Computers, Materials & Continua DOI:10.32604/cmc.2022.029002
Article

Sensitive Information Protection Model Based on Bayesian Game

Yuzhen Liu1,2, Zhe Liu3, Xiaoliang Wang1,2,*, Qing Yang4, Guocai Zuo5 and Frank Jiang6

1School of Computer Science and Engineering, Hunan University of Science and Technology, Xiangtan, 411201, China
2Hunan Key Laboratory for Service computing and Novel Software Technology, Xiangtan, 411201, China
3College of computer and information engineering, Hunan University of Technology and Business, Changsha, China
4School of Computer Science and Information Engineering, Guangzhou Maritime University, Guangzhou, China
5Hunan Software Vocational and Technical University, Xiangtan, China
6School of Engineering and IT, University of New South Wales, NSW, Australia
*Corresponding Author: Xiaoliang Wang. Email: fengwxl@163.com
Received: 22 February 2022; Accepted: 06 April 2022

Abstract: A game measurement model considering the attacker's knowledge background is proposed based on the Bayesian game theory aiming at striking a balance between the protection of sensitive information and the quality of service. We quantified the sensitive level of information according to the user's personalized sensitive information protection needs. Based on the probability distribution of sensitive level and attacker's knowledge background type, the strategy combination of service provider and attacker was analyzed, and a game-based sensitive information protection model was constructed. Through the combination of strategies under Bayesian equilibrium, the information entropy was used to measure the leakage of sensitive information. Furthermore, in the paper the influence of the sensitive level of information and the attacker's knowledge background on the strategy of both sides of the game was considered comprehensively. Further on, the leakage of the user's sensitive information was measured. Finally, the feasibility of the model was described by experiments.

Keywords: Sensitive information; game theory; Bayesian equilibrium; sensitive level; information entropy

1  Introduction

The importance of information network security has become increasingly prominent with the continuous development of computer technology and information construction. With the rapid development of cloud computing, Internet of Things, big data technology, artificial intelligence and wide spread of cloud services, the communication networks have played a fundamental role in business, entertainment, health care and education. Nevertheless, in these processes of information storage, transmission and processing, there is abundant sensitive information, including even state secrets. Therefore, it is extremely vulnerable to various kinds of hacker attacks from all over the world. While informationization brings about great improvement in the efficiency of production and life, it is accompanied by increasingly serious security threats. However, due to the traditional common network information security technology, the defense strategies are relatively passive, and usually applicable to specific attack scenarios and means. Moreover, the specific quantitative analysis and decision-making framework of the solution is not clear enough. Then game theory can be a feasible mathematical tool in network information security.

2  Preliminary Knowledge

In 1928, Hartley [1] first proposed the initial idea of measuring information. He took the number of symbols m=log⁡n as the amount of information. Shannon put forward the theory of information entropy in 1948 [2], which became the basic theory of information theory and digital communication. In addition, Seys, et al. [3] is the first one to employ the information entropy to measure information leakage in privacy protection in 2002. However, in the paper they don’t propose how to improve the degree of anonymity. Nicol et al. [4] investigated the existing model-based system reliability assessment technology and summarized their effectiveness in system security assessment. Besides, Lye et al. [5] defined the game model with the recovery time needed after the network was attacked as a source of revenue and proposed a game theory method to analyze the security of computer network. And in 2007, Cao et al. [6] put forward a model of using static Bayesian game to predict attacks and the probability was obtained with the simulation of the choice of attack and defense sides choosing various strategies to maximize their own interests in the model. Meanwhile, Ma et al. [7] proposed the application of information entropy as a measure of privacy in Vehicle to Everything (V2X) vehicle network system and took into account the impact of aggregator’s accumulated information on system privacy. However, the authors only measure privacy of individual users which is too simple. Furthermore, in 2010, Yi and Xiao proposed a privacy publishing method based on game theory, which guaranteed not only the protection of privacy, but also the availability of privacy [8]. Moreover, in 2011, Ge and Zhu proposed a scheme to construct the distributed data mining under complete information static game and seek Nash equilibrium solution for analysis [9]. In 2014, Feng et al. [10] analyzed the key technologies related to big data security and privacy protection and their latest progress. What’s more in 2016, a Location Based Service (LBS) privacy measurement framework, a game-based privacy protection model and a more basic information entropy model are proposed [11–13]. Furthermore, in 2018, some new game models of privacy protection based on different technologies [14–17]. Wang et al. [18] aimed at distributed attacks in computer networks, on the basis of cooperation and incomplete information game theory, a quantitative method of existing strategic benefits was proposed, and Bayesian equilibrium was calculated and analyzed comprehensively. Furthermore, in 2019, using incentive motivation for privacy concessions or guiding active attacks, Riahi et al. [19] proposed a privacy protection solution based on a game theory model between two participants (data holders and data requesters). Nevertheless, the authors were concern of only two actors. Meanwhile, Cui et al. [20] proposed a personalized differentiated privacy method based on social distance. They formalized all the payoff functions in the differential privacy sense followed by the establishment of a static Bayesian game and derived the Bayesian Nash equilibrium with a modified reinforcement learning algorithm. Besides, Shi et al. [21] proposed a comprehensive evaluation model of privacy protection based on probability statistics and Del entropy method, which realizes the evaluation of data privacy protection level under block confusion. Moreover in 2019, He et al. [22] introduced a general condition called “coarser inter-player information” which proved to be necessary and sufficient for the validity of several fundamental properties on pure-strategy equilibria in Bayesian games, such as existence, purification from behavioral strategies, and convergence for a sequence of games. But the authors didn’t tell us how to deal with asymmetric information. And then, Zhang et al. [23] proposed an anti-fraud scheme based on improved Bayesian game model. In 2021, Dahiya et al. [24] proposed a reputation score policy and Bayesian game theory based incentivizied mechanism for Distributed Denial of Service (DDos) attacks mitigation and cyber defense. Specially, Zarreh et al. in 2020 design a cyber-physical security evaluation in manufacturing systems with a Bayesian game model [25].

Nowadays, because of the importance of information safety, in [26–35], the authors research sensitive information protection for information security. And then they obtain many important conclusions. Some of the authors, going a step further, propose novel anonymous authentication scheme based on edge computing in internet of vehicles.

3  Basic Knowledge

3.1 Concepts Related to Game the Theory [36]

Definition 1: Static game, refers to the simultaneous choice of actions by participants. Or even though the participants take action in sequence, the person who takes action later does not know what kind of actions the person who takes action first takes.

Definition 2: Bayesian Game (G (T) or G (∞, δ)): It means that at least one participant cannot determine the income function of another participant, as the income function is not common knowledge among all participants.

The strategic formulation of n-person static Bayesian game includes: type space of participants {Θ1,…,Θn} conditional probability {p1,…, pn}, type dependency strategy space {A1(θ1), …, An(θn)} and type dependent payment function u1 (a1,…,an; θ1),…, uN (a1,…,an; θn).

Participant i knows its own type θi∈Θi, and conditional probability pi = pi (θ−i|θi) describes, given that it belongs to θi, the uncertainty of participant i about other participating human type θ−i∈Θ−i. We use G = {A1,…, An;θ1,…,θn;p1,…,pn;u1,…,un}, representing the game.

Definition 3: Bayesian Equilibrium: The pure strategic Bayesian Nash equilibrium of n humans static game with incomplete information G = {A1,…,An;θ1,…,θn;p1,…,pn;u1,…,un} is a type-dependent strategic combination {ai*(θi)}, i = 1,…,n, where each participant i chooses action ai*(θi) to maximize his expected utility functioni given his own type θi and other participating human-type dependency strategies {a−i*(θ−i)}.

3.2 Principles of Statistical Grouping

Definition 4: The principles of statistical groupings are as follows. [37]

The principle of consistency. In a grouping, once the grouping criteria are selected, the meaning cannot be changed. However, in a composite grouping, the grouping criteria at different levels should be different. But in the same level of grouping, the grouping criteria should be consistent. Therefore, the consistency principle of grouping should be called the consistency principle of grouping standard.

The principle of proportionality. After grouping, the total number of elements contained in each group, in this sense, should be exactly equal to the sum of its groups, also known as completeness.

The principle of mutual exclusion. This principle is also called the principle of incompatibility or the principle of difference. In general, the relationship between groups at the same level should be a mutually exclusive relationship between two groups, that is to say, there should be no general public unit in any two groups.

The principle of hierarchy. It means that the statistical grouping should be hierarchical, and the phenomenon of over-grading should not be allowed. Therefore, the hierarchical principle of grouping can also be called the hierarchical principle or the orderly principle.

4  Analysis of Sensitive Information Protection Model Based on Bayesian Game

In this paper, a privacy protection model is proposed based on Bayesian game theory. Through the influence of attacker’s knowledge background and user’s demand for sensitivity level of information on game strategy selection in game model, a new game model is constructed based on static Bayesian game to provide users with personalized sensitive information protection.

Sensitivity level of information is a key factor to decide whether the services of service providers will be provided or not, but it can be set by users according to their own needs for information protection intensity or service quality. The range of values is generally [0,1]. This sensitivity level of information reflects the tolerance of users for sensitive information leakage and the requirement of service quality under the condition of observing the principle of statistical grouping. Then users can dynamically classify the level of information sensitivity in real-time according to the dynamic state of the network environment, the tolerance of sensitive information leakage and the requirement of quality of service. Tab. 1 is a correspondence between the sensitivity level and the sensitivity level parameter SSI. SSI is calculated by formula (2) which is shown Section 4.2.

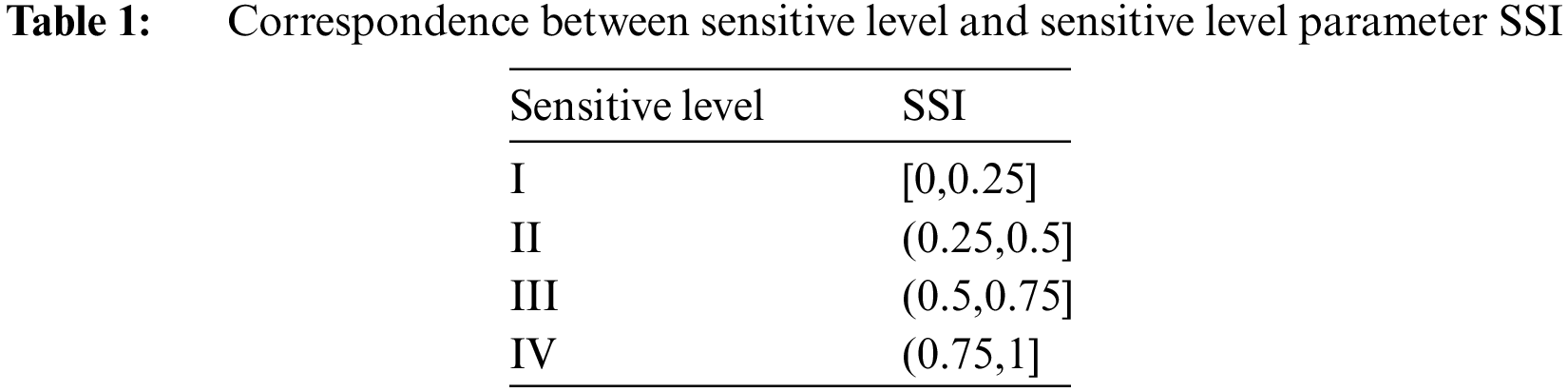
4.1 Privacy Protection Model Flow Chart Based on Bayesian Game

The algorithm of sensitive information protection model based on Bayesian game is given in Fig. 1. And the Fig. 2 shows framework of sensitive information protection model.

4.2 Grading of Individualized Sensitivity

Aiming at keeping the balance between information protection and quality of service in sensitive information protection, this paper explores the user’s information protection intensity and data accuracy requirements, and quantifies the user’s needs, by which the sensitive level of information is determined.

(1) Protection strength of user input and query accuracy.

Suppose N is the highest level of protection strength and data accuracy. PSi(PSi∈[1,N], and PSi∈Z) is the protection strength required by the user, and DAi (DAi∈[1,N], and DAi∈Z) is the data accuracy required by the user, the weight coefficient of data accuracy is k (k∈ [0,1]), and the user' s sensitive information is i (i∈[1,n], and i∈Z).

(2) According to the basic principles of consistency, proportionality, mutual exclusion and hierarchy of statistical grouping, the judgment rules are obtained by using the protection intensity and data accuracy [10].

(1) The two parameters are negatively correlated, which means that the accuracy decreases while the protection intensity increases.

(2) When the requirements of protection intensity and the data accuracy intensity are low, reducing protection intensity and sensitivity level, and improving data accuracy should be given priority in order to achieve Pareto optimum as far as possible.

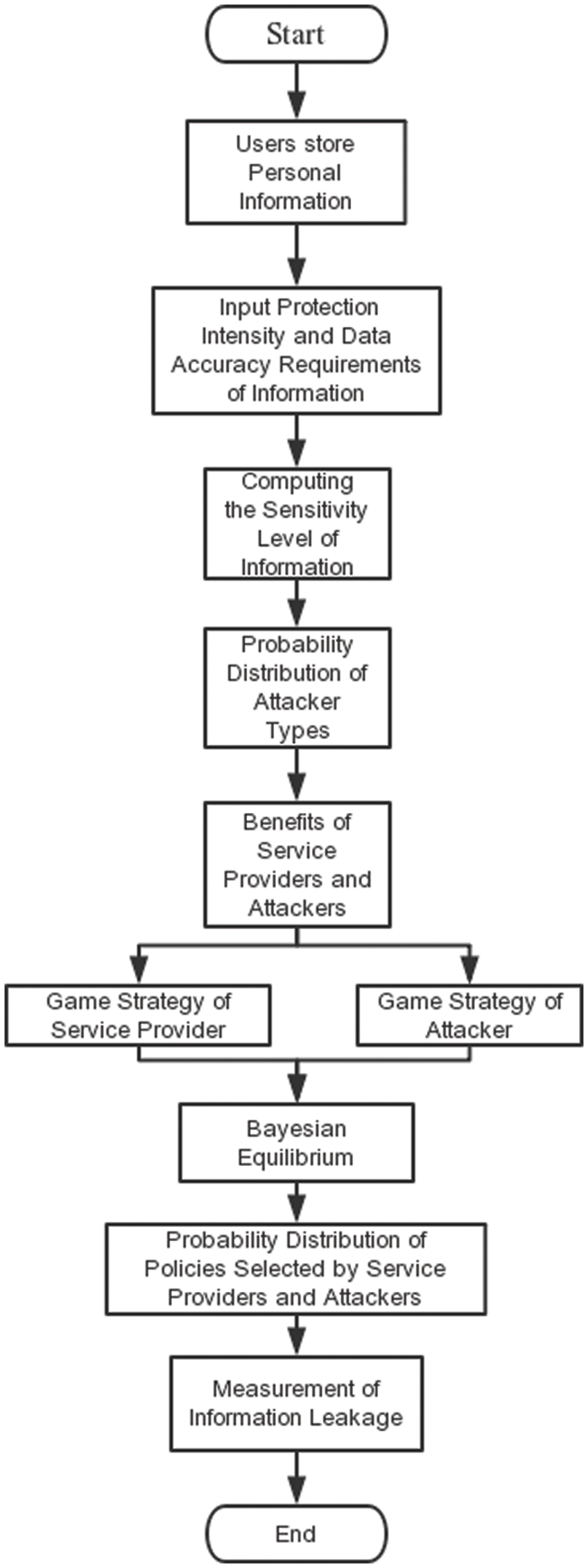
Figure 1: Flow chart of sensitive information protection model based on Bayesian game

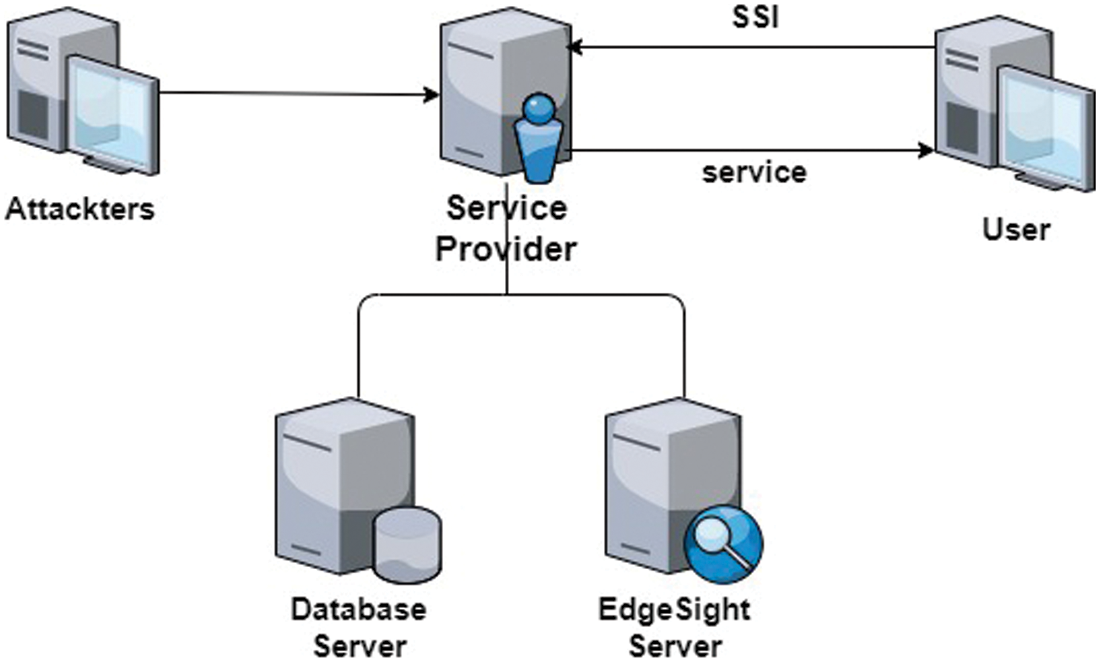
Figure 2: Framework of Sensitive Information Protection Model

(3) When there is a contradiction between the requirements of protection intensity and accurate data intensity, it is necessary to integrate the two requirements to meet the higher requirement of the preference.

(3) The protection strength and the accurate data strength are fused into sensitive level parameters SIi(PSi,DAi), and the sensitive level parameters are obtained.

SIi(PSi,DAi)=PSi−k∗DAiPSi+DAi(1)

The data of SIi (PSi, DAi) will be scaled up and standardized to the range of [0,1] by deviation standardization method to facilitate the division of sensitive levels and obtain standard sensitive levels.

SSIi(i,SIi(PSi,DAi))=SIi(PSi,DAi)−(SIj(PSj,DAj))min(SIj(PSj,DAj))max−(SIj(PSj,DAj))min(2)

4.3 Establishment of Game Model

In this paper, we provide users with personalized sensitive information protection based on static Bayesian game according to the user’s demand for sensitive level of data, which affects the choice of game strategy in game model.

Definition 5: The game model of sensitive information protection is a quintuple: [I, TA, P, U, S].

(1)   I is a set of players participating in the game. Whatever the strategic choices made by any player, other players will choose a certain strategy. Each player’s equilibrium strategy is to achieve the maximum expected return, and the combination constitutes their own dominant strategy. In order to simplify the calculation, the players are sensitive information protection service provider P and attacker A, i.e., I = {SP, A}.

(2)   TA is a type space consisting of the combination of efficient (E) attackers and inefficient (UE) attackers in decision-making under the influence of the knowledge background of service providers, namely TA = {tUE, tE}.

(3)   P is the conditional probability that the service provider is an efficient service provider or an inefficient attacker and combination of service provider policy. P = {pUE, pE}.

(4)   S is the policy space of service providers and attackers, namely S = {SSP, SA}. SSP is the policy space of sensitive information protection service provider P. If the standard sensitivity level is higher, the service level is also higher. In order to simplify the representation, four service levels are assumed to be weak (I) when SSI∈ [0,0.25], general (II) when SSI∈ (0.25,0.5], strong (III) when SSI∈ (0.5,0.75], and very strong (IV) when SSI∈ (0.75,1]. Considering that service providers do not provide services, SSP = {sI, sII, sIII, sIV, sOFF} is obtained. SA is the strategy space of attacker A. In this paper, attacker’s strategy is divided into malicious attack strategy (H) and general goodwill attack strategy (N). Combining the two types of attackers, we get the strategy space SA, namely SA = {sH(θE), sN(θE), sH(θUE), sN(θUE)}.

(5)   U is the revenue function of service providers and attackers, i.e. U = {USP, UA}. USP is the revenue function of sensitive information protection service provider P, which is determined by the choice of different combinations of sensitive information protection service providers P. UA is a revenue function of attacker A determined by different combinations of attacker A’s actions.

4.4 Analysis of Game Model

The static Bayesian game is constructed according to the user’s sensitive level requirement, the attacker’s type space TA and the attacker’s type probability distribution P. The game tree is given by Harsanyi transformation, and the utility functions of both sides of the game are analyzed. Fig. 3 shows game tree between service providers and attackers after Harsanyi Conversion. Tab. 2 shows income matrix of Service Provide (SP) and Attacker (A).

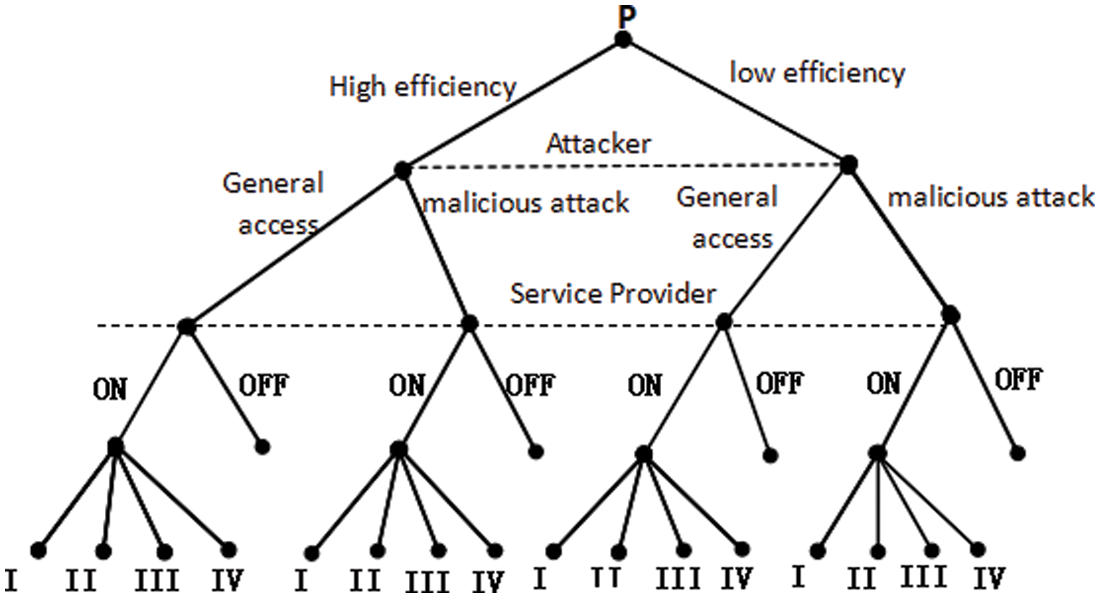
Figure 3: Game Tree between service providers and attackers after Harsanyi Conversion

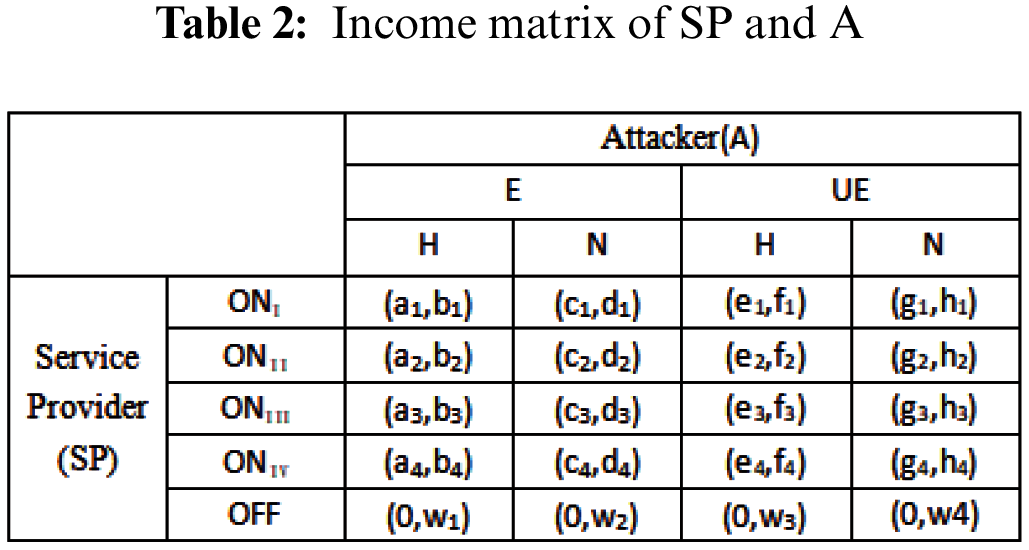
ai, ci, ei, gi (i∈{1,2,3,4}) are the profit functions of the attackers in the corresponding game situation.

bi, di, fi, hi, wi (i∈{1,2,3,4}) are the revenue functions of service providers in the corresponding game situations.

(1) {(ONj, (E, H)), (ONj, (E, N))} (j∈ {I, II, III, IV})represents the benefits of both sides of the game when an efficient attacker chooses either malicious attack or general goodwill access while the service provider chooses to provide the service. However, when the attacker chooses a lower attack strategy than a higher one under the same service level strategy, the loss of profit is lower. Therefore, the attacker chooses a lower attack strategy than a higher one, and it can be obtained: b1 ≧ b2 ≧ b3 ≧ b4, d1 ≧ d2 ≧ d3 ≧ d4.

(2) {(ONj, (UE,H)), (ONj, (UE,N))} (j∈ {I, II, III, IV}) represents the benefits of both sides of the game when the service provider chooses to provide the service, while the inefficient attacker chooses either malicious attack or general goodwill access. The same as (1) can be obtained: f1 ≧ f2 ≧ f3 ≧ f4, h1 ≧ h2 ≧ h3 ≧ h4.

(3) {(OFF, (E, H)), (OFF, (E, N))} denotes the benefits of both sides of the game when an efficient attacker chooses either malicious attack or general goodwill access, while the service provider chooses not to provide the service.

(4) {(OFF, (UE, H)), (OFF, (UE, N))} denotes the benefits of both sides of the game when the service provider chooses not to provide the service, while the inefficient attacker chooses either malicious attacks or a group of good-faith visits.

4.5 Proof of Existence of Hybrid Bayesian Equilibrium

The existence theorem of mixed strategy Bayesian Nash equilibrium is a direct extension of the existence theorem of Nash equilibrium. In the paper the game scenario of sensitive information protection model can be judged as a limited game based on Bayesian game because the attacker type set TA, conditional probability p, action set SSP and SA, revenue function USP and UA are all limited in this model. At the same time, according to Nash’s relevant proof, there is a Bayesian Nash equilibrium of pure strategy or mixed strategy in all finite games, and the Bayesian Nash equilibrium of pure strategy is a special case of Bayesian Nash equilibrium of mixed strategy. Thus, there is a Bayesian Nash equilibrium of mixed strategy in this game model.

4.6 Computation of Mixed Bayesian Equilibrium

According to the benefit matrix of the game, the mixed Bayesian equilibrium of the participants is calculated.

Assuming in the game, the attacker is the corresponding probability distribution (p, 1 − p) of high-efficiency and low-efficiency. Moreover, the common knowledge of the participants in the Bayesian game, i.e., p, (1 − p) is a parameter known to both sides of the game. The probability distribution of the two strategies of service providers in the game is (q, 1 − q), indicating the service providers’ preference to use and withdraw. The probability of providing corresponding sensitive level services is q, while the probability of using closed corresponding sensitive level services is 1 − q. The probability distribution of attackers choosing malicious attack and general goodwill access strategies is (r, 1 − r). That is, the probability of attackers preferring malicious attack (H) is r, while the probability of using general access (N) is 1 − r.

(1) The expected return of the attacker

When an attacker chooses a malicious attack, the expected benefits of the attacker are as follows.

EA(H)=p(qbi+(1−q)w1)+(1−p)(qfi+(1−q)w3)(3)

When an attacker chooses a general goodwill visit, the expected benefits of the attacker are as follows.

EA(N)=p(qdi+(1−q)w2)+(1−p)(qhi+(1−q)w4)(4)

If the policy combination is the best choice for service providers, then EA(H) = ESP(N), that is as follows.

p(qbi+(1−q)w1)+(1−p)(qfi+(1−q)w3)=p(qdi+(1−q)w2)+(1−p)(qhi+(1−q)w4)(5)

Calculations are available as follows.

qi=p(w2−w1)+(1−p)(w4−w3)p(bi−di+w2−w1)+(1−p)(fi−hi+w4−w3)(6)

(2) Expected revenue of service providers

When choosing to provide services, the expected benefits of service providers are as follows.

ESP(ONi)=p(rai+(1−r)ci)+(1−p)(rei+(1−r)gi)(7)

When choosing not to provide services, the expected benefits of service providers are as follows.

ESP(OFF)=0(8)

If the policy combination is the best choice for service providers, ESP(ONi) = ESP(OFF), that is as follows.

p(rai+(1−r)ci)+(1−p)(rei+(1−r)gi)=0(9)

Calculations are available as follows.

ri=−pci−(1−p)gip(ai−ci)+(1−p)(ei−gi)(10)

In summary, when service providers provide level-i standard-sensitive services, the mixed Bayesian equilibrium results between service providers and attackers are as follows.

{qi=p(w2−w1)+(1−p)(w4−w3)p(bi−di+w2−w1)+(1−p)(fi−hi+w4−w3)ri=−pci−(1−p)gip(ai−ci)+(1−p)(ei−gi)(11)

4.7 Measurement of Sensitive Information Leakage

In a sense, Nash equilibrium is a fixed point. In the process of service providers providing services based on users’ needs for information protection and data accuracy, and playing games with attackers, both sides are striving for maximum benefits for their own sake. After calculating the Bayesian equilibrium by utilizing the utility matrix of both sides, the distribution probability of two kinds of service providers, high-efficiency and low-efficiency, can be obtained in the game. Based on the calculation of game theory and the monotonicity of information entropy, this paper introduces information entropy into game theory to solve the measurement problem of sensitive information leakage in the process of service providers’ service measurement [13].

Formulas for calculating information entropy are follows.

H(X)=−C∑x∈χp(x)logp(x)(12)

Among them, C is a constant and normalized to 1.

In this paper, i is the information sensitive level, q is the probability of providing services for service providers, and 1 − q is the probability of not providing services for service providers to express the sensitive information disclosure entropy.

H=−qilog⁡qi−(1−qi)log⁡(1−qi)(13)

And in (13) we set H = 0 when qi = 0.

5  Relevant Work Comparison

The results in Tab. 3 are obtained in terms of the types of information needs, the number of attackers, and the number of service providers by comparing with literature [8], literature [12], literature [14], literature [15]. There is information leakage no matter whether the confidentiality and integrity of information are taken into account.

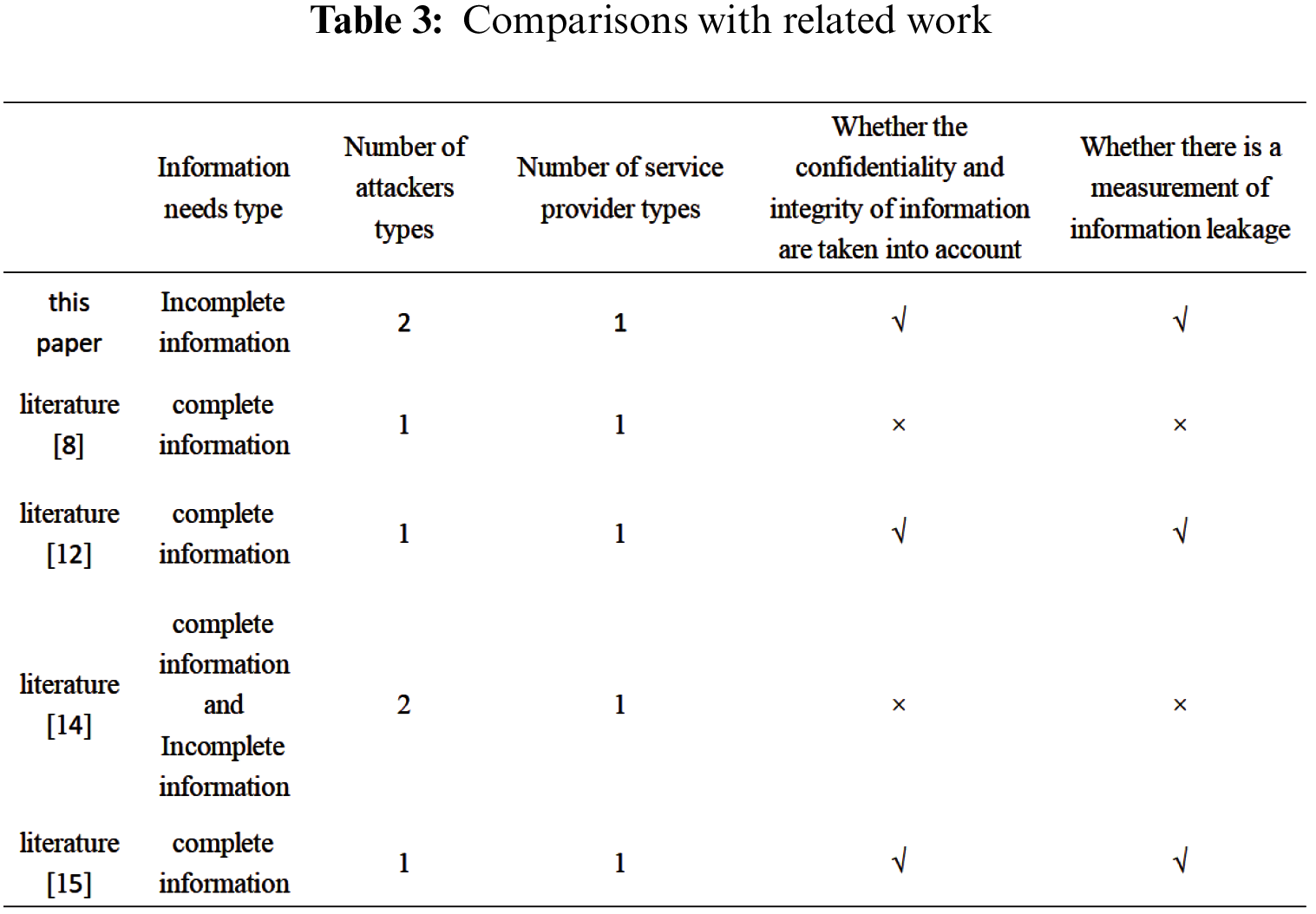
(1) In this paper, we consider that participants do not fully know the return function of other participants and assume that attackers can be divided into efficient and inefficient types.

(2) In order to consider the confidentiality and integrity of information, this paper considers the user’s information protection intensity and data accuracy requirements that are integrated into sensitive level parameters SIi(PSi,DAi), and the sensitive level parameters are obtained. It quantifies the user requirements and determines the information sensitivity level.

(3) By using the monotonicity of information entropy, this paper introduces information entropy to measure information leakage.

6  Experimental Analyses

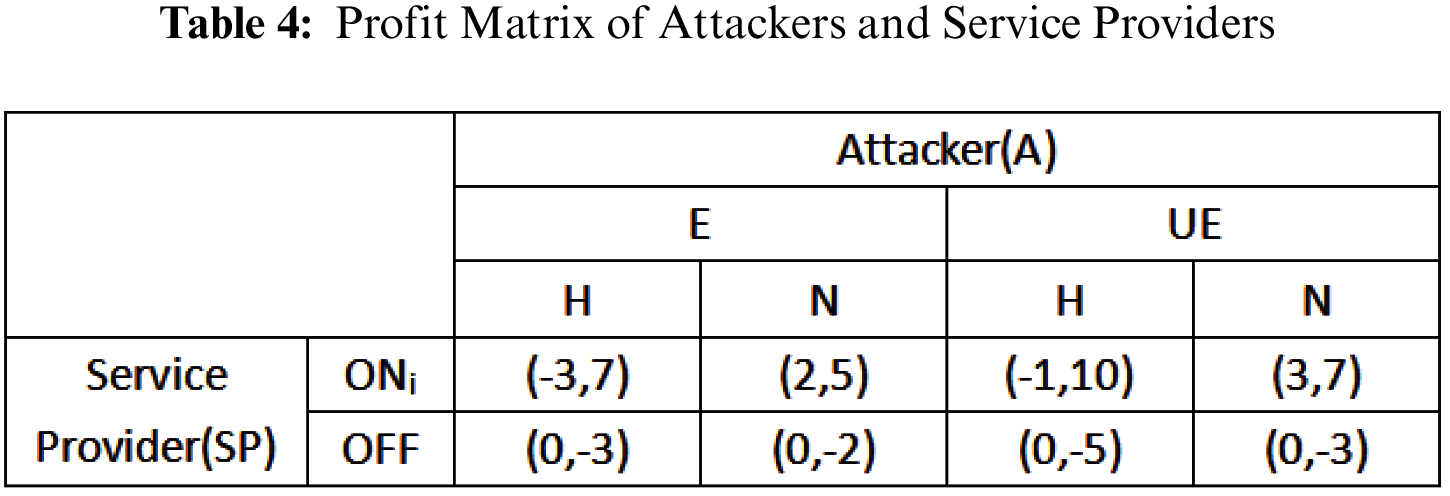
The GAMBIT [38] is a software package designed to help analysts and designers build and grid up Computational Fluid Mechanics (CFD) models and other scientific applications game analysis tool. GAMBIT is used to test the sensitive information protection model. And then the experimental results are analyzed. The relationship between the parameters is plotted by Matlab. In the experiment, this model is applied to the protection of sensitive information in medical treatment. In the context of attacker’s knowledge, it tests the impact of attacker’s high-efficiency probability P on service provider’s service probability, and it also tests attacker’s choice of malicious attack probability in sensitive information protection model given the initial parameters of the revenue function. The following Tab. 4 is as follows.

The experimental results are shown in Figs. 4–7.

In Fig. 4, Abscissa shows probability of efficient attackers and ordinate shows probability of providing corresponding sensitive level services.

In Fig. 5, Abscissa shows probability of efficient attackers and ordinate shows probability of attackers chooses to malicious attack.

In Fig. 6, Abscissa shows ratio of efficient attackers and ordinate shows radio of information entropy.

Fig. 4 shows that the probability of service providers choosing to provide services increases with the increasing of ratio of efficient attackers. Fig. 5 shows that the probability of attackers who chooses malicious attack increases with the increasing of ratio of efficient attackers. Fig. 6 shows that with the increasing of ratio of efficient attackers, the disclosure entropy of sensitive information decreases. Fig. 7 shows Bayesian equilibrium changes with the probability of efficient attacker. To sum up, in the process of protecting sensitive information related to sensitive information, we should consider and attach importance to the impact of attacker’s knowledge and technology background on the actual protection effect and service quality.

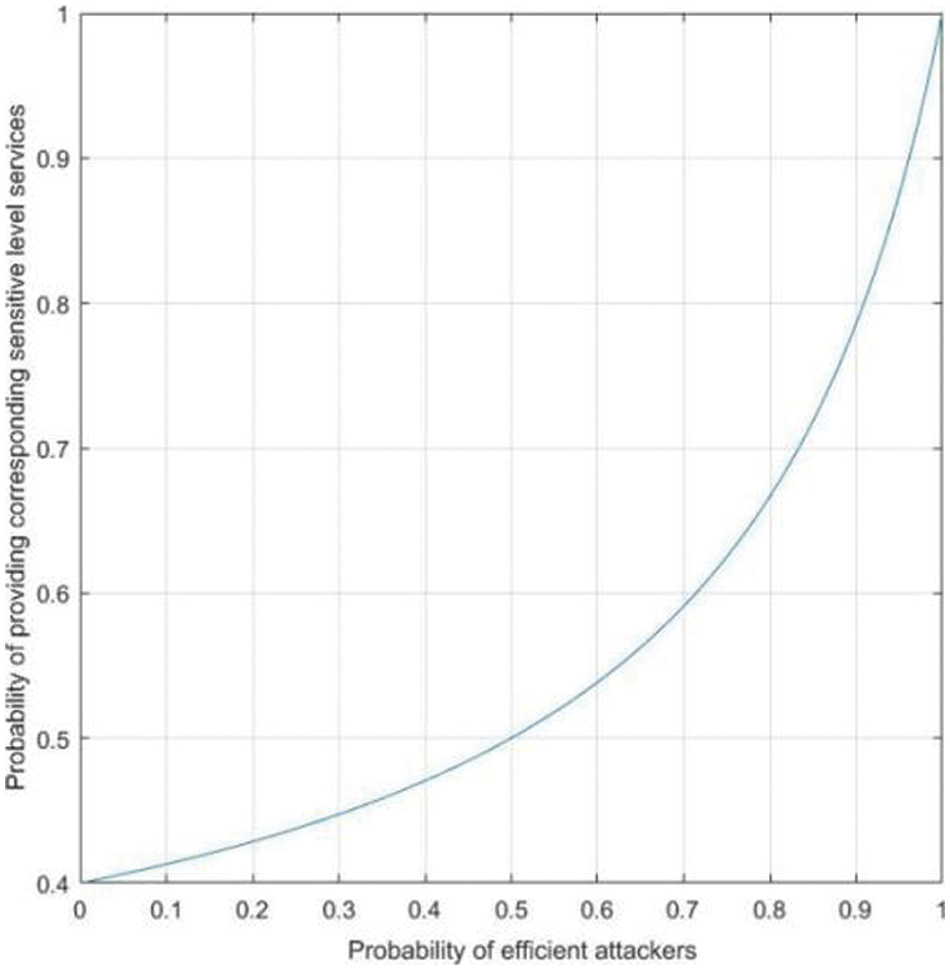
Figure 4: Impact of p on Service Provider’s Choice of Service Provision

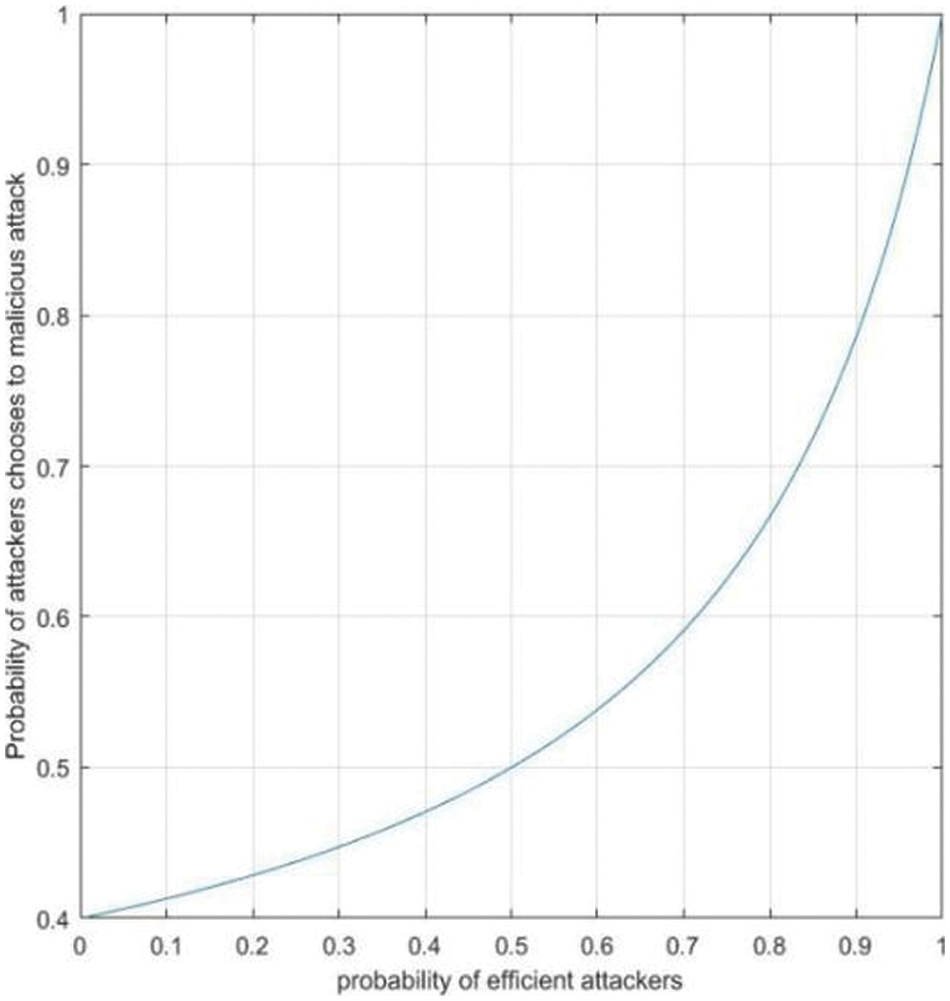
Figure 5: Impact of p on attacker’s choice of attack

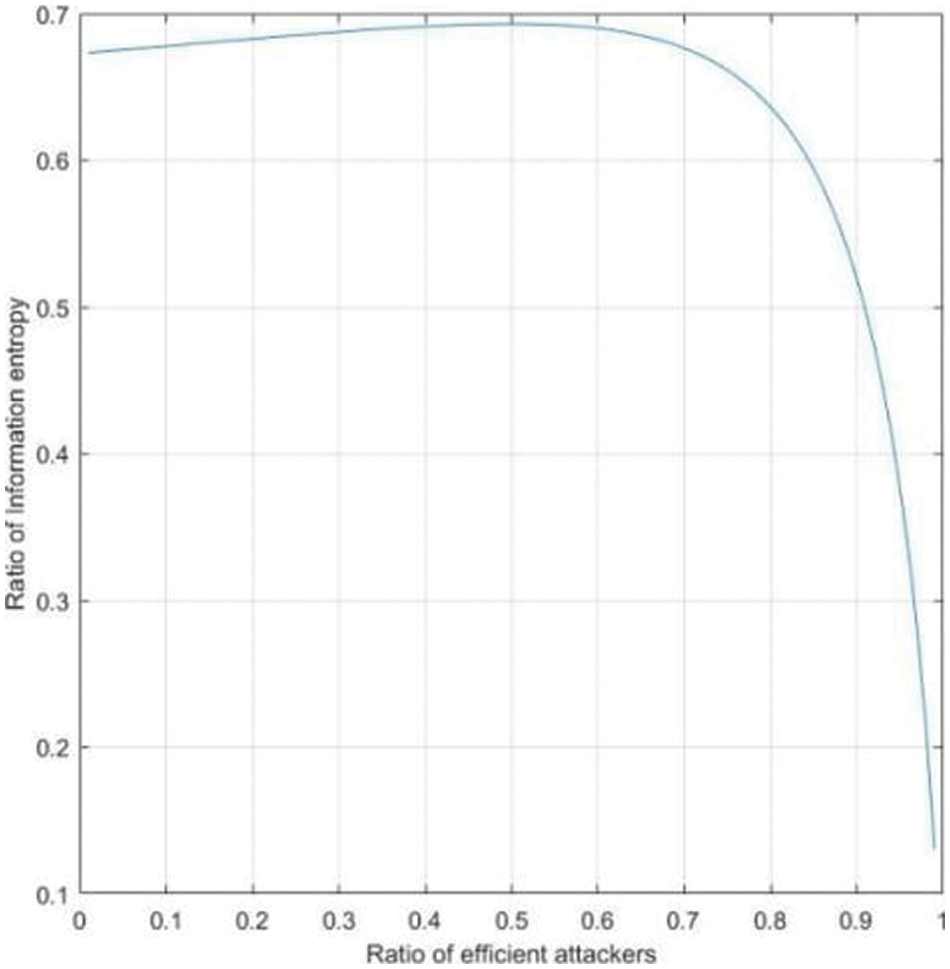
Figure 6: The influence of p on the leakage entropy of sensitive information

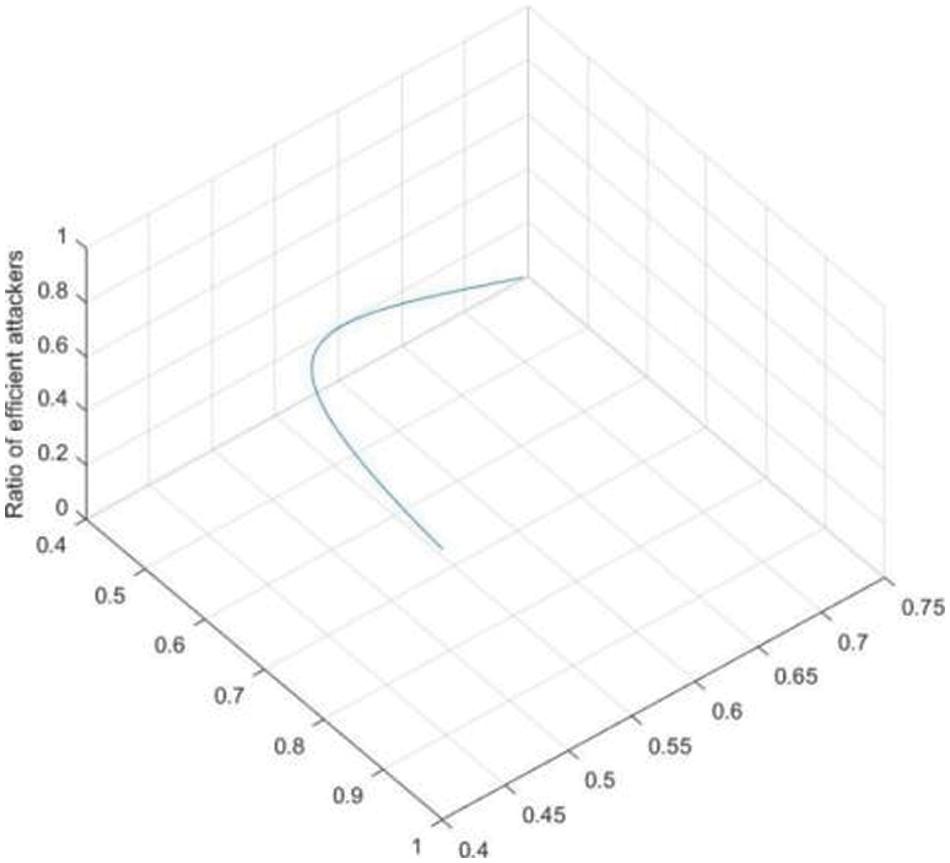
Figure 7: Bayesian equilibrium

7  Conclusion

The author innovatively proposes a sensitive information protection model in order to balance the protection of information and the quality of service in the process of sensitive information protection. Furthermore, the author advances the model based on Bayesian game with information sensitive level, considering the decision-making of attackers and service providers and the impact of attacker’s knowledge background and service provider’s defense level in the process of sensitive information protection.

This model divides the attackers and defenders into many types. Then the model analyses and proves the equilibrium of the game. Compared with the relevant research, more factors are considered influencing service providers and decision maker’s decision-making, more practically and comprehensively. The experiment proves the availability of the model by analyzing the impact of the attacker’s high efficiency probability P on the result of the game. According to their own knowledge background and sensitivity of sensitive information, service providers can take the presented results of sensitive information protection model as a reference to better carry out targeted technical updates and strengthen protection, so as to protect sensitive information and reduce the amount of information leakage.

Funding Statement: This work was supported by Key project of Hunan Provincial Education Department (20A191), Hunan teaching research and reform project (2019-134), Cooperative Education Fund of China Ministry of Education (201702113002, 201801193119), Hunan Natural Science Foundation (2018JJ2138), Hunan teaching research and reform project (2019), Natural Science Foundation of Hunan Province (2020JJ7007).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  R. V. L. Hartley, “Transmission of information,” Bell System Technical Journal, vol. 14, no. 12, pp. 56, 1961. [Google Scholar]

 2.  C. E. Shannon, “A mathematical theory of communication,” Bell Labs Technical Journal, vol. 27, no. 4, pp. 379–423, 1948. [Google Scholar]

 3.  S. Seys, J. Claessens and B. Preneel, “Towards measuring anonymity,” Privacy Enhancing Technologies, Springer Berlin Heidelberg, vol. 2002, pp. 54–68, 2003. [Google Scholar]

 4.  D. M. Nicol, W. H. Sanders and K. S. Tricedi, “Model-based evaluation: From dependability to security,” IEEE Transactions on Dependability and Security, vol. 1, no. 1, pp. 48–55, 2004. [Google Scholar]

 5.  K. Lye and J. Wing, “Game strategies in network security,” International Journal of Information Security, vol. 4, no. 1/2, pp. 71–82, 2005. [Google Scholar]

 6.  H. Cao, Q. Wang, Y. Ma and P. Luo, “Attack prediction model based on static Bayesian game,” Computer Applied Research, vol. 24, no. 10, pp. 122–124, 2007. [Google Scholar]

 7.  Z. Ma, F. Kargl and M. Weber, “Measuring location privacy in V2X communication systems with accumulated information,” in IEEE Int. Conf. on Mobile Ad hoc & Sensor Systems, Macau, China, pp. 322–331, 2009. [Google Scholar]

 8.  R. Yi and Z. Xiao, “A privacy data release method based on game theory,” in 2nd Int. Conf. on E-Business and Information System Security (EBISS 2010), Wuhan, China, pp. 1–4, 2010. [Google Scholar]

 9.  X. Ge and J. Zhu, “Privacy protection distributed data mining based on game theory,” Computer Science, vol. 38, no. 11, pp. 161–166, 2011. [Google Scholar]

10. D. Feng, M. Zhang and H. Li, “Big data security and privacy protection,” Journal of Computer Science, vol. 37, no. 1, pp. 246–258, 2014. [Google Scholar]

11. Y. Zhu, C. Peng, J. Li and H. Ma, “A LBS privacy measurement framework combining query privacy and location privacy,” Information Network Security, vol. 2, pp. 47–53, 2016. [Google Scholar]

12. Y. Zhang, J. He, B. Zhao and N. He, “A privacy protection model based on game theory,” Chinese Journal of Computers, vol. 39, no. 37, pp. 615–627, 2016. [Google Scholar]

13. C. Peng, H. Ding, Y. Zhu, Y. Tian and Z. Fu, “Information entropy model of privacy protection and its measurement method,” Journal of Software, vol. 27, no. 8, pp. 1891–1903, 2016. [Google Scholar]

14. M. Rong, S. Feng, J. Xiong, B. Jin and L. Wang, “Privacy protection method based on security game model,” Journal of Wuhan University: Science Edition, vol. 64, no. 2, pp. 165–174, 2018. [Google Scholar]

15. P. Pang, C. Peng and C. Hao, “A privacy protection model based on privacy preference and its quantitative method,” Computer Science, vol. 45, no. 6, pp. 136–140, 2018. [Google Scholar]

16. B. Subba, S. Biswas and S. Karmakar, “A game theory based multi layered intrusion detection framework for VANET,” Future Generation Computer Systems, vol. 82, no. 3, pp. 12–28, 2017. [Google Scholar]

17. H. Wu, W. Wang, C. Wen and Z. Li, “Game theoretical security detection strategy for networked systems,” Information Sciences, vol. 453, no. 4, pp. 346–363, 2018. [Google Scholar]

18. W. Wang and W. Zhao, “The self-learning network defense based on game theory,” in Int. Conf. Advanced Engineering & Technology Research, Incheon, South Korea, pp. 393–398, 2018. [Google Scholar]

19. S. Riahi, Y. Challal Arbia, P. Moyal and E. Natalizio, “A game theoretic approach for privacy preserving model in IoT-based transportation,” IEEE Transactions on Intelligent Transportation Systems, vol. 20, no. 12, pp. 4405–4414, 2020. [Google Scholar]

20. L. Cui, Y. Qu, M. R. Nosouhi, S. Yu, J. Niu et al., “Improving data utility through game theory in personalized differential privacy,” Journal of Computer Science and Technology, vol. 34, no. 2, pp. 272–286, 2019. [Google Scholar]

21. Y. Shi, W. Zhou, S. Zang and Y. Chen, “Comprehensive evaluation model of privacy protection based on probability statistics and del entropy method,” Journal of Computer Science, vol. 42, no. 7, pp. 786–799, 2019. [Google Scholar]

22. W. He and Y. Sun, “Pure-strategy equilibria in Bayesian games,” Journal of Economic Theory, vol. 180, pp. 11–49, 2019. [Google Scholar]

23. R. Zhang, H. Xia, F. Chen, L. Li and X. Cheng, “Privacy protection: An anti-fraud scheme based on improved Bayesian game model in multimedia communication system,” IEEE Access, vol. 8, pp. 12316–12326, 2020. [Google Scholar]

24. A. Dahiya and B. B. Gupta, “A reputation score policy and Bayesian game theory based incentivized mechanism for DDos attacks mitigation and cyber defense,” Future Generation Computer Systems, vol. 117, no. 12, pp. 193–204, 2021. [Google Scholar]

25. A. Zarreh, Y. Lee, R. A. Janahi, H. Wan and C. Saygin, “Cyber-physical security evaluation in manufacturing systems with a Bayesian game model,” Procedia Manufacturing, vol. 51, pp. 1158–1165, 2020. [Google Scholar]

26. R. M. Saqib, A. S. Khan, Y. Javed, S. Ahmad, K. Nisar et al., “Analysis and intellectual structure of the multi-factor authentication in information security,” Intelligent Automation & Soft Computing, vol. 32, no. 3, pp. 1633–1647, 2022. [Google Scholar]

27. X. R. Zhang, X. Sun, X. M. Sun, W. Sun and S. K. Jha, “Robust reversible audio watermarking scheme for telemedicine and privacy protection,” Computers, Materials & Continua, vol. 71, no. 2, pp. 3035–3050, 2022. [Google Scholar]

28. L. Xiang, J. Qin, X. Xiang, Y. Tan and N. N. Xiong, “A robust text coverless information hiding based on multi-index method,” Intelligent Automation & Soft Computing, vol. 29, no. 3, pp. 899–914, 2021. [Google Scholar]

29. X. Wang, X. She, L. Bai, Y. Qing and F. Jiang, “A novel anonymous authentication scheme based on edge computing in internet of vehicles,” Computers, Materials & Continua, vol. 67, no. 3, pp. 3349–3361, 2021. [Google Scholar]

30. Y. Liu, X. Wang, X. She, M. Yi, Y. Li et al., “Design of intelligent mosquito nets based on deep learning algorithms,” Computers, Materials & Continua, vol. 69, no. 2, pp. 2261–2276, 2021. [Google Scholar]

31. X. R. Zhang, W. F. Zhang, W. Sun, X. M. Sun and S. K. Jha, “A robust 3-D medical watermarking based on wavelet transform for data protection,” Computer Systems Science & Engineering, vol. 41, no. 3, pp. 1043–1056, 2022. [Google Scholar]

32. S. Shang, X. Li, R. Lu, J. Niu, X. Zhang et al., “A privacy-preserving multi-dimensional range query scheme for edge-supported industrial IoT,” IEEE Internet of Things Journal, pp. 1, 2022. [Google Scholar]

33. X. Li, J. He, P. Vijayakumar, X. Zhang and V. Chang, “A verifiable privacy-preserving machine learning prediction scheme for edge-enhanced HCPSs,” IEEE Transactions on Industrial Informatics, pp. 1, 2021. [Google Scholar]

34. W. Sun, G. Z. Dai, X. R. Zhang, X. Z. He and X. Chen, “TBE-Net: A three-branch embedding network with part-aware ability and feature complementary learning for vehicle re-identification,” IEEE Transactions on Intelligent Transportation Systems, pp. 1–13, 2021. [Google Scholar]

35. W. Sun, L. Dai, X. R. Zhang, P. S. Chang and X. Z. He, “RSOD: Real-time small object detection algorithm in UAV-based traffic monitoring,” Applied Intelligence, vol. 92, no. 6, pp. 1–16, 2021. [Google Scholar]

36. R. Gibbons, “The basis of game theory,” China Social Sciences Press, Beijing, China, 1999. [Google Scholar]

37. H. Wang, “On the four logical principles of statistical grouping: Also on the errors in the division of some basic statistical concepts,” Forum on Statistics and Information, vol. 4, pp. 29–32, 1998. [Google Scholar]

38. R. D. Mckelvey, A. M. Mclenn and T. L. Turocy, “Gambit: Software tools for game theory,” [EB/OL], 2004. [Online]. Available: http://econweb.tamu.edu/gambit/. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.