Computers, Materials & Continua DOI:10.32604/cmc.2022.028876
Article

A Highly Secured Image Encryption Scheme using Quantum Walk and Chaos

Muhammad Islam Kamran1, Muazzam A. Khan1, Suliman A. Alsuhibany2, Yazeed Yasin Ghadi3, Arshad4, Jameel Arif1 and Jawad Ahmad5,*

1Department of Computer Science, Quaid-i-Azam University, Islamabad, 45320, Pakistan
2Department of Computer Science, College of Computer, Qassim University, Buraydah, 51452, Saudi Arabia
3Department of Computer Science and Software Engineering, Al Ain University, Abu Dhabi, 15551, UAE
4Institute for Energy and Environment, University of Strathclyde, Glasgow, G1 1XQ, UK
5School of Computing, Edinburgh Napier University, Edinburgh, EH10 5DT, UK
*Corresponding Author: Jawad Ahmad. Email: J.Ahmad@napier.ac.uk
Received: 20 February 2022; Accepted: 30 March 2022

Abstract: The use of multimedia data sharing has drastically increased in the past few decades due to the revolutionary improvements in communication technologies such as the 4th generation (4G) and 5th generation (5G) etc. Researchers have proposed many image encryption algorithms based on the classical random walk and chaos theory for sharing an image in a secure way. Instead of the classical random walk, this paper proposes the quantum walk to achieve high image security. Classical random walk exhibits randomness due to the stochastic transitions between states, on the other hand, the quantum walk is more random and achieve randomness due to the superposition, and the interference of the wave functions. The proposed image encryption scheme is evaluated using extensive security metrics such as correlation coefficient, entropy, histogram, time complexity, number of pixels change rate and unified average intensity etc. All experimental results validate the proposed scheme, and it is concluded that the proposed scheme is highly secured, lightweight and computationally efficient. In the proposed scheme, the values of the correlation coefficient, entropy, mean square error (MSE), number of pixels change rate (NPCR), unified average change intensity (UACI) and contrast are 0.0069, 7.9970, 40.39, 99.60%, 33.47 and 10.4542 respectively.

Keywords: Cryptography; chaotic maps; logistic map; quantum walk; security

1  Introduction

User privacy has emerged as one of the most serious security problems in recent years, especially when it comes to sharing information via the internet and other publicly available communication channels [1]. This is especially true for images, which are now widely used as a source of information, such as medical reports, blueprints, and other sensitive images [2]. Cryptography is used to ensure the protection and security of data. The art of dealing with information in such a way that it is not revealed to an unauthorized person is known as cryptography [3]. Many techniques have been proposed by researchers to secure such sensitive information in the literature, such as advanced encryption standard (AES) and data encryption standard DES [4]. These encryption algorithms are suitable for textual data, but because digital images are known to have a high correlation between consecutive pixels, a small change in one pixel may not harm the overall image. Similarly encrypting an image with a textual encryption algorithm will not completely hide the information need to be secured [5]. Therefore, encrypting images and multimedia data with a conventional encryption technique is not appropriate. Multimedia data is significantly greater in size than text data and requires more computational power and time. Traditional techniques have slow encryption and decryption speed resulting in delay in real-time applications like video conferencing and using a text technique to encrypt them will yield a poor result [6]. Researchers implemented numerous chaos-based encryption algorithms that proved to be effective considering the challenges with multimedia encryption.

Chaotic maps are being utilized for image encryption to improve encryption quality by leveraging the chaotic maps’ erratic behavior [7,8]. Normally, chaotic maps are employed to generate the pseudo-random sequences needed to encrypt images. The logistic map is one of the simplest chaotic maps and is largely used for image encryption because of its faster encryption, low complexity, and higher security, as well as low computation overheads [9].

The relationship between the plain text image and the cipher image is referred to as diffusion, an encryption algorithm is considered more secure if a small change in the pixels of the original image results in a drastic change in the encrypted image. Confusion, on the other hand, is the relationship between the key and the encrypted image, which means a small change in the key results in a completely different encrypted image [9]. Image encryption relies heavily on diffusion and confusion [10].

S-Boxes (substitution boxes) are vector Boolean functions that are used as a fundamental component of cryptography. The S-Box function used in cryptography is of the form S: FG(B)n→G(B)m where B={0,1} and when B={0,1} then GF(2) is the Galois Field (GF) of two elements. The basic idea behind this function is to take m-bits input and convert it to n-bits output. Traditional cryptography includes algorithms like DES and AES, in which the S-Box is the only nonlinear component [11]. The strength of an S-Box against attacks is determined by the non-linearity of the S-Box. It is constructed in such a way that it meets Shannon’s confusion property. In the literature, various S-Boxes are utilized to create confusion.

Image encryption technique based on a two-dimensional chaotic map was proposed by Zhang Han et al. [12] . to solve the self-similarity problem. Guan et al. [13] developed a chaos-based picture encryption technique in which Arnold cat map was used to mix pixels and grayscale values were also modified after pixel shuffling to make it resistant to assault. Anwar et al. [14] suggested an image encryption technique based on a chaotic pixel permutation form of Arnold’s cat map. Anees et al. [15] introduced a new chaotic image encryption technique based on the dynamic allocation of multiple S-Boxes, utilizing three S-Boxes for pixel substitution. Sam et al. [16] suggested an image encryption technique based on the logistic map XOR operation with row and column permutation.

Pisarchik et al. [17] proposed a technique of chaotically coupled maps for image encryption. This algorithm achieved a higher level of security, due to its good diffusion and confusion properties achieved through chaotic mixing. The technique of efficient permutation and bidirectional diffusion through a chaotic system was proposed by Zhang et al. [18]. Liu et al. [19] proposed a technique for encrypting color images that used piecewise linear chaotic map (PWLCM) as a key generator; this algorithm has higher UACI and the NPCR values. Liu et al. [20] used Chen’s chaotic map and PWLCM for substitution and permutation of color images.

Shyamala et al. [21] suggested a novel technique based on a chaotic map to change plain text image statistical features to entirely random distribution. Zeng et al. [22] combined cellular automata and particle swarm optimization to construct hyper-chaotic image encryption technique; the application of cellular automata was for the diffusion of every pixel value. Most substitution-based image encryption techniques performed well, although they frequently suffer from a high degree of correlation coefficient between the encrypted image pixels. Shafique et al. [23] introduced the dynamic S-Box allocation through the chaotic map technique to address this issue, which reduced correlation between encrypted picture pixels. Alvarez et al. [24] suggested a technique for examining the performance of cryptosystems based on chaotic dynamical systems and demonstrated its superiority over the encryption methods Ahmad et al. [25] proposed a new image encryption technique based on chaos-based diffusion and replacement to reduce autocorrelation in digital data with lower gray values. The substituted image is broken down into blocks of size Z×Z pixels, the logistic map generates random values, and those values are put in a Z×Z block to achieve diffusion. The replaced image is further XOR-ed with the random values supplied by the logistic map to minimize co-relation in the final cipher image. This technique had a smaller impact on encrypted photos when a plain image with a little modified pixel value is used, the correlation coefficient is large.

Although numerous image encryption techniques have been presented in previous studies, many of them have been proven to be insecure [26–28] due to a variety of drawbacks such as computational cost, limited key space, and reduced resilience to distinct differential attacks. This study attempts to fill in the gap by providing a new chaotic Quantum-substitution encryption scheme for images based on a Logistic Map, Quantum Walks, and AES S-Box.

In comparison to existing cryptosystems, the proposed scheme results in a highly-secured encrypted image with highly scrambled pixels. In comparison, the proposed scheme has a high level of attack resistance and efficiency. The proposed scheme is sensitive to small changes in the plain image pixel element values, resulting in great resistance to differential attacks. A number of evaluation parameters such as correlation coefficient, entropy, histogram, NPCR, UACI, contrast, are used to evaluate the proposed scheme.

Based on the existing literature, the authors believe the following to be the novel contributions of this work.

1.    The proposed quantum image encryption scheme is more secure and lightweight.

2.    In the proposed scheme, a slight change in the pixels of plaintext image will result in a completely different cipher image.

3.    The proposed scheme enhances image security and provides high resistance against attacks with less computational power.

The rest of the paper is organized as follows. The background of the Quantum walk is presented in Section 2. In Section 3, the proposed scheme is elaborated and discussed. Section 4 evaluates the proposed encryption scheme against attacks with the conclusion presented in Section 5.

2  Quantum Walk

2.1 Quantum Walk Overview

Quantum information theory is of high interest for the past few years. The laws of quantum are employed in different aspects [29]. The most common aspects are computation and cryptography using quantum [30,31]. Quantum computation had tremendous achievements in the last decade. In this paper, the potential applications of a commonly used quantum computation model; the quantum walk is investigated for image encryption. Quantum walk has inbuilt nonlinear chaotic dynamic behavior which helps in generating pseudo-random numbers. There are several chaotic systems available, but due to the periodic nature of their maps, they are unstable, and encryption based on these maps are prone to attacks [32,33]. Quantum computation is a fast-emerging field that had several achievements in the past decades. Quantum walk is a universal model of quantum computation developed as a useful tool for solving several problems, like data clustering [34], element distinctness [35], triangle finding [36], and so on. In this paper, the latent application of quantum walk is investigated in image encryption. Again, thanks to the inherent chaotic nonlinear dynamic nature of the quantum walk. A new scheme is constructed for image encryption using quantum walk along with a logistic chaotic map. The quantum walks-based scheme has merits like; unpredictability, pseudo-randomness, sensitivity to initial values, and parameters of the system. At the same time, it also possesses non-periodicity and stability [37].

2.2 Quantum Walks Chaotic Behavior

Quantum walks have two main types, discrete and continuous [38], several studies show how the properties of quantum walks differentiate from classical counterparts [39–41].

The basic discrete quantum walk includes two sub-quantum systems i.e., coin and walker. A vector in Hilbert space Ht is used to denote the state of the walker-coin. Mathematical representation of Ht is given in Eq. (1)

Ht=Hp⊗Hc(1)

where Ht represents the walker, Hc represents the coin. For a line of grid-length one the space Ht is spanned by the base states i.e., {|x⟩:x∈Z} The walker Hp is operated by a coin and in turn the coin is operated in two base states {|↑⟩,|↓⟩}, which take a spin space of half in the previous section. The motion of the walker that is operated with a coin, is through a conditional shift operator. Mathematical representation of the shift operator S is given in Eq. (2)

S=∑x(|x+1,0⟩⟨x,0|+|x−1,1⟩⟨x,1|)(2)

The S in above equation transforms the base states such that (|↓⟩⊗|i⟩) to (|↓⟩⊗|i+1⟩) and (|↑⟩⊗|i⟩) to (|↑⟩⊗|↑+i⟩) . Summation represents the sum of all the possible position. The quantum walk computation system operates such that a coin is flipped, and it is followed by a shift operator. We want to have an unbiased walk i.e., shifting (|−1⟩) with probability (−1/2) and (|1⟩) with probability (1/2) . For this we use a balanced unitary coin i.e., Hadamard coin H where the mathematical representation of H is given bellow in Eq. (3).

H=121/2(111−1)(3)

To see Hadamard coin is balanced it is quite easy as shown in Eqs. (4) and (5) respectively:

|↑⟩⊗|0⟩→H121/2(|0⟩+|1⟩)⊗|0⟩(4)

→s121/2(|↑⟩⊗|1⟩+|↓⟩⊗|−1⟩)(5)

In classical random walks, the coin state measurement in standard basis gives probability of 1/2 for both |↓⟩⊗|1⟩ and |↓⟩⊗|−1⟩ , no correlation left between the positions after this measurement. If we continue quantum walk with such rules and measurements after every iteration, we obtain classical random walk on the line. Fig. 1 show this distribution with Galton’s board of this measurement of classical random walk [39]. Galton’s board is a device with array of pins at equal distance, allow bead to drop with equal probability of falling left or right. After passing the beads are collected at the bottom.

Figure 1: Galton board for classical random walk

In quantum random walks, the intermediate iterations are not measure, but rather the co-relations between different positions are kept letting them interfere with subsequent steps. This interference will result in completely different behavior of quantum walk.

The total quantum systems can be evaluated by a repetitive sequence of coin flips and the shift operator as S in discrete time (step by step), which is mathematically expressed by Eq. (6):

U=S(I⊗C)(6)

The C represents a coin flip and I represent the walker’s identity operator. The final state |ψ⟩r after several (r) steps is mathematically expressed by Eq. (7):

|ψ⟩r=(U^)r|ψ⟩initial =∑x∑vλx,v|x,v⟩(7)

The probability of locating the position of walker (x) after several (r) steps is expressed by Eq. (8):

P(x,r)=∑v∈{0,1}|⟨x,v|(U^)r|ψ⟩initial |2(8)

where |ψinitial⟩ represents quantum system initial state. To illustrate how quantum random walk departure away from its classical random walk the following example is presented. The walk is evolved without measuring intermediate step, let the initial step be Eq. (9) and the consecutive steps are solved in Eqs. (10)-(12) respectively:

|ψin⟩=|↓⟩⊗|0⟩(9)

|Φin ⟩→U1212(|↑⟩⊗|1⟩−|↓⟩⊗|−1⟩)(10)

→u12(|↑⟩⊗|2⟩−(|↑⟩−|↓⟩)⊗|0⟩+|↓⟩⊗|−2⟩)(11)

→U12(212)(|↑⟩⊗|3⟩+|↓⟩⊗|1⟩+|↑⟩⊗|−1⟩(12)

Tabs. 1 and 2 show the classical random walk and quantum random walk respectively, see how at T=3 the values of quantum walks differ from the classical walks.

Fig. 2 show probability distribution of quantum walk after T=200 steps that is starting with initial step of |↓⟩⊗|0⟩. The pattern of quantum random walk is much more complicated as compared to Gaussian distribution in classical random walk

Figure 2: Quantum random walk, probability distribution for T = 200 with initial state |↓〉⊗|0〉

3  Proposed Method

3.1 Proposed Scheme Overview

The proposed image encryption scheme is filling the gaps of the previously designed encryption algorithms. Quantum walk is used along with a chaotic map to achieve an optimal level of efficiency and security. Quantum walk, chaotic map, substitution, and XOR are the basis of this scheme. The proposed algorithm provides efficient security against different attacks with less consumption of resources.

3.2 Proposed Scheme

The flowchart of the proposed encryption scheme is presented in Fig. 3.

Figure 3: Proposed algorithm flow diagram

3.3 Proposed Scheme Design and Implementation

For reduction of co-relation in the image and improving overall result, the proposed scheme produced a new encryption algorithm using Quantum walks along with a chaotic map. The image used for the proposed scheme is Lena.jpg with size 256×256.

The following steps explain the implementation of the proposed encryption scheme:

1.    Take plain-text image RGB.

2.    Convert it into greyscale.

3.    Separate the most significant bits (MSB) and least significant bits (LSB) of each pixel that are just converted into 8-bits greyscale.

4.    Convert the MSB and LSB into their respective decimal values.

5.    Now the MSB decimal value will correspond towards the i−th row position of the S-Box and the LSB decimal value will correspond towards the j−th column position.

6.    The point where the i−th and j−th will intersect with each other, that value of the S-Box will be replaced with the pixel value of the greyscale image.

7.    There are 3 S-Boxes and one of them will be selected randomly for each pixel value, for selection of the s-box, a chaotic map is used.

8.    For chaotic map, the value of r should be between 3.56 to 4 and x0 should be between 0 to 1 for random chaotic output.

9.    Now to convert the output produced in step 8 to a finite precision value, multiply the value with 1014.

10.   There are 3 S-Boxes and the number produced by the finite precision is too high, take MOD3 of the number to make the value between 0−2. Every time it will produce a number randomly between 0,1,2, and we will choose that respective S-Box for the replacement of the pixel value.

11.   An initial level cipher image is produced.

12.   Now convert the initial cipher image in Z×Z blocks, in this case we converted it into 16×16 pixels blocks.

13.   Repeat step 8 and 9

14.   This time convert the big value in MOD256 so that we get values between 0−255 which is greyscale pixels values limit.

15.   Arrange the 256 numbers in Z×Z block, in the proposed scheme case, 16×16 block.

16.   XOR the block produced in step 16 with the first block of cipher image produced in step 12.

17.   XOR the next block with the current block. i.e., XOR K−th block with (K−th)−1 block, of the image produced in step 16.

18.   This produces a secondary-level cipher image.

19.   Now generate random noise using Quantum walk and produce a noise of 65336(256×256) numbers. i.e., the total noise number generated must be equal to the number of pixels in a grayscale image.

20.   Convert to the data into the range of grayscale image i.e., 256×256 take MOD256 so that we get values between 0−255.

21.   Reshape the produced values in to Z×Z block in the proposed scheme case 256×256.

22.   XOR the values produced in step 22 with the secondary cipher image produced in step 19.

23.   Final level Cipher image is produced, using the Quantum Random Walk computation model.

Fig. 4 show the original image used for encryption. The results of the proposed and state-of-the-art schemes are given below such that: Figs. 5a and 5b show Anees et al. [15] result of the encrypted image and histogram, Figs. 6a and 6b show Ahmad et al. [6] result of the encrypted image and histogram and finally Figs. 7a and 7b shows the proposed scheme results of the encrypted image and histogram.

Figure 4: Grey scale Lena image (256×256)

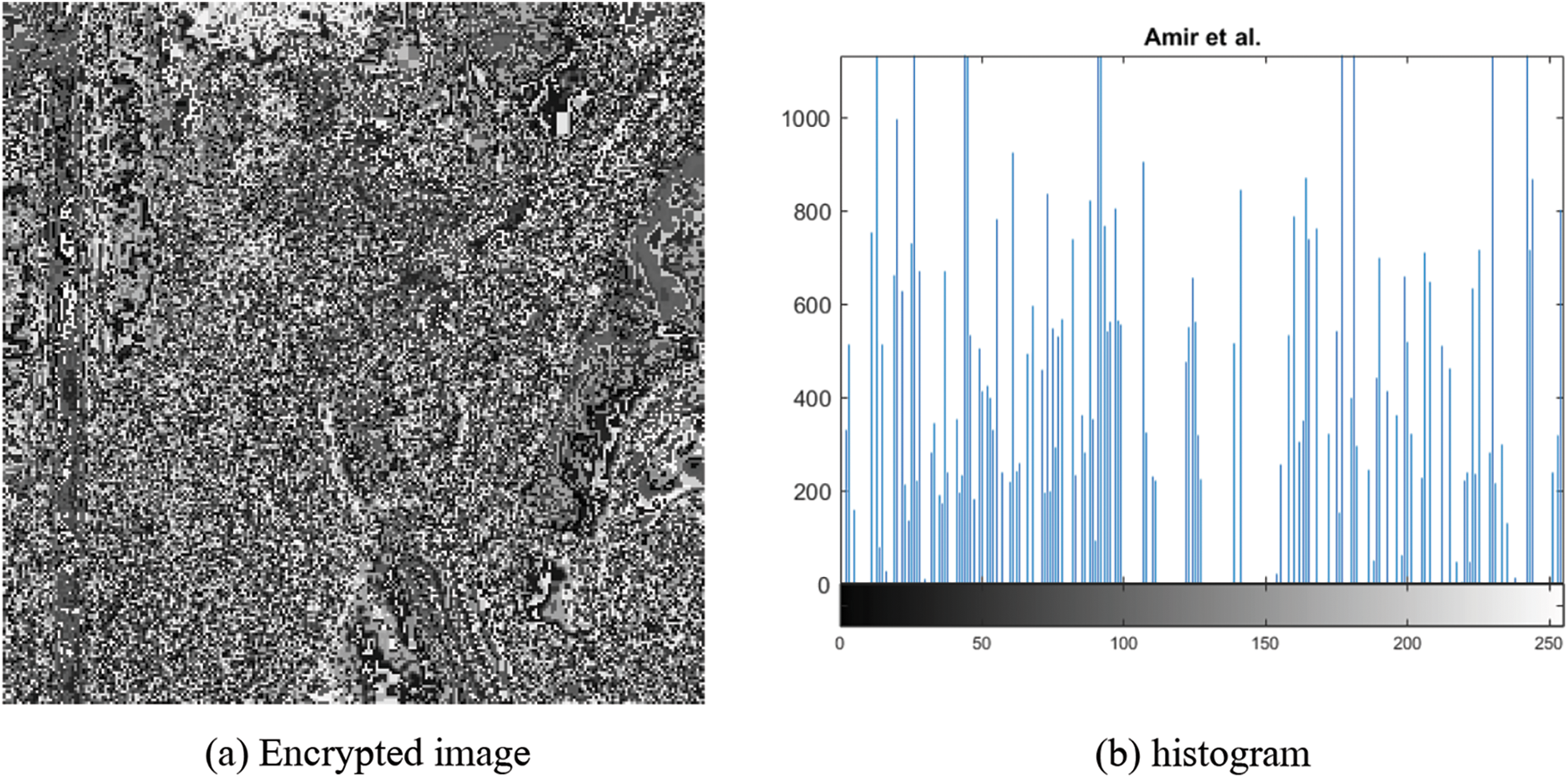
Figure 5: Anees et al. [15] image and histogram

Figure 6: Ahmad et al. [6] image encryption scheme and histogram results

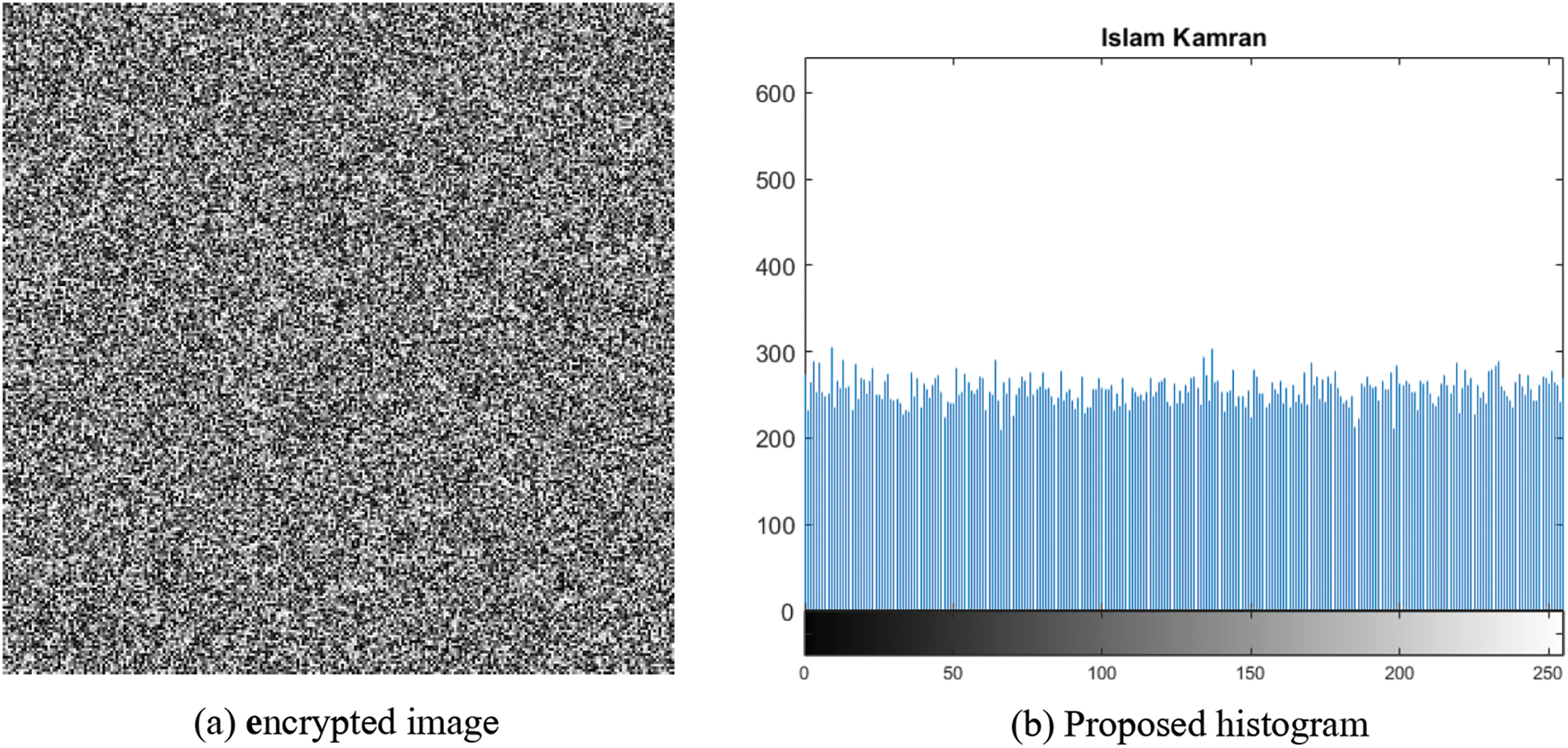
Figure 7: Proposed image encryption scheme and histogram results

4  Evaluation

An encryption algorithm can be evaluated through statistical security parameters that are presented in various papers [5,42,43]. Statistical security evaluation of Ahmad et al. [6], Anees et al. [15], and the proposed scheme are carried out by various parameters such as co-relation, MSE, entropy, contrast analysis, NPCR, and UACI.

4.1 Correlation Coefficient

Correlation coefficient is used to find the degree of similarity between two variables. It is widely used in the field of cryptography. It is used to find out how much two variables depend upon each other. To know if the variables are correlated, we check its value. If the value is close to zero it means the variables are highly uncorrelated, on increasing the value, it increases the dependence on each other. In encryption if the value is closer to zero it means the two variables are independent of each other and the encryption scheme is good. Correlation coefficient can be mathematically presented by Eq. (13):

Corr Coff=Cov(x,y)σx×σy(13)

where Cov is covariance at pixel position x and y, σx and σy are the values of standard deviation at position x and y, the mathematical presentation of covariance and standard deviation are given in Eqs. (14) and (15) respectively.

Cov(x,y)=1N∑i=1N(xi−E(x))(yi−E(y))(14)

σx= Variance (x)σy= Variance (y)(15)

Correlation coefficient is calculated for the images encrypted by Anees et al. [15], Ahmad et al. [6] and compared to the proposed encryption scheme. The results are shown in the Tab. 3. The table shows result for Lena image 256×256. The proposed algorithm shows better result for the correlation coefficient.

4.2 Entropy

Entropy is the rate of uncertainty in a communication system. Elwood Shannon presented this concept which is known by Shannon entropy. Entropy is defined as the measurement of expected values of information in a message. Entropy can be calculated mathematically by Eq. (16)

H=∑i=0N−1p(mi)×log2⁡1p(mi)(16)

where N is the representation of total gray levels and p(mi) is the probability of occurrence of the mi symbol. A source will generate 28 symbols that contains mi with equal probability, if it is truly random, where m={m1…m28}, i.e., the entropy values will be equal to 8.

The result of the simulation is shown in Tab. 4. The resulted value by the proposed method shows better results than Ahmad et al [6] and Anees et al. [15]. According to the obtained entropy results, the leakage of information in the proposed scheme is negligible and can resist attacks better than Anees et al [15] and Ahmad et al. [6]

4.3 Diffusion Characteristics of Encryption Algorithms

An algorithm must have the diffusion property to protect multimedia contents from different attacks. Changing a single bit in the key must change the entire cipher text in an unpredictable way. Diffusion is one of the desiring properties of encryption algorithm.

4.3.1 Avalanche Effect

Avalanche effect can be measured using mean square error (MSE). This metric is used for checking the diffusion characteristic. MSE can be calculated mathematically by Eq. (17):

MSE=1M×N∑i=0N−1∑j=0M−1[C1(i,j)−C2(i,j)]2(17)

The C1 and C2 represent two cipher images whose corresponding keys are different by one bit only, M×N represent the cipher text image size, whereas C1(i,j) and C2(i,j) are the pixel values of the images on the index i, j. higher the value of MSE the better the quality of encryption is, also it means there is sufficient difference between the images. The result of the proposed solution is shown in Tab. 5. The proposed algorithm shows better result than Anees et al. [15] and same result as Ahmad et al. [6] The higher values here show higher diffusion property.

4.3.2 NPCR and UACI

Checking the variance rate of pixels in encrypted image that is caused by single bit change in the original image, NPCR and UACI are used. The detail mathematical details can be found in [46,47].

Tabs. 6 and 7 show NPCR and UACI values of the algorithm respectively. In both tables the proposed algorithm shows better results than Anees et al. [15] and Ahmad et al. [6]

4.4 Contrast Analysis

The difference in intensities of pixels in their neighborhood can be computed by Contrast Analysis. The Goal is that the texture should not be homogeneous. The higher the value of contrast mean the more it is non-homogeneous. Image encryption requires high contrast value.

Mathematically contrast is computed by Eq. (18) :

C=∑i,j=1N|i−j|2p(i,j)(18)

p(i,j) represents the number of gray-level co-occurrence matrix (GLCM); a method that is used to calculate the spatial relationship of an image pixel [48]. N represent the number of Rows and Columns. Tab. 8 show the values of contrast for the proposed scheme and the other techniques the results show that the proposed algorithm contrast values is much greater than Ahmad et al. [6] it also shows that Anees et al. [15] algorithm will still give homogeneous result after encryption.

4.5 Time Analysis

The considered proposed algorithm has been tested through MATLAB 2018a on a system with 2.0 GHZ CPU, 12 GB memory and the size of image is 256×256. Tab. 9 show the time required for the Anees et al. [15] and Ahmad et al. [6] it also shows a good value of time by the proposed algorithm.

5  Conclusion

In this paper, an efficient encryption scheme is proposed which works on highly auto correlated data for the security enhancement of digital images. Some interesting properties of Quantum Walk, S-boxes and chaotic map are the basis of this proposed scheme. The Values obtained from Quantum walk enhance security of the encryption scheme by adding randomness to it. By using diffusion analysis and statistical analysis, the proposed scheme is compared with other traditional techniques. The Results shows that the use of chaotic map and quantum walk in proposed scheme has advantage over the traditional encryption techniques. Time analysis shows that the proposed scheme is quite faster as compared to traditional techniques. The proposed method will be evaluated against other attacks such as plaintext attacks and ciphertext attacks in future.

Acknowledgement: The researchers would like to thank the Deanship of Scientific Research, Qassim University for funding the publication of this project.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  K. M. Sadique and P. Johannesson, “Layered architecture for end-to-end security, trust, and privacy for the internet of things,” in Intelligent Computing and Innovation on Data Science, Berlin: Springer, pp. 289–298, 2021. [Google Scholar]

 2.  J. Ibada, P. Ehkan, R. Ngadiran, D. A. Hammood and A. Alkhayyat, “Rgb image encryption using hill algorithm and chaos system,” Journal of Physics: Conference Series. IOP Publishing, vol. 1962, no. 1, pp. 12061, 2021. [Google Scholar]

 3.  O. C. Abikoye, K. S. Adewole and A. J. Oladipupo, “Efficient data hiding system using cryptography and steganography,” International Journal of Accounting Information Systems, vol. 4, no. 11, pp. 6–11, 2012. [Google Scholar]

 4.  D. Buell, “Modern symmetric ciphers—Des and Aes,” in Fundamentals of Cryptography (FC), First ed., Berlin: Springer, Cambridge University Press, pp. 123–147, 2021. [Google Scholar]

 5.  J. Ahmad and F. Ahmed, “Efficiency analysis and security evaluation of image encryption schemes,” Computing, vol. 23, pp. 25, 2010. [Google Scholar]

 6.  J. Ahmad and S. O. Hwang, “Chaos-based diffusion for highly auto-correlated data in encryption algorithms,” Nonlinear Dynamics, vol. 82, no. 4, pp. 1839–1850, 2015. [Google Scholar]

 7.  M. Andrecut, “Logistic map as a random number generator,” International Journal of Modern Physics B, vol. 12, no. 9, pp. 921–930, 1998. [Google Scholar]

 8.  L. Kocarev, “Chaos-based cryptography: A brief overview,” IEEE Circuits and Systems Magazine, vol. 1, no. 3, pp. 6–21, 2001. [Google Scholar]

 9.  J. Arif, M. A. Khan, J. Ahmad, B. Ghaleb, A. Munir et al., “A novel chaotic permutation-substitution image encryption scheme based on logistic map and random substitution,” IEEE Access, vol. 10, pp. 12966–12982, 2022. [Google Scholar]

10. S. Gao, W. Ma and J. Zhu, “Nonlinearity profile test for an s-box,” in Future Wireless Networks and Information Systems, vol. 143. Berlin, Heidelberg: Springer, pp. 639–644, 2012. [Google Scholar]

11. M. Khan, “A novel image encryption scheme based on multiple chaotic s-boxes,” Nonlinear Dynamics, vol. 82, no. 1, pp. 527–533, 2015. [Google Scholar]

12. Z. Han, W. X. Feng, L. Z. Hui, L. D. Hai and L. Y. Chou, “A new image encryption algorithm based on chaos system,” in IEEE Int. Conf. on Robotics, Intelligent Systems and Signal Proc., Changsha, Hunan, China, vol. 2, pp. 778–782, 2003. [Google Scholar]

13. Z. H. Guan, F. Huang and W. Guan, “Chaos-based image encryption algorithm,” Physics Letters A, vol. 346, no. 1–3, pp. 153–157, 2005. [Google Scholar]

14. S. Anwar and S. Meghana, “A pixel permutation-based image encryption technique using chaotic map,” Multimedia Tools and Applications, vol. 78, no. 19, pp. 27569–27590, 2019. [Google Scholar]

15. A. Anees, A. M. Siddiqui and F. Ahmed, “Chaotic Substitution for highly autocorrelated data in encryption algorithm,” Communications in Nonlinear Science and Numerical Simulation, vol. 19, no. 9, pp. 3106–3118, 2014. [Google Scholar]

16. I. S. Sam, P. Devaraj and R. Bhuvaneswaran, “Chaos based image encryption scheme based on enhanced logistic map,” Distributed Computing and Internet Technology, vol. 6536, pp. 290–300, 2011. [Google Scholar]

17. A. N. Pisarchik and M. Zanin, “Image encryption with chaotically coupled chaotic maps,” Physica D: Nonlinear Phenomena, vol. 237, no. 20, pp. 2638–2648, 2008. [Google Scholar]

18. Z. Zhang and Z. Zhao, “Chaos-based image encryption with total shuffling and bidirectional diffusion,” Nonlinear Dynamics, vol. 75, no. 12, pp. 319–330, 2014. [Google Scholar]

19. H. Liu and X. Wang, “Color image encryption based on one-time keys and robust chaotic maps,” Computer and Mathematics with Applications, vol. 59, no. 10, pp. 3320–3327, 2010. [Google Scholar]

20. H. Liu and X. Wang, “Color image encryption using spatial bit-level permutation and high-dimension chaotic system,” Optics Communication, vol. 284, no. 16, pp. 3895–3903, 2011. [Google Scholar]

21. P. Shyamala, “Chaos based image encryption scheme,” Int. Conf. on Logic, Information, Control and Computation, vol. 140, pp. 312–317, 2011. [Google Scholar]

22. J. Zeng and C. Wang, “A novel hyperchaotic image encryption system based on particle swarm optimization algorithm and cellular automata,” Security and Communication Networks, vol. 2021, no. 5, pp. 1–15, 2021. [Google Scholar]

23. A. Shafique and F. Ahmed, “Image encryption using dynamic s-box substitution in the wavelet domain,” Wireless Personal Communications, vol. 115, no. 3, pp. 2243–2268, 2020. [Google Scholar]

24. G. Alvarez, P. Montoya, M. Romera and G. Pastor, “Chaotic cryptosystems,” in IEEE Proc. 33rd Annual International Carnahan Conference on Security Technology, Madrid, Spain, pp. 332–338, 1999. [Google Scholar]

25. J. Ahmad and S. O. Hwang, “Chaos-based diffusion for highly auto-correlated data in encryption algorithms,” Nonlinear Dynamics, vol. 82, no. 4, pp. 1839–1850, 2015. [Google Scholar]

26. M. Khan and T. Shah, “A novel image encryption technique based on non chaotic map and s8 symmetric group,” Neural Computing and Applications, vol. 25, no. 7–8, pp. 1717–1722, 2014. [Google Scholar]

27. M. Khan and T. Shah, “A construction of novel chaos base nonlinear component of block cipher,” Nonlinear Dynamics, vol. 76, no. 1, pp. 377–382, 2014. [Google Scholar]

28. M. Khan, T. Shah and S. I. Batool, “A color image watermarking scheme based on affine transformation and S4 permutation,” Neural Computing and Applications, vol. 25, no. 7–8, pp. 2037–2045, 2014. [Google Scholar]

29. M. A. Nielson, I. Chuang and L. K. Grover, Quantum computation and quantum information, First ed., New York: Cambridge University Press, pp. 13–15, 2000. [Google Scholar]

30. R. J. Hughes, D. M. Alde, P. Dyer, G. G. Luther, G. L. Morgan et al., “Quantum cryptography,” Contemporary Physics, vol. 36, no. 3, pp. 149–163, 1995. [Google Scholar]

31. N. Gisin, G. Ribordy, W. Tittel and H. Zbinden, “Quantum cryptography,” Reviews of Modern Physics, vol. 74, no. 1, pp. 145–195, 2002. [Google Scholar]

32. C. Li, S. Li and K. T. Lo, “Breaking a modified substitution-diffusion image cipher based on chaotic standard and logistic maps,” Communication in Nonlinear Science and Numerical Simulation, vol. 16, no. 2, pp. 837–843, 2011. [Google Scholar]

33. R. Rhouma and S. Belghith, “Cryptanalysis of a new image encryption algorithm based on hyper chaos,” Physics Letters A, vol. 372, no. 38, pp. 5973–5978, 2008. [Google Scholar]

34. Q. Li, Y. He and J. P. Jiang, “A hybrid classical-quantum clustering algorithm based on quantum walks,” Quantum Information Processing, vol. 10, no. 1, pp. 13–26, 2011. [Google Scholar]

35. A. Ambainis, “Quantum walk algorithm for element distinctness,” SIAM Journal on Computing, vol. 37, no. 1, pp. 210–239, 2007. [Google Scholar]

36. F. Magniez, M. Santhaand and M. Szegedy, “Quantum algorithm for the triangle problem,” SIAM Journal on Computing, vol. 37, no. 2, pp. 413–424, 2007. [Google Scholar]

37. Y. G. Yang, Q. X. Pan, S. J. Sun and P. Xu, “Novel image encryption based on quantum walks,” Scientific reports, vol. 5, no. 1, pp. 1–9, 2015. [Google Scholar]

38. S. E. V. Andraca, “Quantum walks: A comprehensive review,” Quantum Information Processing, vol. 11, no. 5, pp. 1015–1106, 2012. [Google Scholar]

39. J. Kempe, “Quantum random walks—An introductory overview,” Contemporary Physics, vol. 44, no. 4, pp. 307–327, 2003. [Google Scholar]

40. D. Shapira, O. Biham, A. J. Bracken and M. Hackett, “One-dimensional quantum walks with unitary noise,” Physical Review A, vol. 68, no. 6, pp. 062315, 2003. [Google Scholar]

41. P. Blanchard and M. O. Hongler, “Quantum random walks and piecewise deterministic evolutions,” Physical Review Letters, vol. 92, no. 12, pp. 120601, 2004. [Google Scholar]

42. E. F. Nawal and O. M. A. Zaid, “Quality of encryption measurement of bitmap images with RC6, MRC6, and rijndael block cipher algorithms,” International Journal of Network Security, vol. 5, no. 3, pp. 241–251, 2007. [Google Scholar]

43. E. A. Hossam, M. K. Hamdy and S. F. Osama, “Implementation of RC5 block cipher algorithm for image cryptosystems,” International Journal of Computing and Information Systems Control Engineering, vol. 1, no. 8, pp. 245–250, 2007. [Google Scholar]

44. X. Y. Wang, L. Yang, R. Liu and A. Kadir, “A chaotic image encryption algorithm based on perceptron model,” Nonlinear Dynamics, vol. 62, no. 3, pp. 615–621, 2010. [Google Scholar]

45. X. Wang, L. Teng and X. Qin, “A novel colour image encryption algorithm based on chaos,” Signal Processing, vol. 92, no. 4, pp. 1101–1108, 2012. [Google Scholar]

46. Z. Y. Qian and W. X. Yuan, “A new image encryption algorithm based on non-adjacent coupled map lattices,” Applied Soft Computing, vol. 26, pp. 10–20, 2015. [Google Scholar]

47. Z. Y. Qian and W. X. Yuan, “A symmetric image encryption algorithm based on mixed linear-nonlinear coupled map lattice,” Information Sciences, vol. 273, pp. 329–351, 2014. [Google Scholar]

48. H. A. Leopold, A. Singh, S. Sengupta and V. Lakshminarayanan, “Deep learning for ophthalmology using optical coherence tomography,” in State of the Art in Neural Networks and their Applications, Academic Press, vol. 1, pp. 239–269, 2021. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.