Computers, Materials & Continua DOI:10.32604/cmc.2022.028789
Article

A Secure and Lightweight Chaos Based Image Encryption Scheme

Fadia Ali Khan1, Jameel Ahmed1, Fehaid Alqahtani2, Suliman A. Alsuhibany3, Fawad Ahmed4 and Jawad Ahmad5,*

1Department of Electrical Engineering, Riphah International University, Islamabad, 44000, Pakistan
2Department of Computer Science, King Fahad Naval Academy, Al Jubail, 35512, Saudi Arabia
3Department of Computer Science, College of Computer, Qassim University, Buraydah, 51452, Saudi Arabia
4Department of Cyber Security, Pakistan Navy Engineering College, NUST, Karachi 75350, Pakistan
5School of Computing, Edinburgh Napier University, Edinburgh, EH10 5DT, United Kingdom
*Corresponding Author: Jawad Ahmad. Email: J.Ahmad@napier.ac.uk
Received: 17 February 2022; Accepted: 25 March 2022

Abstract: In this paper, we present an image encryption scheme based on the multi-stage chaos-based image encryption algorithm. The method works on the principle of confusion and diffusion. The proposed scheme containing both confusion and diffusion modules are highly secure and effective as compared to the existing schemes. Initially, an image (red, green, and blue components) is partitioned into blocks with an equal number of pixels. Each block is then processed with Tinkerbell Chaotic Map (TBCM) to get shuffled pixels and shuffled blocks. Composite Fractal Function (CFF) change the value of pixels of each color component (layer) to obtain a random sequence. Through the obtained random sequence, three layers of plain image are encrypted. Finally, with each encrypted layer, Brownian Particles (BP) are XORed that added an extra layer of security. The experimental tests including a number of statistical tests validated the security of the presented scheme. The results reported in the paper show that the proposed scheme has higher security and is lightweight as compared to state-of-the-art methods proposed in the literature.

Keywords: Chaos; fractals; fibonacci; tinkerbell chaotic map; confusion; diffusion; brownian motion

1  Introduction

With the advancement in technology, a large number of digital images are transmitted through the Internet. Generally speaking, digital images are not transmitted or stored in encrypted form [1]. Confidentiality of digital images are important in a number of applications that demands restricted access to image data through secure communication. In symmetric cryptography algorithms, the utilized key during the encryption and decryption processes is always same across both the transmitting and receiving ends [2]. As a result, both endpoints need to examine the key exchange protocol for data transmission before initiating the communication. Encrypted keys play a vital role, and the key length determines the strength of any cryptographic scheme [3–5]. The Data Encryption Standard (DES), Advanced Encryption Standard (AES), and Blowfish encryption technique are currently available in symmetric schemes. Chaos based cryptography is one of the emerging areas that researchers and cryptographers are using for image encryption purpose. The intention of utilizing chaos-based cryptography facilitates security to sensitive data because of its high sensitivity towards initial conditions, ergodic performance, and unpredictability [6,7].

Chaos theory has been extensively used in the image encryption method due to its non-periodic nature, susceptibility to initial values, and uncertainty [8,9]. Many schemes are designed by a combination of dynamical phenomena of chaos theory and fractals complex patterns. These (fractal patterns) are never ending complicated shapes that appear to be conscience at various scales. These shapes can be generated using the simple mechanism consistently and systematically [10]. Fractals are depictions of chaotic environments that resembling with the images of chaos and are controlled by iteration. Nature is comprised of fractal geometry, and different patterns are quite ubiquitous. For example, trees, rivers, beaches, mountains, clouds, seashells, and hurricanes are natural occurrences. A function based on fractals possesses dynamic behavior and thus is highly sensitive to its original state, making it a better choice for constructing a robust cryptographic algorithm [11–14]. A fractal image does have a lot of detailed variability at different dimensions with several choices of the key space. Mandelbrot set is a well-known fractal designed by Benoit Mandelbrot in 1979, a remarkably sophisticated and perturbed architecture [11–14]. A computer may generate abstraction fractals, such as the Mandelbrot Set, by constantly computing a mathematical equation [14,15]. The research contribution of the proposed work are as follow:

•   This research proposes an encryption algorithm that utilizes multi-stages symmetric encryption algorithm to generate maximum random sequencing.

•   Multi-stage random sequencing will apply to multimedia data such as images to obtain substitution and permutation-based cryptosystem.

•   Initial step is based on the diffusion process where pixels are permuted using Tinkerbell chaotic map (TBCM). The latter part is based on the bitwise XOR process utilizing Mandelbrot set of fractals (MSF) and Brownian particles (BPM) to get higher entropy value and maximum randomness.

•   Several existing schemes are investigated, and results are added next to the proposed scheme using various statistical standard tests.

2  Research Background

This section discusses chaos-based multi-stage cryptosystem using Fibonacci series-based permutation process, fractals key generation, and Brownian particles.

Chaos-based multi-stage cryptosystems can be iterated rapidly because of their ease in functionalities [16]. As a result, multi-stage techniques are fast in practical uses, especially for image encryption techniques. Chaotic maps are extremely sensitive to initial conditions with deterministic behavior of pseudo-randomness [17]. Confusion and diffusion phenomena are two significant components that are to be considered when designing block cipher. Both contribute to the concealment of plain image structure and a reduction in the statistical dependency of pixels during the image encryption process [18,19]. The enhancement of security is added by integrating it with the sequence generated by the Fibonacci series. Moreover, this sequence is XORed with the extracted real values of the Mandelbrot set of fractals and Brownian particles; thus chaos-based multi-stage encryption scheme is achieved.

2.1 Tinkerbell Chaotic Map (TBCM)

Tinkerbell chaotic map is a two-dimensional chaotic system based on discrete time. TBCM is illustrated as:

wn+1=wn2−xn2+awn+bxn,xn+1=2wnxn+cwn+dxn(1)

whereas, in the Eq. (1) w and x are the sequences generated by the TBCM equation and (a, b, c, & d) are the constants. The initial condition w0 and x0 of the two dimensional chaotic generates random sequencing. Both constants and initial conditions w0 and x0 effects the random sequencing when any of them are altered. Here we applied a = 0.3; b = 0.6000; c = 2.0; and d = 0.27 constants. The initial condition w0 and x0 along with TBCM constants utilized for shuffling of pixels are as follows:

w0=∑k⁡BS1(k)×(2k−1)232,(2)

x0=∑k⁡BS2(k)×(2k−1)232.(3)

whereas BS1and BS2are the two binary strings and Ksub(sub key) that are as follows:

BS1=Ksub(1)Ksub(5)Ksub(3),(4)

BS2=Ksub(4)Ksub(2)Ksub(6).(5)

2.2 Mandelbrot Set of Fractals (MSF)

Fractals are a combination of numeric sequences encompassing many terms in a complex space. These are image-based reiterative and repetitious geometry patterns. They also have the same degrees of variance in all proportions and act identically when iterated. Benoit Mandelbrot (1924–2010) investigated the complicated pattern of recurring shapes in each other, which later he termed it as Mandelbrot set of fractals. A new composite fractal function (CFF) was proposed by the author in, which combines two separate Mandelbrot set (MS) functions with a single control parameter to produce an interesting feature. The results of the CFF simulation show that the proposed map in has a high initial value sensitivity, a complex structure, a larger chaotic region, and a more complex dynamical behaviour than the standard map. CFF is written as:

zn+1=zn2+q+L×(zn4+q)(6)

where z0=q, where points q in the complex plane for which the orbit of zn does not tend to infinity are in the set and 0 < L < 1.

2.3 Brownian Particles Movement (BPM)

The most employed stochastic or random process is Brownian particles motion. It is the representation of the movement of a particle or a point in three-dimensional space. Mathematically the movement of particles in three axis is defined as:

A=rsin⁡acos⁡b,(7)

B=rsin⁡asin⁡b.(8)

whereas a=wi×2×π,b=xi×π,0≤r≤+∞,0≤b≤2π, and 0≤a≤π

Where A and B denote the horizontal and vertical direction distances, respectively; r denotes the movement step length; a and b denote the particle’s movement direction; and wi, xi denote the chaotic sequences produced by chaotic systems.

2.4 Substitution Box

An S-Box (Substitution-Box) is a component of symmetric key algorithms that is responsible for substitution operations in cryptography. Shannon’s property of confusion is commonly utilised in block cyphers to disguise the relationship between the key and the message being encrypted. In many circumstances, the S-Boxes are carefully selected in order to provide resistance to cryptanalysis. In work, we have proposed a novel S-Box which is also known as Fadia’s S-Box. In this paper, we are using Fadia’s S-Box to get a highly secured image in the diffusion stage.

3  The Proposed Image Encryption Scheme

Flowchart of the proposed encryption scheme is shown in Fig. 1 One can see that the proposed scheme has both confusion and diffusion processes using TBCM, CFF and BMP, respectively.

Figure 1: The proposed encryption flowchart

Detailed encryption steps are explained as below:

Designing steps for Multistage Cryptographic Algorithm

4  Performance Analyses

The performance analyses of our proposed encryption scheme are discussed in this section. The plaintext and encrypted images are shown in Figs. 2 and 3, respectively. It is clear from Fig. 3 that the encrypted images conceal original information. Further detailed analyses are based on NIST randomness suite histogram analyses entropy, Adjacent pixels’ correlation, pixel difference analyses and sensitivity analyses etc.

Figure 2: Plaintext images

Figure 3: Encrypted images

4.1 NIST Randomness Test

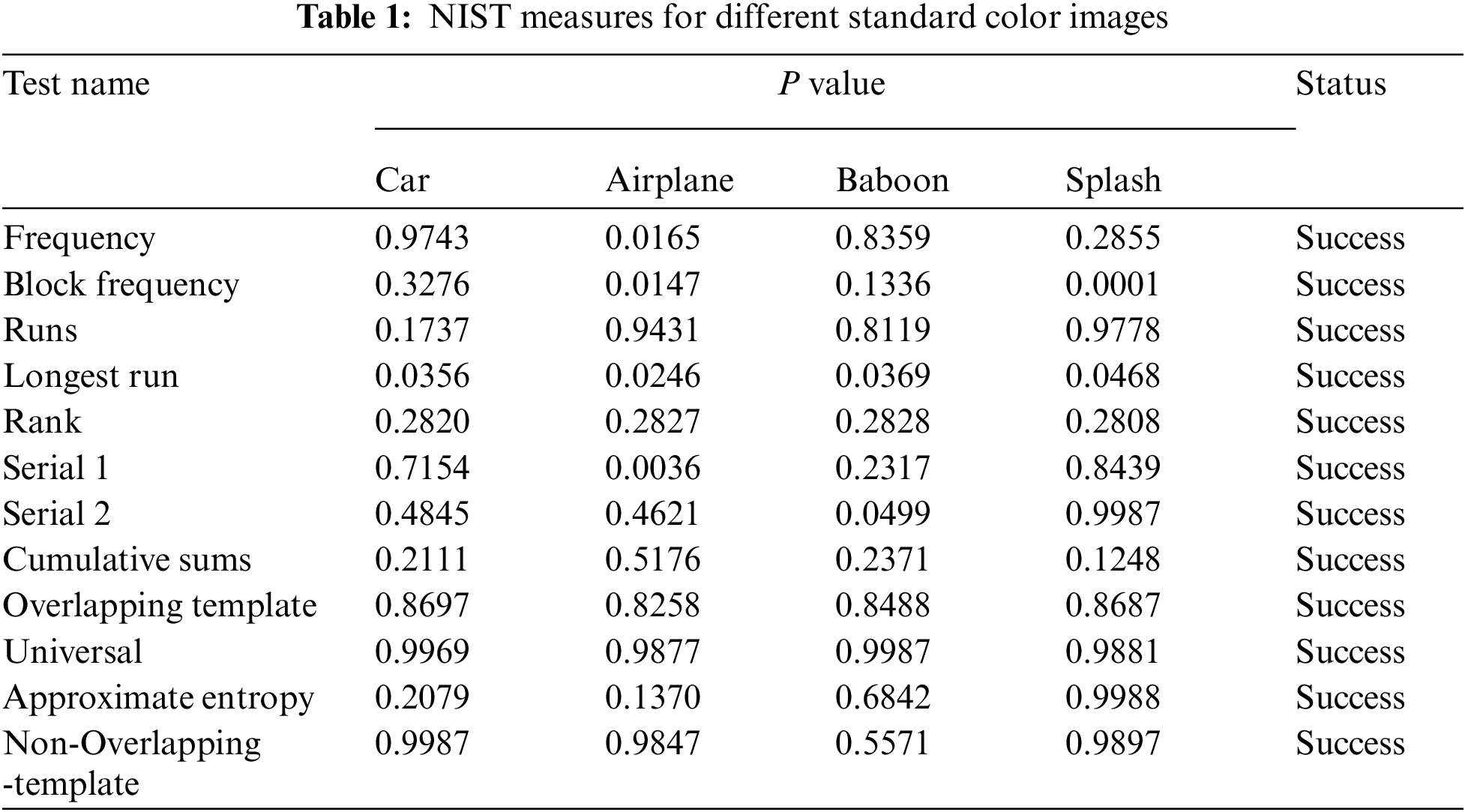
Through NIST (National Institute of Standards and Technology) tests, one can find the unpredictability and randomness. We analyzed chaos based random sequences using multi-stage cryptographic algorithm using TBCM, CFF and BPM. The sequence of random numbers is produced by transforming the decimal system to binary. The NIST test divides the data into ten categories, each comprising 1, 000, 000-bit sequences. The randomness of sequence’s using chaos dynamical system and other sequences is validated, and the encryption’s privacy is guaranteed as highlighted in Tab. 1. Tab. 1 shows that for all tests, the status is a success and it is clear that none of the tests has a failure status.

4.2 Histogram Analyses (HA)

Histogram of an image shows the number of occurrence of pixels. In image encryption, the histograms before and after encryption can be seen significantly different and the encrypted histogram should be flat. From the Figs. 4, and 5, one can see that the histogram is completely different and the ciphertext histogram is almost flat that is near to ideal values.

Figure 4: Plaintext car image having three grey channels (size = 512 × 512 dimension) with histogram plots

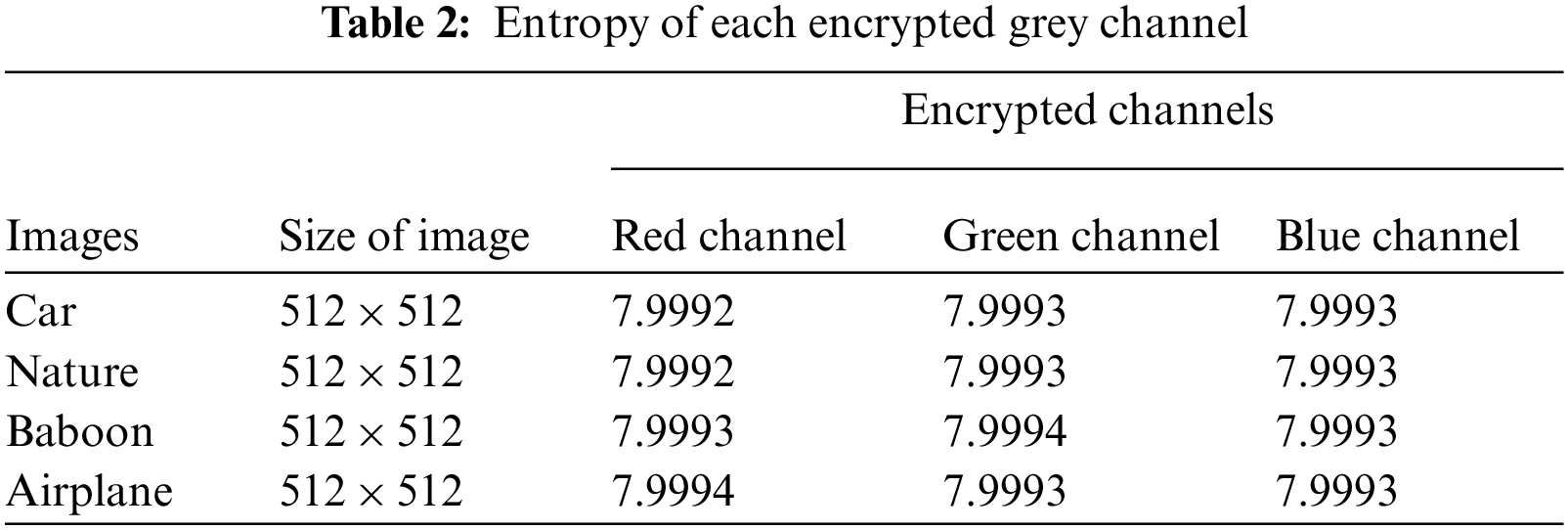
4.3 Information Entropy Analyses

Through the entropy test, one can determine the unpredictability and randomness of an encryption scheme. Entropy is measured by evaluating encrypted images to understand the strength of the proposed system. It is defined as:

H=−∑j=0N−1⁡p(xj)logbp(xj),  (9)

In the above Eq. (9) p(xj)depicts an event-based Probability Masses Function (PMF) whereas xj is the input event of the PMF. ‘X’ shows random number having different outcomes that is referred as n-outcomes. The value obtained should be nearly equal to 8 if all the pixels/numbers have equal probability; therefore, the an ideal scheme should have entropy value 8. Tabs. 2 and 3 shows the findings of the presented scheme. The results demonstrate that the proposed system’s aggregate encrypted image results are closer to 8 and is higher than the schemes that are already available as shown in Tab. 4, intimating that the scheme effectively combats this assault.

Figure 5: Encypted images and it’s histogram plots

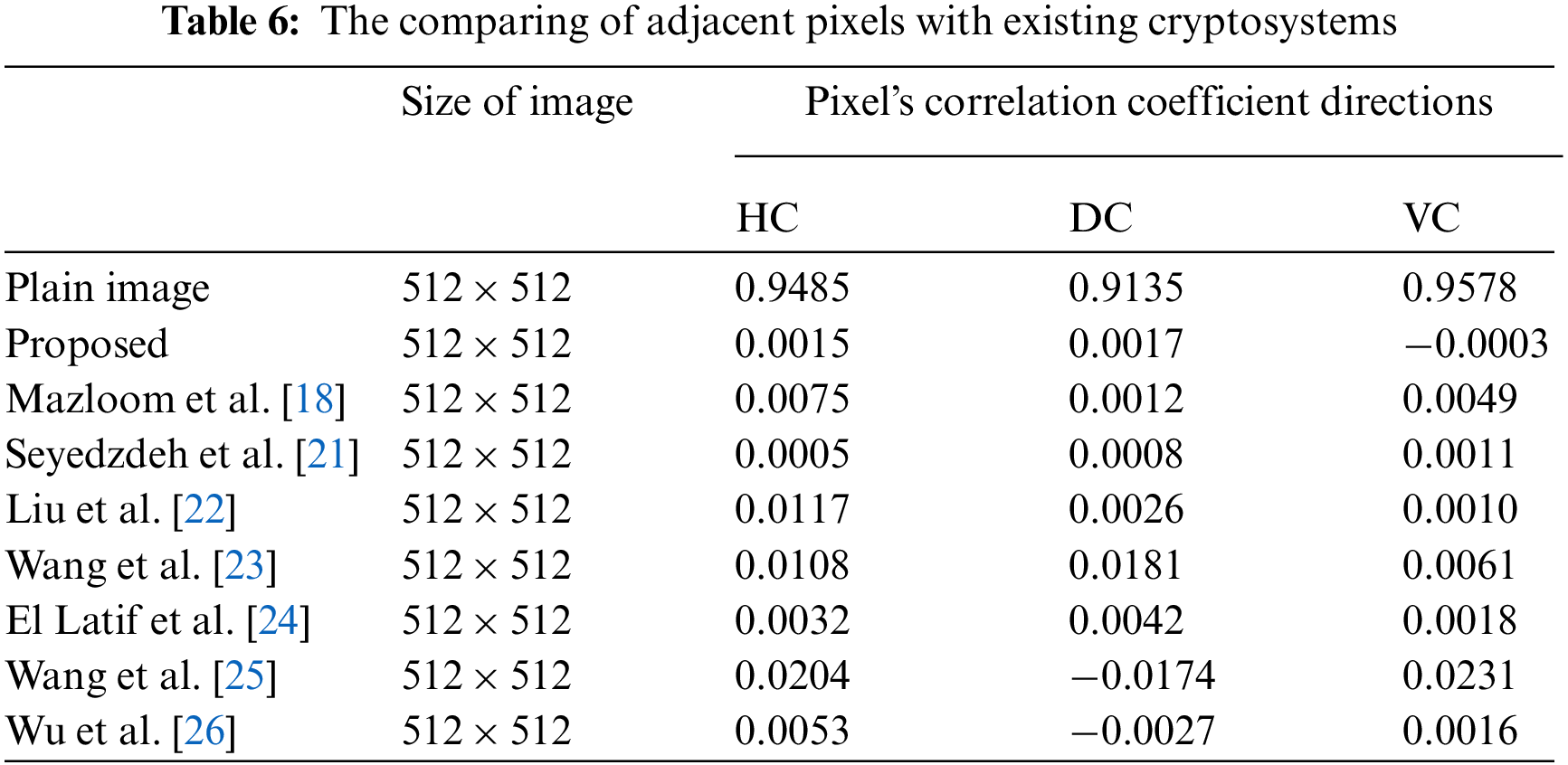
4.4 Adjacent Pixels Correlation (APC)

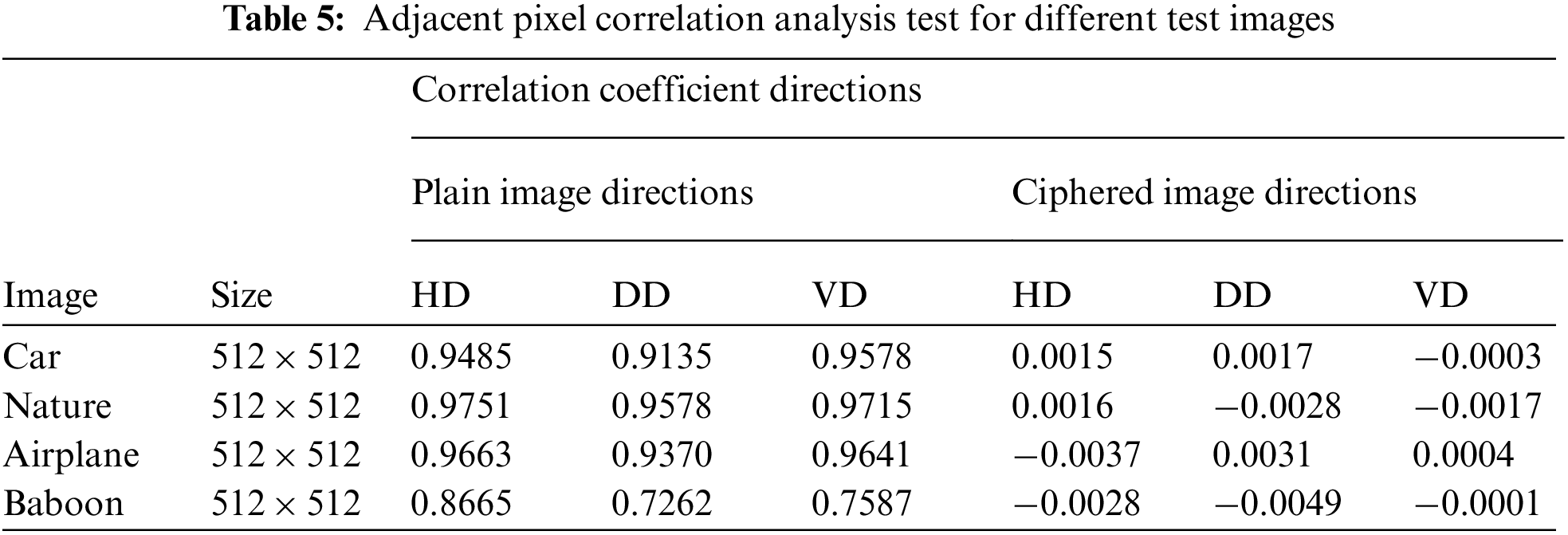
In terms of a linear relation, correlation measures the similarity or closeness among two or more variables [17]. Mathematically APC is illustrated as:

r=SxySxSy,(10)

In the above Eq. (10) sxy shows covariance and standard deviations based on random variables x and y and is denoted by sx, and sy. The valid range for APC is 0 to 1. In the given range ‘0’ shows pixels having no similarity while ‘1’ show full/higher similarity among adjacent pixels. In case of images, neighboring pixels in a plain image are often relatively identical and have a high correlation level. However, in a cipher-text, it’s often desirable to always have a weak relationship among neighboring pixels, which indicates that the adjacent pixels are unique. It is because if there is any resemblance among pixels in an encrypted image, an attacker or cryptologist can readily exploit it by using the neighboring pixel to determine the content of another pixel. Compared to previous results, the suggested method can break the relationship among neighborhood pixels and has least correlation coefficient values. Tab. 5 depicts calculated correlation values for five images in various directions such as Horizontal Direction (HD), Vertical Direction (VD), and Diagonal Direction (DD). In Tab. 6, the calculated value for the presented scheme is compared to traditional art of schemes. One can confirm from Tabs. 5 and 6 that the proposed scheme has low correlation in all directions. Moreover, Fig. 6 shows original and ciphertext correlation plot. From Fig. 6, it is evident that plaintext image has correlation while encrypted images has no correlation and pixels are dispersed.

4.5 Pixels Difference Analyses

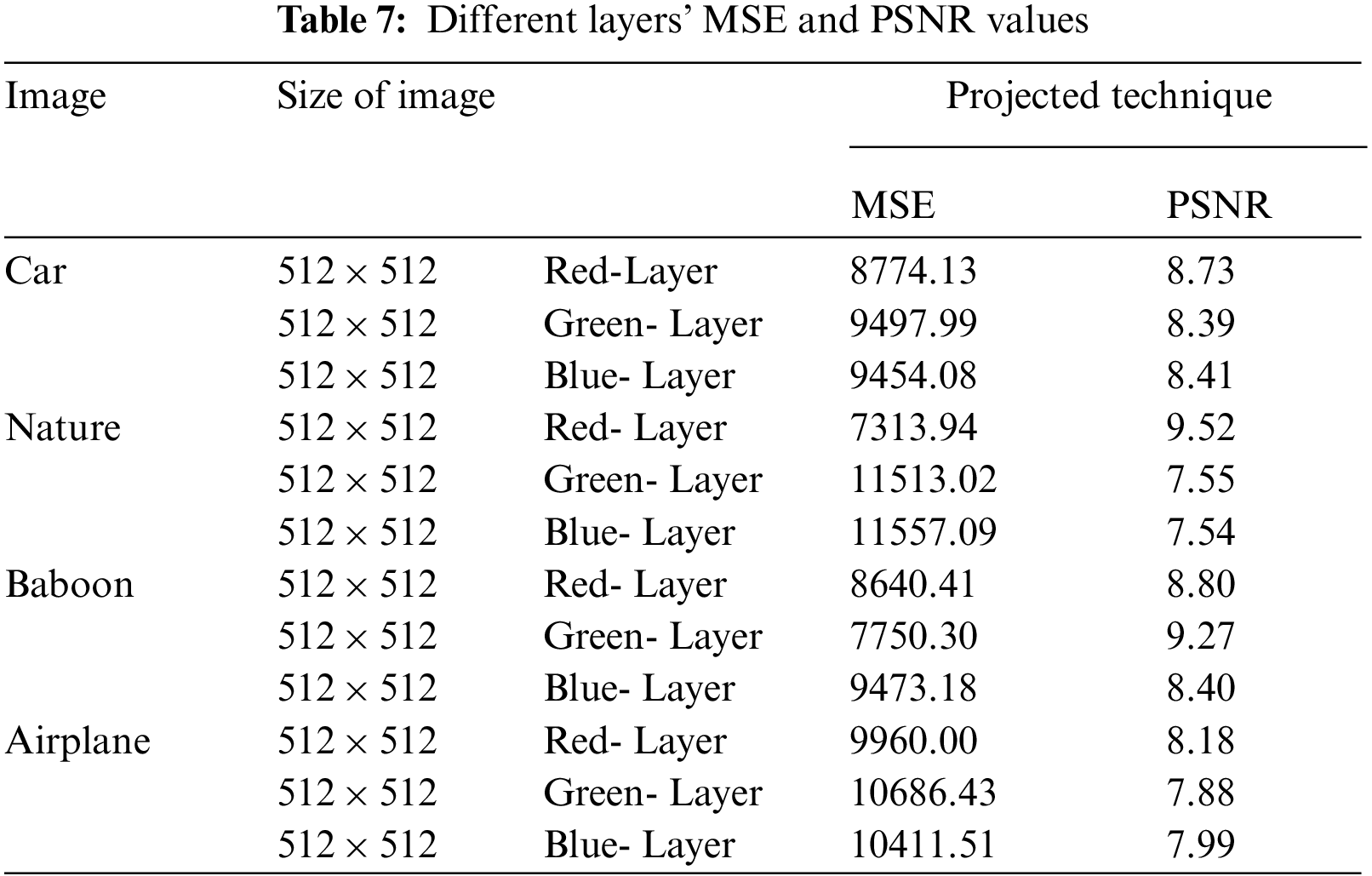
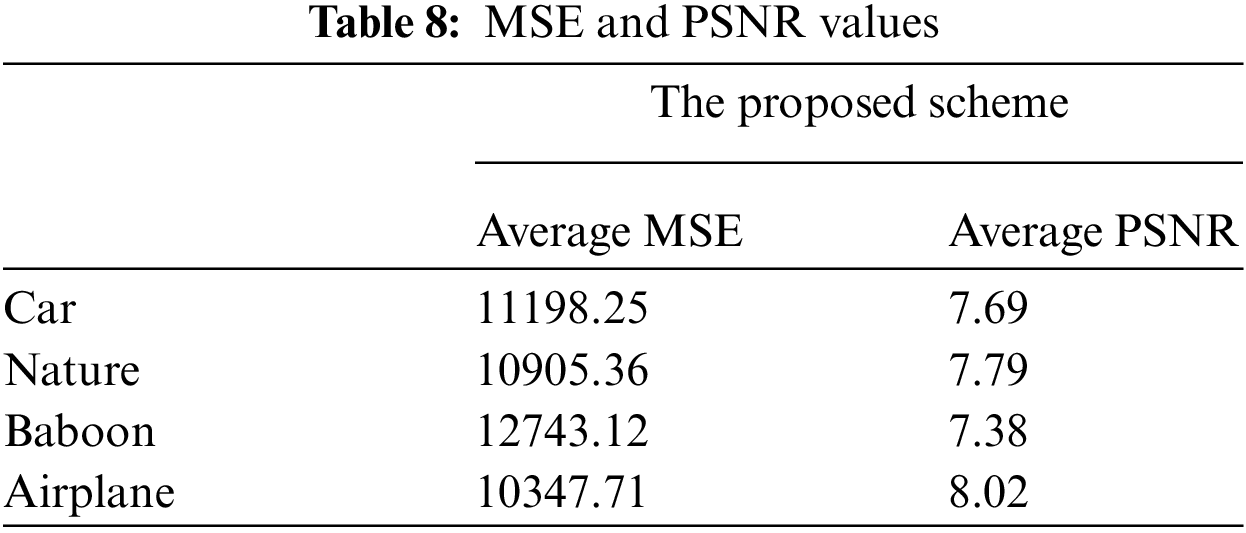
Pixel difference analysis compares plain image content and scrambled image data. The difference between pixels in a plain and encrypted image is assessed utilizing two parameters: (i) Mean Square Error (MSE) and the peak to signal to noise ratio is another (PSNR).

The MSE between the cipher-text image and the plaintext image is measured to assess the proposed algorithm’s efficiency. It shows the average squared disparity among cipher-text image and plaintext image pixels. The below equation can mathematically be expressed as MSE [17]:

Figure 6: Correlation of pixels for three different direction

MSE=1M×N∑i=1M⁡∑j=1N⁡(P(i,j)−C(i,j))2(11)

PSNR is a metric of the logarithmic (base 10) proportion between value calculated from peak signal and mean square error in image encryption assessment. Mathematically PSNR expresses as:

PSNR=10log2(Imax2MSE)(12)

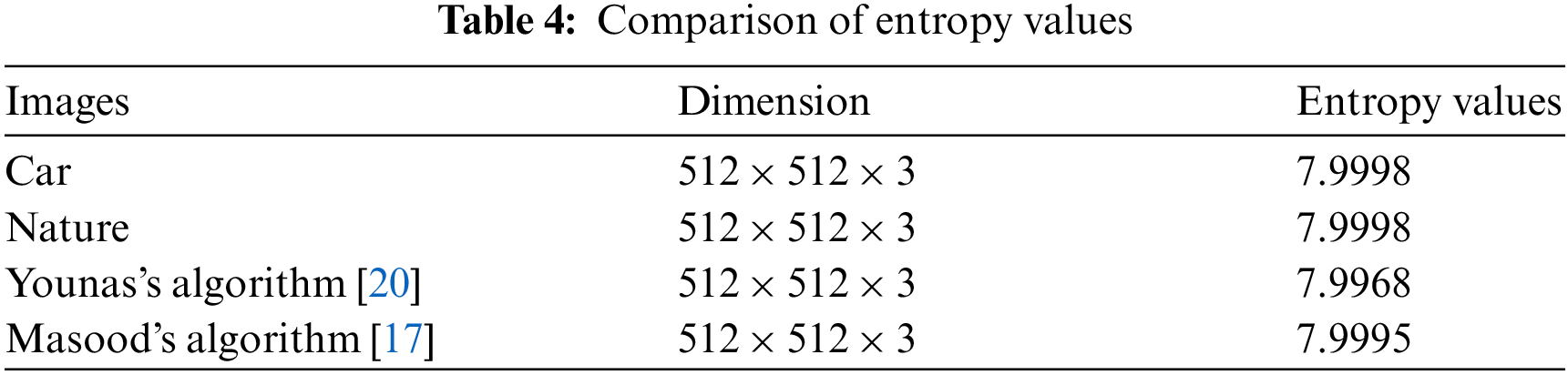
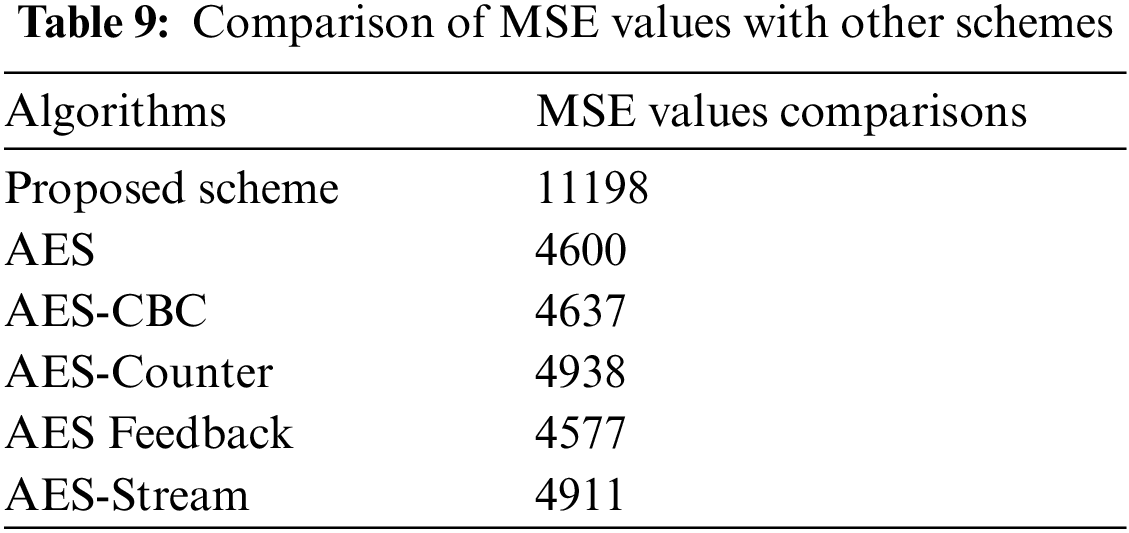
In the above Eq. (12) ‘Imax’ shows calculated maximum value of the pixel. The calculated value for PSNR should be low for a good encryption scheme. The calculated value for the presented scheme is shown in Tabs. 7 and 8. Moreover, calculated value is compared to several existing schemes as shown in Tab. 9.

4.6 Sensitivity Analyses

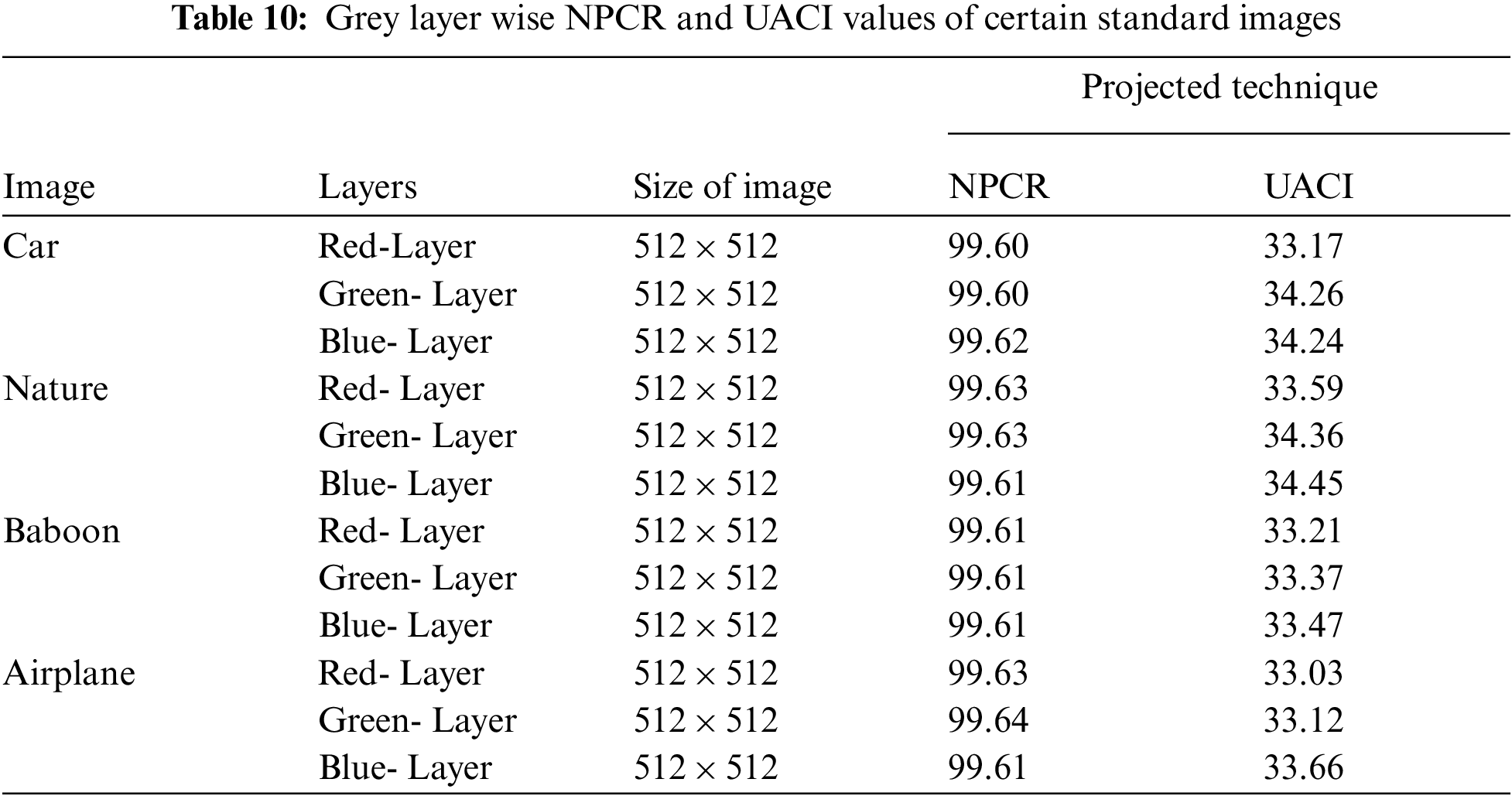
Confidentiality of an image can be compromised if the plaintext and the encrypted images are identified. Differential attack has become very popular method for detecting this sort of relationship. The small variances in the plaintext message and corresponding scrambled images are discovered through statistical attacks. If a pattern emerges from these findings, the attacker can understand the relation between the encrypted message and the plain text and easily decrypt the message. As a result, employing an encryption scheme that ensures a radical shift in the cipher-text whenever the plain image is modified that would be beneficial from an encryption perspective. Three components are done to gauge and assess the effectiveness of an encryption scheme in this aspect. These are the unified average changing intensity (UACI) and the number of Changing Pixel Rates (NPCR). For our algorithm, these parameters were examined, and their corresponding values were compared. These fall into the category of strong encryption. Attackers seek to establish a bridge between the plain image and the encrypted image by analyzing how changes in an input affect the consequent variation at the outputs to infer the key. The encrypted image transforms when an attacker attempts to adjust the plaintext message, including altering even one pixel.

NPCR is a metric that assesses the number of unique pixels in plain and encrypted images in terms of percentage. Higher NPCR results reflect a significant variation between the plain and encrypted images. One can measure the NPCR values for various four encrypted images with a binary number adjustment and matched it to previously published standards. The NPCR comparison table affirmed our proposed technique for mitigating against differential assaults. The two cipher images are C1(i,j) and C2(i,j)are two ciphertext images which are differ by only pixel. Mathematically NPCR is defined as [17]:

NPCR=∑i,j⁡D(i,j)W×H×100(13)

where D(i,j)is calculated as:

D(i,j)={0,C1(i,j)=C2(i,j)1,C1(i,j)≠C2(i,j)(14)

NPCR should be higher for secure systems. The ideal value is 100%. For the presented scheme calculated values are ≥ 99.60 which shows better security.

UACI is metric used to find the intensity level of plain and encrypted image. It is defined as:

UACI=1W×H∑i,j⁡[C1(i,j)−C2(i,j)255]×100(15)

In the above Eq. (15), W×H shows total dimension of an image. C1(i,j) and C2(i,j)are the two encrypted image which is different by only pixel difference. The calculated results for UACI are shown in Tab. 10 for various test images. If the values of NPCR ≥ 100 and UACI ≥ 33, it means that the scheme is highly secure.

5  Conclusion

In this article, we applied the principle of confusion and diffusion for the development of multi-stage image encryption scheme. Initially, an image (red, green, and blue layers) is converted into blocks with an equal number of pixels where each block is shuffled via TBCM and BPM to get shuffled blocks and shuffled pixels, respectively. In the proposed scheme, CFF to get highly random sequence and used in XOR operation. Using the obtained random sequencing, three layers of permuted images are XORed with random values obtained from MSF. Finally, the final ciphetext is obtained using Fadia’s substitution box. A number of experiments are used to assess the robustness of the proposed scheme and to authenticate the randomness of the newly proposed scheme. These tests include NIST-800–22 and other statistical tests that validated the strength of multi-stage scheme. In future, the aim is to extend this research for audio and video content encryption. Other multimedia data, such as audio and video, will be investigated and analysed using the suggested encryption technique.

Acknowledgement: The researchers would like to thank the Deanship of Scientific Research, Qassim University for funding the publication of this project.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  J. Ahmad and F. Ahmed, “Efficiency analysis and security evaluation of image encryption schemes,” Computing, vol. 23, pp. 25, 2010. [Google Scholar]

 2.  N. Munir, M. Khan, Z. Wei, A. Akgul, M. Amin et al.., “Circuit implementation of 3D chaotic self-exciting single-disk homopolar dynamo and its application in digital image confidentiality,” Wireless Networks, pp. 1–18, 2020. [Google Scholar]

 3.  A. Alghafis, N. Munir, M. Khan and I. Hussain, “An encryption scheme based on discrete quantum map and continuous chaotic system,” International Journal of Theoretical Physics, vol. 59, no. 4, pp. 1227–1240, 2020. [Google Scholar]

 4.  I. Bashir, F. Ahmed, J. Ahmad, W. Boulila and N. Alharbi, “A secure and robust image hashing scheme using Gaussian pyramids,” Entropy, vol. 21, no. 11, pp. 1132, 2019. [Google Scholar]

 5.  M. Khan and F. Masood, “A novel chaotic image encryption technique based on multiple discrete dynamical maps,” Multimedia Tools and Applications, vol. 78, no. 18, pp. 26203–26222, 2019. [Google Scholar]

 6.  X. R. Zhang, W. F. Zhang, W. Sun, X. M. Sun and S. K. Jha, “A robust 3-D medical watermarking based on wavelet transform for data protection,” Computer Systems Science & Engineering, vol. 41, no. 3, pp. 1043–1056, 2022. [Google Scholar]

 7.  X. R. Zhang, X. Sun, X. M. Sun, W. Sun and S. K. Jha, “Robust reversible audio watermarking scheme for telemedicine and privacy protection,” Computers, Materials & Continua, vol. 71, no. 2, pp. 3035–3050, 2022. [Google Scholar]

 8.  F. Masood, J. Ahmad, S. A. Shah, S. S. Jamal and I. Hussain, “A novel hybrid secure image encryption based on julia set of fractals and 3D lorenz chaotic map,” Entropy, vol. 22, no. 3, pp. 274, 2020. [Google Scholar]

 9.  M. Khan, F. Masood and A. Alghafis, “Secure image encryption scheme based on fractals key with fibonacci series and discrete dynamical system,” Neural Computing and Applications, vol. 32, no. 15, pp. 11837–11857, 2020. [Google Scholar]

10. S. Agarwal, “Image encryption techniques using fractal function: A review,” International Journal of Computer Science and Information Technology, vol. 9, no. 2, pp. 53–68, 2017. [Google Scholar]

11. S. Agarwal, “Symmetric key encryption using iterated fractal functions,” International Journal of Computer Network & Information Security, vol. 9, no. 4, pp. 1--9, 2017. [Google Scholar]

12. S. Agarwal, “Secure image transmission using fractal and 2D-chaotic map,” Journal of Imaging, vol. 4, no. 1, pp. 17, 2018. [Google Scholar]

13. B. B. Mandelbrot, pp. C. J. Evertsz and M. C. Gutzwiller, in Fractals and Chaos: The Mandelbrot set and Beyond, vol. 3. New York, USA: Springer, 2004. [Online]. Available: https://link.springer.com/book/10.1007/978-1-4757-4017-2. [Google Scholar]

14. Y. Y. Sun, R. Q. Kong, X. Y. Wang and L. C. Bi, “An image encryption algorithm utilizing mandelbrot set,” in Int. Workshop on Chaos-Fractal Theories and Applications, Kunming, China, pp. 170–173, 2010. [Google Scholar]

15. S. Agarwal, “A new composite fractal function and its application in image encryption,” Journal of Imaging, vol. 6, no. 7, pp. 70--97, 2020. [Google Scholar]

16. F. A. Khan, J. Ahmed, J. S. Khan, J. Ahmad, M. A. Khan, “A novel substitution box for encryption based on lorenz equations,” in Int. Conference on Circuits, System and Simulation, London, UK, pp. 32–26, 2017. [Google Scholar]

17. F. Masood, M. Driss, W. Boulila, J. Ahmad, S. U. Rehman et al., “A lightweight chaos-based medical image encryption scheme using random shuffling and XOR operations,” Wireless Personal Communications, pp. 1–28, 2021. [Google Scholar]

18. S. Mazloom and A. M. E. Moghadam, “Color image encryption based on coupled nonlinear chaotic map,” Chaos Solitons Fractals, vol. 42, no. 3, pp. 1745–1754, 2009. [Google Scholar]

19. A. Akhshani, A. Akhavan, S. -C. Lim and Z. Hassan, “An image encryption scheme based on quantum logistic map,” Communications in Nonlinear Science and Numerical Simulation, vol. 17, no. 12, pp. 4653–4661, 2012. [Google Scholar]

20. Y. Irfan and M. Khan, “A new efficient digital image encryption based on inverse left almost semi group and lorenz chaotic system,” Entropy, vol. 20, no. 12, pp. 913, 2018. [Google Scholar]

21. S. M. Seyedzdeh and S. Mirzakuchaki, “A fast color image encryption algorithm based on coupled two-dimensional piecewise chaotic map,” Signal Process, vol. 92, no. 5, pp. 1202–1215, 2012. [Google Scholar]

22. S. Liu, J. Sun, and Z. Xu, “An improved image encryption algorithm based on chaotic system,” J. Comput, vol. 4, no. 11, pp. 1091–1100, 2009. [Google Scholar]

23. X. Wang, T. Lin and Q. Xue, “A novel colour image encryption algorithm based on chaos,” Signal Processing, vol. 92, no. 4, pp. 1101–1108, 2012. [Google Scholar]

24. A. El-Latif, A. Ahmed, L. Li, N. Wang, Q. Han et al., “A new approach to chaotic image encryption based on quantum chaotic system, exploiting color spaces,” Signal Processing, vol. 93, no. 11, pp. 2986–3000, 2013. [Google Scholar]

25. W. Xingyuan and L. Yang, “A novel chaotic image encryption algorithm based on water wave motion and water drop diffusion models,” Optics Communications, vol. 285, no. 20, pp. 4033–4042, 2012. [Google Scholar]

26. Y. Wu, Y. Zhou, J. P. Noonan and S. Agaian, “Design of image cipher using latin squares,” Information Sciences, vol. 264, pp. 317–339, 2014. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.