DOI:10.32604/cmc.2022.028550

| Computers, Materials & Continua DOI:10.32604/cmc.2022.028550 |  |
| Article |
Improved Prediction of Metamaterial Antenna Bandwidth Using Adaptive Optimization of LSTM
1Department of Computer Sciences, College of Computer and Information Sciences, Princess Nourah Bint Abdulrahman University, Riyadh, 11671, Saudi Arabia
2Department of Communications and Electronics, Delta Higher Institute of Engineering and Technology, Mansoura, 35111, Egypt
3Faculty of Artificial Intelligence, Delta University for Science and Technology, Mansoura, 35712, Egypt
4Computer Engineering and Control Systems Department, Faculty of Engineering, Mansoura University, Mansoura, 35516, Egypt
5Department of Computer Systems Engineering, Faculty of Engineering at Shoubra, Benha University, Egypt
6Department of Computer Science, Faculty of Computer and Information Sciences, Ain Shams University, Cairo,11566, Egypt
7Department of Computer Science, College of Computing and Information Technology, Shaqra University, 11961,Saudi Arabia
*Corresponding Author: Amel Ali Alhussan. Email: AAAlHussan@pnu.edu.sa
Received: 12 February 2022; Accepted: 14 March 2022
Abstract: The design of an antenna requires a careful selection of its parameters to retain the desired performance. However, this task is time-consuming when the traditional approaches are employed, which represents a significant challenge. On the other hand, machine learning presents an effective solution to this challenge through a set of regression models that can robustly assist antenna designers to find out the best set of design parameters to achieve the intended performance. In this paper, we propose a novel approach for accurately predicting the bandwidth of metamaterial antenna. The proposed approach is based on employing the recently emerged guided whale optimization algorithm using adaptive particle swarm optimization to optimize the parameters of the long-short-term memory (LSTM) deep network. This optimized network is used to retrieve the metamaterial bandwidth given a set of features. In addition, the superiority of the proposed approach is examined in terms of a comparison with the traditional multilayer perceptron (ML), K-nearest neighbors (K-NN), and the basic LSTM in terms of several evaluation criteria such as root mean square error (RMSE), mean absolute error (MAE), and mean bias error (MBE). Experimental results show that the proposed approach could achieve RMSE of (0.003018), MAE of (0.001871), and MBE of (0.000205). These values are better than those of the other competing models.
Keywords: Metamaterial antenna; long short term memory (LSTM); guided whale optimization algorithm (Guided WOA); adaptive dynamic particle swarm algorithm (AD-PSO)
Machine learning is an active research field that is widely used in data analysis for numerous domains. On the other hand, the design of antennas becomes complex every day; which encourages antenna designers to benefit from the powerful capabilities of machine learning to build reliable models to be used for intelligent and fast optimization of antenna designs. Optimization techniques based on machine learning algorithms; such as particle swarm optimization and genetic algorithms are used recently to optimize the structure of antennas while retaining their significant target performance. These optimization techniques are essential especially when the structure of the antenna is complex. In this case, the machine learning algorithms are effective in discovering the best antenna design parameters. In addition, the tools used in the simulation and analysis of electromagnetic (EM), which can be used to measure the fitness of antennas, require a lot of effort and time by antenna designers to get the proper results from the optimization process performed by these tools. The solution to this bottleneck is offered by machine learning that can be used to overcome the limitations of these simulation tools. The advantage of machine learning is embedded in its ability to provide approximate and proper antenna structures without the need to use EM simulations [1,2].
Machine learning techniques; such as K-nearest neighbors (KNN), artificial neural network (ANN), and least absolute shrinkage and selection operator (LASSO) were used recently in integrated and unified frameworks to optimize the parameters of antennas and to discover their optimal design parameters [3]. One of the key benefits of machine learning is the reduction of the computation time observed in EM approaches. This benefit is obvious when optimizing several parameters or when it is needed to build a large model structure. The geometries of microstrip antennas, particularly complicated geometrical antennas, or the new model structures are still challenging to be handled efficiently using the established theories of antennas. This can be shown when given some of these geometries have low accuracy. In real-time, machine learning may be used to model and forecast scattering problems as well as evaluate and improve antennas performance. In the literature, many research efforts employed machine learning models for optimizing the parameters of antennas. The most commonly used model to perform this optimization is the neural network. However, the antenna structure determines the number of geometrical parameters needed in the optimization process, and as this number increases, it becomes hard for the model to derive a better relationship among these parameters [4].
Many antennas are designed with variable performance and usage. The rectangular antenna is considered the simplest design that can be simply designed based on machine learning. The relevant parameters are the length and width of the rectangular patch, the dielectric, the height of the substrate, and the resonant frequency. A circular patch antenna is another essential type of antenna. The parameters of this design are similar to the rectangular patch antenna but with a radius of the patch antenna instead of the length and width of the rectangular type. An elliptical patch antenna is a special design of a circular antenna, where the shape is an ellipse. Similar parameters to the circular antenna are specified to be optimized using machine learning. In addition, in a fractal antenna, the perimeter (outer structure or inner sections of antenna) can be increased, and the effective length can be maximized based on the self-similar design structures/fractals of the material that can transmit or receive electromagnetic radiation within a given volume or a total surface area. This type of antenna consists of several parameters to be optimized, requiring a suitable dataset with enough samples to predict some of these parameters efficiently. Another type of microstrip antenna is the monopole antenna. The class of monopole antennas consists of a conductor in the form of a straight rod shape. In addition, there is a type of conductive surface, namely, a ground plane used to hold the conductor perpendicularly. When this antenna works as a receiver, the output signal is taken between the ground plane and the lower end of the monopole. Moreover, to the lower end of the monopole, one side of a feedline is attached to the ground plane, and the other side is attached to the antenna. There are other types of microstrip antennas that are designed with particular configurations. These types include substrate integrated waveguide, planar inverted-F antenna, reflect-array, and other special patch designs. Each type of these design has a set of configuration parameters that can be optimized and adjusted using machine learning [5].
One of the main outcomes of the field of computational electromagnetics is known as metamaterial antenna. This type of antenna has a significant advantage which is the possibility of designing this type of antenna using computations and optimization methods without relying on the modeling of its broader type [6]. The field of study of metamaterial antenna is based on customizing the light molecule interactions using complex geometric shapes. However, the other types of conventional antennas use Maxwell’s equations in their inherent design. Therefore, the metamaterial antenna is the best antenna that can benefit from the current advances in machine learning. The material of metamaterial antenna has special properties; which can not be regenerated using the natural material. This type of material is used in many other fields; such as microwave components, revolutionary electronics, and compact antennas. The design of antennas is considered the most important application of this material [7].
Recently, many optimization approaches have emerged in the literature with promising performance [8–11]. These methods are necessary for the tasks where the optimization process grows with time and is thus complex. When the conventional techniques cannot solve complex problems, the metaheuristic approaches are the best choice to handle these cases. The metaheuristic approaches are based on the idea of starting with a random population then selecting the best candidate solution to be passed to the next generation. This dynamic nature of metaheuristic algorithms makes it a proper choice for optimizing the parameters of metamaterial antenna.
Tab. 1 presents some of the key achievements in the literature in which machine learning approaches are employed for optimizing the parameters of antennas. As shown in the table, it can be noted that the most common method used for parameter optimization is neural networks in the form of MLP or SVR that can be harnessed with other approaches in ensembles. In addition, most of the parameters targeted by the parameter optimization are the resonance frequency given the geometrical information of the antenna as an input. Moreover, the table shows the achieved results of each approach in optimizing the target parameters.

Metaheuristic algorithms are capable of handling problems with unexpected behavior. These algorithms are distinguished by their intelligence which is based on the random search methodology. In addition, these algorithms can efficiently avoid local perfections as usually referred to as simple and flexible approaches. This type of algorithm has two main processes namely exploitation and exploration that are running while searching the population for the optimal solution. In the exploration process, the search space is examined thoroughly to find the best solution. In recent decades, many global optimization approaches were developed based on observing natural objects in the real life. One of these global optimization approaches is known as population-based metaheuristic algorithms that can be used in a variety of situations. Two types of metaheuristic approaches are widely spread in the field namely metaphor and non-metaphor base approaches. The metaphor approach is based on observing human behavior or a natural phenomenon in its inherent details [18].
In this paper, we propose a novel approach for predicting the bandwidth of the metamaterial antenna based on optimized long short-term memory (LSTM). The optimization of LSTM is performed in terms of the recently emerged algorithm referred to as adaptive dynamic particle swarm algorithm (AD-PSO) with a guided whale optimization algorithm (Guided WOA) [19,20]. The resulting optimized LSTM with optimum hyperparameters are used to robustly predict the bandwidth of the metamaterial antenna.
The rest of this paper is organized as follows. The description of the dataset along with a detailed discussion of the proposed methodology are explained in Section 2. The achieved results are comparisons are presented and investigated in Section 3. Then, the conclusions are examined in Section 4.
The proposed methodology used to improve the prediction of the metamaterial antenna bandwidth is discussed in this section. The section starts with presenting the dataset employed in this research, followed by discussing the main components of the proposed approach.
The metamaterial dataset used in this work contains eleven features, which are described in Tab. 2. Using Kaggle [21], we were able to access the dataset. There are 572 records in this collection, which is rather large. Each record in the dataset represents the optimum design of a metamaterial antenna. The columns of this dataset represent the features that describe the configurations of the antenna. The bandwidth of the antenna is adopted as the target feature that we need to robustly predict given the other features. A short description of these features is presented in Tab. 2. To get a better understanding of these features, Fig. 1 shows the distribution of the bandwidth from the dataset records. As shown in the figure, the majority of samples in the dataset have a bandwidth in the range from 0.9 to 1.0. This means that the changes in the bandwidth among the samples are very small; which requires a robust predictor to predict the bandwidth value of a given set of parameters accurately.
Figure 1: Distribution of bandwidth feature in the metamaterial dataset
As the dataset is collected from electromagnetic simulation tools, it has been noted that some samples were recorded in the dataset with missing values. To deal with the missing values (denoted by null in the dataset) in a certain feature column, we replaced these values with the average of the surrounding not-null values in the same column. In addition, it is noted that the values of the features in the dataset do not lay in the same range; which might affect the performance of the predictor. Therefore, we applied the min-max normalization. After applying this step, each feature in the dataset has the lowest value of zero and the greatest value of one. Fig. 2 depicts the correlation matrix of the features of the dataset after dealing with the null values and normalizing the feature. As shown in the figure, the values of Tm and Wm are highly correlated with the metamaterial antenna bandwidth.
Figure 2: Correlation matric of features in the metamaterial antenna dataset
As explained in [22], the LSTM model is an improvement on the ANN model and may be used to solve a variety of issues. Long-term memory retention is one of LSTM’s key advantages. Fig. 3 depicts the LSTM design. In the LSTM model, the initial step is to determine which data from the cell state should be disregarded.
Figure 3: LSTM neural network architecture
2.2 Adaptive Dynamic Technique
After the optimization process has been initialized, and for each solution in the population, a fitness value is calculated. To get the highest possible fitness value, the optimization algorithm selects the optimum agent for the situation (solution) [23]. To initiate the adaptive dynamic process, the optimization algorithm divides the population of agents into two groups, which are referred to as the exploitation group and the exploration group. Folks in the exploitation group are mostly concerned with moving toward the ideal or best answer, while individuals in the exploration group are primarily concerned with searching the region surrounding the leaders. The exchange of information (update) between the agents of the various population groupings occurs dynamically. The optimization method is started with a (50/50) population to establish a balance between the exploitation group and the exploration group. The process is then iterated over and over again until it finds the best or optimum solution [24].
The Guided WOA refers to a modified version of the original WOA algorithm [25], which is used in this research. By changing the search strategy via a single agent, the guideline-based WOA overcomes one of the disadvantages of the original WOA. Using a modified algorithm, the agents are directed toward prey or the optimal solution depending on the input from more than one agent. In the original WOA algorithm, agents are forced to roam randomly around each other to get the results of the global search. Agents are forced to follow three random agents instead of just one when they are using the Guided WOA algorithm, which results in a more efficient exploration process. More exploration may be obtained by requiring agents not to be impacted by a single leader position. The updating positions mechanism of the algorithm three random solutions of
A variety of swarming patterns in nature, such as those shown by birds, are represented by the PSO algorithm, which replicates their social behavior. By shifting their places, the agents in the PSO algorithm look for the optimal solution or meal based on the most recent velocity. The following algorithm shows the detailed steps of the AD-PSO-Guided WOA algorithm employed in this research.

A set of experiments were conducted to evaluate the proposed model and compare it with the other competing models in the literature. These models are the Multilayer Perceptron (MLP), K-Nearest Neighbors (KNN), LSTM, in addition to the proposed AD-PSO-Guided WOA for the LSTM model which is used to select the optimal hyperparameters value of the LSTM network for predicting the bandwidth of metamaterial antenna. The evaluation of these models is based on the criteria listed in Tab. 3. These metrics are the mean absolute percentage error (MAPE), the root mean square error (RMSE), the relative root mean square error (RRMSE), and Pearson’s correlation coefficient (R). In addition, the modified agreement index (d) was employed to determine agreement (WI), where M is the number of observations in the subset;

It was necessary to utilize around 80 percent of the dataset obtained at each site for training, with the remaining 20 percent being used to test for the dependability of the models that had been constructed. A uniform distribution was used to provide random sampling and assignment of data to the two subgroups, rather than using a chronological partitioning method. This is done to lessen the reliance of the produced models on the particular data that was used in the fitting process and to guarantee that the models behave in the same manner when dealinsg with other datasets. In addition, the calculation of validation metrics is performed to present non-dimensional error estimates.
After preparing the training and testing sets, a set of values were selected for the configuration parameters of the adaptive PSO-guided WOA algorithm to train the LSTM model. The settings of these values are presented in Tab. 4. As shown in the table, the initial parameters are chosen as follows. The maximum number of iterations is set to 20 and the number of runs is chosen as 20 for the training set. The initial size of the population is selected as 20. In addition, the values of Wmin and Wmax that represent the main parameters of the PSO algorithm are set to 0.6 and 0.9. Moreover, the values of α and β as assigned to 0.99 and 0.1, respectively.
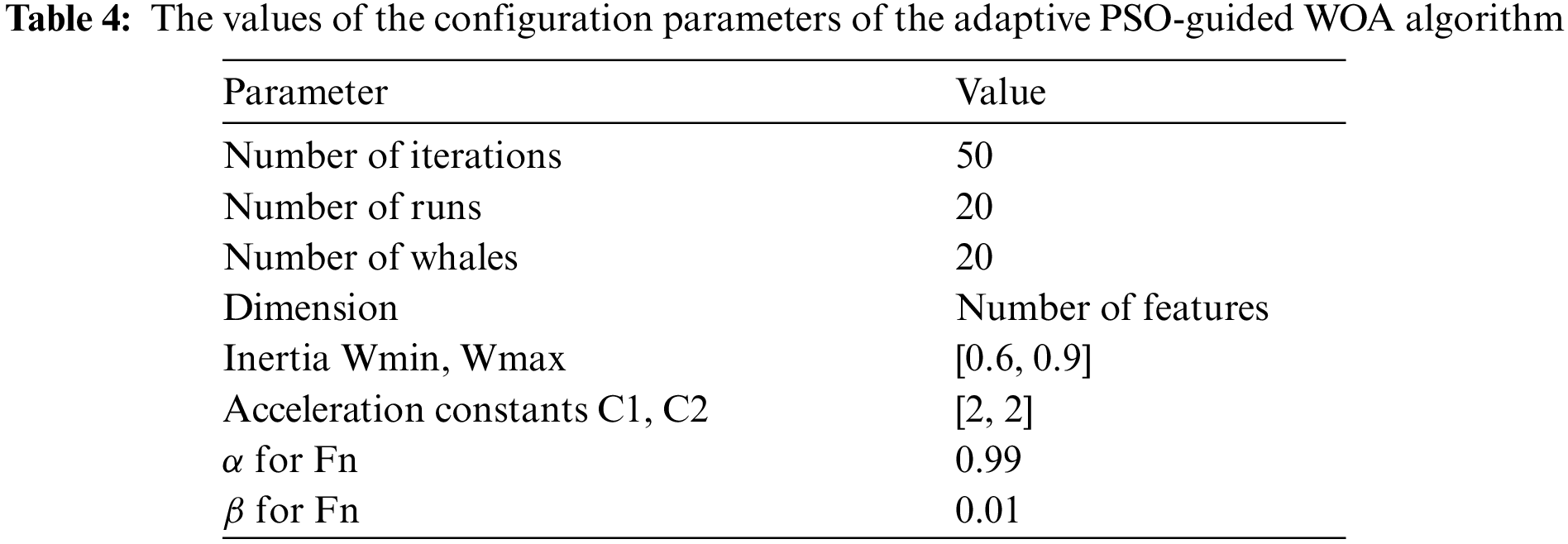
The parameters listed in Tab. 4 are used in the running of the optimization process of the LSTM parameters. The progress of the training process follows the behavior depicted in Fig. 4. In this figure, the model optimization reaches its best values near the 20th iteration. During the optimization process, the exploration and exploitation operations vary depending on the recorded optimized values until reaching the saturation level, then the recorded values of the optimized LSTM parameters are saved to be used in predicting the metamaterial antenna bandwidth.
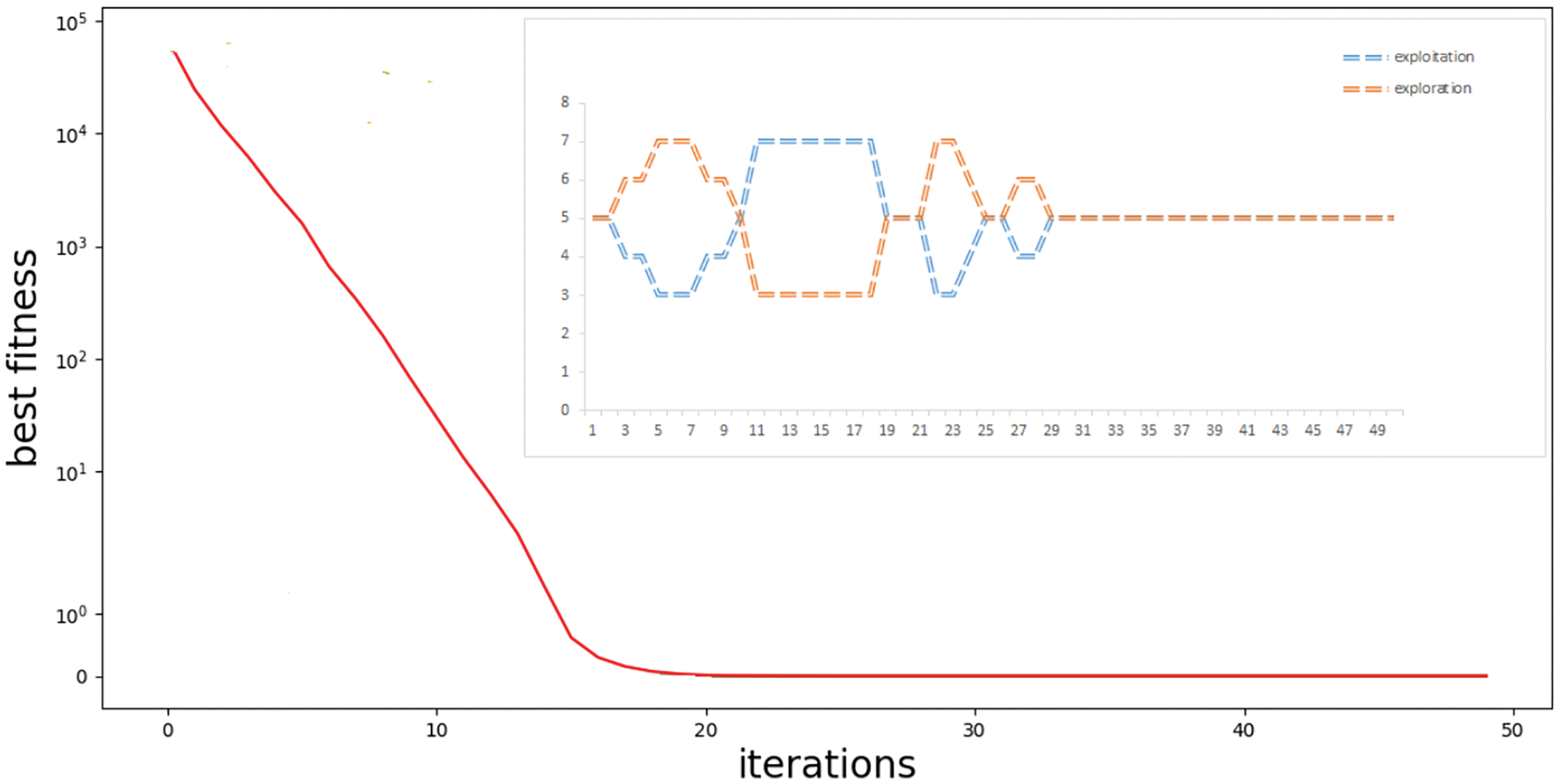
Figure 4: The updating of the groups of exploitation and exploration using AD-PSO-Guided WOA algorithm [22]
The prediction results of the metamaterial antenna bandwidth using the proposed optimized model are shown in Fig. 5. In this figure, the actual values of the bandwidth are shown in green color and the predicted values are presented in red color. As shown in the figure, the predicted values are too close to the actual values, which indicates the effectiveness of the proposed model in accurately predicting the bandwidth of metamaterial antenna.
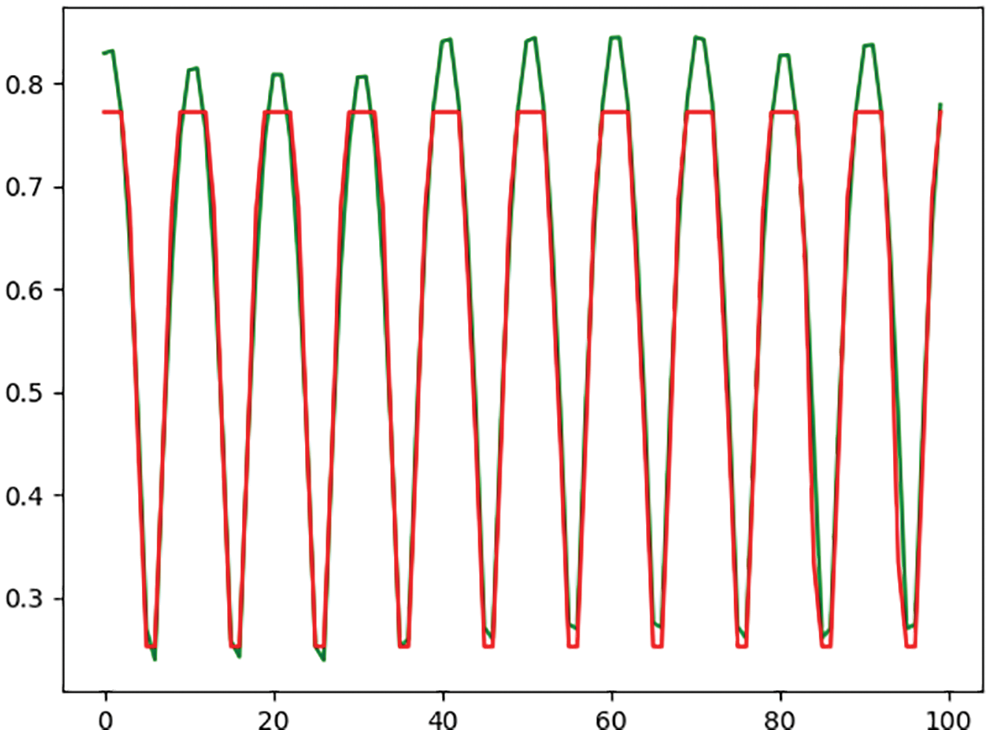
Figure 5: Green color refers to actual values, and red color refers to predicted values using the proposed model
Fig. 6 shows the heat map and quantile-quantile (QQ) plot of the prediction results. As shown in the figure, the points of the QQ plot are distributed in a way that fits the diagonal line between the predicted and the actual residuals. This fitting confirms the performance of the optimized LSTM model in predicting the bandwidth of the metamaterial antenna.

Figure 6: Heat map and QQ plot of the prediction results using the proposed model
The plots depicted in Fig. 7 show the residuals and the homoscedasticity of the prediction results using the proposed optimized LSTM model. As shown in the figure, the values of the residual error are close to zero which confirms the effectiveness of the proposed approach. In addition, a homoscedasticity plot is useful to show if the independent variables have the same error term, which is confirmed from the plot values.
Figure 7: Residual and homoscedasticity plots of the prediction results using the proposed model
Moreover, the plots of Fig. 8 show the receiver operating characteristics (ROC) of the proposed optimized LSTM. The figure shows also the RMSE values of the proposed LSTM and the other competing models. As shown in the figure, the area under the curve is high for the proposed model with the minimum value of RMSE. These values emphasize the superiority of the proposed approach.
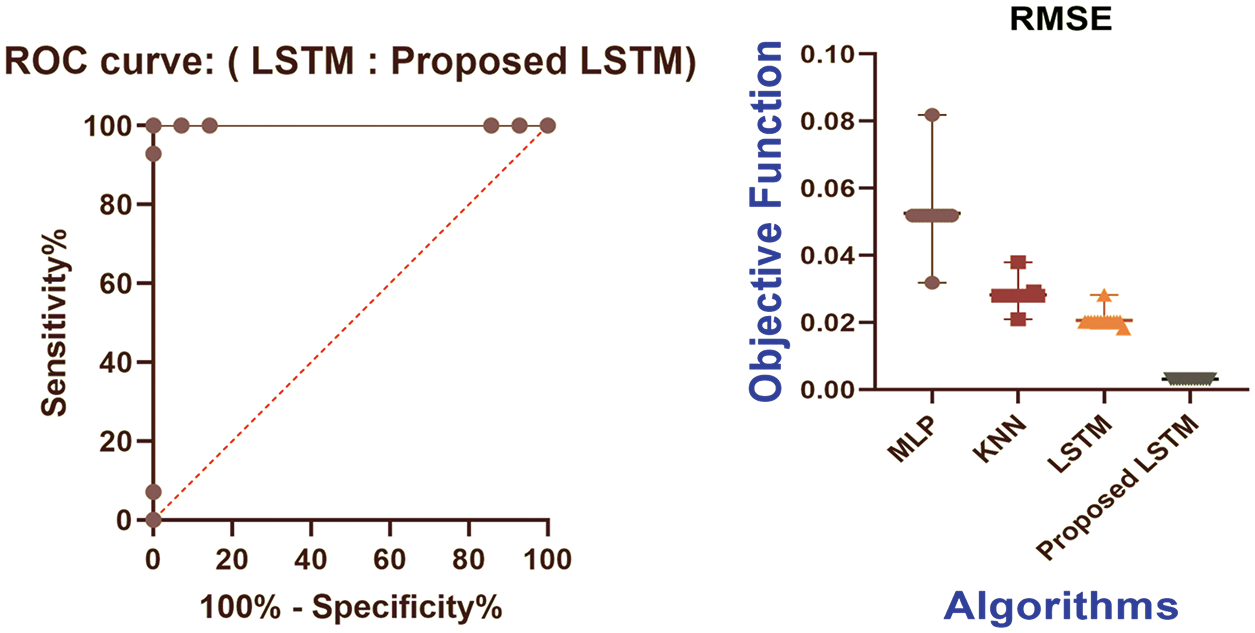
Figure 8: ROC and RMSE for the prediction results of the proposed model
Fig. 9 depicts the histogram of the RMSE values resulting from the prediction of the bandwidth using the proposed model and the other three competing approaches. In this figure, the RMSE values approximately follow a straight line with a few peaks, which reflects the stability of the proposed approach in predicting the bandwidth of the metamaterial antenna.
The evaluation criteria listed in Tab. 2 are used to measure the performance of the proposed approach along with the other competing approaches. Tab. 5 presents the evaluations of these criteria based on the metamaterial antenna test set. As shown in the table, the results achieved by the proposed model are RMSE of (0.003108), MAE of (0.001871), MBE of 0.000205), and R of (0.999888). These values outperform those of the other competing approaches (MLP, KNN, and LSTM). More evaluation criteria are presented in the table with their measured values which are also much better than the values achieved by the other models.
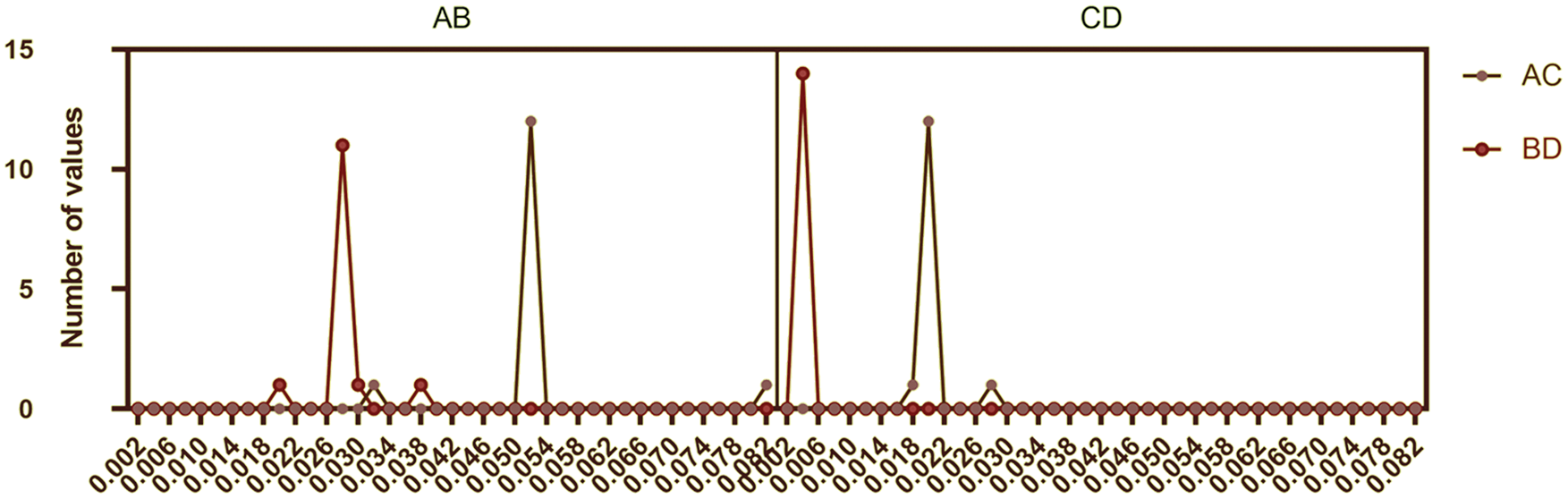
Figure 9: Histogram of the RMSE values measured from the bandwidth predictions
The ANOVA test, using the prediction results achieved by the proposed model, is presented in Tab. 6. The values presented in these tables indicate the stability of the proposed approach. In addition, Tab. 7 shows the descriptive statistics of the proposed approach over 20 runs. The calculated values of these statistics using the proposed approach is promising when compared with the corresponding values calculated from the results achieved by the other approaches, as shown in the table. These values confirm the efficiency and superiority of the proposed model in predicting the bandwidth of metamaterial antenna.
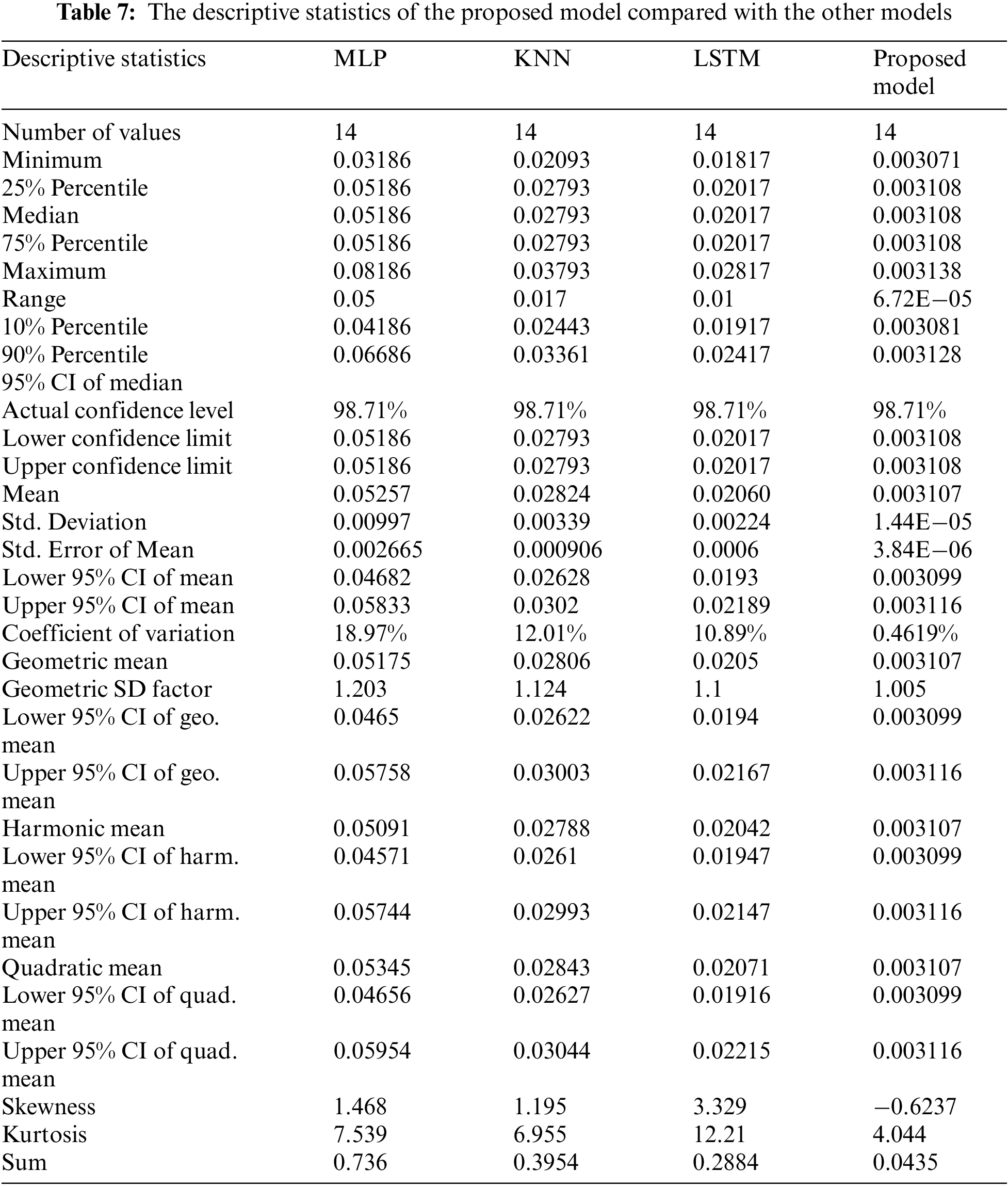
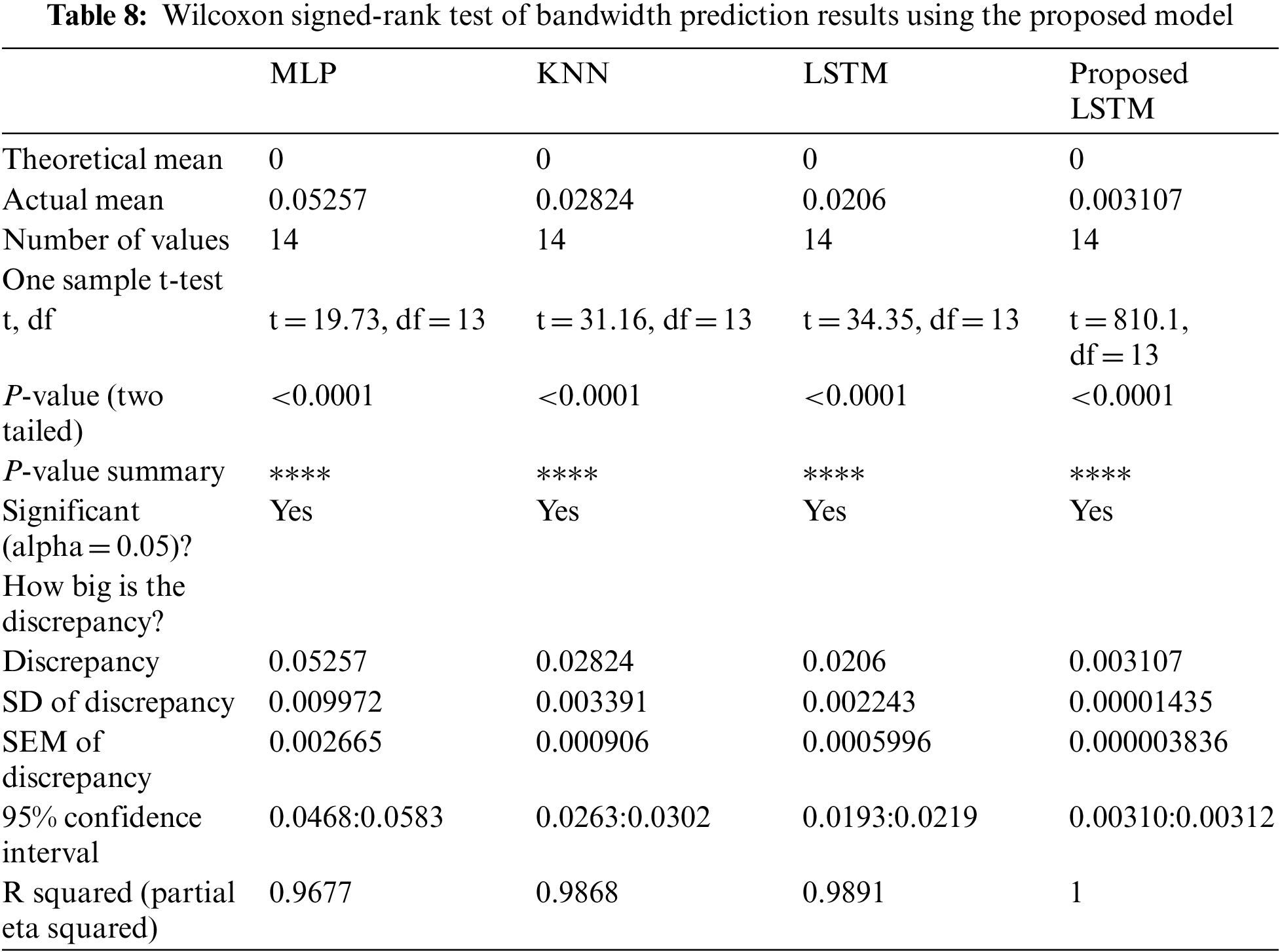
The Wilcoxon signed-rank test is performed on the metamaterial test set and the results are recorded in Tab. 8. As shown in the table, the proposed approach achieves the lowest discrepancy values over the test set when compared with the other methods. This proves the stability of the proposed approach in predicting the bandwidth of the metamaterial antenna.
Machine learning is considered the backbone of the ongoing research efforts which contributes significantly to many fields of today’s technology. The choice of a machine learning model usually affects the accuracy of the predictions of the task results. In this paper, we adopted the application of the recently emerged optimization algorithm, which is referred to as Adaptive PSO-Guided WOA, to search for the best parameters of the LSTM deep network. This network is then used to predict the bandwidth of the metamaterial antenna. The choice of metamaterial antenna in this work was due to its capability to overcome the bandwidth constraints imposed by tiny sizes of antennas. On the other hand, the interesting features and capabilities of deep learning allow it to be widely used in almost all fields of science. LSTM is one of the most significant types of deep networks which is optimized using the adaptive guided whale algorithm to fit the task of predicting the bandwidth. To emphasize the superiority of the proposed approach, other competing models were incorporated in the conducted experiments. The findings of this work indicate that the prediction accuracy using the proposed approach outperforms the standard LSTM, MLP, and KNN models.
Acknowledgement: Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2022R308), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.
Funding Statement: Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2022R308), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. A. Ibrahim, H. Abutarboush, A. Mohamed, M. Fouad and E. El-kenawy, “An optimized ensemble model for prediction the bandwidth of metamaterial antenna,” CMC-Computers, Materials & Continua, vol. 71, no. 1, pp. 199–213, 2022. [Google Scholar]
2. J. Suganthi, T. Kavitha and V. Ravindra, “Survey on metamaterial antennas,” IOP Conference Series: Materials Science and Engineering, vol. 1070, no. 1, pp. 12086, 2021. [Google Scholar]
3. L. Cui, Y. Zhang, R. Zhang and Q. Liu, “A modified efficient KNN method for antenna optimization and design,” IEEE Transactions on Antennas and Propagation, vol. 68, pp. 6858–6866, 2020. [Google Scholar]
4. P. Abbassi, N. Badra, A. Allam and A. El-Rafei, “Wifi antenna design and modeling using artificial neural networks,” in Int. Conf. on Innovative Trends in Computer Engineering (ITCE), Aswan, Egypt, pp. 270–274, 2019. [Google Scholar]
5. H. El Misilmani, T. Naous and S. Al Khatib, “A review on the design and optimization of antennas using machine learning algorithms and techniques,” International Journal of RF and Microwave Computer-Aided Engineering, vol. 30, no. 10, pp. 1–28, 2020. [Google Scholar]
6. S. Campbell, D. Sell, R. Jenkins, E. Whiting, J. Fan et al., “Review of numerical optimization techniques for meta-device design,” Optical Material Express, vol. 9, no. 4, pp. 1842, 2019. [Google Scholar]
7. E. El-kenawy, A. Ibrahim, S. Mirjalili, Y. Zhang, S. Elnazer et al., “Optimized ensemble algorithm for predicting metamaterial antenna parameters,” CMC-Computers Materials & Continua, vol. 71, no. 3, pp. 4989–5003, 2022. [Google Scholar]
8. M. Fouad, A. El-Desouky, R. Al-Hajj and E. El-Kenawy, “Dynamic group-based cooperative optimization algorithm,” IEEE Access, vol. 8, pp. 148378–148403, 2020. [Google Scholar]
9. E. El-Kenawy, A. Ibrahim, S. Mirjalili, M. Eid and S. Hussein, “Novel feature selection and voting classifier algorithms for COVID-19 classification in CT images,” IEEE Access, vol. 8, pp. 179317–179335, 2020. [Google Scholar]
10. E. El-Kenawy, M. Eid, M. Saber and A. Ibrahim, “MBGWO-SFS: Modified binary grey wolf optimizer based on stochastic fractal search for feature selection,” IEEE Access, vol. 8, pp. 107635–107649, 2020. [Google Scholar]
11. B. Singh, “Design of rectangular microstrip patch antenna based on artificial neural network algorithm,” in Int. Conf. on Signal Processing and Integrated Networks (SPIN), Noida, India, pp. 6–9, 2015. [Google Scholar]
12. S. Ulker, “Support vector regression analysis for the design of feed in a rectangular patch antenna,” in Int. Symp. on Multidisciplinary Studies and Innovative Technologies, Turkey, pp. 1–3, 2019. [Google Scholar]
13. Z. Zheng, X. Chen and K. Huang, “Application of support vector machines to the antenna design,” International Journal of RF and Microwave Computer-Aided Engineering, vol. 21, pp. 85–90, 2010. [Google Scholar]
14. N. Tokan and F. Gunes, “Support vector characterization of the microstrip antennas based on measurements,” Progress in Electromagnetics Research, vol. 5, pp. 49–61, 2008. [Google Scholar]
15. N. Turker, F. Gunes and T. Yildirim, “Artificial neural design of microstrip antennas,” Turkish Journal of Electrical Engineering and Computer Sciences, vol. 14, pp. 445–453, 2006. [Google Scholar]
16. L. Xiao, W. Shao, F. Jin and B. Wang, “Multiparameter modeling with ANN for antenna design,” IEEE Transactions on Antennas and Propagation, vol. 66, pp. 3718–3723, 2018. [Google Scholar]
17. E. S. M. El-Kenawy, S. Mirjalili, S. S. M. Ghoneim, M. M. Eid, M. El-Said et al., “Advanced ensemble model for solar radiation forecasting using sine cosine algorithm and newton’s laws,” IEEE Access, vol. 9, pp. 115750–115765, 2021. [Google Scholar]
18. A. Ibrahim, A. Tharwat, T. Gaber and A. E. Hassanien, “Optimized superpixel and AdaBoost classifier for human thermal face recognition,” Signal, Image and Video Processing, vol. 12, no. 4, pp. 711–719, 2018. [Google Scholar]
19. A. A. Salamai, E. -S. M. El-kenawy and A. Ibrahim, “Dynamic voting classifier for risk identification in supply chain 4.0,” CMC-Computers, Materials & Continua, vol. 69, no. 3, pp. 3749–3766, 2021. [Google Scholar]
20. M. M. Eid, E. -S. M. El-kenawy and A. Ibrahim, “A binary sine cosine-modified whale optimization algorithm for feature selection,” in National Computing Colleges Conference (NCCC), Taif, Saudi Arabia, pp. 1–6, 2021. [Google Scholar]
21. R. Machado, Metamaterial Antennas, 2019 [Online]. Available: https://www.kaggle.com/renanmav/metamaterial-antennas, accessed: 2022–02–10. [Google Scholar]
22. A. Ibrahim, S. Mirjalili, M. El-Said, S. S. M. Ghoneim, M. Alharthi et al., “Wind speed ensemble forecasting based on deep learning using adaptive dynamic optimization algorithm,” IEEE Access, vol. 9, pp. 1–18, 2021. [Google Scholar]
23. E. -S. M. El-Kenawy, S. Mirjalili, A. Ibrahim, M. Alrahmawy, M. El-Said et al., “Advanced meta-heuristics, convolutional neural networks, and feature selectors for efficient COVID-19 X-ray chest image classification,” IEEE Access, vol. 9, pp. 36019–36037, 2021. [Google Scholar]
24. E. S. M. El-kenawy, H. F. Abutarboush, A. W. Mohamed and A. Ibrahim, “Advance artificial intelligence technique for designing double T-shaped monopole antenna,” CMC-Computers, Materials & Continua, vol. 69, no. 3, pp. 2983–2995, 2021. [Google Scholar]
25. E. -S. M. El-kenawy and M. Eid, “Hybrid gray wolf and particle swarm optimization for feature selection,” International Journal of Innovative Computing, Information and Control, vol. 16, no. 3, pp. 831–844, 2020. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |