DOI:10.32604/cmc.2022.028292

| Computers, Materials & Continua DOI:10.32604/cmc.2022.028292 |  |
| Article |
Energy Price Forecasting Through Novel Fuzzy Type-1 Membership Functions
1Centre of Research in Data Science, Computer, and Information Sciences Department, Universiti Teknologi PETRONAS, Seri Iskandar, 32610, Perak, Malaysia
2Petroleum Engineering Department, Universiti Teknologi PETRONAS, Seri Iskandar, 32610, Perak, Malaysia
3Institute of Computing, Kohat University of Science and Technology, Kohat, 26000, K.P.K, Pakistan
*Corresponding Author: Mohd Hilmi Hasan. Email: mhilmi_hasan@utp.edu.my
Received: 07 February 2022; Accepted: 10 March 2022
Abstract: Electricity price forecasting is a subset of energy and power forecasting that focuses on projecting commercial electricity market present and future prices. Electricity price forecasting have been a critical input to energy corporations’ strategic decision-making systems over the last 15 years. Many strategies have been utilized for price forecasting in the past, however Artificial Intelligence Techniques (Fuzzy Logic and ANN) have proven to be more efficient than traditional techniques (Regression and Time Series). Fuzzy logic is an approach that uses membership functions (MF) and fuzzy inference model to forecast future electricity prices. Fuzzy c-means (FCM) is one of the popular clustering approach for generating fuzzy membership functions. However, the fuzzy c-means algorithm is limited to producing only one type of MFs, Gaussian MF. The generation of various fuzzy membership functions is critical since it allows for more efficient and optimal problem solutions. As a result, for the best and most improved results for electricity price forecasting, an approach to generate multiple type-1 fuzzy MFs using FCM algorithm is required. Therefore, the objective of this paper is to propose an approach for generating type-1 fuzzy triangular and trapezoidal MFs using FCM algorithm to overcome the limitations of the FCM algorithm. The approach is used to compute and improve forecasting accuracy for electricity prices, where Australian Energy Market Operator (AEMO) data is used. The results show that the proposed approach of using FCM to generate type-1 fuzzy MFs is effective and can be adopted.
Keywords: Fuzzy logic; fuzzy C-means; type-1 fuzzy membership function; electricity price forecasting
Electricity is a unique and special commodity which is economically non storable, therefore, it is very essential for power system stability to keep a balance between the demand and supply of the electricity [1]. The electricity price depends on multiple parameters such as the weather, demand, and the rate of business and daily activities. Since, the world is moving towards digitalization, so the demand of electric power is also increasing simultaneously. In order to decide the price of electricity different stakeholders such as the consumers and the electricity producing companies need to meet in the market place [2]. Electricity price forecasts have become one of the most important input for the corporate markets, which helps energy companies to make decisions more efficiently [3].
Over the years, major utilities have dominated the electric power business, with control over all activities in power generation, transmission, and distribution within their zone of operation [4]. During the crises of California between 2000 to 2001, it was seen that electric utilities got most affected, as they cannot pass their cost onto the consumer [5]. Both producers and consumers need price estimates to establish their respective market bidding strategies in today’s competitive energy marketplaces, so forecasting electricity prices is essential. Moreover, it helps the electricity providing companies to plan more efficiently as they have the prior information of the consumption and demand, which minimize their risk as with this information their decisions can be more economically more viable.
Fuzzy Logic is a sub branch of soft computing, which focuses of approximation of the values. Many duties, such as caring for backpacks, consuming meals, and travelling from one location to another, appear to be quite basic and straightforward while you’re a person. The same tasks can be extremely difficult for robots or computers. The ability of humans to manage ambiguous and unclear data made such tasks fairly straightforward, but computers lacked this skill. To get machines to behave like humans, we need to give them the ability to handle the ambiguous and uncertain data. That is exactly what fuzzy logic achieves [6]. Fuzzy logic systems construct a model in such a way that it can manage uncertain data, making unduly complex tasks simple for computers [7].
Because of uncertainties in the power system, such as machine wear and tear, various dips in the transmission line, voltage and frequency instability, fluctuations, and weather changes, dealing with power system problems by mathematical formulation is extremely challenging. Fuzzy logic is a type of multivalve logic that evaluates data using Boolean logic (yes or no, true or false). The importance of fuzzy logic in such complex problems is that it doesn’t require the mathematical model mapping of inputs to the outputs and also it doesn’t require discrete input as due to its ability to handle linguistic variables [8]. Hence, fuzzy logic can be very essential in forecasting electricity prices.
Membership functions perform key role in fuzzy logic as it represents how the data values between 0 and 1 are mapped to their membership degrees in the input space [9]. With the popularity of fuzzy logics, the methods to generate membership function also became very essential as it converts the conventional crisp data into fuzzy input, few methods of generating membership functions are presented in [10] and [11]. Because of the fact that membership functions are such an important part of fuzzy logic, it’s important to choose the right one for the system you’re designing. Gaussian, triangular, and trapezoidal membership functions are the most commonly utilized fuzzy membership functions.
There are two popular ways to generate fuzzy membership functions, expert knowledge approach, in which an expert provides the parameters for the development of fuzzy MFs, and data-centric approach, in which MFs are automatically formed based on data [12]. Expert knowledge approach to MF generation has drawbacks such as lack of precision [13], time consuming [14], and expert availability at all times [15]. On the other hand, data-centric approaches reduce, if not remove, the disadvantages of expert knowledge approaches. As a result, the majority of research is focused on the autonomous generation of MFs using a data-centric approach, which involves learning from historical data. [16] conducts a quick assessment of all past techniques to generating fuzzy MFs. The MF generation issue has been briefly described through FCM in the study by [17] and their longer work presented in [18]. They used a heuristic approach to approximate MF, although the shape of triangular and trapezoidal MFs is not always exact when using this method. Furthermore, this restriction has a progressive impact on the precision, efficiency as well as the accuracy of the results. As a result, a method for generating the proper linear type-1 triangular and type-1 trapezoidal membership functions is still needed. As a result, we suggest adopting FCM to build type-1 fuzzy triangular and type-1 fuzzy trapezoidal MFs in this study. The objective of this research paper is to discuss how to generate type-1 fuzzy triangular and type-1 fuzzy trapezoidal MFs through FCM algorithm and to provide the fair comparison to verify the accuracy and effectiveness of the proposed method.
Prior research has been focused on either producing Gaussian MF with FCM or incorporating Gaussian MF created by FCM into solutions. There is further work to be done to enhance the FCM-based MF generating approach such that triangular and trapezoidal MFs can be generated. The method allows flexibility in selecting the type of MF, thus improving FIS efficacy by taking advantage of the strengths that each of the three MF types can provide. Hence the two major motivation behind this work are (a) as it can be seen from the literature that FCM algorithm more effective in MF generation so an approach is needed to generate MF using FCM and (b) FCM cannot produce triangular and trapezoidal MFs which are simplest and effective MF types, therefore, this approach focuses to generate type-1 fuzzy triangular and trapezoidal MFs through FCM algorithm.
Fuzzy Logic has a lot of applications in the field of decision making. The work presented in [19] and [20] used fuzzy logic approach as a decision making approach in the Assessment of Value of Information (VOI) for oil and gas industry. Moreover, [21] utilizes fuzzy logic approach to predict current control for the speed control of Non-Silent Permanent Magnet Synchronous Motors. The work presented in [22] uses fuzzy logic approach for improving the accuracy of classification problems, while [23] discusses the fuzzy based control model for the networked control systems. Fuzzy Logic also find its application in protection of data and privacy [24,25].
The remainder of the paper is organized as follows: In Section 2, the background of the fuzzy set and logic system and classification is given, and then in Section 3, the proposed method and methodology are discussed. Sections 4 and 5 show the results of the tests and simulations, as well as the research’s future path and conclusion.
2.1 Type-1 Fuzzy Set and Fuzzy Logic System
In a type-1 fuzzy logic system, crisp inputs are mapped to outputs using the type-1 fuzzy logic systems (T1FLSs) theory. The crisp values of inputs are turned into fuzzy values throughout the fuzzification process using the fuzzy rules in the fuzzy rule base. In the inference engine, fuzzy decisions are taken, and then in final stage during the process of defuzzification an output is defuzzified into a crisp value. The fuzzifier, fuzzy rule base, fuzzy inference engine, and defuzzifier are the four key functions in a T1FLS. Fig. 1 shows the T1FLS block diagram.
Fuzzification is the first phase in a fuzzy system, and it involves converting a crisp input to a fuzzy input [26] and assigning a membership degree to it. For example, a crisp input x = (x1; x2; : ; x(n)) in the universe of discourse X, is passed by the fuzzifier which assigns it the degree of MF μAi(xi) to every input between interval 0 and 1 and converts it into a T1FS, A. The effectiveness of the membership function formed during the fuzzification process determines how well a fuzzy logic system works.
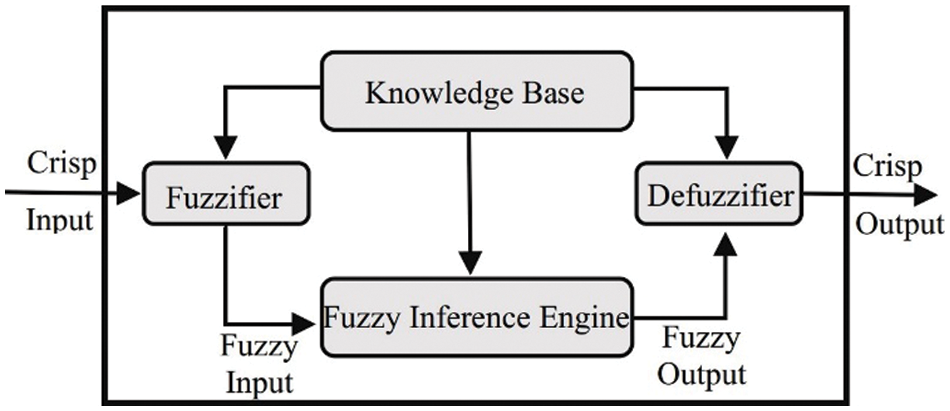
Figure 1: Type-1 fuzzy logic system
It compares fuzzy input degrees using fuzzy rules and makes decisions on how to apply rules to the input field. As it provides the system’s decision-making logics, the inference engine acts as a brain for the fuzzy system, emulating human thinking and decision-making.
2.1.3 Fuzzy Knowledgebase (Rule-Base)
It comprises of IF-THEN statements and fuzzy rules for making decisions based on linguistic data. Fuzzy rules can either be obtained by experts’ knowledge or data driven approach [27,28].
IF-THEN conditional statements are used to create fuzzy rules. In order to conclude the THEN part (known as consequents), the IF part (also known as antecedents) must be fulfilled. The following are some linguistic examples of fuzzy rules:
• If temperature is high, then weather is hot.
• If height is small, then person is short.
• If mood is good, then person is happy.
In this stage of a fuzzy system, a fuzzy set generated by the inference engine is turned to crisp output [6]. It is known as defuzzification as it is the opposite of the fuzzification process.
In fuzzy logic a membership function (MF) is a curve that maps all values in the input space from 0 and 1 to their membership degrees. In other terms, a set’s MF can be defined as a link between both the set’s various components and their degree of belonging [12]. Fig. 2 depicts three common and frequently used fuzzy MFs which are gaussian MF. Triangular MF, and trapezoidal MF, respectively. The three parameters of the triangular MF are a, c, and b, which indicate the floor and peak values, respectively. Trapezoidal MF is created using four parameters: a, b, c, and d, where a < b < c < and d, respectively. Finally, a gaussian MF is created using the center c and width w values.
The study done by [29] describes how clustering analysis was used to generate MF. The triangular MF is created using an improved density-based clustering technique. Their approach, however, did not use the FCM technique to generate MFs. In [10] a circuit for generating MF was demonstrated. The MF generator was actually based on a circuit that did not rely on data. Furthermore, it was restricted to generate only gaussian MF and did not use FCM. For ordinal binary classification, [30] introduced evolutionary fuzzy rules. To construct fuzzy rules, the rough set approach was implemented, and the K-means clustering algorithm was being used; but, the work did not focus to generate fuzzy triangular and fuzzy trapezoidal MFs using FCM. The stability analysis of polynomial fuzzy model-based control systems was investigated in where two sets of MFs were constructed both for the polynomial fuzzy model as well as the controller. For non-linear FIS that were not generated using data clustering, general formed MFs were proposed. The study done in [17] and their further work published in [31] had established a new foundation of FCM generation. Nevertheless, the approach has not always been successful in generating the correct and desired shape of MFs [16]. This constraint may have an impact on the precision and accuracy of the results. As a result, regardless of the sort of dataset on which it is based, there is still a requirement for an approach and technique that can generate correct type-1 fuzzy triangular and trapezoidal MFs shapes.
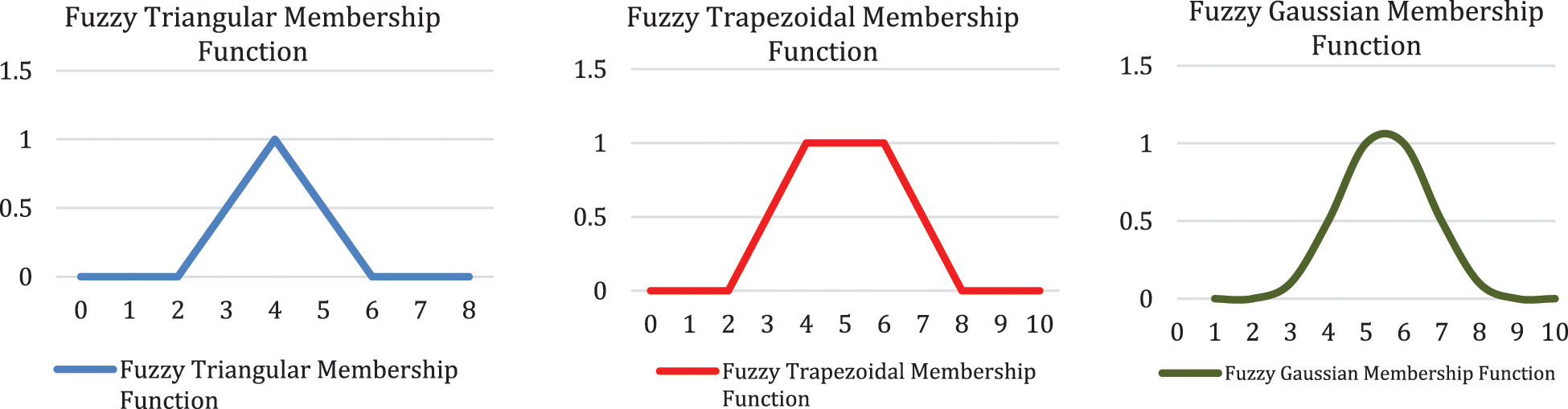
Figure 2: Fuzzy membership functions
The proposed approach for generating type-1 fuzzy triangular as well as type-1 fuzzy trapezoidal MFs is presented in Fig. 3. First of all, a data set is passed through FCM algorithm to calculate fuzzy cluster centers and membership matrix. Proposed fuzzy triangular and fuzzy trapezoidal MFs are then approximated based on the values of cluster center and membership matrix. The detail explanation for the approximation of proposed triangular as well as trapezoidal MFs is presented in Algorithm 1 and Algorithm 2, respectively. Finally, the proposed type-1 fuzzy MFs are tested for electricity forecasting data against comparative approaches for generating fuzzy MFs which are gaussian MF generated through FCM and gaussian as well as triangular MF generated using grid partitioning (GP) algorithm to check the effectiveness and accuracy of the approach.
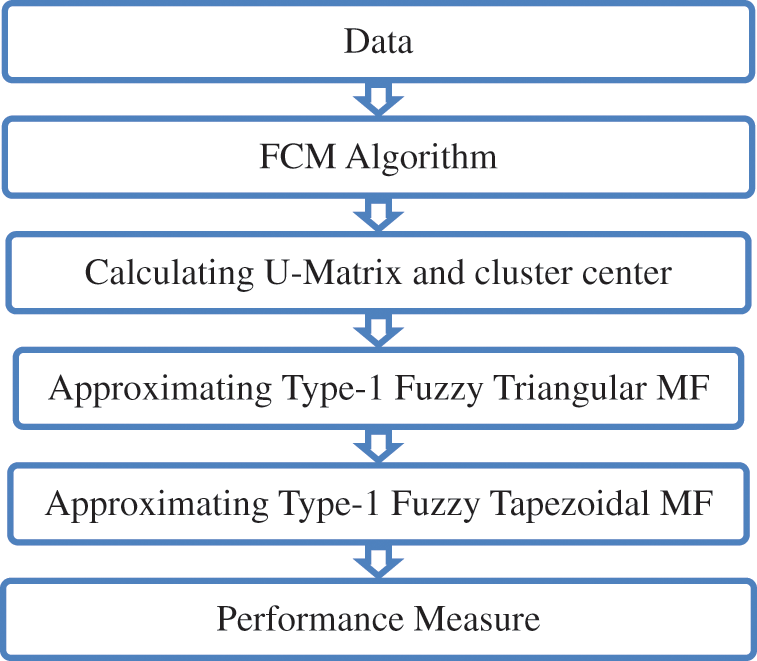
Figure 3: Proposed methodology
Australian Energy Market Operator (AEMO) data for the state of Queensland, Australia [32], is chosen for forecasting the electricity price. The electricity data set contains 3 attributes named as demand, temperature, and price. The data in divided into two parts, the data values recorded between 01-01-2002 and 20-01-2002, comprise of 960 values, are used as training data set while data values recorded between 21-01-2002 and 31-01-2002, comprised of 510 data values, are used as testing data. The model is trained based on the training data, which is then tested against testing data in order to check the accuracy of electricity price forecast. Testing is divided into three phases, in the first phase the data is prepared, and its outliners are removed, while in second phase the data is used to generate triangular and trapezoidal MFs using proposed approach along with gaussian MF generated using FCM and gaussian as well as triangular MFs generated through GP algorithm, after which their FIS is formulated. Finally, in the last phase, the FIS is evaluated against testing data to check the accuracy of future price forecast. The measures of evaluation used are mean absolute square error (MAPE), root mean square error (RMSE), and percentage accuracy. Electricity price is forecasted based on historical demand and temperature data using proposed approach. AEMO Electricity data is presented in Fig. 4.
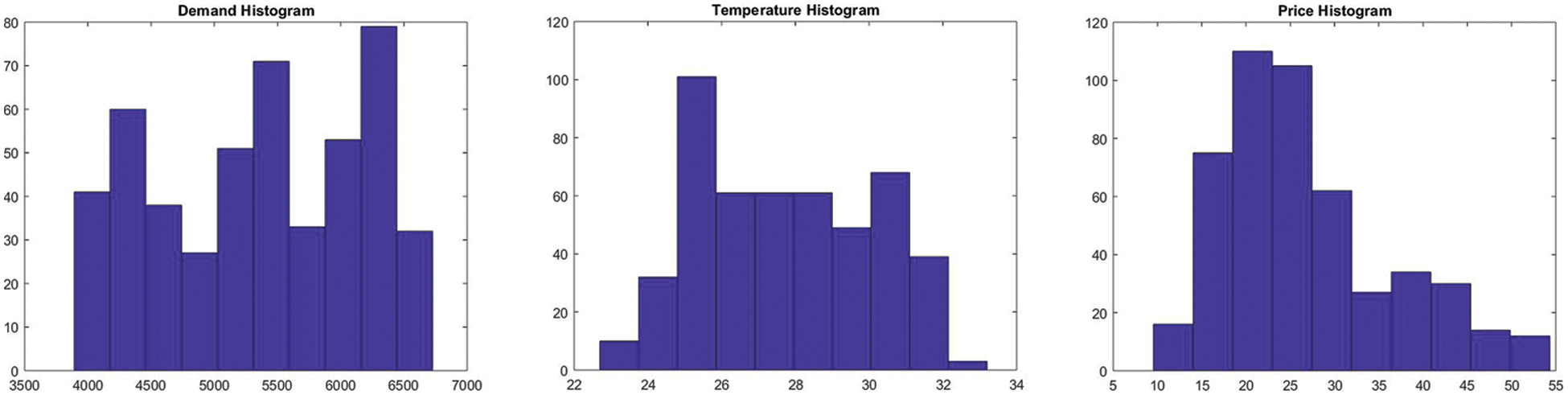
Figure 4: AEMO electricity data representation
The dataset is divided into training and testing data and their outliners are removed. The training and testing dataset with and without outliners being removed is presented in the Fig. 5.
3.2 Fuzzy C-Means (FCM) Algorithm
The Fuzzy C-Means is one of the popular and essential clustering technique based on fuzzy logics. It is an unsupervised clustering algorithm that permits us to build fuzzy partition from data. It was developed by Dunn in 1973 and enhanced by Bezdek in 1981. However, limitation and disadvantage of FCM algorithm is that it performs poorly on datasets which contains clusters of unequal sizes or densities, and it is sensitive to noise and outliners. To overcome this limitation, the dataset is prepared carefully and the outliners are removed. FCM algorithm divides data into clusters and calculates the U-matrix and cluster centers, that would be utilized to approximate proposed type-1 fuzzy triangular as well as type-1 fuzzy trapezoidal MFs. The flow of FCM Algorithm is presented in Fig. 10. The following steps can be used to implement the FCM algorithm:
i. Determine the cluster centers (c) i.e., (2 ≤ c ≤ n) and choose a value for parameter n.
ii. Instantiate a membership matrix (partition matrix) Uij.
iii. For each step, calculate cluster centers (fuzzy centers).
iv. Update the membership matrix (partition matrix)
Here, m is a parameter for facinis (fuzziness).
v. Examine the convergence
vi. If || U(k−1)–U(k) || ≤ E2 is true than stop otherwise go back to step 3.
In this case, E2 represents the threshold, while djk represents the Euclidean distance between jth data and kth cluster center.
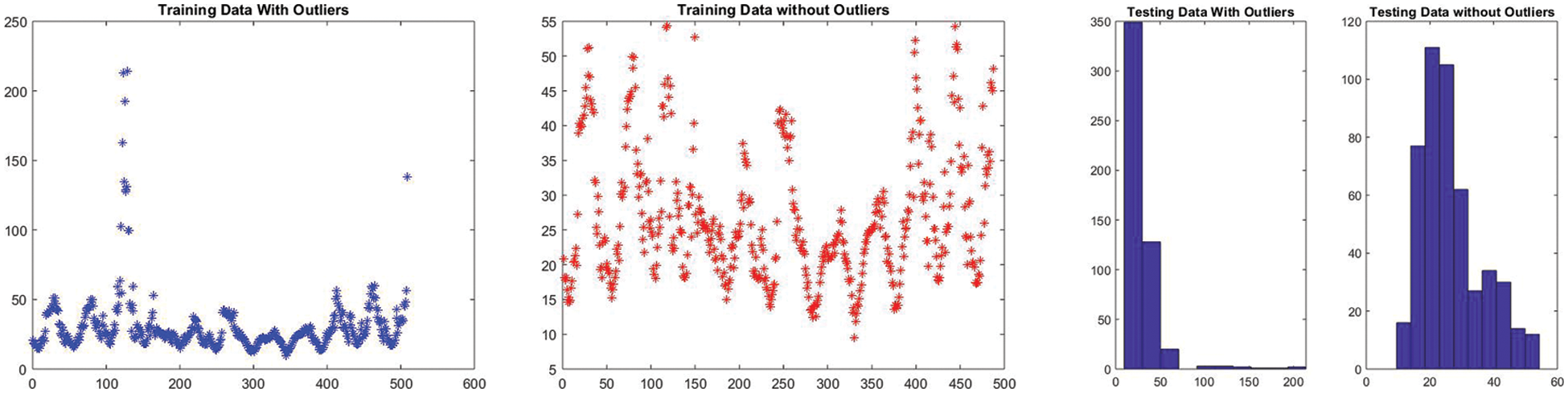
Figure 5: Training and testing dataset with and without outliners
Fig. 6 shows the flow of the FCM Algorithm.
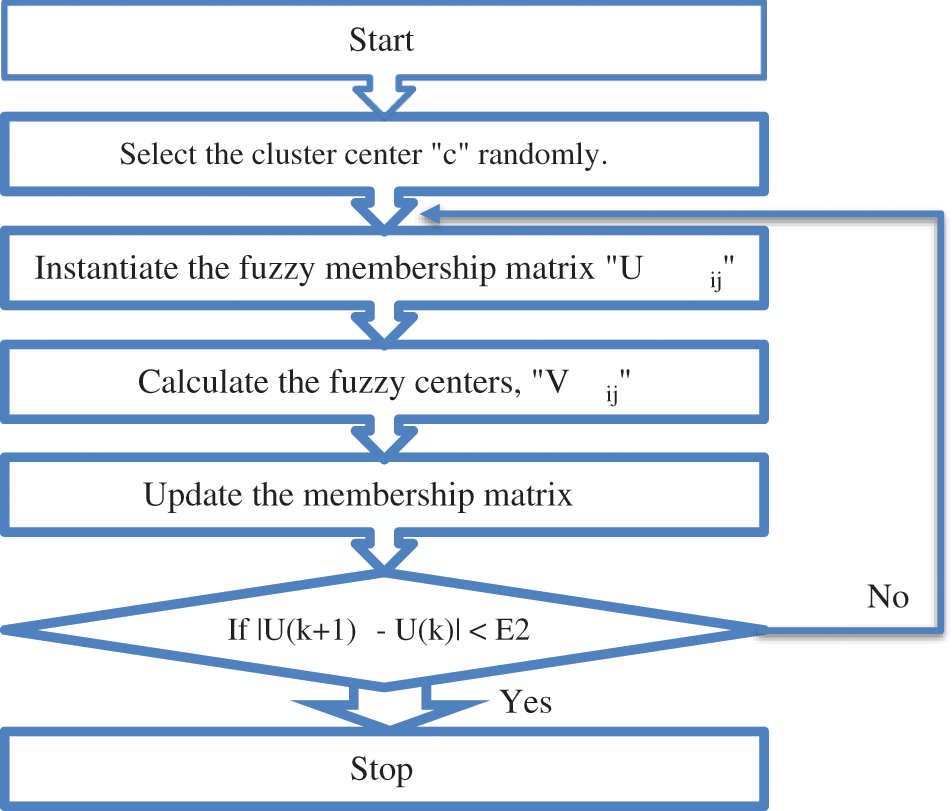
Figure 6: Fuzzy c-means working flowchart
3.3 Approximating Fuzzy Type-1 Triangular MF
FCM is used to process data, resulting in a cluster center and fuzzy membership matrix also known as U-Matrix. As demonstrated in step 5 of Algorithm 1, both the U-matrix and cluster center are combined, mathematical calculations are done, and parameter values needed for generating triangular MF are computed. The triangular MF is generated using these parameter values and the formulated mathematical expressions. The algorithm 1 explains the process in detail.

The parametric values to approximate triangular MF are calculated using a formula set, and the cluster centers and U-Matrix are also calculated, respectively. The formulas used in this method are as follows:
a=α–β*γ;
b=α;
c=α+β*γ;
The values a and c represent the floor value while b is the peak values of triangular MF, respectively. The values α and γ are acquired from the cluster centers and U-matrix, respectively. While β is a constant, whose value is derived based on the outcomes of experiments and simulations.
The values a, b, c, and d are used for generating triangular MF. The proposed triangular MF representation is shown in Fig. 7.
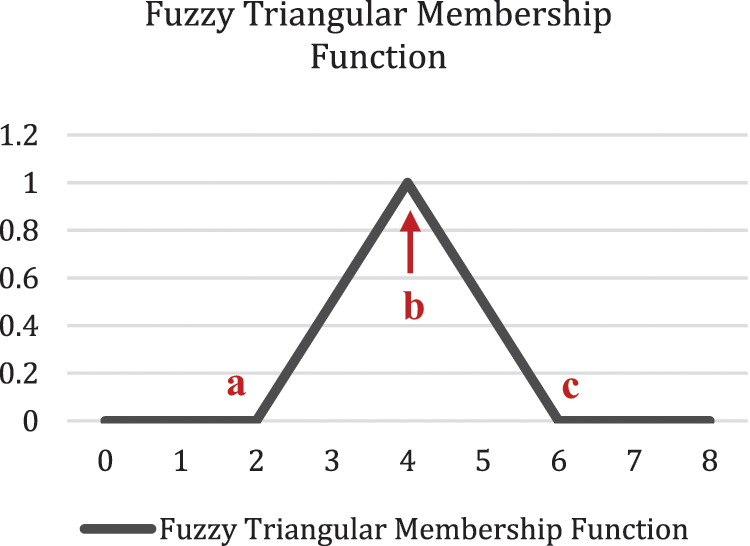
Figure 7: Type-1 fuzzy triangular MF approximation
3.4 Approximating Fuzzy Type-1 Trapezoidal MF
The data is processed using FCM to obtain cluster center as well as membership matrix (U-Matrix), much like the triangular MF approximation. The cluster centers and membership matrix (U-Matrix) are transformed into fuzzy trapezoidal sets, after the mathematical formulation. Resulting the parametric values for the construction of fuzzy trapezoidal MF as an outcome, which is a < b < c < d, respectively. The Algorithm 2 explains the procedure.

The parametric values to approximate trapezoidal MF are calculated using a formula set, and the U-Matrix and cluster centers are also calculated, respectively. The formulas used in this method are as follows:
The values a and d represent the floor value while b and c are peak values of trapezoidal MF, respectively. The values of α as well as γ are acquired from the cluster centers and U-matrix, respectively. While β and
The values a, b, c, and d are used for generating type-1 fuzzy trapezoidal MF. The trapezoidal MF representation is shown in Fig. 8.
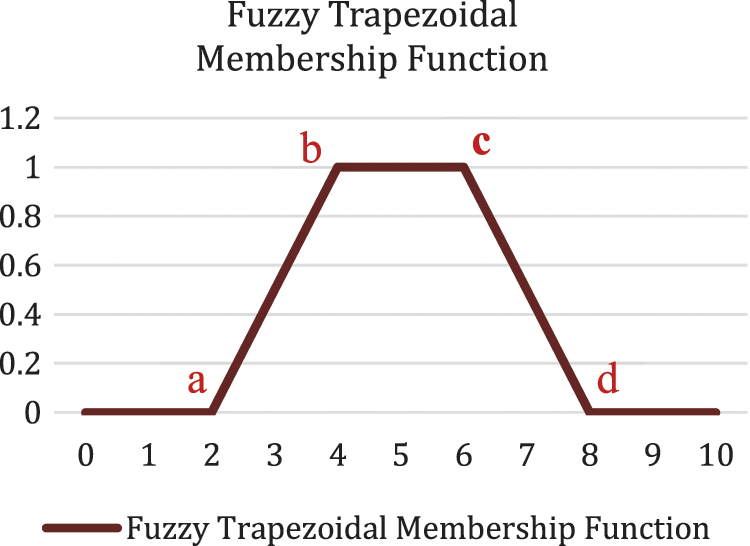
Figure 8: Type-1 fuzzy trapezoidal MF approximation
3.5 Application of Proposed Approach
Electricity training data is used to generate proposed triangular as well trapezoidal MF along with gaussian MF generated through FCM and gaussian and triangular MFs generated using GP algorithm. FCM-based triangular, trapezoidal, and trapezoidal MFs are shown in Fig. 9. The proposed approach is applied and developed in MATLAB 2019a. MATLAB fuzzy logic toolbox is used to design the FIS model of the proposed approach.
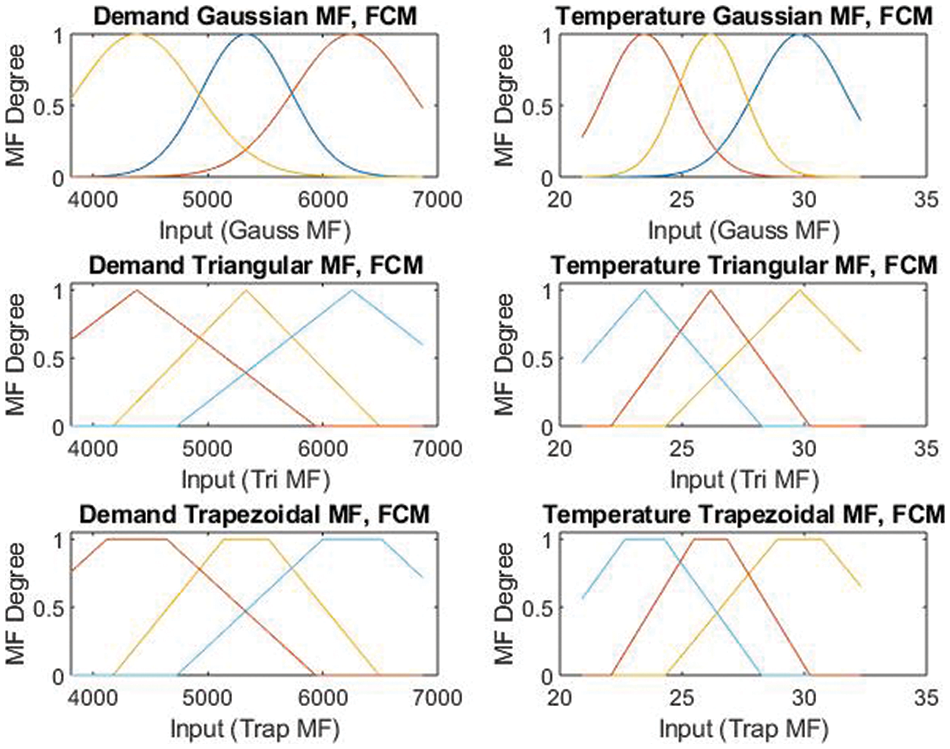
Figure 9: FCM-based MFs for electricity forecasting
Gaussian and triangular MFs generated through GP algorithm using the data are presented in Fig. 10.
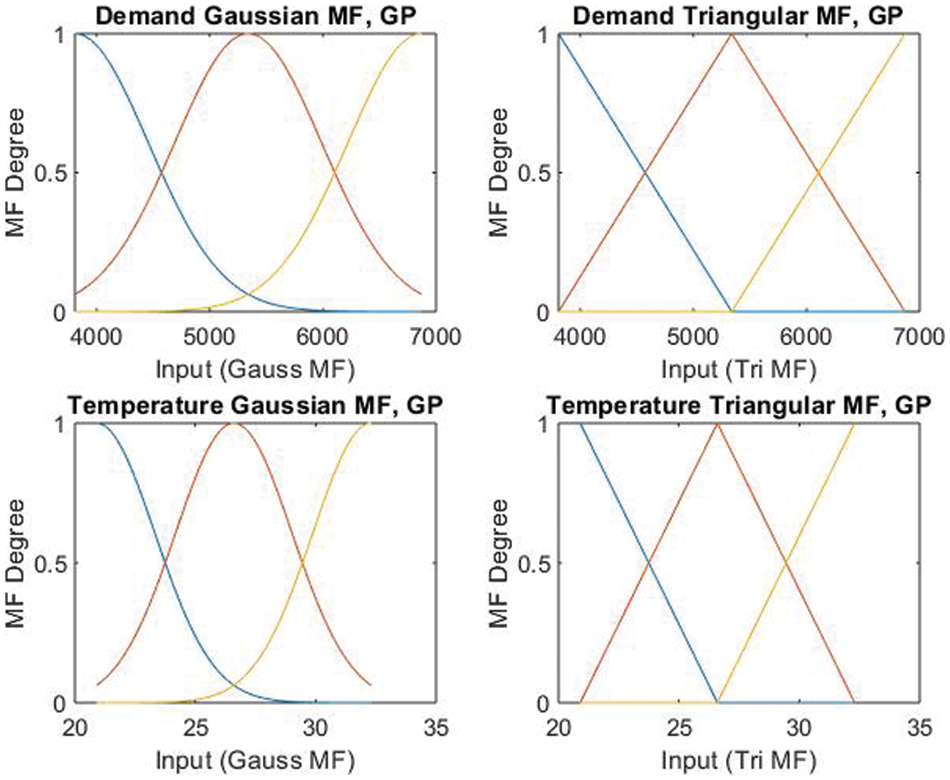
Figure 10: GP-based MFs for electricity forecasting
Once MFs are generated, they are formulated into FIS. The FIS for proposed triangular MF is presented in Fig. 11 respectively.
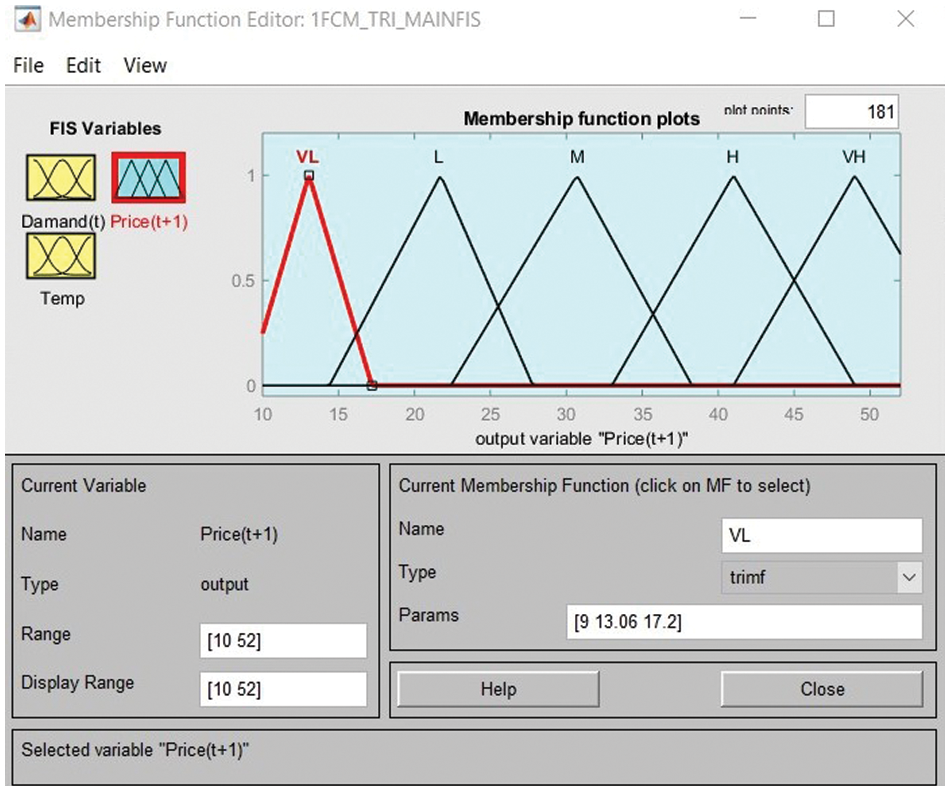
Figure 11: FIS for FCM triangular MF for electricity forecasting
It can be seen from Fig. 11, that the FIS consist of two input MF variables named as demand and temperature and 1 output forecasting MF variable price, which is divided in 5 clusters of the price value, which can be very low ‘VL’, low ‘L’, medium ‘M’, high ‘H’, and very high ‘VH’.
To validate the results of forecast the Mean Absolute Percentage Error (MAPE) as well as Root Mean Square Error (RMSE) and the percentage accuracy for proposed type-1 fuzzy triangular as well as type-1 fuzzy trapezoidal MFs are calculated. The results are also calculated for the comparative approaches of gaussian MF generated using FCM as well as gaussian and triangular MFs generated using grid partitioning (GP) approach are calculated. The outcome proposed type-1 fuzzy triangular as well as type-1 fuzzy trapezoidal MFs are compared against gaussian MF generated through FCM as well as gaussian and triangular MFs generated through GP approach for competitive analysis.
Percentage accuracy is a measure of performance used to validate the forecast. The percentage accuracy is calculated based on the actual and forecasted values which validates either price forecasting using a proposed method is effective or not. The forecasted value is subtracted from the actual value which is then divided by actual value and multiplied by 100 to calculate the percentage accuracy. The formula to calculate the percentage accuracy is presented in Eq. (2).
3.6.2 Mean Absolute Percentage Error (MAPE)
Mean Absolute Percentage Error (MAPE) is a widely used error measure to validate the forecasting results [33]. The formula for calculating MAPE is presented in Eq. (3).
Here M represents MAPE, n shows the number of times the summation iteration happens while At and Ft represents the actual and forecasted prices.
3.6.3 Root Mean Square Error (RMSE)
Root Mean Square Error (RMSE) is also one of very popular error measure used to validate the forecasting results [34]. RMSE can be calculated based on the formula presented in Eq. (4).
Here, N represents number of summation iteration, Ft represent the forecasted price while At represents the actual price value.
In order to validate the outcome of the approach, the electricity forecasting datasets are used for the proposed algorithms, their percentage accuracy as well as MAPE and RMSE are calculated. Electricity price forecasting is done based on 2 input parameters that are demand and temperature. The Electricity price forecasting results for proposed type-1 fuzzy triangular and trapezoidal and well as gaussian MF generated through FCM and gaussian as well as triangular MFs generated using GP algorithms are presented in this section.
After FIS is developed, it is then used to forecast the prices of electricity. The price forecasting results of proposed type-1 fuzzy triangular MF is presented in Fig. 12.
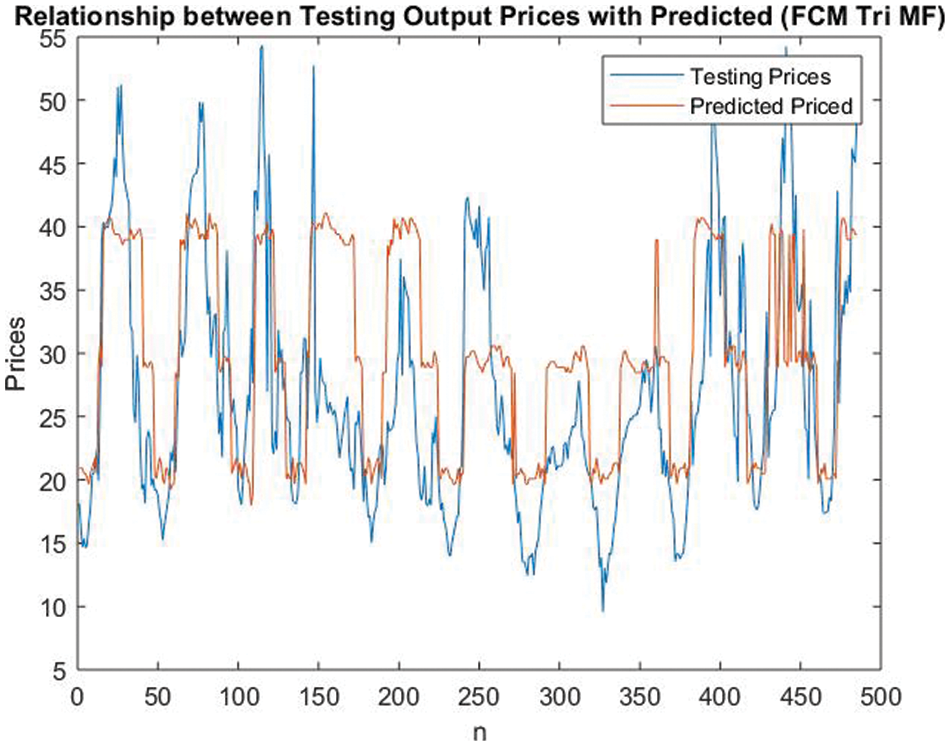
Figure 12: Electricity price forecasting for type-1 fuzzy triangular MF
Similarly, the price is forecasted for proposed type-1 fuzzy trapezoidal MF and is presented in Fig. 13.
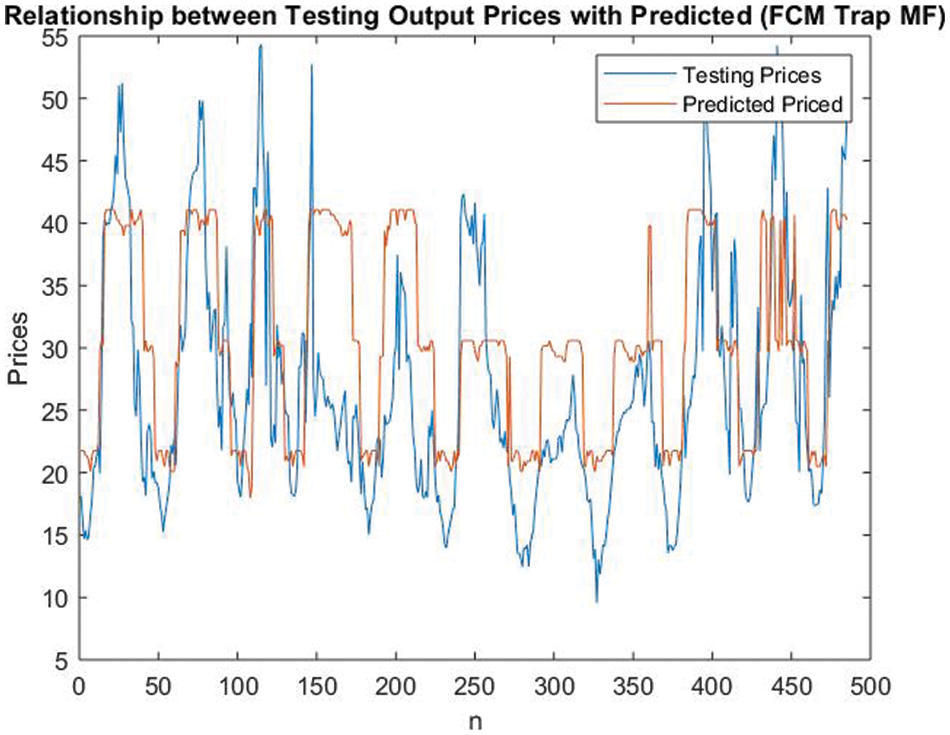
Figure 13: Electricity price forecasting for type-1 fuzzy trapezoidal MF
Electricity price is forecasted for the FCM-based gaussian MF in similar manner, which is used as competitive MF generation approach, the result of the forecast is presented in Fig. 14.
The results for electricity price forecasting are calculated for GP-based triangular MF and are presented in Fig. 15.
The results for electricity price forecasting are calculated for GP-based triangular MF and are presented in Fig. 16.
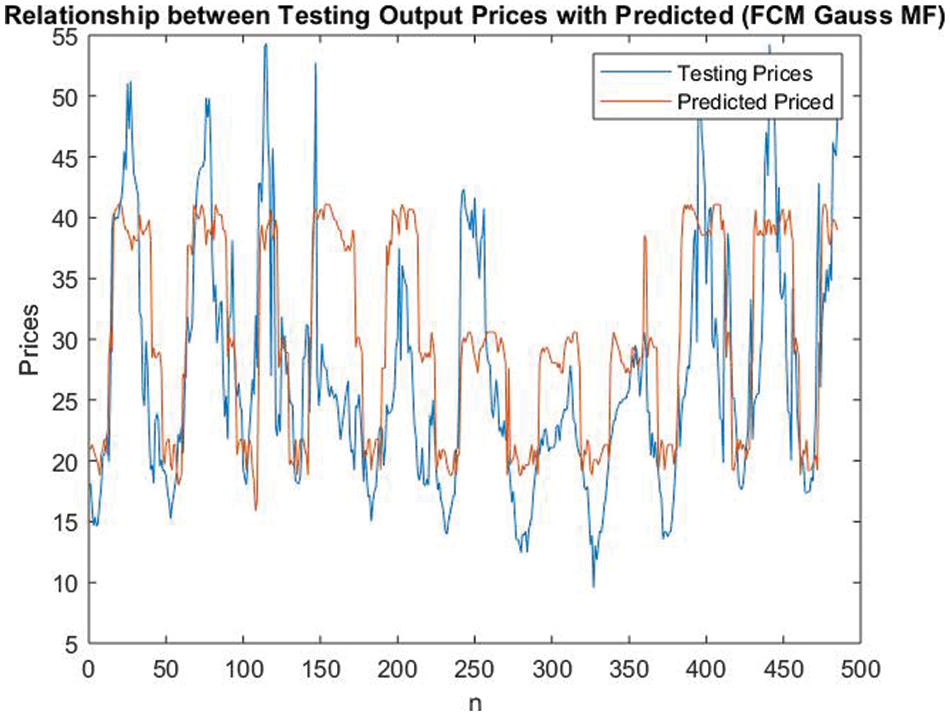
Figure 14: Electricity price forecasting for FCM-based gaussian MF
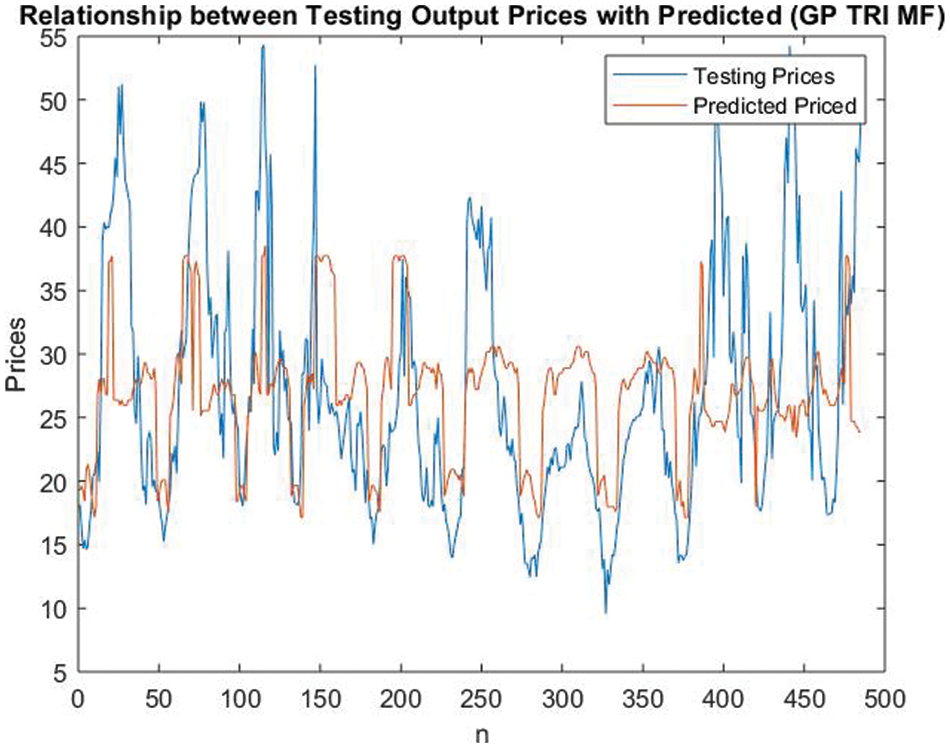
Figure 15: Electricity price forecasting for GP-based triangular MF
To evaluate the results of the approach MAPE, RMSE and percentage accuracy are calculated and presented in Tab. 1 shows that the results of proposed type-1 fuzzy triangular as well as type-1 fuzzy trapezoidal MFs outperforms the results of gaussian MF generated through FCM as well as gaussian and triangular MFs generated using GP algorithm.
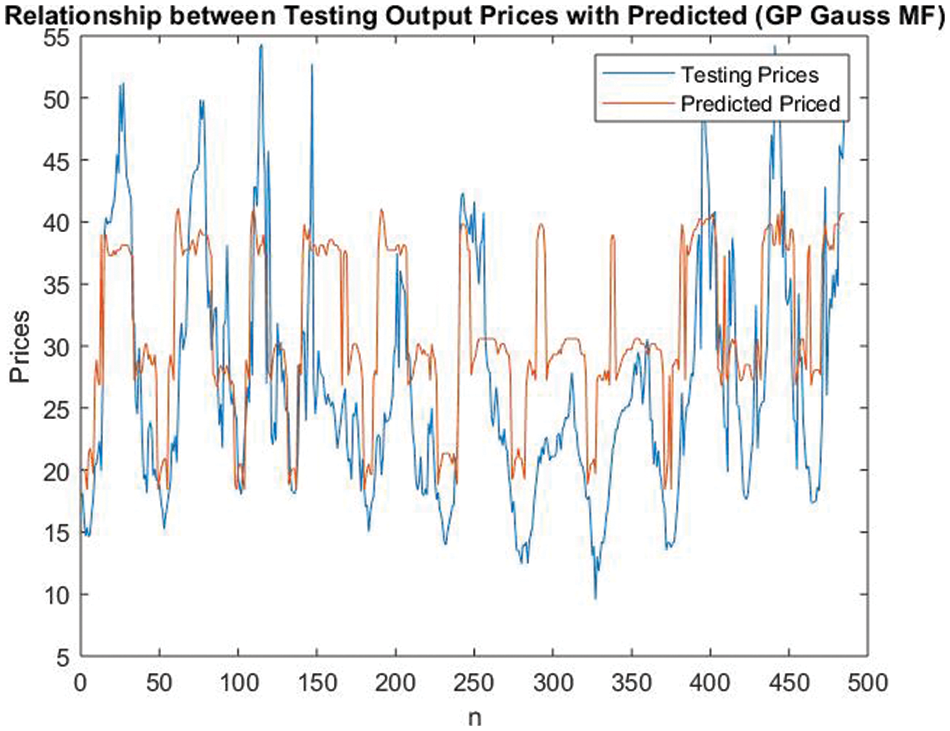
Figure 16: Electricity price forecasting for GP-based gaussian MF
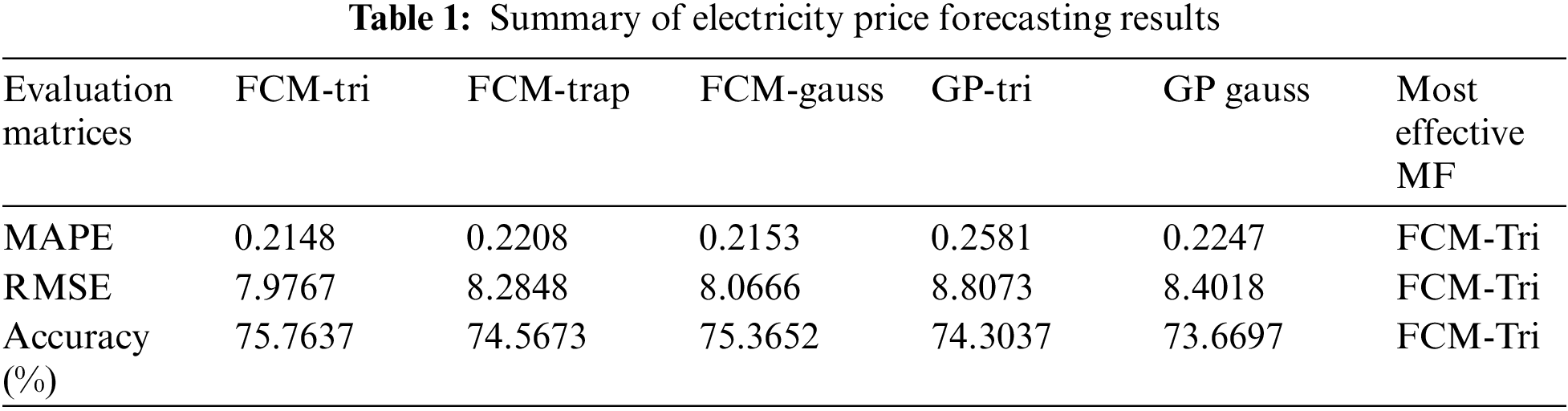
This paper proposes an approach to generate type-1 fuzzy triangular as well as type-1 fuzzy trapezoidal MFs through FCM. The proposed method is tested against electricity price forecasting dataset. It can be analyzed by Tab. 1, that the proposed algorithm-based type-1 triangular MF gives better results as compared to other methods. Type-1 triangular MF based on proposed approach has the least MAPE and RMSE errors as well as the highest percentage accuracy value compared to other approach. It can be concluded that for the under-study electricity forecasting data set, type-1 fuzzy MF generated through proposed algorithm is the most suitable and effective MF compared to others, the proposed approach of generating MFs beats gaussian MF generated through FCM as well as gaussian and triangular MF generated through GP algorithm, according to the results. This proposed approach has a lot of potential in the data science sector, especially for prediction related problems. The proposed approach can be used to handle a variety of real-world data science challenges, such as prediction, classification, regression and data protection. The approach will be used to calculate the accuracy of regression datasets in the future. In the future, we intend to generate triangular and trapezoidal MFs using fuzzy type-2 and fuzzy interval-type-2.
Author Contributions: This paper is equally contributed by all of the authors. The published version of the manuscript has been read and approved by all authors.
Funding Statement: This research is an ongoing research supported by Yayasan UTP Grant (015LC0-321& 015LC0-311) and Fundamental Research Grant Scheme (FRGS/1/2018/ICT02/UTP/02/1); a grant funded by the Ministry of Higher Education, Malaysia.
Conflicts of Interest: The authors declare that they have no conflicts of interset to report regarding the present study.
1. R. Weron, “Electricity price forecasting: A review of the state-of-the-art with a look into the future,” International Journal of Forecasting, vol. 30, no. 4, pp. 1030–1081, 2014. [Google Scholar]
2. A. Eydeland and K. Wolyniec, “Energy and power risk management: New developments in modeling, pricing, and hedging,” in Wiley Finance Series, 1st ed., vol. 1. N.J. Hoboken, N.J, United States: John Wiley & sons Inc., pp. 1–17, 2003. [Google Scholar]
3. F. Schweppe, M. Caramanis, R. Tabors and R. Bohn, “Spot pricing of electricity,” European Journal of Political Economy, vol. 6, no. 4, pp. 591–593, 1990. [Google Scholar]
4. D. Singhal and K. S. Swarup, “Electricity price forecasting using artificial neural networks,” International. Journal of Electrical Power & Energy System, vol. 33, no. 3, pp. 550–555, 2011. [Google Scholar]
5. P. L. Joskow, “California’s electricity crisis,” Oxford Review of Economical Policy, vol. 17, no. 3, pp. 365–388, 2001. [Google Scholar]
6. E. Zuliana and A. M. Abadi, “Sugeno fuzzy inference method and matlab application program for simulation of student performance evaluation in the elementary mathematics learning process,” International. Journal of Advanced Trends Computer Science and Enggineering, vol. 9, no. 4, pp. 4223–4228, 2020. [Google Scholar]
7. M. H. Azam, M. H. Hasan, S. J. A. Kadir and S. Hassan, “Prediction of sunspots using fuzzy logic: A triangular membership function-based fuzzy C-means approach,” International Journal of Advanced Computer Science and Applications, vol. 12, no. 2, pp. 357–362, 2021. [Google Scholar]
8. M. Kumar and S. S. Hans, “Load forecasting using fuzzy logic tool Box,” GRD Journal of Enggineering, vol. 3, no. 8, pp. 12–19, 2018. [Google Scholar]
9. M. H. Azam, M. H. Hasan, S. Hassan and S. J. Abdulkadir, “Fuzzy type-1 triangular membership function approximation using fuzzy C-means,” in Int. Conf. on Computational Intelligence (ICCI), Seri Iskandar, Perak, Malaysia, pp. 115–120, 2020. [Google Scholar]
10. R. Khayatzadeh and M. B. Yelten, “A novel multiple membership function generator for fuzzy logic systems,” in SMACD - 15th Int. Conf. on Synthesis, Modeling, Analysis and Simulation Methods and Applications to Circuit Design, Prague, Czech Republic, pp. 101–104, 2018. [Google Scholar]
11. S. Moshfe, A. Khoei, K. Hadidi and B. Mashoufi, “A fully programmable nano-watt analogue CMOS circuit for Gaussian functions,” in Int. Conf. on Electronic Devices, Systems and Applications, ICEDSA 2010-Proc., Kuala Lumpur, Malaysia, pp. 82–87, 2010. [Google Scholar]
12. M. H. Hasan, J. Jaafar and M. F. Hassan, “Fuzzy C-means and two clusters’ centers method for generating interval type-2 membership function,” in 3rd Int. Conf. on Computer and Information Sciences, ICCOINS 2016 - Proc., Kuala Lumpur, Malaysia, pp. 627–632, 2016. [Google Scholar]
13. J. C. Dunn, “A fuzzy relative of the ISODATA process and its use in detecting compact well-separated clusters,” Journal of Cybernetics, vol. 3, no. 3, pp. 32–57, 1973. [Google Scholar]
14. S. Guillaume, “Designing fuzzy inference systems from data: An interpretability-oriented review,” IEEE Transaction on. Fuzzy System, vol. 9, no. 3, pp. 426–443, 2001. [Google Scholar]
15. J. S. R. Jang, “ANFIS: Adaptive-network-based fuzzy inference system,” IEEE Transactions on System, Man and Cybernetics, vol. 23, no. 3, pp. 665–685, 1993. [Google Scholar]
16. S. H. Khairuddin, M. H. Hasan, M. A. Hashmani and M. H. Azam, “Generating clustering-based interval fuzzy type-2 triangular and trapezoidal membership functions: A structured literature review,” Symmetry, vol. 13, no. 2, pp. 1–25, 2021. [Google Scholar]
17. R. B. Bhatt, S. J. Narayanan, I. Paramasivam and M. Khalid, “Approximating fuzzy membership functions from clustered raw data,” in Annual IEEE India Conference, INDICON 2012, Kochi, Kerala, India, pp. 487–492, 2012. [Google Scholar]
18. G. K. Koduru, K. Nageswararao and A. Namburu., “T1 weighted MR brain image segmentation with triangular intuitionistic fuzzy Set,” International Journal of Innovative Technology and Exploring Engineering, vol. 9, no. 4, pp. 762–768, 2020. [Google Scholar]
19. M. Vilela, G. Oluyemi and A. Petrovski, “A holistic approach to assessment of value of information (VOI) with fuzzy data and decision criteria,” Decision Making: Applications in Management Enggineering, vol. 3, no. 2, pp. 97–118, 2020. [Google Scholar]
20. M. Vilela, G. Oluyemi and A. Petrovski, “A fuzzy inference system applied to value of information assessment for oil and gas industry,” Decision Making: Applications in Management Enggineering, vol. 2, no. 2, pp. 1–18, 2019. [Google Scholar]
21. M. Usama and K. Jaehong, “Simplified model predicted current control method for speed control of non-silent permanent magnet synchronous motors,” in 3rd Int. Conf. on Computing, Mathematics and Engineering Technologies: Idea to Innovation for Building the Knowledge Economy, iCoMET, 2020, Sukkur, Sindh, Pakistan, pp. 1–5, 2020. [Google Scholar]
22. M. H. Azam, M. H. Hasan, S. Hassan and S. J. Abdulkadir, “A novel approach to generate type-1 fuzzy triangular and trapezoidal membership functions to improve the classification accuracy,” Symmetry 2021, vol. 13, no. 10, pp. 1932, 2021. [Google Scholar]
23. R. E. Precup, S. Preitl, E. Petriu, C. A. Bogan-Dragos, A. I. Szedlak-Stinean et al., “Model-based fuzzy control results for networked control systems,” Reports in Mechenical Engineering, vol. 1, no. 1, pp. 10–25, 2020. [Google Scholar]
24. X. Zhang, W. Zhang, W. Sun, X. Sun and S. K. Jha, “A robust 3-D medical watermarking based on wavelet transform for data protection,” Computer Systems Science and Engineering, vol. 41, no. 3, pp. 1043–1056, 2022, https://doi.org/10.32604/CSSE.2022.022305. [Google Scholar]
25. X. Zhang, X. Sun, X. Sun, W. Sun and S. K. Jha, “Robust reversible audiowatermarking scheme for telemedicine and privacy protection,” Computers, Materials & Continua, vol. 71, no. 2, pp. 3035–3050, 2022. [Google Scholar]
26. K. O. Oluborode, O. O. Obe, O. Olabode and O. T. Adeboje, “Adaptive neuro-fuzzy controller for double lane traffic intersections,” International Journal of Advanced Trends in Computer Science and Engineering, vol. 9, no. 4, pp. 6455–6463, 2020. [Google Scholar]
27. J. L. Castro, J. J. Castro-Schez and J. M. Zurita, “Learning maximal structure rules in fuzzy logic for knowledge acquisition in expert systems,” Fuzzy Sets and Systems, vol. 101, no. 3, pp. 331–342, 1999. [Google Scholar]
28. M. Y. Chen and D. A. Linkens, “Rule-base self-generation and simplification for data-driven fuzzy models,” Fuzzy Sets and Systems, vol. 142, no. 2, pp. 243–265, 2004. [Google Scholar]
29. H. Cao, L. Jia, G. Si and Y. Zhang, “A Clustering-analysis-based membership functions formation method for fuzzy controller of ball mill pulverizing system,” Journal of Process Control, vol. 23, no. 1, pp. 34–43, 2013. [Google Scholar]
30. C. Moewes and R. Kruse, “Evolutionary fuzzy rules for ordinal binary classification with monotonicity constraints,” Studies in Fuzziness and Soft Computing:State of the Art Theory, vol. 291, pp. 105–112, 2013. [Google Scholar]
31. S. J. Narayanan, I. Paramasivam, R. B. Bhatt and M. Khalid, “A study on the approximation of clustered data to parameterized family of fuzzy membership functions for the induction of fuzzy decision trees,” Cybernetics and Information Technology, vol. 15, no. 2, pp. 75–96, 2015. [Google Scholar]
32. A. E. M. Operator, “AEMO | NEM data dashboard,” 2002. https://aemo.com.au/energy-systems/electricity/national-electricity-market-nem/data-nem/data-dashboard-nem (accessed Jun. 03, 2021). [Google Scholar]
33. I. Shah, H. Iftikhar, S. Ali and D. Wang, “Short-term electricity demand forecasting using components estimation technique,” Energies, vol. 12, no. 13, pp. 2532, 2019. [Google Scholar]
34. S. Bouktif, A. Fiaz, A. Ouni and M. A. Serhani, “Optimal deep learning LSTM model for electric load forecasting using feature selection and genetic algorithm: Comparison with machine learning approaches,” Energies, vol. 11, no. 7, pp. 1636, 2018. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |