Computers, Materials & Continua DOI:10.32604/cmc.2022.028211
Article

Game Theory Based Decision Coordination Strategy of Agricultural Logistics Service Information System

Long Guo1, Dongsheng Sun1,*, Abdul Waheed2 and Huijie Gao3

1Institute of Agricultural Economics and Development, CAAS, Beijing, 100081, China
2School of Business and Economics, University of Management and Technology, Lahore, 54660, Pakistan
3Beijing Information Science and Technology University, Beijing, 100192, China
*Corresponding Author: Dongsheng Sun. Email: zgnkynjs@163.com
Received: 05 February 2022; Accepted: 23 March 2022

Abstract: Under the background of “Internet plus” rapid development, the agricultural logistics industry should apply information technology to every link of the agricultural product logistics industry chain. By making full use of the decision making module of the agricultural logistics information system, we can realize the full sharing of information and data resources, which makes the decision-making scheme of the agricultural logistics information system more optimized. In real economic society, the uncertainty and mismatch between the customer’s logistics service demand and the logistics service capability that the logistics service function provider can provide, that is, when the two information are asymmetric, how to use the third-party contract to coordinate the income and profit distribution of the two, to make the information system decision making more reasonable? This paper mainly studies the coordination scheme of agricultural logistics information system decision making under uncertain output and demand information by introducing the spot market. A joint coordination strategy based on revenue sharing and penalty feedback contracts proposes decentralized decision making based on game theory. Experiments show that the flexible ordering strategy proposed in this paper can reduce the logistics service supply chain’s uncertainty and significantly improve the logistics service supply chain’s overall income level through coordination contracts.

Keywords: Game theory; decision coordination strategy; agricultural logistics; information system; logistics service supply chain (LSSC)

1  Introduction

Agricultural product logistics is an essential link in the rapid development of agriculture. It occupies a critical position in the national social and economic development and is related to agricultural modernization and the fundamental interests of farmers. As an essential part of the agricultural service industry, the agricultural product logistics industry is a composite, primary, and leading industry integrating agricultural production, transportation, warehousing, freight forwarding, and information industry. Modern technology plays an essential role in promoting the transformation and upgrading of traditional agricultural logistics. With the rapid development of emerging technologies such as intelligent sensing, the Internet of things, big data, and artificial intelligence, agricultural product logistics systems’ analysis, decision-making, and execution ability have been dramatically improved [1]. Decentralized, inefficient, and high-cost logistics services gradually transform into an industrial chain with complementary and integrated resources, mutual connection, and division of labor. Different types of logistics service providers have begun to enter the integration stage and are moving steadily towards the trends of mobile logistics, platform and ecosystem, supply chain, and cross-border logistics, and the whole agricultural logistics service industry has ushered in a new period of rapid development [2].

Agricultural logistics informatization is a series of processing activities which logistics enterprises use to collect, classify, transmit, summarize, identify, track and query the information generated in agricultural logistics operations, which aims to realize the control in logistics activities with information technology and to realize the control in the process of logistics activities, to improve the efficiency of logistics and reduce the total cost of agricultural logistics. Informatization is an essential prerequisite for the development of agricultural logistics and provides information technology support for each link in the operation process of agricultural logistics [3].

In the rapid development of informatization, there are some problems in the agricultural logistics service industry, such as imperfect logistics network systems, many intermediate links, and high circulation costs. At the same time, the management process of the agricultural logistics service industry has the problem of uncertain customer logistics service demand and logistics service capability that logistics service function providers can provide. Therefore, to improve the overall competitiveness of the agricultural logistics industry, it is necessary to integrate the logistics resources of promising agricultural products enterprises and deeply integrate them into the agricultural products supply chain [4]. Strengthen the research on the integrated operation of agricultural logistics service resources, and give the corresponding solutions and Countermeasures to form the synergy and scale benefits of agricultural materials agricultural products logistics chain, improve the logistics efficiency of agricultural products and reduce the logistics cost. Which undoubtedly has essential theoretical value and practical significance for building a fast track for the production and marketing of agricultural products, improving circulation efficiency, reducing logistics costs, realizing high-quality agricultural development, and promoting the supply-side reform of the agricultural logistics service industry [5].

There are many differences between the logistics information systems of agricultural products, and their actual characteristics and various requirements for information are also different. Because of the uncertainty and mismatch between customers’ logistics service demand and the logistics service capability provided by logistics service function providers in the information management process of the agricultural logistics service industry, this paper studies the coordination of the logistics service supply chain by introducing the spot market [6].

2  Literature Review

Internet informatization can combine the main factors in agricultural products, strengthen their interoperability, and then ensure the logistics efficiency of agricultural products. The agricultural logistics management information system collects agricultural logistics information and stores it. After processing and maintenance, it is output in text, tables, graphics, and reports to help logistics managers or leaders control logistics operation activities [7]. Then they can calmly handle various businesses, share resources with customers. Furthermore, improve work efficiency and benefits. The real-time analysis of data can provide business decision support for enterprises, help enterprises formulate strategies and tactics, and enhance their competitiveness. With the improvement of the integrity and complexity of logistics service outsourcing, logistics takes the customer’s logistics demand as the starting point to form a service process of mutual supply and demand relationship to complete a complete supply process of logistics services. This supply and demand relationship constitutes the logistics service supply chain. As a vital decision-making function of logistics management information systems, the logistics service supply chain has attracted the attention of scholars at home and abroad in recent years [8–11].

Karl Inderfurth described the infrastructure of logistics management information systems from the technical level and introduced the development of relevant theories of a logistics information system [12]. P. H. Ketikidis et al. systematically studied the logistics information collection, resource allocation, resource sharing, resource control, and other management systems of supply chain logistics starting from the supply chain [13]. Article [14] makes a qualitative analysis on the motivation, process, and advantages of logistics enterprise alliance from the level of strategic management. However, this research still analyzes the organizational form of logistics service provision from the unilateral perspective of logistics service providers. It does not take the demander of logistics service into account. Choy et al. [15] considered that the logistics service supply chain is a supply chain with the basic structure of “functional provider logistics service integrator customer.” They proposed using an integrated logistics information management system (ILIMS) to manage the uncertainty of this service supply chain. Cui et al. [16] analyzed the complementarity and interaction between different types of logistics enterprises in logistics service value creation from two aspects of network and capability based on resource dependence and the analysis of the industrial network method. Lu et al. [17] studied the income distribution in the logistics service supply chain, established a two-level supply chain composed of logistics service integrators (LSI) and multiple functional logistics service providers (FLSP), and established an improved income distribution model considering FLSP’s unfair aversion. Wang et al. [18] introduced fairness preference into the channel coordination of the logistics service supply chain. They proposed that channel coordination cannot be realized when LSI is in adverse unfairness. This study is about the LSSC composed of LSI and FLSP. Liu et al. [19] studied a two-stage supply chain composed of one LSI and multiple FLSPs. They established an order allocation model, which considers the fairness preference caused by demand update and peer attention between FLSPs. Weihua Liu and Yijia Wang [20] studied the influence of logistics service integrator (LSSC) composed of a logistics service integrator (LSI) and a logistics service provider (LSP) on the behavior of logistics service integrator (LSSC) under risk preference in a fuzzy decision-making environment. Considering the LSSC composed of green innovation cost and demand, this paper establishes an essential quality control game model and studies the risk attitude in supply chain quality control. Weihua Liu and Yijia Wang [21] think that the basic quality control game model is established in LSSC composed of (LSI) and (FLSP), and the problem of risk attitude in supply chain quality control is studied.

It can be seen from the above research that there are still some gaps in this field: on the one hand, although the concept of logistics service supply chain has been popularized, it is relatively rarely applied in the agricultural industry; on the other hand, there is relatively little research on the demand and output of logistics services under uncertain conditions. To sum up, although scholars have carried out theoretical and technical research on logistics management information systems, the research on logistics management information systems in the agricultural industry is not deep enough and is basically in a blank state. Aiming at all links of agricultural logistics management, especially the construction of agricultural coordination strategy of the agricultural logistics service supply chain, and then the construction of an information system will provide more scientific and modern support for its development.

3  Model Construction

Fig. 1 shows a typical agricultural logistics system architecture that provides infrastructure functions such as data storage, security, and system load balancing service at the IaaS layer. In the automatic operation and maintenance layer of PaaS, platform services such as Docker, production environment, system monitoring, and role management are provided [22]. In the application layer, the system provides logistics traceability, supplier app, driver app, logistics operation, and other applications for agricultural logistics [23]. Decision service is the core of the whole logistics system in the internal basic service layer. The service needs to reasonably allocate resources to solve the problem of uncertainty and mismatch between customer logistics service demand and logistics service capability. It is provided by logistics service function providers in the information management process of the agricultural logistics service industry, which aims to determine the maximum procurement quantity and minimum procurement quantity of agricultural logistics service capability and improve the overall interests of participants.

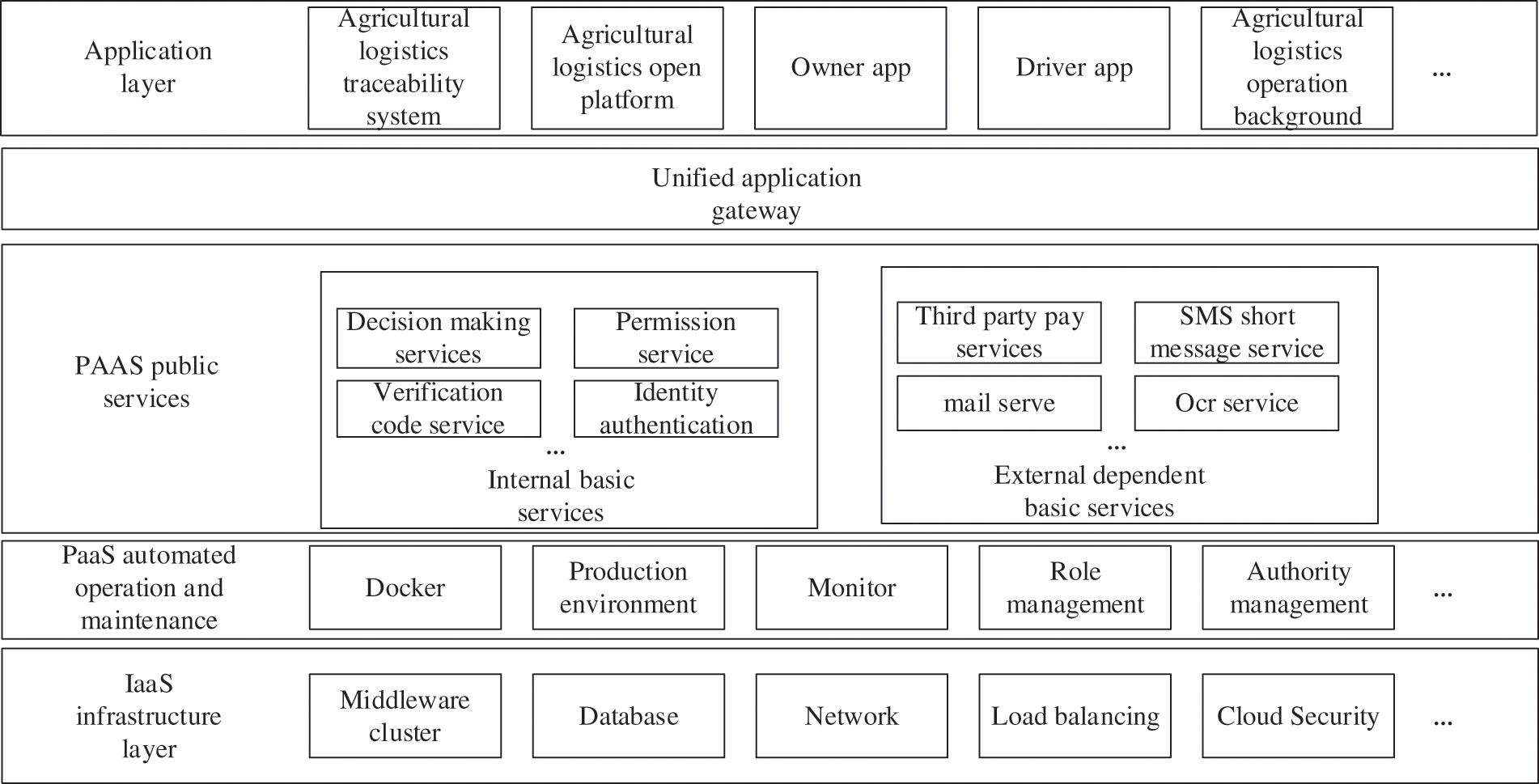
Figure 1: A typical agricultural logistics system architecture

This paper focuses on the analysis of the decision service module. Consider a two-level logistics service supply chain composed of an agricultural logistics service function provider facing the stochastic output of logistics service capability and a logistics service integrator facing the uncertainty of logistics service capability demand (as shown in the Fig. 2). In the process of integrators purchasing logistics service capabilities and functional providers investing in logistics service capabilities, this paper studies the functional relationship between logistics service integrators and functional providers through game theory. This paper assumes that the agricultural logistics service integrator is the leader and the follower is the agricultural logistics service, function provider. It is assumed that both function providers and integrators make decisions according to their expected profit maximization, and the information between them is entirely symmetrical.

Figure 2: Logistics service supply chain with uncertain output and demand

L represents the maximum output of logistics service capacity that agricultural logistics service function providers can provide. ε is the stochastic output factor of logistics service function providers about logistics service capability. Then, the logistics service function provider’s actual output about logistics service capability is εL, where ε∈[a,b], 0≤a≤b≤1, E(ε)=μ1, this paper assumes that the output of logistics service providers about logistics service capability is random. Its cumulative probability density and distribution functions are g(y) and G(y), respectively.

A random function represents the customer logistics service demand faced by logistics service integrators. Its cumulative probability density and distribution functions are f(x) and F(x), E(x)=μ2, F¯(x)=1−F(x) respectively. At the same time, the wholesale price of unit logistics service capability provided by logistics service function providers to logistics service integrators is defined as w. The investment cost per unit logistics service capability of agricultural logistics service providers and the operation cost per unit logistics service capability of logistics service integrators are expressed by C1 and C2, respectively.

Let the price of logistics service integrator selling unit logistics service capability to customers be p. To ensure the overall profitability of the logistics service supply chain, obviously p>cI+cF/μ1.

On the other hand, define D as the number of service capabilities delivered by the logistics service function provider to the logistics service integrator. Then, D={q,εL≤q;εL,q<εL<Q;Q,εL≥Q. Then, q and Q represent the minimum and maximum logistics service capacity purchased by logistics service integrators from logistics service function providers, respectively.

This paper assumes that the agricultural logistics service integrator adopts the Flexible Ordering Policy. The quantity of logistics service capacity purchased by the logistics service integrator from the logistics service function provider is (q,Q). When the number of random logistics service capacity provided by the logistics service function provider is less than q, the function provider will dispatch part of the logistics service capacity from the spot market. Other logistics service function providers make up for their own logistics service capacity shortage. The number of logistics service capacity received by the logistics service integrator is q. When the number of random logistics service capabilities provided by the logistics service function provider is more significant than Q, the logistics service integrator’s number of logistics service capabilities is Q. When the number of random logistics service capabilities provided by logistics service function providers is between q and Q, the number of logistics service capabilities received by logistics service integrators is also between q and Q.

Assuming that the agricultural logistics service integrator is the leader and the agricultural logistics service function provider is the follower, the decision-making order of the logistics service function provider and the integrator is as follows:

Step 1: The agricultural logistics service integrator determines a flexible procurement strategy, that is, the quantity of logistics service capacity purchased from the agricultural logistics service function provider is (q,Q);

Step 2: After receiving the purchase order from the agricultural logistics service integrator, the agricultural logistics service function provider determines the maximum investment reserve of logistics service capacity L, and the corresponding stochastic output quantity of logistics service capability is zL. When zL<q, the logistics service function provider dispatches the logistics service capacity of unit q−zL from the spot market, that is, other logistics service function providers, to make up for its shortcomings. Assume that the scheduling cost of unit logistics service capacity is s. When zL>Q, the logistics service integrator only receives the logistics service capability of unit Q. Quantity of service capacity delivered by agricultural logistics service function providers to logistics service integrators, D={q,εL≤q;εL,q<εL<Q;Q,εL≥Q..

Step 3: the logistics service capacity provided by the agricultural logistics service integrator to customers is min(D,X).

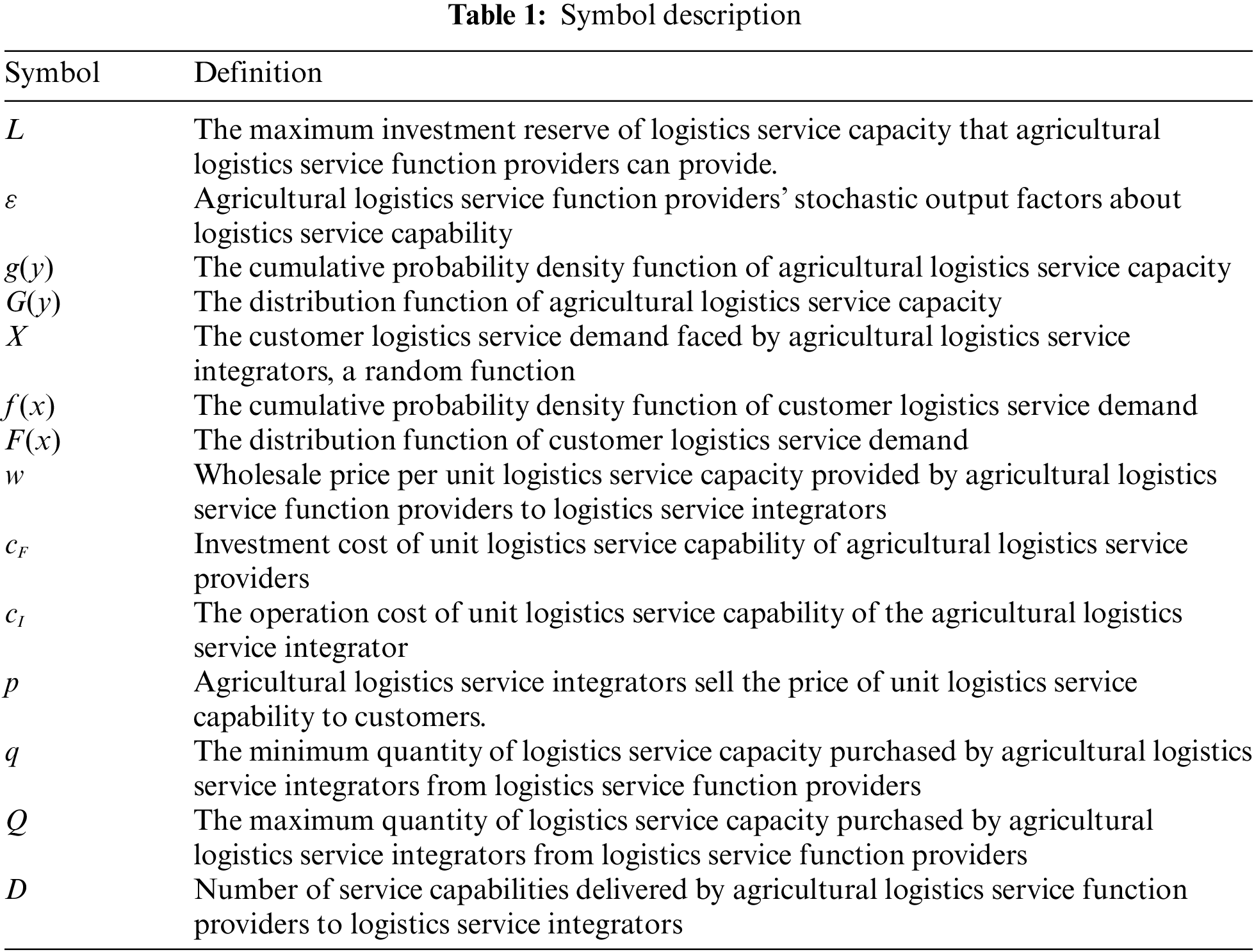
The symbols designed in this paper are shown in Tab. 1.

3.1 Centralized Decision Model of Agricultural Logistics Service Supply Chain

In order to provide a benchmark for decentralized decision-making and the establishment of subsequent coordination contracts, this paper first studies the model under centralized decision of agricultural logistics service supply chain. When the output of logistics service capacity of agricultural providers is random, and customer demand is random. The core goal of the agricultural logistics information system is to determine the optimal investment reserve of logistics service capacity and maximize the expected profit of the supply chain system of logistics service. At this time, the expected revenue of LSSC can be expressed by Eq. (1):

πLC(q,Q,L)=E[pmin(D,X)−s(q−εL)+−cFD]−cIL=p{∫aq/LE[pmin(q,X)]g(y)dy+∫q/LQ/LE[pmin(yL,X)]g(y)dy+∫Q/LbE[pmin(Q,X)]g(y)dy}−s∫aq/L(q−yL)g(y)dy−cI{q∫aq/Lg(y)dy+L∫q/LQ/Lyg(y)dy+Q∫Q/Lbg(y)dy}−cFL(1)

Under centralized decision-making, the expected revenue function of the agricultural logistics service supply chain is mainly composed of four parts. They are sales revenue of agricultural logistics service capacity. When the investment reserve of agricultural logistics service providers is less than Q, the cost of dispatching logistics service capacity from the spot agricultural market. The operation cost of agricultural logistics service integrators on logistics service capability and the cost of logistics service capability invested and reserved by logistics service function providers.

Further simplified Eq. (1), agricultural logistics service

The expected revenue function of the supply chain can be expressed as:

πLC(q,Q,L)=∫aq/L{pE[min(q,X)]−s(q−yL)−cIq}g(y)dy+∫q/LQ/L{pE[min(yL,X)]−cFyL}g(y)dy+∫Q/Lb{pE[min(Q,X)]−cIQ}g(y)dy−cFL(2)

When q=Q, D≡Q, the purchased quantity of agricultural logistics service integrator about logistics service capability remains unchanged, called Invariable Ordering Policy, at this time, the expected revenue function of the agricultural logistics service supply chain is:

πLIOP(Q1,L1)=E[pmin(Q1,X)−s(Q1−εL1)+]−cFL1−cIQ1=p{∫0Q1xf(x)d(x)+Q1F¯(Q1)} −s∫aQ1/L1(Q1−yL1)g(y)dy−cFL1−cIQ1(3)

Theorem 1: When (q,Q,L)=(F¯−1((s+cI)/p),F¯−1(cF/p),LC), The expected revenue of the logistics service supply chain obtains the optimal value, and LC meets the following equation:

s∫aqC/LCyg(y)dy+∫qC/LCQC/LC[pF¯(yLC)−cI]yg(y)dy−cF=0(4)

At this time, the optimal expected revenue of the agricultural logistics service supply chain is:

πLC∗=πLC∗(qC,QC,LC)=p{∫aqC/LC(∫0qCxf(x)dx)g(y)dy+∫qC/LCQC/LC(∫0yLCxf(x)dx)g(y)dy+∫QC/LCb(∫0QCxf(x)dx)g(y)dy}(5)

Prove: Omitted.

When q=qC,Q=QC, the following inference can be drawn from Proposition 5.1:

Corollary 1 If q=Q, when the purchasing quantity Q1C of logistics service capacity of agricultural integrator and the material capacity investment reserve L1 of function provider meet the Eqs. (6) and (7), the expected revenue of logistics service supply chain can be optimized. The optimal value is shown in Eq. (8):

pF¯(Q1C)−sG(Q1CL1C)−cI=0(6)

s∫aQ1C/L1Cyg(y)dy−cF=0(7)

πLIOP∗=πLIOP(Q1C,L1C)=p∫0Q1Cxf(x)dx(8)

From Proposition 1 and Corollary 1, the following conclusions can be drawn:

Theorem 2: The expected revenue of logistics service supply chain under flexible ordering strategy is greater than that under fixed ordering strategy. That is, there is a relationship πLC(qC,QC,LC)>πLIOP(Q1C,L1C).

Prove: Omitted.

It can be seen from Theorem 2 that agricultural logistics service integrators adopt a flexible ordering strategy, which is better than a fixed ordering strategy. Therefore, logistics service integrators can flexibly adjust procurement decisions according to practical needs.

3.2 Optimal Procurement Decision of Agricultural Logistics Service Integrator

For the investment reserve quantity L of any given function provider about service capacity, the expected revenue of agricultural integrator satisfies the relationship (9):

πID(q,Q,L)=pE[min(D,X)]−(w+cI)E(D)(9)

The expected income of an integrator is mainly composed of the sales revenue of agricultural logistics service capacity and the operation cost of providing service to customers. Eq. (9) can be expressed as follows:

πID(q,Q,L)=∫aq/L{pE[min(q,X)]−(w+cI)q}g(y)dy+∫q/LQ/L{pE[min(yL,X)]−(w+cI)yL}g(y)dy+∫Q/Lb{pE[min(Q,X)]−(w+cI)Q}g(y)dy(10)

The same as Theorem 1, it can be obtained that for any given investment reserve of logistics service L of agricultural logistics service provider, when (q,Q) satisfies Eq. (11), the expected income of logistics service integrator is optimal.

(qD,QD)=(F¯−1(w+cIp),F¯−1(w+cIp))(11)

Eq. (11) shows that the logistics service provider’s investment reserve of any logistics service capability is L without coordination. The logistics service integrator can maximize its expected revenue by adopting the same procurement quantity qD of logistics service capability. By introducing Eq. (11) into Eq. (10), the optimal expected revenue of the logistics service integrator at this time can be obtained as follows:

πID∗(qD,QD)=p∫0qDxf(x)dx(12)

3.3 Optimal Investment and Production Decision of Agricultural Logistics Service Providers

After the agricultural logistics service integrator determines the optimal procurement strategy, the expected revenue function of the agricultural logistics service provider can be expressed as follows:

πFD(qD,QD,L)=E[wD−s(qD−εL)+]−cFL=wqD−∫aqD/L(qD−yL)g(y)dy−cFL(13)

The revenue of function providers consists of three parts: the revenue of integrators purchasing logistics service capability, the cost of dispatching logistics service capability from the spot market, and the cost of investment reserve.

According to Eq. (13), the optimal investment reserve L of logistics service function providers on logistics service capability under decentralized decision-making can be obtained, which satisfies the following relationship:

s∫aqD/LDyg(y)dy−cF=0(14)

According to Eq. (14), qD/LD≡C, under decentralized decision-making, the ratio of the optimal purchase quantity q of logistics service integrator on logistics service capability and the optimal investment reserve L of logistics service function provider on logistics service capability is positive constant. The constant depends on the stochastic output quantity of logistics service capability, the investment reserve cost cF, and the price s of Logistics service capability of spot market dispatching units from the spot market.

By introducing Eq. (14) into Eq. (13), it is obtained that the optimal expected revenue of logistics service function providers under decentralized decision-making is:

πFD∗(qD,QD,LD)=[w−sG(C)]qD(15)

If the distribution function F(x) has a generalized increasing failure rate, the optimal wholesale price per unit logistics service capability provided by the logistics service function provider to the logistics service integrator can be obtained, that is:

dπFD∗dw=F¯−1(w+cIp)−w−sG(C)pf(qD)(16)

4  Coordination Strategy of Logistics Service Supply Chain under Hybrid Coordination Contract Strategy

The expected revenue of the agricultural logistics service supply chain is a function of the purchase volume of integrators and the maximum investment reserve of the logistics service capacity of agricultural logistics service function providers. General coordination contracts such as feedback contracts and revenue sharing contracts often coordinate the revenue function containing only one decision variable. Therefore, this paper adopts the mixed coordination contract strategy, combined with the revenue sharing contract, designs the Order Penalty and Rebate Contract (OPR) of the integrator to realize the coordination of the logistics service supply chain.

The Order Penalty and Rebate Contract (OPR) designed in this paper combines the revenue-sharing coordination contract. Its basic ideas are as follows: firstly, it is assumed that the agricultural logistics service function provider gives the procurement volume target Q0(qC≤Q0≤QC) of the logistics service capability provided by the logistics service integrator. And then, two different strategies for giving the integrator are determined according to the gap between the stochastic output εL and Q0 of its logistics service capability. When the stochastic output εL of the logistics service capability of the logistics service function provider is less than Q0, the logistics service function provider will provide a specific penalty for the lack of logistics service capability to the logistics service integrator. Then assume that the penalty for the lack of unit logistics service capability is δ1. When the actual purchase quantity of the logistics service integrator about the logistics service capability is greater than Q0, the logistics service function provider will give a certain rebate to the logistics service integrator for the purchased quantity of the logistics service capability exceeding Q0. Then, we will assume that the rebate of the unit logistics service capability is δ2. The logistics service provider will give the integrator an appropriate wholesale price discount by combining the Penalty and Rebate Contract with the revenue-sharing coordination contract. Moreover, the integrator is also willing to revenue part of the sales revenue of logistics service capability to the function provider. Assume that the logistics service integrator is willing to share the sales revenue of logistics service capability in the proportion of ϕ(0<ϕ<1) to the logistics service function provider. The logistics service integrator has the remaining sales revenue in the proportion of 1−ϕ.

Under the joint coordination of Penalty and Rebate Contract and revenue sharing contract, the expected revenue function of logistics service integrator is:

πIOPR(q,Q,L)=∫aq/L{p(1−ϕ)E[min(q,X)]−(w+cI)q+δ1(Q0−q)+}g(y)dy+∫q/LQ0/L{p(1−ϕ)E[min(yL,X)]−(w+cI)yL+δ1(Q0−yL)+}g(y)dy+∫Q0/LQ/L{p(1−ϕ)E[min(yL,X)]−(w+cI)yL+δ2(yL−Q0)+}g(y)dy+∫Q/Lb{p(1−ϕ)E[min(Q,X)]−(w+cI)Q+δ2(Q−Q0)+}g(y)dy(17)

Theorem 3: Under the joint coordination of Penalty and Rebate Contract and revenue sharing contract, the penalty coefficient δ1 and rebate coefficient δ2 of unit logistics service capability meet Eqs. (18) and (19). The corresponding flexible ordering strategy (qC,QC) can optimize the revenue of logistics service integrators to the maximum logistics service investment reserve L of any given logistics service function provider.

δ1=s(1−ϕ)−cIϕ−w(18)

δ2=s(1−ϕ)−δ1(19)

Prove:

Order π2(Z)=p(1−ϕ)E[min(Z,X)]−(w+δ1+cI)Z,

It is easy to conclude that when δ1=s(1−ϕ)−cIϕ−w, π2(Z) is an increasing function of Z in (0,qC] and a decreasing function of Z in (qC,∞). There are two cases to prove it:

(1) If q<Q0, Then:

∂πIOPR(q,Q,L)∂q=∫aq/L{p(1−ϕ)F¯(q)−(w+cI+δ1)}g(y)dy(20)

Therefore, when δ1=s(1−ϕ)−cIϕ−w, the optimal purchase quantity of logistics service integrator qOPR∗=F¯(w+cI+δ1p(1−ϕ))≡qC can be obtained, For any Q and L, there is πIOPR(qC,Q,L)>πIOPR(q,Q,L); that is, the optimal order quantity of the logistics service integrator is qC, and the revenue of the logistics service integrator obtains the optimal value.

(2) If q≥Q0, Then:

πIOPR(qC,Q,L)−πIOPR(q,Q,L)=K1(q,Q,L)+∫Q0/Lq/L[π2(yL)−π2(q)]g(y)dy(21)

where, K1(q,Q,L)=∫aqC/L[π2(qC)−π2(q)−δ1(q−Q0)]g(y)dy+∫qC/LQ0/L[π2(yL)−π2(q)−δ1(q−Q0)]g(y)dy.

Since ∫Q0/Lq/L[π2(yL)−π2(q)]g(y)dy>0, then F¯(q)<F¯(qC)=F¯(w+cI+δ1p(1−ϕ)),

Then dK1(q,Q,L)dq=−∫aQ0/L[p(1−ϕ)F¯(q)−w+cI+δ1]g(y)dy<0

That is, K1(q,Q,L) is the subtractive function of q, we can conclude that:

πIOPR(qC,Q,L)−πIOPR(q,Q,L)>K1(Q0,Q,L)=∫aqC/L[π2(qC)−π2(q)]g(y)dy+∫qC/LQ0/L[π2(yL)−π2(q)]g(y)dy>0(22)

Therefore, for any q≥Q0, there is πIOPR(qC,Q,L)>πIOPR(q,Q,L).

According to the analysis of (1) and (2), when δ1=s(1−ϕ)−cIϕ−w, there is πIOPR(qC,Q,L)>πIOPR(q,Q,L) for all 0<q<Q.

Similarly, when δ2=s(1−ϕ)−δ1, there is πIOPR(qC,QC,L)≥πIOPR(qC,Q,L) for all Q≥qC.

Thus, πIOPR(qC,QC,L)≥πIOPR(q,Q,L). The proposition proved.

Theorem 3 shows that the logistics service integrator will adopt a flexible ordering strategy under the joint coordination of Penalty and Rebate Contract and revenue sharing contract. When the penalty coefficient δ1 and feedback coefficient δ2 of unit logistics service capacity meet Eqs. (2) and (3), the procurement volume of logistics service capacity is between qC and QC. At this time, the expected revenue function of the corresponding logistics service provider is:

πFOPR(qC,QC,L)=∫aqC/L{pϕE[min(qC,X)]+wqC−s(qC−yL)−δ1(Q0−qC)}g(y)dy+∫qC/LQ0/L{pϕE[min(yL,X)]+wyL−δ1(Q0−yL)}g(y)dy+∫Q0/LQC/L{pϕE[min(yL,X)]+wyL−δ2(yL−Q0)}g(y)dy+∫QC/Lb{pϕE[min(QC,X)]+wQC−δ2(QC−Q0)+}g(y)dy−cFL(23)

From the expected revenue function of logistics service providers, we can obtain the following proposition:

Theorem 4: When the target purchase quantity Q0 of the logistics service integrator set by the logistics service function provider satisfies the relationship (24), the revenue function of the logistics service function provider is the concave function of its maximum investment reserve L. There is a unique L=LC so that the revenue of the logistics service function provider can obtain the maximum value:

s∫aQ0/LCg(y)dy=cF(24)

Prove: Omitted.

According to Theorem 4, when the logistics service supply chain realizes coordination, the target purchase quantity Q0 set by the logistics service function provider is a function of its investment reserve L. Therefore, from Theorem 1 and Theorem 2, the following conclusions can be drawn:

Theorem 5: When the penalty coefficient δ1 for the lack of unit logistics service capability and the feedback coefficient δ2 for unit logistics service capability satisfy Eqs. (21) and (22). The logistics service function provider’s target purchase quantity Q0 of the logistics service integrator satisfies Eq. (24). The logistics service integrator adopts the flexible ordering strategy. The logistics service supply chain can achieve coordination under the combined action of the penalty and feedback contract and the revenue sharing contract.

According to Theorem 5, when the revenue sharing coordination contract is introduced into the punishment and feedback contract, the logistics service supply chain can coordinate under decentralized decision-making. At this time, the revenue functions of logistics service integrators and logistics service function providers are:

πIOPR=(1−ϕ)πLC∗+V(Q0)(25)

πFOPR=ϕπLC∗−V(Q0)(26)

where, V(Q0)=Q0[s(1−ϕ)G(Q0LC)−ϕcI−w]

Theorem 6: Under the joint coordination of punishment and feedback contract and revenue sharing contract, when the penalty coefficient δ1 and feedback coefficient δ2 of unit logistics service capability satisfy Eqs. (21) and (22). The target purchase quantity Q0 of logistics service integrator set by logistics service function provider satisfies Eq. (24). The wholesale price per unit logistics service capacity given by the logistics service function provider to the integrator satisfies Eq. (27), and the logistics service function provider and the integrator can realize any distribution of the revenue of the logistics service supply chain by adjusting the revenue sharing coefficient ϕ:

wOPR=s(1−ϕ)G(Q0LC)−ϕcI(27)

Prove: Omitted.

From Eq. (27), we can see that under the joint coordination of punishment and feedback contract and revenue sharing contract, the coordinated wholesale price wOPR of the logistics service supply chain is lower than the wholesale price w under decentralized decision-making. It may even be a negative value. However, under the coordination contract, logistics service integrators and function providers adjust revenue sharing share ϕ by implementing the revenue-sharing contract. It can realize that their respective benefits are greater than those under decentralized decision-making. Logistics service function providers can still obtain benefits higher than those under decentralized decision-making. Order:

Δ=πLC∗−(πFD∗+πID∗)(28)

ϕ=πFD∗+αΔπLC∗(0<α<1)(29)

Then,

πFOPR=πFD∗+αΔ(30)

πIOPR=πID∗+(1−α)Δ(31)

According to Eqs. (30) and (31), under the joint coordination of punishment and feedback contract and revenue sharing contract, logistics service function providers and logistics service integrators can obtain additional revenue compared with decentralized decision-making. Introducing revenue-sharing contracts into punishment and feedback contracts can realize the coordination of the logistics service supply chain to realize the win-win situation between logistics service function providers and logistics service integrators.

When the logistics service supply chain realizes coordination, it can be obtained from Eqs. (21), (22), (24) and (27): δ1=s(1−ϕ)(1−G(Q0LC))<s−w, δ2=ws(1−ϕ)G(Q0LC)>w−s. Therefore, for logistics service function providers, when the stochastic output εL of logistics service capability is greater than the minimum procurement volume of logistics service capability of logistics service integrators. Regardless of whether its stochastic output εL is greater than or less than its set target procurement volume Q0 of logistics service capability, logistics service function providers will not schedule logistics service capability from the spot market. A flexible ordering strategy helps to reduce the uncertainty of the logistics service supply chain. It makes logistics service integrators bear more uncertainty under flexible ordering strategy, encouraging them to purchase flexibly between qC and QC. The logistics service function provider will also compensate the logistics service integrator by adjusting the penalty coefficient δ1 for the lack of unit logistics service capability and the feedback coefficient δ2 for unit logistics service capability.

5  Simulation Analysis

In order to further study the coordination of agricultural logistics service supply chain under uncertain conditions, and verify that the flexible ordering strategy proposed in this paper can significantly improve the expected revenue of logistics service supply chain than the constant ordering strategy, and the impact of stochastic demand and stochastic output on the revenue of agricultural logistics service supply chain. Next, an example is used to verify the above solution results. The parameter values refer to the research of literature [24] and are compared with the research results under a fixed ordering strategy.

Under the assumption of uncertainty, the stochastic output of the logistics service capability of agricultural logistics service providers follows a uniform distribution, and the customer logistics service demand follows a normal distribution. The values of relevant parameters are as follows: p=15, s=10, cF=4, cI=2, μ1=0.65, σ1=0.15, μ2=1200, σ2=500.

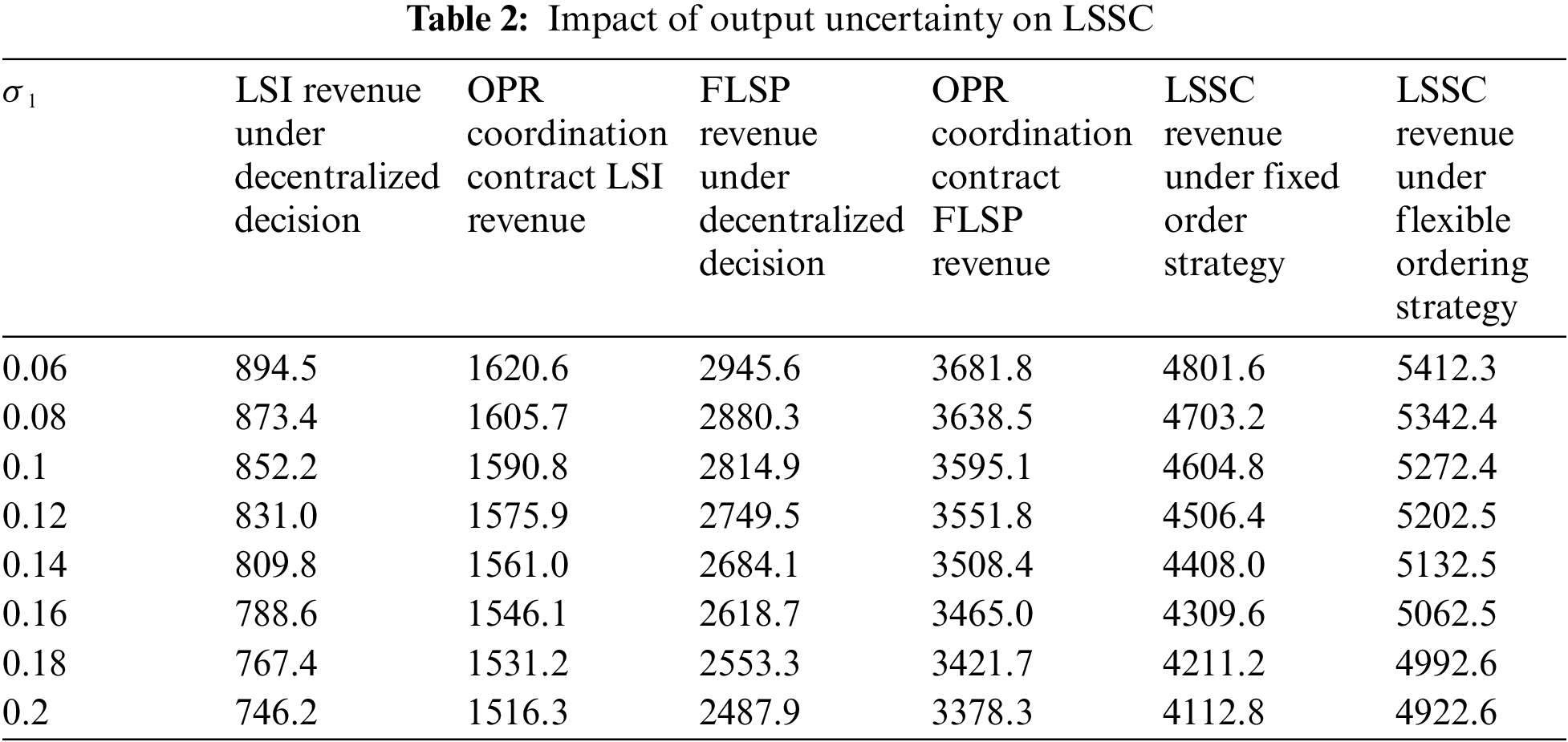
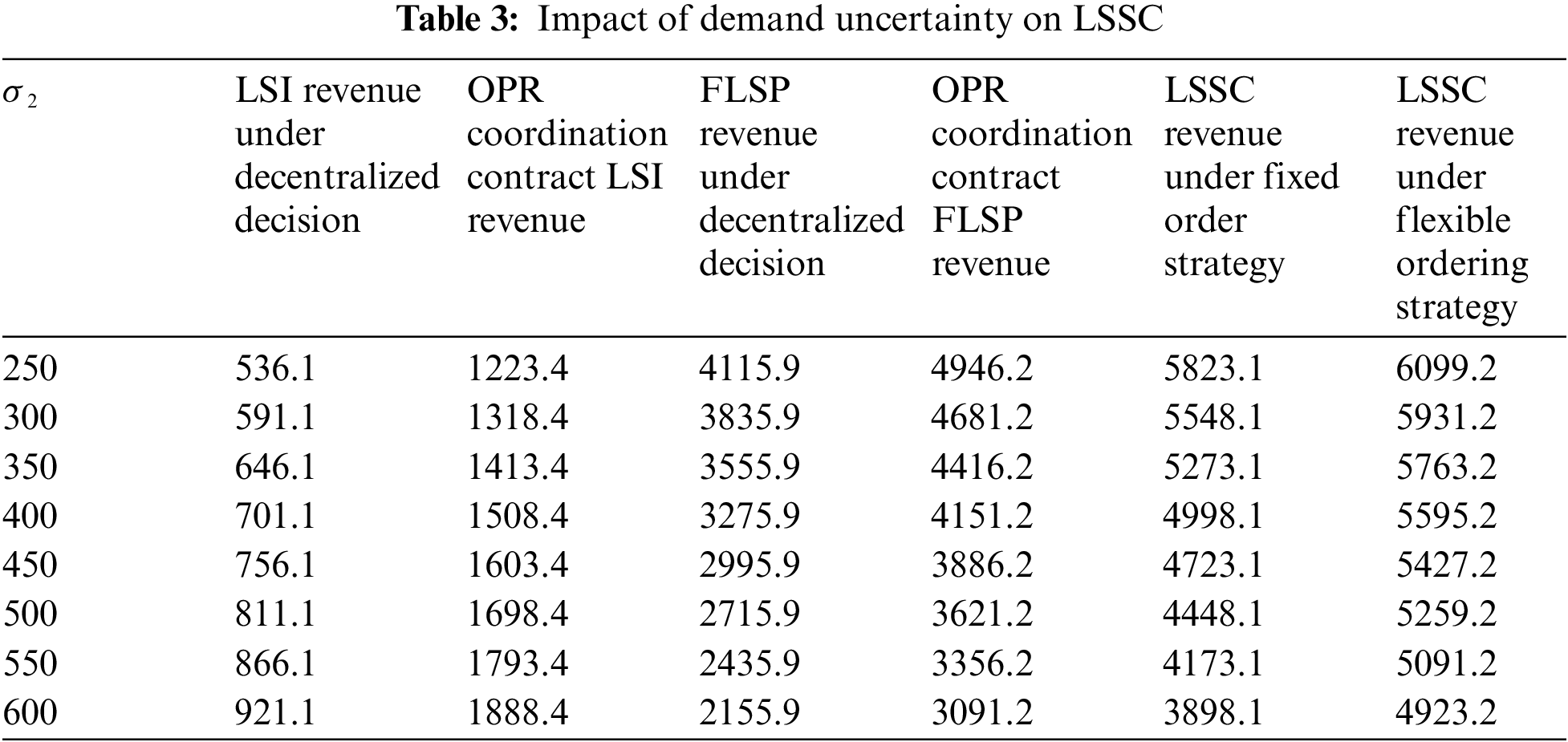
After calculation, the corresponding data results are obtained. These results are then substituted into MATLAB software to obtain the final simulation diagram [25]. Thereinto, Figs. 3 and 4 show the expected revenue of the logistics service supply chain under the stochastic output of agricultural logistics service providers and the stochastic demand of customer logistics service capability. The revenue-sharing distribution coefficient of function providers and integrators is ϕ=πFD∗+Δ2πLC∗. It can be seen from the figure that under random output and stochastic demand, with the increase of uncertainty of agricultural logistics service capacity output and demand, the income of agricultural logistics service supply chain under centralized decision-making shows a downward trend. Compared with the fixed ordering strategy, the revenue of the logistics service supply chain under the flexible ordering strategy is greater than that under the fixed ordering strategy. That shows that the flexible ordering strategy proposed in this paper under the joint coordination of punishment and feedback contract and revenue sharing contract improves the overall revenue and efficiency of the agricultural logistics service supply chain. In addition, under the joint coordination of punishment and feedback contract and revenue sharing contract, it can be found from Figs. 3 and 4 that the revenue of agricultural logistics service function providers and integrators is greater than that under decentralized decision-making. That shows that both can benefit under the coordination contract. With the combined effect of punishment and feedback contract and revenue sharing contract, we can realize the win-win of logistics service supply chain under flexible ordering strategy.

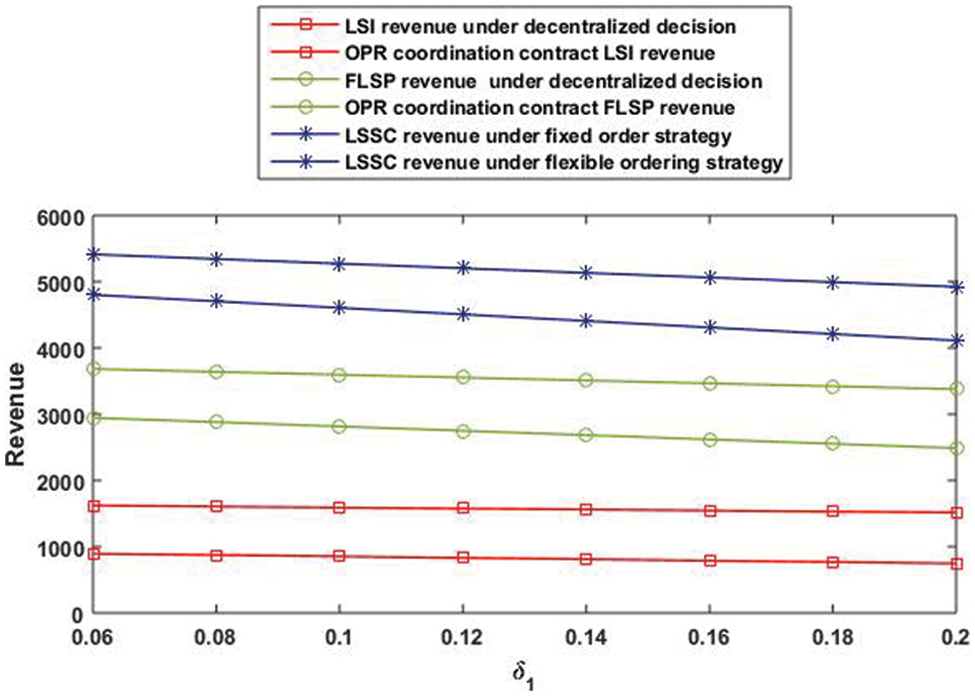
Figure 3: Impact of output uncertainty on logistics service supply chain

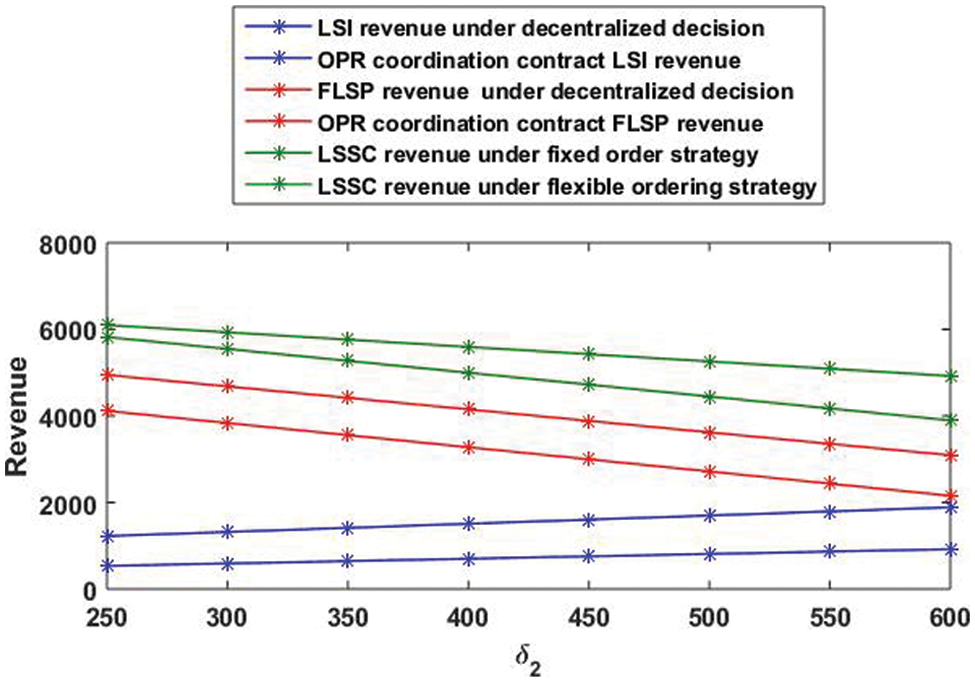
Figure 4: Impact of demand uncertainty on logistics service supply chain

For example, it can be seen from the Tab. 2, when σ1=0.12, under the joint coordination of punishment, feedback, and revenue sharing contract, the revenue of logistics service function provider is πFOPR∗=3551.8, and the revenue of logistics service integrator is πIOPR∗=1575.9. Under the decentralized decision, the revenue of agricultural logistics service function provider is πFD∗=2749.5, and the revenue of agricultural logistics service integrator is πID∗=831.0. Under the coordination contract, the revenue of agricultural logistics service providers and agricultural integrators increased by 29.2% and 89.6% respectively; Similarly, Tabs. 3 and 4 also show the corresponding results.

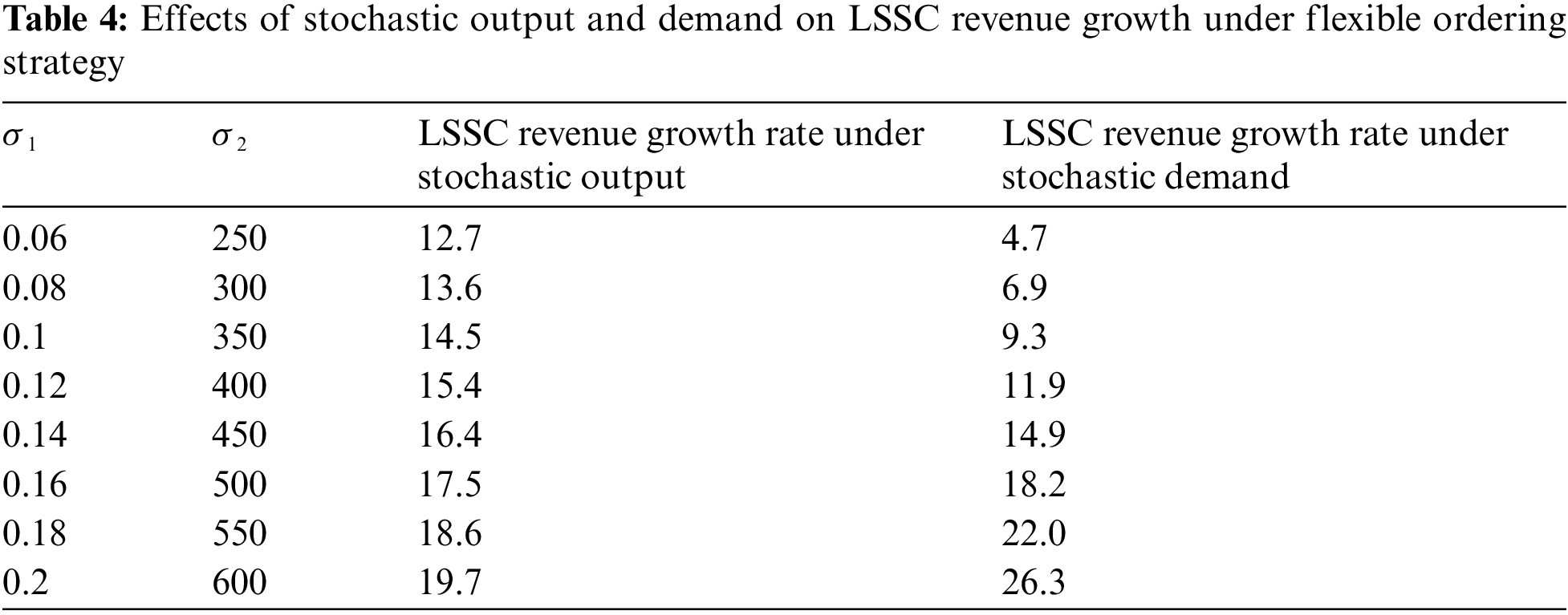
By comparing with the research results of literature [17] under fixed order strategy, Figs. 5 and 6 show the growth of LSSC revenue under flexible ordering strategy compared with that under fixed ordering strategy, and the revenue growth rate is ρ=(πLC∗πT∗−1)×100%.

As can be seen from Figs. 5 and 6, the overall revenue of LSSC gradually decreases with the increase of logistics service capacity output and demand uncertainty. Its revenue growth rate gradually increases with output uncertainty and demand uncertainty. However, the LSSC revenue growth rate with demand uncertainty is significantly greater than that with output uncertainty. The above results show that adopting a flexible ordering strategy can reduce the uncertainty of LSSC and improve the expected revenue of LSSC.

All these results show that: Firstly, under the condition that output and demand are uncertain, the revenue of logistics service supply chain and logistics service function provider decreases with the increase of uncertainty of logistics service capacity output and demand, the income of logistics service integrators shows a steady change trend with the increase of output and demand uncertainty, and the growth rate of logistics service supply chain income gradually increases with the increase of output uncertainty and demand uncertainty. Secondly, the penalty-reward joint coordination contract based on the revenue sharing contract can realize the coordination of the logistics service supply chain, and the logistics service function provider and integrator can realize the reasonable distribution of the logistics service supply chain income by adjusting the revenue sharing coefficient, reflecting the flexibility of the logistics service supply chain. Finally, it is found that the proposed flexible ordering strategy can not only reduce the uncertainty of the logistics service supply chain, but also significantly improve the overall revenue level of the logistics service supply chain through the coordination contract.

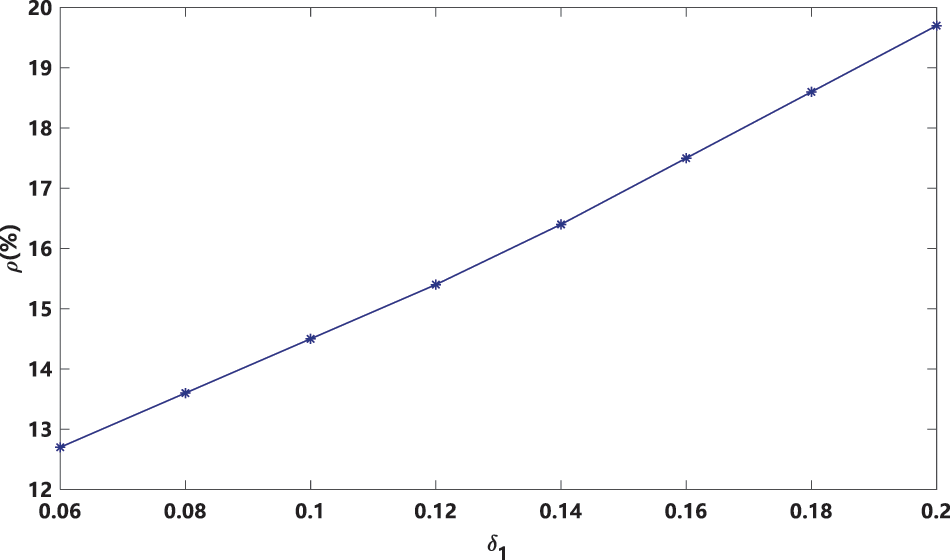
Figure 5: Impact of output uncertainty of flexible ordering strategy on LSSC revenue growth

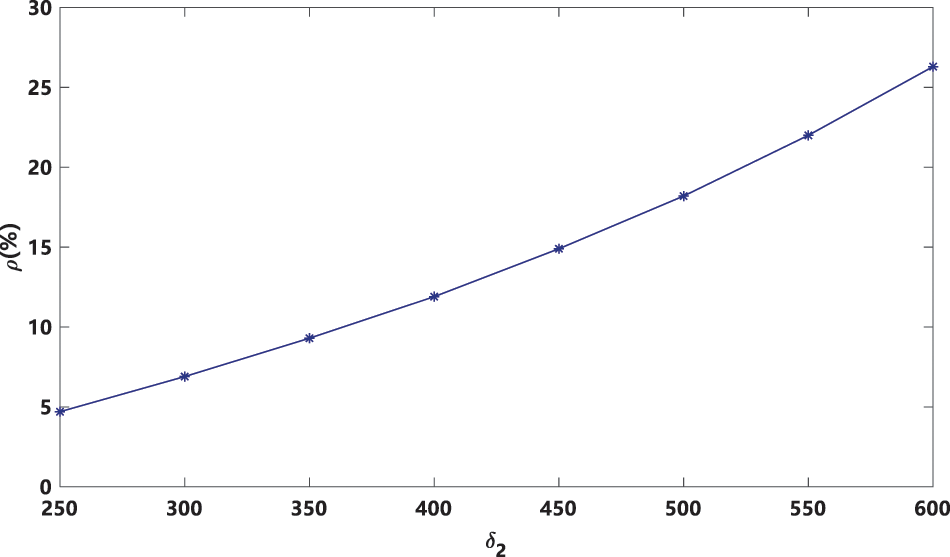
Figure 6: Impact of demand uncertainty of flexible ordering strategy on LSSC revenue growth

6  Conclusion

For the decision-making process in the construction of agricultural logistics information system, this paper focuses on the production and procurement management of the logistics service supply chain composed of an agricultural logistics service function provider and agricultural logistics service integrator. The research process assumes that there is both output uncertainty of agricultural logistics service capability and demand uncertainty of agricultural logistics service capability. We propose a flexible ordering strategy because of this uncertainty. The agricultural logistics service integrator and the agricultural logistics service function provider sign a contract on the purchased quantity of the logistics service capability to determine the maximum purchase quantity and the minimum purchase quantity of the agricultural logistics service capability [26]. A joint coordination strategy based on revenue sharing contract and penalty feedback contract is proposed for the decentralized decision-making situation.

This paper focuses on the agricultural logistics service supply chain composed of an agricultural logistics service provider and an agricultural logistics service integrator, analyzes the situation that the output and demand of agricultural logistics services are uncertain at the same time, and does not study the complex agricultural logistics supply chain composed of multiple logistics service providers or multiple logistics service integrations, as well as the situation that the output and demand of agricultural logistics services are single and random. On the basis of this study, we will further explore the supply chain of complex agricultural logistics services, logistics service capacity output stochastic or demand stochastic.

Acknowledgement: Grateful acknowledgement is made to my supervisor Professor Sun who gave me considerable help by means of suggestion, comments and criticism. His encouragement and unwavering support have sustained me through frustration and depression. Without his pushing me ahead, the completion of this thesis would be impossible. In addition, I deeply appreciate the contribution to this thesis made in various ways by my friends and my sister.

Funding Statement: The Agricultural Science and Technology Innovation Program (ASTIP-IAED-2021-08).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  W. J. Liu and J. Dai, “Agricultural products logistics under supply chain management system in Hubei Province,” Hubei Agricultural Sciences, vol. 53, no. 21, pp. 5296–5298, 2014. [Google Scholar]

 2.  N. Wang and L. P. Huang, “A study on agricultural product logistics supply chain management mode based on information network,” Research of Agricultural Modernization, vol. 26, no. 2, pp. 126–129+144, 2005. [Google Scholar]

 3.  J. Singh, T. Gera, F. Ali, D. Thakur, K. Singh et al., “Understanding research trends in android malware research using information modelling techniques,” Computers Materials & Continua, vol. 66, no. 3, pp. 2655–2670, 2021. [Google Scholar]

 4.  A. Brezulianu, O. Geman, M. Arif, I. Chiuchisan, O. Postolache et al., “Epidemiologic evolution platform using integrated modeling and geographic information system,” Computers Materials & Continua, vol. 67, no. 2, pp. 1645–1663, 2021. [Google Scholar]

 5.  Y. G. Zhong, F. F. Guo, H. J. Tang and X. M. Chen, “Research on coordination complexity of e commerce logistics service supply chain,” Complexity, vol. 18, no. 2, pp. 1–21, 2020. [Google Scholar]

 6.  Y. H. Du, R. Y. Zhang, X. Zhang, A. Ouyang, X. D. Zhang et al., “Protein secondary structure prediction with dynamic selfadaptation combination strategy based on entropy,” Journal of Quantum Computing, vol. 1, no. 1, pp. 21–28, 2019. [Google Scholar]

 7.  S. Khan, X. C. Ren, H. Ali, C. Tanougast, A. Rauf et al., “Reconfigurable compact wideband circularly polarised dielectric resonator antenna for wireless applications,” Computers Materials & Continua, vol. 68, no. 2, pp. 2095–2109, 2021. [Google Scholar]

 8.  W. H. Liu, X. C. Xu and A. Kouhpaenejad, “Deterministic approach to the fairest revenue-sharing coefficient in logistics service supply chain under the stochastic demand condition,” Computers & Industrial Engineering, vol. 66, no. 1, pp. 41–52, 2013. [Google Scholar]

 9.  W. H. Liu, D. Xie and X. C. Xu, “Quality supervision and coordination of logistic service supply chain under multi-period conditions,” International Journal of Production Economics, vol. 142, no. 2, pp. 353–361, 2013. [Google Scholar]

10. W. H. Liu and D. Xie, “Quality decision of the logistics service supply chain with service quality guarantee,” International Journal of Production Research, vol. 51, no. 5, pp. 1618–1634, 2013. [Google Scholar]

11. X. Liu, K. Zhang, B. Chen, J. Zhou and L. Miao, “Analysis of logistics service supply chain for the One Belt and One Road initiative of China,” Transportation Research Part E: Logistics and Transportation Review, vol. 117, no. 7, pp. 23–39, 2018. [Google Scholar]

12. K. Inderfurth and J. Clemens, “Supply chain coordination by risk sharing contracts under random production yield and deterministic demand,” OR Spectrum, vol. 36, no. 2, pp. 525–556, 2014. [Google Scholar]

13. P. H. Ketikidis, S. C. L. Koh, N. Dimitriadis, A. Gunasekaran and M. Kehajova, “The use of information systems for logistics and supply chain management in South East Europe: Current status and future direction,” Omega, vol. 36, no. 4, pp. 592–599, 2008. [Google Scholar]

14. V. Carbone and M. A. Stone, “Growth and relational strategies used by the European logistics service providers: Rationale and outcomes,” Transportation Research Part E: Logistics and Transportation Review, vol. 41, no. 6, pp. 495–510, 2005. [Google Scholar]

15. K. L. Choy, C. Li, S. C. K. So, H. Lau, S. K. Kwok et al., “Managing uncertainty in logistics service supply chain,” International Journal of Risk Assessment & Management, vol. 7, no. 1, pp. 19–43, 2007. [Google Scholar]

16. L. Cui and S. Hertz, “Networks and capabilities as characteristics of logistics firms,” Industrial Marketing Management, vol. 40, no. 6, pp. 1004–1011, 2011. [Google Scholar]

17. F. Lu, L. Wang, H. Bi, Z. Du and S. Wang, “An improved revenue distribution model for logistics service supply chain considering fairness preference,” Sustainability, vol. 13, no. 12, pp. 6711, 2021. [Google Scholar]

18. N. Wang, Z. P. Fan and X. Wang, “Channel coordination in logistics service supply chain considering fairness,” Mathematical Problems in Engineering, vol. 2016, no. 4, pp. 1–15, 2016. [Google Scholar]

19. W. H. Liu, S. Q. Wang, D. L. Zhu, D. Wang and X. R. Shen, “Order allocation of logistics service supply chain with fairness concern and demand updating: Model analysis and empirical examination,” Annals of Operations Research, vol. 268, no. 1, pp. 177–213, 2018. [Google Scholar]

20. S. N. Wang and Z. H. Hu, “Green logistics service supply chain games considering risk preference in fuzzy environments,” Sustainability, vol. 13, no. 14, pp. 8024, 2021. [Google Scholar]

21. W. Liu and Y. Wang, “Quality control game model in logistics service supply chain based on different combinations of risk attitude,” International Journal of Production Economics, vol. 161, no. 3, pp. 181–191, 2015. [Google Scholar]

22. N. Lutsiv, T. Maksymyuk, M. Beshley, O. Lavriv, V. Andrushchak et al., “Deep semisupervised learning-based network anomaly detection in heterogeneous information systems,” Computers, Materials & Continua, vol. 70, no. 1, pp. 413–431, 2022. [Google Scholar]

23. X. Tang, W. Tu, K. Li and J. Cheng, “DFFNet: An IoT-perceptive dual feature fusion network for general real-time semantic segmentation,” Information Sciences, vol. 565, no. 12, pp. 326–343, 2021. [Google Scholar]

24. H. Yong and Z. Xuan, “Coordination in multi-echelon supply chain under supply and demand uncertainty,” International Journal of Production Economics, vol. 139, no. 1, pp. 106–115, 2012. [Google Scholar]

25. X. R. Zhang, W. F. Zhang, W. Sun, X. M. Sun and S. K. Jha, “A robust 3-D medical watermarking based on wavelet transform for data protection,” Computer Systems Science & Engineering, vol. 41, no. 3, pp. 1043–1056, 2022. [Google Scholar]

26. X. R. Zhang, X. Sun, X. M. Sun, W. Sun and S. K. Jha, “Robust reversible audiowatermarking scheme for telemedicine and privacy protection,” Computers, Materials & Continua, vol. 71, no. 2, pp. 3035–3050, 2022. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.