Computers, Materials & Continua DOI:10.32604/cmc.2022.028152
Article

FPGA Implementation of Elliptic-Curve Diffie Hellman Protocol

Sikandar Zulqarnain Khan1,*, Sajjad Shaukat Jamal2, Asher Sajid3 and Muhammad Rashid4

1Department of Aeronautical Engineering, Estonian Aviation Academy, Tartu, 61707, Estonia
2Department of Mathematics, College of Science, King Khalid University, Abha, 61413, Saudi Arabia
3Department of Electrical Engineering, Bahria University, Islamabad, 44000, Pakistan
4Department of Computer Engineering, Umm Al-Qura University, Makkah, 21955, Saudi Arabia
*Corresponding Author: Sikandar Zulqarnain Khan. Email: sikandar.khan@eava.ee
Received: 03 February 2022; Accepted: 06 March 2022

Abstract: This paper presents an efficient crypto processor architecture for key agreement using ECDH (Elliptic-curve Diffie Hellman) protocol over GF(2163). The composition of our key-agreement architecture is expressed in consisting of the following: (i) Elliptic-curve Point Multiplication architecture for public key generation (DESIGN-I) and (ii) integration of DESIGN-I with two additional routing multiplexers and a controller for shared key generation (DESIGN-II). The arithmetic operators used in DESIGN-I and DESIGN-II contain an adder, squarer, a multiplier and inversion. A simple shift and add multiplication method is employed to retain lower hardware resources. Moreover, an essential inversion operation is operated using the Itoh-Tsujii algorithm with similar hardware resources of used squarer and multiplier units. The proposed architecture is implemented in a Verilog HDL. The implementation results are given on a Xilinx Virtex-7 FPGA (field-programmable gate array) device. For DESIGN-I and DESIGN-II over GF(2163), (i) the utilized Slices are 3983 and 4037, (ii) the time to compute one public key and a shared secret is 553.7 μs and 1170.7 μs and (iii) the consumed power is 29 μW and 57 μW. Consequently, the achieved area optimized and power reduced results show that the proposed ECDH architecture is a suitable alternative (to generate a shared secret) for the applications that require low hardware resources and power consumption.

Keywords: Elliptic curve cryptography; point multiplication; key-agreement; diffie hellman; area optimized; architecture; FPGA

1  Introduction

In recent years, demand for the secure transmission of reliable information over any network is increasing dramatically. Various applications such as healthcare [1], automotive [2,3], aviation [4,5] smart cards [6,7], Internet of Things (IoT) [8–12], and several others require the secure exchange of sensitive information on insecure public channels. The cryptographic algorithms (both symmetric and asymmetric) are available in the literature to provide several security services like a public key exchange, signature generation/verification, authentication and encryption/decryption. Elliptic-curve cryptography (ECC) is a form of asymmetric cryptography, which provides an equivalent security level with a smaller key size in respect to other public-key cryptosystems such as RSA (Rivest-Shamir-Adleman) [13,14]. Moreover, many organizations such as IEEE (Institute of Electrical and Electronics Engineering), NIST (National Institute of Standards and Technology), ANSI (American National Standards Institute) and SEC (Standards for Efficient Cryptography) accepted ECC as standardization.

The security strength of ECC relies on solving the discrete logarithms problem [15]. It comprises four layers of a model [13]. The highest layer is the protocol that defines a set of rules to perform encryption/decryption, signature generation/verification and public key exchange. The Elliptic-curve point multiplication (ECPM) is the most critical operation. Its computation depends on the execution of point addition (PA) and double (PD) operations. Arithmetic operations (such as addition, multiplication, square and inversion) are needed to perform point addition and double computations.

There are different settings in the literature to implement ECC protocols. These settings indicate choices for (i) two different basis (polynomial and Gaussian normal) for the representation of the initial & final point and (ii) availability for two different coordinate systems (affine and projective). The polynomial basis is considered in this paper as it is more beneficial to acquire faster modular multiplications while a Gaussian normal basis is valuable where frequent squares are needed to compute [13,16]. Moreover, a projective coordinate system is selected because it requires minimum inversion operations when compared to an affine coordinate system [15].

1.1 Related Work

Several hardware architectures are published in the state-of-the-art to accelerate the performance of ECC operations [16–24]. Mostly the hardware implementations are considered for the optimizations of point multiplication (PM) operation in terms of various parameters such as frequency, area, power and throughput [16–21].

In [16], low-cost and high-speed PM architectures are described for Binary Edward Curves (BEC). Low cost means lower hardware resource utilization. The use of a pipelined digit serial multiplier results in low area utilization. The high-speed is attained with the employment of three pipelined multipliers. Over GF(2163) and GF(2233), the synthesis results are given on Virtex-5 FPGA device. In [17], an efficient PM architecture using Lopez Dahab algorithm is presented over GF(2m) with m=163. Towards clock cycles reduction, a hybrid Karatsuba multiplier is utilized. The reduced hardware resources are achieved with the utilization of multiplier and squarer units for the computation of modular inversion using the Itoh-Tsujii algorithm. The implementation results are reported on Xilinx Virtex-7 device, where the architecture takes 25.3 μs for one PM computation and utilizes only the 3657 slices. Another area optimized architecture over GF(2163) for PM computation is described in [18] where bit/digit serial multipliers are utilized. On Virtex-5 FPGA, their architecture requires 0.11 ms for one PM operation and utilizes 473 slices.

In [19], a high-speed and low-latency ECC processor implementation over GF(2m) on Virtex-4, Virtex-5 and Virtex-7 FPGA devices is presented. They reported implementation results using single and three modular multipliers. Their singular multiplier-based ECC processor provides the highest speed on Virtex4, Virtex5 and Virtex7 FPGA devices. Finally, on same FPGA devices, the use of three multipliers results in a decrease in the number of clock cycles. A dual binary field PM implementation of ECC over GF(2283) and GF(2571) on Virtex-5 and Virtex-7 FPGA devices is described in [20]. A Karatsuba multiplication method is employed to reduce the utilization of required clock cycles.

In [21], a high-performance hardware architecture of ECPM over GF(2m) field is presented. Their design is consists of a Montgomery ladder method and employs a polynomial basis for finite field arithmetic operations. A single Karatsuba multiplier is used to improve the performance of the PM architecture. Other operators (adder and squarer) with the consideration of a small number of hardware resources are utilized in parallel with the multiplier. These architectural employments ultimately reduce the clock cycles and lead to improving performance. For GF(2163) on Virtex-4 FPGA, their design utilizes 10417 slices and achieves an operational clock frequency of 121 MHz.

There are very few hardware designs where key-agreement using Elliptic-curve Diffie Hellman is considered for the optimizations on FPGA [22–24]. A hardware/software implementation of an ECDH protocol is described in [22]. The objective was to reduce the hardware resources and processing power for area-constrained applications. The implementation of their architecture was realized on a Virtex-5 FPGA device with the integration of a MicroBlaze softcore processor. A high-level synthesis (HLS) method is used in [23] to offload the ECDH operations on FPGA for the area and power reductions. Recently in [24], for wireless sensor nodes, a low-cost ECC hardware accelerator architecture is presented on FPGA. Their accelerator architecture was validated using a hardware/software codesign of the ECDH scheme (integrated into the MicroZed FPGA board). The ECDH protocol is operated in 4.1 ms for one shared key generation.

The related implementations, reported in [16–24], shows that the several modern applications such as healthcare [1], automobile [2,3], smart cards [6,7] and IoT [8–10] demand the key agreement architectures. Although, some limited designs are available [22–24], we believe further improvements in area and power can be achieved with use of different settings and strategies. Consequently, the aim of this work is to provide the FPGA implementation of ECDH protocol with different settings and optimization strategies to achieve low area and power values.

1.2 Contributions and Settings

Our contributions and employed strategies to reduce area and power values are as follows:

•   Elliptic-curve PM design (DESIGN-I): With the attention of flexible input/output interfaces, we have presented a low-area crypto processor architecture for Elliptic-curve PM computation over GF(2163). The flexible input/output interfaces determine that for generating coordinates of a public key, users can take x and y coordinates of an initial point on ECC either by using the constant (inside the crypto core) or user-dependent values (from the outside to the crypto core).

•   Key-agreement architecture (DESIGN-II): Generation of a shared key (or) key agreement between two different users/parties using the integration of DESIGN-I with two additional routing multiplexers and an efficient controller.

•   Dedicated controllers: For various control activities, we have used two dedicated finite state machine (FSM) based controllers.

•   Employed strategies to achieve low area and power: To achieve the low area and power values, a schoolbook multiplication method is used in the proposed crypto processor architectures (DESIGN-I and DESIGN-II). Moreover, similar hardware resources of squarer and multiplier units are used to compute the essential inversion operation. To further reduce the hardware resources, we set a design goal from balanced to area reduction during the logic synthesis in the Vivado IDE tool.

1.3 Critical Findings and Significance of This Work

The RTL (register transfer level) implementations of proposed crypto processor designs (DESIGN-I and DESIGN-II) are implemented in a Verilog (HDL). The results are reported on Xilinx Virtex-7 (xc7vx690t-3ffg1930) FPGA device. For DESIGN-I, the utilized Slices, LUTs (look-up-tables) and FFs (flip flops) over GF(2163) are 3983, 10693 and 2389. Similarly, the consumed Slices, LUTs and FFs for DESIGN-II are 4037, 11713 and 2427. The required clock cycles for DESIGN-I and DESIGN-II are 163902 (to generate one public key) and 327804 (to generate one shared secret), respectively. The maximum clock frequency for DESIGN-I and DESIGN-II is 296 and 280 MHz, respectively. The time to operate one public key using DESIGN-I is 553.7 μs. Similarly, the time to generate one shared secret using the ECDH scheme is 1170.7 μs. The DESIGN-I takes 29 μW to generate one public key (or to operate one PM computation) while DESIGN-II consumes 57 μW for one shared secret generation. The achieved area optimized and power reduced results reveal that the DESIGN-II is an appropriate choice (to generate a shared secret) for the applications that demand lower hardware resources without considering the timing characteristics (such as clock cycles, throughput and latency).

The structure of this paper is organized as: Section 2 presents the essential information for the computation of the ECDH scheme and the PM operation, respectively. The proposed crypto processor architecture for generating a public key (DESIGN-I) and shared secret (DESIGN-II) is provided in Section 3. The implementation results are presented in Section 4. Finally, Section 5 concludes the paper.

2  Mathematical Background

The mathematical structure of the ECDH protocol is described in Section 2.1. Moreover, the sequence of instructions for the computation of Elliptic-curve PM and the corresponding point addition and double formulas are provided in Section 2.2.

2.1 ECDH Protocol

A complete layout of the ECDH protocol for key agreement (or shared key generation) between two distinct users is illustrated in Fig. 1.

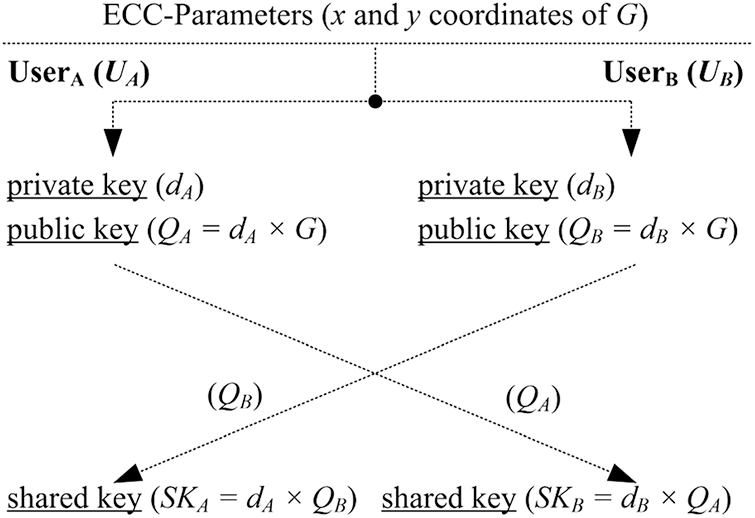
Figure 1: Layout of the ECDH protocol for key-agreement

As shown in Fig. 1, we have two distinct users, i.e., UA, and UB. The UB will generate his/her public key QB by taking a base-point G on the defined curve and a private key dB. A dB is an m-bit random number (or) a scalar multiplier. Based on these parameters (G & dB), the public key will be generated (i.e., QB=dB×G). Similarly, UA will repeat the exact same process to generate his/her public key QA using his/her private key dA and a base point G. The resulting public key will be QA=dA×G. Prior to generate the shared key, both users (UA & UB) will exchange their public keys to each other. Then, the UA and UB will generate their shared keys using SKA=dA×QB and SKB=dB×QA, respectively.

2.2 Elliptic-curve Point Multiplication

The PM operation is the computation of d−1 times the sum of a base (or) initial point G, as presented in Eq. (1):

Q=d×G=G+G+G…+G(1)

In Eq. (1), G is the initial point on the curve, Q is the resultant point and d is a scalar multiplier (or a private key of the corresponding user). There are several algorithms in the literature such as Double and Add, Montgomery ladder, Lopez Dahab, and many more to operate the ECPM operation in ECC. A comprehensive comparison over various ECPM algorithms as hardware accelerators on FPGA and ASIC (application-specific integrated circuits) platforms is shown in [25]. Consequently, we have used the following Montgomery (Algorithm 1) algorithm because (inherently) it counters simple power analysis (SPA) attacks. It is important to note that we are implementing only the SPA attacks at the algorithmic level without realizing on a design level.

The inputs to Algorithm 1 are initial point G and a scalar multiplier d. A sequence dn−1,…,d1,d0 determines the bits of the scalar multiplier in terms of 0′s and 1′s. The output from Algorithm 1 is the x and y coordinates of resultant point Q. The PA and PD operations in Algorithm 1 shows the number of instructions for point addition and double computations, respectively.

3  Proposed Key-Agreement Architecture

The proposed crypto processor architecture for ECDH is shown in Fig. 2. It consists of three blocks, i.e., (i) an ECDH controller, (ii) two routing multiplexers (M1 and M2) and an ECPM (DESIGN-I) unit. Description of these units are as follows:

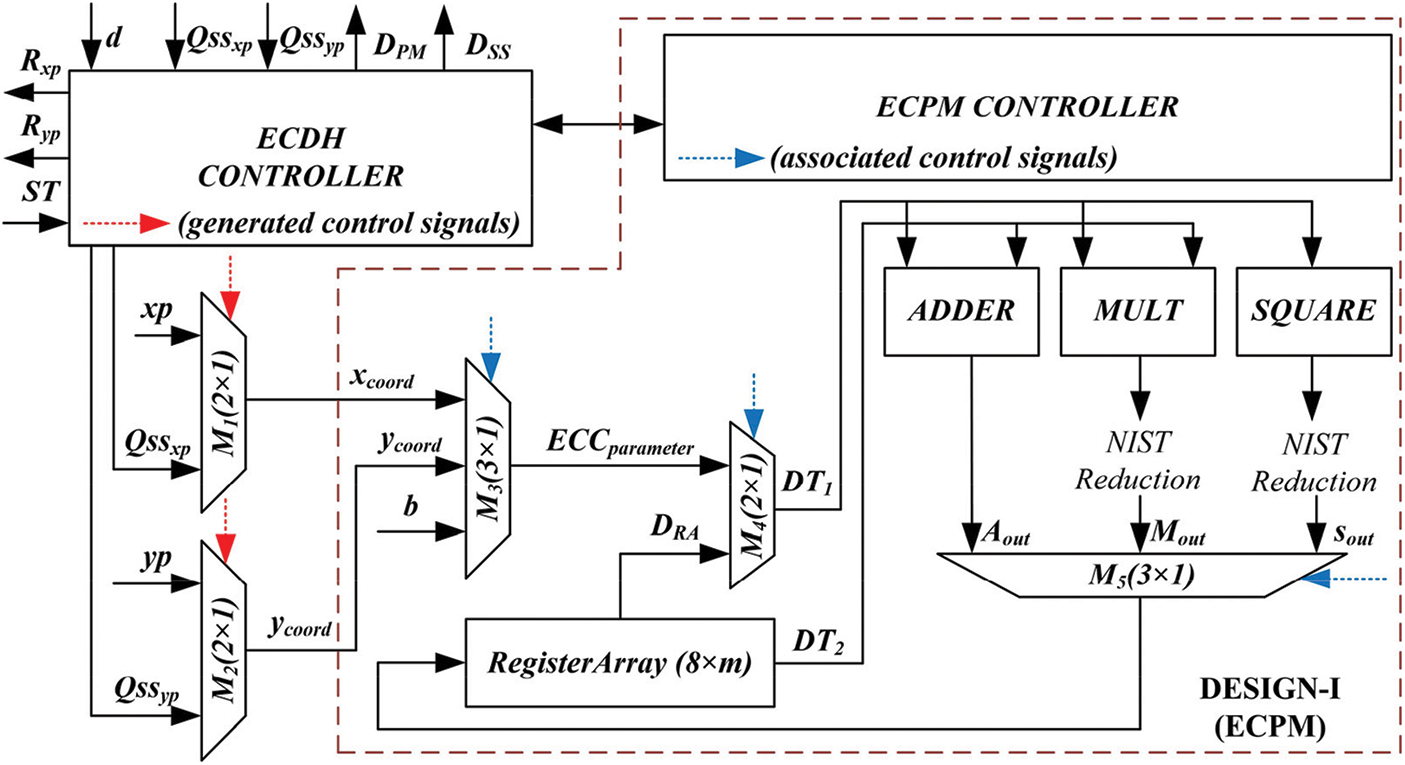
Figure 2: Proposed crypto processor architecture (DESIGN-II) for key-agreement of ECDH protocol

3.1 ECDH Controller

The ECDH controller is responsible for generating control signals for the routing multiplexers M1 and M2, as shown with red color dotted lines in Fig. 2. Moreover, it is responsible for communicating with the ECPM controller for the public and shared key generations. It takes d (an m-bit secret key or a scalar multiplier given in Algorithm 1), QSSxp (x-coordinate of an initial point G (or) public key of another user for the shared secret generation), QSSyp (y-coordinate of an initial point G (or) public key of another user for the shared secret generation) and ST (start signal) as an input. The Rxp and Ryp determines the x and y coordinates of either (i) our generated public key for UA or UB or (ii) shared secret for UA or UB as an output. The DPM and DSS are the one-bit done signals. These signals become true when the corresponding public key or shared secret generation is completed by the ECPM design. The clk and rst signals are input to the proposed ECDH crypto processor architecture and these are not shown in Fig. 2.

The ECDH controller is implemented by adopting a finite state machine (FSM) model. It contains three states, i.e., IDLE, PKG and SKG. As the name implies, IDLE is the initial state of the crypto processor that determines none of the operations is under computation. The PKG shows that the crypto processor is processing a public key. Finally, the SKG means that the processor architecture is computing a shared key. A two-bit input signal “select” from outside to ECDH controller, not shown in Fig. 2, identifies either the generation of a public key (or) shared key. Whenever the two-bit select signal is 00, it means NOP (meaning with no operation and processor will reside in IDLE state). For 01 and 10 cases, the ECDH controller passes the ST signal to the ECPM controller for the generation of corresponding public and shared keys. Once the corresponding public or shared key is generated, the ECPM controller acknowledges the ECDH controller with its associated done signal (DPM when coordinates of a public key is generated and DSS when coordinates of a shared key is generated). Based on the two-bit select signal, the ECDH controller generates the control signals for the routing multiplexers M1 and M2 to select the appropriate inputs (either coordinates of G or a public key of another user for computation of shared key) for DESIGN-I.

3.2 Routing Multiplexers (M1 and M2)

The purpose of M1 and M2 multiplexers is to select the x and y coordinates of either base point G (denoted with xp and yp in Fig. 2) or public key (shown with QSSxp and QSSyp in Fig. 2) of another user. As shown in Fig. 1, the ECDH scheme requires two PM computations. One for public key generation and another for a shared secret generation. Our architecture selects the x and y coordinates of G to generate the public key when the control signals for M1 and M2 are 0. Similarly, it selects the x and y coordinates of public key of another user to generate the shared key when the control signals to M1 and M2 are 1.

3.3 ECPM Unit (DESIGN-I)

The ECPM unit consists of (i) an array of registers, (ii) three routing multiplexers, (iii) adder, squarer, multiplier, polynomial reduction & inversion units and (iv) an ECPM controller. The description of these units are given in the next subsequent sections:

3.3.1 Register Array

The register array in the proposed crypto processor architecture is an 8×m size of register file. A variable m denotes the width of each register while a numerical value 8 shows the total number of register addresses. As a fact, the used register array is liable for preserving the intermediate and the final results during and after the implementation of the Algorithm 1. The inside to register array unit, shown in Fig. 2, comprises two 8×1 multiplexers that are responsible to fetch/reading data from the used register array. Moreover, it includes a 1×8 demultiplexer to modify the contents of each register address. The corresponding control signals for reading and write operations are generated from the ECPM controller (not shown in Fig. 2).

3.3.2 Three Routing Multiplexers (M3, M4 and M5)

The three routing multiplexers in the proposed architecture include M3(3×1), M4(2×1) and M5(3×1). The M3 multiplexer is used to choose an ECC parameter (i.e., xcoord, ycoord and a curve constant b). These parameters are needed during the implementation of Algorithm 1. For our implementations, there are two choices to take xcoord and ycoord of input parameters. The first choice is from the outside to our design using M1 and M2 multiplexers. Another choice is the use of parameters as constants inside the design. For these two choices, we are using always a constant value for parameter b (shown in Fig. 2). For instance, this is the limitation of our proposed architecture. Similarly, the M4 multiplexer drives the output of M3 and an operand from the register array to arithmetic operators. Finally, M5 multiplexer is responsible for selecting an output from arithmetic operators for the register file to perform written back. Noted that, in this paper, the xcoord, ycoord and constant b parameters are selected from NIST (National Institute of Standards and Technology) standardized document [26].

3.3.3 Adder, Squarer, Multiplier, Reduction and Inversion Units

The arithmetic operators, i.e., addition (ADDER), squaring (SQUARE) and multiplication (MULT), perform the PM operation of the ECPM unit. The implementation of a polynomial addition in GF(2m) is rather simple than the prime field. Therefore, the ADDER unit comprises an array of bitwise Exclusive (OR) gates. The polynomials DT1 and DT2 determine the inputs while an m-bit polynomial Aout is output. The implementation of the SQUARE unit is achieved by placing a 0-bit after each successive data bit. It takes an m-bit operand either from the register array or routing multiplexers to perform polynomial squaring. A 2×m−1 bit polynomial (Sout) is generated as an output.

The efficiency of a polynomial multiplier specifies the performance of an ECC-based crypto processor architecture. Based on the available literature, there are four possibilities to implement a multiplier circuit. These possibilities are (i) bit-serial, (ii) digit-serial, (iii) bit-parallel and (iv) digit-parallel. Each aforementioned architectural choice has certain differences. When we consider only the computational cost in terms of clock cycles, the bit-serial multipliers require m cycles. On the other hand, one clock cycle is needed to implement the bit/digit parallel multiplication approaches. The digit-serial multipliers demand ab cycles. A variable a shows the operand size and b presents the length of an incorporated digit. The aforesaid discussion reveals that each multiplication style has its pros and cons as the computational costs are different. Despite the computational costs, the bit-serial multiplication approaches are practical in scenarios where demand for lower hardware resources and power consumption are required. The specific examples include the RFID (radio frequency identification networks) and WSNs (wireless sensor networks) related applications. The bit/digit-parallel multipliers provide high-performance(s). The digit-serial multipliers are useful in applications that require lower hardware area and lower computation time. Consequently, a bit-serial shift and add multiplication method is utilized in our MULT unit to perform two m bit polynomial multiplications. It takes two DT1 and DT2 polynomials as input and yields in 2×m−1 bit polynomial (Mout) as output. In the employed shift and add multiplication approach, the multiplicand (DT1 in our work) is added DT2 times to itself, where DT2 is the multiplier. It takes m cycles to produce one polynomial multiplication.

The size of resultant polynomials generated after MULT and SQUARE units are 2×m−1 bit (not shown in Fig. 2). Therefore, the reduction from 2×m−1 to m bit is essential. The polynomial reduction, in this work, is achieved by using a NIST-specified algorithm (we refer interested readers to Algorithm 2.41 of [15]).

As shown in Algorithm 1, the reconversion from projective to affine requires two polynomial inversion computations. There are several inversion methods in the literature to perform the multiplicative inverse of the polynomial(s). Therefore, the Itoh Tsujii algorithm is extensively employed in the state-of-the-art because it needs multiplications and square operations for computation [13,17,18]. In this paper, we have (also) utilized the implementation resources of our employed MULT and SQUARE units to perform multiplicative inverse over polynomials using the Itoh Tsujii algorithm. Over GF(2163), the cost for execution of nine polynomial multiplications and m−1 squares determine the computational cost of an Itoh Tsujii algorithm [27]. As expressed before, each polynomial multiplication using shift and add method needs m clock cycles when the inputs to our MULT are m-bits. Therefore, the execution of nine multiplications needs 9×m cycles. The m−1 cycles are needed for the squaring as one square takes only the one clock cycle. Thus, the computational cost to perform one inversion is (9×m)+(m−1).

3.3.4 ECPM Controller

The FSM-based ECPM controller is responsible to perform the PM operation of Eq. (1). It generates the control signals to implement the Algorithm 1. The generated control signals for the routing multiplexers and register array are shown with blue color dotted lines in Fig. 2. The details of the ECPM controller is as follows:

•   The proposed crypto processor will remain in state 0 (IDLE state).

•   It starts the computation once it receives the ST signal as 1 from the ECDH controller. After the ST signal becomes 1, the control signals for projective to affine conversions are generated which takes six clock cycles (for six states). For PM computation in projective coordinates, the point addition and double instructions of Algorithm 1 are operated in 14 states as these functions contain seven instructions (from 1 to 7) for each point addition and double operation. Thus, a total of fourteen instructions are involved. During the execution of each state, the value for an inspected key bit, i.e., di, is checked. When the inspected value for di is 1, the corresponding instructions of if statement will be executed. If not, the else statement is operated. In short, these fourteen states will continue to repeat as far as the condition for loop instruction of Algorithm 1 eventually be true.

•   Under different conditions, when the loop instruction of Algorithm 1 becomes true, the processor switches control from PM to projective to affine conversion states.

3.4 Total Clock Cycles (TCC) Calculation for DESIGN-I and DESIGN-II

For the proposed DESIGN-I, Eq. (2) is used to calculate the total clock cycles. Similarly, the total cycles for DESIGN-II are calculated using Eq. (3).

TCCDI=6+[m−1(6×m+8)]+2(inversion)+906(2)

TCCDII=2×TCCDI(3)

In Eq. (2), 6 determines the clock cycles for the affine to projective conversion. The m−1(6×m+8) shows the clock cycles for the PM computation in projective coordinates. More precisely, 6×m are the clock cycles for modular multiplication instructions in point addition and double operations, where m is the clock cycles for one modular shift and add multiplication method. A numerical value 8 shows the clock cycles for the modular addition and square operations in point addition and double instructions (total 8). Hence, the addition of modular multiplications (total six instructions), modular addition (total three instructions) and modular square (total five instructions) becomes the total of fourteen instructions in point addition and double operations. For GF(2163), the proposed DESIGN-I takes 6 clock cycles for affine to projective conversion, 159732 cycles for the PM computation in projective coordinates and 4164 cycles for projective to affine conversions. In projective to affine conversion, each inversion requires 1629 clock cycles and additional 906 cycles are needed to compute the remaining operations of projective to affine conversions. Consequently, the proposed DESIGN-I takes 163902 clock cycles for a public key generation (or for one PM computation).

As shown in Fig. 1, the ECDH scheme consists of dual PM computation (one for a public key generation and another for shared key). Therefore, Eq. (3) confirms that our DESIGN-II needs 163902 + 163902 (327804) clock cycles for one shared key generation between two distinct users (as we mentioned UA and UB in Section 2.1).

4  Implementation Results and Comparisons

The details for the implementation results and comparison to state-of-the-art is given in Section 4.1 and Section 4.2, respectively.

4.1 Implementation Results

Our DESIGN-I and DESIGN-II over GF(2163) is implemented in Verilog HDL using the Vivado IDE tool. The implementation results are reported after running the post-place-and-route design process. A Xilinx Virtex-7 (xc7vx690t-3ffg1930) FPGA device [28] is used for logic synthesis and routing purposes. Before presenting our implementation results, we have reported area utilization of building blocks of DESIGN-I and DESIGN-II in Section 4.1.1. The details for implementation results of our DESIGN-I and DESIGN-II are described in Section 4.1.2. The area comparison of DESIGN-I and DESIGN-II with the sum of Slices and LUTs (look-up-tables) of building blocks are given in Section 4.1.3. Finally, the comparison between DESIGN-I and DESIGN-II is presented in Section 4.1.4.

4.1.1 Area Utilization of Building Blocks of DESIGN-I and DESIGN-II

The area breakdown for building blocks in DESIGN-I and DESIGN-II are shown in Tab. 1. Column one provides the name of the building-blocks of our proposed design. From columns two to four, the area utilization is presented in terms of FPGA LUTs, Slices and FFs (flip-flops).

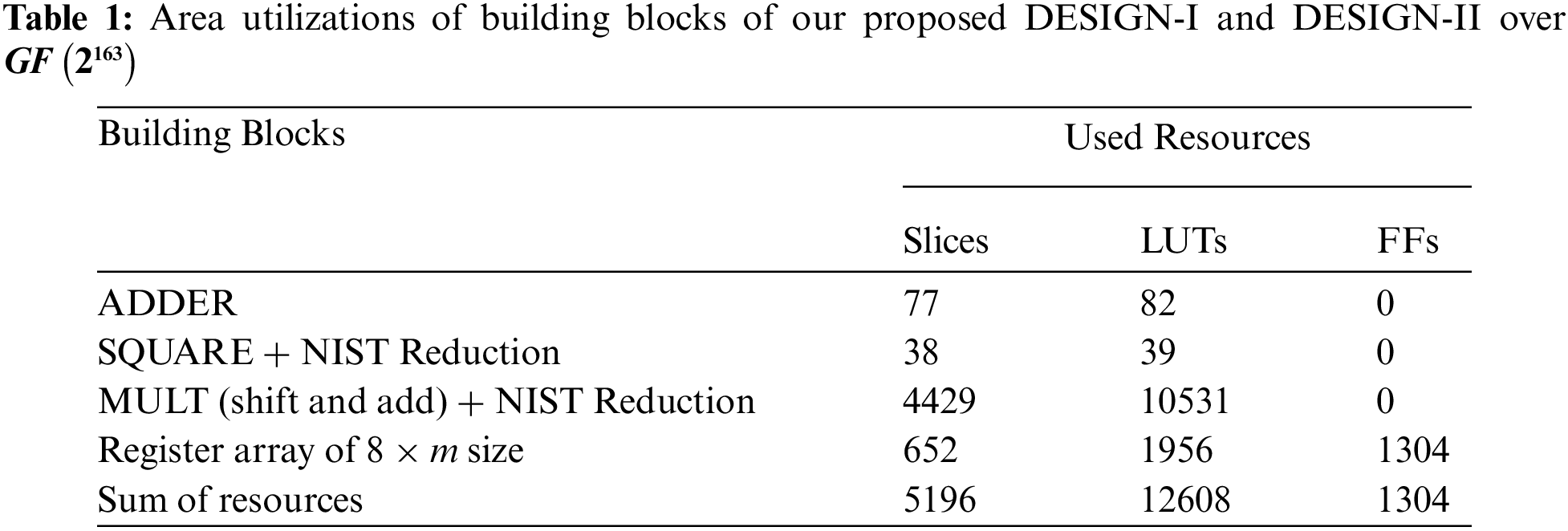
As shown in Tab. 1, the critical building blocks of DESIGN-I and DESIGN-II over Virtex-7 FPGA utilizes 77, 38, 4429 and 652 FPGA Slices for ADDER, SQUARE (including NIST Reduction), MULT (including NIST Reduction) and register array. Similarly, for identical building blocks, the LUTs utilization is 82, 39, 10531 and 1956. The sum of resources for building blocks is 5196 (Slices), 12608 (LUTs) and 1304 (FFs). Tab. 1 reveals that the MULT unit (even with simple shift and add architecture) utilizes more hardware resources as compared to other building blocks. Moreover, the implementation results show that the modular square operation being much simpler in the GF(2m) field than with the array of bitwise Exclusive (OR) gates (in our implemented ADDER unit).

Concerning the sum of resources of building blocks of our DESIGN-I and DESIGN-II, apart from the routing multiplexers, the reported Slices (5196) and LUTs (12608) values in Tab. 1 are still enough in large. Many area-constrained applications such as smart cards, IoT, automotive and several others demand lower hardware resources. In this regard, we have set design goals from balanced to area reduction in the Vivado IDE tool to minimize the hardware resources of our DESIGN-I and DESIGN-II implementations. Therefore, a description of the results is provided in the following section.

4.1.2 Implementation Results for DESIGN-I and DESIGN-II

The detailed implementation results of our proposed DESIGN-I and DESIGN-II are shown in Tab. 2. Column one provides the reference design. The area information in Slices, LUTS and FFs is given in columns two, three and four. Columns five and six provide the total clock cycles and operational clock frequency (in MHz), respectively. Latency is the time for computation of one required cryptographic operation and therefore, the latency (in μs) for one public key and a shared secret generation is given in columns seven to eight, respectively. Finally, the last column presents the total power consumption of our proposed DESIGN-I and DESIGN-II. Note that the reported values for area and clock frequency in Tab. 2 are obtained from the Vivado IDE tool. The total clock cycles are calculated from Eqs. (2) and (3). For both DESIGN-I and DESIGN-II, the latency for one PM computation is calculated using Eq. (4). Similarly, we have used the same Eq. (4) or the calculation of ECDH latency of our DESIGN-II. We clarify that our DESIGN-I does not support ECDH operation, hence its latency is denoted by ‘–’ in Tab. 2.

Latency (in μs)=Total Clock CyclesClock Frequency (in MHz)(4)

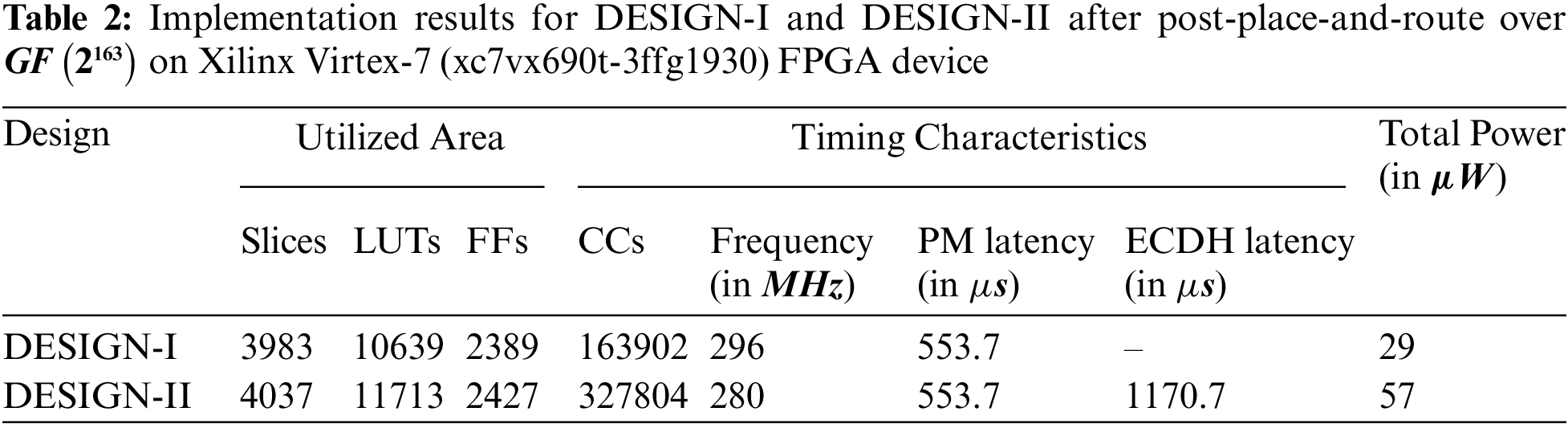
As shown in Tab. 2, the utilized hardware resources of DESIGN-I are 3983 (Slices), 10639 (LUTs) and 2389 (FFs). Similarly, the utilized resources of DESIGN-II are 4037 (Slices), 11713 (LUTs) and 2427 (FFs). The achieved clock frequency for DESIGN-I and DESIGN-II are 296MHz and 280MHz, respectively. The required clock cycle (for DESIGN-I) to generate one public key is 163902. Similarly, the clock cycle (for DESIGN-II) to generate one shared secret is 327804. Both DESIGN-I and DESIGN-II take the 553.7μs to generate one public key, while the DESIGN-II requires 1170.7μs to generate one shared key. As shown in the last column of Tab. 2, the power consumption of our DESIGN-I and DESIGN-II is 29μW and 57μW, respectively.

4.1.3 Area Comparison of DESIGN-I and DESIGN-II with the Sum of Slices and LUTs of Building Blocks

The total sum of Slices and LUTs of building blocks is 1.30 (ratio of 5196 with 3983) and 1.18 (ratio of 12608 with 10639) times higher than the Slices and LUTs of our DESIGN-I. Similarly, when the area resources of DESIGN-II are considered for comparison, the total sum of Slices and LUTs of building blocks is 1.28 (ratio of 5196 with 4037) and 1.07 (ratio of 12608 with 11713) times higher. This indicates that the use of different optimization strategies for synthesis of DESIGN-I and DESIGN-II results in lower resources. The reason is that we set the area optimization as synthesis goal in a Vivado IDE tool.

4.1.4 Comparison Between DESIGN-I and DESIGN-II

As far as the utilized area is concerned, DESIGN-I takes only the 3983, 10639 and 2389 Slices, LUTs and FFs. The reported FPGA area values in terms of Slices, LUTs and FFs for DESIGN-II are 4037, 11713 and 2427 that are comparatively 1.01 (ratio of 4037 with 3983), 1.10 (ratio of 11713 with 10639) and 1.01 (ratio of 2427 with 2389) times higher than our DESIGN-I. The reason for higher hardware resources in DESIGN-II is the use of two additional routing multiplexers (M1 and M2) and an ECDH controller to generate the shared key. On the other hand, the DESIGN-I is only responsible for the computation of a public key (or scalar multiplication). The clock cycles requirement of our DESIGN-I and DESIGN-II is 163902 and 327804 for public key and a shared secret generation. Our DESIGN-I can operate on a maximum clock frequency of 296MHz while DESIGN-II achieves 280MHz. For DESIGN-I and DESIGN-II, the time (or latency) required to compute one public key is 553.7μs. Time to perform a shared secret with our DESIGN-II is twice the time for a public key as in the ECDH scheme, the PM (or scalar multiplication) is essential to compute two times (one for public key and another for shared secret). On Virtex-7 FPGA, DESIGN-I and DESIGN-II consumes 29μW and 57μW for generating the public key and a shared secret, respectively.

4.2 Comparison with State-of-the-Art

The comparison with the most compatible state-of-the-art architectures, published in [13,16–19,22,24], is given in Tab. 3. The column one in Tab. 3 provides the reference design. The implemented PM algorithms and key-agreement protocols are presented in column two. The implementation device for logic synthesis is provided in column three. Column four presents the utilized FPGA slices. Finally, the last two columns (five and six) provide the clock frequency (in MHz) and latency (in μs) parameters, respectively. In Tab. 3, a representation ‘–’ means that the relevant information is not given in the reference design.

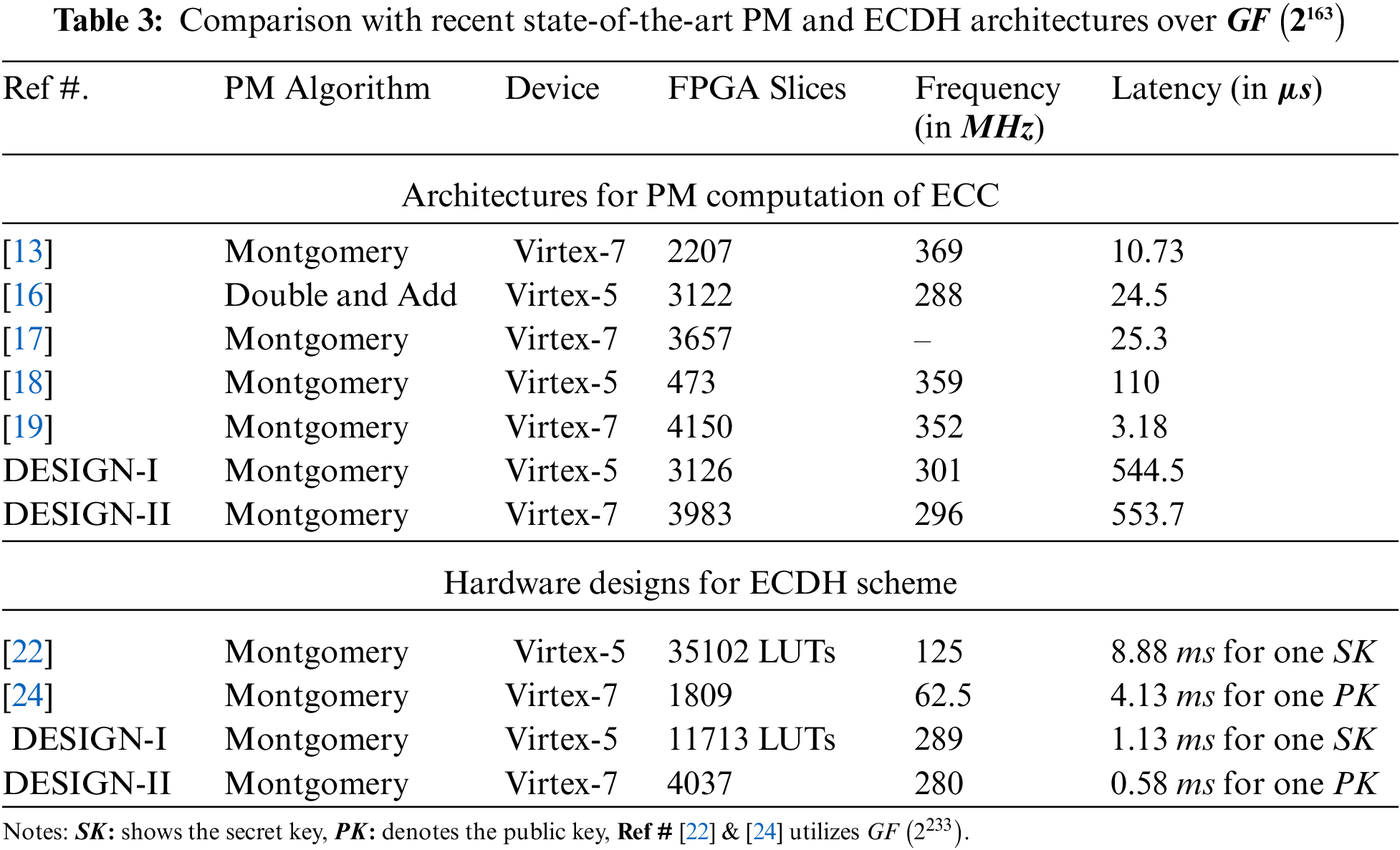
4.2.1 Comparison of our DESIGN-I with [16] and [19]

As compared to the dedicated PM architecture of [16] on Virtex-5 FPGA, our DESIGN-I utilizes 1.09 (3126 over 3122) times lower FPGA Slices. Moreover, in terms of clock frequency, our DESIGN-I is 1.04 (ratio of 301 over 288) times faster than [16]. On the other hand, the time required for one PM computation or public key generation in [16] is 22.2 (ratio of 544.5 over 24.5) times lower than our DESIGN-I. There is always a tradeoff between area and performance (latency) parameters. On Virtex-7 FPGA, a high-speed and latency optimized architecture of [19] for PM computation utilizes 4150 FPGA Slices which is comparatively 1.04 (ratio of 4150 over 3983) times higher than our DESIGN-I. Moreover, their architecture results in higher clock frequency (352MHz) when compared to our design (where we achieved 296MHz). Similar to [16], the PM architecture of [19] requires lower computational time as compared to our DESIGN-I. It is important to note that the main objective of this work was to succeed the minimum hardware resources (FPGA Slices, LUTs and FFs) without concentrating on other design parameters such as clock frequency, power, and latency.

4.2.2 Design Tradeoffs Between [13,17,18] and our DESIGN-I

As shown in Tab. 3, the dedicated PM architectures (reported in [13,17,18]) over Virtex-5 and Virtex-7 FPGA devices show that there is always a tradeoff between several design parameters when implementing the cryptographic algorithms as a hardware accelerator. In the text that follows, a tradeoff by providing the comparison of dedicated PM designs (published in [13,17,18]) with our notion of a flexible crypto processor (DESIGN-I) is described. As reported earlier in this paper, flexibility determines the selection of ECC parameters according to the user’s needs (readers can turn to multiplexer M3 in Fig. 2).

On Virtex-7 FPGA, a 2-stage pipelined PM architecture of [13] utilizes 1.80 (ratio of 3983 over 2207) times lower Slices as compared to our DESIGN-I. The reason for the utilization of lower hardware resources is the use of only one multiplier architecture for both square and polynomial multiplication computations. The square operations are computed by providing similar inputs to the multiplier unit. Additionally, the use of a singular NIST reduction unit also leads to a decrease in hardware resources. Comparatively, we are using a separate MULT and SQUARE unit to operate polynomial multiplications and squaring operations, respectively. In addition, we have two NIST reduction units connected one after each MULT and SQUARE unit in our designs. These architectural differences result in an increase in hardware resources in our work. Due to pipelining in [13], the achieved clock frequency is a bit higher than our crypto processor design. Furthermore, the time to operate one PM computation is lower than our DESIGN-I. In [17], 3657 FPGA Slices is used on Virtex-7 FPGA for the PM computation over GF(2163). This is comparatively 1.08 (ratio of 3983 over 3657) times lower than our DESIGN-I. The clock frequency of their architecture is not presented. Thus, this comparison is not possible to provide. The calculated latency value for [17] is lower than our proposed DESIGN-I as this is a dedicated PM architecture, where the coordinates of the initial point on ECC was applied as a 163-bit constants (inside the core). In our DESIGN-I (shown in Fig. 2), a routing multiplexer M3 takes coordinates of an initial point on ECC as input from outside to DESIGN-I. Therefore, for each public key generation, users can choose different ECC basepoints according to their needs when initiating a setup for public key generation.

As compared to the PM architecture of [18] on Virtex-5 FPGA, our DESIGN-I consumes 6.6 (ratio of 3126 to 473) times higher FPGA Slices. The reason is the employment of two NIST reduction units, one after in each SQUARE and MULT unit in our architecture. Moreover, a segmented digit serial multiplier architecture is used in [18] while in our design, a shift and add multiplication method is used for polynomial multiplication. Similar to the area (FPGA slices), the dedicated PM architecture of [18] achieves higher clock frequency and requires lower computational time as compared to our DESIGN-I. One of the reasons for this is to consider flexibility when selecting different curve parameters as inputs to our DESIGN-I using routing multiplexers M1, M2 and M3. An additional reason is the use of a higher number of input/output interfaces when taking coordinates of a public key as input from outside and producing either public key or shared secret as an output. On the other hand, the dedicated architecture of [18] uses the ECC parameters as constants inside their design.

Remarks: We are not asserting that our DESIGN-I outperforms (in terms of hardware area) in all state-of-the-art PM implementations. There is always a tradeoff when considering several design parameters concurrently for optimizations. Therefore, based on the comparisons presented above, we have noted that the hardware accelerators of ECC for only optimized for PM computation can result in little unfair measurements when scaling the same PM architecture to any ECC protocol (such as ECDH in this work). Therefore, a hardware architecture with the considerations of all four layers could be more beneficial.

4.2.3 Comparison of our DESIGN-II (ECDH) with [22] and [24]

The accelerator architectures of [22,24] for ECDH scheme are presented over GF(2233) while our ECDH design is provided over GF(2163). Although their architectures consider 1.42 (ratio of 233 over 163) times higher key length when compared to our DESIGN-II. On the other hand, our DESIGN-II is 2.312 (ratio of 289 over 125) and 4.48 (ratio of 280 over 62.5) times faster as compared to [22] and [24] over Virtex-5 and Virtex-7 FPGA devices, respectively. When comparing the hardware resources, our DESIGN-II utilizes 2.99 (ratio of 35102 over 11713) times lower FPGA LUTs as compared to [22]. The FPGA Slices used in [24] is 2.23 (ratio of 4037 over 1809) times lower than our DESIGN-II. Apart from hardware resources (FPGA Slices and LUTs) and clock frequency, the time to generate one public key and a shared secret are much lower than the ECDH accelerator architectures of [22] and [24], respectively. In detail, a coprocessor architecture of [22] requires 8.88 ms to generate one shared secret while our DESIGN-II takes only the 1.13 ms, which is comparatively 7.85 (ratio of 8.88 over 1.13) times lower. Similarly, the architecture of [24] on Virtex-7 FPGA requires 4.13 ms to generate one public key while our DESIGN-II takes only the 0.58 ms, which is comparatively 7.12 (ratio of 4.13 over 0.58) times lower.

5  Conclusions

This paper has presented a key-agreement architecture for the ECDH scheme over GF(2163) with the consideration of low hardware resources. Towards hardware resource reduction: (i) a simple shift and add multiplier is used and (ii) a polynomial inversion is computed using the Itoh-Tsujii algorithm with similar hardware resources of squarer and multiplier units. The proposed architecture is implemented in a Verilog HDL using Vivado IDE. The implementation results after the post-place-and-route are given on a Xilinx Virtex-7 FPGA. The utilized Slices over GF(2163) for one shared key generation is 4037. The clock cycles to compute one public key and a shared secret are 163902 and 327804. The time to operate one public key and a shared secret is 553.7 ms and 1170.7 ms, respectively. The consumed power is 29 μW (for one public key calculation) and 57 μW (for singular shared secret computation). We have concluded that the hardware accelerators of ECC for only optimized for PM computation can result in little unfair measurements when scaling same architectures to any ECC protocol (such as ECDH in this work). Subsequently, a hardware architecture with the considerations of all four layers could be more beneficial to achieve better performance(s).

Acknowledgement: We extend our gratitude to the Estonian Aviation Academy, Tartu, Estonia for supporting and funding this research work.

Funding Statement: We acknowledge the support of Deanship of Scientific Research at King Khalid University for funding this work under grant number R.G.P.1/399/42.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  K. Tamilarasi and A. Jawahar, “Medical data security for healthcare applications using hybrid lightweight encryption and swarm optimization algorithm,” Wireless Personal Communication, vol. 114, no. 3, pp. 1865–1886, 2020. [Google Scholar]

 2.  S. Tangade, S. S. Manvi and P. Lorenz, “Trust management scheme based on hybrid cryptography for secure communications in vanets,” IEEE Transactions on Vehicular Technology, vol. 69, no. 5, pp. 5232–5243, 2020. [Google Scholar]

 3.  P. S. Murvay and B. Groza, “Efficient physical layer key agreement for flexray networks,” IEEE Transactions on Vehicular Technology, vol. 69, no. 9, pp. 9767–9780, 2020. [Google Scholar]

 4.  H. Yang, Q. Zhou, M. Yao, R. Lu, H. Li et al., “A practical and compatible cryptographic solution to ADS-B security,” IEEE Internet of Things Journal, vol. 6, no. 2, pp. 3322–3334, 2019. [Google Scholar]

 5.  G. Andrei, T. Polishchuk and M. Wernberg. “Controller–pilot data link communication security,” Sensors, vol. 18, no. 5, pp. 1636, 2018. [Google Scholar]

 6.  Y. Eslami, A. Sheikholeslami, P. G. Gulak, S. Masui and K. Mukaida, “An area-efficient universal cryptography processor for smart cards,” IEEE Transactions on Very Large Scale Integration (VLSI) Systems, vol. 14, no. 1, pp. 43–56, 2006. [Google Scholar]

 7.  R. A. Nelson, “Authentication Techniques for Smart Cards,” United States, 1994. [Online]. Available: https://www.osti.gov/servlets/purl/10141490. [Google Scholar]

 8.  R. Vinoth, L. J. Deborah, P. Vijayakumar and N. Kumar, “Secure multifactor authenticated key agreement scheme for industrial IoT,” IEEE Internet of Things Journal, vol. 8, no. 5, pp. 3801–3811, 2021. [Google Scholar]

 9.  J. Srinivas, A. K. Das, M. Wazid and N. Kumar, “Anonymous lightweight chaotic map-based authenticated key agreement protocol for industrial internet of things,” IEEE Transactions on Dependable and Secure Computing, vol. 17, no. 6, pp. 1133–1146, 2020. [Google Scholar]

10. K. Sahu, S. Sharma and D. Puthal, “Lightweight multi-party authentication and key agreement protocol in IoT-based e-healthcare service,” ACM Transactions on Multimedia Computing, Communications, and Applications, vol. 17, no. 2s, pp. 1–20. 2021. [Google Scholar]

11. S. M. Z. Khan, Y. L. Moullec and M. M. Alam, “An NB-IoT based edge-of-things framework for energy-efficient image transfer,” Sensors, vol. 21, no. 17, pp. 5929, 2021. [Google Scholar]

12. S. M. Z. Khan, M. M. Alam, Y. L. Moullec, A. Kuusik, S. Pärand et al., “An empirical modeling for the baseline energy consumption of an NB-IoT radio transceiver,” IEEE Internet of Things Journal, vol. 8, no. 19, pp. 14756–14772, 2021. [Google Scholar]

13. M. Imran, M. Rashid, A. R. Jafri and M. Kashif, “Throughput/area optimised pipelined architecture for elliptic curve crypto processor,” IET Computers & Digital Techniques, vol. 13, no. 5, pp. 361–368, 2019. [Google Scholar]

14. M. M. Islam, M. S. Hossain, M. Shahjalal, M. K. Hasan and Y. M. Jang, “Area-time efficient hardware implementation of modular multiplication for elliptic curve cryptography,” IEEE Access, vol. 8, pp. 73898–73906, 2020. [Google Scholar]

15. D. Hankerson, A. J. Menezes and S. Vanstone, “Guide to Elliptic Curve Cryptography,” Henderson, NV, USA: Springer, pp. 1–311, 2004. [Online]. Available: https://link.springer.com/book/10.1007/b97644. [Google Scholar]

16. B. Rashidi, “Low-cost and fast hardware implementations of point multiplication on binary edwards curves,” in Electrical Engineering (ICEEIranian Conf. on, Mashhad, Iran, pp. 17–22, 2018. [Google Scholar]

17. M. Imran, M. Rashid and I. Shafi, “Lopez dahab based elliptic crypto processor (ECP) over GF(2163) for low-area applications on FPGA,” in 2018 Int. Conf. on Engineering and Emerging Technologies (ICEET), Lahore, Pakistan, pp. 1–6, 2018. [Google Scholar]

18. Z. U. A. Khan and M. Benaissa, “Low area ECC implementation on FPGA,” in 2013 IEEE 20th Int. Conf. on Electronics, Circuits, and Systems (ICECS), Abu Dhabi, United Arab Emirates, pp. 581–584, 2013. [Google Scholar]

19. Z. U. A. Khan and M. Benaissa, “High-speed and low-latency ECC processor implementation over GF(2m) on FPGA,” IEEE Transactions on Very Large Scale Integration (VLSI), vol. 25, no. 1, pp. 165–176, 2017. [Google Scholar]

20. J. Li, W. Wang, J. Zhang, Y. Luo and S. Ren, “Innovative dual-binary-field architecture for point multiplication of elliptic curve cryptography,” IEEE Access, vol. 9, pp. 12405–12419, 2021. [Google Scholar]

21. S. Liu, L. Ju, X. Cai, Z. Jia and Z. Zhang, “High performance FPGA implementation of elliptic curve cryptography over binary fields,” in 2014 IEEE 13th Int. Conf. on Trust, Security and Privacy in Computing and Communications, Beijing, China, pp. 148–155, 2014. [Google Scholar]

22. A. P. Fournaris, I. Zafeirakis, C. Koulamas, N. Sklavos and O. Koufopavlou, “Designing efficient elliptic curve diffie-hellman accelerators for embedded systems,” in 2015 IEEE Int. Symp. on Circuits and Systems (ISCAS), Lisbon, Portugal, pp. 2025–2028, 2015. [Google Scholar]

23. D. Ionita and E. Simion, “FPGA offloading for diffie-hellman key exchange using elliptic curves,” Cryptology ePrint Archive, Report 2021/065, 2021. [Online]. Available: https://ia.cr/2021/065. [Google Scholar]

24. M. Morales-Sandoval, L. A. R. Flores, R. Cumplido, J. J. Garcia-Hernandez, C. Feregrino et al., “A compact FPGA-based accelerator for curve-based cryptography in wireless sensor networks,” Journal of Sensors, vol. 2021, pp. 13, 2021. [Google Scholar]

25. M. Rashid, M. Imran, A. R. Jafri and T. F. Al-Somani, “Flexible architectures for cryptographic algorithms: A systematic literature review,” Journal of Circuits Systems and Computers, vol. 28, no. 3, pp. 35, 2019. [Google Scholar]

26. NIST. “Recommended Elliptic Curves for Federal Government use,” 1999. [Online]. Available: https://csrc.nist.gov/csrc/media/publications/fips/186/2/archive/2000-01-27/documents/fips186-2.pdf. [Google Scholar]

27. P. Zode, R. B. Deshmukh and A. Samad, “Fast architecture of modular inversion using Itoh-Tsujii algorithm,” in VLSI Design and Test, Singapore: Springer, pp. 48–55, 2017. [Online]. Available: https://www.springerprofessional.de/fast-architecture-of-modular-inversion-using-itoh-tsujii-algorit/15326436. [Google Scholar]

28. XILINX, “7 Series Product Selection Guide,” [Online]. Available: https://www.xilinx.com/products/silicon-devices/fpga/virtex-7.html. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.