DOI:10.32604/cmc.2022.027582

| Computers, Materials & Continua DOI:10.32604/cmc.2022.027582 |  |
| Article |
A Block Cipher Algorithm Based on Magic Square for Secure E-bank Systems
Computer Science Department, University of Technology, Baghdad, 10011, Iraq
*Corresponding Author: Farah Tawfiq Abdul Hussien. Email: Farah.T.Alhilo@uotechnology.edu.iq
Received: 20 January 2022; Accepted: 12 April 2022
Abstract: Nowadays the E-bank systems witnessed huge growth due to the huge developments in the internet and technologies. The transmitted information represents crucial information that is exposed to various kinds of attacks. This paper presents a new block cipher technique to provide security to the transmitted information between the customers and the e-bank systems. The proposed algorithm consists of 10 rounds, each round involves 5 operations. The operations involve Add round key, Sub bytes, Zigzag method, convert to vector, and Magic Square of order 11. The purpose of this algorithm is to make use of the complexity of the Magic Square algorithm, the speed of addition operation, the confusion provided by the zigzag, using these operations with Galois field 28 GF(28), and repeating these operations for several rounds to build fast high secure encryption algorithm. This algorithm is designed to provide fast with high complexity and security which is suitable to encrypt the data that is transmitted over the internet. Speed, complexity, and The National Institute of Standards and Technology Framework NIST suite tests were done. The complexity of the proposed algorithm is = ((256)32)r+1*((256)89)r+1 + (256)121. The proposed technique gives higher speed and security in the encryption and decryption phases, according to the results of the experiments. The degree of randomness has grown by 31.8 percent. Due to a decrease in the time of encrypting and decrypting, as well as the usage of the central processing unit (CPU), efficiency is improved. The encryption process throughput is enhanced by 13%, while the decryption process throughput is increased by 11.6 percent with the recommended approach.
Keywords: Block cipher; magic square order 11; complexity; NIST suite; zigzag; GF(28); MS11
The huge development in lifestyle and technologies results in a daily huge amount of information transmission over the internet [1–3]. Some of this information may contain critical information such as communication between the e-bank and the customers (credit card, payment information, withdrawal money, etc.) [4–6]. Therefore, providing security became an essential issue [7–10]. Many approaches have been applied in this field one of them is encryption algorithms [11–13]. The most important issue in encryption algorithms is the degree of security (complexity) and fast process (performance) [14–16].
Important issues in encryption algorithms that must be balanced are the speed and the security degree. Using many operations with high calculations increases the algorithm complexity that results in a more secure algorithm [17–21]. But on the other hand, increasing complexity leads to an increase in the encryption process time (slow down the encryption algorithm) [22–24]. Which conflicts with the requirement of fast encryption algorithm for real-time systems [25–29]. On the other hand, reducing the complexity to increase the encryption speed will reduce the security level [30–32]. This paper suggests a new block cipher algorithm that is inspired by the Advanced Encryption Standard (AES) encryption algorithm in a trial to balance between the speed and the security level. This algorithm is based on using the magic square of order 11 (MS11) in GF(28), making use of the (MS11) high complexity and fast calculations. To produce fast, high-performance, and high-security encryption algorithms. This is done by running the algorithm into 10 rounds, each round consists of five steps. These steps involve, Add Round Key, Sub Bytes, Zigzag pattern, Convert to vector, and MS11. This algorithm is applied to the communication between an E-banks and the customers to provide security for the payment information and the customer information under the e-bank control. The main contributions of this paper are:
• Creating a novel, new symmetric block cipher algorithm.
• Employing the magic square of order 11(MS11) to increase the encryption complexity and hence increase the security.
• Generate and use 32 different equations as part of the encryption process.
• Create and use 9 different maps by assigning a single map for each round.
• Employ the zigzag algorithm to increase confusion and diffusion.
• Creating a reliable environment to transfer financial information between an e-bank system and the customers.
The remaining organization of the paper is as follows: Sector 2 provides a view of previous works, sector 3 presents the methodologies, sector 4 describes the evaluation and experimental results, and sector 5 explains the conclusions.
Due to the efficiency of the magic square (of different orders) in the encryption process many types of research are performed over years that attempted to create a perfect encryption structure that makes use of the magic square mathematical characteristics, some of them are:
According to M. Sahni and D. B. Ojha Generated a new platform to generate a key using an 8*8 magic square and encrypted the data using Ordeal Random Data Encryption Standard (ORDES) and employing special geometrical figures [27]. Another study by A. S. Rahma and D. A. Jabbar Suggested a protocol to protect the transmitted information between two nodes. This protocol is based on magic square order 3, a linear algebra system. The system is running into several rounds providing complexity of equal to (23*no. of blocks *26*no. of blocks)R where R represents the number of rounds [28]. Also, this study by S. D. Mohammed and T. M. Hasan attempted to improve the permutation and substitution process by removing the frequents. This is performed by concealing the encrypted message into a randomly selected submatrix of size 4*4 which is in turn selected from 16*16 magic square for each encryption process. Magic square and Latin square both of size 3*3 are used for two purposes, providing more permutation and making sure of the availability of inverse matrix for the decrypting phase. This work is good for encrypting databases due to the huge frequents in it [29]. Another study by R. H. AL-Hashemy and S. A. Mehdi Developed an algorithm to encrypt images by investing the wide random keyspace of the chaotic system to generate several keys equal to the image size and based on the magic square. These keys are distributed into non-overlapping submatrices, also the image is divided into sub-images then multiply both matrices to produce a new matrix. System complexity is (((b)46)2)n where b the length of each cell content in the matrix, n represent no. of submatrices [30]. According to I. M. ALattar1 and A. S. Rahma Suggested a block cipher algorithm is based on the magic square of order 7 in Galois Field Prime (GF(P)) and GF(28). They used key length = 35 to be distributed on a certain position of magic square and message of length = 14 to be distributed on the rest positions. The complexity of the developed algorithm is GF(P) = (p)14*(p)35 and GF(28) = (256)14*(256)35 [31].
Another study by I. M. ALattar1 and A. S. Rahma Suggested a new block cipher algorithm based on the magic square. This intended to increase system complexity by using multi-message length. The work is done depending on the round status (even or odd). The key is distributed to preselected places and the remaining locations are filled with the message. The encrypted message is calculated by computing a certain sum. The algorithm complexity is ((P)15 × (256)10)2 × (P)11 × (256)14 for GF(P) and ((256)15 × (256)10)2 × (256)11 × (256)14 for GF(28) [32]. This study by I. M. ALattar1 and A. S. Rahma Employed a magic square of size 5*5 to encrypt text and images using both GF(P) and GF(28). For several rounds, a mask is used depending on the round state (even or odd). For even rounds, addition operation is used while multiplication is used with odd rounds. These sequences are used with two different algorithms. The system complexity for the first algorithm was = ((256) 15)r+1 × (256)10 + or × (256)25 and for the second algorithm was ((256)11)r+1 × (256)14 + or × (256)25 [33]. Later I. M. ALattar1 and A. S. Rahma improved their works to by adding a multilevel key with the matrix of the key to increase speed and complexity. Three different message lengths were used, with three different algorithms. The system complexity was increased of the first, second, and third algorithm to (P)9 × (256)16, (P)9 × (256)16 × 3, and (P)9 × (256)16 × 3 × (P)25 in sequence [34].
All the previous study focuses on using the magic square only depending on the complexity of it without adding any additional complexity. The proposed method utilizing the speed of the magic square and adding additional complexity by utilizing additional operations that are run into several rounds to increase system complexity and security. The proposed algorithm can be used to provide security for applications like smart cities, complex network, traffic flow analysis, cellular network and other applications such as those discussed in [35–40].
This paper aims to create a secure environment for data transmission between e-banks and the customers due to the sensitivity of the information which is involved in this transaction. This is done by suggesting a new block cipher algorithm. This algorithm is consists of five operations to be run into ten rounds. These operations involve Add Round Key, Sub Byte, Zigzag, Convert to vector, and Magic Square of order 11 MS11. These processes will be discussed in detail in the next sections.
3.1 The Proposed Cryptography Technique for Message Length = 32 Using GF(28)
When the characteristics of the normal magic square are examined, 22 equations are found, ten of which are derived by computing the total value of adding the rows, ten more from adding the columns, and two more from adding each diameter derived from the diagonals of MS11. The suggestion is inspired by the standard AES encryption algorithm with some changes: The encryption process consists of several rounds. Each round consists of five operations. The first two operations are Add Round Key and Sub Bytes, these two operations are inspired by AES and performed in the same manner. The third operation is the zigzag method which is implemented instead of the shift row operation in the AES. Next, the result from the zigzag is converted into a vector. The last step is the magic square of order 11. These five operations are repeated in each round. For each round, there will be a unique map for the magic square which is used in this session only.
The suggested algorithm is composed of 5 steps: add round key, sub-byte, zigzag, vector conversion, and magic square order 11, which are performed into 9 rounds.
• The add round key is performed in the same manner as in the standard AES algorithm.
• The sub-bytes step: It consists s-box of 16*16 size and works as the s-box step in the standard AES algorithm.
• The Zigzag pattern A zigzag pattern is applied to increase confusion and diffusion as shown below in Fig. 1.

Figure 1: Initial zigzag pattern
The zigzag pattern can be expressed as a reordering scheme of the characters inside the string to eliminate the statistical relations among them. The zigzag pattern can be described in the zigzag algorithm.

• Convert to vector The state matrix that is resulted from the zigzag step is converted into a vector of 32 sizes. Each cell in the zigzag array is divided into two vales of 4 bits and is stored into successive cells into the vector. For example, if a cell in state matrix consists of the value 2D then it is divided into 20 and 0D. These values are stored into two successive cells as 20 and 0D. The values are taken column by column from the state matrix. For example, if the state matrix after the zigzag step consists of the following values shown in Tab. 1.

The resulted vector will contain the following values shown in Tab. 2.:

Then the values will be stored in predefined places in magic square of order 11
• Magic square order 11 (MS11) In this step, the advantages of the magic square of order 11 (MS11) are taken into consideration, where 11 sums are obtained for the rows, 11 other sums for the columns, and two other sums are for the main and secondary diagonals, so that the final result is 24 sums, as shown in Fig. 2.

Figure 2: The sums of MS11
After examining, studying and applying the resulted equations with each other, it is been found that two of them have dependencies with the rest, so the equations have removed so that, the remaining number of them is 22. As show below:
By adding ten additional equations to obtain the final sum of 32 equations, as shown in Fig. 3. As a result, there will be 10 message locations (maps) and each location corresponds to an equation. The remaining positions in MS11 are 89 for the keys. The proposed algorithm does not restrict the use of specific fixed locations, but rather gives flexibility in choosing the location and values of the keys. To increase the complexity and randomness, the message locations will be fixed only for one session. It means that for each round there will be a fixed map to decide the messages’ locations, but this map is changed from round to round (a different map for each round). Fig. 4 represents the used maps, and Fig. 5 represents the encryption process of the proposed algorithm.

Figure 3: The additional equations

Figure 4: The matrices from 1 to 9 represent the different maps that are used for each round map number is corresponding to the round where to use the map

Figure 5: Light weight AES encryption phase
The additional 10 equations are:

• The add round key
• The inverse sub-bytes
• Inverse zigzag
The Inverse zigzag is the reverse order of the initial zigzag as shown in Fig. 6.

Figure 6: Inverse initial zigzag
The inverse zigzag algorithm is presented in the inverse zigzag algorithm below:

• Convert to vector
• Magic Square
The same equations are used to convert the ciphertext to plaintext using the same maps and the same encryption key. Here the ciphertext will be divided into the maps of the magic square in the same manner as the original message is distributed using the same maps that are shown in Fig. 4. Fig. 7 represents the flowchart of the decryption phase in the new algorithm.

Figure 7: Light weight AES decryption

4 Evaluation and Experimental Results
The updated algorithm’s performance is demonstrated using experimental findings. The NIST test, the time of the encrypting and decrypting phases, and memory use for the files encrypting and decrypting are among the requirements. The system were written in PHP Laravel Framework and simulated on Intel(R) Core(TM) i5-6200U CPU @ 2.30 GHz, 2.40 GHz with 8GB RAM and 64-bit operating system, x64-based processor, Windows 10 Pro.
The National Institute of Standards and Technology (NIST) is the most extensive test that is used for evaluating encryption methods. As a result, it is utilized to measure the traditional AES and the novel block cipher algorithm in this comparison. Comparison is done using three tests: approximation entropy, run test, and linear complexity. These tests offered randomness metrics for both the traditional AES and the novel block cipher algorithms’ encrypted testing. Tab. 3 below summarizes the results.
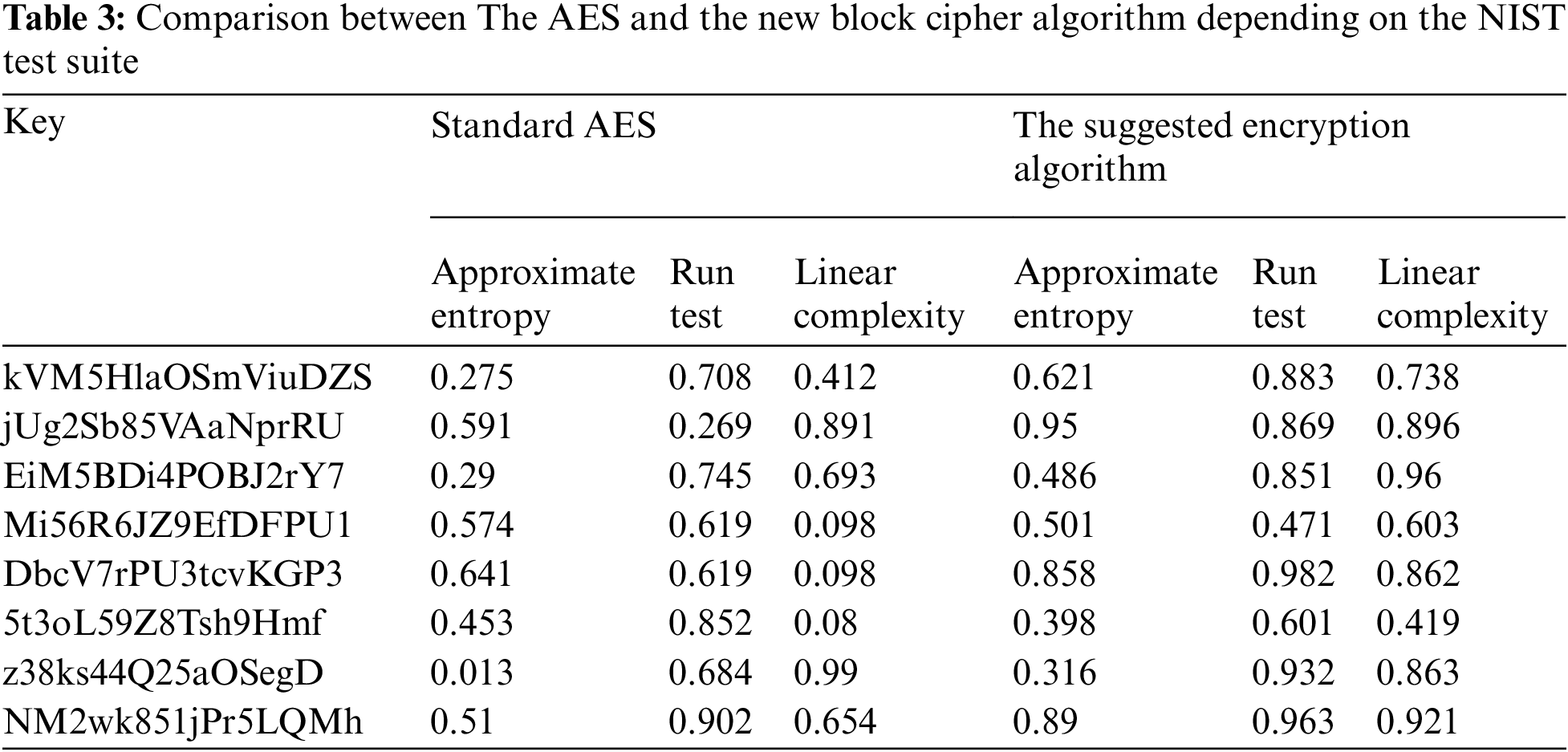
The novel approach provided more unpredictability than the usual AES, according to the findings. As an example, it is proven that on average In comparison to the traditional AES, the proposed encryption algorithm has an approximate entropy of 0.209125, a run test of 0.14425, and a linear complexity of 0.327.
The examination of encrypting and decrypting times is a crucial characteristic for evaluating encryption method performance. The running time of the encrypting and decrypting phases is measured with different file sizes and then compared to the regular AES. The new method is quicker, as seen in Tab. 4 and Figs. 8 and 9. The study’s major purpose is to develop a more efficient encryption method for the data that will be transmitted through the internet.
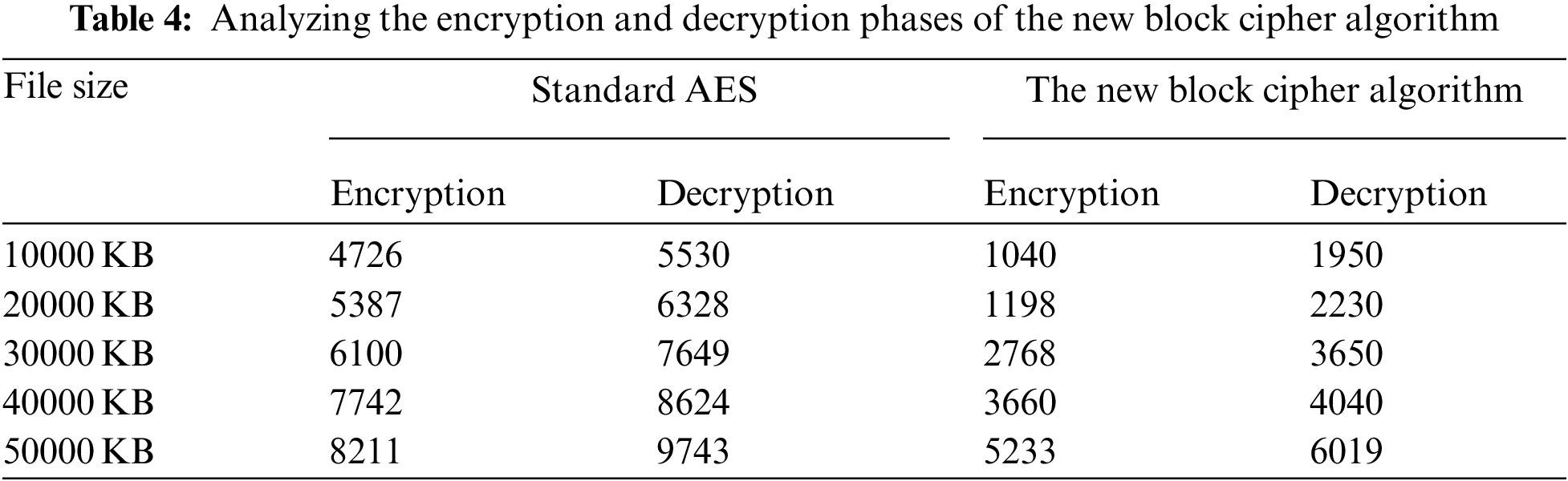

Figure 8: The encrypting time of different file sizes

Figure 9: The time of decrypting files of different sizes
On average, the encryption time of the new block cipher is minus than the AES algorithm by 3653 milliseconds, while the decrypting phase is minus than by 3997 milliseconds.
The new block cipher algorithm requires less memory space than the normal AES during the encrypting phase, according to the analysis of CPU memory using various file sizes. The analysis of the memory use is shown in Fig. 10 and Tab. 5.

Figure 10: Memory utilization of the encrypting phase of various file sizes
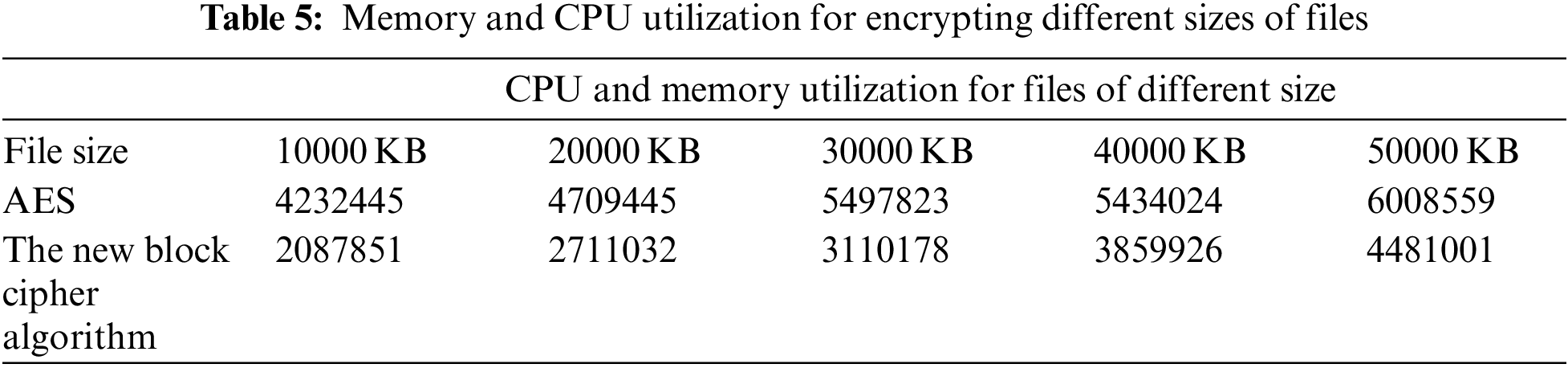
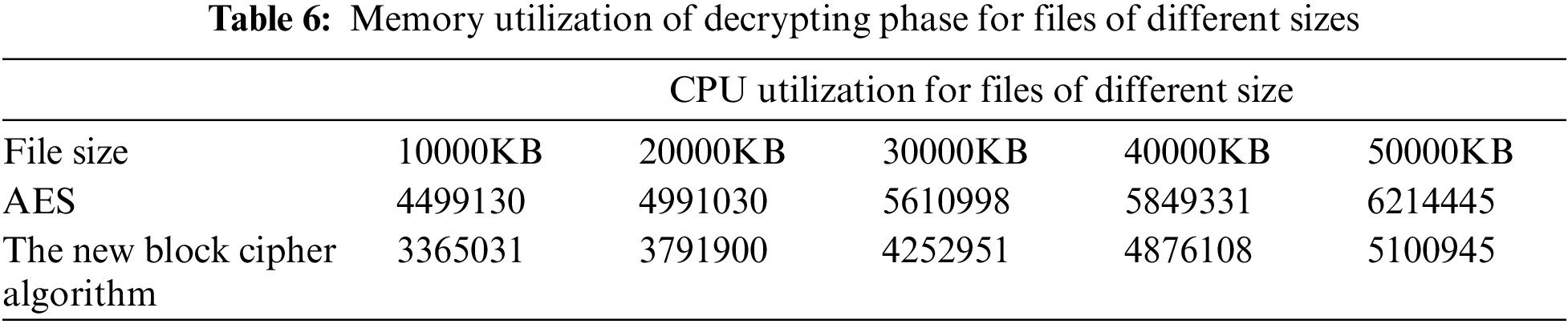
Furthermore, the memory space required for decrypting with the new block cipher algorithm is less than that required by normal AES. Fig. 11 and Tab. 6 illustrate this. The new block cipher algorithm is better at using CPUs than the regular AES, according to prior research.

Figure 11: Memory utilization of the decrypting phase of various file sizes
The development of a new block encryption algorithm employing the MS11 and GF(28) is distinguished by increasing the complexity with little reduction in speed. Applying the GF(28) offers speed and more complexity. On the one hand, the more the number of equations employed, the higher the speed; moreover, the complexity is lowered. Adding more masks to the mix adds a layer of complexity. The addition provides less complexity but it is a fast operation. Also, the zigzag operation provides more confusion and diffusion. This collection provided high speed, high complex encryption algorithm which leads to high performance, with a high degree of a secure encryption algorithm. Which is suitable to be used for encrypting transmitted data over the internet. The experimental results showed that the randomness degree has grown by 31.8 percent, decreasing in the time of encrypting and decrypting and the usage of the CPU, that leads to improving the efficiency. Also, the encryption process throughput is enhanced by 13%, while the decryption process throughput is increased by 11.6 percent with the recommended approach. There are several suggestions to improve system security and complexity some of them such as using MS of even order in the even rounds and using MS of odd order in the odd rounds. Using padding process before starting the work of the algorithm as preprocessing step to increase the confusion and diffusion. Using a specific number and shape of maps is considered as a limitation of the proposed system.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. A. S. Alshammari, “Comparison of a chaotic cryptosystem with other cryptography systems,” Engineering, Technology & Applied Science Research, vol. 10, no. 5, pp. 6187–6190, 2020. [Google Scholar]
2. F. T. Abdul Hussien, “Proposed algorithm to generate encryption key for block and stream cipher using dna computing,” Iraqi Journal of Information Technology, vol. 8, no. 3, pp. 68–82, 2018. [Google Scholar]
3. M. Benssalah, Y. Rhaskali and K. Drouiche, “An efficient image encryption scheme for TMIS based on elliptic curve integrated encryption and linear cryptography,” Multimedia Tools and Applications, vol. 80, pp. 2081–2107, 2021. [Google Scholar]
4. D. A. Jabbar and A. S. Rahma, “Proposed cryptography protocol based on magic square, linear algebra system and finite field,” Journal of Advanced Research in Dynamical & Control Systems, vol. 10, no. 10, pp. 72–75, 2018. [Google Scholar]
5. S. M. M. Najeeb, S. M. Ali and H. Salim “Finding the discriminative frequencies of motor electroencephalography signal using genetic algorithm,” Telkomnika, vol. 19, no. 1, pp. 285–291, 2021. [Google Scholar]
6. O. Z. Akif, S. M. Ali, R. S. Ali and A. K. Farhan, “A new pseudorandom bits generator based on a 2D-chaotic system and diffusion property,” Bulletin of Electrical Engineering and Informatics, vol. 10, no. 3, pp. 1580–1588, 2021. [Google Scholar]
7. Z. K. Obaidand and N. F. Al Saffar, “Image encryption based on elliptic curve cryptosystem,” International Journal of Electrical and Computer Engineering (IJECE), vol. 11, no. 2, pp. 1293–1302, 2021. [Google Scholar]
8. S. D. Mohammed and T. M. Hasan, “Cryptosystems using an improving hiding technique based on latin square and magic square,” Indonesian Journal of Electrical Engineering and Computer Science, vol. 20, no. 1, pp. 510–520, 2020. [Google Scholar]
9. A. E. Ali, N. F. Hassan and M. E. Abdulmunim, “Generate animated CAPTCHA based on visual cryptography concept,” Engineering and Technology Journal, vol. 29, no. 16, pp. 3405–3416, 2011. [Google Scholar]
10. Z. K. Hussein, H. J. Hadi, M. R. Abdul-Mutaleb and Y. S. Mezaal, “Low cost smart weather station using arduino and zigbee,” Telkomnika, vol. 18, no. 1, pp. 282–288, 2020. [Google Scholar]
11. Z. M. Fadhel and A. K. Abdul Hassan, “Design and implementation of a software protection system against software piracy by using cryptographic techniques,” Engineering and Technology Journal, vol. 28, no. 1, pp. 126–148, 2010. [Google Scholar]
12. H. Alrikabi, and H. T. Hazim, “Enhanced data security of communication system using combined encryption and steganography,” International Journal of Interactive Mobile Technologies, vol. 15, no. 16, pp. 144–157, 2021. [Google Scholar]
13. O. A. Dawood, A. S. Rahma and A. J. Abdul Hossen, “New variant of public key based on diffiehellman with magic cube of six-dimensions,” International Journal of Computer Science and Information System (IJCSIS), vol. 13, no. 10, pp. 31–47, 2015. [Google Scholar]
14. A. K. Farhan, R. S. Ali, H. Natiq and N. M. G. Al-saidi, “A new s-box generation algorithm based on multistability behavior of a plasma perturbation model,” IEEE Access, vol. 7, pp. 2169–3536, 2019. [Google Scholar]
15. Y. A. Hussain and Z. A. H. Alobaidy, “Image encryption using chaos and random generation,” Engineering and Technology Journal, vol. 34, Part (Bno. 1, pp. 172–179, 2016. [Google Scholar]
16. S. M. Kareem and A. S. Rahma, “A new multi-level key block cipher based on the blowfish algorithm,” Telkomnika Telecommunication, Computing, Electronics and Control, vol. 18, no. 2, pp. 685–694, 2020. [Google Scholar]
17. R. I. A. Aljazaery, S. K. Al_Dulaimi and H. T. S. Alrikabi, “Generation of high dynamic range for enhancing the panorama environment,” Bulletin of Electrical Engineering, vol. 10, no. 1, pp. 138–147, 2021. [Google Scholar]
18. A. S. Hussein, R. S. Khairy, S. M. M. Najeeb and H. T. S. Alrikabi, “Credit card fraud detection using fuzzy rough nearest neighbor and sequential minimal optimization with logistic regression,” International Journal of Intractive Mobile Technology iJIM, vol. 15, no. 5, pp. 24–41, 2021. [Google Scholar]
19. I. Loth, B. Kargoll and W. Schuh, “Non-recursive representation of an autoregressive process within the magic square,” in the Int. Association of Geodesy Symposia Book Series, (IAG SYMPOSIA), Ukraine, vol. 151, pp. 183–189, 2019. [Google Scholar]
20. I. M. Alattar and A. M. S. Rahma, “A comparison between odd magic squares use in cryptographic algorithms,” Al-Qadisiyah Journal of Pure Science, vol. 26, no. 4, pp. 1–14, 2021. [Google Scholar]
21. H. A. Abdulmohsin, H. B. Abdul Wahab and A. M. J. Abdul Hossen, “A novel classification method with cubic spline interpolation,” Intelligent Automation and Soft Computing, vol. 31, no. 1, pp. 339–355, 2022. [Google Scholar]
22. H. A. Abdulmohsin, H. B. Abdul Wahab and A. J. Abdul Hossen, “A new proposed statistical feature extraction method in speech emotion recognition,” Computers & Electrical Engineering, vol. 93, no. 3, pp. 1–14, 2021. [Google Scholar]
23. F. T. Abdul Hussien, A. S. Rahma and H. B. Abdul Wahab, “A secure environment using a new lightweight aes encryption algorithm for e-commerce websites,” Security and Communication Networks, vol. 6, pp. 1–15, 2021. [Google Scholar]
24. F. T. Abdul Hussien, A. S. Rahma and H. B. Abdul Wahab, “Design and implement a new secure prototype structure of e-commerce system,” International Journal of Electrical and Computer Engineering, vol. 12, no. 1, pp. 560–571, 2022. [Google Scholar]
25. S. Shandal, Y. S. Mezaal, M. Kadim and M. Mosleh, “New compact wideband microstrip antenna for wireless applications,” Advanced Electromagnetics, vol. 7, no. 4, pp. 85–92, 2018. [Google Scholar]
26. Y. S. Mezaal and H. T. Eyyuboglu. “Investigation of new microstrip bandpass filter based on patch resonator with geometrical fractal slot,” PloS one, vol. 11, no. 4, pp. 1–12, 2016. [Google Scholar]
27. M. Sahni and D. B. Ojha, “Magic square and cryptography,” Journal of Global Research in Computer Science, vol. 3, no. 12, pp. 15–17, 2012. [Google Scholar]
28. A. S. Rahma and D. A. Jabbar, “Development cryptography protocol based on magic square and linear algebra system,” Journal of AL-Qadisiyah for Computer Science and Mathematics, vol. 11, no. 1, pp. 72–75, 2019. [Google Scholar]
29. I. Krasbutter, I. Kargoll and W. -D. Schuh, “Magic square of real spectral and time series analysis with an application to moving average processes,” in Kutterer H. et al. (eds.) The 1st International Workshop on the Quality of Geodetic Observation and Monitoring Systems (QuGOMS'11), New York, Springer, pp. 9–14, 2015. [Google Scholar]
30. R. H. AL-Hashemy and S. A. Mehdi, “A new algorithm based on magic square and a novel chaotic system for image encryption,” Journal of Intelligent Systems, vol. 29, no. 1, pp. 1202–1215, 2020. [Google Scholar]
31. I. M. ALattar and A. S. Rahma, “A block cipher algorithm developed using magic square in the seventh order,” Journal of Physics: Conference Series, vol. 1999, pp. 1–12, 2021. [Google Scholar]
32. I. M. ALattar and A. S. Rahma, “A comparative study of researches based on magic square in encryption with proposing a new technology,” Iraqi Journal of Computers, Communications, Control & Systems Engineering (IJCCCE), vol. 21, no. 2, pp. 102–114, 2021. [Google Scholar]
33. I. M. ALattar and A. S. Rahma, “A new block cipher algorithm that adopts the magic square of the fifth order with messages of different lengths and multi-function in GF(28),” Periodicals of Engineering and Natural Sciences, vol. 9, no. 3, pp. 568–578, 2021. [Google Scholar]
34. I. M. ALattar and A. S. Rahma, “A new block cipher algorithm using magic square of order five and galois field arithmetic with dynamic size block,” International Journal of Interactive Mobile Technologies iJIM, vol. 15, no. 16, pp. 63–78, 2021. [Google Scholar]
35. M. N. Al-Mhiqani, R. Ahmad, Z. Z. Abidin, K. H. Abdulkareem, M. A. Mohammed et al. “A new intelligent multilayer framework for insider threat detection,” Computers & Electrical Engineering, vol. 97, pp. 107597, 2022. [Google Scholar]
36. A. Lakhan, M. A. Mohammed, S. Kadry, K. H. Abdulkareem, F. T. Al-Dhief et al. “Federated learning enables intelligent reflecting surface in fog-cloud enabled cellular network,” PeerJ Computer Science, vol. 7, pp. 758, 2021. [Google Scholar]
37. M. J. Awan, O. A. Masood, M. A. Mohammed, A. Yasin, A. M. Zain et al. “Image-based malware classification using VGG19 network and spatial convolutional attention,” Electronics, vol. 10, no. 19, pp. 2444, 2021. [Google Scholar]
38. B. A. Khalaf, S. A. Mostafa, A. Mustapha, M. A. Mohammed, M. A. Mahmoud et al. “An adaptive protection of flooding attacks model for complex network environments,” Security and Communication Networks, vol. 2021, pp. 1–17, 2021. [Google Scholar]
39. S. A. Kashinath, S. A. Mostafa, A. Mustapha, H. Mahdin, D. Lim et al. “Review of data fusion methods for real-time and multi-sensor traffic flow analysis,” IEEE Access, vol. 9, pp. 51258–51276, 2021. [Google Scholar]
40. A. H. Azizan, S. A. Mostafa, A. Mustapha, C. F. M. Foozy, M. H. A. Wahab et al. “A machine learning approach for improving the performance of network intrusion detection systems,” Annals of Emerging Technologies in Computing (AETiC), vol. 5, no. 5, pp. 201–208, 2021. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |