Computers, Materials & Continua DOI:10.32604/cmc.2022.027437
Article

Quantum Remote State Preparation Based on Quantum Network Coding

Zhen-Zhen Li1, Zi-Chen Li1, Yi-Ru Sun2,3,*, Haseeb Ahmad4, Gang Xu5,6 and Xiu-Bo Chen3

1School of Information Engineering, Beijing Institute of Graphic Communication, Beijing, 102600, China
2School of Computer Science and Information Engineering, Zhejiang Gongshang University, Hangzhou, 310018, China
3Information Security Center, State key Laboratory of Networking and Switching Technology, Beijing University of Posts and Telecommunications, Beijing, 100876, China
4Department of Computer Science, National Textile University, Faisalabad, 37610, Pakistan
5School of Information Science and Technology, North China University of Technology, Beijing, 100144, China
6Advanced Cryptography and System Security Key Laboratory of Sichuan Province, China
*Corresponding Author: Yi-Ru Sun. Email: syr@mail.zjgsu.edu.cn
Received: 18 January 2022; Accepted: 08 March 2022

Abstract: As an innovative theory and technology, quantum network coding has become the research hotspot in quantum network communications. In this paper, a quantum remote state preparation scheme based on quantum network coding is proposed. Comparing with the general quantum remote state preparation schemes, our proposed scheme brings an arbitrary unknown quantum state finally prepared remotely through the quantum network, by designing the appropriate encoding and decoding steps for quantum network coding. What is worth mentioning, from the network model, this scheme is built on the quantum k-pair network which is the expansion of the typical bottleneck network—butterfly network. Accordingly, it can be treated as an efficient quantum network preparation scheme due to the characteristics of network coding, and it also makes the proposed scheme more applicable to the large-scale quantum networks. In addition, the fact of an arbitrary unknown quantum state remotely prepared means that the senders do not need to know the desired quantum state. Thus, the security of the proposed scheme is higher. Moreover, this scheme can always achieve the success probability of 1 and 1-max flow of value k. Thus, the communication efficiency of the proposed scheme is higher. Therefore, the proposed scheme turns out to be practicable, secure and efficient, which helps to effectively enrich the theory of quantum remote state preparation.

Keywords: Quantum remote state preparation; quantum network coding; quantum k-pair network

1  Introduction

In 2000, quantum remote state preparation (RSP) was first proposed by Lo [1]. RSP enables the senders to prepare known states for remote receivers with the assistance of entangled resources [2,3] and classical communications [4,5]. With so many years of development, RSP has already made significant advances in theories [6–8] and applications [9–11]. In these researches, respect to the different target state, such as Bell state [12], GHZ state [13], W state [14], cluster state [15] and so on, various kinds of RSP schemes have been proposed. In addition, respect to the different implementation techniques, such as deterministic RSP [16], joint RSP [17] and controlled RSP [18], several schemes have also been proposed.

However, with the development of quantum communication and the requirement for multi-user’s quantum communication, point-to-point communication mode will necessarily toward to the direction of network communication. Thus, the research of RSP over the quantum network have become a meaningful task. In quantum network communications, as a breakthrough technology, quantum network coding (QNC) can effectively improve the quantum communication efficiency and quantum network throughput as compared to the traditional technology of routing. Since the first QNC scheme proposed by Hayashi et al. [19] in 2006, a series of QNC schemes have been put forward in theories [20–23] and applications [24–26] over the past decade. By QNC, the intermediate nodes are allowed to encode the received information and ultimately the destination nodes can recover the original unknown quantum state by decoding. Therefore, it is reasonable to believe that if combining RSP and QNC, the problem of quantum state preparation over quantum networks can be solved effectively.

In this paper, a novel RSP scheme based on QNC is proposed. This scheme is assisted by the resource of prior entanglement and classical communication, and the specified encoding or decoding operations are performed at the corresponding nodes. In terms of the quantum state, an arbitrary unknown quantum state possessed by the source nodes are finally prepared at the sink nodes; in terms of the success probability, this scheme can always achieve the success probability of 1; in terms of the network model, the quantum k-pair network as an expansion of the typical bottleneck network—butterfly network [27–29] in QNC is constructed to propose the scheme. Thus, the proposed scheme can effectively improve the communication efficiency and is more applicable to the scenarios of large-scale quantum networks, which can enrich the theory of quantum remote state preparation over quantum network.

The remainder of this paper is organized as follows. In Section 2, preliminaries including notations, quantum k-pair network, quantum operators and quantum measurements are presented. In Section 3, the specific RSP scheme based on QNC is proposed. In Section 4, the performance analyses including correctness, security, practicability and achievable rate region are discussed. At last, some concluding remarks are given in Section 5.

2  Preliminaries

2.1 Notations

The following notations will be used throughout this paper:

⊕: The addition module d; ⊗: The tensor product of vector space.

Cd: The d-dimension complex field; Zd: The integer ring with respect to addition ⊕ module d.

σx: The Pauli operator over 2-dimension space; X/R: The Pauli operator over d-dimension space.

2.2 Quantum K-Pair Network

Let us consider a directed acyclic graph (DAG) G = (V,E), where V is the set of nodes and E is the set of edges that connect pairs of nodes in V. K pairs of nodes (s1,t1),(s2,t2),…,(sk,tk) constitute a subset of V. Next, a directed acyclic network (DAN) N is deemed a quantum network if it comprises a DAG G and the edge quantum capacity function c:E→Z+. The quantum k-pair network N explored herein is shown in Fig. 1.

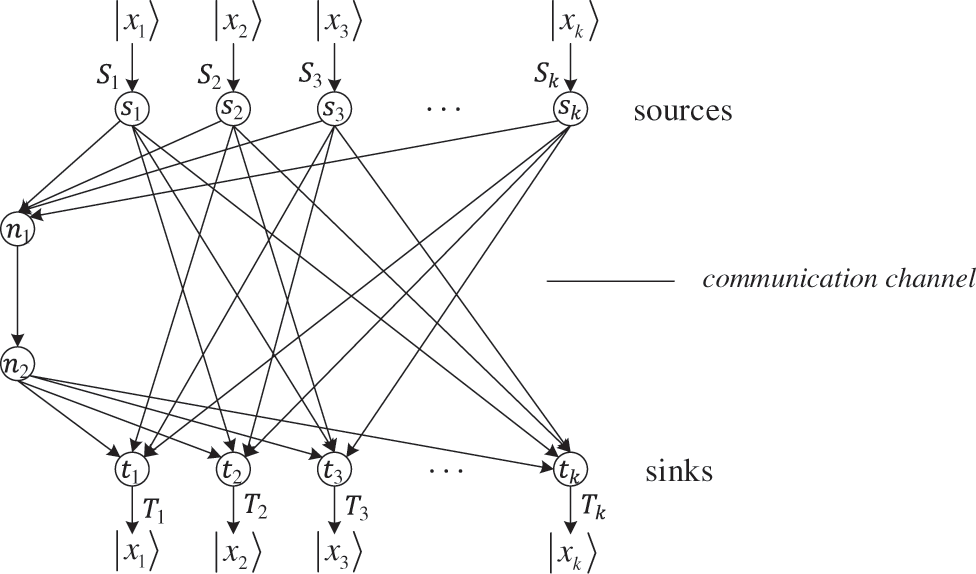
Figure 1: Quantum k-pair network N

In this figure, the solid lines represent the quantum physical channels and the arrows indicate the transmission direction of the quantum information. Let H=Cd denote a Hilbert space. According to the task of the quantum RSP and QNC, one needs to make a quantum state |Ψ⟩S1,…,Sk∈H⊗k supported on the source nodes s1,…,sk (in this order) remotely prepared at the sink nodes t1,…,tk (in this order) through N, under the condition that c(e)≡1,e∈E, i.e., each edge of N can transmit no more than one qudit state over H. For i∈{1,2,…,k}, each quantum register Si is possessed by the source node si, while the quantum register Ti is possessed by the sink node ti. A RSP scheme based on QNC over the quantum k-pair network refers to the corresponding protocol, which contains certain quantum operations for all nodes in V that enable the above preparation to be accomplished successfully.

2.3 Quantum Operators

Firstly, let us introduce the controlled-X operation on a d-dimension quantum system H=Cd, which is written as follows:

ΛXA→B:=∑r∈ℤd|r〉〈r|A⊗XBr,(1)

where X|i⟩=|i⊕1modd⟩ is an analogue of the unitary Pauli operator σx on qubits [30,31]. Based on this, for ∀t∈Zd, the quantum operation constructed by performing t times the controlled-X operation in d-dimension quantum system H=Cd is also presented here, defined as

ΛXA→Bt:=∑r∈ℤd|r〉〈r|A⊗XBrt.(2)

Then, another quantum operation named controlled-R operation on d-dimension quantum system H=Cd is also presented here, defined as

ΛRA→B:=∑i=0d−1|i⟩⟨i|A⊗RBi,(3)

where R|i⟩=|i−1modd⟩ is the reverse transformation of X on qudits.

2.4 Quantum Measurements

In the quantum system H=Cd, quantum Fourier transform F is a unitary transformation that transforms the computing basis states {|k⟩}k∈Zd to the Fourier basis as

|wk⟩=F|k⟩=1d∑l=0d−1e2πιkl/d|l⟩,(4)

where ι2=−1, F=1d∑l,k=0d−1e2πιkl/d|l⟩⟨k|. Thus, the basis states {|wk⟩}k∈Zd are called quantum Fourier basis and the quantum measurement in Fourier basis is called quantum Fourier measurement [21,22]. Quantum Fourier measurement is usually used to measure a single-particle state over H=Cd.

In the quantum system H=Cd, the Bell states (EPR pair) are represented as follows:

|ϕ(M1,M2)〉=1d∑j=0d−1e2πιjM1/d|j,j⊕M2〉,M1,M2∈ℤd.(5)

Hence, the basis states {|ϕ(M1,M2)⟩}M1,M2∈Zd are called the Bell basis, and the quantum measurement in the Bell basis is called the Bell measurement. In general, Bell measurement is typically used to jointly measure a two-particle state over H=Cd.

3  A Quantum Remote Preparation Scheme Based on Quantum Network Coding

3.1 Protocol Specification

Suppose that the arbitrary k-qudit quantum state originally possessed at the source nodes s1,…,sk or desired to be prepared at the sink nodes t1,…,tk is written as

|Ψ⟩S=∑x1,…,xk∈Zdαx1,…,xkeιθx1,…,xk|x1⟩S1⊗⋅⋅⋅⊗|xk⟩Sk,(6)

where all the amplitude coefficient αx1,…,xk and the phase coefficient θx1,…,xk are real numbers such that ∑x1,…,xk∈Zd|αx1,…,xk|2=1, the Si(i∈{1,2,…k}) represent the registers possessed by the source node si. And then suppose that the source nodes s1,…,sk and the sink nodes t1,…,tk initially share a 2k-qudit entangled GHZ state as

|ϕ⟩ST=1d∑h∈Zd|h,h,…,h⟩S1′,…,Sk′,T1′,…,Tk′,(7)

where for i∈{1,2,…,k}, each quantum register Si′ is possessed by the source node si , while quantum register Ti′ is possessed by the sink node ti.

Thus, the whole quantum system now becomes as

|Ψ⟩0=1d∑x1,…,xk,h∈Zdαx1,…,xkeιθx1,…,xk|x1,x2,…,xk⟩S1,…,Sk⊗|h,h,…,h⟩S1′,…,Sk′,T1′,…,Tk′.(8)

According to the task of RSP over the quantum k-pair network N, the coefficients of |Ψ⟩S(k) is known only for the source nodes s1,…,sk and ultimately this desired k-qudit quantum should be prepared at the sink nodes t1,…,tk. Now, the specific steps of the proposed RSP scheme based on QNC are described below in detail.

Step 1: At each source node si(i∈{1,2,…,k}), ancillary registers Rii and Ri,i+1 are introduced, in which each quantum state is initialized to |0H⟩. Then, the quantum operators ΛXSi→Rii and ΛXSi′→Rii are applied to the registers Si , Si′ and Rii, the operator ΛRSi→Ri,i+1 is applied to the registers Si and Ri,i+1. Thus, the quantum state becomes

|Ψ⟩1=1d∑x1,…,xk,h∈Zdαx1,…,xkeιθx1,…,xk⊗i=1k⁡|xi⟩Si|h⟩Si′|h⟩Ti′|xi⊕h⟩Rii|−xi⟩Ri,i+1.(9)

Then, for i∈{1,2,…,k}, the quantum registers Rii are sent from each node si to node n1; for i∈{1,2,…,k−1}, registers Ri,i+1 are sent to the sink nodes ti+1; for i=k, register Ri,i+1 is sent to the sink nodes t1. And the registers Si and Si′ are maintained at the node si.

Step 2: At the intermediate node n1, the ancillary register Rn initialized to |0H⟩ is introduced. Afterwards, the quantum operators ΛXRii→Rn are applied on the registers Rii(i=1,2,…k) and Rn, we have the quantum state:

|Ψ⟩2=1d∑x1,…,xk,h∈Zdαx1,…,xkeιθx1,…,xk|⊕i=1k⁡xi⊕kh⟩Rn⊗i=1k⁡|xi⟩Si|h⟩Si′|h⟩Ti′|xi⊕h⟩Rii|−xi⟩Ri,i+1.(10)

Then, the quantum register Rn is sent from the node n1 to the node n2 and the registers Rii(i=1,2,…k) are kept at the node n1.

Step 3: At the intermediate node n2, quantum registers ri(i=1,2,…,k) each initialized to |0H⟩ are introduced and then the quantum operator ΛXRn→ri is applied to the registers Rn and ri. Thus, the quantum state becomes

|Ψ⟩3=1d∑x1,…,xk,h∈Zdαx1,…,xkeιθx1,…,xk|⊕i=1k⁡xi⊕kh⟩Rn⊗i=1k⁡|⊕i=1k⁡xi⊕kh⟩ri|xi⟩Si|h⟩Si′|h⟩Ti′|xi⊕h⟩Rii|−xi⟩Ri,i+1.(11)

Then, k quantum registers ri(i=1,2,…,k) are transmitted from the node n2 to the sink nodes ti respectively, and the register Rn are maintained at the node n2.

Step 4: For each sink node ti(i∈{1,2,…,k}), the quantum register Ti initialized to |0H⟩ is introduced. Remembering that node ti(i∈{2,…,k}) has received the register Ri−1,i and the node t1 has received the registers Rk,1 in Step 1, and register ri in Step 3, now the quantum operator ΛXri→Ti is applied to ri and Ti, ΛXRi−1,i→Ti(i∈{2,…,k}) is applied to Ri−1,i and Ti( ΛXRk,1→T1 is applied to Rk,1 and T1). And then the quantum operator ΛXTi′→Ti−k is applied to Ti′ and Ti, hence the resulting state becomes

|Ψ⟩4=1d∑x1,…,xk,h∈Zdαx1,…,xkeιθx1,…,xk|⊕i=1k⁡xi⊕kh⟩Rn⊗i=1k⁡|⊕i=1k⁡xi⊕kh⟩ri|xi⟩Si|h⟩Si′|xi⟩Ti|h⟩Ti′|xi⊕h⟩Rii|−xi⟩Ri,i+1.(12)

Step 5: At the intermediate node n1, quantum Fourier measurement is performed on Rii(i=1,2,…k), giving measurement results mi. Because of

|l⟩=1d∑k=0d−1e−2πιkl/d|k⟩,(13)

we have the quantum state:

|Ψ⟩5=1d∑x1,…,xk,h∈Zdαx1,…,xkeιθx1,…,xk∏i=1k⁡e−2πι(xi⊕h)mi/d|⊕i=1k⁡xi⊕kh⟩Rn⊗i=1k⁡|⊕i=1k⁡xi⊕kh⟩ri|xi⟩Si|h⟩Si′|xi⟩Ti|h⟩Ti′|−xi⟩Ri,i+1.(14)

Then, k⌈log⁡d⌉ bits classical information mi is sent from node n1 to the node si.

Step 6: At each source node si(i∈{1,2,…,k}), once receiving the information mi, the quantum unitary operator mapping of the state |xi⟩ to e2πιmixi/d|xi⟩ for each xi∈Zd is applied on the register Si, and the quantum unitary operator mapping of the state |h⟩ to e2πιmih/d|h⟩ is applied on the register Si′. Thus the phase caused by Bell measurement in step 5 is corrected. Afterward, considering the owned registers Si and Si′, the quantum operation ΛXSi′→Si and then the Bell measurement are performed on this two qudits, providing the measurement result ui1ui2. Because of

|j,j⊕u2⟩=1d∑u1=0d−1e−2πιju1/d|ϕ(u1,u2)⟩,(15)

we obtain the quantum state:

|Ψ⟩6=1d∑x1,…,xk,h∈Zdαx1,…,xkeιθx1,…,xk∏i=1k⁡e−2πι(⊕i=1k⁡xi⊕kh)ui1/d|⊕i=1k⁡xi⊕kh⟩Rn⊗i=1k⁡|⊕i=1k⁡xi⊕kh⟩ri|xi⟩Ti|h⟩Ti′|−xi⟩Ri,i+1.(16)

Then, 2k⌈log⁡d⌉ bits classical information ui1ui2 are sent from the nodes si to the sink node ti+1. Here, the security of classical channels can be guaranteed by message authentication mechanism such as HMAC [32], UMAC [33], etc., preventing outside attackers from tampering the transmitted classical information. It is noted that the classical information transmission involved in the following steps is all the same and there will be no repeated mention.

Step 7: At the sink node ti(i∈{1,2,…,k}), upon receiving the information ui−1,1ui−1,2, the quantum unitary operator mapping of the state |x⟩ to e2πιui−1,1x/d|x⟩ for each x∈Zd is applied on its register ri. Thus the phase caused by Bell measurement in step 5 is corrected. And then quantum Fourier measurement is performed on ri, giving measurement results li. The quantum state becomes

|Ψ⟩7=1d∑x1,…,xk,h∈Zdαx1,…,xkeιθx1,…,xk∏i=1k⁡e−2πι(⊕i=1k⁡xi⊕kh)li/d|⊕i=1k⁡xi⊕kh⟩Rn⊗i=1k⁡|xi⟩Ti|h⟩Ti′|−xi⟩Ri,i+1.(17)

Afterwards, k⌈log⁡d⌉ bits classical information li is sent from node ti to the intermediate node n2.

Step 8: At the intermediate node n2, once receiving the information li, the quantum unitary operator mapping of the state |x⟩ to e2πιlix/d|x⟩ for each xi∈Zd is applied on the register Rn to correct the phase. Following this, quantum Fourier measurement is performed on Rn, giving measurement results p. Thus, we have the quantum state

|Ψ⟩8=1d∑x1,…,xk,h∈Zdαx1,…,xkeιθx1,…,xke−2πι(⊕i=1k⁡xi⊕kh)p/d⊗i=1k⁡|xi⟩Ti|h⟩Ti′|−xi⟩Ri,i+1.(18)

Then, 1⌈log⁡d⌉ bits classical information p are sent from the nodes n2 to the sink node ti.

Step 9: At the sink node ti(i∈{1,2,…,k}), upon receiving the information p, the quantum unitary operator mapping of the state |h⟩ to e2πι(⊕i=1k⁡xi⊕kh)p|h⟩ for each xi∈Zd is applied on the register Ti′ to correct the phase. Then, the Bell measurement is performed on the registers Ri−1,i and Ti′, giving measurement results q1q2. The quantum state becomes

|Ψ⟩9=1d∑x1,…,xk,h∈Zdαx1,…,xkeιθx1,…,xke2πιxiq1/d⊗i=1k⁡|xi⟩Ti.(19)

Next, the phase is corrected by performing the quantum unitary operator mapping of the state |x⟩ to e−2πιq1|x⟩ for each xi∈Zd on the register Ti. Thus, the final quantum state becomes the desired state, as follows:

|Ψ⟩T=∑x1,…,xk∈Zdαx1,…,xkeιθx1,…,xk|x1⟩T1⊗⋅⋅⋅⊗|xk⟩Tk,(20)

That is, the arbitrary k-qudit quantum state originally possessed by the source nodes is successfully prepared remotely at the sink nodes.

3.2 Example: The Butterfly Network Over H=C2

For the quantum k-pair network N illustrated in Fig. 1, when k = 2, the network becomes the typical bottleneck network—butterfly network as shown as Fig. 2. This subsection describes the techniques developed in the previous descriptions using the example of the butterfly network over Hilbert space H=C2.

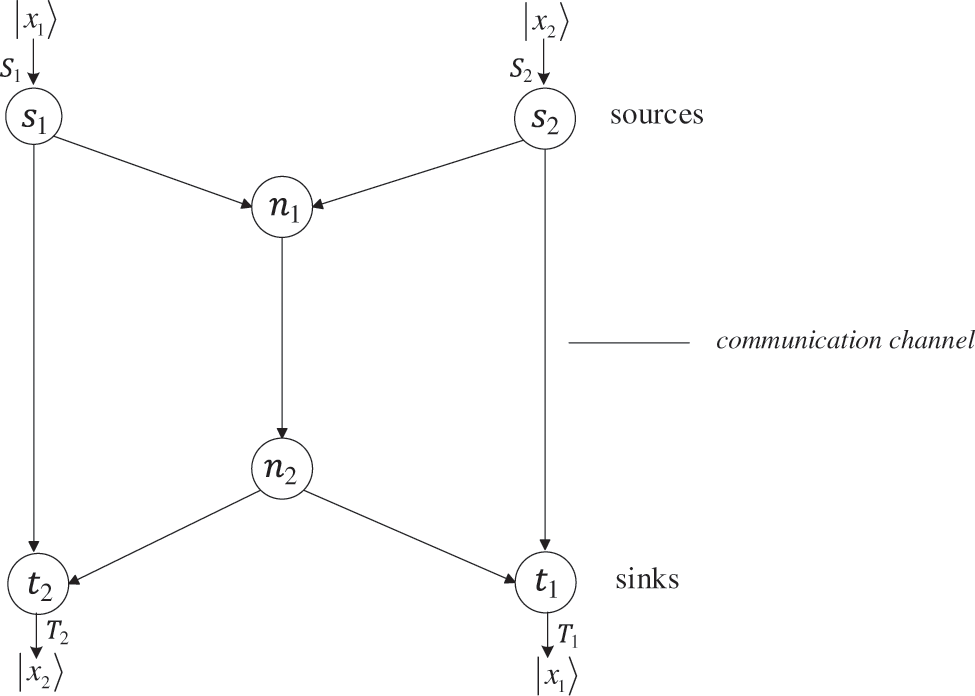
Figure 2: Quantum butterfly network

Here, the arbitrary 2-qubit quantum state originally possessed at the source nodes s1,s2 and desired to be prepared at the sink nodes t1,t2 is written as

|Ψ⟩S(2)=(α00eιθ00|00⟩+α01eιθ01|01⟩+α10eιθ10|10⟩+α11eιθ11|11⟩)S1S2.(21)

And the source nodes s1,s2 and the sink nodes t1,t2 initially share a 4-qubit entangled GHZ state as

|ϕ⟩ST(2)=12(|0000⟩+|1111⟩)S1′S2′T1′T2′.(22)

Thus, the initial quantum state of the whole system is

|Ψ〉0(2)=12(α00eιθ00|00〉+α01eιθ01|01〉+α10eιθ10|10〉+α11eιθ11|11〉)S1S2⊗(|0000〉+|1111〉)S1′S2′T1′T2′.(23)

Hereafter, we proceed to the specific steps of the RSP scheme based on QNC. For step 1-step 4, it can be considered as the encoding process and the object is to make the particles in the quantum registers mutually entangled. The corresponding schematic diagram of quantum circuit can be shown in Fig. 3.

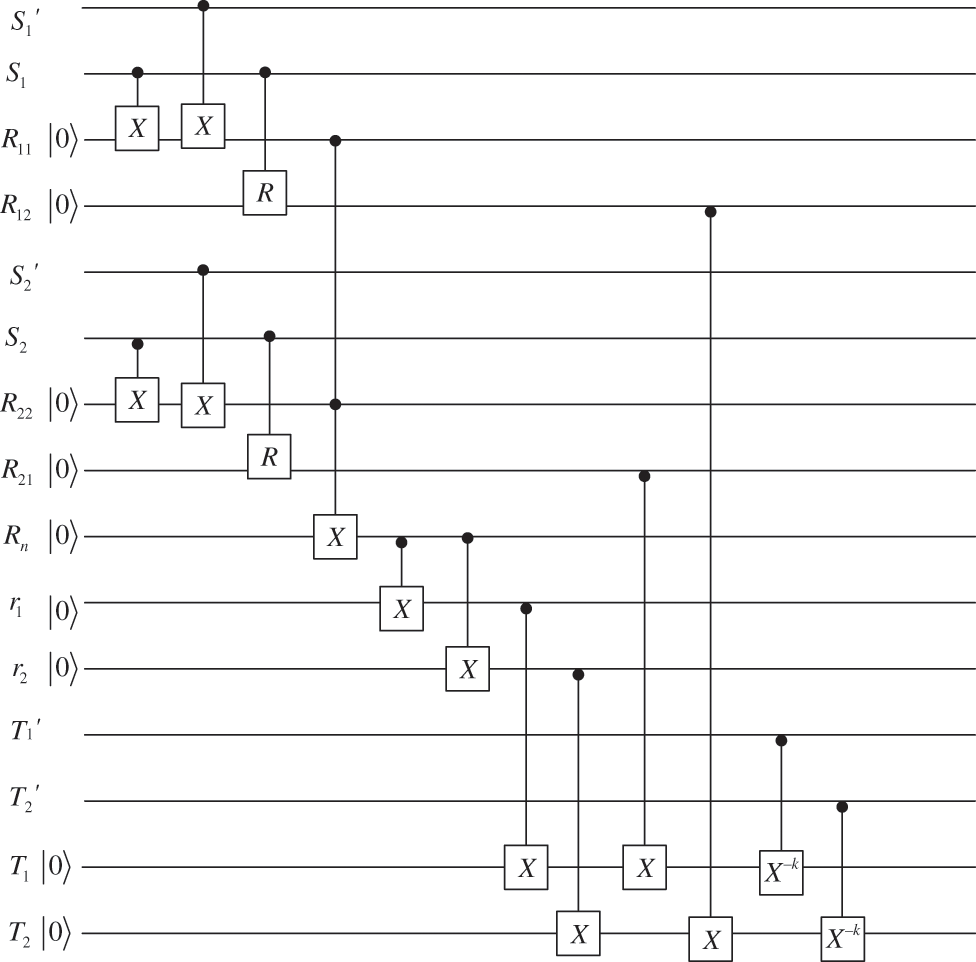
Figure 3: Schematic diagram of quantum circuit for steps 1–4

According to the specific calculations, after Step 1–4, the quantum states of the of the whole system becomes

|Ψ〉5(2)=12[α00eιθ00(|000〉Rnr1r2|00〉S1R12|00〉S2R21|0000〉S1′S2′T1′T2′|00〉T1T2+|000〉Rnr1r2|00〉S1R12|00〉S2R21|1111〉S1′S2′T1′T2′|00〉T1T2)+α01eιθ01(|111〉Rnr1r2|00〉S1R12|11〉S2R21|0000〉S1′S2′T1′T2′|01〉T1T2+|111〉Rnr1r2|00〉S1R12|11〉S2R21|1111〉S1′S2′T1′T2′|01〉T1T2)+α10eιθ10(|111〉Rnr1r2|11〉S1R12|00〉S2R21  |0000〉S1′S2′T1′T2′|10〉T1T2+|111〉Rnr1r2|11〉S1R12|00〉S2R21  |1111〉S1′S2′T1′T2′|10〉T1T2)+α11eιθ11(|000〉Rnr1r2|11〉S1R12|11〉S2R21  |0000〉S1′S2′T1′T2′|11〉T1T2+|000〉Rnr1r2|11〉S1R12|11〉S2R21  |1111〉S1′S2′T1′T2′|11〉T1T2),(24)

Then, For Step 5-Step 9, it can be considered as the decoding process and the object is to remove the particles in the unnecessary quantum registers. The corresponding schematic diagram of quantum circuit can be shown in Fig. 4.

Figure 4: Schematic diagram of quantum circuit for steps 5–9

According to the specific calculations, the quantum states of Step 5–9 are detailed as follows:

|Ψ〉5(2)=12[α00eιθ00(|000〉Rnr1r2|00〉S1R12|00〉S2R21|0000〉S1′S2′T1′T2′|00〉T1T2+|000〉Rnr1r2|00〉S1R12|00〉S2R21|1111〉S1′S2′T1′T2′|00〉T1T2)+α01eιθ01(|111〉Rnr1r2|00〉S1R12|11〉S2R21|0000〉S1′S2′T1′T2′|01〉T1T2+|111〉Rnr1r2|00〉S1R12|11〉S2R21|1111〉S1′S2′T1′T2′|01〉T1T2)+α10eιθ10(|111〉Rnr1r2|11〉S1R12|00〉S2R21  |0000〉S1′S2′T1′T2′|10〉T1T2+|111〉Rnr1r2|11〉S1R12|00〉S2R21  |1111〉S1′S2′T1′T2′|10〉T1T2)+α11eιθ11(|000〉Rnr1r2|11〉S1R12|11〉S2R21  |0000〉S1′S2′T1′T2′|11〉T1T2+|000〉Rnr1r2|11〉S1R12|11〉S2R21  |1111〉S1′S2′T1′T2′|11〉T1T2),(25)

|Ψ〉6(2)=12[α00eιθ00(|000〉Rnr1r2|0〉R12|0〉R21|00〉T1′T2′|00〉T1T2+|000〉Rnr1r2|0〉R12|0〉R21|11〉T1′T2′|00〉T1T2)+α01eιθ01(|111〉Rnr1r2|0〉R12|1〉R21|00〉T1′T2′|01〉T1T2+|111〉Rnr1r2|0〉R12|1〉R21|11〉T1′T2′|01〉T1T2)+α10eιθ10(|111〉Rnr1r2|1〉R12|0〉R21  |00〉T1′T2′|10〉T1T2+|111〉Rnr1r2|1〉R12|0〉R21  |11〉T1′T2′|10〉T1T2)+α11eιθ11(|000〉Rnr1r2|1〉R12|1〉R21  |00〉T1′T2′|11〉T1T2+|000〉Rnr1r2|1〉R12|1〉R21  |11〉T1′T2′|11〉T1T2),(26)

|Ψ〉7(2)=12[α00eιθ00(|0〉Rn|0〉R12|0〉R21|00〉T1′T2′|00〉T1T2+|0〉Rn|0〉R12|0〉R21|11〉T1′T2′|00〉T1T2)+α01eιθ01(|1〉Rn|0〉R12|1〉R21|00〉T1′T2′|01〉T1T2+|1〉Rn|0〉R12|1〉R21|11〉T1′T2′|01〉T1T2)+α10eιθ10(|1〉Rn|1〉R12|0〉R21  |00〉T1′T2′|10〉T1T2+|1〉Rn|1〉R12|0〉R21  |11〉T1′T2′|10〉T1T2)+α11eιθ11(|0〉Rn|1〉R12|1〉R21  |00〉T1′T2′|11〉T1T2+|0〉Rn|1〉R12|1〉R21  |11〉T1′T2′|11〉T1T2),(27)

|Ψ〉8(2)=12[α00eιθ00(|0〉R12|0〉R21|00〉T1′T2′|00〉T1T2+|0〉R12|0〉R21|11〉T1′T2′|00〉T1T2)+α01eιθ01(|0〉R12|1〉R21|00〉T1′T2′|01〉T1T2+|0〉R12|1〉R21|11〉T1′T2′|01〉T1T2)+α10eιθ10(|1〉R12|0〉R21  |00〉T1′T2′|10〉T1T2+|1〉R12|0〉R21  |11〉T1′T2′|10〉T1T2)+α11eιθ11(|1〉R12|1〉R21  |00〉T1′T2′|11〉T1T2+|1〉R12|1〉R21  |11〉T1′T2′|11〉T1T2),(28)

|Ψ⟩9(2)=12(α00eιθ00|00⟩T1T2+α01eιθ01|01⟩T1T2+α10eιθ10|10⟩T1T2+α11eιθ11|11⟩T1T2).(29)