Computers, Materials & Continua DOI:10.32604/cmc.2022.027120
Article

Optimal Beamforming for Secure Transmit in Practical Wireless Networks

Qiuqin Yang1, Linfang Li1, Ming-Xing Luo1,* and Xiaojun Wang2

1The School of Information Science and Technology, Southwest Jiaotong University, Chengdu, 610031, China
2School of Electronic Engineering, Dublin City University, Dublin 9, Ireland
*Corresponding Author: Ming-Xing Luo. Email: mxluo@swjtu.edu.cn
Received: 11 January 2022; Accepted: 07 April 2022

Abstract: In real communication systems, secure and low-energy transmit scheme is very important. So far, most of schemes focus on secure transmit in special scenarios. In this paper, our goal is to propose a secure protocol in wireless networks involved various factors including artificial noise (AN), the imperfect receiver and imperfect channel state information (CSI) of eavesdropper, weight of beamforming (BF) vector, cooperative jammers (CJ), multiple receivers, and multiple eavesdroppers, and the analysis shows that the protocol can reduce the transmission power, and at the same time the safe reachability rate is greater than our pre-defined value, and the analysis results are in good agreement with the simulation results. In this letter, the minimal transmit power is modeled as a non-convexity optimization that is general difficult. Our method is to transform it into a two-level non-convex problem. The outer is a univariate optimization that can be solved by the golden search algorithm. The inner is a convex optimization solved by using the CVX. The solutions are further used to improve the confidentiality rate of the system, and reduce the transmit power of the system and resource consumption in terms of the imperfect CSI. Simulations show the efficiency and robustness of the proposed protocol.

Keywords: Secure transmission; MISO system; imperfect CSI; BF vector; convex optimization

1  Introduction

Physical Layer Security (PLS) has received extensive attention in ensuring the security of data transmission. The main goal of PLS in applications is to ensure the secrecy of messages,which transmitted by legitimate receivers [1]. This is achieved by reducing the signal-to-noise ratio (SNR) of the eavesdropper. One method is to add AN to the legal signal [2–4]. Cooperative relay (CR) is useful in the secure transmit of CR-assisted multi-antenna systems. CR can act as a jammer and expand the interference range [5–7]. At the same time, the status information of the channel should also be considered. It is difficult to obtain accurate CSI because of the time-varying characteristics of the channel. Some schemes have studied robust and secure transmit with imperfect CSI [8–12]. There are two kinds of protocols with uncertain CSI. One is uncertain on one side, that is, only the status information of the eavesdropper or receiver is unknown [13–15]. The other is uncertain on both sides, which mean the CSI of both parties is completely unknown [16–19]. In addition to the secrecy performance, the power consumption of the system is also considered [20–25]. Reference [25] gives the best solution for spectral efficiency and energy consumption issues in 5G communications.

Our motivation comes from the fact that most of cooperative interferences only consider one or a few factors, while the actual factors are not involved in applications, such as imperfect receiver and imperfect CSI of eavesdropper, cooperative jammer, multiple Receivers, and multiple eavesdroppers. In this article, we propose a secure transmit protocol by considering all these factors, which provide a more reliable model for complex networks. The main consideration is coordinated interference, which ensures the confidentiality of the receiver CSI (RCSI) and the eavesdropper CSI (ECSI) under the imperfect premise. At the same time, we will reduce the power required to transmit the signal. Due to the bounded error of CSI, we propose a robust and secure transmit scheme in the MISO downlink network. To further improve the security performance, we also use multi-antenna auxiliary jammers. The main contributions made in this paper are as follows:

(1) Aiming at imperfect RCSI and ECSI, we propose a robust transmit scheme for the eavesdropping model with multi-receiver-eavesdroppers in multicast. We evaluate the minimum transmit power of the transmitter and the CR to meet the transmit reliability and confidentiality, that is, the minimum secrecy rate in the worst case is still greater than what is required to ensure the secure transmission.

(2) We introduce a slack-variable logarithm and semi-definite slack (SDR) to simplify the transmit power optimization, which is due to the non-convexity of the optimization problem involved. At the same time, the Lagrange duality is used to obtain the analytical formula of the constraint conditions. The non-convex problem further becomes a two-level optimization. The external is a univariate optimization, which is solved by using the golden search algorithm. The inner layer is a semi-definite programming (SDP) problem which will be resolved by CVX.

The rest of the paper is organized as follows. Section 2 introduces the system model. In Section 3, we establishes the problem formulationand model the robust transmit power as a non-convex minimization problem. The two-level optimization algorithms will be applied to solve the present problem. Section 4 contributes the simulation that shows the efficiency of the proposed schemes while last section concludes the paper.

2  System Model

Before introducing the system model, we introduce the parameter symbols used in this paper and their meanings, as shown in Tab. 1. The matrix is indicated in bold capital letters. Vectors are represented in bold lowercase letters.

We consider anassisting jammer (AJ)-assisted MISO system as shown in Fig. 1. Alice sends message to multiple receivers Bob1, …, Bobl.The AJ sends AN (here, Gaussian noises will be used in what follows) for the secure transmit by confusing Keavesdroppers Eve. Due to limited feedback, assume that Alice knows the imperfect CSI of each receiver and eavesdropper. The channel estimation error Δ is bounded. The receiver is equipped with an antenna, Eves as same as the receiver. The total number of antennas for the transmitter and assisting jammer is denoted as Nt and Nj, respectively.

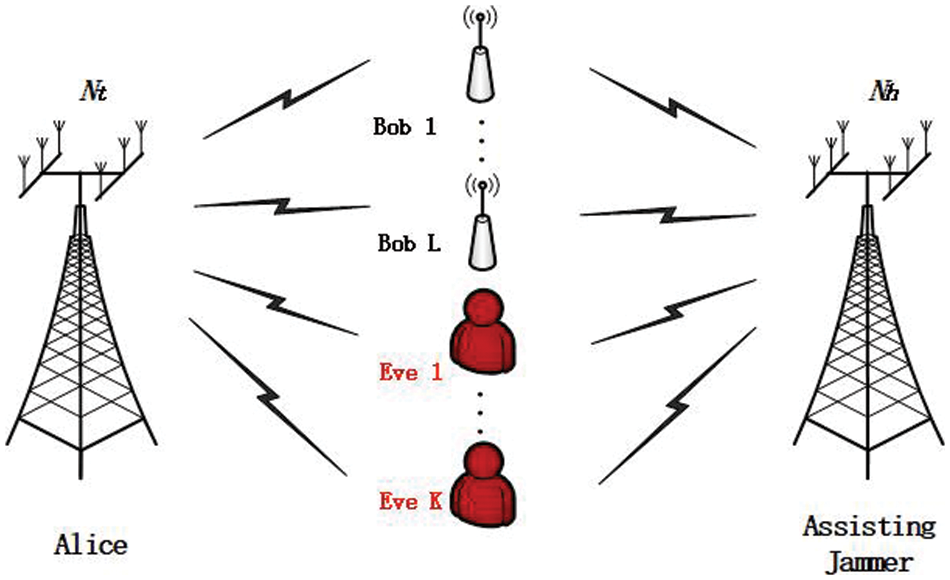
Figure 1: System model for secure transmit with assisting jammer

The signal from the transmitter is expressed by x=ws, which denotes the receiver’s data stream with E[|s|2]=1. Let w∈CNt denote the beamforming (BF) vector of the signal. Let z∈CNt be AN generated by AJ, that is, z∼CN(0, Q),Q⪰0.

Let nl∼CN(0, σb,l2) and nk∼CN(0,σe,k2) denote the standard complex Gaussian noises for Bobl and Evek [26], respectively. Denote gb,l∈CNj and ge,k∈CNj as the channels from AJ to Bobl and Evek, respectively. The signals received by Bobl and Evek are respectively given by

yb,l=hb,lx+gb,lz+nb,l,(1a)

ye,k=he,kx+ge,kz+ne,k,(1b)

where hb,l∈CNt and he,k∈CNt denote the channel vectors from Alice to Bobl and Evek, respectively, l∈L=Δ{1,⋯,L}, and k∈K=Δ{1,⋯,K}. It is assumed that all channels are independent. The SINRs of channels are respectively expressed as

SINRb,l(w,Q)=hb,lwwHhb,lHgb,lQgb,lH+σb,l2(2a)

SINRe,k(w,Q)=he,kwwHhe,kHge,kQge,kH+σe,k2(2b)

3  Optimal Beamforming Schemes

3.1 Channel Mismatch

In this section, we consider the imperfect CSI. The wireless channels of Alice and AJ are estimated in the quadratic form. Therefore, for Alice, its channel modeling [27] is given by

Hb,l=E[hb,lhb,lH]=H~b,l+Δh,b,l=h~b,lh~b,lH+Δh,b,l(3a)

He,k=E[he,khe,kH]=H~e,k+Δh,e,k=h~e,kh~e,kH+Δh,e,k(3b)

where H~b,l and H~e,k are defined by

H~b,l=H~b,lH~b,lH(4a)

H~e,k=H~e,kH~e,kH(4b)

which are the estimated channel covariances in quadratic form, Δh,b,l and Δh,e,k are the CSI errors from Alice to Bobl and Evek, respectively, and l∈L, k∈K.

Suppose that h~b,l is complex Gaussian variable [10], that is, h~b,l∼CN(0,ξb,l), g~b,l∼CN(0,ξb,l). Assume that the uncertainty is bounded in the uncertainty region of the ellipsoid [27,28] that can be modeled as

Hb,l=Δ⁡{Δh,b,l|Δh,b,l∈HN,H~b,l+Δh,b,l⪰0,a1≤1}(5a)

He,k=Δ⁡{Δh,e,k|Δh,e,k∈HN,H~e,k+Δh,e,k⪰0,a2≤1}(5b)

where a1 and a2 are defined as

a1=tr(Δh,b,lDh,b,lΔh,b,l),a2=tr(Δh,e,kDh,e,kΔh,e,k)(6)

Dh,b,l (or Dh,e,k) depends on CSI, which is from Alice to Bobl (or Evek). Both of them are known. Especially, Dh,b,l and Dh,e,k can be decomposed into as follows [27]:

{Dh,b,l=D^h,b,lHD^h,b,lDh,b,l⪰0,{Dh,e,k=D^h,e,kHD^h,e,kDh,e,k⪰0(7)

Similarly, from Eqs. (3a) and (3b), we get the channel model of AJ as follows:

Gb,l=E[gb,lgb,lH]=G~b,l+Δg,b,l=g~b,lg~b,lH+Δg,b,l(8a)

Ge,k=E[ge,kge,kH]=G~e,k+Δg,e,k=g~e,kg~e,kH+Δg,e,k(8b)

where G~b,l and G~e,k are defined by

G~b,l=h~e,kh~e,kh(9a)

G~e,k=g~e,kg~e,kH(9b)

which are the estimated channel covariances in the quadratic form,Δg,b,l and Δg,e,k are CSI errors from AJ to Bobl and to Evek, respectively, and l∈L, k∈K. Let g~b,l∼CN(0,ξb,l) and g~e,k∼CN(0,ξe,k). Similar to Eqs. (5a) and (5b), we have

Gb,l=Δ{Δg,b,l|Δg,b,l∈HN,G~b,l+Δg,b,l⪰0,a3≤1}(10a)

Ge,k=Δ{Δg,e,k|Δg,e,k∈HN,G~e,k+Δg,e,k⪰0,a4≤1}(10b)

where A3 and A4 are defined as follows

a3=tr(Δg,b,lDg,b,lΔg,b,l),a4=tr(Δg,e,kDg,e,kΔg,e,k)(11)

Dg,b,l, and Dg,e,k can be decomposed as follows

{Dg,b,l⪰0Dg,b,l=D^g,b,lHD^g,b,l,{Dg,e,k⪰0Dg,e,k=D^g,e,kHD^g,e,k(12)

3.2 Robust Transmit Power Minimization

The present problem is to minimize the transmit power, while the guarantee the minimum transmit secrecy rate. Here, the estimation error of CSI is considered. For the worst case of secrecy capacity, according to the principle of power minimization, the optimization function after adding AN is given by

Q1:minw,Q⪰0tr(wwH+Q)(13a)

s.t.,minl∈L,k∈K{minΔg,b,l∈Gb,lΔhb,l∈Hb,lRb,l−maxΔg,e,k∈Ge,kΔh,e,k∈He,kRe,k}≥Rs,∀l,∀k(13b)

 tr(wwH+Q)≤Pmax(13c)

where Rs is the pre-defined target secrecy rate. In the model, the secrecy rate is evaluated by the difference between the minimum secrecy capacity of the receiver and the maximum secrecy capacity of the eavesdropper. So, the secrecy rate obtained in the optimization is the minimum secrecy rate of the system. In our setting, the minimum secrecy rate should also be higher than the target secrecy rate. To simplify the secrecy capacity function, we introduce β is used as a slack variable. The optimization problem Q1 is equivalently written into

Q2:minw,Q⪰0tr(wwH+Q)(14a)

s.t.minΔg,b,l∈Gb,lΔhb,l∈Hb,l(Rb,l−log⁡β)≥Rs,∀l,(14b)

maxΔg,e,k∈Ge,kΔh,e,k∈He,kRe,k≤log⁡β,∀k(14c)

 tr(wwH+Q)≤Pmax(14d)

where log⁡(⋅) denotes the base-2 logarithmic function.

According to Shannon’s formula, the achievable secure rate of Bobl and the Evek can be represented as

Cb,l=log⁡(1+tr((H~b,l+Δh,b,l)wwH)tr((G~b,l+Δg,b,l)Q)+σb,l2)(15a)

Ce,k=log⁡(1+tr((H~e,k+Δh,e,k)wwH)tr((G~e,k+Δg,e,k)Q)+σe,k2)(15b)

From Eqs. (14b), (14c), (15a) and (15b), we can obtain

Q3:minw,Q⪰0tr(wwH+Q)(16a)

s.t.minΔg,b,l∈Gb,lΔhb,l∈Hb,l(1+tr(wHb,lwH)tr(Gb,lQ)+σb,l2)≥β2RS,∀l(16b)

maxΔg,e,k∈Ge,kΔh,e,k∈He,k(1+tr(wHe,kwH)tr(Ge,kQ)+σb,l2)≤β,∀k(16c)

tr(wwH+Q)≤Pmax,∀k(16d)

The Q3 is still non-convex problem. We resort to the idea of SDR to deal with Q3. Define W=wwH. It follows that W⪰0,rank(W)=1. By regardless of the constraint rank(W)=1, Q3 is written into

Q4:minw,Q⪰0 tr(W+Q)(17a)

s.t.minΔg,b,l∈Gb,l(tr(Gb,lQF1))+minΔhb,l∈Hb,l(tr(WHb,l))≥−F1,∀l(17b)

maxΔh,e,k∈He,k(tr(WHe,k)+maxΔg,e,k∈Ge,ktr(Ge,kQF2))≤−F2,∀k(17c)

tr(W+Q)≤Pmax(17d)

where F1=1−2Rsβ and F2=1−β

Due to the semi-definite constraints in Eqs. (17b) and (17c), it is difficult to solve the problem Q5. To solve this problem, we firstly transformed into a convex form to get an accurate form. It can be stated as the following proposition.

Proposition 1: For Δ∈HN and two complex Hermitian matrices B and D=DHD, we have

maxD⪰0tr(ΔBΔ)≤1tr(ΔB)=2ϕ(B,D)(18)

where ϕ is a function defined by

ϕ(B,D)=Δ‖(I⊗D~)(I⊗D+DH⊗I)−1vec(B)‖(19)

Its maximum is achieved when Δ is given by

Δopt=(I⊗D~+DH⊗I)−1vec(B)‖(I⊗D~)(I⊗D+DH⊗I)−1vec(B)‖(20)

where I is the identity matrix.

Proposition 2: For Δ∈HN and two complex Hermitian matrices B and D=DHD, we have

minD⪰0tr(ΔBΔ)≤1tr(ΔB)=−2ϕ(B,D)(21)

where its minimum is achieved when Δ is given by

Δopt=−(I⊗D+DH⊗I)−1vec(B)‖(I⊗D~)(I⊗D+DH⊗I)−1vec(B)‖(22)

Proof: See Appendix A.

By using Proposition 2 for the left side of the inequality (17b) and Proposition 1 for the left side of the inequality (17c), we have Proposition 3.

Proposition 3: The optimization problem Q4 is transformed into

Q5:minW⪰,Q⪰0,β tr(W+Q)(23a)

s.t. tr(WH~b,l)−2ϕ(W,Dh,b,l)+tr(QG~b,lF1)−2ϕ(QF1,Dg,b,l)≥F1,∀l(23b)

tr(WH~e,k)−2ϕ(W,Dh,e,k)+tr(QG~e,kF2)−2ϕ(QF2,Dg,e,k)≤−F2,∀k(23c)

tr(W+Q)≤Pmax(23d)

Proof: See Appendix B.

Note that Q5 is still non-convex, because the existence of the slack variable. Fortunately, for a fixed β, it is a convex SDP problem. Thus, the problem Q5 is reconstructed as a two-layer optimization problem. The first layer is a successive approximation problem with slack variables β. while the inner is the convex SDP problem. Hence, Q5 will be transformed into

Q6:minβf(β)(24a)

s.t.1≤β≤1+Pmaxminl∈Ltr(Hh,b,l)(24b)

where f(β) is a function of β, Q6 has an optimal solution when β is fixed.

Proposition 4: β is defined in [1,1+Pmaxτ], where τ=minl∈Ltr(H~b,l).

Proof: From the inequality (16c) and positive semi-definite matrices W,Q,Gg,e,k, we can get

It follows that β≥1.

The upper bound of β can be proved as follows:

β≤1+minl∈L,Δh,b,l∈Hh,b,lΔg,b,l∈Gg,b,ltr(Hh,b,lW)σb,l2+tr(Gg,b,lQ)(25a)

≤1+minl∈Ltr(H~h,b,lW)σb,l2+tr(G~g,b,lQ)(25b)

≤1+Pmaxminl∈Ltr(H~h,b,l)(25c)

Here, the inequality (25a) comes from the inequality (16b) and the fact that Rs may be negative. The inequality (25b) is from the inequality of tr(W)≤Pmax and Eq. (4a) when Q=0 and σb,l2=1. This has completed the proof.

Now, in order to obtain the optimal value of β , we use the one-dimensional search variables method to calculate. Since the inner-level problem is a convex SDP, which will be solved by the CVX [29]. The outer layer problem for a fixed β is solved by using the golden search method [30]. In summary, we obtain a specific algorithm to solve Q6 as shown in Algorithm 1:

4  Simulation Results

This section provides numerical results to verify the performances of the proposed transmit scheme. The main setups are shown in Tab. 2.

The channel uncertainty is given in the following form.:

Dh,b,l=Iγh,b,l2,Dg,b,l=Iγg,b,l2(26a)

Dh,e,k=Iγh,e,k2,Dg,e,k=Iγg,e,k2(26b)

γh,b,l=‖H~b,l‖αb,γg,b,l=‖G~b,l‖αb(26c)

γh,e,k=‖H~e,k‖αe,γg,e,k=‖G~e,k‖αe(26d)

Figs. 2 and 3 show the relationships between Rs, P, R and αb. Fig. 2a presents the actual total transmit power in terms of the target secrecy rate and αe. We set ξb,l=ξe,k=1. It shows that the total transmit power increases as αe increases. Moreover, as the uncertainty of the Eve’s channel increases, the proposed BF scheme requires a higher total transmit power in order to ensure Rs target secrecy rate. From Fig. 2b, the achievable secrecy rate in the worst case is higher than the target secrecy rate, which satisfies the secrecy requirement of the system in Eq. (13b). In addition, although Fig. 2b shows that the larger the αe, the larger the actual secrecy rate when the target secrecy rate takes a certain value, which does not seem to be true. However, when we compare the actual secrecy rate, the consumed power P jointly, as shown in Fig. 3, a reasonable explanation can be obtained. As its shown in Fig. 3, the larger αe is, the smaller the achievable secrecy rate is obtained in the system with the same power. This is because in the present scheme, the power is related to the target secrecy rate, while the achievable secrecy rate in the worst case and the power are correlated. So, the larger the channel uncertainty is, the lower the system secrecy performance is. Fortunately, this can be overcome by increasing the transmit power Pmax.

Figure 2: (a) Actual average total transmit power vs. the pre-defined target secrecy rate. (b) Worst-case achievable secure rate vs. the target secrecy rate Rs for different αe. Here, L = 3, K = 4, αb=0.02, and Pmax=30 dB

Figure 3: The worst-case achievable secrecy rate vs. actual average total transmit power different αb with L=3,K=4, αb=0.02 and Pmax=30 dB

Figure 4: (a) Number of occurrences in terms of actual average total transmit power P with random 100 independent experiments. (b) Number of occurrences in terms of worst-case achievable secrecy ratewith random 100 independent experiments. Here, L = 3, K = 4, αb=αe=0.05, Pmax=30dB and Rs = 2 bit/s/Hz

Fig. 4 shows the system channel capacity and transmit power with random 100 independent experiments. There are more than 90% channels which satisfy the target secrecy rate and the power requirements. This shows that the proposed scheme should be applicable in piratical channels.

Now, we compare the present schemes with previous schemes to show its performances. We mainly consider the LD system model in ref. [23] and CVaR and BTiE in ref. [31], while other schemes may not be consistent with the communication model in this paper or have inconsistent optimization objectives, so no more schemes are selected for comparison.The transmit power and achievable secrecy rate in worst case will be simulated.

Fig. 5a shows a comparison between the present scheme and its in ref. [23] for one receiver and one eavesdropper. In Fig. 5a, the present scheme costs less power than the LD scheme when the system secrecy rate is less than 4.4 provided that the secrecy rate in the worst case reaches the target. However, when the achievable secrecy rate is larger than 4.4, we get converse result. So, when the system secrecy rate is less than 3.8, the present scheme is better than its in ref. [23] to guarantee both the secrecy and power consumption Fig. 5b shows the comparison between the present scheme and the two approaches in ref. [31] for one receiver and multiple eavesdroppers. In both models, the simulations are completed with the same total transmit power of Pmax=30dB. Here, ξb,l=ξe,k=0.002. In Fig. 5b, the present scheme achieves the bettersecrecyperformance when three schemes have the same transmit power. Hence, these results show when both power loss and achievable secrecy rate are involved, our transmit scheme is better than both schemes in refs. [23,31]. Other parameter effects and performance indicators were not considered in this simulation, but it is worth considering.

Figure 5: (a) Achievable secrecy rate vs. average transmit power with L=1,K=1 (b) Average transmit power vs. achievable secrecy rate with L=1 and K=3

5  Conclusion

In this paper, we investigate the robust transmit BF design for MISO wiretapping channels with the imperfect CSI and the minimum transmit power. The covariance-based CSIs of both legitimate receivers and eavesdroppers are imperfect, where the CSI error is restricted to the ellipsoidal model. The communication models are assisted by AJs. We jointly optimized the covariance of the interference signal generated by the auxiliary node and the beamforming vector of the source node in the AJ-assisted system. The SDR method is firstly used to approximate the present non-convex optimization. We then obtained the equivalent tractable semi-infinite constraints by using the Lagrange duality. This transforms the original non-convex optimization into a two-level optimization with univariate optimization in the outer layer and convex SDP in the inner layer. Simulation results show the present scheme is better than previous schemes. This provides an efficient transmit scheme in practical systems.

Funding Statement: This work was supported by the national natural Science Foundation of China (no. 62172341), and Fundamental Research Funds for the Central Universities (no. 2682014CX095).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  I. Qadeer and M. K. Ehsan, “Improved channel reciprocity forsecure communication in next generation wireless systems,” Computers, Materials & Continua, vol. 67, no. 2, pp. 2619–2630, 2021. [Google Scholar]

 2.  R. Negi and S. Goel, “Secret communication using artificial noise,” in VTC-2005-Fall. 2005 IEEE 62nd Vehicular Technology Conf., Dallas, TX, USA, IEEE, pp. 1906–1910, 2005. [Google Scholar]

 3.  X. Liu, Z. Chen, Y. Wang, F. Zhou and S. Ma, “Robust artificial noise-aided beamforming for a secure MISO-NOMA visible light communication system,” China Communications, vol. 17, no. 11, pp. 42–53, 2020. [Google Scholar]

 4.  S. Goel and R. Negi, “Guaranteeing secrecy using artificial noise,” IEEE Transactions on Wireless Communications, vol. 7, no. 6, pp. 2180–2189, 2008. [Google Scholar]

 5.  A. Wolf and E. A. Jorswieck, “On the zero forcing optimality for friendly jamming in MISO wiretap channels,” in 2010 IEEE 11th Int. Workshop on SPAWC, Marrakech, Morocco, pp. 1–5, 2010. [Google Scholar]

 6.  J. E. Giti, B. Srinivasan and J. Kamruzzaman, “Impact of friendly jammers on secrecy multicast capacity in presence of adaptive eavesdroppers,” in 2017 IEEE GC WKSHPS, Singapore, pp. 1–6, 2017. [Google Scholar]

 7.  L. Hu, H. Wen, B. Wu, J. Tang, F. Pan et al., “Cooperative jamming-aided secrecy enhancement in wireless networks with passive eavesdroppers,” IEEE Transactions on Vehicular Technology, vol. 67, no. 3, pp. 2108–2117, 2018. [Google Scholar]

 8.  H. Yu, W. Duan, Q. Sun, X. Wang, J. Wang et al., “Generalized beamforming design for cooperative MIMO multirelay networks with infinite constraints and imperfect CSI,” Mathematical Problems in Engineering, vol. 2018, no. 5, pp. 276–281, 2018. [Google Scholar]

 9.  D. Do, T. Anh Le, T. N. Nguyen, X. Li and K. M. Rabie, “Joint impacts of imperfect CSI and imperfect SIC in cognitive radio-assisted NOMA-V2X communications,” IEEE Access, vol. 8, pp. 128629–128645, 2020. [Google Scholar]

10. H. Ma, J. Cheng and X. Wang, “Cooperative jamming aided robust beamforming for MISO channels with unknown eavesdroppers,” in GLOBECOM, 2017 - 2017 IEEE Global Communications Conf., Singapore, pp. 1450–1454, 2017. [Google Scholar]

11. T. N. Nguyen, M. Tran, P. T. Tran, P. Tran Tin, T. L. Nguyen et al., “On the performance of power splitting energy harvested wireless full-duplex relaying network with imperfect CSI over dissimilar channels,” Security and Communication Networks, vol. 2018, pp. 1–11, 2018. [Google Scholar]

12. Y. Zhang, Y. Dong, L. Wang, J. Liu, Y. Peng et al., “Outagecapacity analysis for cognitive non-orthogonal multiple access downlink transmissions systems in the presence of channel estimation error,” Computers, Materials & Continua, vol. 60, no. 1, pp. 379–393, 2019. [Google Scholar]

13. M. Pei, A. L. Swindlehurst, D. Ma and J. Wei, “Adaptive limited feedback for MISO wiretap channels with cooperative jamming,” IEEE Transactions on Signal Processing, vol. 62, no. 4, pp. 993–1004, 2014. [Google Scholar]

14. J. Huang and A. L. Swindlehurst, “Robust secure transmission in MISO channels based on worst-case optimization,” IEEE Transactions on Signal Processing, vol. 60, no. 4, pp. 1696–1707, 2012. [Google Scholar]

15. T. A. Le, Q. Vien, H. X. Nguyen, D. W. K. Ng and R. Schober, “Robust chance-constrained optimization for power-efficient and secure SWIPT systems,” IEEE Transactions on Green Communications and Networking, vol. 1, no. 3, pp. 333–346, 2017. [Google Scholar]

16. B. Su, Q. Ni and B. He, “Robust transmit designs for secrecy rate constrained misonoma system,” in 2018 IEEE 29th Annual Int. Symp. on PIMRC, Bologna, Italy, IEEE, pp. 1–5, 2018. [Google Scholar]

17. H. Ma, J. Cheng, X. Wang and P. Ma, “Robust MISO beamforming with cooperative jamming for secure transmission from perspectives of QoS and secrecy rate,” IEEE Transactions on Communications, vol. 66, no. 2, pp. 767–780, 2018. [Google Scholar]

18. Z. Chu, H. Xing, M. Johnston and S. Le Goff, “Secrecy rate optimizations for a miso secrecy channel with multiple multiantenna eavesdroppers,” IEEE Transactions on Wireless Communications, vol. 15, no. 1, pp. 283–297, 2016. [Google Scholar]

19. Y. Zhong, F. Zhou, Y. Wang, X. Deng and N. Al-Dhahir, “Cooperative jamming-aided secure wireless powered communication networks: Agame theoretical formulation,” IEEE Communications Letters, vol. 24, no. 5, pp. 1081–1085, 2020. [Google Scholar]

20. H. Song, H. Wen, L. Hu, Y. Chen and R. Liao, “Optimal power allocation for secrecy rate maximization in broadcast wiretap channels,” IEEE Wireless Communications Letters, vol. 7, no. 4, pp. 514–517, 2018. [Google Scholar]

21. D. Jeong and D. Kim, “Power allocation and outage analysis for cognitive radio with jamming signal under primary secrecy outage constraint,” in 2018 28th InITNAC, Sydney, NSW, Australia, IEEE, pp. 1–6, 2018. [Google Scholar]

22. J. Zhou, Y. Sun, Q. Cao, S. Li, Z. Sun et al., “Power minimization for secure multi-user MISO NOMA system with energy harvesting,” IEEE Transactions on Vehicular Technology, vol. 69, no. 9, pp. 10046–10058, 2020. [Google Scholar]

23. Z. Chu, M. Johnston and S. LeGoff, “Robust beamforming techniques for MISO secrecy communication with a cooperative jammer,” in 2015 IEEE 81st VTC Spring, Glasgow, UK, IEEE, pp. 1–5, 2015. [Google Scholar]

24. G. Wang, C. Meng, W. Heng and X. Chen, “Secrecy energy efficiency optimization in an-aided distributed antenna systems with energy harvesting,” IEEE Access, vol. 6, pp. 32830–32838, 2018. [Google Scholar]

25. R. M. Asif, S. Mustafa, N. Jamel, A. U. Rehman, M. Shafiq et al., “Energy efficiency trade-off with spectral efficiency inMIMO systems,” Computers, Materials & Continua, vol. 70, no. 3, pp. 5889–5905, 2022. [Google Scholar]

26. L. Zheng, D. Liu, Z. Wen and J. Zou, “Robust beamforming for multi-user MISOfull-duplex swipt system under non-linear energy harvesting model,” IEEE Access, vol. 9, pp. 14387–14397, 2021. [Google Scholar]

27. G. Zheng, K. Wong and B. Ottersten, “Robust cognitive beam forming with bounded channel uncertainties,” IEEE Transactions on Signal Processing, vol. 57, no. 12, pp. 4871–4881, 2009. [Google Scholar]

28. L. Zhang, L. Jin, W. Luo, Z. Zhong and D. Yu, “Robust artificial noise aided transmit method for multicast MISO wiretap channels with imperfect covariance-based CSI,” in 2015 IEEE 81st VTC Spring, Glasgow, UK, IEEE, pp. 239–243, 2015. [Google Scholar]

29. M. Grant, “CVX: Matlab software for disciplined convex programming,” 2011. [Online]. Available: http://cvxr.com/cvx. [Google Scholar]

30. A. P. Aparna and H. S. Sonalikar, “Fast computation of radomeem parameters with golden section search method for radiation patternpeak detection,” in 2019 IEEE Int. Conf. on Electronics, Computing and Communication Technologies (CONECCT), Bangalore, India , IEEE, pp. 172–176, 2019. [Google Scholar]

31. X. Liu, Y. Gao, G. Zang, N. Sha and M. Guo, “Distributionally robust secure transmission for MISO downlink networks with assisting jammer,” IEEE Access, vol. 7, pp. 119981–119995, 2019. [Google Scholar]

Appendix A.

It can be verified that the convex problem (18) satisfies Slater’s conditions [27]. Hence the strong duality holds between (18) and its dual problem, i.e., they have the same objective value. The Lagrangian of (18) can be written as

L(Δ,λ)=tr(ΔA)−λ(ΔDΔ−1)>0(27)

λ is the dual variable corresponding to the inequality constraint. Differentiating (27) with respect to Δ and setting the derivative to zero, we have

∂L(Δ,λ)∂Δ=A−λΔ−λΔD=0(28)

After applying the identity vec(BXC)=(CT⊗B)vec(X), we have the following equality

λvec(Δ)=Mvec(A),M=(I⊗C+CT⊗I)−1(29)

The Lagrangian dual function for the problem (18) can be written as

L=2λtr(ΔDΔH)−λ(tr(ΔDΔH)−1)=λtr(ΔDΔH)+λ=(1)2λ(30)

where tr(ΔDΔH)=1 if it is in the optimum point, therefore, step 1 in the above formula holds. Due to Δ=ΔH,D=D∼HD~, we can get ‖D~Δ‖2=1, through vec(BXC)=(CT⊗B)vec(X), we can get follow equality:

‖D~Δ‖2=‖(I⊗D~)vec(Δ)‖=1(31)

By combining Eqs. (29) and (31) we can get the value of λ:

λ=λ‖D~Δ‖2=‖(I⊗D~)Mvec(A)‖(32)

By combining Eqs. (30) and (32), we can get

maxtr(ΔB)=2‖(I⊗D~)(I⊗C+CH⊗I)−1vec(A)‖(33)

As a result, we proved Proposition 1 and the optimal Δ, denoted by Δopt which completes the proof.

The proof of Proposition 2 is similar to that of Proposition 1.

Appendix B.

Use Proposition 2, Eqs. (3a) and (5a) for the left side of the inequality (17b)

minΔg,b,l∈Gb,l(tr(Gb,lQF1))=minΔg,b,l∈Gb,l(tr(G~b,lQF1+Δg,b,lQF1))=tr(QG~b,lF1)−2ϕ(QF1,Dg,b,l)(34a)

minΔh,b,l∈Hb,l⁡(tr(WHb,l))=minΔh,b,l∈Hb,l⁡(tr(W~Hb,l+Δh,b,lW))=tr(W~Hb,l)−2ϕ(W,Dh,b,l)(34b)

The above equation holds when Δg,b,l and Δh,b,l takes the following optimal values:

Δg,b,l|opt=(I⊗Dg,b,l+Dg,b,lH⊗I)−1vec(QF1)‖(I⊗D~g,b,l)(I⊗Dg,b,l+Dg,b,lH⊗I)−1vec(QF1)‖(35a)

Δh,b,l|opt=(I⊗Dh,b,l+Dh,b,lH⊗I)−1vec(W)‖(I⊗D~h,b,l)(I⊗Dh,b,l+Dh,b,lH⊗I)−1vec(W)‖(35b)

Similarly, using Proposition 1 and Eqs. (3b) and (5b), from the inequality (17c) we get

maxΔh,e,k∈He,k(tr(WHe,k))=maxΔh,e,k∈He,k(tr(WH~e,k+WΔh,e,k))=tr(WH~e,k)−2ϕ(W,Dh,e,k)(36a)

maxΔg,e,k∈Ge,k(tr(Ge,kQF2))=maxΔg,e,k∈Ge,k(tr(G~e,kQF2)+Δg,e,kQF2))=tr(QG~e,kF2)−2ϕ(QF2,Dg,e,k)(36b)

Eqs. (36a) and (36b) holds when Δh,e,k and Δg,e,k take the following optimal values:

Δh,e,k|opt=−(I⊗Dh,e,k+Dh,e,kH⊗I)−1vec(W)‖(I⊗D~h,e,k)(I⊗Dh,e,k+Dh,e,kH⊗I)−1vec(W)‖(37a)

Δg,e,k|opt=−(I⊗Dg,e,k+Dg,e,kH⊗I)−1vec(QF2)‖(I⊗D~g,e,k)(I⊗Dg,e,k+Dg,e,kH⊗I)−1vec(QF2)‖(37b)

Thus we can transform inequality (17b)and inequality (17c) into the following form:

tr(WH~b,l)−2ϕ(W,Dh,b,l)+tr(QG~b,lF1)−2ϕ(QF1,Dg,b,l)≥F1,∀l(38a)

tr(WH~e,k)−2ϕ(W,Dh,e,k)+tr(QG~e,kF2)−2ϕ(QF2,Dg,e,k)≥−F2,∀k(38b)

Combining optimization problem Q4 with inequalities (38a) and (38b) , we can obtain optimization problem Q5.

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.