DOI:10.32604/cmc.2022.027009

| Computers, Materials & Continua DOI:10.32604/cmc.2022.027009 |  |
| Article |
Characteristics of Climate Change in the Lake Basin Area of Gangcha County
1School of Geographical Sciences, Nanjing University of Information Science & Technology, Nanjing, 210044, China
2School of Environmental Science & Engineering, Nanjing University of Information Science & Technology, Nanjing, 210044, China
3Faculty of Science, The University of Auckland, 1010, New Zealand
*Corresponding Author: Xin Yao. Email: yaoxin@nuist.edu.cn
Received: 08 January 2022; Accepted: 17 March 2022
Abstract: This paper mainly was based on the average temperature, precipitation, humidity, and wind direction of Gangcha county from 1960 to 2013. By using wavelet analysis and Mann-Kendall (M-K) mutation analysis, specifically analyzed the climate change characteristics in the lake basin area of Gangcha county. The result showed that the climatic change in the lake basin area of Gangcha county is noticeable. The average temperature, average minimum temperature, average maximum temperature, and evaporation showed an increasing trend. But the evaporation in the study area was higher than precipitation. The average relative humidity showed a decreasing trend. And the sunshine and the average wind speed percentage showed a significant decreasing trend. Utilizing the Morelet wavelet, The time series of annual mean temperature, annual evaporation and annual sunshine percentage all have quasi3a and quasi4A periods, and the annual mean precipitation has quasi2–3A, quasi2–5A and quasi2–6A periods, which appear in 1996–2005, 1962–1978 and 1978–1996 respectively. The mean annual relative humidity has obvious quasi2–7A and quasi3A time series, which appear from 1960 to 1996, 1997 to 2005 and after 2008, respectively. The annual mean wind speed has quasi3–4A and quasi5A time series characteristics, which appear in 1964–1967, 1984–1995, after 2009 and 1971–1983, respectively. Through Mann-Kendall (M-K) mutation analysis, it is found that the mutations of evaporation and the average speed of wind are significant. The mutation of evaporation started in 2004, and the mutation of average started in 2003.
Keywords: Climate change; the qinghai lake; Morelet wavelet; Mann-Kendall test
Global climate change has an increasingly significant and far-reaching impact on the world’s population, resources, and environment. As the core issue of global change research, climate change is an economic and political issue and has been a broad concern by the international communities. The Tibet Plateau, as the highest plateau in the world, is a “mirror” of the world’s climate change [1,2]. Climate change in Qinghai Lake has a great impact on the Tibet Plateau.
Morlet wavelet analysis and M-K test analysis are widely used for analyzing climate change. Wavelet analysis is a time-frequency analysis method with multi-resolution capability, which can be used in signal information processing and image processing [3–6]. M-K test analysis is a common method in analyzing climate parameters and hydrological series, which can describe the trend characteristics and change the degree of time series data [7,8]. Liu Lei et al. used wavelet analysis and M-K test. They concluded that the precipitation in Wuhu had periodic changes of 40, 10 and 5a, and it is significantly different for the variation trend of precipitation in each season in recent 20 years. [9]. Based on wavelet analysis and M-K test analysis, Qin Wang found that the average wind speed in Inner Mongolia had interannual changes of 4 and 6a and interdecadal periodic change of 14a and from 1981 to 2013, and the average wind speed had a sudden change in the 1990s [10]. Using wavelet analysis and M-K test, Lihua Wu found that there were 2∼6 quasi cycles for some extreme temperature indexes and 4∼6 quasi cycles for 11 extreme precipitation indexes in Lijiang from 1951 to 2017 [11].
Previous studies provided theoretical and methodological support for analyzing climate change characteristics, which showed different results in different study areas [12,13]. The research on climate change in Qinghai is a hot topic for researchers. Researchers often use different methods to study the long-term series of climate change factors such as temperature, precipitation, sunshine duration, wind speed, cloud cover and relative humidity in Qinghai Province based on different scales. For example, Yufang Pei used linear regression and M-K mutation detection to study the climate change characteristics of Haidong City in Qinghai Province from 1961 to 2015 based on annual and seasonal climate factors such as average temperature, precipitation, sunshine duration, wind speed, cloud cover, relative humidity and climate data such as evapotranspiration and precipitation days [14]. Based on the temperature and precipitation data from 1961 to 2015, Zongyan Chen used M-K test and wavelet analysis to analyze the characteristics of climate change in northeastern Qinghai Province [15]. Based on the data of temperature and precipitation from 1961 to 2007, Yuanfu Zhu analyzed the characteristics of climate change in the Republic area of Qinghai Province by using cumulative anomaly analysis and wavelet analysis [16].
The above researchers studied the change characteristics of various climate factors in different time series through different methods. However, M-K test and Morlet wavelet analysis were not used to monitor the long-term change characteristics of all the climate factors in Qinghai Lake basin area. Lake basin area of Gangcha county is located in the northeast of Tibet Plateau, in the perennial westerly belt, is the intersection of the eastern Qinghai-Tibet Plateau monsoon region and climate region. Gangcha county’s unique geographical position makes lake basin area sensitive and vulnerable to climate change. Therefore, based on the annual and monthly data of average temperature, precipitation, relative humidity, sunshine percentage and wind speed from 1960 to 2013, this paper used Morlet wavelet analysis and M-K test to comprehensively analyze the characteristics and trends of climate change in this region. The study of the region is beneficial to understand the trend of global climate change, evaluate the regional ecological environment, and improve agricultural development [17,18].
The remainder of this paper is organized as follows. Section 2 is described the study area. Next, Section 3 should be showed research data and methods. Then, Sections 4, 5 and 6 are demonstrated and discussed the research results in detail, and finally, Section 7 presents the conclusions.
Gangcha county belongs to the Tibetan Autonomous Prefecture of Haibei in Qinghai Province, located in the northeast of Qinghai Province, southwest of Tibetan Autonomous Prefecture of Haibei, the north bank of Qinghai Lake. It is located between 99°20 ‘44 “−100°37’ 24” E and 36°58 ‘06 “−38°04’ 04” N. Gangcha county covers an area of 12,000 square kilometers, and the land type is mainly grassland. Gangcha county is a typical plateau continental climate, long sunshine time, a significant temperature difference between day and night; The average annual precipitation is 370.5 mm, and the annual evaporation is 1500.6∼1847.8 mm. Gangcha county is cool in summer and autumn and cold in winter. The yearly average temperature is only −0.6°C. In this paper, the south of lake basin area was selected as the research area (Fig. 1).
Figure 1: Image of the study area
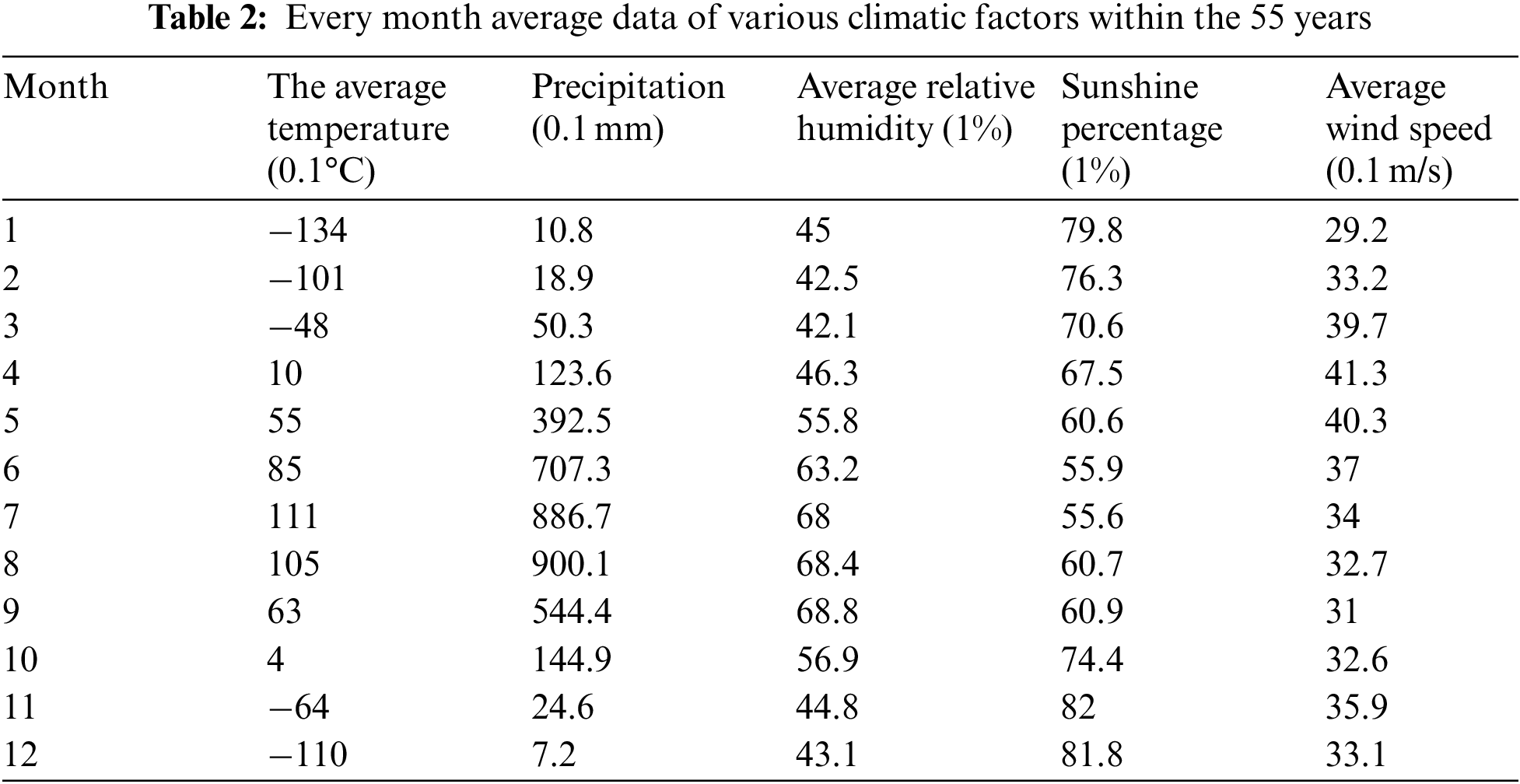
This paper mainly adopted the annual average data and the monthly average data of relevant climate variables. The yearly average data were selected from the China Meteorological Data Service Centre (http://data.cma.cn/). The average annual precipitation and the sunshine percentage data were selected from 1960 to 2013, while the annual average data of other meteorological factors were selected from 1960 to 2014. For example, The monthly average data were also selected from The China Meteorological Science Data Sharing Service network, and the monthly average data of each meteorological factor were chosen from 1960 to 2013 (Tab. 1). Tab. 2 shows the annual average of each climate factor.

Moving average is the most basic method of trend fitting, which is equivalent to a low pass filter. For sequence X with a sample size of n, its moving average sequence is expressed as:
where k is the sliding length, according to the requirements of specific problems and sample size, the sliding length k is determined. n data gives n - k + 1 smoothing value. After the moving average, the period shorter than the sliding length in the sequence is significantly weakened, and the changing trend can be better displayed. In the moving average analysis, the trend of change is mainly diagnosed from the sequence graph [19].
Wavelet analysis is a powerful statistical tool, which is widely used in many fields. The choice of function is critical when wavelet transform is a time series. Orthogonal wavelet functions are generally used for discrete wavelet transform, while non-orthogonal wavelet functions can be used for both discrete wavelet transform and continuous wavelet transform [20]. Generally, we hoped to get smooth and continuous wavelet amplitude when analyzing the time series, so the non-orthogonal wavelet function is more suitable. In addition, to obtain the amplitude and phase information of time series, Complex wavelet transform should be selected because complex wavelet transform has an imaginary part and expresses the phase well. Merlot wavelets (Torrence, 1998) are non-orthogonality and have a good balance between time and frequency localisation [21].
where t is time and ω0 is dimensionless frequency. When ω0 = 6, the wavelet scale s is equal to the Fourier period (λ = 1.03 s) [22], so the scale term and the periodic term can be substituted for each other [23].
The continuous wavelet transform, the discrete-time series xn (n = 1, 2, …, N) with isotime step δt is defined as the convolution of the wavelet function Ψ0 scale change as well as of the xn under the transformation:
where * stands for conjugate complex number, N is the total number of data in time series, is a factor used to normalize a wavelet function so that the wavelet function has unit energy on each wavelet scales [24]. By transforming the wavelet scale s and localizing it along with the time index n,
Wavelet full spectrum can show the unbiased and consistent estimation of the natural power spectrum of time series. The full wavelet spectrum can clearly identify the characteristics and intensity of periodic fluctuation of time series [26].
Although the time-frequency multi-resolution function of wavelet analysis can clearly reveal a variety of features hidden in time series, it is problematic to monitor the period of variation trend. When Jing Liu used Morlet wavelet analysis to analyze the period of measured annual runoff at various hydrological stations in northern Shaanxi province, It is found that the variation of annual runoff series has a certain influence on wavelet analysis period identification [22].
The Mann-Kendall test is a non-parametric statistical test method requiring sample data to follow a specific distribution and is not disturbed by a few outliers. It is suitable for the study of climate change in time series. A time-series x with a sample size of n constructs an order column ri, ri represents the accumulative sample count of xi > xj (1 ≤ j ≤ i). Sk is defined and calculated as follows:
Under the assumption of random independence of time series, define statistics:
In the formula, E(Sk) and Var(Sk) are the mean and variance of the accumulative quantity SK respectively. UFi follows the standard normal distribution, and UF1 = 0 [27].
Put time series x in reverse order; it is arranged as xn, xn−1, …, x. Repeat the above steps while enabling UBk = −UFk, k=n, n−1, …, 1, UB = 0. Give the significance level, α = 0.05, u0.05 = 1.96, is plotted on the same plot as the UFk and UBk two statistical sequence curves. If the value of UFk is greater than 0, the sequence is an upward trend. If the value of UFK is less than 0, the series shows a downward trend. When the two sequence curves exceed the critical straight line, it indicates a significant upward or downward trend. The range beyond the essential line is defined as the time region in which the mutation occurs. If the two curves intersect and the intersection is between the critical line, then the time corresponding to the intersection is when the mutation begins [28].
4 Characteristics of Climate Trends
4.1 The Variation Characteristics of Temperature
The average temperature in Gangcha county showed an obvious upward trend in the past 50 years (Fig. 2a). This warming trend is consistent with the average temperature change in the overall climate background, which passed the significance test with a confidence degree of 99% (trend coefficient R = 0.775 > threshold r0.01 = 0.345). The average temperature in Gangcha county increased at a rate of 0.3°C/10a in the past 55 years. The minimum value of the average temperature was −1.5°C in 1967, while the maximum value was 1.1°C in 2010 and 2013, and the extreme value was 2.6°C. Fig. 2b shows the average temperature of every month within 55 years. The seasonal change was noticeable. The temperature was warmest in July and coldest in January.
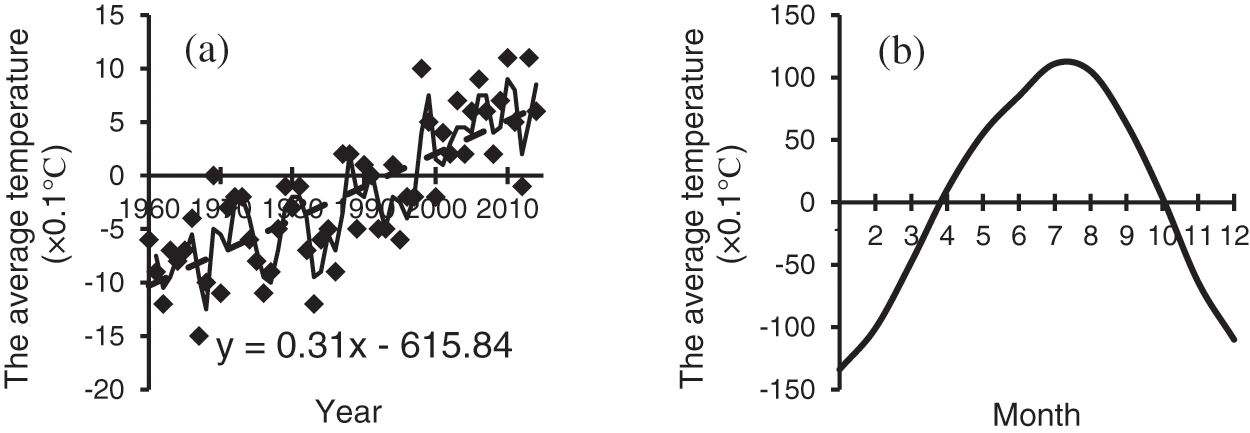
Figure 2: The variation characteristics of mean temperature: (a) the interannual variation; (b) the changes of every month within the 55 years
4.1.2 Mean Annual Minimum Temperature and Mean Annual Maximum Temperature
In recent decades, both the annual mean maximum temperature and annual mean minimum temperature in Gangcha county showed an increasing trend, and both passed the significance test with a confidence level of 99% (trend coefficient R = 0.631 > threshold r0.01 = 0.345. The trend coefficient of annual mean minimum temperature R = 0.860 > threshold r0.01 = 0.345). The warming rates of annual mean maximum temperature and the annual mean minimum temperature were 0.27°C/10a and 0.38°C/10a in the past 55 years respectively, and the extreme values were 3.3°C and 2.9°C respectively. It can be seen that although the warming rate of annual mean maximum temperature was lower than that of mean yearly minimum temperature, the warming range was higher than that of mean yearly minimum temperature (Fig. 3).

Figure 3: The interannual variation of temperature: (a) the annual mean minimum temperature; (b) the annual average maximum temperature
4.2 Variation Characteristics of Precipitation
The annual precipitation in Gangcha county showed a slight upward trend with an increasing rate of 5.6 mm/10a in the past 55 years, but this upward trend was not obvious and did not pass the significance test with a confidence level of 90% (trend coefficient R = 0.169 < threshold r0.1 = 0.226). During the 1960 and 1970s, The fluctuation frequency of annual precipitation was relatively fast. In the 1980s, there was an obvious trend of rising fluctuation. In contrast, in 1990, the precipitation decreased rapidly, and after 1990, there was a trend of increasing slowly, and the annual average of precipitation was 381 mm, (Fig. 4a). Fig. 3b showed the mean precipitation of every month within the 55 years. The precipitation process was mainly concentrated in summer and autumn, with an obvious seasonal distribution.
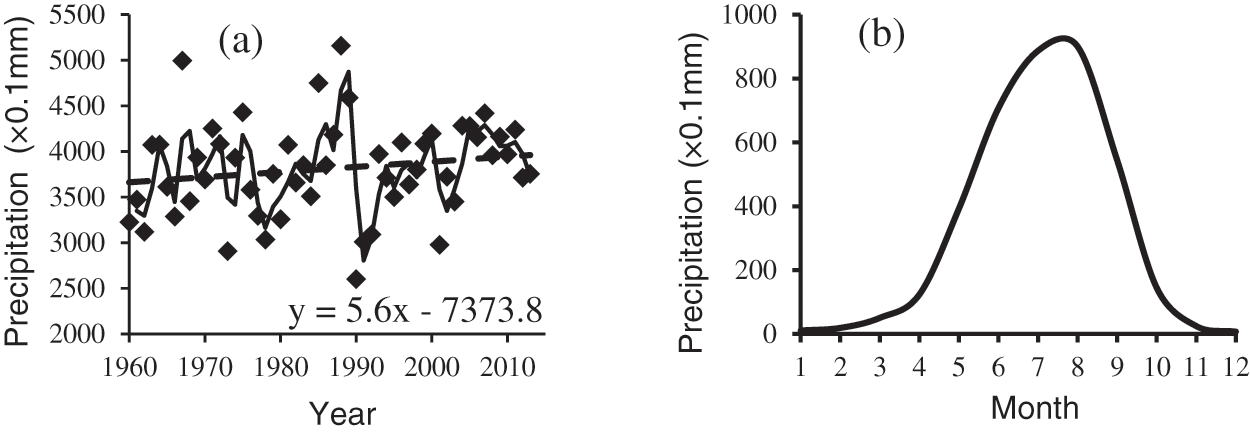
Figure 4: The variation characteristics of precipitation: (a) the interannual variation; (b) the changes of every month within the 55 years
4.3 Variation Characteristics of Evaporation
Evaporation in Gangcha county showed an overall upward trend, with an upward rate of 50 mm/10a in the past 55 years, which passed the significance test with a confidence level of 99% (trend coefficient R = 0.482 > threshold r0.01= 0.345). Fig. 5 shows the variation characteristics of annual evaporation from 1960 to 2014 in Gangcha county. The average annual evaporation in Gangcha county was 1519.8 mm. The increase in evaporation will make the study area drier.
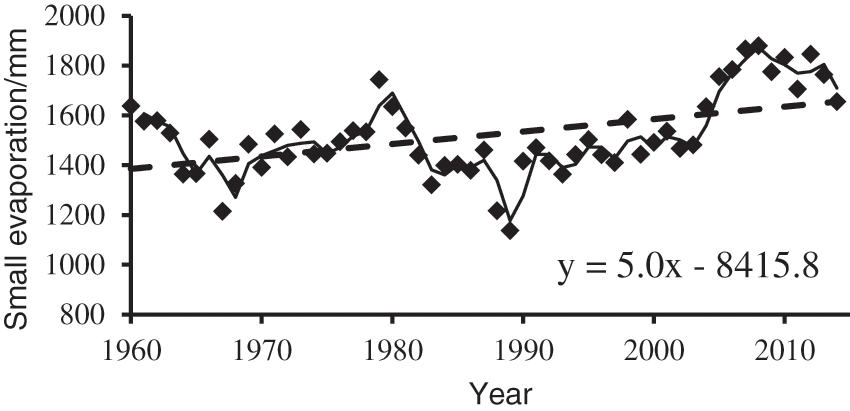
Figure 5: The variation characteristics of annual evaporation
4.4 Variation Characteristics of Average Relative Humidity
The average annual relative humidity in Gangcha County showed a slight downward trend from 1960 to 2014 (Fig. 6a), which was not obvious and failed to pass the significance test with a confidence level of 90% (absolute value of trend coefficient R = 0.115 < threshold r0.1 = 0.224). The average relative humidity was 53.7% within the 55 years. Due to the influence of many factors, the interannual variation characteristics of the average relative humidity showed apparent fluctuation. Although there was an increasing trend of precipitation in Gangcha County, the increasing range was not as large as that of evaporation, which eventually had led to the decline of average relative humidity in Gangcha county. Fig. 6b shows variation characteristics of average relative humidity of every month within the 55 years. Among these, there was an apparent increasing trend from Marche to July in Gangcha county. It was almost unchanged for average relative humidity in July, August and September. And there was an obvious downtrend from September to November.
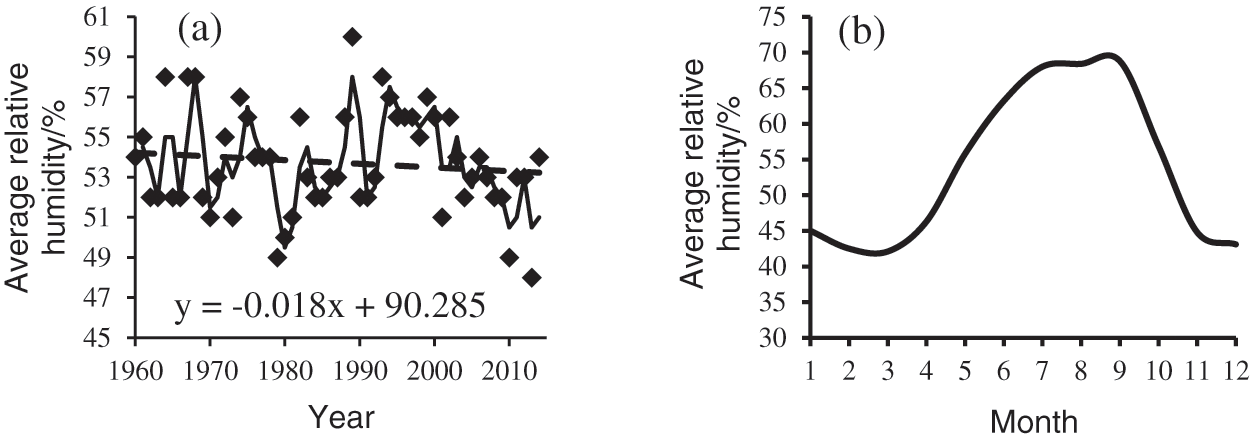
Figure 6: The variation characteristics of mean relative humidity: (a) the interannual variation; (b) the changes of every month within the 55 years
4.5 Variation Characteristics of Sunshine Percentage
The sunshine percentage in Gangcha county showed a decreasing trend year by year, with a decreasing rate of 0.64%/10a, in the past 55 years, (Fig. 7a), which passed the significance test with a confidence of 99% (absolute value of trend coefficient R = 0.409 > threshold r0.01 = 0.345). The average sunshine percentage in Gangcha County was 67.5% within the 55 years. Fig. 7b shows the change of sunshine percentage of every month within the 55 years. Among these, there was a decreasing trend from January to June in Gangcha county. Then there was an overall upward trend from July to December.
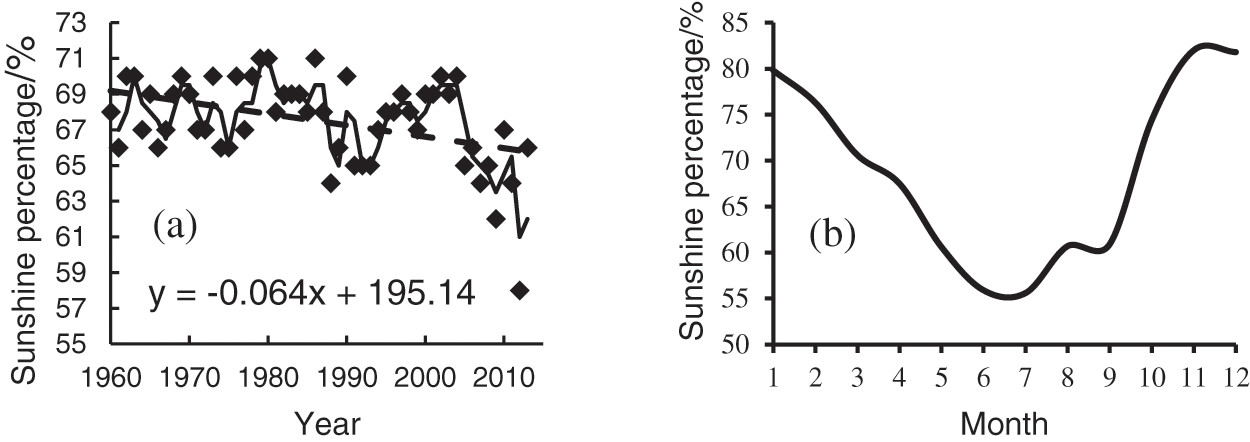
Figure 7: The variation characteristics of sunshine percentage: (a) the interannual variation; (b) the changes of every month within the 55 years
4.6 Variation Characteristics of Mean Wind Speed
The annual average wind speed in Gangcha county showed an obvious downward trend in the past 55 years (Fig. 8). The decreasing rate of mean wind speed reached 0.13 m/s/10a, which passed the significance test of 99% (absolute value of trend coefficient R = 0.580 > threshold r0.01 = 0.345). The annual average wind speed in Gangcha county was 3.5 m/s. It was fluctuant for the trend of mean wind speed of every month within the 55 years. Starting from January, average wind speed increased gradually, to the peak in April, showed a clear trend of decrease, backed to the lowest in September, and then increased, to November, then decreased. There was a trend towards increasing first and then declining in the change mean wind speed of every month within the 55 years.
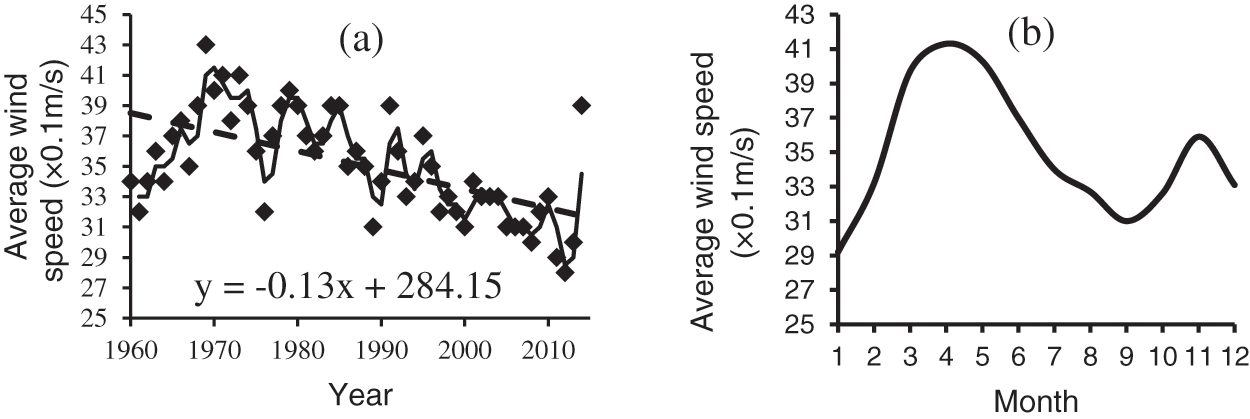
Figure 8: The variation characteristics of mean wind speed: (a) the interannual variation; (b) the changes of every month within the 55 years
5 Characteristics of Climatic Cycles
This section mainly used the Morlet wavelet power spectrum analysis method to study the periodic climate change rule in Gangcha county under the background of global warming.
Fig. 9 shows the power spectra of all meteorological factors in Gangcha county in the past 55 years after the Morlet wavelet transform. The larger the wavelet power, the denser the isolines. The lines with different colors represent the real part of the wavelet coefficient contour. The part surrounded by the thick dotted line indicates that it has passed the scale period of the gaussian red noise test with a significance level of 0.05. The inverted cone * line is the influence cone, and the part surrounded by it is the scale period after removing the boundary effect. In contrast, the edge effect affects the other parts of the wavelet power spectrum, and the periodic characteristics are of great uncertainty [29].
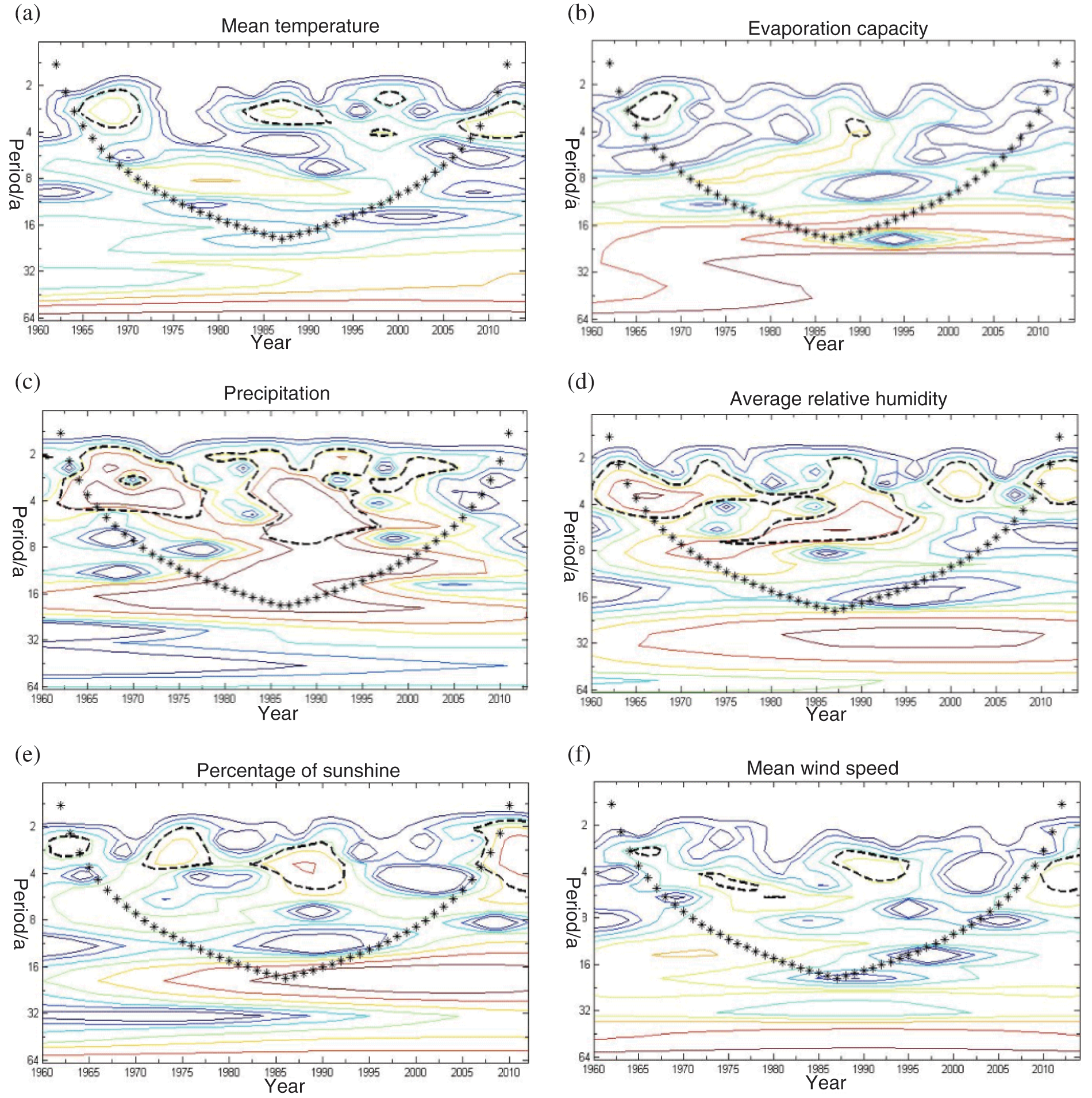
Figure 9: Wavelet power spectrum of meteorological factors in Gangcha county
There were significant quasi3a and quasi4a scale cycles in the time series of annual average temperature in Gangcha county (Fig. 9a), and the intensity of these cycles changed with time. The periodic characteristics of the quasi3a spectrum mainly appeared in the three periods of 1964–1972 (the mean temperature first decreased and then increased), 1982–1993 (the mean temperature fluctuated), and 1997–2001 (the mean temperature first increased and then decreased). After 2006, there was also a significant quasi3a cycle (during which the average temperature showed a rising trend), but there was no closed curve in this period, and differences may appear over time. The quasi4a spectral periodic characteristics mainly occurred from 1996 to 2000, during which the mean temperature fluctuated. Wavelet power spectrum analysis also detected quasi8a period and intergenerational scale period of more than 16a, but they did not pass the significance test at 0.05 level.
Fig. 9b shows the significant quasi-3a and the quasi4a scale cycles in the time series of annulling evaporation in Gangcha county, and the intensity of these cycles changed with time. The periodic characteristics of the quasi3a spectrum mainly appeared in the period from 1964 to 1970, during which annual evaporation decreased, while the periodic characteristics of the quasi4a spectrum mainly appeared in the period from 1988 to 1992, during which annual evaporation first decreased and then increased.
Fig. 9c shows the significant quasi2–3a, 2–5a, and the quasi2–6a scale cycles in the time series of precipitation in Gangcha county, and the intensity of these cycles changed with time. The quasi2–3a periodic characteristics mainly appeared in the period from 1996 to 2005, during which the precipitation variation showed first increased, then decreased, and finally increased. The quasi2–5a periodic characteristics obviously appeared from 1962–1978, during which the precipitation variation fluctuated greatly. The quasi2–6a periodic characteristics were mainly distributed from 1978 to 1996, indicating that the average period of precipitation fluctuation in this period was 4a, and the precipitation in this period had experienced the change of first increase, then decrease and finally increase successively.
Fig. 9d shows that the average relative humidity in Gangcha county had the obvious quasi3a and the quasi2–7a cycle characteristics in time series, and the intensity of these cycles changed with time. The quasi3a periodic feature mainly appeared from 1997 to 2005 and after 2008, and the average relative humidity showed a decreasing trend in the two periods. The quasi2–7a periodic feature mainly occurred in the period from 1960 to 1996, during which there was a noticeable fluctuation of the average relative humidity.
Fig. 9e shows that the sunshine percentage in Gangcha county had significant quasi-3a and quasi-4a scale cycles in time series, and the cycling intensity changed with time. The periodic characteristics of quasi-3a appeared from 1961 to 1965 (the sunshine percentage increased and decreased successively), from 1971 to 1978 (the sunshine percentage decreased first and then increased), and from 2006 (the sunshine percentage continued to decline). In these three periods, The fluctuation cycle of sunshine percentage was mainly 3a. The quasi4a periodic characteristics mainly appeared in the period from 1982 to 1993, during which the sunshine percentage decreased on the whole.
Fig. 9f shows that the mean wind speed in Gangcha county had the significant quasi-3–4a and the quasi-5a scale cycles in time series, and the periodic intensity changed with time. The quasi-3–4a periodic characteristics mainly appeared in the three periods of 1964–1967 (the average wind speed increased), 1986–1995 (the average wind speed showed a decreasing trend of fluctuation), and after 2009 (the average wind speed increased, decreased, and increased). The quasi5a periodic characteristics were mainly distributed in the period from 1971 to 1983. During this period, the fluctuant trend of average wind speed was mainly 5a periodic. Wavelet power spectrum analysis also detected a quasi8a period, but the quasi8a period did not pass the significance test at 0.05 level.
Yuanfu Zhu in Gonghe county of Qinghai province, and analysis of the characteristics of climatic variation with the method of wavelet analysis, it was concluded that the annual mean temperature in Gonghe county were 47.0, 23.5, and 15.7 years change cycles, and had passed the test of significance of 99%, and This is different from the annual average temperature in Gangcha County, but the precipitation cycle is similar. Surong Guo pointed out in the analysis of temporal and spatial characteristics of climate change in Qinghai Province from 1960 to 2010 that the average annual temperature distribution in Qinghai province increased from south to north with a large difference between north and south, while the precipitation increased from northwest to southeast. Both Gonghe county and Gangcha county are lake basin areas of Qinghai Lake, and the time distribution of precipitation is roughly the same [30].
6 Abrupt Analysis of Climate Change
Through M-K test analysis, it can be seen from Fig. 10a that the average temperature in Gangcha county had an evident warming trend, and this warming trend had greatly exceeded the critical line of the significance level of 0.05 (U0.05 = ± 1.96) after 1988, indicating that this rising trend was very significant. This was consistent with previous analyses of interannual variations in average temperature. According to the intersection of the UF curve and UB curve, 1992 May was the abrupt change point of the warming trend in Gangcha county, but this abrupt change point was not within the confidence interval, and its credibility needs further discussion.
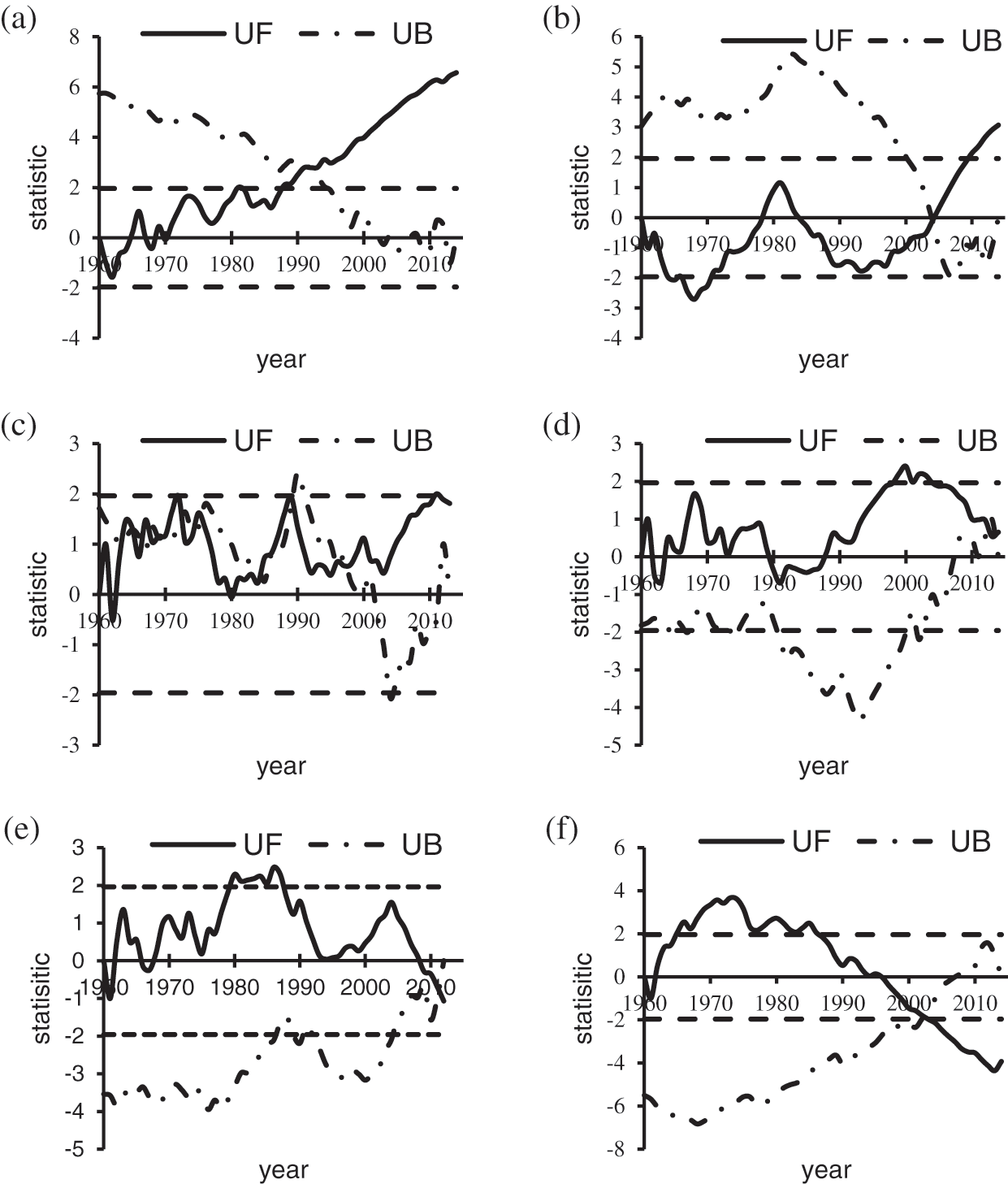
Figure 10: Mann-Kendall statistical curves of various climatic factors in Gangcha county: (a) average temperature; (b) evaporation; (c) precipitation; (d) average relative humidity; (e) sunshine percentage; (f) average wind speed
Evaporation in Gangcha county showed a fluctuated trend with time series, and the increasing trend was gradually intensified after 2004, and the warming trend greatly exceeded the critical line of the significance level of 0.05 (U0.05 = ± 1.96) after 2010, indicating that the increasing trend was significant. This is consistent with previous analyses of interannual variations in evaporation (Fig. 10b). According to the intersection of UF and UB curves, we can confirm that the increasing trend of evaporation after 2004 was a mutation phenomenon, and the specific mutation started in 2004.
As can be seen from Figs. 10c–10e, precipitation, average relative humidity, and sunshine percentage in Gangcha county mainly showed an increasing trend, and the increasing range was in a state of constant fluctuation. However, these increasing trends did not exceed the critical line of the significance level of 0.05, indicating that these increasing trends were not significant.
The annual average wind speed in Gangcha county showed an obvious trend of increase and decrease, and the increasing trend was mainly before 1995, while the average wind speed showed a decreasing trend after 1995 (Fig. 10f). During 1965–1987, the increasing trend of mean wind speed exceeded the critical limit of the significance level of 0.05, indicating that the rising trend was significant. Since the 21st century, the decreasing trend of mean wind speed has been accelerated and gradually exceeded the significance level threshold of 0.05 (U0.05 = ± 1.96), indicating that the decreasing trend was very significant. According to the intersection of UF and UB curves, we found that the decrease of mean wind speed in Gangcha county since the 21st century was a mutation phenomenon, and the mutation started in 2003.
Surong Guo analyzed the abrupt change of climate in Qinghai in recent 50 years and found that there was no obvious abrupt change trend of other climate factors except temperature. When Yufang Pei analyzed the abrupt changes of climate factors in Haidong city in 55 years, he found that the annual average temperature, evaporation, average wind speed, sunshine duration and relative humidity in Haidong City all had abrupt changes, indicating that the abrupt changes of climate factors in local areas were more significant than those in Qinghai Province. Therefore, it was normal for evaporation and wind speed in Gangcha county to have sudden changes.
Through a series of analysis of meteorological data in recent decades, the climate change characteristics in the lake basin area of Gangcha county was analyzed. The average temperature, average minimum temperature, average maximum temperature, and evaporation showed an increasing trend. The average temperature in Gangcha county increased at a rate of 0.3°C/10a. The minimum value of the average temperature was −1.5°C, while the maximum value was 1.1°C. Evaporation had an upward rate of 50 mm/10a. Precipitation increased slightly, with a variable rate of 5.6 mm/10a. The average relative humidity showed a decreasing trend year by year and the annual average relative humidity was 53.7%. Although the precipitation in the study area increased, the evaporation in the study area was higher than precipitation. The sunshine and the average wind speed percentage showed a significant decreasing trend, with the rates of −0.65%/10a and −0.13 m/s/10a, respectively. In general, the climate became drier and hotter, which would intensify the desertification process.
Through Morlet wavelet analysis, The time series of annual mean temperature, annual evaporation and annual sunshine percentage all have quasi3a and quasi4A periods, and the annual mean precipitation has quasi2–3A, quasi2–5A and quasi2–6A periods, which appear in 1996–2005, 1962–1978 and 1978–1996 respectively. The mean annual relative humidity has obvious quasi2–7A and quasi3A time series, which appear from 1960 to 1996, 1997 to 2005 and after 2008, respectively. The annual mean wind speed has quasi3–4A and quasi5A time series characteristics, which appear in 1964–1967, 1984–1995, after 2009 and 1971–1983, respectively.
Through M-K test analysis, it was found that evaporation and the mean wind speed had a significant mutation. The mutation of evaporation started in 2004, and the mutation of mean wind speed started in 2003. Although the average annual temperature changed significantly, the mutation point was outside the confidence interval, so it could not be judged that the change trend was significant. And the average annual precipitation, average relative humidity and sunshine percentage did not change significantly.
Acknowledgement: This work was supported by the Second Tibet Plateau Scientific Expedition and Research Program (STEP) under grant number 2019QZKK0804, and the National Natural Science Foundation of China “Study on the dynamic mechanism of grassland ecosystem response to climate change in Qinghai Plateau” under Grant number U20A2098.
Funding Statement: This work was supported by the National Natural Science Foundation of China “Study on the dynamic mechanism of grassland ecosystem response to climate change in Qinghai Plateau” under grant number U20A2098, and the Second Tibet Plateau Scientific Expedition and Research Program (STEP) under grant number 2019QZKK0804.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. H. Wang, L. Zhang, X. D. Shi and D. L. Li, “Some new changes of the regional climate on the Tibet plateau since 2000,” Advances in Earth Science, vol. 36, no. 8, pp. 785–796, 2021. [Google Scholar]
2. H. Zheng and D. Shi, “A Multi-agent system for environmental monitoring using boolean networks and reinforcement learning,” Journal of Cyber Security, vol. 2, no. 2, pp. 85–96, 2020. [Google Scholar]
3. X. A. Zhu, S. Z. Jin, S. N. Ning and J. Y. Wang, “The application status and outlook of wavelet analysis,” Coal Geology & Exploration, vol. 32, no. 2, pp. 51–55, 2003. [Google Scholar]
4. X. Y. Rong, H. W. Wang and W. Y. Kuang, “Analysis on climate characteristics of rainstormin in shucheng based on wavelet analysis,” Modern Agricultural Science and Technology, vol. 2017, no. 10, pp. 193–195, 2017. [Google Scholar]
5. Y. Zhang, X. Z. Chu, S. M. Yang and C. Guo, “Climate change in north Xinjiang in recent 56 years,” Arid Zone Research, vol. 36, no. 1, pp. 212–219, 2019. [Google Scholar]
6. N. N. Luo, B. T. E. Bake, Y. R. Xue, L. J. Kang and M. H. Wang, “Terng analysis of climate change of maize growth stages in Tacheng city,” Chinese Journal of Agricultural Resources and Regional Planning, vol. 39, no. 4, pp. 22–29, 2018. [Google Scholar]
7. Q. Hu, X. Q. Ma, L. T. Hu, Y. J. Wang, L. Xu et al., “Application of matlab in meteorological teaching——M-K test for the abrupt change analysis of meteorological elements,” Research and Exploration in Laboratory, vol. 38, no. 12, pp. 48–51+107, 2019. [Google Scholar]
8. Y. P. Sui, “Study on climate trend analysis of Mudanjiang city based on M-K method,” M.S. dissertation, Jilin Agricultural University, China, 2020. [Google Scholar]
9. L. Liu, H. Gao, L. Zhang, Y. L. Wang and W. Fu, “Interdecadal variability of precipitation in wuhu in last 140 years,” Research of Soil and Water Conservation, vol. 28, no. 5, pp. 114–120, 2021. [Google Scholar]
10. Q. Wang, B. Zeng and L. Deng, “Characteristics of spatial and temporal changes of wind speed during 1981 to 2013 in inner Mongolia autonomous rigion,” Journal of Inner Mongolia Normal University, vol. 44, no. 5, pp. 674–679, 2015. [Google Scholar]
11. L. H. Wu, P. Cheng, L. Q. Dong, X. P. Cheng, H. D. Gong et al., “Variation characteristics of extreme temperature and precipitation events in Lijiang from 1951 to 2017,” Journal of Nanjing University of Information Science & Technology(Natural Science Edition), vol. 2022, pp. 1–22, 2022. [Google Scholar]
12. C. C. Xu, C. Y. Lu and J. H. Wang, “Characteristics of climate change in Beijing-Tianjin-Hebei region in recent 60 years,” Water Resources and Hydropower Engineering, vol. 52, no. 6, pp. 12–20, 2021. [Google Scholar]
13. X. Q. Huang, Y. H. Qiu, X. Y. Chen, X. H. Sun and Y. R. Lin, “Climate change characteristics and future trend of Fujian province in 1980–2017,” Journal of Wuyi University, vol. 39, no. 9, pp. 27–32, 2020. [Google Scholar]
14. Y. F. Pei, D. L. Qin, Q. F. Zhang and Q. N. Zhao, “Analysis of climate change characteristics and influence factors in Haidong of Qinghai Province in recent 55 years,” Agricultural Research in the Arid Areas, vol. 37, no. 3, pp. 275–282, 2019. [Google Scholar]
15. Z. Y. Chen, “Analysis on characteristics of climate change during 1961–2015 in northeast of Qinghai,” Journal of Qinghai Normal University (Natural Science Edition), vol. 32, no. 4, pp. 1–10. 2016. [Google Scholar]
16. Y. F. Zhu and H. C. Tian, “Analysis of the character of climatic variation for last 50 years in Gonghe district of Qinghai province,” Journal of Anhui Agricultural Sciences, vol. 36, no. 21, pp. 9189–9191. 2008. [Google Scholar]
17. X. Leng, L. Pang, X. T. Jiang and S. Dong, “Analysis and prediction change characteristics and forecast in the Yellow River basin of Qinghai province from 1956 to 2018,” Periodical of Ocean University of China, vol. 52, no. 2, pp. 23–32, 2022. [Google Scholar]
18. Y. C. Yan, S. L. He, G. S. Gao and M. F. Zhao, “Growth period change of brassica campestris L. and the climatic driving factors in the region around Qinghai Lake,” Hunan Agricultural Sciences, no. vol. 6, pp. 86–92, 2021. [Google Scholar]
19. M. Naveed, M. Rafiq, A. Raza, N. Ahmed, I. Khan et al., “Mathematical analysis of novel coronavirus (2019-ncov) delay pandemic model,” Computers, Materials & Continua, vol. 64, no. 3, pp. 1401–1414, 2020. [Google Scholar]
20. N. Pan, Y. Liu, D. Pan, J. Qian and G. Li, “Line trace effective comparison algorithm based on wavelet domain dtw,” Intelligent Automation & Soft Computing, vol. 25, no. 2, pp. 359–366, 2019. [Google Scholar]
21. H. Alhumyani, I. Alrube, S. Alsharif, A. Afifi, C. B. Amar et al., “Analytic beta-wavelet transform-based digital image watermarking for secure transmission,” Computers, Materials & Continua, vol. 70, no. 3, pp. 4657–4673, 2022. [Google Scholar]
22. J. Liu, “Research on the periodicity of annual runoff in north region of Shaanxi,” M.S. dissertation, Northwest A&F Universit, China, 2016. [Google Scholar]
23. W. H. You, X. Duan and M. H. Qi, “Continuous wavelet transforms and their applications to surface air temperature and yearly precipitation variations in yunnan during last one hundred years,” Plateau Meteorology, no. 1, pp. 48–55, 1999. [Google Scholar]
24. X. Shao, C. S. Kim and D. G. Kim, “Accurate multi-scale feature fusion CNN for time series classification in smart factory,” Computers, Materials & Continua, vol. 65, no. 1, pp. 543–561, 2020. [Google Scholar]
25. H. Y. Liu, L. Zou and W. L. Xing, “Temporal and spatial variation of extreme precipitation in Haihe RiverBasin during 1961–2018,” Water Resources and Power, vol. 12, no. 12, pp. 1–6, 2021. [Google Scholar]
26. A. Bachir, I. M. Almanjahie and M. K. Attouch, “The k nearest neighbors estimator of the m-regression in functional statistics,” Computers, Materials & Continua, vol. 65, no. 3, pp. 2049–2064, 2020. [Google Scholar]
27. Y. L. Bi, Y. X. Ouyang, G. Sun, P. Guo, J. J. Zhang et al., “Big data audit of banks based on fuzzy set theory to evaluate risk level,” Journal on Big Data, vol. 2, no. 1, pp. 9–18, 2020. [Google Scholar]
28. W. D. Jiang, J. Wu, G. Sun, Y. X. Ouyang, J. Li et al., “A survey of time series data visualization methods,” Journal of Quantum Computing, vol. 2, no. 2, pp. 105–117, 2020. [Google Scholar]
29. C. Torrence and G. P. Compo, “A practical guide to wavelet analysis,” Bulletin of the American Meteorological Society, vol. 79, no. 1, pp. 61–78, 1998. [Google Scholar]
30. S. R. Guo, “The analysis of temporal and spatial variation of climate in Qinghai province from 1960 to 2010,” M.S. dissertation, Northwest Normal University, China, 2012. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |