DOI:10.32604/cmc.2022.026717

| Computers, Materials & Continua DOI:10.32604/cmc.2022.026717 |  |
| Article |
Reference Selection for Offline Hybrid Siamese Signature Verification Systems
1Department of Electrical Engineering, National Tsing Hua University, Hsinchu, Taiwan
2Department of Information and Finance Management, National Taipei University of Technology, Taipei, Taiwan
3Department of Communications Engineering, National Tsing Hua University, Hsinchu, Taiwan
4Department of Electrical Engineering and the Institute of Communications Engineering, National Tsing Hua University, Hsinchu, Taiwan
*Corresponding Author: Yeong-Luh Ueng. Email: ylueng@ee.nthu.edu.tw
Received: 03 January 2022; Accepted: 23 February 2022
Abstract: This paper presents an off-line handwritten signature verification system based on the Siamese network, where a hybrid architecture is used. The Residual neural Network (ResNet) is used to realize a powerful feature extraction model such that Writer Independent (WI) features can be effectively learned. A single-layer Siamese Neural Network (NN) is used to realize a Writer Dependent (WD) classifier such that the storage space can be minimized. For the purpose of reducing the impact of the high intraclass variability of the signature and ensuring that the Siamese network can learn more effectively, we propose a method of selecting a reference signature as one of the inputs for the Siamese network. To take full advantage of the reference signature, we modify the conventional contrastive loss function to enhance the accuracy. By using the proposed techniques, the accuracy of the system can be increased by 5.9%. Based on the GPDS signature dataset, the proposed system is able to achieve an accuracy of 94.61% which is better than the accuracy achieved by the current state-of-the-art work.
Keywords: Siamese network; offline signature verification; residual neural network; reference selection
Biometric technology uses human biometrics to extract features for implementing an individual identification system. The biological characteristics include physiological traits, such as face or iris, etc., or behavioral traits, such as gestures or signatures, etc. Each feature has strong individual unique biological characteristics, making it difficult to be replicated, stolen or forged, which increases the reliability of identification of the feature and improves the accuracy rate. Choosing the right biometric information plays an important role in recognition performance. A handwritten signature is a particularly important biological feature, mainly because it is used to verify personal identity in the legal, financial, and administrative fields, etc. Another reason is that the process of collecting personal handwritten signatures is non-invasive and is a very common for people to use signatures in their daily lives [1].
In research into signature verification, two methods are used to obtain signatures: Online and Offline. In the online scenario, the signer uses an optical pen to write, while a sensor is used to acquire the images and the handwritten physical features, such as the speed of movement by the hand and the hand stroke, the acceleration between movements, and the pressure applied at various positions, etc., and records the data and signature image movement for verification. The offline scenario refers to the use of optical scanning instruments to obtain handwritten signatures written on paper, represented by digital images for verification.
The process of offline handwritten signature verification poses several challenges. First, offline signatures only provide limited information. In general, the performance when using offline verification is worse than that of online verification because of the lack of movement information [2]. Second, compared to other biometric features, even based on a signature from the same person, there are huge variances, which is why skilled forgeries are often very similar to genuine signatures. Fig. 1 shows a signature that has high intra-class variability in the GPDS dataset [3,4]. An offline handwritten signature verification system can be devised using writer-independent (WI) or writer-dependent (WD) approaches [5]. The advantage of the WI system is that only a single model needs to be trained, but the accuracy of the model is usually lower. In contrast, the advantage of the WD system is its high accuracy, but a large storage space is required and the model needs to be retrained when a new user register. The hybrid systems presented in [6,7] which use WI feature learning and WD classification are able to take advantage of both the WI and WD systems to reduce storage space while retaining a high accuracy. Consequently, this work considers the use of a hybrid approach to devise an offline signature verification system.
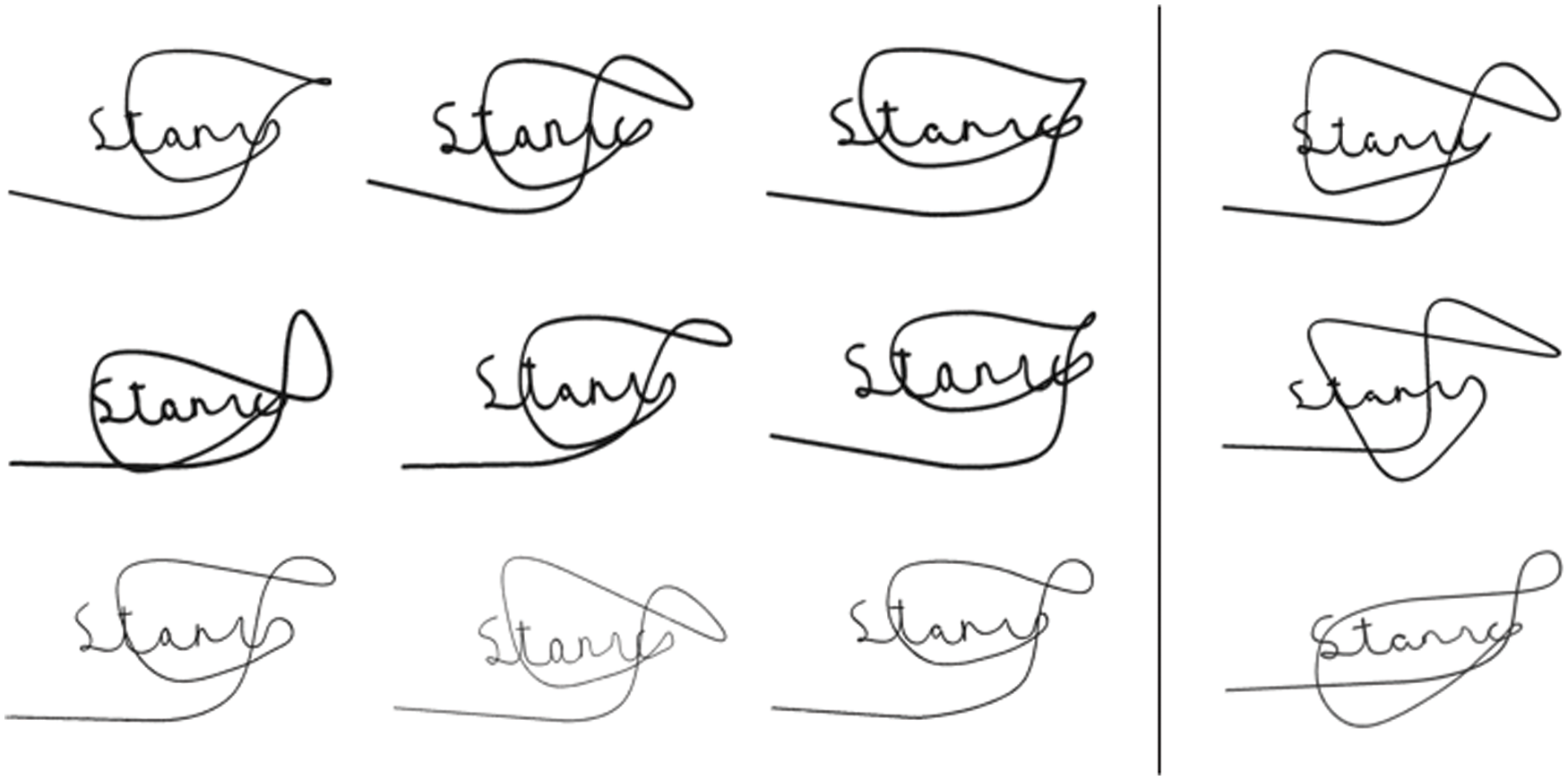
Figure 1: Samples from the GPDS dataset. The left side of the line are all genuine signatures from the same user, and the right side of the line are all skilled forgeries. We notice that each genuine signature is different, showing high intraclass variability, while skilled forged signatures are very similar to the genuine signatures
Much of the previous research in this area is devoted to obtaining a good feature representation for signatures, namely a well-designed feature extractor. A feature extractor utilizes both the hand-crafted method and the learning method. Different hand-crafted features have been proposed for offline signature verification tasks in the past. Many of the studies take into account the global signature image, the geometrical and topological characteristics of local attributes, such as the position, the tangent direction, the blob structure, the connected components, and the curvature [2], or rather applies the projection and contour method to offline signature verification [8]. Due to the high intra-class variability of the signature, it is often difficult to design feature extractors that are widely accepted as “best”. So, feature learning methods, also known as representation learning, have been used to solve issues surrounding offline signature verification in order to devise better feature representation. For example, recent offline signature verification systems are based on texture descriptors, such as Local Binary Patterns [9], and neural networks, such as Multilayer Perceptron [10]. Many studies have proposed using a Convolutional Neural Network (CNN) to learn signature features. Compared to other deep learning structures, a CNN is able to generate better results in terms of image recognition, and requires fewer parameters for estimation. Hafemann et al. [6] proposed using a two-channel CNN architecture to train a WI feature model based on the GPDS dataset.
After the features are extracted, the classifier analyzes these features and then generates a threshold value to determine the authenticity [11] of the signature. Recently, some studies have used either deep learning or user-defining features to train the threshold (or classifier) in the model so as to generate the decision. Pansare et al. [12] used geometric features to train a neural network classifier. Ozgunduz et al. [13] fed grid and mask features into the system to train the support vector machine (SVM) model as a classifier. Diaz et al. [14] considered the situation where there is no reference signature, and then fed the self-defining features into the SVM training model. Arab et al. [15] fed the Local Difference Feature (LDF) information as a new descriptor to train the SVM.
The Siamese network has recently become well known for face recognition and signature verification. The model consists of twin networks that have shared weights, which can train a powerful feature model without relying on hand-crafted features. Since the Siamese model enables the CNN to take advantage of the two-dimensional structure of the input data, Rateria et al. [16] used the Siamese CNN for pure WD offline signature verification.
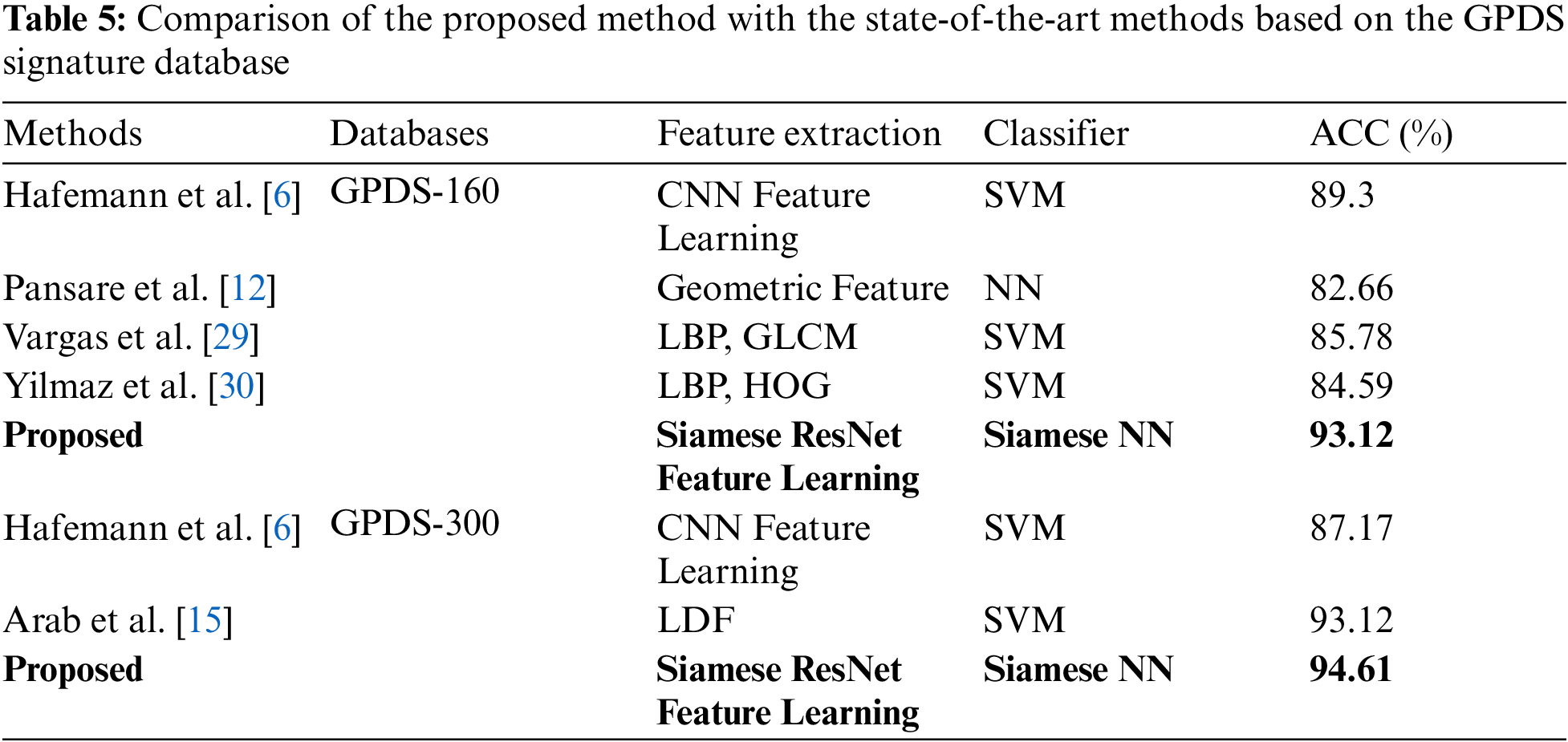
For offline signature verification systems, it is inevitably confronting two challenges: the size of storage space and signature’s high intraclass variability. In order to alleviate these problems, we propose an offline handwritten signature verification system based on a hybrid architecture. Unlike using two-channel CNN in [6], we adopt a Siamese network to learn WI features in order to reduce the number of parameters and hence the storage space during the training process. Additionally, we use Residual neural Network (ResNet) [17] to train the model in a deeper network. In contrast to [16], we choose a Siamese Neural Network (NN) that has a single layer rather than the Siamese CNN to realize the WD classifier for the purpose of minimizing the storage space requirements. To reduce the impact of the high intraclass variability, we use reference selection to ensure that the network is able to learn more effectively, where a genuine signature is selected as a reference input for the Siamese network. To take full advantage of reference selection, we modify the conventional contrastive loss so as to enhance the accuracy. By employing these techniques, accuracy is able to be increased by 5.9%. Based on the GPDS signature dataset, the proposed system achieves an accuracy of 94.61%, which is better than the accuracy of the current state-of-the-art work. To the best of our knowledge, this is the first work to realize an offline hybrid signature verification system using the Siamese ResNet with reference selection.
The remainder of this paper is organized as follows. In Section 2, the details of a conventional signature verification system are discussed. In Section 3, the processes involved, including pre-processing, the selection of a reference signature for each user, the modified contrastive loss function, the extraction and learning of WI features, as well as the WD classifier, are described in detail. The collected test data used in our experiment, together with the experimental results, are presented in Section 4. We make conclusions in Section 5.
A hybrid system architecture was proposed by Hafemann et al. [6] and Eskander et al. [7], as shown in Fig. 2. In these systems, the database is first divided into two groups, a development set (set D) and an exploitation set (set E). Set D is responsible for learning the signature feature, and set E refers to the users to be registered in the system. Set D is used to train the signature feature learning model in WI mode. These WI features are then used to train the WD classifier model using the user signatures from set E. After the training process is complete in the enrollment phase, the weights or parameters for the model will be stored as individual WD classifiers for each user. In the authentication phase, an identity is claimed via the new data, and, after extracting the features through the WI feature model, these features are entered into the individual classifiers to be used for identification purposes.
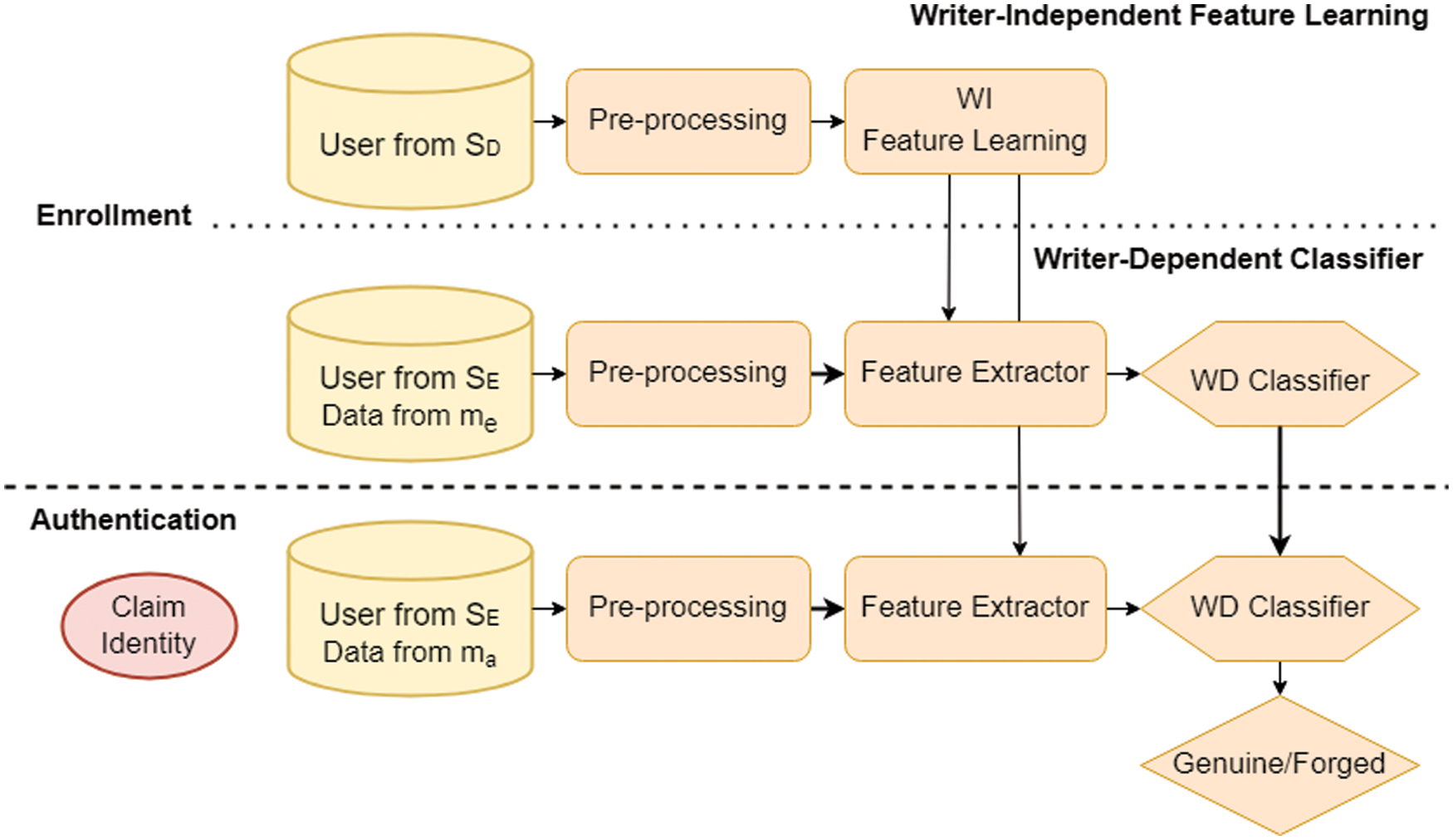
Figure 2: The hybrid system architecture that includes Writer Independent (WI) feature learning and Writer Dependent (WD) classification. If there are a total of S users, where each user is comprised of m data, divide the S users into two groups: A Development set (
Before learning the features, we need to execute a preprocessing stage. The size of the signatures from sets D and E are variable, ranging from 153 × 258 pixels to 819 × 1137 pixels. In order to train the neural network, we need to unify the size of the signature images. First, the OTSU algorithm presented in [16] is used to determine the optimum threshold between the foreground and the background of the images. Second, based on this threshold, the images must be inverted to a monochrome, i.e., binary, style. Then, the input images can be normalized by dividing each pixel by a standard deviation that represents the intensity of all pixels. Finally, we are able to resize the input images to a unified size.
2.2 WI Feature Learning Based on the Siamese CNN Network
When learning the features from the signatures, there is no doubt that the most important target of all is extracting the features and reducing the parameters for the signatures. In [6], Hafemann et al. [6] proposed using a two-channel CNN architecture to train a WI feature model. A CNN is simply a neural network that uses the convolution operation in place of the general matrix multiplication in at least one of network layers. A CNN consists of an input layer, an output layer, and multiple hidden layers. The hidden layers in a CNN typically consist of convolution layers, pooling layers, batch normalization layers, dropout layers, Rectified Linear Unit (ReLU) layers, and fully connected layers. The convolution layer helps us to reduce the number of free parameters and allows the network to be deeper with fewer parameters comparing to the conventional neural networks (e.g. Multilayer Perceptron). Pooling layers are used to reduce the dimensions of the data by combining the outputs of the neuron clusters from one layer into a single neuron in the next layer. The batch normalization layer is used to normalize the inputs of each layer in order to mitigate the internal covariate shift problem. The dropout layer is used to prevent any over-fitting problems. The ReLU layer is used to prevent the exponential growth in the computation, where the spatial and depth information are not changed. Fully connected layers are used to connect every neuron in a single layer to classify the images and send them to every neuron in the next layer.
Networks that are Siamese-like are very popular for different verification tasks, such as online signature verification [18] and facial verification [19,20] etc. Unlike a general neural network, a Siamese network consists of twin networks, which operate by mapping the two images to two subnets, before finally per-forming a Euclidean distance calculation. Lastly, a similarity value is generated, which is used to determine whether the two inputs match each other.
In [21], Dey et al. used the Siamese CNN rather than the two-channel CNN used in [6] for offline signature verification in a pure WI system. Fig. 3 shows the WI feature learning architecture used by the authors of [21]. When learning the weights for the Siamese network, the network is trained according to shared weights, so the network is updated based on a comparative benchmark. During the training process, each training image will be entered into the network for in comparison with the genuine reference signature. The authors of [21] randomly chose a genuine signature as the reference input into the Siamese CNN and adopt the contrastive loss as their loss function,
where i is the index of training example, N is the total number of training examples,
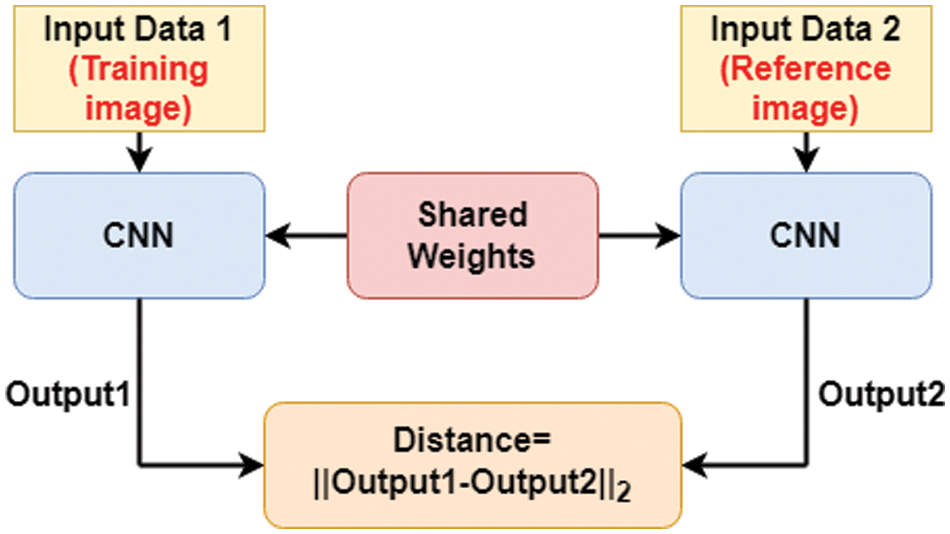
Figure 3: A Siamese network consisting of twin networks accepting two distinct image data sources coming from the tuples that are either similar or dissimilar. In the experiment, the input data is the training and reference signature images, respectively
Since WI signature verification systems have accuracy limitations, this work focuses on the design of a verification system based on a hybrid architecture. This means that WI feature learning and WD classification are considered. Although WI feature learning is also used in [21], there is room for improvement. Because of the high intraclass variability characteristics in the signature, the reference input signature plays a crucial role in the training process. The more relative the reference signature image is to the training image, the higher the performance that will be gained. Consequently, we need an appropriate comparison in order to allow the Siamese network to learn correctly, otherwise it will not be suitable for learning. As a result, we propose a reference selection method that overcomes this problem. We select a genuine signature as the reference signature for each user, and enter it on one side of the Siamese network. In order to achieve a better accuracy, the contrastive loss function used in [21] is modified, where the reference selection is taken into consideration. In order to train in a deeper network, we use ResNet rather than CNN for feature extraction.
In classifier element, not all dimensions are needed to discriminate specific users. Moreover, the dis-similarity thresholds selected in the WI system are not optimal for each user. Therefore, we use the WD architecture to store the features and parameters for each user. Additionally, we can ensure that each user is able to verify their identity in a better environment during the authentication phase.
In order to input the images to the network for training and testing, it is crucial to normalize all signature images. The size of the GPDS signature image varies from 153 × 258 pixels to 819 × 1137 pixels. We first downsize the image to a standard resolution of 128 × 320 pixels, while converting the input image to grayscale. The OTSU algorithm presented in [22] is used to determine the optimal threshold by comparing the intensity of the foreground pixels to those of the background. Any pixel value that is greater than the threshold is set to white (pixel value 255); otherwise, it is set to black (pixel value 0). Consequently, we generate a binary signature image. Since there are two channels in a Siamese network, it is crucial to align signature images for the two channels. In this work, alignment is achieved by applying the Harris corner detection algorithm [23]. We can ensure that the two channels are indeed aligned through the position information from the four corners. Fig. 4 shows the results for each stage in the pre-processing procedure.

Figure 4: Signature images (a) Original (b) Binarized (c) Harris corners (Blue circle) (d) The corners which are closest to the boundaries (e) Four vertices (f) Fixed size
Since the image has been converted to a binary image during the pre-processing stage, the value of pixels will be transformed to either 0 or 1. We now present a method that can be used to select a suitable reference signature. For each genuine signature in the training data, the genuine signature undergoes an XOR operation with other genuine training signatures. When the XOR result is 0, this means that the two images will have a common point. Otherwise, if the XOR result is 1, the result will be seen as a non-common point. We then calculate the number of non-common points for each signature in comparison with the other signatures and select as the genuine reference signature the image which has the fewest non-common points.
Suppose we have a total of M binary genuine signatures, denoted as

Figure 5: Each genuine signature image undergoes an XOR comparison with other genuine images to identify non-common points. The image that has the least number of non-common points is selected as the reference genuine signature image for the user
3.3 Modified Contrastive Loss Function
In the preprocessing stage, we calculate the common points between the training image and the reference image. To take full advantage, we can modify the conventional contrastive loss function to
where
3.4 Writer-Independent Feature Learning
Since we now have a method of selecting a reference signature, our hybrid system is subsequently different from that described in [6,7], as illustrated in Fig. 2. We then add a step for selecting a reference signature at each stage. In the training process, the training image and the reference image will be fed into the feature extractor. After the feature extraction, we store the personal reference signature features and use them in the computation of WD classifier in enrollment as shown in Fig. 6.
As we expect, a higher performance is achieved by forming a deeper network. However, the experimental result shows that training a deeper CNN may lead to a higher training error. To overcome this problem, K. He proposed an architecture named Residual neural Network (ResNet) [17]. ResNet, which is stacked by a set of building blocks named residual blocks. The process of ResNet is defined as: H(x) = F(x,Wi) + x, where x and H(x) are the input and output of the building block. In addition, F(x,Wi) represents the residual mapping to be learned. With x as a shortcut connection, the error can be propagated efficiently during the back propagation. In the conventional CNN, the error is hard to back propagate and may result in degradation.
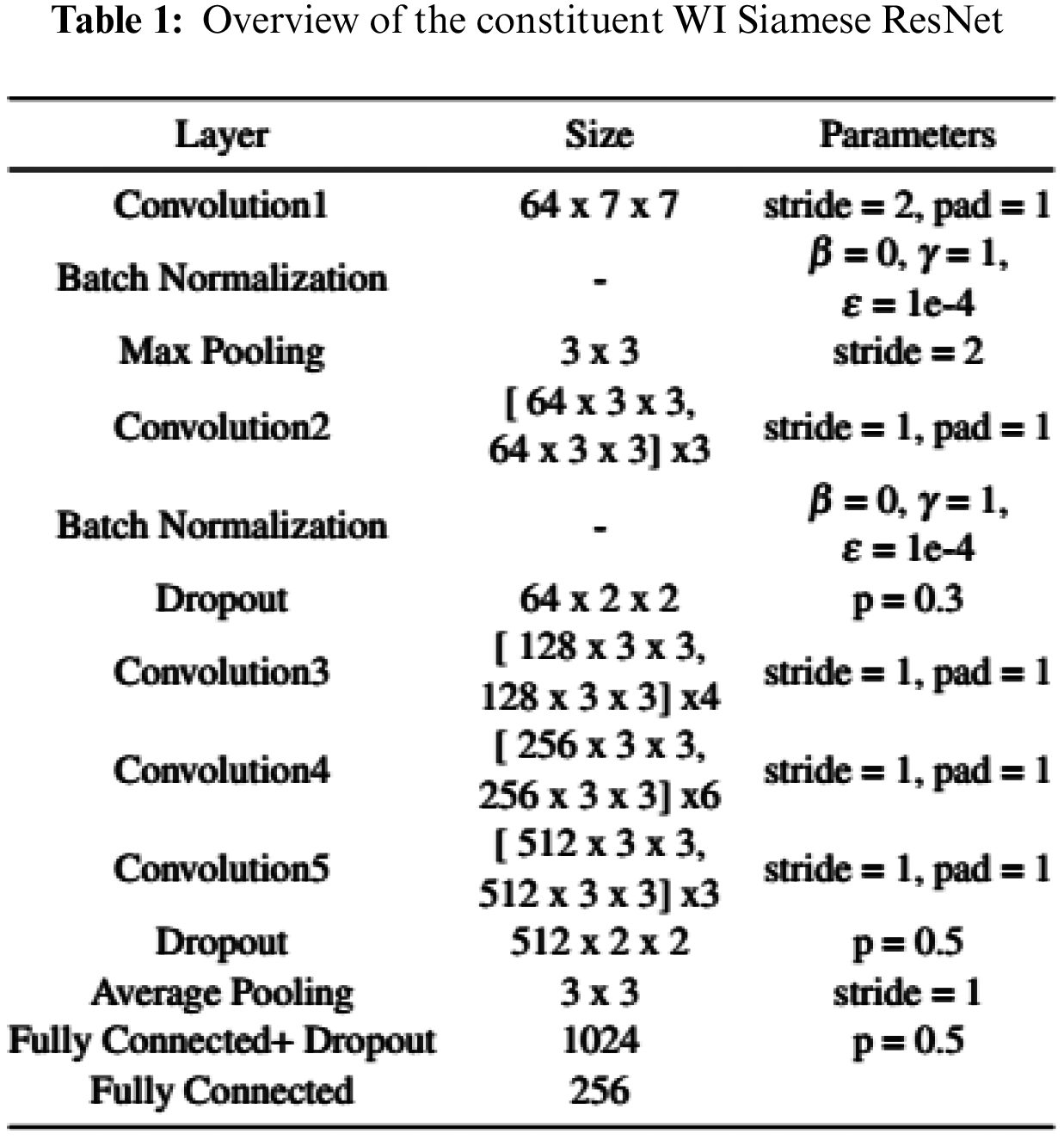
In this paper, we use a ResNet-34 architecture Fig. 7a as the research model. Our proposed Siamese ResNet architecture used to train the WI signature feature is shown in Fig. 7b. As a simple demonstration of our WI feature-learning Siamese ResNet model, a full list of parameters is presented in Tab. 1. For the convolution and pooling layers, we express the size of the filters as F × H × W, where F is the number of filters, H is the height, and W is the width of the corresponding filter. Here, the term stride signifies the distance between the application of the filters for the convolution and the pooling operations and pad indicates the width of the borders to be added to the input.

Figure 6: Proposed hybrid system architecture that includes the use of the Siamese ResNet for WI feature learning and the Siamese NN for WD classification. By claiming identity, the training model will assign a user’s REF and classifier for the authentication application
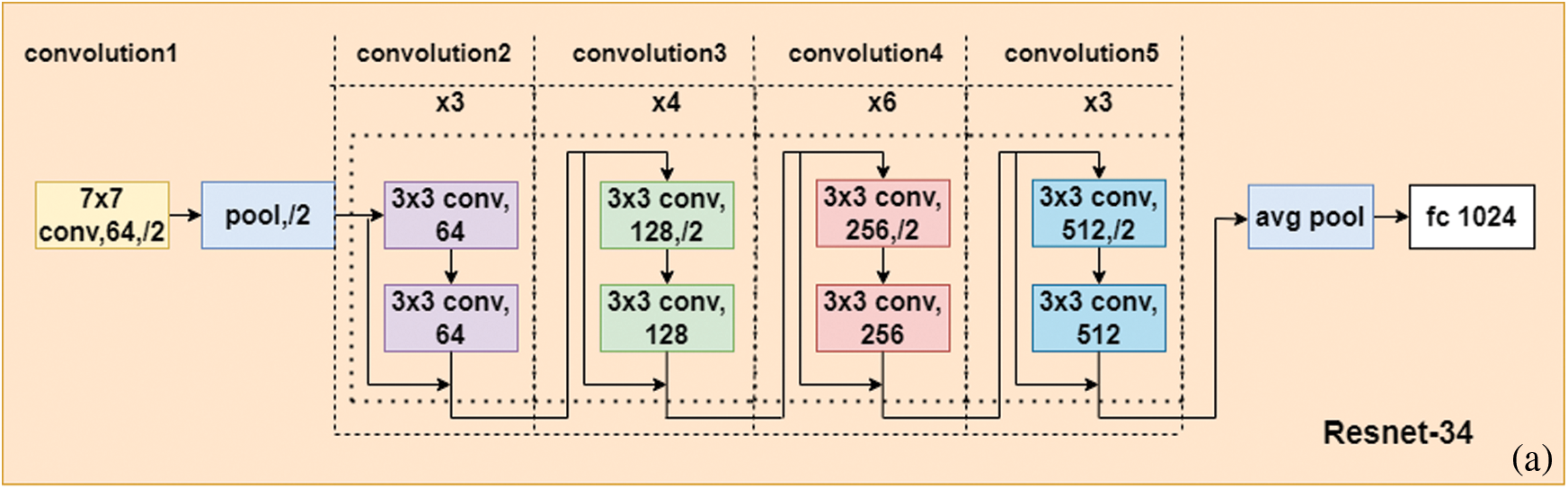
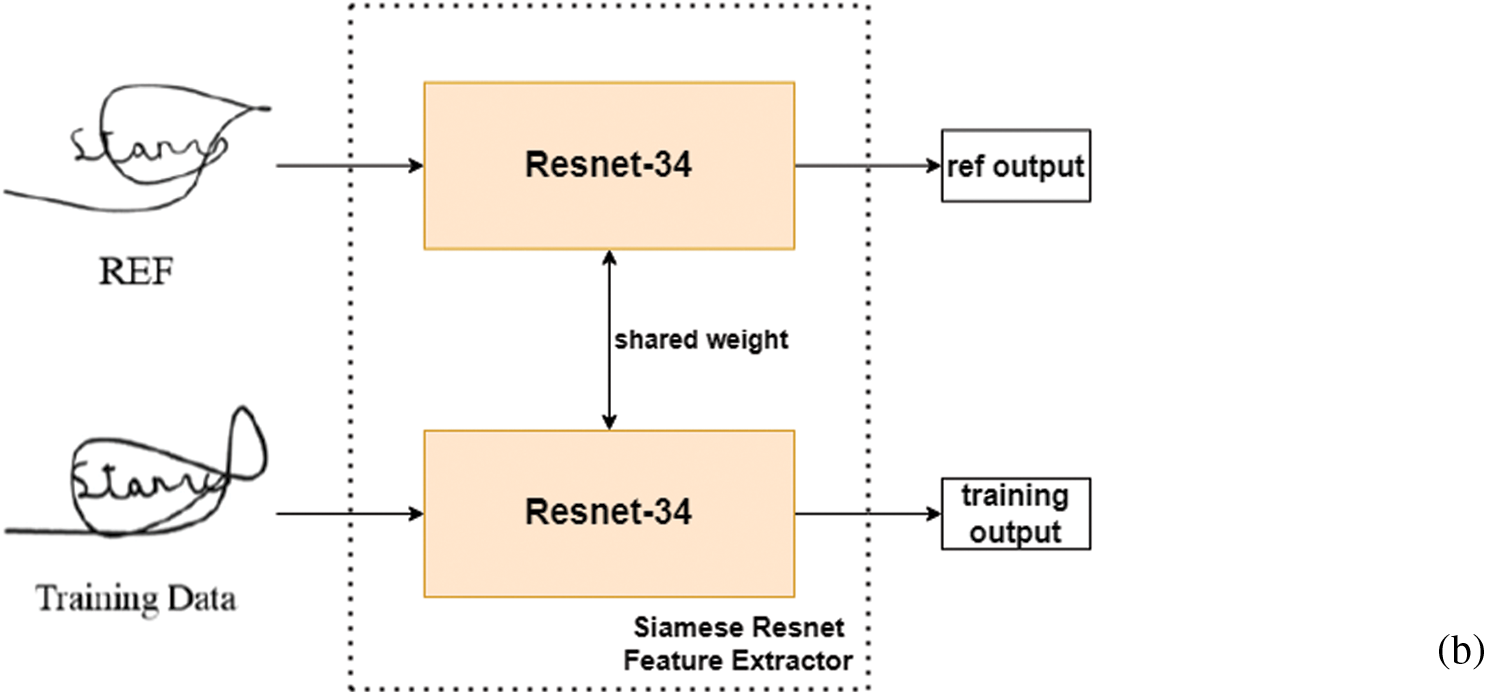
Figure 7: (a) ResNet-34 architecture (b) Process for the proposed Siamese ResNet feature extractor based on ResNet-34
Throughout the network, we use ReLUs as the activation function for all convolution and fully-connected layers. In order to improve the efficiency of the neural-network learning, we use Batch Normalization in the first two convolution layers, which are executed according to [24]. We have three dropout layers [25] following the second convolution layer and the final two fully-connected layers. In [25], Srivastava et al. found that a good value for dropout rate in a hidden layer is between 0.2 and 0.5. So, we tried the dropout rate of 0.1 ~ 0.5 and selected the best combination for our system which are the dropout rate (p) equal to 0.3, 0.5, and 0.5, respectively.
The filter size for the first convolution layer (Convolution1 in Tab. 1 and Fig. 7a) is 7 × 7, and the number of kernels for convolution layer is 64. The remaining four convolution layers (Convolution2 to Convolution5) forms residual blocks. A residual block consists of two layers connected with a shortcut connection. For example, the residual block in Convolution2 consists of two 3 × 3 × 64 convolution layers with a shortcut. The filter size for the convolution layers in Convolution2 to Convolution5 is 3 × 3, and the number of kernels is respectively 64, 128, 256, and 512 for each of the four types of residual blocks. In addition, the number of residual blocks in Convolution2 to Convolution5 is 3, 4, 6, and 3, respectively. The filter size for each of the max pooling layers is 3 × 3. This causes the neural network to learn fewer lower-level features for the smaller receptive fields, and more features for the higher-level fields or more abstract features. The first fully connected layer contains 1024 neurons, followed by the second fully connected layer which has 256 neurons, meaning that the vector dimension is 256.
We initialize the weights of the model according to the work presented by Glorot et al. [26], and initialize the bias to 0. We train the model using Adam [27] for 100 epochs where the batch size is 64. We begin with an initial learning rate equal to
3.5 Writer-Dependent Classifier
In the enrollment phase shown in Fig. 6, we save the features before the second-to-last fully-connected layer in the WI Siamese ResNet feature extractor. Subsequently, we feed those features into a 256-node fully-connected layer (the final layer) and treat it as the WD classifier. The classifier will update the parameters through the user’s features based on the loss result during the training process. After that, reference image and classifier’s weight for the user will be recorded into the database. In the authentication phase, we assign the corresponding classifier and reference from the database once the user claims the identity. This helps our system to verify whether or not the signature is either genuine.
For the experiment, we change the initial learning rate and epoch to
To evaluate the proposed signature verification algorithm, we use the GPDS synthetic database [3,4] since it is commonly used in the recent researches and is the largest available dataset till date. The GPDS dataset is comprised of 4000 signers, where there are 24 genuine and 30 forged signatures for each individual signer. In order to allow a comparison with previous work, we only use the first 881 signers, which were captured in a single session and previously published as GPDS-960. So, there are 881 × 24 = 21144 genuine signatures and 881 × 30 = 26430 forgeries. We test our algorithm using set E, consisting of the first 160 users, and the first 300 users, which were previously published as GPDS-160 and GPDS-300, respectively. The remaining 581 users are assigned to set D to train the WI feature model. Fig. 8 shows how the dataset is split.

Figure 8: The separation of the GPDS dataset into the exploitation set E and the development set D
Since the GPDS dataset contains 24 genuine signatures for each signer, when we establish the training database (set D) for the WI feature learning process, where one reference signature is selected from the 24 genuine signatures for each signer. We then use this reference signature to pair with the remaining genuine signatures. Consequently, there are 23 (genuine, genuine) signature pairs available for each signer. In order to balance the similarity and dissimilarity, we only choose 23 (genuine, forged) signature pairs from each signer. In the training database (set E) for the WD classifier, one reference signature is selected from 16 genuine signatures for each signer. Therefore, we have 15 (genuine, genuine) and 15 (genuine, forged) signature pairs available for each signer. In the set D section, we use 500 signers to train the WI feature and the remaining 81 signers form the basis of the validation set. In the set E section, the data for each user is divided into three segments, 66% training, 17% validation, and 17% testing.
Each pairing must be considered if a reference signature is not selected. There are
Based on the performance metrics presented in [21], we use two metrics to evaluate the performance of our system: True Positive Rate (TPR) and True Negative Rate (TNR). TPR represents the proportion of genuine signatures classified as genuine, while TNR represents the proportion of skilled forgeries classified as forged signatures. The maximum accuracy (ACC) is computed as:
where λ is a decision threshold.
We now discuss the effect of hyperparameter s. Fig. 9 shows the distribution of similarity, i.e.

Figure 9: Similarity distribution for both genuine and forged cases
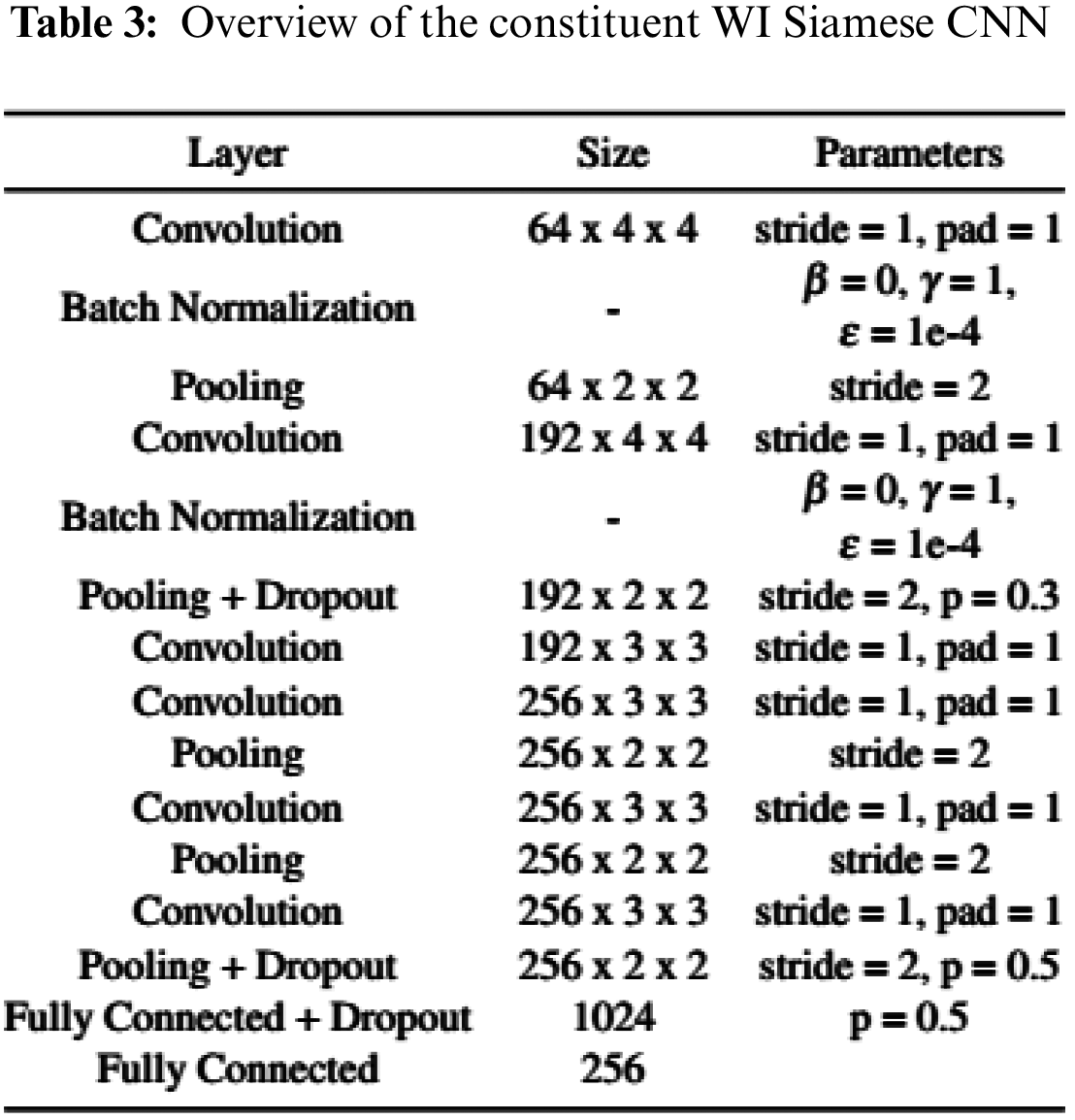
In Tab. 2, we make a comparison of different combinations of WD classifiers and WI feature learning techniques. As shown in table, it can be seen that the accuracy of the NN classifier is significantly improved when combined with the Siamese structure. Then, using ResNet as the feature extractor, the accuracy is 1.78% greater than when using CNN. Regarding to the parameters used in CNN, general filter sizes used are 3 × 3 for the convolution layer for a moderate or small-sized image. We have tried 5 × 5 and 7 × 7 for the filter size and found out the result is not good enough. After our study, we found that the parameters in Tab. 3 are the most suitable for Siamese CNN.
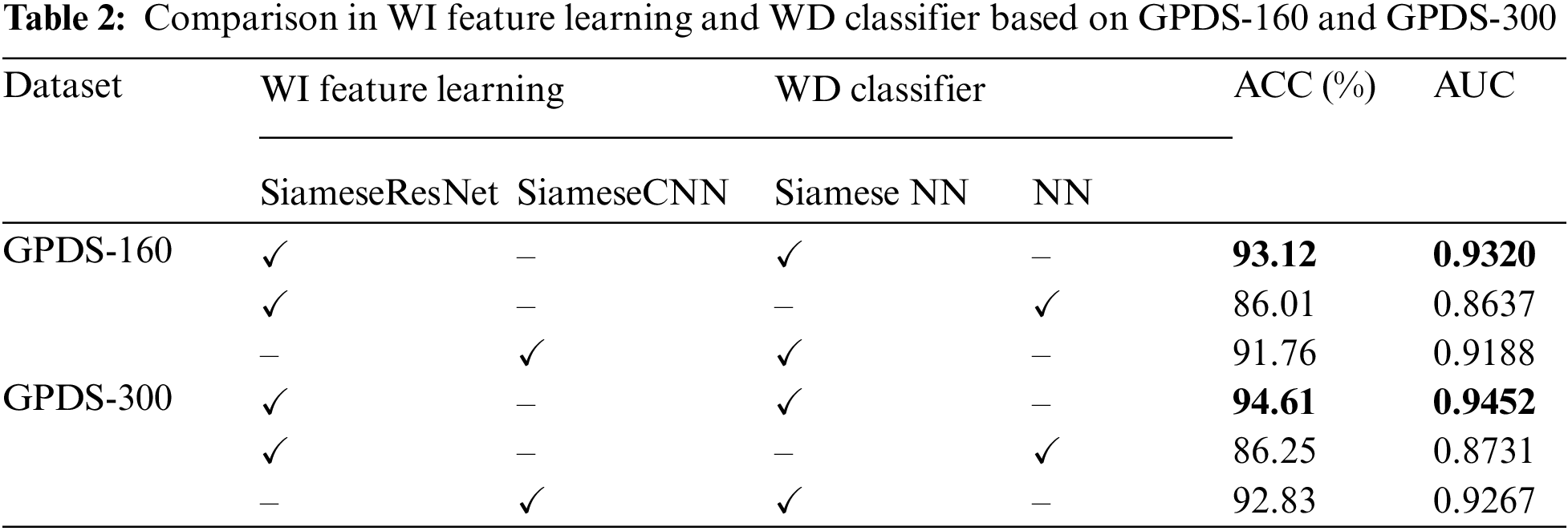
We now evaluate the performance of the proposed reference selection for the Siamese network, where the results are shown in Tab. 4. When the proposed reference selection is not implemented, we need to provide a balance between the similarity and the dissimilarity, so we randomly choose only 276 (genuine, forged) signature pairs from each of the signers. It can be seen that, for the GPDS-300 database, the accuracy is reduced by 5.9% when a reference signature is not selected because the signature has high intraclass variability. The proposed reference selection method is able to effectively reduce the impact from this high intraclass variability characteristic and enable the Siamese network to learn more correctly.

We summarize the accuracy of different hybrid methods based on the GPDS database in Tab. 5. Although the authors of [16] proposed an offline signature verification system based on the Siamese CNN and achieved an accuracy of 92.14%, their scheme is a WD system and, hence, this result is not included in the table. It can be observed that the Siamese network is indeed able to train a good feature model without relying on complex hand-crafted features. In addition, the accuracy of our system based on the GPDS-160 is 3.82% better than the current state-of-the-art CNN method, and 1.49% better when based on the GPDS-300.
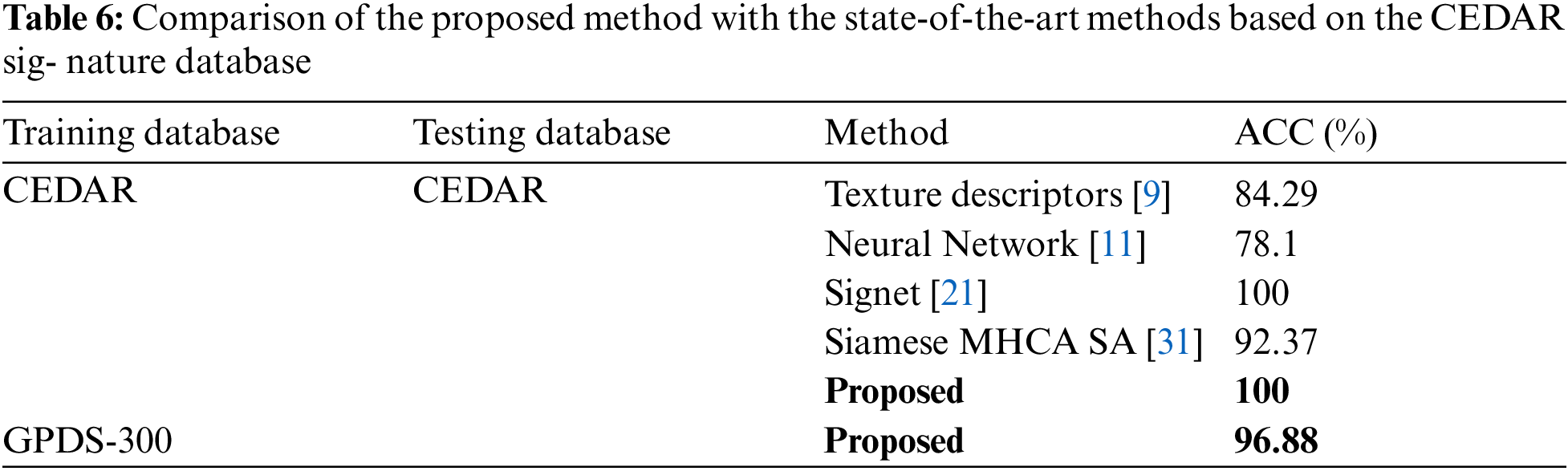
In order to verify whether the proposed model is also suitable for other samples or not, we use the CEDAR database [3,4] to evaluate the performance and compare with different methods in Tab. 6. The CEDAR database consists of offline signatures for signature verification. Each of 55 individuals contributes 24 signatures thereby creating 1,320 genuine signatures and 1,320 forgeries. The accuracy when applying our model on the CEDAR dataset is 96.88%, where we train the model by using the GPDS dataset and evaluate the performance of this trained model on the CEDAR dataset. Consequently, our model is also suitable for other samples and achieve the state-of-the-art performance.
We have presented an off-line signature verification system based on a hybrid architecture, where the Siamese ResNet is used to learn WI signature features, and the Siamese NN is used as a WD classifier to verify the authenticity of the signature. A reference selection method together with the modified loss function is proposed for the Siamese network in order to reduce the impact of the high intraclass variability of the signature and ensure that the Siamese network is able to learn more effectively. Our method can out-perform the current state-of-the-art method in accuracy. For practical applications, we may have no forged signatures. In the future, we will continue to study how to design offline handwritten signature verification systems without any forged signatures. In addition, offline signature verifications for other languages such as Chinese and Russian are interesting and important.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the pre-sent study.
1. L. G. Hafemann, R. Sabourin and L. S. Oliveira, “Offline handwritten signature verification-Literature review,” in Int. Conf. on Image Processing Theory, Tools and Applications, Montreal, Canada, pp. 1–8, 2017. [Google Scholar]
2. M. E. Munich and P. Perona, “Visual identification by signature tracking,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 25, no. 2, pp. 200–217, 2003. [Google Scholar]
3. M. A. Ferrer, M. D. Cabrera and A. Morales, “Synthetic off-line signature image generation,” in Int. Conf. on Biometrics, Madrid, Spain, pp. 1–7, 2013. [Google Scholar]
4. Available at http://www.gpds.ulpgc.es/Download/. [Google Scholar]
5. A. Kumar and K. Bhatia, “A survey on offline handwritten signature verification system using writer dependent and independent approaches,” in Int. Conf. on Advances in Computing, Communication, Automation, Dehradun, India, pp. 1–6, 2016. [Google Scholar]
6. L. G. Hafemann, R. Sabourin and L. S. Oliveira, “Writer-independent feature learning for offline sig-nature verification using deep convolutional neural networks,” in Int. Joint Conf. on Neural Networks, Vancouver, BC, Canada, pp. 2576–2583, 2016. [Google Scholar]
7. G. Eskander, R. Sabourin and E. Granger, “Hybrid writer-independent writer-dependent offline signature verification system,” IET Biometrics, vol. 2, no. 4, pp. 169–181, 2013. [Google Scholar]
8. G. Dimauro, S. Impedovo, G. Pirlo, A. Salzo et al., “A multi-expert signature verification system for bankcheck processing,” International Journal of Pattern Recognition and Artificial Intelligence, vol. 11, no. 5, pp. 827–844, 1997. [Google Scholar]
9. Y. Serdouk, H. Nemmour and Y. Chibani, “Off-line handwritten signature verification using variants of local binary patterns,” in Int. Conf. on Networking and Advanced Systems, Annaba, Algeria, pp. 75, 2015. [Google Scholar]
10. H. Baltzakisa and N. Papamarkosb, “A new signature verification technique based on a two-stage neural network classifier,” Elsevier Journal Engineering Applications of Artificial Intelligence, vol. 14, no. 1, pp. 95–103, 2001. [Google Scholar]
11. M. K. Kalera, S. N. Srihari and A. Xu, “Offline signature verification and identification using distance statistics,” International Journal of Pattern Recognition and Artificial Intelligence, vol. 18, no. 7, pp. 1339– 1360, 2004. [Google Scholar]
12. A. Pansare and S. Bhatia, “Handwritten signature verification using neural network,” International Journal of Applied Information Systems, vol. 1, no. 2, pp. 44–49, 2012. [Google Scholar]
13. E. Ozgunduz, T. Senturk and M. Elif Karsligil, “Off-line signature verification and recognition by support vector machine,” in European Signal Processing Conf., Antalya, Turkey, pp. 1–4, 2005. [Google Scholar]
14. M. Diaz, M. A. Ferrer, S. Ramalingam and R. Guest, “Investigating the common authorship of signatures by off-line automatic signature verification without the use of reference signatures,” IEEE Transactions on Information Forensics and Security, vol. 1, pp. 487–499, 2020. [Google Scholar]
15. N. Arab, H. Nemmour and Y. Chibani, “MultiScale fusion of histogram-based features for robust offline handwritten signature verification,” in Int. Conf. on Computer Systems and Applications, Antalya, Turkey, pp. 1–5, 2020. [Google Scholar]
16. A. Rateria and S. Agarwal, “Off-line signature verification through machine learning,” in IEEE Uttar Pradesh Section Int. Conf. on Electrical, Electronics and Computer Engineering, Gorakhpur, India, pp. 1–7, 2018. [Google Scholar]
17. K. He, X. Zhang, S. Ren and J. Sun, “Deep residual learning for image recognition,” in IEEE Computer Society Conf. on Computer Vision and Pattern Recognition, Las Vegas, Nevada, pp. 770–778, 2016. [Google Scholar]
18. J. Bromley, I. Guyon, Y. LeCun, E. Sackinger and R. Shah, “Signature verification using a Siamese time delay neural network,” International Journal of Pattern Recognition and Artificial Intelligence, vol. 7, no. 4, pp. 669–687, 1994. [Google Scholar]
19. F. Schro, D. Kalenichenko and J. P. Facenet, “A unified embedding for face recognition and clustering,” in Conf. on Computer Vision and Pattern Recognition, pp. 815–823, 2015. [Google Scholar]
20. S. Chopra, R. Hadsell and Y. LeCun, “Learning a similarity metric discriminatively with application,” in Conference on Computer Vision and Pattern Recognition, San Diego, CA, USA, pp. 539--546, 2005. [Google Scholar]
21. S. Dey, A. Dutta, J. I. Toledo, S. K. Ghosh, J. Llados et al., “Signet: Convolutional Siamese network for writer independent offline signature verification,” Computer Research Repository, 2017. [Google Scholar]
22. N. Otsu, “A threshold selection method from gray-level histograms,” IEEE Transactions on Systems, Man, and Cybernetics, vol. 9, no. 1, pp. 62–66, 1979. [Google Scholar]
23. C. Harris and M. Stephens, “A combined corne and edge detector,” in Alvey Vision Conf., Manchester, UK, pp. 147– 151, 1988. [Google Scholar]
24. S. Ioffe and C. Szegedy, “Batch normalization: Accelerating deep network training by reducing internal covariate shift,” in Int. Conf. on Machine Learning, Lille, France, pp. 448–456, 2015. [Google Scholar]
25. N. Srivastava, G. Hinton, A. Krizhevsky, I. Sutskever and R. Salakhutdinov, “Dropout: A simple way to prevent neural networks from overfitting,” Journal of Machine Learning Research, vol. 15, no. 56, pp. 1929–1958, 2014. [Google Scholar]
26. X. Glorot and Y. Bengio, “Understanding the difficulty of training deep feedforward neural networks,” in Int. Conf. on Artificial Intelligence and Statistics, Sardinia, Italy, pp. 249– 256, 2010. [Google Scholar]
27. D. P. Kingma and J. Ba, “Adam: A method for stochastic optimization,” in Int. Conf. for Learning Representations, San Diego, CA, pp. 273–297, 2014. [Google Scholar]
28. L. Prechelt, “Early stopping-but when?,” in Neural Networks: Tricks of the Trade, Berlin, Heidelberg: Springer, pp. 55–69, 1998. [Google Scholar]
29. J. F. Vargas, C. M. Travieso, J. B. Alonso and M. A. Ferrer, “Off-line signature verification based on gray level information using wavelet transform and texture features,” in Int. Conf. on Frontiers in Handwriting Recognition, Kolkata, India, pp. 587–592, 2010. [Google Scholar]
30. M. B. Yilmaz, B. Yanikoglu, C. Tirkaz and A. Kholmatov, “Offline signature verification using classifier combination of HOG and LBP features,” in Int. Joint Conf. on Biometrics (IJCB), Washington DC, pp. 1–7, 2011. [Google Scholar]
31. M. A. Shaikh, T. Duan, M. Chauhan and S. N. Srihari, “Attention based writer independent verification,” in Int. Conf. on Frontiers in Handwriting Recognition (ICFHR), Dortmund, Germany, pp. 373–379, 2020. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |