DOI:10.32604/cmc.2022.026653

| Computers, Materials & Continua DOI:10.32604/cmc.2022.026653 |  |
| Article |
Mode of Operation for Modification, Insertion, and Deletion of Encrypted Data
1Dankook University, Yongin, Gyeonggi, 16890, Korea
2Electronics and Telecommunications Research Institute, Daejeon, 34129, Korea
*Corresponding Author: Nam-Su Jho. Email: nsjho@etri.re.kr
Received: 31 December 2021; Accepted: 11 March 2022
Abstract: Due to the development of 5G communication, many aspects of information technology (IT) services are changing. With the development of communication technologies such as 5G, it has become possible to provide IT services that were difficult to provide in the past. One of the services made possible through this change is cloud-based collaboration. In order to support secure collaboration over cloud, encryption technology to securely manage dynamic data is essential. However, since the existing encryption technology is not suitable for encryption of dynamic data, a new technology that can provide encryption for dynamic data is required for secure cloud-based collaboration. In this paper, we propose a new encryption technology to support secure collaboration for dynamic data in the cloud. Specifically, we propose an encryption operation mode which can support data updates such as modification, addition, and deletion of encrypted data in an encrypted state. To support the dynamic update of encrypted data, we invent a new mode of operation technique named linked-block cipher (LBC). Basic idea of our work is to use an updatable random value so-called link to link two encrypted blocks. Due to the use of updatable random link values, we can modify, insert, and delete an encrypted data without decrypt it.
Keywords: Data encryption; cloud-based collaboration; dynamic data update
Cloud is a technology that can provide various additional services by allowing users to store data in remote storage and use it anywhere [1,2]. With the outbreak of COVID-19, the way of life has changed dramatically. Many of the activities that were conducted face-to-face have been converted to non-face-to-face methods, and accordingly, the demand for technologies suitable for the new environment has increased. Cloud service is a technology specialized for such a non-face-to-face environment, enabling data sharing and collaboration between physically separated users. Until now, a number of researches have been done for the security of cloud-based services [1,2]. Moreover, a number of works focus on the confidentiality, integrity, and availability of data stored in remote cloud storages [3–6]. Some works tried to support users to entrusted some important operations to a cloud server [7].
Many services are being provided in the cloud environment, and services for providing collaboration between users in the cloud environment are also increasing. For example, some service such as the overleaf provides collaborative paper work between researchers online. In particular, papers written or edited by users are reflected in real time and shared between users, so the service enables stable real-time collaboration. For detailed explanation regarding the service, refer to the web-site “https://www.overleaf.com”.
While the importance of collaboration provided in the cloud environment is growing, technology for providing secure collaboration in current services has not been sufficiently researched and developed. The security technology, currently being applied to the cloud-based collaboration service, stores plaintext data in the server, and each client establishes a secure channel with the server to share update information with other collaborators. The current strategy for secure collaboration over cloud server with encryption can be seen in Fig. 1.
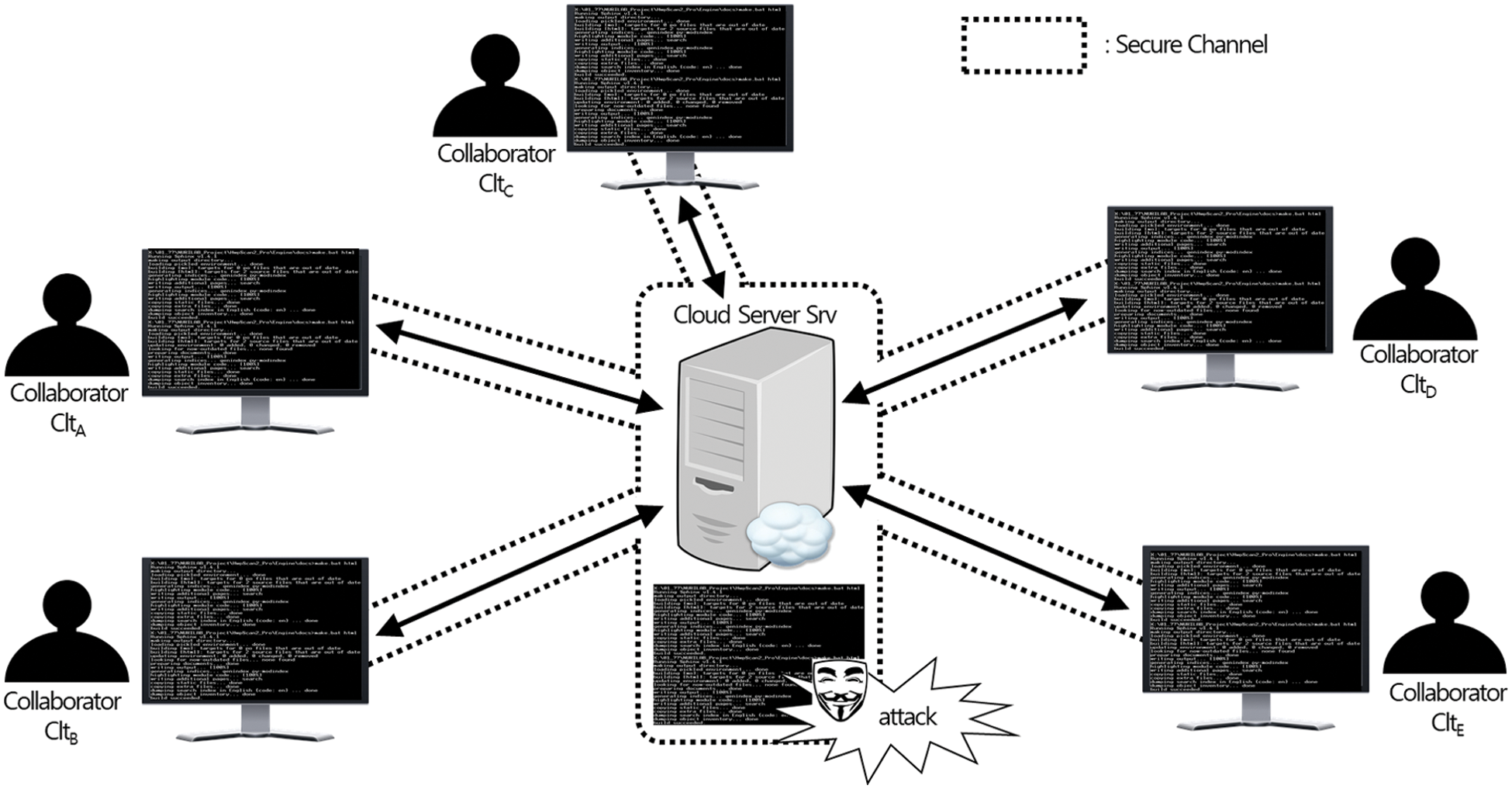
Figure 1: Secure collaboration over cloud server with encrypted channel
As seen in Fig. 1, collaborators can share the same data by the help of the cloud server. Since all communication channels between the server and collaborators are protected by encrypting communicating messages, we can expect secure collaboration if we consider outside adversaries who only can see encrypted communicating messages. But, if we consider the existence of inside adversaries who can see stored data, the current countermeasure cannot guarantee the security of the collaboration. For example, the cloud server could be a malicious-but-curious adversary, which means that the server can exploit high-value collaboration data for its own benefit.
To solve the above described threat against collaboration over cloud environment, it seems inevitable to encrypt data stored in the cloud. So, for secure collaboration, we need a way to encrypt a data for collaboration. For collaboration, an encryption technique should support dynamic data updates, and it is the main goal of this work to give a possible candidate that can permit us to perform secure collaboration by supporting dynamic data updates. Though a number of studies aimed to support dynamic data update operations [8–10], they are not interested in the dynamic update of encrypted data. In this work, we will give a new encryption method for secure collaboration with encrypted dynamic data stored in the remote cloud storage. Specific goal of our research is to design a mode of operation suitable for dynamic data so that the mode can support data updates such as modification, addition, and deletion in an encrypted form. Our strategy to achieve the goal is to use random values. Each random value is used to link two adjacent encrypted blocks. In our construction, the random values are updatable, and so we can update encrypted data by updating link values. Concrete construction can be seen in the following sections. Note that the main contribution of our study is to propose a new mode of operation which can support update operations for encrypted data, and our work is the first approach for secure collaboration with updatable encrypted data, in the literature.
In cryptography, to design secure mode of operations is one of fundamental research topic. In this research direction, it is the most important requirement how to repeatedly apply a cipher’s single-block operation to securely encrypt data which are larger than a block. Though a number of mode of operations have been studied, none of them are designed to encrypt dynamic data.
For security and functionality, error propagation properties of encryption modes have been studied considering various scenarios of data modification. However, the use of dynamic data is not included in the scenarios. Recently, many modes of operation techniques are newly devised, they focus on the way of supporting confidentiality and authenticity in an efficient way, and are known as authenticated encryption modes.
Though a number of techniques have been to support stronger security and better efficiency, none of them are interested in the encryption of dynamic data. By using existing mode of operations, we may support dynamic data by decrypting an encrypted data, updating the data according to required modifications, and encrypting it again. However, it requires cost operations when the data is frequently modified. So, based on the above (brief) remind about related works, we can say that there is no encryption scheme supporting dynamic update in an encrypted form.
From now on, we will briefly review existing mode of operations in terms of dynamic update of encrypted data. Three main functions required for dynamic data are modification, insertion, and deletion. So, we will analyze existing techniques in the viewpoint of the encryption of dynamic data, i.e., the possibility of supporting update operations will be the main goal of our analysis.
There are two kinds of mode of operations. In the first case, mode of operations can support block-wise encryption in the sense that the encryption of a block is not influenced by any other plaintext or ciphertext. Two modes, electronic codebook (ECB) mode and counter (CTR) mode which can be seen in Fig. 2, belong to the first case. The other case includes many mode of operations in which encryption (or decryption) of a plaintext block (or a ciphertext block) is influenced by other blocks. One of representative mode of operation belong to the second case is the cipher block chaining (CBC) mode which works as seen in Fig. 2. Mode of operations belong to the second case are not suitable for dynamic update since the update of single block influence on many blocks. As seen in Fig. 3, two ciphertext blocks should be updated to update one plaintext block. The property is also known as error-propagation though it was not defined to describe the change for updates. It is easy to see that block-wise encryption methods are suitable for dynamic updates since the modification of one block influences on many blocks in the second case.
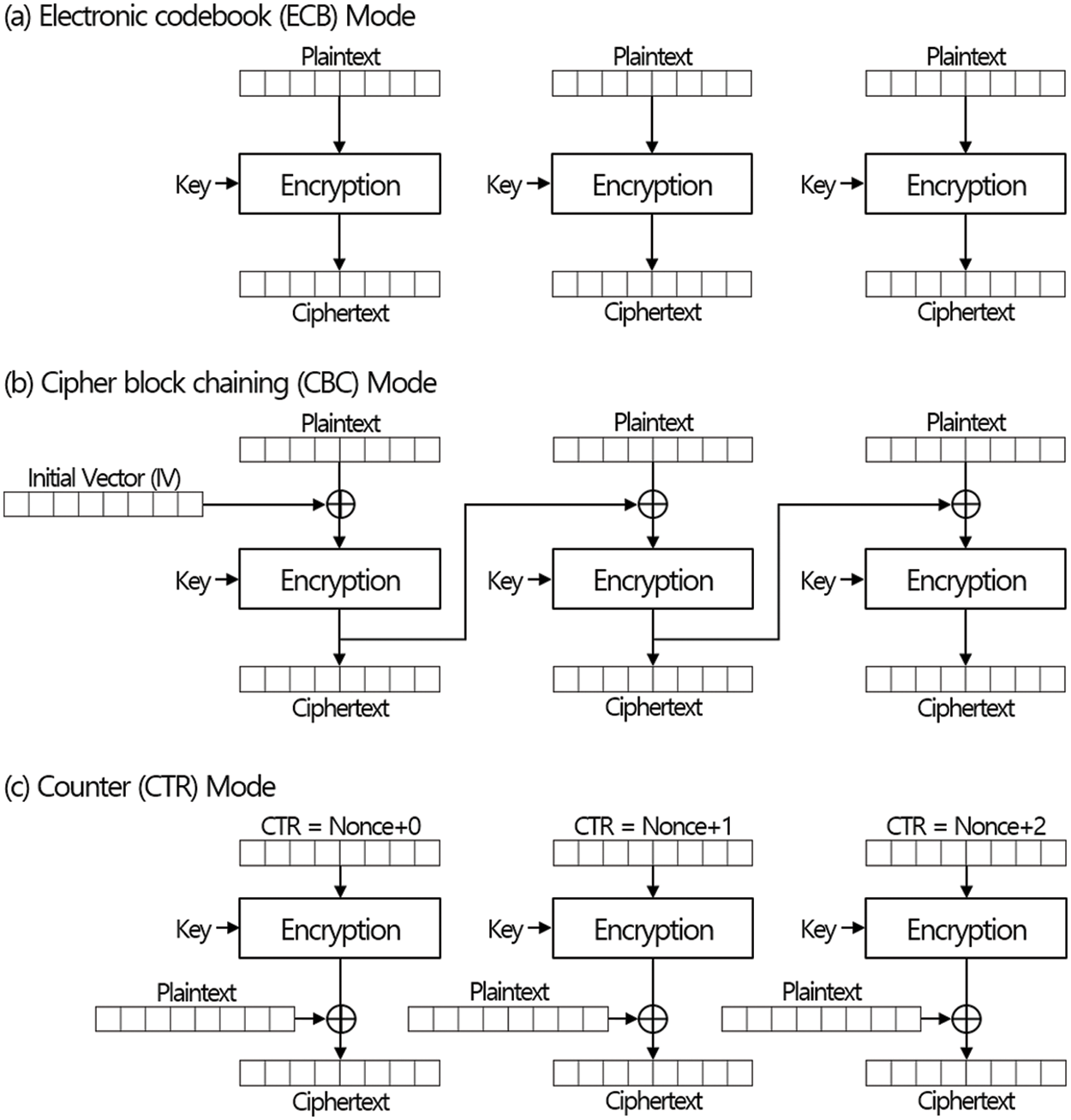
Figure 2: Existing mode of operations
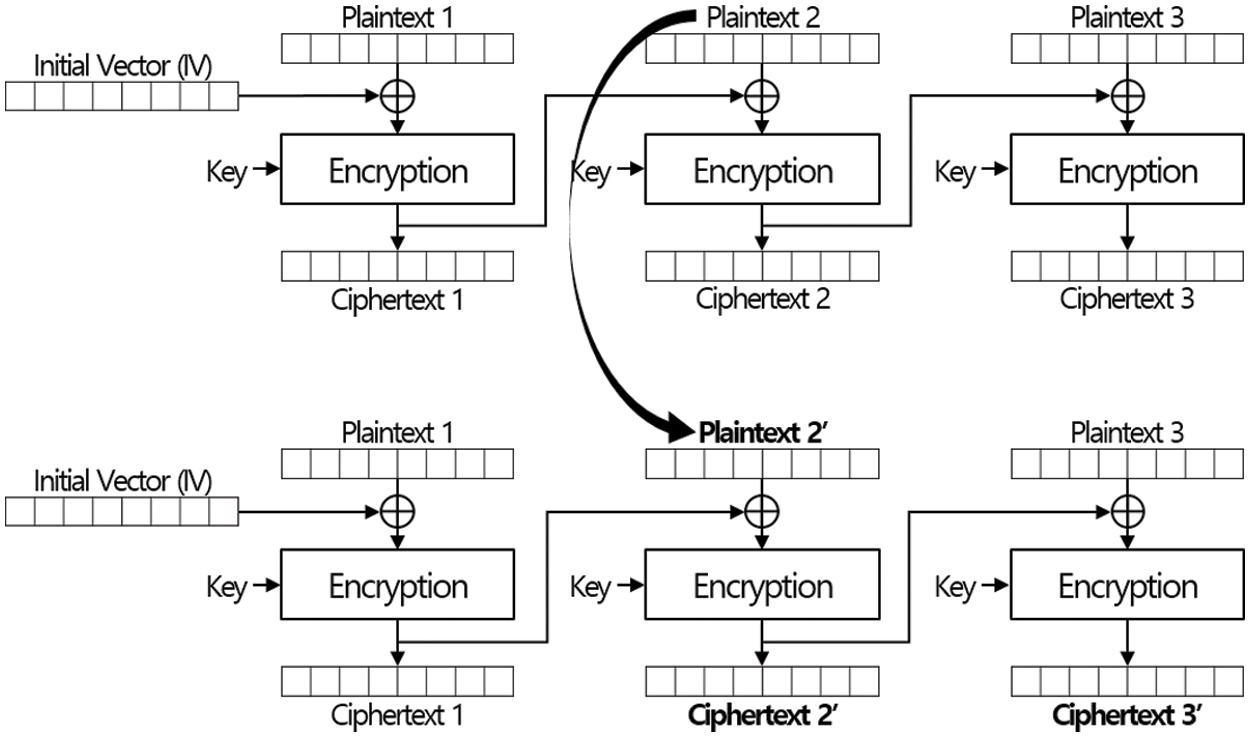
Figure 3: Impact of update in CBC mode
In this section, we describe some basic concepts and definitions.
In order to provide secure collaboration on encrypted data in a cloud environment, key management technology for securely distributing and managing the secret key shared by collaborators or access right management technology for identifying legitimate users is also required. This may require additional system members. However, in this paper, we focus on the problem of storing encrypted data in a cloud server and providing dynamic data update operations for the stored data.
Since we are considering a cloud-based collaboration scenario, the system model consists of a cloud server Srv and a number of collaborators Clts. Each system member has the following roles:
• Server. In order to provide continuous collaboration in an online environment, the server Srv must have the latest version of the data. The update status of data generated through collaboration should always be shared through the server. For secure data access right management, the server must have information that can verify users who are allowed to access data. Since the issue of access control of legitimate users is not dealt with, we assume that secure access control is provided by the server.
• User. Users participating in a collaboration are considered to be sharing a secret key to access the data they collaborate on. Data stored in the cloud must be encrypted, and assuming a shared key among collaborators is an essential part in order to be able to access encrypted data. Users must download the latest version stored in the cloud server at the time of participating in collaboration, and data updates that occur in the middle must be shared to the cloud server in real time. All updates are delivered by the server to collaborating users in real time. Each user proceeds according to the latest version delivered by the server.
From now, we will summarize functional requirements and security requirements for our technique. Before describing the requirements, I would like to note that the technique proposed in this paper is designed to support collaboration with dynamically updated data based on a cloud environment.
In order to support real-time collaboration in a cloud environment, it should be possible to update data stored in the cloud and provided to collaboration participants. The most important factor is to provide data updates in an environment where data is stored in an encrypted form for security. That is, technically, it is the most important requirement to provide data encryption technology that can support all update operations for an encrypted data without decryption.
Since the goal of the proposed technique is to support dynamic update for encrypted data, we assume that a data is stored in a remote storage server in an encrypted form. So, basically, the main security requirement for our scheme is the confidentiality. Differently from ordinary encryption techniques, our technique designed to support dynamic modifications, and so we expect reliability for update operations.
Differently from existing mode of operations for block ciphers, our scheme considers dynamic data which should be changed according to users’ modifications. In ordinary block cipher operation modes, static data is encrypted which means that an adversary cannot obtain two different ciphertexts for similar plaintexts. On the contrary, for dynamic data, an adversary can obtain two different ciphertexts of two similar plaintexts. For example, suppose that one block of a file F is modified to F′ such that
where mi is not equal to mi′. Then, the adversary can obtain two different ciphertexts C = DyEnc(F) and C′ = DyEnc(F′) where DyEnc is an encryption function for dynamic data.
To give formal definition for the security of the proposed scheme, we define an encryption scheme supporting dynamic encryption. From now, we call the encryption scheme as dynamic encryption scheme.
Definition 1. (Dynamic Encryption Scheme) A dynamic encryption scheme is a collection of four polynomial-time algorithms DyEnc = {KeyGen, DyEnc, DyDec, Update} such that,
–KeyGen(λ): For given a security parameter λ, the key generation algorithm returns a secret key sk. Some case, the secret key is a set of secret values.
–DyEnc(sk, M): Let M be a message which is given for encryption. Then the algorithm encrypts M using a secret key sk and returns C as the corresponding ciphertext.
–DyDec(sk, C): For given a ciphertext C, the decryption algorithm uses a secret key sk to recover the message M from the ciphertext.
–Update(sk, C, Q): According to the update query Q, the algorithm modifies the ciphertext C in an encrypted form. i.e., the algorithm updates the ciphertext without decrypting the full ciphertext.
In the above definition, Update is the most important algorithm for dynamic encryption schemes since managing dynamically modified file is the main goal of dynamic encryption schemes. In the definition of Update, the query Q includes the type of update query, required data for update, and (optional) state information such as the version of the file.
The confidentiality is a traditional requirement for encryption schemes since to prevent any adversary from extracting meaningful information from a target ciphertext. The integrity considered in this paper is slightly different from ordinary integrity. We are interested in ‘version integrity’ of our scheme in the sense that an adversary may try to generate a valid encrypted data even if the adversary cannot extract any information from the encrypted data. So, we will call the feature as the version-integrity. The security notion is needed since our scheme support dynamic update of encrypted data without decrypting it. Based on the above reasons, formally, we can define the security of our mode of operation supporting dynamic update as following. The first definition captures the confidentiality of a dynamic encryption.
Definition 2. (Confidentiality of Dynamic Encryption) Let DyEnc(sk, M) be an encryption algorithm supporting dynamic updates. We define the confidentiality for dynamic encryption as similar to the confidentiality of traditional encryption algorithms. For details we consider the following game:
Ind-CCA-DyEnc(sk, A, λ)
–(M0,M1) ← A1OE(sk), OD(sk),OU(sk)(λ), where |M0| = |M1|
–i ← random coin toss
–C = DyEnc(sk, Mi)
–i′ = A2OE(sk),OD(sk),OU(sk)(C, M0,M1,λ)
–if i = i′ then output 1 (the adversary wins the game)
Here the adversary is defined as a tuple of polynomial-time algorithms (A1, A2). A1 is an algorithm that chooses target plaintexts by viewing several sample plaintext-ciphertext pairs which are generated by DyEnc and the secret key sk. We denote encryption oracle, decryption oracle, and update oracle with the secret key sk as OE(sk), OD(sk), OU(sk), respectively. And the second algorithm A2 is an algorithm that determines which plaintext is corresponding to the given ciphertext. Finally, we define the advantage of the adversary as
where sk is a randomly chosen secret key on uniformly distributed key space. Without loss of generality, DyEnc satisfies the confidentiality if there is no polynomial-time algorithm A = (A1, A2), of which the advantage is negligible.
Definition 3. (Integrity of Dynamic Encryption) We define the integrity of our scheme considering the usage that there are multiple users collaborating on the same file. With the integrity, we need to guarantee that the file is not modified by an unprivileged user, the adversary. Therefore, we define the integrity as the following: If there is no polynomial-time adversary which can modify or create proper ciphertexts without a secret key, then the dynamic encryption algorithm satisfies the integrity.
The basic idea of our construction is inspired by chains used in everyday life, and the intuitive concept of the idea is described in Fig. 4. Compared with existing techniques, our technique is designed to provide encryption for dynamic data instead of supporting the optimal ratio of ciphertext to plaintext. In existing encryption techniques, one ciphertext block is generated for one plaintext block, but in our construction, we need redundant value for making link between two blocks as seen in Fig. 4. The redundant value is named Link in the figure. In other words, lb−lL is the size of a plaintext in a block where lb is the size of block for the underlying encryption scheme and lL is the size of a Link.
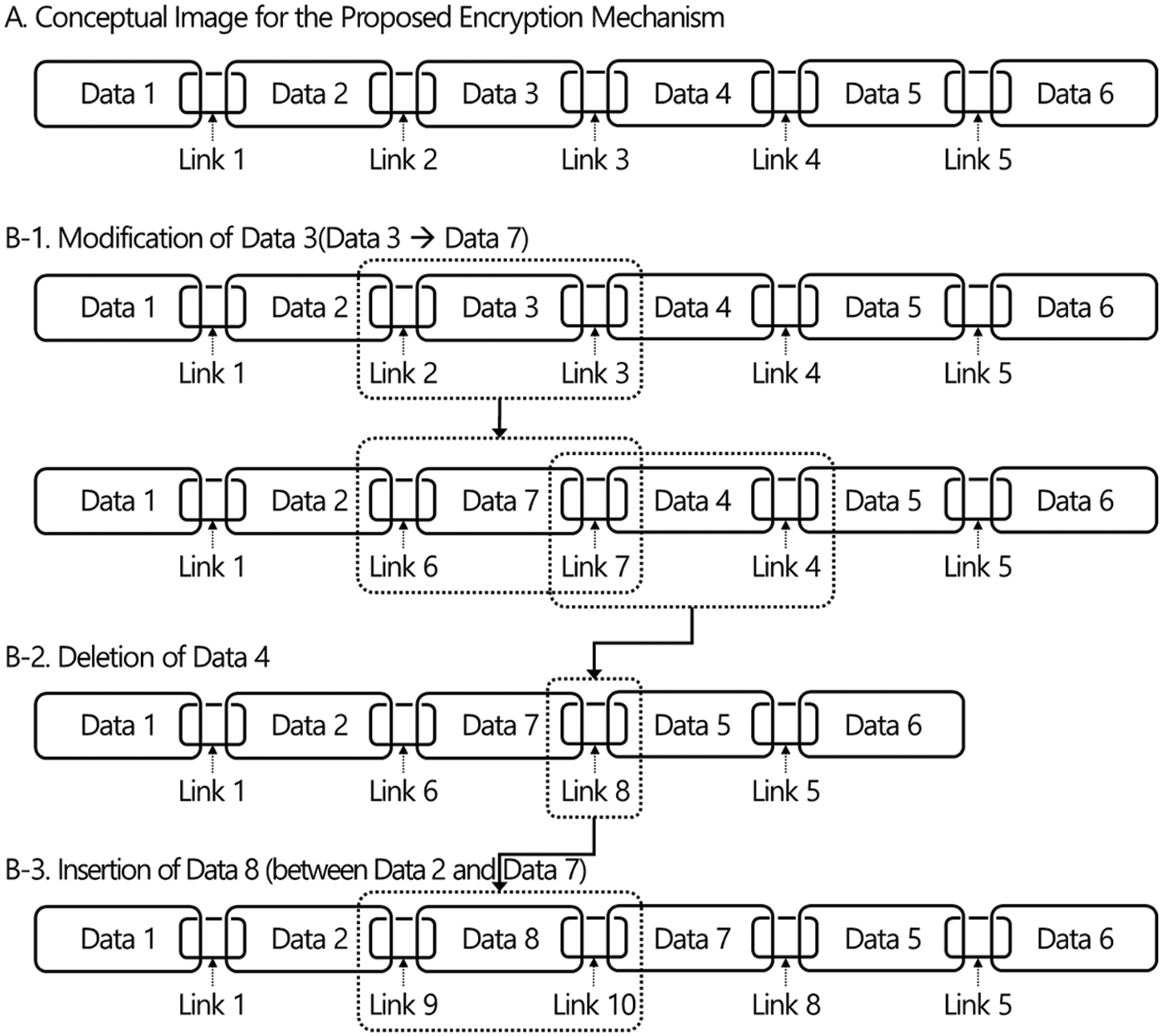
Figure 4: Update operations
For update, we can change encrypted data as seen in Fig. 4. For modification, deletion, and insertion, refer B-1, B-2, and B-3 in Fig. 4. For example, when a data block, Data 3, is modified to Data 7, two links for the block are updated as seen in the figure. It will be easy to understand how the data and links are changed by looking at the specific encryption procedure in the following section.
Here, we will describe detailed algorithms for our dynamic encryption scheme. According to formal definition of a dynamic encryption, we have the following four algorithms: KeyGen, DyEnc, DyDec, and Update.
For encryption, we choose and use a secret key sk. We use the following parameters for our construction. Let lb be the size of a block defined by the underlying block cipher. Let lL be the size of link values used for linking two data blocks.
Note that, for our dynamic encryption scheme, we use a secure encryption algorithm Enc(k,m) as an underlying scheme, which takes a secret key k and a message m to generate the corresponding ciphertext c. Let M be the message to be encrypted. We assume that the size of the message is a multiple of lb − lL. Let |M| = n(lb − lL) which means that M composed with n blocks of length (lb − lL)-bits. Then, the encryption algorithm DyEnc works as followings:
1. Divide the message M into small blocks of length lb − lL-bits. When, we can see that
2. Choose n random values R0, R1, …, and Rn−1, and set IV = R0 where all values are lL-bits such that IV = iv||iv and Ri = ri||ri for i = 1, … , n − 1.
3. Encoded data M′ is computed as
4. Encryption function Enc is applied to
For i = 1 and n, we have
5. Ciphertext is computed as
where ci = Enc(sk,m1′) and sk is the encryption key.
In Fig. 5, we give an example for the encryption procedure. In the example, we consider a message M which can be divided into six blocks such that
Then, we choose six values IV, R1, R2, R3, R4, and R5 where all values are lL-bits such that
Then, an encoded data M′ is computed as
An encryption function Enc is applied to
For i = 1 and 6, we have
Finally, the ciphertext is computed as
where ci = Enc(sk,mi′) and k is the encryption key.
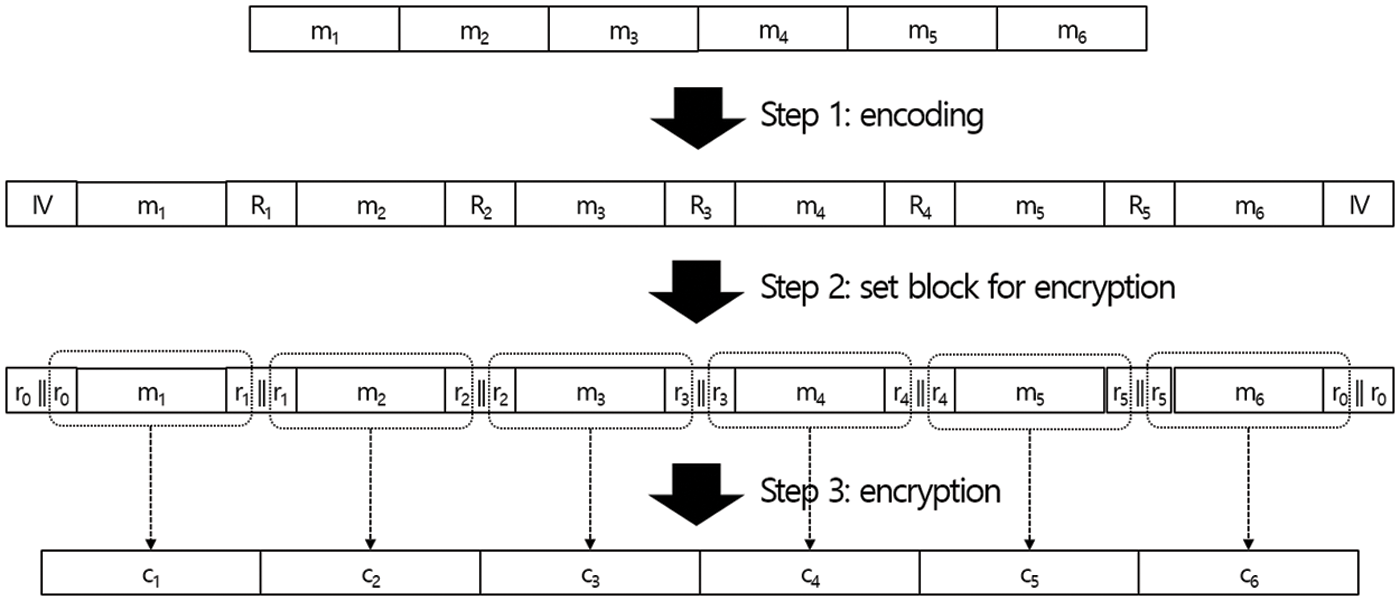
Figure 5: Procedure for proposed encryption technique
To decrypt a ciphertext C, we can use the decryption algorithm Dec(k,c) of the underlying encryption scheme, which returns the corresponding message m for given ciphertext c by using the secret key k.
We can easily recover the data from the ciphertext C by applying block-wise decryption as following steps:
1. Apply the decryption algorithm to each ciphertext block ci for all i = 1, … , n. Then, we can obtain mi′ = Dec(k,ci) for i = 1, … , n.
2. Note that
and
for i = 1 and n. Remove noise values iv and ris and get the plaintext as
Let mi be the message to be updated to m*. To perform update operation, we prepare two new random link values RL= rL||rL and RR = rR||rR. Then, ci the ciphertext of mi′ = ri−1||mi||ri is replaced by
We also have to modify two more ciphertext blocks ci−1 and ci+1. Let
Then, two additional blocks are changed to different ciphertexts
According to the above description, it seems that the proposed technique requires two more additional operation for single modification. However, in general, a number of blocks are modified at once. So, we can see that the additional cost for one modification operation is the modification of two blocks, but the cost is not required for each block. In other words, we need to update lm+2 message blocks to update lm consecutive message blocks. In other words, two more ciphertext blocks are updated for each modification query. A concrete example can be seen in Fig. 4.
Let mi be the message to be deleted. Recall that, encryption of mi−1 and mi+1 are appended at the left and right side of the encryption of mi as
where
To perform update operation, we prepare a new random link value R*= r*||r*. Then, ci the ciphertext of mi is removed from encrypted data, and two ciphertexts ci−1′ and ci+1′ are computed to change link values in two ciphertext ci−1 and ci+1 so that we have the followings:
Then, the encrypted data C is changed to C* as following:
Recall that, two ciphertext blocks are linked when they have the same link values as in the above equation. So, we can see that the message mi is deleted and two ciphertexts are linked as defined. As in the description for modification, the additional cost for one deletion operation is the modification of two blocks. To delete lm consecutive message blocks, we need to update only 2 ciphertext blocks. Refer Fig. 4 for a concrete example.
Let m be the message to be inserted between mi and mi+1, and ci and ci+1 are encryption of two messages such that
To perform insertion operation, we prepare two new random link values RL = rL||rL and RR = rR||rR. Then, c the ciphertext of m′ = rL||m||rR is inserted between ci and ci+1. We also modify two ciphertext ci and ci+1 to update link values. Two ciphertext are computed as
Then, we can see that the message is inserted in the ciphertext C as
To insert lm consecutive message blocks, we need to update only 2 more blocks. Refer Fig. 4 for a concrete example.
To compare our technique with existing techniques, we give the following table. As seen in Tab. 1, existing techniques cannot support all update operations. Though the ECB mode can support dynamic update operations, it is well known that the scheme is not secure since two adjacent blocks are not linked. Two mode of operations, CBC mode and CTR mode, are not suitable for dynamic update. The CTR mode can partially support the modification of a block, but we need somewhat strong assumption that the adversary cannot find two different plaintext blocks for the same position. If an adversary can figure out two different data blocks, the secret encryption key for the position may revealed to the adversary.

In the above, we examine the functionality of our scheme by comparing with existing technique. From now, we will discuss the security of our scheme. The proposed technique is designed based on a secure encryption function Enc, and the security of the proposed technique is guaranteed by the security of the underlying scheme such as the advanced encryption standard (AES) [11]. Extract any information from a ciphertext block is intractable since the underlying scheme is secure under standard security notion which guarantee the hardness of extract any information of encrypted data.
In Section 2.4, we describe a definition for the security of dynamic encryption. As we in Def. 2 and Def. 3, the security of a dynamic encryption is slightly different from ordinary encryption techniques in the sense that any encrypted data are not updated in existing techniques. So, to verify the security of our scheme, we need to prove that it is still hard to guess an encrypted data even if number of update queries can be made by an adversary. From now, we will prove the security of our scheme.
Theorem 1. The proposed dynamic encryption scheme is secure if the underlying block cipher is secure.
Sketch of proof) Assume that our scheme is implemented using a secure block cipher such as AES. Then, we can guarantee the security of encrypted block-sized messages. The goal of the proof is to reduce the security of our scheme to the security of the underlying block cipher. For the goal, we will design an algorithm that can break the security of the underlying scheme using an adversary who can break the security of the proposed scheme.
Proof of Confidentiality) For the proof about the confidentiality, we remind the definition 2. By the definition 2, we need to guarantee there is no adversary that has non-negligible advantage against the ind-CCA-DyEnc game. Suppose that there exists a polynomial-time adversary A = (A1, A2) that
It means that the adversarial algorithm A2 can find out correct i for given C = Enc(sk, ri1||Mi||ri2), M0, and M1 with meaningful probability. For simplicity, we can assume that
where m0t ≠ m1t and m0i = m1i for all other i (i ≠ t). Therefore
where Enc is an embedded encryption algorithm. From the semantic secure property of Enc algorithm, no polynomial-time algorithm can obtain any information about plaintext from a given ciphertext. In other words, Pr[i = i′ | i′ = A2OE(sk),OD(sk),OU(sk)(ct, m0t, m1t, λ), ct = Enc(sk, rL||mit||rR)] – 1/2 is negligible.
Proof of Integrity) To prove the integrity of dynamic encryption, it is needed to guarantee there is no adversary that can construct a proper new cipher block without having the secret key. Without loss of generality, we assume that the adversary’s goal is to construct t-th cipher block. The first strategy of the adversary is to insert a random cipher block into the location of t-th block. However, decrypting the random ciphertext yields a random plaintext, so that links of the resulting plaintext (rL||mt||rR) are random information. It means that rL ≠ rt and rR ≠ rt+1, and it is easy to find out the t-th block is not proper with high probability.
The other way to generate a valid ciphertext can be re-arranging existing valid ciphertexts. In an adversary’s viewpoint, a new valid ciphertext can be made from an existing valid ciphertext only if an inserted block has valid link values. If the adversary has no information about the secret key, then the only possible strategy of an adversary is random guessing of link value. In this case, a randomly chosen link value is valid with probability 1/2lL. Therefore, if we use link values with enough length to obtain the expected security level. For example, we can see that 40-bits link values are enough for our scheme.
Since we use block-wise encryption, the computational complexity of our scheme is almost identical with existing encryption modes since one block-sized message requires one block-encryption. Only the difference is the ciphertext expansion. In existing techniques, the size of ciphertext is almost identical with the data except small-sized padding values. However, our technique requires link values to support dynamic updates. Since we use 40-bits link value, we need one block to encrypt lb-40 bits where lb is the size of a block. Thought the space efficiency is reduced due to the use of link values, our technique is the first encryption mode in the literature, which can support dynamic encryption.
With the development of communication technologies such as 5G and social demands, the importance of cloud-based collaboration is growing. However, since the existing technology is not possible to provide encryption for dynamic data, it is difficult to provide secure cloud-based collaboration. In this paper, we proposed a dynamic encryption technology that can overcome the limitations of these existing technologies. We also proved the security of the proposed technique.
Recall that, in this work, we gave a technique that support dynamic update of encrypted data. One of fundamental requirements for the technique is a way of maintaining the correct version. Since a stored data is frequently updated, collaborators may want to check the version of the data. To guarantee the version of stored data, we need a new authenticating method for dynamically updated data. So, we thought that the most important future work is to design an efficient and effective way to prove the version of a dynamically updated data in an encrypted form. We are also interested in designing efficient technique for collaboration of multimedia data using dedicated encryption technique such as image encryption scheme [12].
Funding Statement: This work was partly supported by Institute of Information & communications Technology Planning & Evaluation (IITP) grant funded by the Korea government (MSIT) (No.2021-0-00779, Development of high-speed encryption data processing technology that guarantees privacy based hardware,50%) and National R&D Program through the National Research Foundation of Korea (NRF) funded by Ministry of Science and ICT (NRF-2021R1F1A1056115,50%).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. K. K. Mar, Z. Hu, C. Y. Law and M. Wang, “Secure cloud distributed file system,” in Proc. of the 11th ICITST, Barcelona, Spain, pp. 176–181, 2016. [Google Scholar]
2. I. Kholod, A. Shorov and S. Gorlatch, “Efficient distribution and processing of data for parallelizing data mining in mobile clouds,” Journal of Wireless Mobile Networks, Ubiquitous Computing, and Dependable Applications, vol. 11, no. 1, pp. 2–17, 2020. [Google Scholar]
3. K. D. Bowers, A. Juels and A. Oprea, “HAIL: A high-availability and integrity layer for cloud storage,” in Proc. of CCS 2009, Chicago, Illinois, USA, pp. 1–12, 2009. [Google Scholar]
4. M. Bellare, S. Keelveedhi and T. Ristenpart, “Message-locked encryption and secure deduplication,” in Proc. of EUROCRYPT 2013, Athens, Greece, pp. 296–312, 2013. [Google Scholar]
5. M. Bellare, S. Keelveedhi and T. Ristenpart, “DupLESS: Server-aided encryption for deduplicated storage,” in Proc. of the 22nd USENIX Conf. on Security, Washington, D.C., USA, pp. 179–194, 2013. [Google Scholar]
6. T.-Y. Youn and N.-S. Jho, “Trapdoor digital shredder: A new technique for improved data security without cryptographic encryption,” KSII Transactions on Internet and Information Systems, vol. 14, no. 3, pp. 1249–1262, 2020. [Google Scholar]
7. Q. Su, R. Hao, S. Duan, F. Kong, X. Liu et al., “Secure computation outsourcing for inversion in finite field,” Journal of Internet Services and Information Security, vol. 10, no. 2, pp. 35–48, 2020. [Google Scholar]
8. Q. Wang, C. Wang, J. Li, K. Ren and W. Lou, “Enabling public verifiability and data dynamics for storage security in cloud computing,” in Proc. of ESORICS 2009, Saint-Malo, France, pp. 355–370, 2009. [Google Scholar]
9. D. Boneh, B. Lynn and H. Shacham, “Efficient dynamic provable possession of remote data via update trees,” ACM Transactions on Storage, vol. 12, no. 9, pp. 1–45, 2016. [Google Scholar]
10. C. C. Erway, A. Kupcu, C. Papamanthou and R. Tamassia, “Dynamic provable data possession,” ACM Transactions on Information and System Security, vol. 17, no. 4, pp. 1–29, 2015. [Google Scholar]
11. United States National Institute of Standards and Technology (NIST“Announcing the advanced encryption standard (AES),” Federal Information Processing Standards Publication, vol. 197, 2012. [Google Scholar]
12. E. Bashier and T. B. Jabeur, “An efficient secure image encryption algorithm based on total shuffling, integer chaotic maps and median filter,” Journal of Internet Services and Information Security, vol. 11, no. 2, pp. 46–77, 2021. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |