Computers, Materials & Continua DOI:10.32604/cmc.2022.025939
Article

Enhanced Archimedes Optimization Algorithm for Clustered Wireless Sensor Networks

E. Laxmi Lydia1, T. M. Nithya2, K. Vijayalakshmi3, Jeya Prakash Kadambaajan4, Gyanendra Prasad Joshi5 and Sung Won Kim6,*

1Computer Science and Engineering, Vignan's Institute of Information Technology (Autonomous), Andhra Pradesh, 530049, India
2Department of Computer Science and Engineering, K. Ramakrishnan College of Engineering, Tiruchirappalli, 621112, India
3Department of Electronics & Communication Engineering, Saveetha School of Engineering, Saveetha Institute of Medical and Technical Sciences, Chennai, 600025, India
4Department of Electronics & Communication Engineering, Kalasalingam Academy of Research and Education, Krishnankoil, 626128, India
5Department of Computer Science and Engineering, Sejong University, Seoul, 05006, Korea
6Department of Information and Communication Engineering, Yeungnam University, Gyeongsan-si, Gyeongbuk-do, 38541, Korea
*Corresponding Author: Sung Won Kim. Email: swon@yu.ac.kr
Received: 09 December 2021; Accepted: 13 January 2022

Abstract: Wireless sensor networks (WSN) encompass a set of inexpensive and battery powered sensor nodes, commonly employed for data gathering and tracking applications. Optimal energy utilization of the nodes in WSN is essential to capture data effectively and transmit them to destination. The latest developments of energy efficient clustering techniques can be widely applied to accomplish energy efficiency in the network. In this aspect, this paper presents an enhanced Archimedes optimization based cluster head selection (EAOA-CHS) approach for WSN. The goal of the EAOA-CHS method is to optimally choose the CHs from the available nodes in WSN and then organize the nodes into a set of clusters. Besides, the EAOA is derived by the incorporation of the chaotic map and pseudo-random performance. Moreover, the EAOA-CHS technique determines a fitness function involving total energy consumption and lifetime of WSN. The design of EAOA for CH election in the WSN depicts the novelty of work. In order to exhibit the enhanced efficiency of EAOA-CHS technique, a set of simulations are applied on 3 distinct conditions dependent upon the place of base station (BS). The simulation results pointed out the better outcomes of the EAOA-CHS technique over the recent methods under all scenarios.

Keywords: Wireless sensor network; CH selection; energy efficiency; clustering; lifetime

1  Introduction

The development of chip or microelectron-mechanical technologies, it is a dramatic improve from utilize of wireless sensor networks (WSN) has been observed [1]. Mainly, this is because of their wide-ranging application in various fields such as military surveillance, healthcare, traffic controlling, disaster-prone zones monitoring, space exploration, environmental monitoring, target tracking, and so on. According to this application, WSN could be underwater, underground, mobile, terrestrial, and multimedia [2]. The resource-restricted and distributed nature of sensor networks makes it crucial to pay more attention to considerable problems such as lifetime enhancement and to energy conservation accomplish better network performances. WSN is the network of powered, cost-effective devices i.e., armed with wireless transmission capacities. This node works collaboratively to monitor their nearby regions. Data sensed by this node was periodically transmitted to central authority that is sink node for other processing. In this study, the terms sink and base station (BS) are interchangeably utilized for the central authority. Behind this activity carried out by the sensors, there are certain requirements that must be satisfied. Such requirements are balancing the energy consumed by the sensors [3]. Energy preservation is the most important problem in WSN which emerges because of the constrained availability of energy with the sensors. Therefore, authors are primarily concerned with the growth of energy aware routing systems [4,5].

Authors pay considerable attention to development of energy effective solutions, but, at the same time network lifetime could also be expanded by designing energy effective models. It is widely agreed that cluster based hierarchical approaches are an effective method to store energy for distributed WSN [6] that increases lifetime of the network by efficiently using the node energy, and assisting dynamic WSN environments. In a cluster based WSN, sensor node (SN) is separated into various sets named as clusters with a group leader called Cluster Head (CH). Each SN senses information and transmits it to their respective CH that eventually transmits it to the BS for other processing. Clustering has many considerable benefits over traditional systems [7]. Firstly, data aggregation is applied to information, received from various SN within a cluster, for reducing the amount of data to be transferred to BS hence energy requirement decreases significantly. Next, rotation of CH assists in ensuring a balanced energy utilization within the networks that avoids getting specific nodes starved because of insufficient energy [8]. But, the appropriate CH selection with optimum capacities while balancing energy efficacy ratio of the network is a well determined NP-hard problem in WSN [9].

Ali et al. [10] design a new clustering method incorporated with heuristic named new ranked-based clustering (NRC) for minimizing the energy utilization of the sensors while effectively balancing lifetime (LT) of system. In contrast to population based algorithms, ARSH-FATI-CHS switches dynamically amongst exploitation as well as exploration of the searching model during runtime to accomplish maximum trade-off and considerably enhance LT of the system. Kadiravan et al. [11] introduce a novel Density Based Clustering (DBC) approach for attaining energy efficacy in WMSN. The DBC method is primarily used for collecting information in medical environments that is based mainly on three input variables namely node centrality, residual energy level, and distance. Additionally, 2 static data collector points named Super Cluster Head (SCH) is established that gather information from standard CH and transmit it to the BS straightaway.

The authors in [12] develop a hybrid metaheuristic approach whereas optimal features of artificial bee colony (ABC) and differential evolution (DE) are integrated to estimate the optimal sets of load-balanced CH. For load-balancing and energy effective clustering, a new objective function is developed on fundamental of average delay, parameter energy, and intracluster distance. Tam et al. [13] consider the problems of optimum relay node deployment to maximize the network life of WSN in 3D terrains. Initially, develop an arithmetical method and redevelop it as a mixed-integer programming method for providing a substructure to find low bound solutions.

Otaibi et al. [14] propose a hybridization of meta-heuristic cluster based routing (HMBCR) approach to WSN. Initially, The HMBCR techniques involve a brainstorm optimization using levy distribution (BSO-LD) based clustering method with fitness function (FF) integrating 4 variables like distance to neighbors, energy, network load, and distance to the base station. In addition, a water wave optimization using hill-climbing (WWO-HC) based routing technique was performed for optimum path selection. In [15], Salp optimization-based method is employed for solving this problem. The presented model is utilized for the selection of CH. The efficacy of the presented system was related to 2 node clustering system under the terms of network lifetime, remaining energy, and energy consumption.

This paper presents an enhanced Archimedes optimization based cluster head selection (EAOA-CHS) technique for WSN. The EAOA-CHS technique intends to optimally choose the CHs from the available nodes in WSN and then organize the nodes into a set of clusters. Besides, the EAOA is derived by the incorporation of the chaotic map and pseudo-random performance. Moreover, the EAOA-CHS technique determines a fitness function involving total energy consumption and lifetime of WSN. The design of EAOA for CH election in the WSN illustrates the novelty of work. For showcasing the enhanced efficiency of EAOA-CHS manner, the set of simulations are applied on 3 distinct conditions dependent upon the place of BS.

2  System Model

An objective function of clustering is for transmitting information to BS in an effective manner which decreases energy utilization. Some of the assumptions made are listed in the following [16].

•   The network has homogeneous with respect to saved, battery level, and sensing range.

•   If the network was functioning, BS as well as SN are stationary.

•   The farness amongst 2 nodes is evaluated in received signal strength indicator (RSSI).

•   When the energy of SN was consumed, it refers that SN is dead, and their battery was entirely consumed.

•   The SN is arbitrarily utilized on target area considered that 100×100m2.

•   The battery of SN has irreplaceable or non-rechargeable.

•   There are no constraints to BS with respect to processing as well as storing.

The radio energy model is employed. It can be also useful for decreasing the energy utilization of network that is utilized in sensing, aggregation, amplification, and broadcast. During the transferring and receiving s bit, energy dissipated is provided as Eqs. (1) and (2).

ETX(S,d)={sEelec+sεfsd2d<d0sEelec+sεmpd4d>d0},(1)

ERX(S)=ERX−elec(s)=sEelec,(2)

where ERX implies the energy required to reception of bit data, ETX signifies the energy utilized for transmission data, d refers the separation amongst transmitting as well as receiving, d0 stands for threshold which defines also free space or multipath method implemented, and it could be computed in Eq. (3). εfs and εamp represents the coefficient of amplifications.

d0=εfsεamp(3)

To a CH, the count of energy consumed from the iteration has been calculated in Eq. (4).

ECH(S)=ns(Eelec+efsdCM+EDA),(4)

where EDA refers the energy utilized from data aggregation.

To a non-CH node, the energy dissipated was calculated in Eq. (5), whereas dCH refers the farness in their CH.

ECM(S)=s(Eelec+efsdCM),(5)

where Eelec stands for the energy consumed for moving a single data bit.

3  The Proposed Model

This study developed a new EAOA-CHS method to optimally choose the CHs from the available nodes in WSN and then organize the nodes into a set of clusters. In addition, the EAOA is derived by the incorporation of the chaotic map and pseudo-random performance. Furthermore, the EAOA-CHS technique determines a fitness function involving total energy consumption and lifetime of WSN. Fig. 1 illustrates the overall working process of EAOA-CHS technique.

Figure 1: Overall process of EAOA-CHS technique

3.1 Design of EAOA Technique

The presented Archimedes optimization algorithm (AOA) is a population-based algorithm whereas the immersed object is assumed as the candidate [17]. Like other meta heuristic-based populations, this approach starts with some amount of arbitrary values that are distributed uniformly in a possible range. The searching method using objects is separated into arbitrary volumes, densities, and accelerations. By taking exploitation and exploration phases into account, AOA could be determined as a global optimization method. The AOA method has been described in the following. Initially, the position of each object has been initiated by:

x(i)=xl(i)+rand×(xu(i)−χl(i))(6)

i=1,2,…,N.

whereas, x(i) represent the ith object using N objects, and xl(i) and χu(i) defines the minimal and maximum limit of solution spaces. From abovementioned, the AOA sets the density (D), acceleration (A), and volume (V), to every i object arbitrarily. Then, upgrade the densities, volumes, and the acceleration for ith object for the iteration t+1:

V(i)=rand(7)

D(i)=rand(8)

A(i)=xl(i)+rand×(xu(i)−xl(i))(9)

Now, the AOA estimates the primary population, and the object with optimal cost values was carefully chosen. This optimal value is determined by xbest,Vbest,Abest, and Dbest.

Next, the candidate is upgraded according to the parameter. The object acceleration is upgraded by taking the collision condition with neighboring objects into account. Next, the upgraded location of the object was attained by three parameters includes volume and density.

Vt+1(i)=Vt(i)+rand×(Vbest−Vt(i))(10)

Dt+1(i)=Dt(i)+rand×(Dbest−Dt(i))(11)

In which, Dbest and Vbest describes the density and volume of optimal object, and rand represents a uniform distributed value. Then, utilize the transfer operator (TF) and density factors for attaining in exploration to exploitation.

TF= exp (t−tmaxtmax)(12)

Here, TF steps up gradually in a period till attaining 1, t and tmax describes the iteration amount and the maximal amount of iterations. Similarly, reducing factors of density (d) try to offer global to local search:

Dt+1= exp (tmax−ttmax)−(ttmax)(13)

In the equation, Dt+1 gradually reduces to offer an appropriate convergence. It assists in making an appropriate trade-off amongst exploitation and exploration.

For exploitation, when TF≤0.5, object have no collision and upgrade the acceleration of the objects for iteration i + 1:

Dt+1= exp (tmax−ttmax)−(ttmax)(14)

whereas, Dt+1 decreases with time that could converge in previously recognized regions. It makes a better trade-off among exploration and exploitation. In such cases, a random material (mr) was carefully chosen to update the object acceleration for t+1 iteration using Eq. (15):

At+1=Dmr+Vmr×AmrDt+1(i)×Vt+1(i)(15)

While, V (i), (i), and A(i) represent, volume, density, and acceleration of ith object, correspondingly. In which Dmr,ymr, and A(i) denotes the density, volume, and acceleration of mr. Carrying out dissimilar values from 0.5 would alter exploration-exploitation behaviors. When TF>0.5, the exploitation was modeled by taking no collision among the objects into account. Now, an update of the object has been attained using Eq. (16):

At+1(i)=Dbest+Vbest×AbestDt+1(i)×Vt+1(i),(16)

Now, Abest determines the optimal object acceleration.

Next, the normalized acceleration is given by:

At+1(i¯)=u×At+1(i)−min(A)max(A)−min(A)+l(17)

Let, At+1(i) be the step variation percentage of every individual, as well as l and u describes the standardization limitations within [0.9, 0.1], correspondingly. Subsequently, when TF≤0.5, the place of update the ith object for t+1 iteration was attained by Eq. (18):

xt+1(i)=xt(i)+c1×rand×At+1(i¯)×D×(xrond−xt(i))(18)

In which C1 indicates a constant equal to 2. Otherwise, when TF>0.5, the object updates its position according to Eq. (19):

xr+1(i)=χbestζ+F×c2×rand×Ar+1(i¯)×D×(T×χbest−xr(i))(19)

whereas, T increases over time among [c3×0.3,1] and take a percentage in the optimal position and c2 describes the constant value equal to 6. This percentage increases with time for reducing the variation among the best and current locations to offer a better trade-off among exploration and exploitation, and F defines the upgrade method of the object according to their position:

F={+1,ifP≤0.5+1,ifP>0.5(20)

While

P=2×rand−c4(21)

It measures every object by f cost function and stores the optimal solution.

Usually, the fundamental AOA offers a well-built outcome to optimize. But, it faces restrictions like premature convergence and local optimization. While the AOA in a primary stage is an optimum diversity, the variance amongst the object reduces then that creates a minimum diverge searching. This occurs in the optimized. For refining this limitation, the current investigation presented a novel 1D chaotic [18]. This process is occurrence as pseudo-random performance which reduces the difficulty of arbitrary numbers creating but maintaining them arbitrarily sufficient. At this point, the chaos logistic map was utilized for changing an arbitrary created by 1, r2, and r3, for instance,

x(i)=x1(i)+r1×(xu(i)−x1(i))(22)

V(i)=r2(23)

D(i)=r3(24)

A(i)=x1(i)+r4×(xu(i)−x1(i))

where, ri(i=1,2,3,4) defines the ith chaotic round value and primary value α1 determined an arbitrary value amongst zero and one.

rik+1=4rik×(1−rik)(25)

where, ri0=0.

3.2 Process Involved in EAOA-CHS Technique

The EAOA aims to choose a set of nodes to effort as CH ensures that minimized the employed energy for data transmission. Specifically, the optimized purpose is for determining an optimum set of nodes to effort as head which delays the network lifespan and minimizes the utilized energy [19]. The main function of this technique is for maximizing the lifespan of network (δnn) which end once the primary node dies and it can be computed as:

δn1=mins∈S⁡δs(26)

where, δs refers the lifespan of node s and S implies the group of nodes from the network. Assume that n sensor nodes were distributed uniformly, and k clusters. So, it is n/k node per cluster (1 CH and (n/k)−1 CM). Entire employed energy by CH (eCH) to a single iteration is provided as:

eCH=(nk−1).ERx(b)+nk.b.EDA+ETx(b,dtoBS).(27)

The CM node sends their information to its CH, since an outcome, entire utilized energy by CM node on iteration is as follows:

eCM=ETx(b,dtoCH).(28)

where, dtoBS and dtoCH signifies the average distance amongst the head node as well as BS, and the average distance amongst member node and CH correspondingly. An entire energy utilization from the cluster in an iteration is

Econsumedcluster=eCH+eCM(29)

The purpose is for maximizing δn1 by minimizing whole employed energy from the network per iteration so that CH rotation is attained to balance utilized energy. Since an outcome, the fitness function (FF) has been provided as:

F=∑i=1k⁡Econsιιmedclιιster(i)a+∑i=1k⁡Econsumedclιιster(i)+(βa+β)(30)

where the amount of CH demonstrated as k,β refer the entire amount of times the chosen node's effort as CH and a refer the constant higher than 0.

4  Experimental Validation

This section inspects the energy efficiency and lifetime analysis of the EAOA-CHS technique under three scenarios based on the location of BS. A comparative analysis is made with low energy adaptive clustering hierarchy (LEACH), Two Level Cluster-based Routing protocol (TLCR), Optimal Clustering Mechanism Fuzzy-C Means (OCM-FCM), enhanced energy proficient clustering (EEPC), and quasi-oppositional butterfly optimization algorithm (QOBOA).

Tab. 1 offers the number of alive nodes (NAN) and total energy consumption (TEC) of the EAOA-CHS technique with BS position of (100, 100). Fig. 2 depicts the comparative NAN analysis of the EAOA-CHS technique with other techniques under dissimilar rounds with BS position of (100, 100). The figure stated that the EAOA-CHS technique has offered increased NAN under all rounds. For instance, with 500 rounds, the EAOA-CHS technique has provided maximum NAN of 100 nodes whereas the LEACH, TLCR, OCM-FCM, EEPC, and QOBOA techniques have attained minimal NAN of 0, 21, 78, 98, and 96 respectively. At the same time, with 1000 rounds, the EAOA-CHS technique has resulted in increased NAN of 63 nodes whereas the LEACH, TLCR, OCM-FCM, EEPC, and QOBOA techniques have demonstrated reduced NAN of 0, 0, 27, 35, and 56 respectively.

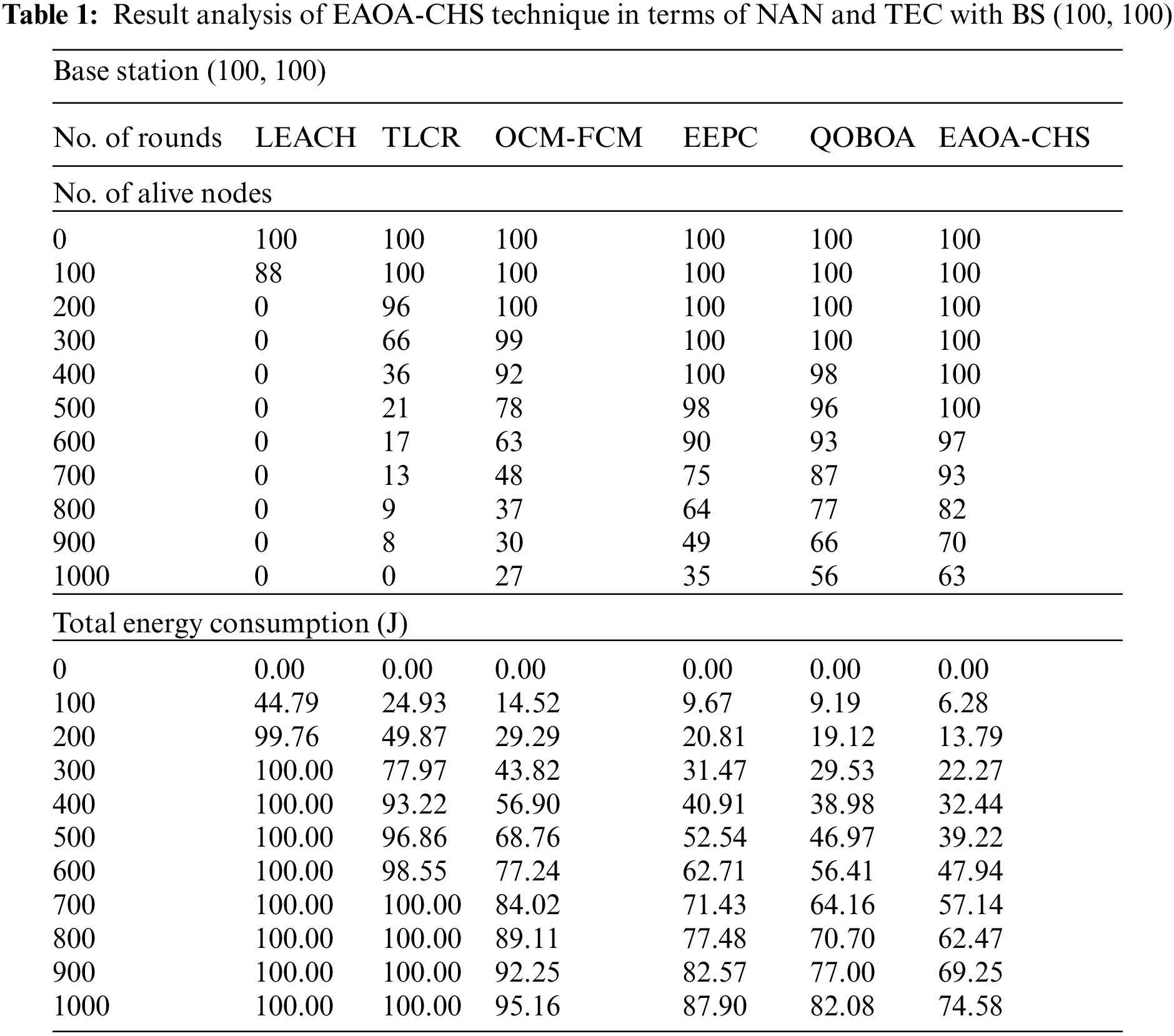
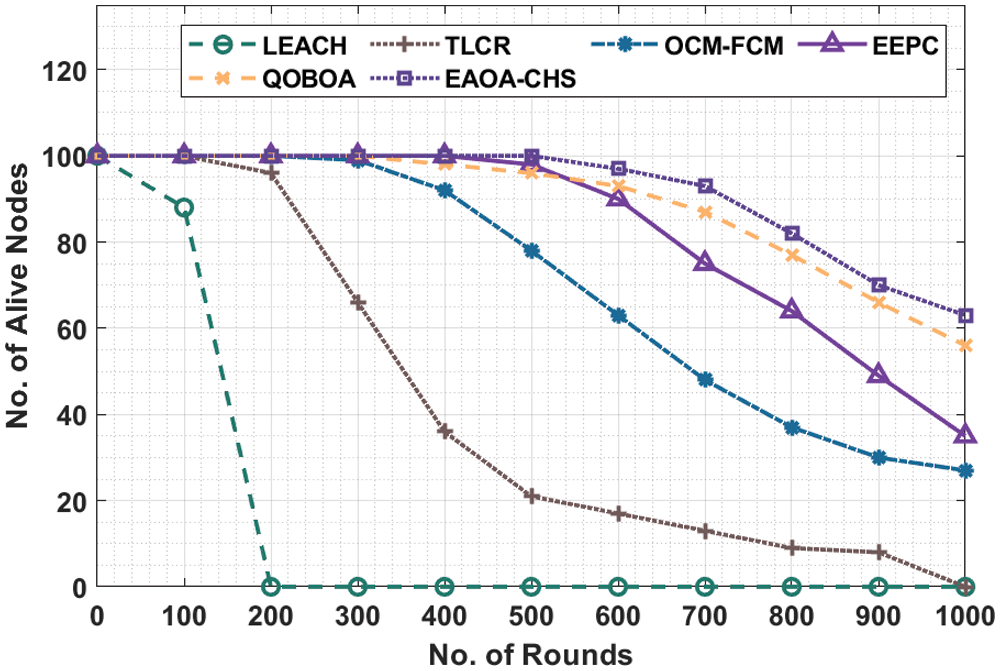
Figure 2: NAN analysis of EAOA-CHS technique with BS (100, 100)

A brief TEC analysis of the EAOA-CHS technique with recent methods with BS position of (100, 100) is given in Fig. 3. From the figure, it is ensured that the EAOA-CHS technique has the ability to attain reduced TEC. For instance, with 500 rounds, the EAOA-CHS technique has depicted least TEC 39.22 J whereas the LEACH, TLCR, OCM-FCM, EEPC, and QOBOA techniques have exhibited increased TEC of 100.00, 96.86, 68.76, 52.54, and 46.97 J respectively. Moreover, with 1000 rounds, the EAOA-CHS technique has gained reduced TEC of 74.58 J whereas the LEACH, TLCR, OCM-FCM, EEPC, and QOBOA techniques have accomplished improved TEC of 100, 100, 95.16, 87.90, and 82.08 J respectively.

Figure 3: TEC analysis of EAOA-CHS technique with BS (100, 100)

Tab. 2 comparative analysis the NAN and TEC of the EAOA-CHS methodology with BS position of (200, 200).

Fig. 4 demonstrates the brief NAN analysis of the EAOA-CHS approach with other methods under dissimilar rounds with BS position of (200, 200). The figure obvious that the EAOA-CHS method has obtainable improved NAN under all rounds. For instance, with 500 rounds, the EAOA-CHS methodology has offered maximal NAN of 57 nodes whereas the LEACH, TLCR, OCM-FCM, EEPC, and QOBOA techniques have attained minimal NAN of 0, 15, 35, 40, and 50 respectively. Likewise, with 1000 rounds, the EAOA-CHS technique has resulted in increased NAN of 35 nodes whereas the LEACH, TLCR, OCM-FCM, EEPC, and QOBOA systems have outperformed lower NAN of 0, 2, 12, 19, and 23 correspondingly.

Figure 4: NAN analysis of EAOA-CHS technique with BS (200, 200)

A detailed TEC analysis of the EAOA-CHS approach with recent manners with BS position of (200, 200) is provided in Fig. 5. From the figure, it can be made sure that the EAOA-CHS technique has the ability to attain reduced TEC. For instance, with 500 rounds, the EAOA-CHS method has depicted least TEC 59.32 J whereas the LEACH, TLCR, OCM-FCM, EEPC, and QOBOA algorithms have exhibited higher TEC of 100.00, 100.00, 88.24, 75.77, and 74.03 J correspondingly. Moreover, with 1000 rounds, the EAOA-CHS system has gained reduced TEC of 81.51 J whereas the LEACH, TLCR, OCM-FCM, EEPC, and QOBOA techniques have accomplished enhanced TEC of 100, 100, 99.72, 92.73, and 91.74 J correspondingly.

Figure 5: TEC analysis of EAOA-CHS technique with BS (200, 200)

Tab. 3 demonstrates brief analysis of the NAN and TEC of EAOA-CHS algorithm with BS position of (100, 200). Fig. 6 illustrates the comparative NAN analysis of the EAOA-CHS manner with other algorithms under dissimilar rounds with BS position of (100, 200). The figure stated that the EAOA-CHS system has obtainable superior NAN under all rounds. For instance, with 500 rounds, the EAOA-CHS manner has provided maximum NAN of 60 nodes whereas the LEACH, TLCR, OCM-FCM, EEPC, and QOBOA techniques have reached decreased NAN of 0, 10, 31, 39, and 55 correspondingly. Simultaneously, with 1000 rounds, the EAOA-CHS technique has resulted in improved NAN of 30 nodes whereas the LEACH, TLCR, OCM-FCM, EEPC, and QOBOA methodologies have showcased lesser NAN of 0, 3, 10, 11, and 23 respectively.

Figure 6: NAN analysis of EAOA-CHS technique with BS (100, 200)

A comparative TEC analysis of the EAOA-CHS technique with recent techniques with BS position of (100, 200) is given in Fig. 7. From the figure, it can be demonstrated that the EAOA-CHS manner has the ability to achieve lower TEC. For instance, with 500 rounds, the EAOA-CHS algorithm has depicted least TEC 66.36 J whereas the LEACH, TLCR, OCM-FCM, EEPC, and QOBOA methodologies have depicted maximum TEC of 100.00, 100.00, 89.28, 83.25, and 80.11 J correspondingly. Followed by, with 1000 rounds, the EAOA-CHS technique has reached minimal TEC of 81.32 J whereas the LEACH, TLCR, OCM-FCM, EEPC, and QOBOA systems have accomplished improved TEC of 100, 100, 99.41, 96.28, and 94.54 J correspondingly.

Figure 7: TEC analysis of EAOA-CHS technique with BS (100, 200)

Finally, the number of packets received at the BS by the EAOA-CHS technique with recent methods take place in Tab. 4 and Fig. 8 [20,21]. The results show that the EAOA-CHS technique has accomplished maximum number of packets over the other techniques.

For instance, with BS (100, 100), the EAOA-CHS technique has received a total of 8805 packets whereas the LEACH, TLCR, OCM-FCM, EEPC, and QOBOA techniques have gained minimal packets of 1169, 2996, 6651, 8174, and 8565 packets respectively. Moreover, with BS (100, 200), the EAOA-CHS technique has attained a total of 5106 packets whereas the LEACH, TLCR, OCM-FCM, EEPC, and QOBOA techniques have gained minimal packets of 1016, 1212, 3801, 4127, and 4649 packets respectively. Therefore, it is apparent that the EAOA-CHS technique has been found to be superior to other techniques.

Figure 8: Comparative analysis of EAOA-CHS technique with recent manners

5  Conclusion

This study developed a new EAOA-CHS technique to optimally choose the CHs from the available nodes in WSN and then organize the nodes into a set of clusters. In addition, the EAOA is derived by the incorporation of the chaotic map and pseudo-random performance. Furthermore, the EAOA-CHS technique determines a fitness function involving total energy consumption and lifetime of WSN. For showcasing the improve performance of EAOA-CHS approach, a series of experiments are applied on 3 distinct conditions dependent upon the location of the BS. The simulation outcomes pointed out the better outcomes of the EAOA-CHS technique over the recent methods under all scenarios. Therefore, it can be ensured that the EAOA-CHS technique has accomplished effective network lifetime and energy efficiency. In future, data aggregation models can be developed to reduce the data transmission at the CHs.

Funding Statement: This research was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (NRF-2021R1A6A1A03039493).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  T. K. Dao, T. T. Nguyen, J. S. Pan, Y. Qiao and Q. A. Lai, “Identification failure data for cluster heads aggregation in wsn based on improving classification of SVM,” IEEE Access, vol. 8, pp. 61070–61084, 2020. [Google Scholar]

 2.  S. Famila, A. Jawahar, A. Sariga and K. Shankar, “Improved artificial bee colony optimization based clustering algorithm for SMART sensor environments,” Peer-to-Peer Networking and Applications, vol. 13, no. 4, pp. 1071–1079, 2020. [Google Scholar]

 3.  A. Shahraki, A. Taherkordi, O. Haugen and F. Eliassen, “A survey and future directions on clustering: From wsns to iot and modern networking paradigms,” IEEE Transactions on Network and Service Management, vol. 18, no. 2, pp. 2242–2274, 2021. [Google Scholar]

 4.  X. Liu, “A survey on clustering routing protocols in wireless sensor networks,” Sensors, vol. 12, no. 8, pp. 11113–11153, 2012. [Google Scholar]

 5.  P. Maheshwari, A. K. Sharma and K. Verma, “Energy efficient cluster based routing protocol for WSN using butterfly optimization algorithm and ant colony optimization,” Ad Hoc Networks, vol. 110, pp. 102317, 2021. [Google Scholar]

 6.  M. Shobana, R. Sabitha and S. Karthik, “Cluster-based systematic data aggregation model (csdam) for real-time data processing in large-scale WSN,” Wireless Personal Communications, vol. 117, no. 4, pp. 2865–2883, 2021. [Google Scholar]

 7.  R. Ahmad, R. Wazirali, Q. Bsoul, T. A. Ain and W. A. Ain, “Feature-selection and mutual-clustering approaches to improve dos detection and maintain WSNs’ lifetime,” Sensors, vol. 21, no. 14, pp. 4821, 2021. [Google Scholar]

 8.  P. S. Rathore, J. M. Chatterjee, A. Kumar and R. Sujatha, “Energy-efficient cluster head selection through relay approach for WSN,” The Journal of Supercomputing, vol. 77, no. 7, pp. 7649–7675, 2021. [Google Scholar]

 9.  M. B. Shyjith, C. P. Maheswaran and V. K. Reshma, “Optimized and dynamic selection of cluster head using energy efficient routing protocol in WSN,” Wireless Personal Communications, vol. 116, no. 1, pp. 577–599, 2021. [Google Scholar]

10. H. Ali, U. U. Tariq, M. Hussain, L. Lu, J. Panneerselvam et al., “ARSH-FATI: A novel metaheuristic for cluster head selection in wireless sensor networks,” IEEE Systems Journal, vol. 15, no. 2, pp. 2386–2397, 2021. [Google Scholar]

11. G. Kadiravan, P. Sujatha, T. Asvany, R. Punithavathi, M. Elhoseny et al., “Metaheuristic clustering protocol for healthcare data collection in mobile wireless multimedia sensor networks,” Computers, Materials & Continua, vol. 66, no. 3, pp. 3215–3231, 2021. [Google Scholar]

12. G. P. Gupta and B. Saha, “Load balanced clustering scheme using hybrid metaheuristic technique for mobile sink based wireless sensor networks,” Journal of Ambient Intelligence and Humanized Computing, 2020, https://link.springer.com/article/10.1007/s12652-020-01909-z. [Google Scholar]

13. N. T. Tam, H. T. T. Binh, V. T. Dat, P. N. Lan and L. T. Vinh, “Towards optimal wireless sensor network lifetime in three dimensional terrains using relay placement metaheuristics,” Knowledge-Based Systems, vol. 206, pp. 106407, 2020. [Google Scholar]

14. S. A. Otaibi, A. A. Rasheed, R. F. Mansour, E. Yang, G. P. Joshi et al., “Hybridization of metaheuristic algorithm for dynamic cluster-based routing protocol in wireless sensor networksx,” IEEE Access, vol. 9, pp. 83751–83761, 2021. [Google Scholar]

15. S. Mirjalili, A. H. Gandomi, S. Z. Mirjalili, S. Saremi, H. Faris et al., “Salp swarm algorithm: A bio-inspired optimizer for engineering design problems,” Advances in Engineering Software, vol. 114, pp. 163–191, 2017. [Google Scholar]

16. A. K. Dwivedi, P. S. Mehra, O. Pal, M. N. Doja and B. Alam, “EETSP: Energy-efficient two-stage routing protocol for wireless sensor network-assisted internet of things,” International Journal of Communication Systems, vol. 34, no. 17, pp. 1–19, 2021. [Google Scholar]

17. F. A. Hashim, K. Hussain, E. H. Houssein, M. S. Mabrouk and W. A. Atabany, “Archimedes optimization algorithm: A new metaheuristic algorithm for solving optimization problems,” Applied Intelligence, vol. 51, no. 3, pp. 1531–1551, 2021. [Google Scholar]

18. B. Yao and H. Hosein, “Model parameters estimation of a proton exchange membrane fuel cell using improved version of archimedes optimization algorithm,” Energy Reports, vol. 7, pp. 5700–5709, 2021, http://dx.doi.org/10.2139/ssrn.3877174. [Google Scholar]

19. W. Osamy, A. A. E. Sawy and A. Salim, “CSOCA: Chicken swarm optimization based clustering algorithm for wireless sensor networks,” IEEE Access, vol. 8, pp. 60676–60688, 2020. [Google Scholar]

20. N. R. Malisetti and V. K. Pamula, “Performance of quasi oppositional butterfly optimization algorithm for cluster head selection in WSNs,” Procedia Computer Science, vol. 171, pp. 1953–1960, 2020. [Google Scholar]

21. K. Guleria, A. K. Verma, N. Goyal, A. K. Sharma, A. Benslimane et al., “An enhanced energy proficient clustering (EEPC) algorithm for relay selection in heterogeneous WSNs,” Ad Hoc Networks, vol. 116, pp. 102473, 2021. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.