Computers, Materials & Continua DOI:10.32604/cmc.2022.025836
Article

Secure Communication Scheme based on A New Hyperchaotic System

Khaled Benkouider1, Aceng Sambas2, Ibrahim Mohammed Sulaiman3, Mustafa Mamat4 and Kottakkaran Sooppy Nisar5,*

1Non Destructive Testing Laboratory, Automatic Department, Jijel University, BP. 98, 18000, Jijel, Algeria
2Department of Mechanical Engineering, Universitas Muhammadiyah Tasikmalaya, Tasikmalaya, West Java, 46196, Indonesia
3School of Quantitative Sciences, College of Art and Sciences, Universiti Utara Malaysia, Sintok, 06010, Kedah, Malaysia
4Faculty of Informatics and Computing, Universiti Sultan Zainal Abidin, Besut Campus, 22200, Kuala Besut, Terengganu, Malaysia
5Department of Mathematics, College of Arts and Sciences, Prince Sattam bin Abdulaziz University, Wadi Aldawaser, 11991, Saudi Arabia
*Corresponding Author: Kottakkaran Sooppy Nisar. Email: n.sooppy@psau.edu.sa
Received: 06 December 2021; Accepted: 16 February 2022

Abstract: This study introduces a new continuous time differential system, which contains ten terms with three quadratic nonlinearities. The new system can demonstrate hyperchaotic, chaotic, quasi-periodic, and periodic behaviors for its different parameter values. All theoretical and numerical analysis are investigated to confirm the complex hyperchaotic behavior of our proposed model using many tools that include Kaplan-Yorke dimension, equilibrium points stability, bifurcation diagrams, and Lyapunov exponents. By means of Multisim software, the authors also designed an electronic circuit to confirm our proposed systems’ physical feasibility. MATLAB and Multisim simulation results excellently agree with each other, which validate the feasibility of our new ten terms hyperchaotic system and make it very desirable to use in different domains especially in chaotic-based communication. Furthermore, by employing the drive response synchronisation, we developed a secure communication strategy for the proposed system. Findings from the proposed scheme show that the proposed approach was successful in completing the encryption and decryption procedure.

Keywords: Hyperchaotic system; synchronization; circuit design; secure communication system

1  Introduction

The high usage of chaotic systems in numerous areas of engineering, such as secure transmission [1–3] prompted the need for the construction of new systems. The researchers in chaos theory have focused their researches to develop more and more systems with complex chaotic behaviors in order to cover the very growing demand of dynamical systems of this kind. The Massachusettsian scientist Edward Lorenz introduced the initial chaotic system [4] in 1963; and proved that we could get chaotic behavior with only three variables. This was the starting point for scientists’ community to develop and construct many chaotic systems in the last few decades [5–7].

Recently, the great development of communication technology and cryptography are leading the researchers to develop new systems with more complex behaviors than the ordinary chaotic systems. As we know, Lyapunov exponents are the famous tool to characterize the complexity of dynamical systems. One positive exponent implies chaos, more than one implies more complexity, which bring us to hyper chaos. The first hyperchaotic model was introduced by the German scientist Otto Rössler [8] in 1979. After that, many of hyperchaotic systems were constructed [9–12].

Recently, several studies are utilizing the hyperchaotic systems for designing different secure communication system methods. For instance, the hyper-chaotic secure asynchronous communication system was investigated by Liu et al. [13]. The stability of the system against noise was very have high, while applying dynamic delay in addition to state variable switching to guarantee the high-pitched security. Wu et al. [14] presented a novel modified generalized projective synchronisation and their applications to secure communication system. Yu et al. [15] studied a new hyperchaotic system of seven-dimension. This system also exhibits quasi-periodic, periodic, hyperchaotic, dynamic, and chaotic behaviors. The electronic circuit of the designed scheme was implemented using confidential communication. The efficiency of the approach was demonstrated via the obtained simulation outcomes. The secure communication system of parameter modulation was investigated by He et al. [16]. The authors obtained the desired results by the synchronization of hyperchaotic systems. A 6th-order cellular neural network (CNN) hyperchaotic system was investigated by Wang et al. [17]. The authors observe that the synchronization of the system is based on a multi-ary number and state observer and communication system. Vaidyanathan et al. [18] constructed of a temperature fluctuations hyperchaotic model, FPGA and electronic circuit execution, and their image encryption application. Peng et al [19] investigated a new hyperchaotic system based on microcontroller unit and its application in decryption and encryption of signal for square wave. Vafamand et al. [20] studied the non-ideal communication channels and present a new method for the hyperchaotic secure communication channels. The authors further investigated the linear matrix inequality (LMI) technique and Takagi–Sugeno (TS) fuzzy model for designing a controller capable of synchronizing the receiver systems and the hyperchaotic transmitter.

This paper presents a novel ten-terms continuous time hyperchaotic system. This system is capable of exhibiting a complex behavior using two positive Lyapunov exponents which make it very desirable to use in cryptography and secure transmission. Also, to prove the new system’s physical feasibility, an electronic circuit was implemented in the system. Lastly, the four signals produced by the defined scheme and the drive response synchronisation are extended to develop an encryption/decryption secure system. Results from the experiment illustrates the robustness of the anticipated scheme for completing the encryption/decryption process.

The main contribution of this paper is

•   The system consists of a total eleven terms and three quadratic nonlinearities.

•   The findings of the bifurcation diagram and Lyapunov spectrum reveal that the system has periodic behavior, quasi-periodic behavior, chaotic behavior and hyperchaotic behavior.

•   The proposed secure communication based on the hyperchaotic system was shown to be successful in completing the secure transmission/reception procedure.

The remaining part of the study is structured in the following way: Section 2 present the proposed hyperchaotic system. The dynamical analysis, bifurcation diagrams and Lyapunov exponents spectrum are investigated in Section 3 and Section 4 present the implementation of the equivalent electronic circuit via Multisim software. In Section 5, we extended the proposed scheme to develop a novel communication secured scheme and present a concluding remark about the study in Section 6.

2  New Hyperchaotic System

2.1 Algebraic Structure

The proposed hyperchaotic system has three positive parameters and three quadratic nonlinearities; it is described using the following algebraic structure:

{x˙1=a(x2−x1)+x2x3x˙2=(b−a)x1+bx2−x1x3+x4x˙3=x1x2−x3x˙4=−cx2(1)

where the positive parameters a, b and c represent the constant and the state variables are defined by x1,x2,x3andx4.

By choosing the parameter values as:

a=17,b=11andc=0.8(2)

and for the initial criteria:

(0.1,0.1,0.1,0.1),(3)

the proposed ten terms dynamical system generates a complex hyperchaotic behaviour. Phase portraits and hyperchaotic attractor of our new system are depicted in Fig. 1.

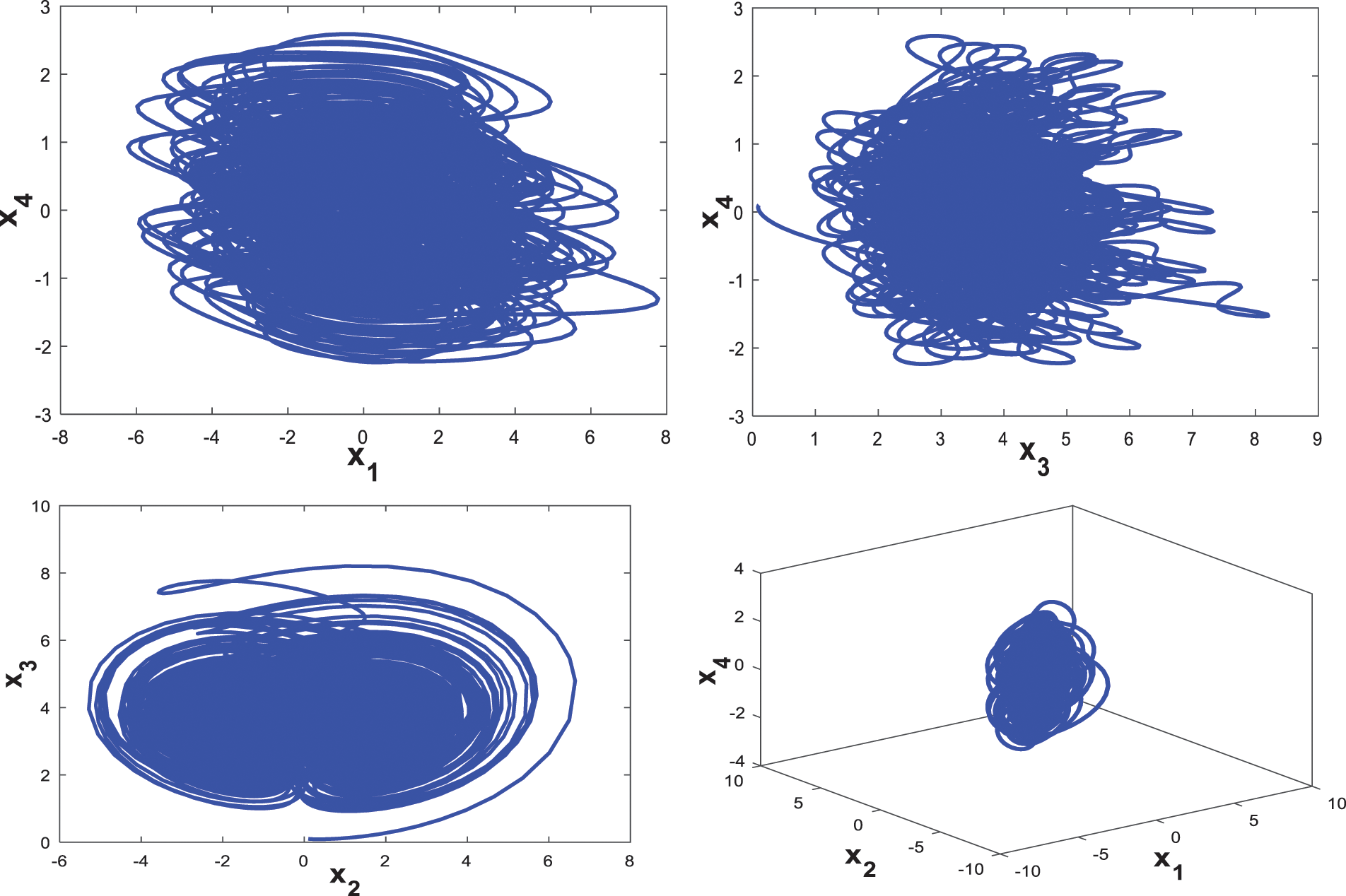
Figure 1: Phase portraits of the announced system (1)

2.2 Lyapunov Exponents and Kaplan-Yorke Dimension

For the previous parameter values, the Lyapunov exponents can be calculated via Wolf’s algorithm [21], the outcome of the experiment is depicted in Fig. 2 as:

L1=0.121,L2=0.057,L3=0.000,L4=−0.698(4)

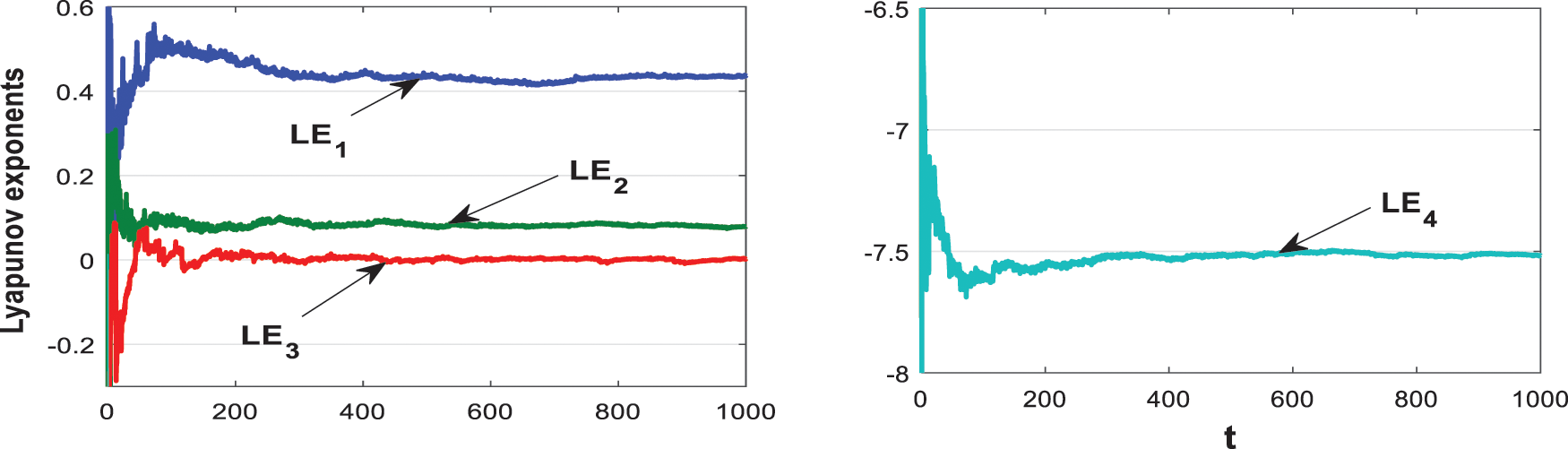
Figure 2: Lyapunov exponent of the proposed complex system (1)

From Fig. 2, it obvious there exist two Lyapunov positive exponents. Thus, the proposed scheme (1) is hyperchaotic. The calculations for the given hyperchaotic system (1) of Kaplan-Yorke dimension can be done as follows:

DKY=3+L1+L2+L3|L4|=3.255(5)

From Eq. (5), It is obvious the dimension of Kaplan-Yorke is fractional. Therefore, it can be concluded the proposed system shows a complex hyperchaotic behaviour.

3  Dynamical Analyses

3.1 Equilibrium Points Stability

To obtain the point of equilibrium for the proposed scheme (1), the given algebraic equations are considered:

{a(x2−x1)+x2x3=0(b−a)x1+bx2−x1x3+x4=0x1x2−x3=0−cx2=0(6)

It is obvious see that (4) has one point of equilibrium S0, that is:

S0=[0000](7)

Next is calculating the corresponding system (1) Jacobian matrix which is as follows

J(S0)=[−aa+x3x20(b−a)−x3b−x11x2x1−100−c00](8)

By linearizing the proposed system (1) at S0, its stability would be investigated by employing the characteristic equation:

|J(S0)−λI |=0(9)

Considering the equilibrium point S0 and parameters values as: a = 17, b = 11 and c = 0.8, characteristic equation is calculated as follows:

λ4+7λ3−79λ2−85λ=0(10)

Then, the roots of (10) are:

λ1=0,λ2=−12.69,λ3=6.69,λ4=−1.(11)

Here, λ2,4<0,λ1=0andλ3>0, thus, the point of equilibrium S0 is unstable, implying that the dissipative systems possess some chaos.

3.2 Dissipativity

To examine the divergence of dynamical system (1), we have:

∇V=∂x˙∂x+∂y˙∂y+∂z˙∂z+∂w˙∂w=−a+b−1=−7<0(12)

which is negative, and thus, produce a decrease in volume (V) at a degree:

dV(t)dt=−7V(13)

Therefore:

dV(t)=V(0)e(−7)t(14)

which affirm the dissipativity of the announced system (1).

3.3 Bifurcation Analysis and Lyapunov Spectrum

The two most important ways of analyzing the main dynamic properties of dynamical systems are the bifurcation diagram and Lyapunov exponents spectrum (LES). As we know, a 4D autonomous system exhibits:

•   Periodic behavior if: LE1=0,LE2,3,4<0

•   Quasi-Periodic behavior if: LE1,2=0,LE3,4<0

•   Chaotic behavior if: LE1>0,LE2=0,LE3,4<0

•   Hyperchaotic behavior if: LE1,2>0,LE3=0,LE4<0

3.3.1 Fix b = 11, c = 0.8 and vary a

The diagram of the bifurcation is depicted by Fig. 3, while Fig. 4 show the Lyapunov exponents spectrum of our proposed ten terms model (1) with respect to parameter a. The two figures show clearly that the diagram of the bifurcation and the Lyapunov spectrum are fully harmonious.

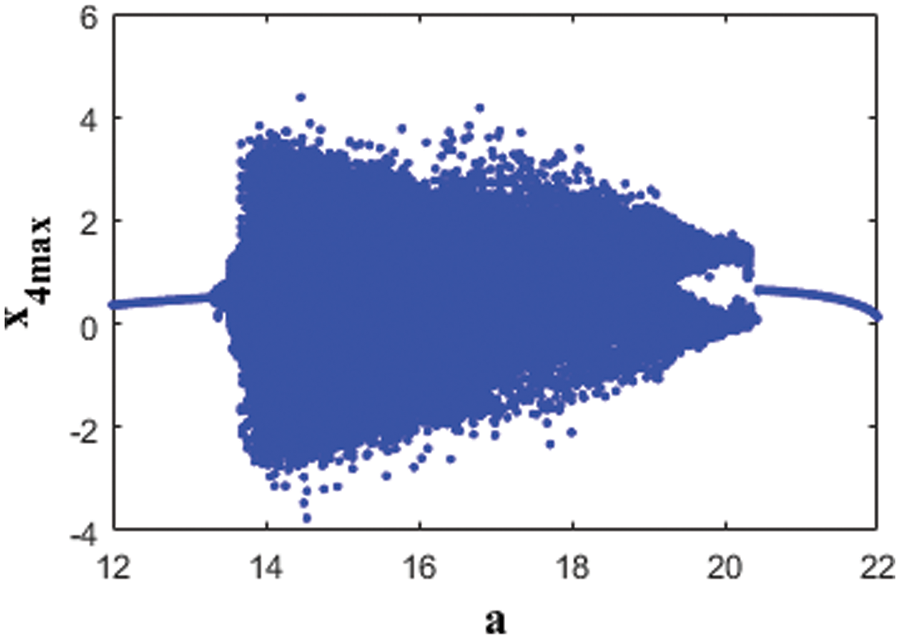
Figure 3: Bifurcation diagram of the announced system (1) fourth state vs. parameter a

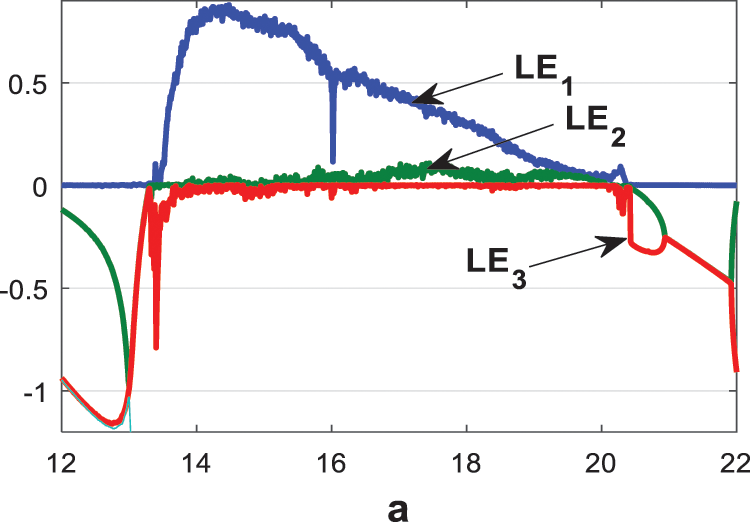
Figure 4: Lyapunov exponents of the announced system (1) vs. parameter a

From Figs. 3 and 4, it is obvious that (1) is capable of generating hyperchaotic, chaotic, and periodic behaviours, while parameter a varies between 12 and 22 as it is clarified in Tab. 1.

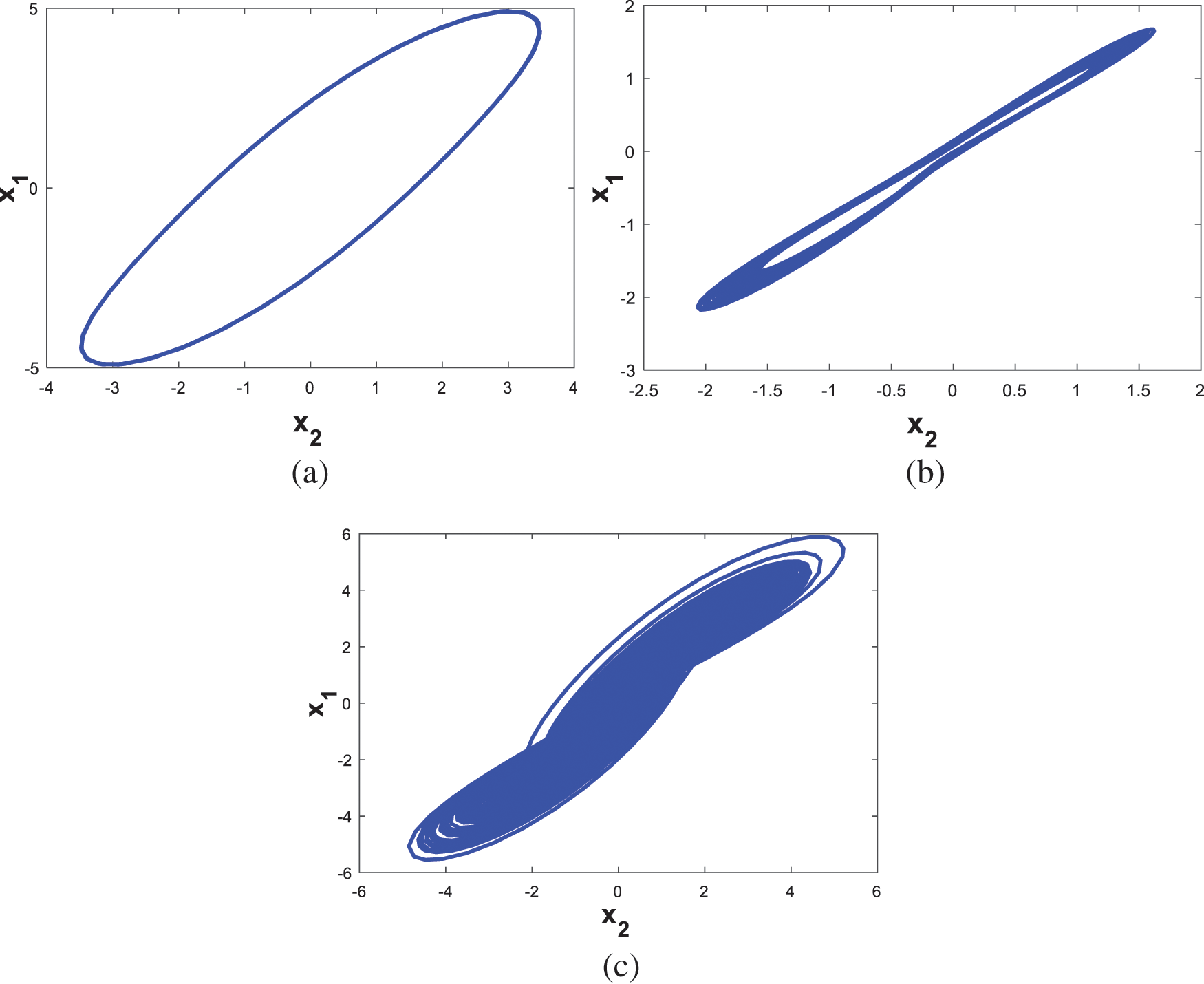
Figure 5: Dynamics of system (1) vs. parameter a

3.3.2 Fix a = 17, b = 11 and vary c

Fig. 6 depict the bifurcation diagram while Fig. 7 represent the Lyapunov exponents spectrum of (1) with respect to parameter c. Also, the dynamics of system (1) vs. parameter c can be seen in Fig. 8.

Figure 6: Bifurcation diagram of the announced system (1) fourth state vs. parameter c

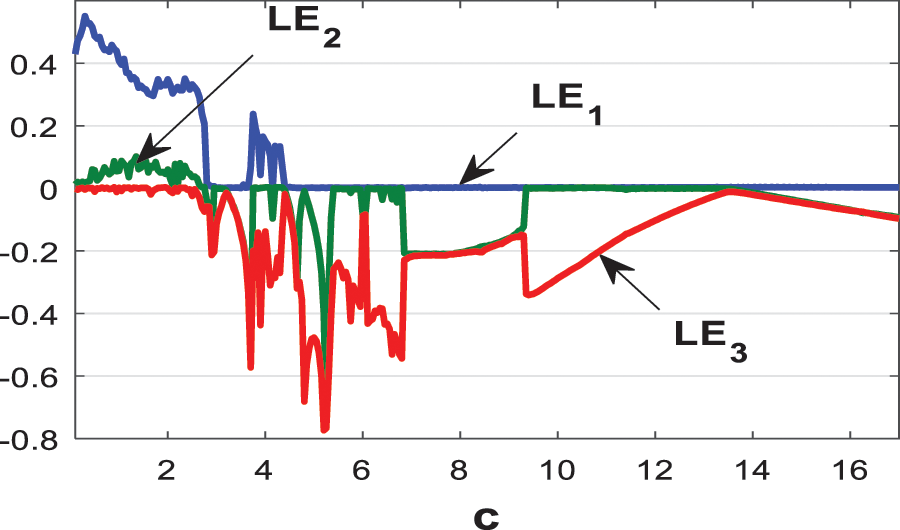
Figure 7: Lyapunov exponents of the announced system (1) vs. parameter c

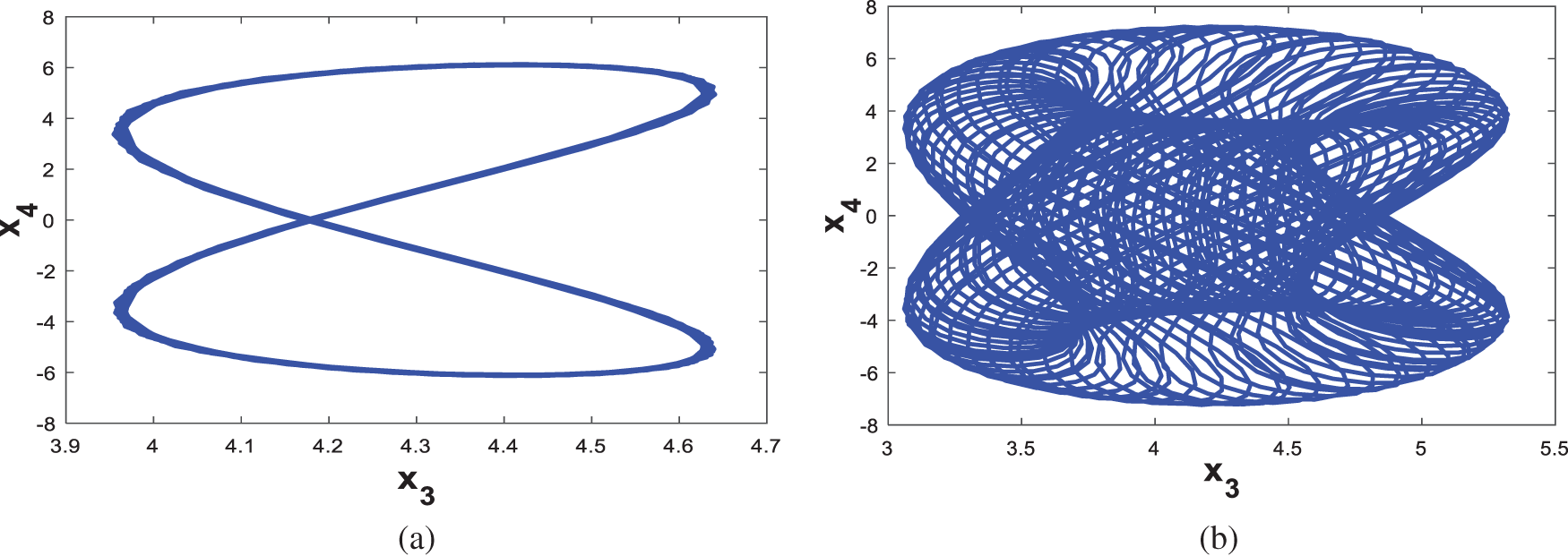
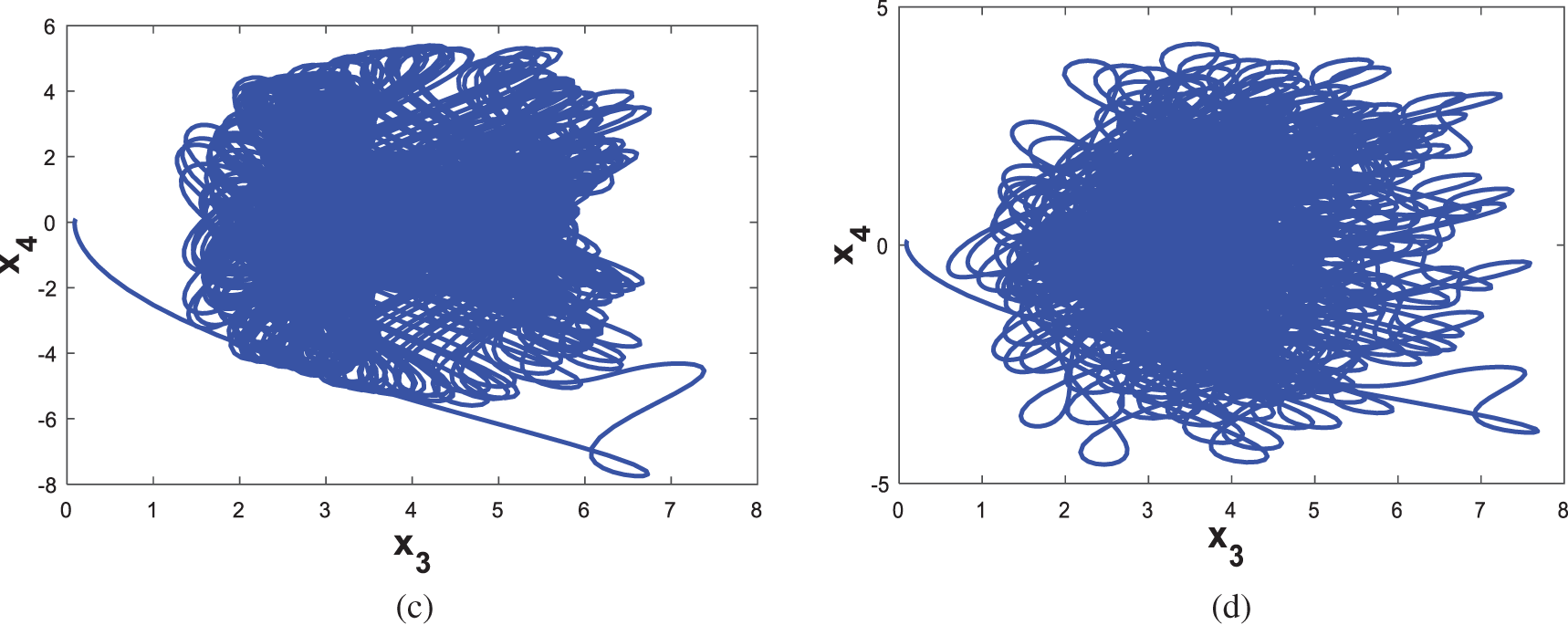
Figure 8: Dynamics of system (1) vs. parameter c

The two figures show that the bifurcation diagram and the Lyapunov spectrum are fully consistent. Figs. 6 and 7 show that our system (1) is capable of exhibiting hyperchaotic, chaotic, quasi-periodic, and periodic behaviours, while the parameter c varies between 0.1 and 17 as it is clarified in Tab. 2.

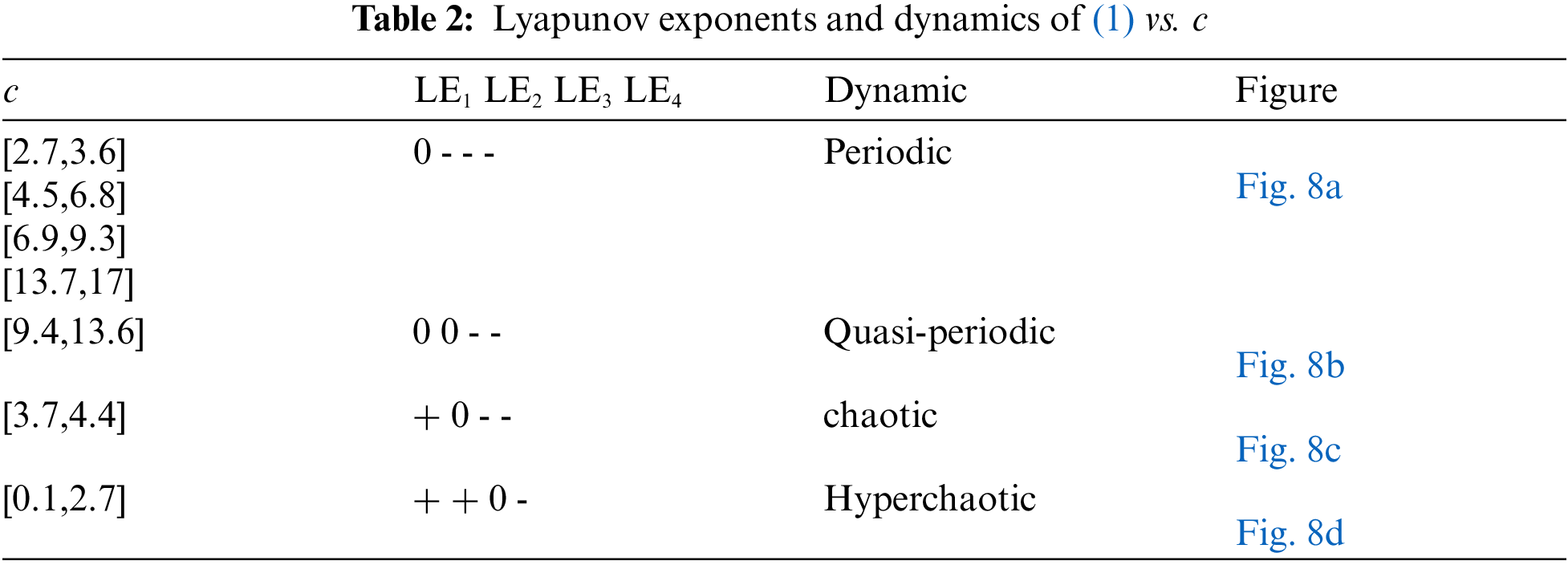
4  Circuit Design of the New System

An electronic circuit is designed in this section. The authors employ Multisim program as depicted in Fig. 9 to illustrate the physical feasibility of our announced Hyperchaotic complex system (1). Based on the dynamical equations of the proposed hyperchaotic scheme (1) and by using Kirchhoff’s theorem to the route in Fig. 9, the equation of the circuit equations for system (1) are defined as:

{x˙1=1R1C1x2−1R2C1x1+1R3C1x2x3x˙2=1R4C2x1+1R5C2x2−1R6C2x1x3+1R7C2x4x˙3=1R8C3x1x2−1R9C3x3x˙4=−1R10C4x2(15)

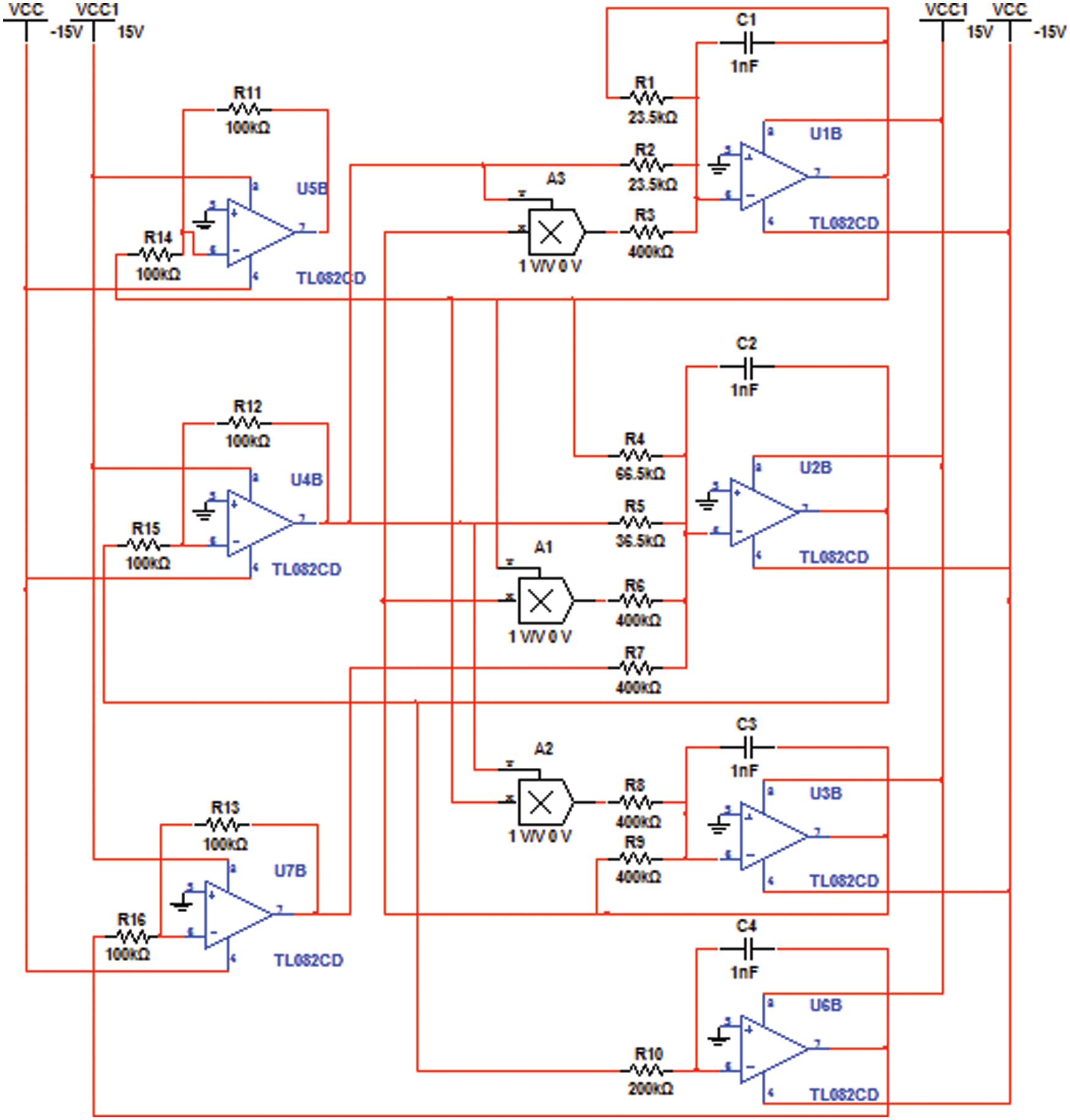
Figure 9: The schematic of the circuit

Now, we choose the values of the components for the electronic circuit using the following process:

{R1,2=23.5kΩ,R3,6,7,8,9=400kΩ,R4=66.5kΩR5=36.5kΩ,R11,12,13,14,15,16=100kΩ,C1,2,3,4=1nFR10=200kΩ(Hyperchaotic)R10=100kΩ(Chaotic)R10=33.5kΩ(Quasi−periodic)R10=26.5kΩ(Periodic)(16)

The chaotic attractor, hyperchaotic attractor, periodic orbit, and the quasi-periodic orbit are shown in Fig. 10. It is obvious the outcomes from the Matlab simulation correspond with the Multisim outcomes. This proved the physical feasibility of proposed ten terms continuous time hyperchaotic system (1).

Figure 10: Multisim result of: (a) The periodic orbit (b) The quasi-periodic orbit (c) The chaotic attractor (d) The hyperchaotic attractor

5  Secure Transmission Schemes for the New Complex Hyperchaotic System

This part presents a new secure transmission scheme. This system follows from the new (1) and use a drive response synchronisation, which possess a strong self-synchronization advantage over other systems. Also, the scheme achieve synchronization by employing only one coordinate [22–25]. Fig. 11 shows a Matlab/Simulink block diagram of the proposed secure transmission/reception technique.

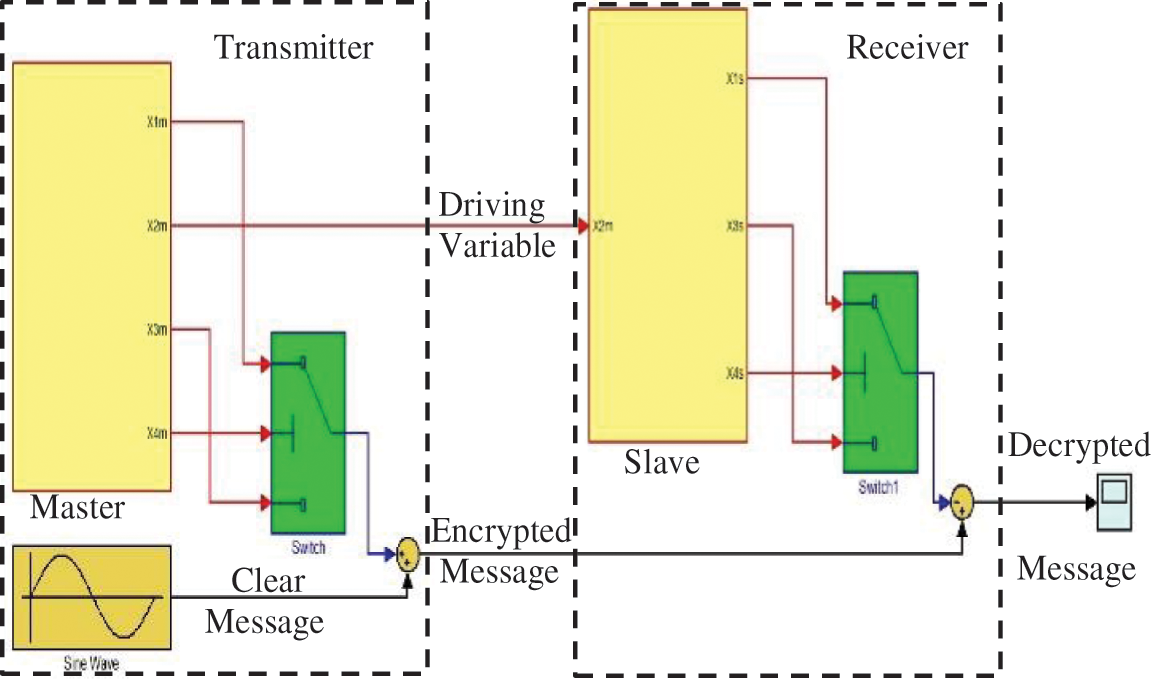
Figure 11: The secure communication scheme Matlab/Simulink bloc diagram

5.1 Drive-response Synchronization

Considering the proposed hyperchaotic system (1) as master system:

{x˙1m=a(x2m−x1m)+x2mx3mx˙2m=(b−a)x1m+bx2m−x1mx3m+x4mx˙3m=x1mx2m−x3mx˙4m=−cx2m(17)

By considering the second state variable of the master system x2m as constraining variable so as to achieve synchronization from the slave system (18) with master system (17), as describe from the following the slave system:

{x˙1s=a(x2m−x1s)+x2mx3sx˙3s=x1sx2m−x3sx˙4s=−cx2m(18)

The errors from the synchronisation between slave systems and the master states are shown in Figs. 12–14. It is obvious that after four seconds, the errors from all the synchronisation converges to zero. These results affirm the efficiency of process of the synchronisation to synchronize the two slave and master hyperchaotic system beginning from varying starting values.

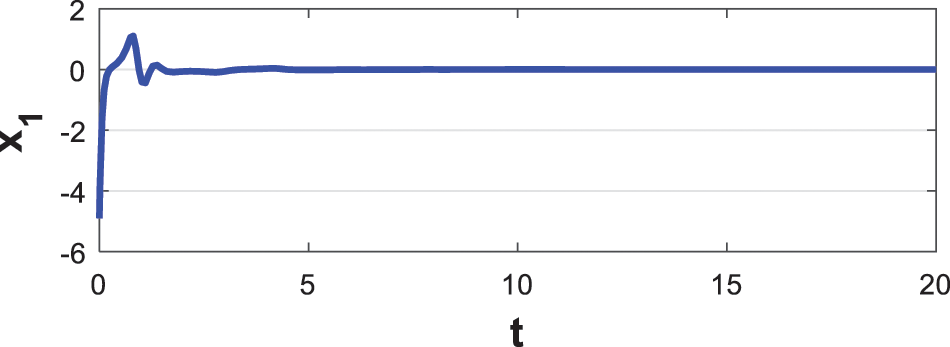
Figure 12: The first state synchronization error

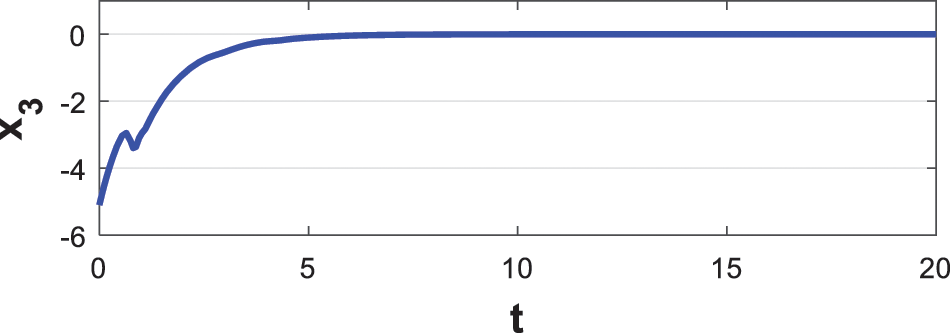
Figure 13: The third state synchronization error

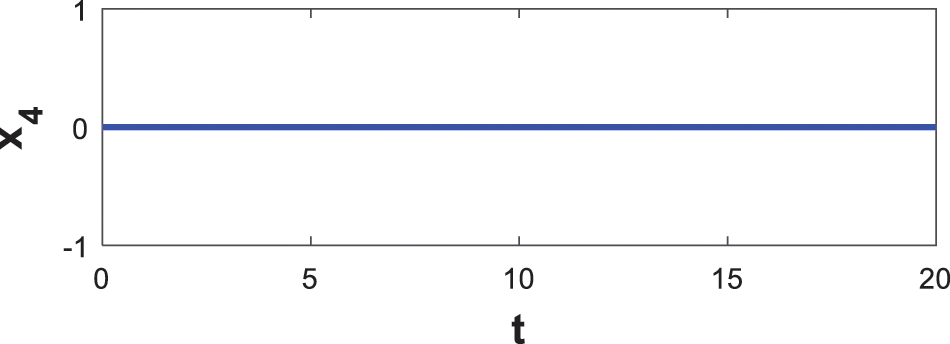
Figure 14: The fourth state synchronization error

5.2 Encryption/Decryption Process

In this subsection, we design a new encryption/decryption approach for the proposed hyperchaotic system based on the drive response synchronization [26–32], as shown in Fig. 11.

By substituting among two different encryption modes, we obtain the encrypted message EM to be transmitted which is based on fourth state master system value x4m as the follows:

If x4m≤0: then, the equation given below would be used to obtain the encrypted:

{EM=F(m,x1)EM=p1m+p2x1(19)

with p1andp2 representing the constant parameters chosen as secret key so as to improve the confidentiality and complexity of process of encryption process and m denoting the clear message to be encrypted.

If x4m>0: then, the equation below will be used to obtain the encrypted message:

{EM=Q(m,x3)EM=k1m+k2x3(20)

where k1andk3 are constant parameters.

After attaining synchronisation in the receiver, amongst the slave system and master system, then, switching between two decrypted modes, we obtain the decrypted message DM. This is based on fourth state slave system values x4s as describe in the algorithm that follows:

If x4s≤0:then, the following equation would be used in obtaining the decrypted message:

{DM=F′(m,x1s)DM=1p1(EM−p2x1s)(21)

where p1andp2 represent the constant parameters similar to those in the transmitter and the encrypted message to be decrypted is denoted as EM.

If x4s>0: we use the following equation to obtain the decrypted message:

{DM=Q′(EM,x3s)DM=1k1(EM−k2x3s)(22)

where k1andk2 represent similar constant parameters as in the transmitter.

•   Simulation Results:

Fig. 15 shows the time evolution of given master system fourth state x4m, which is considered as the switching variable. It can be seen that x4m evolves chaotically around zero, which generates a random switch between the two encryption modes. The clear message to be transmitted is the sine wave as shown in Fig. 16. Fig. 17 depict the complex chaotic behaviour of the EM, confirming the robustness of our proposed encryption scheme for hiding the clear message. Fig. 18 depict the decrypted message, it is obvious that after four second (after attaining synchronisation amongst slave and master systems) the original message corresponds to the obtain message, which confirms the decryption process success to reconstruct the clear message. All simulation outcomes have verified the efficiency of the new Hyperchaotic system for completing the process of decryption/ encryption of the proposed secure communication method.

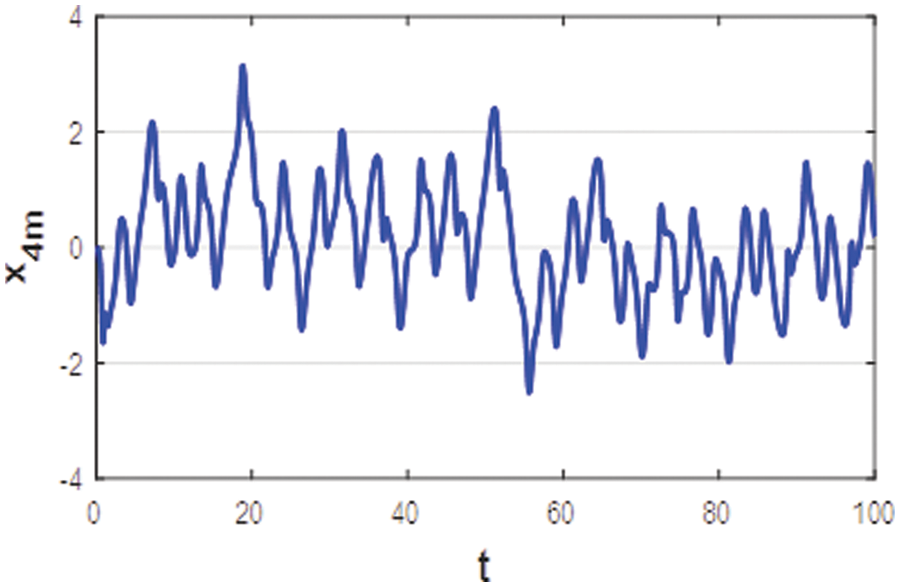
Figure 15: x4m time evolution

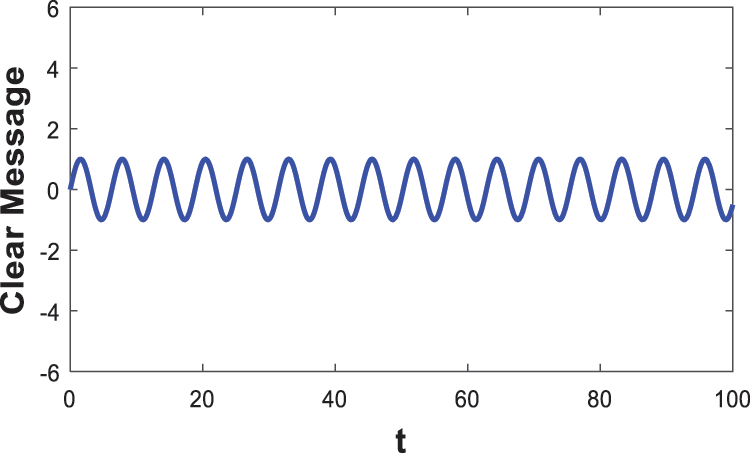
Figure 16: Clear message

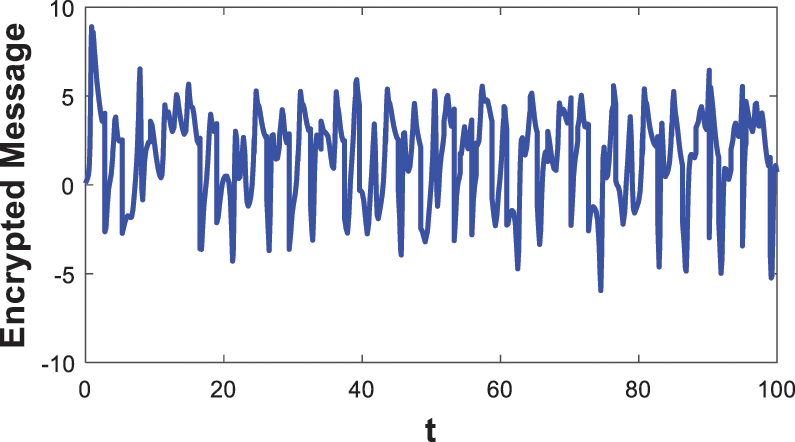
Figure 17: Encrypted message

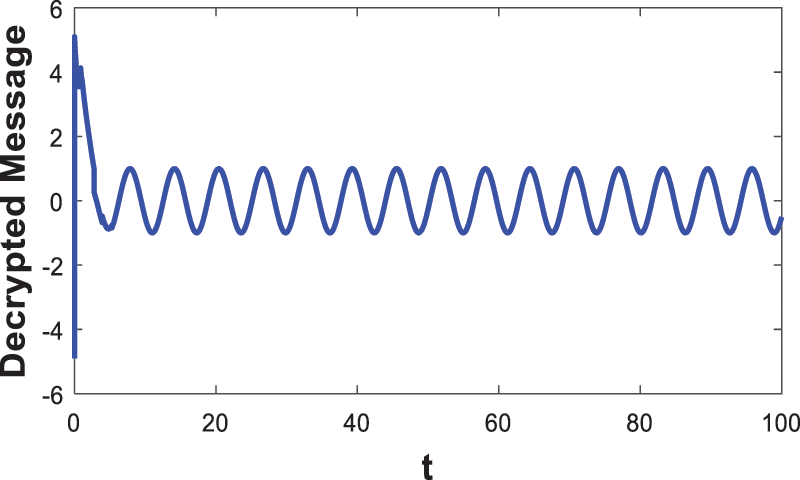
Figure 18: Decrypted message

6  Conclusions

This study proposed a new ten terms continuous time hyperchaotic system. Using two positive Lyapunov exponents, the proposed scheme can exhibit complex hyperchaotic behaviour. Also, using different parameters value, the proposed system is capable of generating chaotic, quasi-periodic and periodic behaviours. Dynamical analysis of the proposed complex system including the points of equilibrium stability, dimension of Kaplan-Yorke, bifurcation and Lyapunov spectrum are studied. Additionally, the Multisim software was employed to implement an electronic circuit schematic, the obtained outcomes are similar to the results from MATLAB and thus, confirming the new system physical feasibility. A new secure communication technique was further tested based on changing between two encryption/decryption modes, to ascertain robustness of our new system when completing the process of encryption/decryption of a clear message. Finally, we believe our proposed hyperchaotic system having a very rich and complex dynamics and its secure communication scheme are desirable to use in real applications in the near future.

Acknowledgement: The authors are grateful to all reviewers for their comments and suggestions.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  K. Benkouider, M. Halimi and T. Bouden, “Secure communication scheme using chaotic time-varying delayed system,” International Journal of Computer Applications in Technology, vol. 60, no. 2, pp. 175–182, 2019. [Google Scholar]

 2.  L. Zhou and F. Tan, “A chaotic secure communication scheme based on synchronization of double-layered and multiple complex networks,” Nonlinear Dynamics, vol. 96, no. 2, pp. 869–883, 2019. [Google Scholar]

 3.  J. Wang, W. Yu, J. Wang, Y. Zhao, J. Zhang et al., “A new six-dimensional hyperchaotic system and its secure communication circuit implementation,” International Journal of Circuit Theory and Application, vol. 47, no. 5, pp. 702–717, 2019. [Google Scholar]

 4.  E. N. Lorenz, “Deterministic nonperiodic flow,” Journal of the Atmospheric Sciences, vol. 20, no. 2, pp. 130–141, 1963. [Google Scholar]

 5.  C. H. Lien, S. Vaidyanathan, A. Sambas, F. Sukono, M. Mamat et al., “A new two-scroll chaotic attractor with three quadratic nonlinearities, its adaptive control and circuit design,” in proc. IOP Conference Series: Materials Science and Engineering, Tangerang, Indonesia, vol. 332, pp. 012010, 2018. [Google Scholar]

 6.  F. Zhang, R. Chen, X. Wang, X. Chen, C. Mu et al., “Dynamics of a new 5D hyperchaotic system of Lorenz type,” International Journal of Bifurcation and Chaos, vol. 28, no. 3, pp. 1850036, 2018. [Google Scholar]

 7.  A. Sambas, S. Vaidyanathan, M. Mamat, M. Sanjaya, S. H. Yuningsih et al., “Analysis, control and circuit Design of a novel chaotic system with line equilibrium,” Journal of Physics Conference. Series, vol. 1090, pp. 1–13, 2018. [Google Scholar]

 8.  O. E. Rossler, “An equation for hyperchaos,” Physics Letters A, vol. 71, no. 2–3, pp. 155–157, 1979. [Google Scholar]

 9.  K. Benkouider, T. Bouden and M. Halimi, “Dynamical analysis, synchronization and circuit implementation of a new hyperchaotic system with line equilibrium,” in in proc. CoDIT, Thessaloniki, Greece, pp. 1717–1722, 2019. [Google Scholar]

10. A. E. Matouk, “Dynamics and control in a novel hyperchaotic system,” International Journal of Dynamics and Control, vol. 7, no. 1, pp. 241–255, 2019. [Google Scholar]

11. S. Vaidyanathan, A. Sambas, M. Mamat and W. S. Mada Sanjaya, “A new 4-D hyperchaotic hyperjerk system with a single equilibrium, its dynamic properties and circuit design,” in in proc. ICoGOIA, Bali, Indonesia, pp. 1–15, 2019. [Google Scholar]

12. K. Benkouider, T. Bouden, A. Sambas, M. A. Mohamed, I. M. Sulaiman et al., “Dynamics, control and secure transmission electronic circuit implementation of a new 3D chaotic system in comparison with 50 reported systems,” IEEE Access, vol. 9, pp. 152150–152168, 2021. [Google Scholar]

13. H. Liu, X. Wang and Q. Zhu, “Asynchronous anti-noise hyper chaotic secure communication system based on dynamic delay and state variables switching,” Physics Letters A, vol. 375, no. 30–31, pp. 2828–2835, 2011. [Google Scholar]

14. X. Wu, H. Wang and H. Lu, “Modified generalized projective synchronization of a new fractional-order hyperchaotic system and its application to secure communication,” Nonlinear Analysis: Real World Applications, vol. 13, no. 3, pp. 1441–1450, 2012. [Google Scholar]

15. W. Yu, J. Wang, J. Wang, H. Zhu, M. Li et al., “Design of a new seven-dimensional hyperchaotic circuit and its application in secure communication,” IEEE Access, vol. 7, pp. 125586–125608, 2019. [Google Scholar]

16. J. He, J. Cai and J. Lin, “Synchronization of hyperchaotic systems with multiple unknown parameters and its application in secure communication,” Optik, vol. 127, no. 5, pp. 2502–2508, 2016. [Google Scholar]

17. X. Wang, B. Xu and H. Zhang, “A multi-ary number communication system based on hyperchaotic system of 6th-order cellular neural network,” Communications in Nonlinear Science and Numerical Simulation, vol. 15, no. 1, pp. 124–133, 2010. [Google Scholar]

18. S. Vaidyanathan, A. T. Azar, K. Rajagopal, A. Sambas, S. Kacar et al., “A new hyperchaotic temperature fluctuations model, its circuit simulation, FPGA implementation and an application to image encryption,” International Journal of Simulation and Process Modelling, vol. 13, no. 3, pp. 281–296, 2018. [Google Scholar]

19. Z. Peng, W. Yu, J. Wang, Z. Zhou, J. Chen et al., “Secure communication based on microcontroller unit with a novel five-dimensional hyperchaotic system,” Arabian Journal for Science and Engineering, vol. 47, no. 1, pp. 813–828, 2022. [Google Scholar]

20. N. Vafamand, S. Khorshidi and A. Khayatian, “Secure communication for non-ideal channel via robust TS fuzzy observer-based hyperchaotic synchronization,” Chaos, Solitons & Fractals, vol. 112, no. April (2), pp. 116–124, 2018. [Google Scholar]

21. A. Wolf, J. B. Swift, H. L. Swinney and J. A. Vastano, “Determining Lyapunov exponents from a time series,” Physica D: Nonlinear Phenomena, vol. 16, no. 3, pp. 285–317, 1985. [Google Scholar]

22. A. Sambas, S. Vaidyanathan, E. Tlelo-Cuautle, B. Abd-El-Atty, A. A. Abd El-Latif et al., “A 3-D multi-stable system with a peanut-shaped equilibrium curve: Circuit design, FPGA realization, and an application to image encryption,” IEEE Access, vol. 8, pp. 137116–137132, 2020. [Google Scholar]

23. K. Benkouider, T. Bouden, A. Sambas, L. Badis, M. A. Mohamed et al., “A new 10-D hyperchaotic system with coexisting attractors and high fractal dimension: its dynamical analysis, synchronization and circuit design,” PLOS One, vol. 1, pp. 1–31, 2022. [Google Scholar]

24. S. Vaidyanathan, A. Sambas, E. Tlelo-Cuautle, A. A. Abd El-Latif, B. Abd-El-Atty et al., “A new 4-D multi-stable hyperchaotic system with no balance point: bifurcation analysis, circuit simulation, FPGA realization and image cryptosystem,” IEEE Access, vol. 9, pp. 144555–144573, 2021. [Google Scholar]

25. S. Vaidyanathan, A. Sambas, B. Abd-El-Atty, A. A. Abd El-Latif, E. Tlelo-Cuautle et al., “A 5-D multi-stable hyperchaotic two-disk dynamo system with no equilibrium point: Circuit design, FPGA realization and applications to TRNGs and image encryption,” IEEE Access, vol. 9, pp. 81352–81369, 2021. [Google Scholar]

26. Z. Li and D. Xu, “A secure communication scheme using projective chaos synchronization,” Chaos, Solitons & Fractals, vol. 22, no. 2, pp. 477–481, 2004. [Google Scholar]

27. X. Wu, C. Zhu and H. Kan, “An improved secure communication scheme based passive synchronization of hyperchaotic complex nonlinear system,” Applied Mathematics and Computation, vol. 252, pp. 201–214, 2015. [Google Scholar]

28. T. Yang and L. O. Chua, “Impulsive control and synchronization of nonlinear dynamical systems and application to secure communication,” International Journal of Bifurcation and Chaos, vol. 7, no. 3, pp. 645–664, 1997. [Google Scholar]

29. X. Wu, Z. Fu and J. Kurths, “A secure communication scheme based generalized function projective synchronization of a new 5D hyperchaotic system,” Physica Scripta, vol. 90, no. 4, pp. 045210, 2015. [Google Scholar]

30. B. Naderi and H. Kheiri, “Exponential synchronization of chaotic system and application in secure communication,” Optik, vol. 127, no. 5, pp. 2407–2412, 2016. [Google Scholar]

31. Y. Liu, G. Ge, H. Zhao, Y. Wang and L. Gao, “Synchronization of hyperchaotic harmonics in time-delay systems and its application to secure communication,” Physical Review E, vol. 62, no. 6, pp. 78–98, 2000. [Google Scholar]

32. P. Trikha and L. S. Jahanzaib, “Secure communication: Using double compound-combination hybrid synchronization,” in In proc. ICAIA, Singapore, Springer, pp. 81–91, 2021. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.