Computers, Materials & Continua DOI:10.32604/cmc.2022.025823
Article

Gaussian Process for a Single-channel EEG Decoder with Inconspicuous Stimuli and Eyeblinks

Nur Syazreen Ahmad*, Jia Hui Teo and Patrick Goh

School of Electrical & Electronic Engineering, Universiti Sains Malaysia, Nibong Tebal, Penang, 14300, Malaysia
*Corresponding Author: Nur Syazreen Ahmad. Email: syazreen@usm.my
Received: 06 December 2021; Accepted: 14 February 2022

Abstract: A single-channel electroencephalography (EEG) device, despite being widely accepted due to convenience, ease of deployment and suitability for use in complex environments, typically poses a great challenge for reactive brain-computer interface (BCI) applications particularly when a continuous command from users is desired to run a motorized actuator with different speed profiles. In this study, a combination of an inconspicuous visual stimulus and voluntary eyeblinks along with a machine learning-based decoder is considered as a new reactive BCI paradigm to increase the degree of freedom and minimize mismatches between the intended dynamic command and transmitted control signal. The proposed decoder is constructed based on Gaussian Process model (GPM) which is a nonparametric Bayesian approach that has the advantages of being able to operate on small datasets and providing measurements of uncertainty on predictions. To evaluate the effectiveness of the proposed method, the GPM is compared against other competitive techniques which include k-Nearest Neighbors, linear discriminant analysis, support vector machine, ensemble learning and neural network. Results demonstrate that a significant improvement can be achieved via the GPM approach with average accuracy reaching over 96% and mean absolute error of no greater than 0.8 cm/s. In addition, the analysis reveals that while the performances of other existing methods deteriorate with a certain type of stimulus due to signal drifts resulting from the voluntary eyeblinks, the proposed GPM exhibits consistent performance across all stimuli considered, thereby manifesting its generalization capability and making it a more suitable option for dynamic commands with a single-channel EEG-controlled actuator.

Keywords: Brain-computer interface; dynamic command; electroence phalography; gaussian process model; visual stimulus; voluntary eyeblinks

1  Introduction

Electroencephalography (EEG) test is the standard approach for measuring oscillations caused by brain activity in most brain-computer interface (BCI) technologies. The measurement was traditionally recorded using multiple wet electrodes (usually more than 32) attached to the scalp with high sensitivity electronics in an attempt to boost the signal-to-noise ratio [1]. Participants involved in the data collection using such a device are typically constrained to laboratory settings and require extensive training in order to produce clean and reliable EEG data [2]. Nonetheless, the past decade has seen the rapid development of wearable EEG-based BCIs such as Neurosky MindWave, Emotive EPOC (+) and Mindo series which offer competitive performance with dry sensor technology and a smaller number of electrodes that overcomes many of the aforesaid barriers. Apart from ease of deployment and suitability for use in complex environments, they are also available at considerably lower prices compared to the laboratory-restricted EEG devices, thus accelerating their adoption by the general public [3–6].

EEG signals measured on the scalp from the BCI device will generate the so-called Event-Related Potentials (ERPs) which refer to the small potential or voltage changes in the signals immediately after the user's attention is invoked by a stimulus. Human inhibitory control using ERP is relatively easier to carry out as it only requires the user's attention in a short duration for transmission of a command to an external device. Examples include switching on/off the lights and stopping an ongoing motor action [7]. However, in reactive BCI applications which require users to consciously generate brain signals for continuous command transmission to an external device such as motorized actuators, the approach via visual evoked potentials (VEPs) which are natural responses when the user's brain is invoked only by a visual stimulus tends to be relatively more prevalent [8].

To improve the quality of EEG data recording and decoding in the aforementioned BCI paradigms, most wearable BCI devices have been equipped with machine learning (ML) algorithms that allow them to safely extract relevant features from the EEG signals and classify them into several states of mind such as relaxation and attention [9]. Linear discriminant analysis (LDA) for instance has been preferred in many EEG classifications due to reduced computational cost which can minimize the transmission delay between the brain and the target system [10]. However, for complex nonlinear EEG data, support vector machine (SVM) can provide more desirable results as it uses a kernel-based transformation to project data into a higher dimensional space where the relationships between variables become linear [11]. The k-Nearest Neighbors (kNN) which is a machine learning (ML) algorithm that identifies a testing sample's class according to the majority class of k-nearest training samples has demonstrated comparable performance in a recent study on EEG-based cognitive tasks [12]. Another popular EEG classification is ensemble learning (EL) which generates multiple ML models and then combines them to attain improved performance [13,14]. A more robust EEG classification can be obtained using a deep convolutional neural network (CNN) using a large number of electrodes with temporal and spatial filters to eliminate redundant information. For BCI applications with a single-channel EEG device, the sequential CNN approach is available but is often employed for passive BCI applications without the purpose of voluntary control such as cognitive monitoring and sleep stage scoring [15,16]. Thus, for reactive BCI applications, applying the CNN methods can be computationally taxing.

To treat issues on ocular artifacts, independent component analysis (ICA) is often employed which utilizes the blind source separation method to detect and reject the contaminated EEG signals [17]. Nonetheless, similar to the many CNN approaches, ICA usually requires EEG data recorded from many channels owing to its intrinsic characteristics, which makes it extremely challenging to eliminate independent components accurately including artifacts when only a few EEG channels are available [18]. Alternatives to the ICA include multiscale principal component analysis [19], signal decomposition methods [20,21], and general filtering methods such as wavelet transform, adaptive and Wiener filters but most of them are frequently adopted for offline analysis due to high computational cost. To minimize delays in real-time BCI application with an external actuator, infinite-impulse response, Kalman and Boxcar filters have been proposed as they can offer better solutions with less demanding computational requirements [22].

Despite promising results in classifying and denoising EEG signals, most of the proposed techniques are either only suitable for passive BCI applications or only applicable to multi-channel EEG devices for optimal performance. A single-channel wearable EEG device, despite being widely accepted due to low cost, convenience, and ease of applications especially in controlling robotic devices in unconstrained environments [9,23], the accuracy and reliability of the transmitted signals are still inconclusive and remain under debate as reported in several recent studies [24,25]. Plus, the use of such a device will pose a great challenge particularly when both eyeblink detection and clean continuous EEG signals are required to control an external actuator in reactive BCI applications [26].

In this work, the focus is on improving the BCI decoding strategy with a single-channel wearable EEG device for reactive BCI applications where a continuous command from the user is transmitted to actuate and drive a motorized actuator. To increase the degree of freedom of the BCI system, voluntary eyeblinks with prespecified durations are leveraged to change the state of the recorded EEG data, thus generating dynamic commands that can modify the speed of the motor while running. The proposed decoding strategy is constructed based on Gaussian Process model (GPM) approach which to-date remains underexplored for such a BCI paradigm. Unlike other ML approaches, a notable advantage of the GPMs lies on their ability to operate on small datasets and provide measurements of uncertainty on predictions. The effectiveness of the proposed approach is demonstrated via a comparative study against other competitive classifiers which have been previously evaluated with a single-channel EEG device in recent works such as multilayer perceptron NN [22], EL [27], LDA [28], kNN, and SVM [29]. In the light of [22] which proposes an alternative to motor imagery BCI that typically entails flickering stimuli and extensive training [30], inconspicuous stationary visual stimuli are introduced in the BCI paradigm to elevate the user's attentiveness while controlling the actuator. The use of such a paradigm is also in line with a recent review in [31] that highlights the significance of selecting suitable stimuli to induce the user's attention. Results demonstrate that a significant improvement can be achieved via the GPM approach with average accuracy reaching over 96% and mean absolute error of no greater than 0.8 cm/s. In addition, the analysis reveals that while the performances of other existing methods deteriorate with a certain type of stimulus due to signal drifts resulting from the voluntary eyeblinks, the proposed GPM exhibits consistent performance across all stimuli considered, thereby manifesting its generalization capability and making it a more suitable option for such applications. The findings of this study will not only increase the degree-of-freedom (DoF) of a single-channel EEG-controlled actuator, but will also redound to the benefit of new BCI users or BCI illiterates who are unable to sufficiently modulate their neuronal signals when controlling an external device.

2  Methodology

2.1 Data Acquisition

NeuroSky® MindWave Mobile 2 Headset has been chosen in this study as it has gained widespread acceptance due to its capability of providing a steady EEG recording over a long length of time. The device consists of a single dry EEG channel placed on Fp1 as depicted in Fig. 1 according to the 10–20 system, which is a worldwide known system that establishes the relationship between the underlying region of the cerebral cortex and the location of the electrodes. Another dry electrode is placed at the A1 position using an ear clip to act as the ground reference.

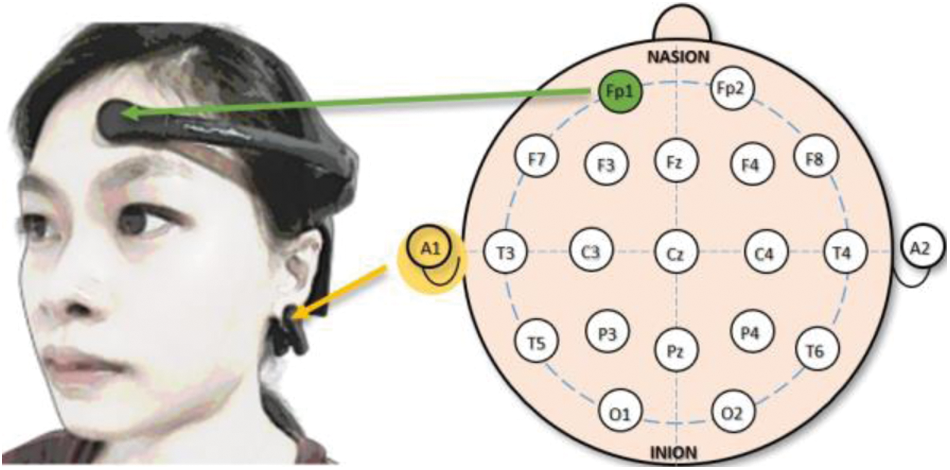
Figure 1: The EEG channel's position with respect to the user's head is placed at Fp1. Another dry electrode in the form of an ear clip is placed at A1 to serve as the ground reference

Another significant characteristic of this device is its portability and lightweight, which allows the user to move around freely without restriction. The MindWave Mobile 2 is equipped with an eSense attention meter, which produces values on a scale of 1 to 100. If the reading falls below 40, the subject is predicted to be in a neutral state. The range (140, 60] implies slightly elevated attention while the range above 60 implies a normal to high attentiveness level.

2.2 Visual Stimuli and Dynamic Command to Actuator

Inspired by the work in [22] which adopts a brain training game-based stimuli to keep the attentiveness high when transmitting signals via a BCI device, this work extends the capability of such a paradigm by introducing voluntary eyeblinks to allow for multiple command changes to the actuator. The proposed paradigm is depicted in Fig. 2 where the subject needs to transmit a continuous dynamic speed command to the actuator (right subplot) while his/her attention is being elevated by the stimulus (left subplot). In the light of [22], two stimuli are employed as shown in Fig. 3 where the first one involves multiple hidden targets which requires the subject to spot differences between two adjacent figures; while the second one involves one hidden target that needs to be localized in a cluttered scene. For performance evaluation purposes, the speed command was designed with a mixture of a step function to indicate a constant velocity and an increasing ramp function to represent acceleration with prespecified durations as follows:

νd(t)={20ift1<t≤t320t/(t5−t3)ift3<t≤t50otherwise(1)

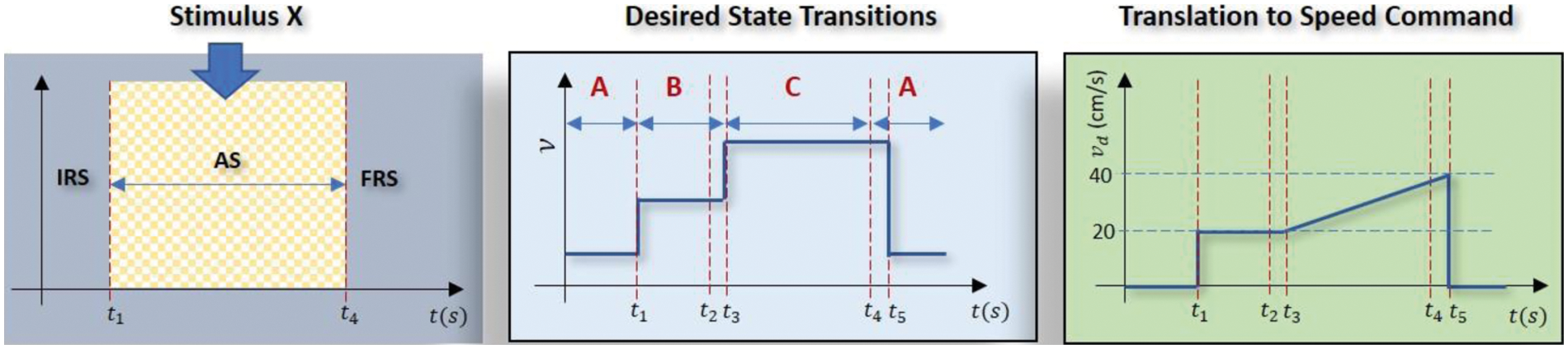
Figure 2: The visual stimulus (left) is used to enhance the subject's capability in controlling the EEG signal to follow the targeted speed command (right) which is a mixture of ramp and step functions. IRS, AS and FRS refer to initial, attentive and final resting stages respectively. The middle subfigure depicts the timeline of the desired state transitions along with voluntary eyeblinks at t=t2 (for b1) and t=t4 (for b2)

Figure 3: Two types of visual stimuli employed in this study [22]; Stimulus 1 (left) involves multiple hidden targets, i.e., the subject needs to spot the differences between the two figures; Stimulus 2 (right) involves one hidden target in a cluttered scene, i.e., the subject needs to find a character named Wally hidden in the crowd

For consistency during the data acquisition, voluntary blinking will only take place at t=t2 and t=t4 which serve as signals for state and speed changes (further details on this strategy are presented in Section 2.3.3) that will take effect at t=t3 and t=t5.

The left subplot of Fig. 2 depicts three major phases in the proposed paradigm; i.e., initial resting state (IRS), attentive state (AS), and final resting state (FRS). During IRS, the subjects are requested to rest and clear their minds before the experiment begins and a timer is displayed on the PC screen as a guide. When the timer hits 10 s (i.e., at t=t1), they must instantly focus on the stimulus to actuate the motor. At t=t2, they are required to blink twice at a rate of approximately 1 blink/second to accelerate the motor, and then continue focusing on the stimulus until t=t4 where they have to blink thrice with a similar rate to stop the motor. The FRS phase begins when t=t5 during which they need to clear their mind to ensure the EEG signal is brought back to the normal state.

While the proposed paradigm is realistically attainable, it can be a significant challenge to distinguish the elevated attention from the normal range during the voluntary blinking events due to drifts and prominent deflections from the recorded EEG data. Such a scenario is illustrated by four recorded trials in Fig. 4 where the blinking starts at t=33s after the stimulus is displayed at t=20s. From the figure, a sudden drop in the EEG data, denoted as ν, and a duration of 2 to 5 s to drive the meter reading back to the attention range is clearly seen within the blue strip. Thus, although the event is instrumental for state or command changes, it can cause undesired delays and increase the chance of misclassification, thereby lowering the BCI's predictive capabilities.

To this purpose, this work proposes a robust decoding strategy that is based on GPM which is a nonparametric Bayesian approach that has the advantages of being able to provide measurements of prediction uncertainties, and a voluntary eyeblink detection that can also be embedded into the motor's control system as illustrated in Fig. 5. To ensure resilience against disturbances within the motor system, the system is assumed to feature a pre-stabilized speed control loop that anticipates a reference speed command rather than a pulse width modulation [32]. Hence, rather than visually assessing the movement of the motor system (e.g., wheeled chair, robotic arm, or mobile robot), which may be influenced by friction with the ground or disturbances within the hardware itself, we focus on the precision of the command received by the system's embedded controller, which also serves as the motion controller in this work. The main decoding strategy is further detailed in the following section.

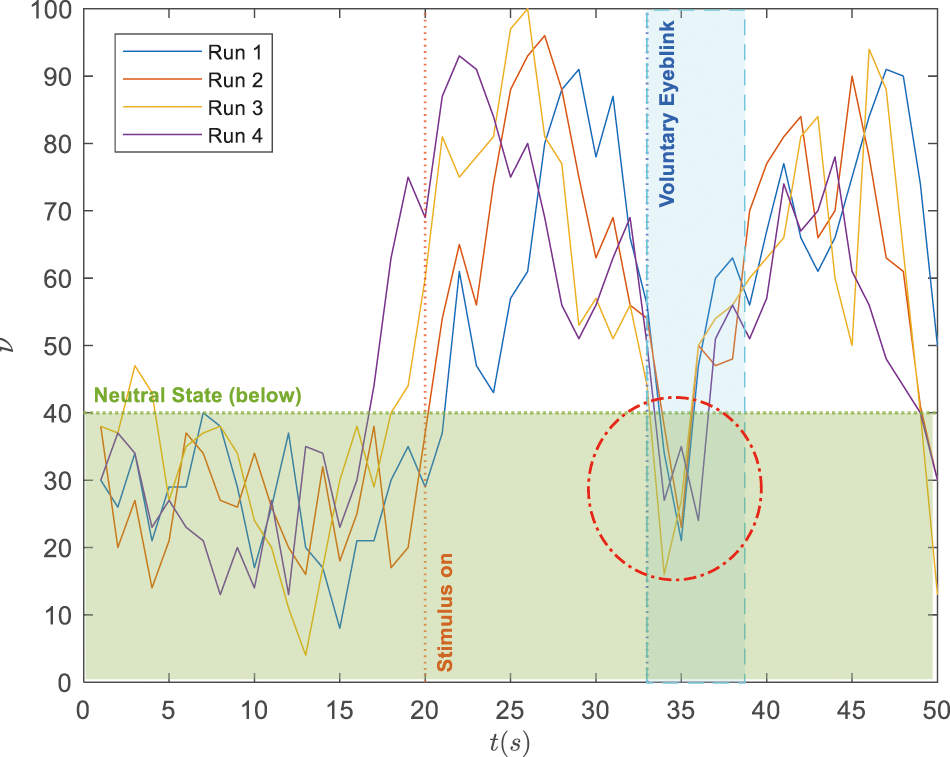
Figure 4: Illustration on signal deflections during voluntary blinking when the subject's attention level is within the elevated range (i.e., ν>40)

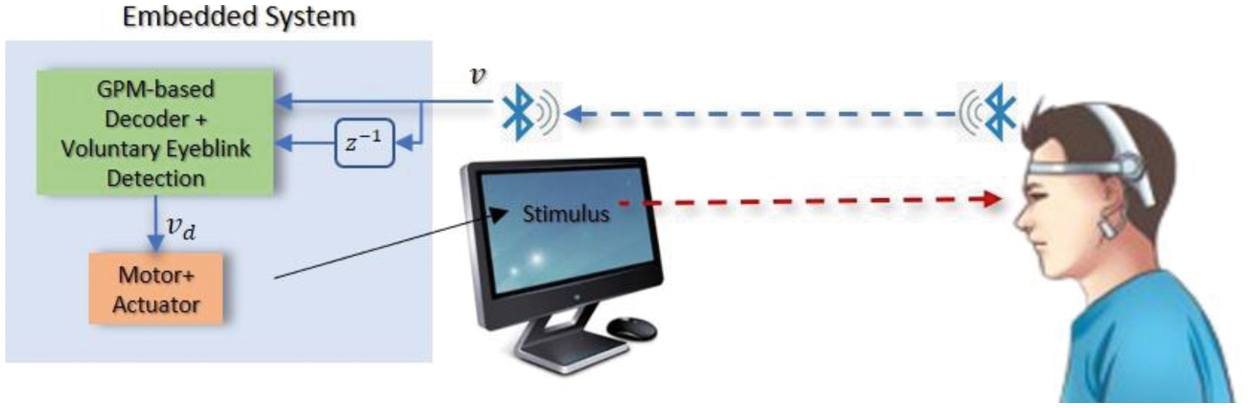
Figure 5: Illustration of the overall flow of the proposed paradigm. The embedded system which consists of the decoder and a motorized actuator is simulated in the PC via MATLAB software. Bluetooth was used for the wireless data transmission from the BCI headset

2.3 Decoding Strategy

Unlike neural network-based predictions which assume that the data distribution can be modeled in terms of a set of a finite number of parameters, GPM works based on nonparametric Bayesian statistics which predicts the target function value in the form of posterior distribution that can be computed by combining the noise (likelihood) model and a prior distribution on the target function. The trained GPM can be embedded into the motor's motion control system in practice using GPML [33], PyGPs [34], GPflow [35] or GPyTorch [36]. Applying the GPM alone, however, may not be adequate if one is to change the speed of the motor when it is running. To treat this issue, voluntary eyeblink detection is introduced since the EEG electrode that is placed at Fp1 will result in prominent signal deflections during the blinking events. In order to construct a stronger prediction model, a Hanning-based filtering stage is also integrated into the system. The overview of the proposed structure for the decoder is presented in Fig. 6 where the green areas illustrate the filtering stage and voluntary eyeblink detection while the blue area represents the GPM with dynamic speed command decoder. Details of each stage are discussed in the subsequent subsections.

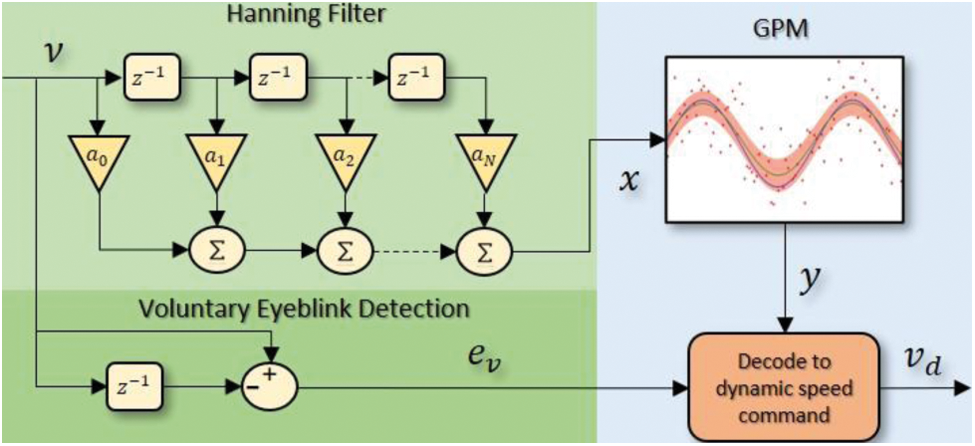
Figure 6: Overview of the proposed decoding strategy which consists of a GPM in cascade with a Hanning filter, and a voluntary eyeblink detection via ev. Both y and ev are required to decode the signal into the desired speed command, vd

2.3.1 Hanning Filter

Hanning filters which are a type of finite impulse response filters with Hanning window are frequently employed with random data as they typically have a moderate impact on the frequency resolution. In this work, as the computation speed is equally important to avoid delay in the wireless communication between the subject and the external device, we propose the Hanning filter as shown in the top left of Fig. 6 with the gain values of a0=0.25,a1=0.5, and a2=0.25 which result in a second-order polynomial as follows:

X(z)=14[ V(z)+2z−1V(z)+z−2V(z) ](2)

or, equivalently in time-domain,

xk=0.25(υk+2υk−1+υk−2)(3)

This filter will have a total gain of unity to preserve the amplitude of the targeted command, and the output that will be fed to the GPM later will only be a scaled average of three sequential inputs, with the center point weighted twice as heavily as its two adjacent neighbours. The performance of this filter will also be compared against the recursive Boxcar filter which has shown superiority over IIR and Kalman filters with a single-channel EEG device in [22].

2.3.2 Gaussian Process Model

Gaussian Process (GP) has an advantage over other ML algorithms in approximating a target function, (denoted as f(x)) since it can express complicated input and output interactions without predefining a set of bases and forecast a target output with uncertainty quantification. For regressions, GP is used as a prior to describe the distribution on the target function. As GP is a stochastic process, the function values f(xi),i=1,…,n are treated as random variables. GP describes the distribution over an unknown function by its mean function m(x)=E[f(x)] and a kernel function k(x,x′) which approximates the covariance E[(f(x)−m(x))(f(x′)−m(x′))]. The covariance function denotes a geometrical distance measure assuming that the more closely located inputs would be more correlated in terms of their function values. That is, the prior on the function values is represented as:

f(x)~GP(0,k(x,x′))(4)

which are from a zero-mean GP with covariance function k(x,x′). Similar to SVM, there are several kernel functions that can be used as covariance functions for GP. A widely employed form is the squared exponential (SE) function which can be described as follows:

k(xi,xj|θ)=σf2exp(−12l(xi−xj)T(xi−xj))(5)

where θ=(l,σf) is the set of hyperparameters. Consider an unknown target function y=f(x), and given a training data set with n samples as defined below:

D={ (xi,yi)|i=1,…,n }(6)

where xi∈Rp denotes the input vector and y∈ {\mathcal R} denotes the corresponding (possibly perturbed) output observations. The aim of GP is to predict the real-valued output fnew=f(xnew) for unseen target input xnew. However, rather than a point estimate, the prediction is given as a probability distribution quantifying uncertainty in the target value (a more detailed description can be found in [37]). Thus, the prior on the function values can be represented as P(f|X)∼N(f|μ,K) where X=[x1,…,xn], f=[f(x1),…,f(xn)], μ=[m(x1),…,m(xn)] and Kij=k(xi,xj). X refers to the observed data points, m is the mean function, and k represents a positive definite kernel function as defined in (5). In practical situations, we do not have access to the true function values, but their noisy versions which can be written as y=f(x)+ε. Assuming there is an additive independent and identically distributed Gaussian noise with variance σn2 in the outputs so that cov(y)=K+σn2I, and by deriving the conditional distribution, the predictive equations for GP model become P(f∗|X,y,X∗)∼N(f¯∗,σ∗) where f¯∗=E[f∗|X,y,X∗]=K∗T[K+σn2I]−1y and σ∗=K∗∗−K∗T[K+σn2I]−1K∗. To predict the function from a new test data, the hyperparameters can be optimized using the log marginal likelihood as follows [37]:

θ∗=argmaxθlogP(y|X,θ).(7)

Thus, with the optimized hyperparameters, a more general predictive equation for GP model can be written as

P(f∗|X,y,X∗,θ∗)~N(f¯∗, σ∗).(8)

In order to predict the dynamic command from the new EEG signal in the test dataset, the mean function of the posterior distribution will be used along with voluntary eyeblinks as described below.

2.3.3 Voluntary Eyeblinks

EEG data from the BCI device would typically have minor fluctuations at all states including normal eyeblink events. In order to identify the voluntary blinks from other events, a preliminary test with ten trials is conducted where the BCI user had to perform voluntary blinking once, twice, and thrice with a rate of approximately 1 Hz when the attention level falls within the elevated range. During the test, the value of ev which refers to the first derivative of ν as depicted at the bottom left of Fig. 6 is computed at each time instant. The magnitudes of ev when ev<0 from voluntary blinks and normal blinks/fluctuations are recorded and visualized in Fig. 7.

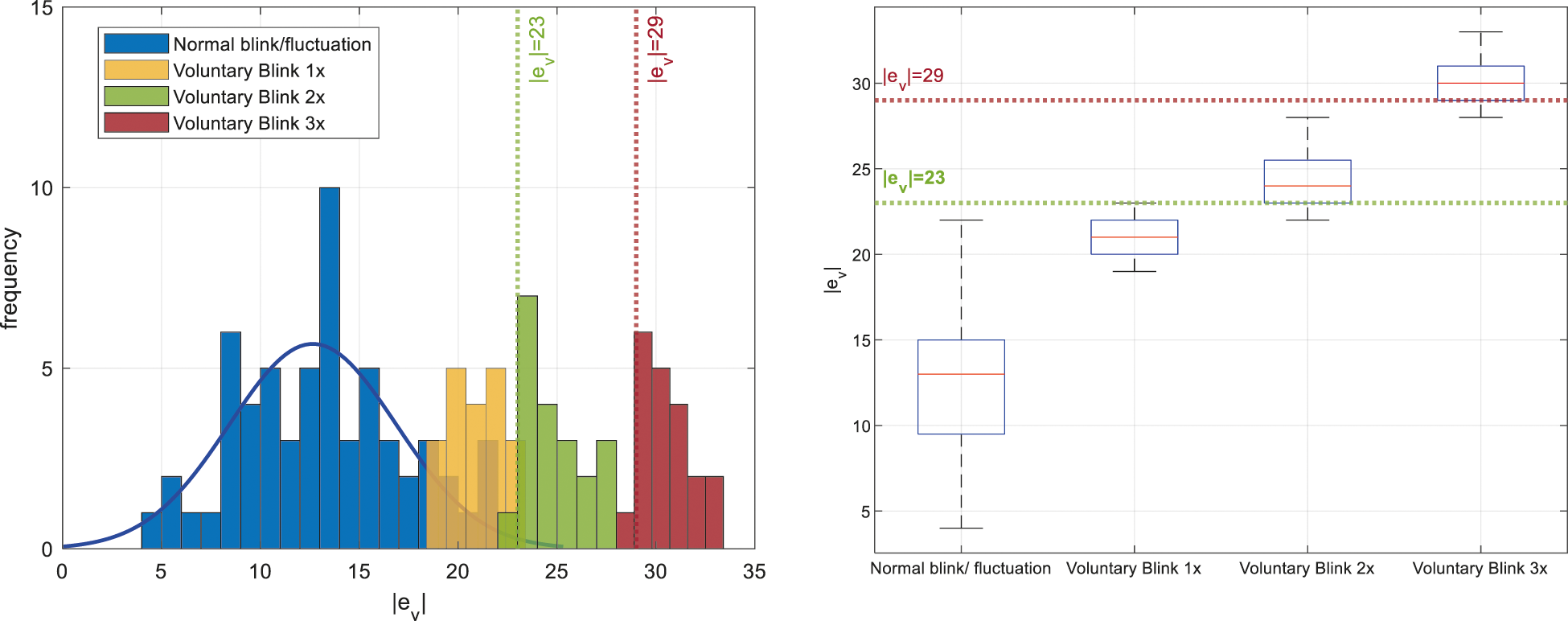
Figure 7: Comparisons of signal deflection magnitude, |ev|, for normal blinks/fluctuations and voluntary blinks. The “1×”, “2×” and “3×” notations refer to once, twice and thrice blinks with a rate of approximately 1 Hz. The left plot shows the histogram while the right plot shows the corresponding box plot

From the left plot of Fig. 7, it can be observed that the |ev| is nearly normally distributed within the (0,23) range during the normal blink or fluctuations. A similar trend is also seen for voluntary blinks that are performed once (1×) where the distribution spans between 19 and 23. On the other hand, the distribution of |ev| when voluntary blinks are performed twice (2×) and thrice (3×) are left-skewed with the highest frequency at |ev|=23 and |ev|=29 respectively. Interestingly, if the 1× voluntary blink is removed, the remaining distributions do not heavily overlap with each other as can be seen in the corresponding box plots on the left side of Fig. 7. Thus, from this observation, a two DoF can be designed with voluntary blinks to change the EEG state when it is elevated, i.e., Voluntary Blink 2× which can be detected when |ev|∈[23,28], and Voluntary Blink 3× which can be detected when |ev|≥29. For brevity, Voluntary Eyeblinks 2× and 3× will be henceforth renamed as b1 and b2 respectively.

2.3.4 Generation of Prediction Models and Performance Metrics

Twenty healthy subjects (ten from each gender) aged between 24 and 29 years participated in the EEG experiments conducted in this study. The subjects had no brain training session or any prior BCI experience before the actual experiment was carried out. During the experiments, the EEG data from the BCI device was captured and recorded in MATLAB software. To obtain consistent and accurate results, descriptions of the experimental protocols and the recommended method for fitting the headset were provided and demonstrated to each participant before the paradigm was carried out.

In order to provide an unbiased evaluation of the prediction model, the data were partitioned into training and test sets where only the performance of the latter would be evaluated. The flowchart of the prediction model generations is illustrated in Fig. 8 (left) where Set MTR and Set FTR which consist of 80% of the data from the male and female subjects respectively are used as training data to construct the prior distribution on the target function and the likelihood model. To further observe whether the gender-based training can enhance the generalization capability of the model, the training is also conducted based on genders as depicted in the first section of the flowchart. This process will generate three types of models, namely Model G (Cg) which is trained based on both male and female data; Model M (Cm) which is trained based on male-only data (i.e., Set MTR); and Model F (Cf) which is trained based on female-only data (i.e., Set FTR).

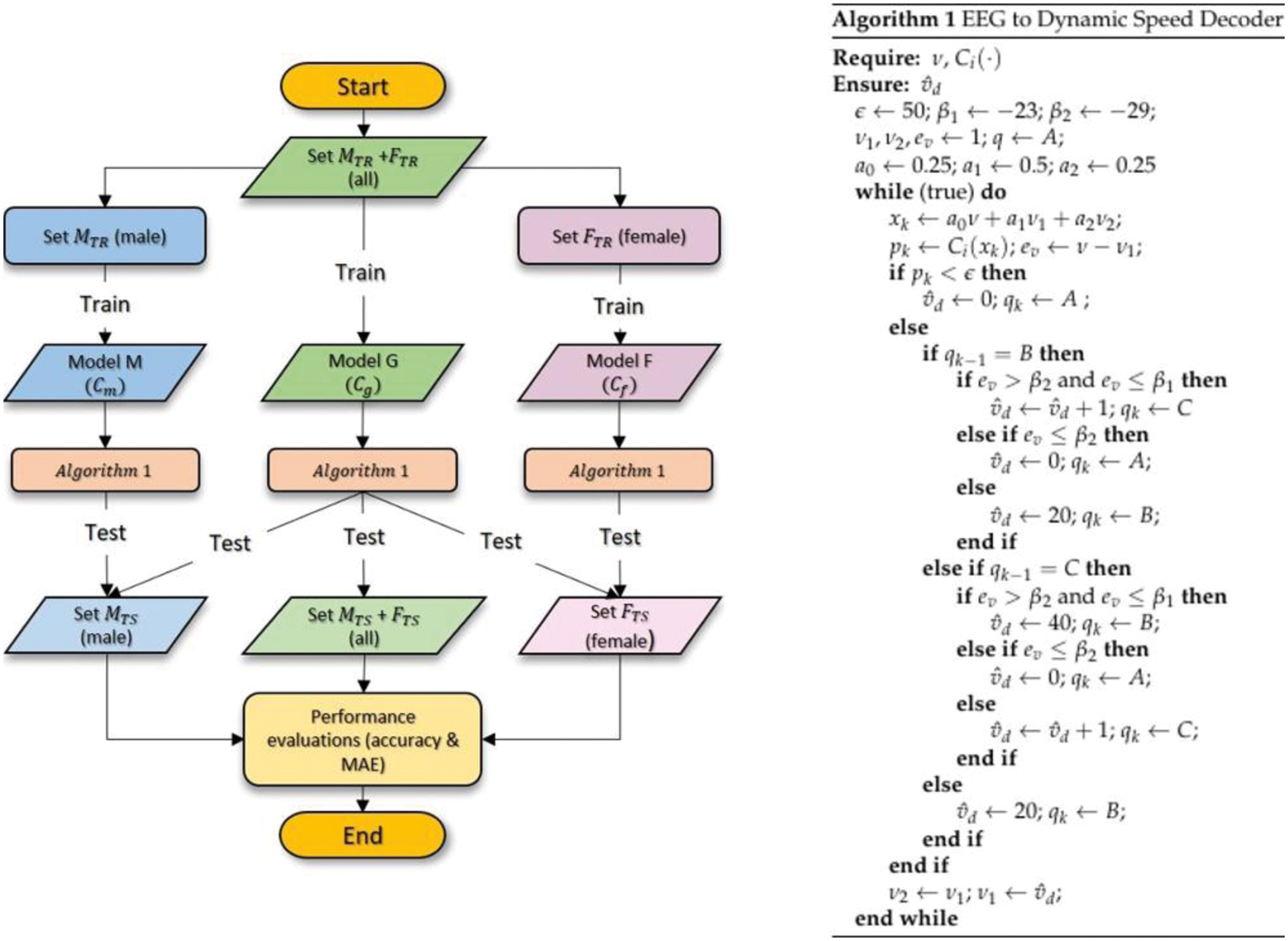
Figure 8: Flowchart of the prediction model generations (left) and the proposed algorithm for EEG to dynamic speed decoder (right)

Algorithm 1 which is detailed on the right side of Fig. 8 presents the proposed EEG to dynamic speed decoding strategy with b1 and b2 detections and heuristic method to reject and reconstruct the EEG data to the desired values during the b1 and b2 events. The actual performance is then tested on new datasets, i.e., Set MTS and Set FTS as defined in Fig. 8, which come from the remaining 20% of the recorded EEG data. Similar to the training process, gender-based evaluations are also conducted to analyse the generalization capability of the gender-based models.

In this study, accuracy which is a measure of correctly classified data is considered as the performance metric for the classification of the states (i.e., A, B and C) as depicted in the middle plot of Fig. 2. This metric can be computed as

Accuracy=TP+TNTP+TN+FP+FN(9)

where TP, TN, FP and FN represent true positive, true negative, false positive and false negative respectively. The ultimate goal is however to ensure the actual dynamic speed command, ν^d, is driven as close as possible to the target command, νd. Thus, to penalize the mismatch between the two, the mean absolute error (MAE) is computed as follows:

MAE=1n∑i=1n| νd,i−ν^d,i |(10)

where n is the total sampled data for each test. This metric will be a more accurate representation of the overall performance since it takes into account the effectiveness of the voluntary blink detection that affects the state transitions. Results from these performance evaluations are presented in the next section.

3  Results

To demonstrate the effectiveness of the proposed GPM in decoding the single-channel EEG data into the desired dynamic commands, the performance is compared against other competitive classifiers using 5-fold cross validations as well as the conventional method (Conv) which relies solely on the eSense meter and the proposed voluntary blink detection for state transitions. The classifiers evaluated in this study are LDA, SVM, kNN, EL and NN which have previously been employed for classification with a single-channel EEG device in recent studies [22,29]. In addition, the results with and without the filters are also recorded for further analyses.

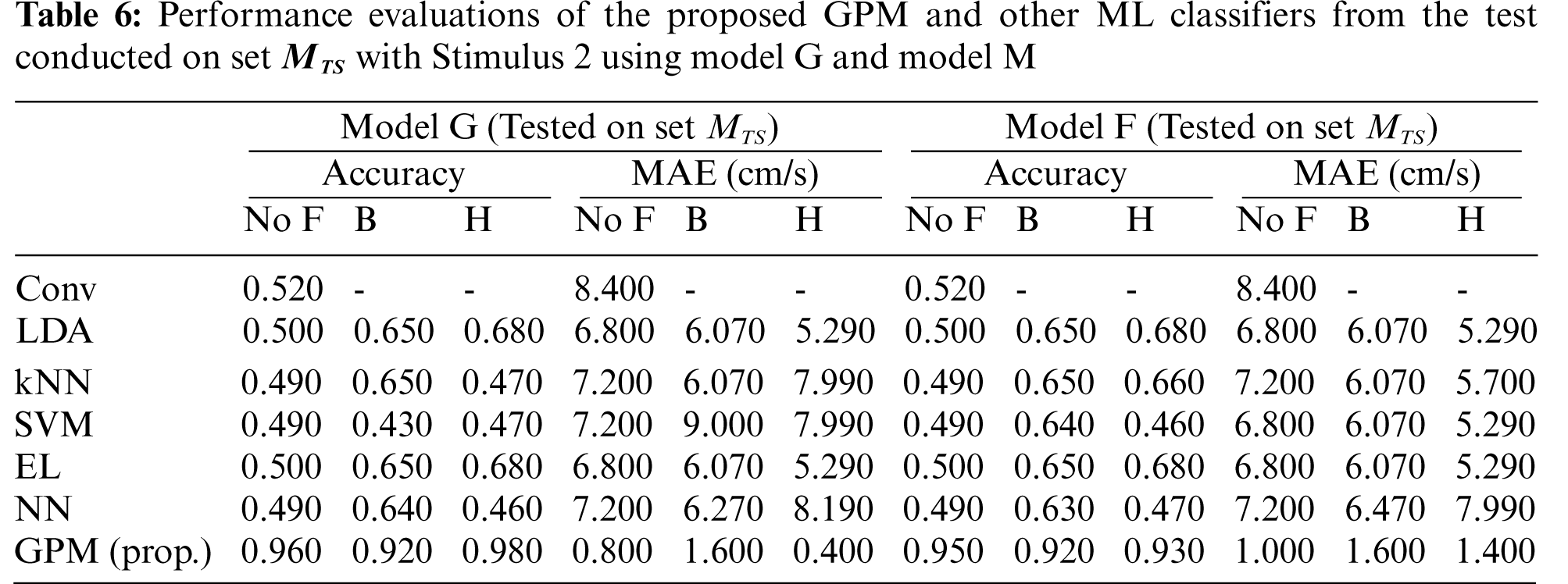
Tab. 1 compares the overall performance of the proposed GPM and other methods from the test conducted on Set FTS+MTS with Stimulus 1 using Model G. “No F”, “B” and “H” denote “No Filter”, “Boxcar filter” and “Hanning filter” respectively. In general, the GPM considerably outperforms the rest in terms of accuracy and MAE, both with and without filters. The highest accuracy and lowest MAE obtained are 96.5% and 0.7 cm/s respectively with Hanning filter.

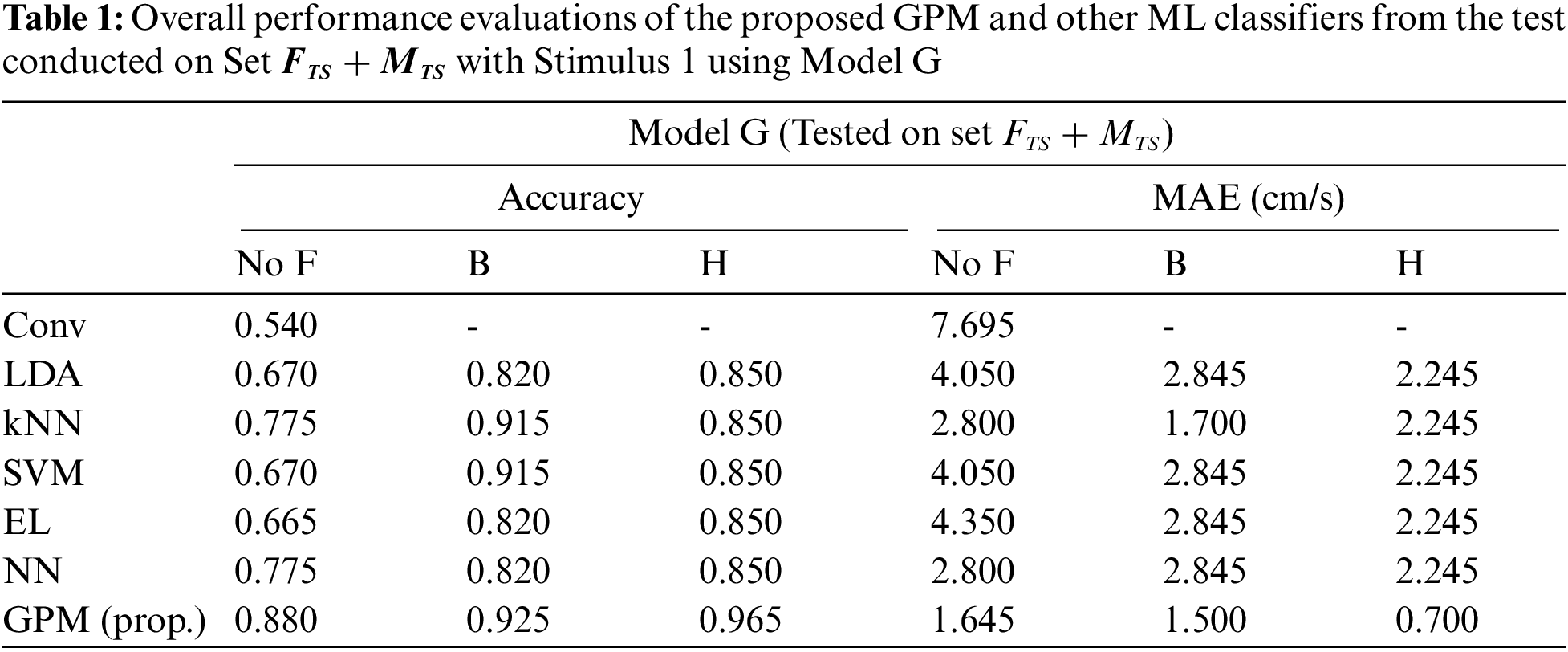
Tabs. 2 and 3 illustrate the difference in the performance of Model G and Model F/M when evaluated based on genders. Via the proposed GPM, no performance differences can be seen between the generic and gender-based models, and both result in the best performance with 96% accuracy and 0.8cm/s MAE with Hanning filter. With regard to male-based evaluations which are presented in Tab. 3, a quite similar trend is seen from the DA, EL and NN classifiers except for kNN and SVM where their generic models outperform their male-based counterparts with MAE of 1.4 cm/s.

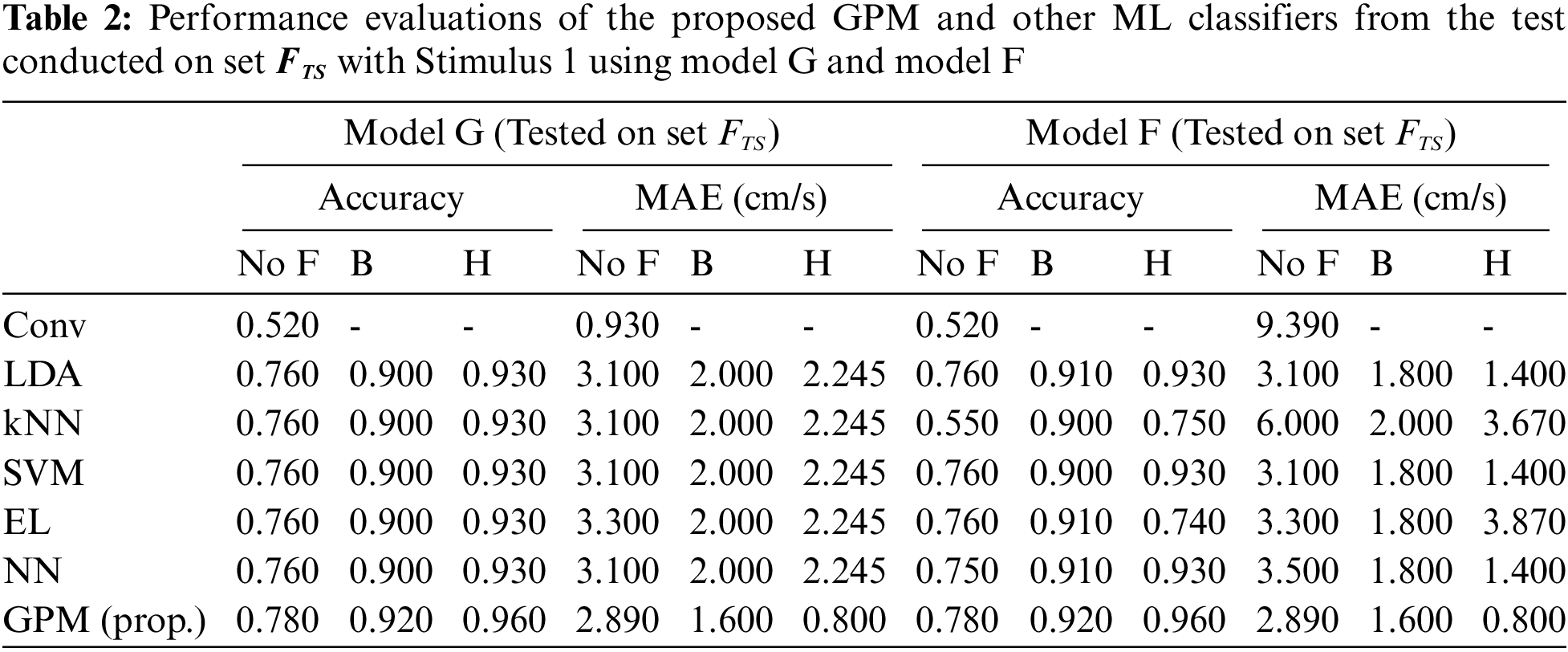
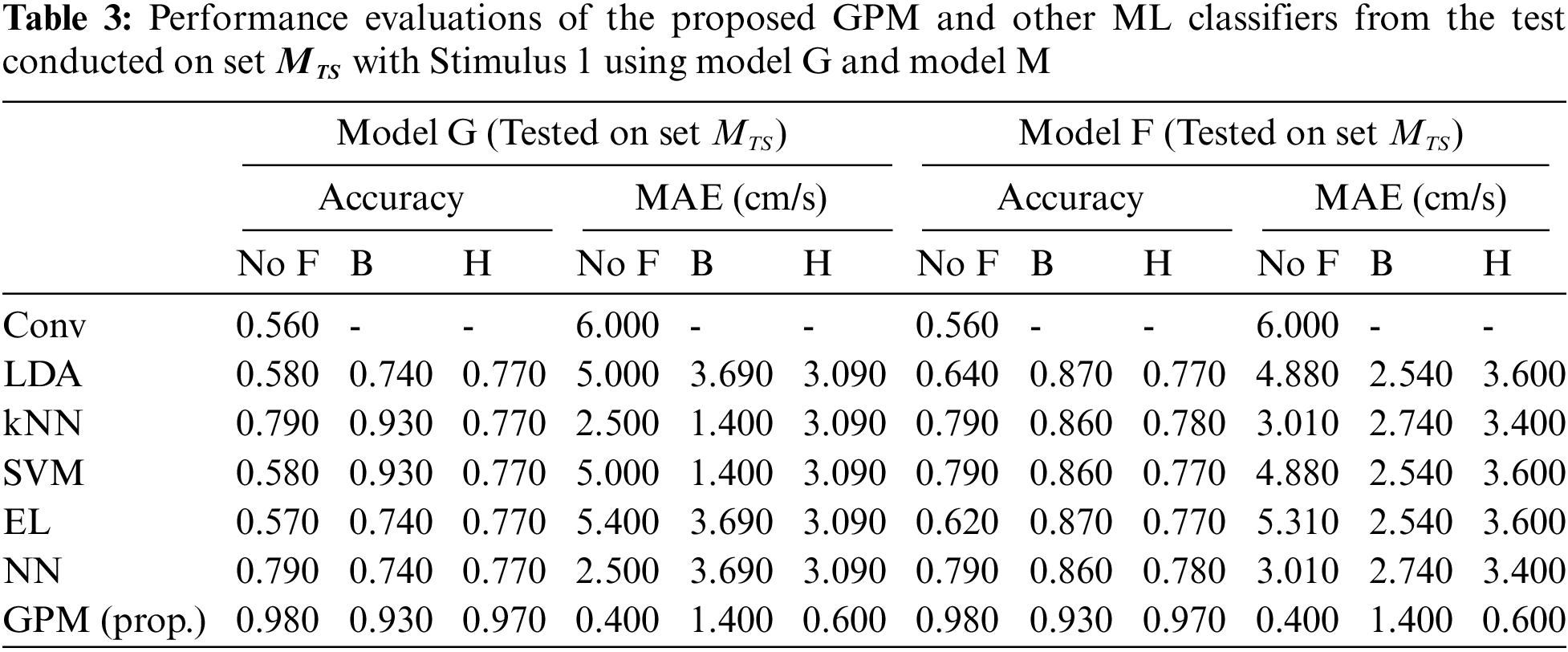
The same evaluations for Stimulus 2 are presented in Tab. 4 for the overall performance, and Tabs. 5 and 6 for the gender-based performances. In contrast to Stimulus 1, the best performance when Stimulus 2 is employed is achieved via the proposed GPM without filter, which results in 92.5% accuracy and 1.5 cm/s MAE. What stands out in Tab. 4 is the big gap in performance between the proposed model and other classifiers where the highest accuracy achieved is only 69.5% via DA and EL, which is considerably lower than that resulted from GPM. Moreover, the resulting gender-based models from the DA, kNN, SVM, EL and NN classifications do not improve the predictive ability as can be observed in Tabs. 5 and 6 where the differences with their generic counterparts are negligibly small. On the contrary, a slight difference in performance is seen between Model G and Model F/M with GPM; i.e., for the female-based evaluations, Model F resulted in a better performance with 91% accuracy and 1.8 cm/s MAE, and for male-based evaluations, Model G with Hanning filter beats Model M with 98% accuracy and 0.4 cm/s MAE.

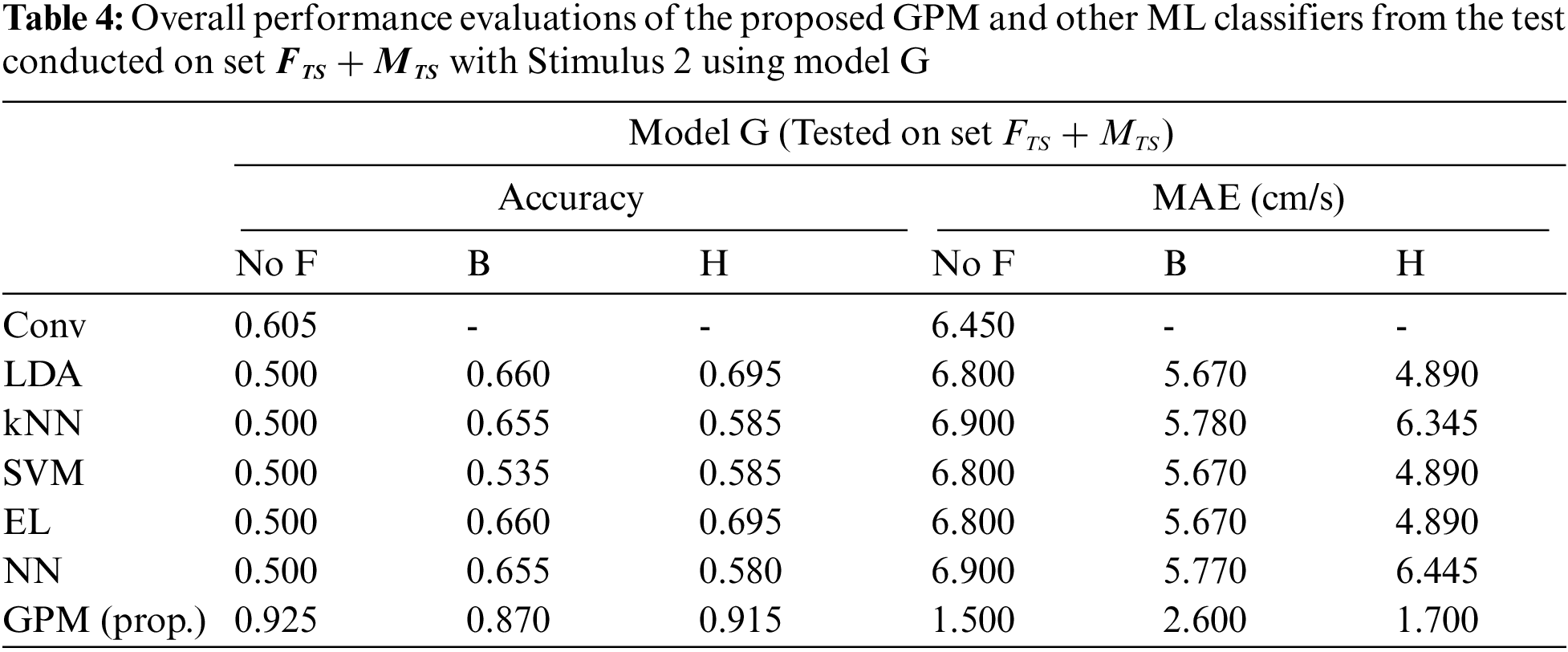
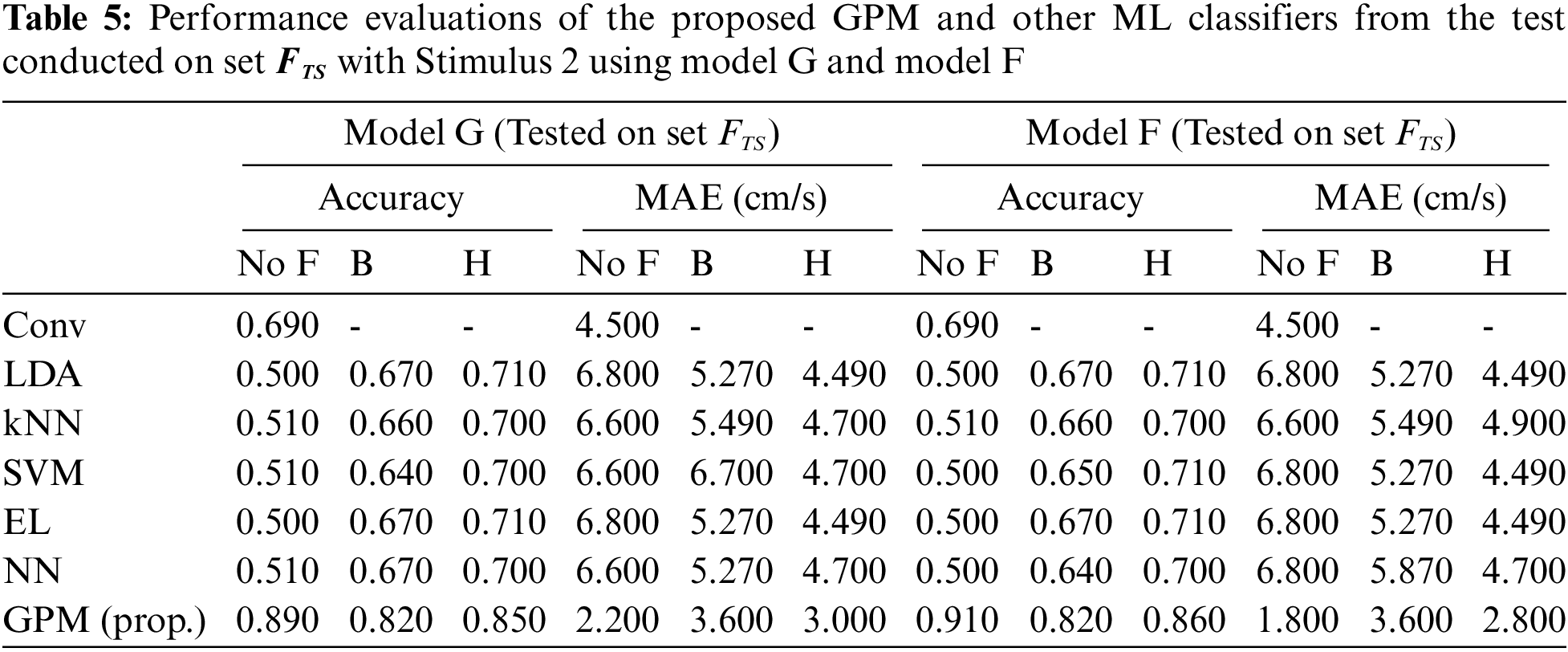
For clarity and brevity, the performance of the proposed GPMs against other best-performing models based on gender and stimulus is summarized in Tab. 7. From the table, it can be generally concluded that while other methods perform substantially worse with Stimulus 2, the GPM approach demonstrates consistent performance across both stimuli with accuracy above 91% and a maximum MAE of 1.80 cm/s. Nonetheless, for such a BCI application, Stimulus 1 with GPM is likely to form a better prediction model since the resulting accuracy reaches 96% with an MAE of no greater than 0.8 cm/s, which is significantly lower than that resulted from Stimulus 2.

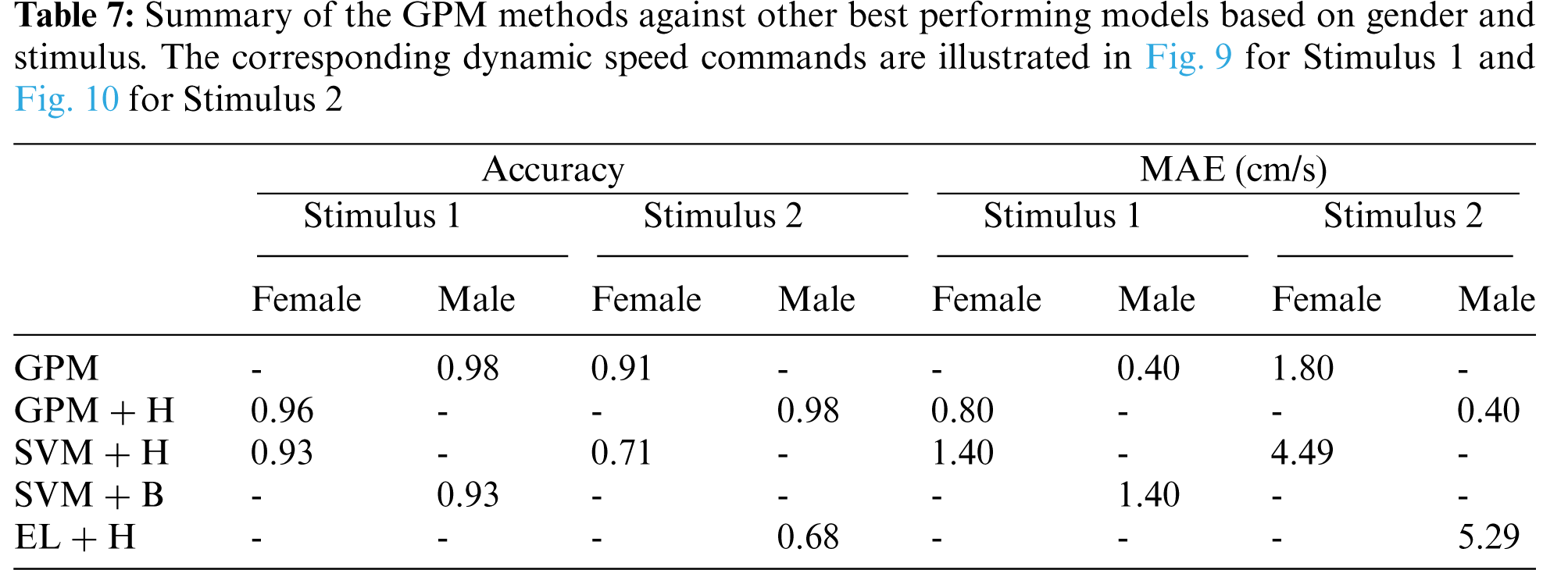
The corresponding dynamic speed commands are visualized in the upper plots of Figs. 9 and 10 along with the derivatives of the EEG data, ev, in the bottom plots. The target speed command, υd, is represented by the dashed black lines, while the voluntary blink events which serve as signals for state transition are denoted by the vertical lines, b1 and b2. Comparing Figs. 9 and 10, it can be clearly seen that Stimulus 2 resulted in a relatively longer delay during the transition from νd=0 to νd=20 cm/s, which accounted for the deteriorating performance when compared to the results from Stimulus 1 in Tab. 7.

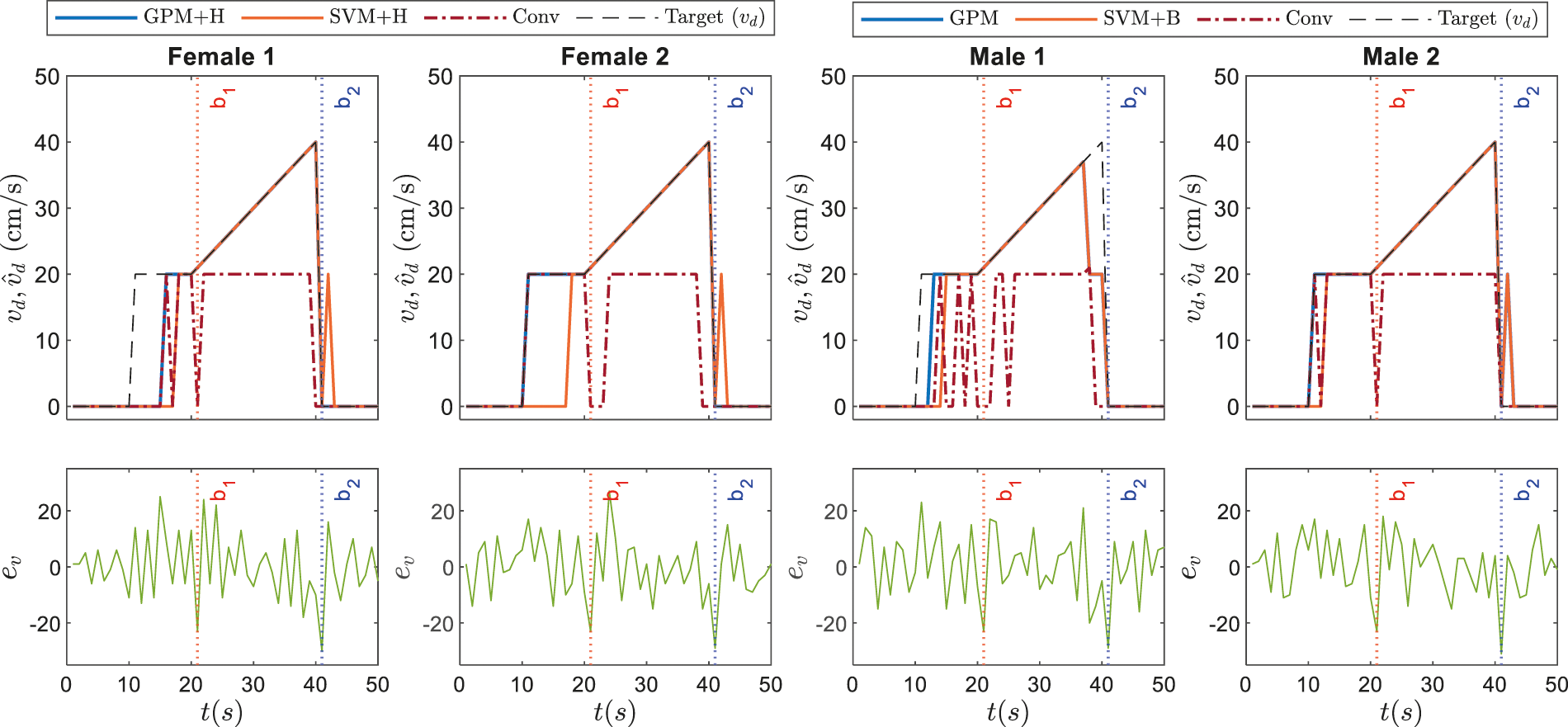
Figure 9: Illustrations on dynamic speed commands based on GPM approach against conventional method and other best performing classifiers as recorded in Tab. 7 for Stimulus 1

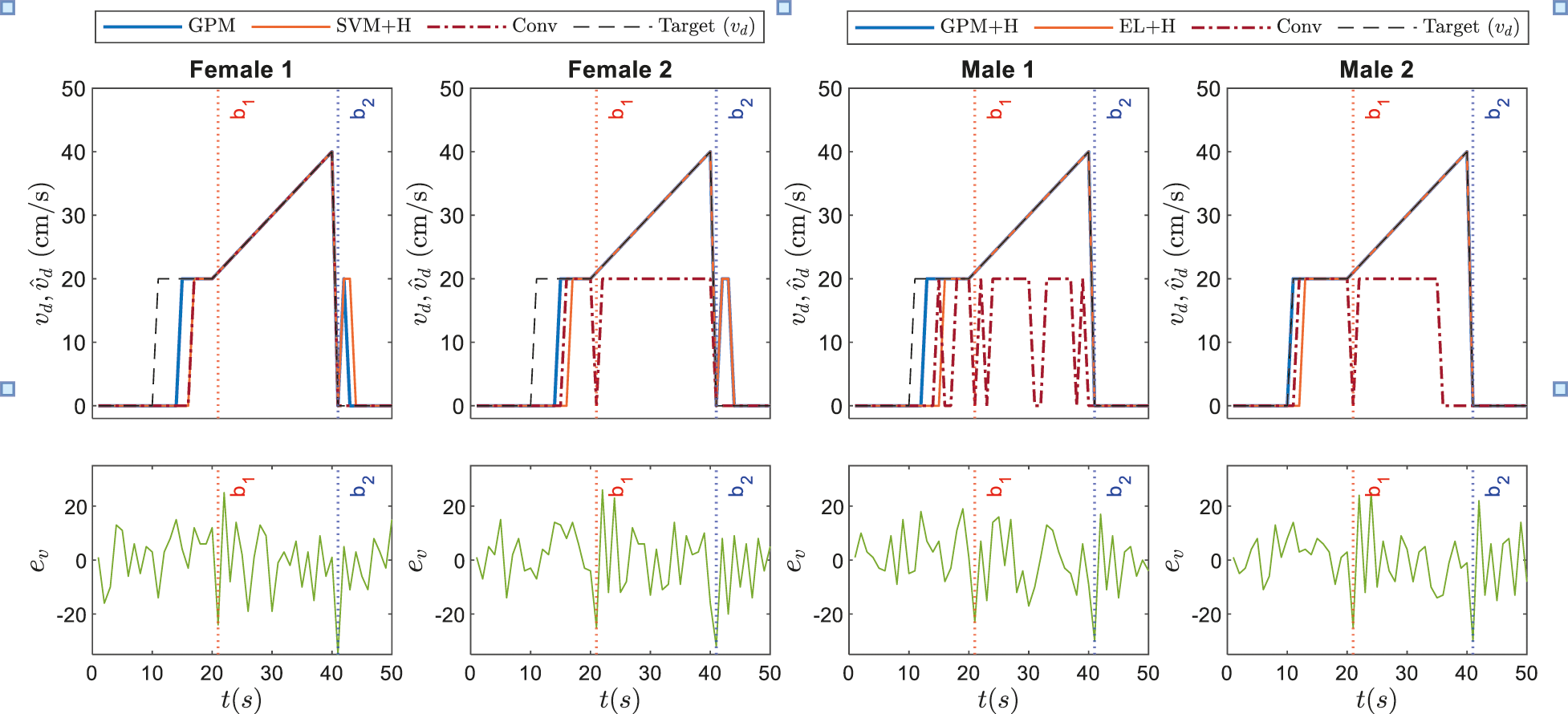
Figure 10: Illustrations on dynamic speed commands based on GPM approach against conventional method and other best performing classifiers recorded in Tab. 7 for Stimulus 2

Referring to the responses of ev on the bottom plots of Figs. 9 and 10, the b2 (b1) events result in the largest (second largest) magnitude when ev<0 in each test. With the proposed voluntary blink detections, the transmitted speed commands have been successfully driven to the desired values for both paradigms as can be seen from the responses of GPM and other classifiers which are represented by the orange and blue lines respectively. On the contrary, the conventional method performs the worst due to the nature of the eSense meter reading which has a greater tendency of misclassification during the voluntary eyeblink events as conjectured in Section 2.2. Another striking observation is that SVM and EL result in significant delays and mismatches between νd and ν^d particularly during the state transitions at t=10s and t=40s compared to the GPM approach which only causes small delays during the transition at t=10s. In practice, such a scenario is undesirable since it will lead to performance deterioration of the closed-loop motor system and eventually instability. By contrast, the GPM approach particularly with Stimulus 1 demonstrates considerably smaller errors between νd and ν^d which only occur when the motor is initially actuated. This is inherently due to the representation flexibility of the trained models that also provide uncertainty measures over predictions.

4  Conclusion and Future Work

Conclusion: In this work, a new BCI decoding strategy via the GPM approach for dynamic speed commands with a single-channel EEG-controlled actuator has been proposed. The experimental outcome has demonstrated the superiority of the GPM approach over other existing classifiers in the literature which include LDA, SVM, kNN, EL and NN. Additionally, further analysis reveals that while the error performance of other existing methods deteriorates with Stimulus 2 due to signal drifts resulting from voluntary eyeblinks, the proposed GPM exhibits consistent performance.

Implications of the study: The current study has proposed an improved BCI decoding strategy based on GPM that can be readily embedded in many affordable off-the-shelf microcomputers. Plus, the combination of an inconspicuous visual stimulus and voluntary eyeblinks has not just increased the DoF of a single-channel EEG-controlled actuator, but also eliminated the need of extensive training that is typically required in most motor-imagery based BCIs. Such an approach will greatly benefit new BCI users as well as BCI illiterates who are unable to sufficiently modulate their neuronal signals when controlling an external device.

Limitations and future work: Despite the significant improvements, the proposed method has only been evaluated with a BCI paradigm that lasted no longer than 50 s. A greater focus on modifying the stimuli to prolong the attention span could produce interesting findings that account more for higher DoF EEG-controlled actuators particularly those used in mobile robots. Thus, future work will encompass the aforementioned research field as well as deployment to robotic platforms which may necessitate some modifications to address unanticipated issues during real-time implementations. For instance, when the actuator is subject to external disturbances and diverts away from the targeted position, a new function to detect such a scenario needs to be embedded in the decoder's algorithm to avoid user distraction that can consequently affect the accuracy of the transmitted EEG signal. In addition, different sizes of datasets may be required to evaluate and further enhance the generalization capability of the GPM-based decoder.

Acknowledgement: The authors would like to thank all volunteers who have participated in this experimental study and the Human Research Ethics Committee for approving the protocol which was conducted in accordance to the ethical principles outlined by the Declaration of Helsinki.

Funding Statement: This work was supported by the Ministry of Higher Education Malaysia for Fundamental Research Grant Scheme with Project Code: FRGS/1/2021/TK0/USM/02/18.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  R. Abiri, S. Borhani, E. Sellers, Y. Jiang and X. Zhao, “A comprehensive review of EEG-based brain-computer interface paradigms,” Journal of Neural Engineering, vol. 16, no. 1, pp. 1741–2552, 2019. [Google Scholar]

 2.  N. Alba, R. Sclabassi, M. Sun and X. Cui, “Novel hydrogel-based preparation-free EEG electrode,” IEEE Transactions on Neural Systems and Rehabilitation Engineering, vol. 18, no. 4, pp. 415–423, 2010. [Google Scholar]

 3.  J. M. Morales, C. D´ıaz-Piedra, H. Rieiro, J. Roca-Gonz´alez, S. Romero et al., “Monitoring driver fatigue using a single-channel electroencephalographic device: A validation study by gaze-based, driving performance, and subjective data,” Accident Analysis & Prevention, vol. 109, pp. 62–69, 2017. [Google Scholar]

 4.  J. Xu and B. Zhong, “Review on portable EEG technology in educational research,” Computers in Human Behavior, vol. 81, pp. 340–349, 2017. [Google Scholar]

 5.  J. Morales, J. Ruiz-Rabelo, C. Diaz-Piedra and L. di Stasi, “Detecting mental workload in surgical teams using a wearable single-channel electroencephalographic device,” Journal of Surgical Education, vol. 76, no. 4, pp. 1107–1115, 2019. [Google Scholar]

 6.  M. Tariq, P. M. Trivailo and M. Simic, “EEG-based BCI control schemes for lower-limb assistive-robots,” Frontiers in Human Neuroscience, vol. 12, no. 312, pp. 1–20, 2018. [Google Scholar]

 7.  R. K. Chikara and L. -W. Ko, “Neural activities classification of human inhibitory control using hierarchical model,” Sensors, vol. 19, no. 3791, pp. 1–18, 2019. [Google Scholar]

 8.  N. Kosmyna, J. Lindgren and A. L´ecuyer, “Attending to visual stimuli versus performing visual imagery as a control strategy for EEG-based brain-computer interfaces,” Scientific Reports, vol. 8, no. 13222, pp. 1–14, 2018. [Google Scholar]

 9.  A. Athanasiou, I. Xygonakis, N. Pandria, P. Kartsidis, G. Arfaras et al., “Towards rehabilitation robotics: Off-the-shelf BCI control of anthropomorphic robotic arms,” BioMed Research International, vol. 2017, no. 5708937, pp. 1–17, 2017. [Google Scholar]

10. M. Hasan, M. Ibrahimy, S. Motakabber and S. Shahid, “Classification of multichannel EEG signal by linear discriminant analysis,” Advances in Intelligent Systems and Computing, vol. 1089, no. 1, pp. 279–282, 2015. [Google Scholar]

11. K. -R. Muller, C. Anderson and G. Birch, “Linear and nonlinear methods for brain-computer interfaces,” IEEE Transactions on Neural Systems and Rehabilitation Engineering, vol. 11, no. 2, pp. 165–169, 2003. [Google Scholar]

12. H. U. Amin, W. Mumtaz, A. R. Subhani, M. N. M. Saad and A. S. Malik, “Classification of EEG signals based on pattern recognition approach,” Frontiers in Computational Neuroscience, vol. 11, no. 103, pp. 1–12, 2017. [Google Scholar]

13. J. Luo, X. Gao, X. Zhu, B. Wang, N. Lu et al., “Motor imagery EEG classification based on ensemble support vector learning,” Computer Methods and Programs in Biomedicine, vol. 193, no. 105464, pp. 1–9, 2020. [Google Scholar]

14. S. F. Abbasi, H. Jamil and W. Chen, “EEG-based neonatal sleep stage classification using ensemble learning,” Computers, Materials & Continua, vol. 70, no. 3, pp. 4619–4633, 2022. [Google Scholar]

15. O. Tsinalis, P. M. Matthews, Y. Guo and S. Zafeiriou, “Automatic sleep stage scoring with single-channel EEG using convolutional neural networks,” ArXiv, 2017. [Online]. Available: https://arxiv.org/abs/1610.01683. [Google Scholar]

16. A. Supratak, H. Dong, C. Wu and Y. Guo, “Deepsleepnet: A model for automatic sleep stage scoring based on raw single-channel EEG,” IEEE Transactions on Neural Systems and Rehabilitation Engineering, vol. 25, no. 11, pp. 1998–2008, 2017. [Google Scholar]

17. T. -P. Jung, S. Makeig, M. Westerfield, J. Townsend, E. Courchesne et al., “Removal of eye activity artifacts from visual event-related potentials in normal and clinical subjects,” Clinical Neurophysiology: Official Journal of the International Federation of Clinical Neurophysiology, vol. 111, pp. 1745–1758, 2000. [Google Scholar]

18. B. R. Schlink, S. M. Peterson, W. D. Hairston, P. Konig, S. E. Kerick et al., “Independent component analysis and source localization on mobile eeg data can identify increased levels of acute stress,” Frontiers in Human Neuroscience, vol. 11, no. 310, pp. 1–13, 2017. [Google Scholar]

19. M. T. Sadiq, X. Yu, Z. Yuan and Z. Aziz, “Motor imagery BCI classification based on novel two-dimensional modelling in empirical wavelet transform,” Electronics Letters, vol. 56, no. 25, pp. 1367–1369, 2020. [Google Scholar]

20. M. T. Sadiq, X. Yu, Z. Yuan, Z. Fan, A. U. Rehman et al., “Motor imagery EEG signals classification based on mode amplitude and frequency components using empirical wavelet transform,” IEEE Access, vol. 7, pp. 127678–127692, 2019. [Google Scholar]

21. M. T. Sadiq, X. Yu and Z. Yuan, “Exploiting dimensionality reduction and neural network techniques for the development of expert brain-computer interfaces,” Expert Systems with Applications, vol. 164, no. 114031, pp. 1–20, 2021. [Google Scholar]

22. J. H. Teo, N. S. Ahmad and P. Goh, “Visual stimuli-based dynamic commands with intelligent control for reactive BCI applications,” IEEE Sensors Journal, vol. 22, no. 2, pp. 1435–1448, 2022. [Google Scholar]

23. H. Hinrichs, M. Scholz, A. K. Baum, J. W. Y. Kam, R. T. Knight et al., “Comparison between a wireless dry electrode EEG system with a conventional wired wet electrode EEG system for clinical applications,” Scientific Reports, vol. 10, no. 5218, pp. 1–14, 2020. [Google Scholar]

24. A. Wexler and R. Thibault, “Mind-reading or misleading? Assessing direct-to-consumer electroencephalography (EEG) devices marketed for wellness and their ethical and regulatory implications,” Journal of Cognitive Enhancement, vol. 3, pp. 131–137, 2019. [Google Scholar]

25. H. Rieiro, C. Diaz-Piedra, J. M. Morales, A. Catena, S. Romero et al., “Validation of electroencephalographic recordings obtained with a consumer-grade, single dry electrode, low-cost device: A comparative study,” Sensors, vol. 19, no. 12, pp. 1–18, 2019. [Google Scholar]

26. W. -D. Chang, H. -S. Cha, K. Kim and C. -H. Im, “Detection of eye blink artifacts from single prefrontal channel electroencephalogram,” Computer Methods and Programs in Biomedicine, vol. 124, pp. 19–30, 2015. [Google Scholar]

27. J. Zhou, Y. Tian, G. Wang, J. Liu, D. Wu et al., “Automatic sleep stage classification with single channel EEG signal based on two-layer stacked ensemble model,” IEEE Access, vol. 8, pp. 57283–57297, 2020. [Google Scholar]

28. A. Cantero, J. Cubero, I. M. Gomez Gonzalez, M. Merino Monge and J. Silva, “Characterizing computer access using a one-channel EEG wireless sensor,” Sensors, vol. 17, no. 7, pp. 1–23, 2017. [Google Scholar]

29. F. Grosselin, X. Navarro-Sune, A. Vozzi, K. Pandremmenou, F. De Vico Fallani et al., “Quality assessment of single-channel EEG for wearable devices,” Sensors, vol. 19, no. 3, pp. 1–17, 2019. [Google Scholar]

30. M. Alimardani, S. Nishio and H. Ishiguro, “Brain-computer interface and motor imagery training: The role of visual feedback and embodiment,” In: Denis Larrivee (Ed.) Evolving BCI Therapy-Engaging Brain State Dynamics, IntechOpen, London, United Kingdom, pp. 73–88, 2018. [Google Scholar]

31. A. H. Alsharif, N. Z. M. Salleh, R. Baharun, E. A. R. Hashem, A. A. Mansor et al., “Neuroimaging techniques in advertising research: Main applications, development, and brain regions and processes.” Sustainability, vol. 13, no. 6488, pp. 1–25, 2021. [Google Scholar]

32. N. S. Ahmad, “Robust H∞-fuzzy logic control for enhanced tracking performance of a wheeled mobile robot in the presence of uncertain nonlinear perturbations,” Sensors, vol. 20, no. 13, pp. 1–27, 2020. [Google Scholar]

33. A. Rasmussen and H. Nickisch, “Gaussian processes for machine learning (GPML) toolbox,” Journal of Machine Learning Research, vol. 11, pp. 3011–3015, 2010. [Google Scholar]

34. M. Neumann, S. Huang, D. Marthaler, K. Kersting and A. Honkela, “PyGPS-a python library for Gaussian process regression and classification,” Journal of Machine Learning Research, vol. 16, pp. 2611–2616, 12 2015. [Google Scholar]

35. A. G. G. Matthews, M. van der Wilk, T. Nickson, K. Fujii, A. Boukouvalas et al., “GPflow: A Gaussian process library using TensorFlow,” Journal of Machine Learning Research, vol. 18, no. 40, pp. 1–6, 2017. [Google Scholar]

36. J. Gardner, G. Pleiss, D. Bindel, K. Weinberger and A. Wilson, “GpyTorch: Blackbox matrix-matrix Gaussian process inference with GPU acceleration,” Advances in Neural Information Processing Systems, vol. 2018, pp. 7576–7586, 2018. [Google Scholar]

37. C. E. Rasmussen and C. K. I. Williams, “Gaussian processes for machine learning,” in Adaptive Computation and Machine Learning, Cambridge, Massachusetts, USA: The MIT Press, pp. 7–30, 2005. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.