Computers, Materials & Continua DOI:10.32604/cmc.2022.025727
Article

Improved Multi-party Quantum Key Agreement with Four-qubit Cluster States

Hussein Abulkasim1,*, Eatedal Alabdulkreem2 and Safwat Hamad3

1Faculty of Science, New Valley University, El-Kharga & the Academy of Scientific Research and Technology, Cairo, Egypt
2College of Computer and Information Sciences, Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia
3Faculty of Computer and Information Sciences, Ain Shams University, Cairo, Egypt
*Corresponding Author: Hussein Abulkasim. Email: abulkasim@scinv.au.edu.eg
Received: 02 December 2021; Accepted: 11 January 2022

Abstract: Quantum key agreement is a promising key establishing protocol that can play a significant role in securing 5G/6G communication networks. Recently, Liu et al. (Quantum Information Processing 18(8):1-10, 2019) proposed a multi-party quantum key agreement protocol based on four-qubit cluster states was proposed. The aim of their protocol is to agree on a shared secret key among multiple remote participants. Liu et al. employed four-qubit cluster states to be the quantum resources and the X operation to securely share a secret key. In addition, Liu et al.'s protocol guarantees that each participant makes an equal contribution to the final key. The authors also claimed that the proposed protocol is secure against participant attack and dishonest participants cannot generate the final shared key alone. However, we show here that Liu et al. protocol is insecure against a collusive attack, where dishonest participants can retrieve the private inputs of a trustworthy participant without being caught. Additionally, the corresponding modifications are presented to address these security flaws in Liu et al.'s protocol.

Keywords: Quantum key agreement; 5G/6G communication networks; collusive attacks; quantum cryptography

1  Introduction

The recent advancement of quantum technology threatens the ability of classical cryptosystems, including 5G/6G communication networks to secure data and communications against growing security attacks [1,2]. In this context, the concept of quantum cryptography or quantum key distribution (QKD) was introduced by Bennet and Brassard [3]. Thanks to the principle of quantum physics, quantum cryptography can provide unconditional security solutions whose security has been proven by [4]. These solutions may be adopted to secure 5G/6G communication networks [5–7]. Subsequently, scholars focused their attention and passion on quantum communication and quantum cryptography, and various quantum protocols were investigated, including quantum secure direct communication [8,9], quantum secret sharing [10–13], quantum teleportation [14], quantum private computation [15–17], quantum signature [18], quantum key agreement (QKA) [19–23], and so on. Currently, QKA is one of the most significant aspects that may be used to generate a secured shared key between two or more distance users using a public quantum channel. It differs from the QKD protocol, which predetermines the key and then distributes it to the users in that no user or subgroup can independently identify the shared key.

In 2004, Zhou et al. [19] presented the pioneering work of the QKA protocol. Several QKA schemes have also been introduced throughout time [20–23]. In the same year, another QKA protocol was proposed based on entangled quantum states. Unfortunately, as Chong et al. [24] pointed out, it was not a true QKA protocol since malicious users may derive the final shared key independently and entirely. In 2010, a QKA protocol based on the BB84 protocol was suggested, which is proved to be secure against inside and outside attacks [24]. In 2014, the authors in [25] developed an efficient two-user QKA protocol using four-qubit cluster quantum states. However, the authors could not extend their protocol to the multi-party case. The multi-party case of the QKA protocol is more complicated, but it is more suitable for real applications. As a result, the multi-party case of the QKA protocol has gotten a lot of interest [26–33].

Recently, Liu et al. [34] (Liu-QKA protocol) presented an interesting multi-party QKA protocol with four-qubit quantum cluster states. Their protocol adopted the four-qubit quantum cluster state as a quantum resource and a unitary operation to generate and share a secure key. Liu-QKA protocol generated and shared quantum key with high efficiency. The authors claimed that their protocol is secure against the outsider and participant attacks. However, our work shows that Liu-QKA protocol cannot resist the collusive attack. Two or more malicious participants can drive the private inputs of the honest ones and execute the protocol without being caught. The rest of this manuscript is organized as follows. A review of Liu-QKA protocol is presented in Section 2. Sections 3 introduces the suggested attack strategy on Liu=-QKA protocol and the suggested improvement. Finally, Section 4 concludes this work.

2  Review of Liu-QKA Protocol

This subsection introduces a brief background of Liu-QKA protocol.

2.1 Preliminaries

Liu-QKA protocol used the X operation to flip qubits, where X|0⟩=|1⟩ and X|1⟩=|0. Here, the X operation represents the matrix |0110|. Liu-QKA protocol also used 4-qubit cluster states as quantum resources, that is

|q⟩1234=((|0000⟩+|0011⟩+|1100⟩−|1111⟩)1234)/2,(1)

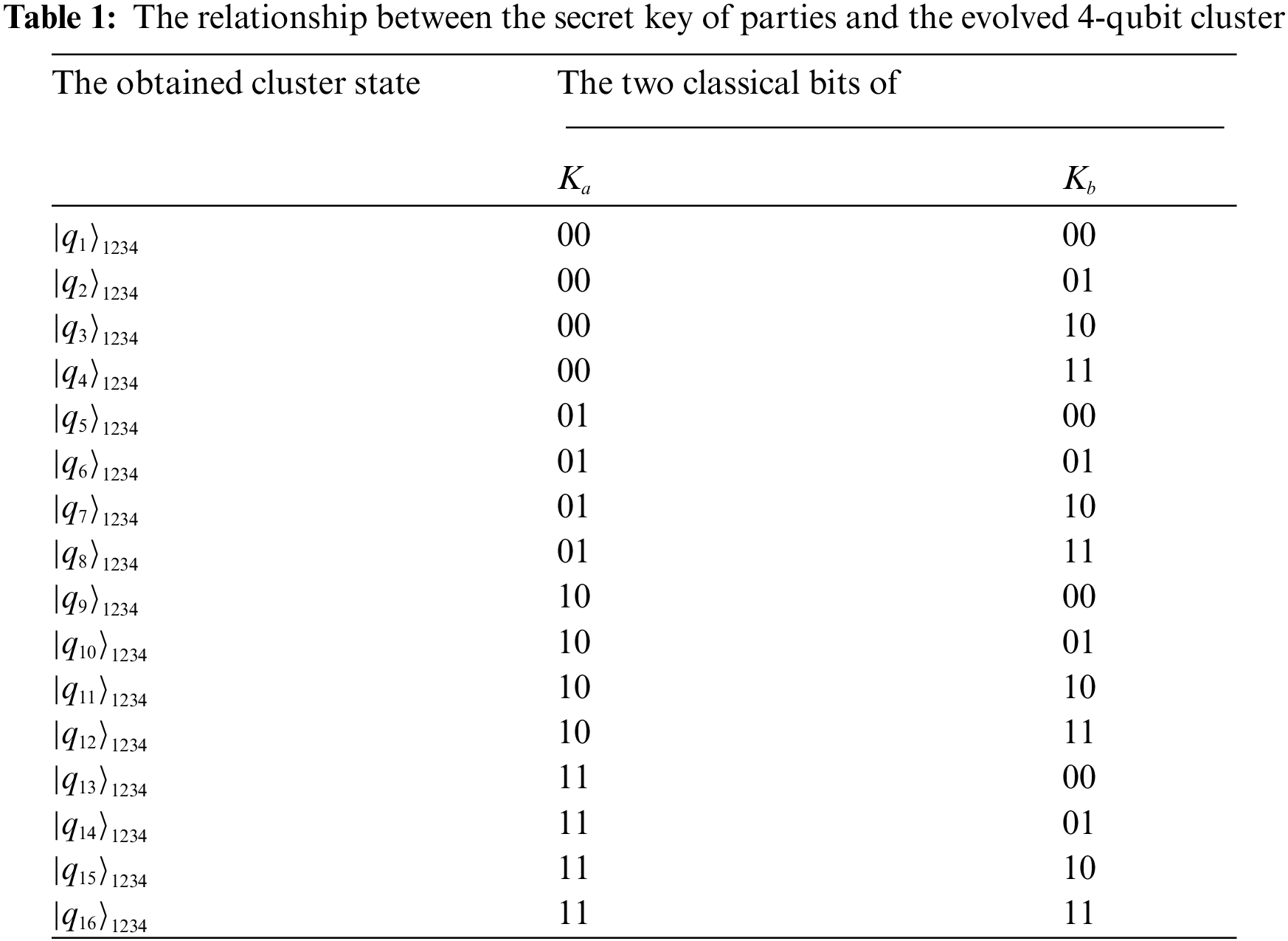
Assume that two parties Alice and Bob have two random secret keys Ka=(Ka1,Ka2,…,KaN) and Kb=(Kb1,Kb2,…,KaN), respectively. Here, Kaj, Kbj∈{00,01,10,11} and j=1,2,3,…,N. According to Ka, Alice applies the X operation to qubits 1 and 2 to the 4-qubit cluster state |q⟩1234 based on the following rule: When the first classical bit of Ka is 0 (1) Alice does not apply any operation to qubit 1 (Alice flips qubit 1). When the second classical bit of Ka is 0 (1) Alice does not apply any operation to qubit 2 (Alice flips qubit 2). Similarly, according to Kb, Bob applies the X operation to qubits 3 and 4 to the 4-qubit cluster state |q⟩1234 based on the following rule: When the third classical bit of Kb is 0 (1) Bob does not apply any operation to qubit 3 (Bob flips qubit 3). When the fourth classical bit of Kb is 0 (1) Bob does not apply any operation to qubit 4 (Bob flips qubit 4). Finally, one cluster state from the below 16 cluster states will be obtained:

|q11234=((|0000+|0011+|1100−|1111)1234)/2,|q21234=((|0001+|0010+|1101−|1110)1234)/2,|q31234=((|0010+|0001+|1110−|1101)1234)/2,|q41234=((|0011+|0000+|1111−|1100)1234)/2,|q51234=((|0100+|0111+|1000−|1011)1234)/2,|q61234=((|0101+|0110+|1001−|1010)1234)/2,|q71234=((|0110+|0101+|1010−|1001)1234)/2,|q81234=((|0111+|0100+|1011−|1000)1234)/2,|q91234=((|1000+|1011+|0100−|0111)1234)/2,|q101234=((|1001+|1010+|0101−|0110)1234)/2,|q111234=((|1010+|1001+|0110−|0101)1234)/2,|q121234=((|1011+|1000+|0111−|0100)1234)/2,|q131234=((|1100+|1111+|0000−|0011)1234)/2,|q141234=((|1101+|1110+|0001−|0010)1234)/2,|q151234=((|1110+|1101+|0010−|0001)1234)/2,|q161234=((|1111+|1100+|0011−|0000)1234)/2,(2)

The relationship between secret key of parties and the evolved 4-qubit cluster is indicated in Tab. 1.

2.2 Liu-QKA Protocol

The steps of Liu-QKA's protocol can be described as follows:

(1)   Each party (Pi) generates m 4-qubit cluster states (|q⟩1234) and forms subsequence Sk,ii by picking up the k−th qubits from every cluster state, where k=1,2,3,and4, i=0,1,…,(n−1). For detecting eavesdropping, Pi randomly generates enough number of decoy-qubits from the states {|0⟩,|1⟩,|±⟩=12(|0⟩±|1⟩)} and randomly puts them in the subsequence Sk,ii getting Sk,ii∗. Subsequently, Pi sends the two subsequences {Si,1i∗, Si,2i∗}* to P(i−1) and sends the other two subsequences {Si,3i∗, Si,4i∗} to P(i+1), respectively, where (i±1)=(i±1)modn.

(2)   Upon P(i−1) (P(i+1)) receiving the subsequences {Si,1i∗, Si,2i∗}({Si,3i∗, Si,4i∗}), Pi and P(i−1) (P(i+1)) check the security of communication. First, Pi publicly announces the position of the decoy-qubits and their measurement bases {Z−basis or X−basis}. Second, P(i−1) (P(i+1)) measures the decoy-qubits by the corresponding measurement bases and sends Pi the measurement results. Finally, they end therotocol if the error rate exceeds a pre-determined value. Otherwise, they perform the next process.

(3)   P(i−1) (P(i+1)) discard the decoy-qubits and recovers the subsequence {Si,1i, Si,2i}({Si,3i, Si,4i}). P(i−1) (P(i+1)) then applies the X operation to the j-th of the Si,1i and the j-th of Si,2i (the j-th of the Si,3i and the j-th of Si,4i) according to K(i−1)j(K(i+1)j) to obtain the subsequences {Si,1(i−1), Si,2(i−2)}({Si,3(i+1), Si,4(i+2)}), where j=1,2,…,N. The governing rule is as follows: When the first classical bit of K(i−1)j is 0 (1) the participant does not apply any operation to the j-th of Si,1(i−1) (the participant flips the j-th of Si,1(i−1)). When the second classical bit of K(i−1)j is 0 (1) the participant does not apply any operation to the j-th of Si,1(i−1) (the participant flips the j-th of Si,1(i−1)). When the first classical bit of K(i+1)j is 0 (1) the participant does not apply any operation to the j-th of Si,3(i+1) (the participant flips the j-th of Si,3(i+1)). When the second classical bit of K(i+1)j is 0 (1) the participant does not apply any operation to the j-th of Si,4(i+1) (the participant flips the j-th of Si,4(i+1)).

(4)   P(i−1) (P(i+1)) inserts enough number of decoy-qubits into the subsequences Si,1(i−1) and Si,2(i−1) (Si,3(i+1) and Si,4(i+1)), at random positions, obtaining Si,1(i−1)∗ and Si,2(i−1)∗ (Si,3(i+1)∗ and Si,4(i+1)∗). P(i−1) (P(i+1)), respectively. Then sends the subsequences Si,1(i−1)∗ and Si,2(i−1)∗ (Si,3(i+1)∗ and Si,4(i+1)∗) to P(i−2)P(i+2)).

(5)   P(i−2),P(i+2),…,P(i−n−32) and P(i+n−32) check the security of communications and then perform the X operation as in steps 3 and 4. The participants continue the process until P(i−n−12) and P(i+n−12) send Si,1(i−n−12) and Si,2(i−n−12) (Si,3(i+n−12) and Si,4(i+n−12)) to Pi.

(6)   Pi and P(i−n−12)(P(i+n−12)) check the security of communications by computing the error rate of the measurement results. They end the protocol of the error rate exceeds a threshold value. Otherwise, they head to the upcoming step.

(7)   After each Pi recovers Si,1(i−n−12) and Si,2(i−n−12) (Si,3(i+n−12) and Si,4(i+n−12)) she/he first combines Si,1(i−n−12) and Si,2(i−n−12) (Si,3(i+n−12) and Si,4(i+n−12)) and then measures them based on the corresponding cluster bases. Finally, the final shared key (K) can be computed using the following expression: K=Ki⊕Ki−1⊕…⊕K(i−n−12)⊕K(i+n−12)⊕…⊕Ki+1, where i=1,2,…,(n−1).

3  Collusive Attack on Liu-QKA Protocol and Improvement

We show in this section that Liu-QKA Protocol is vulnerable to a collusive attack, in which two dishonest players can obtain the secret information of an honest participant. Then, to address this flaw, an improvement is provided.

3.1 The Collusive Attack on Liu-QKA Protocol

The collusive attack on Liu-QKA scheme can be described as follows. Assume that we have three participants P0, P1, and P2. Figs. 1a–1c represent the process of the first cycle that enables P0 from legally obtaining the final shred key, while Fig. 1d represent the collusive attack strategy of the dishonest participants. In this assumption, assume P0. and P2 are two dishonest participants try to reveal the private data of the honest participant (P1). In step (1), P0 generates four subsequences. P0 sends two subsequences to P1 and the other two subsequences two P2. In step (2), P1 and P2 check the security of the quantum channels with P0. If the communications are secure, they continue the protocol. In step (3), P1 and P2 discard the decoy qubits and encode their private data. In step (4), P1 and P2 insert enough number of decoy-qubits to their evolved subsequences and check the security of communication in steps (5) and (6). In step (7), P0 compares the evolved subsequences with original ones, then computes the final key. These processes are sufficient for sharing the final key if performed honestly. However, the dishonest participants (P0 and P2) are able to steal the private information of P1 and can generate the final key alone without being noticed. As indicated in Fig. 1d, P0 sends the two subsequences S3,00 and S4,00 to P1, and may also sends them to if she/he decides to collude with P2. In this case, P2 will be able to extract the private information of P1 by comparing the original S3,00 and S4,00 (that were received from P0) by the evolved S3,00∗ and S4,00∗ that were received from P1. Of course, P2 will ask P0 to send the required information for measuring the S3,00 and S4,00. Based on this strategy, the dishonest participants can easily extract the private information of the honest participants (P1) and generate the final key alone without being detected.

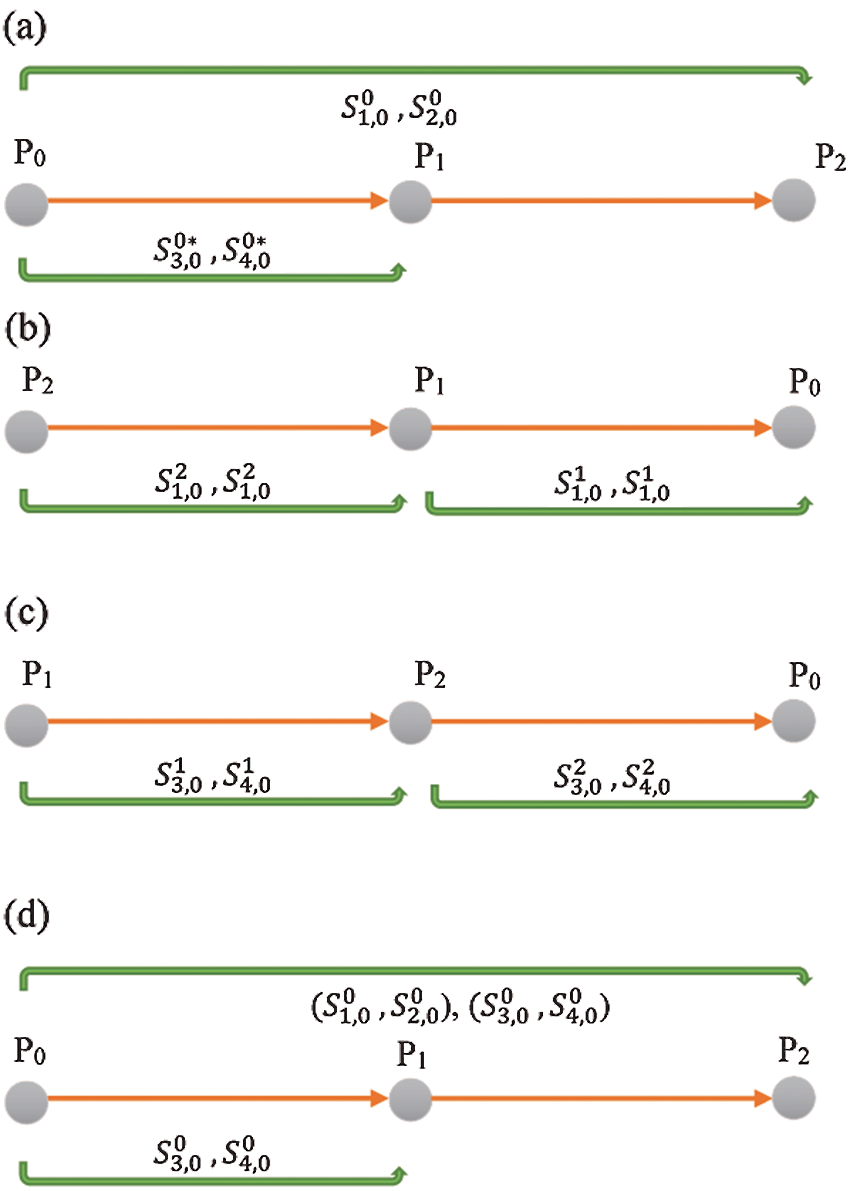
Figure 1: (a), (b), and (c) represent an example of the three-party Liu-QKA protocol, while (d) represents the collusive attack on Liu-QKA's protocol of three participants

3.2 Improvement on Liu-QKA Protocol

A third party is adopted in many exists circular multi-party QKA protocol, such as in Ref. [35] to provide participants random sequences of single-particle quantum states to cover their private keys, and in Ref. [36] to detect dishonest participants. In this work, we adopt a semi-honest third party (TP) with a certain task to address the security pitfall in Liu-QKA's protocol. Semi-honest means here that the TP executes the protocol honestly but not allowed to collude with other dishonest participants. The TP will collaborate with participants to detect internal attacks including the collusive attack. TP generates n random secret keys (KiTPj=(KiTP1,KiTP2,…,KiTPN), where i=1,2,…n, j=1,2,…,N, and KiTPj∈{00,01,10,11}. TP then sends KiTPj to Pi through QKD [3]. Pi encrypts her/his private key with TP's key obtaining a new encrypted key (EKij), i.e., EKij=KiTPj⊕Kij, where Kij is the private key of Pi. The purpose of this process is to protect the private key of Pi form leakage during use in the encoding process. To circumvent the above-mentioned attack, Liu-QKA Protocol should be modified:

Steps (1∗), (2∗), (4∗), (5∗), and (6∗) are the same as steps (1), (2), (4), (5), and (6), in Sub section 2.2, respectively.

The remaining steps should be modified as follows:

(3∗)P(i−1)(P(i+1)) discard the decoy-qubits and recovers the subsequence {Si,1i, Si,2i}({Si,3i, Si,4i}). P(i−1) (P(i+1)) then applies the X operation to the j-th of the Si,1i and the j-th of Si,2i (the j-th of the Si,3i and the j-th of Si,4i) according to EK(i−1)j(EK(i+1)j) to obtain the subsequences {Si,1(i−1), Si,2(i−2)}({Si,3(i+1), Si,4(i+2)}), where j=1,2,…,N. The governing rule is as follows: When the first classical bit of EK(i−1)j is 0 (1) the participant does not apply any operation to the j-th of Si,1(i−1) (the paicipant flips the j-th of Si,1(i−1)). When the second classical bit of EK(i−1)j is 0 (1) the participant does not apply any operation to the j-th of Si,1(i−1) (the participant flips the j-th of Si,1(i−1)). When the first classical bit of EK(i+1)j is 0 (1) the participant does not apply any operation to the j-th of Si,3(i+1) (the participant flips the j-th of Si,3(i+1)). When the second classical bit of EK(i+1)j is 0 (1) the parcipant does not apply any operation to the j-th of Si,4(i+1) (the participant flips the j-th of Si,4(i+1)).

(7∗) After each Pi recovers Si,1(i−n−12) and Si,2(i−n−12) (Si,3(i+n−12) and Si,4(i+n−12)) she/he first combines Si,1(i−n−12) and Si,2(i−n−12) (Si,3(i+n−12) and Si,4(i+n−12)) and then measures them based on the corresponding cluster bases. Finally, the final shared key (K) can be computed using the following expression: K=KiTPj⊕(EKij⊕EK(i−1)j⊕…⊕EK(i−n−12)j⊕EK(i+n−12)j⊕…⊕EK(i+1)j), where i=1,2,…,(n−1).

4  Conclusion

Liu et al. presented an interesting quantum key agreement protocol with four-qubit cluster quantum states, which could be used as an unconditional security solution for enhancing the security of 5G/6G networks against the increasing cyber-attacks. However, this work shows that Liu et al.'s protocol is vulnerable to collusive attacks, where dishonest participants can conspire together to obtain the private information of a trustworthy participant without being caught. With the help of a third party, we suggested an additional process to protect participants’ private data from leakage. Finally, an improvement is suggested to address the security loopholes in Liu et al.'s protocol.

Acknowledgement: The authors acknowledge the Academy of Scientific Research & Technology (ASRT) in Egypt for their financial support.

Funding Statement: This project was financially supported by the Academy of Scientific Research and Technology (ASRT) in Egypt, under the project of Science Up, Grant no. 6626.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  D. J. Bernstein and T. Lange, “Post-quantum cryptography,” Nature, vol. 549, no. 7671, pp. 188–194, 2017. [Google Scholar]

 2.  P. Porambage, G. Gür, D. P. M. Osorio, M. Liyanage, A. Gurtov et al.., “The roadmap to 6G security and privacy,” IEEE Open Journal of the Communications Society, vol. 2, pp. 1094–1122, 2021. [Google Scholar]

 3.  C. H. Bennett and G. Brassard, “Quantum cryptography: Public key distribution and coin tossing,” in Conf. on Computers, Systems and Signal Processing, Bangalore, India, vol. 175, 1984. [Google Scholar]

 4.  P. W. Shor and J. Preskill, “Simple proof of security of the BB84 quantum key distribution protocol,” Physical Review Letters, vol. 85, no. 2, p. 441, 2000. [Google Scholar]

 5.  S. J. Nawaz, S. K. Sharma, S. Wyne, M. N. Patwary and M. Asaduzzaman, “Quantum machine learning for 6G communication networks: State-of-the-art and vision for the future,” IEEE Access, vol. 7, pp. 46317–46350, 2019. [Google Scholar]

 6.  A. Manzalini, “Quantum communications in future networks and services,” Quantum Reports, vol. 2, no. 1, pp. 221–232, 2020. [Google Scholar]

 7.  I. B. Djordjevic, “On global quantum communication networking,” Entropy, vol. 22, no. 8, p. 831, 2020. [Google Scholar]

 8.  C. Wang, F. -G. Deng, Y. -S. Li, X. -S. Liu and G. L. Long, “Quantum secure direct communication with high-dimension quantum superdense coding,” Physical Review A, vol. 71, no. 4, p. 044305, 2005. [Google Scholar]

 9.  R. Qi, Z. Sun, Z. Lin, P. Niu, W. Hao et al., “Implementation and security analysis of practical quantum secure direct communication,” Light: Science & Applications, vol. 8, no. 1, pp. 1–8, 2019. [Google Scholar]

10. H. Abulkasim, S. Hamad, K. El Bahnasy and S. Z. Rida, “Authenticated quantum secret sharing with quantum dialogue based on Bell states,” Physica Scripta, vol. 91, no. 8, p. 085101, 2016. [Google Scholar]

11. H. Abulkasim, S. Hamad, A. Khalifa and K. El Bahnasy, “Quantum secret sharing with identity authentication based on Bell states,” International Journal of Quantum Information, vol. 15, no. 4, p. 1750023, 2017. [Google Scholar]

12. G. Gao, Y. Wang, D. Wang and L. Ye, “Comment on ‘Authenticated quantum secret sharing with quantum dialogue based on Bell states’,” Physica Scripta, vol. 93, no. 2, p. 027002, 2018. [Google Scholar]

13. H. Abulkasim, S. Hamad and A. Elhadad, “Reply to Comment on ‘Authenticated quantum secret sharing with quantum dialogue based on Bell states’,” Physica Scripta, vol. 93, no. 2, p. 027001, 2018. [Google Scholar]

14. D. Bouwmeester, J. -W. Pan, K. Mattle, M. Eibl, H. Weinfurter et al.., “Experimental quantum teleportation,” Nature, vol. 390, no. 6660, pp. 575–579, 1997. [Google Scholar]

15. H. Abulkasim, A. Mashatan and S. Ghose, “Quantum-based privacy-preserving sealed-bid auction on the blockchain,” Optik, vol. 242, p. 167039, 2021. [Google Scholar]

16. H. Abulkasim, A. Farouk, S. Hamad, A. Mashatan and S. Ghose, “Secure dynamic multiparty quantum private comparison,” Scientific Reports, vol. 9, no. 1, pp. 1–16, 2019. [Google Scholar]

17. H. Abulkasim, H. N. Alsuqaih, W. F. Hamdan, S. Hamad, A. Farouk et al., “Improved dynamic multi-party quantum private comparison for next-generation mobile network,” IEEE Access, vol. 7, pp. 17917–17926, 2019. [Google Scholar]

18. G. Zeng and C. H. Keitel, “Arbitrated quantum-signature scheme,” Physical Review A, vol. 65, no. 4, p. 042312, 2002. [Google Scholar]

19. N. Zhou, G. Zeng and J. Xiong, “Quantum key agreement protocol,” Electronics Letters, vol. 40, no. 18, pp. 1149–1150, 2004. [Google Scholar]

20. H. Abulkasim, A. Mashatan and S. Ghose, “Secure multiparty quantum key agreement against collusive attacks,” Scientific Reports, vol. 11, no. 1, pp. 1–8, 2021. [Google Scholar]

21. A. Elhadad, S. Abbas, H. Abulkasim and S. Hamad, “Improving the security of multi-party quantum key agreement with five-qubit brown states,” Computer Communications, vol. 159, pp. 155–160, 2020. [Google Scholar]

22. H. Abulkasim and A. Alotaibi, “Improvement on ‘multiparty quantum key agreement with four-qubit symmetric w state’,” International Journal of Theoretical Physics, vol. 58, no. 12, pp. 4235–4240, 2019. [Google Scholar]

23. H. Abulkasim, A. Farouk, H. Alsuqaih, W. Hamdan, S. Hamad et al.., “Improving the security of quantum key agreement protocols with single photon in both polarization and spatial-mode degrees of freedom,” Quantum Information Processing, vol. 17, no. 11, pp. 1–11, 2018. [Google Scholar]

24. S. -K. Chong, C. -W. Tsai and T. Hwang, “Improvement on “quantum key agreement protocol with maximally entangled states”, International Journal of Theoretical Physics, vol. 50, no. 6, pp. 1793–1802, 2011. [Google Scholar]

25. D. -S. Shen, W. -P. Ma and L. -l. Wang, “Two-party quantum key agreement with four-qubit cluster states,” Quantum Information Processing, vol. 13, no. 10, pp. 2313–2324, 2014. [Google Scholar]

26. H. Zhu, Z. Li, X. Wang and L. Chen, “Multi-party quantum key agreement protocol for smart home environment,” International Journal of Theoretical Physics, vol. 60, no. 10, pp. 3948–3960, 2021. [Google Scholar]

27. J. Tang, L. Shi, J. Wei, Y. Xue and H. Yu, “Novel multi-party quantum key agreement protocols under collective noise,” Modern Physics Letters B, vol. 35, no. 8, p. 2150137, 2021. [Google Scholar]

28. L. Li and Z. Li, “A verifiable multi-party quantum key distribution protocol based on repetitive codes,” Information Sciences, vol. 585, pp. 232–245, 2021. [Google Scholar]

29. X. Ma, C. Wang, Z. Li and H. Zhu, “Multi-party quantum key distribution protocol with new bell states encoding mode,” International Journal of Theoretical Physics, vol. 60, no. 4, pp. 1328–1338, 2021. [Google Scholar]

30. W. Zhao, R. Shi, Y. Feng and X. Ruan, “Conference key agreement based on continuous-variable quantum key distribution,” Laser Physics Letters, vol. 18, no. 7, p. 075205, 2021. [Google Scholar]

31. L. -J. Liu and Z. -H. Li, “A verifiable quantum key agreement protocol based on six-qubit cluster states,” The European Physical Journal D, vol. 75, no. 7, pp. 1–10, 2021. [Google Scholar]

32. J. Kim, “Entanglement of formation and monogamy of multi-party quantum entanglement,” Scientific Reports, vol. 11, no. 1, pp. 1–9, 2021. [Google Scholar]

33. Z. Cai, S. Liu, Z. Han and R. Wang, “A quantum blind multi-signature method for the industrial blockchain,” Entropy, vol. 23, no. 11, p. 1520, 2021. [Google Scholar]

34. H. -N. Liu, X. -Q. Liang, D. -H. Jiang, G. -B. Xu and W. -M. Zheng, “Multi-party quantum key agreement with four-qubit cluster states,” Quantum Information Processing, vol. 18, no. 8, pp. 1–10, 2019. [Google Scholar]

35. H. Cao and W. Ma, “Multi-party traveling-mode quantum key agreement protocols immune to collusive attack,” Quantum Information Processing, vol. 17, no. 9, pp. 1–14, 2018. [Google Scholar]

36. W. -C. Huang, Y. -K. Yang, D. Jiang, C. -H. Gao and L. -J. Chen, “Designing secure quantum key agreement protocols against dishonest participants,” International Journal of Theoretical Physics, vol. 58, no. 12, pp. 4093–4104, 2019. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.