DOI:10.32604/cmc.2022.028391

| Computers, Materials & Continua DOI:10.32604/cmc.2022.028391 |  |
| Article |
Artificial Fish Swarm for Multi Protein Sequences Alignment in Bioinformatics
1Department of Computer Science, College of Computer and Information Sciences, Jouf University, Saudi Arabia (KSA)
2Department of Computer Science, Faculty of Computers and Information, Menoufia University, Egypt
3Department of Information Systems, College of Computer and Information Sciences, Jouf University, Saudi Arabia (KSA)
4Department of Information Systems and Technology, Faculty of Graduates Studies and Research, Cairo University, Egypt
*Corresponding Author: Medhat A. Tawfeek. Email: maelaarg@ju.edu.sa
Received: 09 February 2022; Accepted: 18 March 2022
Abstract: The alignment operation between many protein sequences or DNA sequences related to the scientific bioinformatics application is very complex. There is a trade-off in the objectives in the existing techniques of Multiple Sequence Alignment (MSA). The techniques that concern with speed ignore accuracy, whereas techniques that concern with accuracy ignore speed. The term alignment means to get the similarity in different sequences with high accuracy. The more growing number of sequences leads to a very complex and complicated problem. Because of the emergence; rapid development; and dependence on gene sequencing, sequence alignment has become important in every biological relationship analysis process. Calculating the number of similar amino acids is the primary method for proving that there is a relationship between two sequences. The time is a main issue in any alignment technique. In this paper, a more effective MSA method for handling the massive multiple protein sequences alignment maintaining the highest accuracy with less time consumption is proposed. The proposed method depends on Artificial Fish Swarm (AFS) algorithm that can break down the most challenges of MSA problems. The AFS is exploited to obtain high accuracy in adequate time. ASF has been increasing popularly in various applications such as artificial intelligence, computer vision, machine learning, and data-intensive application. It basically mimics the behavior of fish trying to get the food in nature. The proposed mechanisms of AFS that is like preying, swarming, following, moving, and leaping help in increasing the accuracy and concerning the speed by decreasing execution time. The sense organs that aid the artificial fishes to collect information and vision from the environment help in concerning the accuracy. These features of the proposed AFS make the alignment operation more efficient and are suitable especially for large-scale data. The implementation and experimental results put the proposed AFS as a first choice in the queue of alignment compared to the well-known algorithms in multiple sequence alignment.
Keywords: Multiple sequence alignment; swarm intelligence; artificial fish swarm; protein sequences
The difference between the pairwise alignment and multiple sequence alignment (MSA) is that the pairwise alignment aligns only two sequences, but MSA aligns three or more sequences. The alignment operation finds the similarity and the degree of matching to indicate the sequences relationship [1]. The quality enhancement of the MSA in a short time is still a hot topic of research. Large data set of sequences may result in a narrow bottleneck that causes the alignment process to be lengthy and time consuming. MSA significantly contributes to extracting data from an organic sequence. Traditional techniques are so boring so sequences alignment does not work effectively, and there is a need to develop advanced sequences alignment methods [2].
Deoxyribonucleic Acid (DNA), which is the main singularity, identifies the creature organism. The DNA lies in nucleus and is regulated into chromosomes. DNA conveys multiple genes that hold the cell genetic information [3]. This information aids in how to construct a protein molecule. When protein is needed, the DNA genes are reshaped into Ribonucleic Acid (RNA) (transcription). Protein is constructed outside nucleus-based RNA code. This process is as follows: Information streams from DNA that contains four nucleotides [A, T, C, and G] into RNA that contains four nucleotides [A, U, C, and G] [4]. A refers to Adenine, G refers to Guanine, C refers to Cytosine, T refers to Thymine (T) and U refers to Uracil. Finally, information steams from RNA into protein (20 amino acids) as shown in Fig. 1. The protein sequence can range from modicum to more than thousands of residues [5].
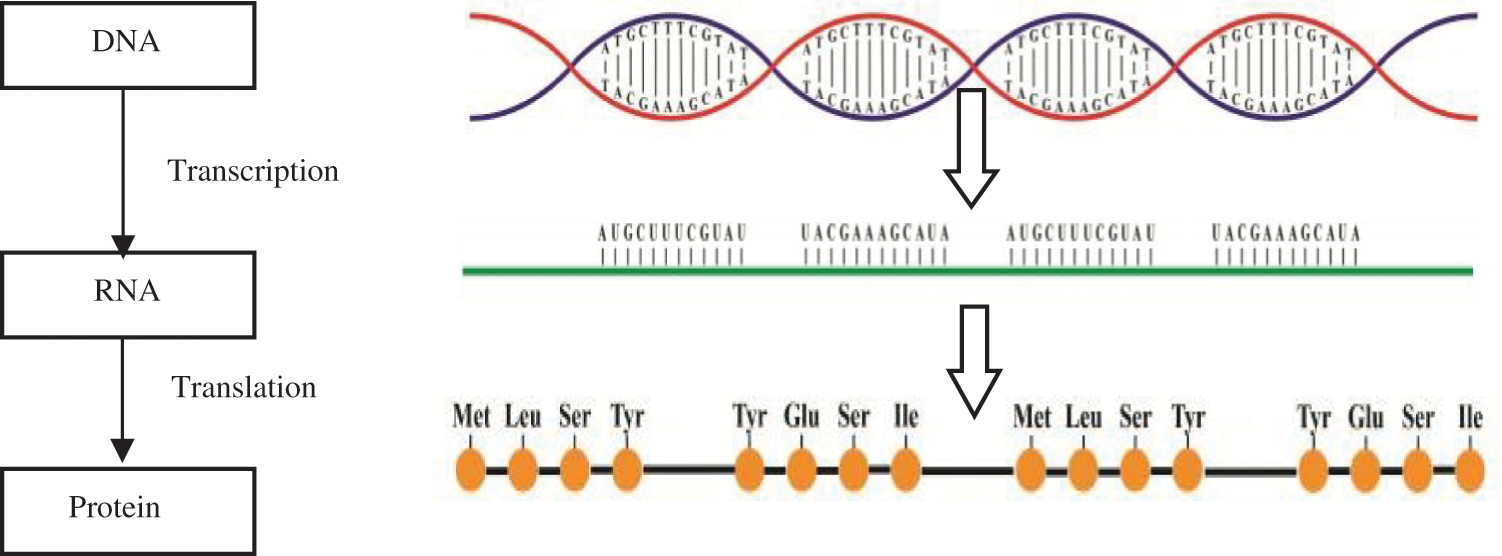
Figure 1: DNA, RNA and protein
DNA holds information of the gene and RNA exploits information to aid cell to produce the protein. Researchers of biology depend on sequences of DNA/RNA/protein in molecular biology, proving genetics and taking treatment decisions. The alignment for different sequences is a mechanism of regulating sequences to distinguish the similar area. Aligning is executed by replacing an element, inserting an element or removing an element repeatedly. The alignment method has a correlated score that should be maximized. Alignment can be categorized into two forms; global form or local form. In the first alignment form, sequences are matched completely for growing the degree of alignment globally. It also exploits the full merit of the bulk of matched up remnants. The most common algorithm for the global alignment form is Needleman-Wunsch. It boosts the bulks of matches of amino acids and lowers the bulks of needed gaps to find the best globally optimal alignment. This form is more efficient when matching mightily related sequences. The second alignment form aligns sub-remnants from the sequences usefully. It boosts the sub-remnants similarity alignment. It searches for the related remnants in two sequences. This form is more elastic than the global alignment form. The most common algorithm for the local alignment form is Smith-Waterman [6].
MSA can be categorized as local or global alignment. MSA is a very intense calculation process, and more powerful hardware that is so expensive needed to manipulate the alignment process. It is not applicable to exploit a practical algorithm to find an optimal solution for MSA problem because it is NP-complete problem. To solve this dilemma, many meta-heuristic methods are adopted and proposed on the basis of various methodologies like progressive, iterative or hybridization [2].
The main aspect of this research is to propose a more effective MSA method for handling the massive multiple protein sequences maintaining the highest accuracy with less time consumption. The proposed method depends on Artificial Fish Swarm (AFS) algorithm that can break down the most challenges of MSA problems. ASF is considered as a type of modern meta-heuristics that is an optimization section in computer science for hard problems expatiating. It belongs to swarm intelligence techniques that can solve complex problems, which overrun the ability of their individuals without needing a central supervision [7]. Multiple sequence alignment can be constructed by several different techniques. A comparative study of the most well-known programs and the proposed AFS for multiple sequence alignment is presented. The MSA programs comparison is necessary for biologist to select the best MSA software corresponding to their needs.
The reminder of this paper is formulated as follows. Section 2 scans a brief background that includes MSA, benchmark datasets and AFS. The related work is presented in Section 3. The proposed Artificial Fish Swarm for Multi Protein Sequences Alignment (AFSMPSA) is introduced in Section 4. The implementation and comparative study are construed in Section 5. Section 6 gives the conclusion of this research and presents future study.
This section includes the most relevant topics to the scope of the study; they are MSA, benchmarks datasets and AFS. Each topic is overviewed separately in a sub-section as follows.
2.1 Multiple Sequence Alignment (MSA)
The MSA is considered as the stretching of Pairwise Sequence Alignment (PSA) as it contains more than two sequences. MSA tries to predict the similarity between more than two biological sequences. It is considered as a generalization to PSA. MSA foretells the texture of new sequences, the synthesis of protein in families, and directs the relationship between the available sequences [8]. Fig. 2 shows an example of four protein sequences alignment. The alignment process is handled by adding gaps (-) into different locations of sequences simultaneously.
The MSA procedures have been categorized into dynamic programming method that is based on divide and conquer and heuristic techniques. The dynamic programming uses match score and mismatch score for alignment. It gets accurate alignment and increases the result function. It applies PSA of the two sequences based on the similarity score. The similarity score is calculated by the substitution matrix or the scoring system. The scoring system sets score values for a match, a mismatch, and a gap [9]. For example, it may set +2 for the match, set −1 for mismatch and set −2 for gap penalty. It can compute the similarity score of the following two sequences as similarity score equals (4*(+2)) + (1*(−1)) + (2*(−2)) = + 3.
Sequence 1: T C T A G T G
Sequence 2: – C T A – T A

Figure 2: Four protein sequences alignment example
Substitution matrix is an array that represents the various scores for the nucleotide substitution. It has a row and a column for each possible letter in the sequence as for the DNA, which uses four rows and four columns [2]. Although dynamic programming gives the optimal solution, it is impossible to apply it to MSA problem, which is very complex, so the heuristic techniques are resorted to. Fig. 3 classifies the various heuristic techniques. It is clarified by Fig. 3 that the heuristic techniques is classified into four types: Progressive techniques such as KALIGN algorithm [10], iterative techniques such as DIALIGN algorithm [11], probabilistic technique such as PROBCONS algorithm [9] and meta-heuristics techniques such as AFS [12], genetic [5] and other algorithms.
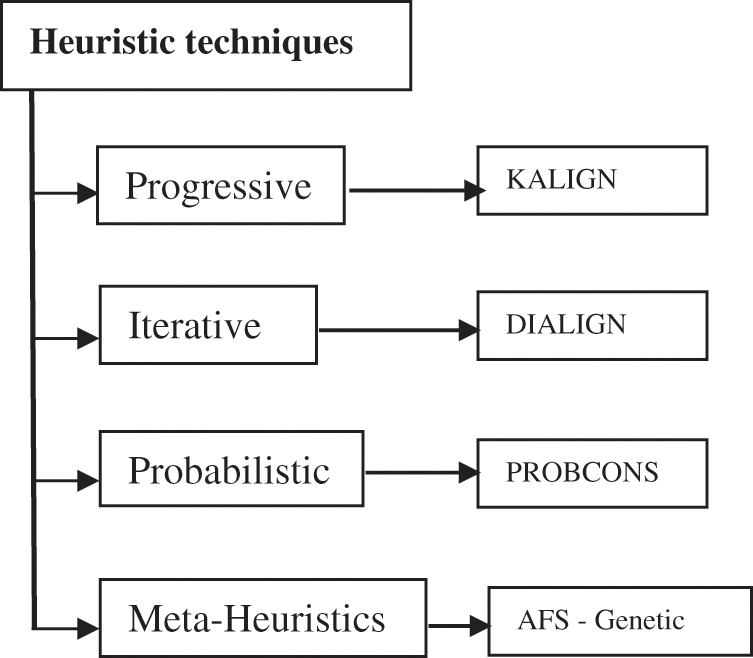
Figure 3: Various heuristic techniques for MSA problem
The progressive techniques depend on dynamic programming for performing sequences alignment. They start alignment in a pairwise method by using its algorithms such as Smith-Waterman or k-mer algorithm [13]. They show the sequences relationship by clustering methods like k-means. After that, a guide tree is regulated depending on score of similarity. Finally, sequences converged one after another by the guide tree. The MSA progressive techniques provide near-optimal solution for alignment and their popular methods are KALIGN [10], CLUSTAL-OMEGA [14], MAFFT algorithm [15], and RETALIGN [16].
The Iterative techniques are a protraction method for progressive MSA techniques, which alter the guide tree construction. They are proposed to enhance the efficiency of the alignment process. Firstly, they establish an initial MSA. After that, they divide them into subgroups. Secondly, they realign each subgroup by dynamic programming. Finally, they renovate the alignment until reaching stopping criteria [17]. The most common MSA iterative techniques are T-Coffee, MUSCLE and DIALIGN [11,18].
The probabilistic techniques carry out gradual consistency-based alignment. They exemplify all insufficient alignment with subsequent probability-based scoring. They exploit two folds of affine insertion penalties, guide tree computation through semi probabilistic clustering, iterative refinement and unsupervised Expectation-Maximization (EM) preparing of hole parameters. The most common MSA probabilistic technique is PROBCONS [9].
The meta-heuristics techniques, which are problem-independent, are high level frame works. It has the flexible ability to inspect the large search space efficiently and effectively using two paradoxical criteria: exploring and exploiting. They propose guidelines series for manipulating the optimization algorithms. They can often find efficient solutions with less computational stress than other MSA techniques. The scientific community has stated that meta-heuristics is a fertile, superior, viable and a substitution to traditional optimization methods. The most common meta-heuristics are genetic algorithms, Ant Colony Optimization (ACO), tabu search, Artificial Fish Swarm (AFS) and many other methods can be found in the literature [19].
2.2 Widespread Datasets of Protein
Many databases have proliferated in recent days. The most common databases of protein which include large amount of protein sequences are Swiss-Prot, HOMFAM [20], SAliBASE [21,22], PIR, Pfam [23], and BAliBASE [24,25]. There is another database for DNA and RNA sequences such as GenBank, HOMSTRAD, PDB, and RefSeq [2].
BAliBASE is considered as a benchmark dataset. It contains more accurate test cases exploited to measure MSA tools accuracy. It has a program of C language that is called bali_score for calculating SPscore and Tcscore that will be explained shortly [24].
SAliBASE is another benchmark dataset. Each dataset part in SAliBASE contains the corresponding alignment that is considered as a standard to evaluate MSA approaches. There are five parameters that control the database generation such as the sequence number, the rate of insertion, the rate of deletion, the length of the sequence, and indel size as in [21].
There are ranking measurements which give scored numeric value to scale the accuracy of MSA. The two most common of these measurements are SPscore and TCscore [6,26]. The SP term of SPscore refers to Sum-of-Pairs function. It decides how well programs can align input sequences in MSA. SP function should calculate the sum of aligned pairwise sequences score. It is a percentage of the sum of the P scores for all remnant pairs in each column line of alignment by the sum of the scores in dataset reference. The highest SPscore is preferred because it indicates the highest accuracy of alignment process. For instance, if we have the following four sequences, the sum of scores for all remnant pairs in each column line of alignment can be computed as follows.
Seq1: A G A
Seq2: – G T
Seq3: A G C
Seq3: C G G
Firstly, the P-score of each corresponding remnants is computed as following: P-score(A,–,A,C), P-score(G,G,G,G), P-score(A,T,C,G), etc.
P-score(A,–,A,C) = score(A,–) + score(A,A) + score(A,C) + score(–,A) + score(–,C) + score(A,C) = −2 + 2–1–2–2–1= −6.
P-score(G,G,G,G) = score(G,G) + score(G,G) + score(G,G) + score(G,G) + score(G,G) + score(G,G) = +2 +2 +2 +2 +2 +2 = +12.
Finally, the total P-scores divided by the sum of the scores in dataset reference produce the SPscore of the alignment process.
The TCscore term refers to Total Column score. TCscore is the binary function of score. It also examines how well programs can align input sequences in MSA correctly [26]. It is computed as the total number of matched columns in alignment to reference alignment. It is computed as the total C scores to the number of columns in the reference alignment. C score will be one if all remnants in the column are aligned similarly in the reference alignment, else C score will be zero. TCscore is computed by Eq. (1).
where, m is the number of columns reference alignment and Ci will be one if all the remnants in the column are aligned as in reference alignment, otherwise, Ci will be zero.
2.3 Artificial Fish Swarm (AFS)
The fishes of the water can reach the extreme nutrition area by two trajectories, alone or by keeping track of other fishes. Therefore, the area with the most fish in general is the region with the farthest food. According to this scenario, the AFS algorithm is based on the idea of synthetic fish that mimic the behavior of fish herds to find the best solution. Any artificial fish (AF) contains its own attitudes and data. All AF focuses on information from the environment through its sensory organs [27]. In AFS algorithm, the AF environment is considered as the solution area.
The main AF attitudes are Prey, Swarm, and Follow. In the Prey attitude, the AF searches for water areas with a high condensation of food and determine to proceed in that orientation. The Swarm attitude permits fishes to associate in groups to avert risks and confirms the swarm presence. The Follow attitude is utilized to follow other fish (one or more fishes) when they have attained the food. Furthermore, each AF has two cases: current case and environmental case. These cases control the next attitude of an AF. The current case contains the AF quality solution. The environmental case shows the case of other AF. Subsequently, the attitude is affected by the environment through special AF activities to construct a solution and other AF activities. Fig. 4 presents the AF visibility concept [28,29].
The AF in the middle of Fig. 4 can recognize the environment by seeing it by means of its vision. The visual reach of the AF is symbolized by Xv. The current state of AF is symbolized by X. If Xv is more preferable than X, then AF offers a step towards this trend and turns in another status called Xnext. Otherwise, the AF sustains exploring in the viewing area. The higher area of exploration refers to the extra knowledge of AF of all possible next situations for a better location [29,30].
AFS has comparable alluring attributes of genetic algorithm (GA), for example freedom from the information of the objective function and the capability to tackle hard nonlinear high dimensional issues. Moreover, it can accomplish quicker assembly speed and not to require many parameters to be changed. Though AFS does not have the hybrid and transformation processes utilized in GA, so AFS may be performed well without any challenges. AFS is likewise an optimizer in light of populace. Firstly, the framework is instated using a set of generated solutions randomly. Secondly it implements the search for the ideal one iteratively [27]. The most well-known AFS applications are used for optimization, management, and control. Additionally, they are used in several vital fields such as image processing, data mining, improving neural networks, networks, scheduling, and signal processing [29].
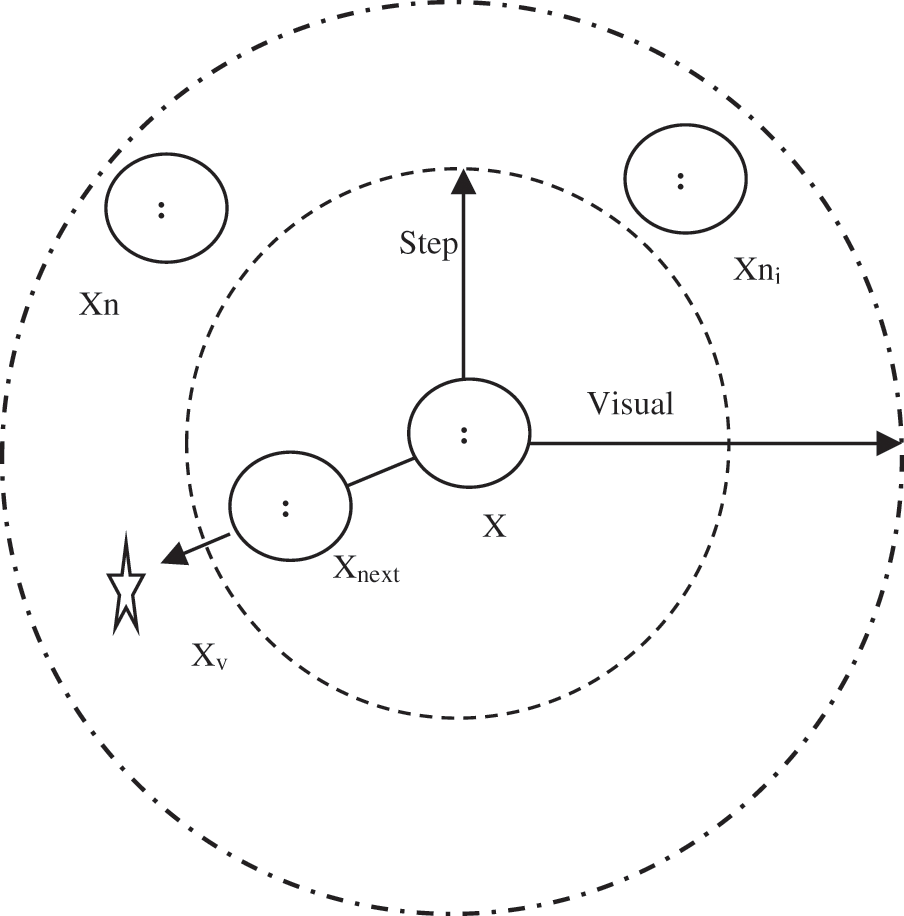
Figure 4: The visibility concept of an AF
The alignment between multiple sequences of protein or DNA is a very complex process of bioinformatics. There are various techniques for aligning multiple strings. In this subsection, the well-known methods for MSA are described.
CLUSTAL techniques that are a widespread particularly weighted variant CLUSTALW and CLUSTAL-OMEGA, are progressive alignment methods. Many applications rely on CLUSTAL-OMEGA due to increased scalability and allowing any number of protein sequences to be aligned faster than previous versions of CLUSTAL technologies [14]. CLUSTAL-OMEGA includes five main steps for handling MSA. The first step constructs equal alignment by the k-tuple method. In the second step, the modified mBed method is exploited to cluster the sequences. In the third step, the k-means in clustering method is applied. In the fourth step, guide tree is structured by employing the UPGMA method. In the fifth step, MSA is generated using HHAlign package.
MUSCLE in [18] that is used for MSA process has three steps. At the end of each step, numerous alignments are obtained and become available so the MUSCLE algorithm can be finished. This algorithm exploits two distance measurements, k-mer distance that is used for non-aligned sequences and Kimura distance method that is used for aligned sequences [13]. It constructs initial alignment depending on the propinquity of the dual alignments. After that it computes the distance matrix and produces rooted tree. The k-mer and Kimura distance matrices are clustered by UPGMA method that enhance the tree by recomposing propinquity. This algorithm also utilizes the log-expectation score as in [31].
MAFFT in [15] uses fast Fourier transform for multiple alignment. It identifies some of the more manifest areas of homology rapidly. The advantage of the first version of MAFFT was speed. It can produce a variety of output formats. It includes interactive phylogenetic trees among its outputs. The MAFFT employs two-cycle heuristics, FFT-NS−2 and FFT-NS-i. Parallelization PROBCONS has been proposed in [9] for MSA. This method is more suitable for large-scale data. PROBCONS that is a tool for MPSA get hold of the expected accuracy, but it has a problem that takes a long time.
As with traditional progressive method, KALIGN works in a very similar way [10]. KALIGN is based on the Wu-Manber algorithm that consumes string matching to improve the speed and the accuracy of MSA. It computes equal distances, then builds a directory tree that aligns the sequences.
RETALIGN in [16] is a progressive corner cutting style. In the incremental alignment, it focuses on determining the suboptimal alignment set. Therefore, it does not define the compressed part of the dynamic table. This technology uses a grid to store the alignment so that the alignment can be used effectively during the gradual phase.
The research that is related to progressive multiple sequence alignment has been proposed in [2]. It improves standard progressive algorithm depending on multithreading techniques. It is basically works on cloud computing. The concepts on swarm techniques have been applied to increase the efficiency of the whole alignment process. Aligning multiple sequences based on particle swarm optimization is proposed in [17]. This algorithm uses the particle motion philosophy to align sequences with great precision.
In this paper, a swarm of artificial fishes is proposed to align the sequences of multiple proteins which is used in related bioinformatics applications that require high alignment accuracy and less execution time in accomplishing the alignment process.
4 Artificial Fish Swarm for Multi Protein Sequences Alignment
Sequence alignment computations are a widespread process implemented in molecular biology and genetics. The continuous growth of dynamic sequencing databases requires an effective alignment implementation. Multi Protein Sequence Alignment is a complete NP problem. To solve this problem, intelligent algorithms based on swarm intelligence techniques are used for obtaining a functional solution.
Thus, the ASF algorithm becomes acclimatized to be utilized with alignment of biological sequences. The basic idea of the ASF algorithm is that a group of fishes randomly scattered over the search area will gradually move to the venue that will extend supreme solutions to the MSA problem, until the swarm of fishes finds a solution that it can no longer improve. In the proposed AFS algorithm, the fish will conform to the sequence alignment. Alignment is outlined as a combination of vectors. Each vector appoints the gaps placements for one of the sequences. The number of gaps allowed per sequence may vary. The set of n sequences coincides to a search space of n dimensions.
Moreover, the minimum value of the alignment length is the length of the largest sequence, and the maximum can be up to twice that length.
The main functions of AF in the proposed AFW are AF-Preying, AF-Swarming, AF-Following, AF-Moving and AF-Leaping.
In AF-Preying, Xi represent the current state of AF. The AF select state in visualization randomly by Eq. (2) that is called Xj.
where, R is a random number between zero and one. Visual stands for visual proportion in the search area.
If the fitness value of Xj is better than Xi, the AF takes a step forward m in this bearing by using Eq. (3). Otherwise, Xj is computed again several times by the Try-Times variable until the previous condition is convinced or a step is selected randomly.
where, Step illustrates the length of step.
In AF-Swarming that is known as huddling behavior, AF will gang to guarantee groups survive and avoid the risk. Suppose nf is the number of AF comrades, Xc represents the center position, δ is overcrowding factor and m is the number of artificial fishes. If the fitness value of Xc is better than Xi and nf/m is less than δ, AF will swarm by Eq. (4).
Eq. (4) shows that the AF will move a step forward to the center when it has a higher fitness and isn’t overcrowded.
In AF-Following, AF explore vicinity comrade (Xv). If the fitness value of Xv is better than Xi and nf/m is less than δ, AF will follow vicinity comrade by Eq. (5).
Eq. (5) shows that the AF will move a step forward vicinity comrade when it has a higher fitness, and his surroundings are not crowded.
In AF-Moving, AF will randomly select a state and advance directly to that state by Eq. (6).
In AF-Leaping, AF will do a leap if it falls into the local maximum area, which means that its fitness value has not changed for some iterations. The AF that wants to leap selects another AF randomly and gathers its parameters. The leaping behavior is handled by Eq. (7).
A placard is used to hold the best state any AF will find. Each AF after each procedure tests its state with the state in placard. If its status is better than placard status, the placard status will be updated. The pseudo code of the proposed AFS for multi protein sequences alignment is shown in Fig. 5.
The initialization phase of the proposed AFS includes step 1 and step 2 in Fig. 5. Initially the proposed AFS parameters must be initialized. The stop criterion is handled by the Tmax argument representing the allowed number of iterations. The number of artificial fish is determined empirically along with the Visual, Step and δ. After that, each AF generates its own random solution. The generated solution comprises set of vectors. Each vector maps the locations of gaps in a sequence.
The iterative phase of the proposed AFS includes step 3 and step 4 in Fig. 5. Step 3 mimics the behavior of a natural fish swarm in foraging. After each action, the placard is updated if a better solution is found. During iterative phase, trapped-in-the-local-optimum problem is treated with Leaping scenario. The proposed AFS has been shown to be insensitive to initial values and has more power for universal search ability. The proposed AFS computational complexity is O (Initialization part + Iterative part). The initialization part that includes the first two steps in Fig. 5 has an arithmetic complexity of O (m × S), where m is the number of artificial fish and S is the number of sequences to align. The iterative part that includes the last two steps in Fig. 5 has an arithmetic complexity of O (Tmax × m × S × L), where L is the length of the longest sequence of the sequences to align.

Figure 5: The proposed AFS for multi protein sequences alignment
The aggregated AFS computational complexity is O ((m × S) + (Tmax × m × S × L)), which can be summed up to O (Tmax × m × S × L), disregarding constants and the minor term value.
5 Implementation & Experimental Results
The proposed AFS for multi protein sequences alignment, called AFSMPSA, was implemented to ensure their efficient alignment. Experiments were applied using the same environment parameters on an HP Intel(R) Core (TM) I7-CPU, 32GB of RAM, and a 1TB HDD.
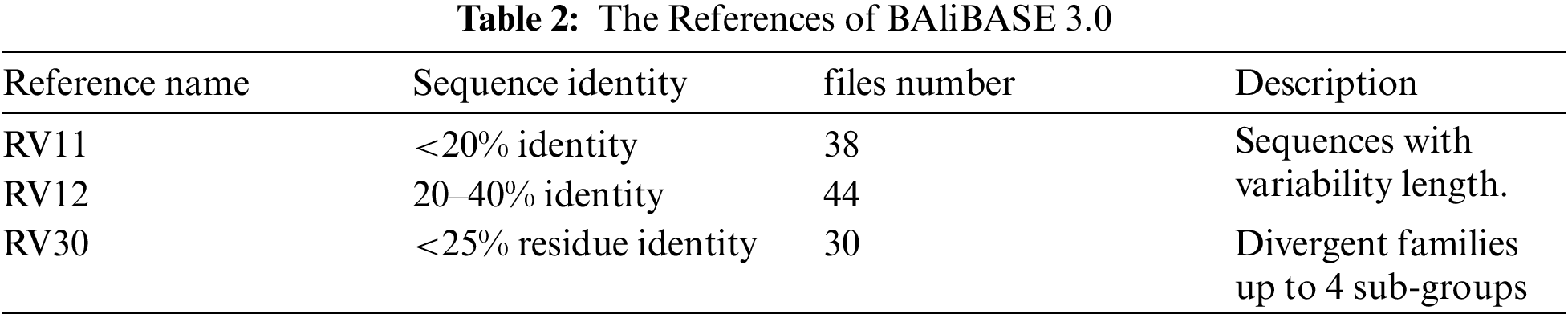
Two standard datasets, BAliBASE and SAliBASE, which simulate a database of sequences, were used. These two datasets are considered as benchmark datasets. Three cases from SAliBASE that are shown in Tab. 1 were used in the implemented experiments. The number of sequences ranges from 100 sequences to 500 sequences of length 500. Three references from BAliBASE 3.0 were used. BAliBASE references contain various file numbers that contain sequences of variable length as shown in Tab. 2.

Tab. 3 shows the proposed AFSMPSA control parameters that were experimentally fine-tuned to improve the performance of the alignment process. The selected number of artificial fishes is set to fifty, the stop criterion is set to one hundred iterations, congestion factor δ is set to thirty five percent, the length of step is set to four and the realized distance to AF (visual) is set to twenty-four. The control parameters of AFSMPSA were determined considering the various sequences of different lengths for more than one database.

Two metrics are measured to prove the quality and efficiency performance of the proposed AFS for multi protein sequences alignment. The first metric is SPscore and second metric is TCscore. The comparative study depending on the experimental results is introduced between the proposed AFS, CLUSTAL-OMEGA in [14], MAFFT in [15], KALIGN in [10], MUSCLE in [18], RETALIGN in [16], PMSA in [2] and PSOMSA in [17]. Fig. 6 shows a SPscore comparison between AFS proposed for multi protein sequences alignment and seven other algorithms from experiments that were applied to three SaliBASE cases. And TCscore comparison is shown in Fig. 7.
Figs. 8 and 9 show SPscore and TCscore comparison from experiments that were applied to three BAliBASE references.
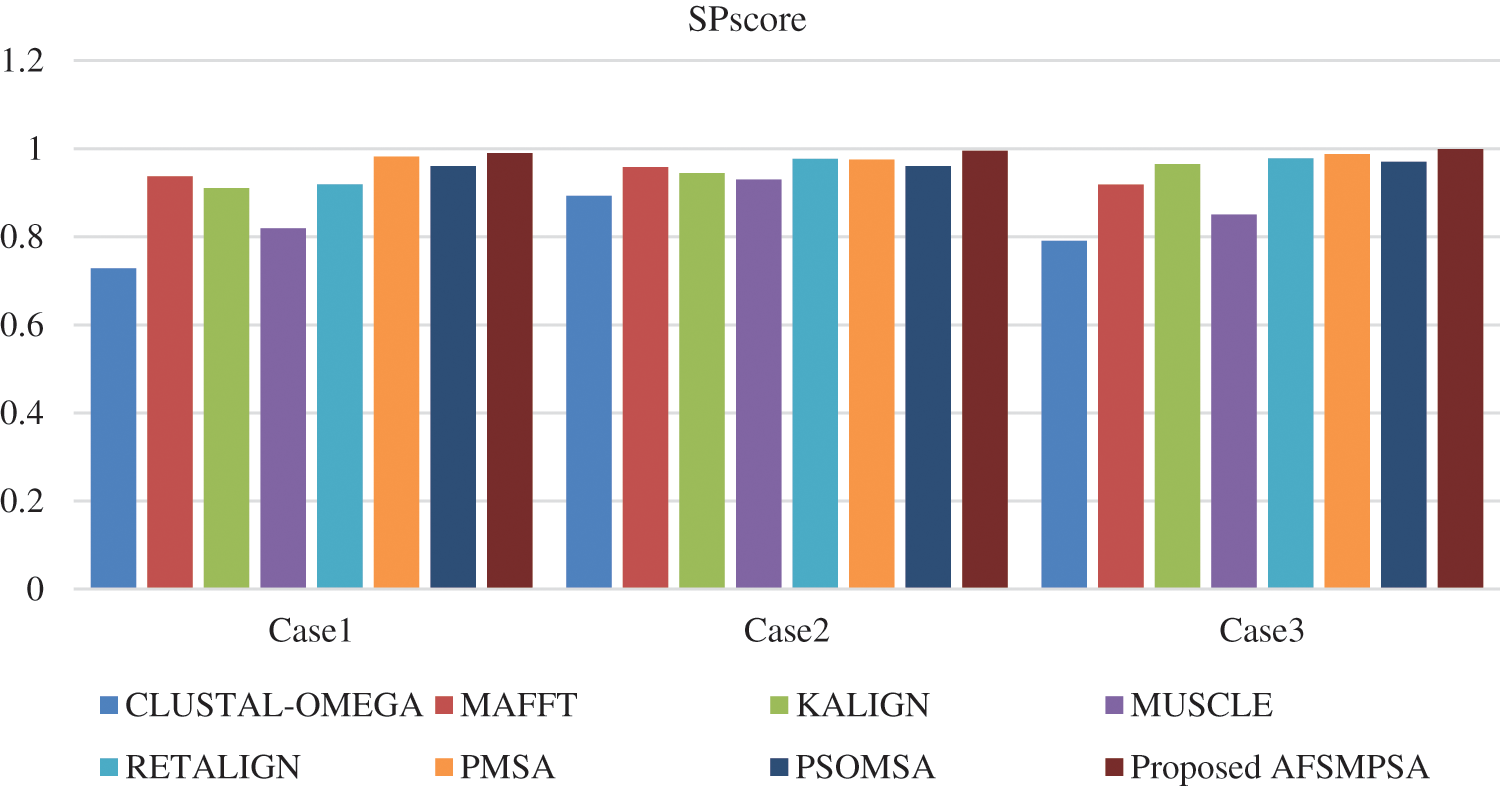
Figure 6: SPscore comparison on SaliBASE dataset
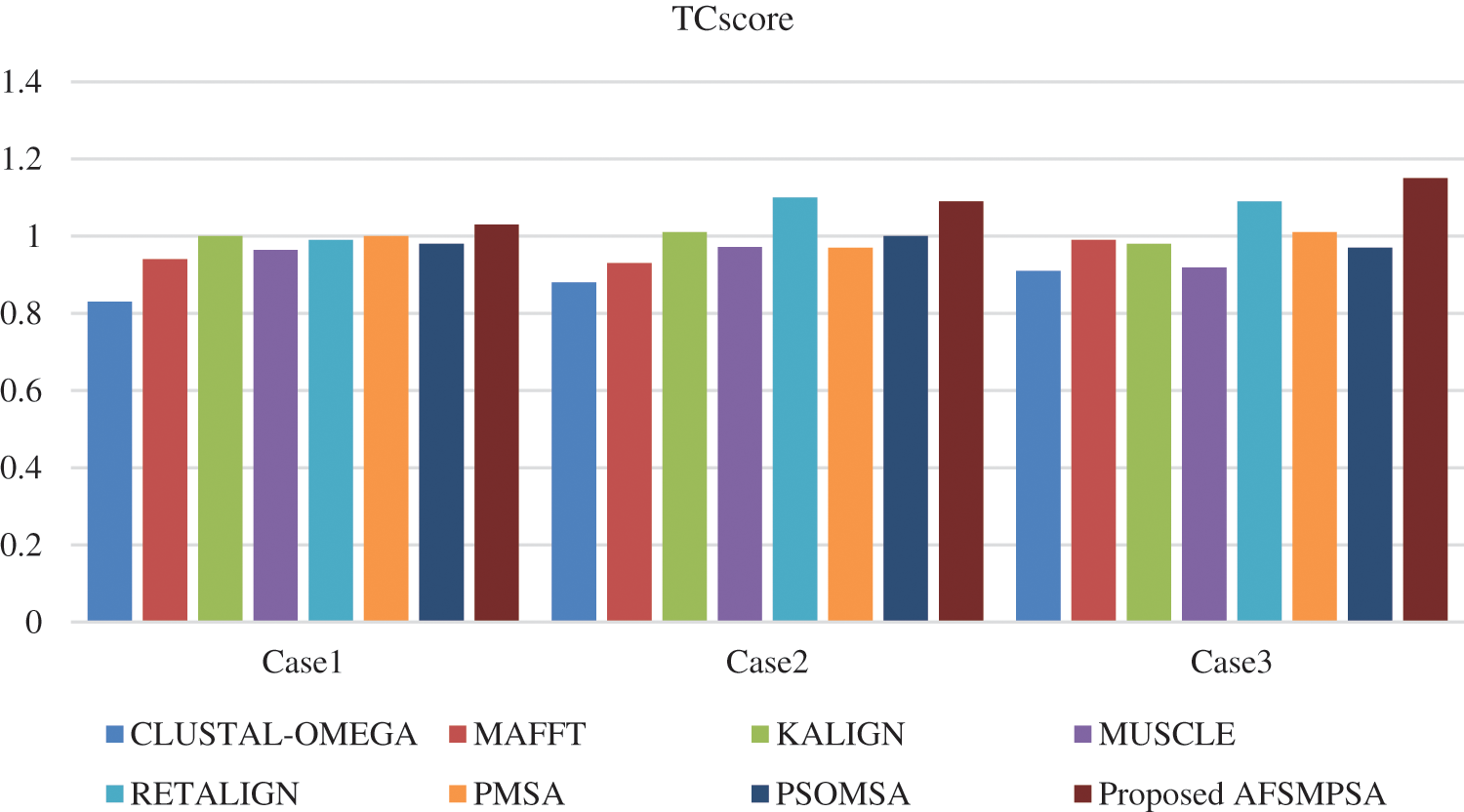
Figure 7: TCscore comparison on SaliBASE dataset
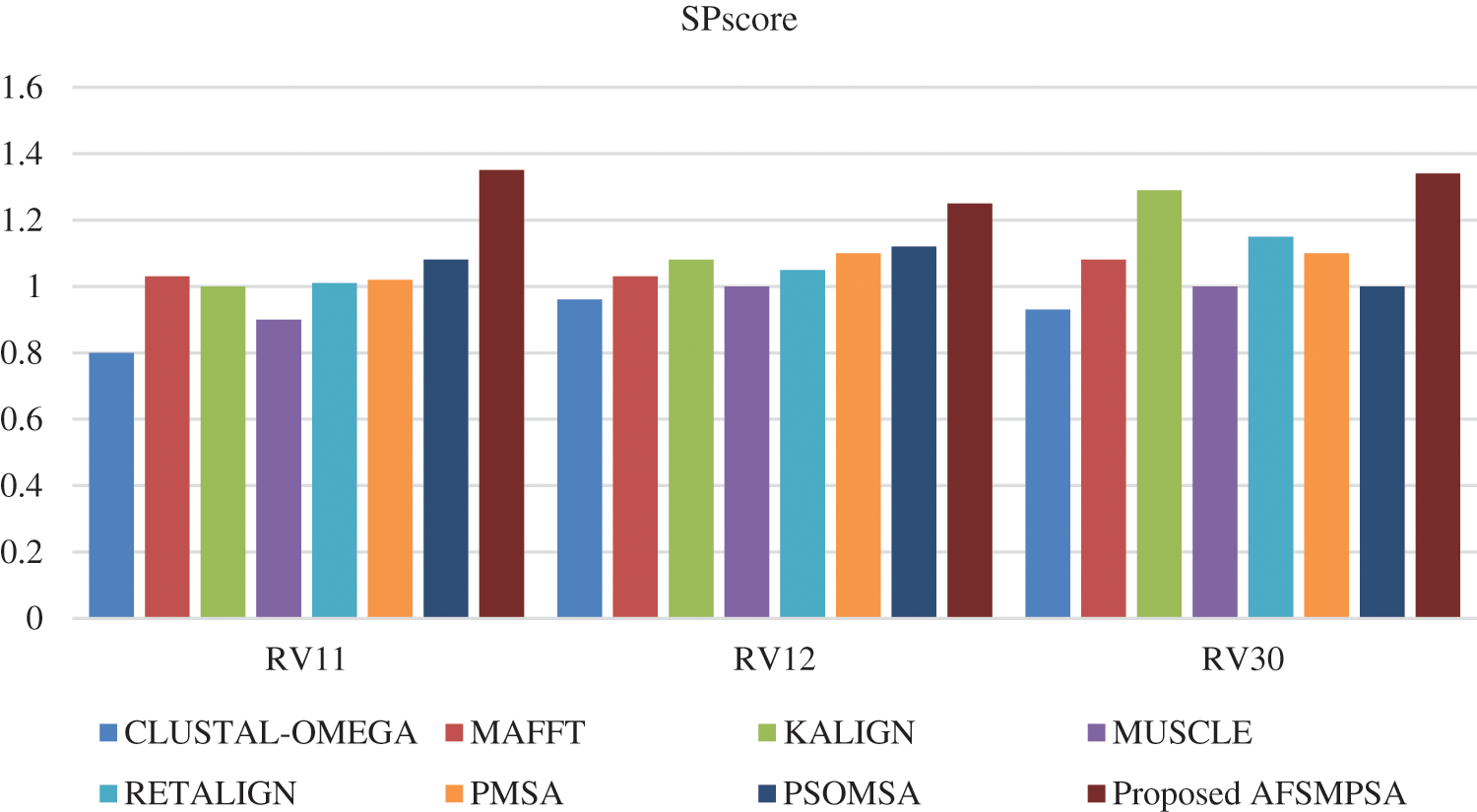
Figure 8: SPscore comparison on BAliBASE dataset
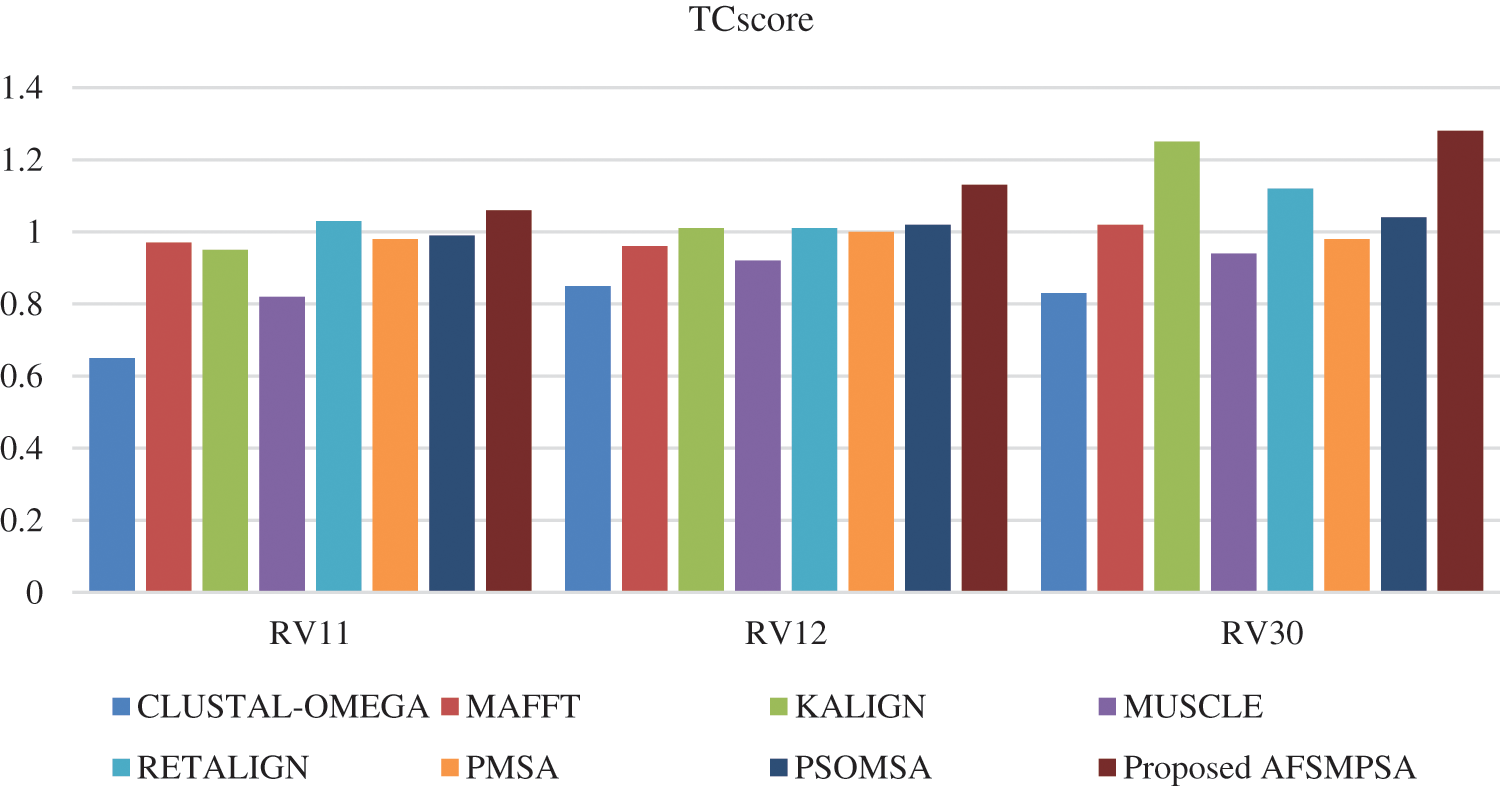
Figure 9: TCscore comparison on BAliBASE dataset
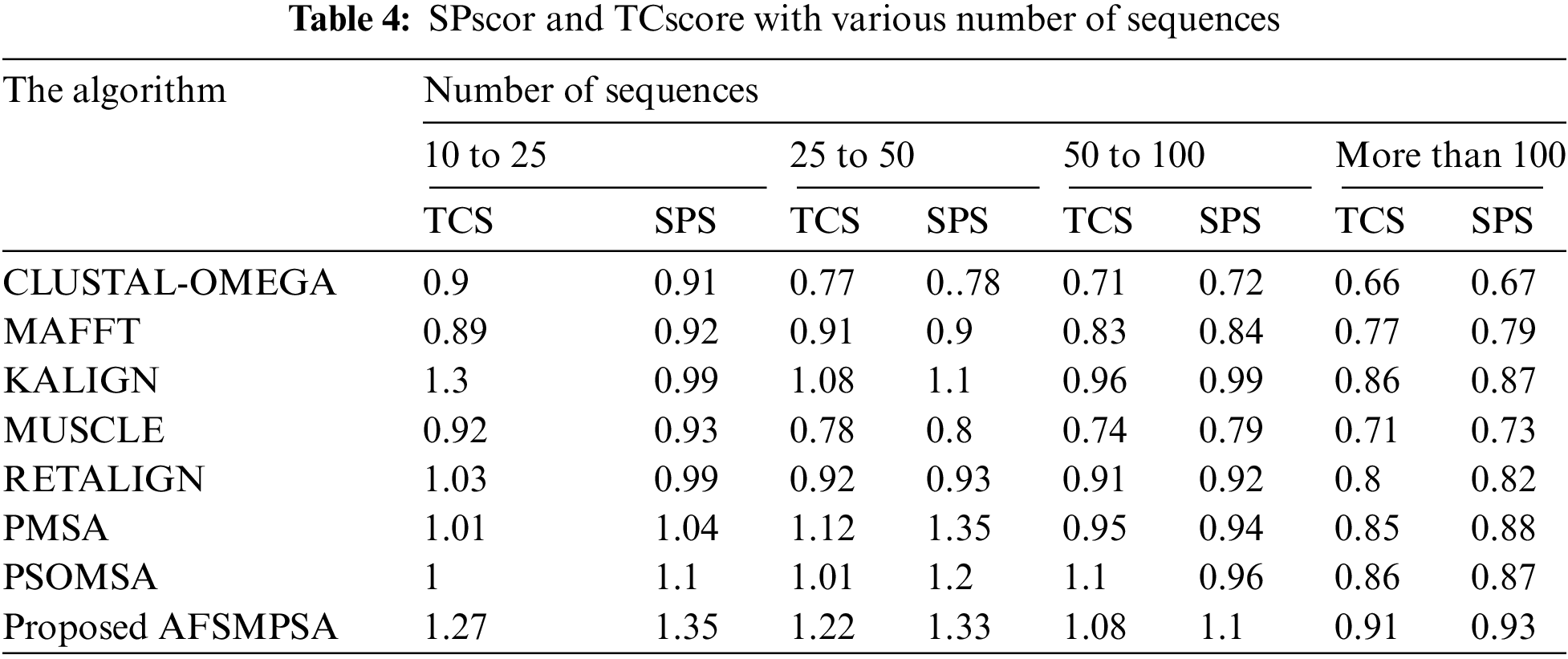
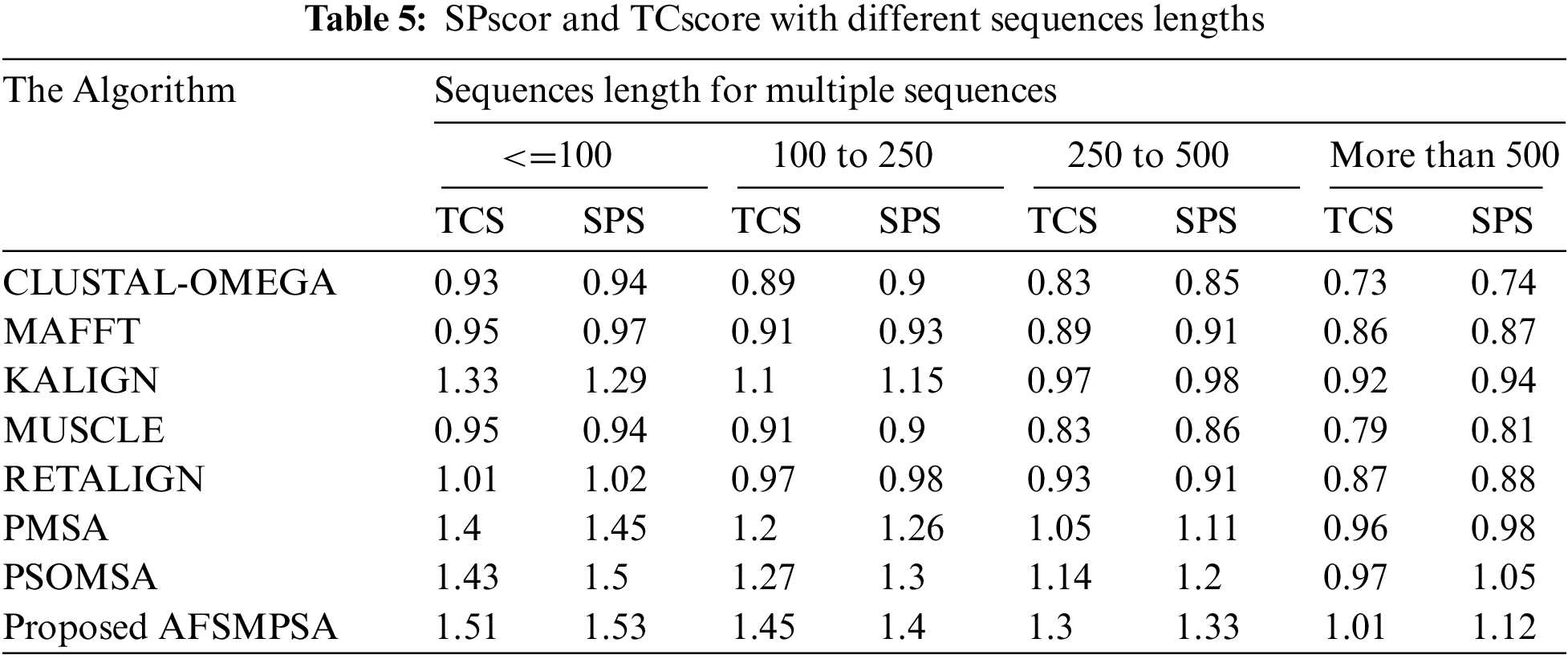
Tab. 4 shows the accuracy of the alignment for a different number of sequences using the average SPscor and TCscore. Five scenarios were tested with 10 to 25 sequences, 25 to 50 sequences, 50 to 100 sequences and more than 100 sequences. Tab. 5 shows the average SPscor and TCscore indicating a measurement of alignment accuracy for different sequence lengths. Five cases with sequence length less than 100, sequence length from 100 to 250 sequences, sequence length from 250 to 500 sequences, and sequence length above 500 were tested. Comprehensive protein sequences based on some protein traits in biology were assembled in the above experiments to attain rigorous alignment. From various practical experiments, it can be said that when the number of sequences and sequence length are increased, it will affect the accuracy of the aligned results in an obvious negative way. Moreover, the alignment processing time will consume more time.
However, the proposed AFSMPSA algorithm gives satisfactory results and is better than other algorithms when increasing the length and number of sequences. It can comprehensively search to reach the highest accuracy of alignment, but it is slow with processing execution in the scenario that contains more than 100 sequences and the case with sequence length above 500. The proposed AFSMPSA is a stochastic algorithm that starts the search for a set of solutions in a random way. Then, it uses the environmental behavior mechanism to teach the fish in the water in the reminder iterations of search process. The main functions of AFSMPSA such as AF-Preying, AF-Swarming, AF-Following, AF-Moving and AF-Leaping are the main factors in increasing the accuracy of the alignment process between different sequences.
The proposed AFSMPSA fits between discovering new solutions and pivoting the best solutions that have been found by adjusting the parameters δ, Visual and Step, which were made by experiments. It turns out that the large values of these parameters force exploration and lessen stability but lower values force exploitation power and optimum local. In AFSMPSA algorithm and PSO algorithm in [17], candidate solutions gravitate towards the solutions of the leading neighbors. In the PSO, At PSO, the selection of attractors is based on the solution of particle and best particle. However, in AFSMPSA, the selection of attractors is based on AF is preferable in its visual ambit and swarm center position.
AFSMPSA, selection rules, which are determined based on jostle factor, do not authorize AFS to crumple nearly optimum plateau. AFSMPSA, selection rules, which are determined based on jostle factor, do not authorize AFS to crumple nearly optimum plateau. This maintains the AFSMPSA with a higher dignity of fluctuation over time and increases its reconnaissance ability. In the AFSMPSA, update rules are sectioned as attitudes that are carried out on AFs under nominated conditions. Each AF can conduct a local search for itself or a social behavior and wags across other attractions. All these factors and strategies are what makes the proposed algorithm ascendant to other algorithms in the process of aligning sequences.
This paper was intended to propose an artificial fish swarm for multi protein sequences alignment. Its parameters have been experimentally tuned to increase the efficiency of the alignment process. Various experiments were applied on two standard data sets to measure the performance of the proposed algorithm using the SPscore and TCscore scales. The first is BAliBASE, where three cases were selected, and the second is SAliBASE, where three references were selected. Experiments were conducted with different sequence lengths ranging from 100 to more than 500 and different numbers of sequences ranging from 25 to more than 100 sequences. The results showed the predominance of the proposed artificial fish swarm algorithm over other algorithms used in the comparison process, which confirms the efficiency of the proposed algorithm in the process of aligning multiple protein sequences. One of the reasons for the preponderant of the proposed algorithm is that it can scan the search area very efficiently to reach the highest possible accuracy in the alignment process. In future work, improving the swarm quickness of the proposed artificial fish is being considered by modifying different behaviors associated with preying, swarming, following, moving and leaping to obtain more enhancements.
Funding Statement: The authors extend their appreciation to the Deanship of Scientific Research at Jouf University for funding this work through research Grant No (DSR2020–01–414).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. Q. Jiang, X. Jin, S. -J. Lee and S. Yao, “Protein secondary structure prediction: A survey of the state of the art,” Journal of Molecular Graphics and Modelling, vol. 76, pp. 379–402, 2017. [Google Scholar]
2. E. M. Mohamed, H. M. Mousa and A. E. keshk, “Improving standard progressive multiple sequence alignment by using multithreading techniques,” in Proc. IEEE 2018 14th Int. Computer Engineering Conf. (ICENCO), Cairo, pp. 156–161, 2018. [Google Scholar]
3. A. S. Alluhaidan, “DNA sequence analysis for brain disorder using deep learning and secure storage,” Computers, Materials & Continua, vol. 71, no. 3, pp. 5949–5962, 2022. [Google Scholar]
4. X. Chen, C. Wang, S. Tang, C. Yu and Q. Zou, “CMSA: A heterogeneous CPU/GPU computing system for multiple similar RNA/DNA sequence alignment,” BMC Bioinformatics, vol. 18, no. 315, pp. 1–10, 2017. [Google Scholar]
5. M. Kumar, “An enhanced algorithm for multiple sequence alignment of protein sequences using genetic algorithm,” EXCLI Journal, vol. 14, pp. 1232–1255, 2015. [Google Scholar]
6. K. Nguyen, X. Guo and Y. Pan, “Multiple Biological Sequence Alignment: Scoring Functions, Algorithms, and Applications,” 1st ed, Wiley & Sons, Inc, New Jersey, pp. 244–248, 2016. [Google Scholar]
7. S. Surender, “Artificial fish swarm optimization algorithm for power system state estimation,” Indonesian Journal of Electrical Engineering and Computer Science, vol. 18, no. 3, pp. 1130–1137, 2020. [Google Scholar]
8. Z. You, M. Zhou, X. Luo and S. Li, “Highly efficient framework for predicting interactions between proteins,” IEEE Transactions on Cybernetics, vol. 47, no. 3, pp. 731–743, 2017. [Google Scholar]
9. B. D. Chuong, M. S. P. Mahabhashyam, M. Brudno and S. Batzoglou, “ProbCons: Probabilistic consistency-based multiple sequence alignment,” Genome Research, vol. 2, no. 15, pp. 330–340, 2005. [Google Scholar]
10. T. Lassmann, O. Frings and E. L. L. Sonnhammer, “ “Kalign2: High-performance multiple alignments of protein and nucleotide sequences allowing external features,” Nucleic Acids Res, vol. 37, no. 7, pp. 858–865, 2009. [Google Scholar]
11. L. Al Ait, Z. Yamak and B. Morgenstern, “DIALIGN at GOBICS-multiple sequence alignment using various sources of external information,” Nucleic Acids Research, vol. 41, no. 1, pp. 3–7, 2013. [Google Scholar]
12. L. Guangqiang, Y. Yang, T. Zhao, P. Peng, Y. Zhou et al., “An improved artificial fish swarm algorithm and its application to packing and layout problems,” in Proc. 2017 36th Chinese Control Conf. (CCC), Dalian, China, pp. 9824–9828, 2017. [Google Scholar]
13. S. C. Manekar and S. R. Sathe, “A benchmark study of k-mer counting methods for high-throughput sequencing,” GigaScience, vol. 7, no. 12, pp. 1–13, 2018. [Google Scholar]
14. F. Sievers and D. G. Higgins, “Clustal omega for making accurate alignments of many protein sciences,” Protein Sci, vol. 27, no. 1, pp. 135–145, 2018. [Google Scholar]
15. K. Katoh and D. Standley, “MAFFT multiple sequence alignment software version 7: Improvements in performance and usability,” Molecular Biology and Evolution, vol. 4, no. 30, pp. 772–780, 2013. [Google Scholar]
16. A. Szabó, A. Novák, I. Miklós and J. Hein, “Reticular alignment: A progressive corner-cutting method for multiple sequence alignment,” BMC Bioinformatics, vol. 11, pp. 570, 2010. [Google Scholar]
17. M. Wallinga, “Multiple sequence alignment using particle swarm optimization,” Ph.D. dissertation, University of South Dakota, 2017. [Google Scholar]
18. R. C. Edgar, “MUSCLE: A multiple sequence alignment methods with reduced time and space complexity,” BMC Bioinformatics, vol. 5, pp. 113–131, 2004. [Google Scholar]
19. J. Swan, S. Adriaensen, A. E. I. Brownlee, K. Hammond, C. G. Johnson et al., “Metaheuristics in the large,” European Journal of Operational Research, vol. 297, no. 2, pp. 393–406, 2022. [Google Scholar]
20. F. Sievers, D. Dineen, A. Wilm and D. G. Higgins, “Making automated multiple alignments of very large numbers of protein sequences,” Bioinformatics, vol. 29, no. 8, pp. 989–995, 2013. [Google Scholar]
21. M. T. Pervez, H. A. Shah, M. E. Babar, N. Naveed and M. Shoaib, “SAliBASE: A database of simulated protein alignments,” Evolutionary Bioinformatics, vol. 15, pp. 1–4, 2015. [Google Scholar]
22. http://www.salibasepak.com/ (accessed May 2019). [Google Scholar]
23. R. D. Finn, A. Bateman, J. Clements, P. Coggill, R. Y. Eberhardt et al., “Pfam: The protein families database,” Nucleic Acids Research, vol. 42, no. 1, pp. D222–D230, 2014. [Google Scholar]
24. J. D. Thompson, P. Koehl, R. Ripp and O. Poch, “BAliBASE 3.0: Latest developments of the multiple sequence alignment benchmark,” Proteins, vol. 1, no. 61, pp. 36–127, 2005. [Google Scholar]
25. https://ftp://ftpigbmc.ustrasbg.fr/pub/BAliBASE3. (accessed May 2019). [Google Scholar]
26. M. Pervez, M. Babar and A. Nadeem, “Evaluating the accuracy and efficiency of multiple sequence alignment methods,” Evolutionary Bioinformatics Online, vol. 10, pp. 205–217, 2014. [Google Scholar]
27. T. Fei, L. Zhang, Y. Li, Y. Yang and F. Wang, “The artificial fish swarm algorithm to solve traveling salesman problem,” in Patnaik S., Li X. (eds)Proc. of Int. Conf. on Computer Science and Information Technology. Advances in Intelligent Systems and Computing, Springer, New Delhi, vol. 255, pp. 1759–1778. 2014. [Google Scholar]
28. M. Alireza, Y. Alinezhad and, K. Kourosh, “Artificial fish swarm algorithm for solving the economic dispatch with valve-point effect,” International Journal of Engineering & Technology Sciences-IJETS, vol. 2, pp. 299–313, 2014. [Google Scholar]
29. Y. Liu, Z. Tao, J. Yang and F. Mao, “The modified artificial fish swarm algorithm for least-cost planning of a regional water supply network problem,” Sustainability, vol. 11, no. 15, pp. 1–12, 2019. [Google Scholar]
30. X. R. Zhang, X. Sun, X. M. Sun, W. Sun and S. K. Jha, “Robust reversible audio watermarking scheme for telemedicine and privacy protection,” Computers, Materials & Continua, vol. 71, no. 2, pp. 3035–3050, 2022. [Google Scholar]
31. L. Yujian and X. Liye, “Unweighted multiple group method with arithmetic mean,” in Proc. Bio-Inspired Computing: Theories and Applications (BIC-TAIEEE Fifth Int. Conf., IEEE, pp. 830–834, 2010. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |