DOI:10.32604/cmc.2022.028272

| Computers, Materials & Continua DOI:10.32604/cmc.2022.028272 |  |
| Article |
Triple Key Security Algorithm Against Single Key Attack on Multiple Rounds
1Department of Computer Science, Superior University Lahore, 54000, Pakistan
2Department of Software Engineering, Superior University Lahore, 54000, Pakistan
3Department of Computer Science, The Institute of Management Sciences (PAK-AIMS), Lahore, 54000, Pakistan
4Department of Computer Science, GC Women University Sialkot, Pakistan
5Department of Computer Science, King Abdulaziz University, Jeddah, Saudi Arabia
6Faculty of Computing and Information Technology, King Abdulaziz University, Jeddah, Saudi Arabia
*Corresponding Author: Muhammad Waseem Iqbal. Email: waseem.iqbal@superior.edu.pk
Received: 06 February 2022; Accepted: 25 March 2022
Abstract: In cipher algorithms, the encryption and decryption are based on the same key. There are some limitations in cipher algorithms, for example in polyalphabetic substitution cipher the key size must be equal to plaintext otherwise it will be repeated and if the key is known then encryption becomes useless. This paper aims to improve the said limitations by designing of Triple key security algorithm (TKS) in which the key is modified on polyalphabetic substitution cipher to maintain the size of the key and plaintext. Each plaintext character is substituted by an alternative message. The mode of substitution is transformed cyclically which depends on the current position of the modified communication. Three keys are used in the encryption and decryption process on 8 or 16 rounds with the Exclusively-OR (XOR) of the 1st key. This study also identifies a single-key attack on multiple rounds block cipher in mobile communications and applied the proposed technique to prevent the attack. By utilization of the TKS algorithm, the decryption is illustrated, and security is analyzed in detail with mathematical examples.
Keywords: Encryption; decryption; cipher; symmetric key cryptography; single key attack
Information plays a very vital role for any organization since it is its asset, and hence must be protected from illegal access. If the Confidentiality integrity availability (CIA) model of any information is lost (compromised), then that information may be used for purposes harmful to the respective organization. It becomes, therefore, very much necessary for any organization to make its data and information resources out of the reach of the illegal users by applying cipher cryptography. In the context of CIA model, the confidentiality is a set of procedures that bounds access, the integrity means to ensure trustworthy and accurate, and availability is assurance of reliability [1]. Securing the information and to maintain the intellectual property and copyright, the best example is watermarking via wavelet transform for data protection [2].
Mostly the ciphers are based on simple functions such as round or iterated block cipher with repeated round function. Encryption is widely used as an effective method to protect data and information in many real-life applications. The cryptographic algorithms are used for encryption using asymmetric and asymmetric keys, some ciphers use the same key for encryption and decryption. The keys may be equal with a simple transformation to go between the two keys. A shared secret for encryption and decryption is used to maintain the information, however, this is the main drawback of symmetric key encryption with respect to the public key. In asymmetric cryptography, a public/private key pair is generated randomly to allow access to the public key. For huge data encryption symmetric algorithm is much faster than asymmetric, but it has some drawbacks that the size of the key should be equal to the size of plaintext otherwise it is repeated continuously and causes repeated histogram. The classes of symmetric block cipher are based on the mode of operation and iterations. The symmetric key block cipher is based on two calculations such as encryption and decryption which takes n bits of plain text by providing a similar number of bits including k bits for the mystery key [3].
Mode of operation determines the methods of using a block cipher to larger plaintexts, this mode is classified into deterministic and probabilistic [4]. Such block cipher methods are planned for mystery and cryptographic primitive which is recognized in figuring texts, these methods are called Electronic codebook (E-C-B). Iterated product ciphers are categorized in unbalanced Feistel cipher, Feistel cipher, and substitution permutation-networks. In unbalanced Feistel “left half” and “right half” are not of equal size therefore these networks are called generalized unbalanced Feistel which consist of a series of rounds [5].
Whereas the Feistel cipher is utilized by adding circular capacity on the normal content to gives encrypted content in which the block cipher calculations use the Data-encryption standard (DES). It comprises 64-bits as input and 64-bits as encryption along with 56-bits key length. Another iterative base cipher is a substitution permutation network in which substitution change is part of a block cipher. The substitution stage is organized by including the round box or S-boxes. The most broadly utilized symmetric cipher is Advanced encryption standard (AES) with 128-block size and incorporates 3 key lengths more likely than not upheld 128, 192, and 256 blocks. If the key size is greater than block size with a uniform distribution, there is more than one key and if a block cipher is designed randomly, then the key space should be into the same classes. So there is a requirement to recover the key of the block cipher [6]. AES lies in its key length options and the time required to crack an encryption algorithm is directly related to the length of the key used to secure the communication for 128-bit, 192-bit, or 256-bit keys. Therefore, AES is exponentially stronger than the 56-bit key of DES. Also, AES uses 10 rounds for 128-bit keys, 12 rounds for 192-bit keys, and 14 rounds for 256-bit keys and each of these rounds uses a different 128-bit round key, which is calculated from the original AES key.
Another utilization of block cipher is in mobile communication particularly for 3GPP evolved radio access and Global system for mobile communication (GSM) networks [7], the 8 round block ciphers are used. This block cipher is called KASUMI and has 64-bit and 128-bit keys with nonlinear S-boxes. Two functions, FO and FL are composed for each round performing logical operations with subkeys. However, there is a single key attack against reduced-round [8] with respect to complexity. In the case of asymmetric key encryption, the public key is available to anyone to encrypt the plaintext on the network and only authentic user can decrypt by using the secret private key. In asymmetric key encryption algorithm, computationally different steps are involved for example in scenario of sender A and receiver B. The following steps are used with different terms and conditions such sender A and receiver B must know the public key while private keys are secret: A can encrypt the plain text by using B’s public key: a can transmit cipher text to B: by using private key B can receive cipher text, Finally, the plain text message is received by B. The problem of asymmetric encryption works slower as compared to symmetric encryption [9].
Most asymmetric algorithms depend on the properties of hard problems in mathematics. These problems are usually work-intensive in one direction and nearly impossible in the other direction. For example, factoring the product of two large prime numbers. If one of the prime numbers is known, then factoring becomes easy [10]. But by knowing only the product it is very difficult to factorize and find the prime numbers. So in the case of the asymmetric algorithm, speed and more computationally costly is a major drawback of using public-key cryptography.
The algorithm TKS is proposed to overcome the said limitations and drawbacks of both symmetric and asymmetric. This study focus on said limitations and to answer the research questions such as, how to manage the key size which must be equal to plaintext in polyalphabetic substitution cipher. The second concern is, how to deal with attack due to the inverse of the underlying mathematical function. The proposed algorithm adds to the subject area compared with other published material that the key is modified on polyalphabetic substitution cipher to maintain the size of key and plaintext.
The rest of paper is structured is sections, the literature review is explained in Section 2, Section 3 presents the comparative study and problem identification, the proposed TKS Algorithm is explained in Section 4, the implementation of proposed algorithm is demonstrated in Section 5, implementation of TKS against attacks on multiple rounds block cipher is explained in Section 6, the results and analytics is validated by mathematical example in Section 7 and the Section 8 presents the conclusions.
Previously various security techniques and encryption algorithms have been carried out for information security. To understand this study, the following security algorithms are discussed for a comparison between the suggested implementation of the triple key security algorithm.
2.1 Enhanced Symmetric Key Cryptography
The study was proposed with a focus on symmetric key encryption-decryption results according to memory consumption and the algorithm is defined for low memory and processing capable devices [11].
The Algorithm equally divides data into blocks for encryption using a key function which is basically a mathematical set with variable key lengths from 65-bytes to 72-bytes. For the decryption, the same key is utilized purely randomly based as shown in Fig. 1 of the conventional model.
A matrix operation is used for permutation column and row mix with an adaptation of AES to protect the data. Matrix form with multiple steps for encryption algorithm in which 16-byte key value has been selected in ten steps. For decryption, the reverse process of the encryption algorithm is used. The throughput of this algorithm is based on the calculation of encryption time, execution time, simulation time, and decryption time with the calculation of memory requirement. The Memory required for implementation is 5.7 KB and Central processing unit (CPU) execution time is 0.23 s for 100 KB. Also, the encryption-decryption time is 0.2 s. According to the results of encryption and decryption time, the proposed algorithm is comparatively better among DES, Triple-DES, Blowfish, and AES, however, there are some limitations of this algorithm such as complex mathematical manipulations, resource constriction, and testing constriction.
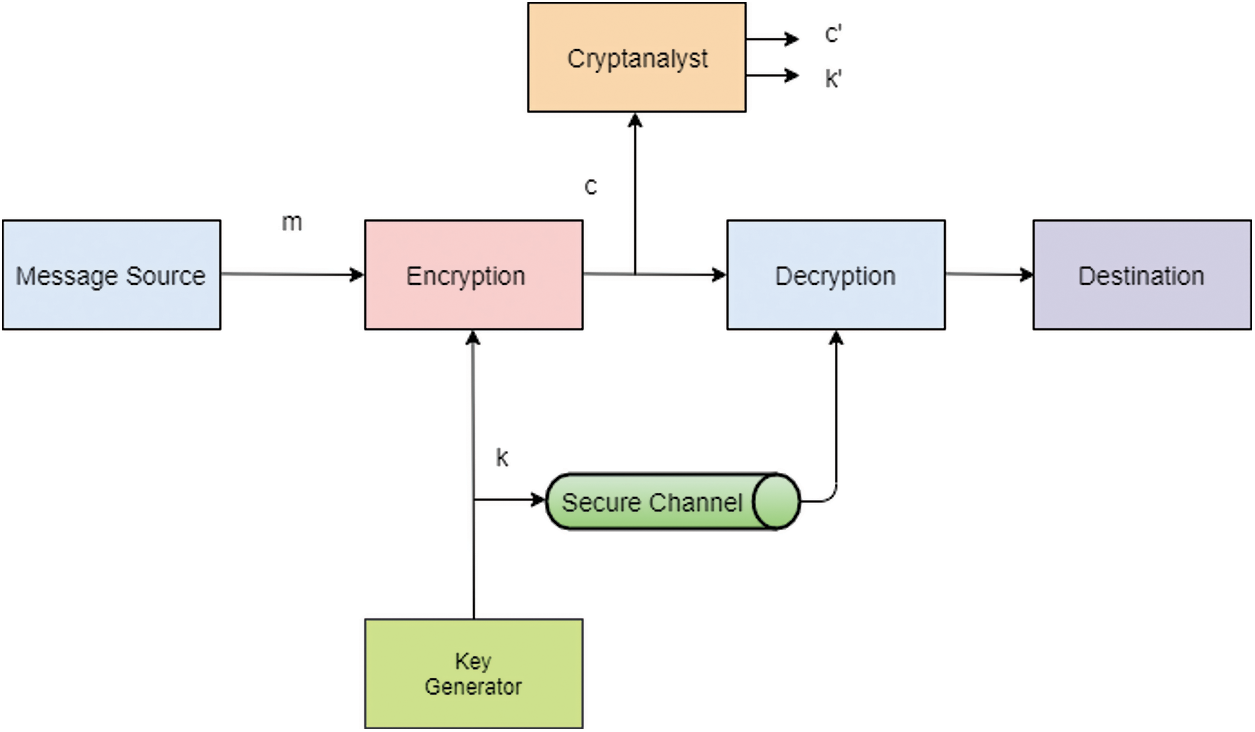
Figure 1: Conventional model
2.2 Data Security with Symmetric Key Cryptography
The symmetric key encryption with some enhanced techniques [12] uses key generation by random number in the algorithm as the concept of internal key generation for the size of 512-bits at the receiver end. In this technique, the sender may store the internal key and send it via another path. Basically, it is a substitution method that is using the block-based technique for encryption of multiple times messages. The proposed key blocks contain ASCII code from 0 to 255 in a random order for all possible words and characters. By using 256 * 2 = 512-bit key size for encryption of a text message at receiving end for decryption of any file, the receiver has to know the key blocks and apply 2512 trial runs. The author proposed the key blocks of all possible worlds comprising of number (n) of characters with ASCII code 0 to 255 and the pattern of the key can be generated by the user. For this purpose, the 256 * 2 = 512-bit key size is used for encryption. At the receiving end the key block must be available for decryption.
The Algorithm is shown in Tab. 1. The decryption time is the same as the encryption time shown in Tab. 2. This algorithm is based on the block cipher method which takes less time for 2 Mb file size however Key transportation has a major problem, due to this, the communication channels may be taped.
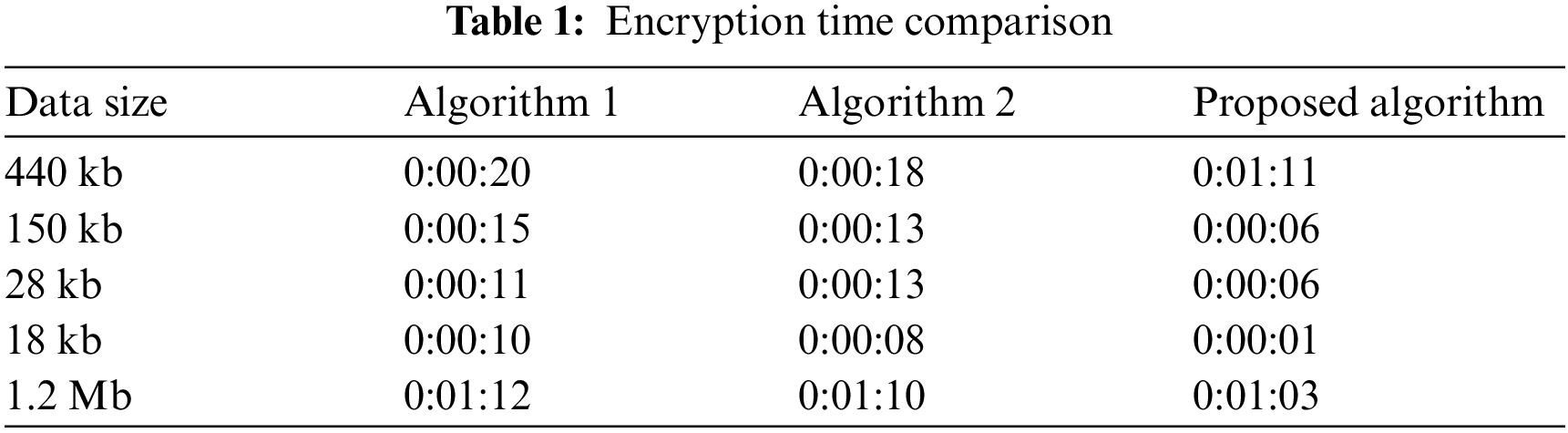
So this algorithm has the following 13 lengthy steps such as: to define variable length, to calculate the random number, calculate the variable total, conversion into a binary string, calculation of random value, selection of another variable value, calculation of encryption number, calculation of encryption value, selection of another variable to represent as an encryption number, availability of random number and encryption number, to store a binary string into a table for next iteration, and exit. According to result evaluation model as shown in Fig. 2, the comparison between the encryption time of proposed Algorithm, with Algorithm 1 is performed.
However, there are some observations symmetric and asymmetric keys have their respective advantages and disadvantages [12] as deficiency of procedures on how to take the function and apposite iterative process so that the convergence is always certain. The second limitation is vulnerability to attack because due to the same key is encoded with the same real number [13].
2.3 Cryptographic Algorithms and Key Lengths
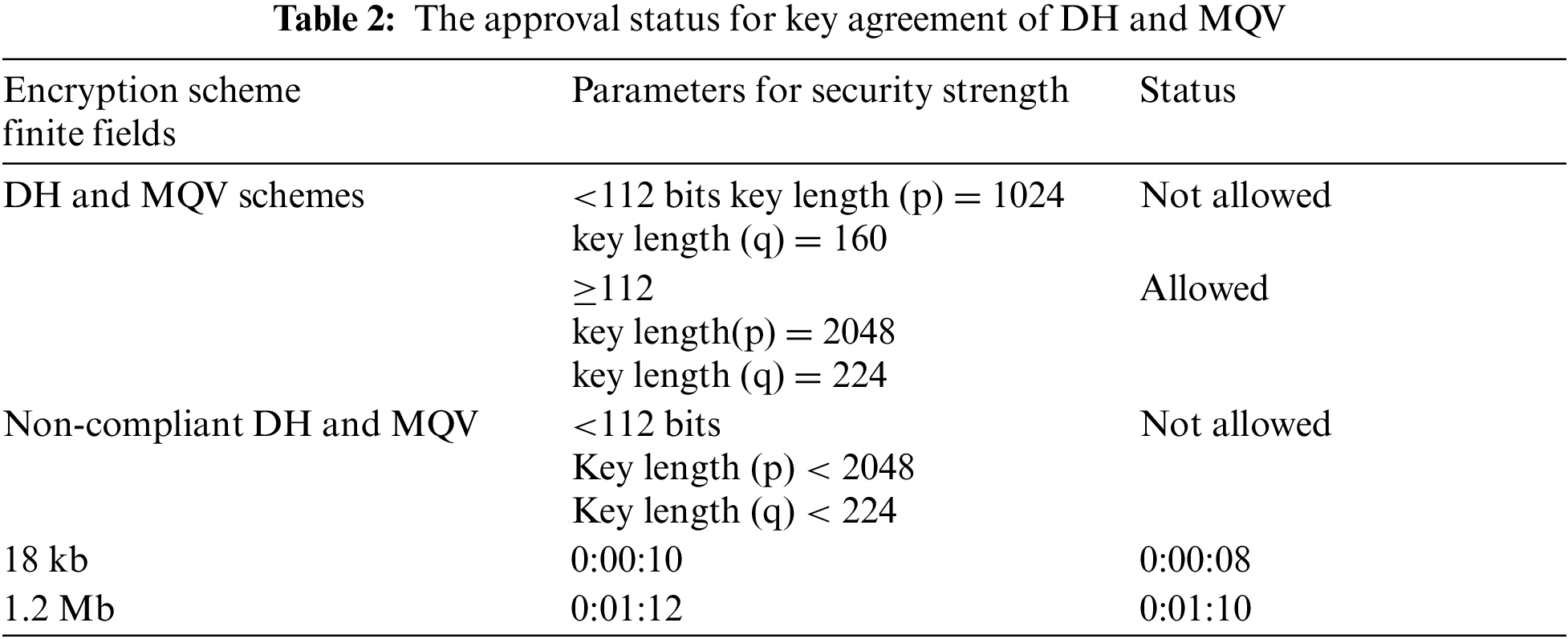
Asymmetric encryption algorithm includes RSA Diffie-hellman (DH) algorithm in which the key exchange is major factor and both sender and receiver need to exchange symmetric secrets key on difficulty of computing discrete logarithms. The key agreement is a technique are used to establish keying material and two related key agreement schemes are DH and RSA. Both schemes have been defined with different mathematical structures, for DH the finite fields and elliptic curves, and for RSA modulus are used [14].
Key agreement using DH and Menezes qu vanstone (MQV) depends on the key-agreement algorithm, based on finite field or elliptic curve which are generated with three domain parameters p, q, and g. while for the elliptic curve, the keys are generated according to domain parameters based on the length of the key. The approval status for the key agreement of DH and MQV is shown in Tab. 2 with schemes, domain parameter, and their status.
Figure 2: Result evaluation model
The approval status for DH and MQV schemes with respect to elliptic curves. The use of RSA for key agreement and transportation of key, additional key-transport scheme is allowed and for agreement, both parties have to contribute the information for the generation of the key. In key transportation technique, only one party controls the key while sending it. RSA keys are modulus n and the length of n is actually the security strength. Asymmetric ciphers are often 2–3 orders of magnitude slower than symmetric ciphers. Public key schemes are neither more secure than private keys (security depends on the key size for both), nor do they replace private key schemes (they are too slow to do so), rather these complement private key ciphers. One of the best known & widely used public-key asymmetric encryption algorithms is RSA, which uses large integers (e.g.,1024-bits) and its security is due to the cost of factoring in large numbers. Cryptographic techniques are also divided into two broad categories depending upon how plaintext is encrypted. Stream ciphers process messages a bit or byte at a time when encrypting or decrypting. Stream cipher processes input elements continuously, producing output one element at a time. The network-based security model uses the DH algorithm for shared secret keys with AES-256 for a key generation [9].
The process begins with a private key then a public key is generated which is a derivative of the private key. Sender A and receiver B then exchange their public keys and now both have their own private key and other systems’ public key. Initially shared secret key can be used in the AES as the round key which encrypts, transmits and the distant end decrypts. This method is limited by its inverse cipher which takes more codes and it does not authenticate the asymmetric exchange [15,16].
3 Comparative Study and Problem Identification
There are some popular parameters used to compare encryption-decryption algorithms. Key management is an important feature of algorithm because the encryption process is completed using this key data. The size of the key and generating process of the key act their role in process of encryption. Symmetric encryption algorithm uses the same key for encryption and decryption but in the asymmetric algorithm different keys are used for encryption and decryption. Throughput is parameter that indicates the power consumption of the algorithm. If throughput increases, the power consumption decreases. Blowfish of symmetric encryption technique is having very high throughput as compared to others. Tenability is used to define encrypted parts [8]. There is no tenability in symmetric encryption algorithm except the blowfish but the asymmetric encryption algorithm used the tenability. The encryption ratio is specifying the measurement of the amount of data to be encrypted. To reduce the complexity of computation the encryption ratio should be minimized. It is high in both the symmetric encryption algorithm and asymmetric encryption algorithm but can be moderate in the 3DES technique of symmetric encryption algorithm.
The cryptography techniques used these days are very many and growing day by day as are the cryptanalysis attacks. Many people have developed cryptographic systems to get the data and information protected from unauthorized persons. Several algorithms offer different levels of strength for various applications. Most of the ciphers are either very complex or less efficient. The computations, permutations, and other operations require considerable effort and time. It is therefore the need to combine their strengths to make our real-life systems more secure, more reliable, and more efficient. TKS algorithm is designed and implemented to secure communication on the networks. Proposed algorithm is expected to play its role in the much-needed secure systems in our daily life. In this research, the algorithm is designed for both network security and data security which is based on symmetric key cryptography. TKS algorithm is a block cipher and uses the same key for encryption and decryption. The size of the data block in the designed algorithm is 128 bits. Three keys are used in encryption and three for the decryption process. The size of the first key is 128-bits, the size of the second key is 64-bits and the size of the third key is also 64-bits [3,7,11,13,16].
It is important for an organization and company to protect its user’s information from unauthorized access. A company and an organization can secure their E-communications by using different cryptographic techniques and different security algorithms. To make communication secure different algorithm are designed. There are two types of security algorithms (1) symmetric algorithms (2) asymmetric algorithms. In symmetric algorithm, user uses the same key for encryption and decryption, DES and AES are the two important symmetric key cryptographic algorithms.
In asymmetric key cryptography user, a uses the public key of user B to encrypt the message and user B uses its private key to decrypt the message. Asymmetric key Algorithms use the public and private key for encryption and decryption. RSA, Al-Gamal are the important asymmetric key algorithms. The designing of proposed algorithm is based on the symmetric key cryptography. This algorithm has a block cipher and uses the same key for encryption and decryption. The size of the data block in the designed algorithm is 128-bits. Three keys are used in the encryption and decryption process. The size of the first key is 128-bits and the size of the second and third key (sub-key) is 64-bits with 8 or 16 iterations or 8 or 16 rounds. Each round consists of 128-bits of data, three keys, and two functions.
First round takes the 128-bits of data and divides the data into two chunks or into two units of 64-bits. These two data units are the input to function-1 and function-2. Function-1 and Function-2 perform the different operations on data and a key is added to the data. Both the function produced the output and this output is swapped and in the end key-1 is added to data which will generate the cipher text. Similarly, 8 rounds are executed and in the end, algorithm generates the cipher text.
There are three keys are used in this algorithm subkey-1 and subkey-2. Key-1 is generated from the shared secret and subkey-1 and subkey-2 is generated from the first and second chunks of 64-bits of key-1, subKey-1, and subkey-2 are used for function one and function two respectively. Round ends with the XOR of the key-1 with data from both functions.
The working process of the key generation can be explained with following steps:
i) Input: It is the 128-bits of secret code. The key generation function will perform the following operation to produce the 8 different round keys.
ii) CON: It means constant. The key generation function will generate the CON by XORing all the bytes of the key. CON will be a byte in size. After finding the value of the CON, each byte of the key XORed with the CON. The whole process is shown in the above diagram. At the end of this function, the whole vector or sub-arrays of bytes is divided into 4 equal chunks of data. The length of each chunk will 32-bits.
iii) CMP&AND: After dividing the key into four parts. Take complement of first array A1 and select the last byte of the first array A1 and perform AND operation and save the result in new array A21. A11 XORed with all other arrays A12, A13, A14 and generate new arrays A22, A23, A24.
iv) Circular Shift: After combining the Arrays A21, A22, A23 and A24 we will get a vector and perform circular shifting on the vector. Again divide the array into four parts and take the complement of the first subarray and perform XOR with all other the array. Combine the sub array into vectors and perform circular shifting two times.
v) Matrix Operations: The resultant vector is then converted into a matrix of 4 * 4 and performs a circular shift on the matrix. There are two types of shifting one is bottom-up and the second is the right-left (row-wise shift and column-wise shift).
vi) Matrix-Vector: Convert the matrix into four sub-arrays and convert these arrays into a vector of 128-bits. The positions of the subarrays are random. For example, we have sub-arrays 1,2,3,4, and the arrangement of the array in vector form will be 4,2,3,1.
For sub key-1, divide the matrix-vector into two parts and first part for the key-1 and second part for the key two. For sub key-1 from part one, determine the constant value CON and perform XOR with all other bytes in the first part of the vector. Further by performing the following operations, we will get the sub key-1 such as reverse the 64-bits vector and perform two-time circular shifts.
For sub key-2, divide the matrix vector into two parts and first part for the key-1 and the second part for the key two. For sub key-1 from part two, determine the constant value CON and perform XOR with all other bytes in the second part of the vector. Further by performing the following operations, we will get the sub key-2 such as performing two time circular shifts.
The round key can be obtained by following operations such as combining results of sub key-1 and sub key-2 into a vector as (subkey-1, subkey-2), performing two-time circular shift on matrix vector perform XOR between sub key vector and matrix vector, perform two-time circular shift to get the final key for the round. Round key is value resultant from the Cipher Key for each round, for implementation of state in the cipher. If the round key were not added in any round, then the block cipher output would not depend on the key at all and it would be an unkeyed permutation.
5 Implementation of Proposed Algorithm
The TKS can be implemented by following steps.
Replacement of plaintext with cipher text is known as substitution, the units of the plaintext are rearranged in complex order. Substitution-box (S-box) are used to hide the relationship between the key and cipher text and S-boxes generation is based on co-set graphs and symmetric groups [17].
The dynamical compound chaotic sequence generator is used for obtaining random chaotic S-box based on the image scrambling method to exploit the randomness of the chaotic system [18,19]. To implement the TKS algorithm the matrix relation S-box for encryption and inverse S-box decryption is used.
Following method is used to generate the S-box,
Here k is the key matrix is shown in Eq. (1). The determinant of the key matrix should not be zero. Following steps are used in the construction of the S-box such as taking the input byte 000000000, to divide the input into two parts 0000 and 0000, to find the inverse of 00 and second part remain same (1111 0000), to convert the above output 1111 into digits which is equal to 15 and 0000 will be 0.
In matrix form
Inverse substitution is reverse in encryption and decryption process; we will use inverse substitution.
Following method is used to generate the inverse S-box,
Here KI is the inverse key matrix is shown in Eq. (2). Following steps are used in the construction of inverse S-box such as to take the input from the S-box which is fd and in decimal form {15:13}, to take the product of a key matrix and message matrix, the result of the matrix product is {15:0}, to take the inverse of the output 15 in binary 0000 and 0000 remain same and the inverse of the fd is 00.
Function one consists of A . C XOR A + C, Reverse, Circular Shift, Swapping, Message Constant, and Key Constant. A . C XOR A + C: In this case, input data which is A & C denotes the key value. First, find the A . C and then A + C. perform the XOR between A . C and A + C. C is the sub key for the function-1. Reverse: Let’s suppose the output of the A . C XOR A + C is 123456 and reverse is 654321. By applying the key derivation function a secret and random derivation function key (DF key) can be generated with three inputs and producing three output keys such as chain key, constant key, and message key [20] as shown in Fig. 3.
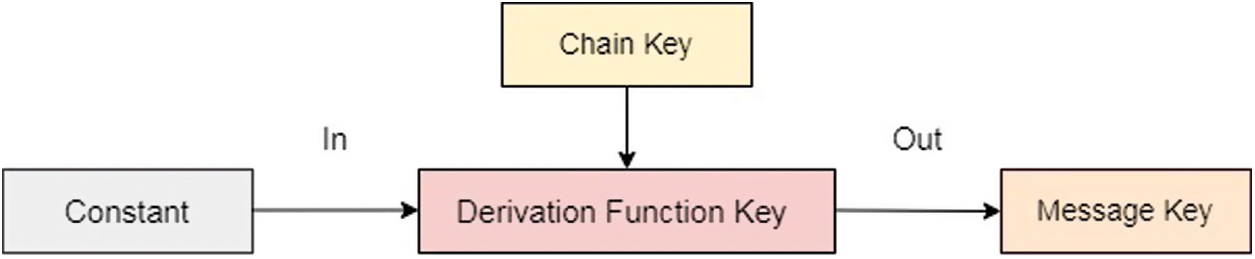
Figure 3: Chain key derivation function for constant and message
Constant (key): The function-1 will generate key constant by XORing all the bytes of the key. After finding the value of the CON, each byte of the Message is XORed with the CON. The function-1 will generate Message constant by XORing all the bytes of the message. After finding the value of the CON, each byte of the message is XORed with the CON. Swapping will be done by dividing the data into two parts e.g., 12345 and 67891. After swapping we have the data 6789112345. The substitution box to substitute the values in data vector is used.
It consists of multiple processes such as substitution, message constant, reverse message constant, and key constant. For substitution, we will replace the values in the input data to the values from the s-box. CON means constant. The function-2 will generate key constant by XORing all the bytes of the subkey-2. CON will be a byte in size, and after finding the value of the CON, each byte of the Message is XORed with the CON.
Message constant: CON means constant. The function-2 will generate Message constant by XORing all the bytes of the message. CON will be 2 bytes in size. After finding the value of the CON, each 2-bytechunk of the Message is XORed with the CON. Reverse message constant: The function-2 will generate message constant by XORing all the bytes of the message. CON will be a 2 bytes in size. After finding the value of the CON, we will find the reverse of the CON and then each 2-byte chunk of the message is XORed with the CON.
Round Cipher (Final): The round cipher is shown in Fig. 4a, each cipher and a number of blocks to create a function multiple times with these steps such as combining the output from the function 1 & 2, performing XOR operation with the round key, 3-time circular shift to output after XOR operation and round cipher. Inverse Round Cipher: In the inverse round the cipher is shown in Fig. 4b, input will be the cipher text from the encryption algorithm or from the previous round. The inverse function-1 will generate key constant by XORing all the bytes of the subkey-1 (according to the round sub key). CON will be a byte in size. After finding the value of the CON, each byte of the Message is XORed with the CON. The whole process is shown in the above Fig. 4, for the inverse function-1. Then the function-1 will generate a message constant by XORing all the bytes of the message. CON will be a byte in size. After finding the value of the CON, each byte of the message is XORed with the CON. The first step of function-1 is operation-1. In operation we will take the 64-bits of data and 64-bits of key. Encrypted message can be obtained by the following relation.
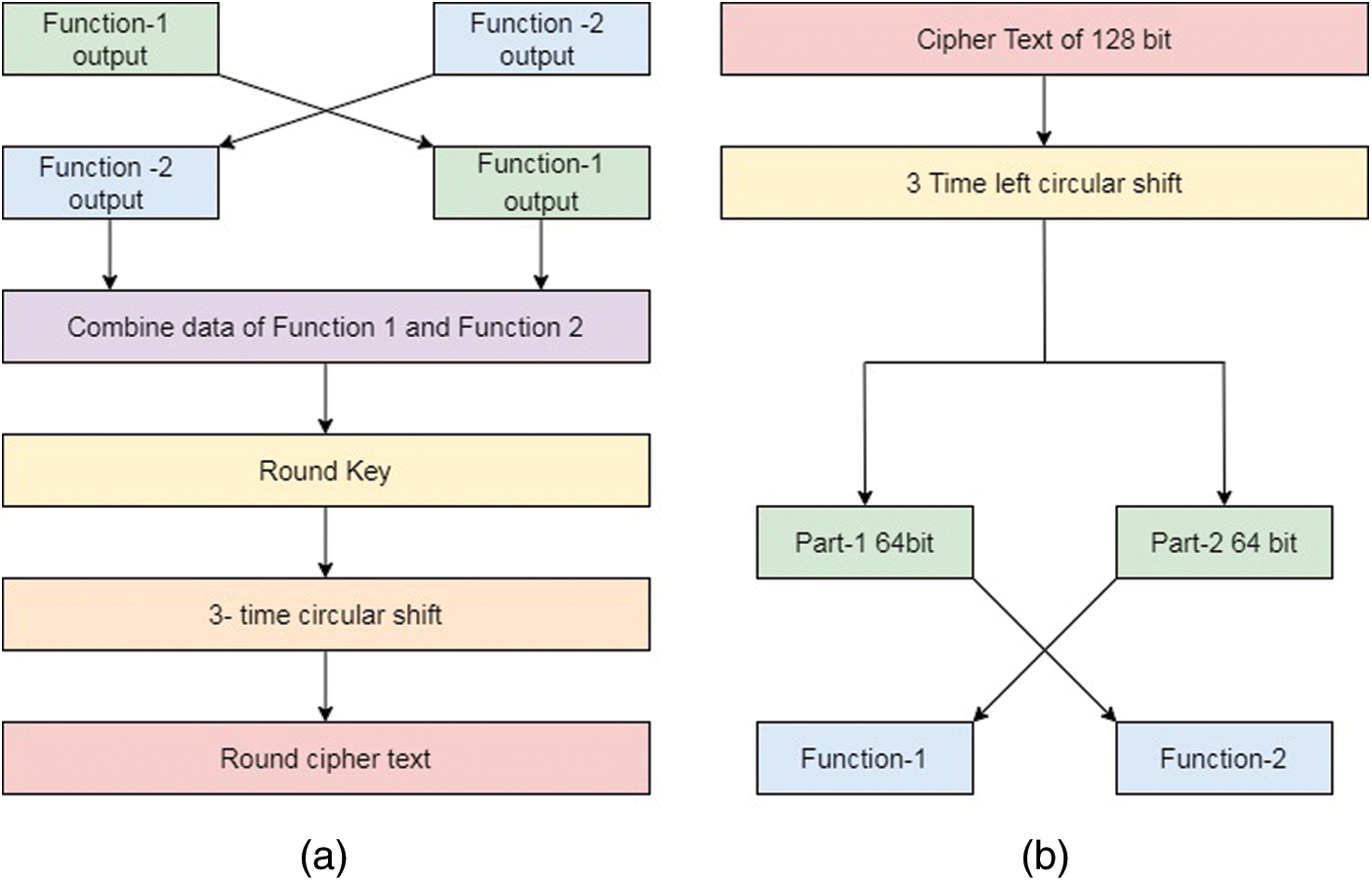
Figure 4: (a) Encryption final round (b) Decryption inverse round
Here A is message, C is the key and Y is the encrypted message in Eq. (3). In decryption algorithm we will use the following relation to recover the message A.
Here A is the message with 64-bits of length and C is also 64-bits in Eq. (4). The reverse function can be explained by example, let suppose the output of the A . C XOR A + C is 123456 and reverse is 654321 by using right and left circular shifts. For inverse function-2 key constant, message constant and reverse message constant via inverse substitution is used. The algorithm will replace the data values in the input data to the values from inverse S-box in order to recover the original text from the cipher text. With reference to key constant the function-1 will generate key constant by XORing all the bytes of the subkey-2 (according to round sub key). CON will be a byte in size. After finding the value of the CON, each byte of the message is XORed with the CON. The whole process is shown in Fig. 4, for the inverse function-2.
With reference to message constant the inverse function-2 will generate message constant by XORing all the bytes of the message. CON will be a 2 bytes in size. After finding the value of the CON, each 2-byte chunk of the message is XORed with the CON. For reverse message constant the inverse function-2 will generate message constant by XORing all the bytes of the message. CON will be a 2 bytes in size. After finding the value of the CON, we will find the reverse of the CON and then each 2-byte chunk of the message is XORed with the CON. For example, let suppose output of the A . C XOR A + C is 123456 and reverse is 654321 by implementing circular shifts.
6 Implementation of TKS Against Attacks on Multiple Rounds Block Cipher
There are different security attacks for the block cipher like rectangle-attack, sandwich-attack and single-key attack. The rectangle attacks for related-key setting are powerful also for key-recovery attack. The sandwich attack is composed of a single S-box layer this attack uses a distinguisher with three layers to have high probability characteristics [17]. To implement TKS for 16-rounds, function is divided into 4 rounds of operation with 16-bit for input and output. The function is processed through even and odd numbers of rounds respectively with 9 bit for input on left and 7-bit for right. The keys of F function are utilized for each round with sub key K of 16-bit. For 32-bit key, two keys Ki1 and Ki2 are further driven by 32-bit key K1 and K2. Mathematically defined in Eq. (5).
Likewise, with respect to above equations the three keys can be formed as shown in Eq. (6).
In above equation n indicates the total number of rounds, in our case 16 rounds to be treated for this each round has a single key like K1 to K16. Let start with 0th round if [n + (integer)] > 15 then the most significant bit can be covered and for nth round to produce key with reference to K1 to K3. As the TKS is based on the S-box as security module of SNOW-3G algorithm as a reference Rijndael’s S1-box for FSM [20,21].
To state two-way interaction formula or other statement the FO function is used within the S-box for remaining rounds as shown in Fig. 5. The 3rd round containing 16-bit is based on s-9 and s7 of S-box for the function of FO(a) which can be splinted in to 9-bit and 7-bit data for next rounds to rotate and cyclic the operation for 16-bit input data. The output results are XOR after rotation and shifting with 16-bit input and output.
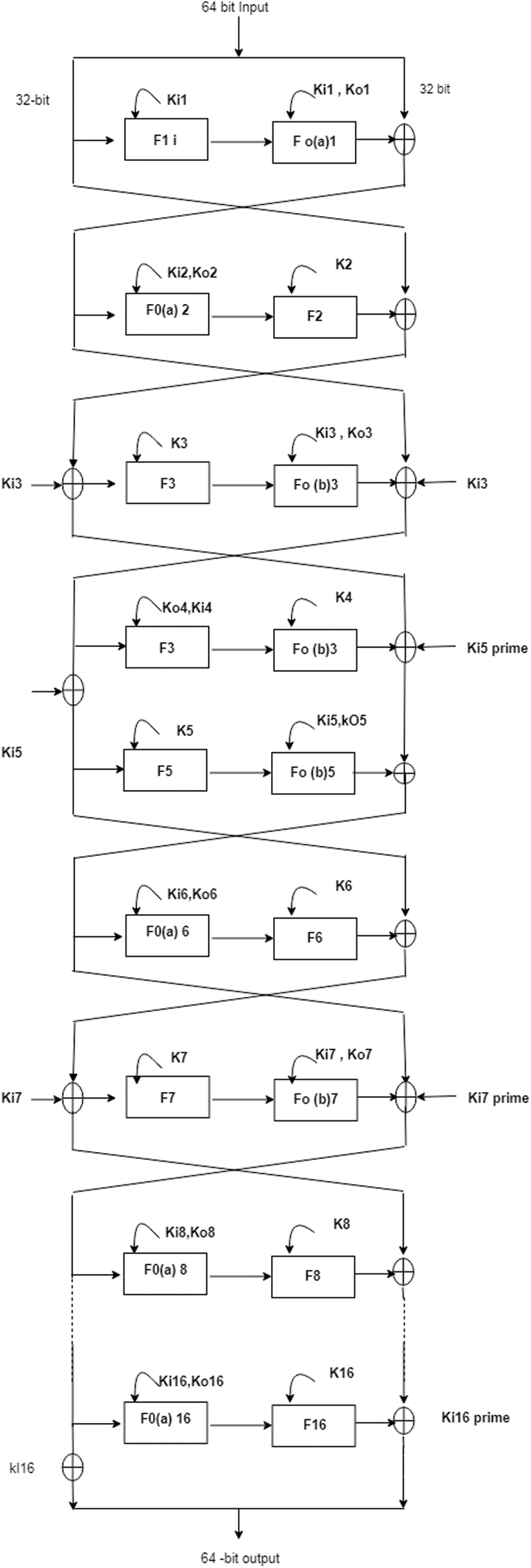
Figure 5: TKS for 16- rounds
7 Results and Analytics by Mathematical Examples
The simulation results can be tested using MATLAB statistical NIST test while the mathematical examples are given to justify the results and analytics.
Plaintext = asdqweqweasdqwea
Key = asdqweqweasdqwea
Below the hex form of the message and key.
Message = 61 73 64 71 77 65 71 77 65 61 73 64 71 77 65 61
Key = 61 73 64 71 77 65 71 77 65 61 73 64 71 77 65 61
Round key and sub -keys are generated from the key generation algorithm.
keyround1 = 17 00 8c 8c 8c 8b 14 98 15 89 15 8d 8d 12 9d 9a
subkey11 = ea f8 66 ec fc 63 fe ea
subkey21 = 67 65 67 72 ed 75 65 66
keyround2 = 01 11 ed ed ec 61 9c 73 9e fa 05 61 60 89 77 ec
subkey12 = 62 66 17 77 60 14 76 76
subkey22 = 12 89 9a 13 fa 15 9a 8a
keyround3 = 88 9f ff ff 66 88 e8 9b ed 72 01 9b 02 76 05 fe
subkey13 = 9b 06 8f 88 04 8d 05 04
subkey23 = 9b 73 72 01 fe 8c 72 64
keyround4 = fb fc 73 73 9a e8 63 fa 73 16 98 fb 12 03 89 72
subkey14 = 64 13 e9 fd 01 fa 00 99
subkey24 = 60 88 88 8d fb fb 88 16
keyround5 = fe 65 03 03 f8 60 05 73 8f 8a ec 76 8d 8f ea 02
subkey15 = 99 11 63 71 11 66 10 f9
subkey25 = 17 e9 ed fd f8 67 ed 9f
keyround6 = ee 89 9f 9f 76 01 8a 13 63 eb f9 11 f8 67 e8 9e
subkey16 = 67 17 01 99 16 02 17 ec
subkey26 = 03 65 66 61 61 03 66 fa
keyround7 = e9 f9 70 70 03 9b ee 88 10 ff 75 14 67 9e e8 71
subkey17 = 8b 03 89 60 06 10 07 ee
subkey27 = 15 03 9e 8e 9e 11 9e 67
keyround8 = f9 76 99 99 02 65 f9 77 16 fc 8e 8a 11 72 73 98
subkey18 = 63 98 73 8c 9a 8c 9b e8
subkey28 = 03 07 fb 67 70 8d fb 07
For the decryption of the cipher text obtained in the final round or in the round 8 we have to perform the following operation. For brevity only the decryption of round 8 will be performed. Divide the received data into two parts. First part is the input to the function-2 and second part is the input to the function-1.
plaintext8 = 9e 8a 87 75 ae d2 79 58 2c 47wQbNPTDJp9hMYdvogK2hAUiHsGeiybwaWe36bwtRQ3UTpYV7YuZ8FV5j9nauFCWwcjM6dTzpL5s2N79Rp5unwdMvc8ZKUperform 3-time right shift then we will get z95. z95 =75 ae d2 79 58 2c 47 93 0c 36 da f3 31 9e 8a 87 in the next step perform XOR operation between round 8 key and z95. The result will be.
Z95 =8c d8 4b e0 5a 47wQbNPTDJp9hMYdvogK2hAUiHsGeiybwaWe36bwtRQ3UTpYV7YuZ8FV5j9nauFCWwcjM6dTzpL5s2N79Rp5unwdMvc8ZKU equal parts of 64 bits.
forf1= e4 1a ca 54 79 20 ec f9
For 16 rounds each function can be explained at encryption and decryption end. With respect to key length, larger length key, higher will be the security. Key length is important to any encryption and decryption algorithm. In our designed algorithm length of the key is 128-bits as shown in Tab. 3. We have used three keys in the designed algorithm in order to encrypt and decrypt the data where the length of the key-1 is 128-bits.
The other two keys are sub keys i.e., Key-2 and key-3, the length of each sub key is 64 bits. More length of the key, makes the brute force attack less feasible. Therefore, in the designed algorithm, the two sub keys are derived from the key-1 and the length of each sub key is 64 bits.

These sub keys are used for encryption and decryption in the different functions. A final area of block cipher design, and one that has received less attention than S-box design, is the key schedule algorithm. With any Feistel block cipher, the key is used to generate one sub key for each round. In general, we would like to select sub keys to maximize the difficulty of deducing individual sub keys and the difficulty of working back to the main key. The data block length in the designed algorithm is 128-bits.
The higher the data block length higher will the data security. The data block in the designed algorithm will be divided into two parts and each part of the 64-bit length. Input to function one is the first chunk and input to the second function is the chunk 2 and the length of each chunk is 64-bits. One noteworthy feature of this structure is that it is not a Feistel structure. Recall that in classic Feistel structure, half of the data block is used to modify another half of the data block, and then the halves are swapped. Two of the AES finalists, including Rijndael, do not use a Feistel structure but process the entire data block in parallel during each round using substitutions.
AES can implement 10, 12, and 14 rounds according to the requirement of the situation and available hardware. DES is designed with 16 rounds and the proposed algorithm TKS can implement with 8 and 16 rounds. The key length of 128-bits is used in AES and a key length of 56 bits is used in DES, but the proposed algorithm TKS is implemented with three keys. The length of the key-1 is 128-bits. The other two keys are sub keys i.e., Key-2 and key-3, the length of each sub key is 64-bits.
Avalanche effect for plain text changed is explained as that a change in one bit of the input should produce a change in many bits of the output. Let us have a message to encrypt “abcdefghijklm000”. This message is our original message. If only one bit will have changed in the original cipher text, then there will be a 64-bit change occurs. Avalanche effect (key changed), let a message encrypt “abcdefghijklm000”. This message is original.
So the number of bits changed in the original message and the corresponding change in the key. Here the key is “abcdefghijklm000”. By using S-box with rotational and cyclic processes to use S9 and S7 boxes, the TKS algorithm makes block cipher strong for discussed security attacks, particularly single key attacks. Keys with XOR and merge operations for each round.
The aim of this work is to improve cipher algorithms limitations by a proposed a new algorithm TKS in which the key is modified on polyalphabetic substitution cipher to maintain the size of key and plaintext. The designed algorithm has shown a good avalanche effect. The algorithm has a sufficient amount of nonlinearity. The designed algorithm has 8 or 16 steps for encryption and decryption which is comparatively less than the symmetric key cryptography and asymmetric key cryptography network-based security model in terms of performance. Each step is consisting of two functions, function-1 and 2. Function-1 and function-2 consist of different operations which are to be performed on the data, for encryption purposes. The performance of this algorithm is more efficient and fast as compared with the symmetric key cryptography and asymmetric key cryptography network-based security model. In the feature, research work can be conducted on this algorithm for evaluation of performance on a different level of network and data security.
Acknowledgement: The authors, acknowledge with thanks to DSR King Abdulaziz University, Jeddah, Saudi Arabia for technical and financial support.
Funding Statement: This project was funded by the Deanship of Scientific Research (DSR), King Abdul-Aziz University, Jeddah, Saudi Arabia under Grant No. (D-63-611-1442).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. N. L. Obiora, “Using the confidentiality, integrity or availability and authentication, authorization, and accounting models to explain cybersecurity Activities,” Project Management (PM) World Journal, vol. 6, no. 1, pp. 1–6, 2017. [Google Scholar]
2. H. B. E. H. Hassan, “Comparative study of different cryptographic algorithms,” Journal of Information Security, vol. 11, no. 3, pp. 138–148, 2020. [Google Scholar]
3. D. N. Lal and D. S. K. Kumar, “Survey on cryptographic block cipher methods to solve the security issues,” International Journal of Engineering and Technology, vol. 9, no. 4, pp. 3115–3129, 2017. [Google Scholar]
4. J. Nazir, M. W. Iqbal, T. Alyas, M. Hamid, M. Saleem et al., “Load Balancing Framework for cross region tasks in cloud computing,” Computers Materials & Continua, vol. 70, no. 1, pp. 1479–1490, 2021. [Google Scholar]
5. Z. Zhang, W. Wenling, H. Sui and B. Wang, “Quantum attacks on type-3 generalized feistel scheme and unbalanced feistel scheme with expanding functions,” Chinese Journal of Electronics, vol. 31, no. 4, pp. 1–9, 2022. [Google Scholar]
6. L. Cheng, Y. Zhao, J. Yang and L. Liu, “A countermeasure of power attack for lightweight cryptographic algorithm using bit permutation operation,” Journal of Physics Conference Series, vol. 1856, no. 1, pp. 1–6, 2021. [Google Scholar]
7. M. Madani and C. Tanougast, “FPGA implementation of an enhanced chaotic-KASUMI block cipher,” Microprocessor and Microsystems, vol. 80, no. 1, pp. 103644, 2021. [Google Scholar]
8. S. K. Yadav, Some problems in symmetric and asymmetric cryptography. In: Information Security, 1st ed., vol. 1. Saarbrucken, Germany: LAP LAMBERT Academic Publishing, pp. 103–114, 2020. [Google Scholar]
9. H. Loriya, A. Kulshreshta and D. Keraliya, “Security analysis of various public key cryptosystems for authentication and key agreement in wireless communication network,” International Journal of Advanced Research in Computer and Communication Engineering (IJARCCE), vol. 6, no. 2, pp. 267–274, 2017. [Google Scholar]
10. B. Ambedkar and S. Bedi, “A new factorization method to factorize RSA public key encryption,” International Journal of Computer Science Issues (IJCSI), vol. 8, no. 6, pp. 242–247, 2011. [Google Scholar]
11. M. Shrivas, A. Boasiako, S. Krishanan and T. Yeboah, “Enhanced simplified symmetric key encryption algorithm,” Texila International Journal of Academic Research, vol. 3, no. 2, pp. 1–27, 2016. [Google Scholar]
12. K. K. Pandey, V. Rangari and S. K. Sinha, “An enhanced symmetric key cryptography algorithm to improve data security,” International Journal of Computer Applications, vol. 74, no. 20, pp. 29–33, 2013. [Google Scholar]
13. E. B. Barker and A. L. Roginsky, “Transitioning the use of cryptographic algorithms and key lengths,” National Institute of Standards and Technology (NIST) Special Publications, vol. 1, no. 1, pp. 1–33, 2019. [Google Scholar]
14. A. Razaq, H. Alolaiyan, M. Ahmad, M. A. Yousaf, U. Shuaib et al., “A novel method for generation of strong substitution boxes based on coset graphs and symmetric groups,” IEEE Access, vol. 8, no. 1, pp. 75473–75490, 2020. [Google Scholar]
15. L. Yi, X. Tong, Z. Wang, M. Zhang, H. Zhu et al., “A novel block encryption algorithm based on chaotic s-box for wireless sensor network,” IEEE Access, vol. 7, no. 1, pp. 53079–53090, 2019. [Google Scholar]
16. S. Zhu, X. Deng, W. Zhang and C. Zhu, “A new one-dimensional compound chaotic system and its application in high-speed image encryption,” Applied Sciences, vol. 11, no. 23, pp. 11206, 2021. [Google Scholar]
17. J. Alwen, S. Coretti and Y. Dodis, “The double ratchet: Security notions, proofs, and modularization for the signal protocol,” in Annual Int. Conf. on the Theory and Applications of Cryptographic Techniques, Darmstadt, Germany, pp. 129–158, 2019. [Google Scholar]
18. B. Zhao, X. Dong, W. Meier, K. Jia and G. Wang, “Generalized related-key rectangle attacks on block ciphers with linear key schedule: Applications to SKINNY and GIFT,” Designs Codes and Cryptography, vol. 88, no. 6, pp. 1103–1126, 2020. [Google Scholar]
19. P. Gundaram, S. N. Allu, N. Yerukala and A. N. Tentu, “Rainbow tables for cryptanalysis of A5/1 stream cipher,” in Second Int. Conf. on Networks and Advances in Computational Technologies, Thiruvananthapuram, India, pp. 251–261, 2021. [Google Scholar]
20. R. Muthalagu and S. Jain, “Modifying LFSR of ZUC to reduce time for key-stream generation,” Journal of Cyber Security and Mobility, vol. 5, no. 1, pp. 257–268, 2017. [Google Scholar]
21. M. Moraitis and E. Dubrova, “Bitstream modification attack on SNOW 3G,” in Proc. of the 23rd Conf. on Design, Automation and Test in Europe (DATE), CA, USA, pp. 1275–1278, 2020. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |