Computers, Materials & Continua DOI:10.32604/cmc.2022.028234
Article

UAV-Aided Data Acquisition Using Gaining-Sharing Knowledge Optimization Algorithm

Rania M Tawfik1, Hazem A. A. Nomer2, M. Saeed Darweesh1,*, Ali Wagdy Mohamed3,4 and Hassan Mostafa5,6

1Wireless Intelligent Networks Center (WINC), School of Engineering and Applied Sciences, Nile University, Giza, 12677, Egypt
2School of Information Technology and Computer Science (ITCS), Nile University, Giza, 12677, Egypt
3Operations Research Department, Faculty of Graduate Studies for Statistical Research, Cairo University, Giza, 12613, Egypt
4Department of Mathematics and Actuarial Science, School of Science and Engineering, The American University in Cairo, Egypt
5Electronics and Communications Engineering Department, Cairo University, Egypt
6University of Science and Technology, Nanotechnology and Nanoelectronics Program, Zewail City of Science and Technology, October Gardens, 6th of October, Giza, 12578, Egypt
*Corresponding Author: M. Saeed Darweesh. Email: mdarweesh@nu.edu.eg
Received: 05 February 2022; Accepted: 10 March 2022

Abstract: Unmanned Aerial Vehicles (UAVs) provide a reliable and energy-efficient solution for data collection from the Narrowband Internet of Things (NB-IoT) devices. However, the UAV’s deployment optimization, including locations of the UAV’s stop points, is a necessity to minimize the energy consumption of the UAV and the NB-IoT devices and also to conduct the data collection efficiently. In this regard, this paper proposes Gaining-Sharing Knowledge (GSK) algorithm for optimizing the UAV’s deployment. In GSK, the number of UAV’s stop points in the three-dimensional space is encapsulated into a single individual with a fixed length representing an entire deployment. The superiority of using GSK in the tackled problem is verified by simulation in seven scenarios. It provides significant results in all seven scenarios compared with other four optimization algorithms used before with the same problem. Besides, the NB-IoT is proposed as the wireless communication technology between the UAV and IoT devices.

Keywords: NB-IoT; UAV; GSK; stop points; optimization

1  Introduction

Internet of Things (IoT) represents the concept of the communication and the data exchange between a massive number of limited-power devices from diverse environments over a large-scale interconnected network without human interference [1]. In recent years, the IoT has been successfully used in various fields such as medical care, intelligent environment, and transportation logistics [1,2]. With the anticipated growth of the IoT market, the number of IoT devices worldwide has been significantly increased from 15.41 billion in 2015 to 23.14 billion in 2018, and it is expected to reach up to 75.44 billion in 2025 [3]. Thus, the efficient data collection of those IoT devices is a major challenging task [4]. There are two significant challenges with traditional data collection methods that use automatic data transmission or human collection [5]. Firstly, the energy of the IoT device is not sufficient to transmit the data to the base station that is located at a distance from the IoT device. Secondly, the data loss and incorrect data transmission problem is caused by poor environments such as basements and far-reaching areas. Therefore, there is a crucial need to develop new IoT data collection methods.

The deployment of the Unmanned Aerial Vehicles (UAVs) as an emerging data collection platform for IoT devices has received wide attention and extensive research due to their mobility, flexibility, capability of establishing Line-of-Sight (LoS) links with the target devices, and ability to provide emergency services to the IoT devices in temporary or unexpected events [6,7]. In addition, the UAV has its own energy and can be frequently recharged. Hence, compared with terrestrial data collection platforms, UAVs can provide a reliable and effective way for the data collection from IoT devices by flying to the target device [8,9].

The UAV’s deployment optimization is a crucial task as a properly deployed UAV can represent a reliable and energy-efficient data collection solution for IoT devices [10]. The deployment procedure is presented in [8] where the total energy consumption of the IoT devices is minimized, and the UAV’s energy required to move efficiently is minimal as well. The total energy consumption of the IoT devices as well as the UAV energy are considered as the optimization goals for efficient data collection. In [6], the optimal deployment of multiple UAVs for data collection from IoT devices is proposed where, a single UAV serves a cluster of IoT devices. In addition, the UAV’s optimal path is determined by dynamic clustering and optimal transmission theory to minimize the UAV’s energy consumption for IoT data collection in mobile and time-varying networks. Authors in [11] present the UAV’s deployment of a UAV-assisted relay system where the UAV is employed as a relay for data transmission from the source nodes and the destination ones. In [12] the UAV’s deployment is studied for a downlink communication converge scheme. Reference [13] proposes the UAV’s deployment optimization by considering the minimum transmission power. Following that, they implement deployment optimization with different requirements of Quality of Service (QoS) [14]. In [5], the problem of the UAV’s deployment optimization is described as a set of UAV’s locations at considerable stop points to collect the data efficiently with minimal overall energy consumption. Moreover, swarm intelligence technology is applied to this problem, and three algorithms; the newer Flower Pollination Algorithm (FPA) [15], the SALP Swarm Algorithm (SSA) [16], and the Sine Cosine Algorithm (SCA) [17] are used for coding to solve the UAV’s deployment optimization problem. The three algorithms have better performance compared with the Differential Evolution Algorithm with Variable Population Size (DEVIPS) proposed in [18]. This paper utilizes a nature-inspired optimization algorithm that is based on the concept of gaining and sharing knowledge during human life, known as Gaining-Sharing Knowledge (GSK) algorithm [19] for solving the problem of the UAV’s deployment optimization for IoT data collection. Furthermore, we propose using the Narrowband-IoT (NB-IoT), which is one of the Low-Power Wide Access Network (LPWAN) technologies [20] as the wireless communication technology between the UAV and the IoT devices. At last, it is shown that using the GSK algorithm has significant performance improvements compared to the algorithms introduced in [5]. The main contributions of this paper are as follows:

■   Deploying of the GSK optimization algorithm on the task of the UAV deployment for IoT data acquisition for the first time.

■   Comparing the GSK results to those of the other optimization algorithms in previous research and proving that GSK outperforms them.

■   Proposing the NB-IoT to be the wireless communication technique between the UAV and IoT devices.

The reminder of the paper is organized as follows. Section 2 describes the problem that this work is tackling. Section 3 introduces the proposed Gaining-Sharing Knowledge (GSK) coding method. Section 4 presents the NB-IoT communication technology for UAV applications. The results and discussions are presented in Section 5. At last, Section 6 concludes this work.

2  Problem Formulation

As shown in Fig. 1, we consider that a UAV is flying horizontally at the height of H, which is used for collecting data from a set of ground N IoT devices with zero height at K stop points, denoted as N=1,2,3,..,n. The red line and the blue line respectively represent the path taken by the UAV through the stop points and the connectivity between M IoT devices and the UAV at each stop point.

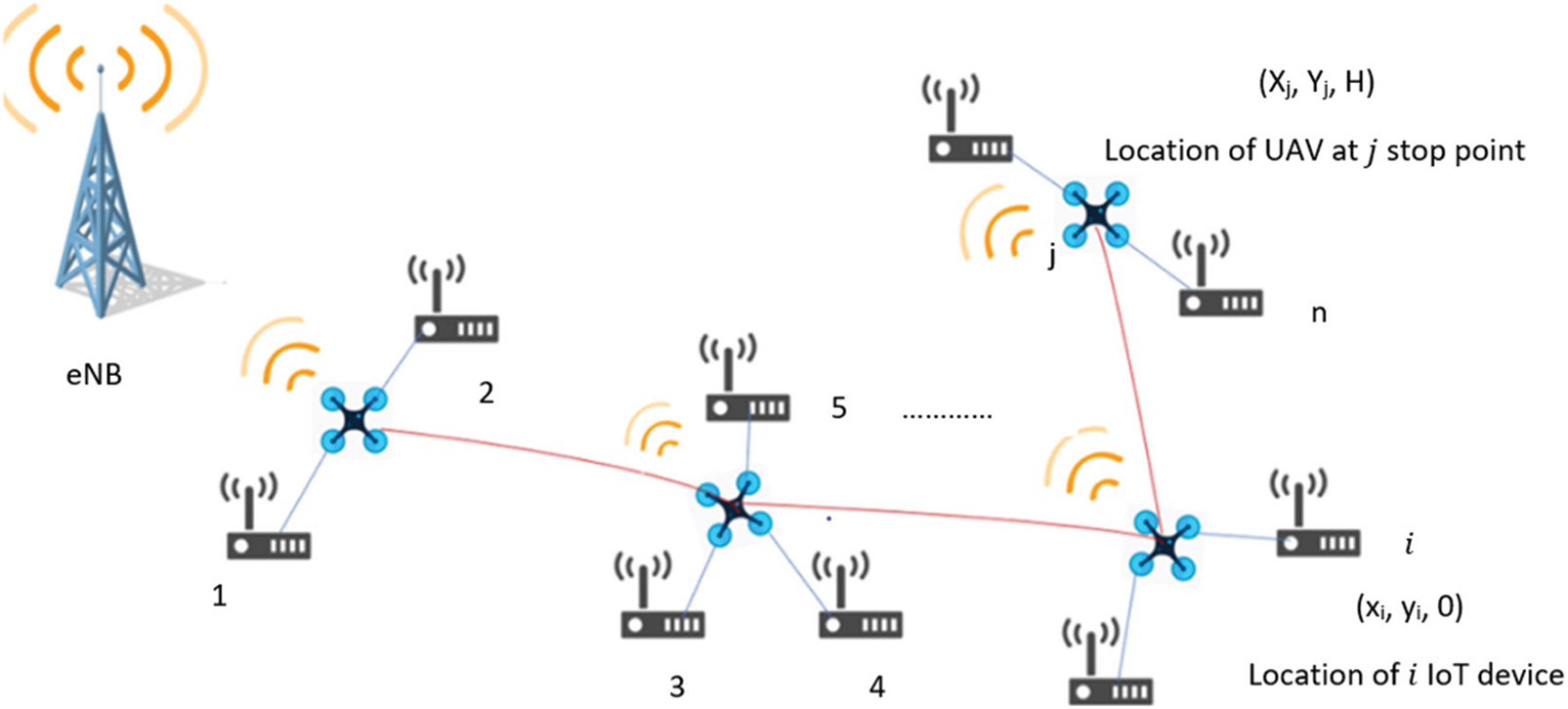
Figure 1: Schematic diagram of UAV collecting data from N IoT devices

Due to UAV’s flexibility and mobility, the locations of its stop points can be modified to guarantee to collect the data from all the IoT devices and reducing the energy consumption of the UAV and IoT devices. Then, the problem can be formulated as shown in Eq. (1) [5].

min(Euav+wEIoT)

s.t.

C1:ai,j∈{0,1},∀i∈N,j∈K

C2:∑j=1k⁡ai,j=1,∀i∈N

C3:∑i=1N⁡ai,j≤M,∀j∈K(1)

C4:∑i=1N⁡∑j=1K⁡ai,j=N

C5:{Xj∈[Xmin,Xmax]Yj∈[Ymin,Ymax],∀j∈K

C6:K∈[Kmin,Kmax]

where Euav is the total UAV’s energy consumption in the data collection process, EIoT is the energy consumption of all IoT devices, and w is the weight between the energy consumption of all IoT devices and that of the UAV as w ≥ 0.

Moreover, the C1 to C6 are the constraint conditions. The ai,j in C1 and C2 is a binary variable that indicates the association between the ith IoT device (i ∈N) and the UAV at the jth stop point (j ∈k). In C1, the ai,j is equal to one if only the distance between the UAV and the target device which can be defined from Eq. (5) is the minimum and the data can be appropriately gathered, as a result. The C2 indicates that each IoT device can send its data only to a one-stop point. From C3, we consider the UAV can receive data from M IoT devices at a single stop point. The C4 indicates that the UAV must collect the data from all N IoT devices. The C5 shows the coordinates of the stop points in X-axis (Xj) and in Y-axis (Yj). At last, the number of the stop points is as shown in C6. The Euav can be calculated as follows:

Euav=∑j=1K⁡Pmax(ai,jTi,j),∀j∈K(2)

The P is UAV’s flight power, and the Ti,j is the time spent by the UAV for collecting the data from device i at the stop point j, and it is defined by dividing the amount of data that the device needs to transmit, Di, by its transmission data rate as shown in Eq. (3) [21].

Ti,j=Di/Ri,j(3)

where the transmission data rate can be defined as follows [22]:

Ri,j=Blog2(1+Piβi,j/σ2)(4)

The B is the system bandwidth, the Pi is the data transmission power of device i, βij is equal to β0dij−2 as β0 is the channel power gain at a reference distance of 1 m [23] and the distance dij can be calculated from Eq. (5). Finally, the σ2 represents the noise power spectral density.

di,j=(Xj−xi)2+(Yj−yi)2+H2(5)

where, the locations of ith IoT device are Xi and Yi in the X-axis and the Y-axis, respectively. For the EIoT, it can be calculated as follows [18]:

EIoT=∑i=1N⁡∑j=1Kai,jEi,j(6)

where the energy consumption for device i can be defined as shown in Eq. (7) [18].

Eij=PiTij,∀i∈N,j∈K(7)

3  Gaining-Sharing Knowledge (GSK) Algorithm

Gaining-Sharing Knowledge algorithm (GSK) is a nature inspired algorithm based on human behavior, and how a single individual can share knowledge and learn from the others. Introduced in [19], GSK has been applied in several optimization problems as feature selection [24–26], scheduling problems [27–29], maximal covering model [30], parameter extraction of photovoltaic models [31] and combinatorial optimization problems as knapsack [32], travelling salesman problem [33], travelling advisor problem [34], and transportation problem [35].

GSK has two main stages: the junior phase and the senior phase, each one has a different mutation rule that is applied to specified number of dimensions. The number of dimensions to be applied by junior or senior mutation rules are determined by a parameter k. The parameter k is called in the original algorithm the knowledge rate, which controls the rate in which the algorithm shifts from the junior phase to the senior phase.

3.1 Basic GSK

The basic version of GSK introduced in [19] has several steps described as the following:

1.    An initial population is generated randomly considering the boundary constraints.

2.    The number of dimensions for each individual to be mutated by the junior mutation scheme is computed using the following formula:

DJ=D∗((MAXNFES−NFES)/MAXNFES)k(8)

DS=D−DJ(9)

3.   Junior phase: All individuals are sorted in ascending order with respect to their objective function values. For each individual in the sized population or the population size (NP) xi (i = 1, 2, …, NP), the nearest best neighbour (xi−1) and the worst neighbour (xi+1) are selected for gaining knowledge, as well choosing an individual (xr) randomly for knowledge sharing then:

xi={xi+kf∗(xi−1−xi+1)+(xr−xi),f(xi)>f(xr)xi+kf∗(xi−1−xi+1)+(xi−xr),f(xi)<f(xr)(10)

4.   Senior phase: Updating individuals are determined as the following: The candidates in the population are divided into three categories (best individuals, middle individuals, and worst individuals). The ratio of best class and worst class is determined by a parameter p, after sorting all individuals in ascending order based on the values of their objective function. Each individual is updated according to the mutation rule:

xi={xi+kf∗(xp−b−xp−w)+(xm−xi),f(xi)>f(xm)xi+kf∗(xp−b−xp−w)+(xi−xm),f(xi)<f(xm)(11)

3.2 GSK Coding Scheme

Unlike previous approaches which either represent the entire population as deployment for an UAV location according to a fixed stop points k or represent each NP individual as a deployment with non-fixed stop points [5,18], in the proposed approach instead the population represents NP entire deployments with fixed stop points. In the approach, the length of each individual is fixed, and the number of dimensions equals to 3 ∗ kmax, in which kmax is the maximum number of stop points for an UAV to collect data from as shown in Fig. 2.

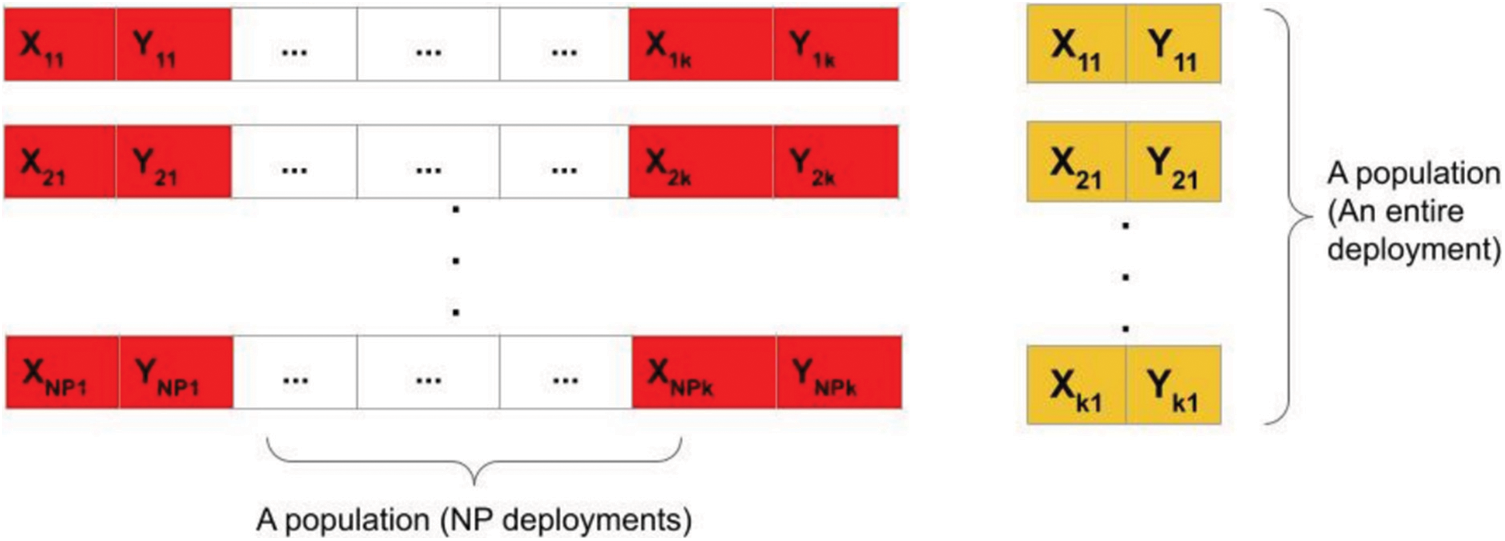
Figure 2: The proposed approach encodes the entire deployment in a single individual, thus there are NP deployments in which the length of each individual is fixed and so is the number of stop points. Other approaches (as DEVIPS) use the population to represent an entire deployment. An update rule updates the population which adapts the number of stopping points

As kmax increases in some environments, the number of dimensions increases, which makes its more challenging for the search algorithm. However, this representation using fixed number of stop points make the search space more stable as the number of dimensions is fixed and not changing. Approaches that represent a deployment as the entire population, uses an update rule to select the best population or merge successful candidates together. The number of candidates in this case is small and remains constant1.

4  NB-IoT Technology for UAV Applications

Narrowband-Internet of Things (NB-IoT) is a cellular technology standard introduced by the 3rd Generation Partnership Project (3GPP) in 2016 in order to serve the massive number of IoT applications [36,37]. This technology provides the main requirements of IoT applications such as long communication range, low power consumption, low data rate, low cost, and large device connectivity [38,39]. NB-IoT is based on the 3GPP Long-Term Evolution (LTE), and therefore it operates in a licensed spectrum and contrary to the other unlicensed wireless technologies (e.g., LoRaWAN and Sigfox) which need new infrastructures, NB-IoT utilizes the same infrastructure of LTE [40]. Most LTE features are inherited in NB-IoT, reducing the complexity of LTE channels and signals to meet the NB-IoT constraints of low cost and low power. In addition, the number of these channels is reduced to fit the new NB-IoT frame structure. As well, the same LTE protocol stacks of the User Equipment (UE) and the Evolved Node B (eNB) are utilized in NB-IoT with reducing the functionalities of each layer [41,42].

The NB-IoT system is designed to occupy one LTE resource block of a 180 kHz bandwidth that is deployed in three different operation modes defined by 3GPP to guarantee the coexistence with LTE carriers without degrading the LTE performance. These operation modes are in-band mode, guard-band mode, and standalone mode, and the details for these modes can be found in [43]. Furthermore, NB-IoT has a large number of repetitions which are up to 128, and 2048 repetitions in uplink and downlink, respectively, and that indeed enhances the coverage [44]. Also, NB-IoT system can be used to improve several applications [45].

The NB-IoT physical downlink channels go through the transmission chain’s blocks at the eNB starting from Cyclic Redundancy Check (CRC) block for the error detection [46]. Then the payload with CRC is encoded [47], a rate matched [48], interleaved, scrambled, modulated, and at last mapped to the Resource Elements (REs) [42]. The overall transmission chain’s processes at the eNB are reversed at the UE receiver (i.e., decoding, channel deinterleaving, etc.) with adding the channel estimation and equalization blocks [49]. While the NB-IoT physical uplink channels at the UE transmitter go through the same transmission blocks, however, the Single-Carrier Frequency-Division Multiple Access (SC-FDMA) modulation techniques are used instead of the Orthogonal Frequency-Division Multiplexing (OFDM) modulation technique used in the downlink in order to reduce the Peak to Average Power Ratio (PAPR), which correspondingly reduces the power consumption [50] and this uplink transmission chain’s blocks are also reversed at the eNB receiver with adding the blocks of the channel estimation and equalization to get better decoding of the received information. The description of each block within the transmission and the reception chains at both eNB and UE sides are stated in [43].

The NB-IoT technology can help several UAV applications and one of the critical applications, telemedicine, to transit the needed data with low power and high data rate. However, the leakage of medical data in telemedicine violates the privacy of patients seriously. So, it’s essential to study how to secure the medical audio data [51] and 3D medical imaging to diagnose the disease accurately [52].

In this work, we propose deploying NB-IoT as the communication technology between the UAV and IoT devices due to its main advantage of low power consumption. Where, NB-IoT has two power saving features which are Power Saving Mode (PSM) and extended Discontinuous Reception (eDRx). These two features extend the NB-IoT devices’ battery lifetime to be 10 years [44]. Accordingly, that makes NB-IoT a good communication solution for the UAV-aided IoT data collection applications. We also consider a relay-based NB-IoT system with N NB-IoT UEs communicating with the NB-IoT base station through a single UAV which collects the data from those IoT devices and delivers it to the NB-IoT base station.

5  Results and Discussions

This section introduces the experimental setup to verify the GSK algorithm for solving the UAV deployment optimization problem. Also, presents the results and the discussions. Experimental simulations are performed according to the coding scheme proposed in this paper using the algorithms SSA, FPA, and SCA as basic algorithms. The algorithm-related parameter settings are listed in Tab. 1.

The F and CR of DEVIPS respectively represent the mutation probability and cross probability. The Eva and MAXNFES in SSA and SCA respectively represent the objective function’s current and maximum evaluation times. In FPA, the P represents the conversion probability, which is the parameter controlling the Lévy distribution. NP represents the population number.

For GSK, we used the same parameter setting as in [19] except for the population size parameter NP, in which we set NP=20 in the scenario where the number of IoT devices is equal to 100, 200, 300, and 400, and NP=50 when the number of IoT devices is equal to 500, 600, and 700. We denote the number of IoT devices as N.

The setting of other key parameters in the experimental environment is the same as that given in reference [18]: the distribution range of IoT devices is (0–1000) m, and the height is set to 200 m. The amount of data each device needs to transmit to the UAV is between 1–1000 MB. It is considered that the UAV can receive at most five information devices at the same location to transmit data simultaneously. The noise power is −30 dB, the data transmission power is 0.1 W, and the flight power of the UAV is 1000 W.

Implementation of GSK and IoT devices locations generation is done in python 3.7, and all experiments were run using python interpreter on Linux environment. MAXNFES is set to 10000. We run the GSK algorithm 30 times for each of the 7 scenarios. We performed the Friedman test, and the Wilcoxon rank-sum test was performed to check its significance level. We calculate both the mean value and standard deviation after the 30 runs. The test level is 0.05, where the symbol ‘ + ’ − ‘ = ’ indicates that the corresponding algorithm is superior to the benchmark algorithm, inferior to the benchmark algorithm, or has no significant difference, respectively.

Fig. 3a through Fig. 4d shows the evolution curve of GSK algorithm when N=100 up to N=700. The evolution curves were plotted for a single run only, which is the median run. It shows that GSK has a common behaviour of steady convergence after less than 100 generations, which implies fast convergence of the GSK algorithm. This appears greatly in cases which N=100, N=200, and N=300. In cases where N is greater than 300, the evolution curve shows a similar but slower convergence of the GSK algorithm.

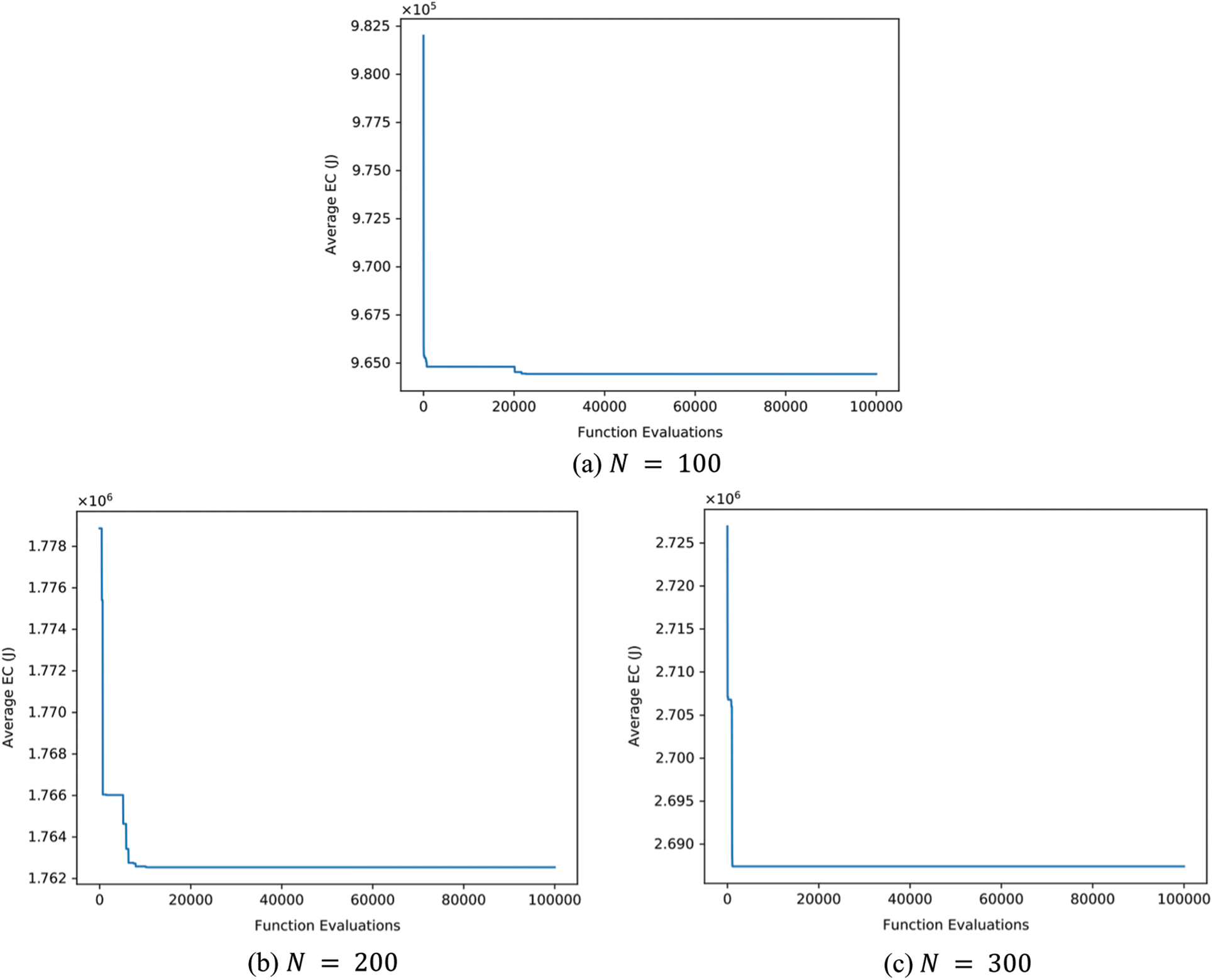
Figure 3: The evolution curve of GSK algorithm when N≤300

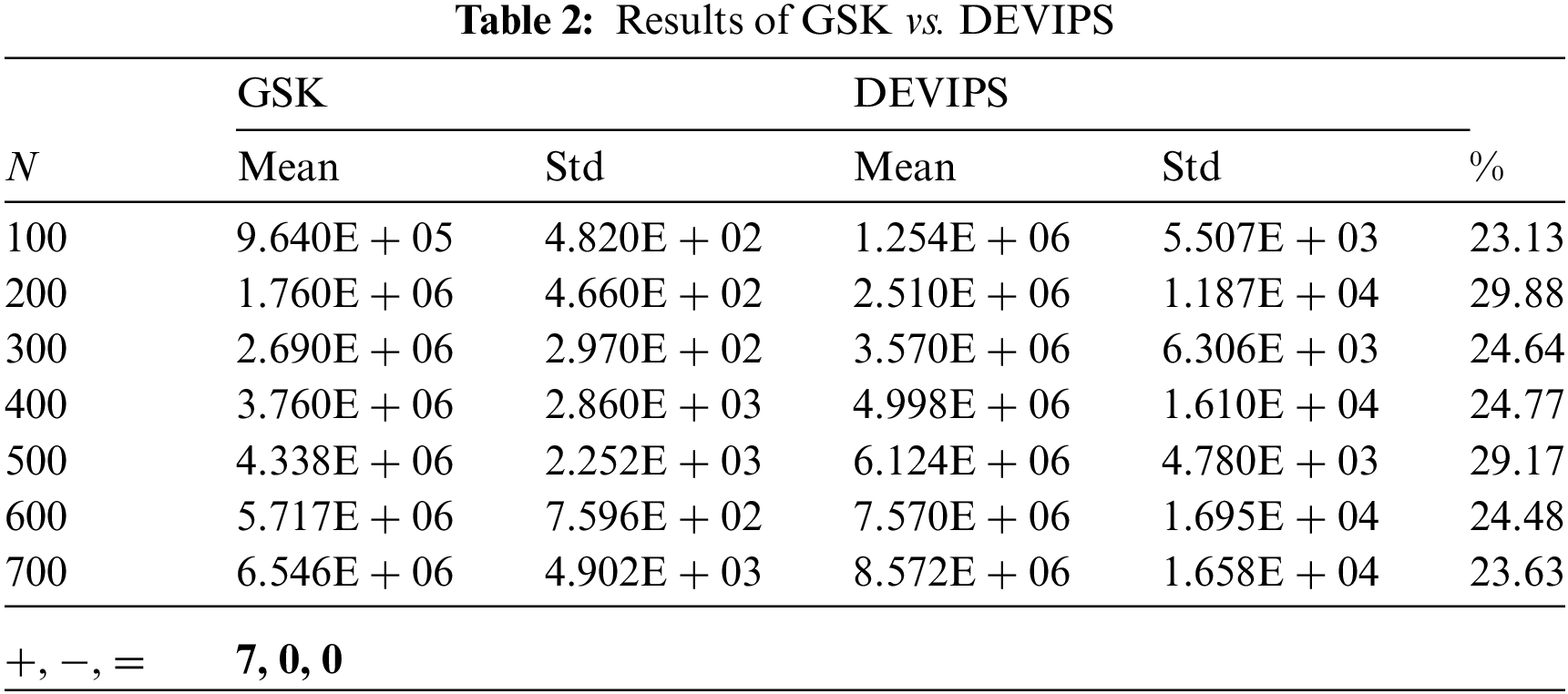
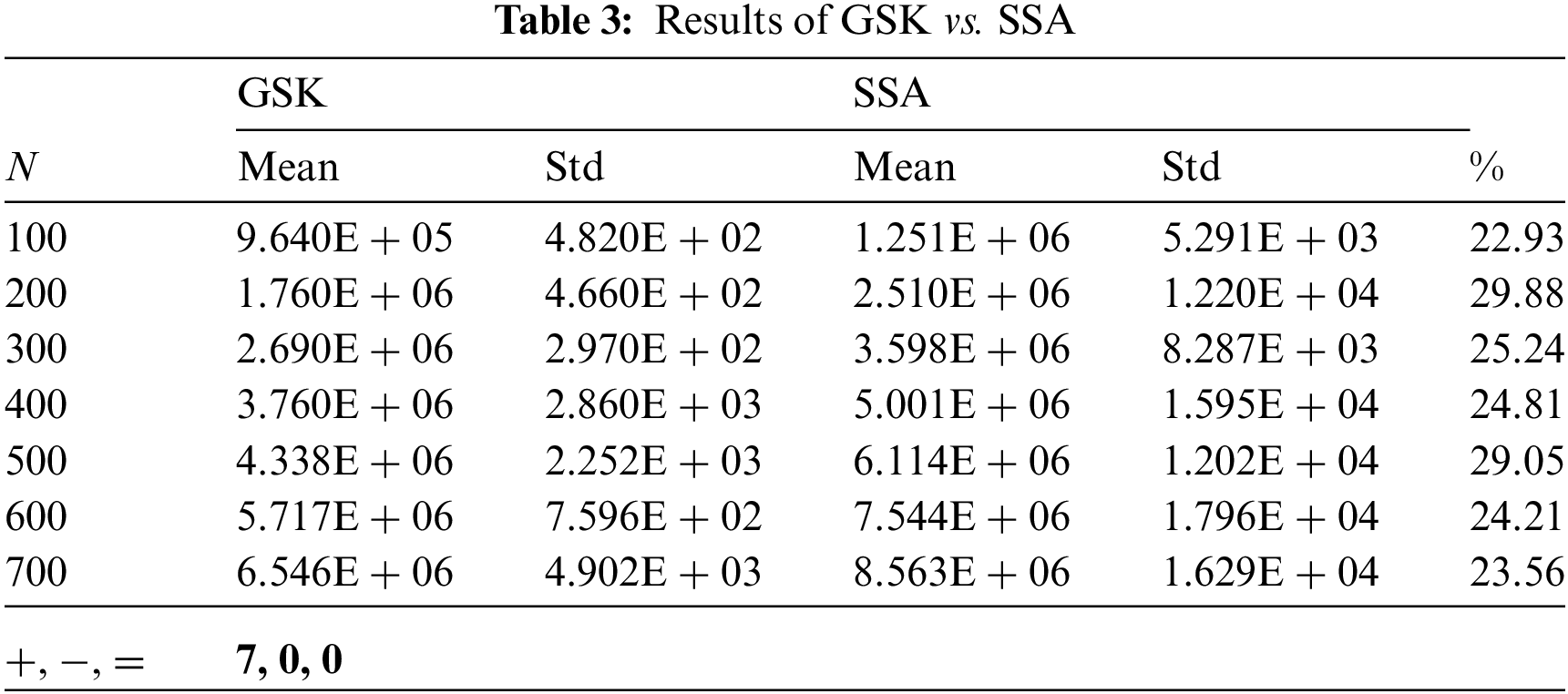
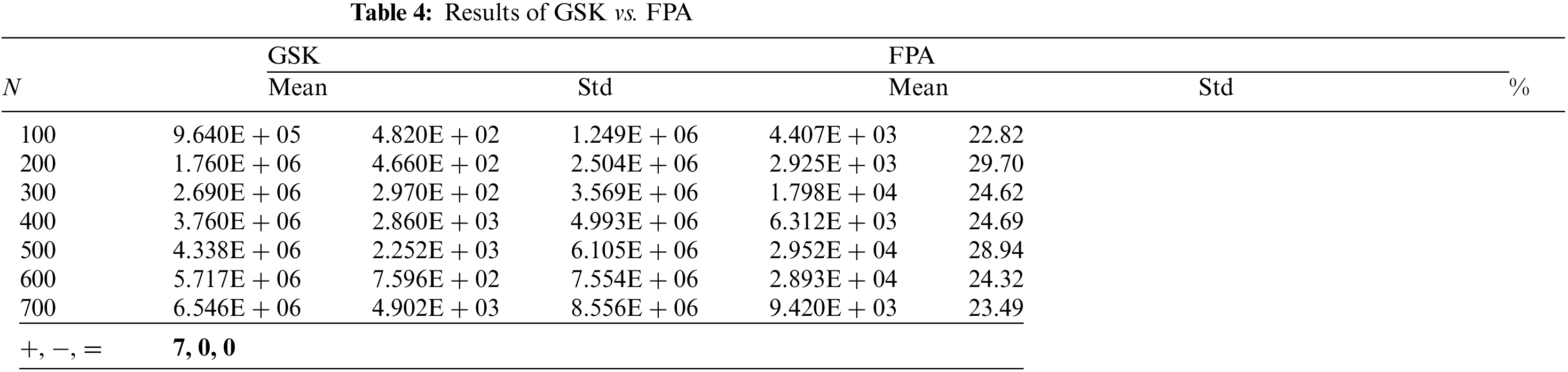
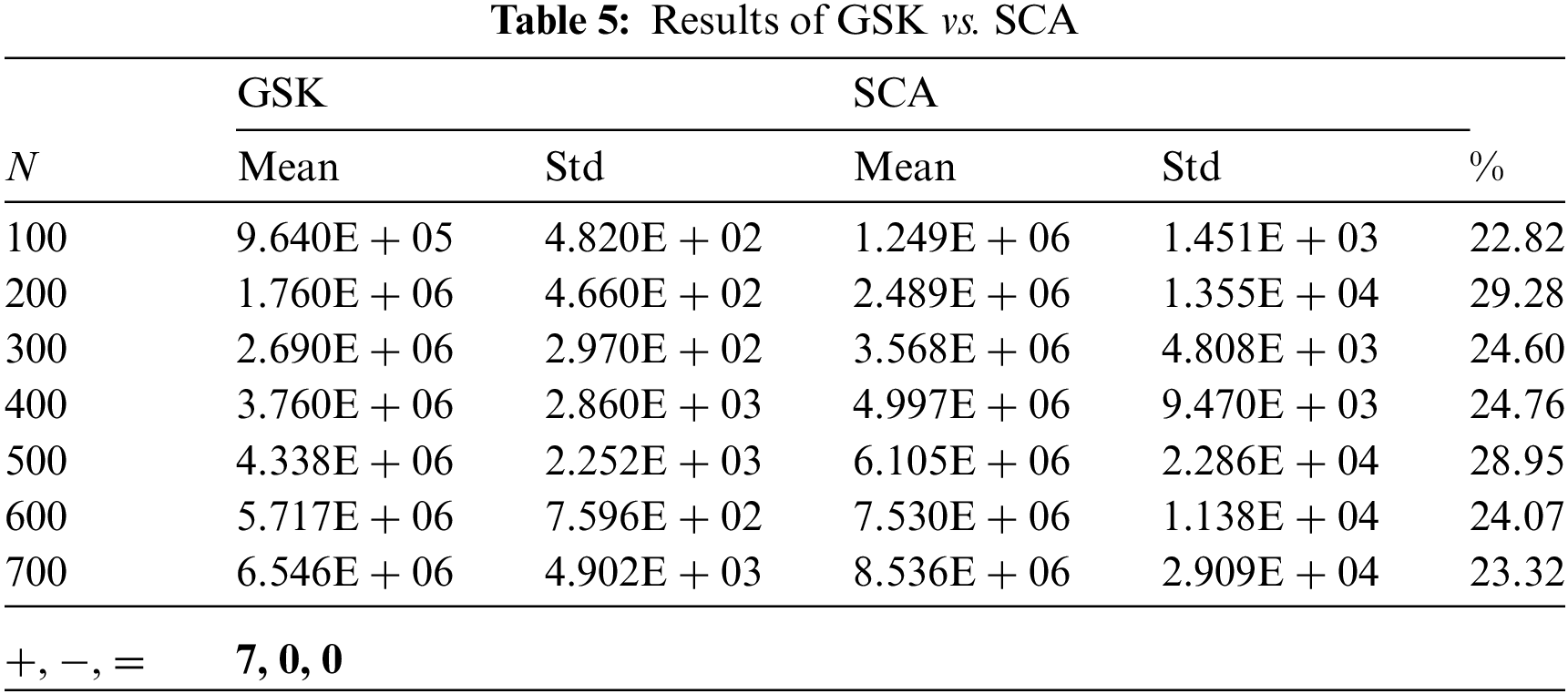
The results of DEVIPS, SSA, FPA, and SCA are all taken from [5]. All numbers are truncated to three decimal places. The Wilcoxon rank-sum test is performed at a significance level of 0.05 for all 4 algorithms. The results are shown in Tab. 2 through Tab. 5. Each Table shows the percentage of improvement of GSK over the compared algorithm. GSK is shown to be superior to all other algorithms and even stable when the number of IoT devices N increases. Note that the search space when N>100 is a high dimensional space (> 1000), the GSK performed well in all these cases, highlighting that GSK can solve high dimensional problems.

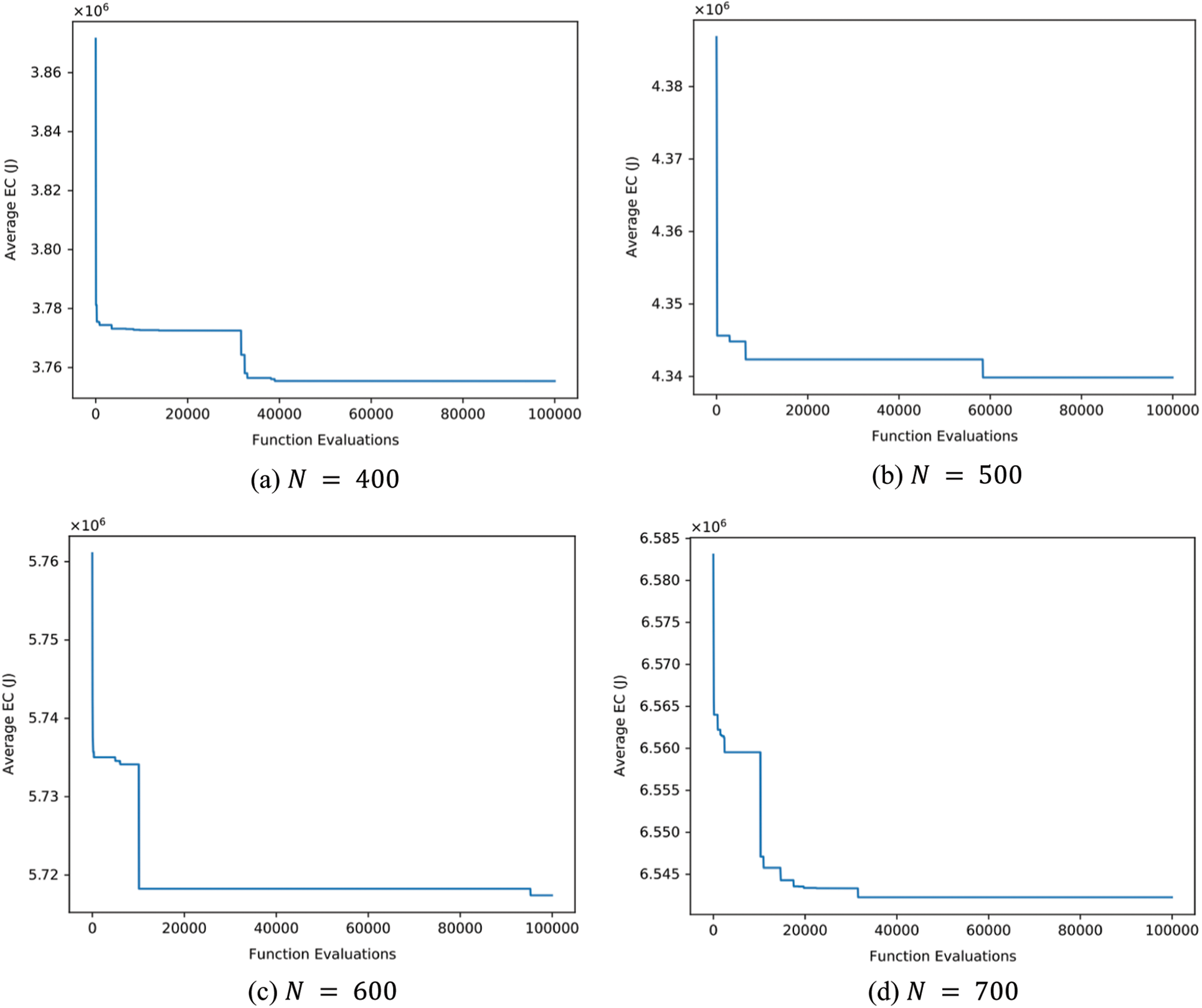
Figure 4: The evolution curve of GSK algorithm when N>300

Tab. 2 shows the result of GSK compared to the DEVIPS algorithm which uses population as a deployment coding scheme and can be considered the state-of-the-art algorithm for UAV deployment. GSK has a very high improvement percentage up to 29.88% and up to 29.17% when N equals 200 and 500, respectively. Also, compared with the SSA algorithm, GSK has almost the same high percentage of improvement up to 29.88% and 29.05% when N equals 200 and 500, respectively as shown in Tab. 3. While the GSK outperforms the FPA algorithm in all scenarios and with 29.7% and 28.94% improvement percentage when N equals 200 and 500, respectively as shown in Tab. 4. Finally, the GSK also outperforms the SCA algorithm with 29.28% and 28.95% when N equals 200 and 500, respectively as illustrated in Tab. 5.

6  Conclusion

This paper studies the UAV’s deployment optimization in UAV-aided NB-IoT data acquisition systems using a natural inspired optimization algorithm based on human behavior named GSK. Minimizing the energy consumption for both the UAV and the IoT devices is the optimization objective for gathering data efficiently, and that can be achievable by optimizing the locations of the UAV’s stop points. In this respect, in GSK, the locations in three-dimensional space of a fixed number of UAV’s stop points present a single individual, which provides an entire deployment. The experimental results of GSK applied in seven IoT devices distribution scenarios prove that GSK is the most suitable algorithm to cope with the UAV’s deployment optimization problems compared with the DEVIPS algorithm and other three swarm intelligence-based algorithms (SSA, FPA, and SCA).

Acknowledgement: The authors would like to thank the Opto-Nano-Electronics laboratory (ONE Lab), Cairo University, and Science, Technology, and Innovation Funding Authority (STIFA), Egypt.

Funding Statement: This research is supported by Science, Technology, and Innovation Funding Authority (STIFA), Egypt, under Grant No. 34876, H. Mostafa received the grant, sponsor website: https://stdf.eg/.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

1In case of population size adaption, the number of candidate solutions will change according to the search space and the algorithm state.

References

 1.  K. Kaur, “A survey on internet of things – Architecture, applications, and future trends,” in 2018 First Int. Conf. on Secure Cyber Computing and Communication (ICSCCC), Jalandhar, India, pp. 581–583, 2018. [Google Scholar]

 2.  L. Atzori, A. Iera and G. Morabito, “The internet of things: A survey,” Computer Networks, vol. 54, no. 15, pp. 2787–2805, 2010. [Google Scholar]

 3.  I. Ticlo, “Is tech the new currency? why you need modern IT,” 2022. [Online]. Available: https://www.insight.com/en_US/content-and-resources/2017/05252017-is-tech-the-new-currency-why-you-need-modern-it.html. [Google Scholar]

 4.  Y. Kawamoto, H. Nishiyama, Z. Fadlullah and N. Kato, “Effective data collection via satellite-routed sensor system (SRSS) to realize global-scaled internet of things,” IEEE Sensors Journal, vol. 13, no. 10, pp. 3645–3654, 2013. [Google Scholar]

 5.  E. Chen, J. Chen, A. W. Mohamed, B. Wang, Z. Wang et al., “Swarm intelligence application to UAV aided IoT data acquisition deployment optimization,” IEEE Access, vol. 8, pp. 175660–175668, 2020. [Google Scholar]

 6.  M. Mozaffari, W. Saad, M. Bennis and M. Debbah, “Mobile unmanned aerial vehicles (UAVs) for energy-efficient internet of things communications,” IEEE Transactions on Wireless Communications, vol. 16, no. 11, pp. 7574–7589, 2017. [Google Scholar]

 7.  Y. Khosiawan, Y. Park, I. Moon, J. M. Nilakantan and I. Nielsen, “Task scheduling system for UAV operations in indoor environment,” Neural Computing and Applications, vol. 31, no. 9, pp. 5431–5459, 2019. [Google Scholar]

 8.  M. Mozaffari, W. Saad, M. Bennis and M. Debbah, “Mobile internet of things: Can UAVs provide an energy-efficient mobile architecture?,” in 2016 IEEE Global Communications Conf. (GLOBECOM), Washington, DC, USA, 2016, pp. 1–6, 2016. [Google Scholar]

 9.  L. Yang, Q. Sun and Z. -S. Ye, “Designing mission abort strategies based on early-warning information: Application to UAV,” IEEE Transactions on Industrial Informatics, vol. 16, no. 1, pp. 277–287, 2020. [Google Scholar]

10. M. Mozaffari, W. Saad, M. Bennis, Y. -H. Nam and M. Debbah, “A tutorial on UAVs for wireless networks: Applications, challenges, and open problems,” IEEE Communications Surveys Tutorials, vol. 21, no. 3, pp. 2334–2360, 2019. [Google Scholar]

11. R. Fan, J. Cui, S. Jin, K. Yang and J. An, “Optimal node placement and resource allocation for UAV relaying network,” IEEE Communications Letters, vol. 22, no. 4, pp. 808–811, 2018. [Google Scholar]

12. W. Du, W. Ying, P. Yang, X. Cao, G. Yan et al., “Network-based heterogeneous particle swarm optimization and its application in UAV communication coverage,” IEEE Transactions on Emerging Topics in Computational Intelligence, vol. 4, no. 3, pp. 312–323, 2020. [Google Scholar]

13. M. Alzenad, A. El-Keyi, F. Lagum and H. Yanikomeroglu, “3-D placement of an unmanned aerial vehicle base station (UAV-BS) for energy-efficient maximal coverage,” IEEE Wireless Communications Letters, vol. 6, no. 4, pp. 434–437, 2017. [Google Scholar]

14. M. Alzenad, A. El-Keyi and H. Yanikomeroglu, “3-D placement of an unmanned aerial vehicle base station for maximum coverage of users with different QoS requirements,” IEEE Wireless Communications Letters, vol. 7, no. 1, pp. 38–41, 2018. [Google Scholar]

15. Y. Chen and D. Pi, “An innovative flower pollination algorithm for continuous optimization problem,” Applied Mathematical Modelling, vol. 83, pp. 237–265, 2020. [Google Scholar]

16. L. Abualigah, M. Shehab, M. Alshinwan and H. Alabool, “Salp swarm algorithm: A comprehensive survey,” Neural Computing and Applications, vol. 32, no. 15, pp. 11195–11215, 2020. [Google Scholar]

17. M. A. Tawhid and V. Savsani, “Multi-objective sine-cosine algorithm (MO-SCA) for multi-objective engineering design problems,” Neural Computing and Applications, vol. 31, no. 2, pp. 915–929, 2019. [Google Scholar]

18. P. -Q. Huang, Y. Wang, K. Wang and K. Yang, “Differential evolution with a variable population size for deployment optimization in a UAV-assisted IoT data collection system,” IEEE Transactions on Emerging Topics in Computational Intelligence, vol. 4, no. 3, pp. 324–335, 2020. [Google Scholar]

19. A. W. Mohamed, A. A. Hadi and A. K. Mohamed, “Gaining-sharing knowledge-based algorithm for solving optimization problems: A novel nature-inspired algorithm,” International Journal of Machine Learning and Cybernetics, vol. 11, no. 7, pp. 1501–1529, 2020. [Google Scholar]

20. K. Mekki, E. Bajic, F. Chaxel and F. Meyer, “A comparative study of LPWAN technologies for largescale IoT deployment,” ICT Express, vol. 5, no. 1, pp. 1–7, 2019. [Google Scholar]

21. K. Wang, P. -Q. Huang, K. Yang, C. Pan and J. Wang, “Unified offloading decision making and resource allocation in ME-RAN,” IEEE Transactions on Vehicular Technology, vol. 68, no. 8, pp. 8159–8172, 2019. [Google Scholar]

22. P. -Q. Huang, Y. Wang, K. Wang and Z. -Z. Liu, “A bilevel optimization approach for joint offloading decision and resource allocation in cooperative mobile edge computing,” IEEE Transactions on Cybernetics, vol. 50, no. 10, pp. 4228–4241, 2020. [Google Scholar]

23. C. Zhan, Y. Zeng and R. Zhang, “Energy-efficient data collection in UAV enabled wireless sensor network,” IEEE Wireless Communications Letters, vol. 7, no. 3, pp. 328–331, 2018. [Google Scholar]

24. P. Agrawal, T. Ganesh and A. W. Mohamed, “A novel binary gaining-sharing knowledge-based optimization algorithm for feature selection,” Neural Computing and Applications, vol. 33, no. 11, pp. 5989–6008, 2021. [Google Scholar]

25. P. Agrawal, T. Ganesh and A. W. Mohamed, “Chaotic gaining sharing knowledge-based optimization algorithm: An improved metaheuristic algorithm for feature selection,” Soft Computing, vol. 25, no. 2, pp. 9505–9528, 2021. [Google Scholar]

26. P. Agrawal, T. Ganesh, D. Oliva and A. W. Mohamed, “S-Shaped and V-shaped gaining-sharing knowledge-based algorithm for feature selection,” Applied Intelligence, vol. 173, pp. 1–32, 2021. [Google Scholar]

27. S. A. Hassan, K. Alnowibet, P. Agrawal and A. W. Mohamed, “Optimum scheduling the electric distribution substations with a case study: An integer gaining-sharing knowledge-based metaheuristic algorithm,” Hindawi, Complexity, vol. 2020, pp. 1–13, 2020. [Google Scholar]

28. S. A. Hassan, P. Agrawal, T. Ganesh and A. W. Mohamed, “Scheduling shuttle ambulance vehicles for covid-19 quarantine cases, a multi-objective multiple 0–1 knapsack model with a novel discrete binary gaining-sharing knowledge-based optimization algorithm,” in Data Science for COVID-19, United States: Elsevier, pp. 675–698, 2021. [Online]. Available: https://www.sciencedirect.com/science/article/pii/B9780128245361000344. [Google Scholar]

29. S. A. Hassan, P. Agrawal, T. Ganesh and A. W. Mohamed, “Optimum distribution of protective materials for covid- 19 with a discrete binary gaining-sharing knowledge-based optimization algorithm,” in Computational Intelligence Techniques for Combating COVID-19, Switzerland: Springer, pp. 135–137, 2021. [Online]. Available: https://link.springer.com/chapter/10.1007/978-3-030-68936-0_8. [Google Scholar]

30. S. A. Hassan, K. Alnowibet, P. Agrawal and A. W. Mohamed, “Optimum location of field hospitals for covid-19: A nonlinear binary metaheuristic algorithm,” Computers, Materials & Continua, vol. 68, no. 1, pp. 1183–1202, 2021. [Google Scholar]

31. G. Xiong, L. Li, A. W. Mohamed, X. Yuan and J. Zhang, “A new method for parameter extraction of solar photovoltaic models using gaining-sharing knowledge-based algorithm,” Energy Reports, vol. 7, pp. 3286–3301, 2021. [Google Scholar]

32. P. Agrawal, T. Ganesh and A. W. Mohamed, “Solving knapsack problems using a binary gaining sharing knowledge-based optimization algorithm,” Complex & Intelligent Systems, vol. 8, pp. 1–21, 2021, https://doi.org/10.1007/s40747-021-00351-8. [Google Scholar]

33. S. A. Hassan, P. Agrawal, T. Ganesh and A. W. Mohamed, “A travelling disinfection-man problem (TDP) for covid-19: A nonlinear binary constrained gaining-sharing knowledge-based optimization algorithm,” in Intelligent Data Analysis for COVID-19 Pandemic, Singapore: Springer, pp. 291–318, 2021. [Online]. Available: https://link.springer.com/chapter/10.1007/978-981-16-1574-0_13. [Google Scholar]

34. S. A. Hassan, Y. M. Ayman, K. Alnowibet, P. Agrawal and A. W. Mohamed, “Stochastic travelling advisor problem simulation with a case study: A novel binary gaining-sharing knowledge-based optimization algorithm,” Hindawi, Complexity, vol. 2020, pp. 15, 2020. [Google Scholar]

35. P. Agrawal, T. Ganesh and A. W. Mohamed, “Solution of uncertain solid transportation problem by integer gaining sharing knowledge based optimization algorithm,” in 2020 Int. Conf. on Computational Performance Evaluation (ComPE), Shillong, India, pp. 158–162, 2020. [Google Scholar]

36. Y. Alharbi, A. Alferaidi, K. Yadav, G. Dhiman and S. Kautish, “Denial-of-service attack detection over IPv6 network based on KNN algorithm,” Wireless Communications and Mobile Computing, vol. 2021, pp. 1–16, 2021. [Google Scholar]

37. Q. Sellat, S. Bisoy, R. Priyadarshini, A. Vidyarthi, S. Kautish et al., “Intelligent semantic segmentation for self-driving vehicles using deep learning,” Computational Intelligence and Neuroscience, vol. 2022, pp. 1–10, 2022. [Google Scholar]

38. M. Chen, Y. Miao, Y. Hao and K. Hwang, “Narrow band internet of things,” IEEE Access, vol. 5, pp. 20557–20577, 2017. [Google Scholar]

39. A. Sharma, D. S. Kapoor, A. Nayyar, B. Qureshi, K. J. Singh et al., “Exploration of IoT nodes communication using LoRaWAN in forest environment,” Computers, Materials & Continua, vol. 71, no. 3, pp. 6239–6256, 2022. [Google Scholar]

40. K. Mekki, E. Bajic, F. Chaxel and F. Meyer, “Overview of cellular LPWAN technologies for IoT deployment: Sigfox, LoRaWAN, and NB-IoT,” in 2018 IEEE Int. Conf. on Pervasive Computing and Communications Workshops (PerCom Workshops), Athens, Greece, pp. 197–202, 2018. [Google Scholar]

41. E. Rastogi, N. Saxena, A. Roy and D. R. Shin, “Narrowband internet of things: A comprehensive study,” Computer Networks, vol. 173, pp. 1–40, 2020. [Google Scholar]

42. M. Kanj, V. Savaux and M. Le Guen, “A tutorial on NB-IoT physical layer design,” IEEE Communications Surveys Tutorials, vol. 22, no. 4, pp. 2408–2446, 2020. [Google Scholar]

43. 3GPP. 3GPP TS 36.211, Physical Channels and Modulation (Release 14, v14.11.0, Technical report, 3GPP, September 2021). 2019. [Google Scholar]

44. C. B. Mwakwata, H. Malik, M. M. Alam, Y. L. Moullec, S. Parand et al., “Narrowband internet of things (NB-IoTFrom physical (PHY) and media access control (MAC) layers perspectives,” Sensors, vol. 19, no. 11, pp. 2613, 2019. [Google Scholar]

45. M. Gupta, K. Gupta, M. Khosravi, P. Shukla, S. Kautish et al., “An intelligent session key-based hybrid lightweight image encryption algorithm using logistic-tent map and crossover operator for internet of multimedia things,” Wireless Personal Communications, vol. 121, pp. 1857–1878, 2021. [Google Scholar]

46. O. Al-Doori and O. Alani, “A multi polynomial CRC circuit for LTE-advanced communication standard,” in 2015 7th Computer Science and Electronic Engineering Conf. (CEEC), Colchester, UK, pp. 19–23, 2015. [Google Scholar]

47. M. A. Mohamed, H. M. Abd-ElAtty, M. E, A. Aboel-Seoud and W. M. Raslan, “Performance analysis of LTE-advanced physical layer,” International Journal of Computer Science Issues, vol. 11, no. 1, pp. 80–87, 2014. [Google Scholar]

48. M. F. Mosleh and M. F. Abid, “Evaluation of rate matching of turbo code for 3GPP LTE system,” in Optical and Wireless Technologies, Lecture Notes in Electrical Engineering, Singapore: Springer, vol. 472, pp. 401–410, 2018. [Google Scholar]

49. M. K. H. Jewel, R. S. Zakariyya and F. Lin, “On channel estimation in LTE-based downlink narrowband internet of things systems,” Electronics, vol. 10, no. 11, pp. 1246, 2021. [Google Scholar]

50. G. Berardinelli, L. A. M. R. de Temino, S. Frattasi, M. I. Rahman and P. Mogensen, “OFDM vs. SC-FDMA: Performance comparison in local area IMT-A scenarios,” IEEE Wireless Communications, vol. 15, no. 5, pp. 64–72, 2008. [Google Scholar]

51. X. R. Zhang, W. F. Zhang, W. Sun, X. M. Sun and S. K. Jha, “A robust 3-D medical watermarking based on wavelet transform for data protection,” Computer Systems Science & Engineering, vol. 41, no. 3, pp. 1043–1056, 2022. [Google Scholar]

52. X. R. Zhang, X. Sun, X. M. Sun, W. Sun and S. K. Jha, “Robust reversible audio watermarking scheme for telemedicine and privacy protection,” Computers, Materials & Continua, vol. 71, no. 2, pp. 3035–3050, 2022. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.