Computers, Materials & Continua DOI:10.32604/cmc.2022.027922
Article

Compact Bat Algorithm with Deep Learning Model for Biomedical EEG EyeState Classification

Souad Larabi-Marie-Sainte1, Eatedal Alabdulkreem2, Mohammad Alamgeer3, Mohamed K Nour4, Anwer Mustafa Hilal5,*, Mesfer Al Duhayyim6, Abdelwahed Motwakel5 and Ishfaq Yaseen5

1Department of Computer Science, College of Computer and Information Sciences, Prince Sultan University, Saudi Arabia
2Department of Computer Sciences, College of Computer and Information Sciences, Princess Nourah Bint Abdulrahman University, Riyadh, 11671, Saudi Arabia
3Department of Information Systems, College of Science & Art at Mahayil, King Khalid University, Saudi Arabia
4Department of Computer Sciences, College of Computing and Information System, Umm Al-Qura University, Saudi Arabia
5Department of Computer and Self Development, Preparatory Year Deanship, Prince Sattam bin Abdulaziz University, AlKharj, Saudi Arabia
6Department of Natural and Applied Sciences, College of Community-Aflaj, Prince Sattam bin Abdulaziz University, Saudi Arabia
*Corresponding Author: Anwer Mustafa Hilal. Email: a.hilal@psau.edu.sa
Received: 28 January 2022; Accepted: 01 March 2022

Abstract: Electroencephalography (EEG) eye state classification becomes an essential tool to identify the cognitive state of humans. It can be used in several fields such as motor imagery recognition, drug effect detection, emotion categorization, seizure detection, etc. With the latest advances in deep learning (DL) models, it is possible to design an accurate and prompt EEG EyeState classification problem. In this view, this study presents a novel compact bat algorithm with deep learning model for biomedical EEG EyeState classification (CBADL-BEESC) model. The major intention of the CBADL-BEESC technique aims to categorize the presence of EEG EyeState. The CBADL-BEESC model performs feature extraction using the ALexNet model which helps to produce useful feature vectors. In addition, extreme learning machine autoencoder (ELM-AE) model is applied to classify the EEG signals and the parameter tuning of the ELM-AE model is performed using CBA. The experimental result analysis of the CBADL-BEESC model is carried out on benchmark results and the comparative outcome reported the supremacy of the CBADL-BEESC model over the recent methods.

Keywords: Biomedical signals; EEG; EyeState classification; deep learning; metaheuristics

1  Introduction

Brain-Computer Interface (BCI) is the growing field in human-computer interaction (HCI). It permits users to communicate with computers via brain-activity [1]. Usually, these kinds of activities are measured by using an electroencephalography (EEG) signal. EEG is a non-invasive physiological method for recording brain electrical activity based on electrodes put on distinct locations on the scalp. classification of Eye condition, the task of identifying the state of eye in case it is opened or closed, is a generic time series problem to identify human cognitive condition [2,3]. Classifying human cognitive state is greater for medical concern in daily lives. Significant use-cases to detect eye condition results in the recognition of eye blinking rate, according to its possibility to forecast diseases like Parkinson's disease or subject suffered from Tourette syndrome [4]. The precise recognition of the eye condition with EEG signal is the challenge however indispensable task for the healthcare sector as well as in our daily lives [5,6]. Different machine learning (ML) based methods were introduced for classifying the EEG-based signal in several applications. Many of them had presented the conventional method. However, it is necessary for correct and accurate classification models that could effectively categorize the eye conditional with electroencephalogram signal [7].

Tahmassebi et al. [8] presented an explainable structure with capability of real time forecast. For demonstrating the analytical power of structure, a test case on eye state recognition utilizing EEG signal was utilized for investigating a deep neural network (DNN) technique that generates a forecast and that predictive was interpreting. The authors in [9] developed the temporal order of data from the place. It can generate several CNN network techniques and choose optimum filter and depth. In CNN feature techniques were effectual became concerned issue dependent and subject independent eye state EEG classifiers. Islam et al. [10] presented 3 frameworks of DL technique utilizing ensemble approach to eye state detection (open/close) in EEG directly. The analysis was implemented on freely accessible publicly EEG eye state data set of 14980 instances. The individual efficiency of all classifiers is detected, and also application of detection efficiency of an ensemble network is related to the present prominent manners.

The authors in [11] established a hybrid classification technique for eye state recognition utilizing EEG signals. This hybrid classifier technique was estimated with other standard ML approaches, 8 classifier techniques (Pre-possessed+Hypertuned), and 6 recent approaches for assessing their suitability and exactness. This presented classifier technique introduces an ML based hybrid method to the classification of eye states utilizing EEG signals with higher accuracy. Nkengfack et al. [12] presented classification model containing approaches dependent upon Jacobi polynomial transforms (JPTs). Discrete Legendre transforms (DLT) and discrete Chebychev transform (DChT) primarily remove the beta (β) and gamma (γ) rhythm of EEG signal. Afterward, various measures of difficulty are calculated in the EEG signal and its removed rhythm and executed as input of least-square support vector machine (LS-SVM) technique with RBF kernel.

In [13], a robust and unique artificial neural network (ANN) based ensemble approach was established in that several ANN was trained separately utilizing distinct parts of trained data. The resultants of all ANNs are joined utilizing other ANN for enhancing the analytical intelligence. The resultant of this ANN has been regarded as vital forecast of user eye state. The presented ensemble technique needs lesser trained time and takes extremely accurate eye state classifier. Shooshtari et al. [14] presented 8 confidence connected property from EEG and eye data that is considered descriptive of determined confidence level from random dot motion (RDM). Since a fact, the presented EEG and eye data property were able of identifying over 9 different levels of confidence. Amongst presented features, the latency of pupil maximal diameter with stimulation performance has introduced that one of the connected to confidence levels.

This study presents a novel compact bat algorithm with deep learning model for biomedical EEG EyeState classification (CBADL-BEESC) model. The major intention of the CBADL-BEESC technique aims to categorize the presence of EEG EyeState. The CBADL-BEESC model performs feature extraction using the ALexNet model which helps to produce useful feature vectors. In addition, extreme learning machine autoencoder (ELM-AE) model is applied to classify the EEG signals and the parameter tuning of the ELM-AE model is performed using CBA. The experimental result analysis of the CBADL-BEESC model is carried out on benchmark results

The rest of the paper is organized as follows. Section 2 offers the proposed model, Section 3 validates the results, and Section 4 draws the conclusion.

2  The Proposed CBADL-BEESC Model

In this study, a novel CBADL-BEESC technique has been developed for biomedical EEG EyeState classification. The main goal of the CBADL-BEESC technique is to recognize the presence of EEG EyeState. The CBADL-BEESC model involves AlexNet feature extractor, ELM-AE classifier, and CBA parameter optimizer. The parameter tuning of the ELM-AE model is performed using CBA. Fig. 1 depicts the overall process of proposed CBADL-BEESC technique.

Figure 1: Overall process of CBADL-BEESC technique

2.1 Feature Extraction Using AlexNet Model

At the initial stage, the AlexNet model can be utilized to generate useful set of feature vectors. AlexNet is a kind of CNN that includes several layers like max pooling, input, dense, output, and convolution layers which are their fundamental structure blocks. It resolves the issue of images classifier in which the input image is one of 1000 distinct classes and the outcome is vector of individual classes [15]. The kth component of resultant vectors are assumed that possibility the input image goes to kth class. It is noticeable the sum of probability of the total resultant vectors is always equivalent to 1. AlexNet gets an RGB image as input containing the size of 256 ∗ 256 that implies each image from the train and test set required to contain the size of 256 ∗ 256. When the input image fails from equivalent to the typical image size, afterward it requires that changed to the typical size, for instance, 256 ∗ 256 before utilize for training the networks. Once the input image utilized is grayscale image, next it can be changed to RGB with replicate the single channel as to 3 channels RGB images. The infrastructure of AlexNet is reformed in the CNN technique that is utilized to computer vision issues and is significantly greater than CNN. AlexNet is 60 million parameters and 650,000 neurons that get a long period to train.

2.2 Classification Using ELM-AE Model

During classification process, the ELM-AE model is applied to classify the EEG EyeState. Autoencoder (AE) is an ANN approach that is usually employed from deep learning (DL). AE is an unsupervised neural network (NN), the resultants of AE are identical to inputs of AE, and AE is a variety of NNs that reproduce the input signals as possible. The ELMAE projected by Kasun et al. is a novel approach of NN that reproduces the input signal and AE. This technique of ELMAE established input, single-hidden, and resultant layers [16]. An j input layer node, n hidden layer (HL) node, j resultant layer node, and the HL activation function g(x). Due to the resultant of HL representing the input signal, ELMAE was separated as to 3 distinct demonstrations as follows.

•   j = n: Equal Dimension Representations: it can be implied feature in an input signal space dimensional equivalent to feature space dimensional.

•   j > n: Compressed Representations: it signifies features in a superior dimension input signal space to lesser dimension feature space. 

•   j<n: Sparse Representations: it demonstrates features in a minimum dimension input signal space to maximum dimension feature space.

There are 2 variances amongst ELMAE and typical ELM. Primarily, ELM is a supervised NN and the resultant of ELM was labeled, however, ELMAE is an unsupervised NN and the resultant of ELMAE is similar to the input of ELMAE. Secondary, the input weight of ELMAE is orthogonal and the bias of HLs of ELMAE is also orthogonal [17], however, ELM is not so. In order to N various instances, xi∈Rn×Rj,(j=1,2, …,N), the resultants of ELMAE technique HL was formulated as (1), and the numerical connection amongst the resultant of HLs and the resultant of resultant layer is written as (2):

h=g(ax+b),  where aTa=I,  bTb=1, (1)

h(xi)V=xiT, i=1, 2,⋯, N. (2)

Employing ELMAE for attaining the resultant weight V is also separated as to 3 steps, yet the computation technique of resultant weight V of ELMAE in Step 3 has distinct in the computation method of resultant weights V of ELM. Fig. 2 demonstrates the structure of ELM method.

Figure 2: ELM structure

For compressed and sparse ELMAE representation, the resultant weight V can be computed by Eqs. (3) and (4). If the amount of trained instances are greater than the amount of HL nodes,

V=(IC+HTH)−1HTX.(3)

Once the amount of trained instances are lesser than the count of HL nodes,

V=HT(IC+HHT)−1X. (4)

To equivalent dimensional ELMAE representation, resultant weights V can be computed as:

V=H−1X.(5)

2.3 Parameter Tuning Using CBA

For tuning the parameters involved in the ELM-AE model, the CBA is applied to it. The purpose of the compact process is for stimulating the operation of population-based BA method [18] in a form with small stored memory. The actual population of solution of BA is converted to the compact process through creating a dispersed data structure, i.e., perturbation vector (PV). PV denotes the probabilistic method to population of solution.

PVt=[μt,δt](6)

Whereas δ and μ denote variables of standard deviation and mean of vector PV, and t indicates the existing time. The δ and μ values are organized in the possibility density function (PDF) and are truncated from 1 and 1. The PDF amplitude can be standardized by keeping its region equivalent to one through gaining around satisfactory in well it is the standard distribution with a complete shape.

A real-value prototype vector was utilized to maintain sampling probability for making arbitrary components of candidate solutions. The vector process is distributed-based evaluated distribution approach (EDA) [19]. The probability is that the evaluated distribution will trend, driving novel candidate forwarding to the FF. The candidate solution is probabilistically created from the vector, and the component from the best solution is utilized for making slight variations to the probability in the vector. The candidate solution χi equivalent to the position of the virtual bat is created as (μi,δi).

P(x)=exp(x−μi)22δi2δi(erf(μi+12δi)−erf(μi+12δi))(7)

Whereas P(x) denotes the likelihood distribution of PV which formulate a truncated Gaussian PDF related to μ and δ. New candidate solutions are created as biased iteratively to a potential region of optimum solution. Then attain all the components of likelihood vector through learning the preceding generation. The erf denotes the error function. The codomain of CDF is ordered within 0 to 1. The CDF determine the real-value arbitrary parameter x with provided likelihood distribution, and the gained values are lesser than or equivalent to xi.

Also, CDF specifies the distribution of multi-variate arbitrary parameters. Therefore, the relations of PDF and CDF are described by CDP=∫01⁡P(x)dx. PV accomplishes the sampling parameter xi through creating an arbitrary value within (0,1). This corresponds to obtaining the parameter through the computation of inverse operation of χj set to inverse (CDF).

For finding an optimal individual from the procedure of compact approach, a comparison of these parameters is implemented. These parameter agents of bat are 2 sampling individuals that accomplished from PV. The “winner” specifies the vector with fitness score is maximum when compared to others, and the “loser” shows that low fitness assessment. The parameters, winner, and loser, are from main function valuation which compared a candidate solution with the preceding optimal global. To update PV,μ and δ are taken into account on the basis of subsequent rules. When the mean value of μ was assumed as 1, the updating rule for the element is μit,δit set forwarding to μit+1,δit+1 as follows:

μit+1=μit+1Np(winneri−loseri)(8)

Whereas Np signifies virtual population. Regarding δ value, the updating rule of element as:

δit+1=(δit)2+(μit)2−(μit+1)2+1Np(winneri2−loseri2)(9)

[winner, loser]=compete(xbesi, xt+1)(10)

Generally, a probabilistic method for compact BA was applied for representing the bat solution set in which the position or velocity is saved, but a recently created candidate is saved. A variable ω is utilized as a weight for controlling the likelihood of μi sampling in PDF among left [−1, μi] i.e., PL(x), for-l ≤x≤μj, and right [1] i.e., PR(x), for μi≤x≤1. The extended edition of PDF for sampling method is employed. The generated new candidate of bat is applied by sampling from PV for example if r<ω it produces coefficient xi∈[1,0] for PL(x) , if not xi∈[1,0] for PR(x)

3  Experimental Validation

The presented CBADL-BEESC model is simulated using the benchmark database from UCI repository (available at https://archive.ics.uci.edu/ml/datasets/EEG+Eye+State). It comprises 14980 samples with two classes namely eye closed with 6723 samples (class 1) and eye open (class 0) with 8257 samples.

The confusion matrix offered by the CBADL-BEESC model with five distinct runs is portrayed in Fig. 3. The figures demonstrated that the CBADL-BEESC model has resulted in effective EEG EyeState classification on all runs. For instance, with run-1, the CBADL-BEESC model has identified 6626 instances under class 1 and 8148 instances under class 2. In addition, under run-2, the CBADL-BEESC model has recognized 6624 instances under class 1 and 8156 instances under class 2. Along with that, run-5, the CBADL-BEESC model has identified 6627 instances under class 1 and 8163 instances under class 2.

Figure 3: Confusion matrix of CBADL-BEESC technique different runs

The classifier results obtained by the CBADL-BEESC model under distinct runs are portrayed in Tab. 1 and Fig. 4. The results demonstrated that the CBADL-BEESC model has resulted in enhanced outcomes under every run. For instance, under run-1, the CBADL-BEESC model has obtained precn of 0.9838, recal of 0.9856, Fscore of 0.9847, and accuy of 0.9862. Eventually, under run-3, the CBADL-BEESC method has gained precn of 0.9856, recal of 0.9851, Fscore of 0.9853, and accuy of 0.9868. Meanwhile, under run-1, the CBADL-BEESC approach has obtained precn of 0.9860, recal of 0.9857, Fscore of 0.9859, and accuy of 0.9873.

Figure 4: Result analysis of CBADL-BEESC technique interms of various measures

Fig. 5 illustrates the ROC analysis of the CBADL-BEESC system on the test dataset. The figure revealed that the CBADL-BEESC technique has gained improved outcomes with the increased ROC of 99.9391.

Tab. 2 provides a brief comparative analysis of the CBADL-BEESC model with recent methods under distinct folds.

Fig. 6 investigates the classifier results analysis of the CBADL-BEESC model with recent models under two-fold. The results indicated that the CBADL-BEESC model has resulted in enhanced outcomes over the other ML models. In addition, the SVM, BGA, and RF models have accomplished lower classification outcomes over the other methods. Moreover, the ET and KNN methods have obtained moderately closer classification outcomes. Furthermore, the proposed CBADL-BEESC model has accomplished superior outcome with the higher precn of 96.42%, recal of 98.40%, Fscore of 97.65%, and accuy  of 98.24%.

Figure 5: ROC analysis of CBADL-BEESC technique

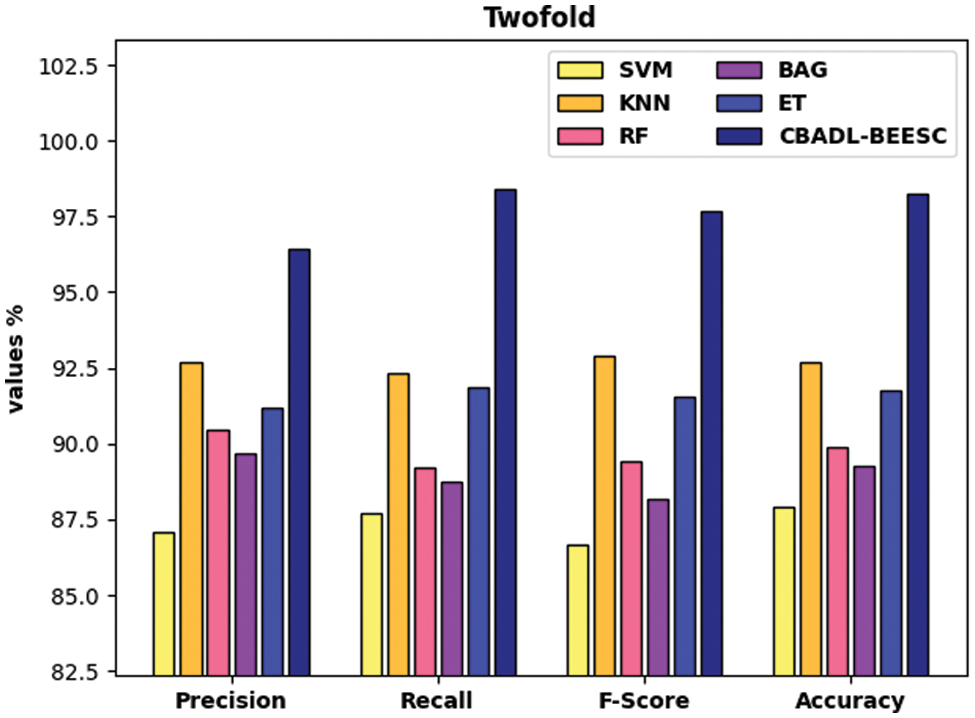
Figure 6: Comparative analysis of CBADL-BEESC technique under two-fold

Fig. 7 examines the classifier results analysis of the CBADL-BEESC system with recent techniques under five-fold. The results demonstrated that the CBADL-BEESC model has resulted in enhanced outcomes over the other ML technique. Besides, the SVM, BGA, and RF models have accomplished lower classification outcomes over the other algorithms. In addition, the ET and KNN techniques have obtained reasonably closer classification outcomes. Eventually, the projected CBADL-BEESC methodology has accomplished superior outcome with the superior precn of 97.97%, recal of 98.52%, Fscore of 98.34%, and accuy of 98.63%.

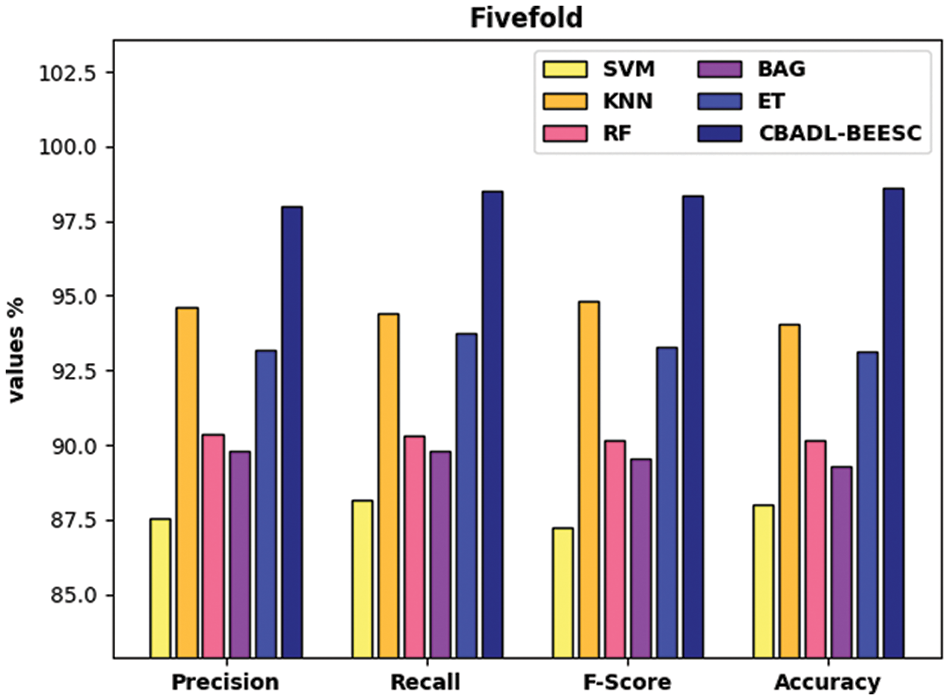
Figure 7: Comparative analysis of CBADL-BEESC technique under five-fold

Fig. 8 defines the classifier results analysis of the CBADL-BEESC technique with recent approaches under ten-fold. The outcomes referred that the CBADL-BEESC model has resulted in maximum outcome over the other ML models. Likewise, the SVM, BGA, and RF models have accomplished lesser classification outcomes over the other methods. Followed by, the ET and KNN approaches have gained moderately closer classification outcomes. At last, the presented CBADL-BEESC method has accomplished higher outcome with the higher precn of 96.55%, recal of 98.80%, Fscore of 97.64%, and accuy of 98.50%.

Finally, a comparative analysis of the CBADL-BEESC model is made with recent methods in Tab. 3 and Fig. 9. The results indicated that the SVM and BAG models have reached lower average accuracy of 88.43% and 89.68% respectively. In line with, the RF model has resulted in slightly increased average accuracy of 90.48%. Along with that, the KNN and ET models have accomplished moderately improved average accuracy of 93.51% and 92.65% respectively. However, the CBADL-BEESC model has outperformed the other methods with an average accuracy of 98.44%. By looking into above mentioned tables and figures, it is ensured that the CBADL-BEESC model has outperformed other models in terms of different measures.

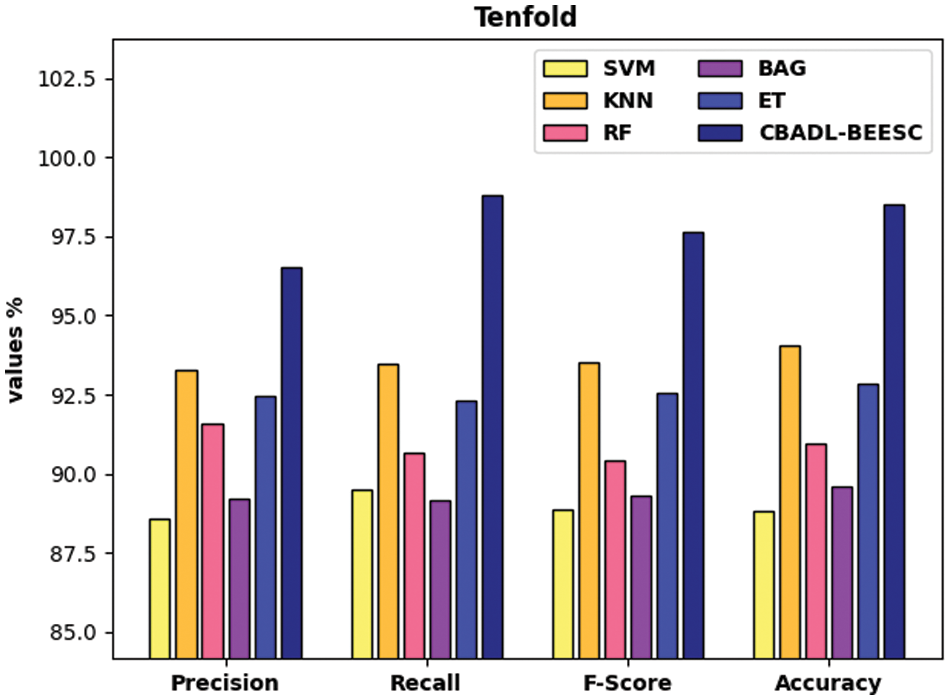
Figure 8: Comparative analysis of CBADL-BEESC technique under ten-fold

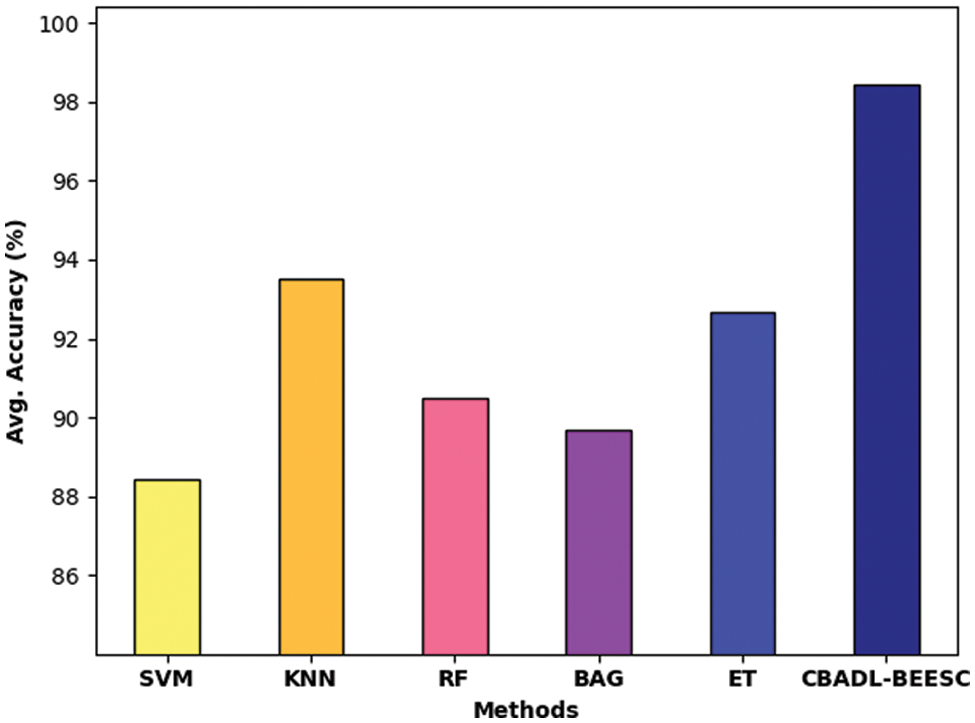
Figure 9: Average accuracy analysis of CBADL-BEESC technique with recent methods

4  Conclusion

In this study, a novel CBADL-BEESC technique has been developed for biomedical EEG EyeState classification. The main goal of the CBADL-BEESC technique is to recognize the presence of EEG EyeState. The CBADL-BEESC model involves AlexNet feature extractor, ELM-AE classifier, and CBA parameter optimizer. At the initial stage, the AlexNet model can be utilized to generate useful set of feature vectors. During classification process, the ELM-AE model is applied to classify the EEG EyeState. For tuning the parameters involved in the ELM-AE model, the CBA is applied to it. The parameter tuning of the ELM-AE model is performed using CBA. The experimental result analysis of the CBADL-BEESC model is carried out on benchmark results and the comparative outcome reported the supremacy of the CBADL-BEESC model over the recent methods. Therefore, the CBADL-BEESC model has appeared as an effective tool for EEG EyeState classification. In future, the classification outcome can be boosted by hybrid DL approaches.

Funding Statement: The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work under grant number (RGP 2/180/43). Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2022R161), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia. The authors would like to thank the Deanship of Scientific Research at Umm Al-Qura University for supporting this work by Grant Code: (22UQU4310373DSR04). The authors would like to acknowledge the support of Prince Sultan University for paying the Article Processing Charges (APC) of this publication.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  A. Khosla, P. Khandnor and T. Chand, “A comparative analysis of signal processing and classification methods for different applications based on EEG signals,” Biocybernetics and Biomedical Engineering, vol. 40, no. 2, pp. 649–690, 2020. [Google Scholar]

 2.  M. T. Sadiq, X. Yu, Z. Yuan, M. Z. Aziz and S. Siuly, “Toward the development of versatile brain–Computer interfaces,” IEEE Trans. Artif. Intell., vol. 2, no. 4, pp. 314–328, Aug. 2021. [Google Scholar]

 3.  X. Yu, M. Z. Aziz, M. T. Sadiq, Z. Fan, and G. Xiaoet al., “A new framework for automatic detection of motor and mental imagery EEG signals for robust BCI systems,” IEEE Trans. Instrum. Meas., vol. 70, pp. 1–12, 2021. [Google Scholar]

 4.  M. T. Sadiq, X. Yu, Z. Yuan, and M. Z. Aziz, “Motor imagery BCI classification based on novel two-dimensional modelling in empirical wavelet transform,” Electron. Lett., vol. 56, no. 25, pp. 1367–1369, 2020. [Google Scholar]

 5.  M. T. Sadiq, X. Yu, Z. Yuan, and M. Z. Aziz, “Identification of motor and mental imagery EEG in Two and multiclass subject-dependent tasks using successive decomposition index,” Sensors, vol. 20, no. 18, pp. 5283, Sep. 2020. [Google Scholar]

 6.  E. Antoniou, P. Bozios, V. Christou, K. D. Tzimourta, K. Kalafatakis et al., “EEG-Based eye movement recognition using brain–computer interface and random forests,” Sensors, vol. 21, no. 7, pp. 2339, 2021. [Google Scholar]

 7.  G. Gaurav, R. S. Anand and V. Kumar, “EEG based cognitive task classification using multifractal detrended fluctuation analysis,” Cognitive Neurodynamics, vol. 15, no. 6, pp. 999–1013, 2021. [Google Scholar]

 8.  A. Tahmassebi, J. Martin, A. M. Baese and A. H. Gandomi, “An interpretable deep learning framework for health monitoring systems: A case study of eye state detection using EEG signals,” in 2020 IEEE Symp. Series on Computational Intelligence (SSCI), Canberra, ACT, Australia, pp. 211–218, 2020. [Google Scholar]

 9.  F. William and F. Zhu, “CNN models for eye state classification using EEG with temporal ordering,” in Proc. of the 12th ACM Conf. on Bioinformatics, Computational Biology, and Health Informatics, Gainesville Florida, pp. 1–8, 2021. [Google Scholar]

10. M. S. Islalm, M. M. Rahman, M. H. Rahman, M. R. Hoque, A. K. Roonizi et al., “A deep learning-based multi-model ensemble method for eye state recognition from EEG,” in 2021 IEEE 11th Annual Computing and Communication Workshop and Conf. (CCWC), NV, USA, pp. 819–824, 2021. [Google Scholar]

11. S. Ketu and P. K. Mishra, “Hybrid classification model for eye state detection using electroencephalogram signals,” Cognitive Neurodynamics, vol. 16, pp. 73–90, 2021, https://doi.org/10.1007/s11571-021-09678-x. [Google Scholar]

12. L. D. Nkengfack, D. Tchiotsop, R. Atangana, V. L. Door and D. Wolf, “Classification of EEG signals for epileptic seizures detection and eye states identification using jacobi polynomial transforms-based measures of complexity and least-square support vector machine,” Informatics in Medicine Unlocked, vol. 23, pp. 100536, 2021. [Google Scholar]

13. M. M. Hassan, M. R. Hassan, S. Huda, M. Z. Uddin, A. Gumaei et al., “A predictive intelligence approach to classify brain–computer interface based eye state for smart living,” Applied Soft Computing, vol. 108, pp. 107453, 2021. [Google Scholar]

14. S. V. Shooshtari, J. E. Sadrabadi, Z. Azizi and R. Ebrahimpour, “Confidence representation of perceptual decision by EEG and eye data in a random dot motion task,” Neuroscience, vol. 406, pp. 510–527, 2019. [Google Scholar]

15. A. Krizhevsky, I. Sutskever and G. E. Hinton, “ImageNet classification with deep convolutional neural networks,” Communications of the ACM, vol. 60, no. 6, pp. 84–90, 2017. [Google Scholar]

16. M. A. Khan, S. Kadry, Y. D. Zhang, T. Akram, M. Sharif et al., “Prediction of COVID-19-pneumonia based on selected deep features and one class kernel extreme learning machine,” Computers & Electrical Engineering, vol. 90, pp. 106960, 2021. [Google Scholar]

17. D. K. Mohanty, A. K. Parida and S. S. Khuntia, “Financial market prediction under deep learning framework using auto encoder and kernel extreme learning machine,” Applied Soft Computing, vol. 99, pp. 106898, 2021. [Google Scholar]

18. B. Alsalibi, L. Abualigah and A. T. Khader, “A novel bat algorithm with dynamic membrane structure for optimization problems,” Applied Intelligence, vol. 51, no. 4, pp. 1992–2017, 2021. [Google Scholar]

19. T. T. Nguyen, J. S. Pan and T. K. Dao, “A compact bat algorithm for unequal clustering in wireless sensor networks,” Applied Sciences, vol. 9, no. 10, pp. 1973, 2019. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.