Computers, Materials & Continua DOI:10.32604/cmc.2022.027807
Article

A Steganography Model Data Protection Method Based on Scrambling Encryption

Xintao Duan1,*, Zhiqiang Shao1, Wenxin Wang1, En Zhang1, Dongli Yue1, Chuan Qin2 and Haewoon Nam3

1Henan Normal University, Xinxiang, 453007, China
2University of Shanghai for Science and Technology, Shanghai, 200093, China
3Hanyang University, Ansan, 15588, Korea
*Corresponding Author: Xintao Duan. Email: duanxintao@htu.edu.cn
Received: 26 January 2022; Accepted: 08 March 2022

Abstract: At present, the image steganography method based on CNN has achieved good results. The trained model and its parameters are of great value. Once leaked, the secret image will be exposed. To protect the security of steganographic network model parameters in the transmission process, an idea based on network model parameter scrambling is proposed in this paper. Firstly, the sender trains the steganography network and extraction network, encrypts the extraction network parameters with the key shared by the sender and the receiver, then sends the extraction network and parameters to the receiver through the public channel, and the receiver recovers them with the key after receiving, to achieve more secure secret communication. In this way, even if the network parameters are intercepted by a third party in the transmission process, the interceptor cannot extract the real secret information. In this paper, the classical Joseph algorithm is used as the scrambling algorithm to scramble the extracted network model parameters of the StegoPNet steganography network. The experimental results show that when the scrambled parameters are used for secret image extraction, a meaningless image independent of the secret image is extracted, it shows that this method can well protect the security of steganography network model. At the same time, this method also has good scalability, and can use a variety of different scrambling algorithms to scramble the parameters.

Keywords: Information hiding; steganography; DCNN; joseph scrambling

1  Introduction

Information hiding is mainly divided into steganography for covert communication and digital watermarking for copyright protection. There are relatively new researches on digital watermarking [1,2]. At present, the information hiding based on carrier modification is the most studied. Because digital image is easy to obtain and modify, and there are a lot of redundant data, digital image is one of the most used cover files in steganography algorithm. The image information hiding in the following refers to the information hiding in steganography. Image information hiding is a communication method that uses images as a carrier to transmit secret information. It requires the carrier image to maintain good visual quality even after the secret information is embedded. According to different implementation methods, image information hiding can be roughly divided into two categories according to different technologies [3], one is called traditional steganography, which mainly designs a specific cost function to minimize the difference between the cover image and the stego image, so as to embed secret information and ensure the visual quality of the cover image. Traditional steganography have many classical algorithms, such as the least significant bit matching (LSBM) [4], close to the optimal coded trellis code STC(syndrome trellis codes) [5], and HUGO (highly undetectable stego) [6], WOW (wavelet obtained weigh) [7] that use the image's own content for adaptive steganography this kind of method usually has high security. Reversible information hiding is a new research hotspot in the traditional information hiding field in recent years. For example, Qin et al. proposed an adaptive reversible data hiding scheme for encrypted images [8]. The other is called deep steganography, which mainly uses deep learning technology based on deep convolutional neural network(DCNN) [9], through designing different network structures and loss functions, using sample data for training to automatically obtain stego images. In 2017, Baluja [10] proposed a CNN based steganography model to hide color image in color image for the first time. In [11] Zhang and Dong proposed a new GAN(generative adversarial networks) structure ISGAN(invisible steganography via GAN), which hides the secret gray-scale image in the color cover image at the sending end, and accurately extracts the secret image at the receiving end. The StegNet proposed by Wu and Yang et al. [12] successfully hides the color secret image into the same-frame cover image. In [13], Yu is based on the structure of CycleGAN and introduces class activation mapping (CAM) [14], and inconsistency loss, to realize effective image information hiding and extraction. The deep convolutional network proposed by Baluja in [15] realizes the hiding of multiple color secret images in one cover image. Recent studies have shown that coverless image steganography can effectively resist the existing steganalysis tools. Therefore, many coverless deep steganography have emerged, such as [16–19].

At present, DCNN-based methods realize information hiding and extraction through synchronous training of the hiding network and extraction network. This means that if the receiver wants to extract secret information in stego image, it must rely on a relatively complete extraction network. Almost all of these methods are based on the premise that the model and parameters will not be leaked in the process of channel transmission. Although only the extracted network structure is leaked, the content of the secret image will not be leaked, but if the model parameters are leaked at the same time, it will inevitably lead to an increase in the risk of leaking secret information, thereby endangering communication security and copyright protection. Therefore, it is necessary to protect the model parameters of the extracted network to prevent the leakage of secret images. Based on the existing image information hiding network model, this article proposes a scrambling encryption method for extracting network parameters. After the sender completes the synchronization training, it scrambles and encrypts the extracted network parameters and sends it through the public channel. After receiving it, the receiver uses the key to restore the parameters of the extraction network, and finally completes the extraction of the secret image. The advantage of this method is that even if the parameter values of the scrambled and encrypted network model are leaked during transmission, the third party still cannot use the intercepted parameter values and the network model to normally extract the secret image, and even cannot know the high frequency of the secret image, such as the approximate outline of the image content.

2  Method

We believe that although the existing DCNN based image information hiding methods have made great progress in capacity, the security of their transmission cannot be guaranteed. Therefore, we propose a scrambling encryption method for extracting the parameter values of the network model to improve the security.

2.1 Joseph Scrambling Encryption Algorithm

Joseph ring is a classic mathematical application problem, which is widely used in scrambling encryption [20]. In recent years, with the development of computers, figures have gradually become an important digital medium, so there have been many Joseph scrambling encryption for images [21]. It is known that there are n people (numbers 1,2,⋯,n respectively) sitting around a round table. Start counting from the person number k, and the person who counts to m will be killed; then his next person starts counting from 1, and the person who counts to m will be killed again, and so on until the round table only one person is sitting around and the remaining n−1 people will all be killed. Joseph scrambling encryption borrowed from this idea, placing the first person killed in the first position of the new array n′, and put the second person killed in the second position of the new array n′ and so on, and then put the last remaining unkilled people in the last position of the new array n′, so that we scramble an ordered array n into a new one array n′. We call the number k the starting position, the interval m is the Joseph distance, and k and m are the keys of the algorithm.

The confusion degree is an objective index used to evaluate the clutter degree of scrambling targets. Li [22] proposed a definition of the confusion degree for the two-dimensional image. He measures the confusion degree of each pixel by calculating the distance of the position change of each pixel before and after scrambling, and obtains the scrambling degree of the image by adding and normalizing the scrambling degree of all points. It is assumed that the gray value of pixel(i,j) in image A is transformed into pixiv(trow(i,j),tcol(i,j)) in image B by scrambling transformation T. Define the confusion degree of image A by this transformation T as:

sT(A)=1(n×m)3∑i=1n∑j=1m(i−trow(i,j))2+(j−tcol(i,j))2(1)

where n and m respectively represent the length and width of the image. The value range of sT is [0, 1]. The larger the value, the higher the confusion degree after scrambling.

We modify it to get the definition of the confusion degree of the one-dimensional sequence. Assuming that the value of the element(i)in sequence A is changed to element(t(i)) in sequence B by scrambling transformation T, the confusion degree of sequence A by transformation T is defined as:

sT(A)=1n2∑i=1n‖i−t(i)‖1(2)

where n represents the length of the one-dimensional sequence. The value range of sT is [0,1]. The larger the value, the higher the confusion degree after scrambling. However, due to the limitations of the scrambling algorithm, the maximum value of the Joseph scrambling algorithm is 0.5. Fig. 1 shows an example of Joseph scrambling.

2.2 The Extraction Network Structure of StegoPNet

In this paper, the extraction network of StegoPNet [23] is selected as the object model for parameter scrambling. Because the extraction network has enough convolutional layers to facilitate our scrambling, and it also has relatively few parameters and FLOPs, can improve the transmission efficiency and save the computing resources of the receiver. The overall framework of the extraction network is shown in Fig. 2, and the detailed architecture information of extraction network is shown in Fig. 3 and Tab. 1. The structure of the extraction network is divided into three modules: down-sampling, pyramid pooling, and up-sampling. Under normal circumstances, the sender uses the hidden network to obtain the stego image and transmits it to the receiver through the public channel. The receiver uses the extraction network to extract the secret image, and the semantics of the extracted secret image is consistent with the original secret image. Our work mainly scrambles encrypts the convolutional layer parameter in the down-sampling and up-sampling modules. This is because these two modules have 4 and 5 convolutional layers, and each layer contains 32 to 256 groups of varying numbers of convolution kernels that have enough parameters. The pyramid pooling module is mainly composed of a pooling layer and a single convolutional layer, with relatively few parameter values, which is not conducive to the operation of scrambling encryption.

Figure 1: Joseph scrambling when k = 6 and m = 5, and the confusion degree is 0.3194 at this time

Figure 2: The extraction network framework

Figure 3: The detailed architecture of extraction network, c, h, w in [c, h, w] represent channel, high, and weight of future map respectively

2.3 Scrambling of Extraction Network Model Parameters

This section will introduce the proposed parameter scrambling method in detail. We mainly scramble the parameters of the convolutional layer, and treat the convolution kernels in the same convolutional layer as independent individuals and scramble them. In the scrambling process, only the position of the convolution kernel changes, and the interior of the convolution kernel remains unchanged. What needs to be clear is that for convolution kernel scrambling, since the number of convolution kernel channels c between different convolution layers is different, we cannot perform cross-layer scrambling on it, that is, the convolution kernel located in the layer A scrambling to layer B. The scrambling steps are as follows:

1)   Read the parameters of each convolutional layer L = {Li}(i=1,2,⋯,n) from the parameter file of the trained extraction network model;

2)   For the convolutional layer Li, we perform Joseph scrambling encryption on the key K shared by the sender and receiver to obtain the encrypted convolutional layer Li′;

3)   Write the scrambled convolutional layer Li into the location corresponding to the model parameter file of the extracted network, and send it to the receiver along with the model;

4)   After receiving the extracted network, the receiver only needs to inverse scramble the model parameters according to the key K to obtain the correct network model parameters, to correctly extract the secret image.

Since in this process, we only scrambled the position of the parameter without changing the original value of the parameter, the receiver can restore the parameter losslessly without affecting the accuracy of the extraction network.

3  Experiment

The network is trained for 150 iterations. GPU-NVIDIA GeForce 1080, the PyTorch version we use is 1.2.0, and the version of python is 3.6.5. From the test images of the network, we randomly selected a part as the data set of the experiment, and selected a pair of images (one is the cover image and the other is the secret image) as an example image, as shown in Fig. 4. At the same time, we selected 7 different confusion degrees (0.20, 0.25, 0.30, 0.35, 0.40, 0.45, and 0.50) for comparative experiments to analyze and study the effect of parameter scrambling under different confusion degrees. For the 9th layer of convolution, that is, the last layer of convolution of the extraction network, because the number of convolution kernels is too small (only 3), the confusion degree has only 3 values, which are 0, 0.2222, 0.4444, therefore, this experiment uses uniform randomness parameter is 0.4444 when scrambling as the ninth layer the convolution kernel. We will prove in the last subsection of the experiment that the 9th layer of convolution mainly acts on the color generation of the image, and has little effect on the generation of image semantic information.

Figure 4: (a) Is a cover image, and (b) is a secret image

In this section, we refer to the image extracted by the extraction network without parameter scrambling as s′, and the image extracted by the extraction network after parameter scrambling as s′′. In this experiment, two indexes are used to evaluate the quality of generated images, namely peak signal-to-noise ratio (PSNR) [24] and structural similarity (SSIM) [25]. PSNR is an index used to evaluate the ratio between the maximum signal and background noise. The larger its value, the smaller the distortion of the image. SSIM is an index to measure the similarity of two images. The value range of SSIM is between 0 and 1. The larger the value, the smaller the difference between the two images. When SSIM is equal to 1, it means that the two images are the same.

3.1 Single Convolutional Layer Scrambling

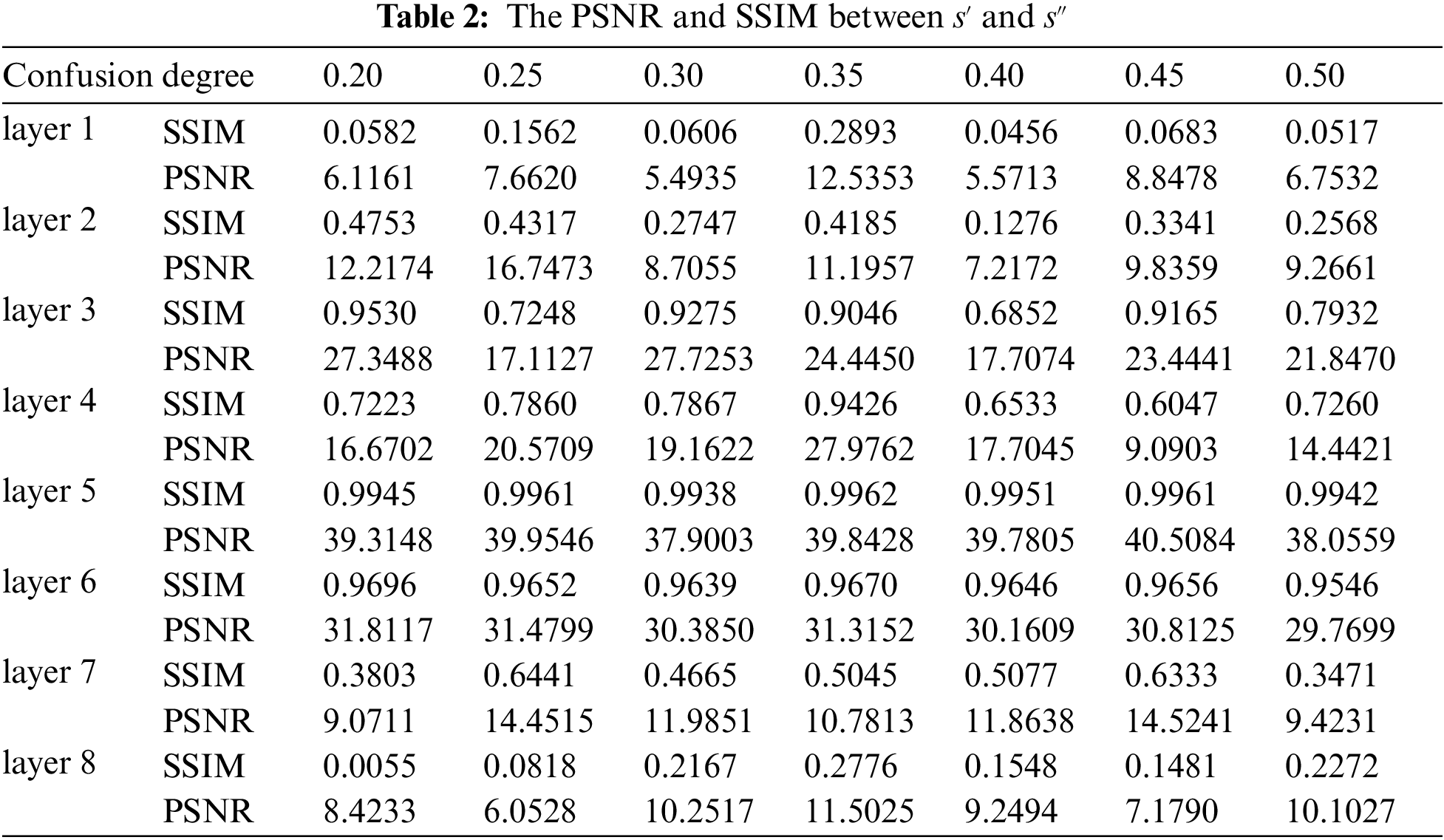
First of all, we only scramble a certain layer of convolution kernel separately. When the confusion degree is 0.35, the experimental results are shown in Fig. 5. And Fig. 6 shows the images extracted by the extraction network when only the first layer is scrambled under different confusion degrees. It can be seen that although only scrambling the single-layer parameters has an effect. But the effect is not obvious, and the outline of the secret image can still be seen, and even (f) and (g) of Fig. 5 are not much different from the original image intuitively. Then we further performed a single-layer scrambling experiment on all seven confusion degrees, and calculated the PSNR and SSIM between s′ and s′′, as shown in Tab. 2. From Tab. 2, we can see that for the fifth-layer convolution kernel of the extraction network, that is, the first-layer convolution kernel of the up-sampling part, regardless of the confusion degree, the SSIMs of s′ and s′′ are close to 1 (actually they are all more than 99.3%). This means that extracting the fifth layer of the network has little effect on the generation of image semantics. Therefore, we believe that the first layer of the up-sampling part of the convolutional layer, its role may only be to enlarge the feature to facilitate subsequent calculations, instead of directly calculating the feature map.

Figure 5: (a) Is the image extracted by the network when the parameters are not scrambled. (b)–(j) are the images extracted by the network when only the first to ninth layers are scrambled

Figure 6: (a) shows the image extracted by the network parameters are not scrambled (b)–(h) are the images extracted from the network after only scrambling the first layer when the confusion degrees is 0.20 to 0.50

In addition, from Tab. 2 we can also see that the closer the convolution layers at both ends are scrambling, the lower the values of PSNR and SSIM between s′ and s′′, and the closer the convolution layer in the middle re scrambling, the higher the values of PSNR and SSIM between s′ and s′′. This means that when the computing power resources are limited, and we can only scramble the single-layer convolution kernel, we can choose to scramble the first layer or the penultimate layer of the extraction network. The SSIM and PSNR value between s′ and s′′ are the smallest, that is, the scrambling effect at this time is the best.

Although we can achieve our goal by scrambling the convolution layer of the first layer and the penultimate layer, the third party cannot extract the secret image normally, but the effect is not very ideal at this time, we can still see the secret image's outline from s′′.

3.2 Multi-Layer Convolution Layer Scrambling

Since the effect of scrambling only on a single layer is not ideal, in this part of the experiment, we decided to perform multi-layer scrambling according to the network module of the extracted network. That is, only the down-sampling module is scrambled, only the up-sampling module is scrambled, and the entire extraction network is scrambled. Fig. 7 shows the image extracted by the extraction network when the confusion degree is 0.35, only scrambling down-sampling, only scrambling up-sampling, and all scrambling. It can be seen that when only the down-sampling module is scrambled, the obtained s′′ can see the outline of cover images, when only the up-sampling module is scrambled, the obtained s′′ can not only see the outlines of some secret images but also the outlines of some cover images, when the entire extraction network is scrambled, the obtained s′′ can also see the outline of cover images, this means that there is no need to waste additional computing resources to scramble the convolution layer of the whole extraction network. But in the above three cases, their visual effect is worse than that when only single convolutional layer is scrambled, this shows that we can scramble the multi-layer convolution kernel to achieve better target effect when the computational resources allow. Similarly, we compared the PSNR and SSIM between s′ and s′′ obtained by the three scrambling methods under different confusion degree. The specific data is shown in Fig. 8.

Figure 7: (a) Is the figure extracted by the network parameters are not scrambled, (b) is the figure extracted by the network when only scrambled down-sampling, (c) is the figure extracted by the network when only scrambled up-sampling, (d) is the figure extracted when the network is all scrambled

As can be seen from Fig. 8, for these three cases, the maximum PSNR does not exceed 9, and the maximum SSIM does not exceed 0.16. This shows that for scrambling only down-sampling and scrambling only up-sampling, although it can see some contour information, it still achieves our expected goal. For all scrambling, it does not significantly improve the scrambling effect.

Figure 8: PSNR and SSIM when scrambling different module

3.3 Convolutional Layer and Convolution Kernel Channel Scrambling

In the first two experiments, we have always regarded the convolution kernel as a whole, and scrambled the whole convolution kernel. But in fact, the convolution kernel is composed of C one-dimensional filters with the size of H×W, where C is the number of channels of the convolution kernel, and H and W are the length and width of the convolution kernel respectively. We can treat all N convolution kernels in a convolutional layer as N×C, one-dimensional filters for scrambling, which greatly increases the complexity of our scrambling, and can achieve better results, where N is the number of convolution kernels in each convolution layer. Because of the extraction network used in this experiment, the size of the convolution kernel of each layer is not the same, so we still only scramble the same layer in this part. For some CNNs where the size of each layer of the convolution kernel is the same, you can put the convolution kernels of all layers together for scrambling, but it should be noted that this will greatly increase the time complexity. We directly scramble it in multiple layers, that is, scramble it according to the lower sampling module, the upper sampling module, and the whole extraction network. The results are shown in Fig. 9.

Figure 9: (a) Is the image extracted by the network parameters are not scrambled, (b) is the image extracted by the network when only scrambled down-sampling, (c) is the image extracted by the network when only scrambled up-sampling, (d) is the figure extracted when the network is all scrambled

We can see that due to the increased complexity of the scrambling, the s′ effect obtained after the scrambling is better than the effect obtained in the first two parts. No matter which module is scrambled, the result is an image completely unrelated to the secret image.

3.4 Role of the Ninth Layer of Convolution

Because the 9th layer of convolution has only 3 convolution kernels, we experimented with all 5 (According to the combination arrangement, there are a total of A33=6 cases, one of which is not scrambled) scrambling cases. Fig. 10 shows the images extracted by the extraction network when only the 9th layer is scrambled under different scrambling situations. From a visual point of view, s′ and s′′ have almost no difference in semantic information except for color. We convert s′ and s′′ under different scrambling conditions into grayscale images through the rgb2gray function that comes with Matlab. The transformation formula is shown in Eq. (3):

GRAY=0.30R+0.59G+0.11B(3)

where R, G and B represent the red channel, green channel, and blue channel respectively in the original color image, GRAY represents the grayscale image obtained after the original color image is converted.

Figure 10: (a) Is the image extracted by the network parameters are not scrambled, (b)–(f) are the images extracted by the network after the ninth layer is scrambled under different confusion degrees

Then calculate the SSIM between the converted gray-scale images, and the experimental results are shown in Fig. 11. It can be seen that the SSIM is above 0.8 in each case of scrambling, indicating that the semantic information of the image obtained before and after the 9th layer parameter scrambling is not much different. Therefore, we believe that the 9th convolutional layer of the extraction network, that is, the last convolutional layer of the extraction network, is mainly responsible for the generation of image colors, and has little to do with the generation of image semantic information.

Figure 11: from left to right shows the SSIM between s′ and s′′ corresponding to 10 test images in the case of scrambling corresponding to Figs. 10b–10f

4  Conclusion

In the past, the security of the DCNN information hiding method is to consider the encrypted image itself. This paper proposes an extraction network of steganography model data protection method based on scrambling encryption, avoid the leakage of secret information caused by the exposure of the extracted network in the public channel. We choose Joseph scrambling algorithm to scramble the extraction network of StegoPNet. Considering the different computing resources of the receiver, we divided the experiment into three parts according to the increasing demand for computing resources. The first is to scramble the single-layer convolution layer. The experimental results show that a good result can be obtained by scrambling the first and penultimate layers of the extraction network under the condition of limited computing resources. Then, the multi-layer convolution layer is scrambled. Although this method can achieve better results, it can still see the contour information from the image extracted from the scrambled extraction network. Finally, we scramble the convolution layer and the number of channels. This method can achieve the best effect. The extracted image is almost a pure color image. In future work, we will focus on the universality of the algorithm, that is, whether it can achieve good results in other extraction networks. At the same time, we will also look for some better scrambling algorithms to make the algorithm achieve better results.

Funding Statement: This work was supported in part by the National Natural Science Foundation of China under Grant 62172280, U1904123 and U20B2051, the Key Laboratory of Artificial Intelligence and Personalized Learning in Education of Henan Province, Henan, China.

Conflicts of Interest: We declare that we have no conflicts of interest to report regarding the present study.

References

 1.  X. R. Zhang, W. F. Zhang, W. Sun, X. M. Sun and S. K. Jha, “A robust 3-D medical watermarking based on wavelet transform for data protection,” Computer Systems Science & Engineering, vol. 41, no. 3, pp. 1043–1056, 2022. [Google Scholar]

 2.  X. R. Zhang, X. Sun, X. M. Sun, W. Sun and S. K. Jha, “Robust reversible audio watermarking scheme for telemedicine and privacy protection,” Computers, Materials & Continua, vol. 71, no. 2, pp. 3035–3050, 2022. [Google Scholar]

 3.  A. M. Alhomoud, “Image steganography in spatial domain: Current status, techniques, and trends,” Intelligent Automation & Soft Computing, vol. 27, no. 1, pp. 69–88, 2021. [Google Scholar]

 4.  A. D. Ker, “Improved detection of LSB steganography in grayscale images,” in Int. Conf. on Information Hiding, Berlin, Germany, pp. 97–115, 2019. [Google Scholar]

 5.  T. Filler, J. Judas and J. Fridrich, “Minimizing additive distortion in steganography using syndrome-trellis codes,” IEEE Transactions on Information Forensics and Security, vol. 6, no. 3, pp. 920–935, 2011. [Google Scholar]

 6.  T. Pevný, T. Fillr and P. Bas, “Using high-dimensional image models to perform highly undetectable steganography,” Lecture Notes in Computer Science, vol. 6387, pp. 161–177, 2010. [Google Scholar]

 7.  V. Holub and J. Fridrich, “Designing steganographic distortion using directional filters,” in 2012 IEEE Int. Workshop on Information Forensics and Security (WIFS), Tenerife, Spain, pp. 234–239, 2012. [Google Scholar]

 8.  C. Qin, W. Zhang, F. Cao, X. P. Zhang and C. C. Chang, “Separable reversible data hiding in encrypted images via adaptive embedding strategy with block selection,” Signal Processing, vol. 153, pp. 109–122, 2018. [Google Scholar]

 9.  Z. J. Fu, E. L. Li, X. Cheng, Y. F. Huang and Y. T. Hu, “Recent advances in image steganography based on deep learning,” Journal of Computer Research and Development, vol. 58, no. 3, pp. 548–568, 2021. [Google Scholar]

10. S. Baluja, “Hiding images in plain sight: deep steganography,” in In Proceedings of the 31st International Conference on Neural Information Processing Systems (NIPS’17), New York, NY, USA, pp. 2066–2076, 2017. [Google Scholar]

11. R. Zhang, S. Dong and J. Liu, “Invisible steganography via generative adversarial networks,” Multimedia Tools and Applications, vol. 78, pp. 8559–8575, 2019. [Google Scholar]

12. W. Pin, Y. Yang and X. Q. Li, “StegNet: Mega image steganography capacity with deep convolutional network,” Future Internet, vol. 10, no. 6, pp. 54, 2018. [Google Scholar]

13. C. Yu, “Attention based data hiding with generative adversarial networks,” Proceedings of the AAAI Conference on Artificial Intelligence, vol. 34, no. 1, pp. 1120–1128, 2020. [Google Scholar]

14. B. L. Zhou, A. Khosla, A. Lapedriza, A. Oliva and A. Torralba, “Learning deep features for discriminative localization,” in IEEE Conf. on Computer Vision and Pattern Recognition, (CVPR), Las Vegas, USA, pp. 2921–2929, 2016. [Google Scholar]

15. S. Baluja, “Hiding images within images,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 42, no. 7, pp. 1685–1697, 2020. [Google Scholar]

16. Q. Liu, X. Xiang, J. Qin, Y. Tan, J. Tan and Y. Luo, “Coverless steganography based on image retrieval of DenseNet features and DWT sequence mapping,” Knowledge-Based Systems, vol. 192, no. 2020, pp. 105375–105389, 2019. [Google Scholar]

17. R. Meng, Z. Zhou, Q. Cui, X. Sun and C. Yuan, “A novel steganography scheme combining coverless information hiding and steganography,” Journal of Information Hiding and Privacy Protection, vol. 1, no. 1, pp. 43–48, 2019. [Google Scholar]

18. Y. Luo, J. Qin, X. Xiang and Y. Tan, “Coverless image steganography based on multi-object recognition,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 31, no. 7, pp. 2779–2791, 2021. [Google Scholar]

19. X. Chen, Z. Zhang, A. Qiu, Z. Xia and N. Xiong, “A novel coverless steganography method based on image selection and StarGAN,” IEEE Transactions on Network Science and Engineering, vol. 9, no. 1, pp. 219–230, 2022. [Google Scholar]

20. F. Qian, Y. Tian and M. Lei, “Algorithm design and application research of josephus problem,” Computer Engineering & Applications, vol. 43, no. 1, pp. 61, 2007. [Google Scholar]

21. M. Naima, A. Ali Pachaa and C. Serief, “A novel satellite image encryption algorithm based on hyperchaotic systems and josephus problem,” Advances in Space Research, vol. 67, no. 7, pp. 2077–2103, 2021. [Google Scholar]

22. Y. J. Li, “Research on digital image scrambling algorithm,” Ph.D. dissertation, XiDian University, China, 2010. [Google Scholar]

23. X. T. Duan, W. X. Wang, N. Liu, D. L. Yue, Z. M. Xie and C. Qin, “StegoPNet: Image steganography with generalization ability based on pyramid pooling module,” IEEE Access, vol. 8, pp. 195253–195262, 2020. [Google Scholar]

24. Y. B. Tong, Q. S. Zhang and Y. P. Qi, “Image quality assessing by combining PSNR with SSIM,” Journal of Image and Graphics, vol. 11, no. 12, pp. 1758–1763, 2006. [Google Scholar]

25. Z. Wang, A. C. Bovik, H. R. Sheikh and E. P. Simoncelli, “Image quality assessment: From error visibility to structural similarity,” IEEE Transactions on Image Processing, vol. 13, no. 4, pp. 600–612, 2004. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.