Computers, Materials & Continua DOI:10.32604/cmc.2022.027725
Article

Efficient Routing Protection Algorithm Based on Optimized Network Topology

Haijun Geng1,2, Zikun Jin1, Jiangyuan Yao3,*, Han Zhang4, Zhiguo Hu6, Bo Yang5, Yingije Guo7, Wei Wang1, Qidong Zhang1 and Guoao Duan8

1School of Computer and Information Technology, Shanxi University, Shanxi, 030006, China
2School of Automation and Software Engineering, Shanxi University, Shanxi, 030006, China
3School of Computer Science and Technology, Hainan University, Haikou, 570228, China
4Department of Computer Science & Technology, Tsinghua University, Beijing, 100084, China
5Department of Urban & Regional Planning San José State University, San José, CA, 95192, USA
6Key Laboratory of Embedded System and Service Computing (Tongji University), Ministry of Education, Shanghai, 201804, China
7Institute of Fundamental and Frontier Sciences, University of Electronic Science and Technology of China, Chengdu, 610054, China
8Beijinng University of Technology, Beijing-Dublin International College, Beijing University of Technology, Beijing, 100124, China
*Corresponding Author: Jiangyuan Yao. Email: yaojy@hainanu.edu.cn
Received: 24 January 2022; Accepted: 08 March 2022

Abstract: Network failures are unavoidable and occur frequently. When the network fails, intra-domain routing protocols deploying on the Internet need to undergo a long convergence process. During this period, a large number of messages are discarded, which results in a decline in the user experience and severely affects the quality of service of Internet Service Providers (ISP). Therefore, improving the availability of intra-domain routing is a trending research question to be solved. Industry usually employs routing protection algorithms to improve intra-domain routing availability. However, existing routing protection schemes compute as many backup paths as possible to reduce message loss due to network failures, which increases the cost of the network and impedes the methods deployed in practice. To address the issues, this study proposes an efficient routing protection algorithm based on optimized network topology (ERPBONT). ERPBONT adopts the optimized network topology to calculate a backup path with the minimum path coincidence degree with the shortest path for all source purposes. Firstly, the backup path with the minimum path coincidence with the shortest path is described as an integer programming problem. Then the simulated annealing algorithm ERPBONT is used to find the optimal solution. Finally, the algorithm is tested on the simulated topology and the real topology. The experimental results show that ERPBONT effectively reduces the path coincidence between the shortest path and the backup path, and significantly improves the routing availability.

Keywords: Routing protection algorithm; network availability; network failure; shortest path; backup path

1  Introduction

With the development of the Internet, the range of supported applications has shown significant changes. Initially, the Internet mainly supported some non-real-time applications, such as e-mail, file transfer, etc. Nowadays, a large amount of real-time business data [1,2] is widely spread over the Internet, such as Voice over Internet Protocol (VoIP), online stock trading, remote surgery, video streaming, instant messaging, and so forth. These new applications put forward higher requirements for routing availability [3,4]. Thus, routing availability will directly affect the property security and even users’ life quality. Relevant studies have shown that network failures frequently occur [5,6], and are unavoidable. During the failure repair period, the routing protocol needs to go through a period of the convergence process. In this process, there will be routing black holes, routing loops [7–9], which lead to network interruption, packet loss, and greatly reduce routing availability. Previous studies [10] demonstrated that when an OC-48 link is disconnected for 10 s, 3 million 1KB packets will be lost. In real-time applications, it is usually required to repair the failures in milliseconds. For current intra-domain routing protocols, e.g., OSPF and IS-IS, it takes several or even tens of seconds to complete convergence, which fails to meet the requirements of real-time applications for routing availability [11]. Therefore, how to improve the availability of intra-domain routing [12] has become an urgent Internet research problem. More research are focused on the problem of how to improve the network’s ability to respond to failures quickly.

Current algorithms aiming to improve the availability of intra-domain routing can be divided into two categories [13], passive recovery algorithms and routing protection algorithms. Among them, the passive recovery algorithm [14] mainly investigates how to speed up the route convergence when the network fails, and shorten the network interruption time as much as possible. However, when the links in a network are frequently disconnected, the algorithm may cause routing instability. According to the relevant rules, the routing protection algorithm [15] calculates the backup routes in advance. When the network fails, the backup routes calculated in advance are used to forward packets, which minimizes the loss of messages and shortens the network service interruption time. In comparison, the routing protection algorithm is more favored by the academic community.

As the earliest routing protection algorithm applied to the Internet, Equal Cost Multiple Paths (ECMP) proposed that if there are multiple paths from the source node to the destination node with the same minimum cost, they can be used as a backup path. Although the algorithm is simple to implement and easy to deploy, it requires the backup path to have the same minimum cost. Therefore, the ECMP algorithm does not contribute much to routing availability. Research [16] was developed to configure the shortest path with the same cost by adjusting the link weights, but this problem was proved to be an NP-Hard problem.

In response to the problems of ECMP, the Internet Engineering Task Force (IETF) released a framework for fast rerouting. On the basis of this framework, Loop-free alternates (LFA), Not-Via-based routing protection scheme [17] and tunnel-based routing protection scheme [18] are proposed. In all routing protection schemes, LFA has received close attention from the industry for its simplicity, and has been deployed and supported by router manufacturers such as Huawei and H3C. Although LFA is simple and easy to deploy, it has a fatal disadvantage—LFA cannot protect all possible single failure scenarios in the network. In order to solve the problems, the author used the theoretical knowledge of graph theory to analyze the problem of LFA failure coverage in the paper [19]. The routing availability of LFA is increased by adjusting the cost of the link in the network, but this method does not necessarily guarantee to deal with all single failure situations. For this reason, the author theoretically analyzed in-depth relationship between LFA’s routing availability and network topology [20], and improved the single-failure protection situation of LFA by adding links.

Reference [21] was proposed to use the routing deflection algorithm to improve the routing availability, that is, first use the loop-free rule to calculate all the optional next hops from the source node to the destination node, and then use the label technology to realize the flexible forwarding of the message. Although this algorithm can improve routing availability, its implementation is complicated and expensive, making it difficult to actually deploy.

Multiple Routing Configurations (MRC) [22] proposes to save multiple configuration diagrams for each router. Each configuration includes all nodes and links. By adjusting link weights, some nodes and links are protected in this configuration. Finally, a configuration diagram for all possible single failures is constructed. When the message encounters a failure in the forwarding process, the pre-configured route can be used to forward the message. However, in real networks, this algorithm needs to consume a lot of computing resources and storage overhead.

Failure Carrying Packet (FCP) [23] proposes to store the failure information encountered in the forwarding process of the message in the header of the message. When the message reaches a node, the node first detects the failure information field in the header of the message, constructs a new topology according to the field, and then re-calculates the shortest path using the new topology, so as to realize the loop-free forwarding of messages. The major advantage of this algorithm is that it eliminates the routing convergence process. However, it has high computational complexity and large changes to the routing protocol, so it is not easy to deploy in practice.

In order to solve the problem that the existing routing protection methods have low failure protection ration and can not be deployed in practice, this paper proposes an Efficient Routing Protection Algorithm Based on Optimized Network Topology (ERPBONT).

The contributions of the paper can be summarized as follows:

1.    ERPBONT is easy to implement and deploy in the real networks.

2.    ERPBONT can effectively solve the problem of low failure recovery ratio caused by network failures.

3.    ERPBONT can significantly reduce the path coincidence degree, and has the ability to quickly recover from the failed network.

2  Network Model and Problem Description

2.1 Network Model

The network topology can be represented by an undirected connected graph [24–26] G=(V,E,W). Where V,E,W respectively represents the set of nodes, the set of links, and the set of costs of links in the network, E¯ is the complement of E. For link (u,v)∈E in the network, w(u,v) represents the cost of the link. Currently, the intra-domain routing protocols deployed on the Internet, such as OSPF and IS-IS, take G=(V,E,W) as input and use the Dijkstra algorithm to calculate the shortest path of all source-destination pairs. When the network is in a normal state, all source-destination pairs use the shortest path to transmit packets, but when a failure occurs in the network, the packets passing through the failure will be discarded. Therefore, the routing protection method is widely used in the industry to minimize the message loss caused by network failure. The routing protection method is to calculate some backup paths for all source-destination pairs in the network. When the shortest path fails, the backup path can be used to forward packets, thereby greatly reducing the packet loss ratio caused by network failures. However, the existing routing protection algorithm calculates multiple backup paths for all source-destination pairs in order to increase the probability of the message being successfully forwarded, which not only increases the calculation overhead, but is also not easy to be deployed in actual networks. In order to solve the above-mentioned problems of existing routing protection algorithms, this paper calculates only one backup path for all source-destination pairs, and uses path coincidence to measure the difference between the backup path and the shortest path.

The following details the path coincidence degree. Given a network topology G=(V,E,W), for any source-destination pair s and d in the network, SP(s,d) represents the set of edges in the shortest path between the pair of nodes s and d in network topology G=(V,E,W). The optimized network topology is G′=(V,E′,W′), BP(s,d) represents the set of edges in the shortest path between node pairs s and d in network topology G′=(V,E′,W′).

The path coincidence degree between the pair of nodes can be expressed as:

CD(s,d)=|SP(s,d)∩BP(s,d)||SP(s,d)∩SP(s,d)|(1)

The path coincidence degree between all node pairs in the network can be expressed as:

C(G,G′)=∑s,d∈VCD(s,d)|V|∗(|V|−1)(2)

The network model defined above is explained by a specific example. The figure on the left in Fig. 1 shows a network topology with four nodes and four links, E={(a,b),(a,d),(b,c),(c,d)}, E¯={(a,c),(b,d)}, w(a,b)=w(b,a)=3. The shortest path SP(a,c)=(a,b,c) between node pairs a−c and the shortest path SP(b,d)=(b,c,d) between node pairs b−d. The figure on the right in Fig. 1 shows the optimized network topology, the backup path between node pair a−c is BP(a,c)=(a,c),CD(a,c)=02=0. Similarly, the backup path between node pairs b−d is BP(b,d)=(b,d), CD(b,d)=02=0.

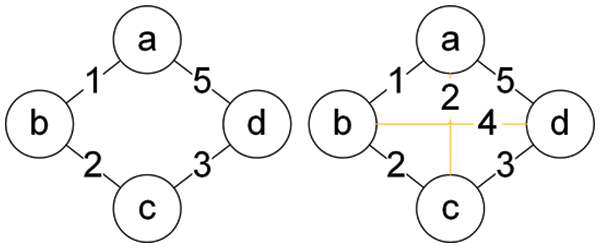
Figure 1: Original network topology (left) and optimized network topology (right)

2.2 Problem Description

This paper aims to calculate two paths with the minimum coincidence degree for all source-destination pair in the network, which are the shortest path and backup path. Given a network topology G=(V,E,W), the Dijkstra algorithm can be used to calculate the shortest path of all source-destination pairs. How to calculate the backup path is the key issue that this article needs to solve.

Given a network topology G=(V,E,W), there are many ways to calculate the backup path between all pairs of nodes. In order to be easy to deploy in the network, we choose the straightforward calculation method. That is, by expanding the original network topology structure, a new network topology structure is obtained, and the shortest path of the source-destination pair calculated in the new network topology structure is the backup path between the node pair. The problem can be expressed as:

Given a network topology G=(V,E,W), how to construct an extended topology G′=(V,E′,W′) of the topology G=(V,E,W), and use the extended topology G′=(V,E′,W′) to calculate the backup path, so as to minimize the overlap of the network path. According to the original network topology, the method of constructing the extended network topology mainly includes: (1) Adjust the link weight (2) Virtually delete the link (3) Increase the link (4) Increase the nodes in the network. Method (1) and method (2) are relatively simple. Method (2) does not actual delete links in the network, but saves these links when calculating the backup path. Method (3) needs to add a certain number of links in the network. If the increased number of links is controlled within a certain range, this method will not introduce large additional overhead. Method (4) requires an additional increase in the number of nodes, and the deployment overhead is relatively large. In summary, this article adopts fusion methods (2) and (3) to construct the extended network topology. Mathematically,

minC(G,G′)(3)

|AL|=min{|E|∗0.1,5},AL∈E¯(4)

w(x,y)=C(x,y)−min{w(u,v)},(x,y)∈E¯,(u,v)∈E(5)

|DL|=min{|E|∗0.1,5},DL∈E(6)

|E′|=|E|+|AL|−|DL|(7)

w(x,y)=w(y,x),(x,y)∈E(8)

w(x,y)=w(y,x),(x,y)∈E′(9)

Eq. (1) is the objective function to minimize the path coincidence between the shortest path and the backup path. Eq. (2) indicates that the number of added links is the minimum value between 0.1 times and 5 of the number of links in the original network, where AL is the set of added links. Eq. (3) shows that the cost of adding links satisfies the triangle rule, that is, the cost of links in the network is the minimum of all path costs. Eq. (4) indicates that the number of deleted links is the minimum value between 0.1 times and 5 of the number of links in the original network, where DL is the set of deleted links. Eq. (5) indicates that the number of links in the extended network topology is equal to the number of links in the original network topology plus the increased number of links, and then minus the number of deleted links. Eqs. (6) and (7) show that the cost of links in the network is symmetrical. Eqs. (8) and (9) show that the link cost of the network used in this paper is symmetrical.

3  Algorithm

The scientific problem solved in this paper is an NP-Hard problem, and it is difficult to obtain the optimal solution in limited computing time. Therefore, in order to reduce the deployment cost, this paper uses the heuristic method ERPBONT to calculate the approximate optimal solution. The algorithm are described in detail below.

3.1 ERPBONT Algorithm

ERPBONT is a two-stage algorithm, which is composed of adding link algorithm AddLink and Deleting Link algorithm DeleteLink. AddLink and DeleteLink expand the original network topology by adding and deleting links in the network, respectively. Through AddLink and DeleteLink, a better extended network topology can be calculated, thereby reducing the coincidence of network paths.

Algorithm 1 introduces the execution process of ERPBONT in detail. The input of the algorithm is the original network topology, the shortest path set. The output of the algorithm is the extended network topology and the backup path. First use the AddLink algorithm to calculate the final added link set AL⊂L, and then use the DeleteLink algorithm to calculate the deleted link set DL⊂L. Finally, the extended network topology G′=(V,E′,W′) is obtained, and E′=E−DL+AL. According to the extended network topology, the backup path BP of all source-destination pairs in the network is calculated.

3.2 Add Link Algorithm

The AddLink algorithm needs to solve the following three problems: (1) How many links to be added (2) Which links to be added (3) How to set the cost of adding links. The solutions to the three problems will be described below.

As for the problem (1), adding too many links will change the original network topology and increase the cost of service providers. On the contrary, adding too few links will not significantly improve the performance of the network. This paper uses a compromise method to solve this problem, increasing the number of links to |AL|=min(5,|E|∗0.1) increase the number of links will not exceed five.

As for the problem (2), the links added by the topology G=(V,E,W) can be selected from the set E¯. The complexity of calculating the added link is C|E¯||AL|, and the computational complexity is high, so this paper uses a simulated annealing algorithm to select the added link.

As for the problem (3), if the link cost is set too large, the shortest path between all nodes in the network will not pass through the link, and the value of increasing the link will be lost. For any additional link (u,v)∈E¯, the cost of the link is w(u,v)=cost(u,v)−min(W), Where cost(u,v) represents the cost between the shortest path between node u and node v, min(W) represents the minimum cost of all links in the network.

The input of the AddLink algorithm is the original network topology, the shortest path set and the initial temperature, where the initial temperature indicates the number of iterations of the algorithm, and the output is the increased link set. The variable T is set to T0, the extended network topology is initialized to G, the set AL of added links is initialized to an empty set, and the original records the path coincidence degree between all pairs of nodes in the network (lines 1–4). The algorithm requires an iterative process to calculate the set of increased links. When the current path coincidence degree is equal to 0 or the system temperature is equal to 0 or the number of increase links is 5, the program execution is completed. In each iteration process, select a link (u,v) from the set E¯ to join the network, at this time C(G,G′) has the minimum value. Update the parameters of the extended network topology (lines 7–8), delete the link (u,v) from the set E¯, and calculate the current network coincidence degree (line 10). When original<current or the temperature in the system at this time is greater than the temperature generated by the random function, the link (u,v) is added to the set AL (lines 12–14); Otherwise, the operation of adding links (u,v) will be canceled (line 15 of the algorithm), and finally return to the set of adding links AL (line 19).

3.3 DeleteLink Algorithm

The Deletelink algorithm needs to solve the following two problems: (1) how many links are deleted and (2) which links are deleted. The solutions to the two problems will be described below.

For problem (1), the number of links added by the DeleteLink algorithm is |DL|=min(5,|E|∗0.1). In order to keep the number of edges in the network unchanged, the number of links deleted by the DeleteLink algorithm is |DL|.

For problem (2), the deleted link can be selected from set DL⊂E. The complexity of calculating the deleted link is C|E||DL|, which is high. Therefore, this paper uses a simulated annealing algorithm to select the deleted link.

The input of the DeleteLink algorithm is the original network topology, the output AL of AddLink and the initial temperature, where the initial temperature indicates the number of iterations of the algorithm, and the output is the deleted link set. Set the variable t to T0, initialize the extended network topology to the union of G and AL, initialize the set DL of deleted links to an empty set, initialize the set L to E, and original records the path coincidence degree between all node pairs in the network (lines 1–5). The algorithm needs to calculate the set of deleted links through an iterative process. When the current path coincidence degree is equal to 0 or the system temperature is equal to 0 or the number of deleted links is 5, the program execution is completed. In each iteration process, a link (u,v) is selected from the set L to join the network, and C(G,G′) has the minimum value at this time. If the network G′ is a connected graph at this time, update the parameters of the extended network topology, delete the link (u,v) from the set E, and calculate the current network coincidence degree (lines 7–11). If the network G′ is not a connected graph, the previous operation of updating G′ is canceled, and the next iteration process is executed. When original<current or the temperature in the system is greater than the temperature generated by the random function at this time, the link (u,v) is added to the set DL (lines 16–19); Otherwise, the operation of adding links (u,v) will be canceled (line 21), and finally return to the set of adding links AL (line 25).

3.4 Algorithm Example

The following will use the form of a table to show the entire process of ERPBONT algorithm calculation on the topology of Fig. 2. The left picture of Fig. 2 represents the original topology, and the right picture is the topology optimized by the ERPBONT algorithm. The yellow edge represents the newly added link, and the red edge represents the virtual deleted link. The table only shows the change in the shortest path of the update link. A blank item indicates that the shortest path has not changed in the current state and is the same as the shortest path shown in the second column. The original topology generates links (a,c) and (b,d) under the action of the AddLink algorithm. At this time, the shortest path of the node to a−c,b−d,c−a,d−b changes, as shown in the third column. It is continuing to calculate the previous topology by the DeleteLink algorithm, the shortest path of the node to a−b,b−a,c−d,d−c has also changed, as shown in the fourth column. According to the path coincidence degree formula, the path coincidence degree of the backup path calculated by the optimized topology is 25%. It can be concluded from Tab. 1 that the public link of the backup path obtained by the ERPBONT algorithm is greatly reduced, and the path coincidence degree decreases significantly.

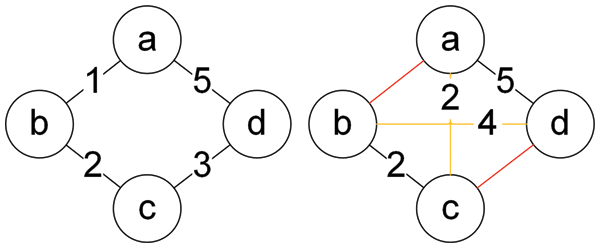
Figure 2: Algorithm example topology

3.5 Algorithm Complexity Analysis

Theorem 1: The time complexity of the AddLink algorithm is:

min(T0,cd1)×[|Com|×O (V2+V2)+O (V2)](10)

Proof: It takes min(T0,cd1) cycles to find the link set that needs to be added. In each cycle, it is necessary to find the structure G′ through the for loop, so as to calculate the shortest path and path coincidence degree of all nodes of G′. At the end of the for loop, the shortest path and path coincidence degree calculation is performed. The time complexity of this algorithm is |Com|×O (V2+V2)+O (V2). Therefore, the time complexity of AddLink is min(T0,cd1)×[|Com|×O (V2+V2)+O (V2)].

Theorem 2: The time complexity of the DeleteLink algorithm is:

min(T0,cd1)×[|Com|×O (V2+V2)+O (V2)](11)

Proof: The same as the AddLink proof process.

Theorem 3: The time complexity of the ERPBONT algorithm is:

min(T0,cd1)×[|Com|×O (V2+V2)+O (V2)](12)

Proof: ERPBONT mainly includes five steps: (1) To construct an undirected connected graph, the time complexity is O (V2). (2) AddLink and DeleteLink, the time complexity is 2×min(T0,cd1)×[|Com|×O (V2+V2)+O (V2)]. (3) The shortest path algorithm and the path coincidence degree algorithm, the time complexity is 2×O (V2). Therefore, the time complexity of ERPBONT is: 2×min(T0,cd1)×[|Com|×O (V2+V2)+O (V2)]+3×O (V2).

4  Experiment Analysis

This section uses experiments to evaluate the path coincidence degree of ERPBONT, AddLink and DeleteLink. The following first introduces the network topology used in the experiment, and then describes the performance of different algorithms.

4.1 Network Topology

This paper uses three types of network topologies for experiments, the real network topology, the network topology published by Rocketfuel and the network topology generated by Brite. The real network topology includes Abilene, NJLATA, TORONTO and USLD [27]. The topologies published by Rocketfuel [27,28] are 1755 (Ebone), 3257 (Tiscali), and 3967 (Exodus). When using Brite to generate the topology, it is assumed that the link weights are symmetrical. Brite’s model is set to Waxman, the number of nodes is 50 to 1000, the values of alpha and beta are 0.15 and 0.2, respectively, and the average degree of nodes is set between 2 and 10. The mode is set to the router, the node position obeys heavy-tail distribution, the size of the link bandwidth is between 10 and 1024, and the link cost is the inverse of the bandwidth.

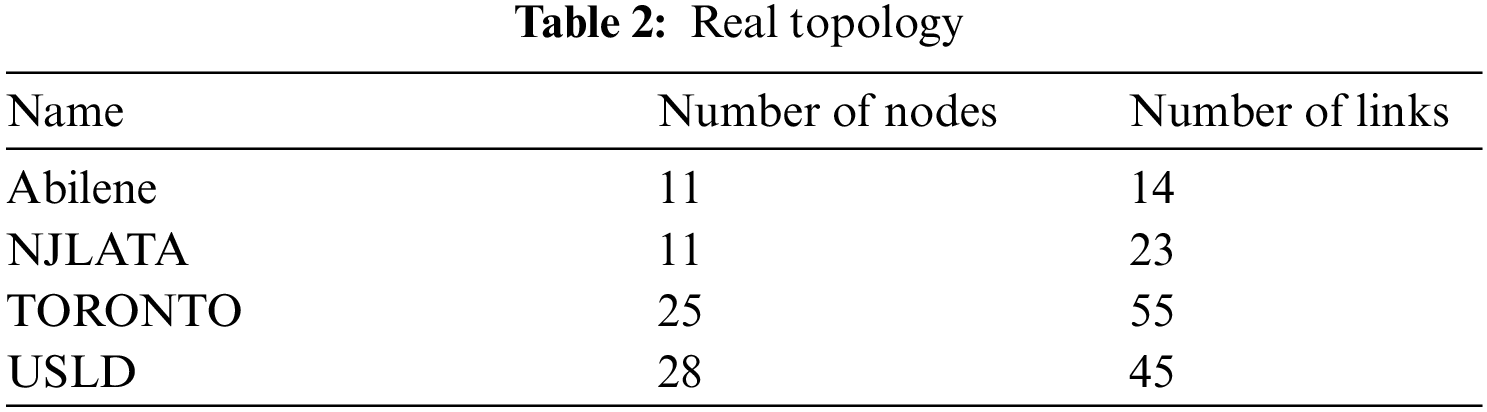
The real topology used in the experiment is shown in Tab. 2:

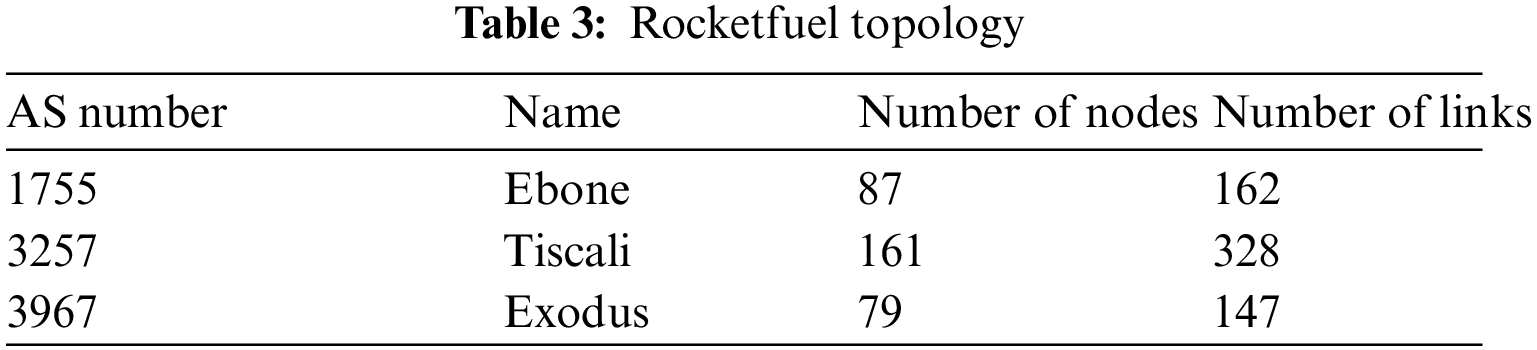
The Rocketfuel topology used in the experiment is shown in Tab. 3:

The Brite topology used in the experiment is shown in Tab. 4:

4.2 Path Coincidence Degree

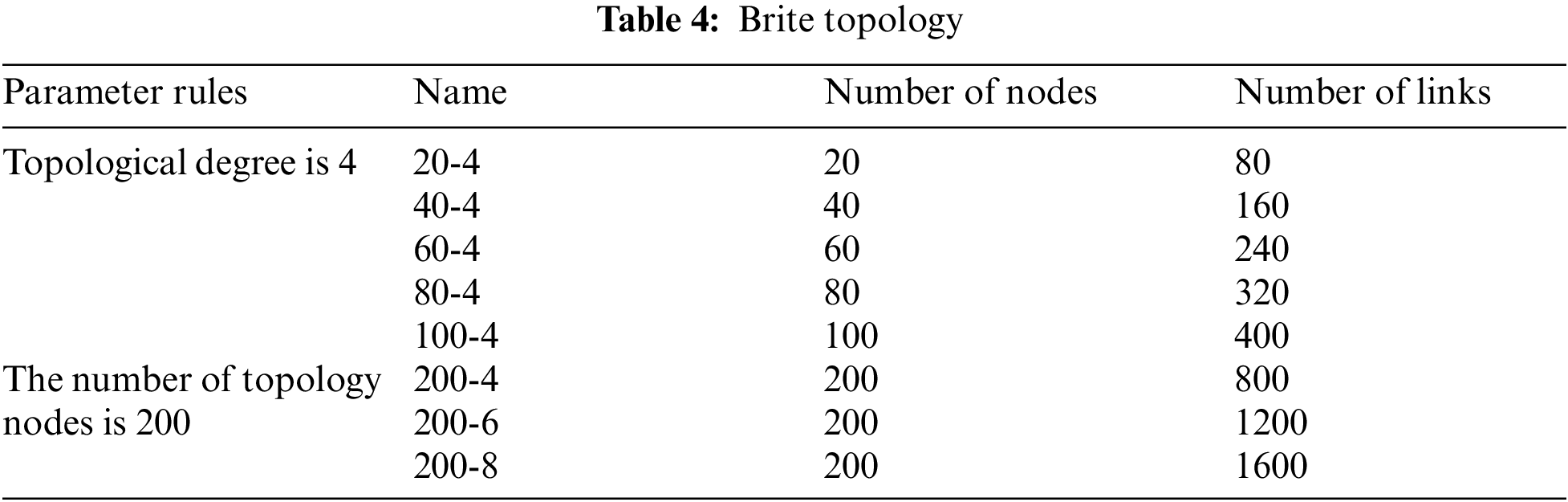
Figs. 3 and 4 show the path coincidence degree corresponding to different algorithms in the real network topology and the measured network topology. As shown in Figs. 3 and 4, in the real topology and measurement network topology, the ERPBONT algorithm’s performance is considerably better than the AddLink algorithm and the DeleteLink algorithm. Compared with the two algorithms, the path coincidence degree of the ERPBONT algorithm is reduced by 23.6% and 6.9%, respectively, and on the Rocketfule topology, the path coincidence degree of the ERPBONT algorithm is reduced by 17.8% and 3.7%, respectively.

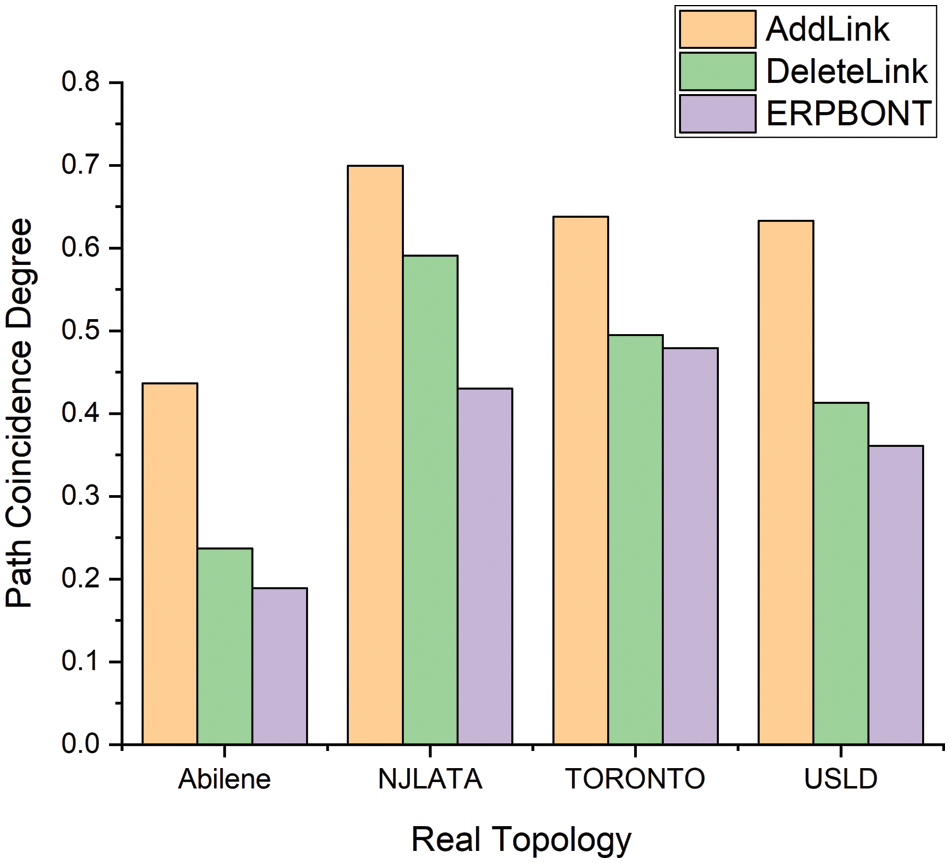
Figure 3: Comparison of path coincidence degree of three algorithms in real topology

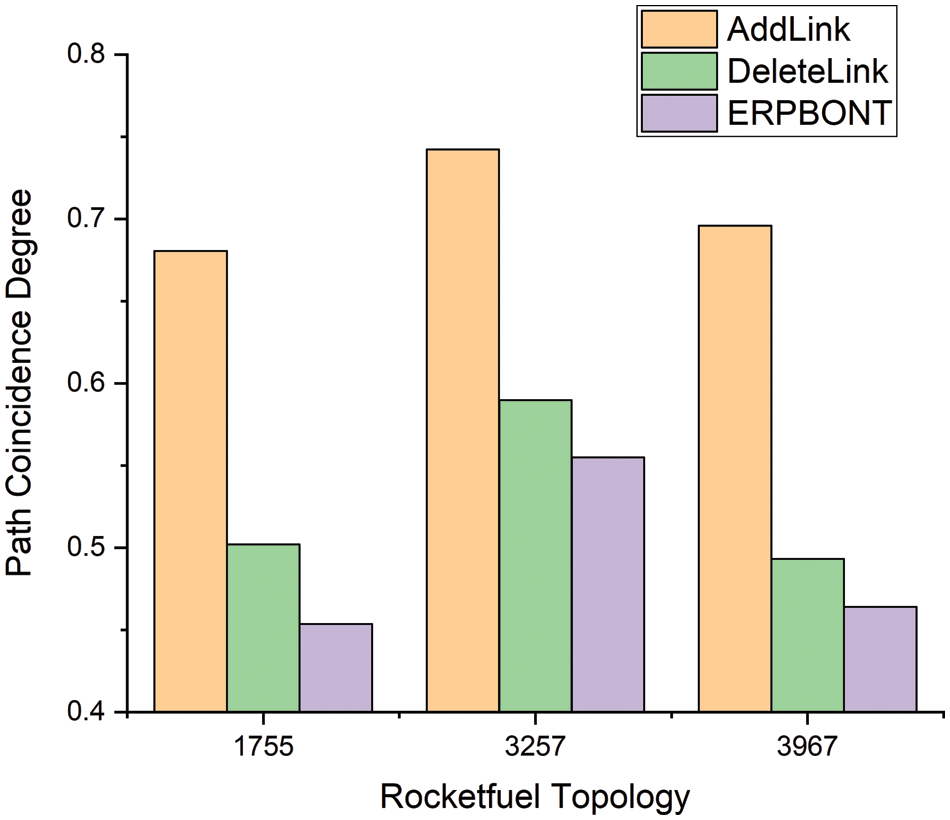
Figure 4: Comparison of path coincidence degree of three algorithms in Rocketfuel topology

Fig. 5 shows how the path coincidence degree of different algorithms changes with the size of the network topology when the average degree of nodes is 4 in the network. Fig. 6 shows the relationship between the path coincidence degree of different algorithms and the average degree of network nodes when the network topology size is 200. It can be seen from Fig. 5 that ERPBONT reduces the path overlap by 18.9% and 5.8%, respectively, compared with the AddLink algorithm and the DeleteLink algorithm. It can be seen from Fig. 6 that the path coincidence degree of ERPBONT is 9.3% and 2.1% lower than that of the AddLink algorithm and the DeleteLink algorithm, respectively.

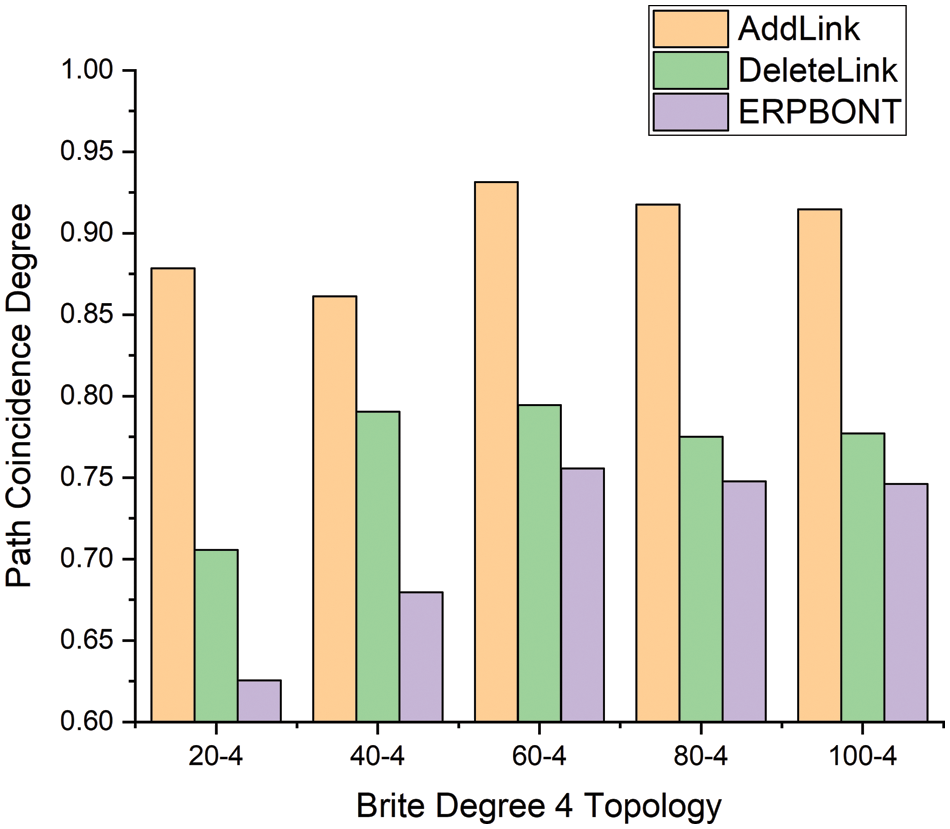
Figure 5: Comparison of path coincidence degree of three algorithms in Brite degree 4 topology

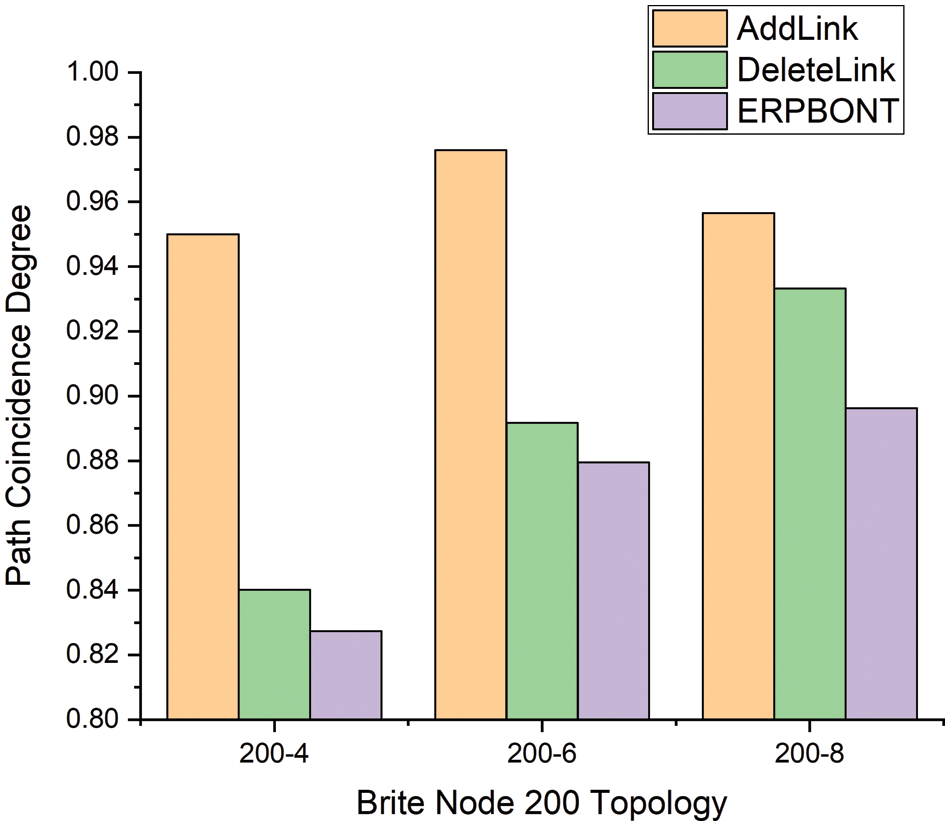
Figure 6: Comparison of path coincidence degree of three algorithms in Brite node 200 topology

5  Conclusion and Future Work

The redundancy problem of backup path calculated by the existing routing protection methods is serious. The use of path coincidence degree as a measurement index is not considered in the selection of backup path, resulting in a large number of duplicate links between backup path and best path, which greatly reduces the routing availability. In order to solve the above problem, this paper proposes a routing protection method ERPBONT based on optimizing network topology. ERPBONT can be employed in the following scenarios, such as Voice over Internet Protocol (VoIP), online stock trading, remote surgery, video streaming, instant messaging, and so forth. ERPBONT takes the path coincidence degree as the index to select the backup path, calculates only one backup path for all source-destination pairs. ERPBONT has the minimum path coincidence degree between the backup path and the original path, which greatly improves the routing availability. According to the simulation experiment, it can be seen that the path coincidence degree of the backup path calculated by ERPBONT algorithm under the real topology and the simulated topology is significantly reduced.

At present, ERPBONT algorithm only stays in the stage of calculating the backup path to improve the routing availability. In the future, we will test the algorithm in a real network, and apply the algorithm ERPBONT to SDN network. We also consider how to improve ERPBONT to deal with the single node failures and concurrent failures scenarios in the network.

Funding Statement:This work is supported by the Hainan Provincial Natural Science Foundation of China (620RC562), the Natural Science Foundation of Shanxi Province (Grant Nos. 20210302123444,20210302123455), the China University industry university research innovation fund (No. 2021FNA02009), the Open Project Program of the Key Laboratory of Embedded System and Service Computing of Ministry of Education (Tongji University) ESSCKF 2021-04, the National Natural Science Foundation of China (Grant Nos. 61702315, 61802092), the Applied Basic Research Plan of Shanxi Province (No. 201901D211168), the Program of Hainan Association for Science and Technology Plans to Youth R&D Innovation (QCXM201910), and the Key R&D Program (International Science and Technology Cooperation Project) of Shanxi Province China (No. 201903D421003).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the study.

References

 1.  H. J. Geng, H. Zhang, X. G. Shi, Z. L. Wang and X. Yin, “Efficient computation of loop-free alternates,” Journal of Network and Computer Applications, vol. 151, no. 5, pp. 1–12, 2020. [Google Scholar]

 2.  J. Tapolcai, G. Rétvári, P. Babarczi, E. R. Bérczi-Kovács, P. Kristóf et al., “Scalable and efficient multipath routing: Complexity and algorithms,” in Proc. ICNP, San Francisco, CA, USA. IEEE, pp. 376–385, 2015. [Google Scholar]

 3.  P. Mérindol, P. Francois, O. Bonaventure, S. Cateloin and J. J. Pansiot, “An efficient algorithm to enable path diversity in link state routing networks,” Computer Networks, vol. 55, no. 5, pp. 1132–1149, 2011. [Google Scholar]

 4.  S. Petale and J. Thangaraj, “Link failure recovery mechanism in software defined networks,” IEEE Journal on Selected Areas in Communications, vol. 38, no. 7, pp. 1285–1292, 2020. [Google Scholar]

 5.  Y. Yang, M. Xu and Q. Li, “Tunneling on demand: A lightweight approach for IP fast rerouting against multi-link failures,” in Proc. IWQoS, Beijing, China. IEEE, pp. 1–6, 2016. [Google Scholar]

 6.  S. Antonakopoulos, Y. Bejerano and P. Koppol, “Full protection made easy: The DisPath IP fast reroute scheme,” IEEE/ACM Transactions on Networking, vol. 23, no. 4, pp. 1229–1242, 2015. [Google Scholar]

 7.  W. Braun and M. Menth, “Loop-free alternates with loop detection for fast reroute in software-defined carrier and data center networks,” Journal of Network and Systems Management, vol. 24, no. 3, pp. 470–490, 2016. [Google Scholar]

 8.  M. W. Xu, M. J. Hou, D. Wang and J. H. Yang, “An efficient critical protection scheme for intra-domain routing using link characteristics,” Computer Networks, vol. 57, no. 1, pp. 117–133, 2013. [Google Scholar]

 9.  S. Petale and J. Thangaraj, “Link failure recovery mechanism in software defined networks,” IEEE Journal on Selected Areas in Communications, vol. 38, no. 7, pp. 1285–1292, 2020. [Google Scholar]

10. X. W. Yang and D. Wetherall, “Source selectable path diversity via routing deflections,” in Proc. SIGCOMM, Pisa, Italy, pp. 159–170, 2006. [Google Scholar]

11. J. Yallouz, O. Rottenstreich and P. Babarczi, “Optimal link-disjoint node-somewhat disjoint paths,” in Proc. ICNP, Singapore. IEEE, pp. 1–10, 2016. [Google Scholar]

12. F. Klaus-Tycho, P. Yvonne-Anne, S. Stefan and T. Gilles, “Local fast failover routing with low stretch,” ACM Sigcomm Computer Communication Review, vol. 48, no. 1, pp. 35–41, 2018. [Google Scholar]

13. K. T. Foerster, A. Kamisinski, Y. A. Pignolet, S. Schmid and G. Tredan, “Improved fast rerouting using postprocessing,” in Proc. SRDS, Lyon, France. IEEE, pp. 1–10, 2019. [Google Scholar]

14. P. Francois, C. Filsfils, J. Evans and O. Bonaventure, “Achieving sub-second igp convergence in large ip networks,” Computer Communication Review, vol. 35, no. 3, pp. 35–44, 2005. [Google Scholar]

15. M. W. Xu, Y. Yang and Q. Li, “Selecting shorter alternate paths for Tunnel-based IP fast ReRoute in linear time,” Computer Networks, vol. 56, no. 2, pp. 845–857, 2012. [Google Scholar]

16. A. Sridharan, R. Guerin and C. Diot, “Achieving near-optimal traffic engineering solutions for current ospf/is-is networks,” IEEE/ACM Transactions on Networking, vol. 13, no. 2, pp. 234–247, 2005. [Google Scholar]

17. G. Enyedi, G. Rétvári, P. Szilágyi and A. Császár, “IP fast ReRoute: Lightweight Not-Via without additional addresses,” in Proc. INFOCOM, Rio de Janeiro, BRAZIL. IEEE, pp. 2771–2775, 2009. [Google Scholar]

18. J. Zheng, H. Xu, X. Zhu, G. Chen and Y. Geng, “We’ve got you covered: Failure recovery with backup tunnels in traffic engineering,” in Proc. ICNP, Singapore. IEEE, pp. 1–10, 2016. [Google Scholar]

19. G. Rétvári, L. Csikor, J. Tapolcai, G. Enyedi, A. Császár et al., “Optimizing IGP link costs for improving IP-level resilience,” in Proc. DRCN, Krakow, Poland. IEEE, pp. 62–69, 2011. [Google Scholar]

20. G. Rétvári, J. Tapolcai, G. Enyedi and A. Császár, “Ip fast reroute: Loop free alternates revisited,” in Proc. INFOCOM, Shanghai, China. IEEE, pp. 2948–2956, 2011. [Google Scholar]

21. X. W. Yang and D. Wetherall, “Source selectable path diversity via routing deflections,” in Proc. SIGCOMM, Pisa, Italy, pp. 159–170, 2006. [Google Scholar]

22. A. Kvalbein, A. F. Hansen, T. Čičić, S. Gjessing and O. Lysne, “Fast IP network recovery using multiple routing configurations,” in Proc. INFOCOM, Barcelona, Catalunya, Spain, pp. 1–11, 2006. [Google Scholar]

23. K. Lakshminarayanan, M. Caesar, M. Rangan, T. Anderson, S. Shenker et al., “Achieving convergence-free routing using failure-carrying packets,” in Proc. SIGCOMM, Kyoto, Japan, pp. 241–252, 2007. [Google Scholar]

24. Z. L. Wang, H. Zhang, X. G. Shi, X. Yin, H. J. Geng et al., “Efficient scheduling of weighted coflows in data centers,” IEEE Transactions on Parallel and Distributed Systems, vol. 30, no. 9, pp. 2003–2017, 2019. [Google Scholar]

25. R. Jin, X. Zhou and Y. Wang, “An efficient energy routing protocol based on gradient descent method in wsns,” Journal of Information Hiding and Privacy Protection, vol. 2, no. 3, pp. 115–123, 2020. [Google Scholar]

26. S. Perumal, M. Tabassum, G. Narayana, S. Ponnan, C. Chakraborty et al., “Ann based novel approach to detect node failure in wireless sensor network,” Computers, Materials & Continua, vol. 69, no. 2, pp. 1447–1462, 2021. [Google Scholar]

27. H. J. Geng, H. Zhang and Y. Y. Zhang, “Efficient routing protection algorithm in large-scale networks,” Computers, Materials & Continua, vol. 66, no. 2, pp. 1733–1744, 2021. [Google Scholar]

28. Y. Guo, K. Huang, C. Hu, J. Yao and S. Zhou, “Traffic engineering in dynamic hybrid segment routing networks,” Computers, Materials & Continua, vol. 68, no. 1, pp. 655–670, 2021. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.