Computers, Materials & Continua DOI:10.32604/cmc.2022.027672
Article

Frequency Domain Adaptive Learning Algorithm for Thoracic Electrical Bioimpedance Enhancement

Md Zia Ur Rahman1,*, S. Rooban1, P. Rohini2, M. V. S. Ramprasad3 and Pradeep Vinaik Kodavanti3

1Department of Electronics and Communication Engineering, Koneru Lakshmaiah Education Foundation, K L University, Vaddeswaram, Guntur, 522502, Andhra Pradesh, India
2Department of Computer Science and Engineering, Faculty of Science and Technology, ICFAI Foundation for Higher Education, Hyderabad, 500082, Telangana, India
3Department of Electrical, Electronics and Communication Engineering, GITAM Institute of Technology, GITAM Deemed to be University, Visakhapatnam, 530045, Andhra Pradesh, India
*Corresponding Author: Md Zia Ur Rahman. Email: mdzr55@gmail.com
Received: 23 January 2022; Accepted: 08 March 2022

Abstract: The Thoracic Electrical Bioimpedance (TEB) helps to determine the stroke volume during cardiac arrest. While measuring cardiac signal it is contaminated with artifacts. The commonly encountered artifacts are Baseline wander (BW) and Muscle artifact (MA), these are physiological and non-stationary. As the nature of these artifacts is random, adaptive filtering is needed than conventional fixed coefficient filtering techniques. To address this, a new block based adaptive learning scheme is proposed to remove artifacts from TEB signals in clinical scenario. The proposed block least mean square (BLMS) algorithm is mathematically normalized with reference to data and error. This normalization leads, block normalized LMS (BNLMS) and block error normalized LMS (BENLMS) algorithms. Various adaptive artifact cancellers are developed in both time and frequency domains and applied on real TEB quantities contaminated with physiological signals. The ability of these techniques is measured by calculating signal to noise ratio improvement (SNRI), Excess Mean Square Error (EMSE), and Misadjustment (Mad). Among the considered algorithms, the frequency domain version of BENLMS algorithm removes the physiological artifacts effectively then the other counter parts. Hence, this adaptive artifact canceller is suitable for real time applications like wearable, remove health care monitoring units.

Keywords: Adaptive learning; artifact canceller; block processing; frequency domain; thoracic electrical bioimpedance

1  Introduction

In various reports the World Health Organization (WHO) states that mortality is increasing globally due to most of the patients are not treated timely who suffered with cardiovascular diseases (CVD) [1]. The most noncommunicable diseases are cardiovascular diseases and it is having 17.8 million deaths globally, to reduce this death rate WHO member states providing drug treatment for 50% of diseased cardiovascular problems by 2025 [2]. American Heart Association [3] states that the heart strokes encountering not only adults, but also children in the age group of 12–19 years. Therefore, continuous monitoring of physiological vitals becomes a key task in health care industry. In such a scenario, medical telemetry is a promising tool for remote health care monitoring of the patients. The prime physiological events to measure the functionality of cardiac activity are electrocardiogram (ECG) and Thoracic Electrical Bioimpedance (TEB). Among these, TEB is much useful to estimate the stroke volume and helps to treat the patient. In this contest, providing a high-resolution signal to the doctors for proper diagnosis is the main motivation of this work. But, during the signal acquisition, several artifacts contaminate the signal and mask the tiny features of physiological quantities, causes ambiguities in the diagnosis. Therefore, eliminating these artifacts before presenting TEB component for diagnosis is the scientific problem in our work. Several contributions were made in the literature for the analysis of TEB signal and to help the diagnosis process.

Massari et al. [4] explained bioimpedance vector analysis, to check the impedance vector to predict length of stay of acute heart failure patients. Panagiotou et al. [5] demonstrated the non-invasive methods to measure cardiac output in pulmonary artery hypertension using thermodilution method in patients who are under treatment of pulmonary artery hypertension. By using cardiometry precision and accuracy of cardiac out is calculated [6]. Sangkum et al. [7] proved the cardiac output measurement by pulmonary artery catheterization using non-invasive method. Shin et al. [8] analyzed the phase angle assessed method to predict clinical outcomes by impedance analysis for hemodialysis patients. TEB also called as impedance plethysmography [9] is mainly used to study about the flow of blood in body, particularly in to find blood flow in heart using haemodynamic method. Blood flow causes variations in current, then by using cardiac device from impedance waveform we can measure cardiac output. This device is used as an alternate device to the invasive methods for heart related management conditions like calibration of pace maker, transplantation of heart and heart failure [10]. TEB is used to find stroke volume in heart and there after several methods come into appearance in between invasive techniques like thermodilution and non-invasive technique of TEB [11–13]. By analyzing TEB, resistance will be calculated by passing a current through thorax area. Thorax area means the area between neck and the abdomen, in this area set of electrodes are placed and current is passed through these electrodes [14]. The combination of stroke volume and heart rate is known as cardiac output and it is used to determine delivery of oxygen to organs [15]. Transportation of oxygen is main function of cardiac output and by estimating cardiac output we can measure blood volume pumped by heart in one minute. Among these methods, TEB is explored rapidly to know cardiac signals [16], so that we are using this method. By using TEB method cardiac output is calculated by identifying changes in body impedance to electrical currents. Blood and tissue stop electrical current to flow but impedance and volume of tissues remain constant during cardiac cycle [17].

Therefore, the analysis of TEB is useful in CVD diagnosis as well as in treatment. But, during sensing and recording the TEB several physiological artifacts contaminate the actual TEB signal. This effects the resolution of cardiac activity and hides some minute features of the electrical component which are very much important for diagnosis. Hence, some signal conditioning has to be applied, to provide a clean TEB component for accurate diagnosis and treatment. As the occurrence of TEB is non-stationery, the conventional signal conditional techniques are not suitable for processing. In such a case, adaptive learning-based techniques are appropriate. In [18] authors presented a methodology of stroke volume and intensity determination, artifact elimination. Several adaptive filtering techniques are presented in [19–21] to remove the noise in cardiac output signal calculation. Several related techniques are presented in [22,23]. Most of the conventional signal enhancement techniques adopt overlapping blocks. In which the processing needed many numbers of iterations and large computations. To avoid this in our work, we proposed a block based adaptive learning scheme. In which the entire signal is divided into several blocks and processed. Again, to improve filtering ability data normalization, error normalization is performed in both time domain as well frequency domains. The second section of the paper demonstrates the mathematical modeling of the block-based techniques in time domain (TD) and frequency domain (FD). The third section elaborates the ability of proposed schemes in the contest of TEB signal enhancement in clinical scenarios and calculates the ability of the techniques by computing SNRI, EMSE, Mad.

2  Modeling Block Based Adaptive Learning for Artifact Cancellation in TEB Signals

Let us consider a block adaptive learning-based noise canceller for TEB enhancement as detailed in Fig. 1. Here, the TEB data vector x(n) and is divided into small blocks of size P and are fed to an adaptive filter of dimension L. The adaptive learning technique in which the data is processed block by block is called as block least mean square (BLMS) algorithm. In conventional techniques sample by sample processing takes place, as a result samples are processed multiple times. This causes the computational complexity. However, in block processing due to averaging the signal quality in terms of amplitude usually decreases.

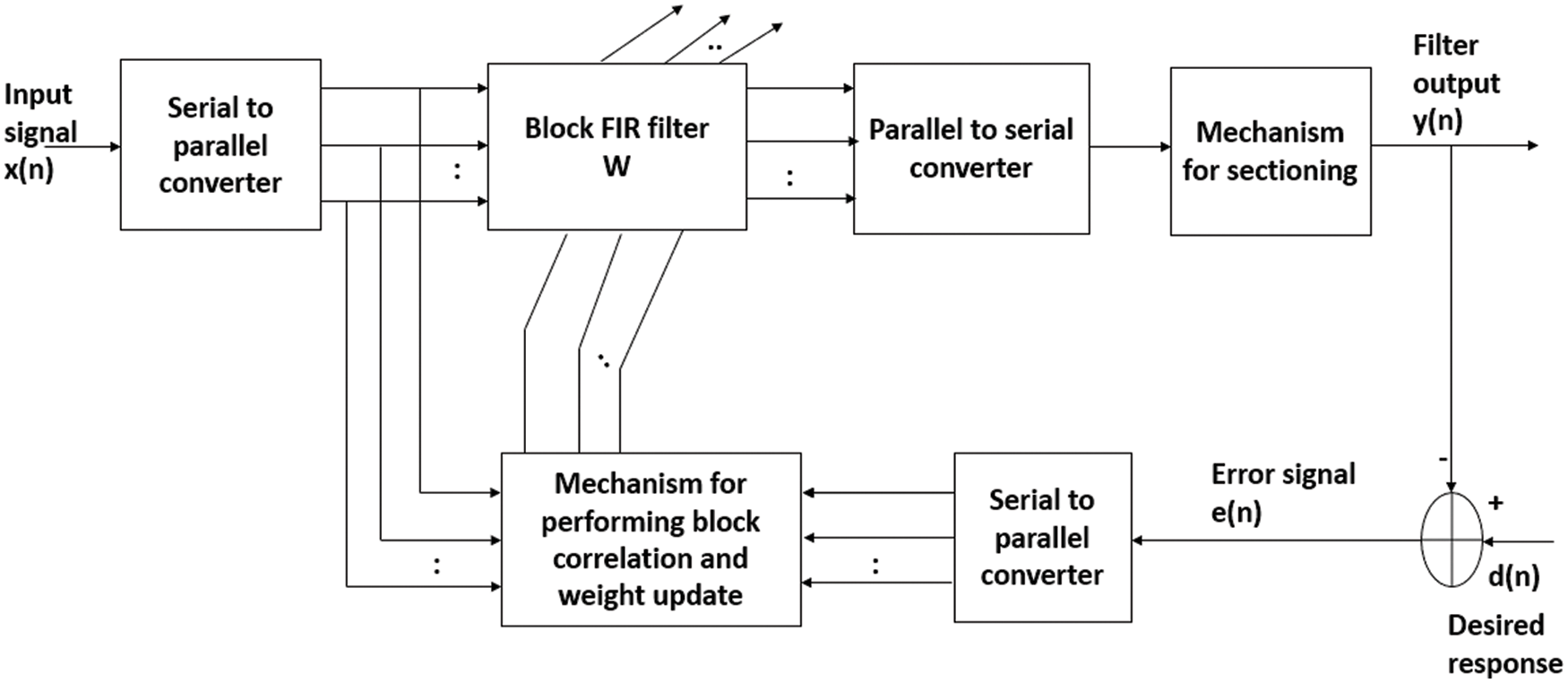
Figure 1: A typical block diagram of block processing based adaptive learning scheme

The weight coefficient vector of BLMS is given by,

w(j+1)=w(j)+μ∑i=0P−1x(jP+i)e(jP+i)(1)

k refers to the block index.

w(j)=[w0(j),w1(j),…,wP−1(j)]t is coefficient vector corresponding to jth portion, x(jP+i)=[x(jP+i),x(jP+i−1),…,x(jP+i−P+1)]t, e(jP+i) is error vector written as,

e(jP+i)=d(jP+i)−y(jP+i)(2)

In block processing, for the jth segment, the product x(jP+i)e(jP+i) takes the values of “i” for the formation of the weight recursion equation given by (1).

The vector d(jP + i) is desired response and is obtained during the training phase of the algorithm and y(jP + i) is filtered and clean TEB signal,

y(jP+i)=wt(j)x(jP+i)(3)

The scalar µ is step size value, has the limits as 0 < µ < 2P∗trR.

With reference to block length P and filter length L, the BLMS operates in the following combinations.

1.    P = L, this is an optimal choice from computational complexity point of view.

2.    P < L, this offers an advantage of reduced processing delay. Moreover, this results an adaptive filter computationally efficient when compared to LMS algorithm.

3.    P > L, gives redundant operations in the adaptive learning process.

In our experiments, we have developed the optimal choice i.e., P = L.

Fast Fourier transform (FFT) algorithm uses a key method for applying fast correlation, convolution operations. The fast block LMS (FBLMS) is the FD version of BLMS. In FD, multiplication is done on element-by-element, followed by IFFT and proper window result to get output vector. Here signals are converted from TD to FD and back words using FFT and IFFT respectively. For fast convolution procedures, overlap save method and overlap add methods are used with help of discrete Fourier transform. The overlap save method is the most commonly used filtering technique. Hence BLMS method is widely used to improve convergence rate and computational efficiency due to FFT. Output filter vector is represented as (3) is computed by convolving the input vector x(n) with weight vector w0(j),w1(j),…,wL−1(j) and it is developed using overlap-save method. Also, the weight vector in (1), viz., ∑r=0P−1x(jP+r)e(jP+r) is calculated by circular correlation of M point FFT and setting the last P − 1 output bits as zero. This method is used for realizing the FBLMS method. For computation, in this technique an N-point FFT is used, where N = 2M. Finally, the N-by-1 weight vector is represented as,

W(j)=FFT[w(j)0](4)

denote FFT coefficients of zero padded, tap weight vector w (j). In Eq. (4), 0 is M-by-1 null vector. The FD weight vector W (j) is twice as long as the TD weight vector w (j). Let X (j) is a diagonal matrix determined by Fourier transforming two successive blocks of the input vector.

X(k)=diag{FFT[u(kL−L),…,u(kL−1),u(kL),…,u(kL+L−1)]}(5)

and d (j) is the L-by-1 desired response vector.

By applying an overlap-save method to the linear convolution of (3) gets the L-by-1 vector,

YT(k)=last L elements of IFFT [X(j) W(j)](6)

Now corresponding L-by-1 error signal vector is given by

e(j)=d(j)−y(j)(7)

In the implementation of linear convolution described in Eq. (6), the first L elements are discarded from the output.

Error vector e(j) in FD is denoted as,

E(j)=FFT[0e(j)](8)

Hence, the weight coefficient vector in (1) is determined in FD as,

W(j+1)=W(j)+μFFT[Φ(j)0](9)

Based on the above mathematical analysis FBLMS in FD filtering and weight updating will be done using FFT i.e., convolution is efficiently done by block processing further by applying FFT for the entire block. Here Φ(j) is a matrix of first M elements of IFFT [D (j) X (j) E (j)]. Where D (j) is the diagonal matrix of average signal power, X(j) is the diagonal matrix obtained by Fourier transform two successive blocks of input data, E (j) is transformed of error vector. The flow diagram of FD adaptive learning based BLMS is shown in Fig. 2.

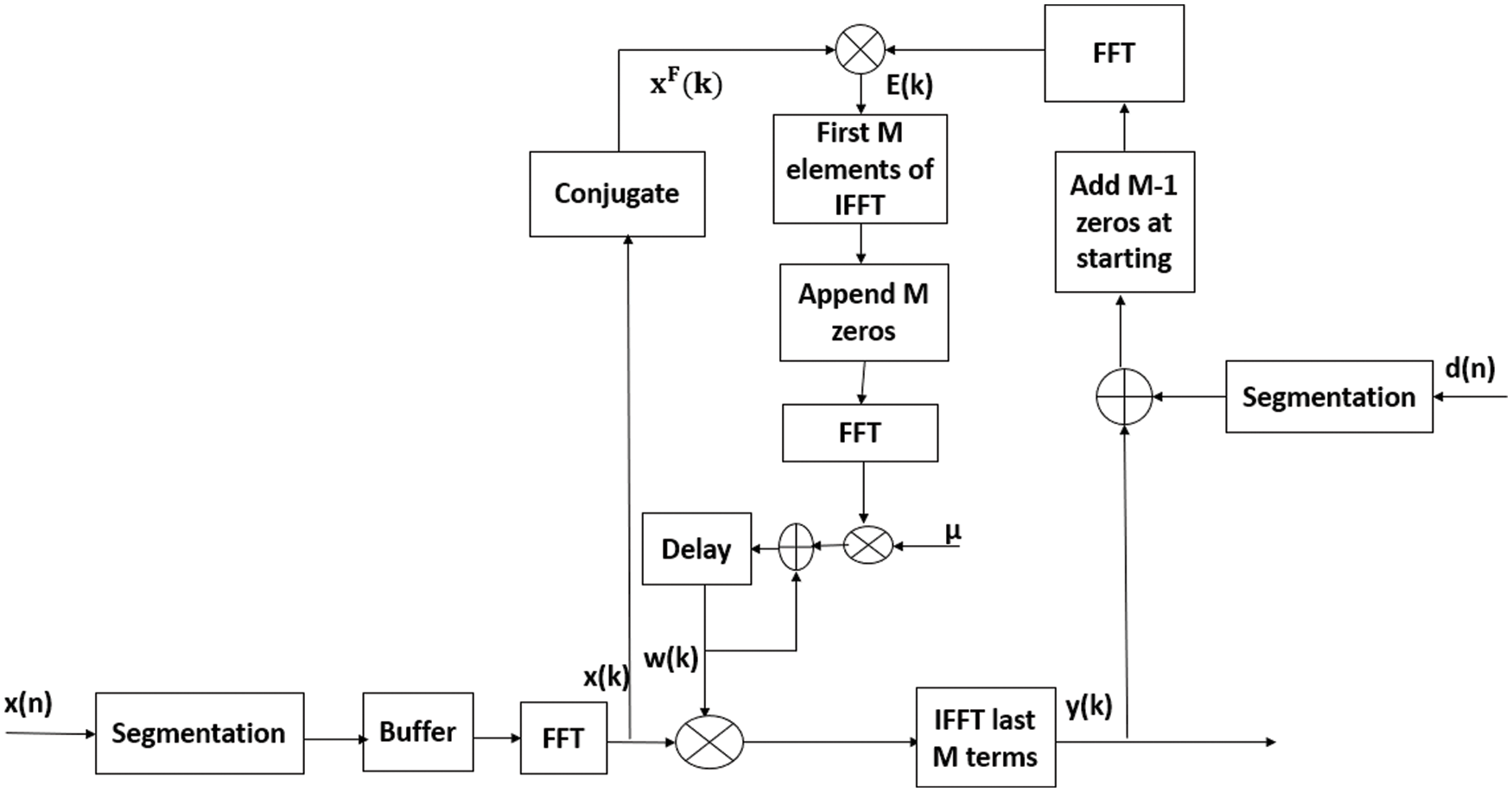
Figure 2: The flow chart of frequency domain adaptive learning algorithm

Further, the convergence rate and filtering ability of the proposed block-based techniques are improved using normalization operations. After data normalization, the step parameter is represented as,

μ(n)=με+||x(n)||2(10)

The resultant weight update equation of BNLMS is expressed as

w(j+1)=w(j)+μ(n)∑r=0P−1x(jP+r)e(jP+r)(11)

Therefore, the change in weight coefficient vector w(n) is inversely proportional to norm of x(n). This normalized algorithm converged quicker than the LMS algorithm because it uses variable step size aims at minimizing in instantaneous output error.

Instead of data normalization, the weight update recursion is normalized with respect to the error component and results in error normalization. Then the step size of BENLMS is represented as

β(n)=με+‖e(n)‖2(12)

Now the weight update recursion for BENLMS is represented as,

w(j+1)=w(j)+β(n)∑r=0P−1u(jP+r)e(jP+r)(13)

For BENLMS, time varying step value is inversely proportional to squared norm of error, whereas in BNLMS algorithm it is inversely proportional to input data.

The realization of BNLMS and BENLMS algorithms follows the same methodology as that of for FBLMS. The frequency domain versions of BNLMS and BENLMS are known as FD BNLMS (FBNLMS) and FD BENLMS (FBENLMS) algorithms.

W(j+1)=W(j)+μ(n)FFT[Φ(j)0](14)

and

W(j+1)=W(j)+β(n)FFT[Φ(j)0](15)

where µ(n) and β(n) are variable step sizes due to data and error normalizations respectively.

In biotelemetry applications, the physiological, non-physiological, and channel noises fades the features of cardiac signal. Moreover, in practical cases, large data rates are used to send the bulk data in less time. In order to process such bulk data, the conventional filter length has to be increased, the computational complexity of the filter increases. In this aspect to reduce the complexity FFT based block processing is the suitable candidate.

The convergence curves of BLMS and its variants in both TD, FD are shown in Fig. 3 and it is clear that convergence characteristics of BLMS are approximately similar to LMS algorithm. However, by adopting normalization fast convergence is achieved in both BNLMS and BENLMS algorithms. Because of normalization, step size is varied iteratively; this step size is proportional to inverse of total expected energy of instantaneous values of the input data vector coefficients. The BNLMS and BENLMS algorithms usually converge faster than LMS algorithm, because it uses a variable convergence factor aims at minimizing instantaneous output error. Advantage of the BNLMS and BENLMS algorithms is that step size is chosen independent of input signal power and number of tap weights. Therefore, these algorithms has a steady state error and convergence rate better than BLMS algorithm. As a result of frequency domain implementation, Fast block least mean square (FBLMS) algorithm is widely used to improve convergence rate due to the use of FFT.

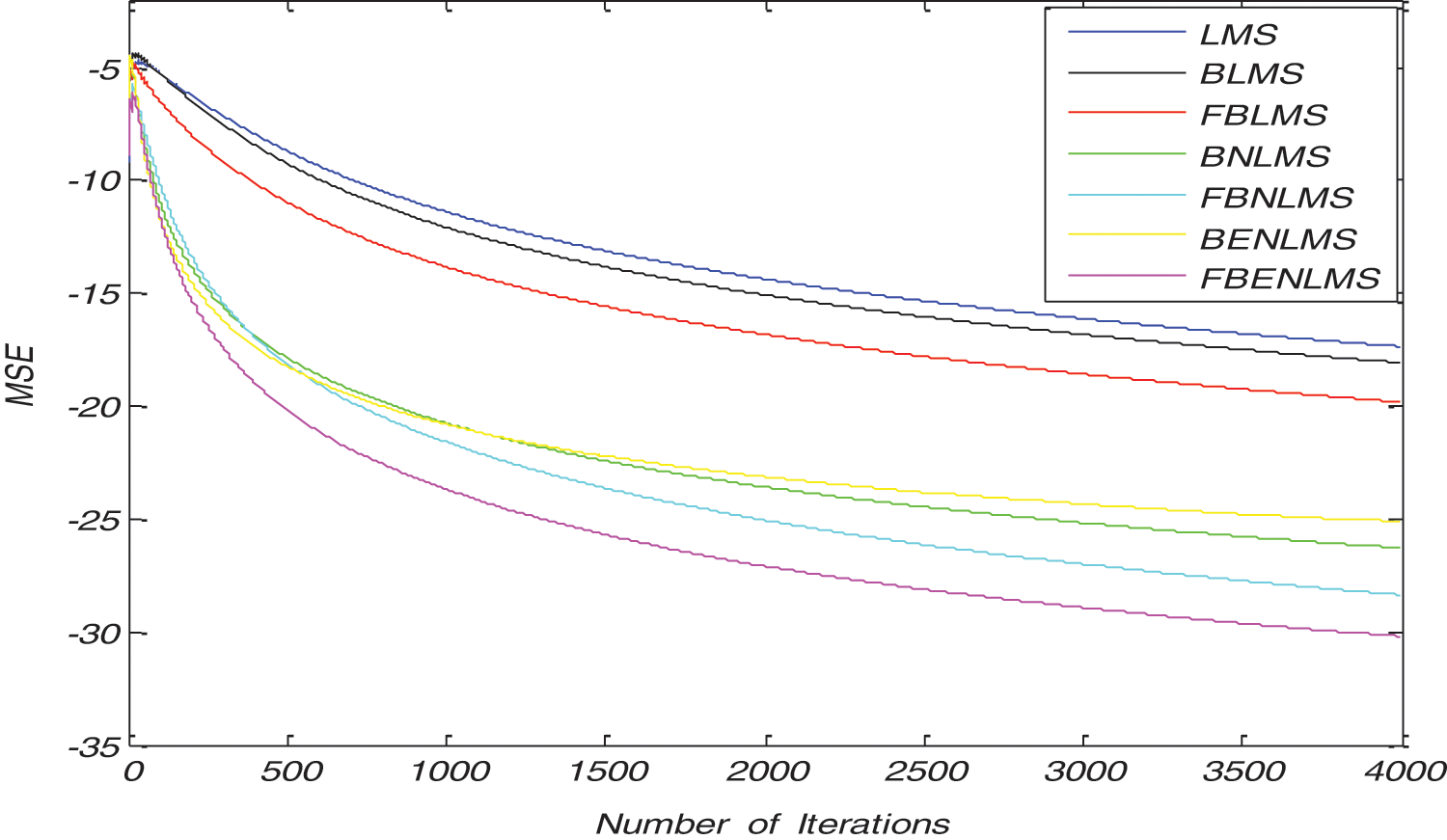
Figure 3: Typical convergence characteristics of various block adaptive learning algorithms in time domain and frequency domain

3  Adaptive Learning Based Artifact Elimination and Discussion

To test the ability of proposed algorithm in clinical situations several experiments are performed on read TEB signals. TEB signals with different artifact components are obtained using VU-AMS ambulatory system. For TEB recordings, system uses Kendall ARBO H98SG ECG electrodes. For simulations, 10,000 samples of TEB components are recorded from five different persons. But to get high resolution signals processed only 1000 samples of data and length of the filter is 10. For evaluation process of the proposed method, signal to noise ratio (SNR), excess mean square error (EMSE) and misadjustment are calculated and averaged over ten experiments. A Gaussian noise of variance of 0.01 is added to TEB component in telemetry system to show the similarity free space effect. For experiments records 1, 2, 3, 4, and 5 are used and these are contaminated with physiological artifacts. For TEB enhancement signal enhancement unit is developed using block LMS algorithm and its variants. The BLMS, its variants, and block based normalized algorithms; its variants are two different independent categories of block adaptive filters. However, we have considered both categories in noise removal experiments and compared them individually. In the former case, we process non overlapping blocks, whereas in the latter case we process overlapping blocks. Input signal is partitioned into non overlapping blocks using serial to parallel converter then it generates synthetically four types of artifacts with help of real artifacts are obtained from MIT-BIH database. Artifact canceller compares contaminated input signal PSD then from obtained reference generator artifact is synthesized. Reference generator can identify noise type in the input signal. Adaptive learning-based artifact cancellation is carried for artifacts like BA and MA.

3.1 Adaptive Baseline Wander Removal from TEB Signals

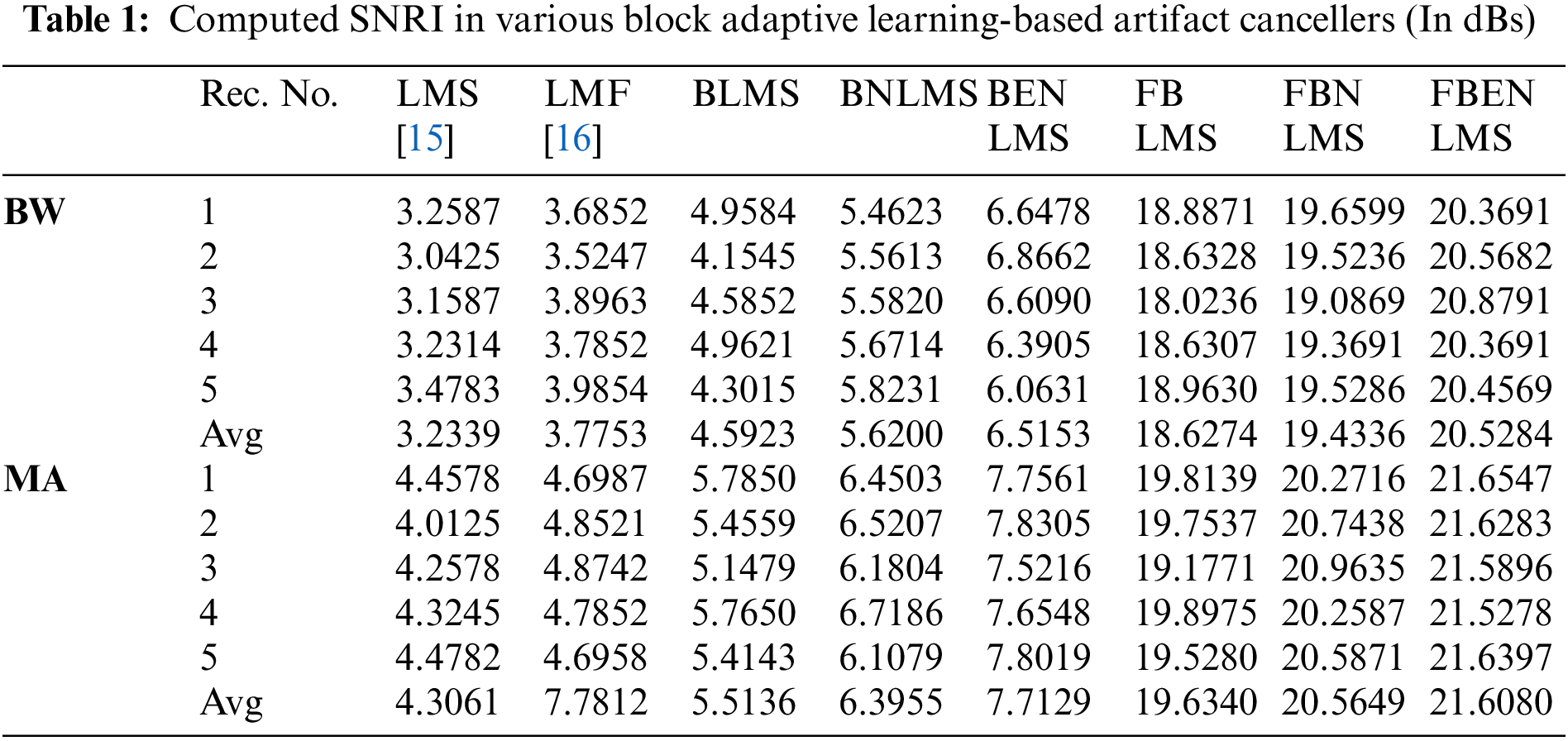
It demonstrates cancellation of BW; it is a non-stationary noise cancellation. The input to the filter is TEB signal is contaminated with respiration baseline wander it is applied to a noise canceller shown in Fig. 1. Reference signal is a real BW obtained from MIT-BIH Database. Contaminated TEB signal is applied as input x(n) and output is y(n). Various filter structures are implemented using nonoverlapping block filters in time domain and frequency domain to eliminate the artifact components from TEB signals. The simulation results for adaptive BW removal using BLMS, its variants are shown in Fig. 4. SNRI contrast for this case is shown in Tab. 1. The EMSE and Mad are calculated for different types of artifacts, averaged values are tabulated in Tabs. 2 and 3 respectively.

Figure 4: Adaptive artifact cancellation results for base line wander (a) TEB with BW, (b) enhanced TEB due to LMS based adaptive learning, (c) enhanced TEB due to BLMS based adaptive learning, (d) enhanced TEB due to BNLMS based adaptive learning, (e) enhanced TEB due to BENLMS based adaptive learning, (f) enhanced TEB due to FBLMS based adaptive learning, (g) enhanced TEB due to FBNLMS based adaptive learning, (h) enhanced TEB due to FBENLMS based adaptive learning

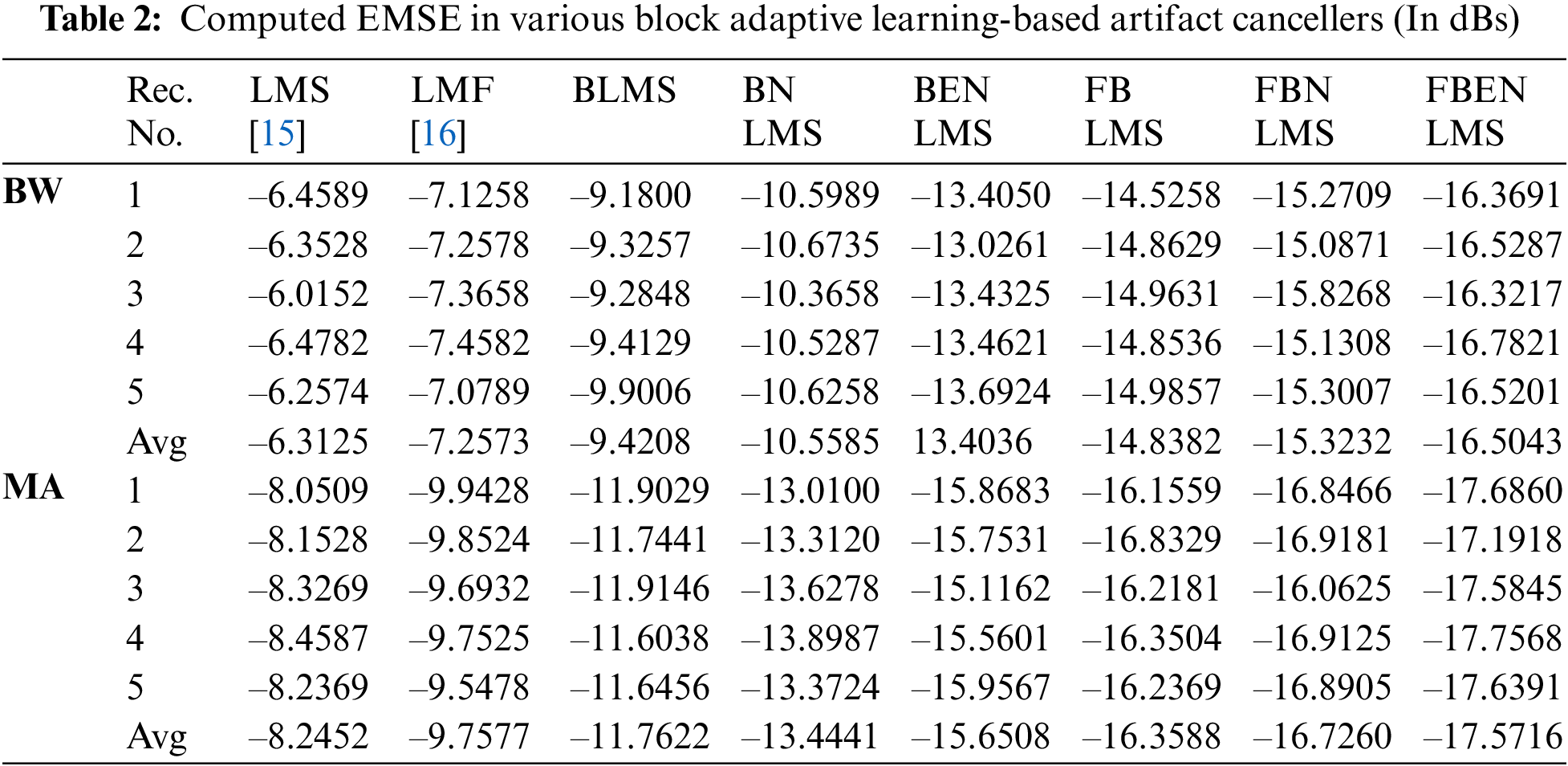
From Figs. 4c–4e it is observed that the amplitude of the TEB signals is decreased due to signal averaging. This in turn decreases the SNRI in the time domain-based block processing. The problem of signal averaging could be avoided using frequency domain analysis, where better filtering ability can be achieved. More accurate estimate of gradient vector is used in BLMS because of time averaging and estimation accuracy increasing as the block size P is increased. The filtering capability of BLMS based ANC is better when compared to LMS, moreover the smoothing capability of BLMS algorithm is better. In Fig. 5, difference signals after base line wander elimination with various block-based methods are presented. Fig. 6 illustrates the nature of EMSE in the BW elimination process. The experimental results confirm that FBENLMS based artifact elimination performs better than the other counterparts and is well suited for remote health care systems.

Figure 5: Difference signals after base line wander elimination (a) Real BW artifact, (b) difference signal after LMS based adaptive learning, (c) difference signal after BLMS based adaptive learning, (d) difference signal after BNLMS based adaptive learning, (e) difference signal after BENLMS based adaptive learning, (f) difference signal after FBLMS based adaptive learning, (g) difference signal after FBNLMS based adaptive learning, (h) difference signal after FBENLMS based adaptive learning

Figure 6: EMSE variations for BW cancellation using block adaptive learning algorithms

3.2 Adaptive Muscle Artifact Removal from TEB Signals

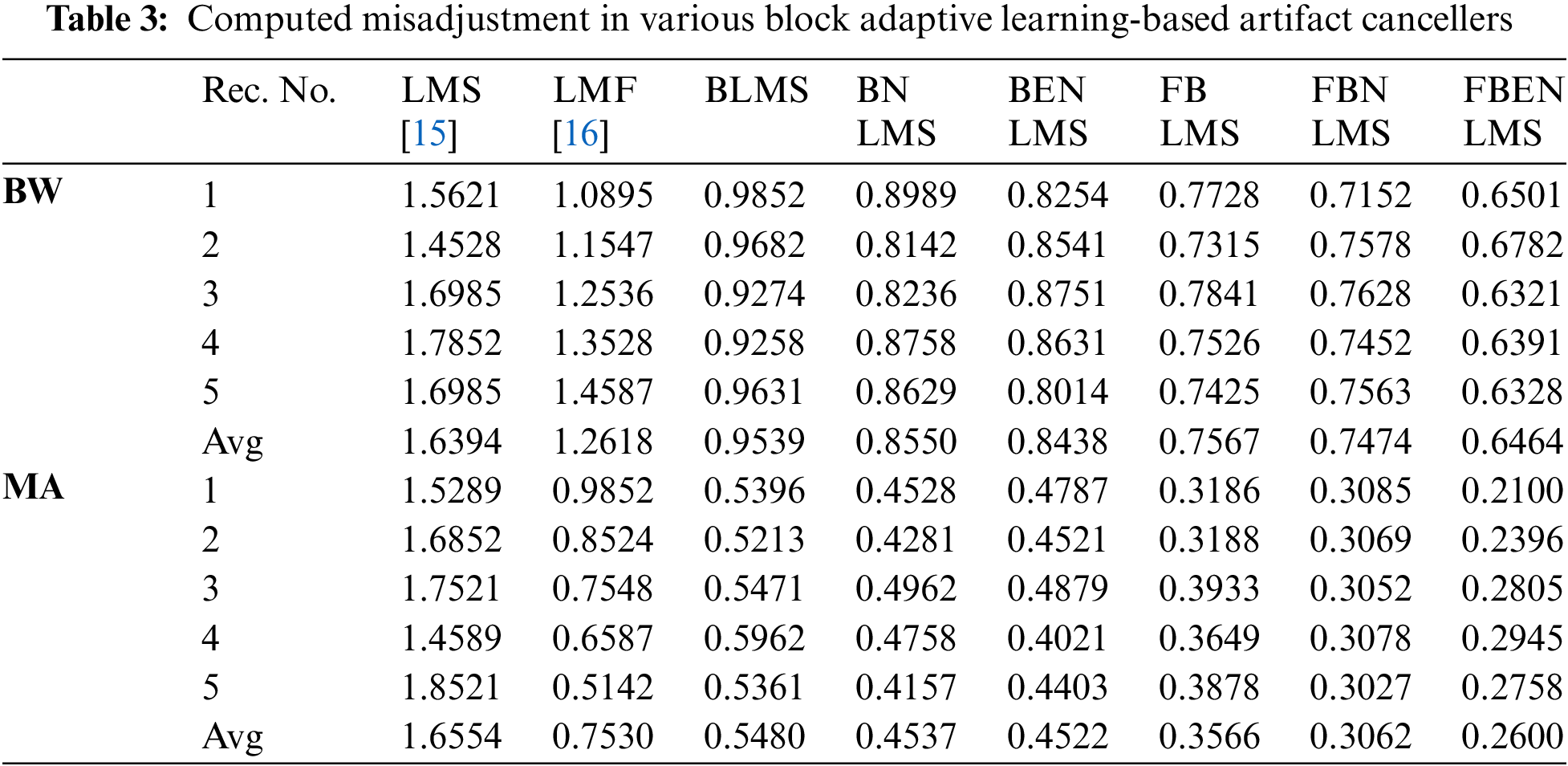
In these experiments the TEB contaminated with MA is given as input to the adaptive artifact canceller as shown in Fig. 1. The reference signal is a real MA obtained from MIT-BIH database. MA originally had a sampling frequency of 360 Hz and they are anti-alias resampled to 128 Hz in order to match sampling rate of the TEB. Various filter structures are developed using non overlapping based block adaptive learning techniques. The experimental results for MA removal using block processing are shown in Fig. 7, difference signals after muscle artifact elimination are shown in Fig. 8. The variations in EMSE are shown in Fig. 9. From Fig. 7, it is clear that the signal averaging due to block processing reduces the amplitude of the filtered signals. Even though the noise is eliminated but due to amplitude reduction, the calculated SNRI and other performance measures are less. The SNRI, EMSE, Mad are tabulated in Tabs. 1–3 respectively. Experimental results confirm that in the case of MA also FBENLMS eliminates the artifact component better than the other block adaptive learning algorithms.

Figure 7: Adaptive artifact cancellation results for muscle artefact (a) TEB with MA, (b) enhanced TEB due to LMS based adaptive learning, (c) enhanced TEB due to BLMS based adaptive learning, (d) enhanced TEB due to BNLMS based adaptive learning, (e) enhanced TEB due to BENLMS based adaptive learning, (f) enhanced TEB due to FBLMS based adaptive learning, (g) enhanced TEB due to FBNLMS based adaptive learning, (h) enhanced TEB due to FBENLMS based adaptive learning

Figure 8: Difference signals after muscle artifact elimination (a) Real muscle artifact, (b) difference signal after LMS based adaptive learning, (c) difference signal after BLMS based adaptive learning, (d) difference signal after BNLMS based adaptive learning, (e) difference signal after BENLMS based adaptive learning, (f) difference signal after FBLMS based adaptive learning, (g) difference signal after FBNLMS based adaptive learning, (h) difference signal after FBENLMS based adaptive learning

Figure 9: EMSE variations for MA cancellation using block adaptive learning algorithms

4  Conclusion

In this paper, we have developed several block adaptive learning algorithms in both TD and FD to eliminate physiological artifacts from TEB signals. The proposed implementations are improved by including normalization with respect to data and error components. This demonstrates significant improvements in filtering ability and convergence characteristics. Again, the frequency domain analysis also presented to avoid signal averaging due to block processing. To judge the performance of the proposed block adaptive learning methods, several performance measures like SNRI, EMSE, Mad, and convergence characteristics are determined. Among the considered classes of block-based techniques, the frequency domain block error normalized adaptive learning algorithm proved that this technique is better than other block processed algorithms. This technique seems to be suitable for implementing real-time remote health monitoring devices in a medical telemetry network.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  World Health Organization, World Health Statistics 2018—A Wealth of Information on Global Public Health. Geneva: World Health Organization, 2018. [Google Scholar]

 2.  World Health Organization cardiovascular disease risk charts: Revised models to estimate risk in 21 global regionsLancet Global Health, vol. 7, no. 10, pp. 1332–1345, 2019. [Google Scholar]

 3.  Heart Disease and Stroke Statistics—2020 Update: A Report from the American Heart Association, Circulation, vol. 141, no. 9, pp. 139–156, 2020. [Google Scholar]

 4.  F. Massari, “Bioimpedance vector analysis predicts hospital length of stay in acute heart failure,” Nutrition, vol. 61, pp. 56–60, 2019. [Google Scholar]

 5.  M. Panagiotou, I. Vogiatzis, G. Jayasekera, Z. Louvaris, A. Mackenzie et al., “Validation of impedance cardiography in pulmonary arterial hypertension,” Clinical Physiology Functional Imaging, vol. 38, no. 2, pp. 254–260, 2018. [Google Scholar]

 6.  M. Sanders, S. Servaas and C. Slagt, “Accuracy and precision of non-invasive cardiac output monitoring by electrical cardiometry: A systematic review and meta-analysis,” Journal of Clinical Monitoring and Computing, vol. 33, no. 3, pp. 433–460, 2019. [Google Scholar]

 7.  L. Sangkum, “Minimally invasive or noninvasive cardiac output measurement: An update,” Journal of Anesthesia, vol. 30, no. 3, pp. 461–480, 2016. [Google Scholar]

 8.  J. Ho Shin, C. Rim Kim and K. Hyun Park, “Predicting clinical outcomes using phase angle as assessed by bioelectrical impedance analysis in maintenance hemodialysis patients,” Nutrition, vol. 41, pp. 7–13, 2017. [Google Scholar]

 9.  F. T. Wang, H. L. Chan, C. L. Wang, H. M. Jian and S. H. Lin, “Instantaneous respiratory estimation from thoracic impedance by empirical mode decomposition,” Sensors, vol. 15, no. 7, pp. 16372–16387, 2015. [Google Scholar]

10. S. F. Khalil, M. S. Mohktar and F. Ibrahim, “The theory and fundamentals of bioimpedance analysis in clinical status monitoring and diagnosis of diseases,” Sensors, vol. 14, no. 6, pp. 10895–10928, 2014. [Google Scholar]

11. B. Saugel, M. Cecconi and L. A. Hajjar, “Noninvasive cardiac output monitoring in cardiothoracic surgery patients: Available methods and future directions,” Journal of Cardiothoracic and Vascular Anesthesia, vol. 33, no. 6, pp. 1742–1752, 2019. [Google Scholar]

12. L. S. Nguyen and P. Squara, “Non-invasive monitoring of cardiac output in critical care medicine,” Frontiers of Medicine, vol. 20, no. 4, pp. 1–8, 2017. [Google Scholar]

13. G. L. Yung, P. F. Fedullo, K. Kinninger, W. Johnson and R. N. Channick, “Comparison of impedance cardiography to direct fick and thermodilution cardiac output determination in pulmonary arterial hypertension,” Congestive Heart Failure, vol. 10, no. s2, pp. 7–10, 2004. [Google Scholar]

14. R. D. Smith, P. Levy and C. M. Ferrario, “Value of noninvasive hemodynamics to achieve blood pressure control in hypertensive subjects,” Hypertension, vol. 47, no. 4, pp. 771–777, 2006. [Google Scholar]

15. S. S. Mirza and M. Z. Ur Rahman, “Efficient adaptive filtering techniques for thoracic electrical bio-impedance analysis in health care systems,” Journal of Medical Imaging and Health Informatics, vol. 7, no. 6, pp. 1126–1138, 2017. [Google Scholar]

16. M. Z. U. Rahman and S. S. Mirza, “Process techniques for human thoracic electrical bio-impedance signal in remote healthcare systems,” Healthcare Technology Letters, vol. 3, no. 2, pp. 124–128, 2016. [Google Scholar]

17. A. Sulthana, M. Z. U. Rahman and S. S. Mirza, “An efficient Kalman noise canceller for cardiac signal analysis in modern telecardiology systems,” IEEE Access, vol. 6, pp. 34616–34630, 2018. [Google Scholar]

18. M. D. N. Salman, P. Trinatha Rao and M. D. Z. U. Rahman, “Novel logarithmic reference free adaptive signal enhancers for ECG analysis of wireless health care monitoring systems,” IEEE Access, vol. 6, pp. 46382–46395, 2018. [Google Scholar]

19. C. S. L. Prasanna and M. Z. U. Rahman, “Noise cancellation in brain waves using a new diffusion normalized least power-based algorithm for brain computer interface applications,” Measurement: Sensors, vol. 14, no. 3, pp. 1–8, 2021. [Google Scholar]

20. G. V. S. Karthik, S. Y. Fathima, M. Z. U. Rahman, S. R. Ahamed and A. Lay-Ekuakille, “Efficient signal conditioning techniques for brain activity in remote health monitoring network,” IEEE Sensors Journal, vol. 13, no. 9, pp. 3276–3283, 2013. [Google Scholar]

21. M. Z. U. Rahman, R. A. Shaik and D. V. R. K. Reddy, “Efficient and simplified adaptive noise cancellers for ECG sensor based remote health monitoring,” IEEE Sensors Journal, vol. 12, no. 3, pp. 566–573, 2012. [Google Scholar]

22. X. R. Zhang, W. F. Zhang, W. Sun, X. M. Sun and S. K. Jha, “A robust 3-D medical water marking based on wavelet transform for data protection,” Computer Systems Science & Engineering, vol. 41, no. 3, pp. 1043–1056, 2022. [Google Scholar]

23. X. R. Zhang, X. Sun, X. M. Sun, W. Sun and S. K. Jha, “Robust reversible audio watermarking scheme for telemedicine and privacy protection,” Computers, Materials & Continua, vol. 71, no. 2, pp. 3035–3050, 2022. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.