DOI:10.32604/cmc.2022.027523

| Computers, Materials & Continua DOI:10.32604/cmc.2022.027523 |  |
| Article |
Intelligent Networks for Chaotic Fractional-Order Nonlinear Financial Model
1Department of Statistics, Faculty of Science, Khon Kaen University, Khon Kaen 40002, Thailand
2Department of Mathematics and Statistics, Hazara University, Mansehra, Pakistan
3Department of Electrical Engineering, COMSATS Institute of Information Technology, Attock, Pakistan
4Department of Mathematics and Engineering Physics, Faculty of Engineering, Mansoura University, Egypt
5Université Française D’Egypte, Ismailia Desert Road, El-Shorouk, Cairo, Egypt
6Department of Mathematics, Faculty of Science, Khon Kaen University, Khon Kaen 40002, Thailand
*Corresponding Author: Thongchai Botmart. Email: thongbo@kku.ac.th
Received: 19 January 2022; Accepted: 16 March 2022
Abstract: The purpose of this paper is to present a numerical approach based on the artificial neural networks (ANNs) for solving a novel fractional chaotic financial model that represents the effect of memory and chaos in the presented system. The method is constructed with the combination of the ANNs along with the Levenberg-Marquardt backpropagation (LMB), named the ANNs-LMB. This technique is tested for solving the novel problem for three cases of the fractional-order values and the obtained results are compared with the reference solution. Fifteen numbers neurons have been used to solve the fractional-order chaotic financial model. The selection of the data to solve the fractional-order chaotic financial model are selected as 75% for training, 10% for testing, and 15% for certification. The results indicate that the presented approximate solutions fit exactly with the reference solution and the method is effective and precise. The obtained results are testified to reduce the mean square error (MSE) for solving the fractional model and verified through the various measures including correlation, MSE, regression histogram of the errors, and state transition (ST).
Keywords: Financial model; chaotic; fractional-order; reference dataset; artificial neural networks; levenberg-marquardt backpropagation
During the last few years, the terminology of econophysics has been used to simulate real-life models describing the complex behavior of financial models and economic systems. This terminology was invented by those researchers who are working in the field of simulating financial and economic systems. Economic data, erratic and microeconomic fluctuations, irregular growth, and overlapping developments of economic systems are some of these newly rising topics in the financial field that needs some new tools to understand. The researchers are describing these models in a simple form without the effect of any external forces and undergo stationary equilibrium behavior. Then, the system is augmented with some shock variables whose behavior can be assumed to come from external forces outside the system along with their effects. These variables are displaying irregular behavior with the effect of these forces is assumed to be random. These variables may have various forms including weather behaviors, political events, and human or other related factors. The irregular behavior may be translated through chaotic behavior in the economic system and this may provide some explanations to the complexity of the behavior of these systems [1]. This was one of the main reasons that reach recently tries to invest deep in the application of Chaotic behaviors in similar systems.
Fractional calculus has been used in mathematical modeling in science, engineering, and biology since it was first established back in the last century. It has proven to be an effective tool to simulate such problems and to better understand the dynamics of various physical processes and systems [2,3]. These systems include biological forms, fluid dynamics, neurons processes, analytical chemistry, and life science [4]. Likewise, it has been used to simulate the financial models of regular and chaotic behaviors. For example, Wen et al. [5] investigated the complex evolution of some chaotic financial systems from the stability point of view of the fractional equilibrium point and the chaotic phenomenon. A brief preview of the application of fractional calculus in the field of finial systems was introduced in [6] by Tarasov. In addition, a new algorithm based on the definition of the variable-order fractional calculus was examined for a chaotic financial system by Soradi-Zeid in [7]. A numerical verification and circuit realization in the perspective of fractional calculus have been presented in [8] by Chen et al. The application of the fractional calculus has been whitened to expand to more physical as in [9] while dealing with problems in the field of nanotechnology. Kulish et al. in [10] investigated the application of fractional calculus in the field of fluid mechanics through some model problems. The branch of viseloacitity has its share in simulating through the fractional calculus and was studied in [11] by Bagley et al. by proposing a well-known Bagley-Torvik equation. Some new insights through novel results were found while simulating some of the basic problems in the view of fractional calculus by Rossikhin et al. in [12]. Other related problems of fractional order include economic systems [13], solid propellants simulation [14], and duffing type equations [15], and other nonlinear systems of paramount significance [16–20].
This study aims to present a real-life financial model with the effect of memory and chaos in the presented system. The memory effect can be witnessed clearly in the fractional-order models and this was the reason behind studying the presented model. The presence of financial variables such as the foreign exchange rate, interest rates, and stock market prices has a long memory effect [21,22]. The basic model of the fractional incommensurate-order model can take the following form:
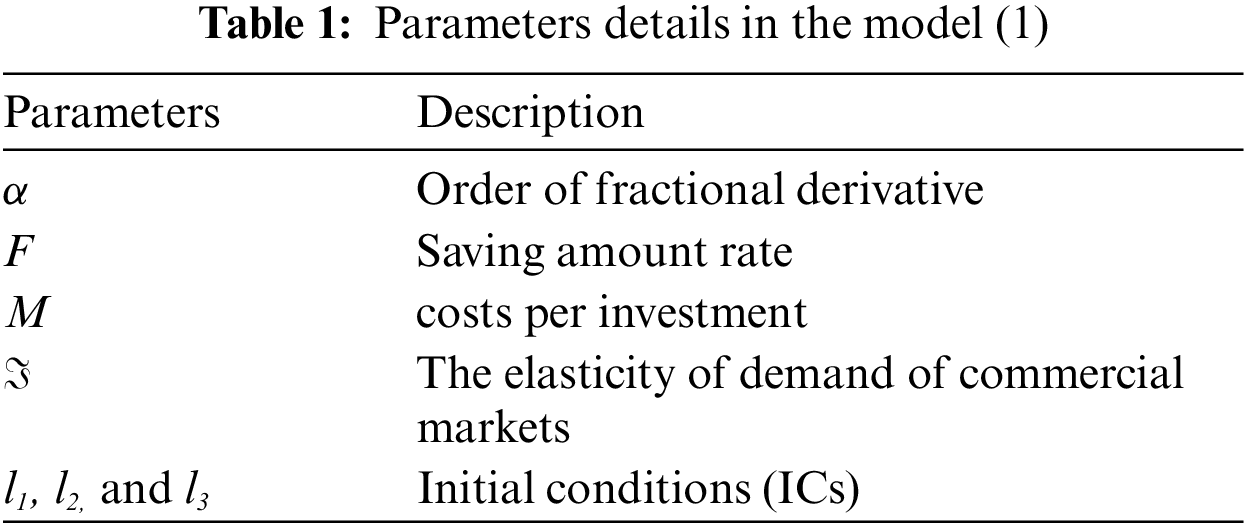
The detail of each parameter is presented in Tab 1 as:
With the importance of model (1) in the field of financial systems, the need for an effective tool for simulating this was a priority. One of the most effective methods that have been developed is artificial neural networks (ANNs). This tool has been used extensively during the last few years to simulate stiff and complicated problems. For example, a singular model with Neumann–robin and Dirichlet was investigated in [23] by Sabir et.al using the last-mentioned method. The application of this effective approach has been used in the field of neuroscientists as in [24]. The application of the ANNs technique has been used in the field of medicine as well. For example, El-Mahelawi et al. in [25] investigated the simulation of the models representing the classification of the types of tumors through applying this effective approach. Also, the method has some application in microgrids has been indicated in [26] by Lopez-Garcia et al. which proves to be a tool to help overcome said challenges in the electrical network. In addition to the last-mentioned areas of application, and has been used to simulate some of the small-world topologies as in [27]. Liu et al. in [28] investigated the application of the proposed technique in modeling composite materials revealing some of the new constitutive laws with some new potential solutions. Generating some urban and architectural designs which may help to customize some geometric data structures through trained ANN as in [29]. With these wide and several applications of this method, researchers have been trying to expand the application of the basic technique and apply some modifications to it to make it more suitable to other related more complex applied problems.
This work aims to solve the nonlinear chaotic financial system represented in Eq. (1) using a modification of the artificial neural networks (ANNs) method inspired from recent relevant reputed reported studies [30–32]. This modification includes the merging of the (ANNs) along with the Levenberg-Marquardt backpropagation (LMB), i.e., ANNs-LMB. This ANN-LMB is based on authentication, testing, and training of some sample data and the results proves the method to be accurate and reliable. The ANNs have proven to be an effective numerical tool to simulate such problems. For example, Raja et al. in [33] investigated the application of a novel stochastic computing paradigm for simulating the heat-conducting model that presents the distribution of heat in the human head representing these through a nonlinear singular problem to be able to better understand their dynamics. In addition, the ANNs procedures have been used to solve a nonlinear multi-singular third-order Emden–Fowler equation in [34] by Sabir et al. [35]. Also, Sabir et al. in [36] adopted a new solver based on the fractional Meyer neuro-evolution computing method for solving a doubly singular multi-fractional order Lane–Emden system. Other fields of application are pantograph models as in [37–39] and some fractional-order models [40,41]. The previously mentioned advantages have driven us to investigate more on the application of the existing technique for simulating the presented model. To the best of our knowledge, the ANNs-LMB is applied the first time to solve this model.
The novel features of the ANNs for solving the fractional order financial model are itemized as:
• A new stochastic numerical procedure with the aid of the ANNs-LMB method is adapted to simulate the chaotic financial models in the system (1).
• Three different cases based on the fractional-order have been presented to solve the chaotic financial models.
• The correction of the proposed scheme is observed through the comparison of the proposed and reference solutions.
• The absolute error (AE) is performed in good measures to authenticate the accuracy of the proposed ANNs-LMB solver.
• The combined features of the ANNs with the LMB enhance the accuracy of the obtained results in terms of error for solving the financial problem.
• The error histograms (EHs), MSE presentations, correlation metrics, and regression measures authenticate the novel computing stochastic numerical procedure based on ANNs-LMB.
The organization of the paper is as follows: Section 2 presents the numerical procedure for solving the chaotic financial models using the ANNs-LMB method. The performance of this novel technique is illustrated through several measures in tables and figures presented in Section 3. The conclusion for the work along with the future work can be found in Section 4.
In this section, the proposed method based on the ANNs-LMB is given in detail for solving the chaotic financial model. The main steps for solving the system can be categorized in the following main steps:
1. Some explanation regarding the use of the stochastic numerical-based ANNs-LMB technique is provided.
2. The implementation of the proposed technique for solving the chaotic financial model validates the exactness and effectiveness of the method for solving the chaotic financial system.
These steps for approximating the solution of the financial model with the proposed technique for simulating the financial model are illustrated in Fig. 1 via actions of the multilayer procedure. In addition, Fig. 2 shows the solution based on a single neuron based on SNNs-LMBT. The solution is presented through ‘nftool’ build-in command in ‘Matlab’ using the selection of data for solving the fractional-order chaotic financial model are selected as 75% for training, 10% for testing, and 15% for certification.

Figure 1: Workflow diagram of the proposed ANNs-LMB for the fractional-order chaotic financial model

Figure 2: Proposed framework of the single neuron
In this section, the performance of the obtained results is presented for solving problem 1 with different three cases using the proposed ANNs-LMB technique. The mathematical representation of each of the obtained cases is solved for
The ICs for system (2) is
The numerical simulations are done through the application of the proposed ANNs-LMB for solving the fractional-order chaotic financial model with the input span of [0, 1]. Fifteen numbers neurons have been used to solve the fractional-order chaotic financial model. The selection of the data to solve the fractional-order chaotic financial model are selected as 75% for training, 10% for testing, and 15% for certification. The performance of the obtained results is tested in Fig. 3.

Figure 3: Schematic diagram for the proposed technique for solving the financial chaotic system
The plotted graphs for solving the fractional financial system using the proposed technique are given in Figs. 4–8. The efficiency of the used technique is first demonstrated in Figs. 4a–4d using the performance and transitions of the method. The measures for the MSE are provided in Figs. 4a–4c and the values of the STs are given in Figs. 4d–4f for all three cases. It can be noticed from these figures that the best curves, training, and testing for case I are drawn at epoch 63 which produces an error between 4.93 × 10−10, 4.11 × 10−08, and 9.58 × 10−08, respectively for each case. Also, the gradient values for solving the financial system using the ANNs-LMB are found to be 9.52 × 10−08 for case I, 3.26 × 10−08 for case II, and 4.78 × 10−08 for case III. In addition, the last-mentioned performance measures showed by the graphical representation of the convergence based on the ANNs-LMB method can be observed in Figs. 5a–5f, which presents the fitting curves and the comparison and EHs for each of the presented three cases. This validates the obtained results and their comparison with the reference solutions. It can be observed from Figs. 5a–5c, which demonstrates the comparison of the obtained output results through authentication, testing, and training for the ANNs-LMB technique that the comparison is the best fitting for all three cases. Also Figs. 5d–5f gives the EHs values for the three cases and we can notice that the maximum EHs for case I are around −8.3 × 10−05, 1.7 × 10−05 and 6.69 × 10−05 compared to −9.3 × 10−05, 6.97 × 10−05 and 1.24 × 10−04 for case II and finally, −4.5 × 10−05, −4.5 × 10−06 and 3.61 × 10−05 for case III. The correlation measures of all three cases for solving the fractional financial model are illustrated in Figs. 6–8 and based on that it indicates the correctness of the proposed ANNs-LMB technique based on the verification, training, and testing. Tab. 2 gives the training, epochs, authentication, testing, backpropagation measures, and complexity for solving the fractional financial model using the ANNs-LMB method.


Figure 4: MSE and state transitions to solve the chaotic financial system


Figure 5: Comparisons and EHs values for solving problem (2) using ANNs-LMB

Figure 6: Regression measures for case I using the ANNs-LMB

Figure 7: Regression measures for case II using the ANNs-LMB


Figure 8: Regression measures for case III using the ANNs-LMB

The plot of the comparison for different cases is illustrated in Figs. 9 and 10 for solving the chaotic financial model. The obtained results and the reference solutions overlapped, which indicates that the proposed technique is efficient in simulating the chaotic financial model using the ANNs-LMB. Fig. 9 gives the obtained results for the three cases compared to the reference solutions for solving the chaotic financial model. Fig. 10 provides the measures of the absolute error for the three cases using the ANNs-LMB method. It can be noted that the presented solutions using the ANNs-LMB method are precise and accurate for solving the chaotic financial model.

Figure 9: Comparison of the results for the financial system
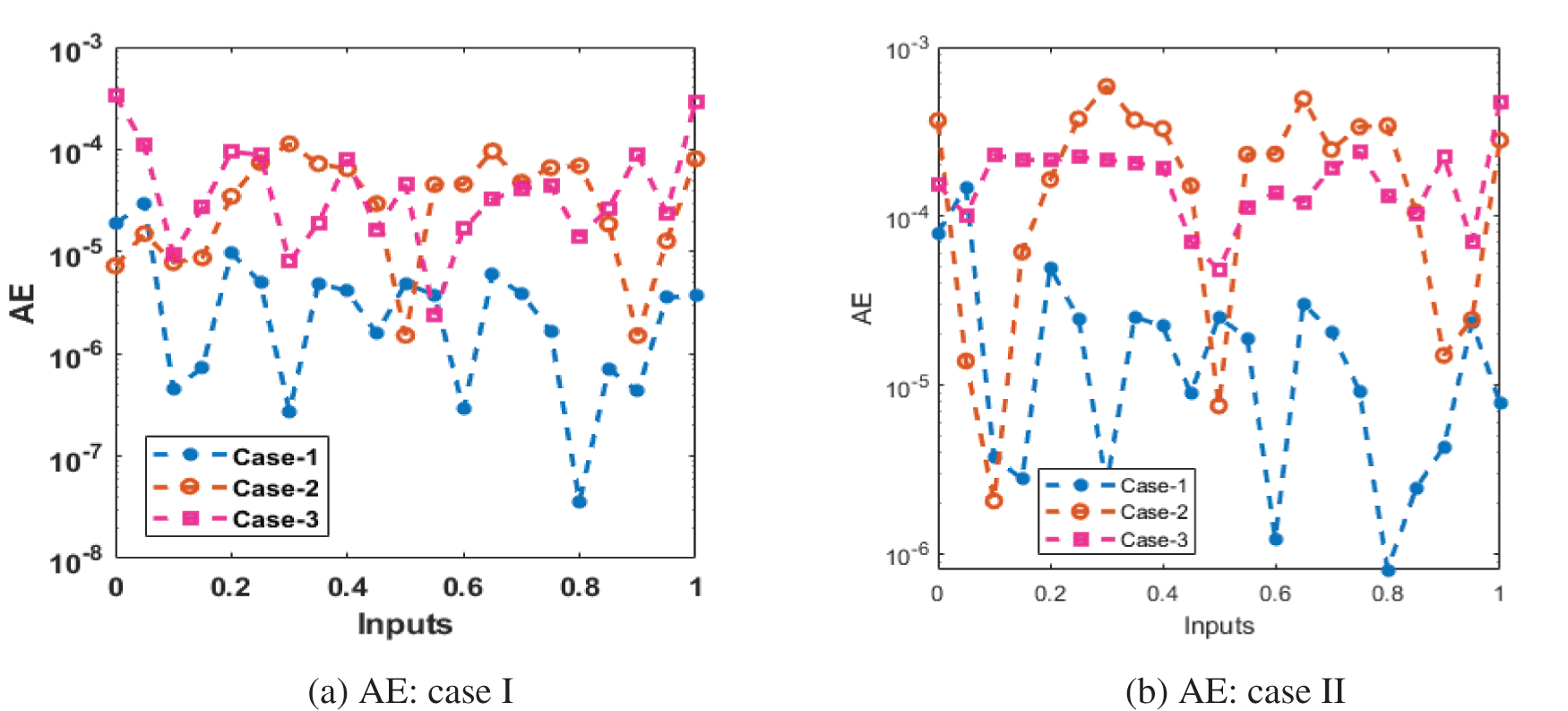

Figure 10: Measure of AE for the financial system
The purpose of this article is to investigate the dynamics of the fractional nonlinear chaotic financial system using a new modification of the ANNs-LMB technique. This technique is performed using the form of the ANNs method combined with the LMB for simulating the proposed system. The fractional-order derivative is defined in the Caputo sense and the method is tested for several values of the fractional-order through three cases. The solutions of the nonlinear, fractional order, financial differential model is not easy to present, however, ANN-LMB is an efficient solver to solve these types of models. The solution is presented through ‘nftool’ build-in command in ‘Matlab’ using the selection of data for solving the fractional-order chaotic financial model are selected as 75% for training, 10% for testing, and 15% for certification. The results acquired by the ANNs-LMB method are demonstrated through the graphs representing the proportional measures of MSE, correlation, EHs, regression, and STs. This indicates that the proposed algorithm is effective in simulating the fractional system with high performance and can be extended in the future for solving the different problems related to biology, fluid mechanics as well as other problems in science and engineering [42–46].
Funding Statement: This research received funding support from the NSRF via the Program Management Unit for Human Resources & Institutional Development, Research and Innovation (Grant Number B05F640088).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. A. Serletis, “Is there chaos in economic time series,” The Canadian Journal of Economics/Revue Canadienne D’Economique, vol. 29, pp. 210–212, 1996. [Google Scholar]
2. P. Arena, Nonlinear Noninteger Order Circuits and Systems: An Introduction, vol. 38, Singapore: World Scientific Publishing Co. Pte. Ltd., 2000. [Google Scholar]
3. I. Podlubny, Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications, California, USA: Academic Press, 1998. [Google Scholar]
4. W. M. Ahma and R. El-Khazali, “Fractional-order dynamical models of love,” Chaos, Solitons & Fractals, vol. 33, no. 4, pp. 1367–1375, 2007. [Google Scholar]
5. C. Wen and J. Yang, “Complexity evolution of chaotic financial systems based on fractional calculus,” Chaos, Solitons & Fractals, vol. 128, pp. 242–251, 2019. [Google Scholar]
6. V. E. Tarasov, “On history of mathematical economics: Application of fractional calculus,” Mathematics, vol. 7, no. 6, pp. 1–28, 2019. [Google Scholar]
7. S. Soradi-Zeid, H. Jahanshahi, A. Yousefpour and S. Bekiros, “King algorithm: A novel optimization approach based on variable-order fractional calculus with application in chaotic financial systems,” Chaos, Solitons & Fractals, vol. 132, pp. 1–9, 2020. [Google Scholar]
8. S. B. Chen, H. Jahanshahi, O. A. Abba, J. E. Solís-Pérez, S. Bekiros et al., “The effect of market confidence on a financial system from the perspective of fractional calculus: Numerical investigation and circuit realization,” Chaos, Solitons & Fractals, vol. 140, pp. 1–15, 2020. [Google Scholar]
9. D. Baleanu, Z. B. Güvenç and J. T. Machado, New Trends in Nanotechnology and Fractional Calculus Applications, New York: Springer, 2010. [Google Scholar]
10. V. V. Kulish and J. L. Lage, “Application of fractional calculus to fluid mechanics,” Journal of Fluids Engineering, vol. 124, no. 3, pp. 803–806, 2002. [Google Scholar]
11. R. L. Bagley and P. J. Torvik, “A theoretical basis for the application of fractional calculus to viscoelasticity,” Journal of Rheology, vol. 27, no. 3, pp. 201–210, 1983. [Google Scholar]
12. Y. A. Rossikhin and M. V. Shitikova, “Application of fractional calculus for dynamic problems of solid mechanics: Novel trends and recent results,” Applied Mechanics Reviews, vol. 63, no. 1, pp. 1–52, 2010. [Google Scholar]
13. V. E. Tarasov, “Mathematical economics: Application of fractional calculus,” Mathematics, vol. 8, no. 5, pp. 1–3, 2020. [Google Scholar]
14. C. Fang, X. Shen, K. He, C. Yin, S. Li et al., “Application of fractional calculus methods to viscoelastic behaviors of solid propellants,” Philosophical Transactions of the Royal Society A, vol. 378, no. 2172, pp. 1–16, 2020. [Google Scholar]
15. Y. A. Z. I. D. Gouari, Z. O. U. B. I. R. Dahmani and I. Q. B. A. L. Jebril, “Application of fractional calculus on a new differential problem of duffing type,” Advances in Mathematics: Scientific Journal, vol. 9, no. 12, pp. 10989–11002, 2020. [Google Scholar]
16. J. Tariboon, S. K. Ntouyas and P. Agarwal, “New concepts of fractional quantum calculus and applications to impulsive fractional q-difference equations,” Advances in Difference Equations, vol. 2015, no. 1, pp. 1–19, 2015. [Google Scholar]
17. P. Agarwal and A. A. El-Sayed, “Non-standard finite difference and chebyshev collocation methods for solving fractional diffusion equation,” Physica A: Statistical Mechanics and Its Applications, vol. 500, pp. 40–49, 2018. [Google Scholar]
18. R. Singh, A. U. Rehman, M. Masud, H. A. Alhumyani, S. Mahajan et al., “Fractional order modeling and analysis of dynamics of stem cell differentiation in complex network,” AIMS Mathematics, vol. 7, no. 4, pp. 5175–5198, 2022. [Google Scholar]
19. A. Sunarto, P. Agarwal, J. Sulaiman and J. V. L. Chew, “Computational approach via half-sweep and preconditioned AOR for fractional diffusion,” Intelligent Automation and Soft Computing, vol. 31, no. 2, pp. 1173–1184, 2022. [Google Scholar]
20. M. Bataineh, M. Alaroud, S. Al-Omari and P. Agarwal, “Series representations for uncertain fractional IVPs in the fuzzy conformable fractional sense,” Entropy, vol. 23, no. 12, pp. 1–20, 2021. [Google Scholar]
21. B. J. West and S. Picozzi, “Fractional langevin model of memory in financial time series,” Physical Review E, vol. 65, no. 3, pp. 1–3, 2002. [Google Scholar]
22. E. Panas, “Long memory and chaotic models of prices on the London metal exchange,” Resources Policy, vol. 27, no. 4, pp. 235–246, 2001. [Google Scholar]
23. K. Nisar, Z. Sabir, M. A. Z. Raja, A. A. Ag Ibrahim, J. J. P. C. Rodrigues et al., “Artificial neural networks to solve the singular model with neumann–Robin, dirichlet and neumann boundary conditions,” Sensors, vol. 21, no. 19, pp. 1–15, 2021. [Google Scholar]
24. G. R. Yang and X. J. Wang, “Artificial neural networks for neuroscientists: A primer,” Neuron, vol. 107, no. 6, pp. 1048–1070, 2020. [Google Scholar]
25. J. K. El-Mahelawi, J. U. Abu-Daqah, R. I. Abu-Latifa, B. S. Abu-Nasser and S. S. Abu-Naser, “Tumor classification using artificial neural networks,” International Journal of Academic Engineering Research, vol. 4, no. 11, pp. 8–15, 2020. [Google Scholar]
26. T. B. Lopez-Garcia, A. Coronado-Mendoza and J. A. Domínguez-Navarro, “Artificial neural networks in microgrids: A review,” Engineering Applications of Artificial Intelligence, vol. 95, pp. 1–14, 2020. [Google Scholar]
27. S. Kaviani and I. Sohn, “Application of complex systems topologies in artificial neural networks optimization: An overview,” Expert Systems with Applications, vol. 180, pp. 1–14, 2021. [Google Scholar]
28. X. Liu, S. Tian, F. Tao and W. Yu, “A review of artificial neural networks in the constitutive modeling of composite materials,” Composites Part B: Engineering, vol. 224, pp. 1–15, 2021. [Google Scholar]
29. H. Zheng and P. F. Yuan, “A generative architectural and urban design method through artificial neural networks,” Building and Environment, vol. 205, pp. 1–16, 2021. [Google Scholar]
30. S. R. K. Somayaji, M. Alazab, M. K. Manoj, A. Bucchiarone, C. L. Chowdhary et al., “A framework for prediction and storage of battery life in IoT devices using DNN and blockchain,” in 2020 IEEE Globecom Workshops (GC Wkshps), Taipei, Taiwan, pp. 1–6, 2020. [Google Scholar]
31. S. Bhattacharya, P. K. R. Maddikunta, I. Meenakshisundaram, T. R. Gadekallu, S. Sharma et al., “Deep neural networks based approach for battery life prediction,” Computers, Materials & Continua, vol. 69, pp. 2599–2615, 2021. [Google Scholar]
32. Z. Sabir, T. Botmart, M. A. Z. Raja, R. Sadat, M. R. Ali et al., “Artificial neural network scheme to solve the nonlinear influenza disease model,” Biomedical Signal Processing and Control, vol. 75, no. 103594, pp. 1–13, 2022. [Google Scholar]
33. M. A. Z. Raja, M. Umar, Z. Sabir, J. A. Khan and D. Baleanu, “A new stochastic computing paradigm for the dynamics of nonlinear singular heat conduction model of the human head,” The European Physical Journal Plus, vol. 133, no. 9, pp. 1–21, 2018. [Google Scholar]
34. Z. Sabir, M. Umar, J. L. Guirao, M. Shoaib and M. A. Z. Raja, “Integrated intelligent computing paradigm for nonlinear multi-singular third-order emden–Fowler equation,” Neural Computing and Applications, vol. 33, no. 8, pp. 3417–3436, 2021. [Google Scholar]
35. M. A. Z. Raja, J. Mehmood, Z. Sabir, A. K. Nasab and M. A. Manzar, “Numerical solution of doubly singular nonlinear systems using neural networks-based integrated intelligent computing,” Neural Computing and Applications, vol. 31, no. 3, pp. 793–812, 2019. [Google Scholar]
36. Z. Sabir, M. A. Z. Raja, M. Shoaib and J. G. Aguilar, “FMNEICS: Fractional meyer neuro-evolution-based intelligent computing solver for doubly singular multi-fractional order lane–Emden system,” Computational and Applied Mathematics, vol. 39, no. 4, pp. 1–18, 2020. [Google Scholar]
37. Z. Sabir, J. L. Guirao and T. Saeed, “Solving a novel designed second order nonlinear lane–Emden delay differential model using the heuristic techniques,” Applied Soft Computing, vol. 102, pp. 1–12, 2021. [Google Scholar]
38. Z. Sabir, D. Baleanu, M. A. Z. Raja and J. L. Guirao, “Design of neuro-swarming heuristic solver for multi-pantograph singular delay differential equation,” Fractals, vol. 29, no. 5, pp. 2140022, 2021. [Google Scholar]
39. Z. Sabir, M. A. Z. Raja, H. A. Wahab, M. Shoaib and J. G. Aguilar, “Integrated neuro-evolution heuristic with sequential quadratic programming for second-order prediction differential models,” Numerical Methods for Partial Differential Equations, vol. 2020, pp. 1–17, 2020. [Google Scholar]
40. Z. Sabir, M. A. Z. Raja and D. Baleanu, “Fractional mayer neuro-swarm heuristic solver for multi-fractional order doubly singular model based on lane-emden equation,” Fractals, vol. 29, no. 5, pp. 2140017, 2021. [Google Scholar]
41. Z. Sabir, M. A. Z. Raja, J. L. Guirao and M. Shoaib, “A novel design of fractional meyer wavelet neural networks with application to the nonlinear singular fractional lane-emden systems,” Alexandria Engineering Journal, vol. 60, no. 2, pp. 2641–2659, 2021. [Google Scholar]
42. M. T. Gençoğlu and P. Agarwal, “Use of quantum differential equations in sonic processes,” Applied Mathematics and Nonlinear Sciences, vol. 6, no. 1, pp. 21–28, 2021. [Google Scholar]
43. H. M. Baskonus, H. Bulut and T. A. Sulaiman, “New complex hyperbolic structures to the lonngren-wave equation by using sine-gordon expansion method,” Applied Mathematics and Nonlinear Sciences, vol. 4, no. 1, pp. 129–138, 2019. [Google Scholar]
44. E. İlhan and İ.O.A. Kıymaz, “Generalization of truncated M-fractional derivative and applications to fractional differential equations,” Applied Mathematics and Nonlinear Sciences, vol. 5, no. 1, pp. 171–188, 2020. [Google Scholar]
45. E.İ. Eskitaşçıoğlu, M. B. Aktaş and H. M. Baskonus, “New complex and hyperbolic forms for ablowitz–Kaup–Newell–Segur wave equation with fourth order,” Applied Mathematics and Nonlinear Sciences, vol. 4, no. 1, pp. 93–100, 2019. [Google Scholar]
46. A. Yokuş and S. Gülbahar, “Numerical solutions with linearization techniques of the fractional harry Dym equation,” Applied Mathematics and Nonlinear Sciences, vol. 4, no. 1, pp. 35–42, 2019. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |