Computers, Materials & Continua DOI:10.32604/cmc.2022.027048
Article

Evolutionary Algorithsm with Machine Learning Based Epileptic Seizure Detection Model

Manar Ahmed Hamza1,*, Noha Negm2, Shaha Al-Otaibi3, Amel A. Alhussan4, Mesfer Al Duhayyim5, Fuad Ali Mohammed Al-Yarimi2, Mohammed Rizwanullah1 and Ishfaq Yaseen1

1Department of Computer and Self Development, Preparatory Year Deanship, Prince Sattam bin Abdulaziz University, 16278, AlKharj, Saudi Arabia
2Department of Computer Science, College of Science and Arts, King Khalid University, Mahayil, Asir, 62529, Saudi Arabia
3Department of Information Systems, College of Computer and Information Sciences, Princess Nourah Bint Abdulrahman University, Riyadh, 11671, Saudi Arabia
4Department of Computer Sciences, College of Computer and Information Sciences, Princess Nourah Bint Abdulrahman University, Riyadh, 11671, Saudi Arabia
5Department of Natural and Applied Sciences, College of Community - Aflaj, Prince Sattam bin Abdulaziz University, 16278, Saudi Arabia
* Corresponding Author: Manar Ahmed Hamza. Email: ma.hamza@psau.edu.sa
Received: 09 January 2022; Accepted: 04 March 2022

Abstract: Machine learning (ML) becomes a familiar topic among decision makers in several domains, particularly healthcare. Effective design of ML models assists to detect and classify the occurrence of diseases using healthcare data. Besides, the parameter tuning of the ML models is also essential to accomplish effective classification results. This article develops a novel red colobuses monkey optimization with kernel extreme learning machine (RCMO-KELM) technique for epileptic seizure detection and classification. The proposed RCMO-KELM technique initially extracts the chaotic, time, and frequency domain features in the actual EEG signals. In addition, the min-max normalization approach is employed for the pre-processing of the EEG signals. Moreover, KELM model is used for the detection and classification of epileptic seizures utilizing EEG signal. Furthermore, the RCMO technique was utilized for the optimal parameter tuning of the KELM technique in such a way that the overall detection outcomes can be considerably enhanced. The experimental result analysis of the RCMO-KELM technique has been examined using benchmark dataset and the results are inspected under several aspects. The comparative result analysis reported the better outcomes of the RCMO-KELM technique over the recent approaches with the accuy of 0.956.

Keywords: Epileptic seizures; eeg signals; machine learning; kelm; parameter tuning; rcmo algorithm

1  Introduction

Machine Learning (ML) method is a subarea of artificial intelligence (AI) technique, where the term represents the capacity of information technology (IT) system to independently find solutions to the problem by recognizing patterns in data bases. The ML method allows IT systems to identify patterns on the basis of current datasets and algorithms and develop satisfactory solution concepts. Thus, in ML method, artificial knowledge is created on an experience basis [1]. In ML, mathematical and statistical models are utilized for learning datasets. There are two major schemes i.e., symbolic and sub-symbolic models. During symbolic system, e.g., propositional system where the knowledge content, that is the induced rules and they are explicitly characterized, while sub-symbolic system is artificial neuronal network [2]. It works on the principles of human brain, where the knowledge content is implicitly characterized. The key problems of ML for big data are high speed of streaming data, largescale of data, different types of data, incomplete and uncertain data. The three major kinds of ML are reinforcement, supervised, and unsupervised learning.

Epilepsy is a common brain disorder, represented as recurring seizure [3]. Around 50 million people worldwide suffer from epilepsy, and 80% of them are in developing nations. Yearly, over 2 million new cases of epilepsy are detected across the world. Electroencephalogram (EEG) signal is extensively employed for detecting epilepsy by recording the brain's electrical activities directly [4]. Generally, seizure happens unpredictably and infrequently, an automatic diagnosis scheme which is capable of classifying epileptic EEG signal from normal one is extremely useful in making diagnosis. In this method, the recorded EEG signal is the input, whereas the classification of EEG signal is the output. In general, two stages are included in an automatic diagnoses method: (i) the feature extraction from EEG input signal and (ii) the classification of feature extraction for seizure diagnosis [5]. Various classification technique has been employed for the automatic diagnosis of seizure. Generally, the experiment result shows that EEG signal contains useful feature for the diagnosis of seizure event and that most automatic seizure diagnosis system is very efficient [6].

The major problem in the automated diagnosis of epileptic seizures is selecting the distinguishing feature to differentiate among distinct phases (involving ictal, pre-ictal) [7]. But, in the earlier studies, initially, time-frequency, several time, frequency, and statistical features are extracted, later, the optimal discriminator feature is chosen manually or utilizing traditional feature selection (FS) method that is a time-consuming process that demands higher computation difficulty because of higher dimension and are computationally intensive and are typically not strong [8]. Moreover, the optimal feature in one case/subject mayn't be regarded as optimal for other ones. Thus, a generalized model which learns the appropriate feature corresponds to all the cases/subjects is important.

Kaur et al. [9], proposed a secure and smart medical data scheme with advanced security and ML mechanisms for handling big data in healthcare field. The novelty lies in the integration of data security layer and optimum storage utilized for maintaining privacy and security. Distinct methods such as activity monitoring, masking encryption, dynamic data encryption, end point validation, and granular access control were integrated. Abdelaziz et al. [10] presented an approach for HCS based cloud environments with Parallel (PPSO) to enhance the selection of virtual machine (VM). Additionally, a new method for chronic kidney disease (CKD) prediction and detection is presented for measuring the efficiency of these VM models. The predictive method of CKD is performed by two successive methods, that is, logistic regression (LR) and neural network (NN).

Nilashi et al. [11] a prediction model has been developed for the diagnosis of heart disease with ML method. Then, the presented model is designed by supervised and unsupervised learning models. Particularly, the study is based on principal component analysis (PCA), Self-Organizing Map, Fuzzy support vector machine (FSVM), and two imputation methods for missing value imputation. Moreover, employing the incremental FSVM and PCA to incremental learning of the information for reducing the computational time of disease prediction.

Dinh et al. [12] estimate the capability of ML methods in diagnosing at-risk patients with laboratory results and find key parameters within the data that contributed to these diseases amongst the patients. With distinct feature sets and time-frames for the laboratory data, various ML methods have been estimated on the classification accuracy. Elhoseny et al. [13] presented an automatic heart disease (HD) diagnosis (AHDD) which incorporates a binary convolutional neural network (CNN) with multiagent feature wrapper (MAFW) method. The agent instructs the genetic algorithm (GA) to implement a global searching on HD feature and adjusts the weight at the time of early classification.

This article develops a novel red colobuses monkey optimization with kernel extreme learning machine (RCMO-KELM) technique for epileptic seizure detection and classification. The proposed RCMO-KELM technique initially extracts the features from the actual EEG signals and the min-max normalization approach is employed for the pre-processing. In addition, KELM model is used for the detection and classification of epileptic seizures utilizing EEG signals. Also, the RCMO technique was employed to the optimal parameter tuning of KELM model in such a way that the overall detection outcomes can be considerably enhanced. The experimental result analysis of the RCMO-KELM technique has been examined using benchmark dataset and the results are inspected under several aspects.

2  The Proposed Model

In this article, a novel RCMO-KELM technique has been developed for epileptic seizure detection and classification. The proposed RCMO-KELM technique initially extracts the chaotic, time, and frequency domain features in the actual EEG signal. Besides, the RCMO-KELM technique involves several stages of operations namely feature extraction, min-max normalization based preprocessing, KELM based classification, and RCMO based parameter tuning. Fig. 1 demonstrates the overall process of RCMO-KELM technique.

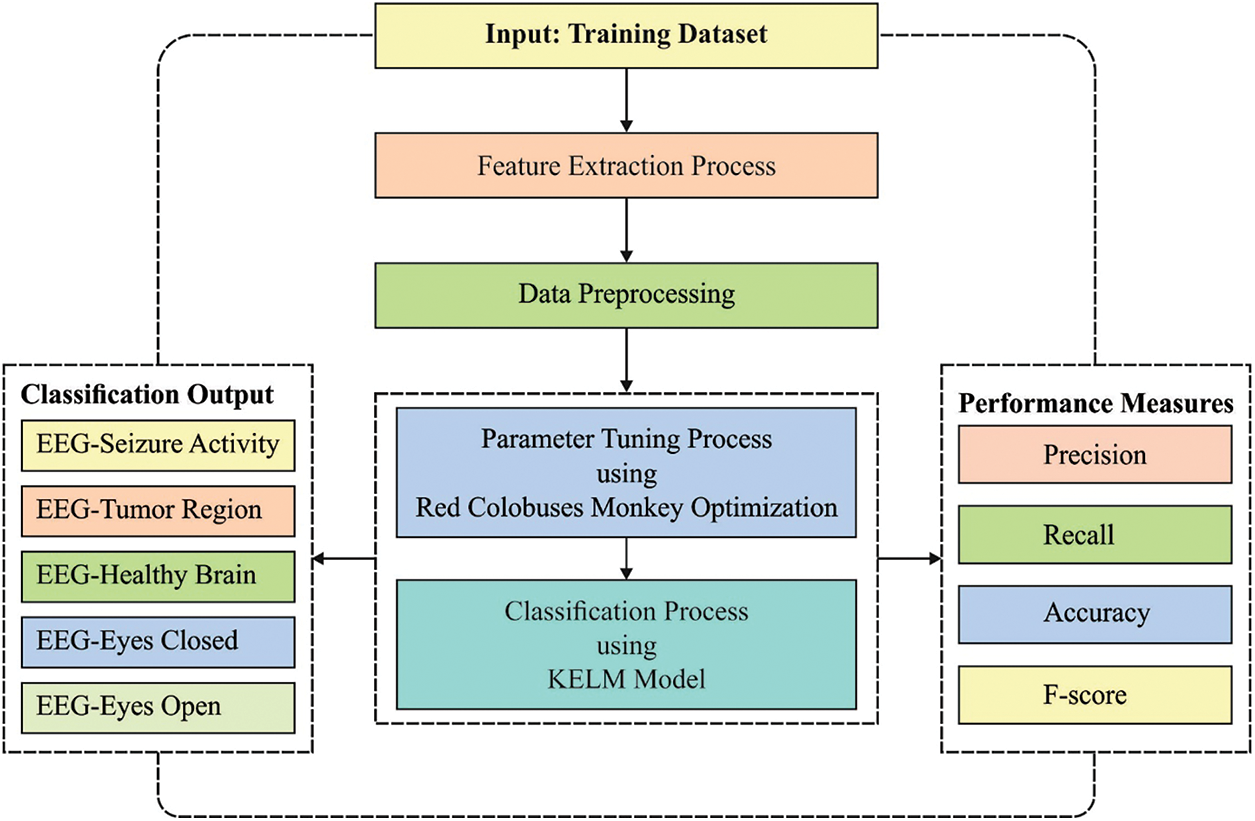
Figure 1: Overall process of RCMO-KELM technique

2.1 Feature Extraction

The proposed RCMO-KELM technique initially extracts the chaotic, time, and frequency domain features from the actual EEG signal. During all the raw EEG signals, there are 178 points. For extracting important data in these EEG signals, 31 distinct features are removed in these EEG signals to all the classes. These features are skewness, maximal value, clearance factor, minimal value, sample entropy, average value, shape factor, kurtosis, median, mod, fast Fourier transform (FFT) coefficients (first 15 values), approximate entropy, and Auto-Regressive (AR) coefficients (first 5 values).

2.2 Pre-processing

The procedure of normalized to raw input is an enhanced result of creating the data that is suitable to train. This approach rescales the resultant or feature in one range of values to a novel range of values. Most frequently, the feature was being rescaled to lie from the range of zero to one or from -l to 1. This rescale was accomplished frequently with utilize of linear interpretation equation as:

y′=(ymax−ymin)×(xi−xmin)(xmax−xmin)+xmin(1)

where (ymax−ymin)=0; if (xmax−xmin)=0 to a feature, it defines the continuous rate for that feature from the data. When the value of feature was detected with constant value from the data, it supposes that unconcerned as it doesn't provide some data to NN. When the min-max normalized was implemented, all the features lie from the novel range of values that turn remain similar. The normalized utilizing min-max is the advantage of maintaining every connection from the data exactly.

2.3 KELM Based Classification

Information on the ELM utilized by IPEELM technique. The ELM utilizes a Single hidden layer feedforward neural network (SLFN) with learning speed greater than typical feedforward network learning techniques (BP). Because of their simplicity, remarkable performance, and impressive efficiency on generalized, the ELM was executed from a variety of domains namely data classification, computer vision, control and robotics, bioinformatics, and system identification [14].

The resultant of SLFN containing L amount of hidden nodes are demonstrated in Eq. (2);

fL(x)=∑i=1L⁡βi.G(ai,bi,x);x∈Rn,ai,bi∈R(2)

where ai and bi implies the learning parameter of hidden nodes βi signifies the weight linking the ith hidden to resultant nodes. G(ai,bi,x) refers to the resultant of hidden nodes in terms of input χ. Usually, the additive hidden node with activation function (AF) has g(x):R→R. At time, G(ai,bi,x) was provided as;

G(ai,bi,xj)=g(ai.xj+bi);bi∈R,j=1,…,N(3)

Eq. (4) is expressed as:

Hβ=T(4)

where

H(a1,…,aL,b1,…,bL,x1,…,xN)

H=[g(a1⋅x1+b1)⋯g(aL⋅x1+bL)⋮⋯⋮g(a1⋅xN+b1)⋯g(aL⋅xN+bL)]N×L(5)

β=[β1T⋮βNT]L×mandT=[t1T⋮tNT]N×m(6)

H is named as hidden state resultant matrix of SLFN; the i−th column of H is jth hidden nodes resultant in terms of input x1,x2,…,xN.h(x)=G(a1,b1,x),…,g(aL,bL,x) is termed as hidden state feature map. The ith row of H signifies the hidden state feature map interms of ith input xi:h(xi). It is demonstrated that interpolation ability viewpoint when the AF g has infinitely differentiable from some interval the hidden state parameters are arbitrarily created [15]. Fig. 2 depicts the framework of KELM.

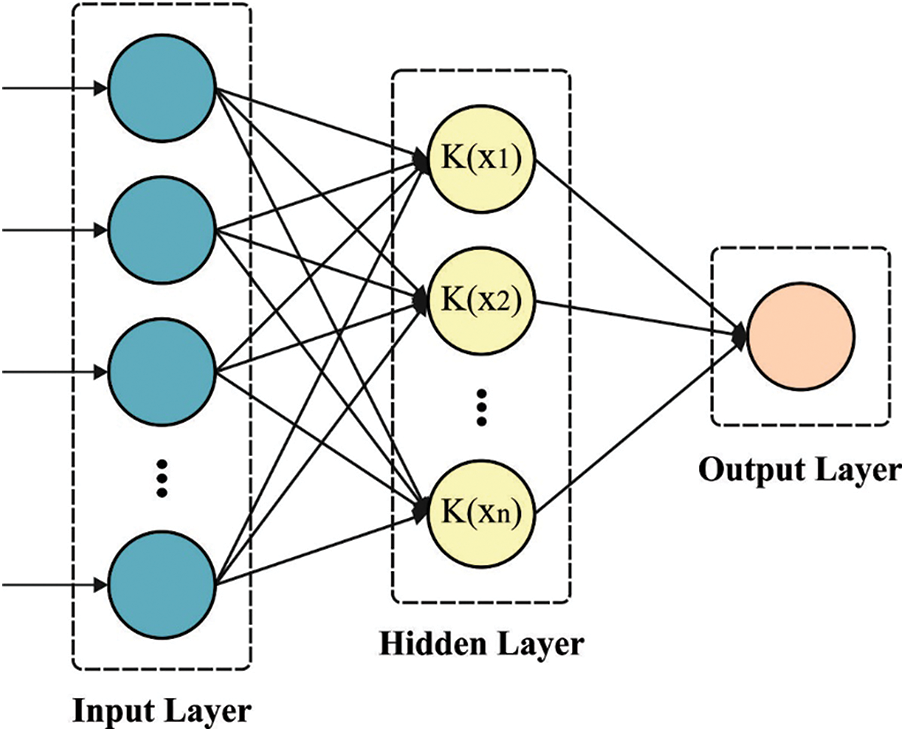
Figure 2: KELM structure

Activation functions (AF): The ELM defines a solution on unified learning structure to SLFN. The AF is also named as Transfer Function (TF) defines the result of node because of a provided input or group of inputs. Specifically, AFs were utilized for restricting and limiting the resultant value to particular finite value range. With respect to this calculation, AF is a vital play. At this point, it is examining the performances of AFs and implements them experimentally. This technique utilizes 4 distinct AFs. All the processors from the parallel calculation environment utilize or choose one of these AFs arbitrarily under the optimized procedure. This AFs utilized by IPE-ELM technique are:

Sigmoid function: is a mathematical process containing a characteristic “S”-shaped curve or sigmoid curve. During these conditions, sigmoidal function signifies to special case of logistic function, determined as the equation:

sig(x)=11+e−x(7)

where n refers the weighted sum of inputs. Its range is amongst zero and one. It can be simple for understanding and applying however it has main challenge. Primary, it is a vanishing gradient problem that means in specific cases, the gradient is vanishingly small, efficiently preventing the weight from altering its value. Secondary, its resultant is not zero centered. It generates gradient upgrades that get carried away from distinct directions.

Hyperbolic Tangent function: Its mathematic equation as:

tanh(x)=1−e−2x1+e−2x(8)

Its outcome is zero centered as their range was amongst −1 to 1, for instance, −1<output<1. Therefore, the optimization was simpler under this technique practically. It can be sometimes desired on Sigmoid function. However, it also undergoes vanishing gradient problems.

Sine function: Although, one of the AFs utilized from SLFN or deep neural network (DNN) are non-periodic, it is also utilized periodic functions like sine and cosine.

sin(x)=−1≤output≤1(9)

Whether a NN model with sine activation, the whole solutions are repeating periodically and the system is training to some resultant classes. The NN with one hidden state is estimated some function, provided the AF was improving and is set (with min and max) where The sine function could not improve function and input to sine function which has extremely lower and extremely higher are producing the similar outcome.

Cosine function: is utilized to compare with sine function however it could not be a regularly utilized AF. Its outcomes are experimental because of their periodic nature w.r.t.sine functions.

cos(x)=−1≤output≤1(10)

For N trained instance (xi,ti)∈Rd×Rm, while ri denotes the ith class vector coded as {−1,1}m, and thereby ELM using G(w,b,x) activation function can be arithmetically expressed by Hβ=T,

H=[G(w1⋅x1+b1)⋯G(wL⋅x1+bL)⋮⋯⋮G(w1⋅xN+b1)⋯G(wL⋅xN+bL)]N×L(11)

β=[β1T⋮βNT]L×m,T=[t1T⋮tNT]N×m(12)

Now, β is evaluated as: β^=H†T, whereas H† signifies the Moore Penrose generalized inverse of matrix H,H†=(HTH)−1HT if HTH denotes non-singular or H†=HT(HHT)−1 when HHT is non-singular. Usual, the spectral analysis case, N<L. To enhance the stability of ELM, β^ is evaluated as: β^=HT(1C+HHT)−1T whereas C represents a normalized coefficient. A kernel matrix for ELM is determined by: =HHT,Ωij=h(xi)h(xj)=K(xi,xj), later the output function of ELM is formulated by [16]:

f(x)=[K(x,x1)⋮K(x,xN)]TB(13)

In which

B=(IC+Ω)−1T(14)

For unknown samples x~, its class is attained as follows:

category(x~)=argmax(f(x~))(15)

It is notable that the computations of Eqs. (13) and (14) does not need to directly estimate the hidden function h(x) through kernel conversion that brings several benefits: (1) the oscillation of hidden neuron output matrix of ELM is resolved, also the arbitrariness is a major problem in chemometrics. (2) the amount of hidden nodes does not need to be stated. Thus, the computational time of kernel matrix for KELM would be much lesser when compared to the searching time of hidden node number in ELM, when the amount of trained samples is smaller i.e., normal situations in spectroscopy-related chemometrics.

2.4 RCMO Based Parameter Tuning

At the final stage, the RCMO algorithm is utilized for the optimal parameter tuning of the KELM model in such a way that the overall detection outcomes can be considerably enhanced. The RCMO algorithm is stimulated by the characteristics of red monkeys. The RCMO algorithmic program was simulating the red monkey performance. In order to modeling, these connections, all clusters from the monkey region units needed maneuvering on the search region. While it is referred that earlier, during this case, it can be separated to teams, all the teams of monkeys are consumed one male, and no needed the male was leader, but the stronger monkey could not from the scope of convention vision. Besides, it could not be several connections amongst male Cercopithecus mitis and young ones [17]. The young male has to come out fast because of territorial aspects connected with Cercopithecus mitis that best performing, as it enters problems with dominant male in another family. When it is defeated that male, it can be leader from the family and proposal place to live, food supply, and socialized to the young males.

The place upgrade considering each one of the red monkeys from the set was dependent upon the place of an optimum red monkey of group; as performance is delineating with the subsequent equation:

PBi+1=(PAi×PBi)+(Wleader−Wi)×rand×(Xbest−Xi)(16)

Xi+1=Xi+PBi+1(17)

PBi+1=PAi×rand(18)

where,

•   PBZ implies the monkey body power (an arbitrary number amongst -5 and 5);

•   PAZ refers the monkey battle power (an arbitrarily selected number among zero and one);

•   WleaderZ signifies the leader weight;

•   WiZ stands for the monkey weight (arbitrary numbers from the range of four and six);

•   XZ denotes the place of red monkey;

•   XbestZ indicates the place of leaders. Conversely, rand defines the some number amongst zero and one.

For updating the place compared with the children of red monkeys, the next formulas are employed as:

PBchi+1=(PAi×PBchi)+(Wchleader−Wchi)×rand×(Xchbest−Xchi)(19)

Xchi+1=Xchi+PBchi+1(20)

PAchi+1=PAchi×rand(21)

where,

•   PBch implies the rate of power of the child body;

•   PAch has demonstrated the child fighting rate of power;

•   WchleaderZ defining the weight of the child of leaders

•   WchiZ signifying the child weight in which every weight is indicated to being arbitrary numbers from the range of four and six;

•   XchZ denotes the place of children;

•   XchbestZ indicates the place of leader child's, and

•   “rand” refers an arbitrary number from the range of zero and one. Moreover, this place is transformed from every iteration.

It can be worth declaring that every parameter of RCMO is fixed also to be experimental or based on the issues in nature that are resolved [18]. The RCMO was considered as some parameters which generate it simple for executing; the RCMO is also balancing amongst exploitation as well as exploration stages, creating it appropriate for solving several optimized problems.

3  Experimental Validation

The performance validation of the RCMO-KELM technique takes place using the Epileptic Seizure Recognition Data Set from the UCI repository [19]. The dataset comprises 5 class labels namely eyes open, eyes closed, with tumor region, healthy brain, and epileptic seizure in the dataset. The dataset holds a set of 11500 instances. Tab. 1 offers the classification result analysis of the RCMO-KELM technique under a distinct number of hidden layers (NHL) and runs. Fig. 3 portrays the classification results obtained by the RCMO-KELM technique under run-1 with distinct NHLs. With NHLs of 10, the RCMO-KELM technique has obtainedprecn of 0.9462, recal of 0.9509, accuy of 0.9472, and Fscore of 0.9469. Concurrently, with NHLs of 30, the RCMO-KELM methodology has reached precn of 0.9353, recal of 0.9223, accuy of 0.9301, and Fscore of 0.9375.

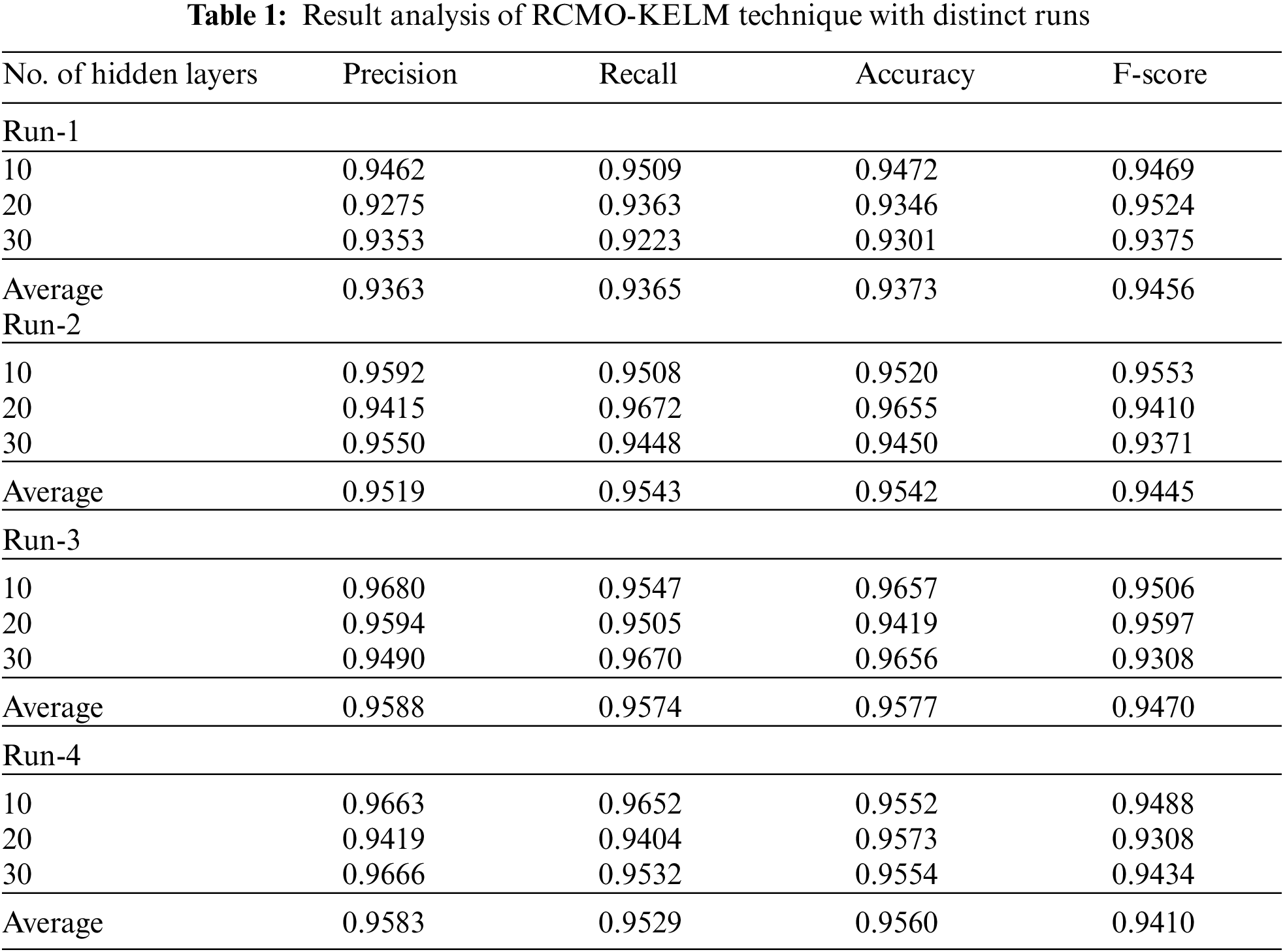
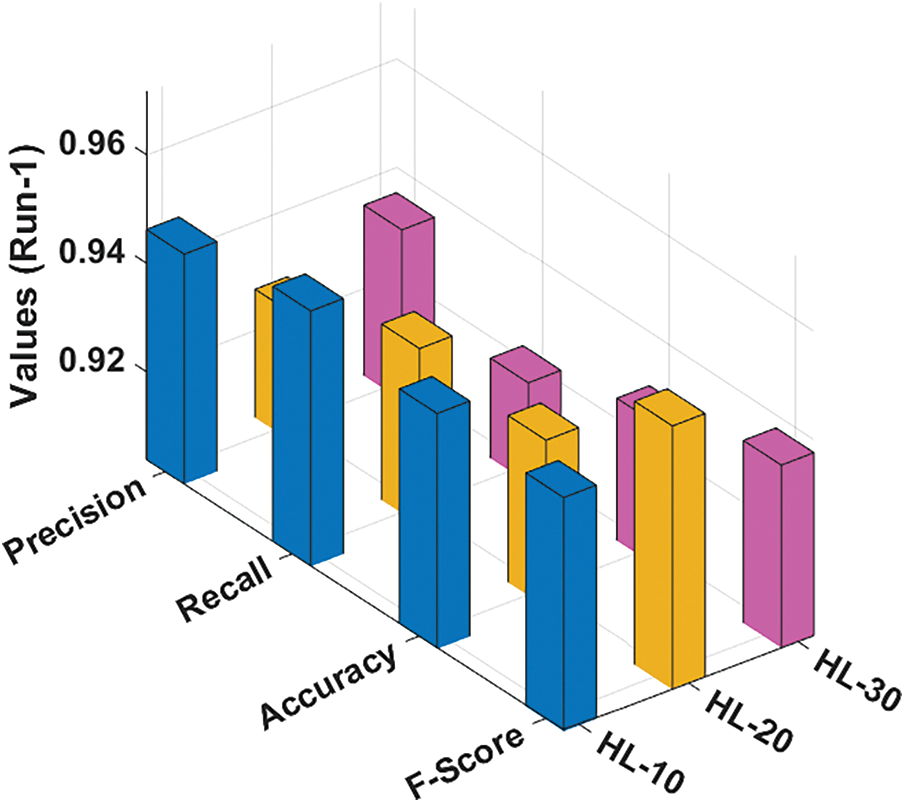
Figure 3: Result analysis of RCMO-KELM technique under run-1

Fig. 4 depicts the classification outcomes attained by the RCMO-KELM system under run-2 with several NHLs. With NHLs of 10, the RCMO-KELM approach has obtained precn of 0.9592, recal of 0.9508, accuy of 0.9520, and Fscore of 0.9553. Likewise, with NHLs of 30, the RCMO-KELM approach has gained precn of 0.9550, recal of 0.9448, accuy of 0.9450, and Fscore of 0.9371.

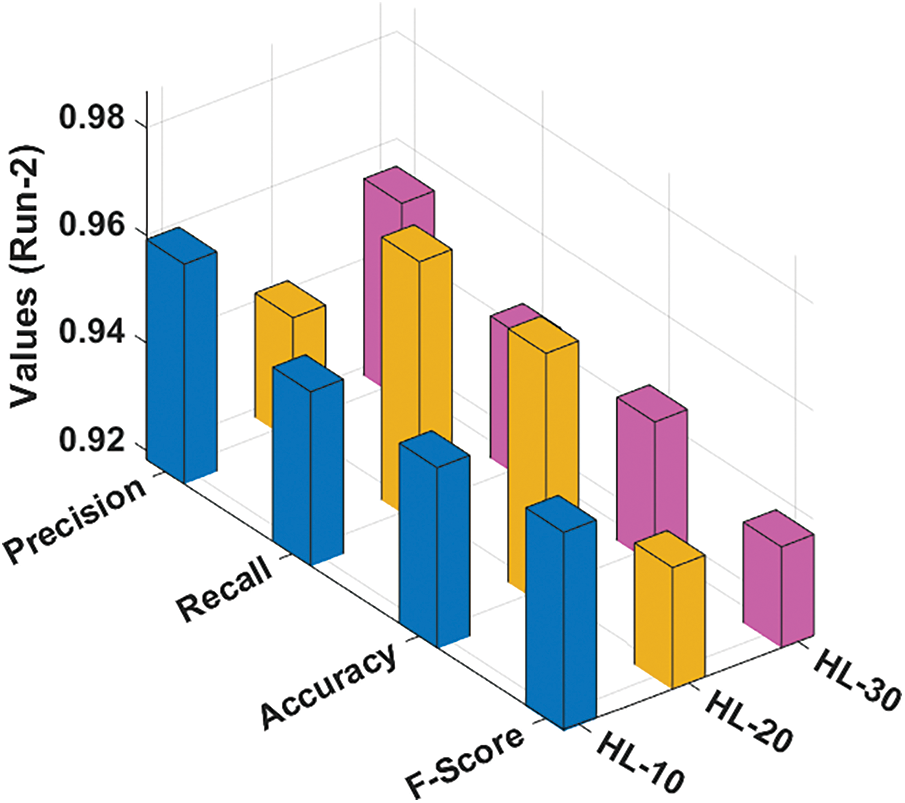
Figure 4: Result analysis of RCMO-KELM technique under run-2

Fig. 5 portrays the classification results reached by the RCMO-KELM method under run-3 with various NHLs. With NHLs of 10, the RCMO-KELM algorithm has achieved precn of 0.9680, recal of 0.9547, accuy of 0.9657, and Fscore of 0.9506. Eventually, with NHLs of 30, the RCMO-KELM method has obtained precn of 0.9490, recal of 0.9670, accuy of 0.9656, and Fscore of 0.9308.

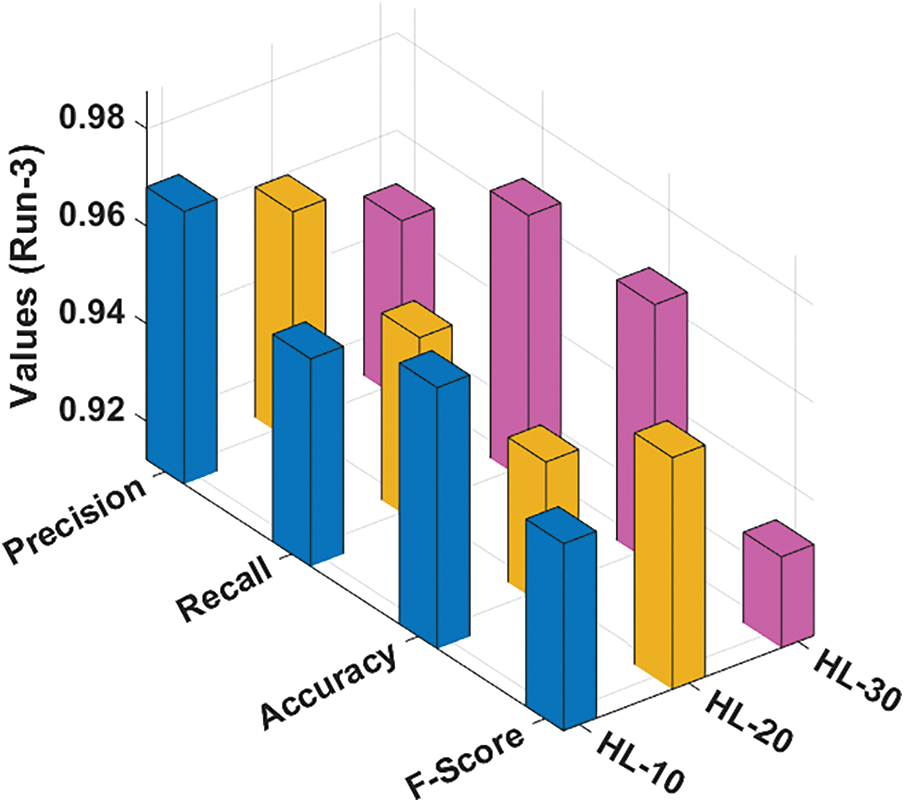
Figure 5: Result analysis of RCMO-KELM technique under run-3

Fig. 6 illustrates the classification results gained by the RCMO-KELM method under run-4 with several NHLs. With NHLs of 10, the RCMO-KELM approach has obtainedprecn of 0.9663, recal of 0.9652, accuy of 0.9552, and Fscore of 0.9488. Finally, with NHLs of 30, the RCMO-KELM approach has reachedprecn of 0.9666, recal of 0.9532, accuy of 0.9554, and Fscore of 0.9434.

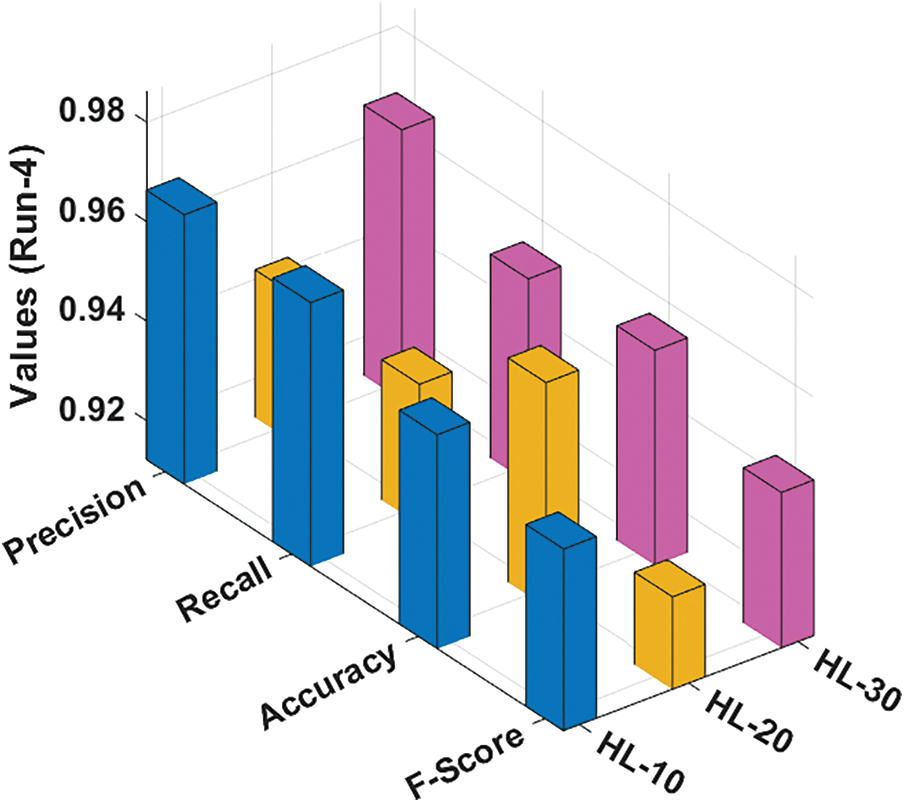
Figure 6: Result analysis of RCMO-KELM technique under run-4

Tab. 2 and Fig. 7 investigate the overall average result analysis of the RCMO-KELM technique under distinct runs. The results reported the enhanced outcomes of the RCMO-KELM technique under every run. For sample, with run1, the RCMO-KELM system has attained precn of 0.9363, recal of 0.9365, accuy of 0.9373, and Fscore of 0.9456. In addition, with run2, the RCMO-KELM approach has reached precn of 0.9519, recal of 0.9543, accuy of 0.9542, and Fscore of 0.9445. Moreover, with run3, the RCMO-KELM system has gained precn of 0.9588, recal of 0.9574, accuy of 0.9577, and Fscore of 0.9470. Finally, with run4, the RCMO-KELM methodology has obtained precn of 0.9583, recal of 0.9529, accuy of 0.9560, and Fscore of 0.9410.

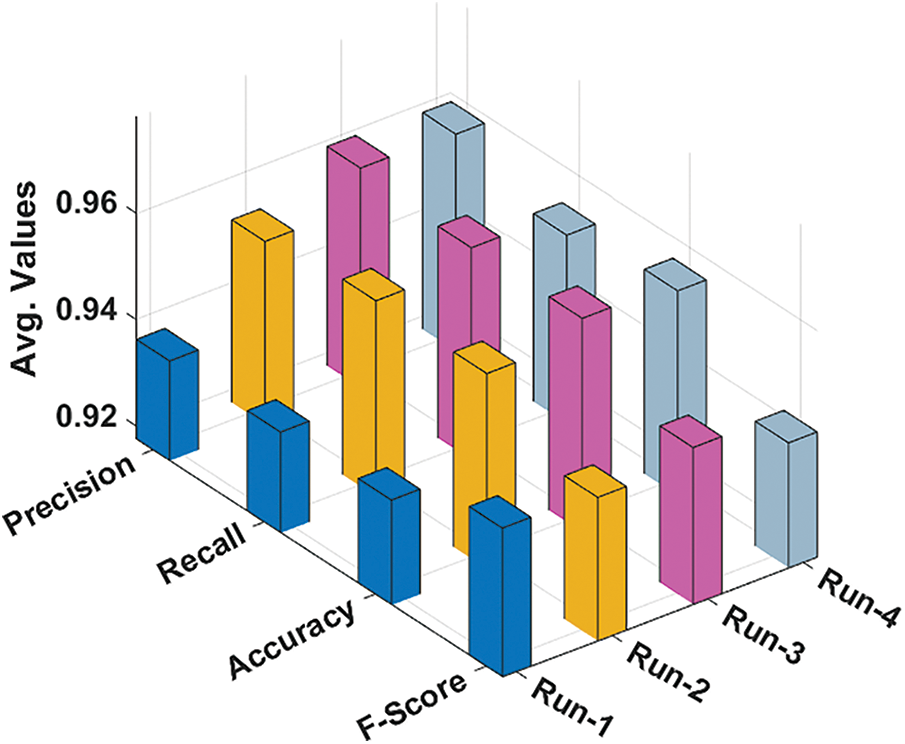
Figure 7: Average analysis of RCMO-KELM technique with different measures

Fig. 8 provides the accuracy and loss graph analysis of the RCMO-KELM technique on the test dataset. The results show that the accuracy value tends to increase and loss value tends to decrease with an increase in epoch count. It is also observed that the training loss is low and validation accuracy is high on the test dataset.

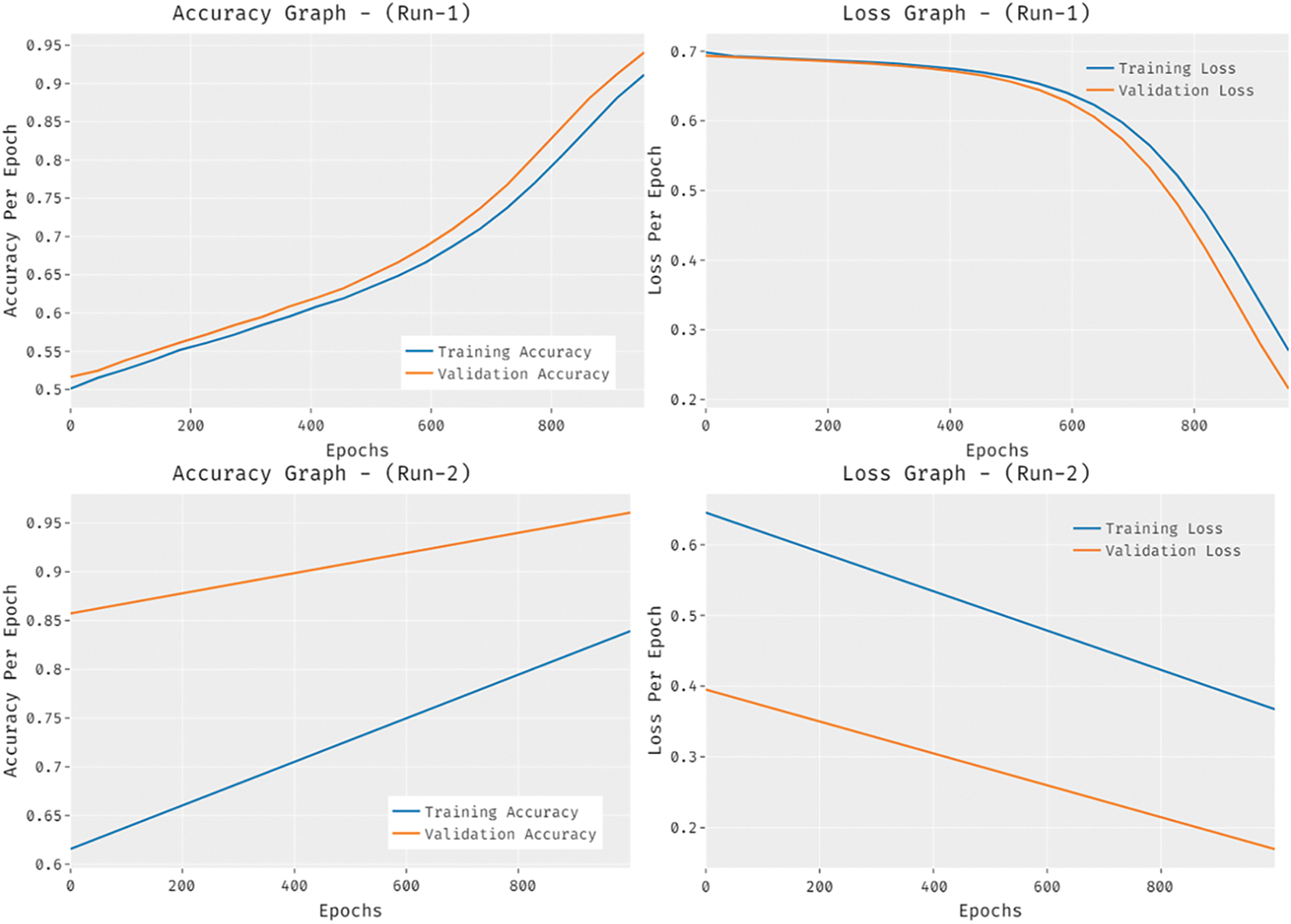
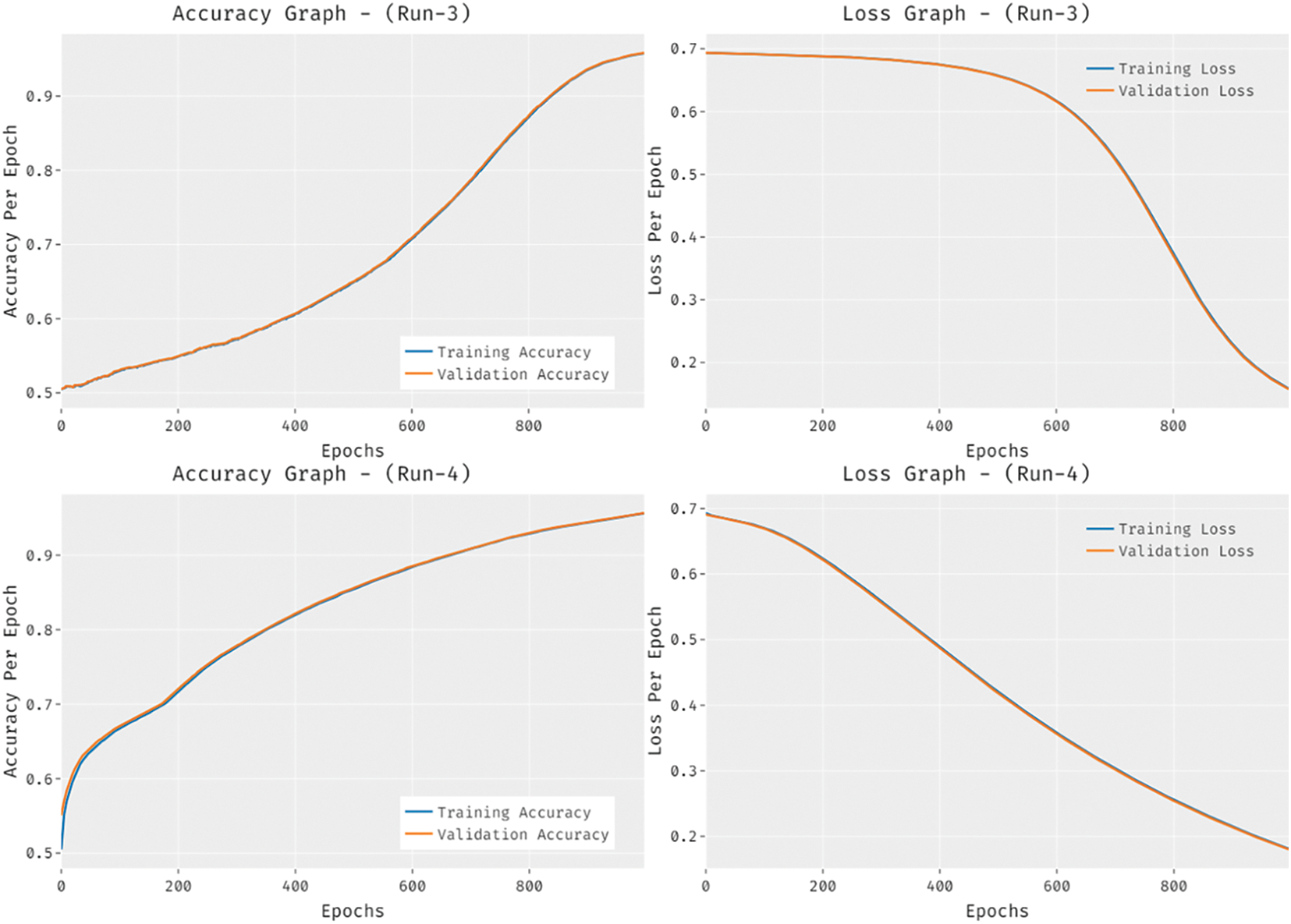
Figure 8: Accuracy and loss graph analysis of RCMO-KELM technique

Finally, an extensive comparative study of the RCMO-KELM technique has been made with recent methods interms of accuy in Tab. 3 and Fig. 9 [20]. The results reported that the MADN-LSVM, WN-LSVM, ZSN-LSVM, and MNN-LSVM techniques have obtained lower accuy of 0.767, 0.769, 0.771, and 0.772 respectively. Followed by, the ZSN-CSVM, WN-CSVM, MADN-CSVM, and MNN-CSVM techniques have reached moderately closer accuy values of 0.823, 0.824, 0.824, and 0.825 respectively. However, the RCMO-KELM technique has accomplished maximum accuy of 0.956. From the result analysis, it is ensured that the RCMO-KELM technique outperformed the other techniques on the test dataset applied.

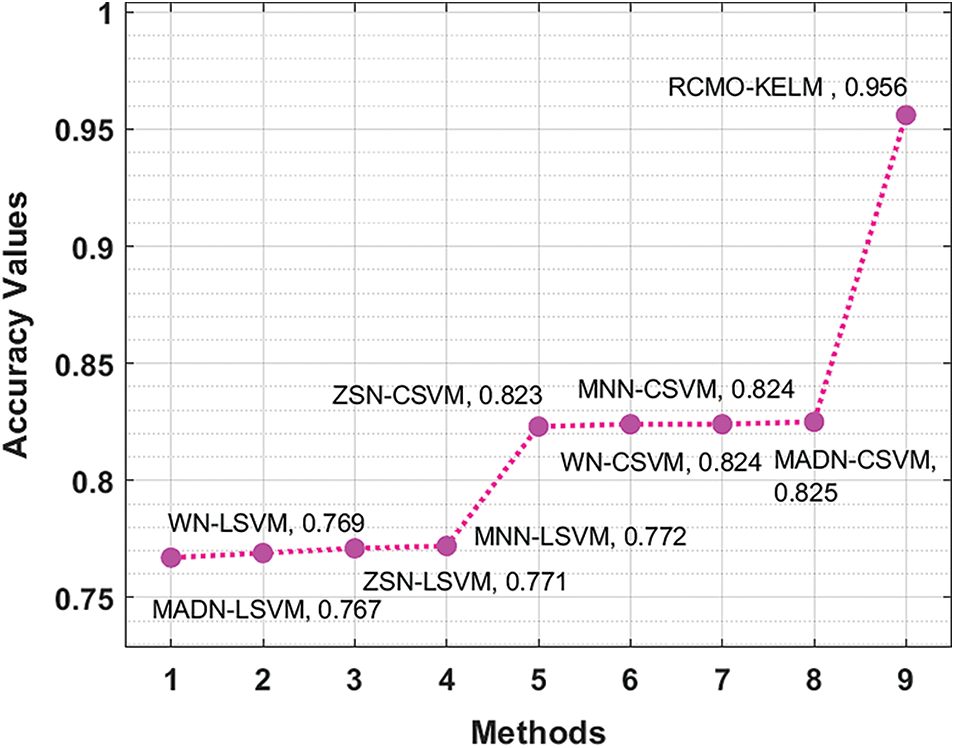
Figure 9: Accuracy analysis of RCMO-KELM technique with recent algorithms

4  Conclusion

In this article, a novel RCMO-KELM technique has been developed for epileptic seizure detection and classification. The proposed RCMO-KELM technique initially extracts the chaotic, time, and frequency domain features in the actual EEG signal. Besides, the RCMO-KELM technique involves several stages of operations namely feature extraction, min-max normalization based preprocessing, KELM based classification, and RCMO based parameter tuning. The RCMO technique was utilized for the optimal parameter tuning of the KELM method in such a way that the overall detection outcomes can be considerably enhanced. The experimental result analysis of the RCMO-KELM technique has been examined using benchmark dataset and the results are inspected under several aspects. The comparative result analysis reported the better outcomes of the RCMO-KELM technique over the recent approaches with accuy of 0.956. In future, hybrid DL models can be included to enhance the overall performance.

Funding Statement: The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work under Grant Number (RGP2/42/43). Princess Nourah bint Abdulrahman University Researchers Supporting Project Number (PNURSP2022R136), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  M. Diykh, Y. Li and P. Wen, “Classify epileptic EEG signals using weighted complex networks based community structure detection,” Expert Systems with Applications, vol. 90, pp. 87–100, 2017. [Google Scholar]

 2.  R. S. Segundo, M. G. Martín, L. F. D'Haro-Enríquez and J. M. Pardo, “Classification of epileptic EEG recordings using signal transforms and convolutional neural networks,” Computers in Biology and Medicine, vol. 109, pp. 148–158, 2019. [Google Scholar]

 3.  A. Y. Mutlu, “Detection of epileptic dysfunctions in EEG signals using hilbert vibration decomposition,” Biomedical Signal Processing and Control, vol. 40, pp. 33–40, 2018. [Google Scholar]

 4.  P. Boonyakitanont, A. L. uthai, K. Chomtho and J. Songsiri, “A review of feature extraction and performance evaluation in epileptic seizure detection using EEG,” Biomedical Signal Processing and Control, vol. 57, pp. 101702, 2020. [Google Scholar]

 5.  E. B. Assi, D. K. Nguyen, S. Rihana and M. Sawan, “Towards accurate prediction of epileptic seizures: A review,” Biomedical Signal Processing and Control, vol. 34, pp. 144–157, 2017. [Google Scholar]

 6.  G. Wang, D. Ren, K. Li, D. Wang, M. Wang et al. “EEG-Based detection of epileptic seizures through the use of a directed transfer function method,” IEEE Access, vol. 6, pp. 47189–47198, 2018. [Google Scholar]

 7.  A. B. Das and M. I. H. Bhuiyan, “Discrimination and classification of focal and non-focal EEG signals using entropy-based features in the EMD-DWT domain,” Biomedical Signal Processing and Control, vol. 29, pp. 11–21, 2016. [Google Scholar]

 8.  U. R. Acharya, S. L. Oh, Y. Hagiwara, J. H. Tan and H. Adeli, “Deep convolutional neural network for the automated detection and diagnosis of seizure using EEG signals,” Computers in Biology and Medicine, vol. 100, pp. 270–278, 2018. [Google Scholar]

 9.  P. Kaur, M. Sharma and M. Mittal, “Big data and machine learning based secure healthcare framework,” Procedia Computer Science, vol. 132, pp. 1049–1059, 2018. [Google Scholar]

10. A. Abdelaziz, M. Elhoseny, A. S. Salama and A. M. Riad, “A machine learning model for improving healthcare services on cloud computing environment,” Measurement, vol. 119, pp. 117–128, 2018. [Google Scholar]

11. M. Nilashi, H. Ahmadi, A. A. Manaf, T. A. Rashid, S. Samad et al. “Coronary heart disease diagnosis through self-organizing map and fuzzy support vector machine with incremental updates,” International Journal of Fuzzy Systems, vol. 22, no. 4, pp. 1376–1388, 2020. [Google Scholar]

12. A. Dinh, S. Miertschin, A. Young and S. Mohanty, “A Data-driven approach to predicting diabetes and cardiovascular disease with machine learning,” BMC Medical Informatics and Decision Making, vol. 19, no. 1, 2019. [Google Scholar]

13. M. Elhoseny, M. A. Mohammed, S. A. Mostafa, K. H. Abdulkareem, M. S. Maashi et al. “A new multi-agent feature wrapper machine learning approach for heart disease diagnosis,” Computers, Materials & Continua, vol. 67, no. 1, pp. 51–71, 2021. [Google Scholar]

14. G. B. Huang, Q. Y. Zhu and C. K. Siew, “Extreme learning machine: a new learning scheme of feedforward neural networks,” in 2004 IEEE Int. Joint Conf. on Neural Networks (IEEE Cat. No.04CH37541), Budapest, Hungary, vol. 2, pp. 985–990, 2004. [Google Scholar]

15. T. Dokeroglu and E. Sevinc, “Evolutionary parallel extreme learning machines for the data classification problem,” Computers & Industrial Engineering, vol. 130, pp. 237–249, 2019. [Google Scholar]

16. W. Zheng, H. Shu, H. Tang and H. Zhang, “Spectra data classification with kernel extreme learning machine,” Chemometrics and Intelligent Laboratory Systems, vol. 192, pp. 103815, 2019. [Google Scholar]

17. W. J. AL-kubaisy, M. Yousif, B. Al-Khateeb, M. Mahmood and D. -N. Le, “The red colobuses monkey: A new nature–inspired metaheuristic optimization algorithm,” International Journal of Computational Intelligence Systems, vol. 14, no. 1, pp. 1108, 2021. [Google Scholar]

18. E. Worch, “Play behavior of red colobus monkeys in kibale national park, Uganda,” Folia Primatologica, vol. 81, no. 3, pp. 163–176, 2010. [Google Scholar]

19. W. Qiuyi and E. Fokoue, https://archive.ics.uci.edu/ml/datasets/Epileptic+Seizure+Recognition, 2017. [Google Scholar]

20. K. Polat and M. Nour, “Epileptic seizure detection based on new hybrid models with electroencephalogram signals,” Innovation and Research in BioMedical Engineering, vol. 41, no. 6, pp. 331–353, 2020. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.