Computers, Materials & Continua DOI:10.32604/cmc.2022.026556
Article

Optimal Machine Learning Enabled Intrusion Detection in Cyber-Physical System Environment

Bassam A. Y. Alqaralleh1,*, Fahad Aldhaban1, Esam A. AlQarallehs2 and Ahmad H. Al-Omari3

1MIS Department, College of Business Administration, University of Business and Technology, Jeddah, 21448, Saudi Arabia
2School of Engineering, Princess Sumaya University for Technology, Amman, 11941, Jordan
3Faculty of Science, Computer Science Department, Northern Border University, Arar, 91431, Saudi Arabia
*Corresponding Author: Bassam A. Y. Alqaralleh. Email: b.alqaralleh@ubt.edu.sa
Received: 30 December 2021; Accepted: 08 March 2022

Abstract: Cyber-attacks on cyber-physical systems (CPSs) resulted to sensing and actuation misbehavior, severe damage to physical object, and safety risk. Machine learning (ML) models have been presented to hinder cyberattacks on the CPS environment; however, the non-existence of labelled data from new attacks makes their detection quite interesting. Intrusion Detection System (IDS) is a commonly utilized to detect and classify the existence of intrusions in the CPS environment, which acts as an important part in secure CPS environment. Latest developments in deep learning (DL) and explainable artificial intelligence (XAI) stimulate new IDSs to manage cyberattacks with minimum complexity and high sophistication. In this aspect, this paper presents an XAI based IDS using feature selection with Dirichlet Variational Autoencoder (XAIIDS-FSDVAE) model for CPS. The proposed model encompasses the design of coyote optimization algorithm (COA) based feature selection (FS) model is derived to select an optimal subset of features. Next, an intelligent Dirichlet Variational Autoencoder (DVAE) technique is employed for the anomaly detection process in the CPS environment. Finally, the parameter optimization of the DVAE takes place using a manta ray foraging optimization (MRFO) model to tune the parameter of the DVAE. In order to determine the enhanced intrusion detection efficiency of the XAIIDS-FSDVAE technique, a wide range of simulations take place using the benchmark datasets. The experimental results reported the better performance of the XAIIDS-FSDVAE technique over the recent methods in terms of several evaluation parameters.

Keywords: Cyber-physical systems; explainable artificial intelligence; deep learning; security; intrusion detection; metaheuristics

1  Introduction

Cyber-physical systems (CPS) being a strongly coupled combination of physical systems, computing systems, and communication devices, have proved to pose many security problems because of their basic complex design [1]. The CPS has wide-ranging applications includes transport industry, aviation, chemical and consumer appliances, civil, and also in the fields of healthcare and manufacturing. The attack on a CPS might cause a failure of the system and lose sensitive data to the attackers [2]. This could result in multiple losses. For preventing damages to systems and users, it is necessary to deploy and design secure CPS. It could assist in maintaining privacy and security for CPS and also improve the quality of applications [3]. The security of CPS is an extension of traditional cybersecurity, wherein the process of the physical model is further taken into account. One of the most significant privacy problems in the traditional cybersecurity fields because of the risks of private data leaks are password cracking, which is password recovery method for the systems [4]. In CPS security, simple data leaks by the password cracking could not damage the CPSs; but, the operation of the physical process by illegal access with a password could affect the dynamics of the physical system.

Hence, different CPS security researches have been carried out by modelling physical dynamics with control theory [5]. But CPS is impacted by several factors, namely unexpected events, quick environment changes, and physical system-based CPS security suffers from false alarm that degrades recognition accuracy against cyber-physical attacks. Furthermore, the CPS becomes larger and the relationship of all the CPS components becomes difficult, the accuracy levels exhibited by a real CPS and the traditional CPS reduces which creates further attack vectors [6]. From a control theoretical perspective, complex and massive models could be characterized as higher-order differential equations, in which arithmetical models with higher-order terms are susceptible to noise on the state variable. Hence, it is hard to attain accurate arithmetical models of complicated physical systems, as well as unconsidered arithmetical terms of the incorrect dynamic models, which turn out to be the vulnerability of the system-based attack detectors, which leads to incorrect recognition [7].

In order to conquer the limitation of legacy method-based CPS security, the data-driven anomaly recognition method (wherein abnormal information is attained from many controlled experiments and simulations) is adapted in CPS security [8]. Especially, machine learning (ML) that shows correlation among input and output using large number of information without modelling based physical laws, is adapted in CPS security for satisfying reliability concerns and higher-level security [9]. Moreover, ML technique enables a method to be made for the complex and massive relations of all the components of the CPS, involving several physical models in the real-time, complex application software, and heterogeneous network protocol in the cyberworld, the generated method could improve the safety levels of the CPSs. Fig. 1 illustrates the process of explainable artificial intelligence (XAI) technique [10].

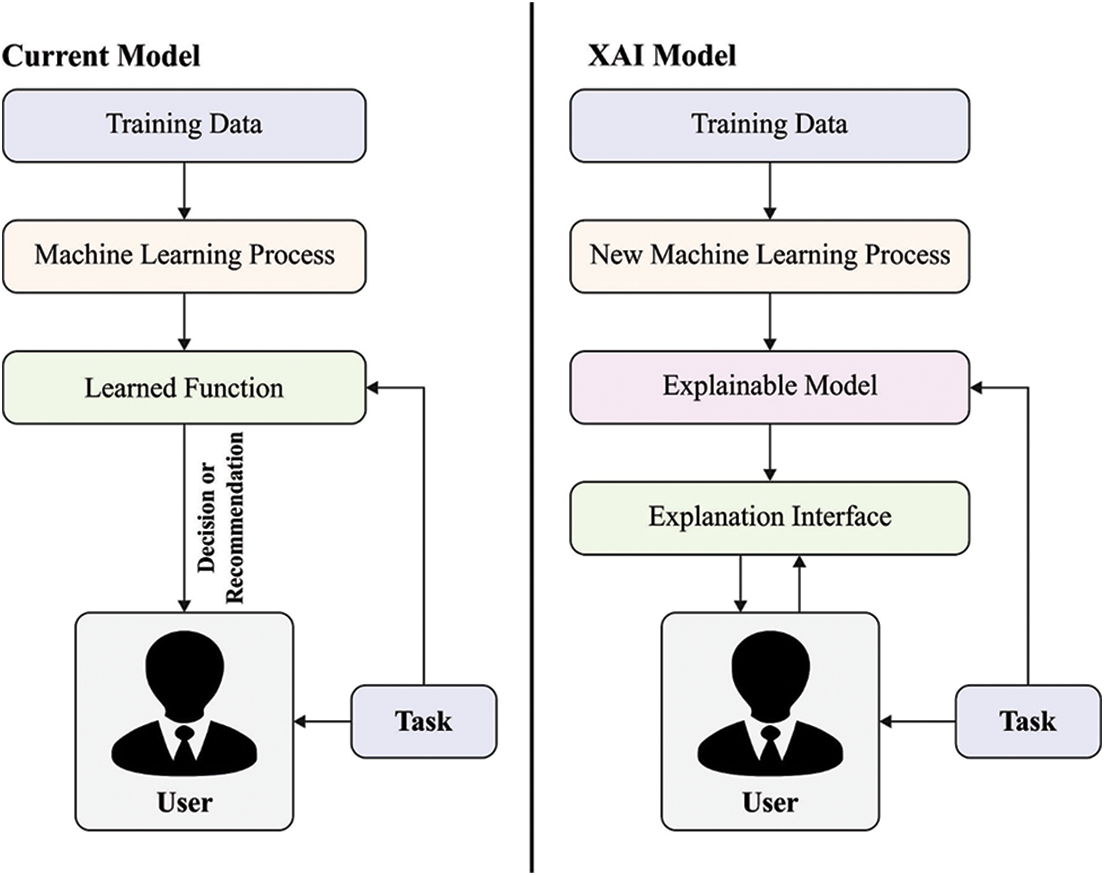
Figure 1: Process of XAI

This paper presents an XAI based intrusion detection system (IDS) using feature selection with Dirichlet Variational Autoencoder (XAIIDS-FSDVAE) model for CPS. The presented strategy encompasses the design of coyote optimization algorithm (COA) based FS model is derived to elect an optimal subset of features. Next, an intelligent DVAE technique is employed for the anomaly detection process in the CPS environment. Finally, the parameter optimization of the DVAE takes place using a manta ray foraging optimization (MRFO) algorithm to tune the parameters of the DVAE. In order to determine the enhanced intrusion detection efficacy of the XAIIDS-FSDVAE technique, a wide range of simulations take place using the benchmark datasets.

2  Related Works

Aljehane [11] presented a parameter-tuning deep-stacked autoencoder (PT-DSAE) based deep learning (DL) method for the IDS in CPS. The presented method comprises feature extraction, preprocessing, classification, and parameter tuning. Firstly, preprocessing is performed for eliminating the noise existing in the information. Followed by, a DL-based DSAE method is exploited for finding anomalies in the CPS. Furthermore, hyperparameter tuning of the DSAE performs by a search-and-rescue optimization model for parameter tuning the DSAEs, namely the learning rate, epoch count, batch size, and the number of hidden layers.

Hariri et al. [12] introduced customized malware scripts to manipulate and sniff data and demonstrate the capacity of the malware for triggering false positives in the neural network response. The malware is proposed to be a vaccine to reinforce the IDS against data processing attacks by improving the capacity of the neural network to adapt and learn those threats. Li et al. [13] presented a federated DL method, termed DeepFed, to identify cyberattacks against industrial CPS. Especially, developed a new DL-based IDS for industrial CPSs, by using a gated recurrent unit (GRU) and convolutional neural network (CNN). Later, designed a federated learning architecture, which allows various industrial CPS models to jointly construct a wide-ranging IDS in a privacy-preserving method.

Gifty et al. [14] aimed at the privacy and security factors in handling big data for CPS and review current challenges in data integrity. As well, introduce a security architecture for IDS recognition and investigate the failure rate, performance parameter, and reliability in a malicious big data context. Belenko et al. [15] examined generative adversarial artificial neural network (ANN) for detecting security intrusion in largescale network of cyber devices. As per the outcomes of the experiment, a calculation is composed of applicability of generative adversarial ANN to identify privacy anomalies, and real-world recommendation is deliberated for using interconnected CPS.

Khan et al. [16] presented an architecture named Intrusion detection through electromagnetic-signal analysis (IDEA) which exploits electromagnetic (EM) side-channel signals for detecting malevolent activities on embedded and CPSs. First, IDEA records EM emanation from uncompromised reference devices to determine a starting point of reference EM pattern. Then, IDEA monitors the targeted device’s EM emanation. Filho et al. [17] designed an fog based intrusion detection using generative adversarial network (FID-GAN). The IDS is presented for a fog framework that brings computational resources nearer to the end node and consequently contributes to meeting lower-latency requirements. To accomplish high detection rate, the presented framework computes a reconstruction loss-based reconstruction of data sample mapped to the latent space.

3  The Proposed Model

In this study, a novel XAIIDS-FSDVAE technique has been presented for the detection and classification of intrusion in the CPS environment. The XAIIDS-FSDVAE technique encompasses different subprocesses namely pre-processing, COA based election of features, DVAE based classification, and MRFO based parameter tuning. The COA application reduces the computational complexity and MRFO algorithm helps to accomplish maximum intrusion detection performance. Fig. 2 illustrates the overall process of proposed XAIIDS-FSDVAE technique.

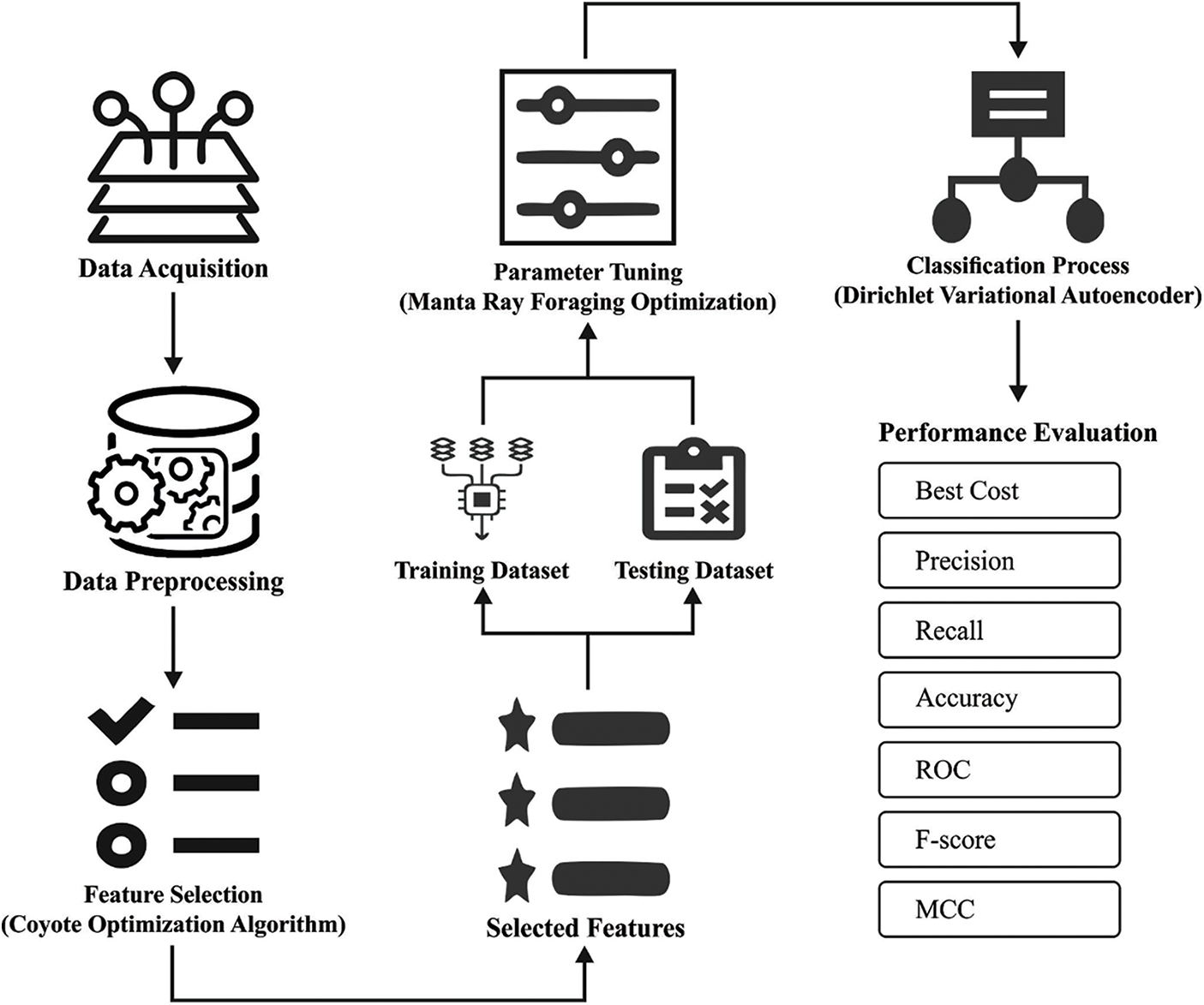
Figure 2: Overall process of XAIIDS-FSDVAE technique

3.1 Data Pre-Processing

Primarily, the pre-processing of data is carried out to transform the actual data into a useful format and thereby improve the performance of the applied model. To accomplish this, a min-max normalization technique is performed, which rescales the output or features from a range of values into new ones (0 to 1 or −1 to +1). The rescaling process is performed by the utilization of linear interpolation process, as given below.

y′=(ymax−ymin)×(xi−xmin)(xmax−xmin)+xmin(1)

where (ymax−ymin)=0; when (xmax−xmin)=0 for a feature, it defines a continuous value for the feature.

3.2 Process Involved in COA Based Feature Selection Approach

At this stage, the preprocessed data is applied as input into the COA model to choose a useful set of features. COA is a recently established meta-heuristic technique which is presented by Pierezan et al. [18]. This technique was dependent upon the alteration performance of coyotes by the environment and also the coyote experiences replacing. COA is a stimulating approach for obtaining a balance amongst exploration as well as exploitation. This technique begins with NP amount of populations and Nc count of coyotes as candidate solution:

SOCcp,t=x=[x1, x2, …, xD](2)

where c represents the number and p refers to the group and t indicates the time of inspiration to the design variable. Primary, a few arbitrary coyotes are created as candidate solution from the search space. The subsequent formula demonstrated this procedure modeling:

SOCc,jp,t=LBj+η×(Urj−Lrj)(3)

where η∈[0,1] refers to an arbitrary value and Lrj and Urj signifies the lower as well as upper ranges of jth variable from the search space:

objcp,t=f(SOCc,jp,t)(4)

This technique upgrades the group’s place arbitrarily. In addition, the candidate upgrades its place by leaving its groups to another one. The subsequent formula defines the leaving procedure dependent upon the probability design:

P1=0.05×Nc2(5)

An optimum solution of all iterations is regarded as the alpha coyote and attained by the subsequent formula:

αp,t=soccp,tfor min objcp,t(6)

The general property of coyotes to the culture alteration is as follows:

culjp,t={Rp,tNC+12,j, Nc is odd number12(RNc2,jp,t+RNC2+1,jp,t)0.W.(7)

where, Rp,t indicates the coyotes, social state ranking to group number p at time t to the variable j:

Blejp,t={socr1,jp,t, rj<prs or j=j1socr2,jp,t, rj≥prs+pra or j=j2σj, O.W.(8)

where, rj∈[0,1] implies the arbitrary value and r2 defines an arbitrary coyote from the groups p,σj signifies the arbitrary value from the design variable limit [19], j1 and j2 represents the arbitrary design variables, and pra and prs demonstrates the connection and scatter probability correspondingly that announce the coyote cultural diversity in the group. The arithmetical process to pra and prs is as follows:

prs=1d(9)

Pra=12(1−pr)(10)

where d stands for the dimensional to variables. The cultural transitions amongst the group were determined by 2 features containing δ1 and δ2 as:

δ1=αp,t−soccr1p,t(11)

δ2=culp,t−soccr2p,t(12)

where δ1 stands for the culture variances amongst the leader (alpha) and chosen coyote (cr1) and δ2 implies the culture variance amongst group culture trending and the chosen coyote (cr2):

nsoccp,t=soccp,t+r1×δ1+r2×δ2(13)

where r1 and r2 represents the arbitrary numbers amongst zero and one. With assuming the upgrade formulas, a novel cost was lastly attained by the subsequent formula:

nobjcp,t=f(nsoccp,t)(14)

soccp,t+1={nsoccp,t, nobjcp,t<objcp,tsoccp,t, O.W.(15)

An essential part of these approaches is their ability to escape at the local optimal point.

The feature selection using the FS approach can be denoted as a N sized vector where N indicates the feature count [20]. Here, every location of the vectors can consider the values as 0 or 1 in which 0 signifies the features which are unselected and 1 denotes the chosen features. The transfer function approach signifies the possibility of varying a position vector component from 0 to 1 and vice versa more easily and effectively. A transfer function considerably influences the outcome of the FS technique at the time of searching the optimal set of features related to avoiding local optimal problems and maintaining the tradeoff among exploration as well as exploitation processes:

V(new−soccp,t)=|newS0Ccp,l1+(new−soccp,t)2|

where new−soccp,t indicates the upgraded social condition vector by considering the constant values [21].

3.3 Intrusion Detection Using DVAE Model

During the intrusion detection process, the DVAE model can be employed for the detection and classification of intrusions in the CPS environment. The major difference of the generative approaches is the preceding distribution supposition on the latent parameter z. Rather than the utilization of the uniform Gaussian distribution, the Dirichlet distribution can be employed, representing a conjugate prior distribution of the multi-nomial distribution [22].

z∼p(z)=Dirichlet(α),x∼pθ(x|z)(17)

The probabilistic encoding unit with an approximation of the posterior distribution q∅(z|x) can be defined as Dirichlet (α^). The approximation of the posterior variable α^ can be defined using the multilayer perceptron (MLP) from the observation x in data set D with positive outcome functions like softplus function, therefore, the outcome could be positive value limited by the Dirichlet distribution. Initially, it is considered that v∼ MultiGamma (α, β 1K). Afterward, v is normalized to the summation ∑⁡vi. The objective function aims in the optimization of the model variables θ and ∅. The loss function used for the optimization next to the composition is presented in Eq. (18). The inverse Gamma cumulative distribution function (CDF) approach allows the flow of backpropagation into the input with stochastic gradient descent (SGD). Then, the Dirichlet distribution with inverse Gamma CDF approximation and softmax Gaussian approach can be compared, assume αk=1−1/K when μk=0 and Σk=1; and β=1.

L(x)=Eq∅(z|x)[ log pθ(x|z)]

−∑k ⁡(log⁡Γ(αk)−log⁡Γ(α^k)+(α^k−αk)ψ(α^k))(18)

The approximation with inverse Gamma CDF. When if ∼Gamma(α, β), and if F(x;α,β) is a CDF of the arbitrary variable X [23], the inverse CDF undergo approximation by F−1(u;α, β)≈β−1(uαΓ(α))1/α. Therefore, the secondary parameter u∼Uniform(0,1) for considering the arbitrariness of X, and the Gamma undergoes sampling X as a deterministic value for α and β.

3.4 Parameter Optimization Using MRFO Algorithm

Finally, the parameter tuning of the DVAE model takes place using the MRFO algorithm such that the recognition rate could be improvised. Zhao et al. [24] projected a state-of-the-art meta-heuristic optimized manner called MRFO simulated in the foraging approach then manta ray from catch its prey. In 3 foraging functions like somersault, chain, and cyclone foraging. The chain foraging procedure is written as:

xi(t+1)={xi(t)+r⋅(xbest(t)−xi(t))+α(xbest(t)−xi(t))i=1xi(t)+r⋅(xi−1(t)−xi(t))+α(xbest(t)−xi(t))i=2,…,N(19)

where xi(t) refers the ith individuals place at iterations t,r implies the arbitrary vector from range; xbest(t) indicates the optimum solution at iterations t,N characterizes the amount of manta rays and α means the weighting coefficient as:

α=2×r×| log (r)| (20)

Mentioning to Eq. (7), the place of ith individual excepts a primary one is based on the place of (i−1)th individuals (xi−1(t)) and optimum one (xbest(t)). Once the place of the plankton patch was detected by manta ray, it is join creating chain, and afterward swim near the prey from spiral shapes. Also, the spiral swimming, all individuals swim near the manta ray in front, it can be monitored in cyclone foraging [25]. This effort was expressed as:

{Xi(t+1)=Xbest+r⋅(Xi−1(t)−Xi(t))+ebω⋅ cos (2πω)⋅(Xbest−Xi(t))Yi(t+1)=Ybest+r⋅(Yi−1(t)−Yi(t))+ebω⋅ sin (2πω)⋅(Ybest−Yi(t))(21)

where ω stands for an arbitrary number from range, the cyclone foraging stage is demonstrated as:

xi(t+1)={xbest+r.(xbest(t)−xi(t))+β(xbest(t)−xi(t))i=1xbest+r.(xi−1(t)−xi(t))+β(xbest(t)−xi(t))i=2, …,N(22)

where β implies the weighting factors determined as:

β=2er1(T−t+1T) sin (2πr1)(23)

where t refers to the present iterations, T stands for the maximal count of iterations and r1 indicates the arbitrary number from range. The cyclone foraging is an optimum use to better solutions region as every manta ray do exploring method to the food-dependent upon its reference places. Also, this procedure improves the exploration procedure using the strength of individuals for searching novel places that are far from the present optimum. This performance is carried out by allocating an arbitrary place from the search space as:

χrand=Lb+r.(Ub−Lb)(24)

xi(t+1)={xrand+r. (xrand−xi(t))+β(xrand−xi(t)) i=1xrand+r. (xi−1(t)−xi(t))+β(xrand−xi(t)) i=2,…,N(25)

where Lb and Ub defines the lower as well as upper limits of problem variable, χrand refers to the arbitrary place allocated to the search spaces. The last stage monitored in MRFO was somersault foraging whereas the food was detected as hinge. During this phase, all manta rays prefer swim back and forth about the hinge as well as tumble to novel place. It could be mathematically written as:

xi(t+1)=xi(t)+S.(r2. xbest−r3. xi(t)) i=1,2,…N(26)

where S implies the factor of somersault utilized from determining the manta ray somersault range, r2 and r3 represents the arbitrary numbers from the range. As regards Eq. (20), all individuals are moved to someplace from the search space amongst their present place and symmetrical one around the hinge. In this stage, the distances amongst the manta rays places an optimum one decreases that means converging to optimum solutions. Therefore, the somersault foraging range was adaptably decreased with iteration.

The MRFO approach develops a fitness function (FF) for attaining enhanced classification efficiency. It defines a positive integer for representing the optimum efficiency of the candidate solution. During this analysis, the minimized classifier error rate was assumed as FF, as provided in Eq. (27). The optimum solutions have a lesser error rate and the worst solution gains a higher error rate.

fitness(xi)=ClassifierErrorRate(xi)=numerb of misclassified instancesTotal number of instances∗100(27)

4  Results and Discussion

The experimental validation of the XAIIDS-FSDVAE technique takes place using the CICIDS-2017 [26] and NSL-KDD-2015 [27] datasets. The first NSL-KDD 2015 data set has 125973 instances with two classes, 41 features, and five kinds of attacks. Secondly, the CICIDS-2017 data set includes 2830743 samples with two classes and 80 features. The best cost (BC) analysis of the COA-FS model with other FS models takes place in Tab. 1 and Fig. 3. The results show that the COA-FS technique has chosen a set of 16 and 42 features on the test NSL-KDD-2015 and CICIDS-2017 datasets. On the test NSL-KDD-2015 dataset, the COA-FS technique has depicted minimum BC of 0.05321 while the grey wolf optimization (GWO)-FS, ant colony optimization (ACO)-FS, and particle swarm optimization (PSO)-FS models have attained maximum BC of 0.06495, 0.10646, and 0.12680 respectively. Likewise, on the test CICIDS-2017 datasets, the COA-FS procedure has offered lower BC of 0.05341 while the GWO-FS, ACO-FS, and PSO-FS systems have resulted in higher BC of 0.09486, 0.12543, and 0.13557 respectively.

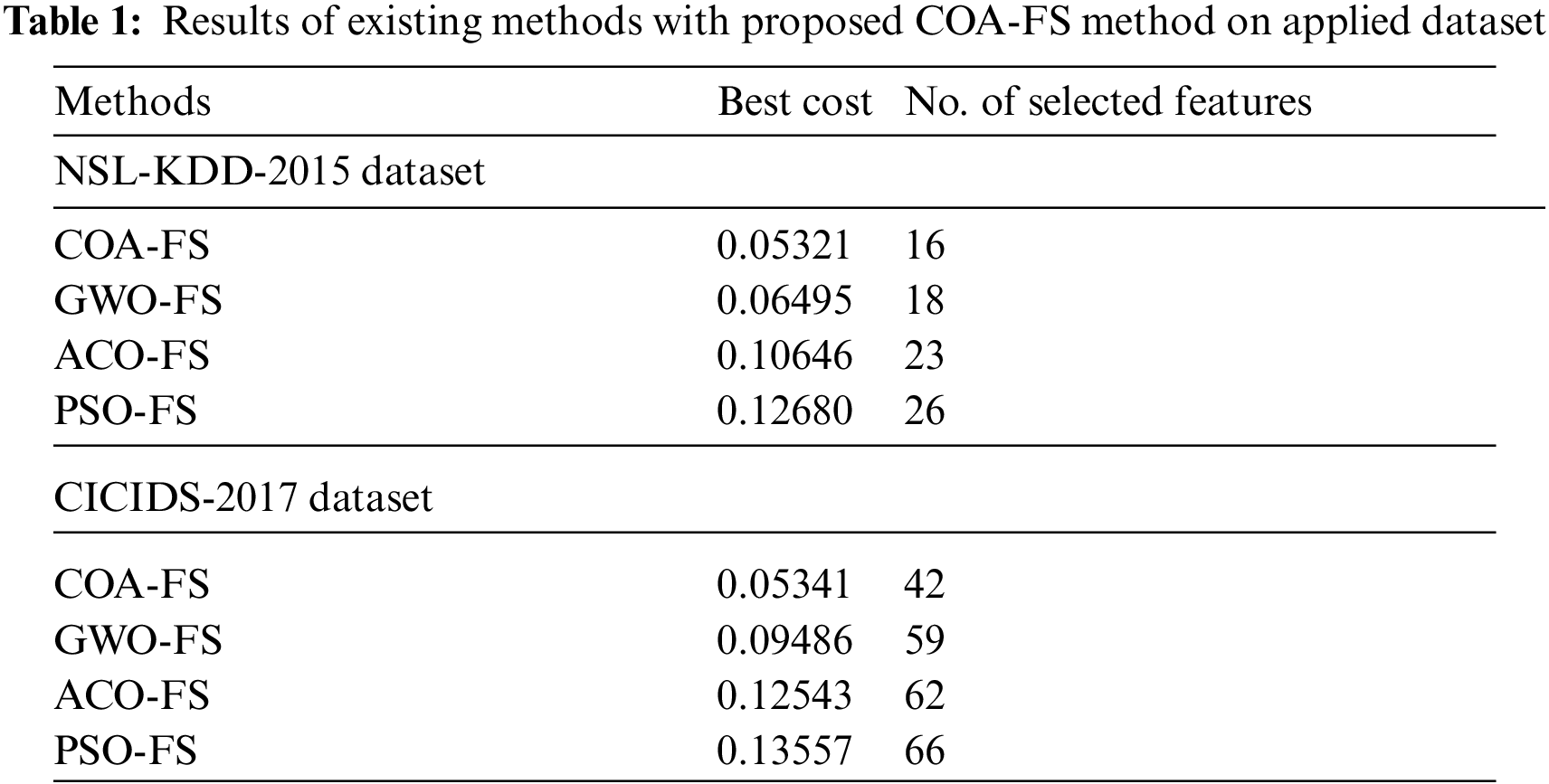
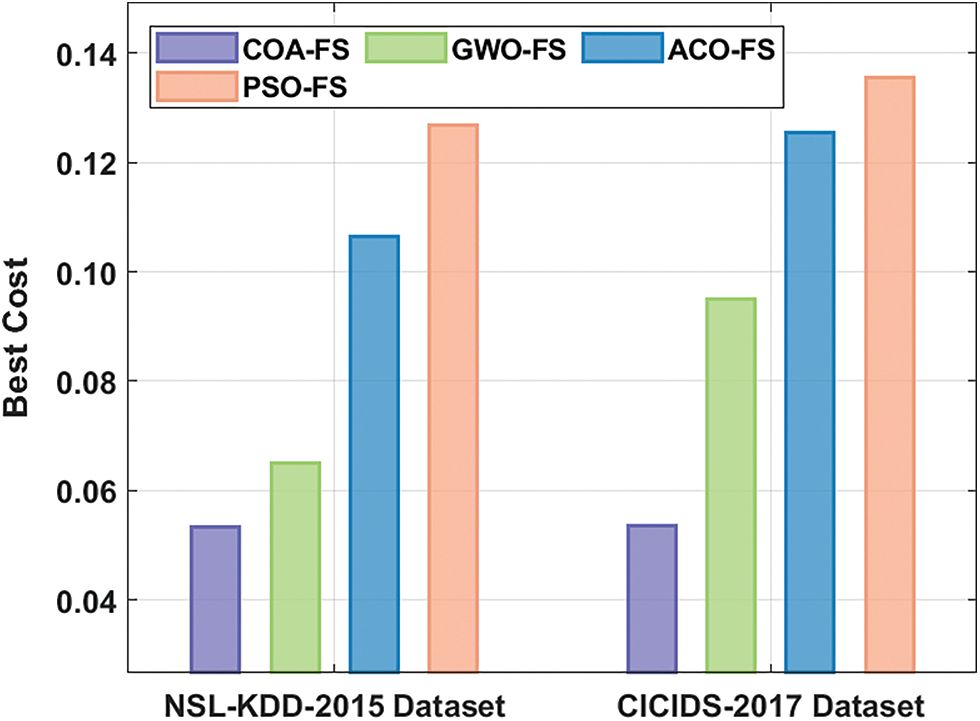
Figure 3: BC analysis of COA-FS technique

Tab. 2 offers a detailed intrusion detection result analysis of the XAIIDS-FSDVAE technique on the test NSL-KDD-2015 dataset. Fig. 4 illustrates the brief result analysis of the XAIIDS-FSDVAE technique under BS of 64 on the test NSL-KDD-2015 datasets. The figure displayed that the XAIIDS-FSDVAE technique has gained improved performance under all epochs. For instance, with 100 epochs, the XAIIDS-FSDVAE technique has provided en, recl, Fmeasure, and accy of 99.21%, 99.38%, 99.32%, 99.54%, and 99.42% respectively. Similarly, with 500 epochs, the XAIIDS-FSDVAE technique has resulted to en, recl, Fmeasure, and accy of 99.34%, 99.18%, 99.52%, 99.34%, and 99.28% respectively.

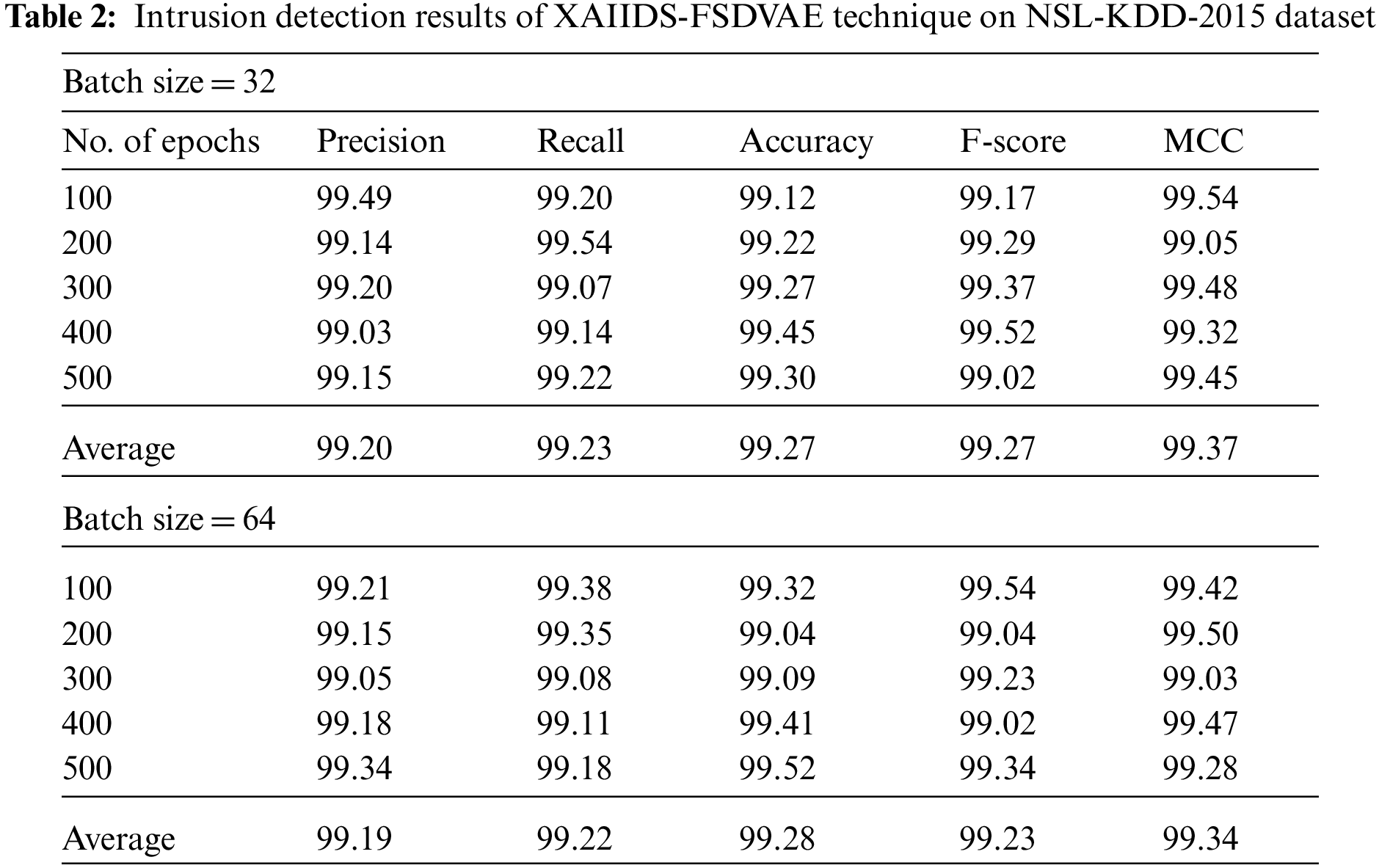
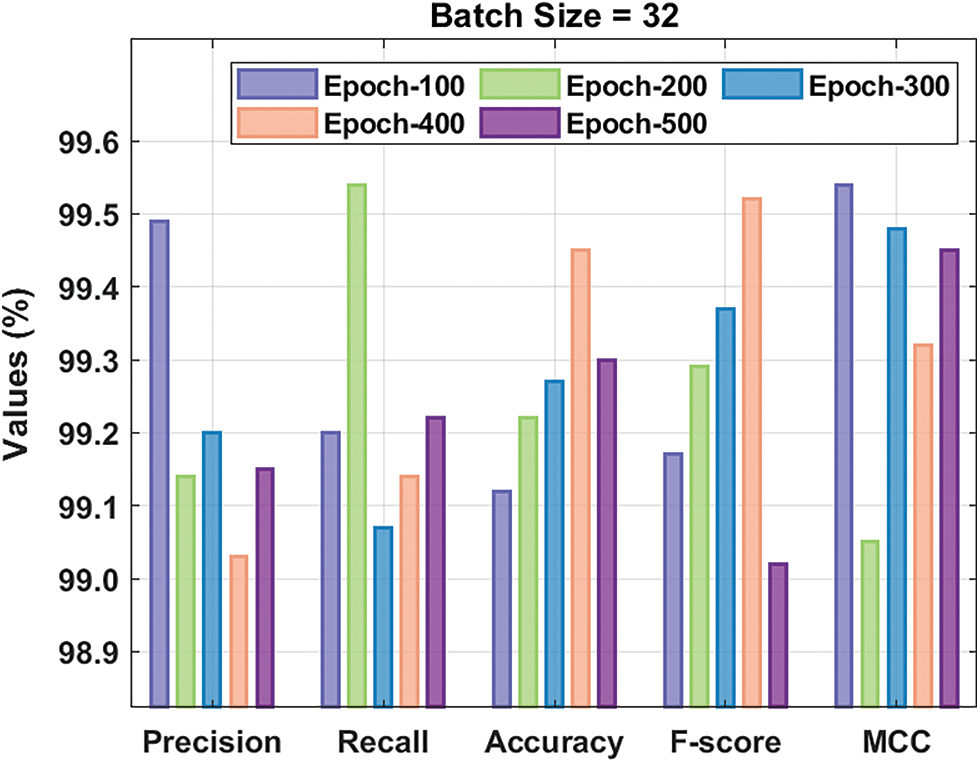
Figure 4: Result analysis of XAIIDS-FSDVAE technique under BS of 32 on NSL-KDD-2015 dataset

Fig. 5 demonstrates the overall intrusion detection result analysis of the XAIIDS-FSDVAE technique under BS of 32 on the test NSL-KDD-2015 datasets. The figure shows that the XAIIDS-FSDVAE technique has obtained effective outcomes under all epochs. For instance, with 100 epochs, the XAIIDS-FSDVAE technique has provided en, recl, Fmeasure, and accy of 99.49%, 99.20%, 99.12%, 99.17%, and 99.54% respectively. Likewise, with 500 epochs, the XAIIDS-FSDVAE technique has attained en, recl, Fmeasure, and accy of 99.15%, 99.22%, 99.30%, 99.02%, and 99.45% respectively.

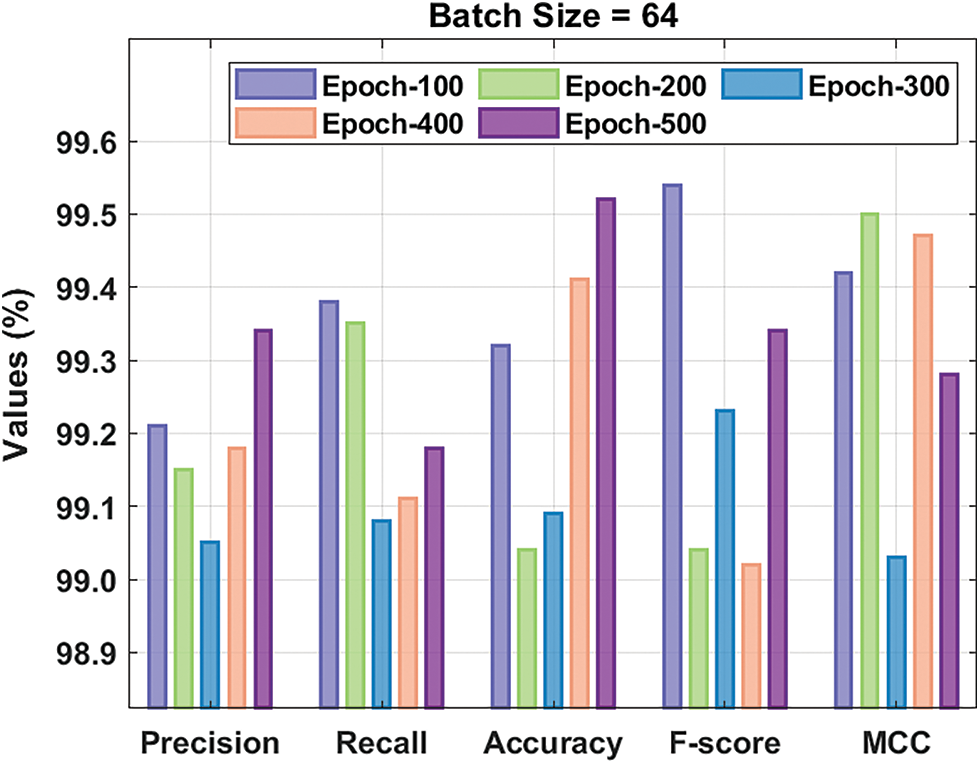
Figure 5: Result analysis of XAIIDS-FSDVAE technique under BS of 64 on NSL-KDD-2015 dataset

Fig. 6 depicts the receiver operating characteristic (ROC) analysis of the XAIIDS-FSDVAE approach on NSL-KDD-2015 dataset. The figure clear that the XAIIDS-FSDVAE process has reached increased outcome with the minimal ROC of 99.8110.

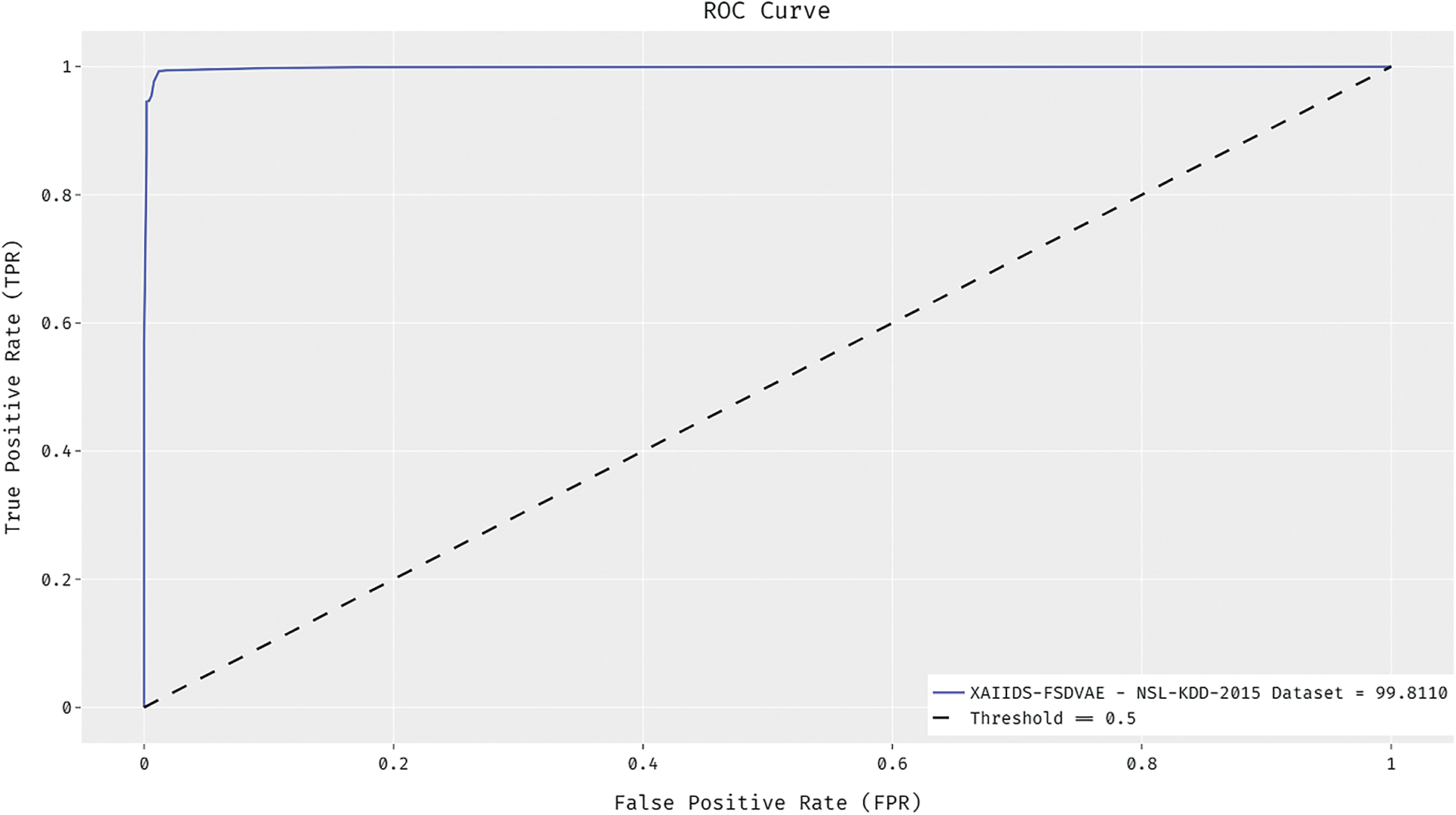
Figure 6: ROC analysis of XAIIDS-FSDVAE technique on NSL-KDD-2015 dataset

Tab. 3 illustrates a comprehensive intrusion detection result analysis of the XAIIDS-FSDVAE technique on the test CICIDS-2017 dataset.

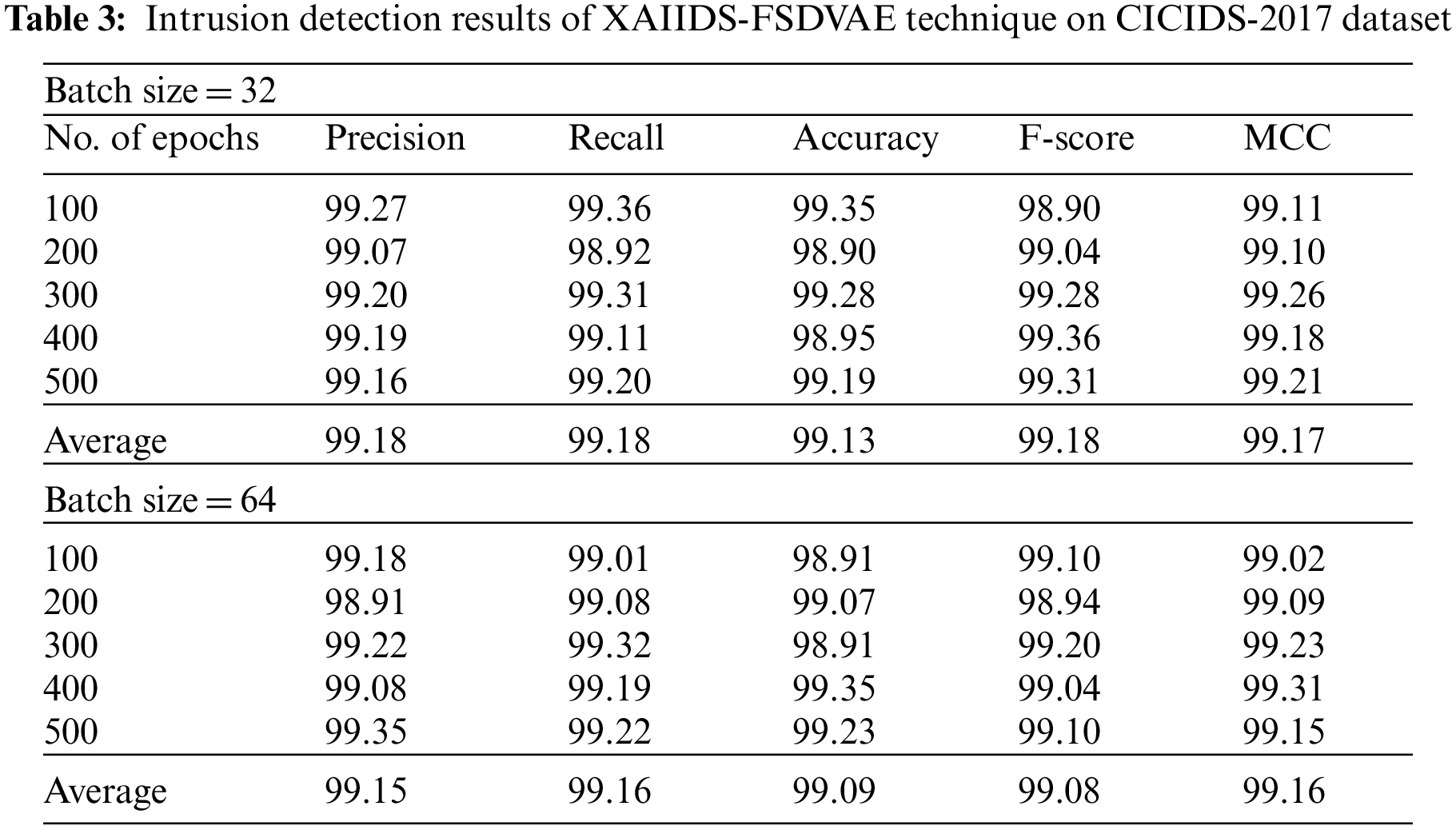
Fig. 7 exhibits the overall intrusion detection result analysis of the XAIIDS-FSDVAE technique under BS of 32 on the test CICIDS-2017 dataset. The figure revealed that the XAIIDS-FSDVAE technique has obtained operational outcomes under all epochs. For instance, with 100 epochs, the XAIIDS-FSDVAE technique has provided en, recl, Fmeasure, and accy of 99.27%, 99.36%, 99.35%, 98.90%, and 99.11% respectively. Simultaneously, with 500 epochs, the XAIIDS-FSDVAE technique has attained en, recl, Fmeasure, and accy of 99.16%, 99.20%, 99.19%, 99.31%, and 99.21% respectively.

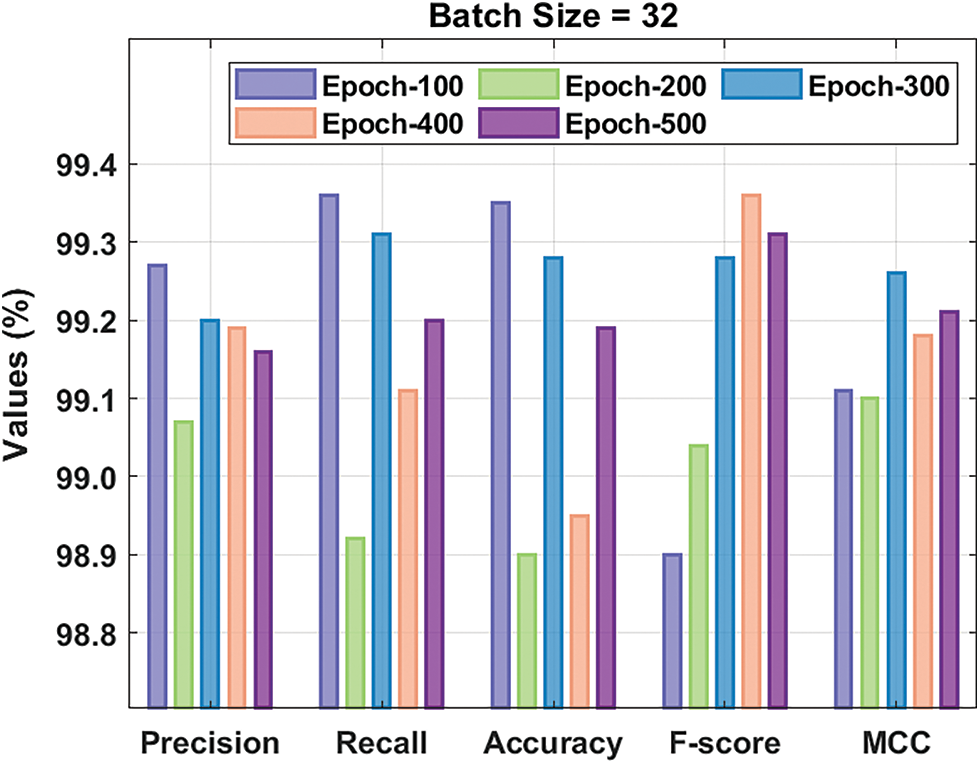
Figure 7: Result analysis of XAIIDS-FSDVAE technique under BS of 32 on CICIDS-2017 dataset

Fig. 8 validates the brief result analysis of the XAIIDS-FSDVAE technique under BS of 64 on the test CICIDS-2017 dataset. The figure exhibits that the XAIIDS-FSDVAE algorithm has extended better performance under all epochs. For instance, with 100 epochs, the XAIIDS-FSDVAE technique has provided en, recl, Fmeasure, and accy of 99.21%, 99.38%, 99.32%, 99.54%, and 99.42% respectively. In the same way, with 500 epochs, the XAIIDS-FSDVAE technique has led to en, recl, Fmeasure, and accy of 99.35%, 99.22%, 99.23%, 99.10%, and 99.15% respectively.

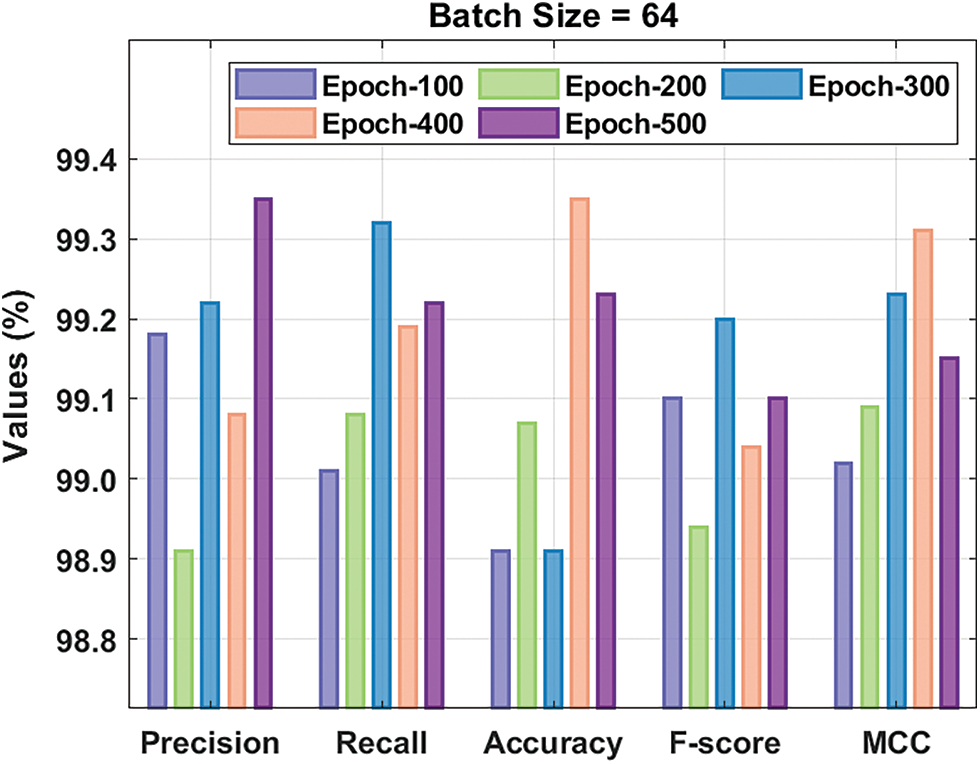
Figure 8: Result analysis of XAIIDS-FSDVAE technique under BS of 64 on CICIDS-2017 dataset

Fig. 9 demonstrates the ROC analysis of the XAIIDS-FSDVAE technique on CICIDS-2017 dataset. The figure exposed that the XAIIDS-FSDVAE technique has reached enhanced outcome with the minimum ROC of 99.6543.

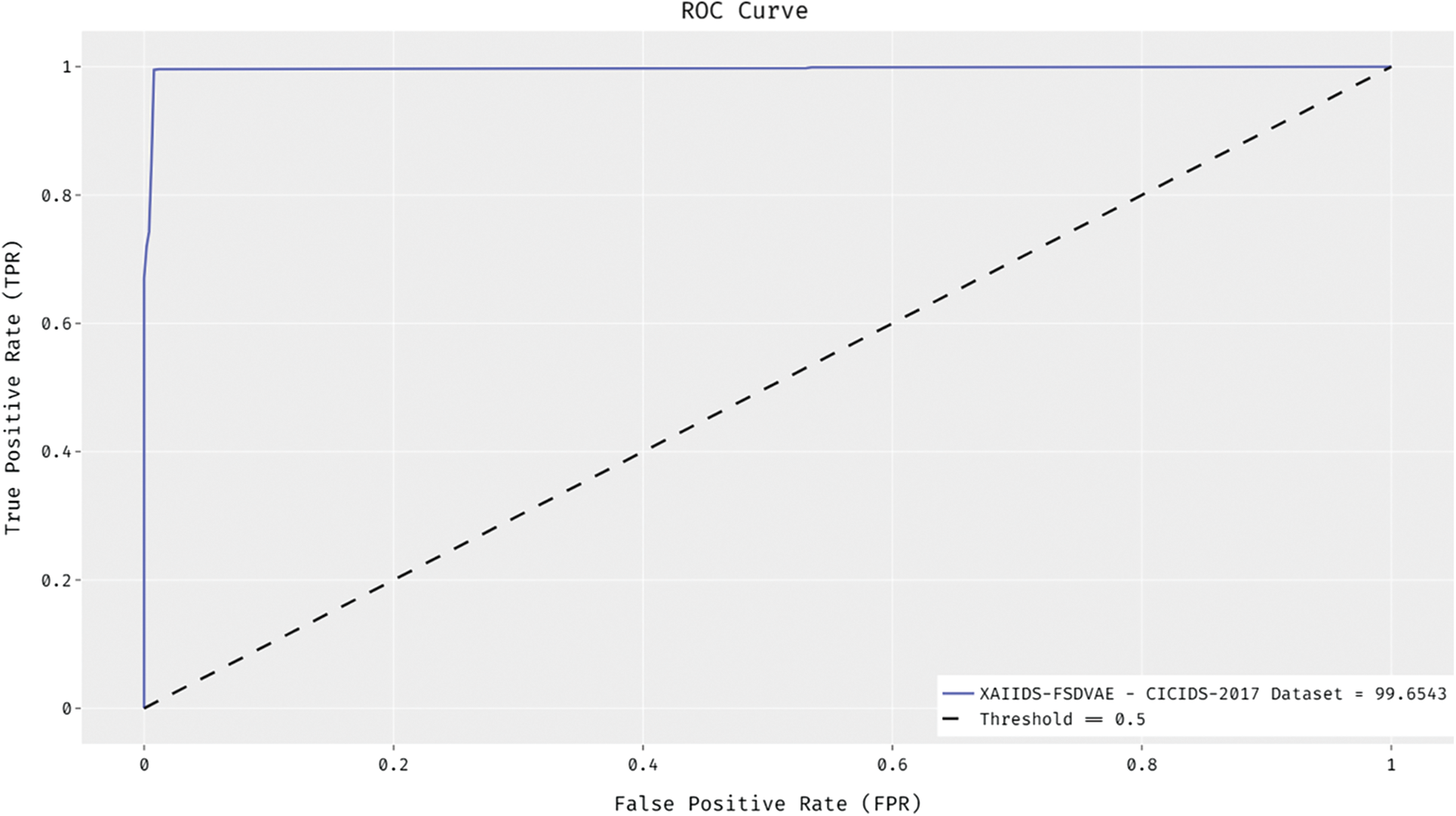
Figure 9: ROC analysis of XAIIDS-FSDVAE technique on CICIDS-2017 dataset

Tab. 4 and Fig. 10 provide a brief result analysis of the XAIIDS-FSDVAE technique with recent methods. The figure reported that the decision tree (DT), random forest (RF), and Adversarially Learned Anomaly Detection (ALAD) techniques have showcased poor performance with least values of en, recl, and Fmeasure. Followed by, the FID-GAN and Multivariate Anomaly Detection with GAN (MAD-GAN) techniques have resulted in slightly improved values of en, recl, and Fmeasure. Along with that, the DVAE and PT-DSAE techniques have reached moderately closer values of en, recl, and Fmeasure. But the XAIIDS-FSDVAE technique has outperformed the other methods with the en, recl, and Fmeasure of 99.20%, 99.23%, and 99.27% respectively.

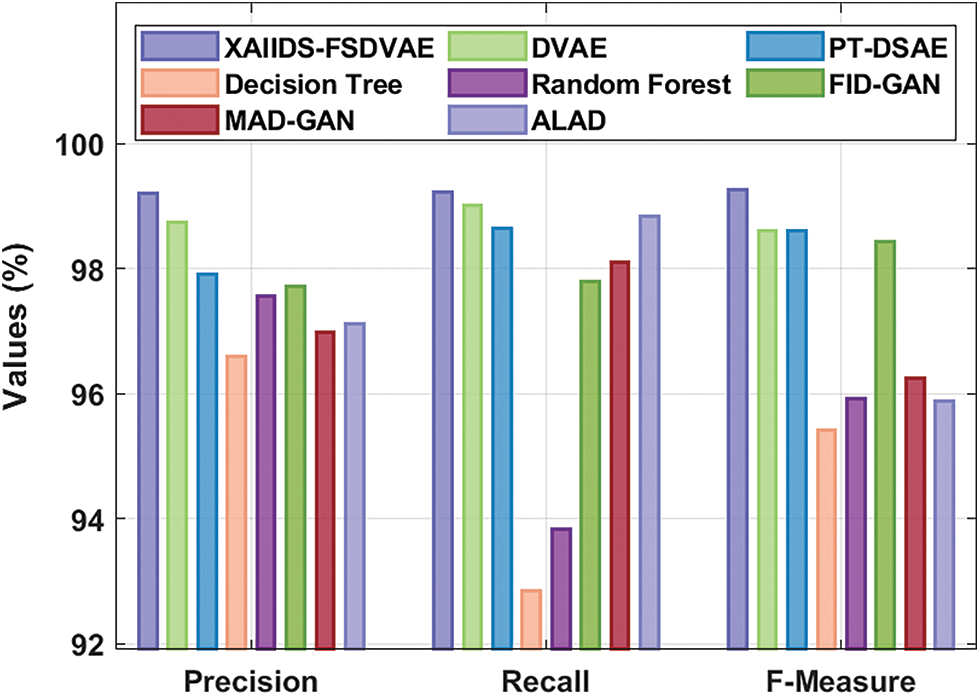
Figure 10: Comparative analysis of XAIIDS-FSDVAE technique

A comparative accy analysis of the XAIIDS-FSDVAE system with existing methodologies are shown in Fig. 11. The figure reported that the DT and ALAD techniques have obtained lower accy values of 93.65% and 94.10% respectively. In line with, the MAD-GAN, FID-GAN, and RF techniques have attained moderately closer accy values of 96.80%, 96.07%, and 95.98% respectively. Moreover, the DVAE and PT-DSAE technique has resulted in reasonable accy of 99.02% and 98.49% respectively. However, the XAIIDS-FSDVAE methodology has outperformed the existing systems with the highest accy of 99.27%.

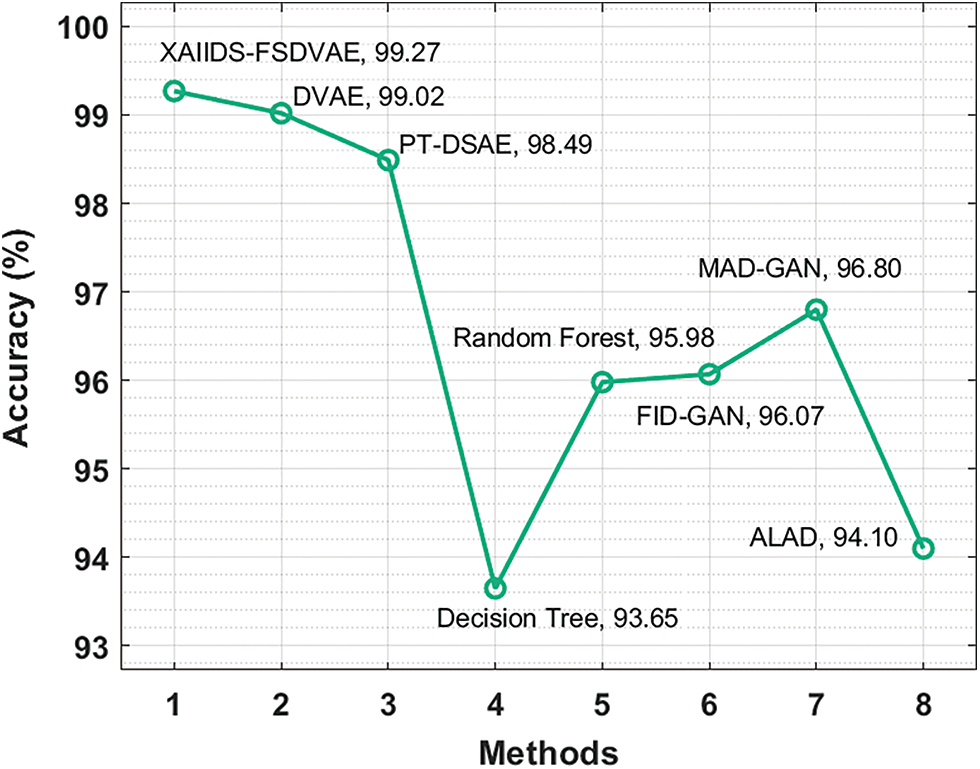
Figure 11: Accuracy analysis of XAIIDS-FSDVAE technique

5  Conclusion

In this study, a novel XAIIDS-FSDVAE approach has been presented for the detection and classification of intrusion in the CPS environments. The XAIIDS-FSDVAE technique encompasses different subprocesses namely pre-processing, COA based election of features, DVAE based classifiers, and MRFO based parameter tuning. The COA application reduces the computational complexity and MRFO algorithm helps to accomplish maximum intrusion detection performance. For demonstrating the enhanced intrusion detection efficiency of the XAIIDS-FSDVAE technique, a wide range of simulations take place using the benchmark datasets. The experimental results reported the better performance of the XAIIDS-FSDVAE technique over the recent methods in terms of several evaluation parameters. As a part of future extension, outlier detection and cluster-based approaches can be designed to boost the detection rate of the XAIIDS-FSDVAE technique.

Funding Statement: This Research was funded by the Deanship of Scientific Research at University of Business and Technology, Saudi Arabia.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  D. Ding, Q. L. Han, Y. Xiang, X. Ge and X. M. Zhang, “A survey on security control and attack detection for industrial cyber-physical systems,” Neurocomputing, vol. 275, pp. 1674–1683, 2018. [Google Scholar]

 2.  C. M. Paredes, D. M. Castro, V. I. Junquera and A. G. Potes, “Detection and isolation of DoS and integrity cyber-attacks in cyber-physical systems with a neural network-based architecture,” Electronics, vol. 10, no. 18, pp. 2238, 2021. [Google Scholar]

 3.  C. Liang, B. Shanmugam, S. Azam, A. Karim, A. Islam et al., “Intrusion detection system for the internet of things based on blockchain and multi-agent systems,” Electronics, vol. 9, no. 7, pp. 1120, 2020. [Google Scholar]

 4.  D. Midi, A. Rullo, A. Mudgerikar and E. Bertino, “Kalis—A system for knowledge-driven adaptable intrusion detection for the internet of things,” in 2017 IEEE 37th Int. Conf. on Distributed Computing Systems (ICDCS), Atlanta, GA, USA, pp. 656–666, 2017. [Google Scholar]

 5.  R. Mitchell and I. R. Chen, “A survey of intrusion detection techniques for cyber-physical systems,” ACM Computing Surveys, vol. 46, no. 4, pp. 1–29, 2014. [Google Scholar]

 6.  K. D. Kim and P. R. Kumar, “An overview and some challenges in cyber-physical systems,” Journal of the Indian Institute of Science, vol. 93, no. 3, pp. 341–352, 2013. [Google Scholar]

 7.  R. C. B. Hink and K. G. Popstojanova, “Characterization of cyberattacks aimed at integrated industrial control and enterprise systems: A case study,” in 2016 IEEE 17th Int. Symp. on High Assurance Systems Engineering (HASE), Orlando, FL, USA, pp. 149–156, 2016. [Google Scholar]

 8.  S. Krishnamurthy, S. Sarkar and A. Tewari, “Scalable anomaly detection and isolation in cyber-physical systems using Bayesian networks,” in Proc. of the ASME 2014 Dynamic Systems and Control Conf., American Society of Mechanical Engineers, San Antonio, Texas, USA, pp. V002T26A006, 2014. [Google Scholar]

 9.  A. Jones, Z. Kong and C. Belta, “Anomaly detection in cyber-physical systems: A formal methods approach,” in Proc. of the 2014 IEEE 53rd Annual Conf. on Decision and Control, Los Angeles, CA, USA, pp. 848–853, 2014. [Google Scholar]

10. J. Vallverdú, “Approximate and situated causality in deep learning,” Philosophies, vol. 5, no. 1, pp. 2, 2020. [Google Scholar]

11. N. O. Aljehane, “A secure intrusion detection system in cyberphysical systems using a parameter-tuned deep-stacked autoencoder,” Computers, Materials & Continua, vol. 68, no. 3, pp. 3915–3929, 2021. [Google Scholar]

12. M. E. Hariri, E. Harmon, H. F. Habib, T. Youssef and O. A. Mohammed, “A targeted attack for enhancing resiliency of intelligent intrusion detection modules in energy cyber physical systems,” in 2017 19th Int. Conf. on Intelligent System Application to Power Systems (ISAP), San Antonio, TX, USA, pp. 1–6, 2017. [Google Scholar]

13. B. Li, Y. Wu, J. Song, R. Lu, T. Li et al., “DeepFed: Federated deep learning for intrusion detection in industrial cyber–physical systems,” IEEE Transactions on Industrial Informatics, vol. 17, no. 8, pp. 5615–5624, 2021. [Google Scholar]

14. R. Gifty, R. Bharathi and P. Krishnakumar, “Privacy and security of big data in cyber physical systems using weibull distribution-based intrusion detection,” Neural Computing and Applications, vol. 31, no. S1, pp. 23–34, 2019. [Google Scholar]

15. V. Belenko, V. Chernenko, M. Kalinin and V. Krundyshev, “Evaluation of GAN applicability for intrusion detection in self-organizing networks of cyber physical systems,” in 2018 Int. Russian Automation Conf. (RusAutoCon), Sochi, Russia, pp. 1–7, 2018. [Google Scholar]

16. H. A. Khan, N. Sehatbakhsh, L. N. Nguyen, R. L. Callan, A. Yeredor et al., “IDEA: Intrusion detection through electromagnetic-signal analysis for critical embedded and cyber-physical systems,” IEEE Transactions on Dependable and Secure Computing, vol. 18, no. 3, pp. 1150–1163, 2019. [Google Scholar]

17. P. F. d. A. Filho, G. Kaddoum, D. R. Campelo, A. G. Santos, D. Macedo et al., “Intrusion detection for cyber–physical systems using generative adversarial networks in fog environment,” IEEE Internet of Things Journal, vol. 8, no. 8, pp. 6247–6256, 2021. [Google Scholar]

18. J. Pierezan and L. D. S. Coelho, “Coyote optimization algorithm: A new metaheuristic for global optimization problems,” in 2018 IEEE Congress on Evolutionary Computation (CEC), Rio de Janeiro, Brazil, pp. 1–8, 2018. [Google Scholar]

19. Z. Yuan, W. Wang, H. Wang and A. Yildizbasi, “Developed coyote optimization algorithm and its application to optimal parameters estimation of PEMFC model,” Energy Reports, vol. 6, pp. 1106–1117, 2020. [Google Scholar]

20. B. Crawford, R. Soto, G. Astorga, J. García, C. Castro et al., “Putting continuous metaheuristics to work in binary search spaces,” Complexity, vol. 2, pp. 1–19, 2017. [Google Scholar]

21. R. C. T. d. Souza, C. A. d. Macedo, L. d. S. Coelho, J. Pierezan and V. C. Mariani, “Binary coyote optimization algorithm for feature selection,” Pattern Recognition, vol. 107, pp. 107470, 2020. [Google Scholar]

22. W. Joo, W. Lee, S. Park and I. C. Moon, “Dirichlet variational autoencoder,” Pattern Recognition, vol. 107, pp. 107514, 2020. [Google Scholar]

23. D. A. Knowles, “Stochastic gradient variational Bayes for gamma approximating distributions,” arXiv preprint arXiv:1509.01631, 2015. [Google Scholar]

24. W. Zhao, Z. Zhang and L. Wang, “Manta ray foraging optimization: An effective bio-inspired optimizer for engineering applications,” Engineering Applications of Artificial Intelligence, vol. 87, pp. 103300, 2020. [Google Scholar]

25. A. Fathy, H. Rezk and D. Yousri, “A robust global MPPT to mitigate partial shading of triple-junction solar cell-based system using manta ray foraging optimization algorithm,” Solar Energy, vol. 207, pp. 305–316, 2020. [Google Scholar]

26. M. Tavallaee, E. Bagheri, W. Lu and A. Ghorbani, http://www.unb.ca/research/iscx/dataset/iscx-NSL-KDD-dataset.html. 2015. [Google Scholar]

27. I. Sharafaldin, A. H. Lashkari and A. A. Ghorbani, https://www.unb.ca/cic/datasets/ids-2017.html. 2018. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.