DOI:10.32604/cmc.2022.025865

| Computers, Materials & Continua DOI:10.32604/cmc.2022.025865 |  |
| Article |
Imbalanced Classification in Diabetics Using Ensembled Machine Learning
1School of Information Technology and Engineering, Vellore Institute of Technology, Vellore, Tamil Nadu, 632014, India
2Department of Computer Science and Information, Taibah University, Medina, Saudi Arabia
3College of Computer Science and Engineering, Taibah University, Medina, Saudi Arabia
*Corresponding Author: Mohammad Zubair Khan. Email: zubair.762001@gmail.com
Received: 07 December 2021; Accepted: 16 February 2022
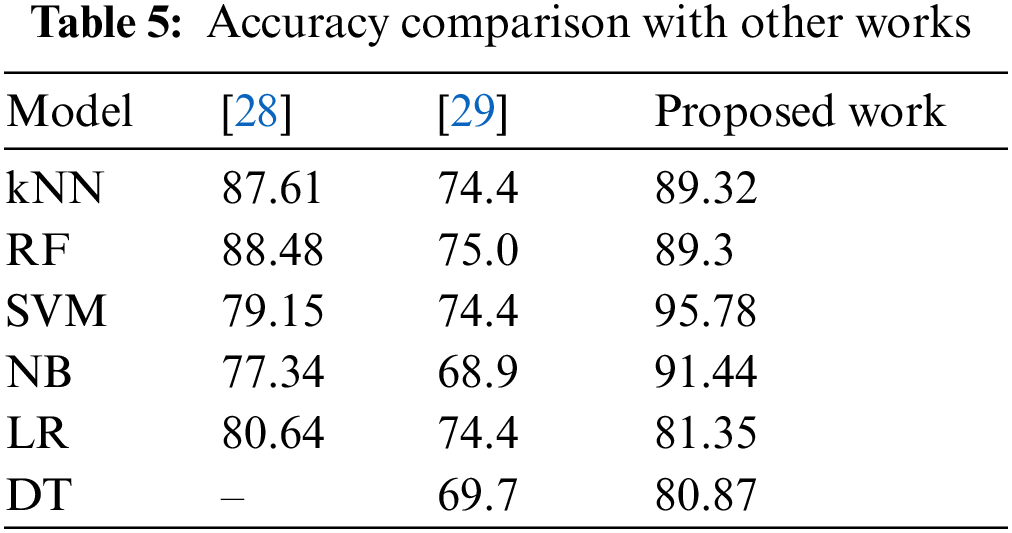
Abstract: Diabetics is one of the world’s most common diseases which are caused by continued high levels of blood sugar. The risk of diabetics can be lowered if the diabetic is found at the early stage. In recent days, several machine learning models were developed to predict the diabetic presence at an early stage. In this paper, we propose an embedded-based machine learning model that combines the split-vote method and instance duplication to leverage an imbalanced dataset called PIMA Indian to increase the prediction of diabetics. The proposed method uses both the concept of over-sampling and under-sampling along with model weighting to increase the performance of classification. Different measures such as Accuracy, Precision, Recall, and F1-Score are used to evaluate the model. The results we obtained using K-Nearest Neighbor (kNN), Naïve Bayes (NB), Support Vector Machines (SVM), Random Forest (RF), Logistic Regression (LR), and Decision Trees (DT) were 89.32%, 91.44%, 95.78%, 89.3%, 81.76%, and 80.38% respectively. The SVM model is more efficient than other models which are 21.38% more than exiting machine learning-based works.
Keywords: Diabetics classification; imbalanced data; split-vote; instance duplication
Classification-based models such as kNN, SVM, RF, and so on suffer from a problem called a class imbalance. Imbalanced classification is a situation where there are a significantly different number of instances across the various classes. Specifically, during the binary classification, if there are number of instances in one class (called as majority class) than the number of instances in the other class (called as minority class), then there is an imbalanced classification. When the frequency of instances among all the classes is not equally distributed, then the classifier understands more about a single class and very little about other classes. A classifier may produce high False Negative rates during the imbalance data scenario [1] because the classifier wrongly classifies an instance of one class to another. Imbalanced data causes problems many classification applications such as spam detection [2], bug prediction [3], sentimental analysis [4], credit card classification [5], and much more.
There are many ways the researchers are handling this imbalanced data problem. One of the methods is called the weighting-based approach [6]. In this approach, the classifier is allowed to learn from the training set with imbalanced instances. Later, a weight is assigned to the classifier to reduce the classification error. This approach can be very dangerous sometimes because it is very highly error-prone. Consider an imbalanced data scenario in which a classifier is deployed to determine a patient is having heart disease or not. The cost of wrongly predicting a heart patient as a normal patient is more dangerous than predicting a normal patient as a heart patient.
The second method to deal with the imbalance problem is under-sampling [7], where the instances of the majority class are removed one by one until there is an equal instance distribution among all classes. The important drawback of this approach is the loss of information [8]. The key information that determines the important attributes of a feature may get lost and the classifier may produce a high false rate during the testing phase. Many researchers omit this method due to the above-mentioned reason. In some cases, few samples may be noisy or redundant. If they are used in the training process, it creates unusual problems such as increased computation cost, degrading the performance, high false rates, and so on. These samples can be removed using the under-sampling method to eliminate the noises in the dataset. Few research works like [9] develop under-sampling from majority class to find the class boundary. Once the class boundary of the minority class is found, the original dataset is used for classification.
The third method is over-sampling which increases the instance of the minority classes by adding new samples. The newly added samples are done statistically so that it is not a duplicate of already existing instances. In recent years, over-sampling is used by many research works [10,11]. The main drawback of this approach is it increases the chances of overfitting. A combination of both under-sampling and over-sampling can also increase the performance of a classifier [12,13]. The generated dummy instances should not alter the original dataset and should obey the distribution of the minority class. An unbiased classification can be done only if the whole dataset distribution is unaltered. If the data distribution is known, it is very easy to generate the samples; however, in most cases, the distribution of the dataset is unknown. In that case, estimation should be done in such a way that the estimated parameters more or less match the original dataset. If not, then there will be misleading samples that will ruin the performance of the classification.
One of the efficient methods in handling the imbalance problem is the ensemble approach where multiple classifiers collectively are used to classify an instance into a class [14,15]. Despite many popular embedded-based binary imbalanced classifiers, the performance of the imbalanced classification still degrades. Over the years, this has attracted much attention in the research community to build more powerful imbalanced classifiers. Many research works focus on developing dynamic classification, where the classification is done by selecting subsets of the data. Finally, either selecting the best or combining multiple classifiers is done in the embedded process. The main novelty of this embedded process relay on how the merging is done. This paper focuses on using this ensemble approach to handle the imbalance problem by two methods called as split-vote method and dummy instance generation. We have used an ensemble of two approaches called as split-vote method and instance generation method. In the split-vote method, the dataset is first to split into multiple sub-datasets and then each subset is used to train various machine learning models. We pick the best machine learning models for each sub-set and then finally perform the voting operation to predict the final class of an instance. During the splitting process, there is a high chance that a set of important features might get missed out in a particular set, so hence we perform instance duplication to each set. The subsets are generated by both unique instances as well as mixed instances. The mixed instances can assure that the same instance is present in more than one sub-set. The next step is instance duplication, where a clustering algorithm is used to group similar data points in the feature space and generate dummy instances without affecting the characteristics of a cluster. Finally, the voting is done from the two approaches with the original dataset and the final class is found out.
In this paper, we propose an ensemble machine learning model that efficiently classifies an imbalanced dataset for diabetics. The main contributions are listed below
• To develop a split-vote methodology for dividing an imbalanced dataset into a finite number of balanced datasets.
• To generate dummy instances without affecting the statistical properties of an imbalanced dataset.
• To use model weighting and feature selection to enhance the voting process.
The above-mentioned contributions aim to convert an imbalanced dataset into a balanced one. The proposed method first uses the under-sampling method by duplicating the dataset into finite number of times and at each set, random data samples were discarded to make all the classes evenly distributed. Then over-sampling is performed by generating dummy instances. The dummy instances are not an exact replicate of any original instances, but share only the statistical properties. Finally, the performance of the proposed system is increased by assigning weights based on how well each model has been learned.
The rest of the paper is organized as follows. Section 2 briefs the literature related to imbalanced classification. Section 3 contains the working of the proposed algorithms. Section 4 presents the experimental results and the comparison with existing machine learning models and with other existing works. Finally, the conclusion is present in Section 5.
A research work done by [16] proposes an ensemble classification approach. They aim to reduce the rate of overfitting by proposing implicit regularization. They have considered the binary imbalanced data classification problem. 12 datasets were considered by the authors for validating the proposed method. Generating two new virtual spaces along with the original dataset and feeding the same to the SVM classifier can significantly reduce the imbalance problem as per [17]. They have incorporated fuzzy concepts in their proposed architecture and found that the searching time is reduced.
Random sampling is one of the widely used methods to handle imbalanced data; however, the use of random sampling can lead to undesirable results. Hence [18] proposes a stable method for determining sampling ratios based on genetic algorithms. They have used 14 datasets to validate the performance of their proposed work.
A work done by [19] focuses on optimizing the AdaBoost algorithm. They have proposed a new weighting approach that can boost the weak classifiers. Two synthetic datasets and four original datasets were used to test the performance of the proposed work.
Reference [20] uses the Hellinger Distance Weighted Ensemble model for tackling imbalanced data. Feature drift is one of the problems in spam detection which the authors consider for generating appropriate features. Using these features, spam detection is done efficiently.
Many oversampling techniques such as [21] add the synthetic instance to minority class so that the number of minority class is equal to the majority class instances. However, there is a high chance that the synthetic instances can create noise in the dataset. Even the synthetic instances can also modify the decision boundary of the classifiers [21].
Data resampling can cause important instances to be lost forever and often leads to oversampling, a work by [22] focuses on gaining advantages of both data level and the ensemble of classifiers. They apply a few pre-processing steps to the training phase of each classifier and compare them using eight datasets.
Fuzzy-based methods are used in [23] where the authors have used two families of classifiers. One is purely based on bag level and another one is based on instance level. Using these two types they have solved the imbalance problem with the help of multi-instances.
As many methods work on alternating the original dataset [24], a research work proposed by [22] aims to develop a balanced dataset from an imbalanced dataset and perform an ensemble to consolidate the result. This process prevents important data to be lost in the classification. Tab. 1 shows a few existing research works in the field of imbalance classification.
Four stage imbalance handling were proposed by [25] which includes component analysis, feature selection, SVM based minor classification and sampling. They have used coloring scheme to classify buildings and their connected components. Four machine learning models were used by the authors to classify 3D objects. They show that after using SVM, the performance of the classification increases to a promising amount.
Another research [26] provided a cost sensitive classification by assigning weights to majority and minority data. This creates a strong bias which helps in reducing the classification errors.
From the above-mentioned literature, the imbalanced classification needs lots of improvement in the areas of over-sampling and under-sampling. The proposed work introduces split-vote method for sub set creation and instance duplication for dataset balancing. We have used sim machine learning models are compared the results with existing works.
3 Imbalance Data Classification
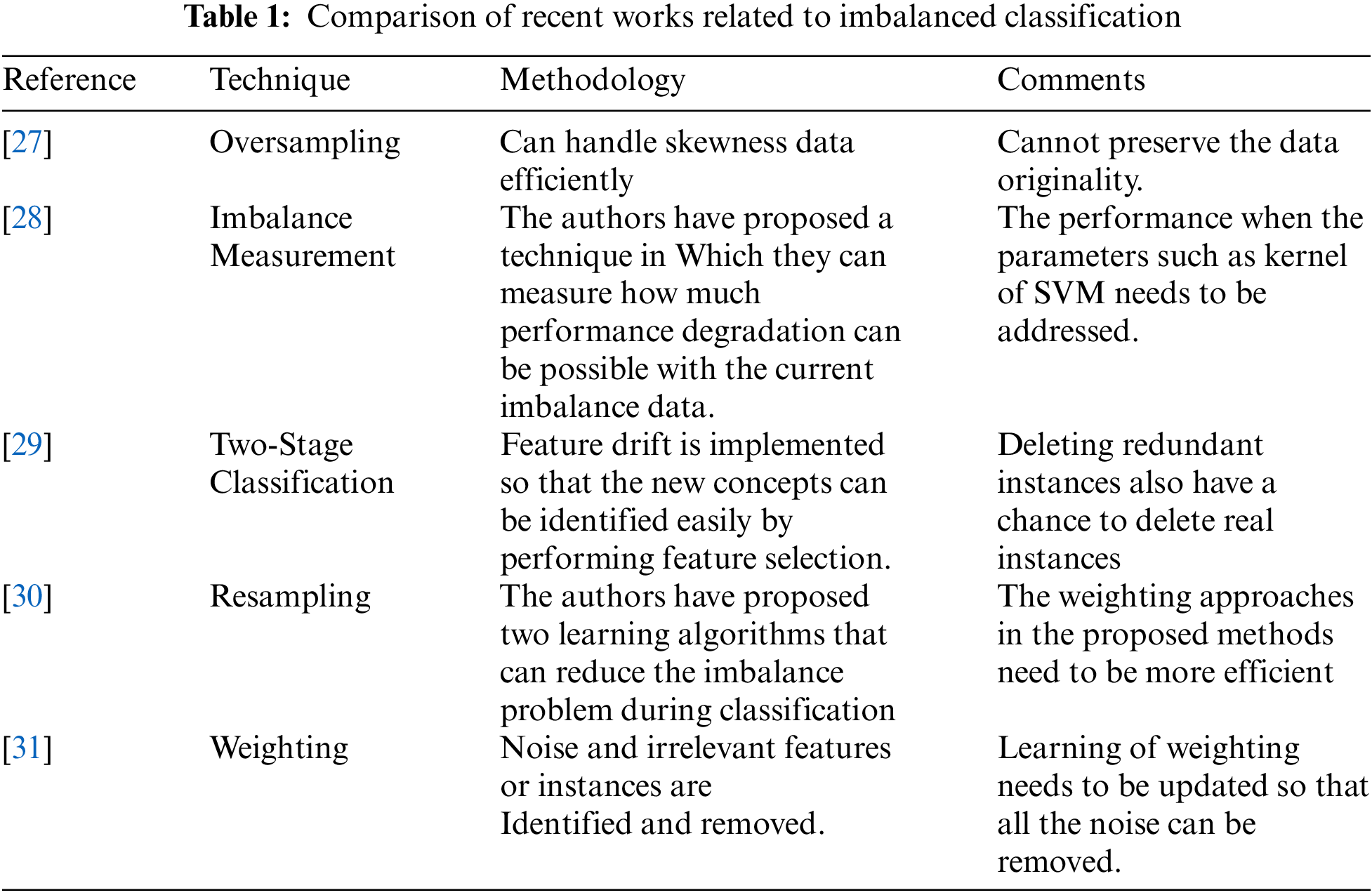
A classifier expects all the classes in the training set to be balanced. However, in real-time, it is very difficult to find a dataset with balanced classes. Several techniques shown in Section 2 have been used by various researchers to overcome the imbalance problem. In this section, we present an embedded-based machine learning model which works in three stages as shown in Fig. 1.
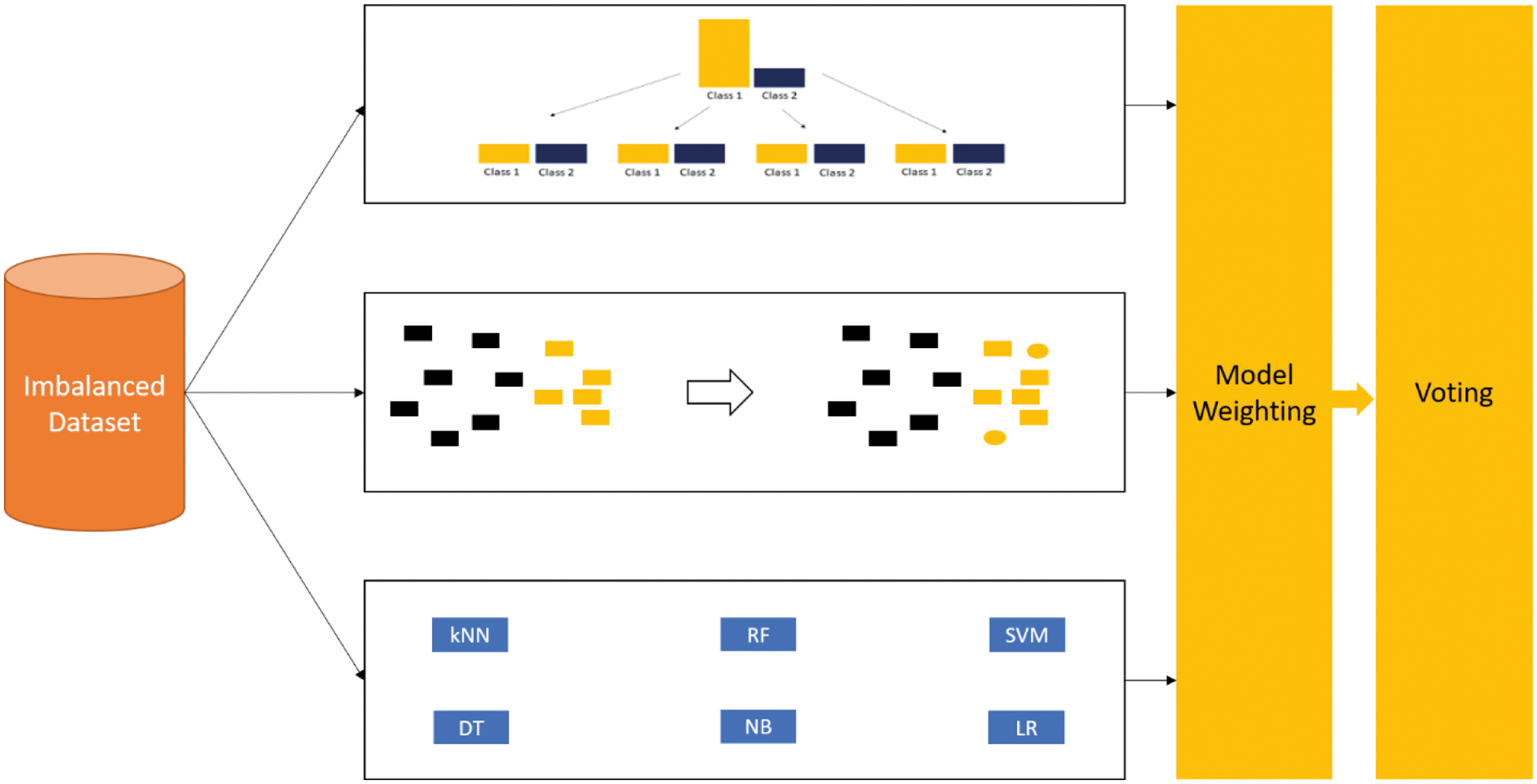
Figure 1: Architecture of the proposed embedded based model
A good performance can be achieved if proper preprocessing is done before classification [32]. In this paper, we do the preprocessing in many stages. In the first stage, the dataset is divided into multiple subsets such that each subset contains an equal number of instances in both positive and negative classes. The next stage generates dummy instances without affecting the statistical properties of the dataset. The last stage is the normal machine learning model which uses the raw dataset for classification. The output of each stage is passed to a weighting step where the classification output is given some priority based on the performance of each machine learning model. The working of each stage is explained in more detail in the following subsections.
Let us consider D as the set of all instances as defined by 1. X is the input feature defined by Eq. (2) and Y is considered as binary value in this research work, where C1 represents the first class and C2 represents the second class. An imbalance problem is when the number of instances of both C1 and C2 is different and the difference exceeds the tolerable amount IM as defined by Eq. (3).
The generation of sub sets is defined as per Eq. (4). Each subset is generated by balancing the number of instances of both classes. During the process of training, there is a high chance that very important instances fall in only a few of the sub-sets. Thus, the majority of the subsets may yield poor results. To tackle this problem, we have performed instance shuffling where a portion of random instances are duplicated across multiple sub-sets. This step largely reduces the risk of an important instance being missed out in the majority of the subsets.
Unlike the first stage, the dataset is not divided into sub-datasets; moreover, dummy instances are generated in the minority class to match the number of classes in the majority class. To perform the instance generation, clustering is used to group instances into distinct classes. The clustering algorithm is explained in Algorithm 1.

Algorithm 1 is used to cluster each instance into one class. Then instance duplication can be done using the normal distribution as shown in Eq. (5). The generated instances ensure that the statistical parameters of each cluster are not affected. If there are 500 instances of the majority class and 200 instances of the minority class, then 300 instances are generated from the minority class to match the majority class instances. Here we use clustering for finding out the commonality between the instances. Suppose, there are 5 clusters formed within the 200 instances, then 60 dummy instances are created in each cluster to match the majority class.
The final step is that the classifiers use the raw pre-processed dataset to classify diabetics. Four standard machine learning models are used for classification. Each machine learning model is briefed in the following sub-sections.
KNN is one of the simple machine learning models that work by the concept of neighbors. When an instance needs to be classified, the kNN considers k closest neighbors, and the target class is fixed by majority voting. The value of K should be fixed before starting the classification process. Based on the investigational study, the value of K is always an odd number. This classifier is called a lazy classifier because it does nothing during the training phase. The actual implementation is only done during the testing phase, where the distance between all the exiting points is calculated and sorted in ascending order. Finally, the first k values are picked to determine the class of the instance.
Naive Bayes is one of the frequently used ML models. This model utilizes the concepts of probability to find out the target class of the instance. NB groups similar instances based on the Bayes probability theorem. Naïve Bayes is the second most used machine learning model after SVM for classifying diabetics.
Support Vector Machines can be used for classifying both linear and non-linear data. It maps all the instances into a hyperplane; afterward, it ideally finds a linear separation among them. The separation is done using the endpoints which are also called support vectors because it is used to decide the separation.
RF is an ensemble model of multiple DTs. All the DTs are independently trained and hence with better prediction can be achieved. Every DT selects a class based on its trained knowledge and finally, a bagging strategy is performed to pick the class with the highest frequency.
LR considers one or more independent features and tries to approximate the relationships within them. Several types of LR exist such as binary model, multi-class model, ordered model, and conditional model. LR seems to produce less performance when compared with other models because it is highly error-prone.
DT works with the concept of decision-making. It constructs tree-like structures where each branch represents a decision. If there are multiple decisions, then there are multiple branches. High-dimensional data can be easily processed using decision trees.
After the classification is done, a weight should be given to each stage for the ensemble to happen. The weight is just the accuracy of the classifier. Suppose a machine learning model produces 75% accuracy, its weight is 75 because the model is 75% effective. The higher the accuracy, the better learning capacity the model has. The cumulative weights across all stages are considered to predict the final class. For example, if the cumulative weight of the negative class is 400 and the cumulative weight of the positive class is 350, then the patient data is classified as diabetic negative. Two weights are given for each classifier. The first weight considers all the features and the second weight considers only the 5 most important features. The most important feature is considered using correlation values. Fig. 2 shows how each model receives two sets of features.
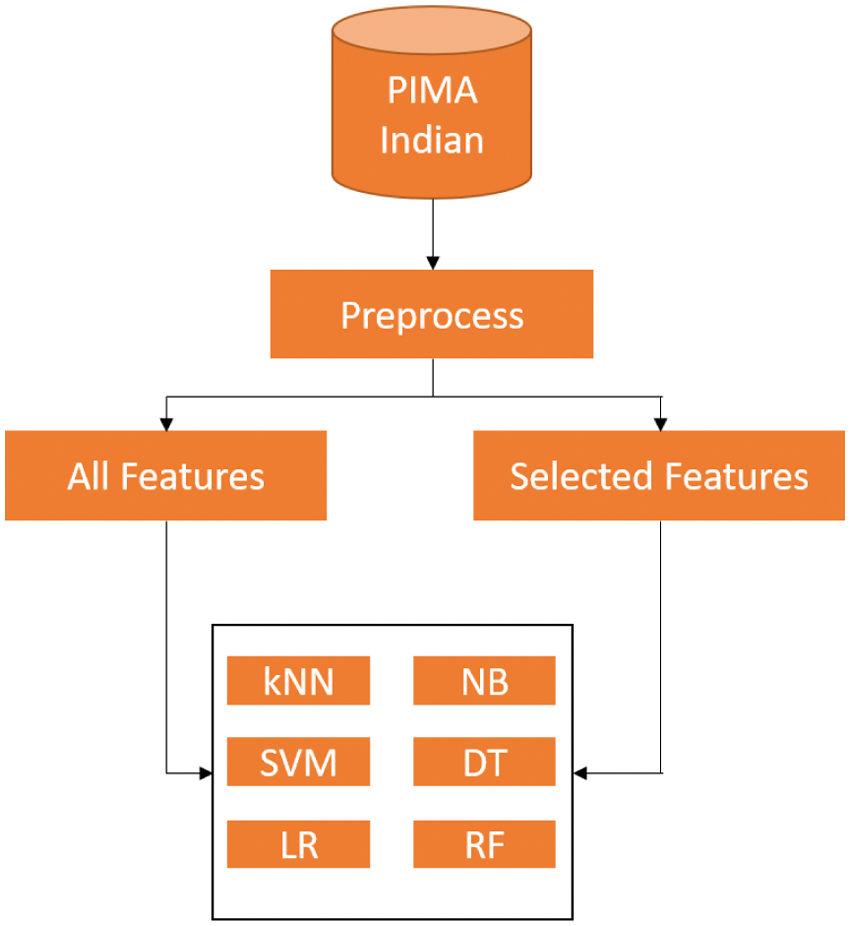
Figure 2: Feature selection in model weighting
We have used PIMA Indian dataset for testing the proposed model and the analysis results were compared with existing machine learning models. We have used k fold validation (k = 10) for the experiment.
The dataset contains 768 instances with nine attributes. The details of the attributes are listed in Tab. 2.
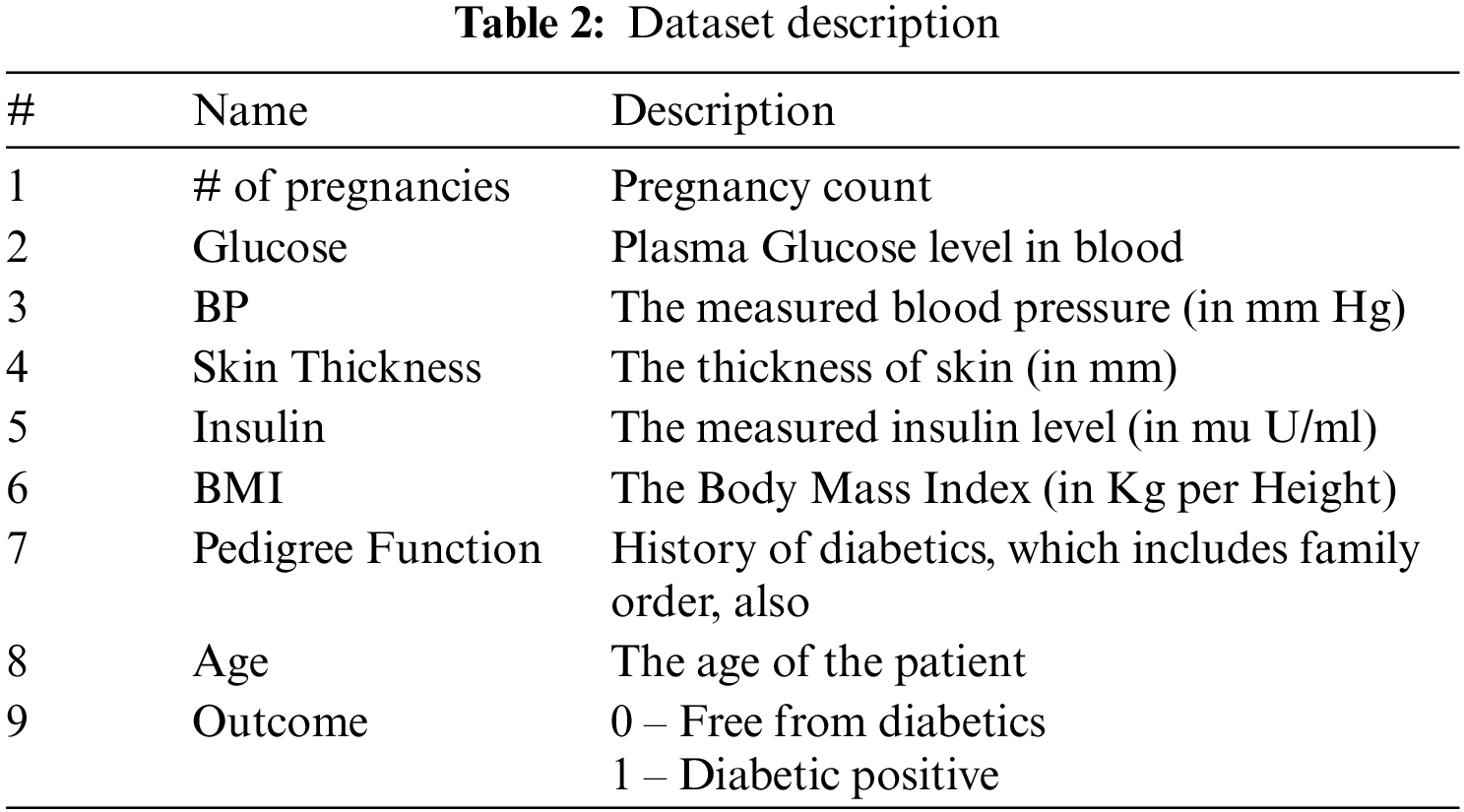
The dataset contains lots of missing values. We have used mean values to replace the missing values. Tab. 3 contains the missing values and the details of the mean value for each feature.
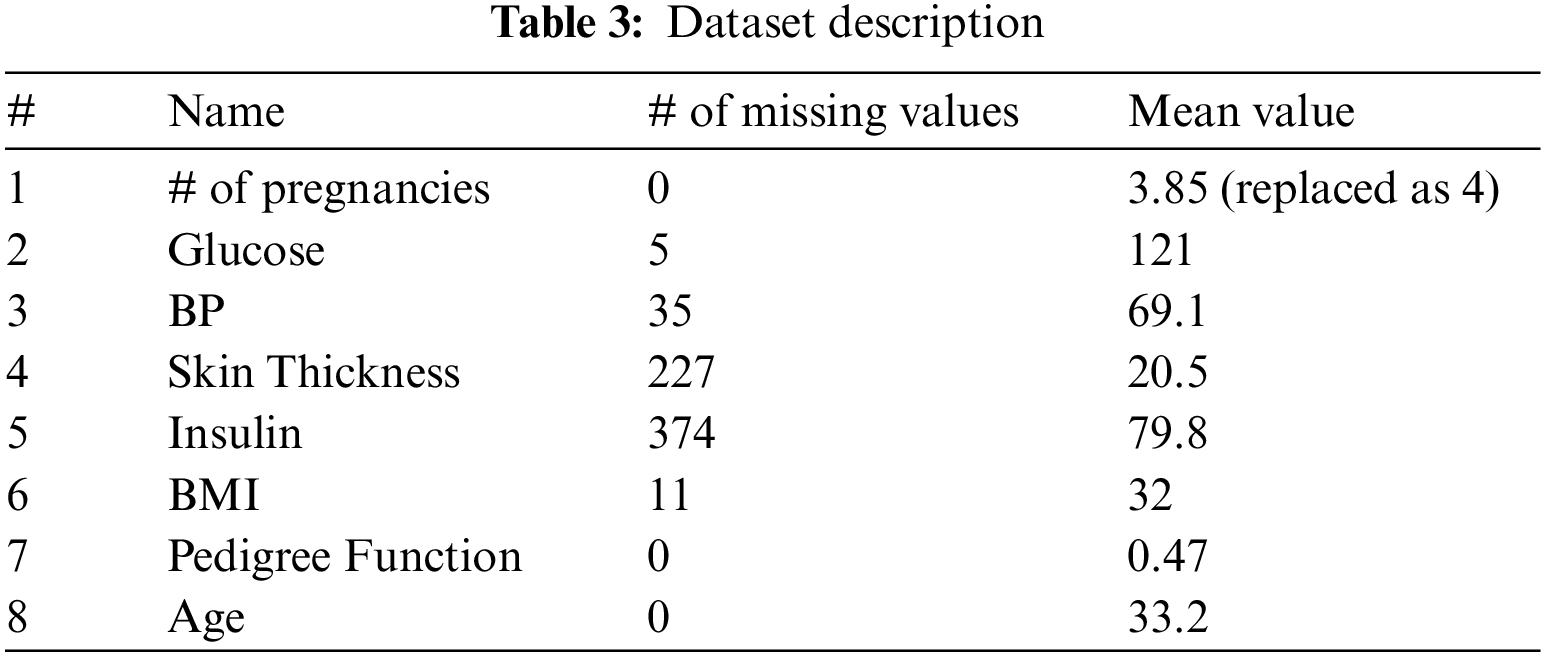
For the second weighting value, five features are selected based on correlation with the output feature. The five selected features are # of pregnancies, Glucose, BP, Skin Thickness, and Insulin. Tab. 3 lists; they just preserve the statistical properties of the original dataset. The proposed model does not use sample generating methods such as interpolation because there is a high chance to disturb the distribution of the dataset. The experimental results prove that the proposed method increases the performance of the imbalance classification.
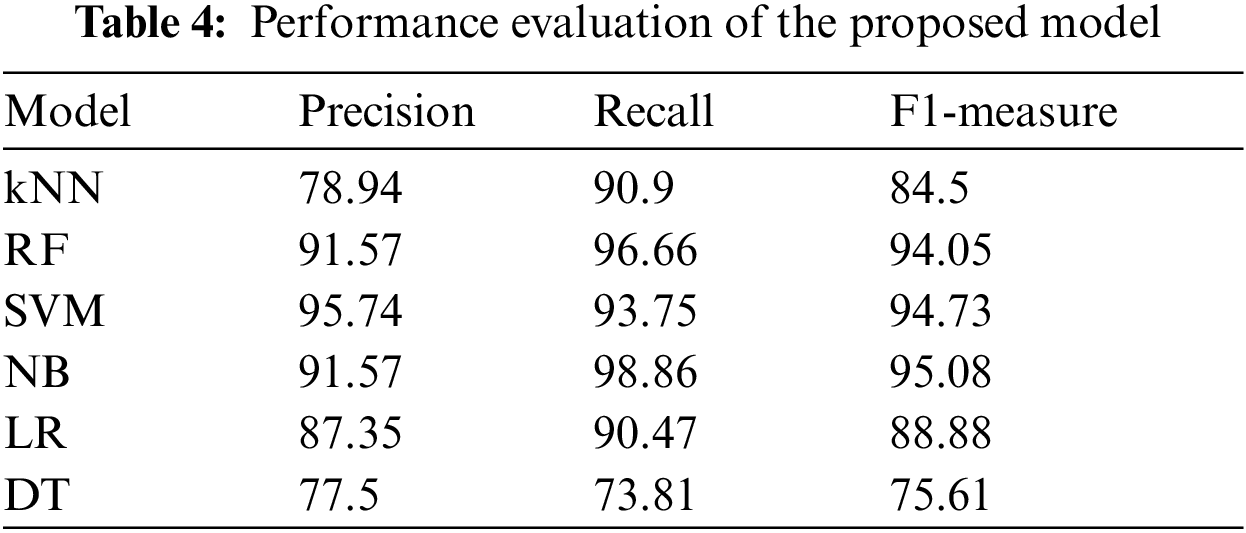
We have compared our work with two other recent works related to diabetic classification. Shown in Fig. 3. Tabs. 4 and 5 shows the complete comparison in terms of accuracy. In some cases, the majority of the data points reside near the class borders. Hence, it becomes difficult for the classifier to judge the boundary and decide the class for new samples. Models which don’t consider hyperparameters face difficulty in classifying samples that are falling near the class borders. Models such as SVM handle this situation better and outputs better performance. The first step in the proposed model generates balanced sub sets, this can eliminate many border data points and hence it becomes easy to separate both classes, this is another reason why the accuracy of the proposed model is more than the existing ones.
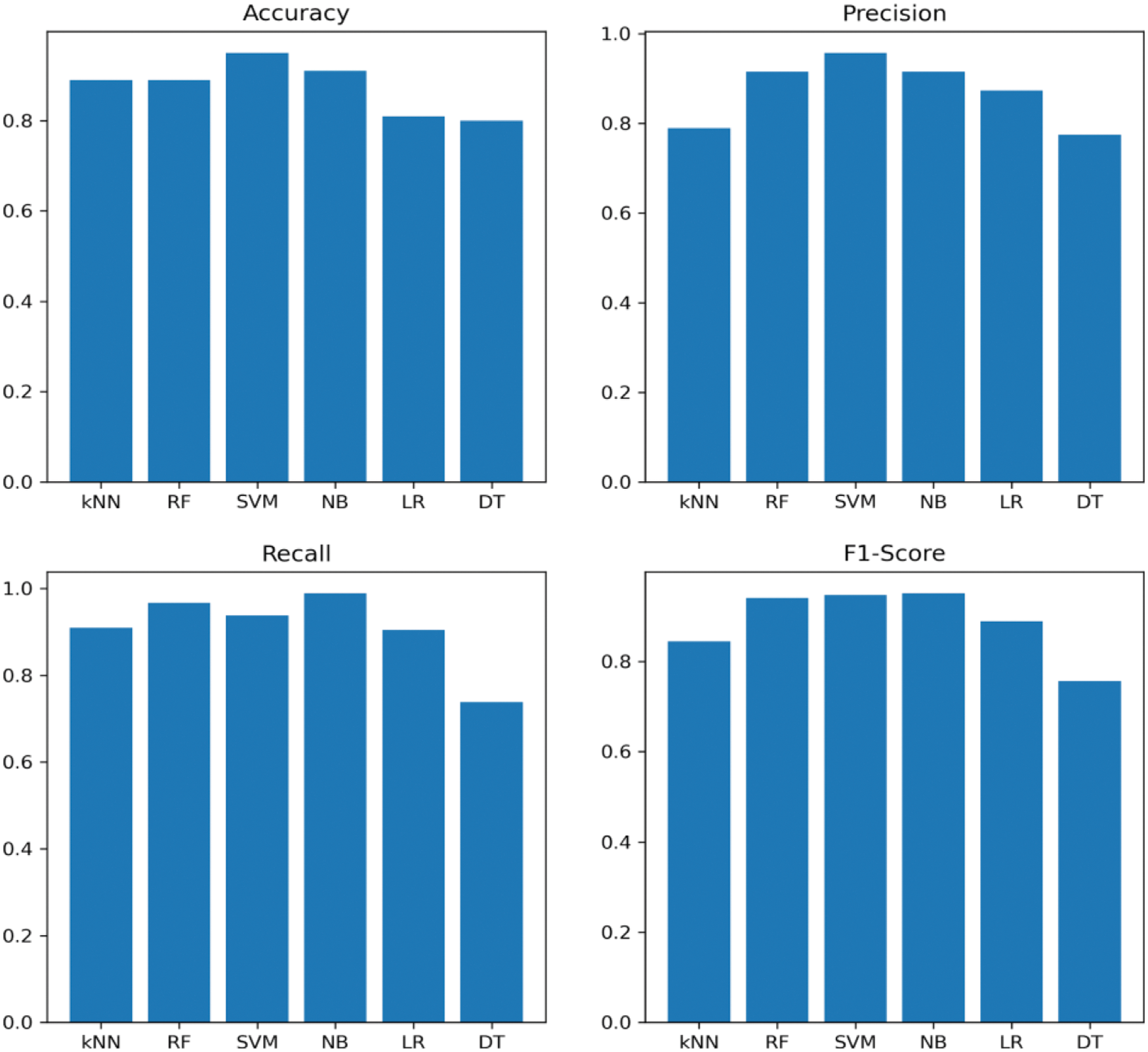
Figure 3: Performance evaluation of proposed model
Diabetes is one of the worst diseases in the medical domain. Nearly 422 million people are affected by diabetes. The risk of diabetes can be reduced significantly if the diabetes is predicted at an early stage. In this paper, we focus on developing a machine learning model which can predict whether a patient has diabetes or not. In this work, we have used both over-sampling and under-sampling at different stages. The results show that the combination has significantly increased the performance of classification in the imbalanced dataset. The over-sampling used in the work ensures that all the class has equal memberships by selecting and generating samples from the minority class until they are balanced. As random sampling is not used, the risk of oversampling is prevented, and also, since the samples are generated within the distribution, the statistical properties are preserved. The under-sampling generates many sub sets, each sub sets have a high chance of removing border values and thus makes it easy to place the classification margin. We have used six machine learning models kNN, SVM, RF, NB, LR, and DT, and used the PIMA Indian dataset. We have measured the performance of all these models with and without the proposed algorithm. We have used the standard four metrics known as accuracy, precision, recall and F1 to evaluate the model. The results revealed that the Support Vector Machine was most effective than the other modes in predicting diabetes in terms of accuracy. In future work, we aim to develop a cross model that works on multiple datasets to overcome imbalanced classification.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that there is no conflict of interest to report regarding the present study.
1. S. Shubham, N. Jain, V. Gupta, S. Mohan, M. M. Ariffin et al., “Identify glomeruli in human kidney tissue images using a deep learning approach,” Soft Computing, vol. 25, pp. 1–12, 2021. [Google Scholar]
2. S. Mohan, A. John, M. Adimoolam, S. Kumar Singh et al., “An approach to forecast impact of Covid-19 using supervised machine learning model,” Software - Practice and Experience, 2021. [Google Scholar]
3. X. Xia, D. Lo, E. Shihab, X. Wang, X. Yang et al., “Elblocker: Predicting blocking bugs with ensemble imbalance learning,” Information and Software Technology, vol. 61, no. 3, pp. 93–106, 2015. [Google Scholar]
4. Y. Li, H. Guo, Q. Zhang, M. Gu and J. Yang, “Imbalanced text sentiment classification using universal and domain-specific knowledge,” Knowledge-Based Systems, vol. 160, pp. 1–15, 2018. [Google Scholar]
5. J. Xiao, Y. Wang, J. Chen, L. Xie and J. Huang, “Impact of resampling methods and classification models on the imbalanced credit scoring problems,” Information Sciences, vol. 5, pp. 506–528, 2021. [Google Scholar]
6. N. Japkowicz and S. Stephen, “The class imbalance problem: A systematic study,” Intelligent Data Analysis, vol. 6, no. 5, pp. 429–449, 2002. [Google Scholar]
7. A. Guzmán-Ponce, J. S. Sánchez, R. M. Valdovinos and J. R. Marcial-Romero, “Dbig-us: A two-stage under-sampling algorithm to face the class imbalance problem,” Expert Systems with Applications, vol. 168, pp. 114301, 2021. [Google Scholar]
8. S.-J. Yen and Y.-S. Lee, “Cluster-based under-sampling approaches for imbalanced data distributions,” Expert Systems with Applications, vol. 36, no. 3, pp. 5718–5727, 2009. [Google Scholar]
9. V. Gupta, N. Jain, P. Katariya, A. Kumar, S. Mohan et al., “An emotion care model using multimodal textual analysis on covid-19,” Chaos, Solitons & Fractals, vol. 144, pp. 110–118, 2021. [Google Scholar]
10. V. García, J. S. Sánchez, A. I. Marqués, R. Florencia and G. Rivera, “Understanding the apparent superiority of over-sampling through an analysis of local information for class-imbalanced data,” Expert Systems with Applications, vol. 158, pp. 113026, 2020. [Google Scholar]
11. F. Ren, P. Cao, W. Li, D. Zhao and O. Zaiane, “Ensemble based adaptive over-sampling method for imbalanced data learning in computer aided detection of microaneurysm,” Computerized Medical Imaging and Graphics, vol. 55, no. 1, pp. 54–67, 2017. [Google Scholar]
12. A. Zughrat, M. Mahfouf, Y. Yang and S. Thornton, “Support vector machines for class imbalance rail data classification with bootstrapping-based over-sampling and under-sampling,” IFAC Proceedings, vol. 47, no. 3, pp. 8756–8761, 2014. [Google Scholar]
13. M. Bach, A. Werner, J. Żywiec and W. Pluskiewicz, “The study of under and over-sampling methods utility in analysis of highly imbalanced data on osteoporosis,” Information Sciences, vol. 384, pp. 174–190, 2017. [Google Scholar]
14. A. Palanivinayagam and S. Nagarajan, “An optimized iterative clustering framework for recognizing speech,” International Journal of Speech Technology, vol. 23, no. 4, pp. 767–777, 2020. [Google Scholar]
15. N. Jain, S. Jhunthra, H. Garg, V. Gupta, S. Mohan et al., “Prediction modelling of covid using machine learning methods from B-cell dataset”,” Results in Physics, vol. 21, pp. 103813, 2021. [Google Scholar]
16. C. Wang, C. Deng, Z. Yu, D. Hui, X. Gong et al., “Adaptive ensemble of classifiers with regularization for imbalanced data classification,” Information Fusion, vol. 69, pp. 81–102, 2021. [Google Scholar]
17. Y. Tian, B. Bian, X. Tang and J. Zhou, “A new non-kernel quadratic surface approach for imbalanced data classification in online credit scoring,” Information Sciences, vol. 563, pp. 150–165, 2021. [Google Scholar]
18. M. Zheng, T. Li, L. Sun, T. Wang, B. Jie et al., “An automatic sampling ratio detection method based on genetic algorithm for imbalanced data classification,” Knowledge-Based Systems, vol. 216, pp. 106800, 2021. [Google Scholar]
19. W. Wang and D. Sun, “The improved AdaBoost algorithms for imbalanced data classification,” Information Sciences, vol. 563, no. 6, pp. 358–374, 2021. [Google Scholar]
20. J. Grzyb, J. Klikowski and M. WoÅžniak, “Hellinger distance weighted ensemble for imbalanced data stream classification,” Journal of Computational Science, vol. 51, no. 2, pp. 1013–1014, 2021. [Google Scholar]
21. N. V. Chawla, K. W. Bowyer, L. O. Hall and W. P. Kegelmeyer, “Smote: Synthetic minority over-sampling technique,” Journal of Artificial Intelligence Research, vol. 16, no. 1, pp. 321–357, 2002. [Google Scholar]
22. P. Ashokkumar and S. Don, “Link-based clustering algorithm for clustering web documents,” Journal of Testing and Evaluation, vol. 47, no. 6, pp. 20180497, 2019. [Google Scholar]
23. A. Puri and M. Kumar Gupta, “Knowledge discovery from noisy imbalanced and incomplete binary class data,” Expert Systems with Applications, vol. 181, no. 1, pp. 115179, 2021. [Google Scholar]
24. U. R. Salunkhe and S. N. Mali, “Classifier ensemble design for imbalanced data classification: A hybrid approach,” Procedia Computer Science, vol. 85, no. 4, pp. 725–732, 2016. [Google Scholar]
25. S. Vluymans, D. S. Tarragó, Y. Saeys, C. Cornelis and F. Herrera, “Fuzzy rough classifiers for class imbalanced multi-instance data,” Pattern Recognition, vol. 53, pp. 36–45, 2016. [Google Scholar]
26. Y. Sun, Y. Sun and H. Dai, “Two-stage cost-sensitive learning for data streams with concept drift and class imbalance,” IEEE Access, vol. 8, pp. 191942–191955, 2020. [Google Scholar]
27. Z. Sun, Q. Song, X. Zhu, H. Sun, B. Xu et al., “A novel ensemble method for classifying imbalanced data,” Pattern Recognition, vol. 48, no. 5, pp. 1623–1637, 2015. [Google Scholar]
28. B. E. Aissou, A. B. Aissa, A. Dairi, F. Harrou, A. Wichmann et al., “Building roof superstructures classification from imbalanced and low density airborne LiDAR point cloud,” IEEE Sensors Journal, vol. 21, no. 13, pp. 14960–14976, 2021. [Google Scholar]
29. Q. Wu, B. Hou, Z. Wen, Z. Ren and L. Jiao, “Cost-sensitive latent space learning for imbalanced PolSAR image classification,” IEEE Transactions on Geoscience and Remote Sensing, vol. 59, no. 6, pp. 4802–4817, 2021. [Google Scholar]
30. R. Rustogi and A. Prasad, “Swift imbalance data classification using smote and extreme learning machine,” in Int. Conf. on Computational Intelligence in Data Science (ICCIDS), Chennai, India, pp. 1–6, 2019. [Google Scholar]
31. Y. Lu, Y. M. Cheung and Y. Y. Tang, “Bayes imbalance impact index: A measure of class imbalanced data set for classification problem,” IEEE Transactions on Neural Networks and Learning Systems, vol. 31, no. 9, pp. 3525–3539, 2020. [Google Scholar]
32. P. Ashokkumar, G. Siva Shankar, G. Srivastava, P. K. Maddikunta and T. R. Gadekallu, “A two-stage text feature selection algorithm for improving text classification,” ACM Transactions on Asian and Low-Resource Language Information Processing, vol. 20, no. 3, pp. 1–19, 2021. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |