Computers, Materials & Continua DOI:10.32604/cmc.2022.024204
Article

A Sustainable WSN System with Heuristic Schemes in IIoT

Wenjun Li1, Siyang Zhang1, Guangwei Wu2, Aldosary Saad3, Amr Tolba3,4 and Gwang-jun Kim5,*

1School of Computer and Communication Engineering, Changsha University of Science and Technology, Changsha, 410114, China
2College of Computer and Information Engineering, Central South University of Forestry and Technology, Changsha, 410114, China
3Computer Science Department, Community College, King Saud University, Riyadh, 11437, Saudi Arabia
4Mathematics and Computer Science Department, Faculty of Science, Menoufia University, Egypt
5Department of Computer Engineering, Chonnam National University, Gwangju, 61186, Korea
*Corresponding Author: Gwang-jun Kim. Email: kgj@chonnam.ac.kr
Received: 08 October 2021; Accepted: 20 December 2021

Abstract: Recently, the development of Industrial Internet of Things has taken the advantage of 5G network to be more powerful and more intelligent. However, the upgrading of 5G network will cause a variety of issues increase, one of them is the increased cost of coverage. In this paper, we propose a sustainable wireless sensor networks system, which avoids the problems brought by 5G network system to some extent. In this system, deploying relays and selecting routing are for the sake of communication and charging. The main aim is to minimize the total energy-cost of communication under the precondition, where each terminal with low-power should be charged by at least one relay. Furthermore, from the perspective of graph theory, we extract a combinatorial optimization problem from this system. After that, as to four different cases, there are corresponding different versions of the problem. We give the proofs of computational complexity for these problems, and two heuristic algorithms for one of them are proposed. Finally, the extensive experiments compare and demonstrate the performances of these two algorithms.

Keywords: Industrial Internet of Things; sustainable wireless sensor network system; combinatorial optimization problem; heuristic algorithms

1  Introduction

With the improvement of intelligent level of manufacturing industry, sensors or smart devices with capabilities of sensing, monitoring, data transmission and simple calculation are used in industry. It promotes the development of Industrial Internet of Things (IIoT). Moreover, it also brings a great number of problems and numerous challenges, which have attracted a great attention from a large number of engineers and scientists [1,2]. Among all the parts of IIoT, wireless sensor networks (WSN) play an important role in it.

In the past few years, with the maturity of 5G technology, 4G network is gradually replaced by 5G network due to its advantages, such as high speed, large capacity and low delay [3]. Nevertheless, it has its own shortages. Compared with 4G signal, 5G signal transmission distance is shorter. Hence, the coverage of 5G station is smaller than 4G station. To deal with this problem, a reasonable way is to deploy a large number of 5G stations. Fig. 1 shows an instance of the coverage comparison between 5G station and 4G station. Obviously, this method results in a very high cost. To avoid the problem mentioned above to some extent, we proposed a sustainable WSN system with simple topological structure.

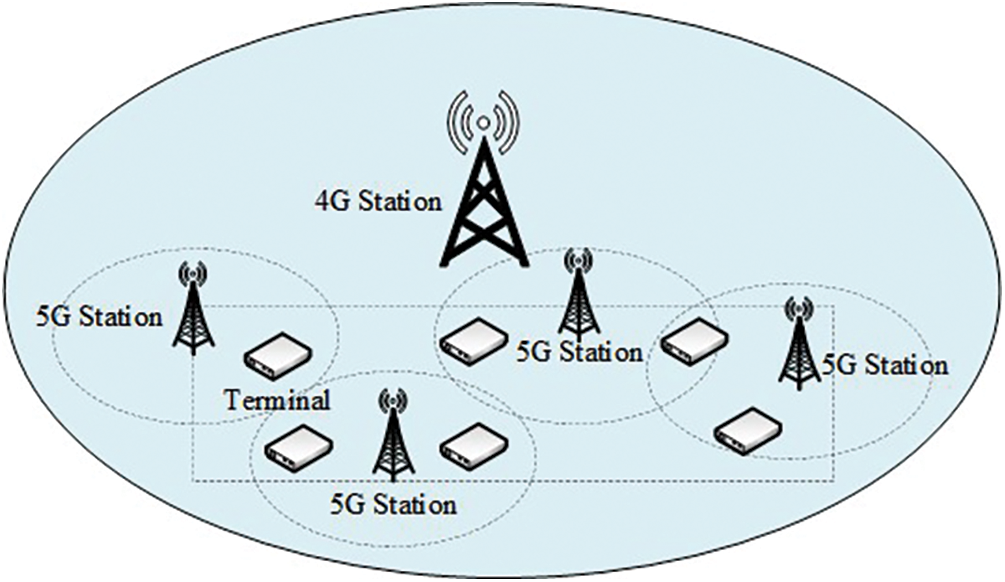
Figure 1: An instance of coverage comparison between 5G station and 4G station

In our proposed system, some terminals and a sink are given. The terminals with low-power can be charged by relays and wireless information can be transmitted via relays. More precisely, the information can be transmitted in multi-hop, but the energy can only be transmitted in one-hop since the energy loss is too large in the process of wireless power transmission. The tasks of the system include deploying relays to make up a communication network and selecting routing for each terminal. Further, the aim of it is to minimize the energy assumption of communication (communication cost) under the restriction that each terminal can be charged by at least one relay. We extract a combinatorial optimization problem, called Sustainable Communication (SC) Problem, from the system mentioned above.

The followings are the main contributions of this paper: (a) proposing a sustainable wireless sensor network system framework; (b) showing some models and corresponding combinatorial problems for different cases of the system; (c) proving the computational complexity of the problems, and (d) giving two heuristic algorithms and some simulation results for one of the problems.

The structure of the rest of paper is composed of the following four sections. Section 2 is about related works. Section 3 presents our proposed sustainable wireless sensor network system, including description and some explanations of the system, some models and corresponding combinatorial optimization problems of the system, computational complexity proofs and two heuristic algorithms for the problems. In Section 4, we give the performance analysis for the two algorithms showed in Section 3 and an instance of engineering application. The last section concludes this paper.

2  Related Work

In this section, we will show some related work about our proposed sustainable wireless sensor network system. Since relay deployment and routing selection are the two tasks needed to construct the system, we review the major related works about these two items.

The relay deployment problem has attracted a lot of attentions. The authors in [4] studied the energy provisioning and relay deployment problem in two-tiered WSN. They modeled this problem as an NP-hard problem (Mixed-integer Nonlinear programming), and proposed a heuristic algorithm to address it. Patel et al. [5] considered the nodes (including sensor, relay and base station) deployment problem in WSN. On the basis of ensuring the coverage, connectivity, bandwidth and robustness, they proposed several different strategies based on the number of sensors, network lifetime and energy consumption. The authors in [6] modeled the relay sensor deployment problem as the Steiner Minimum Tree problem, where the amount of steiner points is minimum and the edge length is bounded. Liu et al. [7] investigated the problem in WSN inspecting tunnels. Based on the comprehensive consideration of energy cost, coverage, connectivity, network lifetime and data latency, they proposed a strategy of deploying relays. Furthermore, the authors studied the same problem in the application of pipeline inspection [8]. The authors in [9] considered designing WSN with relays, where the networks are deployed underground, but relays are placed above ground. The authors in [10] studied the relay deployment problem in the same network with the constraints of load balance.

For the IEEE 802.16j WiMAX networks, there is a long history of research for the relay deployment problem. The authors in [11] considered the relay station deployment problem for minimizing the network operational cost. Based on the Bender's decomposition method, they divided the original problem into some small subproblems expressed by Boolean variables. Yu et al. [12] investigated the problem of base and relay station deployment in relay networks with multi-hop. Later, the authors considered the same problem in [13]. They proposed a clustering approach, the main idea of which is similar to the Divide and Conquer method [14]. Huang et al. considered the relay selection problem in relaying network with two hops, the aim of which is to maximize the system capacity [15]. The authors in [16] studied the relay station deployment cooperative communications problem, which aims to deploy minimum relay stations such that the data rate requests of the subscriber stations are satisfied. They proved that the problem is NP-complete firstly, where NP is the abbreviation of nondeterministic polynomial. And then, they proposed an O(logn)-approximation algorithm for the problem. Furthermore, they developed an approximation algorithm with a constant ratio for it in the case that any relay station is connected to constant subscriber stations. Lu et al. [17] investigated the relay station deployment problem aiming to maximize network capacity under the cost constraint. For this problem, they considered two different kinds of relay stations. The one is Transparent Relay Station, and the other is Non-Transparent Relay Stations. These two types of relay stations hold different functions and have different prices. They proved that the problem is NP-hard. Furthermore, they developed a heuristic scheme to achieve a suboptimal solution for it. Chang et al. [18] studied this problem with bandwidth constraint of relay stations. This problem aims to deploy relays in right locations such that the network throughput is maximized under the restriction of bandwidth requirement. Since the bandwidth constraint of relay stations may lead to load unbalance and bandwidth starvation, the authors put forward some measures to avoid these two situations. The most crucial measure is to divide the original region into several parts, which have the same traffic demands.

The authors in [19] developed a cooperative network, which is focused on maximizing energy efficiency under QoS (Quality of Service) constraints. The proposed strategies for the cooperative network include how to deploy relays at the right locations under consideration of energy efficiency and QoS.

It should be pointed out that relay deployment problem and relay selected problem have great similarity. Because selecting some relays from the deployed relays is the same as deploying some relays to candidate relay locations from the combinatorial optimization perspective. If all the relays are deployed in the wireless networks, then relay selection becomes another important task with respected to some optimization targets in this case. Zappone et al. [20] studied an energy efficiency problem in networks with users and relays. The aim of it is to optimize the relay assignment and transmit powers jointly such that the user-fairness are considered and the minimum bit/J efficiency is maximized. They modeled it as a mixed-integer optimization problem. The authors in [21] considered a relay selection problem with fairness of users in relay networks, which are decoded-and-forwarded and full-duplex. They proposed a relay selection algorithm for two different models. There have been some research works considering user cooperation problems in other types of relay networks.

During the wireless network construction, relay deployment usually includes routing selection operation implicitly. Routing selection is a trivial problem in the networks with only one or two hops. However, if the wireless network has multi hops, then it becomes an important and complicated problem for minimizing energy consumption and maximizing network lifetime. Chai et al. [22] considered the routing selection problem in Mesh Networks, which aims to minimize the end-to-end delay. Their main contribution is based on a delay-and interference-aware routing method. Mahmood et al. proposed a search based genetic algorithm for routing selection in wireless mesh network [23]. Li et al. [24] considered an optimization problem, called Superposed Data Uploading Problem, in multi-hop wireless network with smart devices. In the problem, the task is to select routing for each terminal, and the aim is to minimize the total energy cost. There were some other works showing theoretical or practical studies about routing selection, which are modeled as some corresponding optimization problems. Furthermore, some efficient heuristic algorithms or schemes are proposed.

3  Our Proposed Sustainable WSN System

In this section, we show the framework of our proposed system first. Later, some models and corresponding formal mathematical definitions of combinatorial optimization problems are given. And then, the NP-hardness of the combinatorial problems are presented. At last, two heuristic algorithms for one of the NP-hard problems are shown.

3.1 System Framework

In this part, we will show details of our proposed sustainable wireless sensor network system framework. In the system, there are some fixed terminals and a fixed sink. And there are some relays which not only can transmit data but also can charge of terminals. The system should satisfy the following two conditions: Communication condition. Each terminal's data can be transmitted to the sink via some relays; Sustainability condition. Each terminal can be charged by at least one relay. The first condition is trivial, since communication is the fundamental function of the system. The second condition is to ensure sustainable running of the whole system.

To construct such a sustainable wireless sensor network system, we have to accomplish two tasks: (1) Relays deployment task (deploying a limited or unlimited number of relays at the restricted or unrestricted locations); and (2) Routing selection task (for each terminal, select a routing of the transmission from it to the sink). The optimization target of the system is to minimize the communication cost under the case that the system satisfies the communication condition and sustainable condition. It should be remarked that we will not consider energy consumption of terminal charging, since only a few of terminals are in the state of lower battery and need to be charged in practice. Moreover, we assume the possibility of data transmission from each terminal to the sink is the same. In order to introduce our proposed system clearly, we will give some necessary explanations on some issue about the system, such as relay deployment, energy consumption of wireless communication, energy loss of wireless charging, and the topology of the constructed network.

Firstly, the system should focus on the number of relays and the candidate locations for deploying relays. Since relays may be expensive, it is reasonable that the number of relays is usually limited. For the reason that the environment may be complex and there are some constraints of the applications, relays should not be deployed at somewhere. It means that the candidate locations for deploying relays may be restricted. Secondly, in our system, we just consider the energy loss during the RF (Radio Frequency) transmission in our system. And we assume energy consumption (communication cost) function is EC (Dist (a, b)) = c*Dist (a, b)q, where Dis t (a, b) is the distance between sender a and receiver b, and c, q are constants. Thirdly, there is a valid distance from relays and the charged terminals, called charging radius (Rcha). Generally, the radius of charging is smaller than that of the wireless communication, called communication radius (Rcom). Last, for the network in our proposed system, there is a fixed sink s, which connects the communication network with extranet. And we assume the communication radius of the terminals, relays and sink are the same.

Fig. 2 shows an instance of communication and charging network for our proposed system. In the network, c, e, f and g are the deployed relay nodes. We omit all the candidate locations nodes except the deployed relay nodes. Here, a, b and d are the fixed terminated nodes, and h is a fixed sink node. The charging radius Rcha = 15 and the communication radius Rcom = 25. Paths a→c→g→h, b→c→g→h and d→f→g→h are valid communication paths from relay nodes a, b and d to h, respectively. In this instance, terminal c can charge a and b since Dist(a,c)=Dist(b,c)=10≤Rcha. However, relay f cannot charge terminal d for the reason that Dist(d,f)=25>Rcha, and path d→e→g→h is an invalid communication path since Dist(e,g)=50>Rcom. Therefore, in this instance, the sustainable wireless sensor network system has to use at least 4 relays though only three relays used for communication.

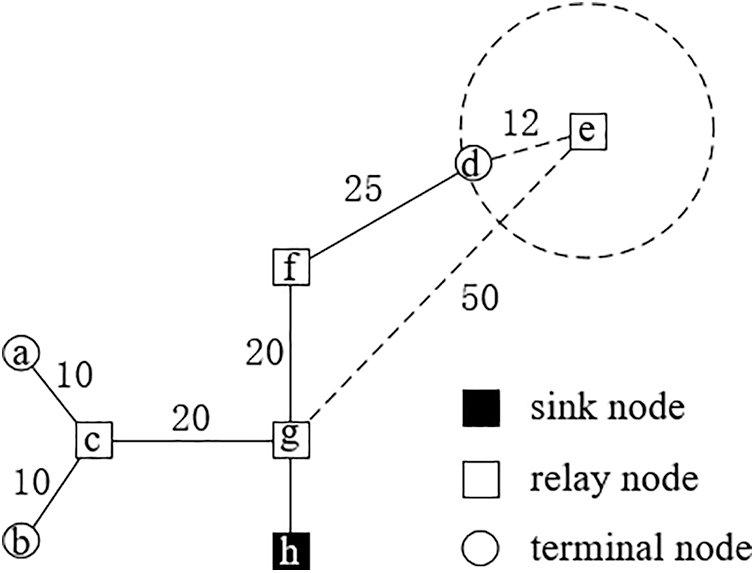
Figure 2: An instance of communication and charging network. Rcha = 15 and Rcom = 25. Since the distance between node d and f is 25 (larger then Rcha), terminal d can only be charged by e though it not on any communication path from terminal d to s

3.2 Models and Combinatorial Optimization Problems

In this part, based on the proposed sustainable wireless sensor network system mentioned in the previous subsection, we extract four different models for four different cases, and show the corresponding formal definitions of combinatorial optimization problems.

Assume the scenario of the communication system is in three-dimensional Euclidean space (R3). Ster is a set of fixed terminal node, s is a fixed sink node, the aim is to deploy a set Srel of relay nodes satisfying that (a) for each terminal node v∈Ster, there is a relay node u∈Srel with Dist(u,v)≤Rcha; (b) for each terminal node v∈Ster, there is a communication path Pv (a routing path) from v to the sink node s such that the distance of any two adjacent nodes on Pv is no larger than Rcom, and (c) the total communication cost (energy consumption) W(p)=∑v∈VterW(Pv) is minimized, where W(Pv)=∑(a,b)∈E(Pv)EC(Dist(a,b)). For the total communication cost function, there is an implied assumption that each terminal work at the same frequency. Actually, the terminals do not work all the time. This fact leads to the trouble of calculating the total communication cost. Our assumption can deal with it and seems rational.

Obviously, for different models of the proposed sustainable wireless sensor network system, the corresponding combinatorial optimization problems will be different. In this paper, we consider two issues about the system. The one is the limitation for the number of relays to be deployed, and the other is candidate location restriction. For the former, the number of relays deployed in the system could be finite or infinite. For the latter, candidate locations could be anywhere or restricted to some fixed positions. Above all, we consider the following four cases (Case 1–4) which correspond to the problems SC-1, -2, -3 and -4, respectively:

(a)  Case 1: The number of relays is finite and the candidate locations are restricted;

(b)  Case 2: The number of relays is infinite and the candidate locations are restricted;

(c)  Case 3: The number of relays is finite and the candidate locations are unrestricted;

(d)  Case 4: The number of relays is infinite and the candidate locations are unrestricted.

Now, we are going to present the formal definition of the four problems as follows:

Definition 1. New Sustainable Communication Problem 1 (SC-1): Given a set Ster of terminals nodes, a set Srel of candidate location nodes and a sink node s in R3, communication cost function EC, wireless communication radius Rcom and wireless charging radius Rcha, choose at most k candidate location nodes (the chosen candidate location node is a deployed relay node) such that:

(a)  for each v∈Ster, there is a relay node u with Dist(u,v)≤Rcha;

(b)  for each v∈Ster, there is a path Pv from v to the sink node s via relay nodes, where the distance of any two adjacent nodes on Pv is no larger than Rcom;

(c)  the total communication cost is minimized.

Definition 2. New Sustainable Communication Problem 2 (SC-2): Given a set Ster of terminals nodes, a set Srel of candidate location nodes and a sink node s in R3, communication cost function EC, wireless communication radius Rcom and wireless charging radius Rcha choose some candidate location nodes (the chosen candidate location node is a deployed relay node) such that:

(a)  for each v∈Ster, there is a relay node u with Dist(u,v) ≤ Rcha;

(b)  for each v∈Ster, there is a path Pv from v to the sink node s via relay nodes, where the distance of any two adjacent nodes on Pv is no larger than Rcom;

(c)  the total communication cost is minimized.

Definition 3. New Sustainable Communication Problem 3 (SC-3): Given a set Ster of terminals nodes, and a sink node s in R3, communication cost function EC, wireless communication radius Rcom and wireless charging radius Rcha, deploy at most k relay nodes such that:

(a)  for each v∈Ster, there is a relay node u with Dist(u,v)≤Rcha;

(b)  for each v∈Ster, there is a path Pv from v to the sink node s via relay nodes, where the distance of any two adjacent nodes on Pv is no larger than Rcom;

(c)  the total communication cost is minimized.

Definition 4. New Sustainable Communication Problem 4 (SC-4): Given a set Ster of terminals nodes, a set Srel of candidate location nodes and a sink node s in R3, communication cost function EC, wireless communication radius Rcom and wireless charging radius Rcha, deploy some relay nodes such that:

(a)  for each v∈Ster, there is a relay node u with Dist(u,v)≤Rcha;

(b)  for each v∈Ster, there is a path Pv from v to the sink node s via relay nodes, where the distance of any two adjacent nodes on Pv is no larger than Rcom;

(c)  the total communication cost is minimized.

3.3 Computational Complexity Proofs

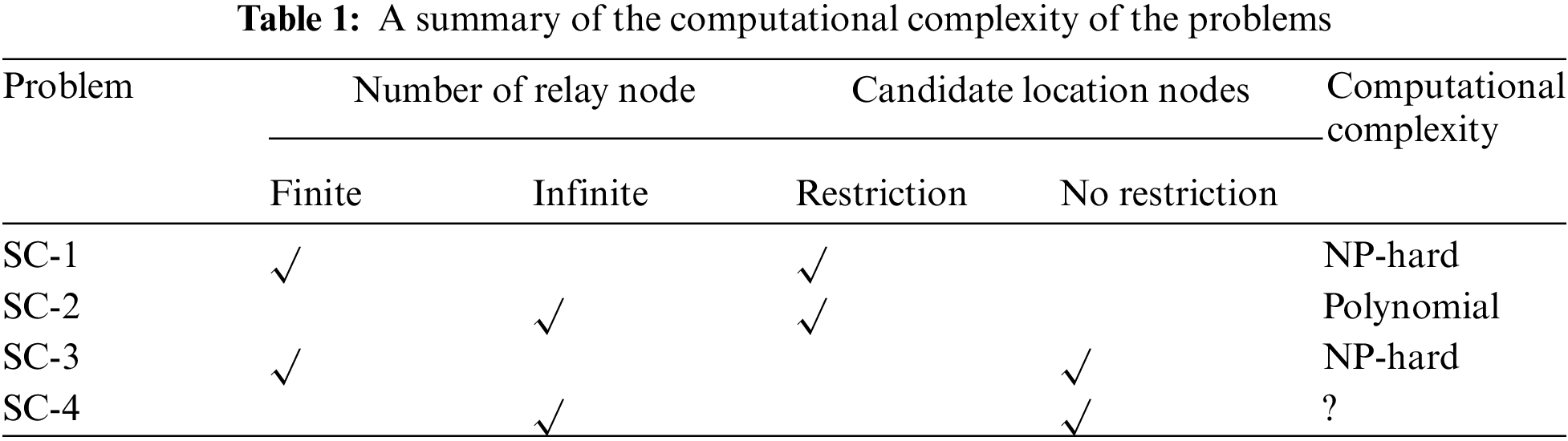
In this subsection, we will prove the computational complexity of the problems SC-1, -2, and -3. The results are summarized in the Tab. 1. It shows that the two problems SC-1 and SC-3 are NP-hard, and the problem SC-2 is in P. However, the computational complexity of SC-4 is still open.

In our proposed new communication system model, the relays not only can be used for transmitting data but also can be used for charging terminals. Moreover, from the definitions of SC-1, we know that the number of relay nodes is limited. Furthermore, there is a simple observation that finding a minimum number of relays to charge all the terminals in R2 in polynomial time is impossible unless P=NP. Because of these, we reduce the NP-hard problem Discrete Unit Disk Cover problem (DUDC) and the Unit Disk Cover problem (UDC) in Euclidean plane to a special version of SC-1 and SC-3 respectively, which proves the NP-hardness of SC-1 and SC-3. We prove the problem SC-2 is in P by providing an optimal polynomial algorithm for it. The details are as follows.

Theorem III.1. The problem SC-1 is NP-hard.

Proof: Note that the problem DUDC in Euclidean plane is NP-complete. Before proving the NP-hardness of the problem SC-1, we show the formal definition of the optimization and the decision versions of the problem DUDC.

Definition 5. Minimum Discrete Unit Disk Cover problem (MDUDC): Given a set S of n points and a set D of m unit disks in the Euclidean plane, find a minimum set D′⊆D such that S∩D′=S.

Definition 6. Parameterized Discrete Unit Disk Cover problem (PDUDC): Given a set S of n points, a set D of m unit disks in the Euclidean plane and a parameter k, does there exist a set D∗⊆D with cardinality at most k such that S∩D∗=S?

Let IDUDC= (S, D, k) be an instance of PDUDC in R2, where S = {p1, p2, …, pn} is a set of n nodes, D={d1, d2, …, dm} is a set of unit disks in R2, and a parameter k. Now, we are going to construct an instance ISC−1∗=(Vter∗,Vloc∗,vsink∗,Rcha∗,Rcom∗,k∗) for a special version of the problem SC-1 (assume SC-1*) based on IDUDC as follows:

(1)   For each node pi∈S, create a terminal node ti∈Vter∗ with the same coordinates of pi;

(2)   For each disk di∈D, create a candidate location node ri∈Vloc∗ with the same coordinates of the center of di;

(3)   Let Rcha∗ be the radius of the unit disks in D;

(4)   Create a sink node vsink∗ at any location such that Dist(ti,vsink∗)>Rcha∗ for any terminal ti∈Vter∗;

(5)   Let Rcom∗ be the value max {Dist(ti,vsink∗)|ti∈Vter∗}.

(6)   Let k∗=k.

Fig. 3 shows an instance of ISC−1∗. Compared with SC-1, SC-1∗ holds three particularities. The first one is that all the terminal nodes, all candidate location nodes and the sink node are in a Euclidean plane (a special case of R3). The second one is that for any terminal node v, the inequality Dist(v,vsink∗)≤Rcom holds. In other words, each terminal can communicate with sink node directly. It means that the instance satisfies the communication condition even though no relay can be used to data transmission. The last one is that Dist(ti,vsink∗)>Rcha for any terminal ti∈Vter, which implies that the sink cannot charge any terminal.

Figure 3: An instance of ISC−1∗, where each terminal can communicate with the sink directly, the distance between each terminal and the sink is smaller than Rcom

In the following, we will prove that SC-1∗ is NP-hard by contradiction. Assume there is an algorithm A that solves SC-1* in polynomial time. This means that if for any instance I∗ of SC-1∗, A can find a subset Vloc′⊂Vloc∗ with size at k∗ (if exists) such that for each terminal node vter∗∈Vter∗, there exists at least one node vloc∈Vloc∗ with Dist(vter,Vloc)≤Rcha, and there is a communication path from vter to vsink∗ via the nodes in Vloc′. If k∗ is the minimum number of relays charging all the nodes in Vter∗, then A can outputs a valid solution for I∗, since Rcom∗ has the value max {Dist(ti,vsink∗)|ti∈Vter∗}. Thus, A can find a minimum set D′⊆D such that S∩D′=S in polynomial time, which contradicts to the fact that PDUDC is an NP-hard problem.

Corollary III.1. The problem SC-3 is NP-hard.

Proof: The NP-hardness proof of the problem SC-3 is almost the same as that of SC-1. The only difference between them is that we make a reduction from the UDC problem (not from the problem DUDC) in R2 to a special version of SC-3. In the problem DUDC, there is a given set of discrete unit disks, which are corresponding to the chosen candidate locations nodes or the deployed relay nodes in the problem SC-1. But in the problem UDC, the solution space is continuous, which can be corresponding to the solution space of the problem SC-3.

Theorem III.2. The problem SC-2 is in P.

Proof: Since there is no limitation for the number of relay nodes, we can choose all of them first. And then, by using Dijkstra's algorithm, we find a shortest transmission path from each terminal to the sink. Obviously, it is a polynomial optimal algorithm.

3.4 Two Heuristic Algorithms for SC-1

Note that once a problem is proved to be NP-hard, then it is reasonable to design heuristic algorithm for it. In this subsection, we give two heuristic algorithms for SC-1. The similar main idea of these two algorithms could be used to solve the other three problems.

The input of our algorithms consists of a set of candidate location nodes Sloc, a set of terminal nodes Ster, a sink node s, a parameter k, wireless communication radius Rcom and wireless charging radius Rchar. The main idea of our algorithms can be summarized as follows:

(A)  construct a graph based on the input instance of the problem SC-1;

(B)  for each terminal node, find a shortest path from it to the sink node on G (assume P is the path set of these paths);

(C)  find a minimal set D (a charging node set) of candidate location nodes such that for each terminal node u, there is at least one node v∈D such that in Dist(u,v)≤Rcom; and

(D)  use Local Search method to reduce the relay nodes of Vrel=Vlov∩(D∩V(P)) if the number of vertices in Vrel is larger than the number limitation of relays (parameter k).

For two different approaches of Local Search, we obtain two different algorithms. The whole algorithm can be divided into two phases. The first phase consisting of steps (A)-(C) is a subroutine to choose a set of candidate location nodes which satisfy the communication condition and the sustainability condition, but may not satisfy the number limitation of relays. Algorithm 1 (called Relays Deployment Initialization, abbreviated as RDI)) shows this phrase. The second phase, step (D), is to reserve k by two different algorithms (Algorithm 2 and 3), which are called Relays Compression on Path(RCOP) and Relays Compression in Graph (RCIG), respectively. Therefore, our first algorithm for the problem SC-1 is made up of RDI and RCOP, and the second one consists of RDI and RCIG.

Now, we are going to show the details of steps (A)-(D) of our algorithms.

Step (A): It is natural to construct a graph based on the topology of network derived from the proposed system. In the following, we will show constructing an edge weighted-and-colored undirected graph G=V=(Vloc∪Vter∪{vsink},E=(Egrey∪Eblack)):

(a)  for each candidate location node a in Sloc, create a candidate location vertex va and add it to Vloc;

(b)  for each terminal node a in Ster, create a terminal vertex vb and add it Vter;

(c)  for the sink node s, create a sink vertex vsink;

(d)  for each terminal node a and each candidate location node b, if Dist(a,b)≤Rcha, then create a black edge (va, vb) with weight c∗Dist(va,vb)q and add it to Egrey; and

(e)  for each candidate location node a and each candidate location (or terminal) node b, if Dist(va,vb)≤Rcom and there is no black edge between them, create a grey edge (va, vb) with weight c∗Dist(va,vb)q and add it to Eblack.

Step (B): For each vertex v∈Vter, the algorithm uses Dijsktra's algorithm to find a shortest path form v to the sink vertex.

Step (C): This step is to find a charging node set D of Vter with small size as possible. In our algorithms, the vertex set D can be divided into two sets D1 and D2, where D1⊂V(P) consists of all the vertices adjacent to some vertex in Vter by black edges. In the following, we just to show how to find the vertex set D2. Let Gblack=((V1,V2),Eblack) be the graph induced by the edge set Eblack, where V1 = Vter, V2 = V (Eblack)\V1. From the construction of G, we know that Gblack is a bipartite graph, and D1⊂V2. Let V2∗=V2∖D1, and V1∗=Vter∖NGblack(D1), where NGblack(D1) is the vertex set of D1's neighbors in Gblack. Let G∗=(V∗=(V1∗,V1∗)),E∗) be a subgraph of Gblack induced by the vertex set V∗. Then, we use a simple greedy algorithm to find a minimal set D2⊂V2∗ dominating all the nodes of V1∗ in G*. The greedy strategy is to choose a vertex from V2∗ with maximum degree in G∗ step by step until all the nodes of V1∗ are dominated, and the vertex set D2 consists of all these chosen vertices.

Step (D): If |Vrel=Vloc∩(D∪V(P))|>k, then we have to decrease the number of vertices in Vrel until it is no larger than k. To achieve this goal, we have two different ways (two different Local Search rules). They lead to two different heuristic algorithms, which are shown as the algorithms RCOP (Algorithm 2) and RCIG (Algorithm 3), respectively. Let graph GP be the union of all paths in P. And if a vertex v∈Vrel∖D is a degree−2 vertex in GP, then we color it with black. The strategy of our local search rules is to remove the black vertices under the communication condition and sustainability condition. Assume v is a black vertex on a path P (a, vsink) of P, and v+, v− are the two neighbors of a on P (a, vsink), where v+, v− are on the path P (a, v) and P (v, vsink) in GP, respectively. In the first rule, we consider the case that (v+,v−)∈E. If so, we replace the sub-path (v+, v, v−) by (v+, v−) in all paths containing (v+, v, v−) in P (an example is shown in Fig. 4a). After the implementation of such an operation, the number of vertices in Vrel is decreased by 1. The algorithm RCOP executes this operation repeatedly until |Vrel|≤k. In the second rule, we refine the selection of black vertex as follows. If there exists a vertex u∈(V(P)∖Vter) such that (u,v+)∈E, then we replace the sub-path P (v+, vsink) by (v+, v−) and P (u, vsink) in all paths containing P (v+, vsink) in P, where P (v+, vsink), P (u, vsink) are the paths in GP from v+ to vsink, and from u to vsink, respectively (an example is shown in Fig. 4b). This operation implementation makes the cost of communication increased but the number of vertices in Vrel decreased at least 1. For the greedy strategy, we define an evaluation indicator as Δ(v,u)=Δcost(v,u)Δrelay(v,u), where Δcost(v,u) and Δrelay(v,u) are the increment of communication cost and number of relay vertices decrement after replacing the sub-path P (v+, vsink) by (v+,u)∪P(u,vsink) in all paths containing (P(v+, vsink)) in P. Let Δ(v)=min{Δ(v,u)|u∈(V(P)∖Vter)}. In order to make the increment as small as possible, we pick the vertex v’ with minimum Δ(v′) among all the vertices in B, and execute the paths replacement operation as the local search rule for each step in the algorithm RCIG until a relay vertex set with size of at most k is found.

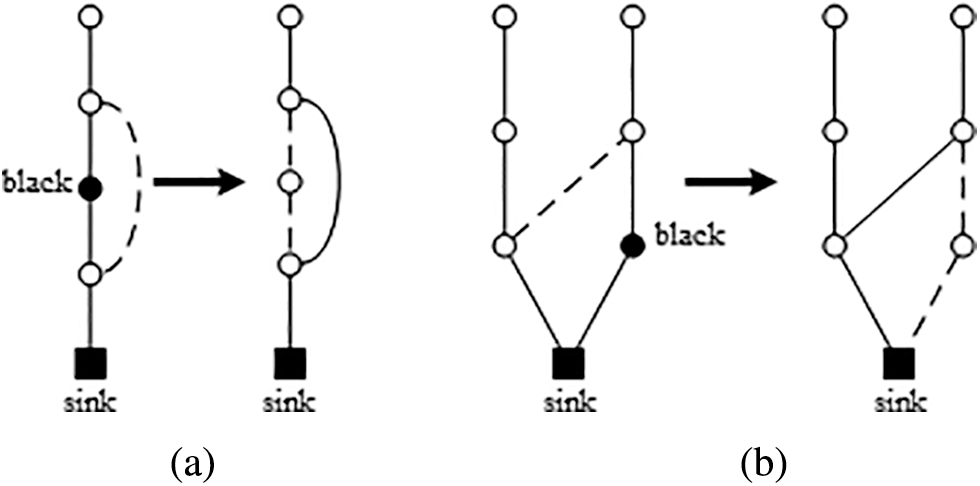
Figure 4: Two instances of local search rules, where the subgraph (a) shows the local search rule for the algorithm RCOP, and the subgraph (b) shows that of RCIG

4  Performance Analysis and Engineering Applications

In this section, we will illustrate some simulation experiments to evaluate the proposed two heuristic algorithms first. And then, we present an instance of communication system in a chemical plant as an engineering application of our proposed sustainable wireless sensor network system.

4.1 Performance Analysis

As we mentioned, the function of energy consumption is EC (Dist (a, b)) = c∗Dist (a, b)q, 2 ≤ q ≤ 4. For sake of simplification, we set in our c = 1 and q = 2 in our experiments. Taking into account the reality, we set the wireless communication radius Rcom = 40 m and the wireless charging radius Rcha = 15. Each experiment was performed 1000 times, and the value of each result is an average. All the terminals, candidate locations and the sink are randomly generated in a limited R3.

Tab. 2 shows the simulation experiment results on the algorithm RDI. There are four different simulation scenarios, the size of which are 100 m*100 m*10 m, 150 m*150 m*15 m, 200 m*200 m*20 m, and 250 m*250 m*25 m, and the number of candidate location nodes in the scenarios are 100, 225, 400, and 625, respectively. For each scenario, there are five different values of terminal nodes number, which are 10, 20, 30, 40, and50. It is easy to see that the communication cost and number of charging nodes increase with the growth of the number of terminal nodes. The reason is that the total communication cost is related to the number of communication path, which is determined by the number of terminal nodes.

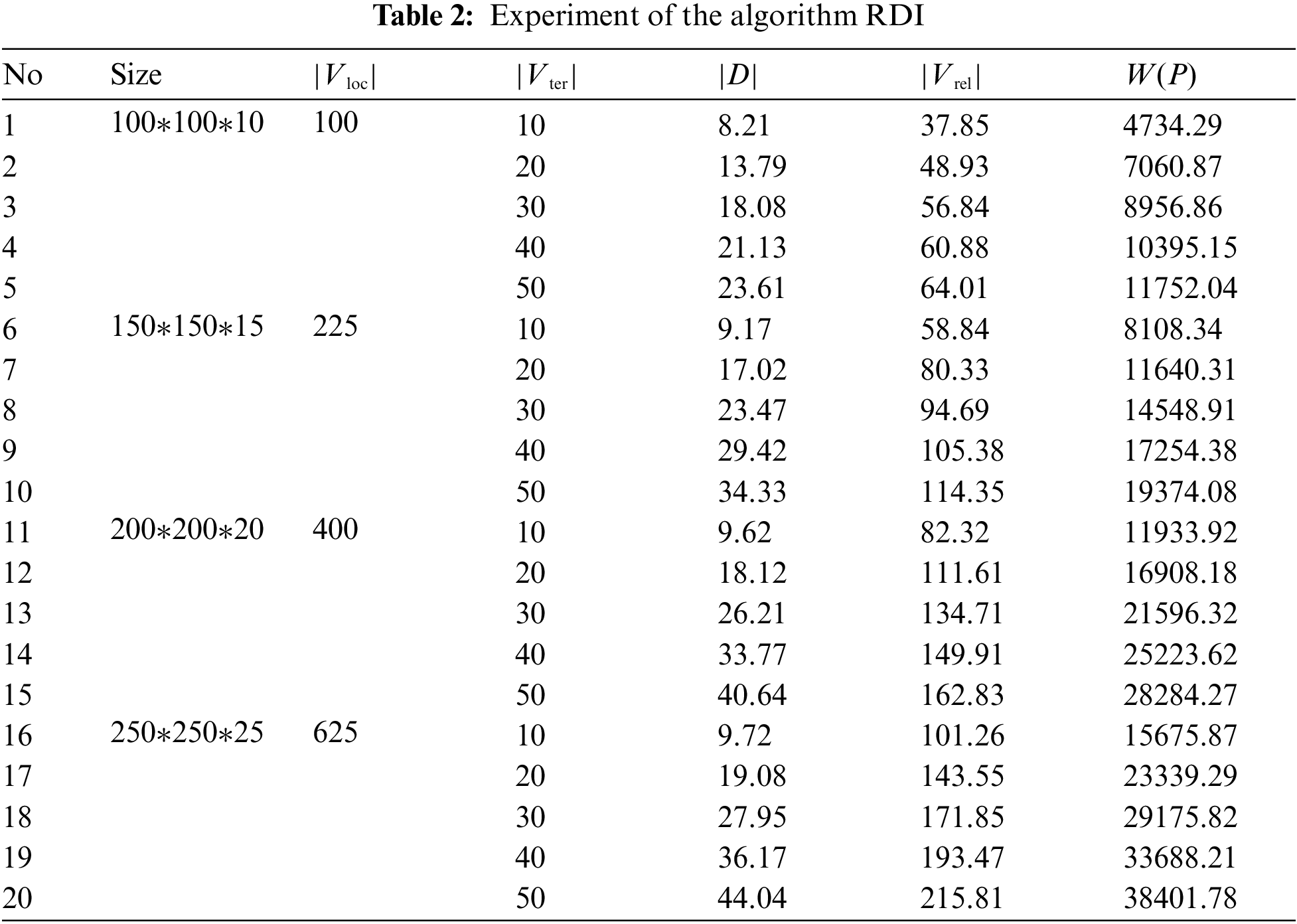
Fig. 5 shows the performance of the algorithm RCOP and RCIG. In the experiments, there are four simulation scenarios (four cases) which are the same as that showed in Tab. 2, and the number of candidate location nodes are also the same. However, the number of terminal nodes is fixed at 20. The horizontal axis shows different number limitation of relay nodes (parameter k), and the vertical axis shows the total communication cost W(P). For the one hand, in each case, the total communication cost decreases with the growth of number of relay node. It is because of that the limitation of the deployed relay makes some shortest path deserted. On the other hand, the communication cost of algorithm RCOP is slightly larger than that of the algorithm RCIG. The reason is that, the local search rule in the algorithm RCOP just tries to find substituted edge between the nodes on some path. But, the local search rule in the algorithm RCIG tries to find that between any two nodes in the whole graph. However, less communication cost is obtained by more running time. For the algorithm RCOP, the total running time is (O (|V|3)). And the time complexity of RCIG is (O (|E||V|3)), which is larger than that of RCOP.

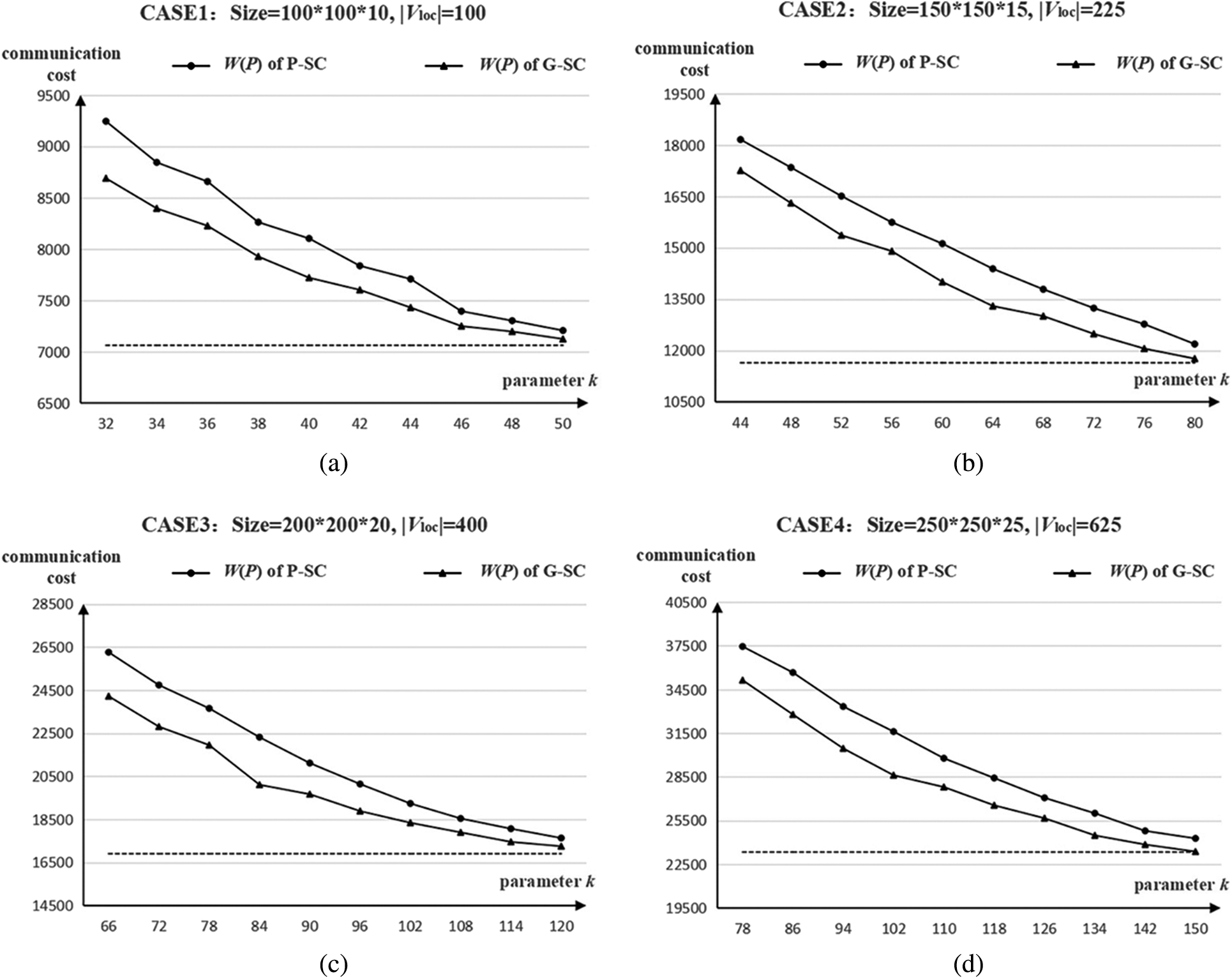
Figure 5: Performance of two algorithms RCOP and RCIG. The subgraphs (a)–(d) show the cases 1–4, where the size of simulation scenarios are 100*100*10, 150*150*15, 200*200*20 and 250*250*25, and the number of candidate location nodes in the scenarios are 100, 225, 400, and 625 respectively

4.2 Engineering Applications

Now, we are going to show an engineering application of our proposed sustainable wireless sensor network system. Let us see the scenario shown in Fig. 6. In a large chemical plant, there are some fixed terminals, which are used to monitor, collect and transmit various parameters of reactors, storage equipment or environment, such as pressure, temperature, humidity, concentration of various chemical elements, etc. Moreover, there is a sink node, which connects the communication network with external network. At the side of the plant, there is a 4G station, which could deliver data to the control center. Assume there is a project that will last one to two weeks, the task of which is to gather the collection data from the terminals to the control center. Due to the reason that each parameter is very important for the running of equipments and the safety of the chemical plant, timely collection and transmission of collected data to a server or controller binding to the station is important and particularly necessary. Due to the needs of the project itself, the 4G station should be replaced by a 5G station. However, there is a problem for the coverage of the 5G station. In the scenario, the size of the plant is no less than 2000 m*1500 m. Nevertheless, generally, the 5G signal cannot be transmitted beyond 400 m. Moreover, compared with 4G signal, 5G signal is more easily blocked by obstacles such as plant buildings and equipments. Hence, a 5G station cannot cover all the terminals. This will lead to two problems for the uncovered terminals. The one is that the data collected by them cannot send data to the control center. The other one is that if a terminal runs out of power it will not work, which makes the whole system cannot run properly. One reasonable way is to deploy a number of 5G stations such that all the terminals are covered. But this will cost a lot.

In this case, it is easy to see that using some relays to make up a wireless communication network with relays is a feasible way. In order to ensure that the terminal has continuous power supply, the relay deployed in the network should hold the function of wireless charging. If a terminal's power is in the state of low-level, then the relays which are not far more than a certain value (radius of wireless charging) can charge this terminal. And more precisely, our proposed sustainable wireless sensor network system can be used to accomplish the extremely project shown in Fig. 6.

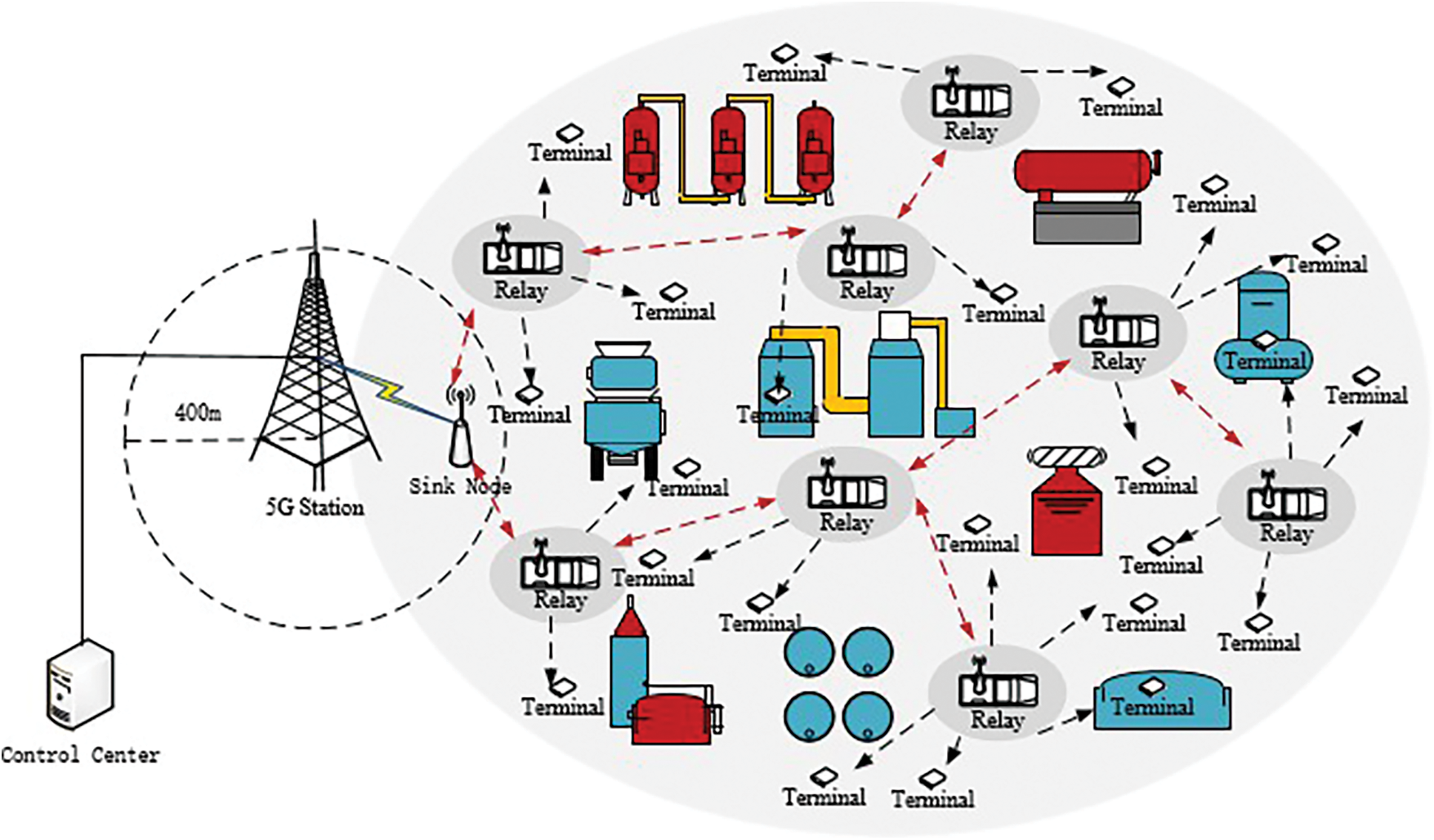
Figure 6: An instance of chemical plant with fixed terminals, where a large part of terminals cannot communicate the 5G station directly

5  Conclusions

In this paper, we proposed a sustainable wireless sensor network communication system which holds the property of sustainable communication via charging the terminals by relays. And we extracted some combinatorial optimization problems from it for different cases under some reasonable assumptions. We have investigated these problems from the aspects of computational complexity, heuristic algorithms and engineering application. It is possible that our proposed system can be also suitable for some other applications in IoT.

Funding Statement: The authors would like to extend their gratitude to King Saud University (Riyadh, Saudi Arabia) for funding this research through Researchers Supporting Project number (RSP-2021/260). And this work was supported by the Natural Science Foundation of Hunan Province, China (Grant No. 2020JJ4949), and the Postgraduate Scientific Research Innovation Project of Hunan Province (Grant No. CX20200883).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  S. Balaji, K. Nathani and R. Santhakumar, “IoT technology, applications and challenges: A contemporary survey,” Wireless Personal Communications, vol. 108, pp. 363–388, 2019. [Google Scholar]

 2.  R. Yu, W. Lu, H. Lu, S. Wang, F. Li et al., “Sentence pair modeling based on semantic feature map for human interaction with IoT devices,” International Journal of Machine Learning and Cybernetics, vol. 12, pp. 3081–3099, 2021. [Google Scholar]

 3.  R. N. Mitra and D. P. Agrawal, “5G mobile technology: A survey,” ICT Express, vol. 1, no. 3, pp. 132–137, 2015. [Google Scholar]

 4.  Y. T. Hou, Y. Shi, H. D. Sherali and S. F. Midkiff, “On energy provisioning and relay node placement for wireless sensor networks,” IEEE Transactions on Wireless Communications, vol. 4, no. 5, pp. 2579–2590, 2005. [Google Scholar]

 5.  M. Patel, R. Chandrasekaran and S. Venkatesan, “Energy efficient sensor, relay and base station placements for coverage, connectivity and routing,” in PCCC 2005. 24th IEEE Int. Performance, Computing, and Communications Conf., Phoenix, AZ, USA, pp. 581–586, 2005. [Google Scholar]

 6.  X. Cheng, D. -Z. Du, L. Wang and B. Xu, “Relay sensor placement in wireless sensor networks,” Wireless Networks, vol. 14, pp. 347–355, 2008. [Google Scholar]

 7.  R. Liu, I. J. Wassell and K. Soga, “Relay node placement for wireless sensor networks deployed in tunnels,” in 2010 IEEE 6th Int. Conf. on Wireless and Mobile Computing, Networking and Communications, Niagara Falls, Canada, pp. 144–150, 2010. [Google Scholar]

 8.  D. Wu, K. Youcef-Toumi, S. Mekid and R. Ben Mansour, “Relay node placement in wireless sensor networks for pipeline inspection,” in 2013 American Control Conf., Washington, DC, USA, pp. 5905–5910, 2013. [Google Scholar]

 9.  B. Yuan, H. Chen and X. Yao, “Optimal relay placement for lifetime maximization in wireless underground sensor networks,” Information Sciences, vol. 418, no. c, pp. 463–479, 2017. [Google Scholar]

10. N. T. Tam, H. T. T. Binh, D. A. Dung, P. N. Lan, L. T. Vinh et al., “A hybrid clustering and evolutionary approach for wireless underground sensor network lifetime maximization,” Information Sciences, vol. 504, pp. 372–393, 2019. [Google Scholar]

11. A. So and B. Liang, “Optimal placement of relay infrastructure in heterogeneous wireless mesh networks by bender's decomposition,” in Ser. QShine ‘06, New York, NY, USA: Association for Computing Machinery, pp. 22–es, 2006. [Google Scholar]

12. Y. Yu, S. Murphy and L. Murphy, “Planning base station and relay station locations in IEEE 802.16j multi-hop relay networks,” in 2008 5th IEEE Consumer Communications and Networking Conference, Las Vegas, NV, USA, pp. 922–926, 2008. [Google Scholar]

13. ——, “A clustering approach to planning base station and relay station locations in IEEE 802.16j multi-hop relay networks,” in 2008 IEEE Int. Conf. on Communications, Beijing, China, pp. 2586–2591, 2008. [Google Scholar]

14. T. Cormen, C. Leiserson, R. Rivest and C. Stein, “Introduction to algorithms,” 3rd ed., The MIT Press, 01 2009. [Google Scholar]

15. J. H. Huang, L. C. Wang, W. S. Chang and C. -J. Su, “Design of optimal relay location in two-hop cellular systems,” Wireless Networks, vol. 16, pp. 2179–2189, 2010. [Google Scholar]

16. D. Yang, X. Fang, G. Xue and J. Tang, “Relay station placement for cooperative communications in WiMAX networks,” in 2010 IEEE Global Telecommunications Conf. GLOBE-COM 2010, Miami, FL, USA, pp. 1–5, 2010. [Google Scholar]

17. H. Lu, W. Liao and F. Y. Lin, “Relay station placement strategy in IEEE 802.16j WiMAX networks,” IEEE Transactions on Communications, vol. 59, no. 1, pp. 151–158, 2011. [Google Scholar]

18. C. Y. Chang, C. T. Chang, T. C. Wang and L. Ming Hsien, “Throughput-enhanced relay placement mechanism in WiMAX 802.16j multihop relay networks,” IEEE Systems Journal, vol. 9, no. 3, pp. 728–742, 2015. [Google Scholar]

19. J. H. Huang and S. Y. Hsu, “QoS provisioning in energy-efficient cooperative networks with power assignment and relay deployment planning,” Wireless Networks, vol. 26, pp. 5207–5222, 2020. [Google Scholar]

20. A. Zappone, S. Atapattu, M. Di Renzo, J. Evans and M. Deb- bah, “Energy-efficient relay assignment and power control in multi-user and multi-relay networks,” IEEE Wireless Communications Letters, vol. 7, no. 6, pp. 1070–1073, 2018. [Google Scholar]

21. S. Atapattu, P. Dharmawansa, M. Di Renzo, C. Tellambura and J. S. Evans, “Multi-user relay selection for full-duplex radio,” IEEE Transactions on Communications, vol. 67, no. 2, pp. 955–972, 2019. [Google Scholar]

22. Y. Chai and X. -J. Zeng, “Delay-and interference-aware routing for wireless mesh network,” IEEE Systems Journal, vol. 14, no. 3, pp. 4119–4130, 2020. [Google Scholar]

23. K. Mahmood, B. Nazir, I. A. Khan and N. Shah, “Search-based routing in wireless mesh network,” EURASIP Journal on Wireless Communications and Networking, vol. 2017, no. 36, 2017. [Google Scholar]

24. W. Li, H. Xu, H. Li, Y. Yang, P. K. Sharma et al., “Complexity and algorithms for superposed data uploading problem in networks with smart devices,” IEEE Internet of Things Journal, vol. 7, no. 7, pp. 5882–5891, 2020. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.