DOI:10.32604/cmc.2022.022824

| Computers, Materials & Continua DOI:10.32604/cmc.2022.022824 |  |
| Article |
Task Scheduling Optimization in Cloud Computing by Rao Algorithm
1Faculty of Computers and Information, Department of Computer Science, Sohag University, Sohag, 82524, Egypt
2Department of Computer Science and Artificial Intelligence, College of Computer Science and Engineering, University of Jeddah, Jeddah, 21959, Saudi Arabia
*Corresponding Author: A. Younes. Email: a.yhamed@yahoo.com
Received: 19 August 2021; Accepted: 03 December 2021
Abstract: Cloud computing is currently dominated within the space of high-performance distributed computing and it provides resource polling and on-demand services through the web. So, task scheduling problem becomes a very important analysis space within the field of a cloud computing environment as a result of user's services demand modification dynamically. The main purpose of task scheduling is to assign tasks to available processors to produce minimum schedule length without violating precedence restrictions. In heterogeneous multiprocessor systems, task assignments and schedules have a significant impact on system operation. Within the heuristic-based task scheduling algorithm, the different processes will lead to a different task execution time (makespan) on a heterogeneous computing system. Thus, a good scheduling algorithm should be able to set precedence efficiently for every subtask depending on the resources required to reduce (makespan). In this paper, we propose a new efficient task scheduling algorithm in cloud computing systems based on RAO algorithm to solve an important task and schedule a heterogeneous multiple processing problem. The basic idea of this process is to exploit the advantages of heuristic-based algorithms to reduce space search and time to get the best solution. We evaluate our algorithm's performance by applying it to three examples with a different number of tasks and processors. The experimental results show that the proposed approach significantly succeeded in finding the optimal solutions than others in terms of the time of task implementation.
Keywords: Heterogeneous processors; RAO algorithm; heuristic algorithms; task scheduling; multiprocessing; cloud computing
One of the main pre-performance measurements of any computing system is the execution time, and to reduce execution time processors have been developed faster but have physical limitations, and the multi-processing system has therefore been used. In the multiprocessor system, the program will be divided into tasks, so that each task is performed on a processor. The task assignment association and processors are called task scheduling in the multi-processing system.
To access optimal task scheduling and processor used in a heterogeneous multiprocessor system is a mathematically difficult goal. The optimal term may refer to many of the objectives combined. The main goal is usually to reduce the length of the schedule (makespan). Finding optimal task scheduling is NP-complete, [1,2]. Accordingly, heuristic algorithms are a good candidate for addressing this problem. Meta-heuristics are problem-independent improvement techniques that give an optimum resolution by exploring and exploiting the whole search area iteratively. These techniques have been successfully engaged to resolve distinct real-life and multidisciplinary issues. An honest quantity of literature has been already published on the design and role of assorted meta-heuristic algorithms and their variants. The aim of this study [3] was to present a comprehensive analysis of nature-inspired meta-heuristic utilized within the domain of feature choice. Chaotic Interior Search Algorithm (CISA) was proposed in [4]. Interior Search Algorithm (ISA) is a recently proposed meta-heuristic impressed by the change of state of objects and mirrors. However, the same as most of the meta-heuristic algorithms, ISA, in addition, encounter two issues, i.e., entrapment in local optima and slow convergence speed. Stress is that the most prevailing and international psychological condition that inevitably disrupts the mood and behavior of individuals. Chronic stress might gravely affect the physical, mental, and social behavior of victims and consequently, induce myriad crucial human disorders. Herein, a review has been presented where supervised learning (SL) and soft computing (SC) techniques used in stress diagnosis have been meticulously investigated to focus on the contributions, strengths, and challenges faced in the implementation of those strategies in stress diagnostic models [5]. Salp Swarm Algorithm (SSA) is a recently created bio-inspired improvement algorithm that relies on the swarming mechanism of salps. Despite the high performance of SSA, slow convergence speed and obtaining stuck in local optima are two disadvantages of SSA. This paper [6] introduces a novel Chaotic Salp Swarm Algorithm (CSSA) to avoid these weaknesses. A Computer-Aided Diagnosis (CAD) system that employs a brilliant learner to diagnose the presence or absence of a disease has been developed. Each clinical dataset is preprocessed and split into a training set (60%) and a testing set (40%). A wrapper approach that uses three bio-inspired algorithms, namely, Cat Swarm Optimization, Krill Herd, and Bacterial Foraging Optimization with the classification accuracy of Support Vector Machine because the fitness function has been used for feature choice. The chosen features of each bio-inspired algorithm are stored in three separate databases. The features selected by each bio-inspired algorithm are used to train three Back Propagation Neural Networks independently using the Conjugate Gradient Algorithm [7]. A bio-inspired technique called Bat Algorithm hybridized with a Naive Bayes classifier has been presented [8]. When the amount of data and information is said to double in every 20 months approximately, feature selection has become extremely vital and helpful. Any enhancements in feature selection will positively affect a wide array of applications in fields like pattern recognition, machine learning, or signal process.
In this paper, a multi-processing system was studied. Heterogeneous multi-processing has different processing capabilities. Task processing time can only be determined when the task is assigned to a specific processor, i.e., the task processing time depends on the processor. A new efficient approach based on RAO's algorithm, [9,10], called Proposed RAO (PRAO) was developed to find an ideal task scheduling set to a heterogeneous multi-processing system. We evaluate our algorithm's performance by applying it to three examples with a different number of tasks and processors. The results show that the proposed approach succeeded in finding the optimal solutions than other algorithms in terms of the time of task implementation.
The paper is organized as follows. The notations are given in Section 2. Section 3 presents some related work for task scheduling problems for different structures of multiprocessing systems. Section 4 introduces the problem description. Section 5 shows the RAO optimization algorithm. In Section 6 describes the PRAO approach. The results were obtained by applying the PRAO and compared with other results presented in Section 7. Section 8 draws conclusions and future work.

The goal of scheduling tasks in the multiprocessor system is to assign a processor task and reduce the processing time. To reduce the processing time, a Genetic Algorithm (GA) may apply to the processors for different solutions faster processing time.
Task scheduling is two aspects: Earliest Start Time (EST) and Number of Tasks dependencies (NTD). This comparison was made using java simulation and the result obtained is the proposed algorithm minimum EST solution achieves faster processing time than the EST maximum [1,2]. The study addressed the problems of scheduling multi-processors referred to a Directed Acyclic Graph (DAG) task targeted with communications costs. The authors suggested based on GA, priority/shorter first processor schedule to provide better solutions than existing algorithms about the completion time of the resulting schedules and reduce the time of effective execution of the task [1,2].
Task scheduling algorithms using an Effective Space Search Genetic Algorithm (ESSGA) use the benefits of heuristic-based algorithms to reduce space search and time for effective solutions [11]. The processor assignment was performed using an early, heuristic-based end-time policy, which reduces the time for the time task is performed.
GA for scheduling tasks in multiprocessor systems has indicated that the priority of carrying out the task depends on a higher mission graph to scheduling. This method is simulated and used to compare with the basic genetic algorithm [12].
GA efficiency can be achieved through the improvement of different parameters such as mutation, crossover, selection function, and crossover probability. These GA parameters on reducing bi-criteria fitness functions and parameter development will be accomplished through a central composite design approach with design experiments. Experiments use these parameters and analyze contrast that reduces the total completion time and makespan [13].
Modified Critical Path (MCP) algorithms are used to solve problems in task graph scheduling. The algorithm relies entirely on the new approach to reducing the cost of communications from processors and critical length of time. To solve the scheduling of the graph, the GA has been applied effectively. The GA has proposed to schedule this graph of the task that can be obtained effectively with low time. The results obtained from the study stated that the graph algorithm without the cost of communication could work quickly compared with others [14].
GA chromosomes such as Task List (TL), Processor List (PL), and Integration of Both Task List Processor List Combination (TLPLC). Experiments on the graph of real-world application such as Gaussian elimination, Gauss Jordan, the equation for Laplace, and Lower-Upper (LU) decomposition. Task List Processor List Combination Genetic Algorithm (TLPLCGA) is associated with GA and heuristic algorithms regarding the time and efficiency of the processor have been conducted. The result is an experienced hybrid approach performing better than other algorithms [15].
The NP problem is solved using the integration of heuristic and search techniques. GAs offers a robust and stochastic solution for many optimization problems. Design and implement the schedule of the length of the task graph performed on the processors. To solve the scheduling problem, the GA has been applied [16].
The fitness assessment approach is a time-consuming process of a genetic algorithm that affects the performance of the GA synchronous master-slave algorithm performs better than a sequential algorithm on a large and difficult number of generation problems. This GA search is used in a scheduling program to solve the multiprocessor scheduling problem. A schedule is a simple tool for scheduling the task and modeling on the multiprocessor system. The complex task graph can easily be adjusted to a specific multiprocessor architecture. The result obtained from the study indicated that changing the number of processors on the system by users and small changes in the program would manage delays in communication between processors and overhead costs [17].
The Node Duplication Genetic Algorithm (NGA) approach is based on existing inevitable scheduling techniques to reduce traffic connections between processors. The results you get from the simulation indicate that the GA can use the scheduled task to meet deadlines and get high processor use. Compare NGA performance analysis with GA, First Come First Serve (FCFS), and list scheduling [18].
One such effective technique is known as Ant Colony Optimization (ACO). This improvement technique is inspired by the capabilities of ant colonies to find the shortest route between food sources and their nests. Consequently, an ACO-based algorithm was proposed, to solve the task scheduling problem. The algorithm uses a priority-based heuristic and pheromone, known as the upward rank value, as well as an insertion-based policy and a pheromone aging mechanism to guide the ants to high-quality solutions [19].
The scheduling method based on the Open Computing Language (OpenCL) framework was proposed [20]. It executes a matching degree scheduling algorithm based on a heterogeneous multiprocessor system. Before the actual scheduling, the static task feature value and therefore the processor core configuration feature value is mapped into the same European space, and the “program-core-distance” matching value is calculated by using the wed. Within the actual scheduling, the matching value and the size of the input byte are obtained, and the tasks are matched with the processor under the influence of the two to determine the execution order of the tasks on every processor.
Energy-aware task allocation of embedded systems is one of the most important problems in recent decades. A classical solution to solve the problem is Integer Linear Programming (ILP). However, given the considerable time consumption, it's effective solely to the extent that the scale of the matter is small. A way to use ILP to solve large allocation issues on heterogeneous multiprocessor systems to minimize energy consumption is still a challenge. The authors propose [21] two ILP formulations to deal with it. One complete ILP(1) is used to derive a feasible allocation, and therefore different simplified ILP(2) is for calculating the desired minimum energy.
Reference [22] an efficient technique based on genetic algorithms is developed to solve the problem of task scheduling. To efficiently implement programs in parallel on multiprocessor scheduling problems should be resolved to determine the assignment of tasks to the processors and the execution order of the tasks so that the execution time is decreased.
Reference [23] suggested an ACO based on a task scheduling algorithm to reduce the makespan of the application in cloud environments. Cloud computing is that the development of distributed computing, parallel computing, and grid computing, or defined as the commercial implementation of these computer science concepts. One of the fundamental problems in this environment is related to task scheduling. Cloud task scheduling is an NP-hard improvement problem.
Reference [24] addresses the problem of scheduling tasks through the effective use of evolutionary algorithms. Genetic algorithms are promising to provide near-perfect results even in a large problem area but at the same time the complexity of the time of genetic algorithms are higher but the proposed algorithm, the Performance Effective Genetic Algorithm (PEGA) not only provides near the optimal schedule but also has low time complexity.
The task scheduling model numbers in this work, which can be described as distributed N tasks to be performed on M processors, can be processors with different computing capabilities in general. G can be set to descript the structure of the problem. It is a DAG consisting of n nodes n1, n2, n3, … nn. Each node of the graph is described as a task. The task is supposed to be a set of instructions that must be performed sequentially in a particular processor. The task (node) may have pre-required data (inputs) before they are executed. When you receive all entries, the node can run to execute.
These entries are expected to be delivered after some other tasks have been completed, and these tasks are evaluated for them. We have named reliance on task reliance. If the task (t) depends on other task data, we consider that tasks are tasks that serve as important parents (t), and task (t) is their child. A node without an entry node is called an entry node and is called a node without a child, a termination node [25].
As shown in Fig. 1. The time to perform a task we call the cost of the computation. Whenever the cost of calculating a ni node is indicated by (ni) weight. The graph also contains E direct edges that represent a partial order between tasks. The partial arrangement offers a DAG group restricted by precedence and means that if it (ni → nj), nj is a child, which cannot begin until the ni asset ends. The weight on the edge represents the cost of communication between tasks referred to by C (ni, nj), and the communication cost is considered only if ni and nj are set in different processors, otherwise, it is calculated to be zero, in which case ni and nj are assigned to the processor itself. If a ni node is set to the p processor, the start time and the end time of the node are indicated by ST (ni, p) and FT (ni, p) respectively. After assuming scheduling, the length of the schedule is defined as the max{FT (ni, p)} across all processors.
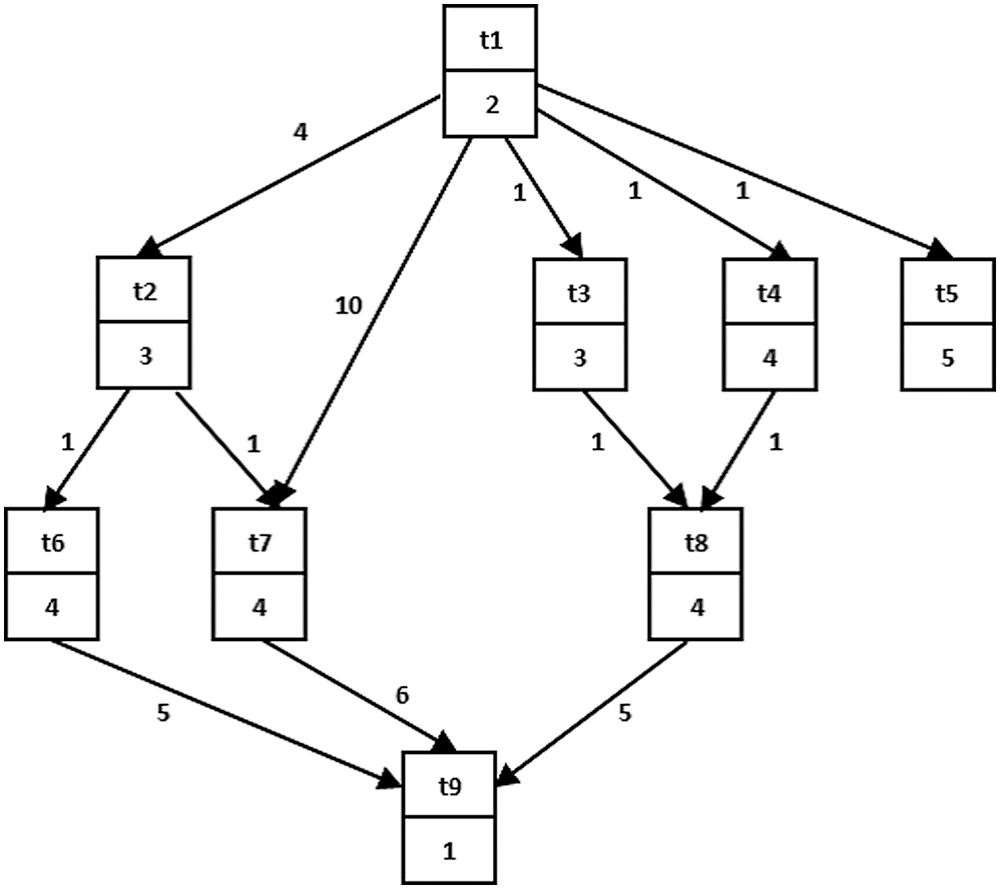
Figure 1: An example of DAG [25]
The task scheduling problem is to find the task schedule in the processors so that the length of the schedule is minimized across possible schedules, where task dependency restrictions are retained. Task dependency restrictions state that no task can be initiated until all parents are finished. Let pj be the processor that Kth original tk task of Ti task is scheduled. The Data Arrival Time (DAT) of ti in the pj processor is the time when the data is available for each required to perform the task, in defined as in [25] as follows:
C(ti, tk) = 0 if task i and k are scheduled on the same processor.
Rao [9] introduced Rao's algorithm. Rao algorithm is a population algorithm on a simple and easy to execute basis for optimization problems. This algorithm has neither specific algorithm parameters nor metaphorical explanations. The general control parameter, i.e., population size, is the only parameter that needs to be adjusted once the termination standard has been fixed. Therefore, it becomes much easier to implement these algorithms for engineering applications.
During the repetitive process, these algorithms use the best iteration solution, the worst iteration solution, and random interactions among the population to explore and exploit the search area. The flow of these three algorithms is similar, but the motion equation used is different for each algorithm. The steps needed from Rao's algorithms to improve objective function G(y) are as follows [10].
Step 1: Define the number of population (N); define the number of design variables (D) and their boundaries: lower bound, upper bound; termination criterion: it can be a number of function evaluations or level of accuracy required for the objective function.
Step 2: Randomly initialize the population of size N and evaluate the objective function G(y) values.
Step 3: Select the best_solution and worst_solution from the population depending on their objective function value. If the G(y) is a minimization function, then the solution with the minimum G(y) value is the best_solution, and the solution with the maximum G(y) value is the worst_solution. Similarly, if the G(y) is a maximization function, then the solution with the maximum G(y) value is the best_solution, and the solution with the minimum G(y) value is the worst_solution.
Step 4: Locate the new solutions for all the population (pop = 1, 2…N): during the ith iteration, let Yv,p,i be the value of vth variable for the pth solution, Yv,b,i be the value of vth variable for the best solution, Yv,w,i be the value of vth variable for the worst solution, and Yv,p,i be the newly located value of Yv,p,i. Then, For the Rao-1 algorithm, the new solutions are found using the following equation:
For the Rao-2 algorithm, the new solutions are located using the following equation:
where r1,v,i and r2,v,i are the two random numbers selected in the range [0, 1] for the vth variable during the ith iteration.
Step 5: Evaluate the objective function values for the new population and apply the greedy selection process. If the objective function value corresponding to the new solution Yv,p,i is better than that of the old solution, then replace the old solution with the new solution or otherwise discard the new solution.
Step 6: Check for the termination criterion. If the termination criterion is not satisfied, go to Step 3, or else report the optimum solution from the final population.
PRAO algorithm begins with the first set of population solutions. Then, by applying some operators the best solution is selected according to the objective value of the function. In the PRAO algorithm we declare the following steps:
The initial population is randomly generated according to this relation
where LB is a lower bound and UB is upper bound we consider that the value of the upper bound is equal to the number of processors and lower bound value is equal to 1 we see that the representation of a vector is a continuous value, so we will use the Smallest Position Value (SPV) rule [26] and Largest Position Value (LPV) rule [27] and by using modulus function with the number of processors and increasing the value by 1 as shown in Fig. 2.
Where the tasks T2, T6 are scheduled into processor 1 and the tasks T4, T5, T7 are scheduled into processor 2 and T1, T3 are scheduled into processor 3, as shown in Fig. 3.
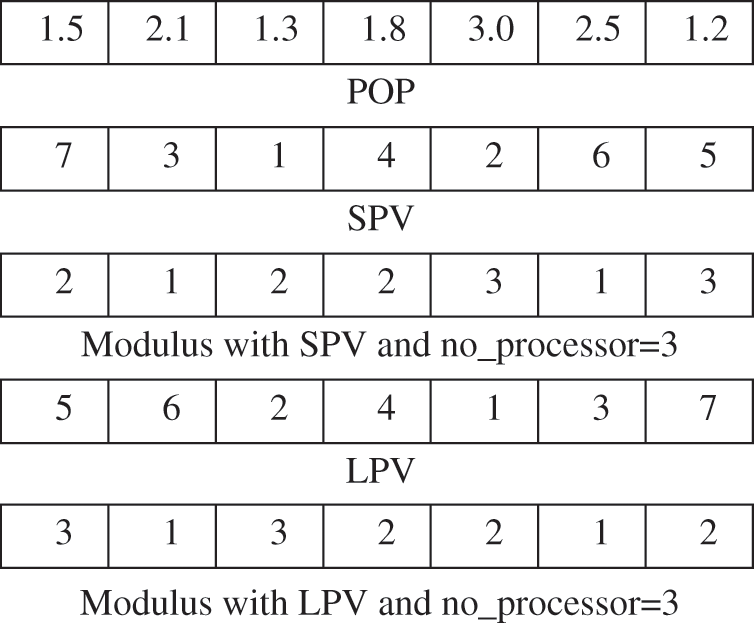
Figure 2: An example of proposed schedule

Figure 3: Proposed schedule
Task priority plays a big role in task scheduling and calculating schedule length. The proposed priority is randomly generated in order that preserves the precedence constraints.
The main objective of the scheduling problem is to reduce schedule length. That is:
where a is a constant and S_Length is the schedule length which is determined by the following equation:
The pseudo-code for the task schedule using the Standard Genetic Algorithm (SGA) [25] is as follows:
For all processor Pj RT[Pj] = 0; j = 1,…N.
For i = 1 to N
{
Remove the first task Ti form list LT.
For j = 1 to M
{
If Ti is scheduled to processor Pj
ST[Ti] = max{RT[Pj], DAT(Ti, Pj)}
FT[Ti] = ST[Ti] + weight[Ti]
RT[Pj] = FT[Ti]
End If
}
}
S_Length = max {FT}
Step 1: Select the best solution
Step 2: Select the worst solution
Step 3: Select a randomly solution but not be the same as the current solution
Step 4: Calculate the objective function
Step 5: If the current solution is less than the randomly chosen solution calculate Ynew and call
function manar(Ynew)
Step 6: If the current solution is greater than the randomly chosen solution calculate Ynew and
call function manar(Ynew)
Step 7: Calculate the schedule length
Step 8: If the new solution is better than the current solution update the current
Step 9: If the minimum value is less than the best update the best value
Step 10: Repeat step 1…step 9 until reaching maximum iteration value
Function manar(s)
R = random number between [1…5]
Switch case (R)
Case 1:
Use SPV rule
Case 2:
Use LPV rule
Case 3:
Use round nearest function
Case 4:
Use floor nearest function
Case 5:
Use ceil nearest function
End case
End function
In this section, we show PRAO effectiveness by applying it to three examples. The first example of 10 tasks and three processors is heterogeneous. The second example is 11 tasks and two heterogeneous processors. The third of 10 tasks and two processors is heterogeneous. PRAO algorithm was implemented as a system by MATLAB 2016. We run our system one more time with the initial population = 100, and the maximum number of iteration = 100 for all three examples.
We consider an example of 10 tasks {T1, T2, T3, T4, T5, T6, T7, T8, T9, T10} as shown in Fig. 4 to be executed on three heterogeneous processors {p1, p2, p3}, the cost of executing each task on different processors is shown in Tab. 1, [28]. The best solution and the schedule obtained by the PRAO are shown in Fig. 5 and Tab. 2 respectively. The results obtained by the PRAO are compared with that obtained by ACO [23], Critical Path on Processor (CPOP), and Heterogeneous Earliest Finish Time (HEFT) [28] as shown in Tab. 3 and Fig. 6 with the proposed task priority {T1, T4, T3, T2, T5, T6, T9, T8, T7, T10}.
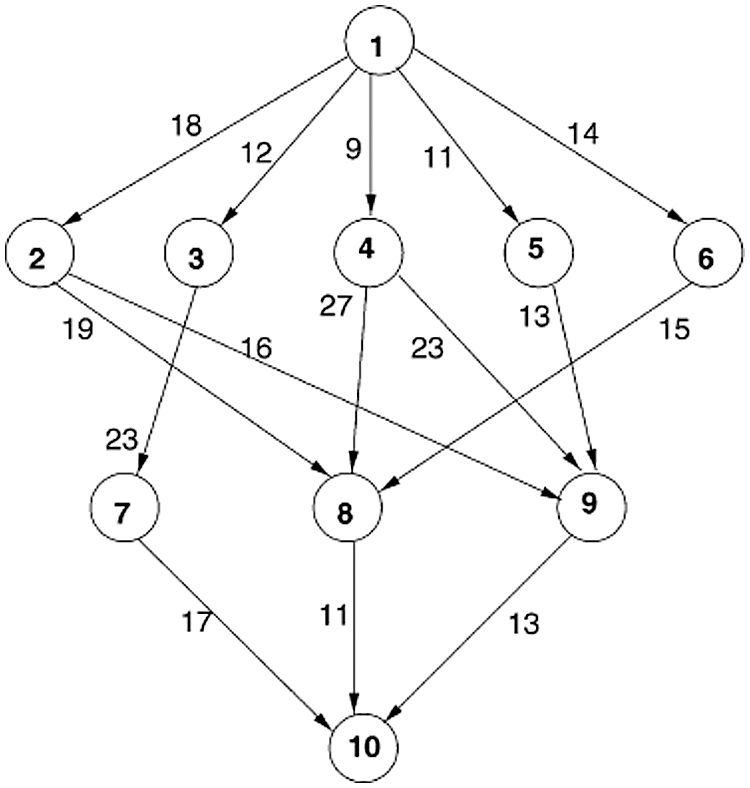
Figure 4: An example of DAG application with 10 tasks [28]


Figure 5: The best solution for example 1
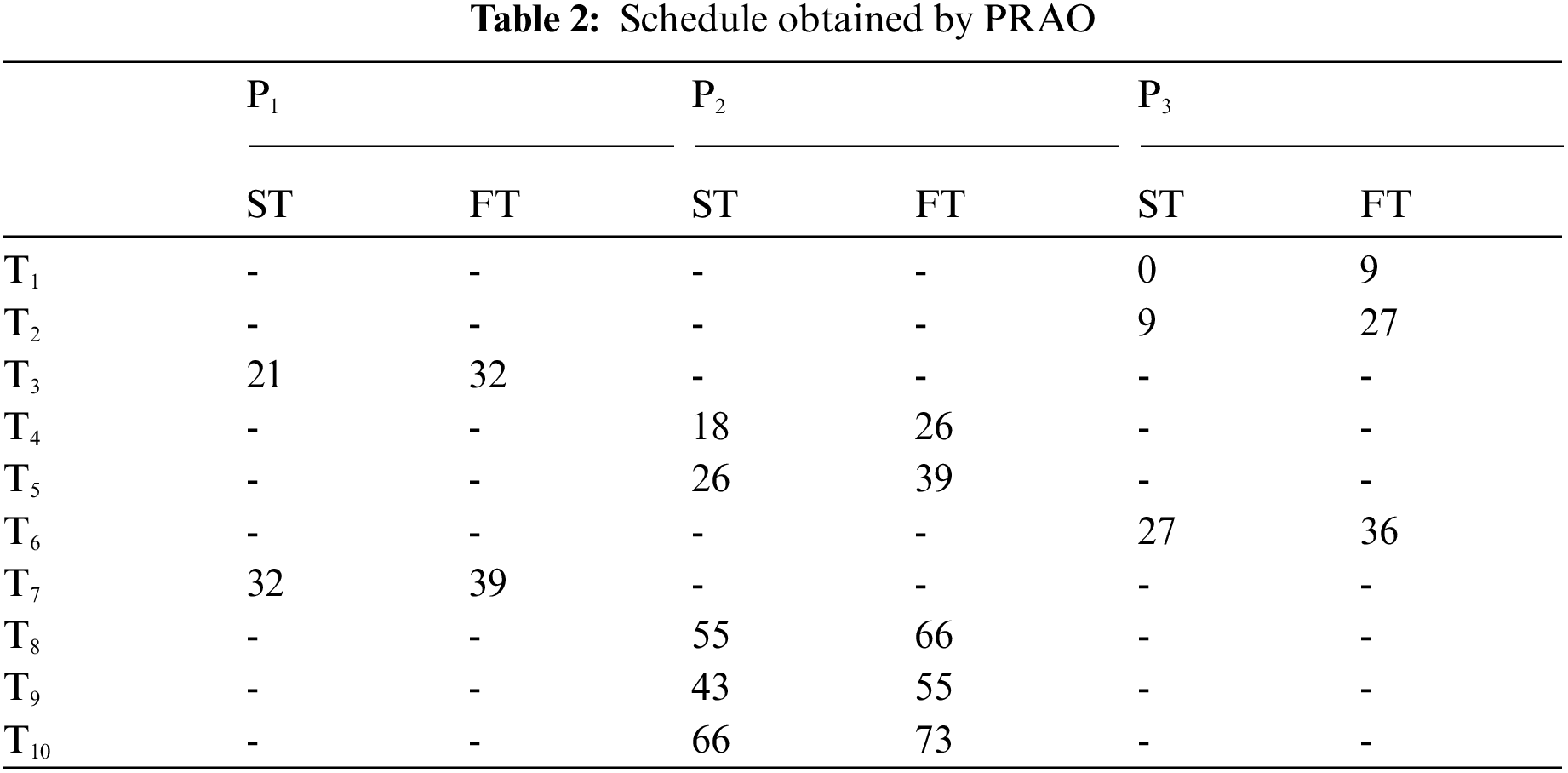
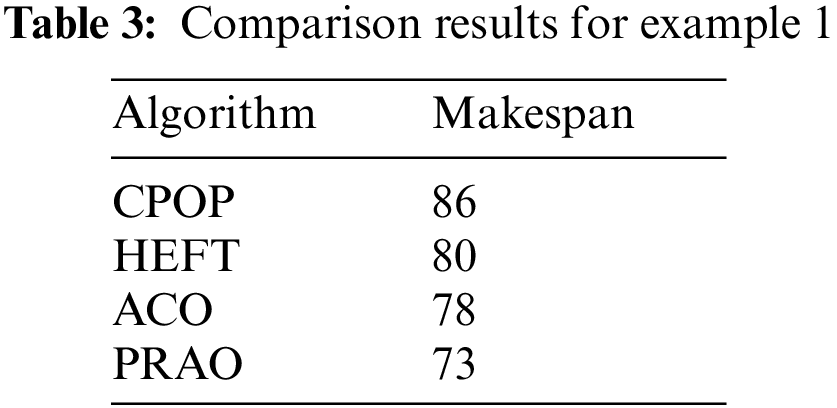
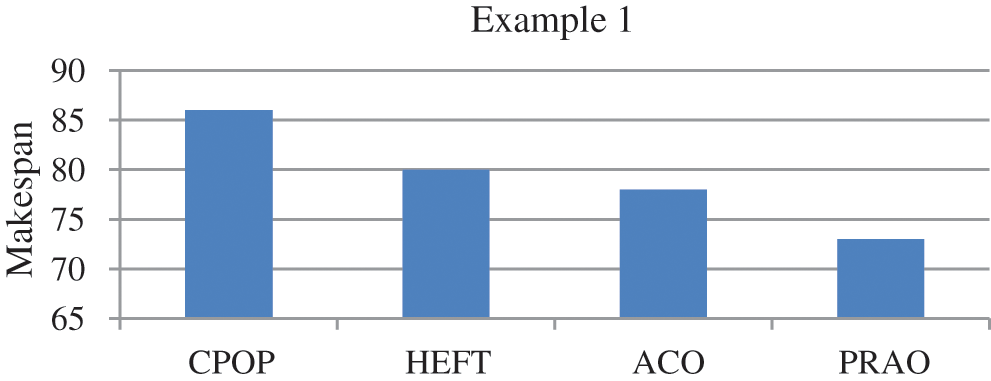
Figure 6: Comparison of makespan for DAG in Fig. 4
In this example, the number of tasks {T1, T2, T3, T4, T5, T6, T7, T8, T9, T10, T11} as shown in Fig. 7 to be executed on two heterogeneous processors {P1, P2}, the cost of executing each task on different processors and inter-task communication cost between the tasks shown in Tab. 4, [29]. The best solution and the schedule obtained by the PRAO are shown in Fig. 8 and Tab. 5 respectively. The obtained results are compared with Upward and Downward [29], GA [30], and Particle Swarm Optimization (PSO) [31] for the proposed task priority {T1, T3, T2, T7, T4, T5, T6, T8, T10, T9, T11}, as shown in Tab. 6 and Fig. 9 respectively.
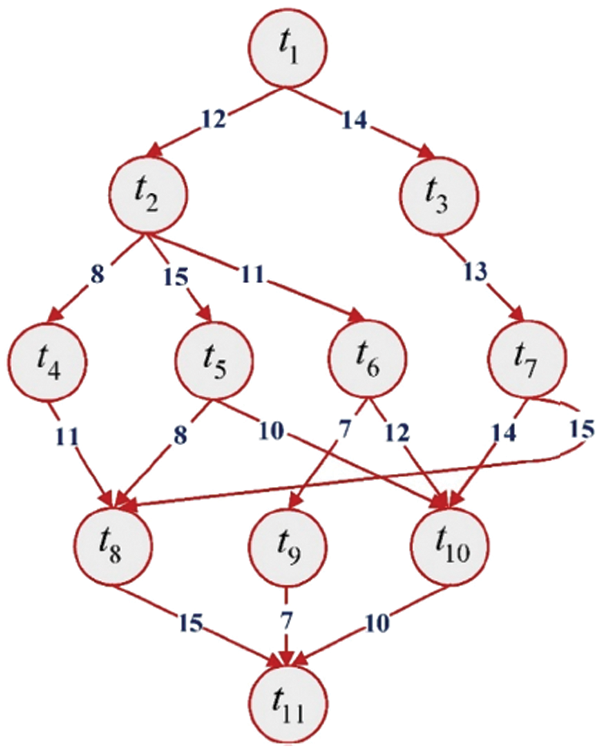
Figure 7: An example of DAG application with 11 tasks [29]
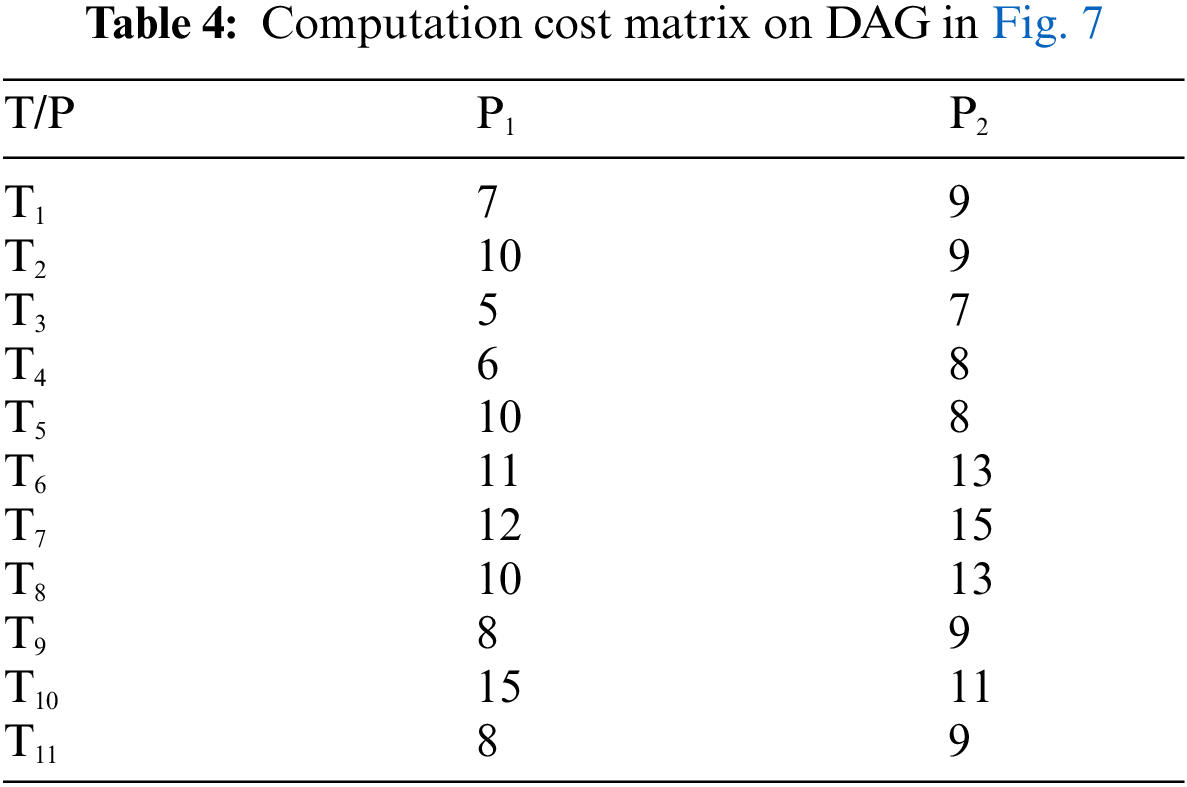

Figure 8: The best solution for example 2
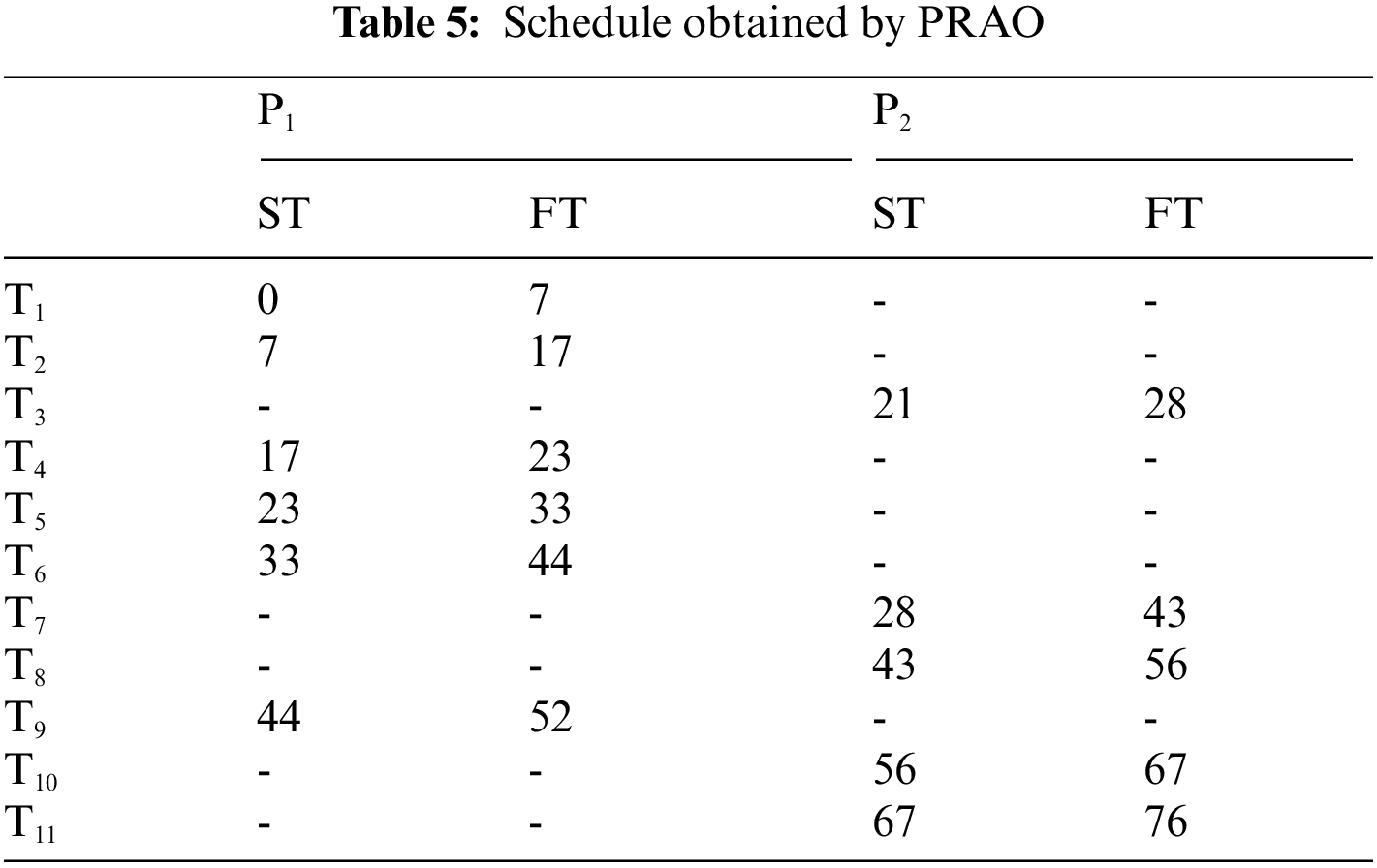
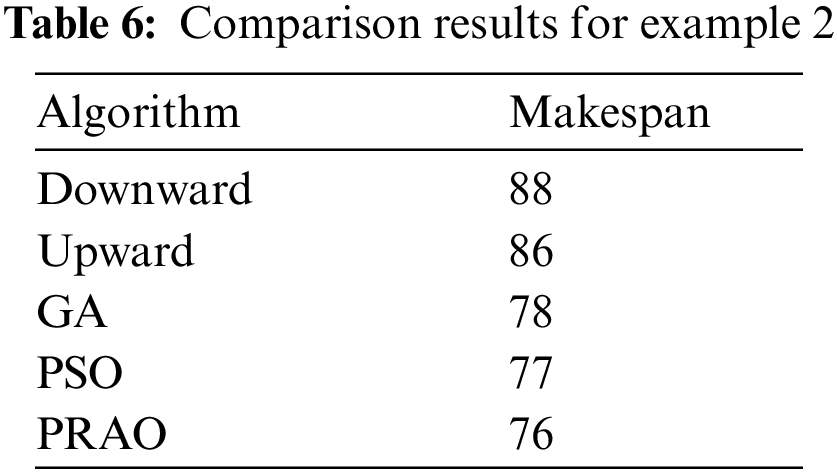
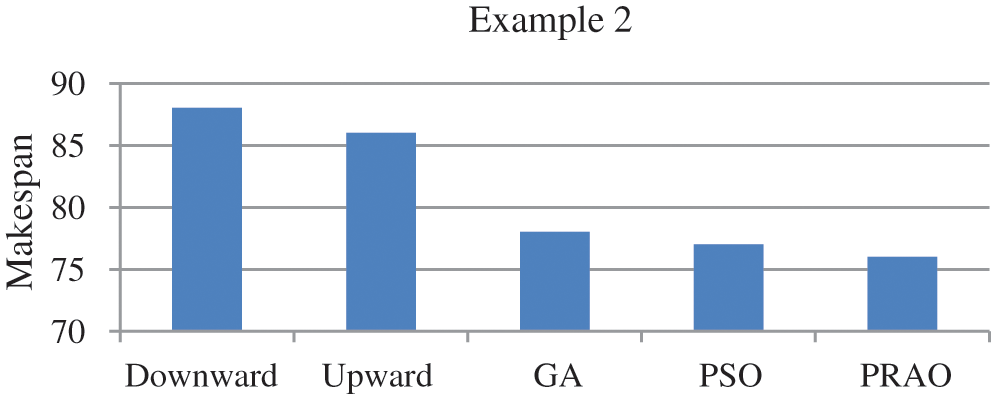
Figure 9: Comparison of makespan for DAG in Fig. 7
In this example, the number of tasks {T1, T2, T3, T4, T5, T6, T7, T8, T9, T10} as shown in Fig. 10 to be executed on two heterogeneous processors {P1, P2}, the cost of executing each task on different processors and inter-task communication cost between the tasks are shown in Tab. 7, [32]. The best solution and the schedule obtained by the PRAO are shown in Fig. 11 and Tab. 8 respectively. We run our proposed algorithm and compare the results with four algorithms Predict Earliest Finish Time (PEFT), HEFT, and Task Scheduling Heterogeneous Computing Systems (TSHCS) [32], Heterogeneous Scheduling with Improved Task Priority (HSIP) [33], and Hybrid List-based Task Scheduling Duplication (HLTSD) [34] with the proposed task priority {T1, T3, T5, T4, T2, T6, T7, T9, T8, T10} as shown in Tab. 9 and Fig. 12 respectively.
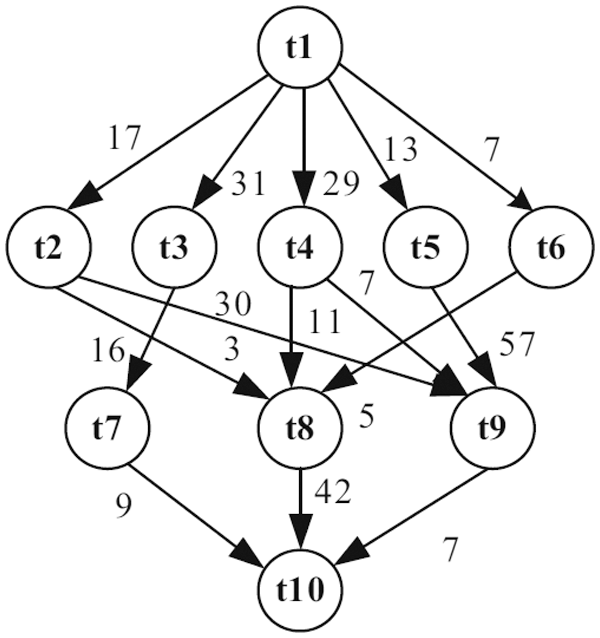
Figure 10: An example of DAG application with 10 tasks [32]
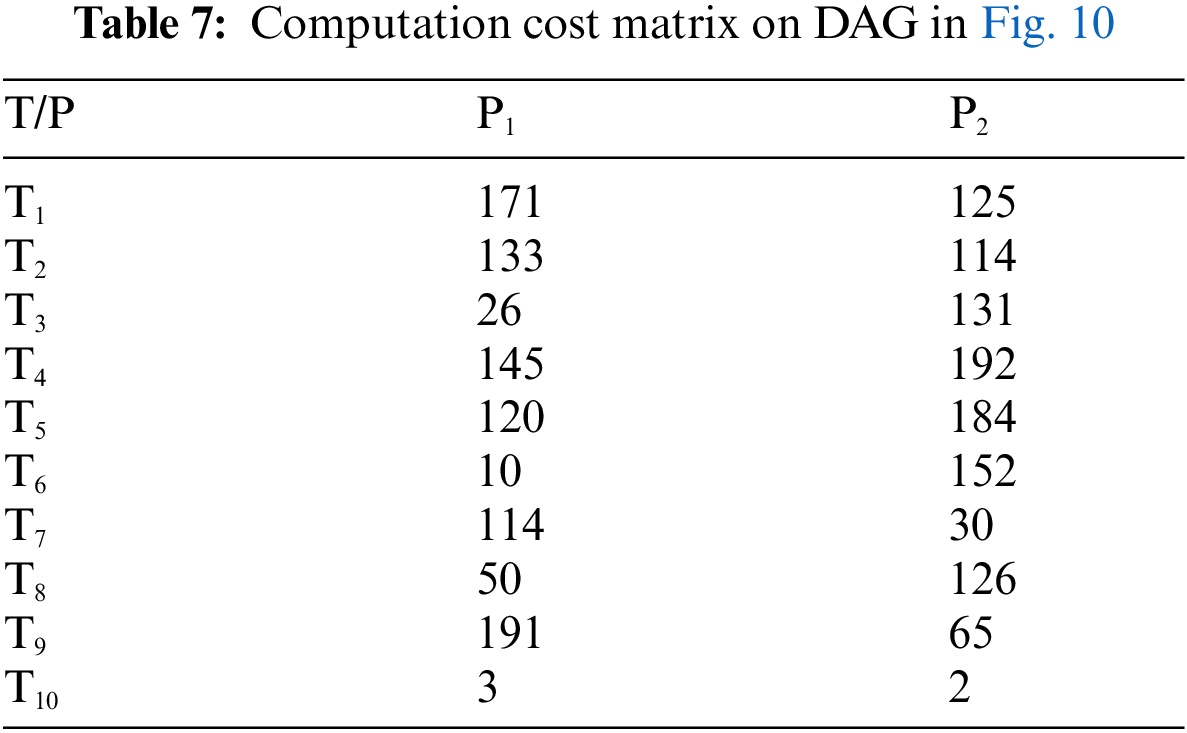

Figure 11: The best solution for example 3
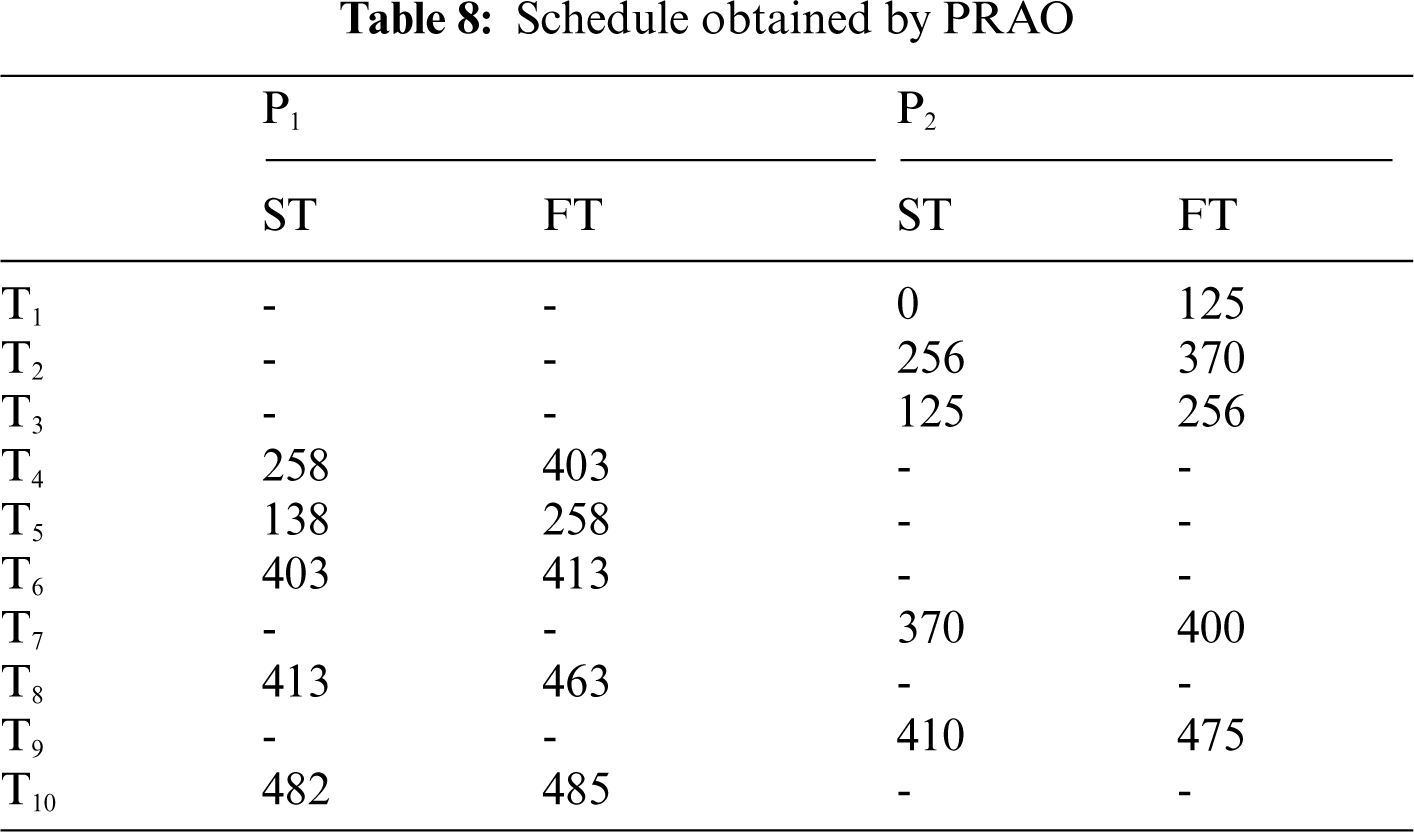
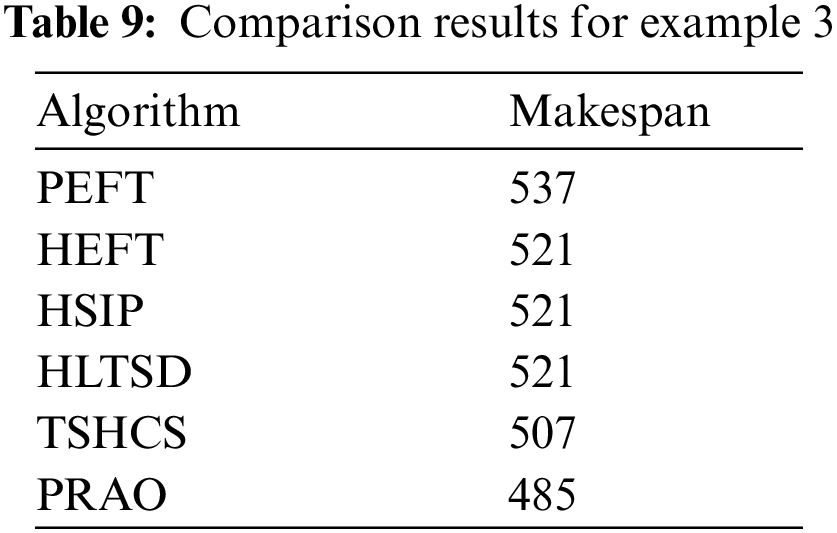
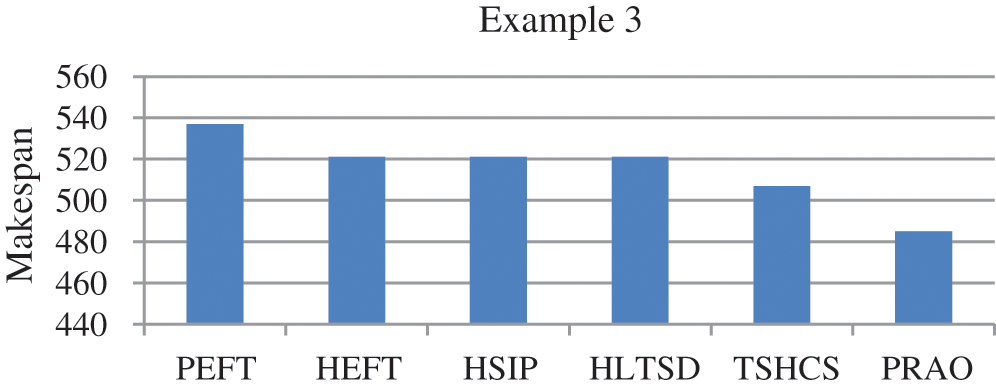
Figure 12: Comparison of makespan for DAG in Fig. 10
In this paper, we introduced PRAO algorithm to solve the task scheduling problem in distributed systems. The system was two processes. The first process consists of a limited number of fully connected homogeneous processors and the second consists of a limited number of fully connected heterogeneous processors. We compared the results of PRAO with ACO, CPOP, and HEFT, it is clear that the length of PRAO's schedule was less than that of CPOP, HEFT, and ACO as shown in Fig. 6. Also, we compared PRAO results in the case of heterogeneous processors, Fig. 9 shows that the length of the PRAO heterogeneous processor schedule was less than that obtained by Upward, Downward, GA and PSO. In addition, the PRAO results were better than those found by PEFT, HEFT, TSHCS, HSIP, and HLTSD as shown in Fig. 12.
The scheduling problem contains many versions of different structures and systems, especially with the current importance of account capabilities. In the meantime, the efficiency of time is strongly required from any system, and this is achieved through new algorithms rather than faster devices. Even the new 5G connection depends on the efficiency of the software account. For future work, PRAO may be used to solve the scheduling problem based on the OpenCL framework. In addition, study the scheduling problem considering Energy in the cloud computing system and solve it by PRAO algorithm.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. E. S. H. Hou, N. Ansari and H. Ren, “A genetic algorithm for multiprocessor scheduling,” IEEE Transactions on Parallel and Distributed Systems, vol. 5, no. 2, pp. 113–120, 1994. [Google Scholar]
2. Q. M. Hussein and A. N. Hasoon, “Dynamic process scheduling using genetic algorithm,” in Proc. NTICT, Baghdad, Iraq, pp. 111–115, 2017. [Google Scholar]
3. M. Sharma and P. Kaur, “A comprehensive analysis of nature-inspired meta-heuristic techniques for feature selection problem,” Archives of Computational Methods in Engineering, vol. 28, no. 3, pp. 1103–1127, 2021. [Google Scholar]
4. S. Arora, M. Sharma and P. Anand, “A novel chaotic interior search algorithm for global optimization and feature selection,” Applied Artificial Intelligence, vol. 34, no. 4, pp. 292–328, 2020. [Google Scholar]
5. S. Sharma, G. Singh and M. Sharma, “A comprehensive review and analysis of supervised-learning and soft computing techniques for stress diagnosis in humans,” Computers in Biology and Medicine, vol. 134, pp. 1–19, 2021. [Google Scholar]
6. A. E. Hegazy, M. A. Makhlouf and G. S. El-Tawel, “Feature selection using chaotic salp swarm algorithm for data classification,” Arabian Journal for Science and Engineering, vol. 44, no. 4, pp. 3801–3816, 2019. [Google Scholar]
7. S. Murugesan, R. S. Bhuvaneswaran, H. K. Nehemiah, S. K. Sankari and Y. N. Jane, “Feature selection and classification of clinical datasets using bioinspired algorithms and super learner,” Computational and Mathematical Methods in Medicine, vol. 2021, pp. 1–18, 2021. [Google Scholar]
8. A. M. Taha, A. Mustapha and S. -D. Chen, “Naive Bayes-guided Bat algorithm for feature selection,” The Scientific World Journal, vol. 2013, pp. 1–9, 2013. [Google Scholar]
9. R. V. Rao, “Rao algorithms: Three metaphor-less simple algorithms for solving optimization problems,” International Journal of Industrial Engineering Computations, vol. 11, no. 1, pp. 107–130, 2020. [Google Scholar]
10. R. V. Rao and H. S. Keesari, “Rao algorithms for multi-objective optimization of selected thermodynamic cyclesn,” Engineering with Computers, vol. 36, pp. 1–29, 2020. [Google Scholar]
11. M. Akbari and H. Rashidi, “An efficient algorithm for compile-time task scheduling problem on heterogeneous computing systems,” International Journal of Academic Research, vol. 7, no. 1, pp. 192–200, 2015. [Google Scholar]
12. A. Sharma and M. Kaur, “An efficient task scheduling of multiprocessor using genetic algorithm based on task height,” International Journal of Hybrid Information Technology, vol. 8, no. 8, pp. 83–90, 2015. [Google Scholar]
13. S. Dhingra, S. Gupta and R. Biswas, “Genetic algorithm parameters optimization for bi-criteria multiprocessor task scheduling using design of experiments,” International Journal of Computer, Electrical, Automation, Control and Information Engineering, vol. 8, no. 11, pp. 661–665, 2014. [Google Scholar]
14. M. Mahi and H. Kodaz, “Genetic algorithm with descendants idea for scheduling tasks graph in the multi-processor architecture,” Journal of Advances in Computer Networks, vol. 2, no. 1, pp. 10–13, 2014. [Google Scholar]
15. M. R. Mohamed and M. Awadalla, “Hybrid algorithm for multiprocessor task scheduling,” International Journal of Computer Science, vol. 8, no. 2, pp. 79–88, 2011. [Google Scholar]
16. N. Al-Angari and A. ALAbdullatif, “Multiprocessor scheduling using parallel genetic algorithm,” International Journal of Computer Science, vol. 9, no. 3, pp. 260–264, 2012. [Google Scholar]
17. M. Bohler, F. Moore and Y. Pan, “Improved multiprocessor task scheduling using genetic algorithms,” in Proc. of the Twelfth Int. FLAIRS. Conf., Orlando, Florida, USA, pp. 140–146, 1999. [Google Scholar]
18. H. Heidari and A. Chalechale, “Scheduling in multiprocessor system using a genetic algorithm,” International Journal of Advanced Science and Technology, vol. 43, pp. 81–94, 2012. [Google Scholar]
19. N. Edward and J. Elcock, “Task scheduling in heterogeneous multiprocessor environments–an efficient ACO-based approach,” Indonesian Journal of Electrical Engineering and Computer Science, vol. 10, no. 1, pp. 320–329, 2018. [Google Scholar]
20. J. Fang, T. Yu and Z. Wei, “Heterogeneous multiprocessor matching degree scheduling algorithm based on OpenCL framework,” in IOP Conf. Series: Materials Science and Engineering IOP Publishing, Kazimierz Dolny, Poland, vol. 490, no. 4, pp. 042045, 2019. [Google Scholar]
21. Y. Qin, G. Zeng, R. Kurachi, Y. Matsubara and H. Takada, “Energy-aware task allocation for heterogeneous multiprocessor systems by using integer linear programming,” Journal of Information Processing, vol. 27, pp. 136–148, 2019. [Google Scholar]
22. M. Golub and S. Kasapović, “Scheduling multiprocessor tasks with genetic algorithms,” in Proc. of the IASTED Int. Conf. Applied Informatics, Insbruck, Austria, pp. 273–278, 2002. [Google Scholar]
23. M. A. Tawfeek, A. El-Sisi, A. E. Keshk and F. A. Torkey, “Cloud task scheduling based on ant colony optimization,” International Arab Journal of Information Technology, vol. 12, no. 2, pp. 129–137, 2015. [Google Scholar]
24. S. G. Ahmad, E. U. Munir and W. Nisar, “PEGA: A performance effective genetic algorithm for task scheduling in heterogeneous systems,” in 2012 4th IEEE Int. Conf. on High Performance Computing and Communication & 2012 9th IEEE Int. Conf. on Embedded Software and Systems, Liverpool, United Kingdom, pp. 1082–1087, 2012. [Google Scholar]
25. A. Younes, A. BenSalah, T. Farag, F. A. Alghamdi and U. A. Badawi, “Task scheduling algorithm for heterogeneous multi processing computing systems,” Journal of Theoretical and Applied Information Technology, vol. 97, no. 12, pp. 3477–3487, 2019. [Google Scholar]
26. I. Dubey and M. Gupta, “Uniform mutation and SPV rule based optimized PSO algorithm for TSP problem,” in Proc. of the 4th Int. Conf. on Electronics and Communication Systems, Coimbatore, India, pp. 168–172, 2017. [Google Scholar]
27. L. Wang, Q. Pan and F. M. Tasgetiren, “A hybrid harmony search algorithm for the blocking permutation flow shop scheduling problem,” Computers & Industrial Engineering, vol. 61, pp. 76–83, 2011. [Google Scholar]
28. H. Topcuoglu, S. Hariri and M. -Y. Wu, “Performance effective and low-complexity task scheduling for heterogeneous computing,” IEEE Transactions on Parallel and Distributed Systems, vol. 13, no. 3, pp. 260–274, 2002. [Google Scholar]
29. M. Shirvani, “A hybrid meta-heuristic algorithm for scientific workflow scheduling in heterogeneous distributed computing systems,” Engineering Applications of Artificial Intelligence, vol. 90, pp. 1–20, 2020. [Google Scholar]
30. Y. Xu, K. Li, J. Hu and K. Li, “A genetic algorithm for task scheduling on heterogeneous computing systems using multiple priority queues,” Information Sciences, vol. 270, pp. 255–287, 2014. [Google Scholar]
31. A. Al Badawi and A. Shatnawi, “Static scheduling of directed acyclic data flow graphs onto multiprocessors using particle swarm optimization,” Computers & Operations Research, vol. 40, pp. 2322–2328, 2013. [Google Scholar]
32. S. AlEbrahim and I. Ahmad, “Task scheduling for heterogeneous computing systems,” Journal of Supercomputing, vol. 73, pp. 2313–2338, 2017. [Google Scholar]
33. G. Wang, Y. Wang, H. Liu and H. Guo, “HSIP: A novel task scheduling algorithm for heterogeneous computing,” Scientific Programming, vol. 2016, pp. 1–11, 2016. [Google Scholar]
34. M. Sulaiman, Z. Halim, M. Waqas and D. Aydin, “A hybrid list-based task scheduling scheme for heterogeneous computing,” Journal of Supercomputing, vol. 4, pp. 1–37, 2021. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |