Computers, Materials & Continua DOI:10.32604/cmc.2022.022417
Article

Fuzzy Decision Model: Evaluating and Selecting Open Banking Business Partners

Ngo Quang Trung, Nguyen Van Thanh*, Nguyen Viet Tinh and Syed Tam Husain

Faculty of Commerce, Van Lang University, Ho Chi Minh City, 70000, Vietnam
*Corresponding Author: Nguyen Van Thanh. Email: thanh.nguyenvan@vlu.edu.vn
Received: 06 August 2021; Accepted: 07 September 2021

Abstract: The finance supply chain has always been a different supply chain compared to product supply chain being a service supply chain. Open Banking (OB) is one of the most important milestones since the beginning of financial technology innovation and service supply chain. As these are activities provided by traditional banks, non-bank financial institutions also provide financial service with access to consumer banking, transactional and other financial data to develop financial applications and services tailored to their customers. The development of financial technology, “Open banking”, promotes financial services to begin this transformation. However, evaluating and selecting open banking business partners from multiple perspectives for banks are underexplored. Thus, the authors in this research proposed a hybrid multi-criteria decision-making model which includes a Spherical Fuzzy Analytical Hierarchy Process (SF-AHP) model and a Multi-Attributive Ideal-Real Comparative Analysis (MAIRCA) model with supports from seasoned domain experts. The contribution of this research is a proposition of a fuzzy decision model for evaluating and selecting open banking business partners. The model successfully determined a suitable open bank provider in order to assist decision makers decide objectively.

Keywords: Open banking; MCDM; SF-AHP; MAIRCA; fuzzy theory

1  Introduction

Banking is an essential service that is often considered a necessity now for many businesses on different scales. With the continuous improvement of bank services with an increase of the number of services that banks can deliver, open banking services are able to increase its attraction to many audiences. Open banking is a collaboration model where businesses’ banking data are shared through APIs between two or more unaffiliated parties to deliver continuous analysis about the marketplace [1]. Although the sound of information sharing to unaffiliated parties may sound daunting and unsafe especially with banking information relating to monetary status, the concept of open banking has allowed businesses to create opportunities for third parties to have a chance into further analyze the financial status of businesses.

All of the aforementioned information shared above, the development application programming interface, or API where Zachariadis defined as a method which two computer applications is able to communicate through a shared network that can be understood using a common language [2], have proven to the significant linkage in order for businesses to collaborate with each other. API has been applied in many industries such as popular social media like Twitter, and Facebook [3], manufacturing in analytical technology [4], and even software engineering [5]. With the expansion of API to the banking industries, it creates other opportunities for the API field to continue growing.

The expansion of API in the open banking services requires a lot of trust built between businesses which is essential since the exchange of confidential information is involved. Therefore, the criteria set out to choosing a suitable open banking strategic partner is very important. As there are numerous methods into choosing alternatives based on a set of criteria, the multicriteria decision making methods have proven to continuously solve selection problems over the years of studies especially the Analytical Hierarchy Process (AHP) combined with Fuzzy set to balance the uncertainties amongst experts’ opinions.

2  Literature Review

The application of multicriteria decision-making (MCDM) methods in solving complicated decision-making problems has been widely studied across different disciplines and industry sectors. Especially in the supply chain management discipline, where MCDM methods are frequently used to solve different complicate decision-making problem such as supplier selection problems [6–10], facility selection problems [11–15], and procurement order allocation problems [16–20]. There are also multiple literatures about the application of MCDM methods in other disciplines such as healthcare [21,22] and renewable energy development [23,24].

MCDM methods are also frequently applied in decision-making processes in the financial and banking industry. One of the most widely application of MCDM in this industry is risk analysis. Kou et al. [25] approach the selection of clustering algorithm problem in financial risk with an MCDM-based approach. An experimental case studied is performed to validate the proposed approach. The case study involves six clustering algorithms which are applied into three real-world credit risk and bankruptcy data sets. The result shows that the repeated-bisection method is the optimal clustering algorithm for the given data set. Wang et al. [26] researched a fuzzy MCDM model to assist the financial performance evaluation process of domestic airlines in Taiwan. The proposed model is based on grey relation analysis method and fuzzy Technique in Order of Preference by Similarity to Ideal Solution (TOPSIS) method. The proposed model is them applied to analyze the performance of three domestic airlines of Taiwan to demonstrate the applicability of the model. Peng et al. [27] developed a MCDM approach to evaluate the performance of eight different machine learning algorithms in predicting credit risk, fraud risk and bankruptcy. The approached is based on Preference Ranking Organization Method for Enrichment of Evaluations (PROMETHEE), TOPSIS and Vlse Kriterijumska Optimizacija Kompromisno Resenje (VIKOR) methods. An empirical studied is performed using seven real-world credit risk and fraud risk datasets from six countries. The results suggest that linear logistics, Bayesian Network, and ensembled methods are the top three algorithms. Ignatius et al. [28] approached the credit scoring problem by developing a fuzzy decision support system. The proposed system is built upon fuzzy Analytic Hierarchy Process (AHP) and TOPSIS methods. Tansei Iç [29] introduced a credit limit allocation model based on fuzzy TOPSIS method and linear programming. Fuzzy TOPSIS is used to calculate the credit risk scores of customers; then a linear programming model is developed, based on the result of the fuzzy TOPSIS model and other constraints, to determine the credit limit allocation among the customers. The proposed model was applied to a real-world case study and obtained satisfactory result. Ouenniche et al. [30] developed an integrated in-sample and out-of-sample bankruptcy risk evaluation framework based on TOPSIS method. The proposed framework is applied to a real-world data set of firms listed on the London Stock Exchange (LSE) during the 2010 - 2014 period. The result demonstrates that the proposed framework has good predictive capability and can be applied in real-world cases.

Another application of MCDM methods in the banking and finance industry is in company performance evaluation processes. Fu et al. [31] developed a fuzzy MCDM based benchmarking tool for the hotel industry. The author employed fuzzy AHP method to calculate the weighting of individual performance criteria and VIKOR model to evaluate the performance of 26 international hotels in order to find the benchmarking enterprise. Abdel-Basset et al. [32] has studied an integrated plithogenic MCDM approach to support the financial performance evaluation process of manufacturing companies. The proposed approach is developed based on neutrosophic AHP, VIKOR, and TOPSIS methods. Zhao et al. [33] introduced a novel hybrid MCDM approach to evaluate innovations strategies of China's banking industry. The model is built upon the Decision-making trial and evaluation laboratory (DEMATEL) technique, DEMATEL-based Analytic Network Process (DANP) and modified VIKOR methods. The authors use DEMATEL and DANP methods to analyze the interrelationships among six criteria and twenty sub-criteria and their weights, while the modified VIKOR method is applied to evaluate the performance gaps of major types of commercial banks in China. Yalcin et al. [34] developed a hierarchical financial performance evaluation model based on accounting-based performance and value-based performance criteria. The model is built using fuzzy AHP, TOPSIS, and VIKOR methods. Wang [35] developed an MCDM model to assist the financial performance evaluation process of Taiwan container shipping companies using fuzzy TOPSIS method. The model is then applied to a real-world case study to demonstrate its feasibility.

While there are many applications of MCDM models in the banking and finance industry, none have looked into the open banking strategic partners, especially under fuzzy decision-making environment. This research aims to propose a fuzzy decision model for evaluating and selecting open banking business partners based on Spherical Fuzzy AHP (SF-AHP) method and Multi-Attributive Ideal-Real Comparative Analysis (MAIRCA) method. The proposed model is them applied into a real-world case study in Vietnam.

3  Methodology

3.1 Research Process

A Fuzzy Multi-Criteria Decision Model (F-MCDM) model by using FANP and MAIRCA in order to decide suitable supplier in garment industry. Three main steps are involved shown in Fig. 1:

Step 1: From the literature review and experts’ opinions, all of the criteria and sub-criteria which are used to determine the supplier selection process are identified and listed.

Step 2: FANP is then applied in order to determine the ranking of significance for each identified criteria and sub-criteria based on literature review and experts’ opinions.

Step 3: MAIRCA is then utilized to determine the final ranking of all options based on the theoretical and real ratings of each criteria and the scoring of each alternative. The ranking is used as evidence to support the decision-maker finalize the optimal supplier.

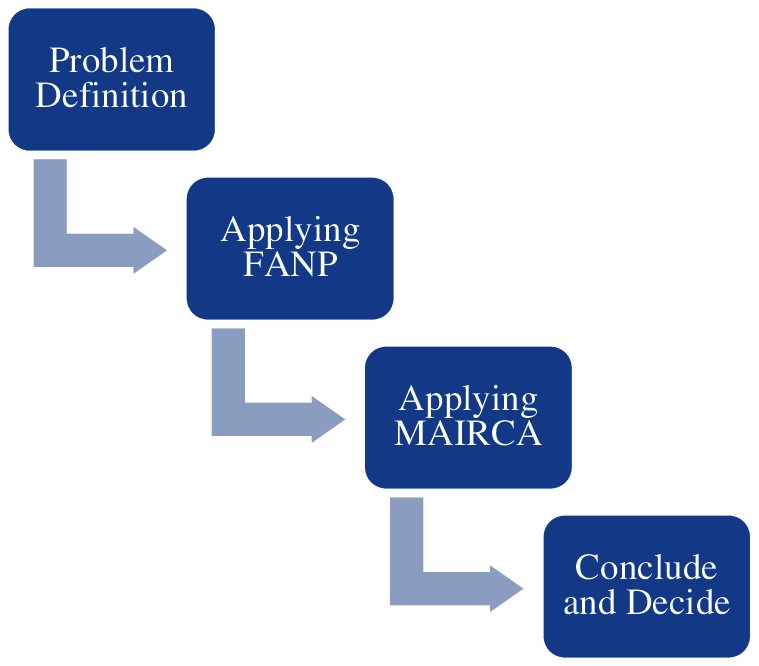
Figure 1: Research process of the paper

3.2 Spherical Fuzzy Sets Theory

Kutlu Gündoğdu et al. [36] first mentioned Spherical Fuzzy Sets Theory as a particular case of Neutrosophic sets theories [37]. Since its introduction recently, the spherical fuzzy sets theory has been utilized in several studies to build MCDM models to solve a multiple of decision-making issues and problems [38]. The membership function of a spherical fuzzy set B~S is described by its degree of membership (mB~S(x)), non-membership (nB~S(x)), and hesitancy (hB~S(x)). Each of these parameters can have a value between 0 and 1 independently and the sum of the squared values of these parameters is at most 1.

A spherical fuzzy set B~S within a universe U1 is defined as:

B~S={x,(mB~S(x),nB~S(x),hB~S(x))|xϵU1}(1)

with:

mB~S(x):U1→[0,1],nB~S(x):U1→[0,1],andhB~S(x):U1→[0,1]

and

0≤mB~S2(x)+nB~S2(x)+hB~S2(x)≤1(2)

with ∀x∈U1

3.3 Spherical Fuzzy Analytic Hierarchy Process (SF-AHP) Model

SF-AHP method is an extension of the AHP with spherical fuzzy sets. The SF-AHP method introduced by Kutlu Gündoğdu et al. [36] has five steps:

Step 1: Develop the hierarchical structure of the model

The model's hierarchical structure consists of three levels. Level 1 is the goal of the model which is calculated based on a performance index. In Level 2, the performance index is calculated with regards to N criteria. In Level 3, a set of M alternative B (M≥2) is defined.

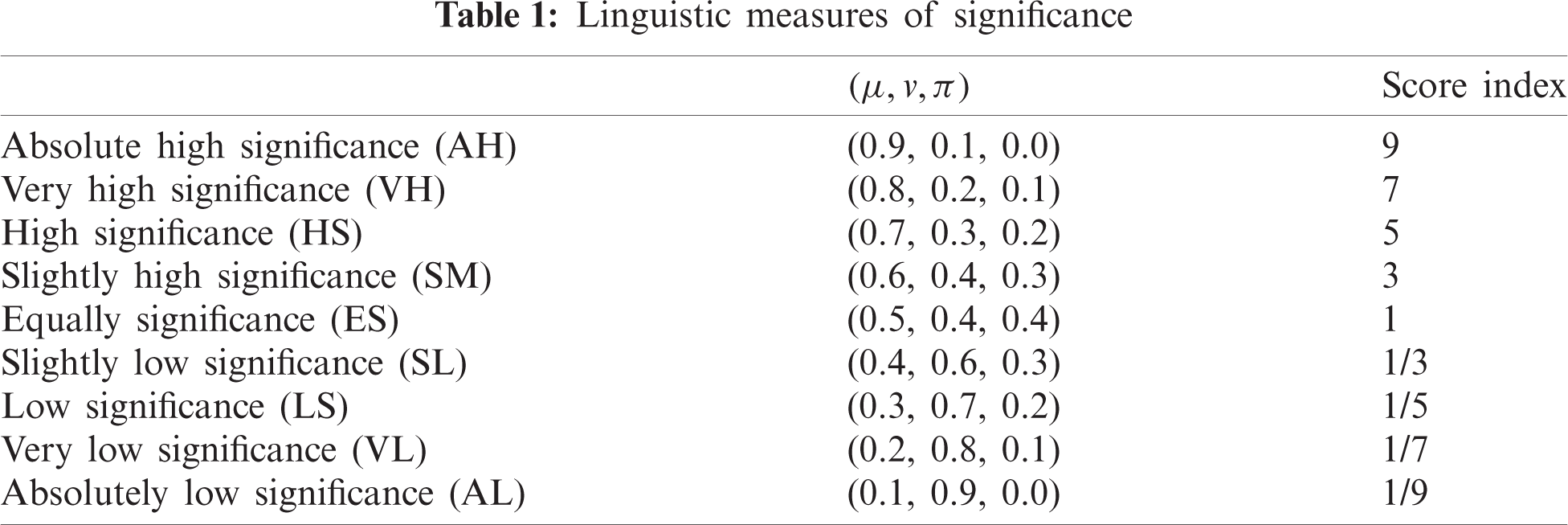
Step 2: Develop a pairwise comparison matrix of the criteria using spherical fuzzy judgement based on qualitative terms using the linguistics measure of importance introduced by Gundogdu and Kahraman [36] as shown in Tab. 1:

Then, the performance index (PI) of each equation is determined using Eqs. (3) and (4):

PI=|100∗[(mB~s−hB~s)2−(nB~s−hB~s)2]|(3)

for AH, VH, HS, SM, and ES.

1PI=1|100∗[(mB~s−hB~s)2−(nB~s−hB~s)2]|(4)

for SL, LS, VL, and AL.

Step 3: Perform consistency check for each pairwise comparison matrix appropriately

The threshold of the Consitency Ratio (CR) is 10%:

CR=CIRI(5)

With the Random Index (RI) is determined based on the number of criteria and the Consistency Index (CI) is calculated as:

CI=λmax−NN−1(6)

With λmax as the highest value of the matrix.

Step 4: Calculate the fuzzy weights of criteria and options.

The fuzzy weightings of each option with respect to each criterion is calculated as:

SWMw(B~S1,…,B~SN)=w1B~S1+…+wNB~SN=⟨[1−∏i=1N⁡(1−mB~Si2)wi]1/2,∏i=1N⁡nB~Siwi,[∏i=1N⁡(1−mB~Si2)wi−∏i=1N⁡(1−mA~Si2−hA~Si2)wi]1/2⟩(7)

with w=1/N.

Step 5: Applying layer sequencing from highest to lowest to calculate the overall weights

The performance index of the options is calculated by combining the fuzzy weights at each level of the model's hierarchical structure. There are two ways to do this:

The first option is using Eq. (8) to de-fuzzify the criteria weights:

S(w~jS)=|100∗[(3mB~s−hB~s2)2−(nB~s2−hB~s)2]|(8)

Then, use Eq. (9) to normalize the criteria weights:

w¯js=S(w~js)∑j=1N⁡S(w~js)(9)

Apply spherical fuzzy multiplication in Eq (10):

B~Sij=w¯js∗B~Si=⟨(1−(1−mB~S2)w¯js)12,nB~Sw¯js,((1−mB~S2)w¯js−(1−mB~S2−hB~S2)w¯js)12⟩(10)

The final performance index (P~) for each option Bi is determined:

P~=∑j=1N⁡B~Sij=B~Si1+B~Si2+…+B~SiN(11)

The second option is to perform the calculation without defuzzying the criteria weights. The spherical fuzzy global weights are calculated as:

∏j=1N⁡B~Sij=B~Si1∗B~Si2∗…∗B~SiN(12)

The final performance index (P~) for each alternative Bi is calculated using Eq. (11)

3.4 MAIRCA Method

There are a total of six steps in the Multi-Attributive Ideal-Real Comparative Analysis (MAIRCA) method as applied by Pamucar et al. [39].

Step 1: The decision-making matrix (X) is initially formed. This starting decision matrix defines the criteria values (xij, i = 1, 2, …, n; j = 1, 2, …, m) for each option collected:

       C1 C2 … CnX=A1A2…Am [ x11 x12 … x1nx21 x22 … x2n… … … …xm1 xm2 … xmn ](13)

The decision-making matrix (13) is used for the declaration of criteria, which can be calculated quantitatively (measurable) or described qualitatively (descriptive) depending on the nature of the criteria. The measureable values of the decision-making matrix (13) is represented by real calculated values that are obtained by quantification methods. The descriptive criteria values are determined by literature and experts’ opinions based on preference.

Step 2: Determining interests for the choice of options, PAi. The decision-maker (DM) is neutral with no judgmental opinion while the options are being gathered. The assumption is that the DM do not have any opinions in the selection process and is totally committed into recognizing the decision based on the calculations.

PAi=1m;∑i=1m⁡PAi=1,i=1,2,…,m(14)

We proceed from the point that the neutrality of the DM for the selection probability of each option by using a decision-making analysis with priori uncertainties. In such case, all interests for the selection of every option are equal individually, i.e.,

PA1=PA2=…=PAm(15)

where m is the overall number of the options chosen.

Step 3: The number of the theoretical values matrix (Tp) calculation method.

The structure of the matrix (Tp) is nxm (where n is defined as the overall number of criteria, and m is the overall number of options). The number of the theoretical values matrix (Tpij) are calculated as a product of interests for the culmination of options PAi and criterion weightings (wi,i=1,2,…,n)

Tp=w1 w2 … wnPA1PA2…PAm[ x11 x12 … x1nx21 x22 … x2n… … … …xm1 xm2 … xmn ]=PA1PA2…PAm w1      w2    …     wn[ PA1⋅w1 PA1⋅w2 … PA1⋅wnPA2⋅w1 PA2⋅w2 … PA2⋅wn… … … …PAm⋅w1 PAm⋅w2 … PAm⋅wn ](16)

The interests (PAi) are the same for all options because of the neutrality of the DM. As the interests (PAi) are the same for all options, matrix (16) in the format nx1 (where n is defined as the overall selection of criteria) is defined as follows:

Tp=w1 w2 … wnPAi[ tp1 tp2 … tpn ]=PAiw1  w2  … wn [ PAi⋅w1 PAi⋅w2 … PA1⋅wn ](17)

where n are defined as the overall selection of criteria, and tpi are theoretical values.

Step 4: Determining the selection of real values matrix

Tr=A1A2…AmC1 C2 … Cn[ tr11 tr12 … tr1ntr21 tr22 … tr2n… … … …trm1 trm2 … trmn ](18)

where n describes the overall selection of criteria, and m the total number of options.

By utilizing the following equations, the number of the real values matrix(Tr) and the number of the theoretical values matrix (Tp) are multiplied with the number of the starting decision-making matrix (X):

For the preferred higher criterion (beneficial criterion):

trij=tpij⋅(xij−xi−xi+−xi−)(19)

For the preferred lower criterion (cost criterion):

trij=tpij⋅(xij−xi+xi−−xi+)(20)

where xij, xi+, xi− are defined as the number of the starting decision-making matrix (X), xi+ and xi− are determined as: xi+=max(x1,x2,…,xm), defined as the highest values of the collected criterion by options, xi−=min(x1,x2,…,xm), defined as the lowest values of the collected criterion by options.

Step 5: The determination of the total difference matrix (G) by calculation. The individual data points of the G matrix are determined as a vector difference between the theoretical (tpij) and real values (trij), i.e., a vector difference between the theoretical individual ratings matrix (Tp) and the corresponding real individual ratings matrix (Tr).

G=Tp−Tr=[g11g12…g1ng21g22…g2n…………gm1gm2…gmn]=[tp11−tr11tp12−tr12…tp1n−tr1ntp21−tr21tp22−tr22…tp1n−tr1n…………tpm1−trn1tp11−tr11…tpmn−trmn](21)

where n are defined as the overall number of criteria, m is overall number of the options being chosen.

The difference of gij is determining the value of the interval gij∈[0,∞), by Eq. (22):

gij=tpij−trij(22)

The interested option is that gij moves towards zero (gij→0), because the decision maker will determine the option with the smallest difference between theoretical values (tpij) and real values (trij). If for criterion Ci, the option Ai has a theoretical rating value and the real rating value which are equal (tpij=trij), the difference for option Ai, with the corresponding criterion Ci, then option Ai is the best (ideal) option (Ai+).

If by criterion Ci option Ai has the value of theoretical values tpij, and the real values trij=0, then the gap for alternative Ai, with the corresponding criterion Ci, is gij=tpij. Additionally, option Ai is the worst (anti-ideal) option (Ai−) with the corresponding criterion Ci.

Step 6: The calculation of the final values of criteria functions (Qi) by options. The values of criteria functions are determined by the summation of the difference (gij) by options, that is, by adding the numbers of matrices (G) by columns, Eq. (23):

Qi=∑j=1n⁡gij;i=1,2,…,m(23)

where n is the overall selection of criteria, and m is the overall selection of the options chosen.

4  Case Study

Currently in Vietnam, a new trend is excelling in the financial services industry that offers a multiple of interesting services that has redefined the structure of the banking industry, which is open banking. Using open banking, banks can provide financial institutions and other third parties with seamless access to and communication with customer data through a standards-based technology called Open Application Programming Interface (Open API).

In this research, the authors proposed a hybrid multi-criteria decision-making model which includes a (SF-AHP) model and a (MAIRCA) with supports from seasoned domain experts for evaluating and selecting open banking business partners.

This study utilizes a domestic bank in Vietnam to model the fuzzy Multi-criteria decision making model evaluation and selection model. The bank's operational performance is well-recognized by domestic and international institutions. To form an opening banking adoption evaluation model the authors invited domain experts from the banking. All the experts have over 15 years’ working experience in the related fields. In the first step, the authors collect information from five potential opening bank business collaboration partners. Information regarding criteria and potential partners is shown in Fig. 2:

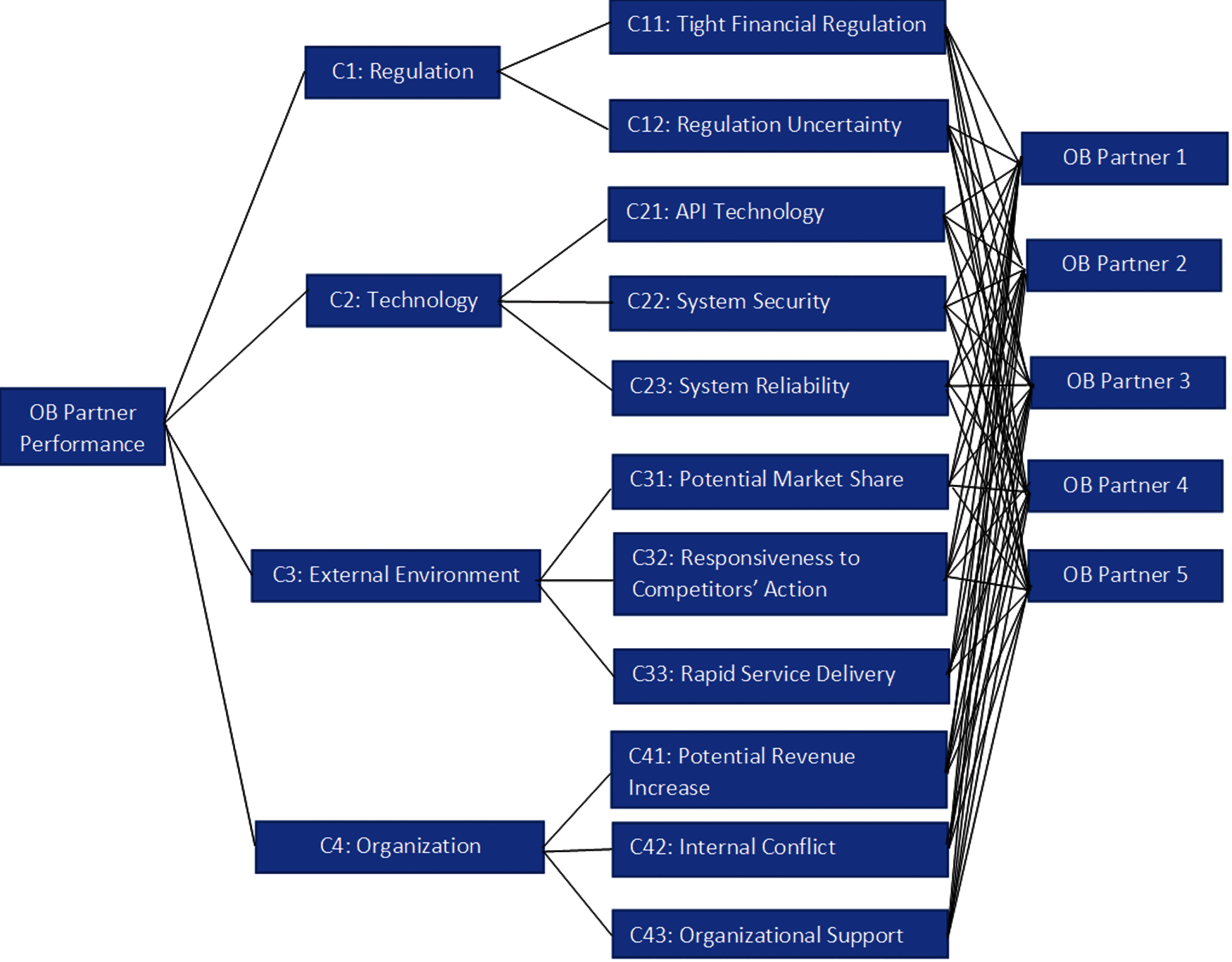
Figure 2: Information regarding criteria and partners

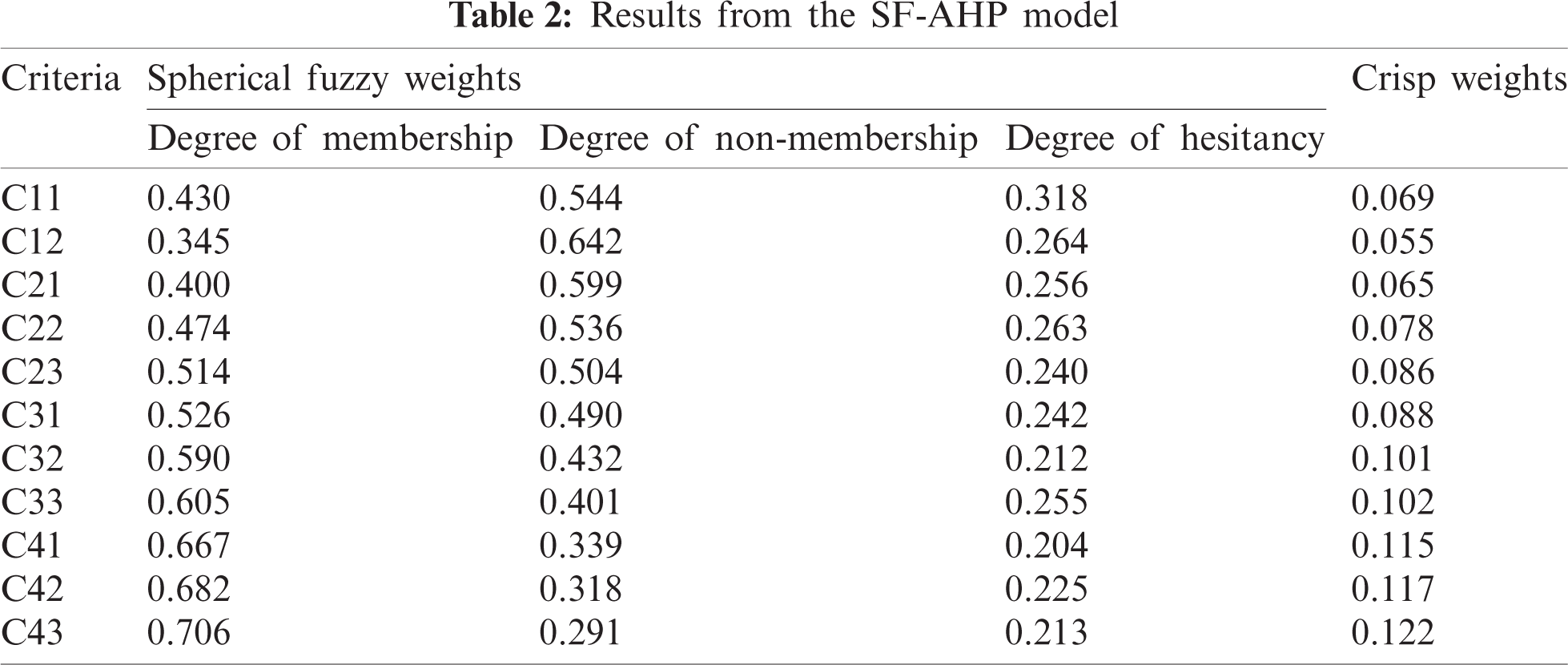
To calculate the weighting of the selected criteria, all input data of the SF-AHP model is determined by the opinions of domain experts from the banking, the weight of criteria is show in Tab. 2:

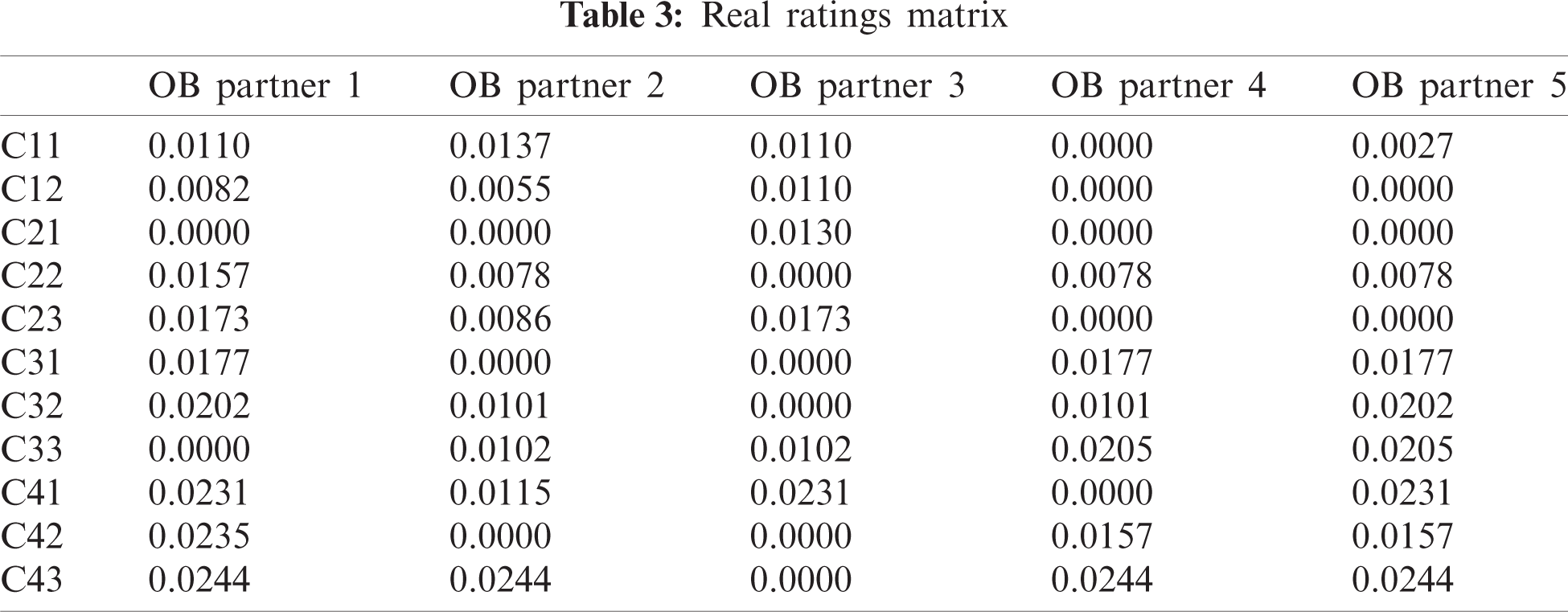
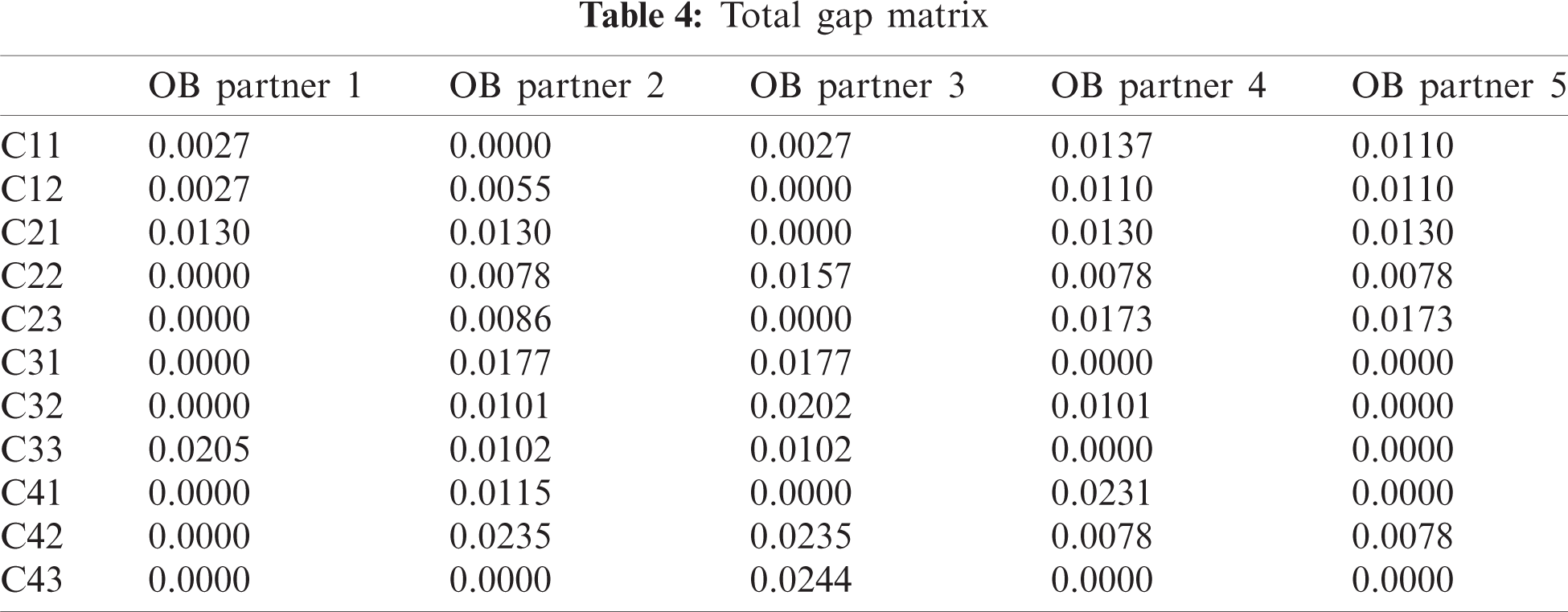
The MAIRCA model is a multi-criteria decision analysis method that then utilizes the weights of the criteria from the SF-AHP and combines with the selected options. In this step, the author applied MAIRCA approach for ranking all five potential opening bank business collaboration partners. The results of MAIRCA model are shown in Tabs. 3 and 4:

In the final stage, an MAIRCA methodology is utilized to determine the final ranking of the options and conclude the decision-making process.

As the results from Tab. 5, alternative OB Partner 1 is the best option that the decision maker should choose to collaborate. From Tab. 4, OB Partner 1 perform well in most of the criteria which result in the final ranking. Furthermore, Tab. 2 shows that the most important criteria of the problem are Organization criteria: C41, C42, and C43; with crisp weights of 0.115, 0.117, and 0.122 respectively. This suggests that to the studied bank in the case study, the impact of the option to its organization is the most important factor to decide on an open banking partner.

5  Conclusion

The study initially wanted to investigate a calculation method that could assist in the determination of an open bank supplier in the finance supply chain. Due to the nature and the similarities of the supplier selection problem, the authors applied MCDM methods into a real case study that helped decision makers in understanding which open banking sources are best for their respective businesses. An application of SF-AHP was first introduced in order to determine the weightings and ranking of the criteria used to judge each alternative. Then the MAIRCA methodology was introduced in order to determine the final ranking for each of the alternatives, being the open banking sources. From the results, the ranking was shown accordingly from highest to lowest and the analysis provided with the Open Banking Partner 1 having the lowest difference between the theoretical and real ratings from the applied methodology.

While the proposed model has demonstrated its feasibility and applicability, its performance has not been compared to others MCDM models. Comparative studies can be used to further understand the relative performance of SF-AHP based models to other fuzzy MCDM models. For further studies in this area, the authors wish to expand the exploration and compare different MCDM methods such as FANP, or FAHP in order to have further understanding of how the behavior of the criteria is managed based on qualitative and quantitative data collection. More alternatives can also be examined with different properties in order diversify the nature of the problem.

Acknowledgement: The authors wish to express their gratitude to Van Lang University, Vietnam for support this research.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  A. Premchand and A. Choudhry, “Open banking & APIs for transformation in banking,” in 2018 Int. Conf. on Communication, Computing and Internet of Things (IC3IoT), Chennai, India, 2018. [Google Scholar]

 2.  M. Zachariadis and P. Ozcan, “The API economy and digital transformation in financial services: The case of open banking,” SSRN Electronic Journal, 2016. [Google Scholar]

 3.  K. Makice, In Twitter API, Sebastopol, California, USA: O'Reilly, 2009. [Google Scholar]

 4.  A. Chanda, A. M. Daly, D. A. Foley, M. A. LaPack, S. Mukherjee et al., “Industry perspectives on process analytical technology: Tools and applications in API development,” Organic Process Research & Development, vol. 19, no. 1, pp. 63–83, 2014. [Google Scholar]

 5.  R. Fung and C. Wong, “Supplier environmental performance evaluation using AHP,” in Proc. – 6th ISAHP 2001 Berne, Switzerland, pp. 111–118, 2021. [Google Scholar]

 6.  R. Handfield, S. Walton, R. Sroufe and S. Melnyk, “Applying environmental criteria to supplier assessment: A study in the application of the analytical hierarchy process,” European Journal of Operational Research, vol. 141, no. 1, pp. 70–87, 2002. [Google Scholar]

 7.  F. Dweiri, S. Kumar, S. Khan and V. Jain, “Designing an integrated AHP based decision support system for supplier selection in automotive industry,” Expert Systems with Applications, vol. 62, pp. 273–283, 2016. [Google Scholar]

 8.  B. Karpak, R. Kasuganti and E. Kumcu, “Multi-objective decision-making in supplier selection: An application of visual interactive goal programming,” Journal of Applied Business Research (JABR), vol. 15, no. 2, pp. 57, 2011. [Google Scholar]

 9.  I. Badi and D. Pamucar, “Supplier selection for steelmaking company by using combined grey-marcos methods,” Decision Making: Applications in Management and Engineering, vol. 3, no. 2, pp. 37–48, 2020. [Google Scholar]

10. C. Wang, V. Nguyen, J. Kao, C. Chen and V. Nguyen, “Multi-criteria decision-making methods in fuzzy decision problems: A case study in the frozen shrimp industry,” Symmetry, vol. 13, no. 3, pp. 370, 2021. [Google Scholar]

11. S. Tadić, M. Krstić, V. Roso and N. Brnjac, “Dry port terminal location selection by applying the hybrid grey MCDM model,” Sustainability, vol. 12, no. 17, pp. 6983, 2020. [Google Scholar]

12. A. Budak, İ Kaya, A. Karaşan and M. Erdoğan, “Real-time location systems selection by using a fuzzy MCDM approach: An application in humanitarian relief logistics,” Applied Soft Computing, vol. 92, pp. 106322, 2020. [Google Scholar]

13. M. Deveci, I. Akyurt and S. Yavuz, “A GIS-based interval type-2 fuzzy set for public bread factory site selection,” Journal of Enterprise Information Management, vol. 31, no. 6, pp. 820–847, 2018. [Google Scholar]

14. P. Liu and Y. Li, “Multiattribute decision method for comprehensive logistics distribution center location selection based on 2-dimensional linguistic information,” Information Sciences, vol. 538, pp. 209–244, 2020. [Google Scholar]

15. P. Kieu, V. Nguyen, V. Nguyen and T. Ho, “A spherical fuzzy analytic hierarchy process (SF-aHP) and combined compromise solution (CoCoSo) algorithm in distribution center location selection: A case study in agricultural supply chain,” Axioms, vol. 10, no. 2, pp. 53, 2021. [Google Scholar]

16. J. Scott, W. Ho, P. Dey and S. Talluri, “A decision support system for supplier selection and order allocation in stochastic, multi-stakeholder and multi-criteria environments,” International Journal of Production Economics, vol. 166, pp. 226–237, 2015. [Google Scholar]

17. C. Chang, H. Chen and Z. Zhuang, “Integrated multi-choice goal programming and multi-segment goal programming for supplier selection considering imperfect-quality and price-quantity discounts in a multiple sourcing environment,” International Journal of Systems Science, vol. 45, no. 5, pp. 1101–1111, 2013. [Google Scholar]

18. S. Hamdan and A. Cheaitou, “Supplier selection and order allocation with green criteria: An MCDM and multi-objective optimization approach,” Computers & Operations Research, vol. 81, pp. 282–304, 2017. [Google Scholar]

19. S. Nazari-Shirkouhi, H. Shakouri, B. Javadi and A. Keramati, “Supplier selection and order allocation problem using a two-phase fuzzy multi-objective linear programming,” Applied Mathematical Modelling, vol. 37, no. 22, pp. 9308–9323, 2013. [Google Scholar]

20. S. Hosseini, N. Morshedlou, D. Ivanov, M. Sarder, K. Barker et al., “Resilient supplier selection and optimal order allocation under disruption risks,” International Journal of Production Economics, vol. 213, pp. 124–137, 2019. [Google Scholar]

21. L. Xiong, G. Sheng, Z. Fan, H. Yang, F. Hwang et al., “Environmental design strategies to decrease the risk of nosocomial infection in medical buildings using a hybrid MCDM model,” Journal of Healthcare Engineering, vol. 2021, pp. 1–17, 2021. [Google Scholar]

22. Y. Ali, M. Khan, U. Mumtaz, A. Salman, N. Muhammad et al., “Identification of factors influencing the rise of cesarean sections rates in Pakistan, using MCDM,” International Journal of Health Care Quality Assurance, vol. 31, no. 8, pp. 1058–1069, 2018. [Google Scholar]

23. C. Wang, J. Kao, Y. Wang, V. Nguyen, V. Nguyen et al., “A multicriteria decision-making model for the selection of suitable renewable energy sources,” Mathematics, vol. 9, no. 12, pp. 1318, 2021. [Google Scholar]

24. F. Chien, C. Wang, V. Nguyen, V. Nguyen and K. Chau, “An evaluation model of quantitative and qualitative fuzzy multi-criteria decision-making approach for hydroelectric plant location selection,” Energies, vol. 13, no. 11, pp. 2783, 2020. [Google Scholar]

25. G. Kou, Y. Peng and G. Wang, “Evaluation of clustering algorithms for financial risk analysis using MCDM methods,” Information Sciences, vol. 275, pp. 1–12, 2014. [Google Scholar]

26. Y. Wang, “Applying FMCDM to evaluate financial performance of domestic airlines in Taiwan,” Expert Systems with Applications, vol. 34, no. 3, pp. 1837–1845, 2008. [Google Scholar]

27. Y. Peng, G. Wang, G. Kou and Y. Shi, “An empirical study of classification algorithm evaluation for financial risk prediction,” Applied Soft Computing, vol. 11, no. 2, pp. 2906–2915, 2011. [Google Scholar]

28. J. Ignatius, A. Hatami-Marbini, A. Rahman, L. Dhamotharan and P. Khoshnevis, “A fuzzy decision support system for credit scoring,” Neural Computing and Applications, vol. 29, no. 10, pp. 921–937, 2016. [Google Scholar]

29. Y. Tansel İç, “Development of a credit limit allocation model for banks using an integrated fuzzy TOPSIS and linear programming,” Expert Systems with Applications, vol. 39, no. 5, pp. 5309–5316, 2012. [Google Scholar]

30. J. Ouenniche, B. Pérez-Gladish and K. Bouslah, “An out-of-sample framework for TOPSIS-based classifiers with application in bankruptcy prediction,” Technological Forecasting and Social Change, vol. 131, pp. 111–116, 2018. [Google Scholar]

31. H. Fu, K. Chu, P. Chao, H. Lee and Y. Liao, “Using fuzzy AHP and VIKOR for benchmarking analysis in the hotel industry,” the Service Industries Journal, vol. 31, no. 14, pp. 2373–2389, 2011. [Google Scholar]

32. M. Abdel-Basset, W. Ding, R. Mohamed and N. Metawa, “An integrated plithogenic MCDM approach for financial performance evaluation of manufacturing industries,” Risk Management, vol. 22, no. 3, pp. 192–218, 2020. [Google Scholar]

33. Q. Zhao, P. Tsai and J. Wang, “Improving financial service innovation strategies for enhancing China's banking industry competitive advantage during the fintech revolution: A hybrid MCDM model,” Sustainability, vol. 11, no. 5, pp. 1419, 2019. [Google Scholar]

34. N. Yalcin, A. Bayrakdaroglu and C. Kahraman, “Application of fuzzy multi-criteria decision-making methods for financial performance evaluation of turkish manufacturing industries,” Expert Systems with Applications, vol. 39, no. 1, pp. 350–364, 2012. [Google Scholar]

35. Y. Wang, “The evaluation of financial performance for Taiwan container shipping companies by fuzzy TOPSIS,” Applied Soft Computing, vol. 22, pp. 28–35, 2014. [Google Scholar]

36. F. Kutlu Gündoğdu and C. Kahraman, “Spherical fuzzy sets and spherical fuzzy TOPSIS method,” Journal of Intelligent & Fuzzy Systems, vol. 36, no. 1, pp. 337–352, 2019. [Google Scholar]

37. R. Yager, “Pythagorean fuzzy subsets,” in 2013 Joint IFSA World Congress and NAFIPS Annual Meeting (IFSA/NAFIPS), Edmonton, Canada, pp. 57–61, 2013. [Google Scholar]

38. F. Kutlu Gündoğdu and C. Kahraman, “A novel spherical fuzzy analytic hierarchy process and its renewable energy application,” Soft Computing, vol. 24, no. 6, pp. 4607–4621, 2019. [Google Scholar]

39. D. Pamucar, S. Tarle and T. Parezanovic, “New hybrid multi-criteria decision-making DEMATEL-mAIRCA model: Sustainable selection of a location for the development of multimodal logistics centre,” Economic Research-Ekonomska Istraživanja, vol. 31, no. 1, pp. 1641–1665, 2018. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.