Computers, Materials & Continua DOI:10.32604/cmc.2022.017378
Article

Impact of Magnetic Field on a Peristaltic Flow with Heat Transfer of a Fractional Maxwell Fluid in a Tube

Hanan S. Gafel*

Department of Mathematics, Faculty of Science, Taif University, Saudi Arabia
*Corresponding Author: Hanan S. Gafel. Email: h.gafel@tu.edu.sa
Received: 28 January 2021; Accepted: 13 April 2021

Abstract: Magnetic field and the fractional Maxwell fluids’ impacts on peristaltic flows within a circular cylinder tube with heat transfer was evaluated while assuming that they are preset with a low-Reynolds number and a long wavelength. Utilizing, the fractional calculus method, the problem was solved analytically. It was deduced for temperature, axial velocity, tangential stress, and heat transfer coefficient. Many emerging parameters and their effects on the aspects of the flow were illustrated, and the outcomes were expressed via graphs. A special focus was dedicated to some criteria, such as the wave amplitude's effect, Hartman and Grashof numbers, radius and relaxation–retardation ratios, and heat source, which were under discussions on the axial velocity, tangential stress, heat transfer, and temperature coefficients across one wavelength. Multiple graphs of physical interest were provided. The outcomes state that the effect of the criteria mentioned beforehand (the Hartman and Grashof numbers, wave amplitude, radius ratio, heat source, and relaxation–retardation ratio) were quite evident.

Keywords: Peristaltic flow; fractional maxwell fluid; mass and heat transfer; magneto-hydrodynamic flow

Nomenclature

1  Introduction

The method of inserting fluids within tubes if a progressive wave of expanded or contradicted area circulates along the boundary's length of a distensible tube that contains fluid is known as peristaltic transport. Physiologically, blood flow or peristalsis is the key application of this mechanism. Saqib et al. [1] evaluated the heat transfer in an MHD flow of Maxwell fluid through emulating a fractional Cattaneo-Friedrich system. Alotaibi et al. [2] handled numerically the MHD flow of Casson nanofluid by convectively heating a nonlinear extending surface with the impacts of injection/suction and viscous dissipation. Crespo et al. [3] discussed the dynamic particles–generated boundary parameters in SPH methods. Khan et al. [4] assessed the heat transfer and MHD flow within a sodium alginate fluid with the impacts of thermal radiation and porosity. While subject to a radially varying magnetic field, the authors of [5] illustrated a Jeffery fluid's peristaltic flow within a tube having an endoscope. Zhao [6] explained the flow of the axisymmetric convection of a fractional Maxwell fluid past a vertical cylinder in the presence of temperature jump and velocity slip. The authors of [7] stated the impacts of the endoscope and the magnetic field on the peristalsis involving a Jeffrey fluid. Rachid [8] examined the effect of the endoscope and heat transfer on a fractional Maxwell fluid's peristaltic flow within a vertical tube. The authors of [9] assessed a long-wavelength peristaltic flow within a tube with an endoscope affected by the magnetic field. Nadeem et al. [10] argued heat transfer's effect in a peristaltic transport with variable viscosity. Novel movements of fractional modeling, as well as mass and heat transfer exploration of (MWCNTs and SWCNTs) in nanofluids flow that is based on CMC over an inclined plate with generalized boundary parameters were assessed by Asjad et al. [11]. Hussain et al. [12] evaluated the heat transfer in a peristaltic flow of MHD Jeffrey fluid in the presence of heat conduction. Mainardi and Spada [13] exhibited the viscosity and relaxation aspects of basic fractional models in theology. Within an asymmetric channel, Mishra and Rao [14] applied a peristaltic transport of a Newtonian fluid. The instable rotating flow of a viscoelastic fluid in the presence of the fractional Maxwell fluid system among coaxial cylinders was explored by Qi and Jin [15]. The impact of the second-order slip and heat transfer on the MHD flow of a fractional Maxwell fluid within a porous medium was depicted by Amana et al. [16]. Ali et al. [17] scrutinized magnetic field's impacts on a Casson fluid and blood flow in an axisymmetric cylindrical tube. Haque et al. [18] analyzed a computational method for the unsteady flow of a Maxwell fluid that has Caputo fractional derivatives. Carrera et al. [19] delivered a fractional-order Maxwell fluid system concerning non-Newtonian fluids. Johnson and Quigley [20] described a viscosity peristaltic Maxwell fluid model for rubber's viscoelasticity. Tripathi et al. [21] presented transporting the viscoelastic fluid with the fractional Maxwell system through peristalsis within a channel affected by long wavelength and low Reynolds number approximations. Dharmendra Tripathi [22] devoted studying the peristaltic transportation of viscoelastic non-Newtonian fluids in the presence of a fractional Maxwell system in the channel. In [23], the electro-osmotic peristaltic flow of a viscoelastic fluid through a cylindrical micro-channel was premeditated. The authors of [24] identified the impacts of initial stress and rotation on peristaltic transportation of fourth-grade fluid with the induction of the magnetic field and heat transfer. Also, Alla et al. [25] studied the impact of the initial stress, magnetic field, and rotation on the peristaltic motion of the micropolar fluid. Several hypotheses of this type of context have been made and attempted by many practitioners and researchers ([26–30]).

Using the fractional Maxwell model, the study aims to explore analytically the impact of heat transfer on the peristaltic flow of a viscoelastic fluid in the gap between two coaxial vertical tubes. It generalizes the two-dimensional equations of heat and motion transfer assuming having low Reynolds numbers and a long wavelength. Regarding solving the reduced equations numerically and analytically, the wave shape is found. The related parameters are defined pictorially in the problem. The collected results are shown and graphically discussed. The results discussed in this paper are valuable for physicists, engineers, and people involved in developing fluid mechanics. It is also expected that the various possible fluid mechanic flow parameters for the peristaltic Jeffrey fluids will serve as similarly good theoretical estimates.

2  Formulation of the Problem

Take the MHD peristaltic flow through uniform coaxial tubes of a viscoelastic fluid in the presence of the fractional Maxwell fluid model. A constant magnetic field Bo applies transversely to the flow when electrical conductivity exists. Flow configuration is presented in Fig. 1. The inner tube is considered, with a sinusoidal wave traveling down its outer tube wall. The outer and inner tube temperatures are T1 and T0, respectively. We picked a cylindrical coordinate system R¯ and Z¯. The equations for the tube walls in the dimensional form, as follows

R1¯=a1(1)

R2¯=a2+b(sin⁡2πλ(Z¯−ct¯))(2)

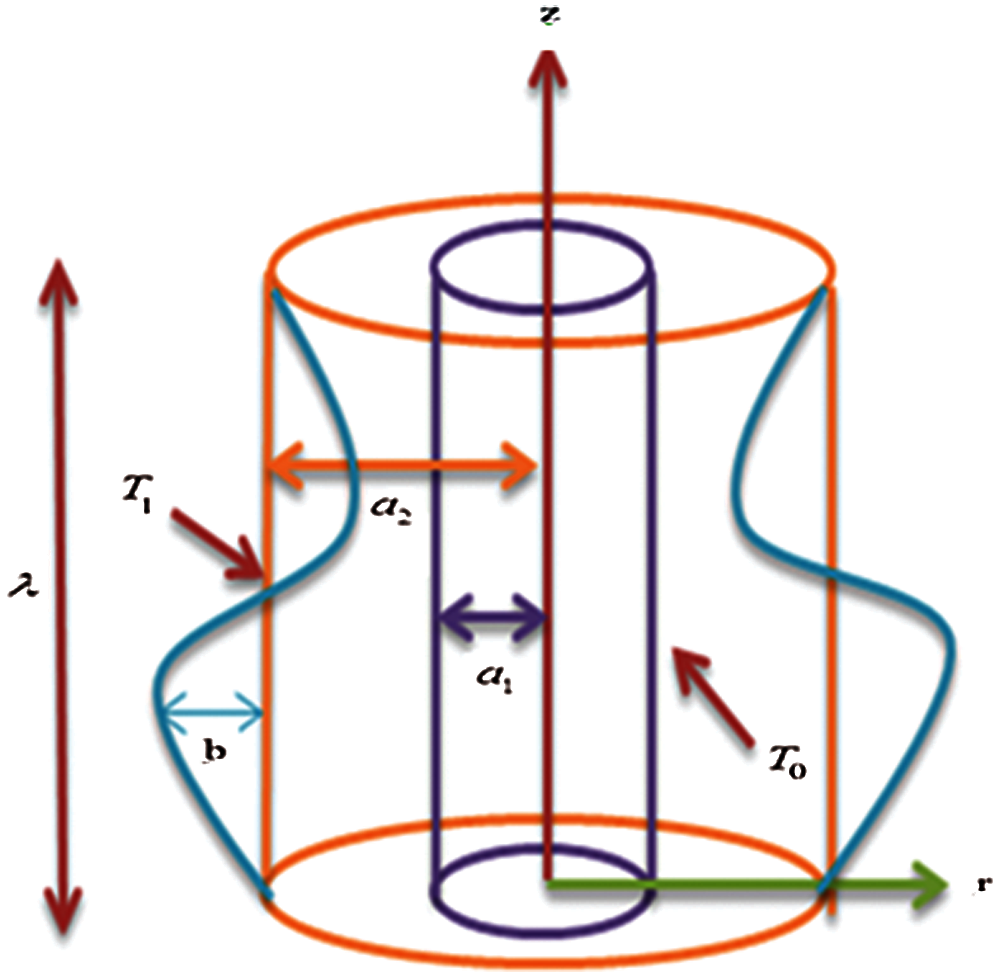
Figure 1: Schematic of the problem

The equation of the fractional Maxwell fluid takes the form

(1+λ1¯α1D~t¯α1)S¯=μγ.(3)

where (0≤α1≤1).

The following equation defines the upper convected fractional derivative D~t¯α1

D~t¯α1(S¯)=Dt¯α1(S¯)+(V¯.∇)(S¯)−L¯(S¯)−(S¯)L¯T(4)

In which

γ.=(∇V¯)+(∇V¯)T(5)

Also, note that Dt¯α1=∂t¯α1, denoting the α1-order fractional differentiation operator concerning t takes the following form:

Dt¯α1f(t)=1Γ(1−α1)ddt∫0tf(ξ)(t−ξ)α1dξ,0≤α1≤1.(6)

In this function, Γ(.) represents the gamma function.

The expression of f is as follows:

f(t)=1+λ1αt−αΓ(1−α1)(6a)

The following equations represent the flow's governing motion equations for an incompressible fluid within the fixed frame (Fig. 1):

ρ(∂∂t¯+U¯∂∂R¯+W¯∂∂Z¯)U¯=−∂p¯∂R¯+1R¯∂∂R¯(R¯S¯R¯R¯)+∂∂Z¯(S¯R¯Z¯)−S¯θ¯θ¯R¯(7)

ρ(∂∂t¯+U¯∂∂R¯+W¯∂∂Z¯)W¯=−∂p¯∂Z¯+1R¯∂∂R¯(R¯S¯R¯Z¯)+∂∂Z¯(S¯Z¯Z¯)+ρgα(T¯−To)−σBo2W¯(8)

ρCp(∂∂t¯+U¯∂∂R¯+W¯∂∂Z¯)T¯=K(∂2∂R¯2+1R¯∂∂R¯+∂2∂Z¯2)T¯+Qo(9)

∂U¯∂R¯+U¯R¯+∂W¯∂Z¯=0(10)

The fixed frame (R¯,Z)¯ has an unsteady flow between the two tubes but grows into a steady flow within a wave frame (r¯,z¯) which moves at the same speed of a wave in the Z¯ direction.

The transformations among the two frames take the following forms:

r¯=R¯,z¯=Z¯−ct¯(11)

u¯=U¯,w¯=W¯−c(12)

The following form shows the applicable boundary settings within the wave frame:

w¯=−c,u¯=0atr¯=r1¯(13)

w¯=−catr¯=r2¯+bsin⁡(2πλz¯)(14)

T¯=T1¯atr¯=r1¯(15)

T¯=T0¯atr¯=r2¯(16)

The following equations represent the motion's governing equations of the movement of the incompressible fluid within the wave frame

ρ(u¯∂∂r¯+(w¯+c)∂∂z¯)u¯=−∂p¯∂r¯+1r¯∂∂r(r¯S¯r¯r¯)+∂∂z¯(Sr¯z¯)−S¯θ¯θ¯r¯(17)

ρ(u¯∂∂r¯+(w¯+c)∂∂z¯)w¯=−∂p¯∂z¯+1r¯∂∂r¯(r¯S¯r¯z¯)+∂∂z¯(S¯Z¯Z¯)+ρgα(T¯−To)−σBo2(w¯+c)(18)

ρCp(u¯∂∂r¯+(w¯+c)∂∂z¯)T¯=K(∂2∂r¯2+1r∂∂r¯+∂2∂z¯2)T¯+Qo(19)

∂u¯∂r¯+u¯r¯+∂w¯∂z¯=0(20)

The extra stress S¯ relies on r and t only. When utilizing the initial setting S¯(t¯=0), the yield was S¯r¯r¯=S¯θ¯θ¯=S¯z¯z¯=S¯r¯θ¯=0 and

(1+λ1¯α1∂α1∂t¯α1)S¯r¯z¯=μ∂(w¯+c)∂r¯(21)

To do more analyses, the authors introduced these dimensionless parameters:

r=r¯a2,z=z¯λ,t=ct¯λ,u=u¯cδ,w=w¯c,λ1=cλ1¯λ,p=a22p¯cλμ,δ=a2λ,θ=T¯−T0T1−T0,Pr=μCPK,Re=ρca2μ,Gr=ρgα(T1−To)a22μc,M=σμB0a2,S=a2S¯μc,r1=r1¯a2=ε<1,r2=r2¯a2=1+φsin⁡(2πz),(22)

where (φ=ba2<1) is the wave amplitude.

3  Solution of the Problem

Regarding the above-mentioned modifications and nondimensional variables (22), the preceding equations are reduced to

Reδ3(u∂∂r+(w+1)∂∂z)u=−∂p∂r+δr∂∂r(rSrr)+δ2∂∂z(Srz)−δ(Sθθr)(23)

Reδ(u∂∂r+(w+1)∂∂z)w=−∂p∂z+1r∂∂r(rSrz)+δ∂∂z(Szz)+Grθ−M2(w+1)(24)

RePrδ(u∂∂r+(w+1)∂∂z)θ=(∂2∂r2+1r∂∂r+δ2∂2∂z2)θ+β(25)

∂u∂r+ur+∂w∂z=0(26)

With boundary settings

w=−1,u=0atr=r1=ε(27)

w=−1atr=r2=1+φsin⁡(2πz)(28)

θ=1atr=r1(29)

θ=0atr=r2(30)

4  The Analytical Solution

Utilizing the aforementioned nondimensional quantities while assuming having long wavelengths approximation and low Reynolds numbers, the equations of motion are

−∂p∂r=0(31)

f[dpdz−Grθ+M2(w+1)]=(∂2w∂r2+1r∂w∂r)(32)

∂2θ∂r2+1r∂θ∂r+β=0(33)

where, from Eq. (31), we conclude that p is independent of r, which depends on z only.

The solutions of Eqs. (24) and (25) limited by (27)–(30) are

w=4c2+4c1log⁡(r)+f×[dpdzr2+M2r2−Gr[r2(log⁡(rr2)−1)log⁡(εr2)+β4(ε2r2(log⁡(rr2)−1)−r22r2(log⁡(rε)−1)log⁡(εr2))−β16r4]/[4−fM2r2](34)

f=(1+λ1α1Dtα1),A=−4−f×[dpdzε2+Gr(ε2(log(εr2)−1)log(εr2)+β4(ε4(log(εr2)−1)+ε2r22)log(εr2))−β16ε4)],B=−4−f×[dpdzr22+Gr(−r22log(εr2)+β4(−ε2r22−r24(log(r2ε)−1)log(εr2))−β16r24)],C1=A−B4log(εr2),C2=Blog(ε)−Alog(r2)4log(εr2).(35)

The following formula expresses the heat transfer coefficient

Zr=∂θ∂r×∂r2∂z(37)

So, The solution of heat transfer is given by

Zr=[−rβ2+1rlog⁡(r1r2)+(r12r−r22r)β4log⁡(r1r2)]×[2φπcos⁡(2πz)](38)

5  Numerical Results and Discussion

For analyzing the performance of solutions, numerical calculation of numerous values of the fractional Maxwell fluid, wave amplitude φ, the Hartman number M, heat source β, and relaxation–retardation ratio λ1, radius ratio ε, and Grashof number Gr were conducted. The axial velocity is plotted against z in Fig. 2 concerning various values of α1,M,φ, and λ1. Note that that axial velocity decreases when increasing the fractional Maxwell fluid but declines and increases when increasing Hartman numbers and wave amplitude, and relaxation–retardation times’ ratio. It is revealed that an increase in Hartman numbers, heat source, and relaxation–retardation times’ ratio declines the axial velocity. Moreover, the axial velocity had an oscillatory performance in the entire range of axial z. Additionally, the results of Fig. 2 indicate that the flow is strongly dependent on α1,φ,φ, and λ1. The effect of wave amplitude ϕ, radius ratio ε, heat source β, and radius r for temperature θ is illustrated in Fig. 3 emulates the impact of ϕ on temperature, where temperature profiles are somehow parabolic and surge and decrease as ϕ increases, while they decrease and increase with increasing radius ratio and heat source. In contrast, they decrease with the increase of radius. Moreover, the temperature profiles are almost parabolic and rise as β increases. Within the entire range of axial z, the temperature had an oscillatory performance.

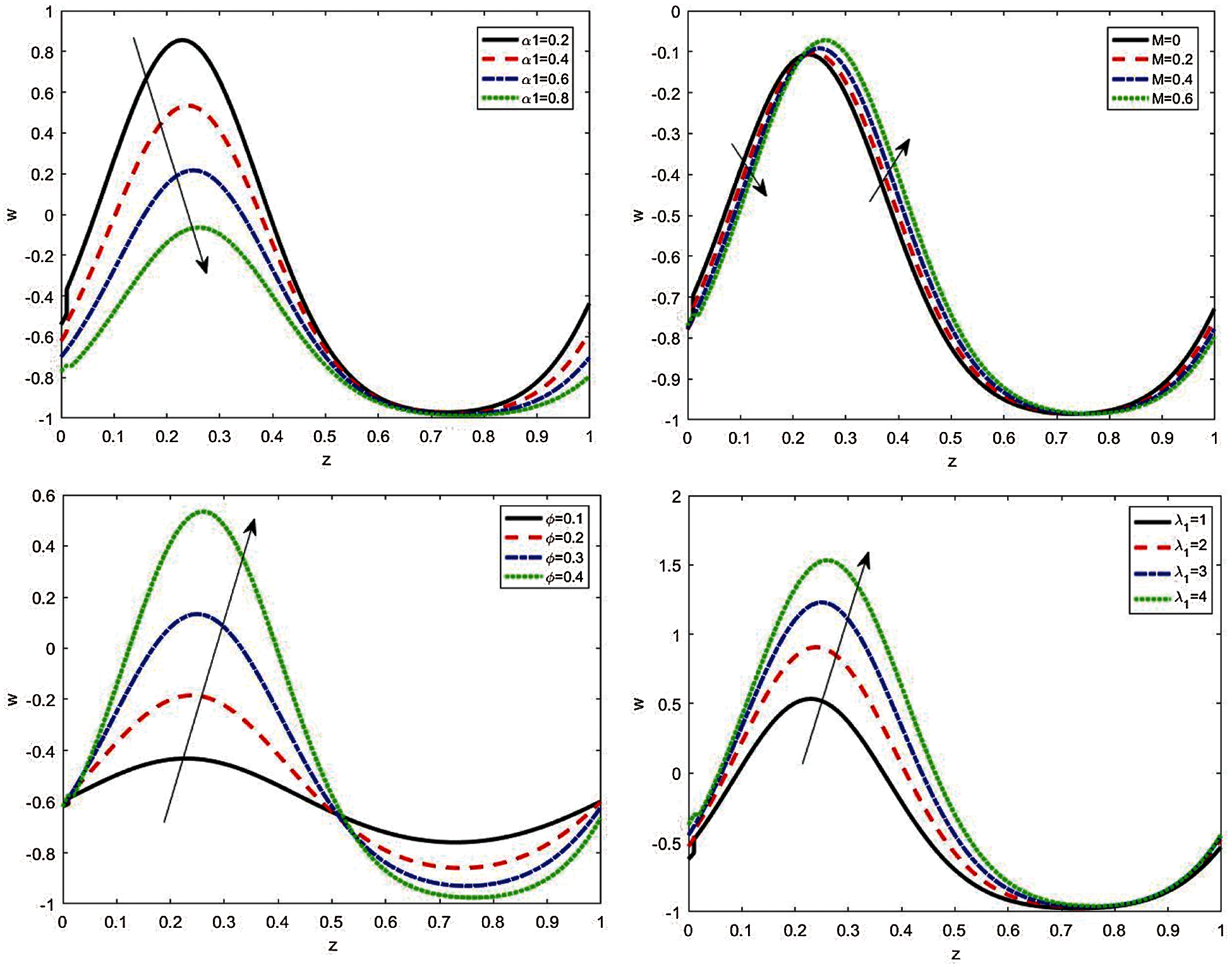
Figure 2: Various values of axial velocity w concerning the z−axis concerning different values of α1,M,φ, and λ1 in the peristaltic flow of the fractional Maxwell fluid within tubes

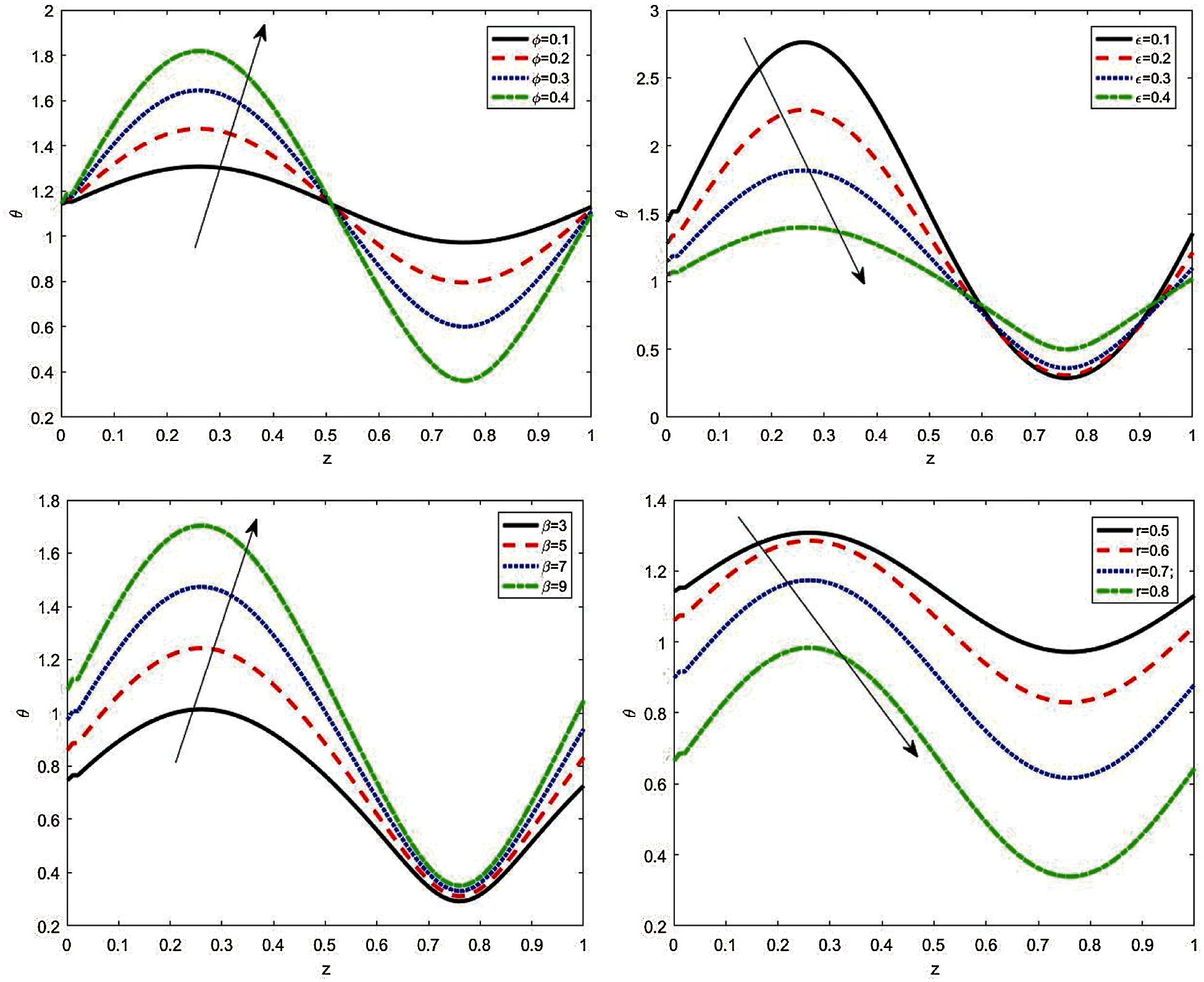
Figure 3: Various values of temperature θ with regard to the z−axis for various values of φ,ε,β, and r in the fractional Maxwell fluid's peristaltic flow within tubes

The effects of the fractional Maxwell fluid α, Hartman number M, wave amplitude φ, and Grashof number Gr can be observed from Fig. 4 in which the tangential stress srz is illustrated for various values of the fractional Maxwell fluid, Hartman and Grashof numbers, and wave amplitude. It was found that the tangential stress diminished inversely with the fractional Maxwell fluid and Hartman number, while it surged directly proportionally with wave amplitude and Grashof number. Within the entire range of axial z, the tangential stress had an oscillatory performance, which may be due to peristalsis. The influence of wave amplitude ϕ, radius ratio ε, heat source β, and radius r on heat transfer coefficient Zr are graphically displayed in Fig. 5 through various values of the amplitude, radius ratio, and heat source and radius. The increasing wave amplitude, radius ratio, heat source, and radius increase and decrease with the amplitude of the heat transfer coefficient in the whole range z. Such an effect may be expected; under the conditions considered, the wave amplitude and heat source resist the flow, and its magnitude is proportional to the heat transfer coefficient. One can observe that the heat transfer coefficient is an oscillatory performance that may be caused by peristalsis. Fig. 6 is plotted in 3D schematics illustrating heat transfer coefficient Zr, temperature θ, and axial velocity w with regard to r and z axes in the presence of the fractional Maxwell fluid α1, Hartman number M, heat source β, and wave amplitude ϕ. Axial velocity diminished with the increase of the fractional Maxwell fluid and Hartman number. Unlike temperature, which surged with the surge of heat source, the heat transfer coefficient increased and decreased with increasing wave amplitude. For all physical quantities, the peristaltic flow is illustrated in 3D overlapping and damping when r and z increase to the state of particle equilibrium. The vertical distance with the most significant curves was acquired. Most of the physical fields move in a peristaltic flow.

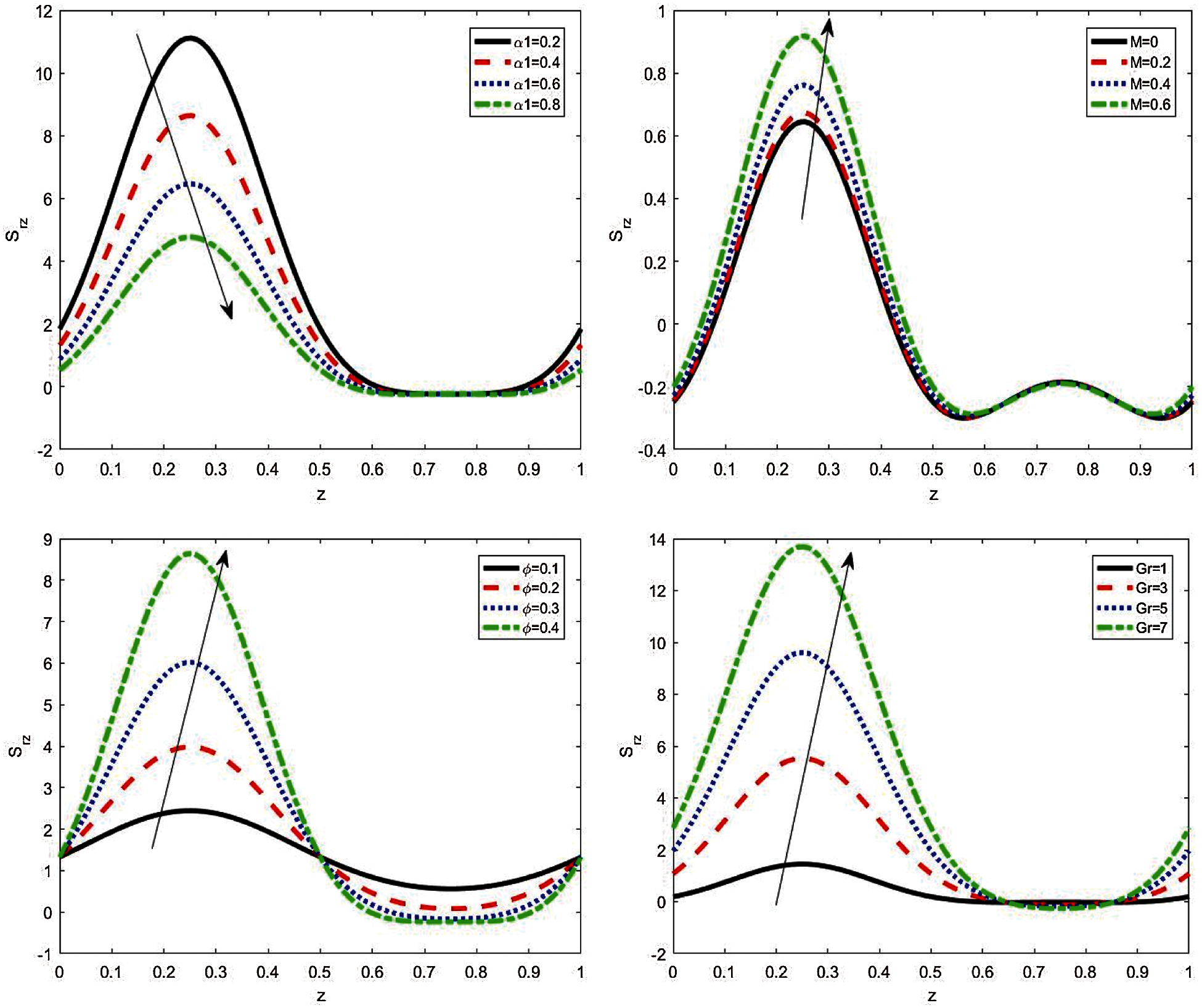
Figure 4: The variations of axial tangential stress srz with regard to the z−axis concerning various values of α1,M,φ, and Gr in the fractional Maxwell fluid's peristaltic flow within tubes

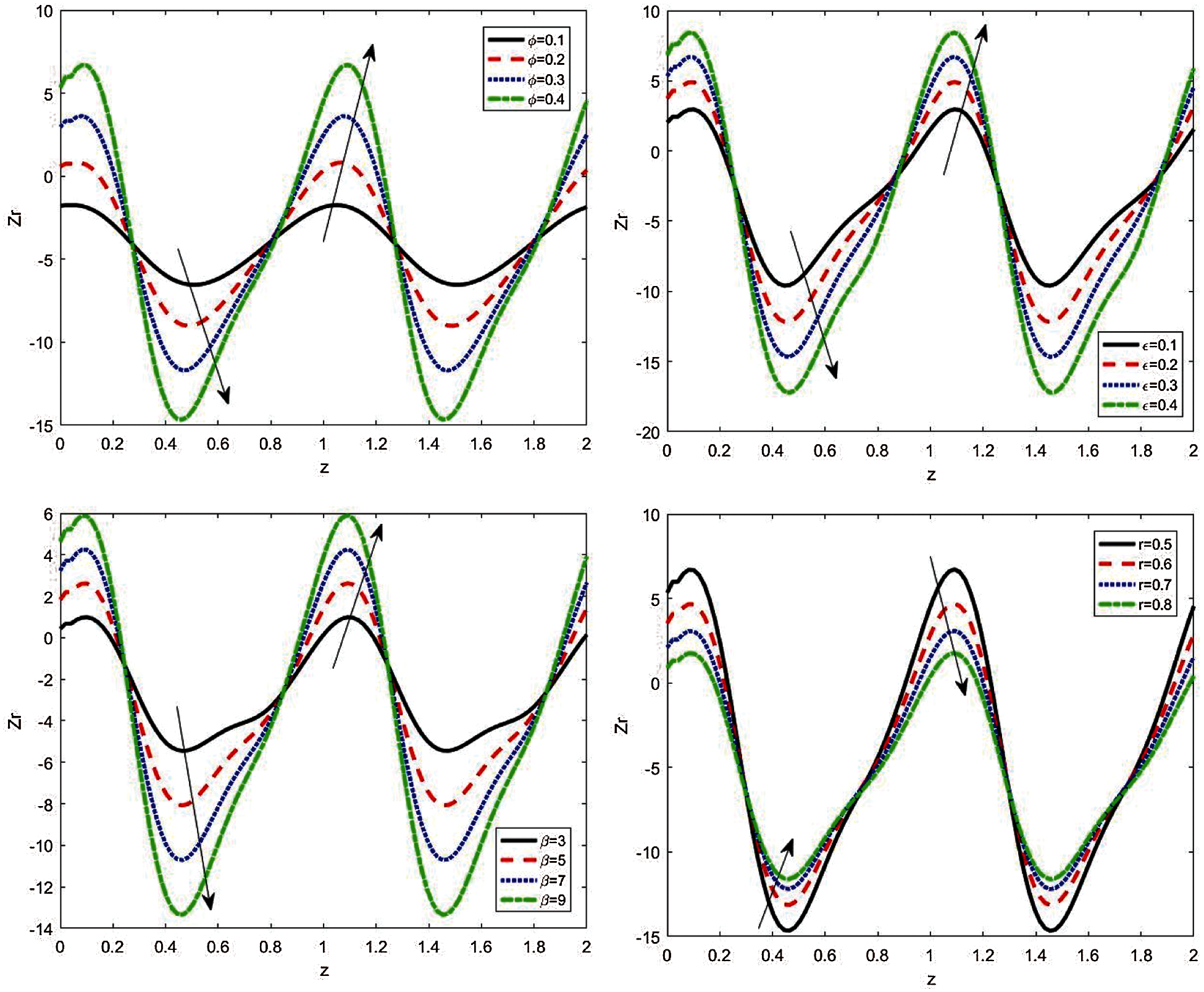
Figure 5: The variations of heat transfer coefficient Zr with regard to the z−axis concerning various values of φ,ε,β, and r in the peristaltic flow of the fractional Maxwell fluid within tubes

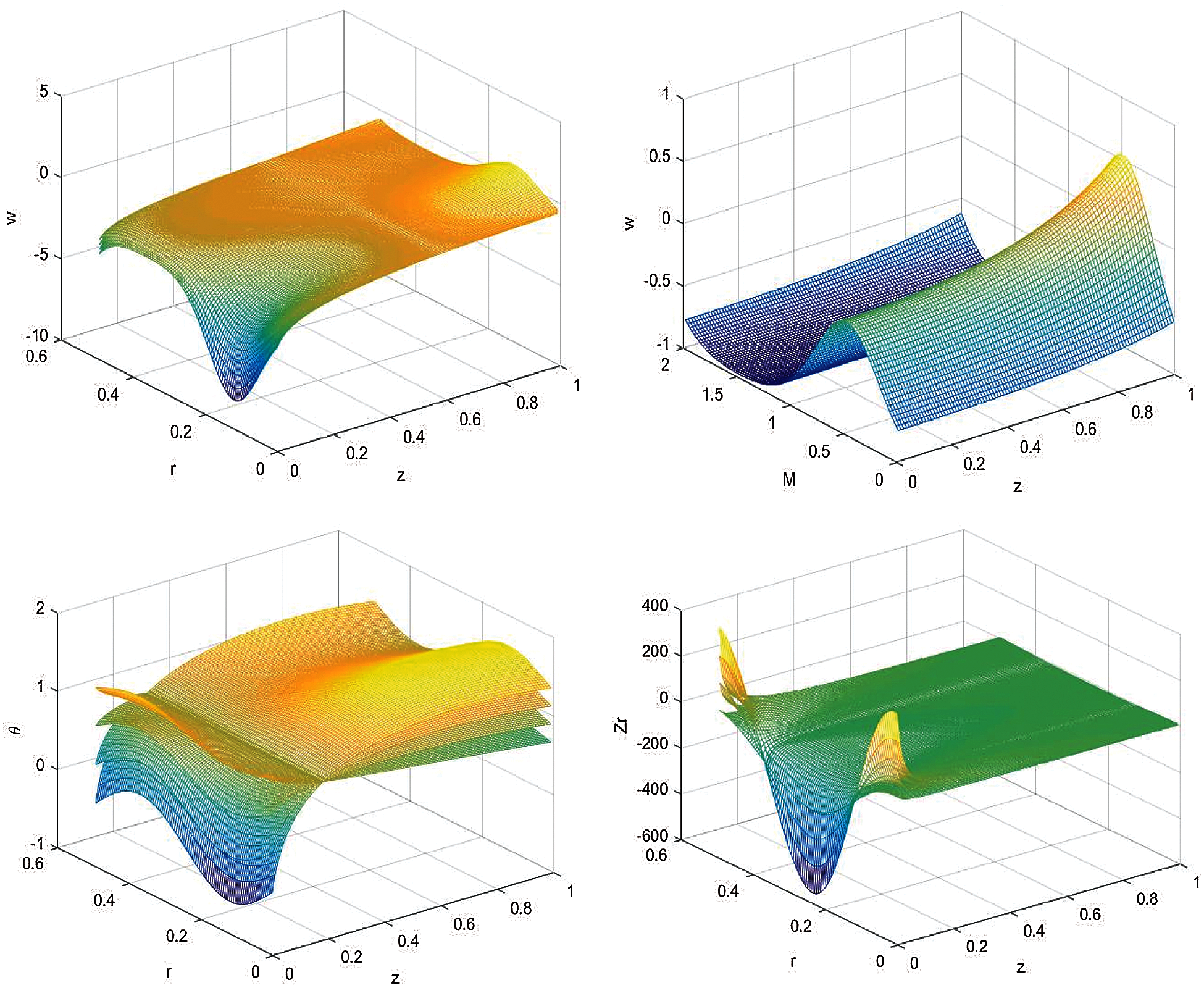
Figure 6: The variations of heat transfer coefficient Zr, temperature θ, and axial velocity w in 3D concerning the r and z axes under the influence of the α1,M,φ, and φ.

If λ¯1α=0, the fractional Maxwell model declines to a Newtonian fluid.

6  Conclusion

The present paper displayed an analytical study of how heat transfer affected the peristaltic flow of the fractional Maxwell model in the gap between two vertical coaxial tubes. It simplified the problem, assuming the low Reynolds number and the approximation of the long wavelength. It solved the problem analytically based on the fractional calculus system. The axial velocity, temperature, tangential stress, and heat transfer coefficient was examined on the endoscope parameters, Hartman number M, Grashof number Gr, the heat parameter β, the relaxation time λ1, the fractional time derivative parameter α1, the amplitude ratio ϕ, and the radius ratio ε. The following solutions were obtained based on the graphs:

1- The axial velocity declines and surges when increasing the fractional Maxwell fluid, relaxation–retardation times, Hartman number, and wave amplitude.

2- The temperature surges and diminishes with increasing wave amplitude and radius ratio.

3- The axial velocity of the Jeffrey fluid declines in comparison with a hydrodynamic fluid within the tube's center.

4- Tangential stress declines and rises with rising the fractional Maxwell fluid, heat source, wave amplitude, radius ratio, and Grash of number.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  M. Saqib, H. Hanif, T. Abdeljawad, I. Khan, S. Shafie et al., “Heat transfer in MHD flow of Maxwell fluid via fractional cattaneo-friedrich model: A finite difference approach,” Computers, Materials & Continua, vol. 65, no. 3, pp. 1959–1973, 2020. [Google Scholar]

 2.  H. Alotaibi, S. Althubiti, M. R. Eid and K. L. Mahny, “Numerical treatment of MHD flow of casson nanofluid via convectively heated non-linear extending surface with viscous dissipation and suction/injection effects,” Computers, Materials & Continua, vol. 66, no. 1, pp. 229–245, 2021. [Google Scholar]

 3.  A. J. C. Crespo, M. Gómez-Gesteira and R. A. Dalrymple, “Boundary conditions generated by dynamic particles in SPH methods,” Computers, Materials & Continua, vol. 5, no. 3, pp. 173–184, 2007. [Google Scholar]

 4.  A. Khan, D. Khan, I. Khan, M. Taj, I. Ullah et al., “MHD flow and heat transfer in sodium alginate fluid with thermal radiation and porosity effects: Fractional model of atangana baleanu derivative of non-local and non-singular kernel,” Symmetry, vol. 11, no. 10, pp. 1295–1305, 2019. [Google Scholar]

 5.  A. M. Abd-Alla, S. M. Abo-Dahab and A. Kilicman, “Peristaltic flow of a jeffrey fluid under the effect of radially varying magnetic field in a tube with an endoscope,” Journal of Magnetism and Magnetic Materials, vol. 384, no. 15, pp. 79–86, 2015. [Google Scholar]

 6.  J. Zhao, “Axisymmetric convection flow of fractional Maxwell fluid past a vertical cylinder with velocity slip and temperature jump,” Chinese Journal of Physics, vol. 67, pp. 501–511, 2020. [Google Scholar]

 7.  T. Hayat, N. Ahmad and N. Ali, “Effects of an endoscope and magnetic field on the peristalsis involving jeffrey fluid,” Communications in Nonlinear Science and Numerical Simulation, vol. 13, pp. 1581–1591, 2008. [Google Scholar]

 8.  H. Rachid,“Effects of heat transfer and an endoscope on peristaltic flow of a fractional Maxwell fluid in a vertical tube,” Abstract and Applied Analysis, vol. 2015, pp. 322–333, 2015. [Google Scholar]

 9.  A. M. Abd-Alla, S. M. Abo-Dahab and R. D. El-Semiry, “Long wavelength peristaltic flow in a tubes with an endoscope subjected to magnetic field,“ Korea-Australia Rheology Journal, vol. 25, pp. 107–118, 2013. [Google Scholar]

10. S. Nadeem, T. Hayat, N. S. Akbar and M. Y. Malik, “On the influence of heat transfer in peristaltic with variable viscosity,” International Journal of Heat and Mass Transfer, vol. 52, pp. 4722–4730, 2009. [Google Scholar]

11. M. I. Asjad, M. Aleem, A. Ahmadian, S. Salahshour and M. Ferrara, “New trends of fractional modeling and heat and mass transfer investigation of (SWCNTs and MWCNTs)-CMC based nanofluids flow over inclined plate with generalized boundary conditions,” Chinese Journal of Physics, vol. 66, pp. 497–516, 2020. [Google Scholar]

12. Q. Hussain, S. Asghar, T. Hayat and A. Alsaedi, “Heat transfer analysis in peristaltic flow of MHD jeffrey fluid with variable thermal conductivity,”Applied Mathematics and Mechanics, vol. 36, pp. 499–516, 2015. [Google Scholar]

13. F. Mainardi and G. Spada, “Creep, relaxation and viscosity properties for basic fractional models in rheology,” The European Physical Journal Special, vol. 193, pp. 133–160, 2011. [Google Scholar]

14. M. Mishra and A. R. Rao, “Peristaltic transport of a newtonian fluid in an asymmetric channel,” Zeitschrift für Angewandte Mathematik und Physik, vol. 54, pp. 532–550, 2003. [Google Scholar]

15. H. Qi and H. Jin, “Unsteady rotating flows of a viscoelastic fluid with the fractional Maxwell model between coaxial cylinders,” Acta Mechanica Sinica, vol. 22, no. 4, pp. 301–305, 2006. [Google Scholar]

16. S. Amana, Q. Al-Mdallala and I. Khan, “Heat transfer and second order slip effect on MHD flow of fractional Maxwell fluid in a porous medium,” Journal of King Saud University–Science, vol. 32, pp. 450–458, 2020. [Google Scholar]

17. F. Ali, N. A. Sheikh, I. Khan and M. Saqib, “Magnetic field effect on blood flow of casson fluid in axisymmetric cylindrical tube: A fractional model,” Journal of Magnetism and Magnetic Materials, vol. 423, no. 4, pp. 327–336, 2017. [Google Scholar]

18. E. Ul Haque, A. U. Awan, N. Raza, M. Abdullah and M. A. Chaudhry, “Computational approach for the unsteady flow of Maxwell fluid with caputo fractional derivatives,” Alexandria Engineering Journal, vol. 57, no. 4, pp. 2601–2608, 2018. [Google Scholar]

19. Y. Carrera, G. Avila-de la Rosa, E. J. Vernon-Carter and J. Alvarez-Ramirez, “A fractional-order Maxwell model for non-newtonian fluids,” Physica A: Statistical Mechanics and its Applications, vol. 482, pp. 276–285, 2017. [Google Scholar]

20. A. R. Johnson and C. J. Quigley, “A viscohyperelastic Maxwell model for rubber viscoelasticity,” Rubber Chemistry and Technology, vol. 65, no. 1, pp. 137–153, 1992. [Google Scholar]

21. D. Tripathi, S. K. Pandey and S. Das, “Peristaltic flow of viscoelastic fluid with fractional Maxwell model through a channel,” Applied Mathematics and Computation, vol. 215, pp. 3645–3654, 2010. [Google Scholar]

22. D. Tripathi, “Peristaltic transport of a viscoelastic fluid in a channel,” Acta Astronautica, vol. 68, pp. 1379–1385, 2011. [Google Scholar]

23. X. Guo and H. Qi, “Analytical solution of electro-osmotic peristalsis of fractional jeffreys fluid in a micro-channel,” Micromachines, vol. 4, no. 341, pp. 341, 2017. [Google Scholar]

24. A. M. Abd-Alla, S. M. Abo-Dahab and H. D. El-Shahrany, “Effects of rotation and initial stress on peristaltictransport of fourth grade fluid with heat transfer and induced magnetic field,” Journal of Magnetism AndMagnetic Materials, vol. 349, pp. 268–280, 2014. [Google Scholar]

25. A. M. Abd-Alla, G. A. Yahya, S. R. Mahmoud and H. S. Alosaimi, “Effect of the rotation, magnetic field and initial stress on peristaltic motion of micropolar fluid,” Meccanica, vol. 47, pp. 1455–1465, 2012. [Google Scholar]

26. T. Muhammad, S. Z. Alamri, H. Waqas, D. Habib and R. Ellahi, “Bioconvection flow of magnetized carreau nanofluid under the influence of slip over a wedge with motile microorganisms,” Journal of Thermal Analysis and Calorimetry, vol. 143, pp. 945–957, 2021. [Google Scholar]

27. D. Tripathi, “Numerical study on peristaltic transport of fractional bio-fluid,” Journal of Mechanics in Medicine and Biology, vol. 11, no. 5, pp. 1045–1058, 2011. [Google Scholar]

28. D. Tripathi, “Peristalticflow of a fractional second grade fluid through a cylindrical tube,” Thermal Science, vol. 15, no. 2, pp. S167–S173, 2011. [Google Scholar]

29. D. Tripathi and O. A. Bég, “Mathematica numerical simulation of peristaltic biophysical transport of a fractional viscoelastic fluid through an inclined cylindrical tube,” Computer Methods in Biomechanics and Biomedical Engineering, vol. 18, no. 15, pp. 1648–1657, 2015. [Google Scholar]

30. M. Veera Krishna, “Hall and ion slip effects on MHD free convective rotating flow bounded by the semi-infinite vertical porous surface,” Heat Transfer, vol. 49, no. 4, pp. 1920–1938, 2020. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.