Computers, Materials & Continua DOI:10.32604/cmc.2022.027074
Article

Fuzzy Logic with Archimedes Optimization Based Biomedical Data Classification Model

Mahmoud Ragab1,2,3,* and Diaa Hamed4,5

1Information Technology Department, Faculty of Computing and Information Technology, King Abdulaziz University, Jeddah 21589, Saudi Arabia
2Centre of Artificial Intelligence for Precision Medicines, King Abdulaziz University, Jeddah 21589, Saudi Arabia
3Department of Mathematics, Faculty of Science, Al-Azhar University, Naser City 11884, Cairo, Egypt
4Department of Mineral Resources and Rocks, Faculty of Earth Sciences, King Abdulaziz University, Jeddah 21589, Saudi Arabia
5Geology Department, Faculty of Science, Al-Azhar University, Naser City 11884, Cairo, Egypt
*Corresponding Author: Mahmoud Ragab. Email: mragab@kau.edu.sa
Received: 10 January 2022; Accepted: 14 February 2022

Abstract: Medical data classification becomes a hot research topic in the healthcare sector to aid physicians in the healthcare sector for decision making. Besides, the advances of machine learning (ML) techniques assist to perform the effective classification task. With this motivation, this paper presents a Fuzzy Clustering Approach Based on Breadth-first Search Algorithm (FCA-BFS) with optimal support vector machine (OSVM) model, named FCABFS-OSVM for medical data classification. The proposed FCABFS-OSVM technique intends to classify the healthcare data by the use of clustering and classification models. Besides, the proposed FCABFS-OSVM technique involves the design of FCABFS technique to cluster the medical data which helps to boost the classification performance. Moreover, the OSVM model investigates the clustered medical data to perform classification process. Furthermore, Archimedes optimization algorithm (AOA) is utilized to the SVM parameters and boost the medical data classification results. A wide range of simulations takes place to highlight the promising performance of the FCABFS-OSVM technique. Extensive comparison studies reported the enhanced outcomes of the FCABFS-OSVM technique over the recent state of art approaches.

Keywords: Clustering; medical data classification; machine learning; parameter tuning; support vector machines

1  Introduction

Computational intelligent system for medical application is an exciting and important research field. Generally, a medical doctor collects their knowledge from the confirmed diagnoses and patient symptoms [1]. In another word, predictive significance of symptoms towards diagnostic and diseases precision of a person are dependent extremely on a physician's knowledge. Since treatment therapy and medical knowledge rapidly progresses, for example, the accessibility of new drugs and the existence of new diseases, it is difficult for a clinician to possess current development and knowledge in medical settings [2]. Alternatively, with the emergence of computing technology, now it is relatively easy to store and acquire lots of data digitally for example in devoted dataset of electronic patient’s record. Intrinsically, the positioning of computerized medicinal decision support system (DSS) becomes a feasible method for helping physicians to accurately and swiftly identify individual patients. Nonetheless, several problems should be resolved beforehand an effective medicinal DSS could be and deployed developed that includes decision making in the existence of imprecision and uncertainty [3]. Though medicinal experience and expert knowledge is significant, ranging from measuring a patient's healthcare status to making diagnoses, advancement in machine learning (ML) methods have paved the way for medicinal practitioner to make use of computational intelligent system for DSS [4]. Fig. 1 depicts the process in medical image processing.

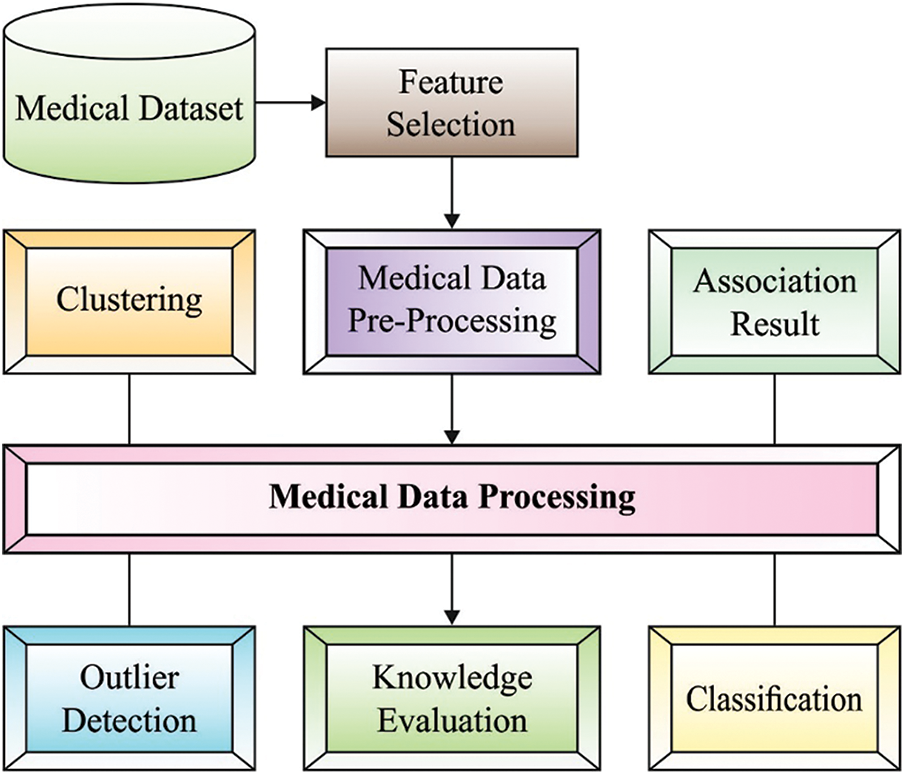
Figure 1: Different processes involved in medical data processing

Data mining (DM) and ML frequently utilize similar methods and they significantly overlap, but ML method on forecast, on the basis of known property learned from the trained information [5], DM methods concentrate on the detection of previously unknown property within the information. DM method employs ML method, for various purposes; at the same time, ML utilizes DM method as unsupervised learning or as a pre-processing stage to improve performance of the learning model [6]. The ML algorithm is developed from the very beginning and utilized for analyzing medicinal datasets. The clustering technique plays a significant role in DM and ML methods. Domestic researcher mostly focusses on the succeeding two characteristics: (a) a clustering model enhances the performance of clustering and (b) a clustering method dynamically determine the amount of cluster centre [7]. A dynamic clustering model based genetic algorithm; the key concept of the algorithm is to efficiently resolve the sensitivity of the primary state value clustering, it employed the maximal feature value ranges partitioning strategy and two phases and dynamic selection model in mutation that attain optimum clustering centre. Clustering analysis is a type of unsupervised method in recognition of patterns [8]. The clustering task split an unmarked pattern based on some condition into various subsets that need equivalent instances have the more equivalents cluster centre and different instances must be separated in various groups. Thus, it is named unsupervised classification. Clustering analysis was widely employed in image processing, DM, radar target detection, object detection, and so on [9].

This paper presents a Fuzzy Clustering Approach Based on Breadth-first Search Algorithm (FCA-BFS) with optimal support vector machine (OSVM) model, named FCABFS-OSVM for medical data classification. The proposed FCABFS-OSVM technique involves the design of FCABFS technique to cluster the medical data which helps to boost the classification performance. In addition, the OSVM model investigates the clustered medical data to perform classification process. Also, Archimedes optimization algorithm (AOA) is utilized to the SVM parameters and boost the medical data classification results. A wide range of simulations takes place to highlight the promising performance of the FCABFS-OSVM technique.

2  Literature Review

Yelipe et al. [10] introduced an enhanced imputation model named Imputation related class-based clustering (IM-CBC). The experiment is conducted on 9 standard data sets and the recorded outcomes with IM-CBC imputation method are compared with 10 imputation models with C4.5, k-nearest neighbor (KNN), and support vector machine (SVM) classification with fuzzy gaussian similarity and Euclidean distance models. Karlekar et al. [11] proposed an approach for medicinal data classifier with an ontology and whale optimization-related SVM algorithm. At first, privacy-preserved data are designed adapting Kronecker product bat model, later, ontology is constructed for the feature selection (FS) model. Then, optimal SVM and Ontology model is presented by incorporating whale optimization algorithm (WOA) and ontology with SVM, where WOA and ontology are utilized for selecting possible kernel parameters.

Karim et al. [12] present an architecture for medicinal data processing that is developed on the basis of energy spectral density (ESD) and deep autoencoder (AE) models. The main innovation of presented method is to integrate ESD process as feature extractor to a unique deep sparse auto-encoder (DSAE). This enables our presented method for extracting more qualified features in a short computation time than the traditional framework. Le [13] proposes a fuzzy c-means (FCM) clustering interval type-2 cerebellar model articulation neural network (FCM-IT2CMANN) model for helping physicians improve diagnosis performance. The presented approach integrates two classifications, where FCM model is the pre-classification and the IT2CMANN is the initial classification. Implementation of gradient descent model, an adoptive laws to update the presented method is derived.

In Kadam et al. [14], the medical data is reduced dimensionally by the PCA method. The reduction dimensionality information is converted by multiplying with weighting factors, i.e., enhanced by WOA, to attain maximal distance among the attributes. Consequently, the information is converted into a label-distinguishable plane where the DBN system is adapted for performing the DL method, and the data classification is implemented.

3  The Proposed Model

In this study, a novel FCABFS-OSVM technique has been developed to classify the healthcare data by the use of clustering and classification models. The proposed FCABFS-OSVM technique encompasses different subprocesses such as data pre-processing, FCABFS based clustering, SVM based classification, and AOA based parameter optimization. Fig. 2 demonstrates the overall process of FCABFS-OSVM technique.

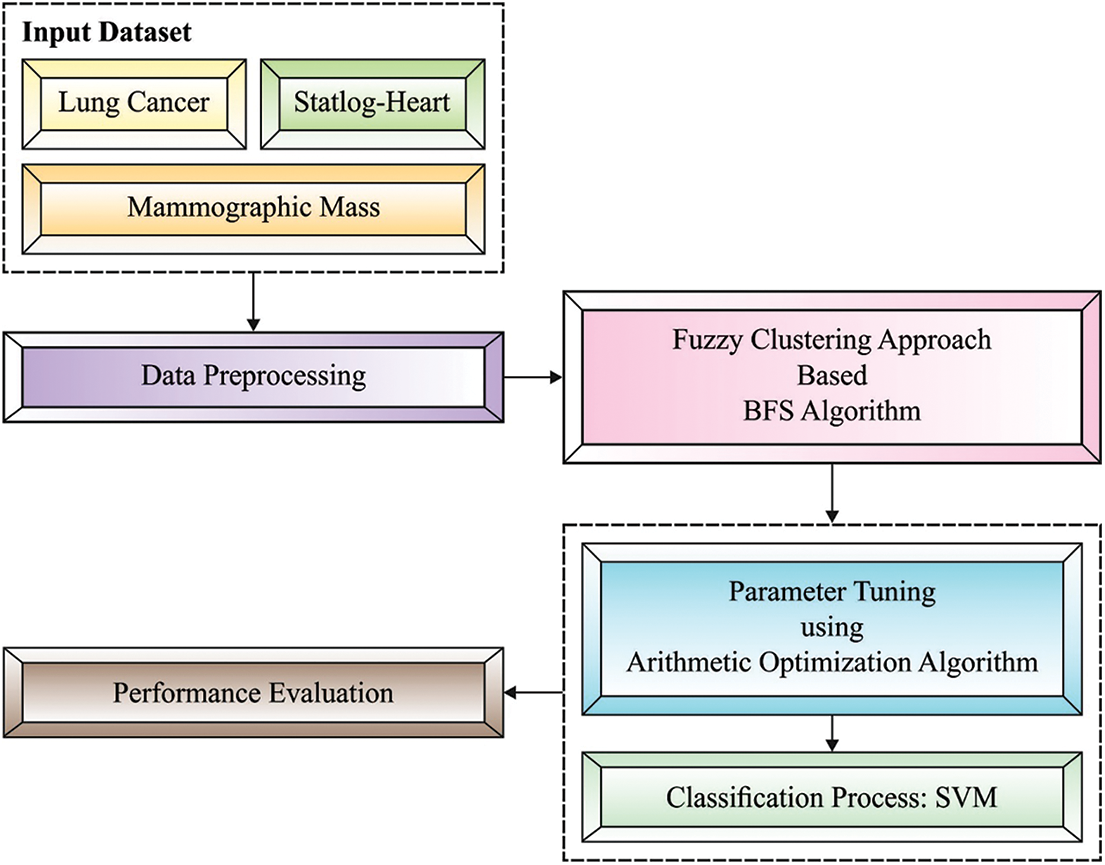
Figure 2: Architecture of FCABFS-OSVM technique

3.1 Design of FCABFS Technique for Clustering Process

At the initial stage, the FCABFS technique has been developed to group the medical data into distinct clusters. The conventional FCM approach reduces the weighted sum of squares of the distance from each data point to the respective cluster center. But FCM considers each property have a similar effect on clustering, nevertheless of the effect on distinct data properties. Still, the clustering unrelated attributes and sample noise attributes exist. Few data objects in a huge sample might have large impact on clustering results because of separation from another object. But, almost all the clustering models, and feature weighting extension, considers each sample to have an equivalent weight at the time of clustering. Consequently, the process is sensitive to noise. The data object in a huge sample might belong to distinct attributes. Few attribute objects might have a greater influence on clustering results and be named as called data with stronger reparability. In contrast, others might have lower contributions towards clustering results and called noise or isolated data. We employ the variation coefficient to minimize the contribution of noise attributes.

In the presented method, the similarity among objects is defined by presenting an extra weight of the variation coefficient model as follows:

minJm(U,V)=∑i=1n∑j=1cuijmdij2w.(1)

in which w=(w1,w2,…,wp)T,wk=vk∑k=1pvk.wk represent the weight of all the attribute factors and X¯=1n∑i=1nXi denotes the sample mean, vx=Sx|X¯| indicates the variation coefficient, m signifies a fuzzy parameter and J shows the loss function, Sx=1n−1∑i=1n(xi−X¯)2 represent standard deviation [15], C implies the number of clusters; and n means the number of data.

The Lagrange multiplier model is utilized for finding the solution. The presented FCM alongside the Lagrange function is formulated by

J(U,V,λ)=∑i=1n∑j=1cuijmdijmw−∑i=1nλi(∑k=1cuik−1).(2)

Let,

∂J∂λ=0

In the early phase of optimization, the succeeding is attained.

∂J∂u11=mu11m−1d112w−λ1=0

⇒u11=(λ1md112w)1m−1.

Likewise, u12 is enhanced by the following equation,

Apply the condition, ∑k=1cuik=1,

We get,

(λ1m)1m−1[∑k=1c(1d1k2w)1m−1]=1.(3)

From, u11=(1d112w)1m−1∑k=1c(1d1k2w)1m−1,⋯⋯,unc=(1dlc2w)1m−1∑k=1c(1d1k2w)1m−1 ,

Likewise, u2c=(1d2c2w)1m−1∑k=1c(1d2k2w)1m−1,⋯,unc=(1dnc2w)1m−1∑k=1c(1dnk2w)1m−1⋅

From the abovementioned, the common form of the center upgrading equation is,

uij=(1dij2w)1m−1∑k=1c(1dik2w)1m−1,⋯⋯dij=‖xi−vj‖.(4)

Generally, to attain vj, the objective function is extended as

Improving the above objective function gives,

J(U,V)∂v1=−2∑i=1nuijw‖xi−v1‖=0

⇒v1=∑i=1nui1mxiw∑i=1nui1mw.

Likewise, v2=∑i=1nui2mxiw∑i=1nui2mw,…,vj=∑i=1nuijmxiw∑i=1nuijmw.

From the abovementioned, the common form of upgrading center is

vj=∑i=1nuijmxjw∑i=1nuijmw.(5)

3.2 Design of Optimal SVM Based Classification Process

Once the medical data has been clustered, they are passed into the SVM model to perform the classification process. Assume that binary classification task: {xi,yi},i=1,…,l,yi∈{−1,1}, xi∈Rd, where xi represents the data points [16], and yi implies the equivalent labels. It can be divided as hyperplane provided as wTx+b=0, where w refers the d dimension co-efficient vector which is normal to hyperplane, and b signifies the offset in the origin. The linear SVM attains a better separate margin with resolving the subsequent optimized task:

s.t.,yi(wTxi+b)≥1−ξi,ξi≥0(6)

With establishing Lagrangian multiplier αi(i=1,2,…,n), a primal issue is decreased to Lagarangian dual issue:

s.t.,αi≥0,i=1,…,n,∑i=1nαiyi=0(7)

It can be obvious a quadratic optimized issue with linear constraint. In KarushKuhnTucker (KKT) condition, it is realized: αi(yi(wTxi+b)−1)=0. If αi>0. The equivalent data points are named SVs. Therefore, the solution gets the subsequent procedure: w=∑i=1nαiyixi, where n implies the amount of support vectors (SVs). At this point, b is attained in yi(wTxi+b)−1=0, where xi are SVs. Then, w and b are defined, the linear discriminant function is provided in Eq. (8).

g(x)=sgn(∑i=1nαiyixiTx+b)(8)

Generally, the 2 classes could not be linearly divided. For the purpose of the linear learning machine for working well from non-linear cases, a common idea was established. Specifically, a novel input space is mapped as to some high dimensional feature spaces in which the trained set was linearly separate. With this mapping, the decision function is formulated as:

g(x)=sgn(∑i=1nαiyi∅(xi)T∅(x)+b)(9)

where xiTx from the input space was signifying as the procedure ∅(xi)T∅(x) from the feature space [17]. It could not essential for knowing the functional procedure of mapping φ(Xi) as it can be implicitly determined as one chosen kernel: (xi,xj)=∅(xi)Tφ(xj). Therefore, the decision function is written as:

g(x)=sgn(∑i=1nαiyiK(xi,x)+b)(10)

Generally, some positive semi-definite function which fulfills Mercer’s criteria is kernel function.

In order to optimally tune the weight and bias values of the SVM model, the AOA is utilized. Usually, along with other techniques, the AOA contains 2 search stages like exploration and exploitation, simulated as mathematics functions namely −,+,∗,and/. Primary, the AOA creates the group of N solutions (agent) [18]. Everyone defines the solution to tested problem. Therefore, the solution or agent signifies the X population as:

X=[x1,1⋯x1,jx1,n−1x1,nx2,1⋯x2,j⋯x2,n⋯⋯⋯⋯⋯⋮⋮⋮⋮⋮xN−1,1⋯xN−1,j⋯xN−1,nxN,1⋯xN,jxN,n−1xN,n](11)

Afterward, the FF of all solutions are calculated for detecting an optimum one Xb. Next, according to the Math Optimizer Accelerated (MOA) value, AOA carries out exploration or exploitation procedures. At that point, MOA has upgraded as the subsequent formula:

MOA(t)= Min +t×(MaxMOA−MinMOAMt)(12)

whereas Mt stands for the entire amount of iterations. MinMOA and MaxOA signifies the minimal and maximal values of accelerated functions correspondingly. In particular, the multiplication (M) and division (D) were utilized from the exploration stage of AOA as projected from the subsequent formula:

Xi,j(t+1)={Xbj÷(MOP+∈)×((UBj−LBj)×μ+LBj),r2<0.5Xbj×MOP×((UBj−LBj)×μ+LBj),otherwise(13)

whereas e implies the small integer value, UBj and LBj denotes the lower as well as upper boundaries of search area at jth dimensional. μ=0.5 defines the control function. Also, Math Optimizer (MOP) is expressed as:

MOP(t)=1−t1/αMt1/α(14)

α=5 demonstrates the dynamic parameter which defines the precision of exploitation stage throughout iteration.

Moreover, addition (A) and subtracting (D) operators were utilized for implementing the AOA exploitation stage utilizing the subsequent formula [19].

xi,j(t+1)={Xbj−MOP×((UBj−LBj)×μ+LBj),r3<0.5Xbj+MOP×((UBj−LBj)×μ+LBj),otherwise(15)

whereas r3 indicates the arbitrary number created from zero and one. Next, the agent's upgrading procedure was executed utilizing the AOA operator. In brief, Algorithm 1 demonstrates the important steps of the AOA.

4  Experimental Validation

The proposed model is tested using three datasets namely lung cancer, mammographic mass, and Statlog-heart dataset [20]. Tab. 1 demonstrates the details of the dataset description. Tab. 2 investigates the classifier result analysis of the FCABFS-OSVM technique under distinct epochs on the lung cancer dataset. With 100 epochs, the FCABFS-OSVM technique has gained true positive rate (TPR), true negative rate (TNR), accuracy, error, and F-measure of 83.08%, 80.88%, 87.04%, 12.96%, and 83.35% respectively. Along with that, with 300 epochs, the FCABFS-OSVM method has received TPR, TNR, accuracy, error, and F-measure of 82.63%, 85.23%, 86.92%, 13.08%, and 85.66% correspondingly. In addition, with 500 epochs, the FCABFS-OSVM technique has gained TPR, TNR, accuracy, error, and F-measure of 83.38%, 82.36%, 87.22%, 12.78%, and 86.78% respectively.

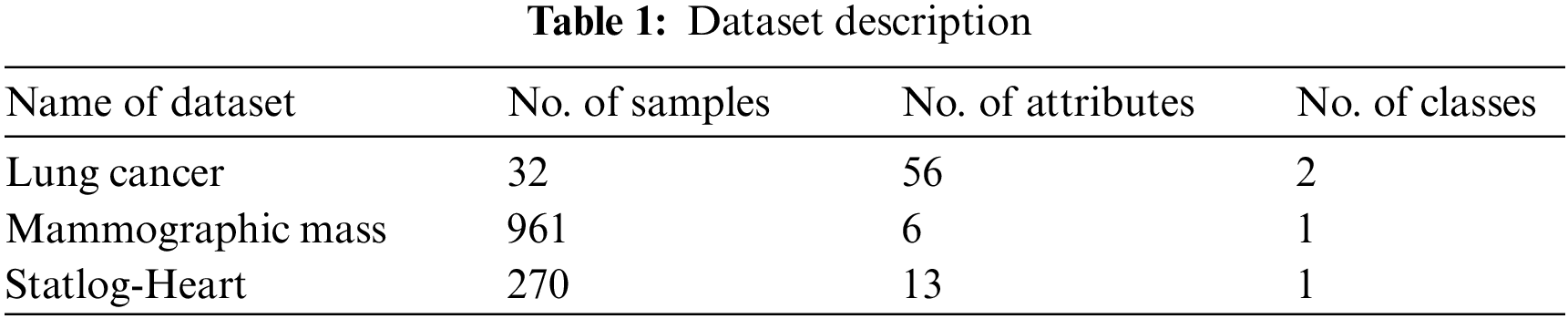
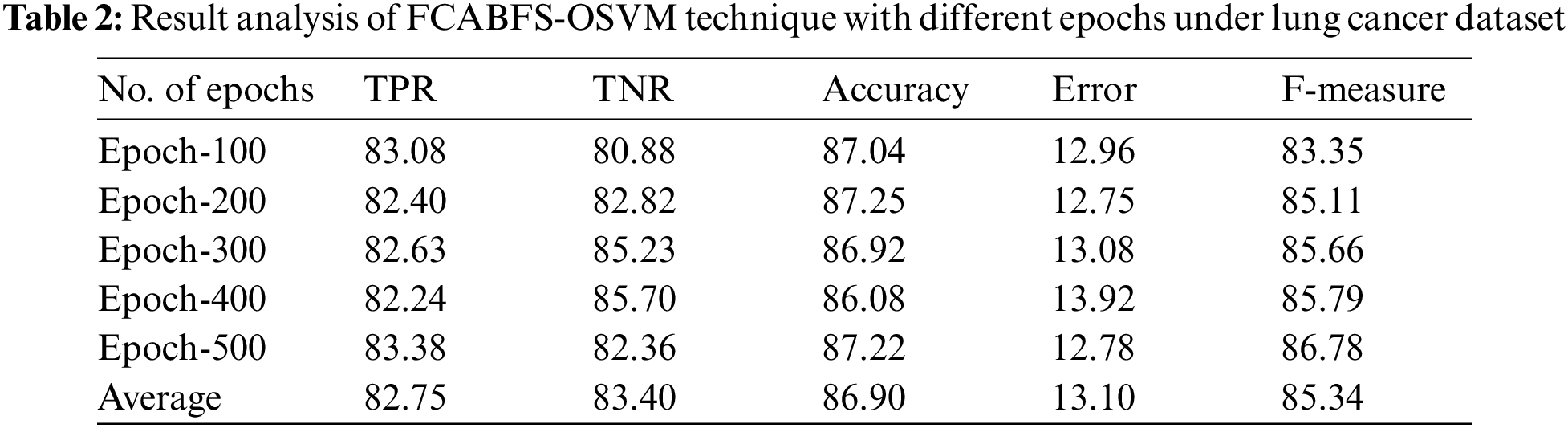
Fig. 3 determines the receiver operating characteristics (ROC) curve analysis of the FCABFS-OSVM system under lung cancer data sets. The figure revealed that the FCABFS-OSVM method has improved outcomes with a high ROC of 95.4070. Tab. 3 examines the classifier analysis of the FCABFS-OSVM system under dissimilar epochs on the Mammographic mass dataset. With 100 epochs, the FCABFS-OSVM method has received TPR, TNR, accuracy, error, and F-measure of 86.59%, 85.82%, 89.41%, 10.59%, and 86.69% correspondingly. Along with that, with 300 epochs, the FCABFS-OSVM procedure has attained TPR, TNR, accuracy, error, and F-measure of 84.15%, 87.58%, 88.51%, 11.49%, and 86.45% correspondingly. In addition, with 500 epochs, the FCABFS-OSVM method has archived TPR, TNR, accuracy, error, and F-measure of 86.66%, 86.81%, 86.26%, 13.74%, and 88.16% correspondingly.

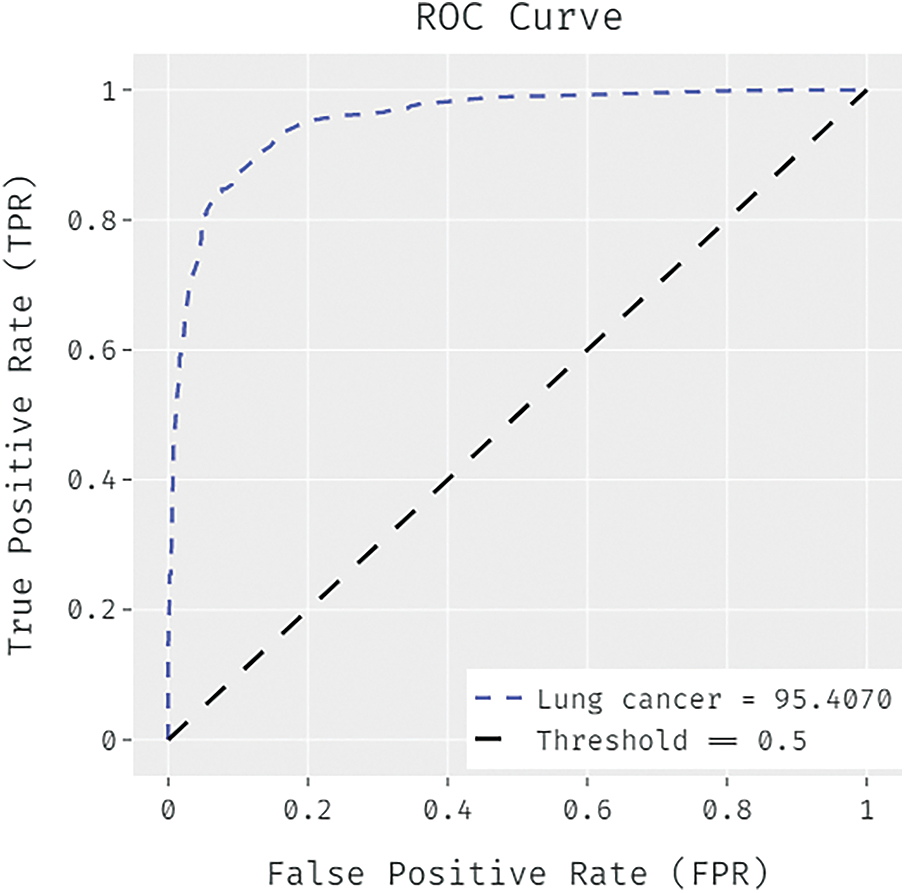
Figure 3: ROC analysis of FCABFS-OSVM technique under lung cancer dataset

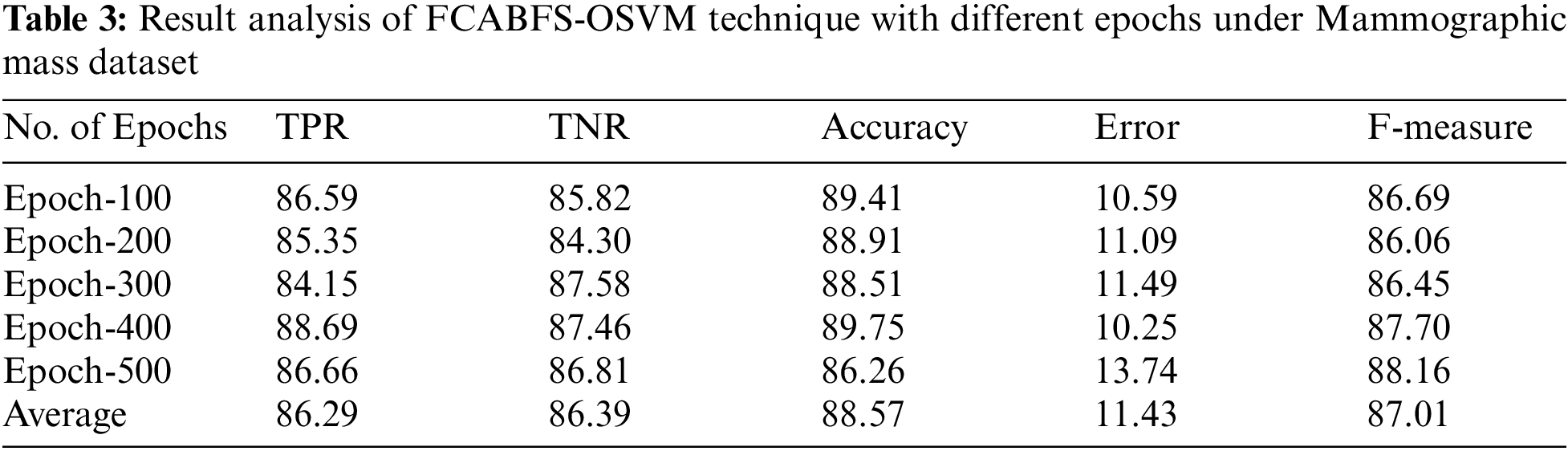
Fig. 4 illustrated the ROC analysis of the FCABFS-OSVM system under Mammographic mass dataset. The figure exposed that the FCABFS-OSVM method has attained improved outcomes with the high ROC of 94.8630.

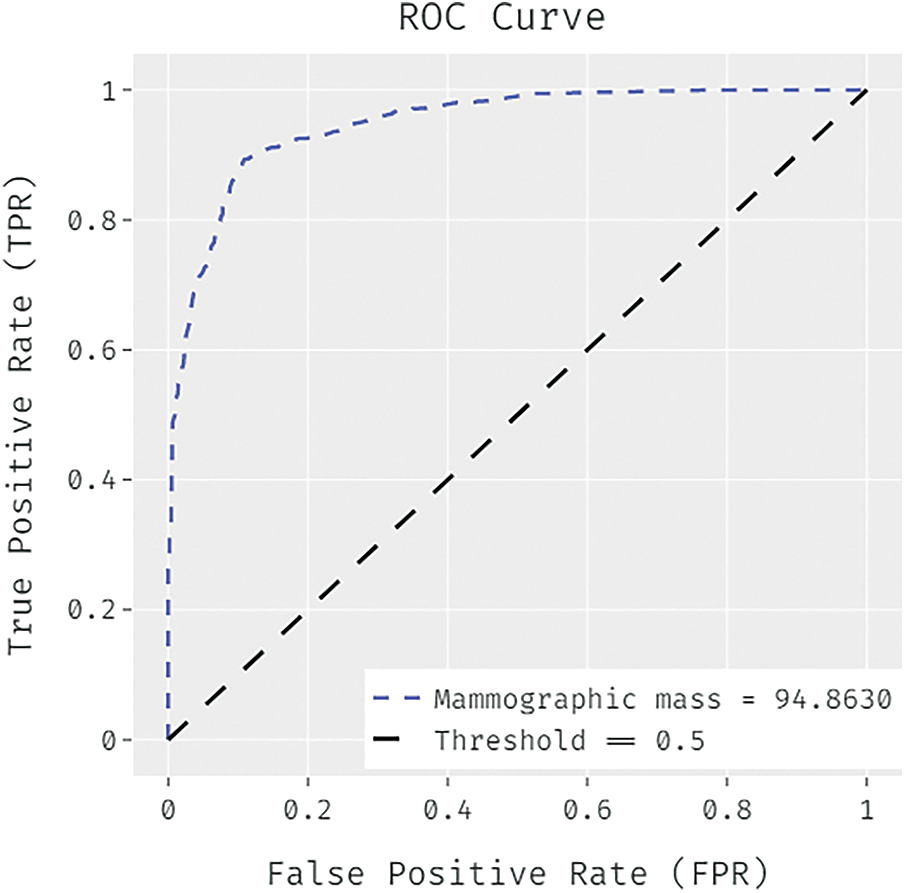
Figure 4: ROC analysis of FCABFS-OSVM technique under Mammographic mass dataset

Tab. 4 explores the classifier analysis of the FCABFS-OSVM model under discrete epochs on the Statlog-Heart dataset. With 100 epochs, the FCABFS-OSVM approach has attained TPR, TNR, accuracy, error, and F-measure of 89.37%, 90.38%, 89.41%, 10.59%, and 93.21% correspondingly. Along with that, with 300 epochs, the FCABFS-OSVM system has achieved TPR, TNR, accuracy, error, and F-measure of 90.40%, 90.87%, 89.48%, 10.52%, and 91.35% correspondingly. In addition, with 500 epochs, the FCABFS-OSVM system has obtained TPR, TNR, accuracy, error, and F-measure of 91.54%, 90.64%, 91.12%, 8.88%, and 92.79% correspondingly.

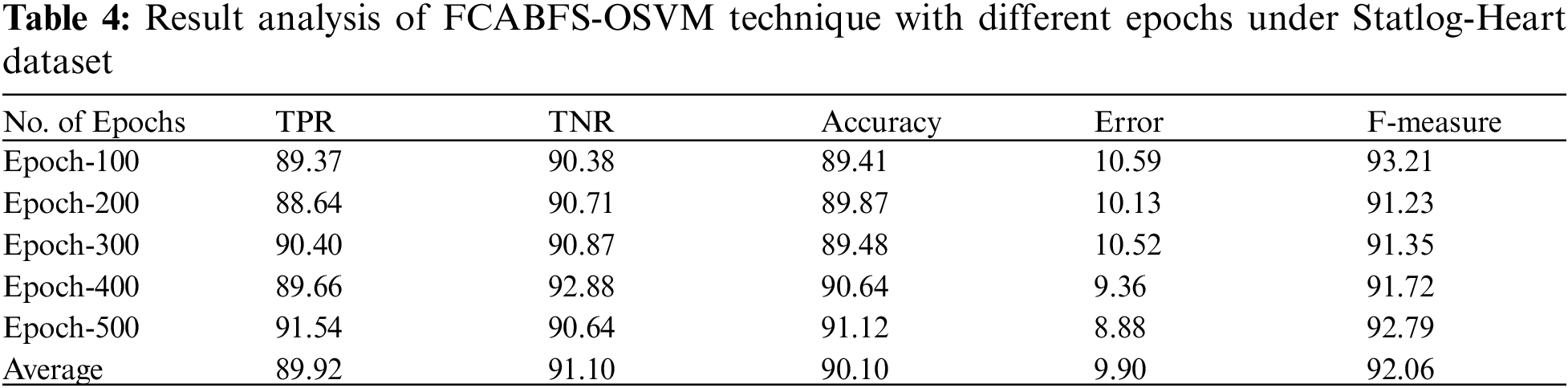
Fig. 5 proves the ROC analysis of the FCABFS-OSVM method under Statlog-Heart data set. The figure revealed that the FCABFS-OSVM method has attained improved outcomes with the maximal ROC of 96.2790.

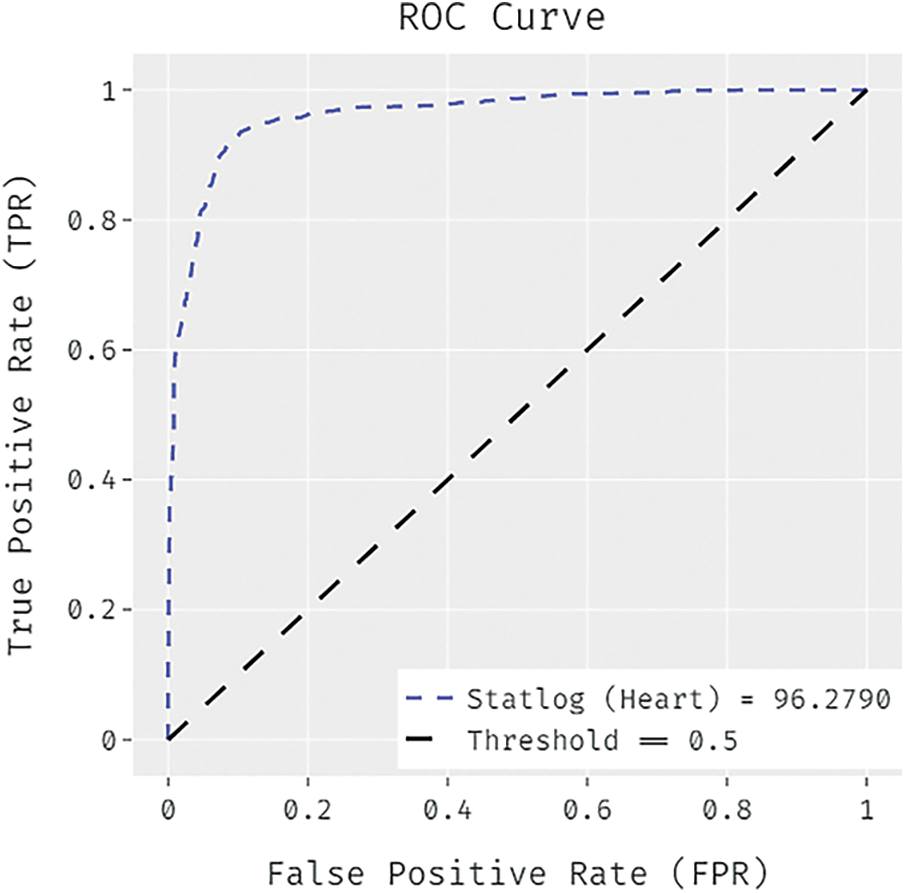
Figure 5: ROC analysis of FCABFS-OSVM technique under Statlog-Heart dataset

Fig. 6 offers the accuracy and loss graph analysis of the FCABFS-OSVM system on the testing data set. The result shows that the accuracy values tend to increase and loss values tend to reduce with an increasing epoch amount. Also, it is observed that the training loss is lower and validation accuracy is higher on the testing datasets.

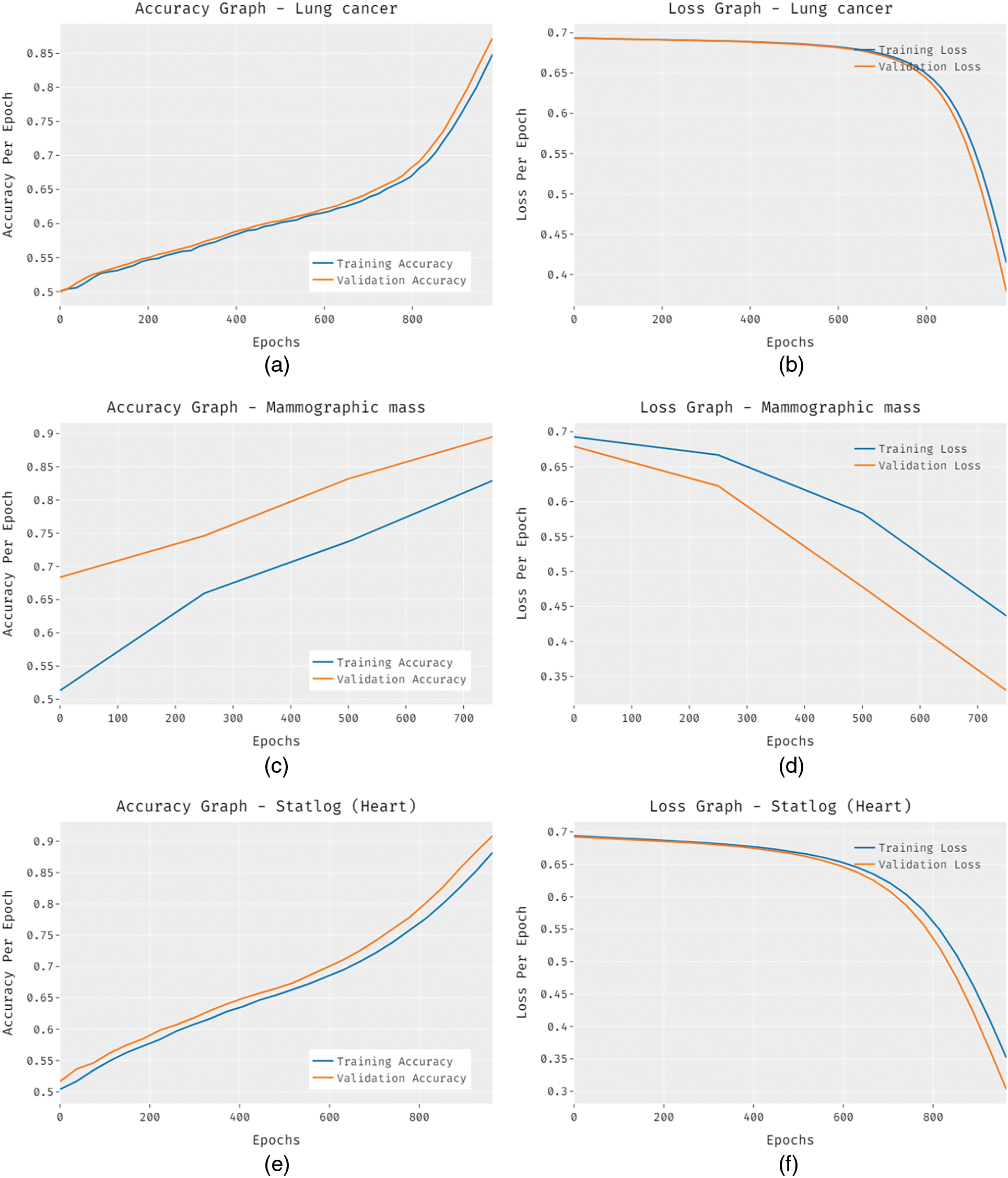
Figure 6: Accuracy and loss graph analysis of FCABFS-OSVM technique

Fig. 7 examine the comparative classification result analysis of the FCABFS-OSVM technique over the other methods [21]. The experimental results indicated that the Decision Stump (DS) and Random Tree (RT) methods have results to lower classification results. In line with this, the DT (J48) and RT algorithms have obtained slightly improved and closer classification performance. Though the Improved ID3 technique has resulted in competitive outcome, the FCABFS-OSVM technique has accomplished maximum outcome with the TPR of 82.75%, TNR of 83.40%, accuracy of 86.90%, error of 13.10%, and F-measure of 85.34%.

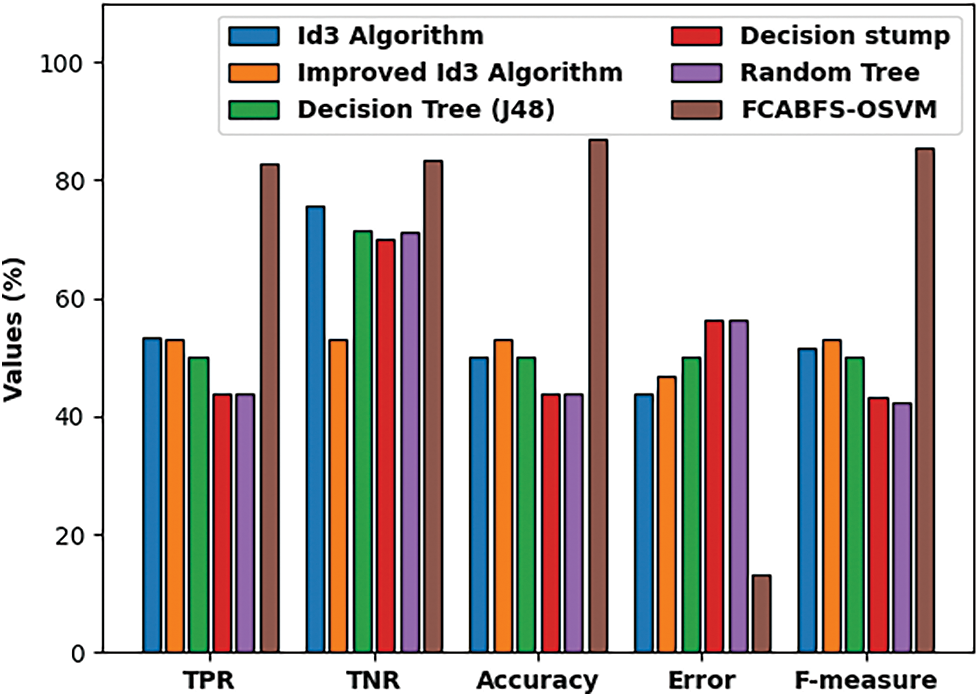
Figure 7: Comparative analysis of FCABFS-OSVM technique under lung cancer dataset

Fig. 8 inspect the comparative analysis of the FCABFS-OSVM method over the other algorithms. The experiment result indicates that the DS and RT methodologies have resulted in low classification results. In line with this, the DT (J48) and RT models have attained improved and closer classification efficiency. Though the Improved ID3 system has resulted in competitive outcome, the FCABFS-OSVM algorithm has accomplished maximal results with the TPR of 86.29%, TNR of 86.39%, accuracy of 88.57%, error of 11.43%, and F-measure of 87.01%.

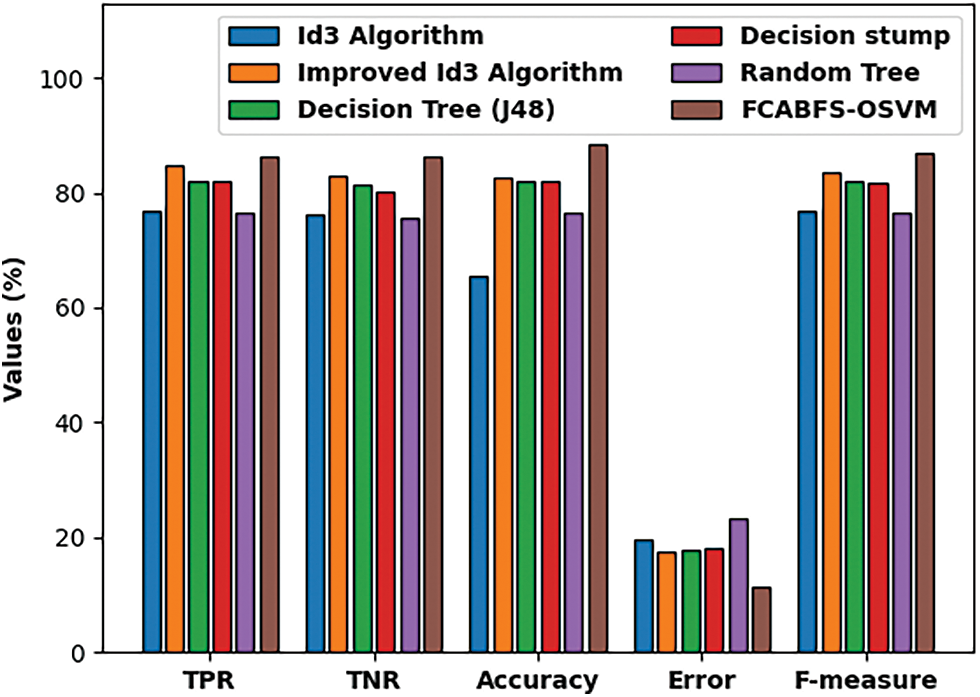
Figure 8: Comparative analysis of FCABFS-OSVM technique under Mammographic mass dataset

Fig. 9 investigate the comparative analysis of the FCABFS-OSVM approach over the other algorithms. The experiment result indicates that the DS and RT methodologies have resulted in low classification outcomes. In line with this, the DT (J48) and RT methods have attained improved and closer classification efficiency. Though the Improved ID3 technique has resulted in competitive outcomes, the FCABFS-OSVM approach has attained maximal results with the TPR of 89.92%, TNR of 91.10%, accuracy of 90.10%, error of 9.90%, and F-measure of 92.06%.

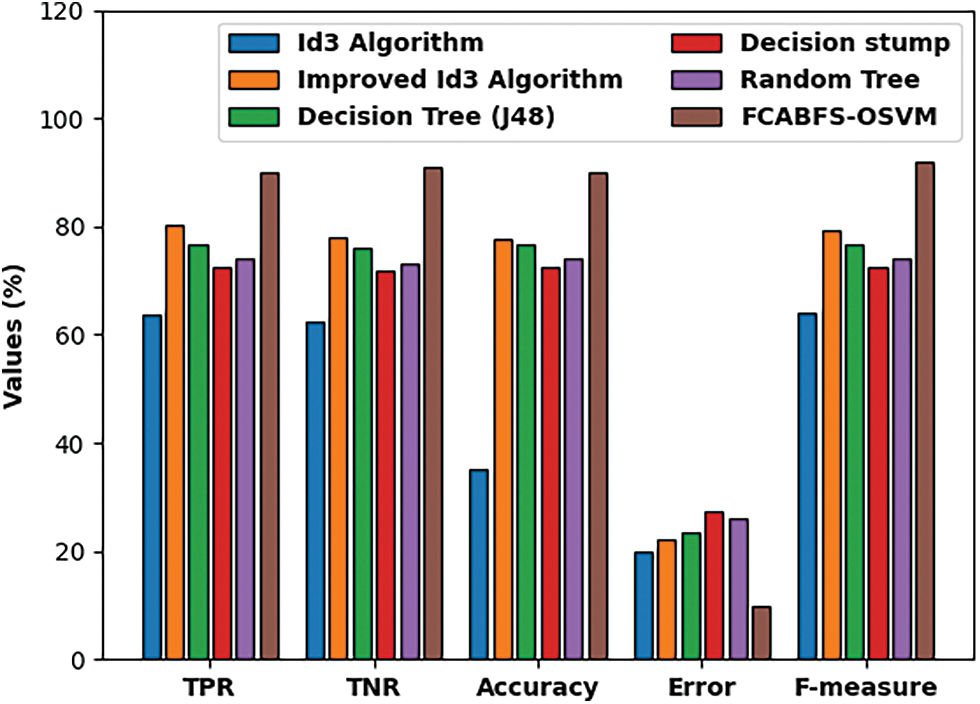
Figure 9: Comparative analysis of FCABFS-OSVM technique under Statlog-Heart dataset

5  Conclusion

In this study, a novel FCABFS-OSVM technique has been developed to classify the healthcare data by the use of clustering and classification models. The proposed FCABFS-OSVM technique encompasses different subprocesses such as data preprocessing, FCABFS based clustering, SVM based classification, and AOA based parameter optimization. The development of clustering and parameter tuning approaches helps to considerably boost the classification results. Furthermore, Archimedes optimization algorithm (AOA) is utilized to the SVM parameters and boost the medical data classification results. A wide range of simulations takes place to highlight the promising performance of the FCABFS-OSVM technique. An extensive comparison study reported the enhanced outcomes of the FCABFS-OSVM technique over the recent state of art approaches. In future, effective feature selection methodologies can be devised to boost the classifier results.

Acknowledgement: The authors extend their appreciation to the Deputyship for Research & Innovation, Ministry of Education in Saudi Arabia for funding this research work through the project number (IFPIP-249-145-1442) and King Abdulaziz University, DSR, Jeddah, Saudi Arabia.

Funding Statement: This project was supported financially by Institution Fund projects under Grant No. (IFPIP-249-145-1442).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  P. Mohapatra, S. Chakravarty and P. K. Dash, “An improved cuckoo search based extreme learning machine for medical data classification,” Swarm and Evolutionary Computation, vol. 24, no. 4, pp. 25–49, 2015. [Google Scholar]

 2.  C. Y. Fan, P. C. Chang, J. J. Lin and J. C. Hsieh, “A hybrid model combining case-based reasoning and fuzzy decision tree for medical data classification,” Applied Soft Computing, vol. 11, no. 1, pp. 632–644, 2011. [Google Scholar]

 3.  M. Z. Alam, M. S. Rahman and M. S. Rahman, “A random forest based predictor for medical data classification using feature ranking,” Informatics in Medicine Unlocked, vol. 15, no. 5, pp. 100180, 2019. [Google Scholar]

 4.  T. Nguyen, A. Khosravi, D. Creighton and S. Nahavandi, “Medical data classification using interval type-2 fuzzy logic system and wavelets,” Applied Soft Computing, vol. 30, no. 2, pp. 812–822, 2015. [Google Scholar]

 5.  R. Tang and X. Zhang, “CART decision tree combined with boruta feature selection for medical data classification,” in 2020 5th IEEE Int. Conf. on Big Data Analytics (ICBDA), Xiamen, China, pp. 80–84, 2020. [Google Scholar]

 6.  V. Sudha and H. A. Girijamma, “Novel clustering of bigger and complex medical data by enhanced fuzzy logic structure,” in 2017 Int. Conf. on Circuits, Controls, and Communications (CCUBE), Bangalore, India, pp. 131–135, 2017. [Google Scholar]

 7.  D. Abd, J. K. Alwan, M. Ibrahim and M. B. Naeem, “The utilisation of machine learning approaches for medical data classification and personal care system mangementfor sickle cell disease,” in 2017 Annual Conf. on New Trends in Information & Communications Technology Applications (NTICT), Baghdad, Iraq, pp. 213–218, 2017. [Google Scholar]

 8.  M. D. d. Lima, J. d. O. R. e. Lima and R. M. Barbosa, “Medical data set classification using a new feature selection algorithm combined with twin-bounded support vector machine,” Medical & Biological Engineering & Computing, vol. 58, no. 3, pp. 519–528, 2020. [Google Scholar]

 9.  A. Tai, A. Albuquerque, N. E.Carmona, M. Subramanieapillai, D. S. Cha et al., “Machine learning and big data: Implications for disease modeling and therapeutic discovery in psychiatry,” Artificial Intelligence in Medicine, vol. 99, pp. 101704, 2019. [Google Scholar]

10. U. Yelipe, S. Porika and M. Golla, “An efficient approach for imputation and classification of medical data values using class-based clustering of medical records,” Computers & Electrical Engineering, vol. 66, no. 12, pp. 487–504, 2018. [Google Scholar]

11. N. P. Karlekar and N. Gomathi, “OW-SVM: Ontology and whale optimization-based support vector machine for privacy-preserved medical data classification in cloud,” International Journal of Communication Systems, vol. 31, no. 12, pp. e3700, 2018. [Google Scholar]

12. A. Karim, M. Güzel, M. Tolun, H. Kaya and F. Çelebi, “A new framework using deep auto-encoder and energy spectral density for medical waveform data classification and processing,” Biocybernetics and Biomedical Engineering, vol. 39, no. 1, pp. 148–159, 2019. [Google Scholar]

13. T. L. Le, “Fuzzy c-means clustering interval type-2 cerebellar model articulation neural network for medical data classification,” IEEE Access, vol. 7, pp. 20967–20973, 2019. [Google Scholar]

14. V. J. Kadam and S. M. Jadhav, “Optimal weighted feature vector and deep belief network for medical data classification,” International Journal of Wavelets, Multiresolution and Information Processing, vol. 18, no. 02, pp. 2050006, 2020. [Google Scholar]

15. Y. Zhang, L. L. Zhai and M. Shahbaz, “A novel fuzzy clustering approach based on breadth-first search algorithm,” Journal of Computers, vol. 30, no. 3, pp. 162–175, 2019. [Google Scholar]

16. C. Cortes and V. Vapnik, “Support-vector networks,” Machine Learning, vol. 20, no. 3, pp. 273–297, 1995. [Google Scholar]

17. H. L. Chen, D. Y. Liu, B. Yang, J. Liu and G. Wang, “A new hybrid method based on local fisher discriminant analysis and support vector machines for hepatitis disease diagnosis,” Expert Systems with Applications, vol. 38, no. 9, pp. 11796–11803, 2011. [Google Scholar]

18. L. Abualigah, A. Diabat, S. Mirjalili, M. A. Elaziz and A. H. Gandomi, “The arithmetic optimization algorithm,” Computer Methods in Applied Mechanics and Engineering, vol. 376, no. 2, pp. 113609, 2021. [Google Scholar]

19. A. Ewees, M. A. A. Al-qaness, L. Abualigah, D. Oliva, Z. Y. Algamal et al., “Boosting arithmetic optimization algorithm with genetic algorithm operators for feature selection: case study on cox proportional hazards model,” Mathematics, vol. 9, no. 18, pp. 2321, 2021. [Google Scholar]

20. http://archive.ics.uci.edu/ml/index.php. [Google Scholar]

21. S. Yang, J. Guo and J. Jin, “An improved Id3 algorithm for medical data classification,” Computers & Electrical Engineering, vol. 65, no. 4, pp. 474–487, 2018. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.