Computers, Materials & Continua DOI:10.32604/cmc.2022.026587
Article

Optimization Agricultural Supply Chain: A Case Study of Fertilizer Supplier Selection

Nguyen Van Thanh1, Nguyen Thi Kim Lan2,*, Syed Tam Husain1, Nguyen Hoang Hai1 and Nguyen Viet Tinh1

1Faculty of Commerce, Van Lang University, Ho Chi Minh City, Vietnam
2International Education Institute, Van Lang University, Ho Chi Minh City, Vietnam
*Corresponding Author: Nguyen Thi Kim Lan. Email: lan.ntk@vlu.edu.vn
Received: 30 December 2021; Accepted: 15 February 2022

Abstract: The 21st century is associated with the Industrial Revolution 4.0 and the organic agriculture trend, making the utilization of high-quality fertilizers, abundant nutritional content, economical, and no affect to environment pollution. According to the new concept, clean agricultural production and organic agricultural products are not allowed to excessively use synthetic chemicals such as chemical fertilizers, and plant protection drugs, but priority is to use manure, organic fertilizers, and natural mineral fertilizers. Fertilizer must meet the balanced nutritional requirements of crops, maintain, and improve the fertility of the ground, protect the surrounding ecosystem, and leave harmful effects in agricultural products, products with high quality, safe for users and high economic efficiency for producers. To achieve the above goal, the selection of a fertilizer supplier is an important decision, supporting the supply chain's sustainable development, fertilizer supplier selection is a multicriteria decision making model, the decision maker must assess all qualitative and quantitative factors. In this paper, the author proposed an integer decision making model including Fuzzy Analytic Hierarchy Process (FAHP) and Complex Proportional Assessment of Alternatives (COPRAS) for fertilizer supplier selection. The weightings of the criteria are calculated by using FAHP, COPRAS is then applied for ranking some potential fertilizer suppliers. The efficiency of the proposed models is proved by a case study conducted in a farm located in the south of Vietnam. This research is the first fertilizer supplier evaluation and se-lection model in Vietnam by interviewing experts and reviewing the literature. Re-search result is to provide a case study on evaluating supplier in agricultural supply chain utilizing the model proposed by the combination of FAHP and COPRAS models.

Keywords: Fertilizer industry; optimization model; fuzzy theory; agricultural supply chain

1  Introduction

Over the years, the agricultural sector of Vietnam has always affirmed its position of contributing to the country's economy. Vietnam's policies have proven to be appropriate and motivated to promote the potentials and advantages of Vietnam's agriculture, turning Vietnam from a food aid recipient to one of food exporter [1]. Vietnam is a developing country; agriculture still plays an important role in the economy today. However, Vietnam's agricultural production is facing many challenges: Due to the increasing population, the demand for food is constantly increasing; agricultural land area is shrinking due to urbanization, so it is necessary to increase agricultural productivity to meet food security; Climate change is taking place strongly, creating great pressure for our country's agriculture; the process of international integration requires higher quality agricultural products [2].

The global supply chain is posing a series of challenges for businesses, including the origin of goods, trade barriers and trade defense mechanisms. Sustainable development requires businesses to form a supply chain of green products and services, and through that change consumer habits [3]. According to the Food and Agriculture Organization of the United Nations FAO, sustainable agricultural development is the process of managing and sustaining organizational, technical and institutional change in agricultural development to meet the growing demand for agricultural products of people in terms of agricultural products and services now and in the future. This development does not harm the environment, does not degrade natural resources in accordance with technology and brings economic efficiency that is acceptable to society [4].

In the context that Vietnamese agriculture is being strongly affected by global climate change today, the issue of synchronous and balanced fertilizer use becomes even more important. However, agricultural production has not paid due attention to environmental protection for a long time. Clean agricultural production, improving the quality of agricultural products to ensure food hygiene and safety and being environmentally friendly are the goals of both the agricultural industry in general and farmers in particular. In agricultural production activities, fertilizer is an important agricultural input and is used quite a lot every year. Fertilizers have contributed significantly to increase crop yield and quality of agricultural products. According to the International Plant Nutrition Institute (IPNI), fertilizers contribute about 30%–35% of total crop production. However, if used incorrectly, it is one of the agents that pollute the agricultural production and living environment [5].

Therefore, choosing the optimal fertilizer supplier is an important task, contributing to ensuring the efficient operation of the agricultural supply chain, and supporting the goal of developing a sustainable supply chain. However, finding proper suppliers involves several variables and it is critically a complex process. This research provides a decision-making tool to solve a fertilizer supplier selection in agricultural supply chain. First, fuzzy analytic hierarchy process (FAHP) is used to calculate the weights to each criterion separately and the final ranking is achieved by Complex Proportional Assessment of Alternatives (COPRAS) for fertilizer supplier selection. This paper has several interrelated objectives. The first aim of this research refers to the development and detailed description of the new fuzzy multicriteria decision making model. The second aim is to improve the efficiency of single MCDM model through hybrid fuzzy MCDM model including fuzzy analytic hierarchy process and Complex Proportional Assessment of Alternatives (COPRAS).

2  Literature Review

The selection of suppliers is a constant process that requires the consideration of a certain number of criteria needed to make a decision on the selection of the most suitable suppliers [6–8]. The supplier selection, according to many authors, is one of the most demanding problems of sustainable supply chain management [9]. Decision-making in the supplier selection domain, as an essential component of the supply chain management, is a complex process since a wide range of diverse criteria, stakeholders and possible solutions are embedded into this process [10].

Liu et al. [11] integrated MCDM model for sustainable supplier selection under interval-valued intuitionistic uncertain linguistic environment. Koganti et al. [12] proposed a MCDM model including Grey Relational Analysis (GRA), Analytical Hierarchy Process (AHP) and Technique for Order Performance by Similarity to Ideal Solution (TOPSIS) for supplier evaluation and selection. Wang et al. [13] provide a new MCDM model for decision-makers in evaluating and selecting suppliers in plastic industry, which is formulated based on the supply chain operation reference (SCOR) model, fuzzy analytic network process (FANP), and VIseKriterijumska Optimizacija I Kompromisno Resenje (VIKOR).

Yazdani et al. [14] showed that supplier evaluation and selection is an important decision for minimizing operational costs and maintaining organizational competitiveness for the purpose of developing business opportunities. Therefore, the author proposed Integrated QFD-MCDM framework for green supplier selection. Jain et al. [15] proposed an integrated fuzzy MCDM techniques for sustainable supplier selection. In this study, they used fuzzy AHP and TOPSIS model. Ghorbani et al. [16] proposes a three-phase approach for supplier selection based on the Kano model and fuzzy MCDM model. Sobhan et al. [17] addressed a critical issue of selection of supplier occurred in supply chain of a manufacturing company. In this project, the authors proposed paper proposes a MCDM method using Decision Making Trial and Evaluation Laboratory (DEMATEL) based on Analytic Network Process (ANP).

Banaeian et al. [18] used fuzzy group decision making methods for green supplier selection for an actual company from the agri-food industry. The incorporation of fuzzy set theory into TOPSIS, VIKOR and GRA methods is thoroughly discussed in this study. Singh et al. [19] applied big data cloud computing framework for a suitable supplier selection in the beef supply chain. The proposed framework would show results in shedding the environmental conduction of beef supply chain as the highest maintainable carbon footprint generated in beef farms.

Cheraghalipour et al. [20] proposed a strong a strong approach, namely best worst method (BWM) along with a well-known MCDM technique with the name of VIKOR for supplier selection in the Iranian agricultural implements industry. Wakeel [21] proposed a hybrid Entropy-Range of Value MCDM Technique for supplier selection in a semiconductor industry.

As literature review, multi-criteria decision-making model is widely applied in many different fields, but there are very few works using the MCDM based on fuzzy sets to develop a decision support system in agricultural supply chain management. Thus, the author proposed fuzzy MCDM model in fuzzy AHP and COPRAS model for fertilizer evaluation and selection in this research.

3  Methodology

This paper introduces a Fuzzy Multi-Criteria Decision-Making (F-MCDM) model for deciding the optimal sustainable supplier in agricultural supply chain using the FAHP and COPRAS methods. This research involves three main steps, as shown in Fig. 1:

Figure 1: Research processes

Step 1: Identifying all criteria and sub-criteria effecting the fertilizer supplier selection process through interviewing experts and literature review.

Step 2: FAHP is a general form of the decentralized process, which includes the feedback and interdependencies of decision attributes and alternatives. FAHP is employed to determining the weights of the identified criteria.

Step 3: The FAHP can be applied for ranking alternatives, but the of selection several suppliers is practically limited because of the number of pairwise comparisons that need to be made, and a disadvantage of the FAHP model is that input data, expressed in linguistic terms, depend on the experience of decision makers, and thus involve subjectivity. Thus, we proposed the COPRAS model to rank alternatives in the final stage. COPRAS model is applied to rank all the alternatives. The decision maker will use this ranking to support the decision-making process.

3.1 Fuzzy Theory

The Triangular Fuzzy Number (TFN) can be symbolized as (k, h, g), with k, h, and g (k ≤h ≤ g) are parameters that determines the smallest likely value, the most likely value and the highest possible value in TFN. TFN are shown in Fig. 2 and can be described as:

μ(xM~)={0,x−kh−kg−xg−h0, x<h,k≤x≤h,h≤x≤g,x>g,(1)

Figure 2: Triangular fuzzy number

A fuzzy number is given as:

M~=(Mo(y),Mi(y))=[k+(h−k)y,\; g+(h−g)y],y ∈[0,1](2)

With o(y)andi(y) showing the left-hand side and the right-hand side of a fuzzy value, respectively. The below shows basic calculations involve two positive TFN, (k1, h1, g1)and(k2, h2, g2).

(k1, h1, g1)+(k2, h2, g2)=(k1+k2, h1+h2,g1+g2)(k1, h1, g1)−(k2, h2, g2)=(k1−k2, h1−h2,g1−g2)(k1, h1, g1)×(k2, h2, g2)=(k1×k2, h1×h2,g1×g2)(k1, h1, g1)(k2, h2, g2)=(k1/k2, h1/h2,g1/g2)(3)

3.2 Fuzzy Analytic Hierarchy Process (FAHP)

Fuzzy Analytical Hierarchy Process (FAHP) is an extension of AHP that utilizes Fuzzy set theory to calculate its limitation in working with uncertain decision-making environments. Let X={x1,x2,…,xn} be the set of objects and K={k1,k2,…,kn} be the final suitable set. According to Chang [22] extent analysis method, for each value taken, an extent analysis of its final solution is calculated. Therefore, the l extent analysis values for each object can be obtained. These values are denoted as:

Lki1,Lki2,…,Lkim,i=1,2,…,n(4)

where Lkj(j=1,2,…,m) are the TFNs

Fuzzy synthetic extent value of the ith object is defined as:

Si=∑j=1m⁡Lkij⊗[∑i=1n⁡∑j=1m⁡Lkij]−1(5)

The possibility that L1≥L2 is defined as:

V(L1≥L2)=supy≥x[min(μL1(x),),(μL2(y))](6)

where the pair (x,y) exists with x≥y and μL1(x)=μL2(y), then we have V(L1≥L2)=1.

Since L1 and L2 are convex fuzzy numbers, we have:

V(L1≥L2)=1,ifl1≥l2(7)

And

V(L2≥L1)=hgt(L1∩L2)=μL1(d)(8)

where d is the ordinate of the highest intersection point D between μL1 and μL2

With L1=(o1,p1,q1) and L2=(o2,p2,q2), the ordinate of point D is calculated by (9):

V(L2≥L1)=hgt(L1∩L2)=l1−q2(p2−q2)−(p1−o1)(9)

In order to compare L1 and L2, we need to calculate the values of V(L1≥L2) and V(L2≥L1).

The possibility for a convex fuzzy number to be greater than k convex fuzzy numbers Li(i=1,2,…,k) is calculated as:

V(L≥L1,L2,…,Lk)=V[(L≥L1)and(L≥L2)](10)

and, (L≥Lk)=minV(L≥Li),i=1,2,…,k

Under the assumption that:

d′(Bi)=minV(Si≥Sk),(11)

for k=1,2,…,nandk#i, the weight vector is determined as:

W′=(d′(B1),d′(B2),…,d′(Bn))T,(12)

where Bi are n elements.

The Normalized weight vectors are shown as:

W=(d(B1),d(B2),…,d(Bn))T(13)

With W is a nonfuzzy number.

An evaluation of a Saaty's matrix is used to test for its consistency.

CR=CIRI=λ¯−n(n−1)×RI≤0.1(14)

where:

•Consistency Ratio (CR);

•Consistency Index (CI);

•Random Index (RI).

3.3 COPRAS Method

The methodology follows of the proposed steps [23]:

Step 1: Determining and selecting contributing criteria (attributes) and the available options

First the attributes which are contributing to the decision in the MCDM problem are determined and the available options are chosen.

Step 2: Prepare the decision matrix between options vs. attributes (X)

The gathered data (options and attributes) are layered in matrix formation as shown in Eq. (15)

X=[x11x12…x1mx21x22…x2m⋮⋮⋮xn1xn2xnm](15)

where n = number of options; m = number of attributes

Step 3: Normalization of decision matrix (X¯)

The normalization of the decision is shown in Eq. (16).

X¯=[ x¯11x¯21⋮x¯n1x¯12x¯22⋮x¯n2…x¯1m…x¯2m⋮x¯nm](16)

where x¯ij=xij∑i=1n⁡xij; I = 1, 2, …, n; and j = 1, 2, …, m

Step 4: Calculation of the weighting of the attributes (Wj)

The attributes’ weightings are calculated by using FAHP calculations.

Step 5: Calculation of the overall normalized matrix (X^)

The calculated weights are multiplied across corresponding attribute value of all options to get the overall normalized matrix.

X^=[ x^11x^21⋮x^n1x^12x^22⋮x^n2…x^1m…x^2m⋮x^nm](17)

where X^ij=x¯ij∗Wj

Step 6: Determination of maximizing index (Pj) and minimizing index (Rj)

Based on the qualitative nature of the attribute, the maximizing index (Pj) and minimizing index (Rj) values are determined. Attribute Pj is determined if it is a maximizing index. Rj will be calculated for minimizing index.

Pj=∑i=1k⁡x^ij(18)

Rj=∑i=k+1m⁡x^ij(19)

where k = number of attributes which is to be maximized

Step 7: Calculation of relative weights of each option (Qj)

Finally, all the attributes overall relative weighting will be determined.

Qj=Pj+∑j=1n⁡RjRj∑j=1n⁡1Rj(20)

The alternative with the highest relative weights is considered as the best alternative.

4  Case Study

From a country that has to depend on imported fertilizers, in the past 30 years, Vietnam's fertilizer industry has made strong progress, taking the initiative in supplying and even exporting products to more 20 countries in the world. Although it has met most of the needs of the domestic market, over the past time, many Vietnamese fertilizer factories have only focused on quantity, not really paying attention to improving product quality and environmental factors [24]. In this paper, the author proposed an integer decision making model including Fuzzy Analytic Hierarchy Process (FAHP) and Complex Proportional Assessment of Alternatives (COPRAS) for fertilizer supplier selection in agricultural supply chain.

In the first step of this research, all criteria and sub-criteria effecting the fertilizer supplier selection process are identified through interviewing experts and literature review. A hierarchy of criteria is shown in Tab. 1.

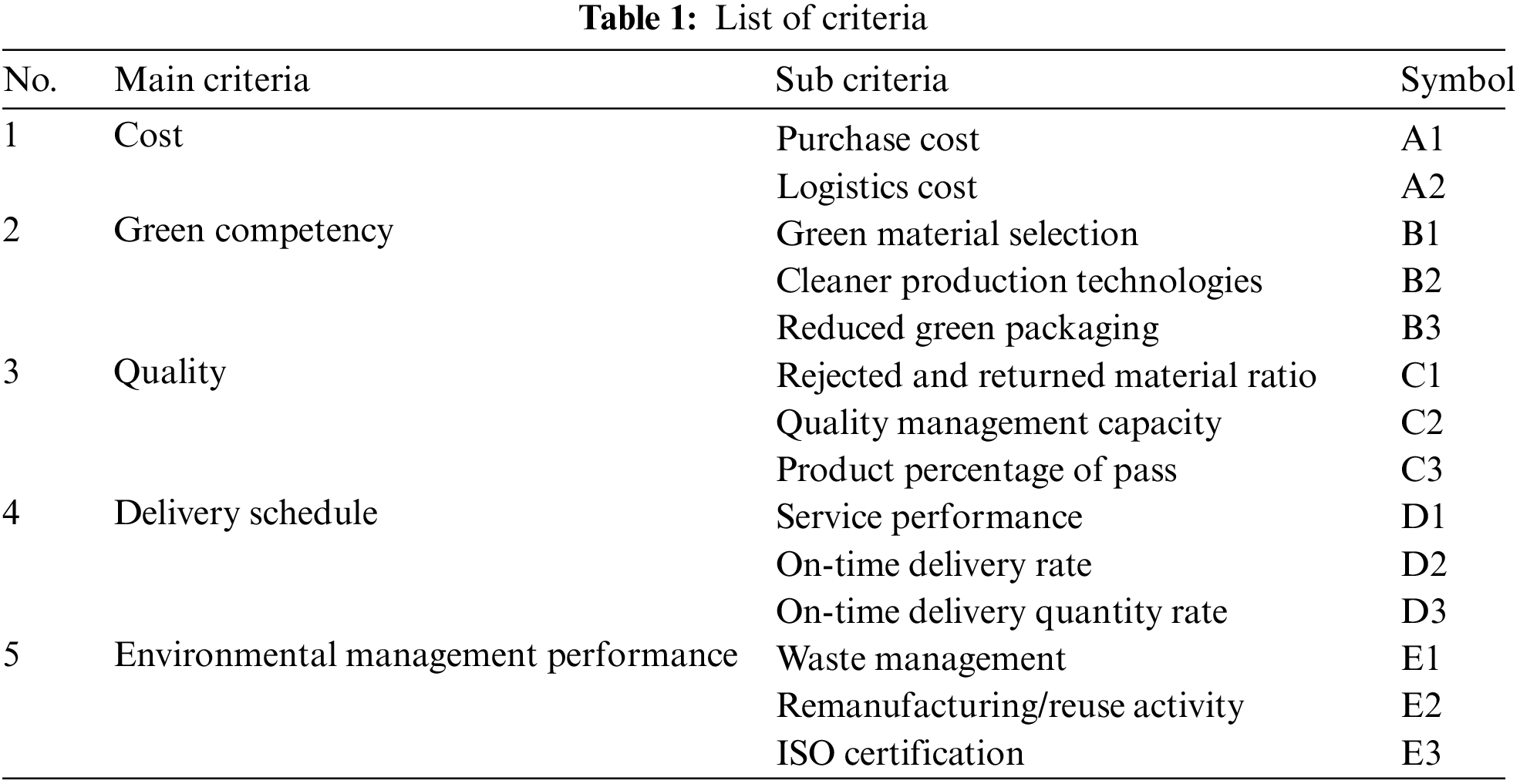
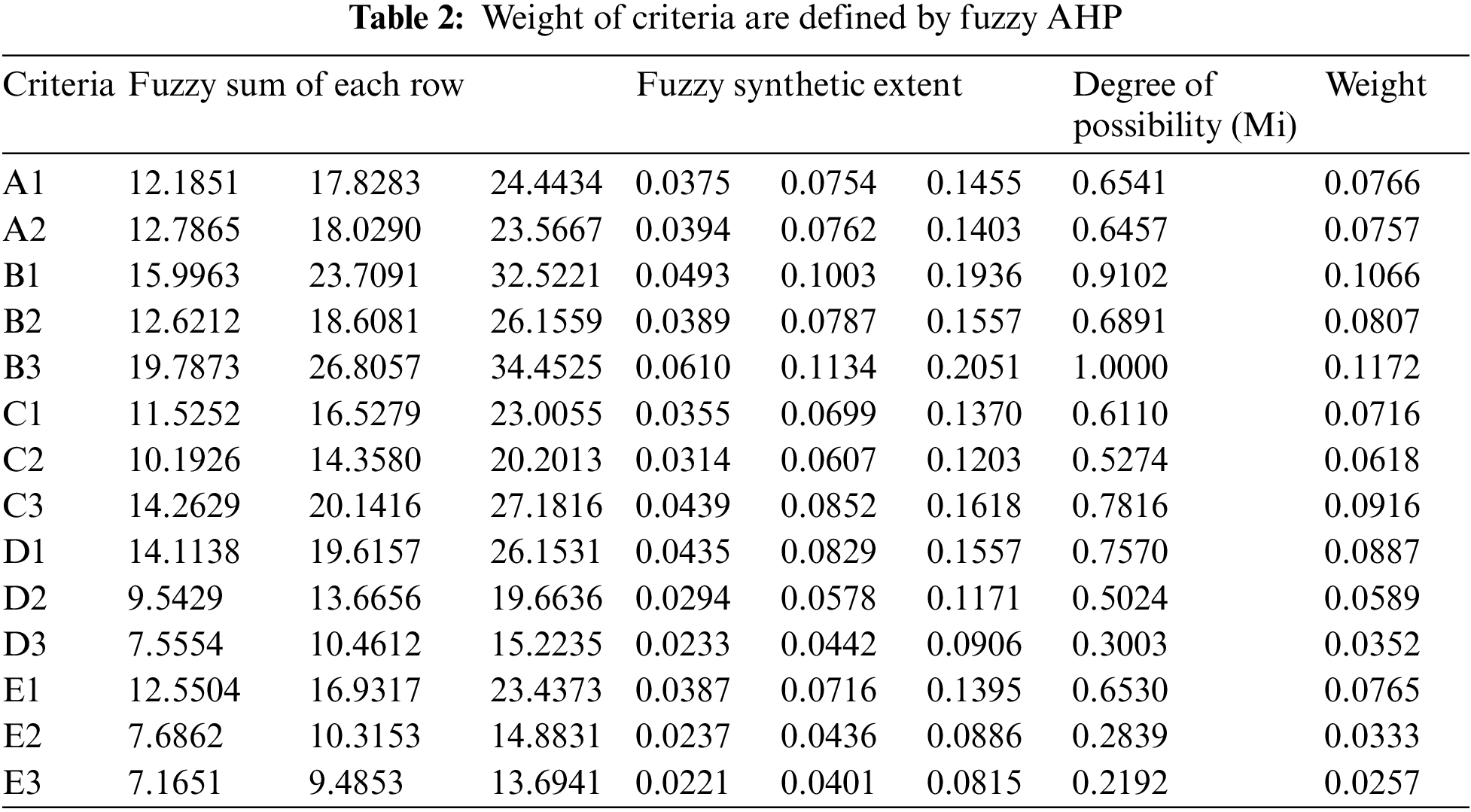
The Fuzzy Analytic Hierarchy Process (FAHP) is a method for organizing and analyzing complex decisions, using math and psychology. It was developed by Thomas L. Saaty in the 1970s and has been refined since then. The weights of the criteria are calculated by using FAHP in second stage. Results of FAHP is shown in Tab. 2.

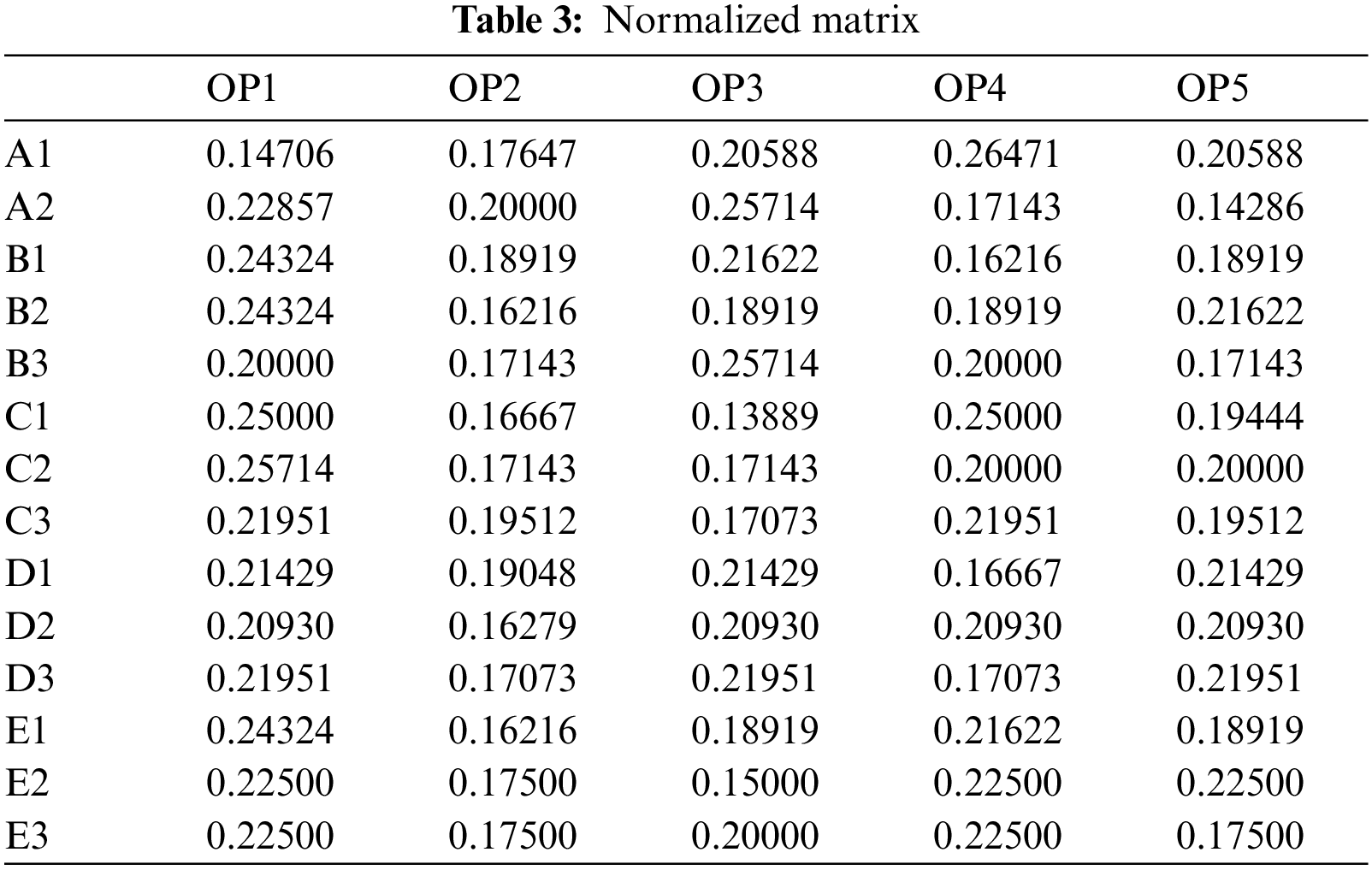
In the final stage of this study, COPRAS is applied to rank all the alternatives. The decision maker will use this ranking to support the decision-making process. Normalized matrix and Weight normalized matrix of COPRAS are shown Tabs. 3 and 4.

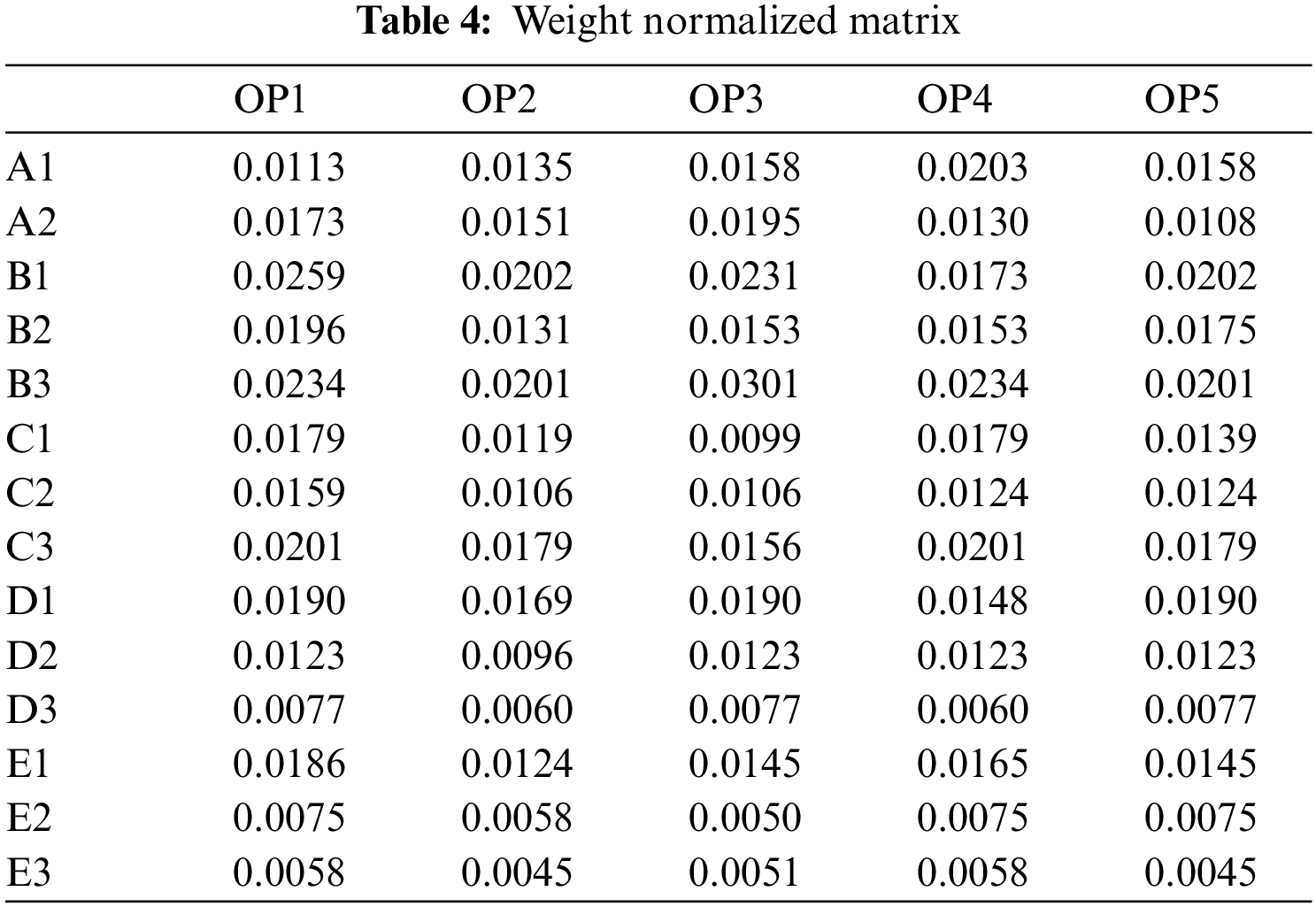
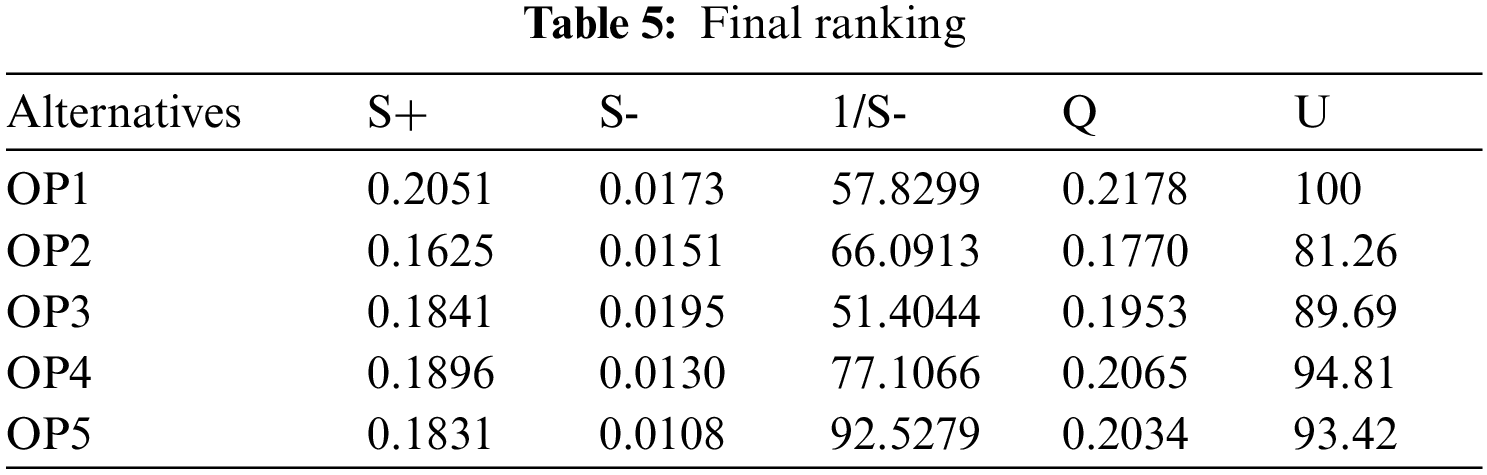
The option with the highest relative weighting overall in all aspects is considered as the optimal option for the selection process. As results from Tab. 5, OP1 is optimal supplier in this case study.

5  Conclusion

In the context of the continuously changing economy, agricultural development needs to focus on connecting supply chains, building brands of agricultural products, and locating the value of Vietnamese agricultural products in the agricultural global market. Developing the sustainable agricultural supply chain will help increase the export of goods by easily meeting the technical and phytosanitary standards of the importing country, helping to control export products of enterprises better, especially towards environmental protection. Selecting the optimal fertilizer supplier is an important task, contributing to ensuring the efficient operation of the agricultural supply chain, and supporting the goal of developing a sustainable supply chain. In this research, the author proposed a fuzzy multicriteria decision making model (FMCDM) including Fuzzy Analytic Hierarchy Process (FAHP) and Complex Proportional Assessment of Alternatives (COPRAS) for fertilizer supplier selection. The model was also utilized in a suitable case. It is an important study in the agricultural supply chain, and it can be extended to optimize the supplier selection in other industries.

However, the number of criteria is currently limited in this research. Thus, the authors should consider more criteria in the supplier selection process in the future. Particular attention should be paid to the sustainable development factor, which is evaluating sustainability, which is increasing rapidly with the expansion of the period of industrialization and modernization

Funding Statement: The authors wish to express their gratitude to Van Lang University, Vietnam for financial support for this research.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  V. T. Le and T. T. Nguyen. (2020, December 21th). “Chuỗi cung ứng sản xuất nông nghiệp việt Nam,” [Online]. Available: https://ictvietnam.vn/chuoi-cung-ung-san-xuat-nong-nghiep-viet-nam-20201225145426779.htm. [Google Scholar]

 2.  T. Tran. (2021, April 18th). “Thực trạng phát triển nông nghiệp cao ở việt Nam,” [Online]. Available: https://tapchicongthuong.vn/bai-viet/thuc-trang-phat-trien-nong-nghiep-cao-o-viet-nam-70642.htm. [Google Scholar]

 3.  Open Development Vietnam. (2019, Octobor 22th). “Phát triển bền vững là chìa khóa để tham gia chuỗi cung ứng toàn cầu,” [Online]. Available: https://vietnam.opendevelopmentmekong.net/vi/news/sustainable-development-key-to-joining-global-chain/. [Google Scholar]

 4.  A. Nguyen. (2021, December 14th). “Phát triển kinh tế nông nghiệp bền vững và thích ứng biến đổi khí hậu,” [Online]. Available: https://amp.tapchicongthuong.vn/bai-viet/phat-trien-kinh-te-nong-nghiep-ben-vung-va-thich-ung-bien-doi-khi-hau-tai-dong-bang-song-cuu-long-85863.htm. [Google Scholar]

 5.  ĐCSVN. “Sử dụng phân bón đồng bộ cho phát triển nông nghiệp bền vững,” 2014. [Online]. Available: https://dangcongsan.vn. [Google Scholar]

 6.  Ž Stević, M. Vasiljević, A. Puška, I. Tanackov, R. Junevičius et al., “Evaluation of suppliers under uncertainty: A multiphase approach based on fuzzy AHP and fuzzy EDAS,” Transport, vol. 34, pp. 34, 2019. [Google Scholar]

 7.  I. Badi and M. Ballem, “Supplier selection using the rough BWM-MAIRCA model: A case study in pharmaceutical supplying in Libya,” Decis. Mak. Appl. Manag. Eng., vol. 1, pp. 16–33, 2018. [Google Scholar]

 8.  I. Badi, A. Abdulshahed and A. Shetwan, “A case study of supplier selection for steelmaking company in Libya by using combinative distance-based Assessemnt (CODAS) model,” Decis. Mak. Appl. Manag. Eng., vol. 1, pp. 1–12, 2018. [Google Scholar]

 9.  G. M. Keshavarz, M. Amiri, E. K. Zavadskas and J. Antucheviciene, “Supplier evaluation and selection in fuzzy environments: A review of MADM approaches,” Econ. Res. Ekon, vol. 30, pp. 1073–1118, 2017. [Google Scholar]

10. G. Petrović, J. Mihajlović, Ž Ćojbašić, M. Madić and D. Marinković, “Comparison of three fuzzy mcdm methods for solving the supplier selection problem,” Facta Universitatis, Series: Mechanical Engineering, vol. 17, no. 3, pp. 455, 2019. [Google Scholar]

11. H. Liu, M. Quan, Z. Li and Z. Wang, “A new integrated MCDM model for sustainable supplier selection under interval-valued intuitionistic uncertain linguistic environment,” Information Sciences, vol. 486, pp. 254–270, 2019. [Google Scholar]

12. V. Koganti, N. Menikonda, S. Anbuudayasankar, T. Krishnaraj, R. Athhukuri et al., “GRAHP TOP model for supplier selection in supply chain: A hybrid MCDM approach,” Decision Science Letters, vol. 8, no. 1, pp. 65–80, 2019. [Google Scholar]

13. N. Wang, N. Thanh, T. Chyou, F. Lin and T. Nguyen, “Fuzzy multicriteria decision-making model (mcdm) for raw materials supplier selection in plastics industry,” Mathematics, vol. 7, no. 10, pp. 981, 2019. [Google Scholar]

14. M. Yazdani, P. Chatterjee, E. Zavadskas and S. Hashemkhani Zolfani, “Integrated QFD-MCDM framework for green supplier selection,” Journal of Cleaner Production, vol. 142, pp. 3728–3740, 2017. [Google Scholar]

15. N. Jain, A. Singh and R. Upadhyay, “Sustainable supplier selection under attractive criteria through FIS and integrated fuzzy MCDM techniques,” International Journal of Sustainable Engineering, vol. 13, no. 6, pp. 441–462, 2020. [Google Scholar]

16. M. Ghorbani, S. Mohammad Arabzad and A. Shahin, “A novel approach for supplier selection based on the kano model and fuzzy MCDM,” International Journal of Production Research, vol. 51, no. 18, pp. 5469–5484, 2013. [Google Scholar]

17. S. Sobhan, L. Vishal, A. Irshad and M. Jhareswar, “Supplier selection in uncertain environment: A fuzzy mcdm approach,” Advances in Intelligent Systems and Computing, vol. 458, pp. 257–266, 2016. [Google Scholar]

18. N. Banaeian, H. Mobli, B. Fahimnia, I. Nielsen and M. Omid, “Green supplier selection using fuzzy group decision making methods: A case study from the agri-food industry,” Computers & Operations Research, vol. 89, pp. 337–347, 2018. [Google Scholar]

19. A. Singh, S. Kumari, H. Malekpoor and N. Mishra, “Big data cloud computing framework for low carbon supplier selection in the beef supply chain,” Journal of Cleaner Production, vol. 202, pp. 139–149, 2018. [Google Scholar]

20. A. Cheraghalipour, M. Paydar and M. Keshteli, “Applying a hybrid BWM-VIKOR approach to supplier selection: A case study in the Iranian agricultural implements industry,” International Journal of Applied Decision Sciences, vol. 11, no. 3, pp. 274, 2018. [Google Scholar]

21. S. Wakeel, S. Ahmad, S. Bingol, M. Bashir, T. Pacal et al., “Supplier selection for high temperature die attach by hybrid entropy-range of value mcdm technique: A semiconductor industry,” in 21st Int. Conf. on Electronic Packaging Technology (ICEPT), In Dalian, China. 2020. [Google Scholar]

22. D. Chang, “Extent analysis and synthetic decision,” Optimization Techniques and Applications, vol. 1, no. 1, pp. 352–355, 1992. [Google Scholar]

23. P. Pitchipoo, D. Vincent, N. Rajini and S. Rajakarunakaran, “Copras decision model to optimize blind spot in heavy vehicles: A comparative perspective,” Procedia Engineering, vol. 97, pp. 1049–1059, 2014. [Google Scholar]

24. Quatest3. (2021, September 19th). “Nâng cao chất lượng sản phẩm phân bón, hướng đến phát triển bền vững-QUATEST 3,” [Online]. Available: http://www.quatest3.com.vn/nang-cao-chat-luong-san-pham-phan-bon-huong-den-phat-trien-ben-vung. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.