Computers, Materials & Continua DOI:10.32604/cmc.2022.026185
Article

A Sparse Optimization Approach for Beyond 5G mmWave Massive MIMO Networks

Waleed Shahjehan1, Abid Ullah1, Syed Waqar Shah1, Imran Khan1, Nor Samsiah Sani2 and Ki-Il Kim3,*

1Department of Electrical Engineering, University of Engineering and Technology Peshawar, Pakistan
2Center for Artificial Intelligence Technology, Faculty of Information Science & Technology, Universiti Kebangsaan, Kajang, 43000, Malaysia
3Department of Computer Science and Engineering, Chungnam National University, Daejeon, 34134, Korea
*Corresponding Author: Ki-Il Kim. Email: kikim@cnu.ac.kr
Received: 17 December 2021; Accepted: 24 January 2022

Abstract: Millimeter-Wave (mmWave) Massive MIMO is one of the most effective technology for the fifth-generation (5G) wireless networks. It improves both the spectral and energy efficiency by utilizing the 30–300 GHz millimeter-wave bandwidth and a large number of antennas at the base station. However, increasing the number of antennas requires a large number of radio frequency (RF) chains which results in high power consumption. In order to reduce the RF chain's energy, cost and provide desirable quality-of-service (QoS) to the subscribers, this paper proposes an energy-efficient hybrid precoding algorithm for mmWave massive MIMO networks based on the idea of RF chains selection. The sparse digital precoding problem is generated by utilizing the analog precoding codebook. Then, it is jointly solved through iterative fractional programming and successive convex optimization (SCA) techniques. Simulation results show that the proposed scheme outperforms the existing schemes and effectively improves the system performance under different operating conditions.

Keywords: 5G; mmwave precoding; massive mimo; complexity

1  Introduction

The fifth generation of mobile communications (5G) intends to use millimeter-wave frequency bands to provide higher system capacity for users in hot spots [1]. Millimeter-wave is considered as one of the key technologies to solve the capacity demand in the fifth-generation (5G) mobile communication system due to its large number of unused frequency bands [2]. The millimeter-wave has a shorter wavelength, so the base station can configure more antennas with a smaller physical array size [3]. In the traditional pure digital baseband precoding scheme, each antenna has a corresponding baseband and radio frequency (RF) link structure [4]. These RF links are not only costly but also consume large power and it is impractical. Compared with the microwave band, the aperture of antenna elements in the millimeter-wave band is usually smaller, and a large number of antenna elements can be integrated at the transmitting end of the millimeter-wave system, thereby using multiple-input multiple-output (MIMO) technology to improve antenna gain through beamforming; at the same time, can solve the problem of high path loss and attenuation in the millimeter-wave band, it also precode multiple data streams for multiple users, improving the spectral efficiency of the system [5–8]. Generally, microwave band communication systems are precoded at the baseband by digital signal processing (DSP) units. However, due to the hardware cost and power constraints in a millimeter-wave system, the system cannot configure an RF link for each antenna, so it is difficult to achieve pure digital precoding [9,10]. In order to achieve spatial multiplexing, a hybrid precoding algorithm using fewer RF chains has become a cost-saving and power-saving alternative to millimeter-wave MIMO systems [11]. In this hybrid structure, analog precoding is used to provide beamforming gain, and digital precoding is used to provide multiplexing gain. In order to solve the above problems, academia proposes to adopt a hybrid digital/analog precoding structure in a millimeter-wave MIMO system [8]. Hybrid digital/analog precoding at the transmitting end maps the data stream to baseband digital precoding processing and maps it to each RF link. Then, a constant mode phase shifter adjusts the phase of the signal on each RF link to complete the analog precoding. In this structure, the number of RF links is much smaller than the number of antennas, thereby reducing the hardware requirements of the communication system without causing a significant loss to the system performance [9,10].

In recent years, due to energy shortages and the effects of the greenhouse effect, the energy consumption of communication systems has also received widespread attention. Energy efficiency as a performance indicator weighing system capacity and system energy consumption has become one of the hotspots in future wireless communication research [5]. At present, there is a large amount of literature that has extensively studied the energy efficiency optimization problem in mmWave MIMO systems. For example, the authors in [12] proposed a beamforming scheme with optimal energy efficiency in a multi-user MISO scenario. The reference [13] design an iterative algorithm to optimize energy efficiency under the interfered with the broadcasting channel.

However, the proposed new hybrid precoding structure under the mmWave communication system brings more new difficulties to the energy efficiency optimization problem:

1) The constant mode limit of the analog precoder brings non-convex limits to the original target problem;

2) The number of RF links has a great impact on the energy efficiency of the system [14], but because its value is directly related to the dimensions of the analog precoding matrix and the digital precoding matrix, therefore, it is difficult to obtain its optimal solution through numerical analysis.

Although there are currently limited literature focusing on energy efficiency optimization problems in mmWave hybrid precoding systems, for example, in [15], given the number of RF links, the energy efficiency optimization problem of mmWave hybrid precoding is transformed into a Euclidean solution. For the problem with the smallest distance, use the orthogonal matching pursuit (OMP) algorithm to obtain the approximate optimal value of the original problem. Reference [16] also uses the OMP method to obtain the optimal value of system energy efficiency after traversing each possible number of RF links. However, the above literature ignores the difficulty 2), and the preset number of RF links is used, which increases the difficulty of solving. Doing so, on the one hand, ignores the impact of the number of RF links on the energy efficiency of the system; on the other hand, when there are a large number of antennas, exhaustively searching for each possible number of RF links will be very time-consuming.

Based on the above research status, this paper proposes an energy efficiency optimization scheme based on RF link selection in a multi-user mmWave MIMO system. Because the original problem is difficult to solve directly, first a preset analog precoding codebook is introduced to convert the problem equivalently to solving sparse digital precoding [17,18], while the analog precoding is an NRF selected from the codebook codeword, where NRF is the optimal number of RF links. Then, since the transformed problem is still a non-convex non-linear problem, we use sequential convex approximation (SCA) theory and Dinkelbach’s theory to turn the problem into a convex problem and solve iteratively. Simulation results show that the performance of the proposed algorithm is very close to the performance of the exhaustive method, and is much higher than the performance of the equal gain transmission (EGT) [19] and other existing algorithms.

The rest of the paper is organized as follows. In Section 2, the system model is described. In Section 3, the proposed algorithms and their principle are analyzed. Section 4 provides the simulation results, while Section 6 concludes the paper.

2  System Model

2.1 Channel Model

Consider the mmWave single-cell downlink scenario, as shown in Fig. 1. The system consists of K single-antenna users and a base station with Nt antennas. The number of RF links at the base station is NRF, and its value range is [K,Nt]. The base station uses a fully connected hybrid digital/analog precoding structure, including a NRF×K baseband digital precoder WBB and an Nt×NRF analog precoder WRF composed of a constant-mode phase shifter.

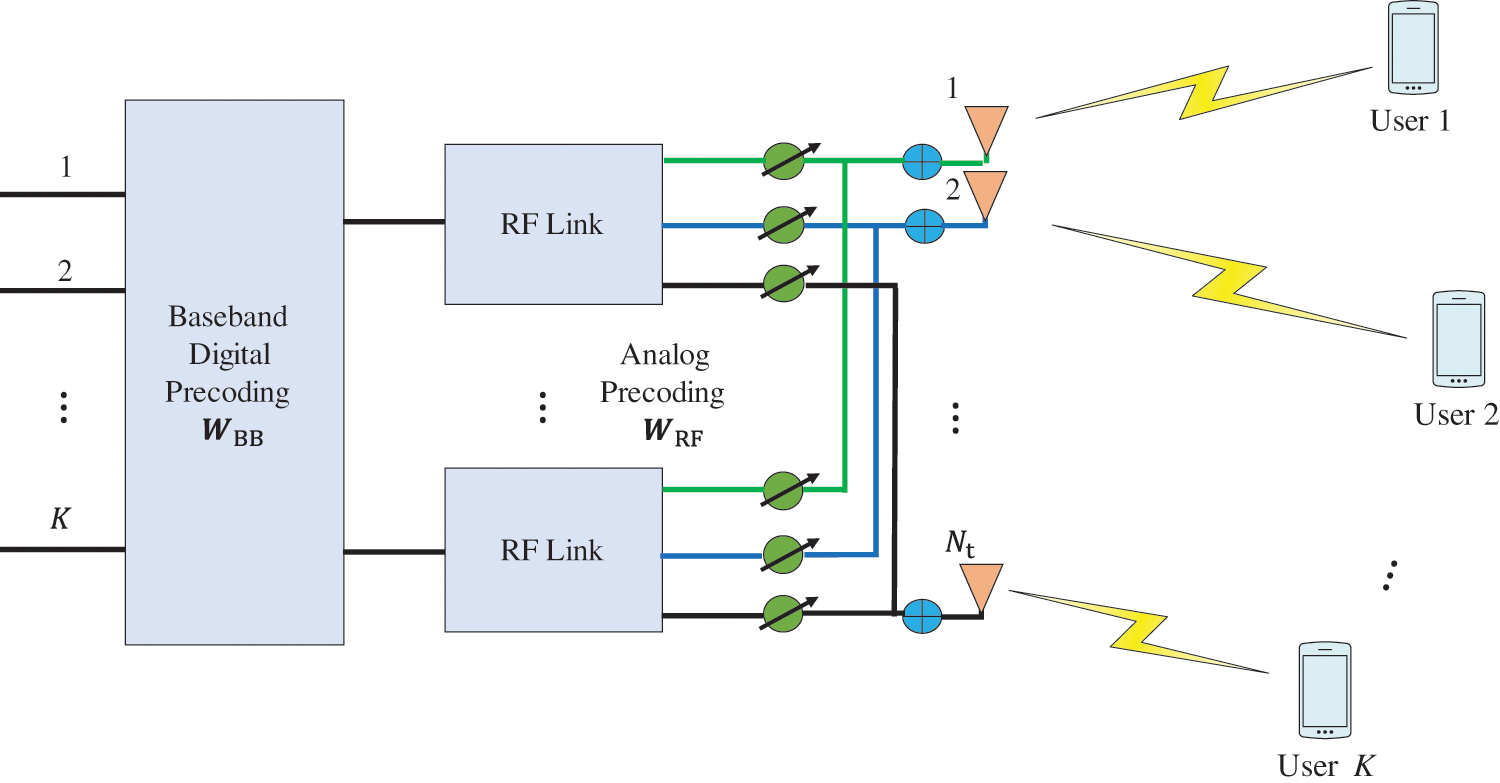
Figure 1: System model

The signal received by the kth user can be expressed as

yk=hkHWRFWBBS+nk(1)

where S=[s1,s2,…,sK]T; sk∼CN(0,1) represents the signal transmitted to the kth user. nk∼CN(0,σ2Ik) is an independent and identically distributed additive Gaussian white noise with a mean of 0 and a variance of σ2. The channel from the base station to the K users is H=[h1,h2,…,hK]H, where hk represents the downlink channel from the base station to the kth user. In this paper, the Saleh-Valenzuela model based on angular expansion is used to characterize mmWave channels [9], which is currently widely used in the research of mmWave hybrid precoding. The downlink channel from the base station to the kth user can be expressed as

hk=NtρkNray∑i=1Nrayαkiu(φi,θi)(2)

where Nray is the number of multipath from the base station to K users; ρk=ξ/rkκ is a large-scale attenuation factor; ξ is a random number that obeys the normal distribution, with a mean value of 0 and a variance of 9.7 dB [20]; rk is the distance between the base station and the kth user; κ is the path loss index; αki is the complex gain of the ith transmission path from the base station to the kth user; φi and θi are the azimuth and elevation angles of the antenna, respectively, and obey the uniform distribution in the range [−π2,π2]. u(φi,θi) represents the transmitting antenna array response vector, which is expressed as

u(φi,θi)=1Nt[1,ej2πλd(psin⁡φisin⁡θi+qcos⁡θi),…,ej2πλd((Nt−1)sin⁡φisin⁡θi+(Nt−1)cos⁡θi)](3)

where λ is the signal wavelength and d is the separation between the antenna elements which is half the wavelength. p and q are the indexes of the antenna in the 2D plane. This article uses a square array, so there are 0≤p≤Nt−1 and 0≤q≤Nt−1.

2.2 Energy Consumption Model

Because the base station accounts for the main power consumption in mobile communication systems, this article does not consider the user's power consumption. The total power consumption of a base station usually includes signal transmission power consumption and circuit power consumption, so the general power consumption model of a mmWave communication system [8] is

Ptotal=1εPt+NRFPRF+Pc(4)

where the coefficient ε<1 of the power amplifier is a constant; Pt is the transmission power consumption and has Pt=‖WRFWBB‖F2. For the sake of convenience, all power consumption unrelated to the transmission power consumption Pt is represented as the circuit power consumption, which includes the dynamic circuit power consumption NRFPRF caused by the radio frequency link, and the basic power at the base station end which is independent of the number of antennas and radio frequency links consume Pc. PRF refers to the power consumption of RF devices, including the sum of all power consumption of the transmit filter, mixer, frequency synthesizer, and A/D and D/A converters.

3  Proposed Hybrid Precoding Algorithm

3.1 Problem Formulation

The energy efficiency optimization problem under the above millimeter-wave system model can be modeled as follows

maxWRF,WBB,NRFRsumPtotal

Subject to |WRF(i,j)|2=1Nt

Rk≥γk,∀k=1,2,…,K

∑k=1K‖WRFWBB,k‖2≤Pmax

NRF≥K(5)

where Pmax is the maximum transmit power; Rk is the rate of the kth user, which can be expressed as

Rk=log2⁡(1+hkWRFWBB,kWBB,kHWRFHhkH∑i=1,i≠kKhkWRFWBB,iWBB,iHWRFHhkH+σ2)(6)

The user’s sum rate is Rsum=∑k=1KRk; γk is the minimum rate requirement for the kth user. This article defines that when each user's rate meets this minimum rate requirement, the system’s quality of service (QoS) is guaranteed. The analog precoder is composed of a constant-mode phase shifter, so each element in the analog precoding matrix satisfies the condition of amplitude 1, which is |WRF(i,j)|2=1Nt. In Eq. (5), the dimensions of WRF and WBB change with the number of RF links NRF, and the number of RF links NRF must satisfy the condition of not less than the number of users. From Eq. (5), it can be seen that the energy efficiency of the system, that is, RsumPtotal is affected by the precoding matrix WRF and WBB, and the maximum transmission power of the system is limited by Pmax, the number of antennas in the system, Nt, and the number of RF links NRF will affect the amplitude and dimensions of the precoding matrix WRF and WBB. When Pmax is larger, the more power can be transmitted on each antenna, the amplitude of the precoding matrix becomes larger, so the user and rate increase, but at the same time the system power consumption also increases. Therefore, the energy efficiency of the system increases with the increase of Pmax in a certain range. At this time, the impact of Pmax on the sum-rate exceeds the impact on system energy consumption. The improvement is limited, while the energy consumption is still increasing linearly. At this time, the energy efficiency of the system will not increase and should remain unchanged. The number of systems transmitting antennas Nt and the number of radiofrequency links NRF will change the dimension of the precoding matrix. When the two become larger, the dimension of the precoding matrix increases, the corresponding sum rate increases, and the energy consumption also increase. This article will further illustrate the impact of the above system parameters on system energy efficiency through simulation in Section 4.

3.2 Problem Model Transformation

In order to maximize the energy efficiency of the system, three variables in Eq. (5) need to be optimized simultaneously: WRF, WBB, and NRF. Since the size of WRF and WBB is directly related to NRF, and the target problem is non-convex and nonlinear, Eq. (5) becomes very complicated and difficult to solve directly. Although the reference [16] searched the energy efficiency of the system under each possible NRF by the exhaustive method to obtain the optimal value, when the number of antennas is large, this reference [16] algorithm takes too much time and the complexity is too high. In order to avoid exhaustive search and make the problem solvable, the original problem will be further transformed to make the original ternary coupled variable optimization problem into a sparse digital precoding optimization problem that contains only one variable. Consider that the analog precoding matrix WRF is composed of NRF codewords selected from a preset codebook. Here, the codebook is represented by the symbol WRF, and the modulus values of all elements in the codebook are constant 1/Nt. An Nt×Nt-sized discrete Fourier transform (DFT) matrix [21] is used to represent the codebook. The reason for this is

1.    Each column vector in the DFT matrix is irrelevant;

2.    The column vectors in the DFT matrix can be combined linearly to synthesize the array response vectors in any direction in space. The Nt×Nt DFT matrix can be expressed as

1Nt[1,ej2πNt(k−1),…,ej2πNt(k−1)(Nt−1)]T,k=1,2,…,Nt(7)

Each column represents a codeword in the codebook WRF. Therefore, the design of analog precoding can be seen as selecting the appropriate codeword from the codebook WRF. Let W~RF=WRFQ be the sparse form of WRF, which means that the matrix after selecting NRF codewords from the codebook WRF and filling them with Nt−NRF all-zero column vectors have a size of Nt×Nt. Q is a diagonal matrix, and the element on the diagonal is a binary 0-1 variable. When the element on the diagonal is 1, it indicates that the column vector in the codebook corresponding to the subscript is selected. Let W~BB be a Nt×K matrix, which contains Nt−NRF all-zero rows and all elements of WBB is a sparse representation of W~BB, and satisfies W~BB all-zero row index corresponding to W~RF all-zero column index. In summary, the following equation holds

WRFWBB=W~RFW~BB=WRFQW~BB=WRFW~BB(8)

where NRF is equal to the number of non-zero rows in W~BB.

Using Eq. (8), Eq. (5) can be equivalently transformed into

maxW~BBRsumPtotal

Subject to Rk=log2⁡(1+|h~kW~BB,k|2∑i≠kK|h~kW~BB,k|2+σ2)≥γk,∀k

‖WRFWBB‖F2≤Pmax

‖diag (W~BBW~BBH)‖0≥K(9)

The total power consumption of the system is that Ptotal=1ε‖WRFWBB‖F2+‖diag (W~BBW~BBH)‖0PRF+Pc and W~BB,k is the kth column vector of W~BB, and h~k=hkWRF,∀k, which is the equivalent channel of the kth user.

Through the above conversion, Eq. (9) contains only one unknown variable, that is, a sparse digital precoding matrix W~BB. The original problem can be seen as a process of sparse digital precoding matrix and codeword selection. Each codeword in the codebook WRF can be regarded as a virtual transmitting antenna, and the virtual channel to the kth user is h~k. When the ith row of W~BB is all zero, it indicates that the ith codeword of WRF is not selected.

3.3 Algorithm Design

The problem in Eq. (9) is a classic fractional programming problem. Using Dinkelbach's theory [22,23], the fractional programming problem is transformed into an equivalent linear programming problem by introducing the parameter η, so as to optimize the single precoding matrix which can be obtained by solving J(η)=0, where J(η) is expressed as

J(η)=maxW~BB∑k=1KRk−ηPtotal(10)

The meaning of the equivalence relationship is that if an optimal value ηopt can be found, so that J(η)=0 holds, then its corresponding optimal solution W~BBopt is the optimal solution to the optimization problem (9). This paper uses the classic binary search method to solve J(η)=0 [22]. It can be seen that the key step in solving the optimization problem in this paper is still to solve the corresponding optimal solution W~BBopt under a given η. Therefore, the following section will discuss the solution method of the given η subproblem.

First, since the DFT matrix is a unitary matrix, there is WRFHWRF=INt. According to this equation, the total power consumption can be written as Ptotal=1ε‖W~BB‖F2+‖diag (W~BBW~BBH)‖0PRF+Pc, and the second constraint in Eq. (9) is also transformed into ‖WRFW~BB‖F2=‖W~BB‖F2≤Pmax.

Next, introduce a few auxiliary variables, and combine the constraints in Eqs. (10) and (9) and get

maxτ

Subject to ∑k=1Klog2⁡(βk+1)≥τ+ηPtotal

‖W~BB‖F2≤Pmax

h~kW~BB,k≥βkzk

zk≥∑i≠kK‖h~kW~BB,i‖2+σ2

1γ¯kh~kW~BB,i≥∑m≠kK‖h~kW~BB,m‖2+σ2

Im(h~kW~BB,k)=0

‖diag (W~BBW~BBH)‖0≥K(11)

Obviously, all constraints in Eq. (11) are optimal when they take the equal sign, so Eq. (11) is the equivalent transformation form of sub-problems. The difficulty in solving the problem (11) lies in its existence of non-convex constraints h~kW~BB,k≥βkzk and zero norm ‖diag (W~BBW~BBH)‖0. For non-convex constraints, h~kW~BB,k≥βkzk uses the order convex approximation [24] to approximate it. Reference [24] showed that βkzk can be replaced by its convex upper bound and the parameters in it are updated iteratively during the solution process. Specifically, define G(ϕk,βk,zk)=ϕk2zk2+12ϕkβk, for a fixed ϕk, ϕk>0, there is G(ϕk,βk,zk)≥βkzk. Therefore, h~kW~BB,k≥βkzk can be converted to h~kW~BB,k≥G(ϕk,βk,zk), in each iteration, for a fixed ϕk, h~kW~BB,k≥G(ϕk,βk,zk) it is a convex constraint. Second, consider the l0 norm of ‖diag (W~BBW~BBH)‖0. Introduce a selection variable xi∈{0,1}, which indicates whether the ith codeword is selected, 1 for selected, and 0 for unselected. Obviously, when the ith codeword is not selected, for all users, the ith element of W~BB,k is 0, that is, xi=0→W¯i=0,W¯i≜[[W1]i,[W2]i,…,[WK]i]T∈CK×1 is the ith row vector of W~BB. The above process is transformed into a constraint form, which can be written as ‖W¯i‖22<fixi, where fi is regarded as the power level corresponding to each codeword. When xi, is relaxed into a continuous variable between 0 and 1, the second-order cone constraint of ‖W¯i‖22<fixi can be written as ‖W~iT,12(fi−xi)‖2<12(fi+xi). Combining all the above results, the solution of the subproblem (11) with a given η is transformed into a convex problem, and the mathematical description of the problem is shown in Eq. (12)

maxτ

Subject to ∑k=1Klog2⁡(βk+1)≥τ+η(1ε∑i=1Ntfi+∑i=1Ntxi×PRF+Pc)

‖W~iT,12(fi−xi)‖2<12(fi+xi)

h~kW~BB,k≥ϕk2zk2+12ϕkβk,∀k

∑i=1Ntfi≤Pmax;

0≤xi≤1,∀i;

∑i=1Ntxi≥K

zk≥∑i≠kK‖h~kW~BB,i‖2+σ2

1γ¯kh~kW~BB,k≥∑i≠kK‖h~kW~BB,i‖2+σ2

Im(h~kW~BB,k)=0(12)

The algorithm solving steps for the entire problem is shown in Algorithm 1. It includes two nested loops. The outer binary search η makes J(η)=0 and the inner loop solves the optimal energy efficiency value corresponding to Eq. (12) under the condition of fixed η.

In Eq. (12), since xiis relaxed into a continuous variable on [0,1], a simple matching principle is adopted: for xi>1−ξ, let xi=1; otherwise, let xi=0. Here ξ is a very small number. The simulation results in the next section show that the impact of this matching algorithm on performance is almost negligible because of most of the xi obtained from the solution are very close to 1 or 0. Through the matched xi, the selected codewords in the codebook can be found, thereby forming an analog precoding matrix WRF. Use h~k=hkWRF and Ptotal=1ε‖WRFWBB‖F2+∑k=1KxiPRF+Pc to replace the new Eq. (12), repeat the steps in Algorithm 1 again, and solve the digital precoding matrix WBB to obtain the optimal value of system energy efficiency.

3.4 Complexity Analysis

The complexity of the proposed algorithm is compared with reference [25] and conventional OMP algorithm [7] in Tab. 1. As can be seen from Tab. 1, the proposed algorithm has a lower computational complexity than the competing alternative which means that the proposed algorithm is easy to implement with simple hardware and less signal processing requirement.

4  Simulation Results and Analysis

This section verify the simulation performance of the above algorithm. Some parameters [8–16] used in the simulation are shown in Tab. 2. The number of users is K=4, the number of transmitting antennas is Nt=64 and the maximum transmission power is Pmax=30dBm.

Fig. 2 compares the spectral efficiency of the proposed algorithm with optimal digital, reference [25] and conventional OMP algorithm [7] under different antenna configurations and SNR levels. In Fig. 2a, the system configuration of NRF=4,Nt=64,Nr=16 is used to evaluate the achievable spectral efficiency of the algorithms under different SNR values. As can be seen from Fig. 2a, the spectral efficiencies of all algorithms increase with increasing SNR. It is also clear from the results that the spectral efficiency of the proposed algorithm is better than reference [25] and conventional OMP algorithm [7]. The proposed algorithm also gives closed performance with the fully digital precoding which verifies it effectiveness. On the other hand, the spectral efficiency of the conventional OMP algorithm [7] is lower than the other algorithms and the rate gap increases with increasing SNR, which makes OMP scheme worst in high SNR channel conditions. In Fig. 2b, the system configuration of NRF=4,Nt=256,Nr=16 is used to evaluate the performance of the proposed and existing algorithms. It can be seen from Fig. 2b that; the proposed algorithm gives better spectral efficiency as compared with reference [25] and conventional OMP algorithm [7] and it also shows closed performance with the optimal digital precoding scheme. It is worth notable that with increasing the number of transmitter antennas Nt, the rate gap between the proposed algorithm and reference [25] and conventional OMP algorithm [7] gets larger whereas, the spectral efficiency of the proposed algorithm reaches that of the optimal digital precoding algorithm. Fig. 2c compare the spectral efficiency performance with system configuration of NRF=4,Nt=1024,Nr=16. It can be seen from Fig. 2c that the spectral efficiency of the proposed algorithm is better than the reference [25] and conventional OMP algorithm [7]. The rate gap of the OMP algorithm [7] gets much larger as in contrast to Figs. 2a and 2b respectively.

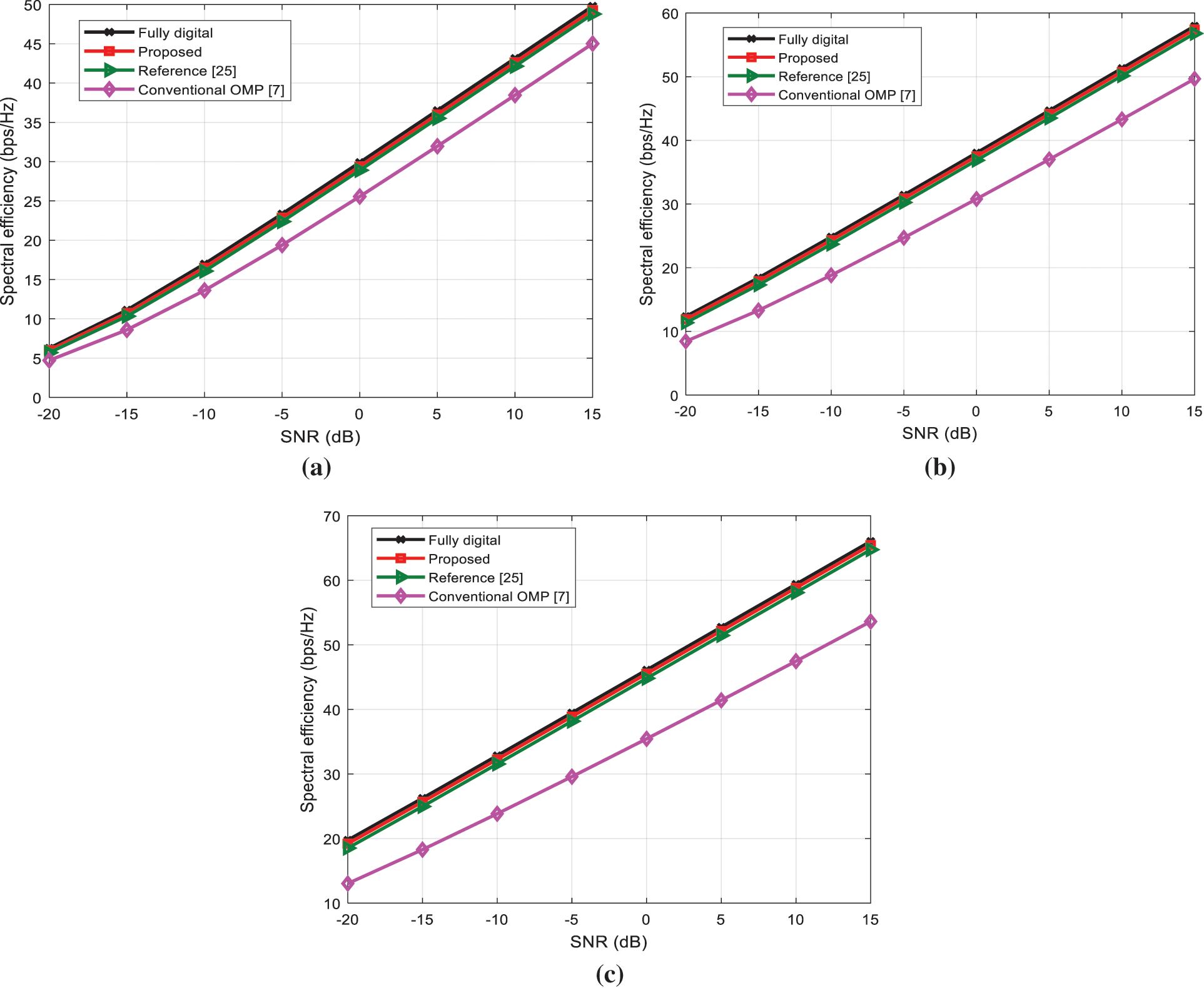
Figure 2: Comparison of the spectral efficiency of the algorithms under different SNR values. (a) NRF=4,Nt=64,Nr=16; (b) NRF=4,Nt=256,Nr=16; (c) NRF=4,Nt=1024,Nr=16

Fig. 3 compares the NMSE of the proposed algorithm with fully digital, reference [25] and conventional OMP [7] algorithm under various SNR values. As can be seen from Fig. 3, the NMSE of all algorithms decreases with increasing SNR. It is also clear from the results that the NMSE of the proposed algorithm is much better than reference [25] and conventional OMP [7] algorithms and gets improved with increasing SNR. This means that the channel quality and quality of service (QoS) to the subscribers is better using the proposed algorithm, and has reliable data transmission. Moreover, the proposed algorithm closely perform with the fully-digital precoding, which also validates the effectiveness of the proposed algorithm.

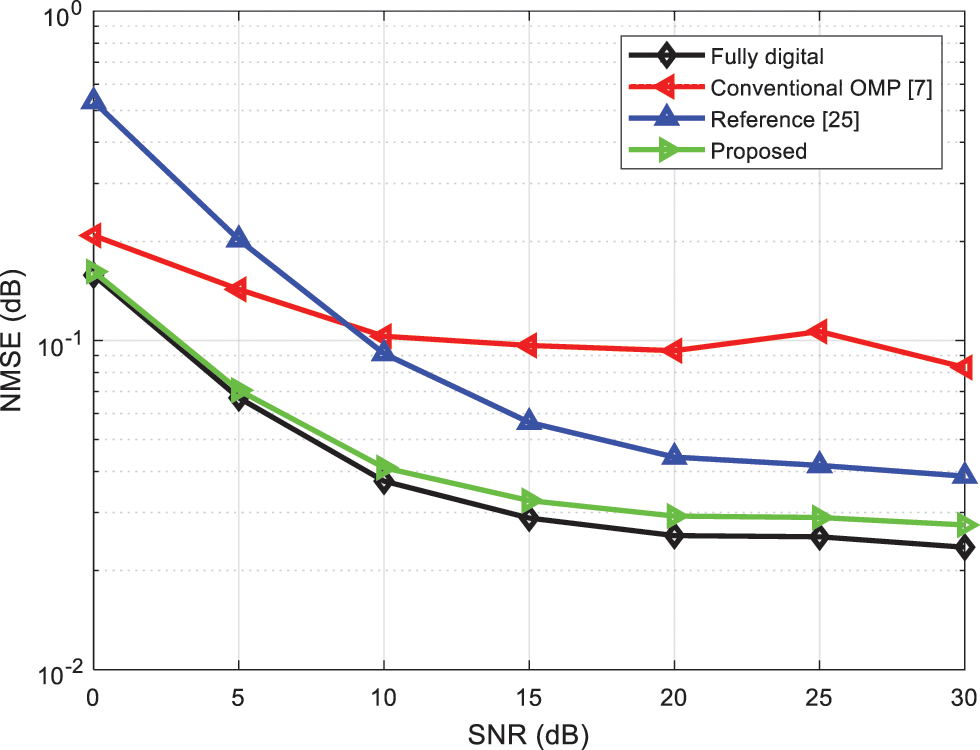
Figure 3: Comparison of the NMSE of the algorithms under different SNR values

To elaborate the effectiveness of the proposed algorithms in terms of hardware energy consumption (energy efficiency), Fig. 4 compares the energy efficiency of algorithms under increasing number of RF chains. As can be seen from Fig. 4, the energy efficiency of all algorithms increases when the number of RF chains range is from 1 to 10. However, when the number of RF chains increases above 10, the energy efficiency of all algorithms starts declining. It can also be seen from the results that the energy efficiency of the proposed algorithm is much better than that of reference [25] and conventional OMP [7] algorithm for each number of RF chains, which makes it more effective from practical implementation perspective which will require less amount of energy per hardware module.

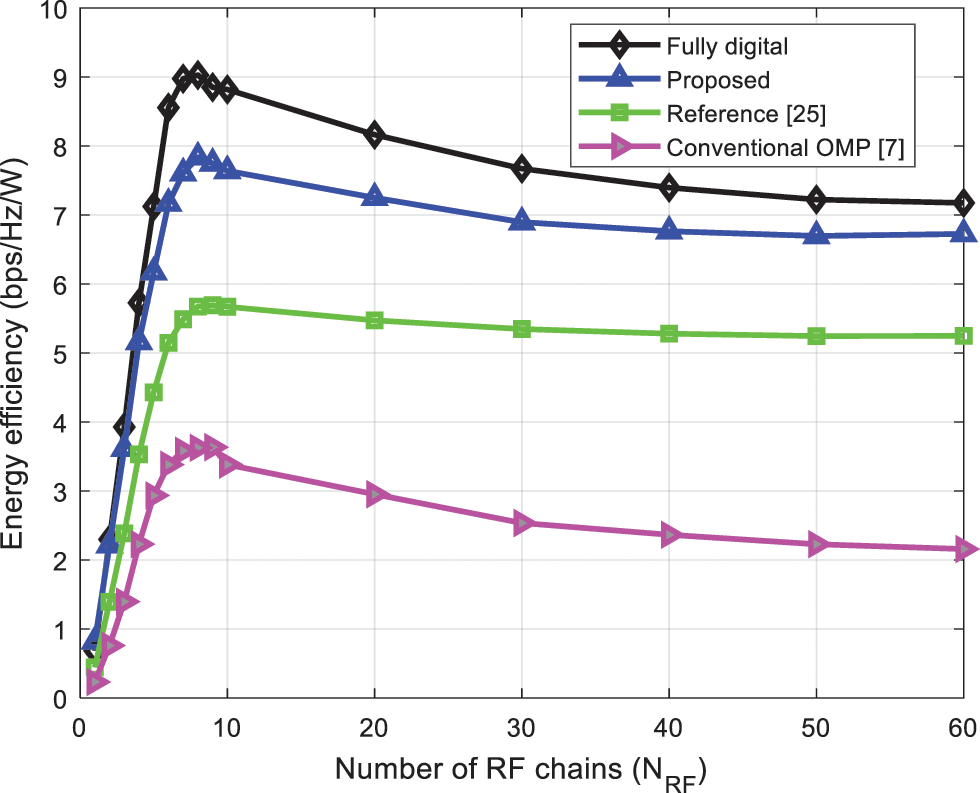
Figure 4: Comparison of the energy efficiency of the algorithms under different number of RF chains

5  Conclusion

With the millimeter-wave hybrid precoding structure, the optimization of system energy efficiency and the number of RF links is very challenging. This paper proposes an energy-efficient hybrid precoding algorithm based on RF link selection. First, using the preset analog precoding codebook, the original problem is equivalently converted into a sparse digital precoding optimization problem, so that the three coupling variables of the original problem are converted into one unknown variable. Then an iterative solution algorithm was designed using Dinkelbach’s theory combined with sequential convex approximation. The results show that the algorithm proposed in this paper can optimize the number of RF links and effectively improve the energy efficiency of the system while avoiding exhaustive search. The results are very close to the performance obtained by the fully digital method and significantly higher than other commonly used algorithms, such as reference [25] and conventional OMP [7]. This work can further be improved by considering the hardware impairment and low-resolution ADC issues and evaluation in different deployment scenarios.

Acknowledgement: This study was supported by the Institute for Information & Communications Technology Planning & Evaluation (IITP) grant funded by the Korean government (MSIT) (No.2019-0-01343, Training Key Talents in Industrial Convergence Security).

Funding Statement: This publication was supported by the Ministry of Education, Malaysia (Grant code: FRGS/1/2018/ICT02/UKM/02/6).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  I. Khan, M. H. Al-Sharif, M. H. Zafar, M. O. Alassafi, M. Ashraf et al., “An efficient algorithm for mmwave MIMO systems,” Symmetry, vol. 11, no. 6, pp. 1–13, 2019. [Google Scholar]

 2.  R. Magueta, S. Teodoro, D. Castanheira, A. Silva, R. Dinis et al., “Multiuser equalizer for hybrid massive MIMO mmwave CE-OFDM systems,” Applied Sciences, vol. 9, no. 16, pp. 1–18, 2019. [Google Scholar]

 3.  D. Castanheira, P. Lopes, A. Silva and A. Gameiro, “Hybrid beamforming designs for massive MIMO millimeter-wave heterogeneous systems,” IEEE Access, vol. 7, pp. 21806–21817, 2017. [Google Scholar]

 4.  S. L. Mohammed, M. Al-Sharif, S. K. Gharghan, I. Khan and M. Albreem, “Robust hybrid beamforming scheme for millimeter-wave massive-MIMO 5G wireless networks,” Symmetry, vol. 11, no. 11, pp. 1–18, 2019. [Google Scholar]

 5.  W. Shahjehan, A. Riaz, I. Khan, A. S. Sadiq, S. Khan et al., “Bat algorithm-based beamforming for mmwave massive MIMO systems,” International Journal of Communications Systems, vol. 33, no. 2, pp. 772–779, 2019. [Google Scholar]

 6.  A. M. Y. Al-Nimrat, M. Smadi and O. A. Saraereh, “An efficient channel estimation scheme for mmwave massive MIMO systems,” in IEEE Int. Conf. on Communication, Networks, and Satellite (ComNetSat), Makassar, Indonesia, pp. 1–6, 2019. [Google Scholar]

 7.  A. A. Bakar, R. Hamdan and N. S. Sani, “Ensemble learning for multidimensional poverty classification,” Sains Malaysiana, vol. 49, no. 2, pp. 447–459, 2020. [Google Scholar]

 8.  A. B. Abdulkareem, N. S. Sani, S. Sahran, Z. A. A. Alyessari, A. Adam et al., “Predicting COVID-19 based on environmental factors with machine learning,” Intelligent Automation & Soft Computing, vol. 28, no. 2, pp. 305–320, 2021. [Google Scholar]

 9.  Z. A. Othman, A. A. Bakar, N. S. Sani and J. Sallim, “Household overspending model amongst B40, M40 and T20 using classification algorithm,” International Journal of Advanced Computer Science and Applications, vol. 11, no. 7, pp. 392–399, 2020. [Google Scholar]

10. L. Liang, W. Xu and X. Dong, “Low-complexity hybrid precoding in massive MIMO systems,” IEEE Wireless Communications Letters, vol. 3, no. 6, pp. 653–656, 2014. [Google Scholar]

11. G. Y. Li, Z. Xu, C. Xiong, C. Yang, S. Zhang et al., “Energy-efficient wireless communications: Tutorials, survey, and open issues,” IEEE Wireless Communications, vol. 18, no. 6, pp. 28–35, 2011. [Google Scholar]

12. N. S. Sani, A. F. M. Nafuri, Z. A. Othman, M. Z. A. Nazri and K. N. Mohamad, “Drop-out prediction in higher education among B40 students,” International Journal of Advanced Computer Science and Applications, vol. 11, no. 11, pp. 550–559, 2020. [Google Scholar]

13. M. Tareq, E. A. Sundararajan, M. Mohd and N. S. Sani, “Online clustering of evolving data streams using a density grid-based method,” IEEE Access, vol. 8, pp. 166472–166490, 2020. [Google Scholar]

14. A. G. Rodriguez, V. Venkateswaran, P. Rulikoski and C. Masouros, “Hybrid analog-digital precoding revisited under realistic rf modeling,” IEEE Wireless Communications Letters, vol. 5, no. 5, pp. 528–531, 2016. [Google Scholar]

15. C. Ma, J. Shi, N. Huang and M. Chen, “Energy-efficient hybrid precoding for millimeter wave systems in MIMO interference channels,” in IEEE 83rd Vehicular Technology Conf. (VTC Spring), Nanjing, China, pp. 1–5, 2016. [Google Scholar]

16. R. Zi, X. Ge, J. Thompson, C. X. Wang, H. Wang et al., “Energy efficiency optimization of 5G radio frequency chain systems,” IEEE Journal on Selected Areas in Communications, vol. 34, no. 4, pp. 758–771, 2016. [Google Scholar]

17. Y. Shi, J. Zhang and K. B. Letaief, “Group sparse beamforming for green cloud-RAN,” IEEE Transactions on Wireless Communications, vol. 13, no. 5, pp. 2809–2823, 2014. [Google Scholar]

18. B. Dai and W. Yu, “Sparse beamforming and user-centric clustering for downlink cloud radio access network,” IEEE Access, vol. 2, pp. 1326–1339, 2014. [Google Scholar]

19. L. Liang, W. Xu and X. Dong, “Low-complexity hybrid precoding in massive multiuser MIMO systems,” IEEE Wireless Communications Letters, vol. 3, no. 6, pp. 653–656, 2014. [Google Scholar]

20. G. R. MacCartney, M. K. Samimi and T. S. Rappaport, “Omnidirectional path loss models in new york city at 28 GHz and 73 GHz,” in IEEE 25th Annual Int. Symp. on Personal, Indoor, and Mobile Radio Communications (PIMRC), Washington DC, USA, pp. 227–231, 2014. [Google Scholar]

21. D. J. Love and R. W. Heath, “Equal gain transmission in multiple-input multiple-output wireless systems,” IEEE Transactions on Communications, vol. 51, no. 7, pp. 1102–1110, 2003. [Google Scholar]

22. Y. Dong, Y. Huang and L. Qiu, “Energy-efficient sparse beamforming for multiuser mimo systems with nonideal power amplifiers,” IEEE Transactions on Vehicular Technology, vol. 66, no. 1, pp. 134–145, 2017. [Google Scholar]

23. S. Schaible and T. Ibaraki, “Fractional programming,” European Journal of Operational Research, vol. 12, no. 4, pp. 325–338, 1983. [Google Scholar]

24. A. Beck, A. Ben-Tal and L. Tetruashvili, “A sequential parametric convex approximation method with applications to nonconvex truss topology design problems,” Journal of Global Optimization, vol. 47, no. 1, pp. 29–51, 2010. [Google Scholar]

25. X. Yu, J. C. Shen, J. Zhang and K. B. Letaief, “Alternating minimization algorithms for hybrid precoding in millimeter wave mimo systems,” IEEE Journal of Selected Topics in Signal Processing, vol. 10, no. 3, pp. 485–500, 2016. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.