DOI:10.32604/cmc.2022.025924

| Computers, Materials & Continua DOI:10.32604/cmc.2022.025924 |  |
| Article |
Optimized Image Multiplication with Approximate Counter Based Compressor
1SRMIST, Chennai, 603203, India
2Vel Tech Multi Tech Dr. Rangarajan Dr. Sakunthala Engineering College, Chennai, 601206, India
3Intel Corportation, California, 93657, USA
*Corresponding Author: M. Maria Dominic Savio. Email: mariadom@srmist.edu.in
Received: 09 December 2021; Accepted: 16 February 2022
Abstract: The processor is greatly hampered by the large dataset of picture or multimedia data. The logic of approximation hardware is moving in the direction of multimedia processing with a given amount of acceptable mistake. This study proposes various higher-order approximate counter-based compressor (CBC) using input shuffled 6:3 CBC. In the Wallace multiplier using a CBC is a significant factor in partial product reduction. So the design of 10-4, 11-4, 12-4, 13-4 and 14-4 CBC are proposed in this paper using an input shuffled 6:3 compressor to attain two stage multiplications. The input shuffling aims to reduce the output combination of the 6:3 compressor from 64 to 27. Design of 15-4, 10-4, 9-4, and 7-3 CBCs are performed using the proposed 6:3 compressor and the results obtained are compared with the existing models. These existing models are constructed using multiplexers and 5-3 CBC. When compared to input shuffled 5-3 the proposed 6:3 compressor shows better results in terms of area, power and delay. An approximation is performed on the 6:3 compressor to further reduce the computational energy of the system which is optimal for multimedia applications. The major contribution of this work is the development of two stage multiplier using various proposed CBC. All designs of the approximate compressor (AC) and true compressor (TC) are analysed with 8 x 8 and 16 x 16 image multiplication. The proposed multipliers also provide adequate levels of accuracy, according to the MATLAB simulations, in addition to greater hardware efficiency. As the result approximate circuits over image processing shows the stunning performance in many deep learning network in the current research which is only oriented to multimedia.
Keywords: Multiplier; PSNR; image processing; approximate; compressor; NED
The digital signal processing (DSP) units are constructed with several arithmetic circuits [1]. The DSP blocks play a major role in the operation of the processor [2]. During the construction of a DSP, design complexity is observed at the multiplier. Over half the computational energy of any DSP occurs at the multipliers [3]. The construction of a multiplier has been a challenging research problem for the last three-decades. Various approaches like Vedic multipliers and well-known algorithmic multipliers using shift and add, Wallace and Dadda tree multiplication, sequential multipliers, and array multipliers are adopted in the construction of a DSP [4]. The processor was injected with the problem of a large data set and a heavy payload in the current scenario [5]. Many studies are being conducted to process data in Cloud computing to overcome this problem. However, when it comes to stand-alone processors for critical applications, the GPU and FPGA board used in cloud computing are insufficient. As a result, research on the circuit level to reduce processor strain continues. The approximate computation is one of the strategies. Approximation is accomplished using a variety of ways, including software, architecture, and circuit hardware. This study concentrated on circuit level approximation. Image processing circuits such as multipliers, dividers, thresholding, and subtractors are investigated. When it comes to multipliers, numerous researchers have considered using a compressor. So the design of a two-stage reduction Wallace tree multiplier using an advanced compression technique is proposed in this work. The compressor architecture is used for partial product reduction in the multiplier which consists of N inputs, (N-3) cin, (N-3) cout, sum and carry [6,7]. Another type of counter-based compressor (CBC) counts the number of 1’s at the input side. The full adder is a basic CBC which counts the three inputs “111” as carry = 1, sum = 1 the output of which is equal to “11” which is equivalent to the decimal value of three [8]. Using the same approach, an N-bit CBC is constructed by stacking the half adder and full adder. Another approach for lowering the bit-length CBC using k-maps relations between the outputs is constructed using logic gates and multiplexer implementation [9].
The concept of input shuffling in 5-3 CBC was introduced to reduce the output combination, thereby improving system efficacy. The 15-4 CBC is constructed using 5-3 CBC in [10] and acquired results are compared to existing results. When compared to the prior 16 x 16 multiplier, this architecture produces better results. The issue with this literature is that the number of full-adders and 5-3 CBCs has increased. Furthermore they have only constructed a 15-4 compressor due to that the multiplier’s design complexity has increased. So the same approach is proposed in 6-3 CBC and the design of 8-4, 9-4, 10-4, 11-4, 12-4, 13-4, 14-4 and 15-4 CBC is performed using the proposed 6-3 CBC and shows attractive results when compared with various existing results. Utilizing the CBC’s in the Wallace tree multiplier improves the energy consumed by DSPs in the processor [11]. When the processor is developed for a specific application of multimedia operation, the output approximation has been opted by many researchers to further improve the circuit performance [12]. After input shuffling, few output approximations in the truth table reduces the circuit complexity. This approximation holds limited error and a trade-off is maintained between circuit parameter and multiplier accuracy. The accuracy of any arithmetic circuit is evaluated through normalized error distance (NED) [13]. These approximate and true multipliers are used in 8-bit and 16-bit image multiplication to evaluate if the multipliers are suitable for multimedia applications. The approximate multiplied images of existing and proposed systems are compared with true multiplication images and the peak signal to noise ratio (PSNR) is computed and [14] provides an introduction to the PSNR parameters. The compressor constructed with 6-3 CBC shows better achievement in power and delay when compared with existing results. The construction of 16-bit multiplier with two-stage reduction using 4-3, 5-3, 6-3, 7-3, 8-4, 9-4, 10-4, 11-4, 12-4, 13-4, 14-4 and 15-4 CBC’s has been proposed in this paper. The rest of the section as follows: 2. Literature. 3. Proposed CBC’s. 4. Multiplier designs. 5. Image multiplication application. 6. Conclusion.
Normal compressors differ from CBCs according to carry and Cout weights. The famous 4:2 compressor introduced by Shen-Fu Hsiao et al. [15] made a revolutionary change in multiplier architecture over the past two decades. It is made up of two full adders and a state-of-the-art method of developing a full-adder using two XOR gates and a multiplexer, invented by Chang et al. [16]. With the same approach, several compressor architectures have been developed. For example, a 6:2 compressor weight are given by Eq. (1)
From the Eq. (1) all the couts and carry having equal weight in the multiplier architecture the carry or couts are generated by the compressor in the ith column will be passed to i + 1 column. The CBC’s are quite different in weights considering the 6-3 CBC having only three outputs and the weights given in Eq. (2).
So the carry outputs of CBC’s in ith stage are given to i + 1, i + 2… depending on its weights. Many CBC’s blocks were involved in multipliers for the last decade. Marimuthu et al. [17] proposed 8-4, 9-4 CBC’s that were constructed using a multiplexer and half adder as shown in Figs. 1 and 2.
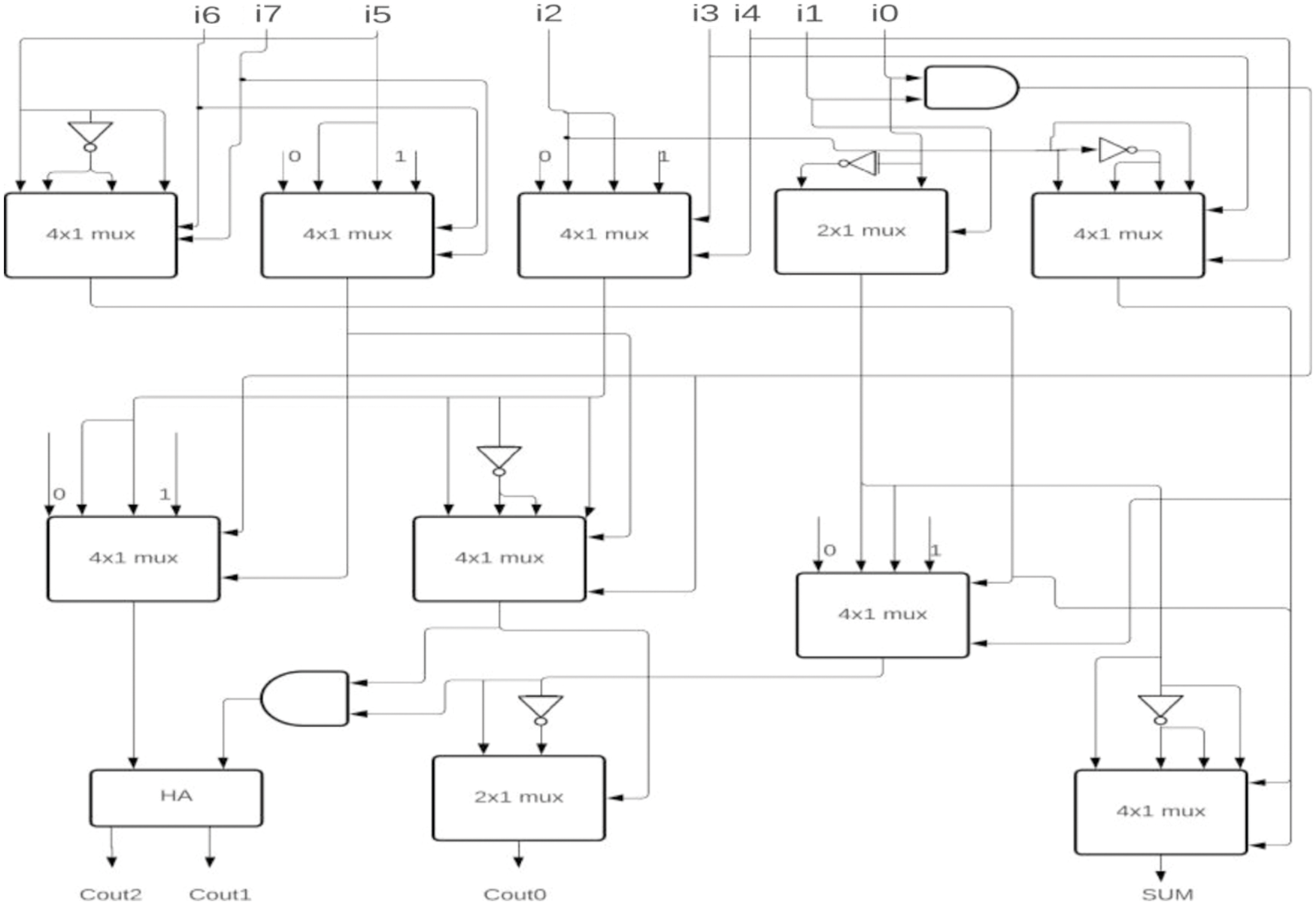
Figure 1: 8-4 CBC [17]
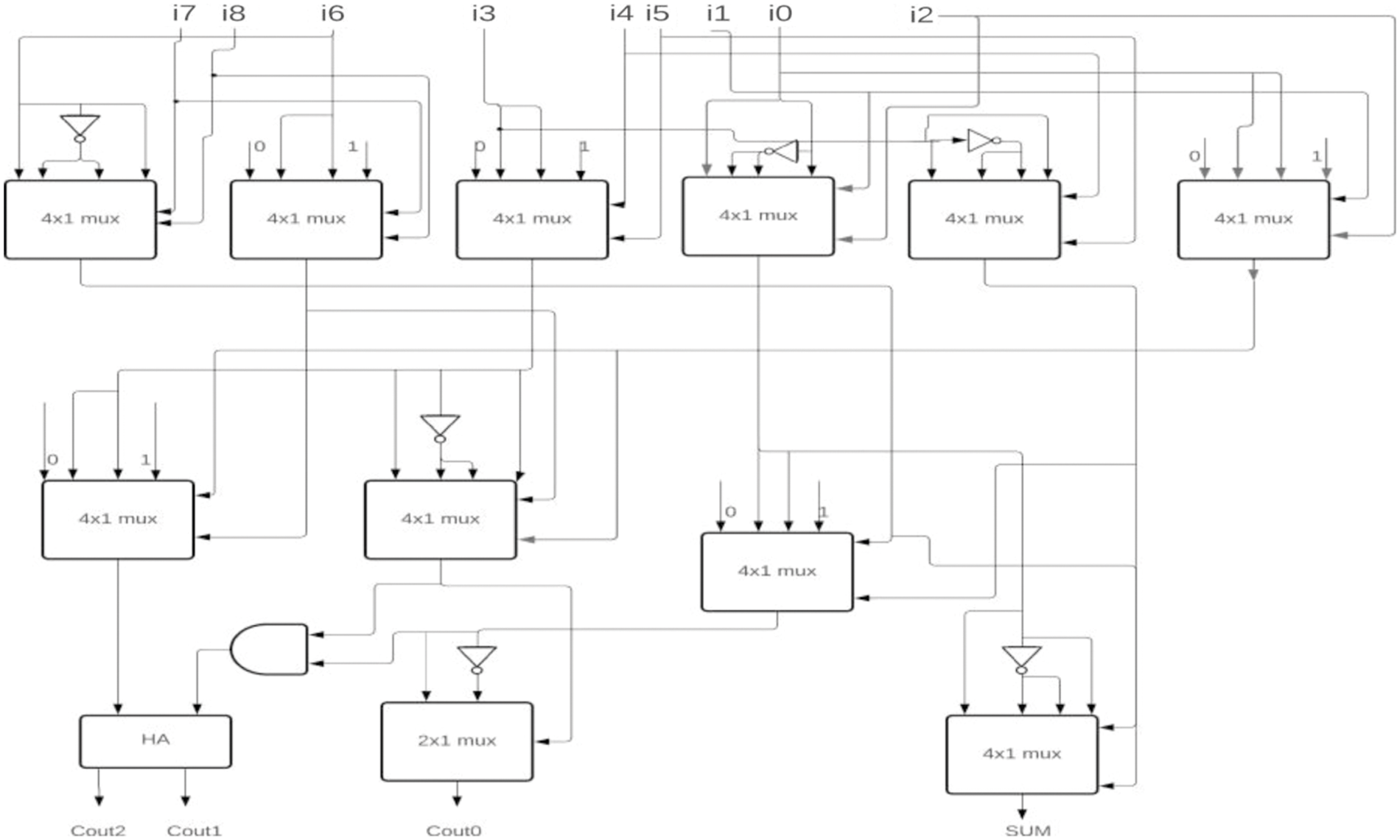
Figure 2: 9-4 CBC [17]
In [18] the author proposed 5-3 CBC and 15-4 CBC developed using 5-3 CBC. Here the 5-3 CBC is constructed using XOR and MUX. The modified 5-3 CBC used in 15-4 CBC was proposed in [19] as shown in Fig. 3. The concept of input reordering in 5-3 CBC was introduced by Krishna et al. [10] shows the significant improvement in the area, power, and delay as shown in Fig. 4. These 5-3 CBCs are also used in 15-4 which is used to construct 16-bit multipliers. The 6-3 and 7-3 CBC’s were proposed using full adder and parallel addition by Anup Dandapat et al. in [20]. A modified architecture of the same using XOR-MUX was proposed in [21] as shown in Figs. 5 and 6.
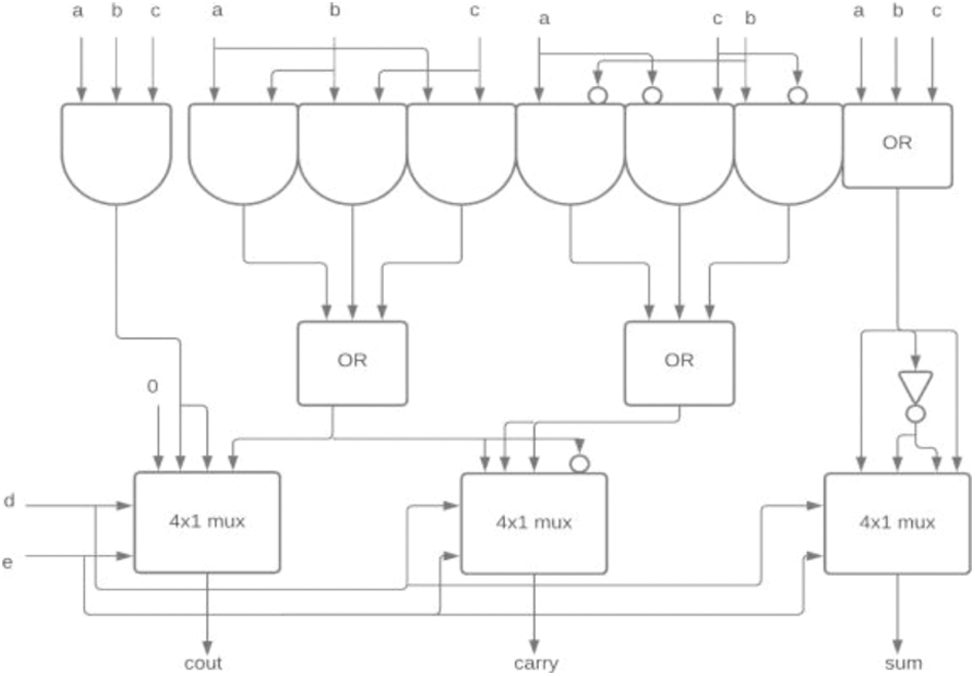
Figure 3: 8-4 CBC [18]

Figure 4: 15-4 CBC [10]
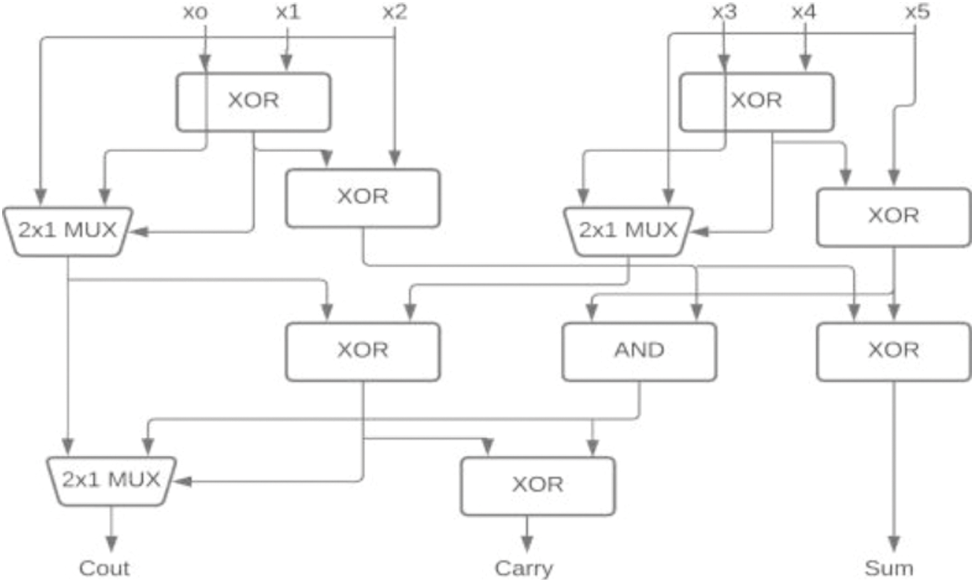
Figure 5: 6-3 CBC [21]
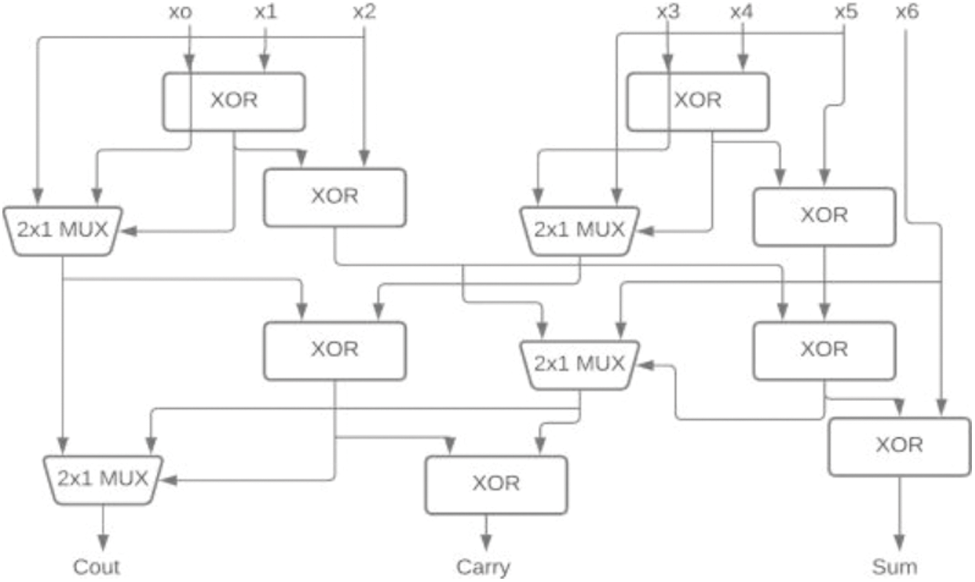
Figure 6: 7-3 CBC [21]
The scheme of approximation has been introduced when the operation is concerned with image or multimedia data format. With the addition of limiting error, approximation generally reduces the hardware. Consider the OR gate, which outputs one as an output if any of the inputs is one. The OR gate has been replaced by a buffer that connects to any of the inputs, leaving the other input free. Due to both inputs turning to one two times out of four cycles, the output comes with an error of one time out of four cycles, resulting in a 75% pass rate. In [21] the approximation in done in the 4:2 compressor using probability method and utilized in 8 * 8 multiplier. The impact approximate multiplier is analyzed with Conventional Neural Network (CNN) in [22]. In [23] the well know VGG deep learning network performance has been enhanced using approximate multiplier.
Hammad et al. [24], developed four approximate multipliers by reducing the gates in 5-3 CBC. In [25] the author proposed an approximate multiplier by using an 8:2 compressor. Another 16-bit multiplier is targeted for error-tolerant application by using a 4:2 compressor in [26]. Taheri et al. [27], have approximated 4:2 and constructed an 8-bit multiplier for image multiplication. Anusha et al. [28], used an approximate full adder to construct an 8 * 8 multiplier that was utilized in image processing.
The major work contributed in this paper is the design of input shuffled 6-3 CBC. The input shuffling is made in such a way that the CBCs count “000001” and “100000” as “001” and likewise “000011” and “110000” as “010”. By the input shuffling circuit, several combinations are reduced. For example, both “000001” and “000010” are treated as “010000”.The output combination is reduced from 64 to 27 and the remaining values are considered as don’t care in the k-maps, thereby optimizing the circuit architecture. The input shuffling circuit equations are termed as a = x [1] . x [0], b = x [1] + x [0], c = x [3] . x [2], d = x [3] + x [2], e = x [5] . x [4], f = x [5] + x [4] . The output of the input shuffling is given in Tab. 1.
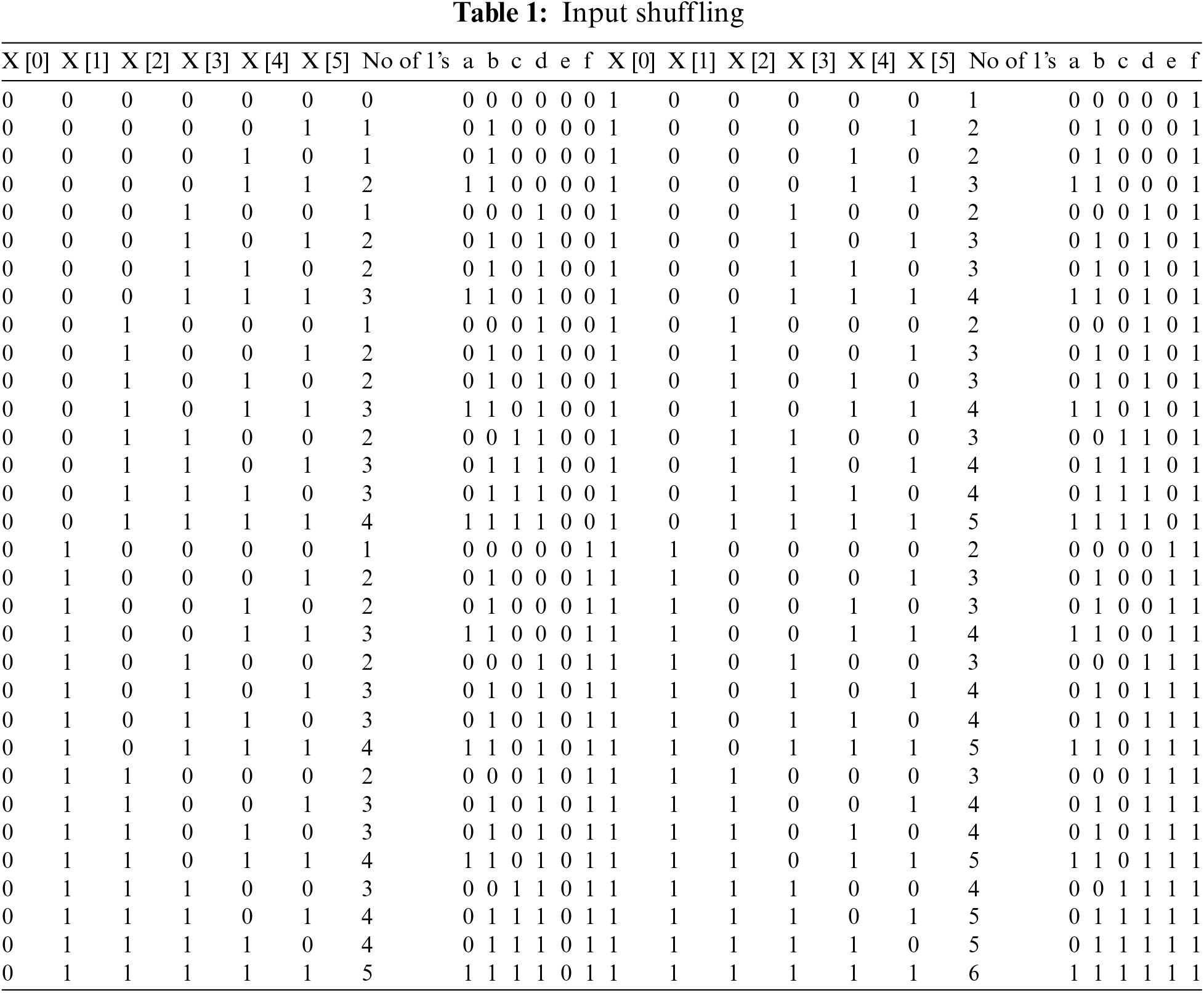
The reduced 27 combinations and time occurrences are shown in Tab. 2. From the Tab. 2, the logic for sum, Cout1, and Cout2 are calculated and given in Eqs. (3)–(5). The circuit for input shuffling is shown in Fig. 7.
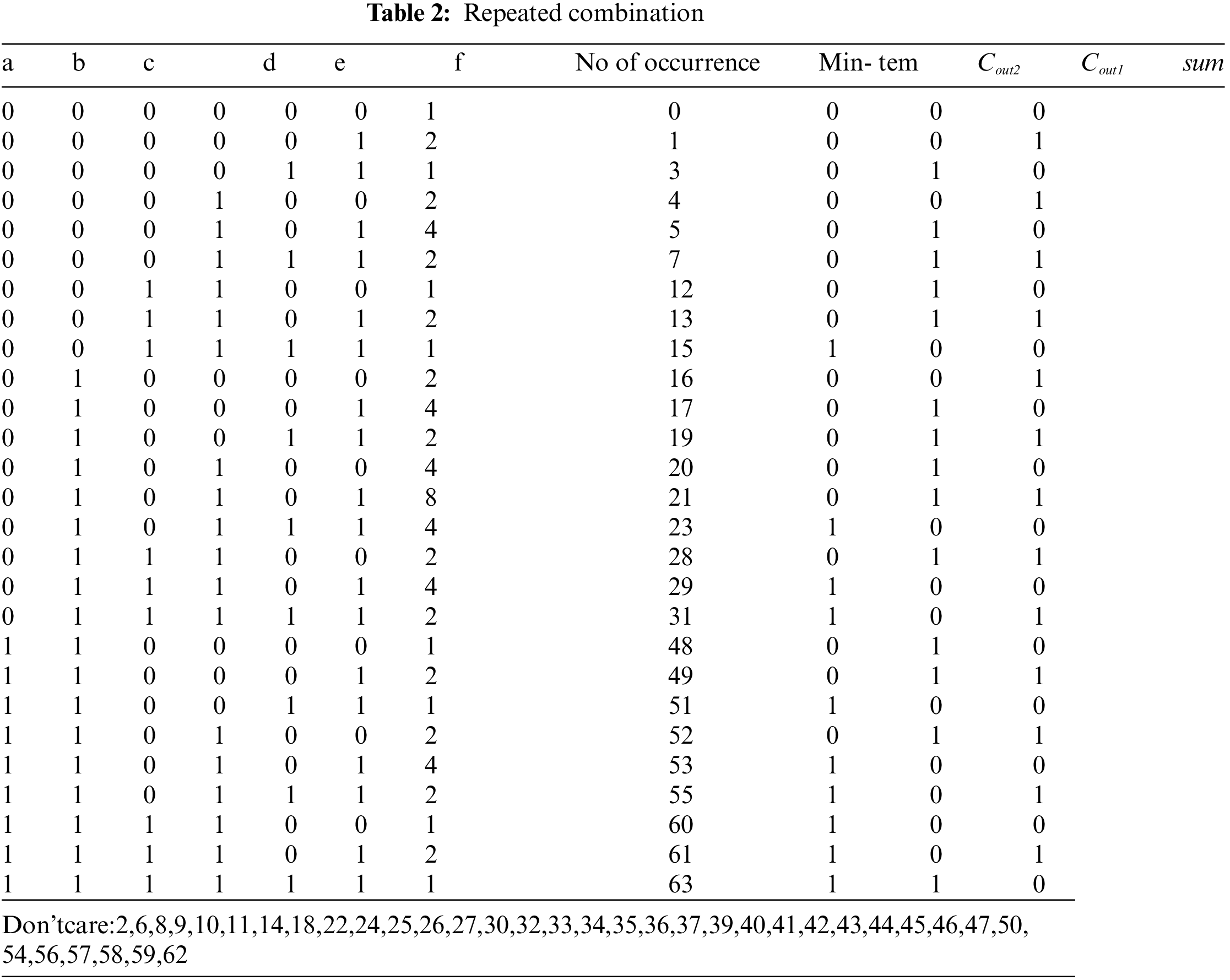

Figure 7: Input shuffling
The proposed 6-3 CBC has been used in the construction of various higher-bit CBCs and compared with existing systems. Some of the examples include (i) 8-4 CBC designed using 6-3 CBC, full adder and half adder as represented in Fig. 8., (ii) 9-4 CBC designed using 6-3 CBC, full adder and half adder as represented in Fig. 9., (iii). 10-4 CBC designed using 6-3 CBC, full adder, and half-adder is represented in Fig. 10. (iv) 15-4 CBC designed using 6-3 CBC, full adder, half adder and an XOR gate as represented in Fig. 11.
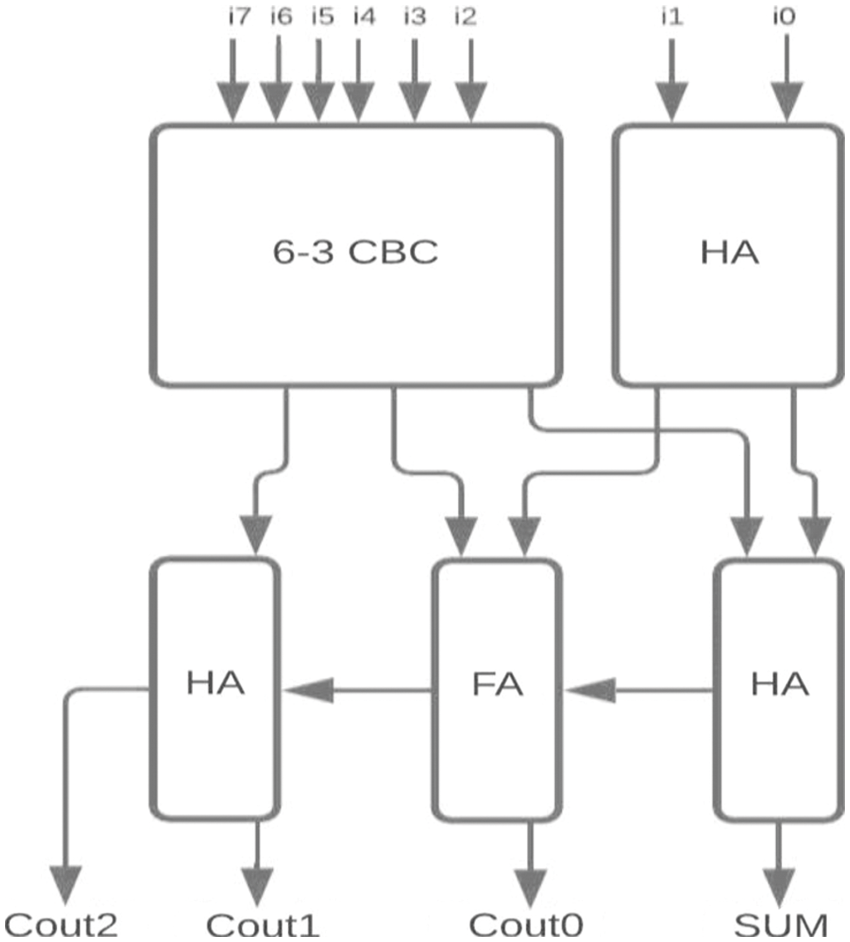
Figure 8: Proposed 8-4 CBC
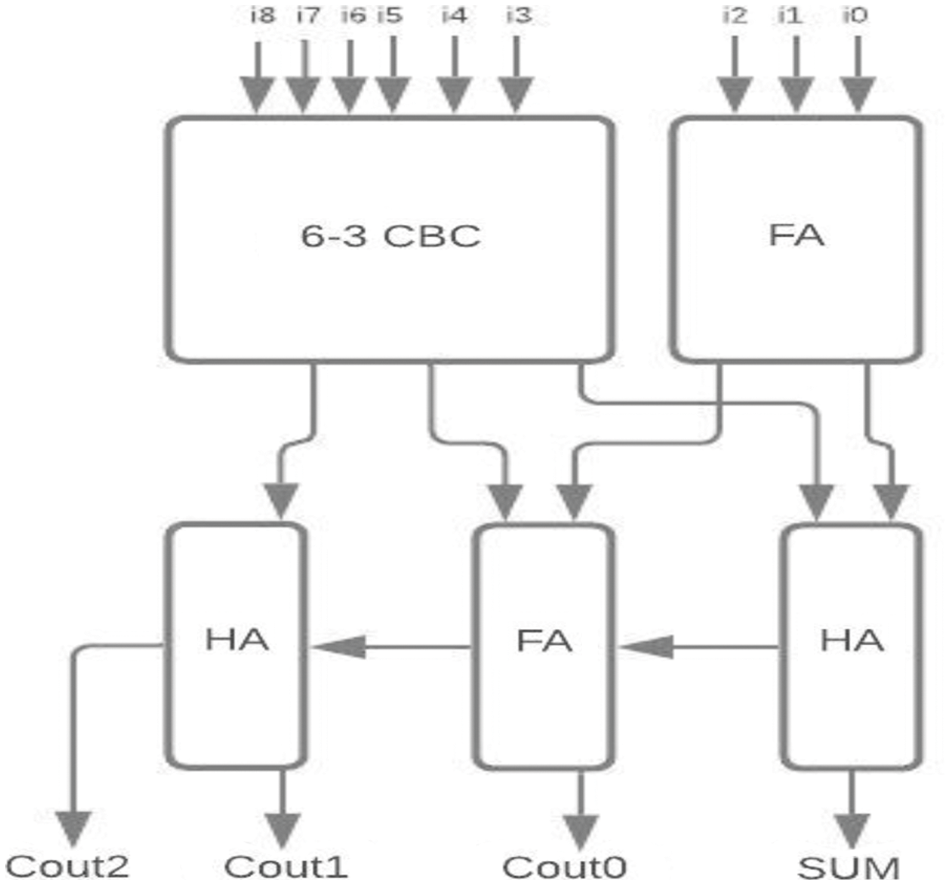
Figure 9: Proposed 9-4 CBC
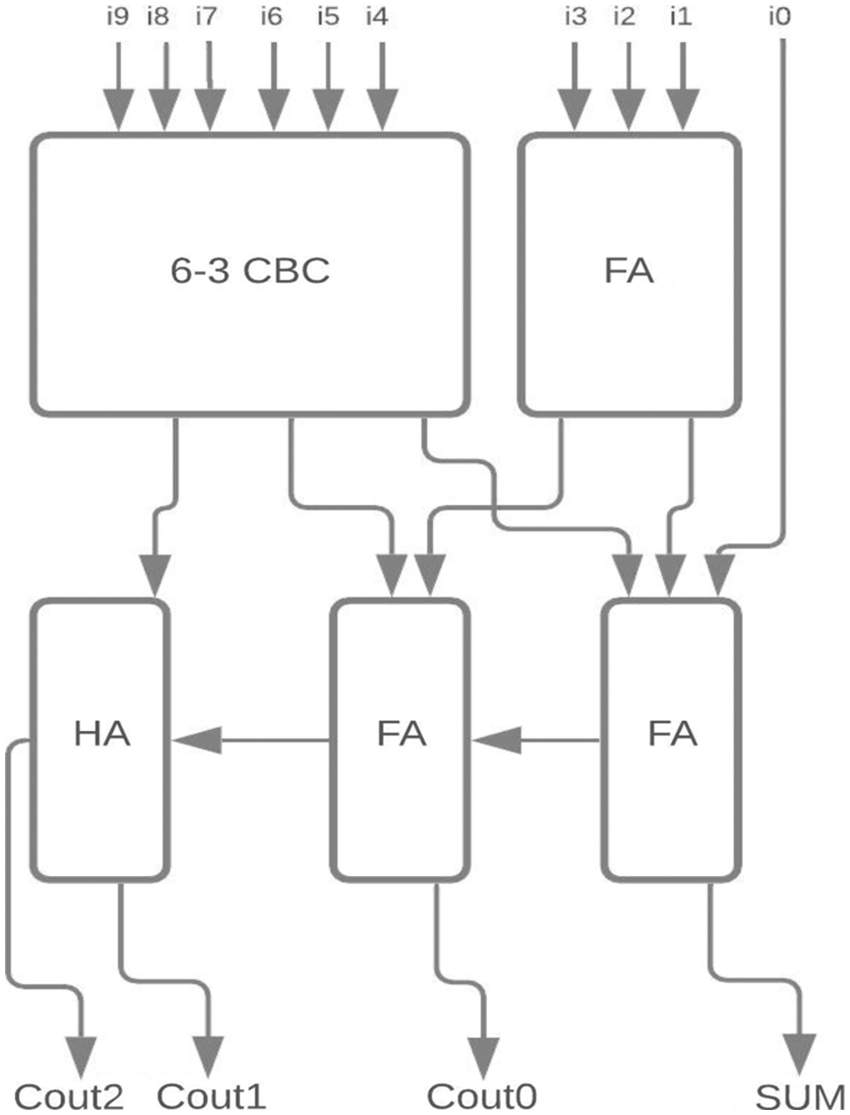
Figure 10: Proposed 10-4 CBC
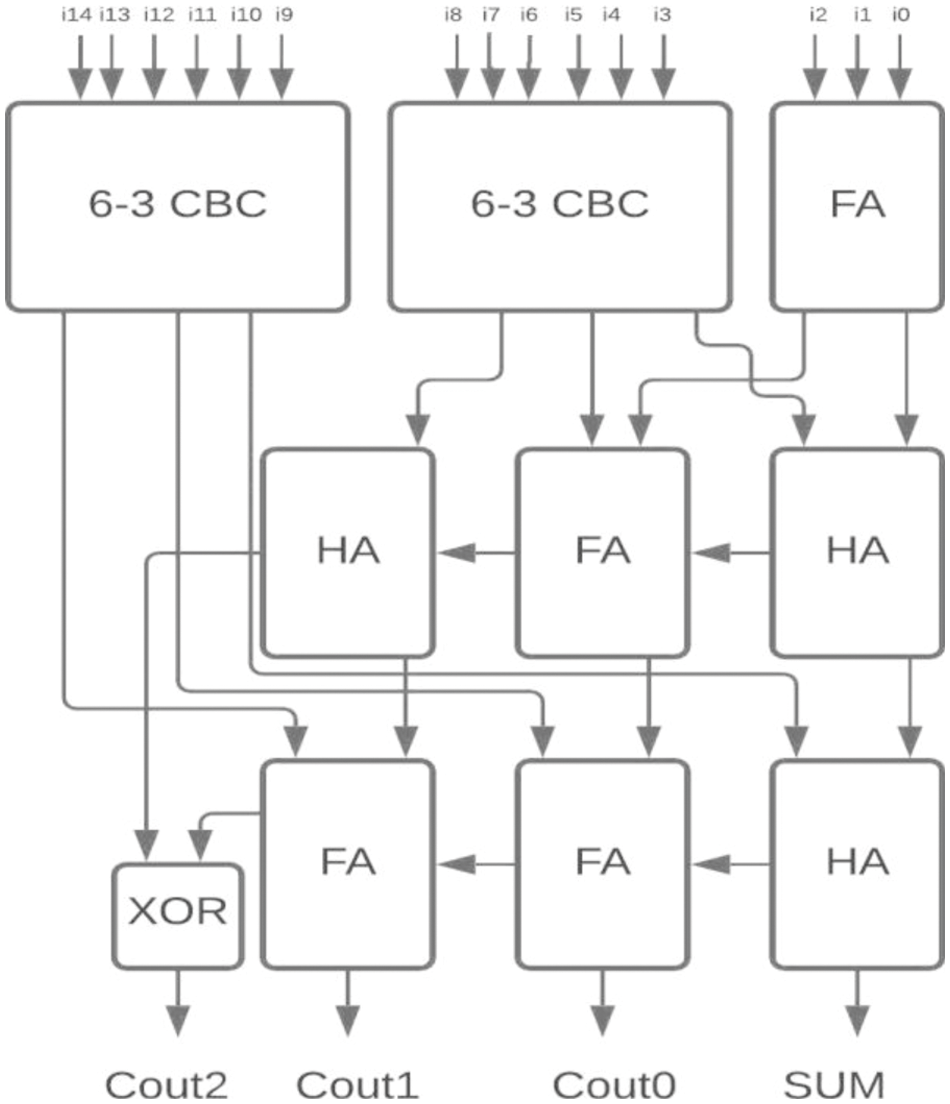
Figure 11: Proposed 15-4 CBC
For the two-stage reduction multiplier, higher bit CBCs are designed using the proposed 6-3 CBC and compared with 5-3 CBC architecture as shown in Figs. 12–15.
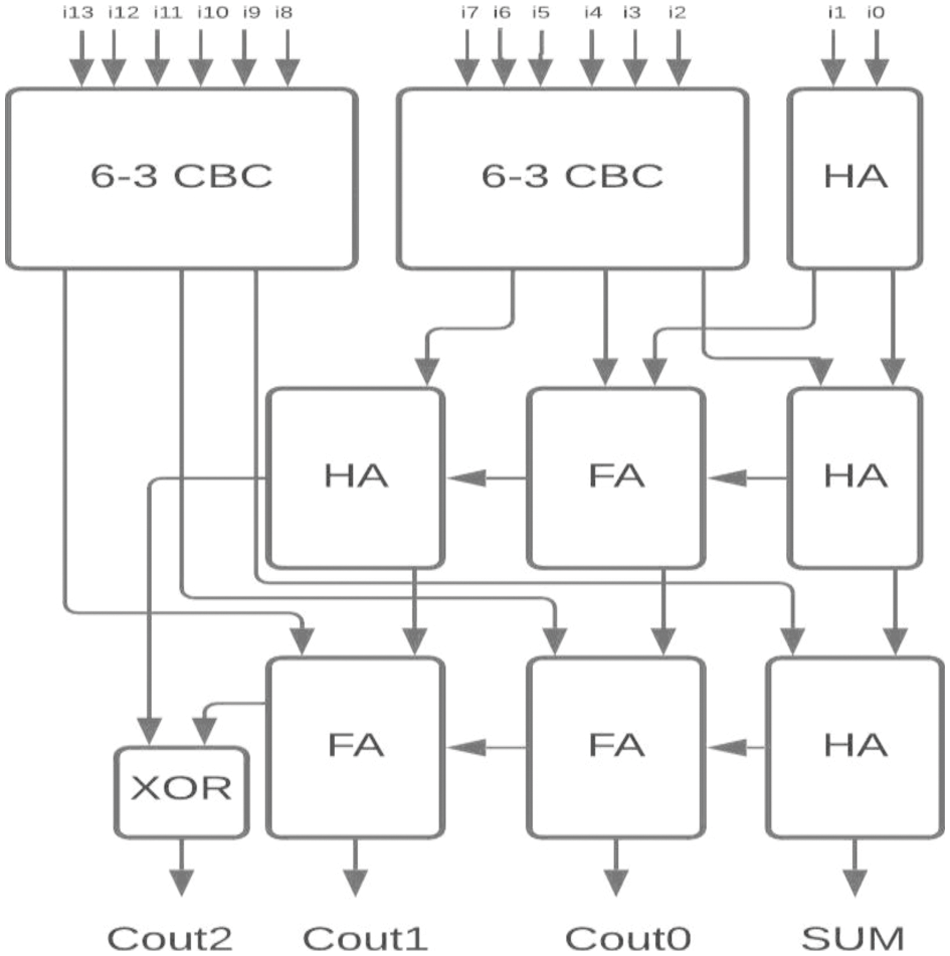
Figure 12: Proposed 14-4 CBC
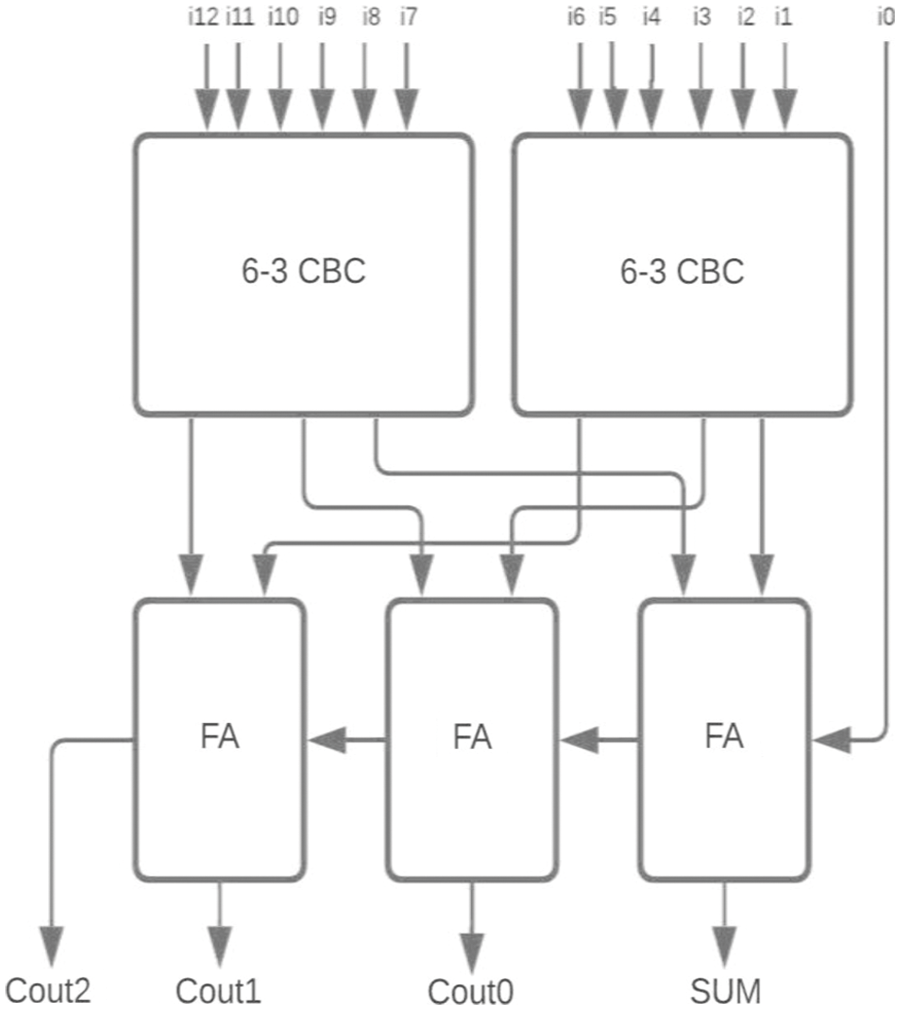
Figure 13: Proposed 13-4 CBC
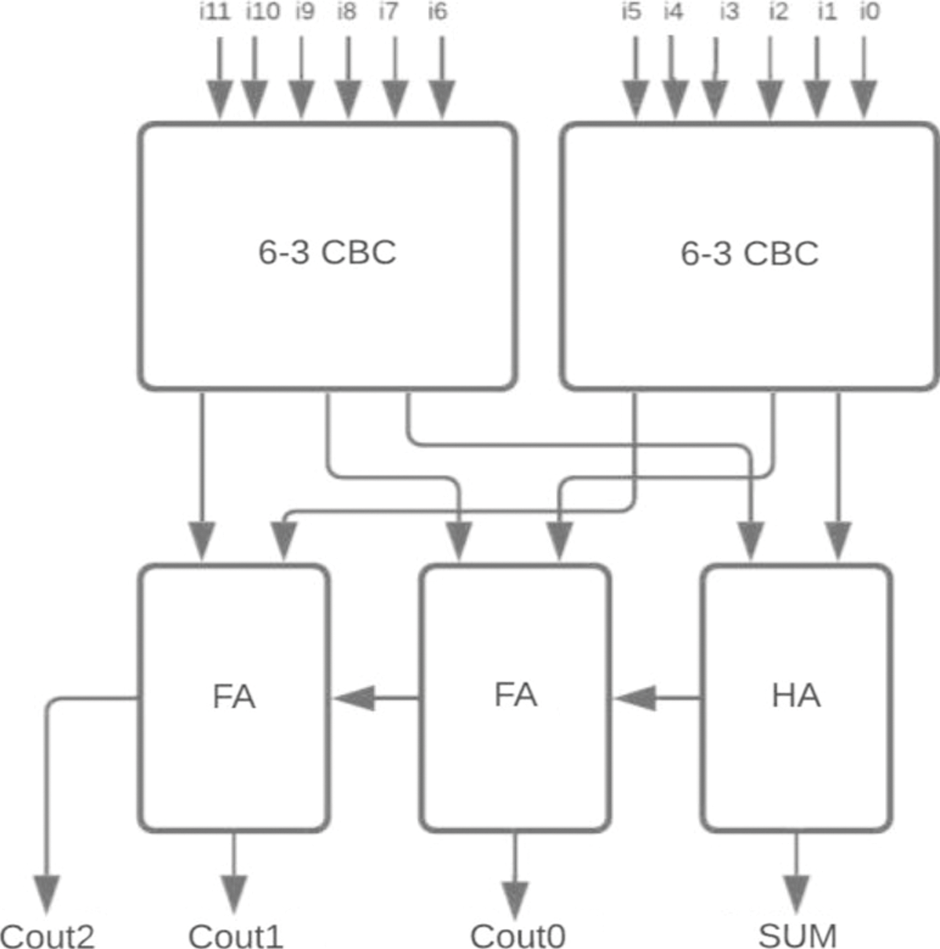
Figure 14: Proposed 12-4 CBC
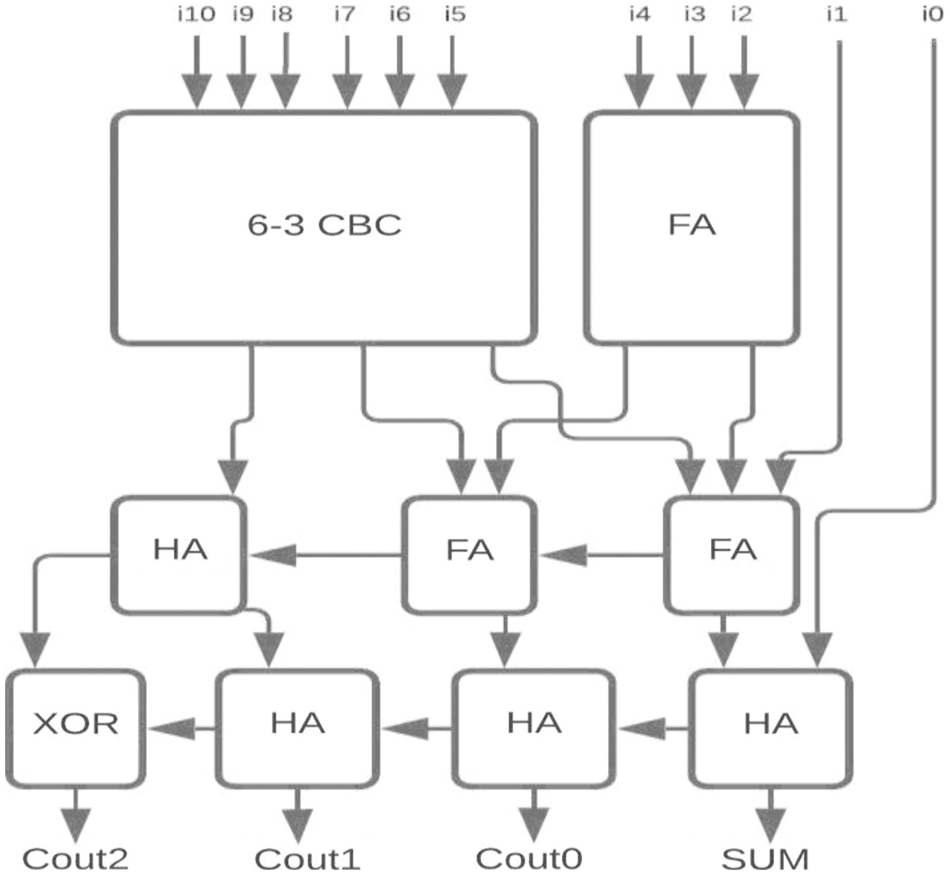
Figure 15: Proposed 11-4 CBC
Two design approximations have been performed in the proposed 6-3 CBCs which makes the design more efficient and suitable for image processing applications. Design-1 approximation is executed in sum term as shown in Eq. (6). Design -2 is executed with both sum as in Eq. (6) and Cout1 term as shown in Eq. (7).
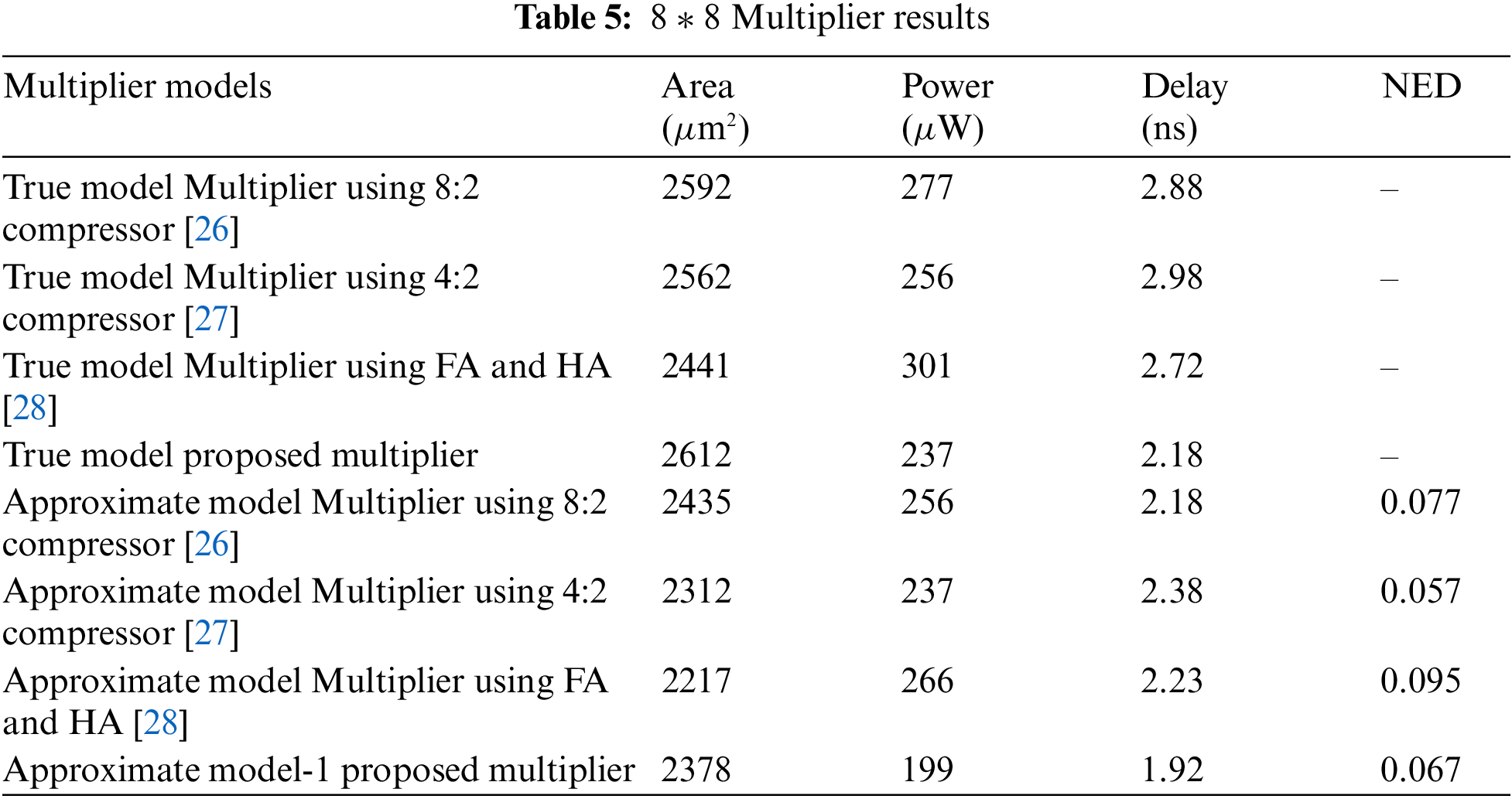
The proposed and existing CBCs functionality are verified through Verilog-HDL. The Cadence RTL compiler is used to calculate the power, speed, and area. All designs are compiled with 90 nm technology and the results are obtained using a typical Cadence library. Tab. 3, shows the area, power, and delay of the proposed and existing CBCs. Tab. 4. shows the approximate compressor area, power, and delay with its pass rate.
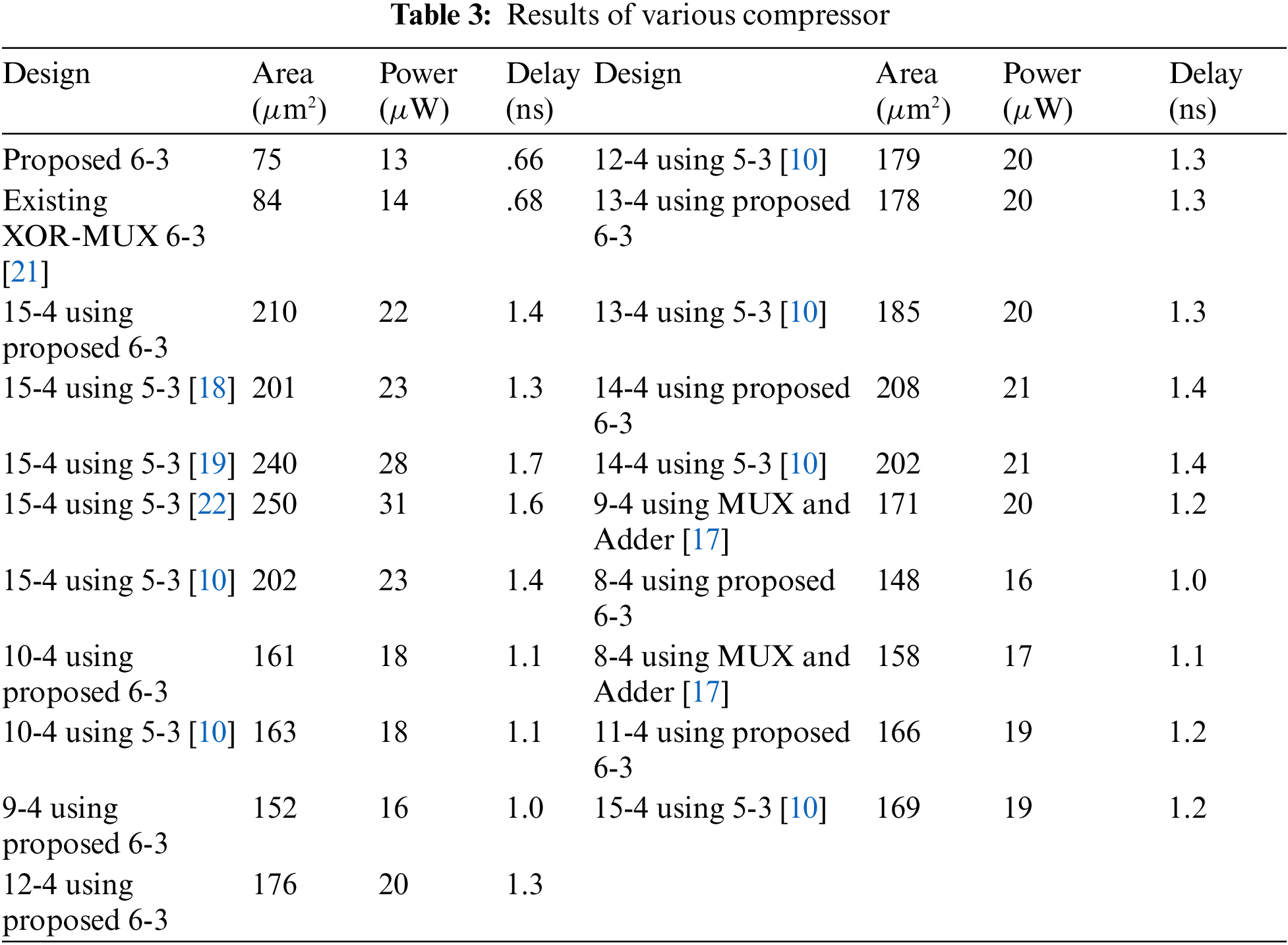
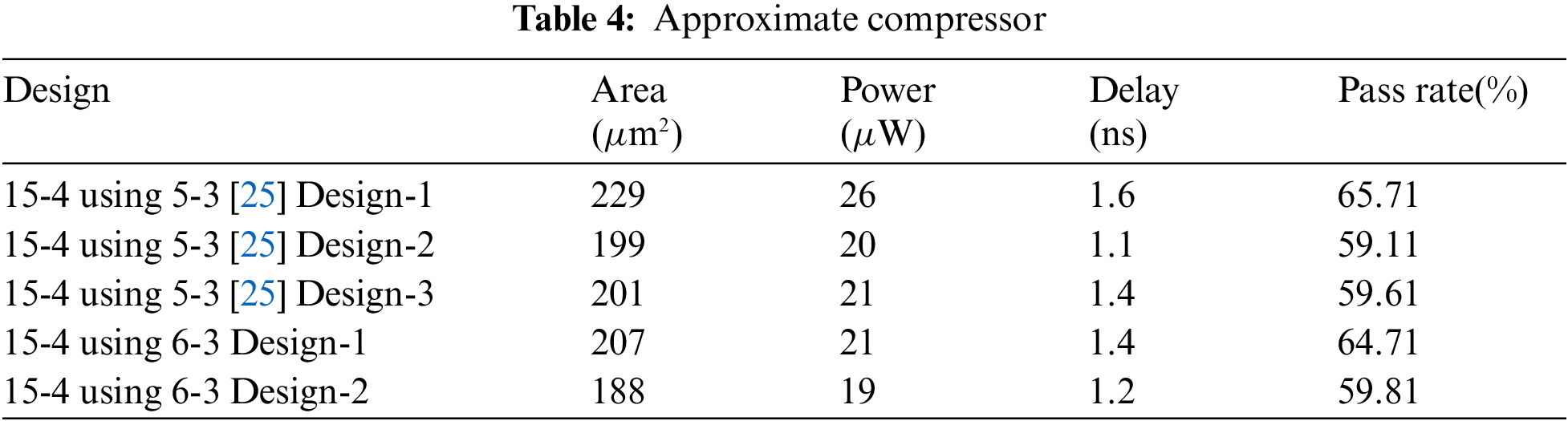
The proposed and existing CBCs are involved in partial product reduction of the 8 x 8, 16 x 16 multiplier designs. The proposed 16 x 16 multiplier utilizes 5-3 to 15-4 CBCs to achieve two-stage reduction. The proposed multiplier is compared with various conventional 16 x 16 multipliers that use only specific CBCs. The 8 x 8 multiplier is designed with the proposed CBC and the performance is evaluated and compared with existing multipliers.
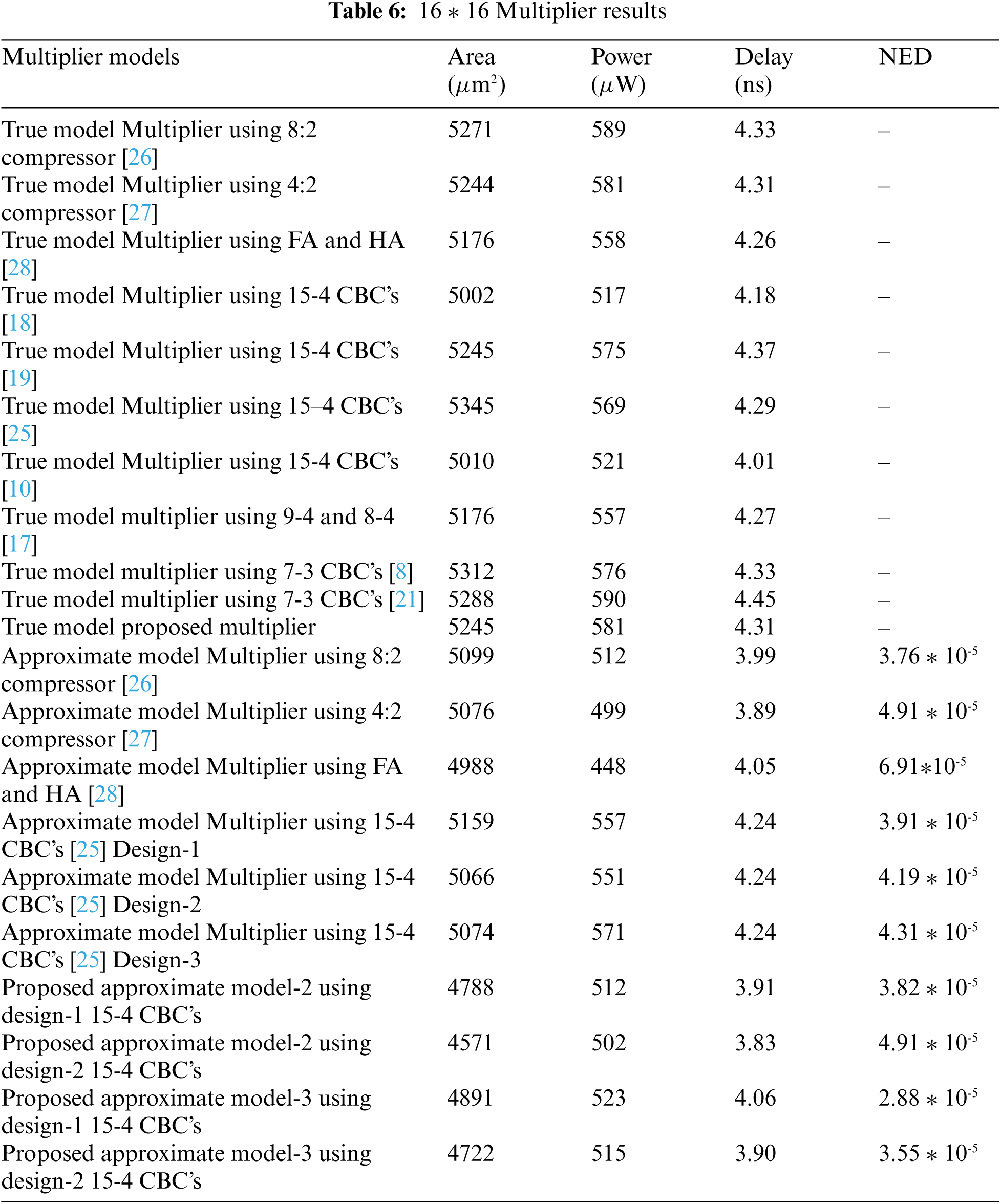
The proposed multipliers are shown in Figs. 16 and 17. The approximate 6-3 compressor is also used in the multiplier design and is compared with related approximate works. In model-1 of 8 x 8 multipliers, approximations are performed in the middle 5 columns. Two approximation models have been developed for 16 x 16 multiplier (i) model-2 approximation on entire CBC where 6-3 is used (ii) model-3 approximation from middle to LSB side CBC where 6-3 is used. Tabs. 5 and 6, give the results of 8 x 8 and 16 x 16 multipliers respectively.
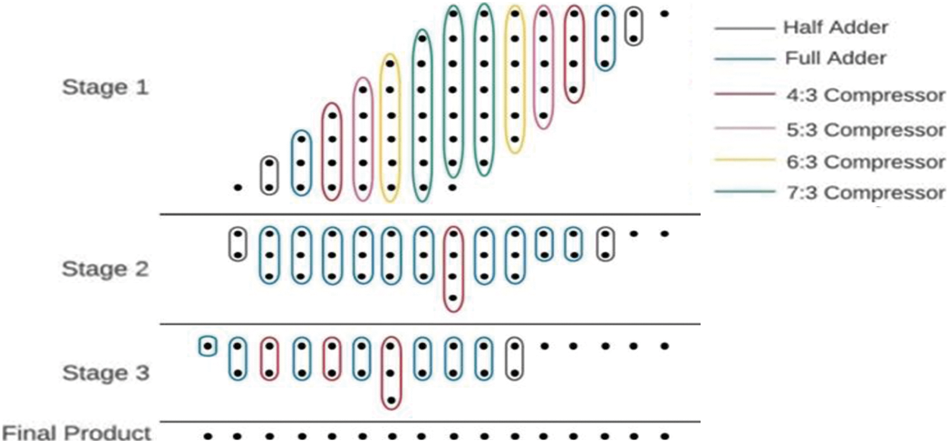
Figure 16: 8 * 8 multiplier
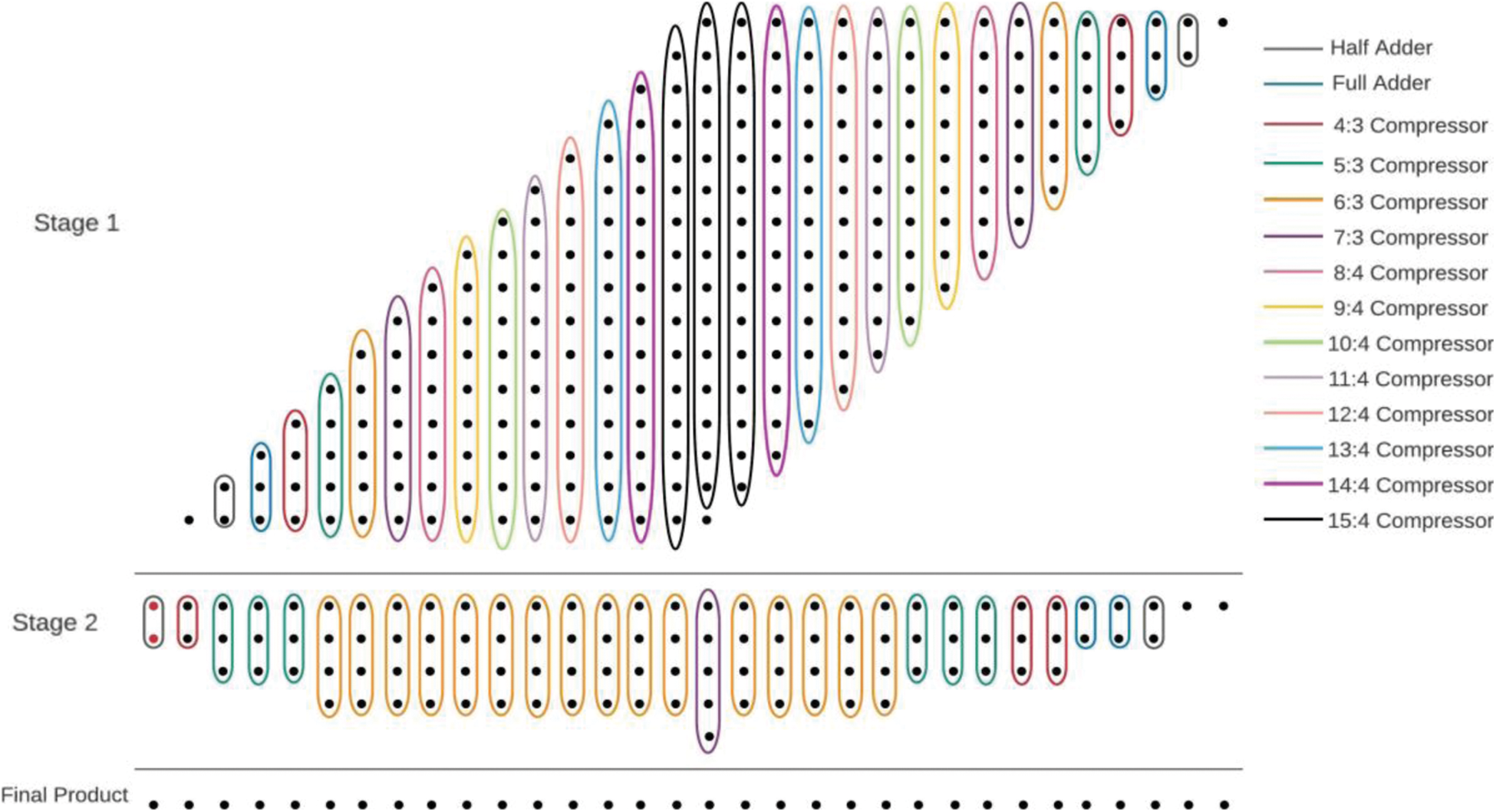
Figure 17: 16 * 16 multiplier
The VLSI arithmetic circuit is essential in many digital applications. In this work, both true and approximate multipliers have been designed using various CBCs. The approximate multiplier can be suitable for any multimedia application. To check the quality of the proposed approximate multiplier, 8-bit and 16-bit images are multiplied using the proposed and existing multipliers. Two different 8-bit test samples were taken from Signal and Image processing Institute (SIPI) of the University of Southern California (USC) (http://sipi.usc.edu/database) data set and multiplied with the true, existing approximate, and proposed approximate multiplier.
The results of multiplication with their corresponding PSNR values are shown in Fig. 18. For contrast scaling applications, the image will be self-multiplied, so the standard test image, Lena is squared using all multipliers and the PSNR values are observed as shown in Fig. 19. The Performance of the 16-bit multipliers is evaluated with two test images taken from (https://sourceforge.net/projects/testimages) data set and multiplied with true, existing approximate, and proposed approximate multipliers as shown in Fig. 20. The standard test image, 16 bit-Lena is squared and the PSNR values are noted as shown in Fig. 21.

Figure 18: 8-bit clock * aeroplane

Figure 19: 8-bit lena * lena

Figure 20: 16-bit lion * pencil

Figure 21: 16-bit lena * lena
The construction of multipliers based on various CBCs has been presented in this paper. The design of an input shuffled 6-3 counter compressor has been presented in this work. Using the proposed 6-3 CBC, several higher-length CBCs have been constructed in this paper. The proposed two-stage reduction multiplier shows an average improvement of 6% in delay and 4% in power. The proposed 6-3 CBC, when used in 15-4 CBC, shows an average improvement of 5% in area, 19% in power, and 7% in delay. The method of approximate computation is used in all compressors and the proposed system shows admirable PSNR results when compared to the conventional techniques. In future the approximate circuit can be involved in much application. This work can extended to construction of convolutional layer with approximate multiplier which is used for imaging application.
Acknowledgement: Ms Anuj Chahal and Ms Antara Ghosh are gratefully appreciated for their support.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. D. Radhakrishnan and A. P. Preethy, “Low power CMOS pass logic 4-2 compressor for high-speed multiplication,” in Proc. of the 43rd IEEE Midwest Sym. on Circuits and Systems (Cat. No. CH37144), Lansing, MI, USA, IEEE, vol.3, pp. 1296–1298, 2000. [Google Scholar]
2. D. Liu, “Embedded DSP processor design: Application specific instruction set processors,” in Morgan Kaufmann Publishers Inc., San Francisco, CA, United States, Elsevier, pp. 808, 2008. [Google Scholar]
3. Y. Kim, Y. Zhang and P. Li, “An energy efficient approximate adder with carry skips for error resilient neuromorphic VLSI systems,” in 2013 IEEE/ACM Int. Conf. on Computer-Aided Design (ICCAD), San Jose, CA, USA, IEEE, pp. 130–137, 2013. [Google Scholar]
4. Y. Bansal, C. Madhu and P. Kaur, “High speed vedic multiplier designs-A review,” in 2014 Recent Advances in Engineering and Computational Sciences (RAECS), March, Chandigarh, India, IEEE, pp. 1–6, 2014. [Google Scholar]
5. X. Yu, A. Aouari, R. F. Mansour and S. Su, “A hybrid algorithm based on PSO and GA for feature selection,” Journal of Cybersecurity, vol. 3, no. 2, pp. 117–124, 2021. [Google Scholar]
6. S. Veeramachaneni, K. M. Krishna, L. Avinash, S. R. Puppala and M. B. Srinivas, “Novel architectures for high-speed and low-power 3-2, 4-2 and 5-2 compressors,” in 20th Int. Conf. on VLSI Design Held Jointly with 6th Int. Conf. on Embedded Systems (VLSID’07), Bangalore, India, IEEE, pp. 324–329, 2007. [Google Scholar]
7. R. Menon and D. Radhakrishnan, “High performance 5:2 compressor architectures,” IEEE Proceedings-Circuits, Devices and Systems, vol. 153, no. 5, pp. 447–452, 2006. [Google Scholar]
8. S. Ghafari, M. Mousazadeh, A. Khoei and A. Dadashi, “A new very high-speed true 7-3 compressor,” in 2019 MIXDES-26th Int. Conf., Rzeszow, Poland, IEEE, pp. 163–166, 2019. [Google Scholar]
9. N. Van Toan and J. G. Lee, “FPGA-based multi-level approximate multipliers for high performance error-resilient applications,” IEEE Access, vol. 8, pp. 25481–25497, 2020. [Google Scholar]
10. H. L. Krishna, M. Neeharika, V. Janjirala, S. Veeramachaneni and N. S. Mahammad, “Efficient design of 15:4 counter using a novel 5:3 counter for high-speed multiplication,” IET Computers and Digital Techniques, vol. 15, no. 1, pp. 12–19, 2021. [Google Scholar]
11. S. E. Abed, B. J. Mohd, Z. Al-bayati and S. Alouneh, “Low power Wallace multiplier design based on wide counters,” International Journal of Circuit Theory and Applications, vol. 40, no. 11, pp. 1175–1185, 2012. [Google Scholar]
12. M. H. Moaiyeri, F. Sabetzadeh and S. Angizi, “An efficient majority- based compressor for approximate computing in the nano era,” Microsystem Technologies, vol. 24, no. 3, pp. 1589–1601, 2018. [Google Scholar]
13. K. N. Vijeyakumar, P. T. N. K. Joel, S. H. S. Jatana, N. Saravanakumar, S. Kalaiselvi et al., “Area efficient parallel median filter using approximate comparator and faithful adder,” IET Circuits, Devices & Systems, vol. 14, no. 8, pp. 1318–1331, 2020. [Google Scholar]
14. L. Li, L. Sun, Y. Xue, S. Li, X. Huang et al., “Fuzzy multilevel image thresholding based on improved coyote optimization algorithm,” IEEE Access, vol. 9, pp. 33595–33607, 2021. [Google Scholar]
15. S. F. Hsiao, M. R. Jiang and J. S. Yeh, “Design of high-speed low-power 3-2 counter and 4-2 compressor for fast multipliers,” Electronics Letters, vol. 34, no. 4, pp. 341–343, 1998. [Google Scholar]
16. C. H. Chang, J. Gu and M. Zhang, “Ultra low-voltage low-power CMOS 4-2 and 5-2 compressors for fast arithmetic circuits,” IEEE Transactions on Circuits and Systems I: Regular Papers, vol. 51, no. 10, pp. 1985–1997, 2004. [Google Scholar]
17. R. Marimuthu, D. Bansal, S. Balamurugan and P. S. Mallick, “Design of 8-4 and 9-4 compressors for high speed multiplication,” American Journal of Applied Sciences, vol. 10, no. 8, pp. 893, 2013. [Google Scholar]
18. S. R. Chowdhury, A. Banerjee, A. Roy and H. Saha, “Design, simulation and testing of a high speed low power 15-4 compressor for high speed multiplication applications,” in 2008 First Int. Conf. on Emerging Trends in Engineering and Technology, Nagpur, India, IEEE, pp. 434–438, 2008. [Google Scholar]
19. R. Marimuthu, M. Pradeepkumar, D. Bansal, S. Balamurugan and P. S. Mallick, “Design of high speed and low power 15-4 compressor,” in 2013 Int. Conf. on Communication and Signal Processing, Melmaruvathur, India, IEEE, pp. 533–536, 2013. [Google Scholar]
20. A. Dandapat, S. Ghosal, P. Sarkar and D. Mukhopadhyay, “A 1.2-ns16× 16-bit binary multiplier using high speed compressors,” International Journal of Electrical and Electronics Engineering, vol. 4, no. 3, pp. 234–239, 2010. [Google Scholar]
21. S. Mehrabi, K. Navi and O. Hashemipour, “Performance analysis and simulation of two different architectures of (6:3) and (7:3) compressors based on carbon nano-tube field effect transistors,” in 2013 IEEE 5th Int. Nanoelectronics Conf. (INEC), Singapore, IEEE, pp. 322–325, 2013. [Google Scholar]
22. K. M. Reddy, M. H. Vasantha, Y. B. N. Kumar and D. Dwivedi, “Design and analysis of multiplier using approximate 4-2 compressor,” AEU-International Journal of Electronics and Communications, vol. 107, no. 9, pp. 89–97, 2019. [Google Scholar]
23. M. S. Kim, A. A. D. B. Garcia, H. Kim and N. Bagherzadeh, “The effects of approximate multiplication on convolutional neural networks,” in IEEE Transactions on Emerging Topics in Computing, Early access, IEEE, pp. 1, 2021. [Google Scholar]
24. I. Hammad and K. El-Sankary, “Impact of approximate multipliers on VGG deep learning network,” IEEE Access, vol. 6, pp. 60438–60444, 2018. [Google Scholar]
25. R. Marimuthu, Y. E. Rezinold and P. S. Mallick, “Design and analysis of multiplier using approximate 15-4 compressor,” IEEE Access, vol. 5, pp. 1027–1036, 2016. [Google Scholar]
26. M. M. D. Savio and T. Deepa, “Design of higher order multiplier with approximate compressor,” in 2020 IEEE Int. Conf. on Electronics, Computing and Communication Technologies (CONECCT), Banglore, India, IEEE, pp. 1–6, 2020. [Google Scholar]
27. M. Taheri, A. Arasteh, S. Mohammadyan, A. Panahi and K. Navi, “A novel majority based imprecise 4:2 compressor with respect to the current and future VLSI industry,” Microprocessors and Microsystems, vol. 73, no. 3, pp. 102962, 2020. [Google Scholar]
28. G. Anusha and P. Deepa, “Design of approximate adders and multipliers for error tolerant image processing,” Microprocessors and Microsystems, vol. 72, no. 7, pp. 102940, 2020. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |