DOI:10.32604/cmc.2022.025660

| Computers, Materials & Continua DOI:10.32604/cmc.2022.025660 |  |
| Article |
Blockchain-Based Robust Data Security Scheme in IoT-Enabled Smart Home
1Center for Security, Theory and Algorithmic Research, International Institute of Information Technology, Hyderabad, 500032, India
2School of Electronics Engineering, Kyungpook National University, Daegu, 41566, Korea
3Department of Mathematics, College of Science, King Khalid University, Abha, Saudi Arabia
*Corresponding Author: YoungHo Park. Email: parkyh@knu.ac.kr
Received: 01 December 2021; Accepted: 09 February 2022
Abstract: The recent surge in development of smart homes and smart cities can be observed in many developed countries. While the idea to control devices that are in home (embedded with the Internet of Things (IoT) smart devices) by the user who is outside the home might sound fancy, but it comes with a lot of potential threats. There can be many attackers who will be trying to take advantage of this. So, there is a need for designing a secure scheme which will be able to distinguish among genuine/authorized users of the system and attackers. And knowing about the details of when and what IoT devices are used by the user, the attacker can trace the daily activities of user and can plan an attack accordingly. Thus, the designed security scheme should guarantee confidentiality, anonymity and un-traceability. Most of the schemes proposed in the literature are either non-blockchain based which involves inherent problems of storing data in a single-server or assuming weaker attack models. In this work, we propose a novel scheme based on blockchain technology, assuming a stronger Canetti and Krawczyk (CK)-threat model. Through the formal and informal security, and comparative analysis, we show that the proposed scheme provides a superior security and more functionality features, with less communication cost and comparable computational cost as compared to other competent schemes. Moreover, the blockchain based simulation study on the proposed scheme has been conducted to show its feasibility in real-life application.
Keywords: Internet of things (IoT); smart home; ubiquitous computing; blockchain; security
Now a days, almost all the utilities are enabled with the Internet connectivity. It benefits users of multiple domains to operate the resources remotely and know their status. Smart home is one such application of the Internet of Things (IoT), where the users can monitor the home appliances and can take decisions accordingly. The system helps in tackling numerous real-life problems, like robberies (by collecting the data from surveillance) and fire accidents (by collecting data from fire detecting sensors) and so on. However, it brings in several challenges which are to be handled and so, there is a need for designing a security scheme very carefully by considering all such challenges and making sure that no sensitive information is compromised.
Since there are many schemes in the literature which ensure secure communication between home gateway and IoT smart devices, we confine ourselves in designing the secure scheme which is subjected to the security aspects/hurdles that either of a user or the home gateway faces when they try to communicate with each other. The blockchain technology has been employed in order to enhance the security of a system. The blockchain has several inherent properties like decentralization, immutability and transparency. Thus, the blockchain technology provides high data integrity, and resilience against Denial-of-Service attacks (DoS) and several cyber security attacks when the data is simply stored in centralized databases. The immutability of the blockchain allows no adversary can update a block, insert fake information into a block or even delete a block once a block is added into the blockchain after running a consensus protocol among a group of nodes, called peer nodes, in a distributed Peer-to-Peer (P2P) blockchain network. To mitigate these issues, we aim to proposed a novel blockchain-based robust security scheme in an IoT-enabled smart home environment, which is light-weight by making the authentication and key establishment between the two authorized parties with minimal resources faster, and it will make a user in smart home deployment to feel that all the resources are at his disposal.
A blockchain-based smart home system is shown in Fig. 1. In this system, we have a trusted registration authority (RA), which takes the responsibility of registering all the authorized entities by providing the corresponding secret parameters of that entity in a secure channel. We maintain a gateway node which acts as a mediator between the network of devices at home and remote users operating through some smart devices with smart cards installed in it. Once the home gateway and the users register with the RA, the users will be installing a smart card in their device, which has some set of parameters (credentials) through which their secrets are hidden. A set of consensus nodes are maintained on a cloud that are responsible for verifying the blocks and adding the blocks into the blockchain stored using these cloud nodes.
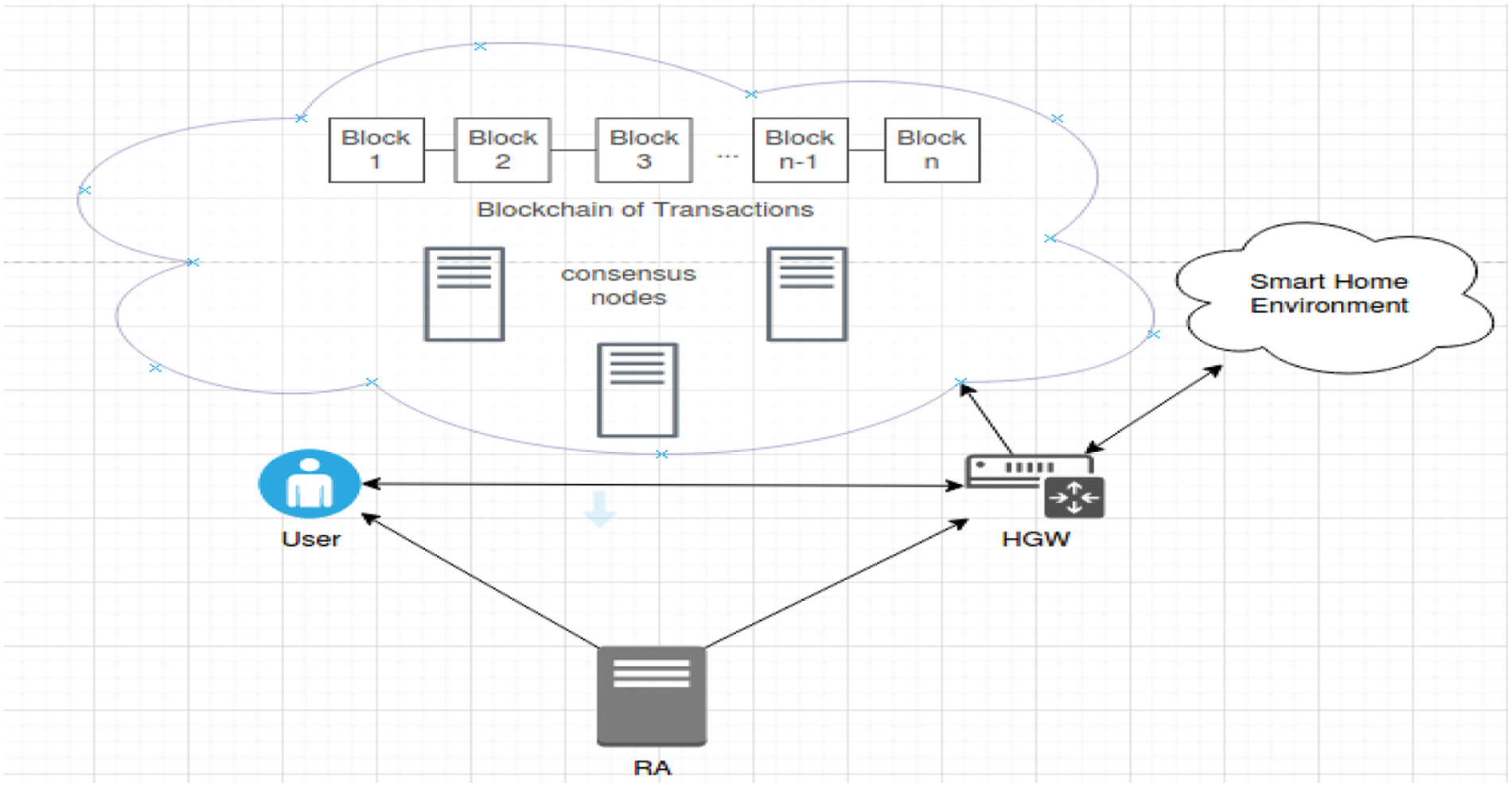
Figure 1: A general IoT network model of blockchain based smart home system
The proposed scheme is evaluated under “Dolev-Yao (DY) threat model” [1], which considers an adversary has capabilities of modifying, replaying, dropping the transactions and requests in transit. The adversary can also impersonate the authorized user(s) and home gateway. The smart devices of the devices with installed smart cards can be lost and all the information from them can be extracted by the adversary. The scheme also adopts the “Canetti and Krawczyk (CK-adversary model)” [2], where the adversary has all the capabilities as in the DY threat model, and in addition, the session state information and previous session keys of the entities in the system can be leaked through the session hijacking attack. The home gateway node can be put under a locking system as in [3] in order to avoid physical capture attack by the adversary. In addition, some smart home IoT devices can be physically capture by the adversary as these devices cannot be always monitored in 24 × 7 time. The adversary can then extract all the credentials stored in a captured smart device using the power analysis attacks [4].
In the following, some important contributions made in the research paper are listed:
• The proposed scheme is light-weight, which makes the authentication and key establishment between the two authorized parties with minimal resources faster, and it will make a user to feel that all the resources are at his disposal. The proposed scheme makes sure that the anonymity of a user is never compromised. In addition, the blockchain technology has been adopted with the scheme to make it highly robust for data storage in P2P blockchain network to provide high data integrity, and resilience against DoS and several cyber security attacks.
• The proposed scheme handles the challenging and risky smart card stolen attacks, and thus, a user needs not to be panic if he lost his smart card. The scheme is designed in such a way that it will resist many attacks, like stolen smart card attack, user impersonation attack, replay attack, gateway impersonation attack, man-in-the-middle attack, and Ephemeral Secret Leakage (ESL) attack, which make the scheme robust. We also consider a stronger notion of user anonymity where even gateway will not know the user's actual identity.
• We show how the proposed scheme is resistant to various potential attacks under the DY and CK-adversary models. A detailed comparative analysis among the proposed scheme and other existing schemes show that the proposed scheme provides a superior security and more functionality features, with less communication cost and comparable computational cost as compared to other competent existing schemes in the literature.
• The practical implementation of the proposed scheme using the blockchain-based experimental study has been shown to exhibit the feasibility in real-life application.
The remainder of this article is as follows. Section 2 describes an in-depth literature study on the related authentication protocols in an IoT environment. Various phases related to the proposed scheme have been discussed in Section 3. A detailed security analysis using both formal and informal security study has been done in Section 4 to show the robustness of the proposed scheme against various types of attacks in an IoT-enabled smart home environment. Section 5 provides a detailed comparative study on various security and functionality features, and communication and computational costs among the proposed scheme and other existing schemes. A blockchain-based implementation on the proposed scheme has been shown in Section 6. Finally, Section 7 provides some concluding remarks on this article.
There has been extensive research on authentication schemes for smart home systems in the last decade. We study some of the most recent schemes relevant to the model developed in our proposed system.
Fakroon et al. [5] proposed an authentication scheme for a smart home system with smart devices to be accessed by users via gateway nodes. This scheme makes use of the user's location that restricts users beyond distance from accessing the smart devices by considering it a malicious access. This scheme has low computation cost, but higher communication cost. It does not consider usage of blockchain.
Shuai et al. [6] proposed an authentication scheme based on elliptic curve cryptography for smart home environment. This scheme is vulnerable to privileged insider attack that can be launched using stolen smart card and offline password guessing attack, user impersonation attack, parallel session attack and password change attack. This scheme was improved by Banerjee et al. [7] to overcome its limitations by considering a stronger notion of threat model, called Canetti and Krawczyk model (CK-adversary model), where the session secret leakage is possible. They adopted smart card-based authentication for user and assumed a central registry to supply secrets to the gateway and the users. This scheme is not block-chain based, and hence, it has all inherent problems of storing the transactions in a single server and also this scheme does not provide anonymity of user at the gateway node. However, this scheme is secure against several attacks such as ESL attack and stolen smart card attack. The same scheme by Shuai et al. [6] was also cryptanalyzed by Kaur et al. [8] by exposing its vulnerability to insecure session key agreement, replay attack, and gateway node bypass attack in addition to the attacks identified by Banerjee et al. [7]. The scheme by Shuai was also considered to be vulnerable against offline dictionary attack and it lacks forward secrecy as identified by Xu et al. [9].
Lin et al. [10] proposed a block-chain based mutual authentication scheme for smart home, where authentication of the users is done by using group signatures and session key establishment between user and the gateway with the help of the elliptic curve integrated encryption scheme (ECIES), and the gateway verification is done using keyed message authentication code (MAC) function generated using ECIES scheme. They confined the scope of the work to secure communication between a user and the gateway, and the same between the gateway and IoT devices are declared beyond the scope of their work. The attack model considered in their work is something like the DY threat model and it does not consider the scope for session secret leakage. Hence, their scheme is vulnerable to ESL attack under the CK-adversary model.
Naoui et al. [11] proposed a user authentication scheme, called LRP-SHAP, for smart home system with a user having a smartphone in a remote environment accessing the smart devices in the smart home via home energy manager (HEM). It uses a Wi-Fi or 4G/5G network for communication. It applies the elliptic curve and hashed message authentication code (HMAC) cryptographic operations in addition to hash functions and cookies for the authentication purpose. However, it has the extra overhead of storing cookies in addition to the parameters required for authentication.
From the above discussion, it is clear that most of the existing schemes are either vulnerable to various attacks including the ESL attack under the CK-adversary model or they are expensive in communication/computational costs. Thus, most of the schemes used in the literature for smart homes consider somewhat weaker notion of security and they are prone to ESL attack under the CK-adversary model, while some of the recent works consider the CK-adversary model but they are either non-blockchain based approaches which will have an inherent disadvantage of storing transactions in a single server or there is no stronger notion of anonymity of user (in the gateway). Moreover, the discussed existing schemes do not adopt the blockchain technology. As a result, the existing schemes lack in providing high data integrity, and they are not resilience against DoS and several cyber security attacks.
To deal with this, we propose a security scheme which can solve these major issues, by adopting the prominent solutions of existing schemes as building blocks with the blockchain technology. The proposed scheme is based on block chain technology and assumes a stronger CK-adversary model. It makes a user anonymous even to the gateway, anonymous and un-traceable to the intruder, and it is also resistant to several attacks for smart home environment.
In this section, we first discuss the main motivation behind the proposal of our blockchain-based security scheme for smart home environment. We then discuss different phases relevant to the proposed scheme.
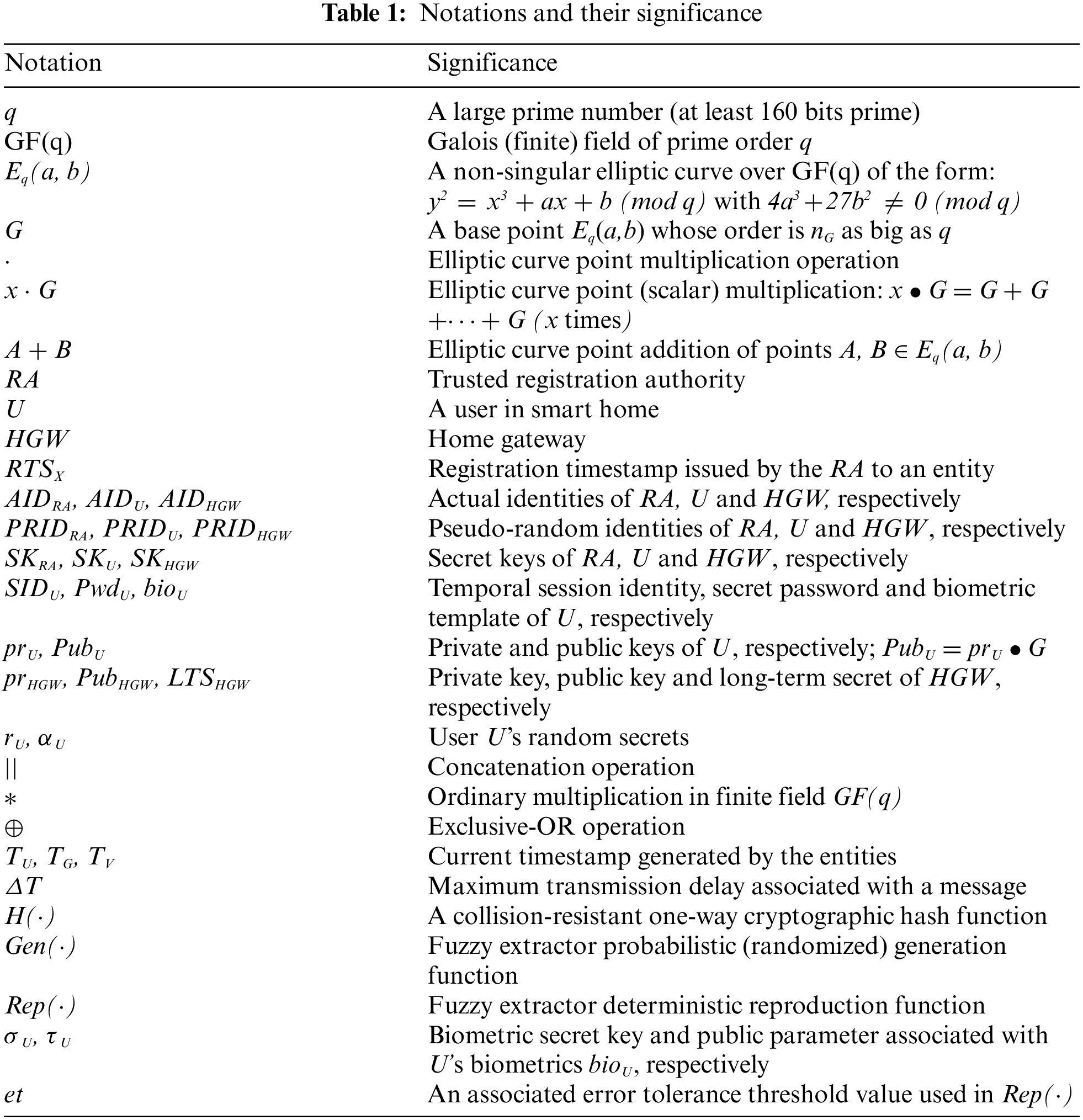
Various notations and their significance are provided in Tab. 1, which are used throughout the paper.
3.2 Description of Various Phases
In the following subsection, we now discuss the details of the various phases involved in the proposed blockchain-based security scheme for ubiquitous computing environment, called BlockUbiHome.
In this phase, the trusted RA sets up the system by generating various public and private parameters by executing the below steps:
• Step 1. The RA selects a non-singular elliptic curve Eq(a, b) of the form: y2 = x3 + ax + b over a finite (Galois) field GF(q), where a and b are constants chosen from Zq = {0, 1, 2, …, q−1}, 4a3 + 27b2 ≠ 0 (mod q) and q is a large prime such that the “Elliptic Curve Discrete Logarithm Problem (ECDLP)” is intractable, a base point G in Eq(a, b) and a “collision-resistant one-way hash function” H(.).
• Step 2. The RA then randomly picks its actual identity AIDRA and a unique secret key (SKRA) from
3.2.2 One-time Registration Phase
This phase is executed by the RA before the actual communication procedure with both gateway node and the user.
1) User registration phase: The user registration phase occurs as follows.
• Step 1. A user U selects an actual identity (AIDu), a secret key SKU, a password PwdU, temporal identity SIDU and registration timestamp RTSU, and calculates pseudo-random identity of the user U as PRIDU = H(AIDu || SKU || PwdU|| RTSU) and sends the credentials {PRIDU, SIDU} to the RA via secure channel.
• Step 2. After receiving the credentials of the user U, the RA computes a secret XRA = H(SIDU || PRIDU || SKRA || AIDRA), stores it in a smart card and returns the smart card to the user U via secure channel.
• Step 3. After receiving the smart card from the RA, the user U enters personal biometric bioU at the sensor of a particular terminal and obtains (σU, τU) using the “fuzzy extractor probabilistic generation function Gen(.)”, that is, Gen(bioU) = (σU, τU). U computes YU = XRA ⊕H(PwdU || σU|| AIDU) and generates a random αU
2) Gateway registration phase: Like the user registration phase, the gateway registration phase occurs as follows.
• Step 1. The RA selects an actual identity (AIDHGW) of the home gateway, registration timestamp RTSHGW and secret key SKHGW
• Step 2. After receiving the registration credentials from the RA, the gateway selects its private key as prHGW
To login to the smart home network, a registered user U needs the following steps:
• Step 1. U inserts his smart card and initiates the process by providing his actual identity AIDU, secret password PwdU, his/her bio-metrics bioU’ at the sensor of a specific terminal, say mobile device.
• Step 2. The smart card regenerates the biometric secret key σU using “fuzzy extractor deterministic reproduction function Rep(.)” as Rep(bioU’, τU) = σU provided that the “Hamming distance between the original registered biometric and current entered biometric is less than or equal to the error tolerance threshold value et”, and computes αU = αU’ ⊕ H(PwdU || σU), RpwdU = RpwdU’ ⊕ H(PRIDU || σU ||PwdU), RbioU = RbioU’ ⊕ H(σU || PRIDU || AIDU ||PwdU) and ZU’ = H(αU || RpwdU || RbioU || AIDU). The smart then checks if ZU’ = ZU. If it is so, the user login is successful. Otherwise, this phase is terminated.
• Step 3. U generates a random secret rU
This phase is summarized in Fig. 2.

Figure 2: Login phase of a user U
3.2.4 Authentication and Key Establishment Phase
In this phase, both the home gateway, HGW and the user, U mutually authenticate each other and set up a common session key between them for secure data exchange. This is achieved by executing the following steps:
• Step 1. The gateway (HGW) receives Msg1 at
• Step 2. The HGW then generates a random secret rG
• Step 3. The user U receives Msg2 at time
• Step 4. The user U generates current timestamp TV and computes a session key verifier as
• Step 5. When HGW receives the
This overall phase is finally briefed in Fig. 3.
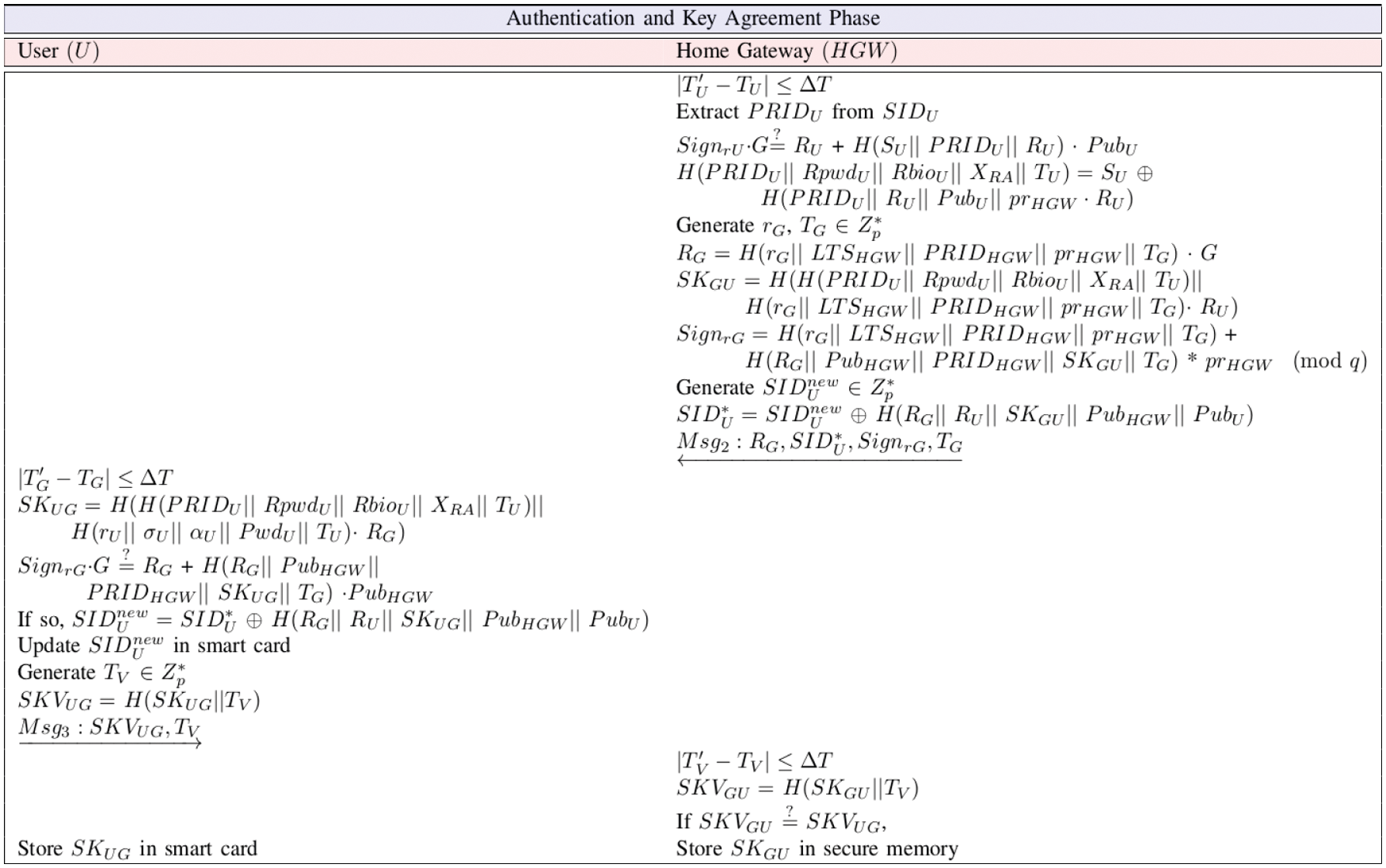
Figure 3: Authentication and key agreement among a user (U) and the home gateway node (HGW)
3.2.5 Secure Data Aggregation Phase
After the successful authentication and key establishment between a user and the gateway node, the transactions can be now sent in encrypted way using the established session key, along with the hash of transactions which will ensure privacy, integrity, and authentication between the communication parties. In this way, the in-charge gateway HGW will securely gather all the transactions, which will be used in forming the blocks for mining into the blockchain.
Once the home gateway (HGW) receives the transactions from the authorized users, it will be routing then to one of the consensus nodes of private blockchain, and once the transactions threshold is reached, the consensus node, being the leader (miner) node in the Peer-to-Peer (P2P) blockchain network, creates a block with the useful parameters which make it immutable. The transactions (Txi) in the block are encrypted with the public key of HGW in order to ensure privacy. Then using the voting-based Practical Byzantine Fault Tolerance (PBFT) consensus algorithm [12], the leader determines whether to add or discard the block. The structure of a block is shown in Fig. 4. A constructed block has two parts: a) block header and 2) block payload. The block header contains the following fields:
• Block version (BV): It is a unique version number attached to each created block into the blockchain.
• Previous block hash (PBH): For creating the chain of blocks into the blockchain, the hash value (using Secure Hash Algorithm (SHA-256) [13] which produces 256-bit hash output) of the previous block of a current block is calculated.
• Merkle Tree Root (MTR): It is created as the hash value of all the transactions present in a block. Note that the Merkle tree is considered as a hash tree is a tree in which each “leaf node” is labelled with the cryptographic hash value of a data block containing the digital information. On the other side, each node that is not a leaf node is also labelled with the cryptographic hash value of the labels of its child nodes. Thus, a hash tree (Merkle tree) is treated as a generalization of a “hash list” and a “hash chain”.
• Timestamp (T): The time when a block was created.
• Owner of block (BO): It represents an entity in the network who has created the block.
• Public key of signer (PubHGW): The public key of the home gateway being the signer is used to verify the signature on the current block hash (CBlock). CBlock is used to create the signature using the “Elliptic Curve Digital Signature Algorithm (ECDSA) signature verification function” with the help of the private key prHGW of HGW.
• List of encrypted transactions: A list of nt encrypted transactions is inserted as block payload. Here, the encryption is done using the public key PubHGW to provide confidentiality or privacy of the transactions which can be viewed by the HGW only.
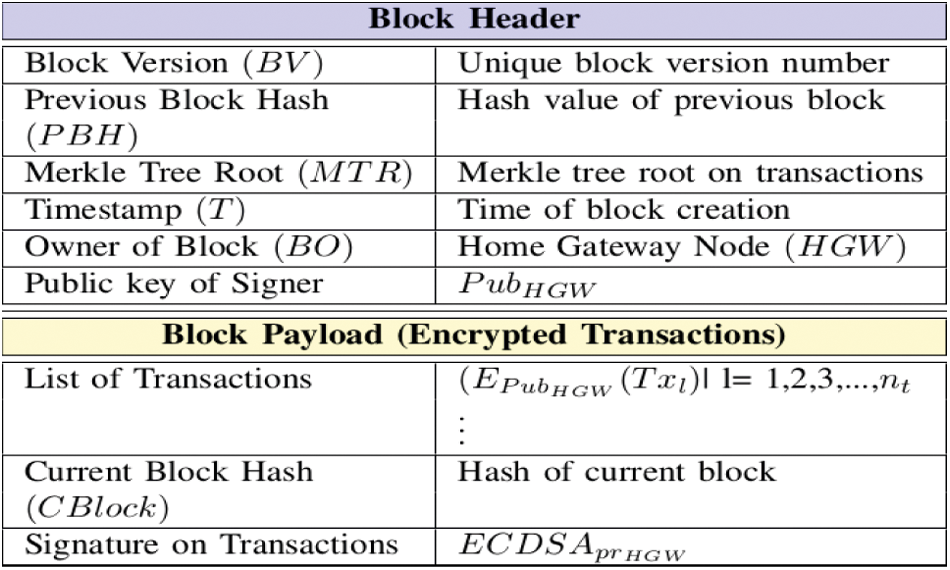
Figure 4: Structure of a block in blockchain
To verify a block, we need three level verification process: 1) Merkle tree root verification helps to checks whether any transactions in the block are modified or not; 2) current block hash verification helps to check whether any block header fields, and the transactions are proper or not; and 3) block signature verification using the ECDSA verification algorithm helps in verifying whether the overall block is authentic or not.
When an authorized user wants to remotely operate the smart devices at his home, he must provide his secret credentials and biometric details, through which the smart card authenticates him as a genuine user and will allow him in exchanging a secret session key. The user then passes all the essential parameters needed to the home gateway for constructing a session key. Through the authentication and key establishment phase of the scheme, the home gateway and the user will share a secret session key. Using the shared session key, the user can encrypt the transactions (with the necessary details of IoT device and commands to it) and can send the transactions to the home gateway securely through the secure data aggregation phase. The home gateway decrypting the transactions will send the commands to the appropriate IoT device(s) and through the block addition phase of the scheme, the transactions will be added into the blockchain. The results from IoT devices are also encrypted with the same key and will be passed to the user.
The overall working flow diagram of the proposed smart home system including the block addition phase is summarized in Fig. 5. In the process flow diagram of the proposed scheme, two types of communication are performed through a) private/secure channel and b) public (open) channel. Here, the private channel is used for registration of the entities in a smart home environment. For instance, a user in smart home can register with the trusted RA in person by submitting the registration credentials to the RA and then receive a smart card from the RA. On the other side, the public channel is used for all other communications excluding the registration phase.
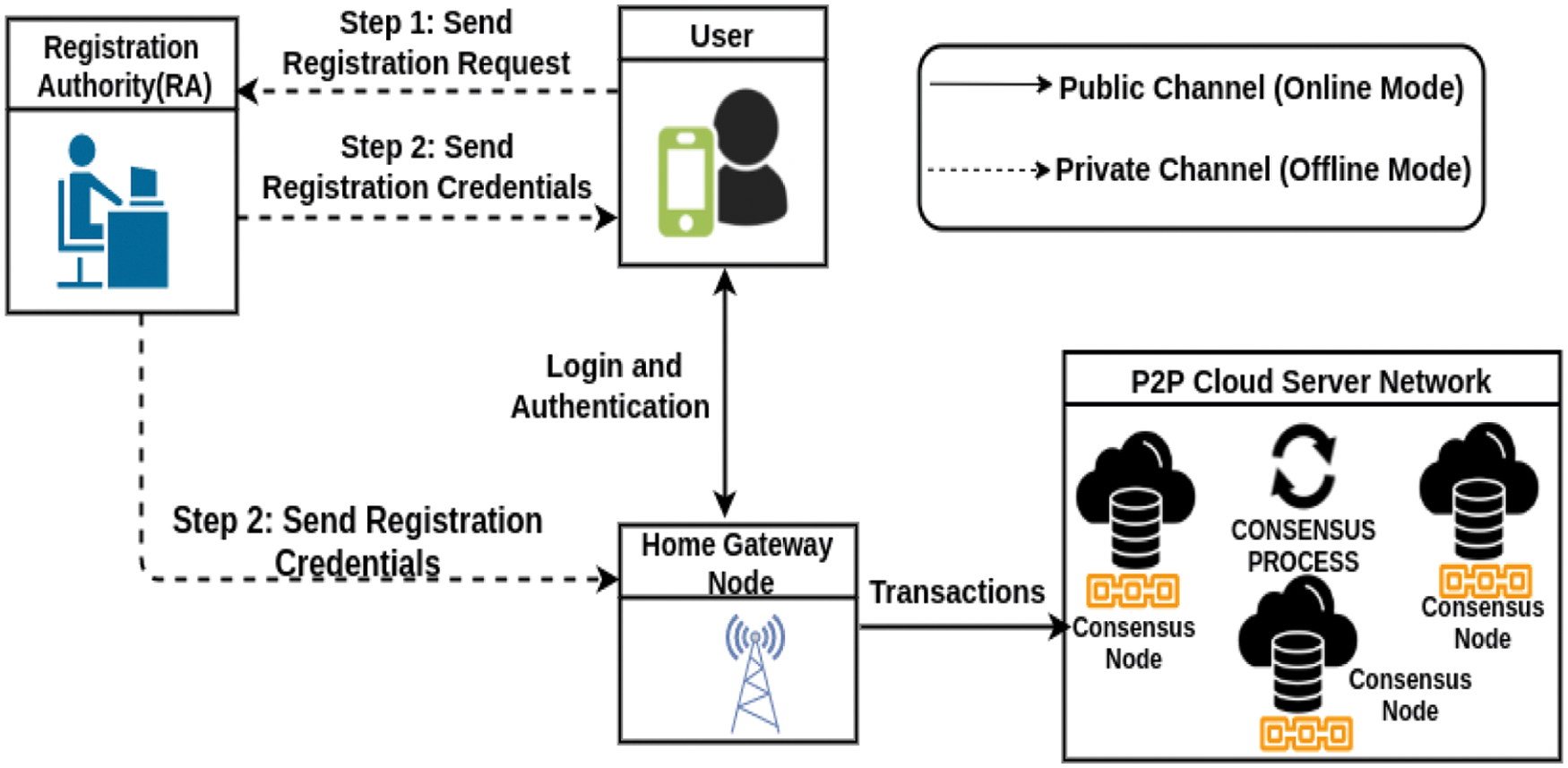
Figure 5: Process flow diagram of the proposed smart home system
In this section, through both the formal and informal security analysis, we show the robustness of the proposed scheme against various potential attacks that are possible in case of a smart home environment.
This section analyses the proposed scheme using the widely adopted Real-Or-Random (ROR) oracle model [14] as follows.
The ROR model models a one-way cryptographic hash function H(•) as a random oracle Hash. Let ΛUw1 and ΛHGWw2 denote the instances of the participants user and the home gateway in the proposed scheme, respectively. The ROR analysis uses the queries defined in Tab. 2.

Definition 1 (Semantic security): A polynomial time adversary A may have an advantage AdvABlockUbiHome(polyt) to derive the session key SKUG( = SKGU) for the proposed scheme BlockUbiHome given by AdvABlockUbiHome(polyt) = |
Theorem 1. Let AdvABlockUbiHome(polyt) be the advantage of a polynomial time adversary A in deriving the session key SKUG ( = SKGU) for the proposed scheme BlockUbiHome such that bitscount be the number of bits in the biometric secret key σU under the Zipf's law, then
where qhash, qsend and |Hash| represent “the number of hash queries, send queries and the range space of H(•)”,
Proof. Four games
•
•
•
•
After the games are played, the adversary now guesses the correct bit
Considering Eqs. (1)–(5), we get
Now, we get
Multiplying both sides by 2 in Eq. (6), we get
4.2 Informal Security Analysis
The informal security analysis proves that the proposed scheme is resistant to various known attacks.
Proposition 1. The proposed scheme BlockUbiHome is secure against ESL Attack.
Proof. In the proposed scheme, the computed session key is constructed as SKGU = H(H(PRIDU || Rpwd U || RbioU || XRA || TU) || RU • H(rG || LTSHGW || PRIDHGW || prHGW || TG)) = H(H(PRIDU || Rpwd U || RbioU || XRA || TU) || H(rU || σU || αU || PwdU || TU) • RG) = SKUG. The session key is constructed using the temporal secrets rU, rG and the long term secrets σU, αU, PwdU, LTSHGW, XRA, Rpwd U, RbioU and prHGW. If only the long-term secrets are revealed, then the short-term secrets protect the session key from compromise. Similarly, if the short-term secrets are compromised, then the long-term secrets ensure that the session key is protected.
Proposition 2. The proposed scheme BlockUbiHome is secure against privileged insider attack.
Proof. The home gateway node registration phase does not require the gateway to share any of its credentials. All the required parameters are pre-loaded by the registration authority into the gateway node's secure memory. The registration of the user ensures that AIDU, SKU, and RTSU are not revealed to the registration authority. The user credentials created do not use any parameters generated by the RA. The only parameter XRA is used in the session key construction but not in any user credentials. In addition, usage of random secret
Proposition 3. The proposed scheme BlockUbiHome is resilient against replay attack.
Proof. Consider that the messages
Proposition 4. The proposed scheme BlockUbiHome is resilient against man-in-the-middle attack.
Proof. Consider that the messages
Proposition 5. The proposed scheme BlockUbiHome is resilient against impersonation attacks.
Proof. Consider that the messages
• User impersonation attack: To launch this attack, the adversary A tries to impersonate the user U. For this, A generates
• Home gateway node impersonation attack: For the adversary A to impersonate the home gateway, it needs to first generate a random secret
Proposition 6. The proposed scheme BlockUbiHome is resilient against DoS attack.
Proof. The fuzzy extractor method used in the scheme employs the Hamming distance concept that helps avoid false acceptance and false rejection rates. This method is better in comparison to the one-way hash functions, perceptual hashing and biohashing, which cannot generate unique results from user biometric data even though they have reduced output error. In addition, the usage of timestamps in ensures message freshness and does not allow the same message from the same sender to be repeatedly received. This ensures that safety against DoS attack.
Proposition 7. The proposed scheme BlockUbuiHome achieves anonymity and untraceability.
Proof. The messages
Proposition 8. The proposed scheme is resilient against stolen smart card attack.
Proof. The user stores the credentials
This section performs thorough analysis of the proposed scheme and compares it with other schemes, such as the schemes of Fakroon et al. [5], Shuai et al. [6] and Naoui et al. [11] for costs undergone like the analysis done in the existing schemes [16–20].
5.1 Testbed Experimentation with MIRACL
The proposed scheme is examined through its execution time with the help of the open source SDK “Multiprecision Integer and Rational Arithmetic Cryptographic Library (MIRACL)” [21] based on C/C++ that gives the execution times of all required cryptographic operations. The notations for representing the cryptographic operations as denoted as
Two scenarios have been considered as follows.
Scenario 1: The platform for a server is taken as “Ubuntu 18.04.4 LTS, with memory: 7.7 GiB, processor: Intel Core i7-8565U CPU @ 1.80 GHz X 8, OS Type: 64-bit and disk: 966.1 GiB”. 100 runs have been executed for each cryptographic operation to record the “maximum, minimum and average run time in milliseconds” for each operation. The results are tabulated in Tab. 3.

Scenario 2: The platform for a user device/smart device is considered as follows: “Raspberry Pi 3 B + Rev 1.3, with CPU: 64-bit, Processor: 1.4 GHz Quad Core, 4-cores, Memory (RAM): 1GiB, and OS: Ubuntu 20.04 LTS, 64-bit” [22] Once again, 100 runs are executed for each operation to record the maximum, minimum and average run-time for each operation. The results are also tabulated in Tab. 3.
5.2 Computational Costs Comparison
The proposed scheme is evaluated to obtain a computation cost of
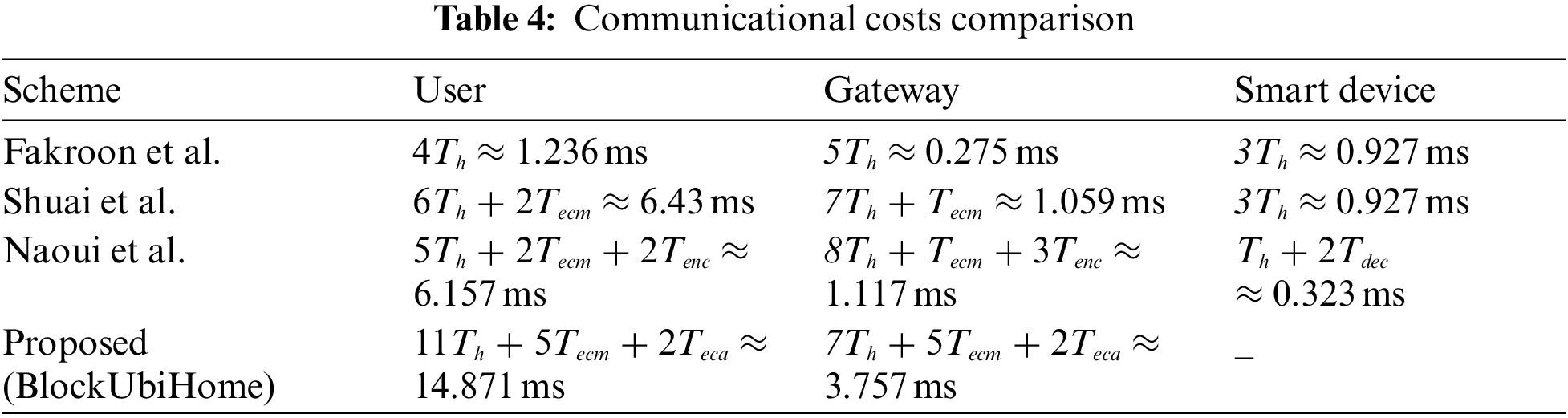
5.3 Communication Costs Comparison
The result of hash function (using SHA-256) takes 256 bits, and the result of “symmetric key encryption/decryption function using AES-128” [23] takes 128 bits. Choice of ECC is taken such that 160-bit ECC provides the same security as 1024-bit RSA algorithm. A given point on the elliptic curve takes 320 bits with each coordinate taking 160 bits. The proposed scheme is evaluated to obtain a communication cost of 1984 bits in 3 messages. The comparison of communication costs is shown in Tab. 5. The proposed scheme BlockUbiHome is observed to take the least communication cost among all compared schemes.

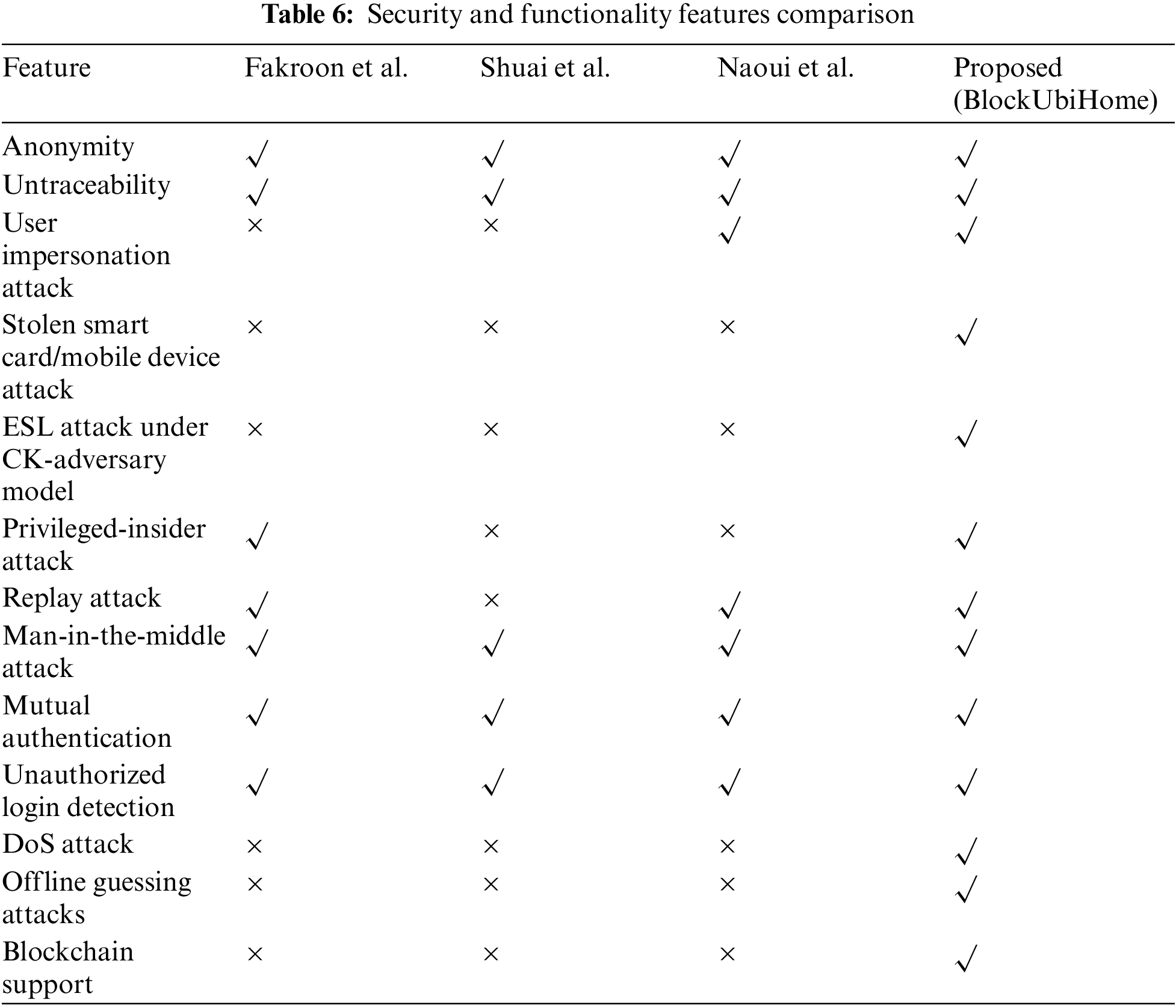
5.4 Security and Functionality Features Comparison
The proposed scheme is compared with the relevant schemes to understand how many of the required security features and functionality features are supported by each scheme. It can be concluded from Tab. 6 that even though the scheme has slightly higher computational cost, its communication cost is very low and it achieves more features compared to the other schemes.
6 Implementation of Blockchain: Simulation Study
The blockchain simulations were performed on a platform “Ubuntu 20.04.3 LTS (Focal Fossa), 64-bit OS with Intel® Core™ i7-6820HQ CPU @ 2.70 GHz, 32 GiB RAM” using the “Practical Byzantine Fault Tolerance (PBFT)” consensus algorithm [12]. The main advantages of using the blockchain simulations for the proposed scheme are to show the effects of computational time needed for three cases: a) a varied number of transactions per each block, b) a varied number of P2P nodes in the blockchain network, and c) a varied number of blocks to be mined in P2P blockchain network. These will measure the effectiveness of the proposed scheme with respect to utilization of the blockchain technology with the traditional user authentication and key agreement procedures in a smart home environment.
The home gateway after receiving a transaction from an authorized user will pass the transaction to a consensus Node for storing it into the blockchain. We can make the consensus node build a block, only after receiving some threshold number of transactions, so that storage overhead will be decreased. It creates a block which has the parameters essential to make the system achieve immutable and non- tampering. The transactions in the block are encrypted with its public key to ensure privacy [24]. It now requests leader for adding the block to the Network. Then using the PBFT algorithm for consensus, the leader determines whether to add or discard the block.
The size of the block <BV, PBH, MTR, T, BO, Signer Public Key, List of Transactions, Block Sign, CBH> can be computed as <32, 256, 256, 32, 160, 160,
Case 1: The number of peer nodes in the network is taken to be 10 and the no of transactions is taken to be 15 in each block. The time for computation as the number of blocks mined is increased from 5 to 25 in steps of 5 as shown in Fig. 6.

Figure 6: Simulation results: Number of blocks mined vs. computational time (in s)
Case 2: The number of peer nodes is taken to be 5 and the number of blocks mined is fixed at 10 while the number of transactions in each block is increased from 5 to 25 in steps of 5 to note the change in computation time as shown in Fig. 7.
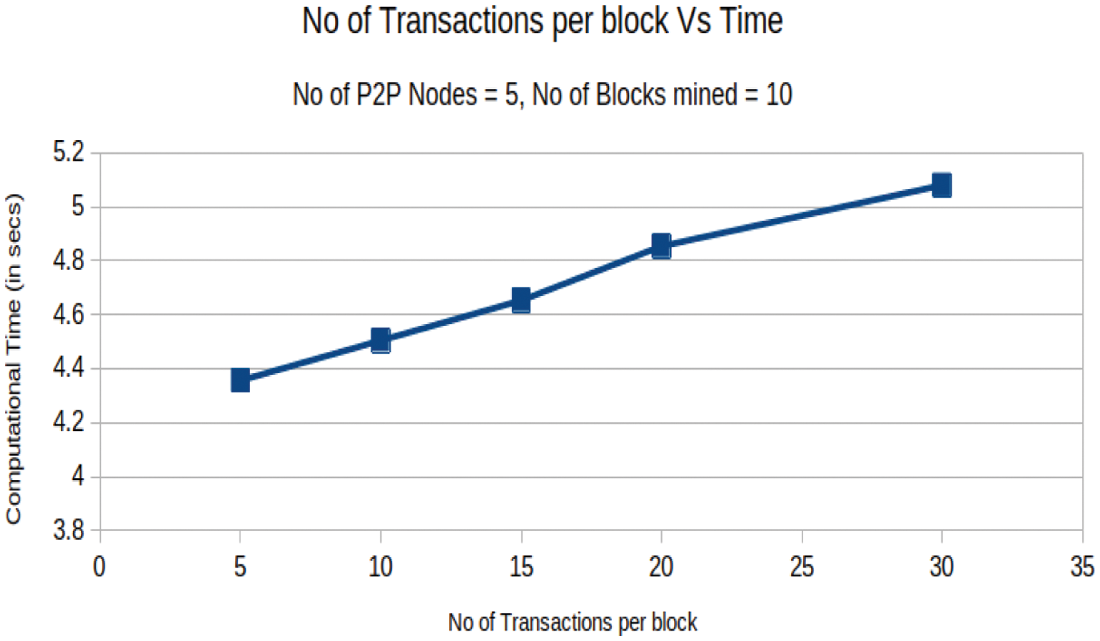
Figure 7: Simulation results: Number of transactions per block vs. computational time (in s)
Case 3: The number of peer nodes is varied from 10 to 30 in steps of 5 while the number of blocks mined is fixed at 10 and the number of transactions per block is fixed at 15. The respective computation time is noted during this variation as shown in Fig. 8.

Figure 8: Simulation results: Number of P2P nodes vs. computational time (in s)
The proposed research work presents a novel authentication protocol for smart home system using blockchain technology. A user can be remotely authenticated by the home gateway network using the proposed scheme. Once authenticated, the user may send any commands or instructions to be executed by a network of devices via the home gateway. Since the user is authenticated before sending commands, any malicious user is restricted from sending harmful commands to the home network. The proposed scheme is analyzed through a detailed analysis of the computation cost, communication cost and security features. In addition, an implementation of the blockchain shows only a linear variation in the increase of execution time with change in the peer nodes or number blocks or number transactions in each block. Future work includes lattice-based cryptographic techniques that can be embedded with the blockchain technology for smart home environment [25].
Acknowledgement: The authors would like to thank their universities for the support provided during this research. The authors would also like to thank the anonymous reviewers and the associate editor for their valuable feedback.
Funding Statement: This work was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education under Grant 2020R1I1A3058605. The authors also extend their gratitude to the Deanship of Scientific Research at King Khalid University for funding this work through research groups program under Grant Number R.G.P. 1/399/42.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. D. Dolev and A. Yao, “On the security of public key protocols,” IEEE Transactions on Information Theory, vol. 29, no. 2, pp. 198–208, 1983. [Google Scholar]
2. R. Canetti and H. Krawczyk, “Universally composable notions of key exchange and secure channels,” in Int. Conf. on the Theory and Applications of Cryptographic Techniques, pp. 337–351, 2002, Springer, Berlin Heidelberg. [Google Scholar]
3. M. Wazid, A. K. Das, V. Odelu, N. Kumar and W. Susilo, “Secure remote user authenticated key establishment protocol for smart home environment,” IEEE Transactions on Dependable and Secure Computing, vol. 17, no. 2, pp. 391–406, 2020. [Google Scholar]
4. T. S. Messerges, E. A. Dabbish and R. H. Sloan, “Examining smart-card security under the threat of power analysis attacks,” IEEE Transactions on Computers, vol. 51, no. 5, pp. 541–552, 2002. [Google Scholar]
5. M. Fakroon, M. Alshahrani, F. Gebali and I. Traore, “Secure remote anonymous user authentication scheme for smart home environment,” Internet of Things, vol. 9, pp. 100158, 2020. [Google Scholar]
6. M. Shuai, N. Yu, H. Wan and L. Xiong, “Anonymous authentication scheme for smart home environment with provable security,” Computers & Security, vol. 86, pp. 132–146, 2019. [Google Scholar]
7. S. Banerjee, V. Odelu, A. K. Das, S. Chattopadhyay and Y. Park, “An efficient, anonymous and robust authentication scheme for smart home environments,” Sensors, vol. 20, no. 4, pp. 1215, 2020. [Google Scholar]
8. D. Kaur and D. Kumar, “Cryptanalysis and improvement of a two-factor user authentication scheme for smart home,” Journal of Information Security and Applications, vol. 58, pp. 102787, 2021. [Google Scholar]
9. M. Xu, Q. Dong, M. Zhou, C. Wang and Y. Liu, “Security analysis on anonymous authentication scheme for smart home environment with provable security,” Wireless Communications and Mobile Computing, Vol. 2020, pp. 1–4. Article ID 8838363. 2020. [Google Scholar]
10. C. Lin, D. He, N. Kumar, X. Huang, P. Vijayakumar et al., “Homechain: A blockchain-based secure mutual authentication system for smart homes,” IEEE Internet of Things Journal, vol. 7, no. 2, pp. 818–829, 2019. [Google Scholar]
11. S. Naoui, M. E. Elhdhili and L. A. Saidane, “Lightweight and secure password based smart home authentication protocol: LSP-SHAP,” Journal of Network and Systems Management, vol. 27, no. 4, pp. 1020–1042, 2019. [Google Scholar]
12. M. Castro and B. Liskov, “Practical byzantine fault tolerance and proactive recovery,” ACM Transactions on Computer Systems, vol. 20, no. 4, pp. 398–461, 2002. [Google Scholar]
13. W. E. May, “Secure hash standard,” FIPS PUB 180-1, National Institute of Standards and Technology (NISTU.S. Department of Commerce, April 1995. [Online]. Available: http://nvlpubs.nist.gov/nistpubs/FIPS/NIST.FIPS.180-4.pdf, accessed on January 2020. [Google Scholar]
14. M. Abdalla, P. A. Fouque and D. Pointcheval, “Password-based authenticated key exchange in the three-party setting,” in Public Key Cryptography (PKC 2005), Lecture Notes in Computer Science, Berlin, Heidelberg: Springer, vol. 3386, pp. 65–84, 2005. [Google Scholar]
15. D. Wang, H. Cheng, P. Wang, X. Huang and G. Jian, “Zipf's law in passwords,” IEEE Transactions on Information Forensics and Security, vol. 12, no. 11, pp. 2776–2791, 2017. [Google Scholar]
16. A. Vangala, A. K. Sutrala, A. K. Das and M. Jo, “Smart contract-based blockchain-envisioned authentication scheme for smart farming,” IEEE Internet of Things Journal, vol. 8, no. 13, pp. 10792–10806, 2021. [Google Scholar]
17. A. Vangala, B. Bera, S. Saha, A. K. Das, N. Kumar et al., “Blockchain-enabled certificate-based authentication for vehicle accident detection and notification in intelligent transportation systems,” IEEE Sensors Journal, vol. 21, no. 14, pp. 15824–15838, 2021. [Google Scholar]
18. A. Vangala, A. K. Das and J. H. Lee, “Provably secure signature-based anonymous user authentication protocol in an internet of things enabled intelligent precision agricultural environment,” Concurrency and Computation: Practice and Experience, pp. e6187, 2021, https://doi.org/10.1002/cpe.6187. [Google Scholar]
19. B. Bera, A. Vangala, A. K. Das, P. Lorenz and M. K. Khan, “Private blockchain-envisioned drones-assisted authentication scheme in IoT-enabled agricultural environment,” Computer Standards & Interfaces, vol. 80, pp. 103567, 2022. [Google Scholar]
20. A. Vangala, A. K. Das, N. Kumar and M. Alazab, “Smart secure sensing for IoT-based agriculture: Blockchain perspective,” IEEE Sensors Journal, vol. 21, no. 16, pp. 17591–17607, 2021. [Google Scholar]
21. “MIRACL cryptograhic SDK: Multiprecision integer and rational arithmetic cryptograohic library,” 2020, [Online]. Available: https://github.com/miracl/MIRACL, accessed on October 2021. [Google Scholar]
22. “Raspberry Pi 3 model B+, ” 2020, [Online]. Available: https://www.raspberrypi.org/products/raspberry-pi-3-model-b-plus/, accessed on May 2021. [Google Scholar]
23. “Advanced encryption standard,” FIPS PUB 197, National Institute of Standards and Technology (NISTU.S. Department of Commerce, November 2001, [Online]. Available: http://csrc.nist.gov/publications/fips/fips197/fips-197.pdf, accessed on June 2020. [Google Scholar]
24. T. Li, H. Wang, D. He and J. Yu, “Permissioned blockchain-based anonymous and traceable aggregate signature scheme for industrial internet of things,” IEEE Internet of Things Journal, vol. 8, no. 10, pp. 8387–8398, 2020. [Google Scholar]
25. R. Chaudhary, A. Jindal, G. S. Aujla, N. Kumar, A. K. Das et al., “LSCSH: Lattice-based secure cryptosystem for smart healthcare in smart cities environment,” IEEE Communications Magazine, vol. 56, no. 4, pp. 24–32, 2018. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |