Computers, Materials & Continua DOI:10.32604/cmc.2022.025477
Article

Supplier Selection Fuzzy Model in Supply Chain Management: Vietnamese Cafe Industry Case

Chia-Nan Wang1, Hoang Tuyet Nhi Thai1,* and Nguyen Van Thanh2

1Department of Industrial Engineering and Management, National Kaohsiung University of Science and Technology, 80778, Taiwan
2Faculty of Commerce, Van Lang University, Ho Chi Minh City, Vietnam
*Corresponding Author: Hoang Tuyet Nhi Thai. Email: tuyetnhi1096@gmail.com
Received: 25 November 2021; Accepted: 12 January 2022

Abstract: Supplier selection is a vital part of the supply chain and is also a current issue that concerns businesses today as supplier quality directly affects the operations of the organization. Choosing the right supplier can help businesses increase productivity, competitiveness in the market, and profits without having to lower the quality of the products. However, choosing a supplier is not a simple matter, it requires businesses to consider many aspects about their suppliers. Therefore, the goal of this study is to propose an integrated model consisting of two models: Fuzzy Analytics Network Process (Fuzzy-ANP) model and Weighted Aggregated Sum Product Assessment (WASPAS) to solve the problem above. The Fuzzy-ANP model was developed to evaluate the weightings of the supplier selection criteria, and the WASPAS Model was used to rank the suppliers. An example of supplier selection in the coffee industry in Vietnam was studied to validate the model, namely 5 main criteria, with 16 sub-criteria, and 7 suppliers. The model test results show that the Fuzzy ANP and WASPAS integration model was suitable. In future, these developing models can apply to other industries or integrate with other models.

Keywords: Fuzzy-ANP; WASPAS; multi-decision; café industry; supplier selection; supply chain management

1  Introduction

Coffee production has been a major source of income for Vietnam since the early 20th century. First introduced by the French in 1857, the Vietnamese coffee industry has developed through the plantations system, becoming a major economic force of the country [1]. Over a long period of time and strong development, now coffee has brought great export value to the Vietnamese people. With an average of about 2.3 tons/ha, Vietnam's coffee yields are significantly higher than any other coffee-producing country in the world. Vietnam has created a unique brand of “high-intensity Robusta” farming, as Robusta produces more coffee beans per hectare than Arabica, which allows Vietnam to become the highest production of coffee. At the same time, it also promotes profits for coffee farmers, because many Vietnamese farmers harvest over 3.5 tons/ha [2].

According to data from the General Statistics Office of Vietnam, Vietnam is the world's second-largest coffee exporter. The EU is the largest coffee-consuming market in the world, with imports from foreign countries of 10 billion USD annually. Currently, Vietnam's coffee exports to the EU account for more than 8.5% of the total EU imports and nearly 40% of Vietnam's coffee exports. From 2010 to 2019, each year our country exports an average of more than 1.5 million tons of coffee for export, the average export value falls to over $3 billion. Coffee exports in September 2020 reached 99,700 tons, worth US $ 188.11 million, down 0.5% in volume but up 2% in value compared to August/2020. Generally, in the first 9 months of 2020, coffee exports decreased by 1.4% in volume and 1.0% in value over the same period in 2019, reaching 1.25 million tons, worth $ 2.16 billion.

Currently, in Vietnam, there are 4 famous types of coffee: Arabica, Robusta, Cherry, Culi. If before, anyone could easily make a traditional cup of coffee, now making coffee is an art. The concept of deliciousness with the new Vietnamese coffee culture today is not only delicious in “quality”, but the presentation must also look “delicious”. To achieve the above, coffee businesses in Vietnam today need to choose the right supply source. Supplier selection is becoming increasingly important to all businesses globally. The quality of the supplier affects the competitiveness of businesses [3]. In order to increase production and business efficiency without having to reduce product quality, increase selling prices, …, choosing a suitable supplier is also one of the important strategies that businesses are interested in and considered. Currently, there are many tools to support businesses in choosing suppliers: Analytical Hierarchical Analysis (AHP), Analytical Network Analysis (ANP), Data Contour Analysis (DEA), … This study proposes the Fuzzy-ANP model and Weighted Aggregated Sum Product Assessment (WASPAS) model to analyze data after consulting experts including 5 main criteria, 16 sub-criteria and 7 suppliers to assist the coffee industry in selecting supplier high quality ensures minimum costs, and maximum quality of raw materials with other factors.

In this study, the FANP model can provide direct supplier queuing results. However, the author wants to combine two models FANP and WASPAS to increase reliability. For the FANP model, the author only uses the evaluation weight results of the criteria from the FANP model and uses it as input of the WASPAS model to rank the supplier.

2  Literature Review

Evaluation and selection of suppliers has attracted the attention of researchers for several decades. Functional role of selected providers in the practice of this new supply chain strategy in the literature references below.

Function selected suppliers are dominated by quantitative methods and mathematical models. Overall, the model focuses on improving the accuracy of the evaluation and performance of the supplier or on the method used to rank and determine suppliers [4]. In Dickson's study, alternative methods have been used to evaluate and select criteria [5]. Most models make decisions about vendor selection based on a set of vendor performance criteria by Pi and Low [6]. Decision-making models differ by having one or more goals or by having different criteria. Timmerman proposed a linear model for decision support, in which the suppliers were ranked by several criteria and these ratings were combined into a single point [7]. Pearson et al. examined the supplier selection and evaluation criteria in small and large electronics companies outlining the criteria used by purchasing managers in choosing suppliers optimally [8].

There are several works applying MCDM approach to selecting suppliers, such as: Samut [9] applied FANP and Mixed Integer Goal Programming model (MIGP) for wind turbine supplier only in wind power plant projects. Tien-Chin Wang et al. [10] presented the MCDM model using FAHP and DEA combined to select solar panel suppliers. Onut et al. [11] have designed a FANP-based approach to the selection of container ports from manufacturing companies for the shipping industry. The MCDM is method to compare support structures for offshore wind turbines [12] or energy plant location selection [13]. Liou et al. [14] combined fuzzy priority programming and ANP to form a model of the selection of strategic alliance partners in the aviation industry. Dubey et al. [15] proposed a framework for green supply chains. Yucel et al. [16] developed a predictive risk assessment model for the hospital information system (HIS) by applying ANP, practical design gap assessment and fuzzy inference system. Büyüközkan et al. [17] have developed a sustainable principles-based supplier selection approach using FANP following a multi-person decision-making scheme with inadequate preference relationships. Vinodh et al. [18] applied FANP to the process of supplier selection in a production organization to remain in the global market. Chen et al. [19] were used in an integrated FANP model with benefits, opportunities, costs, and risks to prioritize smart grid systems. Lee et al. [20] built an integrated fuzzy QFD framework for new product development, with FDM for selecting important factors, fuzzy ISM to define the relationship between important factors and QFD and FANP to calculate the priority of important factors. Carter [21] analysed the role of purchasing in environmental management: Developing cross-functional theory. Chang et al. [22] applied AHP and ANP to evaluating digital video recorder systems.

For the WASPAS model, there are also many case studies such as: Zolfani et al. [23], have developed a multi-criteria decision-making approach to solve the problem of locating shopping centres by how to use SWARA and WASPAS methods. Bagočius et al. [24], proposed a MCDM method based on the WASPAS Method to select and rank viable site sites of wind power farms and to evaluate wind turbines in the external area. Singh et al. [25] applied SWARA and WASPAS methods for supplier selection in an Indian cement industry. Vafaeipour et al. [26] integrated SWARA and WASPAS method to evaluate solar projects based on the priority of the area. Chakraborty et al. [27] applied the WASPAS method to solve a few multi-criteria manufacturing problems such as selection of cutting fluid, electroplating system, forging conditions, arc welding process, etc. Zavadskas et al. [28] extension of weighted aggregated sum product assessment with interval-valued intuitionistic fuzzy numbers (WASPAS-IVIF). Lashgari et al. [29] developed the MCDM approach based on the Quantitative Strategic Planning Matrix (QSPM) and the WASPAS method to define outsourcing strategies.

3  Materials and Methods

To build an effective supplier selection model, the implementation process is carried out according to the main steps as shown in Fig. 1.

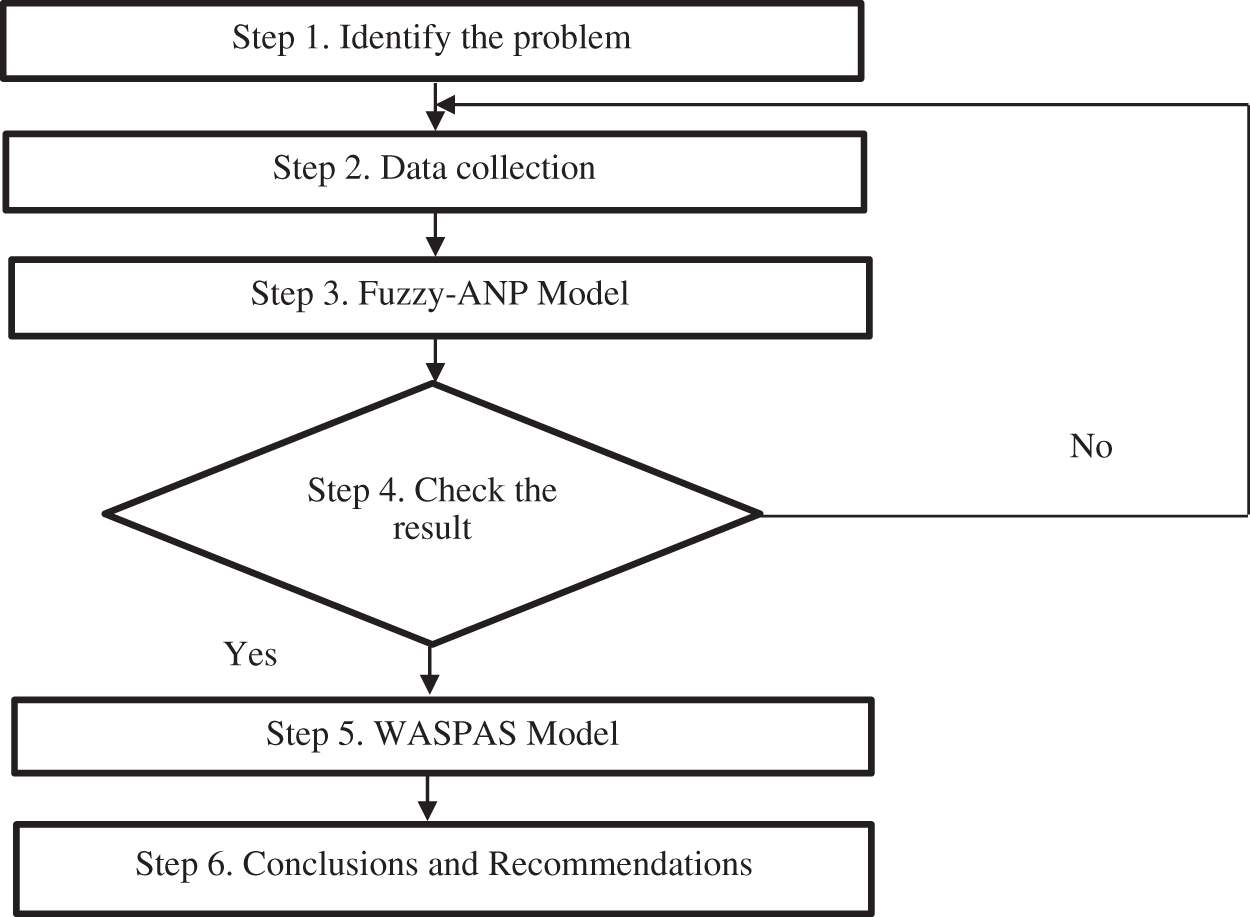
Figure 1: Research process of the paper

Step 1: Identify the problem

To analyze and evaluate the status of the company's supplier selection, the first step is to learn about the purchasing process, the criteria for selecting suppliers at the company through observing the actual operating environment, at the same time, to learn materials related to the problem, in order to make comments more effectively. Identify the core problem that causes ineffective supplier selection, analyze and come up with solutions. Besides, refer to the relevant previous studies to understand the concepts, implementation methods, evaluation and model building of supplier selection.

Step 2: Data collection

Collect coffee bean evaluation criteria, gather information about suppliers, set up a team of experts or outsource to evaluation criteria. Synthesize articles related to research issues, information from the General Statistics Office of Viet Nam, Ministry of Agriculture and Rural Development Viet Nam and information of companies supplying coffee beans.

Step 3: FANP model

Build a FANP model to evaluate and rate suppliers. Using a Fuzzy Network Analysis method (Fuzzy Analysis Network Process-FANP).

Step 4: Check the FANP model result

Check the correctness of the model, if the result is false, go back to identify the problem. Selection of the most optimal supplier.

Step 5: WASPAS model

Optimized supplier rating with a combination of two models FANP and WASPAS. Experts will conduct an initial assessment, combined with the weights from the FANP model.

Step 6: Conclusions and recommendations

Analyze and conclude the results achieved when conducting the research, in addition to propose stakeholders to the issues encountered and unsolved in the research process. In addition, it is recommended to develop models, in combination with other methods used in other decision-making areas.

3.1 Data Collected

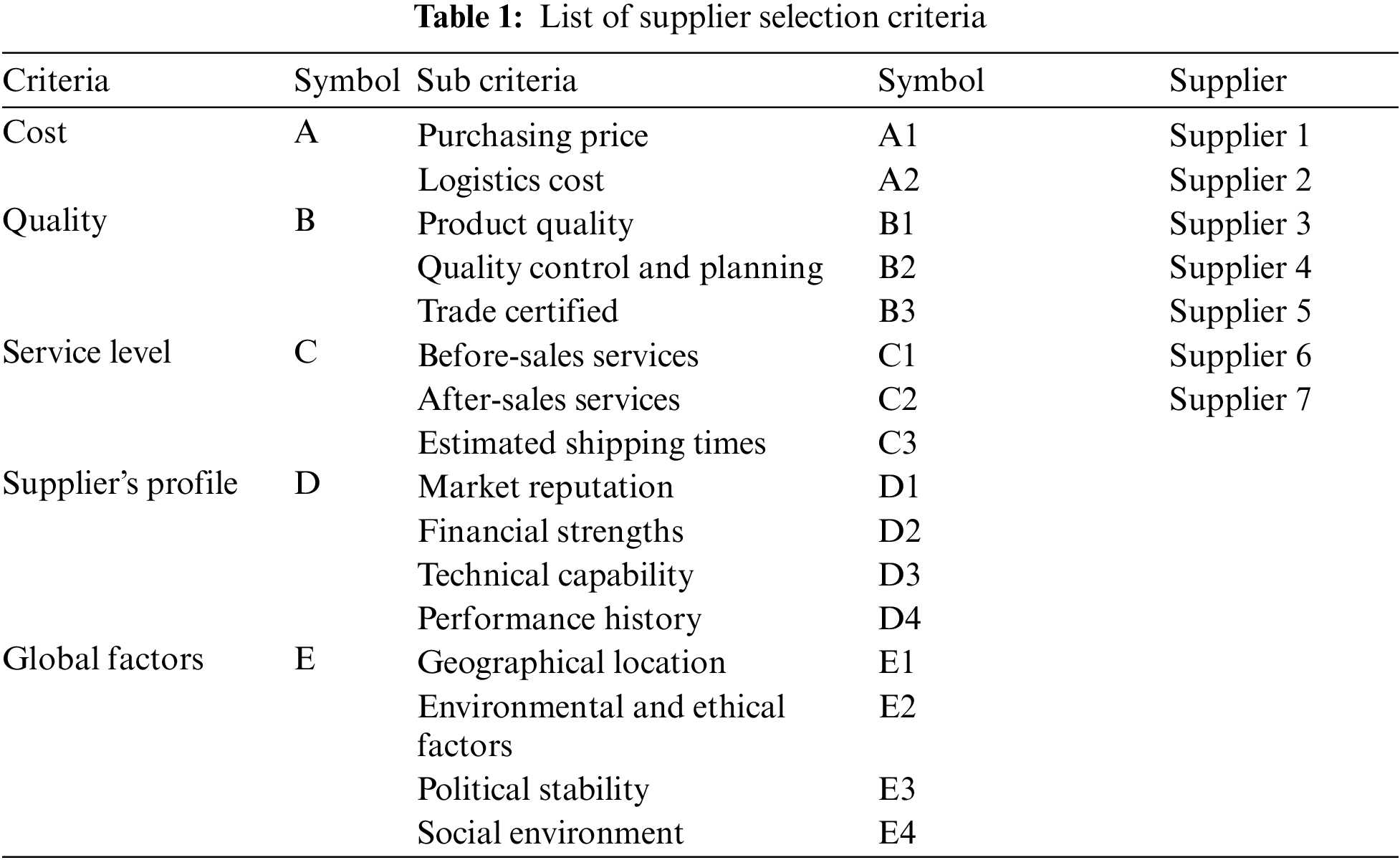
From the reference documents, we identified a list of criteria for the selection of recommended coffee to experts. We have selected five main criteria with sub-criteria and seven suppliers, which can be seen in Tab. 1.

3.2 Fuzzy Analytic Network Process Model

The procedure for implementing the Fuzzy-ANP method is as follows:

Step 1: Building FANP model

Construction of the FANP model structure. Set the Analytic Network Process and define the relationship between the criteria and the suppliers shown on Fig. 2:

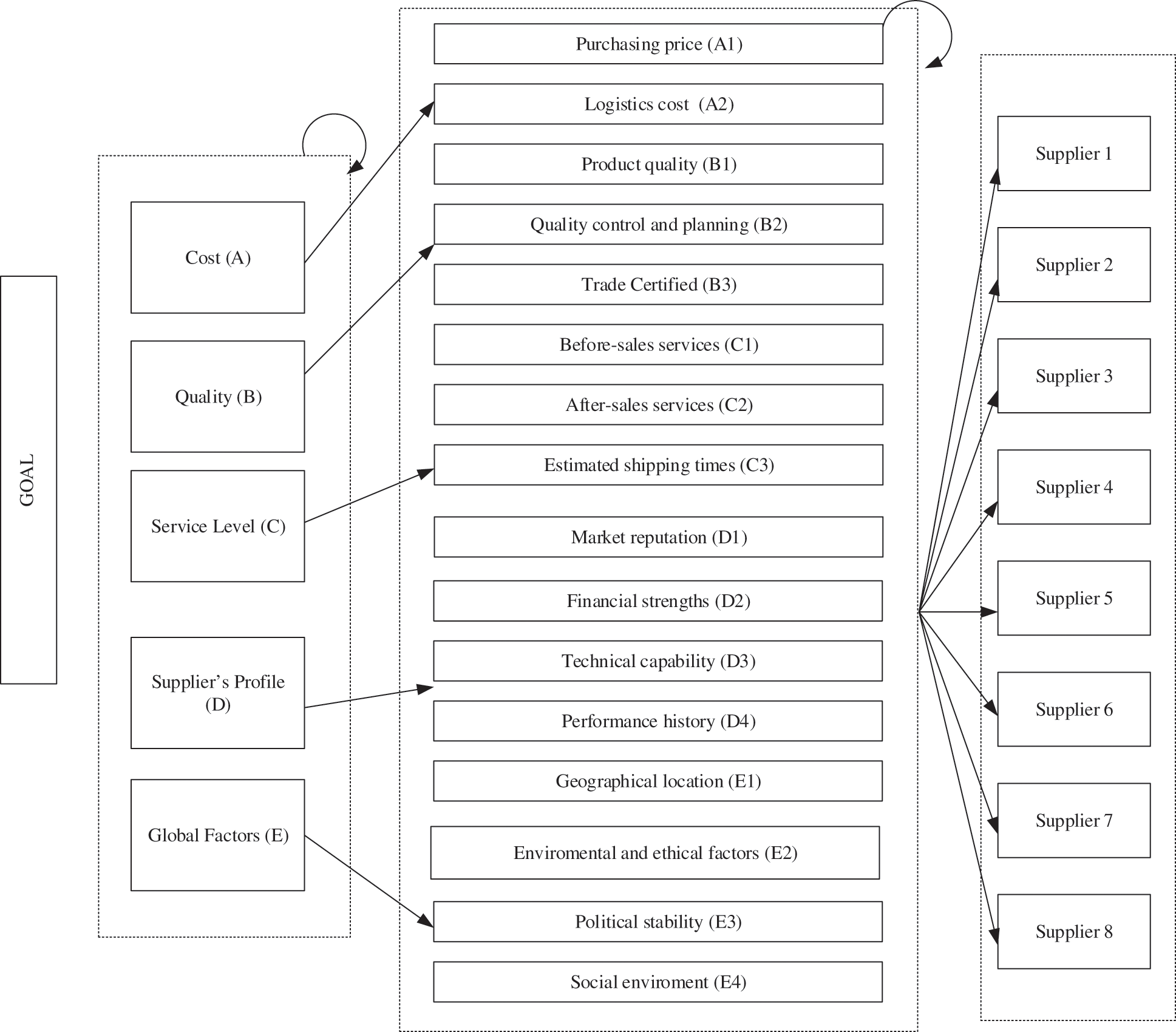
Figure 2: Fuzzy analytics network process structure

Step 2: Set up pair comparison matrix

A pairwise comparison of fuzzy numbers is used to perform a pairwise comparison between criteria. The pair comparison matrix is presented as follows:

Nk~=[n11k~n12k~⋯n21k~⋯n22k~⋯⋯⋯na1k~na2k~⋯n1ak~n2ak~⋯naak~](1)

where:

Nk~ is called a pairwise comparative matrix of fuzzy elements.

naak~ is the triangular fuzzy mean value when comparing the pair of priorities between the elements.

Converting fuzzy numbers to real numbers, triangular fuzzy trigonometric methods are presented as follows [30]:

zα,β(α¯ij)=[β.fα(Lij)+(1−β.fα(Uij)](2)

0≤β≤1,0≤α≤1

where:

fα(Lij)=(Mij−Lij).α+Lij(3)

fα(Uij)=Uij−(Uij−Mij).α(4)

When matching the diagonal matrix, we have:

zα,β(α¯ij)=1zα,β(α¯ij)(5)

0≤β≤1,0≤α≤1,i>j

After comparing the fuzzy pairs matrix, we obtain a matrix that compares the real numbers. This comparison is made between pairs of indicators and is combined into a matrix of a lines and a columns (a: is the number of indicators). Element shows the importance of the indicator i vs. the column criteria

N=(mij)a×a=[1m12m211…m1a…m2a⋮⋮ma1ma2⋮⋮…1](6)

Step 3: Calculate maximum individual value

To calculate the maximum specific value for the indicator, ANP can use different methods. In particular, the most widely used is Lambda Max (max) by Saaty Proposition [31,32]:

|N−λmax.I|=0(7)

where:

λmax: the maximum value of the matrix.

N: Comparative matrix of pairs of elements.

I: unit matrix of the same level with matrix A.

Step 4: Check consistency. Calculates the vector of the matrix

This ratio compares the degree of consistency with the (random) objectivity of the data:

CR=CIRI(8)

where:

CI: Consistency Index

RI: Random Index

If CR ≤0.1 is satisfactory, otherwise if CR ≥ 0.1 then we must conduct a reevaluation of the pair comparison matrix. Randomized index values corresponding to indicators is shown in Tab. 1

CI=  λmax−  nn−1(9)

where:

λmax is the maximum value of the matrix

n is the number of indicators

3.3 Weighted Aggregated Sum Product Assessment

The WSM method is very simple, easy to use and easy to understand. It determines the overall score of an alternative as the weighted sum of the attribute values. This is the most known and most widely used [34] method. WPM was developed to avoid alternatives with poor attribute value. It determines the score of each alternative as a product of the scale rating of each attribute to strength by the attribute's significance weight [35].

The computational procedure of the WASPAS method can be precisely presented as follows:

Step 1: Normalization of the decision matrix

For the WASPAS approach, the approach to normalizing the decision matrix depends on whether the decision criteria are beneficial or not. For the beneficial decision criteria, the normalization of the decision matrix in Tab. 1 is performed as shown in Eq. (10) as follows:

qij=xijmaxxij,i=1,2,…,n;j=1,2,…,m(10)

For non-beneficial decision criteria as shown in Eq. (11):

qij=xijminxij,i=1,2,…,n;j=1,2,…,m(11)

Step 2: Calculate the relative importance of the ith alternative, based on the WSM method as follows:

Si1=∑j=1n⁡qij×wj(12)

Step 3: The performance index of the ith alternative is evaluated by WPM as given in Eq. (14):

Si2=∏j=1n⁡(qij)wj(13)

Step 4: With the combination of Eqs. (12) and (13), we create a WASPAS model to calculate the total relative importance. Sum of relative importance, or more precisely, the general criterion of the weighted synthesis of the addition and multiplication methods as follows:

F=λSi1+(1−λ)Si2=λ∑j=1n⁡qij×wj+(1−λ)∏j=1n⁡(qij)wj(14)

where λ is the coefficient and λ∈ [0,1]

When decision-makers have no preference in relation to the coefficient, its value is set to λ = 0.5.

The alternatives are ranked based on an index of performance, and the optimal alternative is the one with the highest weight of F.

4  Result

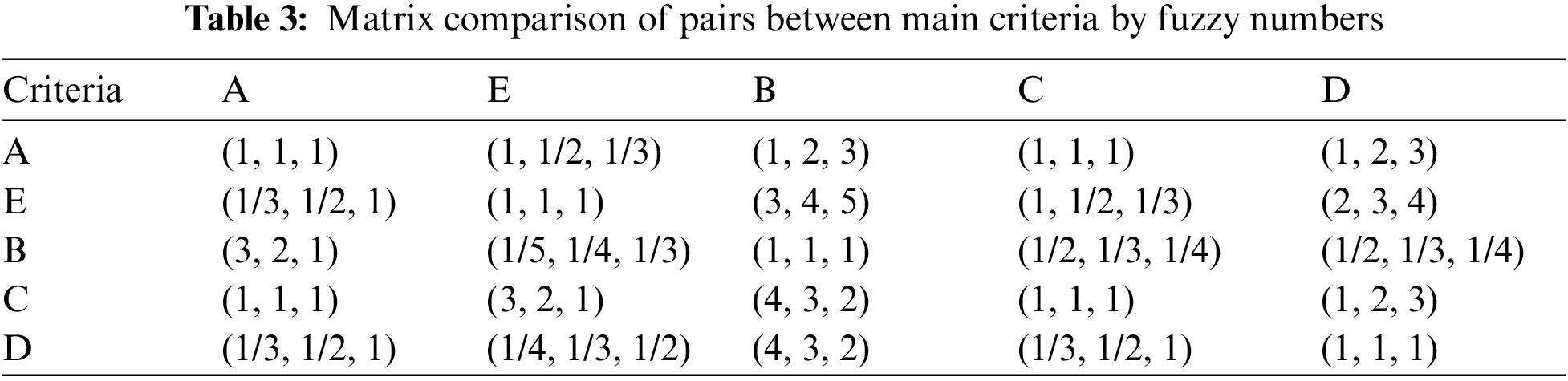
After collecting all the required criteria and suppliers, a fuzzy assessment matrix related to the goal is given in Tab. 3. Then, the decision-maker compares the attributes related to the criterion. The pairwise comparison matrix is made, and weight vector of each matrix is calculated. All properties are compared against each individual criterion by following the same procedure as below:

To convert fuzzy numbers into real numbers, we conduct the fuzzy solution by the triangular fuzzy number method. In the process of solving fuzzy we take the coefficients α = 0.5 and β = 0.5. In particular, α present uncertain environment, β represents the attitude of the assessment is fair.

g0.5,0.5(aA,B¯) = [(0.5 × 1.5) + (1 – 0.5) × 2.5] = 2

f0.5(LA,B) = (2–1) × 0.5 + 1 = 1.5

f0.5(UA,B) = 3–(3–2) × 0.5 = 2.5

g0.5,0.5(aB,A¯) = 1/2

The remaining calculations for other criteria are similar to the above calculation. The real number priority when comparing the main criteria pairs are shown in Tab. 4:

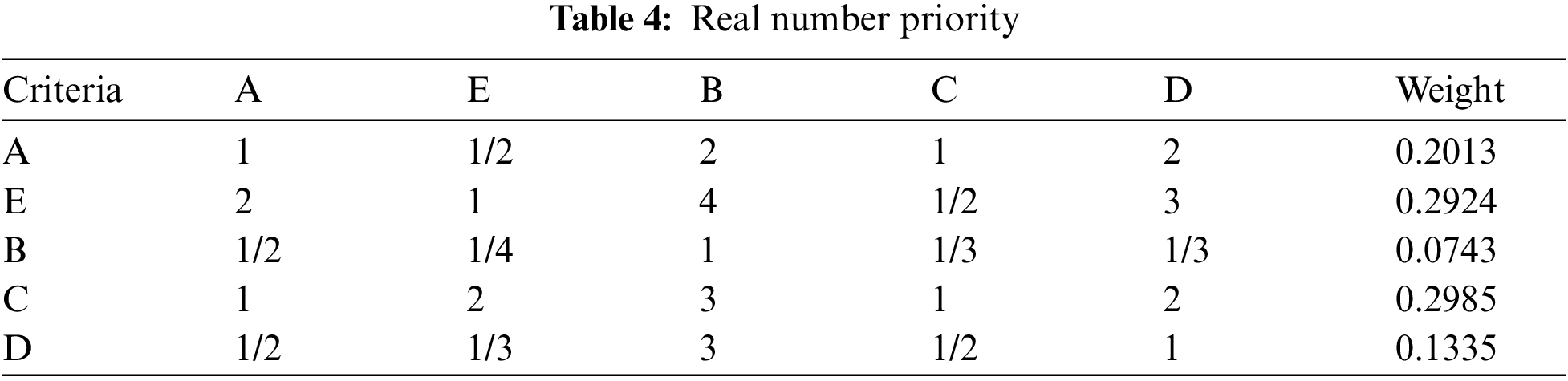
Results of the inputs given by the Software are listed in Tab. 5 which describes the criteria which are more important in criteria and supplier relationship. Each of these attributes may be more or less important in developing assessment criteria for the supplier's selection performance. Results of WASPAS model are shown in Tabs. 6–8.

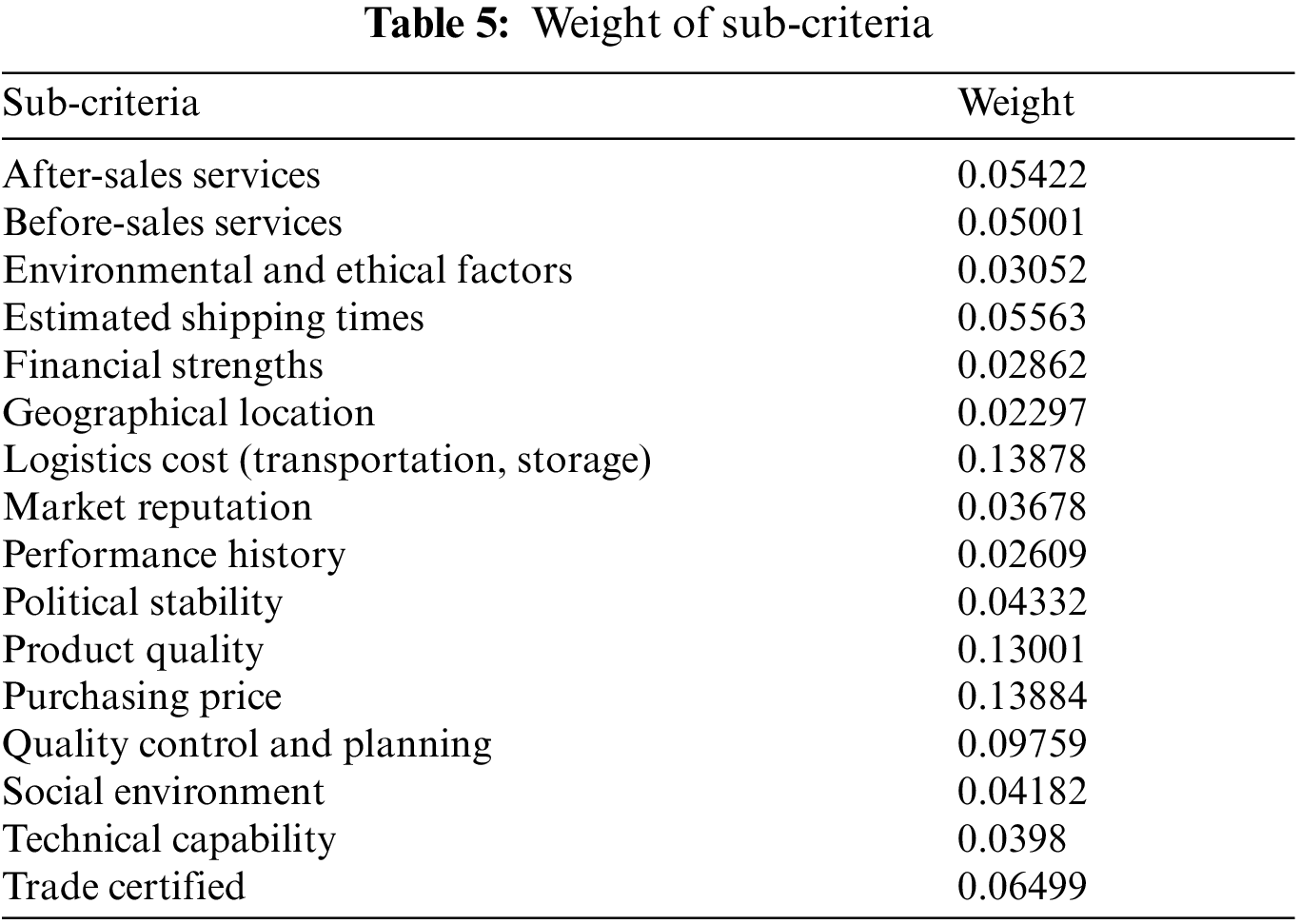
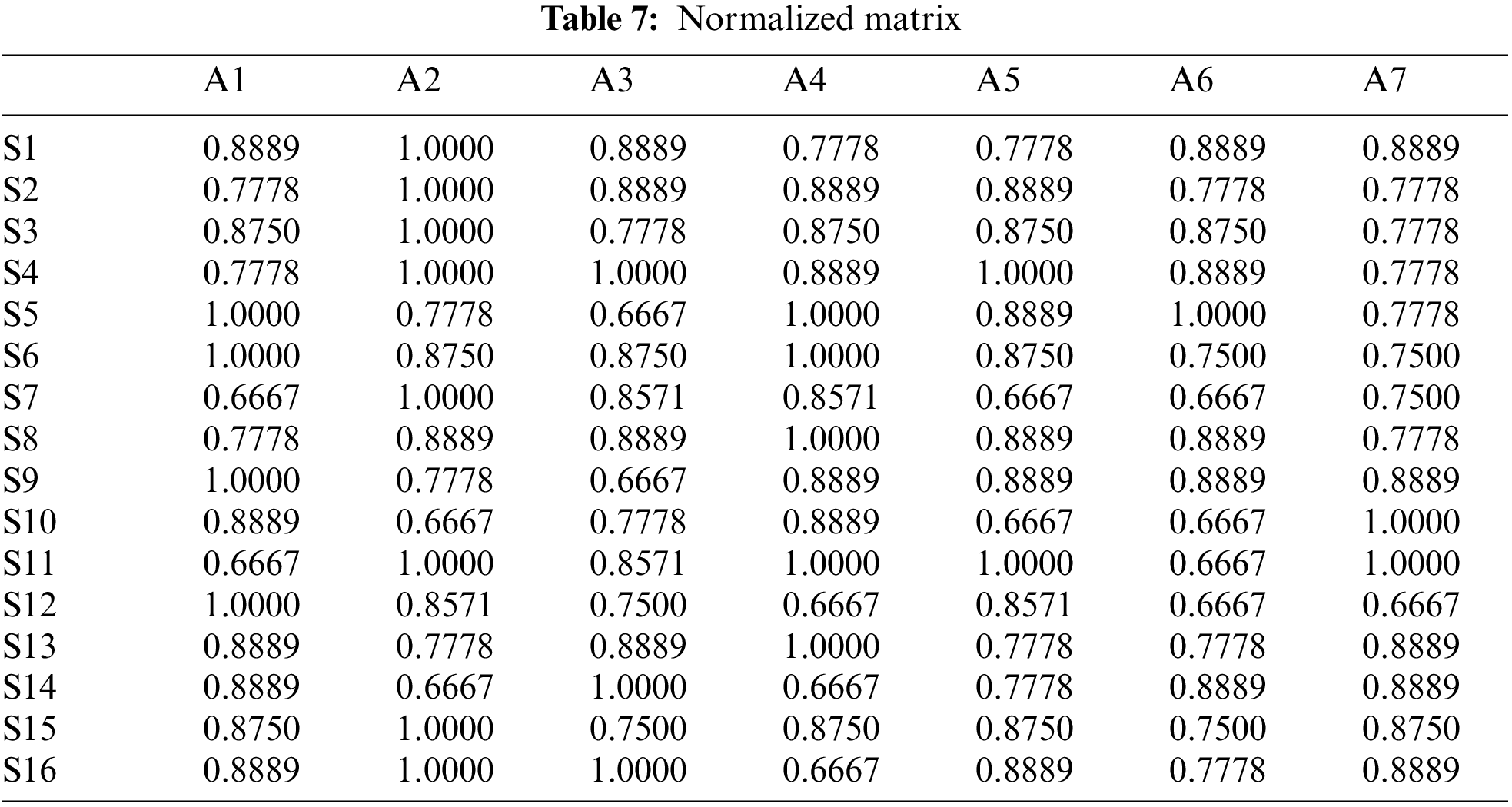
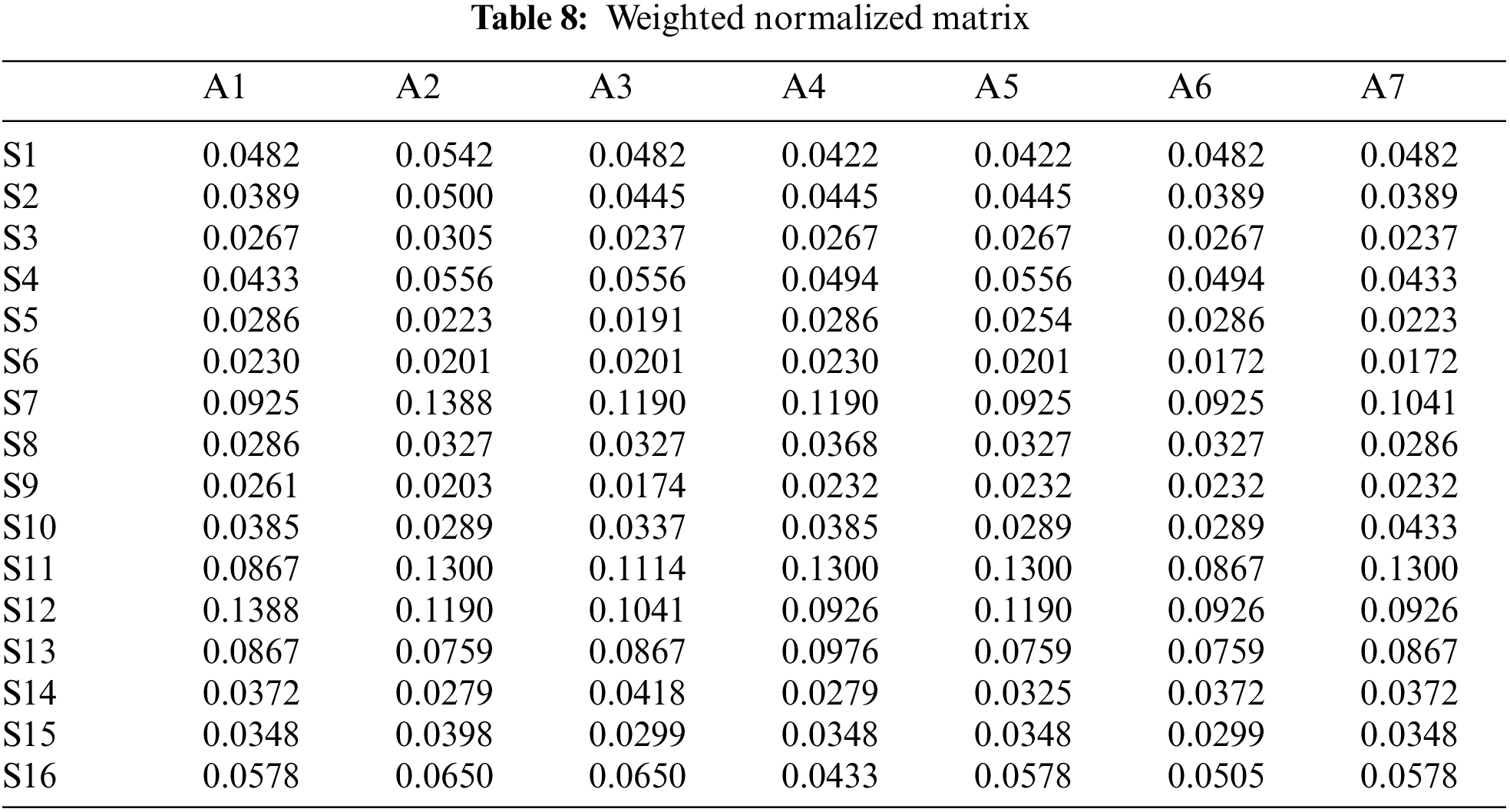
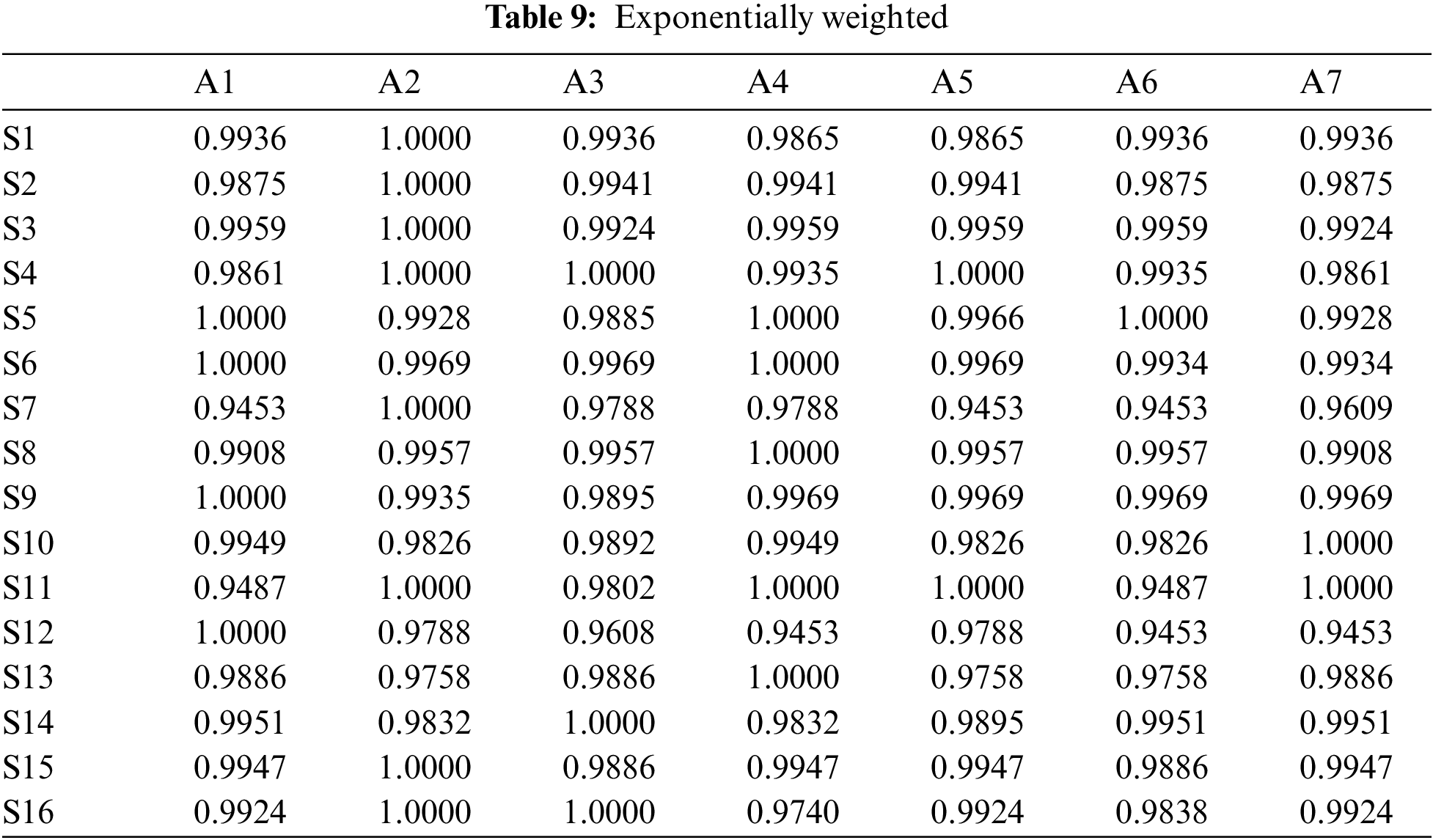
To be able to select the best supplier, after receiving the comparison weights the criteria from the FANP model will be used as input to the WASPAS model. Data input will show in below:

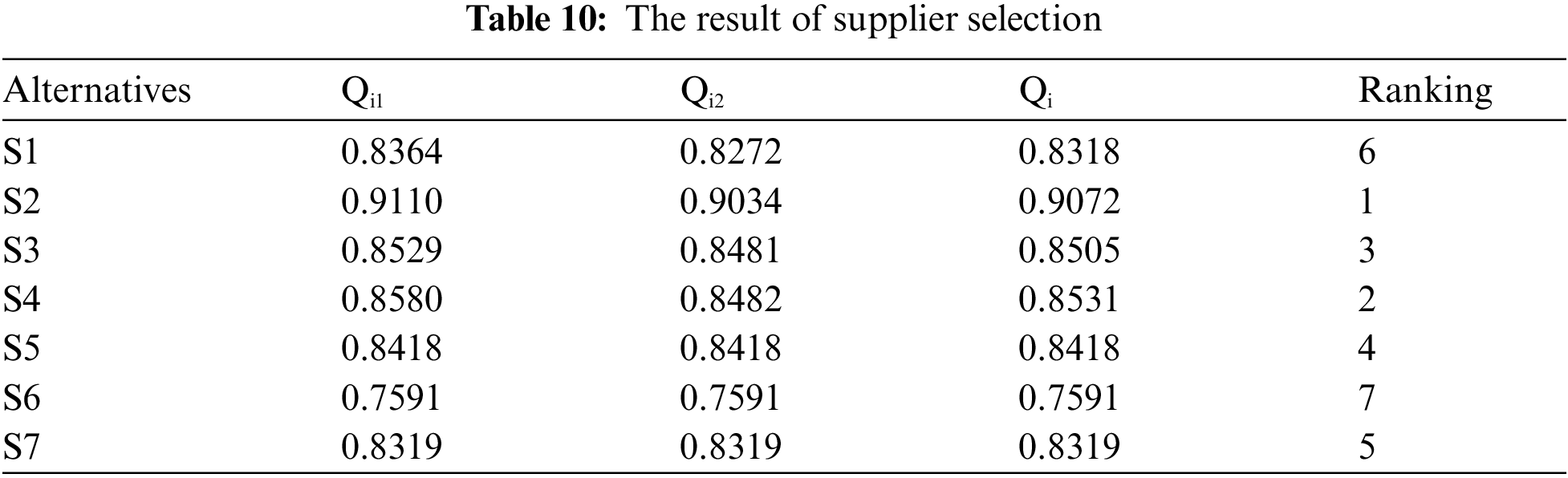
In the WASPAS method, λ represents the parameter and λ ∈ [0, 1]. The results of each alternative with different values of λ are shown in Tab. 10. The Supplier 2 (S2) is the best choice, and the six supplier performs poorly in any case. According to Tab. 10, the alternatives are ranked as S2>S4 >S3 >S5>S7>S1>S6.

5  Conclusion and Discussion

Selecting suppliers is an important activity of the supply chain to boost your business and increase profits in the coffee industry. However, the supplier selection process tends to be based on the decision-maker's experience, inaccurate and ambiguous. Therefore, the objective of this study is to propose an optimal supplier selection model for coffee businesses. The author used the FANP method combined with the WASPAS model, the study used secondary data including books, literatures, and published documents to have empirical knowledge base. A model test problem on supplier selection of coffee beans was performed as follows: Evaluation criteria are listed first through documentary review and interview with experts, and they are used to build a network with 5 criteria, 16 sub-criteria and 7 suppliers. After the experts answered the questionnaire, the Fuzzy ANP was used to calculate the importance of the criteria and sub-criteria and to assess the importance between the criteria. In this case, purchasing price and logistics cost are the most important criterion, followed by the technical capability, quality control and planning, etc. Such results are consistent with the fact that most businesses focus on cost, then quality, followed by global factors, supplier's profile, and service level. The results obtained from the fuzzy ANP model will be used as input data in conjunction with expert evaluation of the WASPAS model to ranking suppliers. The results of ranking suppliers from WASPAS model show that Supplier 1 (S1) is the most suitable. From the result of test, the proposed model is feasible.

The proposed FANP-WASPAS model can support more optimal decision-making because it considers based on many criteria and checks their correlation. It also considers the ambiguity, uncertainty, and subjectivity of many different decision makers and criteria experts. Therefore, the model in this study supports coffee companies to make more accurate decisions. The contribution of this research is to propose a MCDM under fuzzy environment conditions. Although the study is only applicable to the coffee industry in Vietnam, the proposed model can be adapted and applied to other industries or different countries as a reference in the multi-criteria decision making.

Funding Statement: This study was financially supported by Van Lang University, Vietnam and National Kaohsiung University of Science and Technology, Taiwan.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Wikipedia, Coffee production in Vietnam, Wikimedia Foundation Incorporated, 2015. [Online]. Available: https://en.wikipedia.org/wiki/Coffee_production_in_Vietnam. [Google Scholar]

 2.  N. T. H. Van, Lich su du nhap cay ca phe vao Viet Nam, PrimeCoffea, 2021. [Online]. Available: https://primecoffea.com/lich-su-cay-ca-phe-viet-nam.html. [Google Scholar]

 3.  M. Dehghan, M. Esmaeilian and R. T. Moghaddam, “Employing fuzzy ANP for green supplier selection and order allocations: A case study,” International Journal of Economy, Management and Sciences, vol. 2, no. 8, pp. 565–575, 2013. [Google Scholar]

 4.  J. Scott, W. Ho, P. K. Deya and S. Talluri, “A decision support system for supplier selection and order allocation in stochastic, multi-stakeholder and multi-criteria environments,” International Journal of Production Economics, vol. 166, pp. 226–237, 2015. [Google Scholar]

 5.  G. W. Dickson, “An analysis of vendor selection: Systems and decisions,” Journal of Purchasing, vol. 1, no. 2, pp. 5–17, 1966. [Google Scholar]

 6.  W. N. Pi and C. Low, “Supplier evaluation and selection via Taguchi loss functions and an AHP,” International Journal of Advanced Manufacturing Technology, vol. 27, pp. 625–630, 2006. [Google Scholar]

 7.  E. Timmerman, “An approach to vendor performance evaluation,” The Journal of Supply Chain Management, vol. 22, no. 4, pp. 2–8, 1986. [Google Scholar]

 8.  J. N. Pearson and L. M. Ellram, “Supplier selection and evaluation in small versus large electronics firms,” Journal of Small Business Management, vol. 33, no. 4, pp. 53–65, 1995. [Google Scholar]

 9.  P. K. Samut, “Integrated FANP-f-MIGP model for supplier selection in the renewable energy sector,” Journal of Business Economics and Management, vol. 18, pp. 427–450, 2017. [Google Scholar]

10. T. C. Wang and S. Y. Tsai, “Solar panel supplier selection for the photovoltaic system design by using fuzzy multi-criteria decision making (MCDM) approaches,” Energies, vol. 11, pp. 1989, 1989. [Google Scholar]

11. S. Onut, U. R. Tuzkaya and E. Torun, “Selecting container port via a fuzzy ANP-based approach: A case study in the Marmara Region,” Transport Policy, vol. 18, pp. 182–193, 2011. [Google Scholar]

12. A. Kolios, M. Collu, A. Chahardehi, F. P. Brennan and M. H. Patel, “A Multi-criteria decision making method to compare support structures for offshore wind turbines,” European Wind Energy Conference and Exhibition, vol. 6, pp. 4778–4787, 2010. [Google Scholar]

13. C. N. Wang, V. T. Nguyen, D. H. Duong and H. T. N. Thai, “A hybrid fuzzy analysis network process (FANP) and the technique for order of preference by similarity to ideal solution (TOPSIS) approaches for solid waste to energy plant location selection in Vietnam,” Applied Sciences, vol. 8, no. 7, pp. 1100, 2018. [Google Scholar]

14. J. J. H. Liou, G. H. Tzeng, C. Y. Tsai and C. C. Hsu, “A hybrid ANP model in fuzzy environments for strategic alliance partner selection in the airline industry,” Applied Soft Computing, vol. 11, no. 4, pp. 3515–3524, 2011. [Google Scholar]

15. R. Dubey, A. Gunasekaran and S. S. Ali, “Exploring the relationship between leadership, operational practices, institutional pressures and environmental performance: A framework for green supply chain,” International Journal of Production Economics, vol. 160, pp. 120–132, 2015. [Google Scholar]

16. G. Yucel, S. Cebi, B. Hoege and A. F. Ozok, “A fuzzy risk assessment model for hospital information system implementation,” Expert Systems with Applications, vol. 39, no. 1, pp. 1211–1218, 2011. [Google Scholar]

17. G. Büyüközkan and G. Çifçi, “A novel fuzzy multi-criteria decision framework for sustainable supplier selection with incomplete information,” Computers in Industry, vol. 62, no. 2, pp. 164–174, 2011. [Google Scholar]

18. S. Vinodh, R. A. Ramiya and S. G. Gautham, “Application of fuzzy analytic network process for supplier selection in a manufacturing organisation,” Expert Systems with Applications, vol. 38, no. 1, pp. 272–280, 2011. [Google Scholar]

19. H. H. Chen and H. Gu, “A fuzzy ANP model integrated with benefits, opportunities, costs, and risks to prioritize intelligent power grid systems,” Mathematical Problems in Engineering, vol. 2013, 2013. [Google Scholar]

20. A. H. I. Lee and C. Y. Lin, “An integrated fuzzy QFD framework for new product development,” Flexible Services and Manufacturing Journal, vol. 23, pp. 26–47, 2011. [Google Scholar]

21. C. R. Carter and M. Dresner, “Purchasing's role in environmental management: Cross-functional development of grounded theory,” Journal of Supply Chain Management, vol. 37, no. 2, pp. 12–27, 2001. [Google Scholar]

22. C. W. Chang, C. R. Wu, C. T. Lin and H. L. Lin, “Evaluating digital video recorder systems using analytic hierarchy and analytic network processes,” Information Sciences, vol. 177, no. 16, pp. 3383–3396, 2007. [Google Scholar]

23. S. H. Zolfani, M. H. Aghdaie, A. Derakhti, E. K. Zavadskas and M. H. M. Varzandeh, “Decision making on business issues with foresight perspective; an application of new hybrid MCDM model in shopping mall locating,” Expert Systems with Applications, vol. 40, no. 17, pp. 7111–7121, 2013. [Google Scholar]

24. V. Bagočius, E. K. Zavadskas and Z. Turskis, “Multi-person selection of the best wind turbine based on the multi-criteria integrated additive-multiplicative utility function,” Journal of Civil Engineering and Management, vol. 20, no. 4, pp. 590–599, 2014. [Google Scholar]

25. R. L. Singh and S. Modgil, “Supplier selection using SWARA and WASPAS–a case study of Indian cement industry,” Measuring Business Excellence, vol. 24, no. 2, 2020. [Google Scholar]

26. M. Vafaeipour, S. H. Zolfani, M. H. M. Varzandeh, A. Derakhti and M. K. Eshkalag, “Assessment of regions priority for implementation of solar projects in Iran: New application of a hybrid multi-criteria decision making approach,” Energy Conversion and Management, vol. 86, pp. 653–663, 2014. [Google Scholar]

27. S. Chakraborty and E. K. Zavadskas, “Applications of WASPAS method in manufacturing decision making,” Informatica, vol. 25, no. 1, pp. 1–20, 2014. [Google Scholar]

28. E. K. Zavadskas, J. Antucheviciene, S. H. R. Hajiagha and S. S. Hashemi, “Extension of weighted aggregated sum product assessment with interval-valued intuitionistic fuzzy numbers (WASPAS-IVIF),” Applied Soft Computing, vol. 24, pp. 1013–1021, 2014. [Google Scholar]

29. S. Lashgari, J. Antuchevičienė, A. Delavari and O. Kheirkhah, “Using QSPM and WASPAS methods for determining outsourcing strategies,” Journal of Business Economics and Management, vol. 15, no. 4, pp. 1–15, 2014. [Google Scholar]

30. R. Lin, J. J. Lin, C. J. Shu, T. Diodes, H. Chao et al., “Note on group consistency in analytic hierarchy process,” European Journal of Operational Research, vol. 190, no. 3, pp. 627–678, 2008. [Google Scholar]

31. T. L. Saaty, The Analytic Hierarchy Process-Planning, Priority Setting, Resource Allocation, New York: McGraw-Hill International, 1980a. [Google Scholar]

32. T. L. Saaty, The Analytic Hierarchy Process, New York: McGraw-Hill International, 1980b. [Google Scholar]

33. T. L. Saaty, The Analytic Hierarchy Process, New York: McGraw-Hill International, 1980. [Google Scholar]

34. K. R. MacCrimon, Decisionmaking Among Multiple-Attribute Alternatives: A Survey and Consolidated Approach, Santa Monica, California: The Rand Corporation, 1986. [Google Scholar]

35. A. Easton, “One of a kind decisions involving weighted multiple objectives and disparate alternatives,” Multiple Criteria Decision Making, pp. 657–667, 1973. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.