DOI:10.32604/cmc.2022.025233

| Computers, Materials & Continua DOI:10.32604/cmc.2022.025233 |  |
| Article |
Design of Energy Efficient WSN Using a Noble SMOWA Algorithm
1Department of Computer Science and Engineering, Bennett University, Greater Noida, 201310, India
2Department of Information Technology, Asansol Engineering College, Asansol, 713305, India
3Department of Computer and Information Science, Raiganj University, Raiganj, 733134, India
4Department of Computer Science and Engineering, JIS College of Engineering, Kalyani, 741235, India
5School of Computer Science and Engineering, University of New South Wales,Sydney, Australia
6Symbiosis Centre for Applied Artificial Intelligence, Symbiosis International (Deemed University), Pune, India
*Corresponding Author: Ketan Kotecha. Email: head@scaai.siu.edu.in
Received: 17 November 2021; Accepted: 21 February 2022
Abstract: In this paper, the establishment of efficient Wireless Sensor Network (WSN) networks has been projected to minimize the consumption of energy using a new Self-adaptive Multi-Objective Weighted Approach (SMOWA) algorithm for solving a multi-objective problem. The Different WSN nodes deployment policies have been proposed and applied in this paper to design an efficient Wireless Sensor Network to minimize energy consumption. After that, the cluster head for each cluster has been selected with the help of the duty cycle. After configuring the WSN networks, the SMOWA algorithms have been developed to obtain the minimum energy consumption for the networks. Energy minimization, as well as the amount of day-saving, has been calculated for the different WSNs which has been configured through different deployment policies. The major finding of the research paper is to improve the durability of Wireless Sensor Network (i) applying different deployment strategies: (Random, S pattern and nautilus shell pattern), and (ii) using a new Meta-heuristic algorithm (SMOWA Algorithm). In this research, the lifetime of WSN has been increased to a significant level. To choose the best result set from all the obtained results set some constraints such as “equivalent distribution”, “number of repetitions”, “maximum amount energy storage by a node” has been set to an allowable range.
Keywords: Wireless Sensor Network (WSN); Self-adaptive Multi-Objective Weighted Approach (SMOWA); deployment strategies; Meta-heuristic Methods; energy minimization; duty cycle
The WSN can be defined as a network of minute embedded components, called sensor nodes, which can interact with another node using a wireless medium Wang et al. [1]. Sink nodes are the controller node of all controlling sensor nodes. The sensor node contains mainly five microunits such as a sensing unit, data storage unit, power storage unit, communication unit and a processing unit. Specific type sensors are mounted on the nodes to sense the behaviour of the external environment Navarro et al. [2]. The type of sensors varies depending upon the application area. e.g., For sensing the temperature of the external environment, one needs to embed a temperature Sensor with hardware, and if the research is about sensing the humidity the researchers should embed a Humidity Sensor. Here sensing unit acts as the input device of the network. The tiny processor processes the input data and produces the processed data Sara et al. [3]. The sensing data is inputted as raw data in the processor, the tiny but the robust processor process the data and calibrate according to the research and make the output. Now the data storage unit comes into the picture and the processed data are stored in the local storage. The data storage capacity of the WSN nodes is very limited Ren et al. [4]. Therefore, it’s a very important task to differentiate between the desired data and many unwanted as well as unnecessary data through the proper filtering process. The communication unit is used for transmitting and receiving a very limited amount of processed data to the sink node or neighbour nodes. This communication is called node to sink node communication. When the sink receives the data generally it generates some acknowledgement signal to acknowledge the system that it receives data from the terminal nodes. The input processed data may be further refined or processed in the sink node. The power storage unit is used to supply power to every unit of the WSN node. Each and every node consist of this type of tiny power unit generally made up of a lithium-ion battery. This independent battery power supply is used to make the node alive Visconti et al. [5]. Sink node can interact with every node to create the network and establish the path of communication. It transmits as well as receives data to and from the dominant nodes. This type of network system can be considered as a multi-hop communication system Kumar et al. [6]. Nowadays this type of WSN is being used in various fields like agriculture, meteorology, condition monitoring, health care, traffic control, ecological monitoring, war front monitoring etc. Now in the case of our research, The approach [7] (Banerjee et al.) has been implemented keeping mind the research work of Banerjee et al. as follows: At first, the indexing of WSN nodes is done, in this process, each and every node gets a unique identification number, the number is used for future reference to identify easily, then after the clustering process is done. Clustering is the process of segregation of the target area for the deployment of the WSN node by which the target area can be gridded and can easily be divided into many clusters. Those clusters can be used to deploy WSN nodes in future. In the clustering process, some bunches of closely situated nodes are considered a cluster. The clusters are generally are of uniform structure. It may be a square block or it may be a Hexa-diagonal block. In our experiment, the structure of the cluster is considered a square-shaped block. After that, the Deployment of WSN nodes is done. Here it is proposed three different deployment processes namely Random deployment, S pattern deployment and nautilus shell deployment strategies. Depending upon the deployment strategy one can produce different energy-efficient Wireless Sensor networks. at last, the Minimization of consumed energy for the configured WSN with the help of the newly proposed SMOWA algorithm is done. Every process is well described in Section 5 under the solution procedure.
The article has 9 sections and those sections are abstract, Literature Survey, Problem Formulation, Solution Procedure, Numerical Solutions and Discussion, Experimental Result, Result in analysis and conclusion. In the abstract, a very brief idea about the research work has been presented. In the literature survey, there is some discussion about the past work in this research area and tried to find the scope and gap of the further possible research work. The problem formulation is the mathematical model creation of the specific problem. In the solution procedure, there is a detailed description of the various products through which the problem can be solved. The numerical solution is the outcome after applying the solution mechanism to the problem derived by the mathematical model. In the experimental result part, we depicted the numerical result to a tabular form and compared it with different types of experiments. The result for different deployment policies as well as the result obtained by the Ant Colony Optimization (ACO) algorithm has been compared in the experimental result section. The result has been further analysed using a statistical method named “Wilcoxon Rank-Sum Test for the Multi-objective reliability optimization” to determine the significance of a population among other populations. At last, the conclusion has been drawn summarising the contribution of the paper in the field of WSN and describing the future scope of the research work.
Contribution:
The contributions of the paper are as follows:
• In this research, energy minimized Wireless Sensor Network has been constructed. To do so different deployment strategies (Random deployment, S pattern deployment, Nautilus shell shape deployment) and a noble multi-objective optimization technique i.e., Self-adaptive Multi-Objective Weighted Approach (SMOWA) has been used.
• The MWPSO algorithm has been developed to prolong the sustainability of the network by minimizing the energy consumption in the WSN.
• The self-adaptive characteristic of the algorithm (SAMP) is used to screen the population, based on the qualitative nature of the populations; the higher the quality of the population, the better the solution. SAMP's higher-quality populations are supplied into the MWPSO algorithm, increasing the likelihood of a better outcome. The solution set of MWPSO is compared to get even better results.
• Previously, no researcher has concentrated on the self-adaptive nature of the hybrid algorithm (SMWPSO) to achieve a better-quality population set for the minimization of the consumed energy of the WSN, and it has been observed that the suggested algorithm outperforms with respect to the present literature.
Different WSN deployment methods have been developed by the researchers. The deployment process can be divided into WSN model construction and placement optimization. Benatia et al. [8] propose a “multi-objective deployment strategy”, where the integration of each necessary objective has been done. Also, energy can be saved if the sensing task finishes faster. “multi-objective optimization” is frequently used as a solution to the problem. Dai et al. [9] also use the “multi-objective optimization” algorithm of job scheduling for failure-prone sensors in WSN. Another way is provided by Abidinet al. [10] where the author uses a new optimization technique inspired biologically where it studies the behaviour of regional predators marking their regions with their scent. In another work to conquer the difficulty of an optimal resolution, Aitsaadi et al. [11] proposed a combination of “multi-objective deployment algorithm” and Tabu search metaheuristic method. In another paper Champrasert et al. [12], a fitness dependent on crossover operator in a “multi-objective Optimization” is studied and evaluated, that optimizes the cost of the installation and area of the coverage in WSN. In this proposed method, the author uses a population of individuals, that represents the types and positions of the sets of wireless sensor nodes, and develops by using the proposed algorithm for finding the optimal cost of the installation and coverage area.
Another approach has been used by Haider et al. [13] where the author presented an approach that depends on general fuzzy logic. On the other hand, to make energy-saving routing choices for WSN they use fixed metrics. Vimalarani et al. [14] have presented an improved power optimization algorithm based on PSO for WSN. Where the selections of clusters and cluster heads have been done by an improved Particle Swarm Optimization that results in an energy-efficient WSN. In another research Erol-Kantarci et al. [15], the author focuses to minimize the energy consumption of the consumers. To do so, they compare and evaluate iHEM and OREM. In another research Fidanova et al. [16], complex telecommunication problems have been resolved by using a “multi-objective algorithm” with ant colony optimization.
In Xu et al. [17] an approach has been taken to reduce the cost of the network with lifetime limitation. Optical WSN deployment methods are explored by the author to minimize the cost. Among the several approaches that have been proposed by the researchers, recently in Rao et al. [18], The author put forward an algorithm that is based on SMOWA, which is a self-adaptive multi population-based algorithm. It has been used to solve restricted and unrestricted numerical and engineering problems for optimization. The searching technique of this algorithm is enhanced here by using a self-adaptive scheme where populations are divided into subpopulations. In Wang et al. [19], the author concludes that the delay can be reduced with an optimal DC value if the number of SFNS are fixed. When the DC value is greater than the optimal value, it will increase the delay, because more than one node is in the awake situation. Banerjee et al. [20] designed an optimized path with the help of Ant Colony Optimization for reducing energy. Maximization of the Coverage Area is also considered using hybrid Differential Evolution–Quantum behaved Particle Swarm Optimization (DE-QPSO)”. Recently in Banerjee et al. [21], the author discussed a way to optimize the coverage area in Fog Network that consists of WSNs, while minimizing the energy consumption. For deployment of the WSN, random deployment is used and for optimization algorithm, “Ant Colony Optimization (ACO)” has been used.
Many researchers have contributed to different applications like video surveillance [22], Internet of Things [23], internet of multimedia things [24] using different robust infrastructures like a cloud-based wireless network [25], 6G Technology [26], Therefore there are also many possibilities of utilizing WSN in those areas of application such as the WSN technology can be combined with video surveillance which may lead robust security system to some remote or risky place like battlefields.
In this paper, a multi-objective function is suggested to minimize the consumed energy by configuring WSN with different deployment policies. The multi-objective function has been described by Eqs. (2) and (3). There are present several procedures to handle multi-objective problems and some few techniques are as follows:
method 1: Global criteria method.
method 2: Weighted method.
method 3:
method 4: Weighted sum method.
In this paper, two problems related to the consumption of energy in WSN as described through Eqs. (2) and (3) has been considered. In this case, no direct procedure has been used but suggested a new approach is suggested as described in Eq. (1)
All the above-mentioned methods are posterior i.e., all these methods generated Pareto optimal solutions. For a detailed discussion about these problems, one may refer to the book of Branke et al. [27].
Here a new way has been proposed as follows:
Subject to,
and
where
Here n represents the total number of weights considered for different propagation models and
This method looks like a weighted approach introduced by Charnes et al. [28].
This concept has been used for the minimization of the energy consumption for WSN. The energy consumption throughout successful data communication among constructed WSN using three different deployment policies has been reduced using the equations mentioned below [29].
The fitness function is described below:
Subject to,
D
Subject to, D > Do for “two-ray ground propagation model”.
From Eqs. (2) and (3) we can write:
where Do is the “threshold transmission distance”.
In the case of two- ray ground propagation model
In the case of the free space propagation model
Here, the distance between two nodes has been measured within the permissible range i.e., 50 to 100 m [29] in the case of the “free space propagation model”.
Etx = quantity of electronic-energy consumed by each node during the transmission of data packets.
Erx = quantity of electronic-energy consumed for receiving data packets.
where (x1, y1) and (x2, y2) are the coordinates of two head-to-head WSN nodes and the distance between two adjacent WSN nodes is D.
Etr = quantity of electronic-energy needed to a single node for “two-ray ground propagation”.
Ets = quantity of electronic-energy needed to a single node for “free-space propagation”.
Eq. (4) is a multi-objective nonlinear constrained optimization problem. In this problem, the weighted component has been adjusted by prior choices of objective functions.
This may arise in several ways.
Way1: The second constraint is more important than of First i.e.,
Way2: The First constraint is more important than the second constraint i.e.,
Way3: Both constraints have equal priority. i.e.,
In this research work, the priority of both constraints has been chosen as equal, therefore, in this research work, way3 has been adopted.
For solving Eq. (4) hybrid SMOWA algorithm has been used. Now the SMOWA algorithm is being discussed in the solution Procedure section.
Now the approach [21] is as follows:
1. Indexing of nodes: At first the indexing of WSN nodes are done, initially it is just a sequential number to identify the nodes easily. This identification number can be referred to identify in case of locating fault detection as well as to locate the position of the active node. After deployment, the indexing should be attached with cluster number, so that the cluster can be identified in case of fault detection or active participation.
2. Clustering: In this paper, the Clustering mechanism is adopted called the “area wise clustering” process. In the “area wise clustering” process the target area has been divided into some uniform blocks called clusters. In this research, the block shape has been considered square. In each cluster, there is one node that is called active node (cluster head (CH)) and others are considered inactive nodes.
3. WSN node Deployment policies:
A. Random deployment: In random deployment,the nodes are deployed randomly in the target area under a cluster. One may use a random function to get the random position of the nodes in the boundary of the target area under a cluster. Some fixed amount of nodes have been deployed within the target area maintaining a certain period and also keeping a certain time interval. This deployment process is more practical in real-life scenarios especially where the planned deployment of nodes is not possible like on battlefields.
B. S pattern deployment: Here the deployment path is following S shape. Acertain amount of nodes have been deployed within the target area maintaining a certain period and also keeping a certain time interval. In this strategy, the login time for entry to the deployment area and the log out time for exit from the deployment area should be immovable. This deployment is possible in the case of the planned deployment of nodes like WSN node deployment in farmhouses.
C. Nautilus shell shape deployment: In this method of deployment, the path is following the nautilus shell shape. Some fixed numbers of nodes have been deployed within the target area maintaining a fixed quantity of time and also keeping a fixed time interval. In this strategy, the login time for entry to the deployment area and the logout time for exit from the deployment area should be immovable. This deployment process is also possible in the case of the planned deployment of WSN nodes.
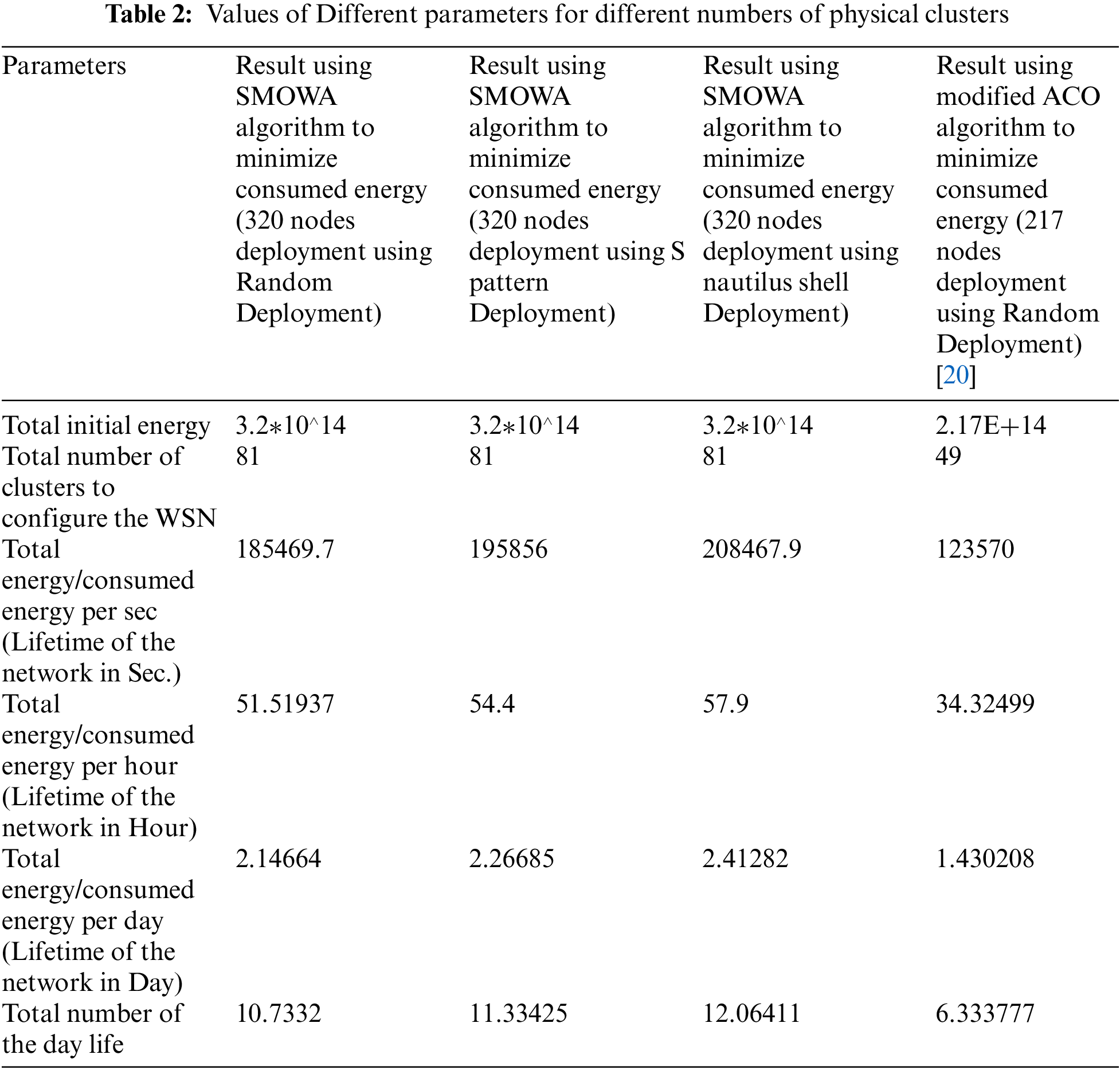
4. Minimization of consumed energy for the configured WSN using SMOWA algorithm: After the deployment of WSN nodes, the wireless sensor network is configured as shown in Figs. 1–3 respectively for random, S-pattern and nautilus shell deployments. After that, the SMOWA Algorithm is used to minimize the energy consumption by different WSN nodes under different networks and the result is depicted in Tab. 2 taking the input parameters from Tab. 1.
SMOWA Algorithm for solving a multi-objective problem
Step 1: Initialize the total populations as P and termination criterion (i.e., the maximum round of fitness function evaluations, repetition of fitness function value for a certain time etc.).
Step 2: calculate the primary candidate solutions (“initial solution”) using the “fitness function” for the problem (See Eqs. (1), (2) and (3)).
Step 3: The entire population is segregated using a new operator called the segregation operator. The whole population is segregated into an equal n number of “sub-populations” depending upon the quality of the solutions. The quality is checked depending upon a predefined threshold value and in this case, the threshold value is the ideal fitness value (See Eq. (1)).
Step 4: Each “sub-population” uses a multi-objective weighted approach algorithm (see Eq. (1)) to modify the solutions for every subpopulation independently.
Step 5: In the selection phase, the selection operator is used to accept the updated solutions if the new solution is better than the previous solution.
Step 6: stopping condition(s) is checked, i.e., the maximum round of fitness function evaluations, repetition of fitness function value for a certain time and the best optimum solution are reported. If the stopping condition is not met go to step 3.
Here it should be mentioned that the SMOWA algorithm is used to determine the minimum distance of the connections between WSN nodes, before different node deployment strategies.
5 Numerical Solutions and Discussion
To demonstrate the proposed approach for solving the “constrained multi-objective optimization problem” by the newly proposed SMOWA algorithm, the following numerical illustration [20] has been adopted.
Tab. 1 has been used to denote the input values used for different parameters in the experiment. The parameters have been chosen from either the existing literature [20] or calculated maintaining the synchronization with some existing literature [20]. After applying different deployment strategies, the following network has been generated.

The axis measuring unit for the below-mentioned figures (Figs. 1–3) is “Meter” in both X-axis and Y-axis and the axis measuring unit for Figs. 4–6 is “objective function value in pico-joule”.
Figure 1: (A) Random deployment (before building connection among nodes). (B) Connection building of WSN after Random deployment
Figure 2: (A) S pattern deployment (before building connection among nodes). (B) Connection building of WSN after S pattern deployment
Figure 3: (A) NautilusShell deployment (before building connection among nodes). (B)Connection building of WSN after nautilus shell deployment
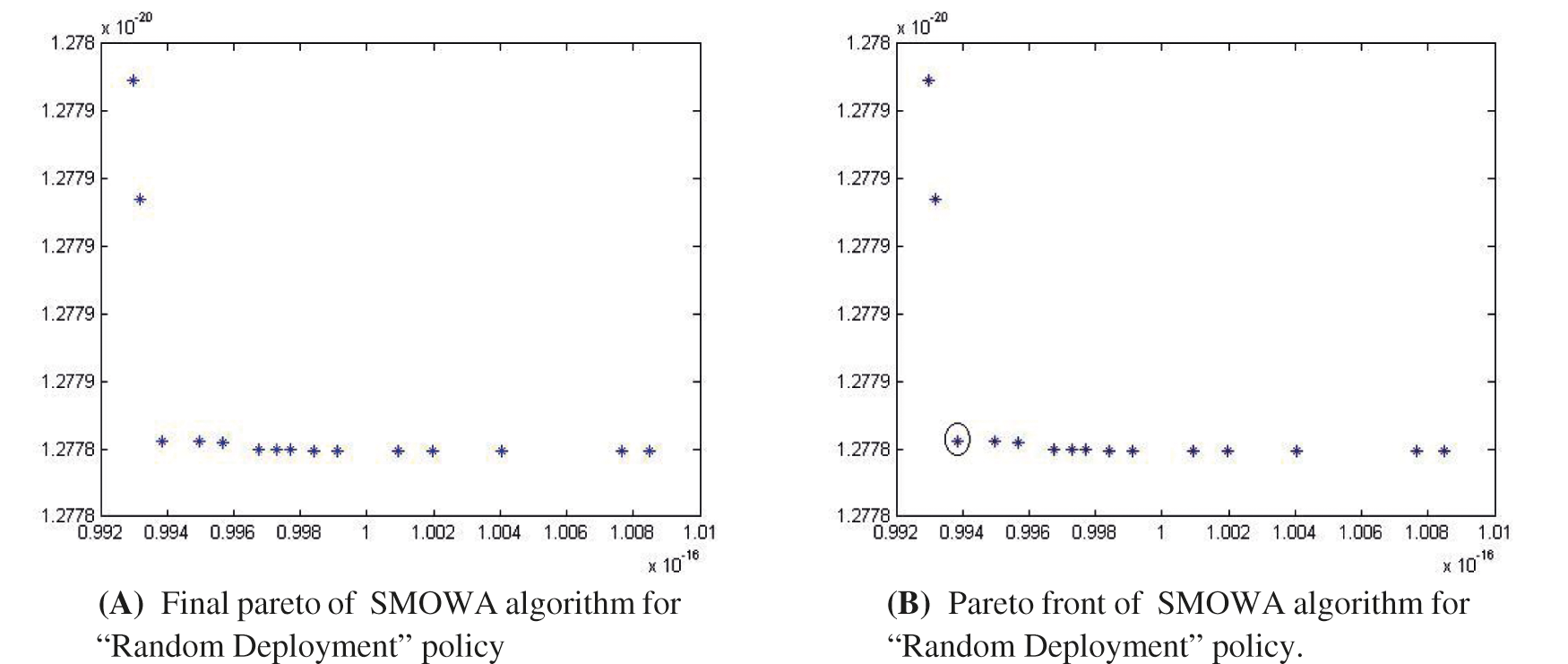
Figure 4: (A) Final pareto of SMOWA algorithm for “Random Deployment” policy. (B) Pareto front of SMOWA algorithm for “Random Deployment” policy
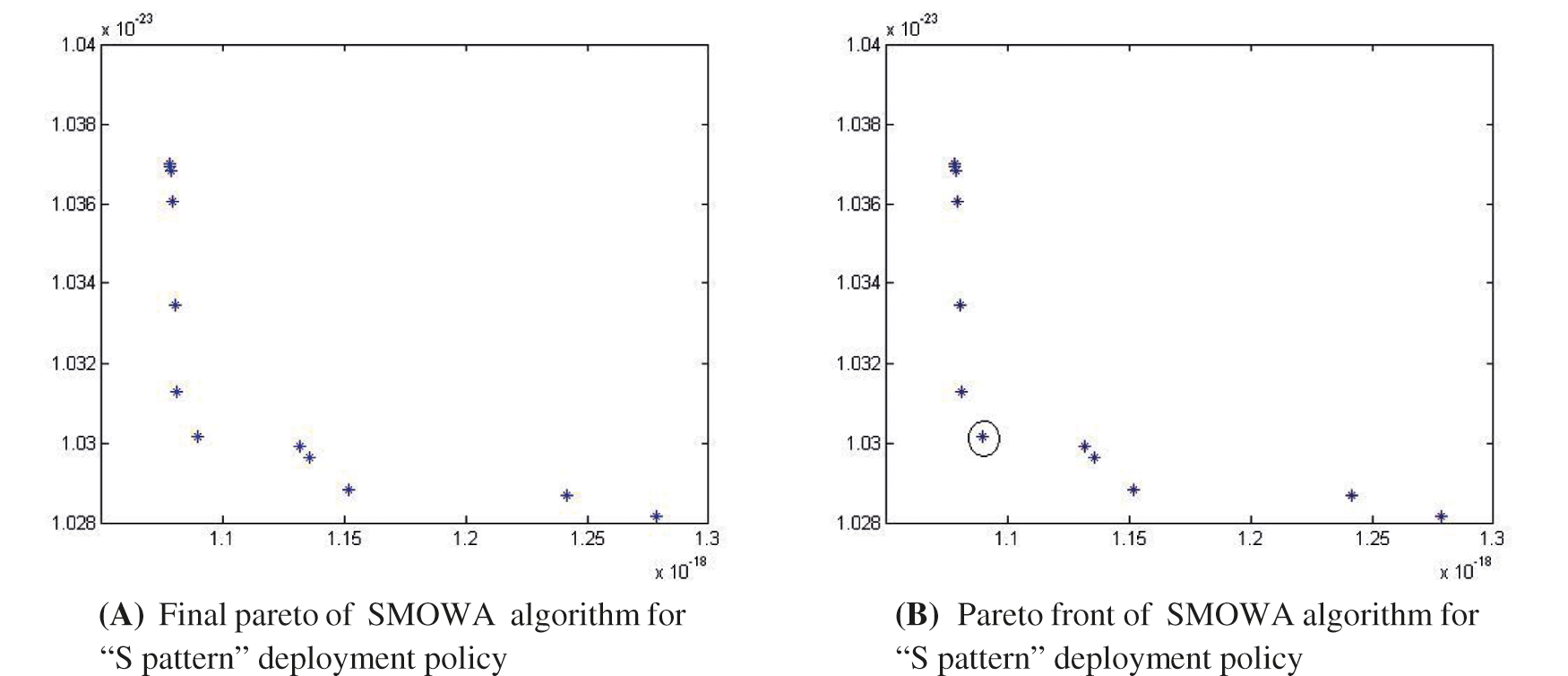
Figure 5: (A) Final pareto of SMOWA algorithm for “S pattern” deployment policy. (B) Pareto front of SMOWA algorithm for “S pattern” deployment policy
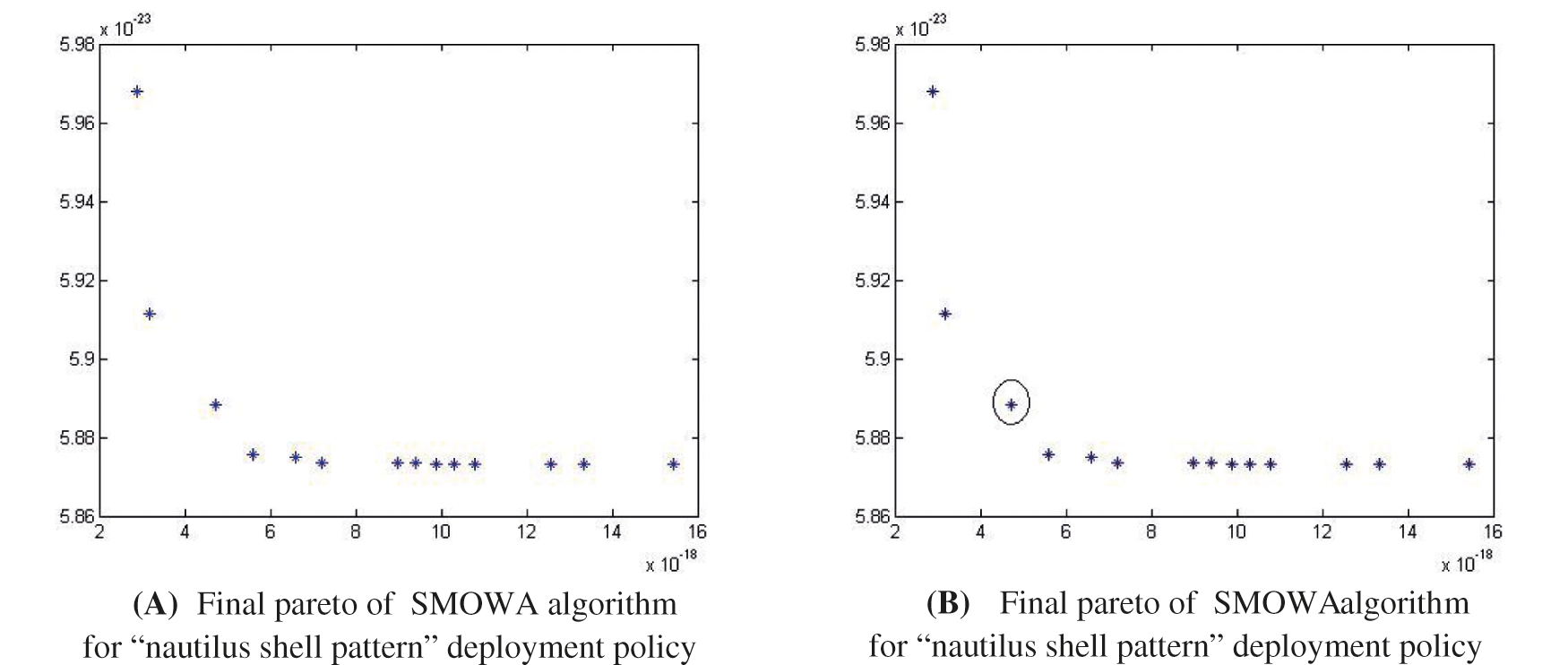
Figure 6: (A) Final pareto of SMOWA algorithm for “nautilus shell pattern” deployment policy. (B) Final pareto of SMOWA algorithm for “nautilus shell pattern” deployment policy
Eq. (4) is used to minimize the consumed energy of the configured WSN network with the help of the SMOWA algorithm. Now the numerical data of results are being signified using the tabular format as depicted below in Tab. 2.
“Python” programming, as well as “Matlab” simulation, is used in the research work to obtain the result set. The desired WSN network has been constructed using “Python” programming for different deployment policies as described in Section no 5 (“Solution Procedure”). The code for simulation of the proposed SMOWA algorithm has been written using “Matlab”. Figs. 4–6 have been constructed using the simulation for different (“Random deployment”, “S Pattern deployment” and “nautilus shell pattern deployment”). There are two parts in each figure denoting the “Final pareto of SMOWA algorithm for different deployment policies” and “Pareto front of SMOWA algorithm for different deployment policies”.
From Tab. 2 we can see that the obtained result using SMOWA algorithm to minimize consumed energy in case of random deployment for 320 nodes using Random Deployment is much better than the obtained result using modified ACO algorithm to minimize consumed energy in case of random deployment 217 nodes using Random Deployment [20]. The compared result has made bold for easy understanding. Ultimately, we can conclude that the total number of day-life is bigger in the case of the proposed algorithm than that of the existing literature [20]. Here the day-life refer to the lifetime of the total WSN. In the below-mentioned figures, the x-axis denotes the energy consumption in free space propagation and the y-axis denotes the energy consumption in the two-ray ground propagation model.
Wilcoxon Rank-Sum Test for the Multi-Objective Reliability Optimization
In Tab. 4 population set is generated by the algorithm SMOWA using our proposed model when
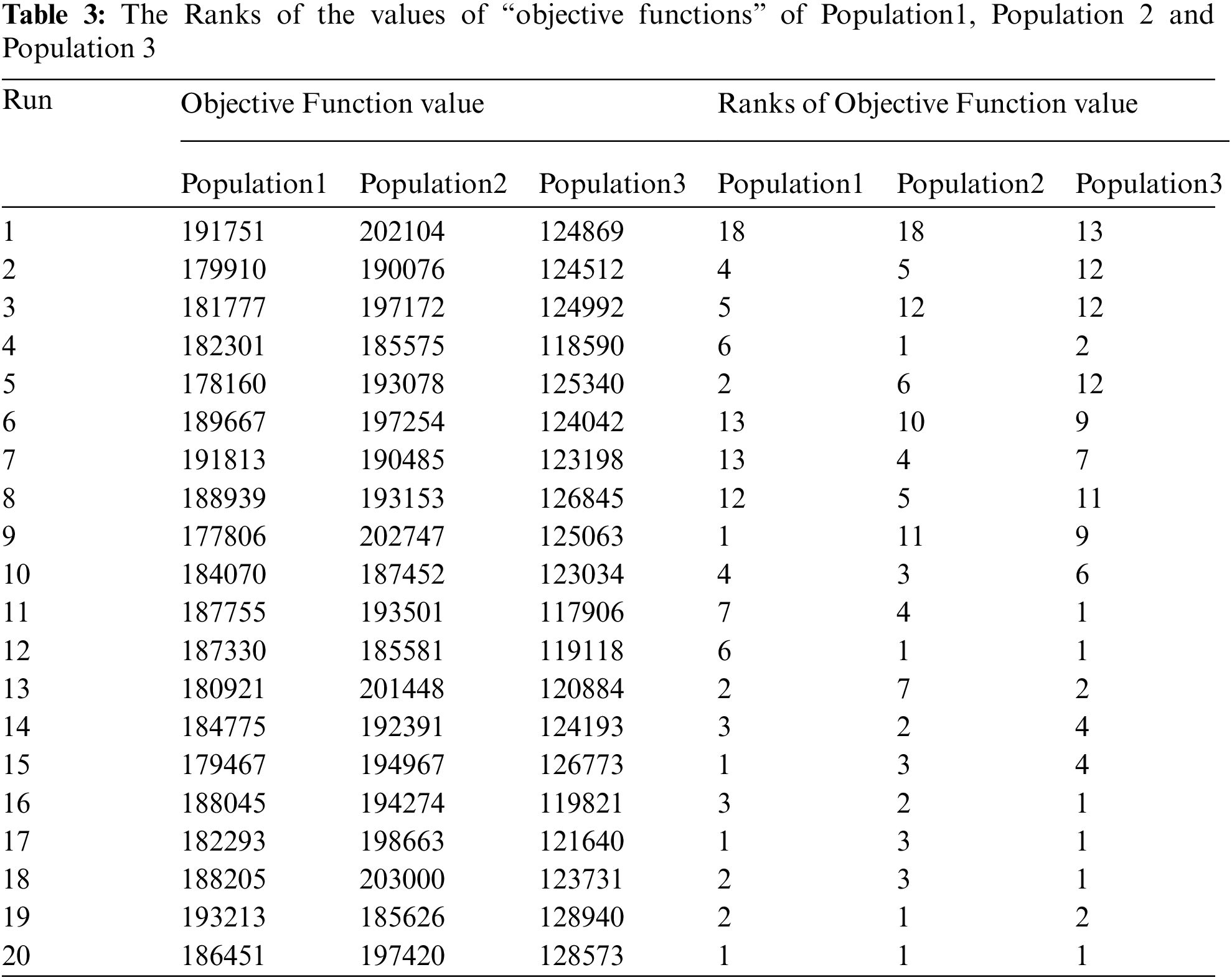
In Tab. 4, the discussion has been made about the statistical data, which leads to deciding the population selection as well as methods involved in the experiment. Here Wilcoxon Rank-Sum Test played an important role to make a decision.
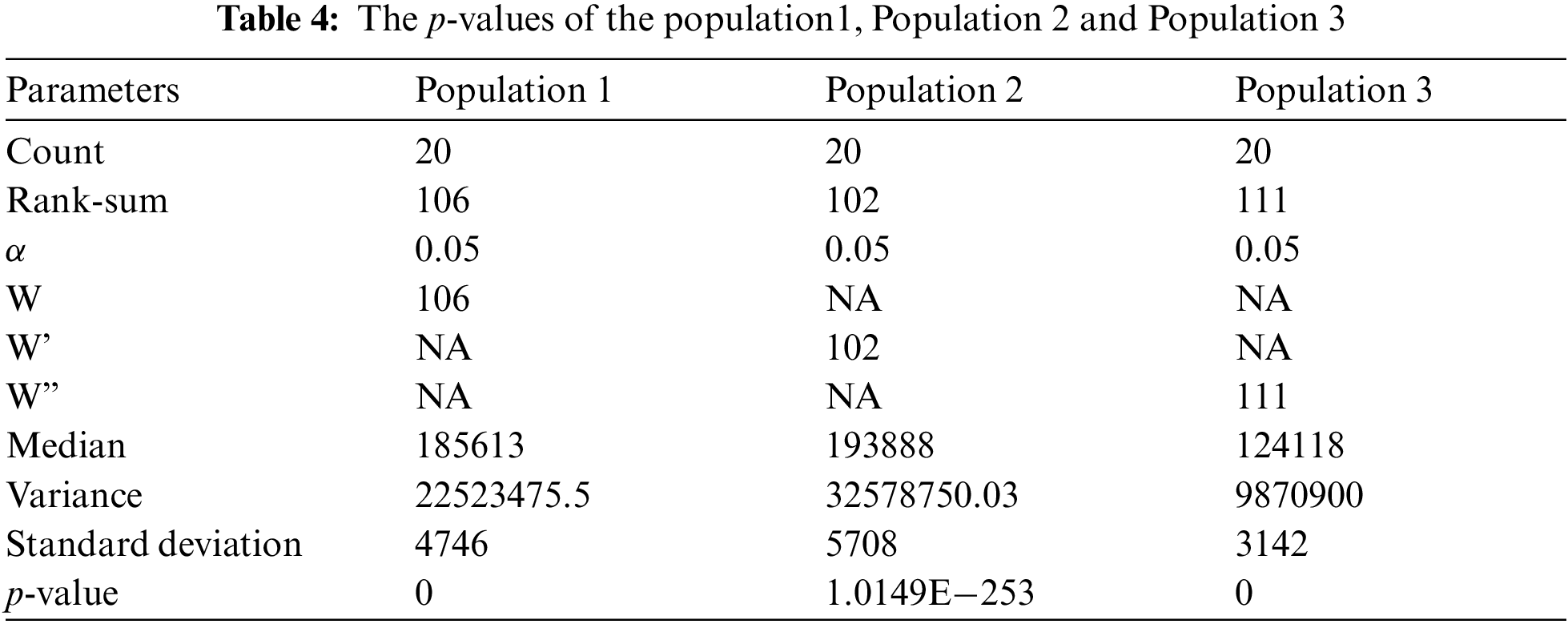
Significance of p-value [30]: Since (p-value for population 2) < (p-value of population 1) = (p-value of population 3) therefore the population2 (sample) has higher significance over population1 and population3. We get the value p-value using the Wilcoxon Rank-Sum Table. Also, from Tab. 2, “a Total number of the day-life” field it is clear the model has the highest sustainability (i.e., 10.7332) in comparison to other models.
The major goal of this research work is to reduce the consumption of energy in Wireless Sensor Networks. Here consumption of energy by the WSN network refers to the total energy consumption by each and individual WSN node. The efficient network may be configured using different deployment strategies as discussed in Subsection 2 of Section 5. The SMOWA algorithm has been used as the minimization technique, which is another novelty of the paper. Through this algorithm, one can select a better population set due to its self-adaptive nature as well as this algorithm can handle the multi-objective problem which is an added feature of the algorithm, therefore, this algorithm has a global context that can lead to solving other problems related to another similar engineering problems. In the result analysis section, different results obtained through different deployment strategies have been analysed. Furthermore, the significance of appropriate population among the different auto-generated population have been discussed and analysed through the Wilcoxon Rank-Sum Test for the Multi-objective reliability optimization. For further research, the proposed approach can be improved with the use of advanced segregation, selection operators and advanced stopping criterion for the SMOWA algorithm. Here SMOWA Algorithm has been used because the main focus is on the convergence for the local optimal rather than global optimal. In this research work, only one case has been considered while setting the priority among the weight of the different propagation models (free space propagation model and two-ray ground propagation model) i.e., the equal priority to both of them but in real life, the priority is rarely equal therefore this is a limitation of the research work. But in the future one can implement the new models by considering the other cases as mentioned in the problem formulation section. For further research, one can modify the proposed approach using advanced segregation techniques, using advanced selection operators, and modified termination criterion of the SMOWA algorithm. There are also many scopes to improve the optimization operators of the used optimization technique. In this research, this unique hybridized approach has been used to solve the minimization problem. This approach can also be applied to solve some maximization problems like area maximization of WSN.
Funding Statement:The authors received no specific funding for this study.
Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.
1. J. Wang, Y. Cao, B. Li, H. J. Kim and S. Lee, “Particle swarm optimization based clustering algorithm with mobile sink for WSNs,” Future Generation Computer Systems, vol. 76, no. 12, pp. 452–457, 2017. [Google Scholar]
2. M. Navarro, T. W. Davis, Y. Liang and X. Liang, “A study of long-term WSN deployment for environmental monitoring,” in 2013 IEEE 24th Annual Int. Symp. on Personal, Indoor, and Mobile Radio Communications (PIMRC), London, UK, pp. 2093–2097, 2013. [Google Scholar]
3. M. Sara, I. Jawharand and M. Nader, “A softwarization architecture for UAVs and WSNs as part of the cloud environment,” in 2016 IEEE Int. Conf. on Cloud Engineering Workshop (IC2EW), Berlin, Germany, pp. 13–18, 2016. [Google Scholar]
4. Y. Ren, Y. Liu, S. Ji, A. K. Sangaiahand and J. Wang, “Incentive mechanism of data storage based on blockchain for wireless sensor networks,” Mobile Information Systems, vol. 2018, pp. 1–10, 2018. [Google Scholar]
5. P. Visconti, R. Ferri, M. Pucciarelliand and E. Venere, “Development and characterization of a solar based energy harvesting and power management system for a WSN node applied to optimized goods transport and storage,” International Journal on Smart Sensing & Intelligent Systems, vol. 9, no. 4, pp. 1637–1667, 2016. [Google Scholar]
6. V. Kumar, V. Kumar, D. N. Sandeep, S. Yadav, R. K. Barik et al., “Multi-hop communication based optimal clustering in hexagon and voronoi cell structured WSNs,” AEU-International Journal of Electronics and Communications, vol. 93, no. 4, pp. 305–316, 2018. [Google Scholar]
7. A. Banerjee, V. Das, A. Mitra, S. Chattopadhyay and U. Biswas, “A power optimization technique for WSN with the help of hybrid meta-heuristic algorithm targeting fog networks”, in Intelligent and Cloud Computing, Singapore: Springer, pp. 105–123, 2019. [Google Scholar]
8. M. A. Benatia, M. H. Sahnoun, D. Baudry, A. Louis, A. El-Hami et al., “Multi-objective WSN deployment using genetic algorithms under cost, coverage, and connectivity constraints,” Wireless Personal Communications, vol. 94, no. 4, pp. 2739–2768, 2017. [Google Scholar]
9. L. Dai, H. Xu, T. Chen, Q. Chao and L. Xie, “A multi-objective optimization algorithm of task scheduling in WSN,” International Journal of Computers Communications & Control, vol. 9, no. 2, pp. 160–171, 2014. [Google Scholar]
10. H. Z. Abidin, N. M. Din and Y. E. Jalil, “Multi-objective Optimization (MOO) approach for sensor node placement in WSN,” in 2013, 7th Int. Conf. on Signal Processing and Communication Systems (ICSPCS), Carrara, Australia, IEEE, pp. 1–5, 2013. [Google Scholar]
11. N. Aitsaadi, N. Achir, K. Boussettaand and G. Pujolle, “Artificial potential field approach in WSN deployment: Cost, QoM, connectivity, and lifetime constraints,” Computer Networks, vol. 55, no. 1, pp. 84–105, 2011. [Google Scholar]
12. P. Champrasert and T. Kumrai, “Coverage and installation cost optimization in wsns using a fitness-based crossover evolutionary algorithm,” in 2013 Int. Conf. on Technology, Informatics, Management, Engineering and Environment, Bandung, Indonesia, IEEE, pp. 83–88, 2013. [Google Scholar]
13. T. Haider and M. Yusuf, “A fuzzy approach to energy-optimized routing for wireless sensor networks,” The International Arab Journal of Information Technology, vol. 6, no. 2, pp. 179–185, 2009. [Google Scholar]
14. C. Vimalarani, R. Subramanian and S. N. Sivanandam, “An enhanced PSO-based clustering energy optimization algorithm for wireless sensor network,” Soft Computational Approaches for Prediction and Estimation of Software Development, The Scientific World Journal, vol. 2016, no. 1, pp. 1–11, 2016. [Google Scholar]
15. M. Erol-Kantarciand and H. T. Mouftah, “Wireless sensor networks for cost-efficient residential energy management in the smart grid,” IEEE Transactions on Smart Grid, vol. 2, no. 2, pp. 314–325, 2011. [Google Scholar]
16. S. Fidanova, P. Marinov and M. Paparzycki, “Multi-objective ACO algorithm for WSN layout: Performance according to number of ants,” International Journal of Metaheuristics, vol. 3, no. 2, pp. 149–161, 2014. [Google Scholar]
17. K. Xu, Q. Wang, H. Hassaneinand and G. Takahara, “Optimal wireless sensor networks (WSNs) deployment: Minimum cost with lifetime constraint,” in WiMob’2005, IEEE Int. Conf. on Wireless and Mobile Computing, Networking and Communications, Montreal, QC, Canada, vol. 3, pp. 454–461, 2005. [Google Scholar]
18. R. V. Rao and A. Saroj, “Saroj, self-adaptive multi-population based SMOWA algorithm for engineering optimization,” Swarm and Evolutionary computation, vol. 37, pp. 1–26, 2017. [Google Scholar]
19. F. Wang, W. Liu, T. Wang, M. Zhao, M. Xieet et al., “To reduce delay, energy consumption and collision through optimization duty-cycle and size of forwarding node set in WSNs,” IEEE Access, vol. 7, pp. 55983–56015, 2019. [Google Scholar]
20. A. Banerjee, V. Das, A. Biswas, S. Chattopadhyay and U. Biswas, “Development of energy efficient and optimized coverage area network configuration to achieve reliable WSN network using meta-heuristic approaches,” International Journal of Applied Metaheuristic Computing (IJAMC), vol. 12, no. 3, pp. 1–27, 2021. [Google Scholar]
21. A. Banerjee, S. K. De, K. Majumder, V. Das, D. Giri et al., “Construction of effective wireless sensor network for smart communication using modified ant colony optimization technique,” in Advanced Computing and Intelligent Technologies, Singapore: Springer, pp. 269–278, 2022. [Google Scholar]
22. A. Reyana, S. Kautish, A. S. Vibithand and S. B. Goyal, “EGMM video surveillance for monitoring urban traffic scenario,” International Journal of Intelligent Unmanned Systems, vol. 36, no. 2, pp. 89, 2021. [Google Scholar]
23. K. Prasanna, K. Ramana, G. Dhiman, S. Kautishand and V. D. Chakravarthy, “PoC design: A methodology for proof-of-concept (PoC) development on internet of things connected dynamic environments,” Security and Communication Networks, vol. 2021, no. 4, pp. 1–12, 2021. [Google Scholar]
24. M. Uppal, D. Gupta, S. Juneja and S. Kautish, “Cloud-based fault prediction using IoT in office automation for improvisation of health of employees,” Journal of Healthcare Engineering, vol. 2021, no. 5, pp. 1–13, 2021. [Google Scholar]
25. S. Juneja, M. Gahlan, G. Dhiman and S. Kautish, “Futuristic cyber-twin architecture for 6G technology to support internet of everything,” Scientific Programming, vol. 2021, pp. 1–7, 2021. [Google Scholar]
26. M. Gupta, K. K. Gupta, M. R. Khosravi, P. K. Shukla, S. Kautishet et al., “An intelligent session key-based hybrid lightweight image encryption algorithm using logistic-tent map and crossover operator for internet of multimedia things,” Wireless Personal Communications, vol. 121, no. 3, pp. 1–22, 2021. [Google Scholar]
27. J. Branke, J. Branke, K. Deb, K. Miettinen and R. Slowiński (Eds.“Multiobjective optimization: Interactive and evolutionary approaches,” in Springer Science & Business Media, Berlin Heidelberg Germany: Springer-Verlag, vol. 5252, 2008. [Google Scholar]
28. A. Charnesand and W. W. Cooper, “Goal programming and multiple objective optimizations: Part 1,” European Journal of Operational Research, vol. 1, no. 1, pp. 39–54, 1997. [Google Scholar]
29. S. B. Landeand and S. Z. Kawale, “Energy efficient routing protocol for wireless sensor networks,” in 2016 8th Int. Conf. on Computational Intelligence and Communication Networks (CICN), Tehri, India, pp. 77–81, 2016. [Google Scholar]
30. de Barros, R. S. Maior, J. I. G. Hidalgo and D. R. de Lima Cabral, “Wilcoxon rank sum test drift detector,” Neurocomputing, vol. 275, pp. 1954–1963, 2018. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |