DOI:10.32604/cmc.2022.025205

| Computers, Materials & Continua DOI:10.32604/cmc.2022.025205 |  |
| Article |
Modeling and Verification of Aircraft Takeoff Through Novel Quantum Nets
1School of Systems and Technology, University of Management & Technology (UMT), C-II Block C 2 Phase 1 Johar Town, Lahore, 54770, Punjab, Pakistan
2Department of Computer Science, COMSATS University Islamabad–Sahiwal Campus, Sahiwal, 57000, Punjab, Pakistan
3Department of Computer Science (CS), College of Computer Science and Information Technology (CCSIT), Imam Abdulrahman Bin Faisal University (IAU), Dammam, 31441, Saudi Arabia
4Department of Computer Information System (CIS), College of Computer Science and Information Technology (CCSIT), Imam Abdulrahman Bin Faisal University (IAU), Dammam, 31441, Saudi Arabia
*Corresponding Author: Atta-ur-Rahman. Email: aaurrahman@iau.edu.sa
Received: 16 November 2021; Accepted: 11 February 2022
Abstract: The formal modeling and verification of aircraft takeoff is a challenge because it is a complex safety-critical operation. The task of aircraft takeoff is distributed amongst various computer-based controllers, however, with the growing malicious threats a secure communication between aircraft and controllers becomes highly important. This research serves as a starting point for integration of BB84 quantum protocol with petri nets for secure modeling and verification of takeoff procedure. The integrated model combines the BB84 quantum cryptographic protocol with powerful verification tool support offered by petri nets. To model certain important properties of BB84, a new variant of petri nets coined as Quantum Nets are proposed by defining their mathematical foundations and overall system dynamics, furthermore, some important system properties are also abstractly defined. The proposed Quantum Nets are then applied for modeling of aircraft takeoff process by defining three quantum nets: namely aircraft, runway controller and gate controller. For authentication between quantum nets, the use of external places and transitions is demonstrated to describe the encryption-decryption process of qubits stream. Finally, the developed takeoff quantum network is verified through simulation offered by colored petri-net (CPN) Tools. Moreover, reachability tree (RT) analysis is also performed to have greater confidence in feasibility and correctness of the proposed aircraft takeoff model through the Quantum Nets.
Keywords: Aircraft takeoff; BB84; quantum cryptography; petri-nets; quantum nets; formal modeling and verification
Takeoff is the initial and critical phase of a flight as it raises the confidence level of overall flight safety. The task of safe aircraft takeoff is also distributed amongst various computer-based controllers. The intense communication between different controllers involved in aircraft takeoff needs to be secure which is perplexed by the dynamic, distributed, and concurrent nature of air traffic control system. These issues make the takeoff process a highly difficult and challenging domain [1]. Furthermore, even a minor system error or abnormal system behavior may lead to severe consequences in term loss of precious human lives and heavy monetary penalties. Also, the possible intrusion of an eavesdropper during communication between aircraft and controller may put the whole takeoff process at a high security risk. Therefore, there is need of modeling and verification of aircraft takeoff process while focusing the overall system security. The BB84 quantum protocol was introduced in 1984 by Bennett et al. [2] that offers a secure way of communication by combining the cryptography with quantum principles [3]. It is among the strongest techniques which guarantees safe transmission between a transmitter and receiver. The presence of an intrusion attack by an eavesdropper is identified through photon polarization [4]. But petri-nets are graphical formal methods which underlies on strong mathematical foundations. Due to their robust expressivity, they are widely used for modeling concurrency and non-determinism. Furthermore, the petri-nets are enriched with strong verification support for inspecting correctness of a system [5]. Undergoing research provides an integration of BB84 with petri-nets for formal modeling and verification of aircraft takeoff procedure while incorporating system security. As the BB84 is a quantum cryptographic protocol which provides the maximum level of security, and the petri-nets are a powerful notation for mathematical modeling and verification of distributed concurrent systems. This integration allows a secure and comprehensive mathematical modeling of aircraft takeoff. Moreover, it allows system verification for presence of potential errors and unexpected system behavior. While the errors spotted during modeling are easier and cheaper to be fixed. This research is important as it provides starting point for integration of quantum cryptography with petri-nets to integrate best features of both approaches. Since the petri-nets offers only three basic notations (place, transition, and arcs) therefore, they cannot model all concepts of BB84 which is a quantum cryptographic protocol. The existing notations and properties of traditional petri-nets are enriched for quantum concepts through the development of a new variant of traditional petri-nets, named as the “Quantum Nets”. The existing work regarding integration of BB84 with petri-nets is novel in a sense that an existing work is found where the integration was performed at an abstract level [6], whereas some existing work just covers the model checking of BB84 protocol. In this study, the strong static foundations of quantum nets are developed to describe distributed network nodes, concurrent bi-directional communication, and flow of different types of data whereas the dynamic properties such as tokenization, external transitions, transition, enabling, and system dynamics are also formalized. Furthermore, the properties like reachability, boundedness, liveness, safety, and concurrency are abstractly defined in this research. The proposed Quantum Nets are applied to develop a formal model of aircraft takeoff which is composed of three quantum nets namely aircraft, runway controller, ground controller. The authentication process is defined through a public and a quantum channel also the secure communication between the quantum nets is modeled through external places and external transitions. To inspect its behavior, the proposed model is verified through CPN tools simulator. The proposed takeoff model is also verified by using mathematical proof technique of reachability tree (RT) analysis which ensures the correctness of proposed model which further makes the study unique.
The article is sectioned as: Section 2 covers a thorough literature survey, the mathematical foundations of proposed quantum nets are enclosed in Section 3. The mathematical properties of quantum network are specified in Section 4 and in Section 5, the practical applicability of quantum nets is demonstrated through the case study of an aircraft takeoff. Finally, Section 5 wraps up the articles with concluding remarks.
Formal modeling and verification of quantum protocols using various mathematical techniques is among the hottest areas of research. The research in [7,8] focused the verification of B94 protocol through PRISM tool. Similarly, some quantum protocols were verified by using a decision procedure which integrates algebraic logic with operational semantics in [9]. The application of a quantum model checker was shown in [10,11]. In [12] process calculus was used to model BB84 protocol which was analyzed by concurrency workbench of the new century (CWB-NC) tool. A new language coined as Communicating Quantum Processes was proposed by combining pi-calculus with quantum theory in [13]. In [14] a Hoare-style logic was proposed for quantum protocols and a semi-automated formal framework was defined for verification of quantum systems in [15]. To analyze the bi-simulation relation of quantum processes a tool was developed in [16] and in [17] an entanglement sampling technique was applied to find the lower bound of entanglement which is required by an eavesdropper for attacking a quantum channel. The measurement in a quantum process calculus was described in [18] by using bi-simulation congruence and protocol equivalency. Distribution-based bi-simulation of quantum process by using process algebra was proposed in [19]. The research in [20] presented an automation of unconditional security proof for quantum key distribution and the quantum information system based on B92 protocol. The process was performed by using PRISM tool in [21]. In [22] a variant of BB84 was modeled by using discrete time Markov chain and probabilistic computation tree logic and its security properties were verified by using PRISM tool. BB84 and B94 were modeled by using Communicating Quantum Processes in [23] which were translated into PRISM model for its verification. IEEE 802.11 standard was integrated with BB84, and some security properties were analyzed by using PRISM tool in [24]. Some important quantum bit commitment approaches were proposed in [25,26] and were reviewed in [27,28]. In [29] the analysis of this protocol was done by using model checking to demonstrate its practical applicability. Few basic correctness properties of the protocol were verified in [30] by using PRISM tool to demonstrate the feasibility of automated verification techniques. A new formal execution technique called equivalence checking was presented in [31,32] for analysis of the protocol. It focused on communicating concurrent components which the authors claimed to be applicable on all input states. The use of PRISM tool was shown for identification of an eavesdropper in a quantum system in [33]. Few ways to attack the quantum network were modeled and verified by using PRISM tool in [5]. Focusing the parameter of eavesdropper and quantum channel, the security of BB84 was analyzed through PRISM tool in [34]. Automated model checking PRISM tool was used in [35] and a direct relation was identified between number of transmitted qubits and evasion of an eavesdropper. The channel disturbance of a quantum channel was modeled and verified by using PRISM tool in [36]. While the entangled photon pairs of BB84 protocol were focused for verification using PRISM tool in [37] and addressed in [38]. Other than cryptosystems, digital watermarking and steganography also used for authentication and verification. Especially, in digital image transmission, the images need to be secure [39]. In digital image watermarking mainly, proprietary, and medical images are watermarked for sake of authentication, integrity and information hiding [40–44]. Similarly, steganography is used for secrecy [45–48].
Based on the extensive review of modeling and verification of BB84 quantum key distribution techniques, the undergoing research was conducted. In the literature, several approaches verified certain dimensions of this protocol but all of them mainly use the PRISM toolset for the verification. However, the investigation of petri-nets for modeling and verification of a quantum cryptographic system has been an uncovered arena of research. Only one related publication was found in which the petri nets were used to model quantum communication protocol at an abstract level [6]. Since quantum cryptography offers a high level of security and it can detect an intrusion attack as well. Modeling and verification of a quantum cryptographic system has a potential benefit of revealing unexpected system behavior. Also, the errors identified before system implementation are easier and cheaper to be fixed. Therefore, the modeling and verification capabilities of petri nets may be fruitful in modeling of BB84 quantum protocol.
In this section the extension of Petri-nets is provided. The BB84 is a quantum key distribution protocol which exploits photon polarization state for transmission of qubits. Using this protocol, the sender and receiver are connected through a quantum channel and a classical channel. Both channels are not secure against intruder attack. The encoding of BB84 lays its foundation on the pairs of orthogonal states named as a basis. A basis can either be rectilinear with vertical polarization state or diagonal with horizontal polarization state. The two bases are used in this protocol as both are conjugate to one another. The conjugate pair of basis is known to both sender and receiver prior to their communication. The sender chooses one of the basis to encode a qubit and sends it to receiver, via its quantum channel. The receiver receives the qubit through its quantum channel, and it decodes the basis of a qubit on random guessing. Once the stream of qubit sent by the sender is decrypted by the receiver, it resends the decrypted basis values back to sender through its public channel for matching. If the number of matching decrypted and encrypted qubits is less than or equal to a threshold then the sender verifies the receiver and sends the secret message safely to receiver via its public channel. Petri-nets are robust graphical formal methods widely used by experts for modeling distributed and concurrent systems. The foundations of petri nets are based on firm mathematical semantics, and they offer strong verification techniques like reachability, boundedness etc. Further, they offer simple place-transition notations which can be extended for complex systems modeling. Subsequently, the integration of BB84 cryptography with petri-nets is provided. To model quantum key cryptography, a new variant of traditional petri-nets, coined as the “Quantum Nets” is defined. Basic petri-nets are mathematically enriched with quantum concepts as described in next section.
A quantum net is defined as, QN = (Ƥ, Ͳ, Ƒ, ϻ0), Ƥ is the set of places defined as Ƥ = ƤI¼PE where PI is the set of internal places of a net and PE is the set of external places, Ͳ is the set of transition, defined as Ͳ = ͲI¼ͲE where ͲI is the set of internal transitions of a net and ͲE is the set of external transitions. An external transition and an external place are not only visible to its resident quantum net but also to all other nets. They can be accessed by any non-resident quantum nets and can change marking of a quantum net. Ƒ is the set of connections between place and transition or vice versa such that Ƒ¹(Ƥ²Ͳ) ¼(Ͳ²Ƥ) and ϻ0 is the initial marking of a quantum net such that ϻ0o Ƥ. A flow arc ƒ is an external arc, such that ƒ (ϯ, ϸ)³Ƒ where transition ϯ is an external transition and ϸ is an external place.
3.2 Quantum Key Distribution System
A quantum key distribution system is defined as a tuple named QDS = (QID, Ǫs, Ǫd, ɋ, ρ) where QID³¤ +which is unique identifier of a quantum net, Ǫs is the source quantum net and its initial marking ϻ0 is |Ǫs.ϻ0|ä1, Ǫd is the destination quantum net and its initial marking ϻ0 is |Ǫd.ϻ0|ä1, ɋ is the qubit interaction channel defined as ɋoͲ²Ƥ such that Õ(ϯ, ϸ)³ɋ. ϯ³ͲEÙϯ³Ǫs.ͲÙϸ³ƤEÙϸ³Ǫd.Ƥ and ρ is the message interaction channel defined as ρoͲ²Ƥ such that Õ(ϯ, ϸ)³ρ. ϯ³ͲEÙϯ³Ǫs.ͲÙϸ³ƤEÙϸ³Ǫd.Ƥ and M(ϸ)ä Ƒ(ϸ, ϯ).
The arc activation rules make the interaction of quantum net possible. These rules are triggered before transporting qubits and messages on their respective channels. The rules for arc activation within a quantum key distribution system QDS is a pair of marking (M, M’) such that M is the marking of source quantum net, Ǫs and M’ is the marking of destination quantum net, Ǫd are defined as follows.
• A transition ϯ³Ǫs, Ͳ is activated in the pair of marking (M, M’) of a quantum key distribution system iff ϯϸ = ¸ and ϯ is activated in M. Then the resultant pair of marking in a source quantum net is defined as (M1, M2) such that MaM1 and M’ = M2, i.e., (M, M’)ª ϯ(M1, M2).
• A pair (ϯ1, ϯ2)³Ǫs.Ͳ²Ǫd, Ͳ is activated in a pair of marking (M, M’) of a quantum key distribution system iff (ϯ1, ϯ2)³ϸ and both ϯ1and ϯ2 are activated in M and M’. Then the resultant pair of marking in a source quantum net is defined as (M1, M2) such that MaM1 in a destination quantum net and M’ = M2, i.e., (M, M’)ª(ϯ1, ϯ2)(M1, M2).
A transition ϯ³Ǫd, Ͳ is activated in a bi-marking (M, M’) of a quantum key distribution system iff ϸϯ=¸ and ϯ is activated in M’. Then the resultant pair of marking in a destination quantum net is defined as (M1, M2) such that M’ªM2 and M = M1, i.e., (M, M’)ªϯ(M1, M2).
3.4 Quantum Key Distribution Network
A quantum key distribution network is defined as a tuple named QDN = (ǪS, ǪD, ᴪ) where ǪS is the set of all source quantum nets and defined as QS =
A token can be of two types: the qubits and bits. The qubit is a specialized token meant to travel on a quantum channel. A qubit is defined as Bit²Basis²Polarization²Ϯ. A bit represents a Boolean value of either 1 or 0 and defined as Bit:1|0, Basis is defined as Rectilinear or Diagonal. A Rectilinear Basis can have a value 0 for vertical and 90 for horizontal state. Likewise, a Diagonal Basis can have a value 45, 135 or a circular basis of left and right handedness. A Rectilinear basis is represented as V and a diagonal basis is represented as D. Polarization represents a photon polarization which is generated from bit and basis value. For instance, basis V with bit 0 is represented as North, N and a bit 1 is shown as Right, R. A basis D with bit 0 is marked as North East, NE and a bit 1 is represented as South East, SE. Ϯ is the time at which the qubit emits from the sender's quantum channel. A bit token is designed to carry message on a classical public channel. A bit token can carry a stream of bits, so it is defined as ¡Bits. At the receiver's end when a qubit is received via quantum channel it appends the time with a delay factor, γ such that at receiver's end Ϯ’ = Ϯ + γ and Ϯ < Ϯ’.
A transition of a petri-net allows token movement from one place to another. To allow external communication, we extend the transition with a new one called channel transition. A channel transition is a kind of transition which is not only visible to a quantum net to which it belongs to but also to outside nets. Any place can connect with it to transmit its tokens. It is important to note that the same transition is defined to work for incoming and outgoing token flow. Based on the flag, channel transition allows incoming flow if flag is set to true and outgoing flow is achieved if flag is set to false. Moreover, for each quantum net two external transitions are mandatory, i.e., a quantum and public channel.The channel transition to represent a quantum channel is capable of transporting qubits whereas a channel transition which represents a public channel can carry public data. Any place with a qubit token can access quantum channel transition whereas any place with a bit token can access a public channel transition.
4 Properties of Quantum Network
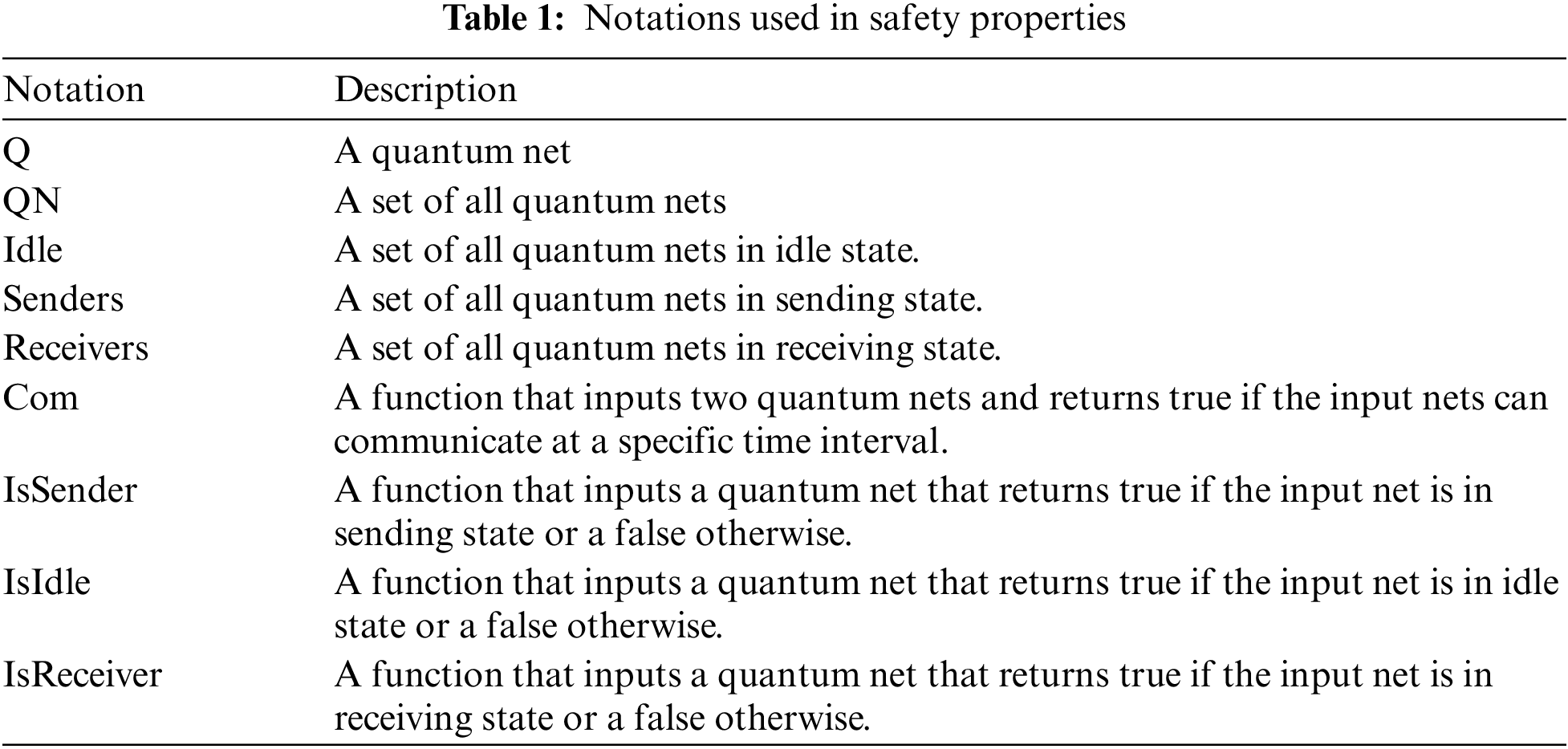
After giving formal foundations to the quantum nets, in this sub-section we define some of its system properties. The system properties help to define overall system behavior. We have defined the following properties for the quantum system. The functions used to define such properties are described in Tab. 1. The proof of following properties is left for the future work.
Every quantum net can send message to another quantum net at any time if the sender is idle and receiver is not a sender or receiver of any other communication.
Õq1, q2: QN; t: ¤ .
Com(q1, q2)@t ª
IsIdle(q1) Ù (Ø IsSender(q2)Ú ØIsReceiver(q2))
Each quantum net of a quantum system must be in an idle state or communicating with another net either as a sender or a receiver.
Õq: QN . q ³ Q Ü
IsIdle(q) Ú IsSender(q) Ú IsReceiver(q)
Every two quantum nets communicating at any time must end their communication after certain interval of time.
Õq1, q2: QN; t, k: ¤ . Com(q1, q2)@t ª
IsIdle(q1)@t + k Ù IsIdle(q2)@t + k Ù t ã t + k
A quantum system is safe if for every sender there is a single receiver and sum of all quantum nets must be equal to idle, sending and receiving nets.
Õq: QN . |Receiver(q)| = 1 Ù
(|QN| = |Idle| + |Senders| + |Receivers|)
In a quantum system any two quantum nets can communicate simultaneously.
Õq1, q2: QN; t: ¤ . q1 ³ Q Ü
((IsSender(q1)@t Ù IsSender(q2)) Ú
(IsReceiver(q1)@t Ù IsReceiver (q2)))Ùq1μ q2
Takeoff is the primary phase of aircraft journey and a safe takeoff raise the confidence level for overall safety. In an earlier study [49] also demonstrated the modeling and analysis of an aircraft takeoff process by using Vienna Development Method Specification Language (VDM-SL). Being the initial flight phase, takeoff should be a secure process to avoid intrusion of any malicious attack. The task of safe aircraft takeoff is also distributed amongst various computer-based controllers and requires secure coordination. Any security loophole may facilitate an intruder to cause immense damage to the whole system. Also, air traffic control system is a complex and highly distributed safety critical system. Its secure modeling and analysis become crucial because even a minor system flaw may lead to catastrophic effects such as monetary loss and risk of human lives.
5.1 Aircraft Takeoff Quantum Network
In this section we have developed a quantum network for an aircraft takeoff. To model takeoff process, as explained earlier, three quantum nets are defined. An aircraft is represented by an aircraft quantum net and the controllers of gate and runway are depicted through a gate controller quantum net and runway quantum net respectively as shown in Fig. 1. The labels assigned to all transition of each quantum nets are shown in Tab. 2. The aircraft quantum net has twenty-two internal places (pa1 to pa22) and two external places; qaio for a quantum channel and paio for a public channel. Also, the aircraft quantum net has four external transitions (ta1, ta13, ta7 and ta14) and the other nineteen are internal transitions. The gate controller quantum net has twenty-four internal places (pa1 to pa24) and two external places; qgio for a quantum channel and pgio for a public channel. Also, the gate controller quantum net has four external transitions (tg1, tg13, tg7 and tg14) and the remaining twenty are internal transitions. The runway controller quantum net has twenty-five internal places (pa1 to pa25) and two external places; qrio for a quantum channel and prio for a public channel. Also, the runway controller quantum net has four external transitions (tr1, tr13, tr7 and tr14) and the remaining twenty-one are internal transitions.
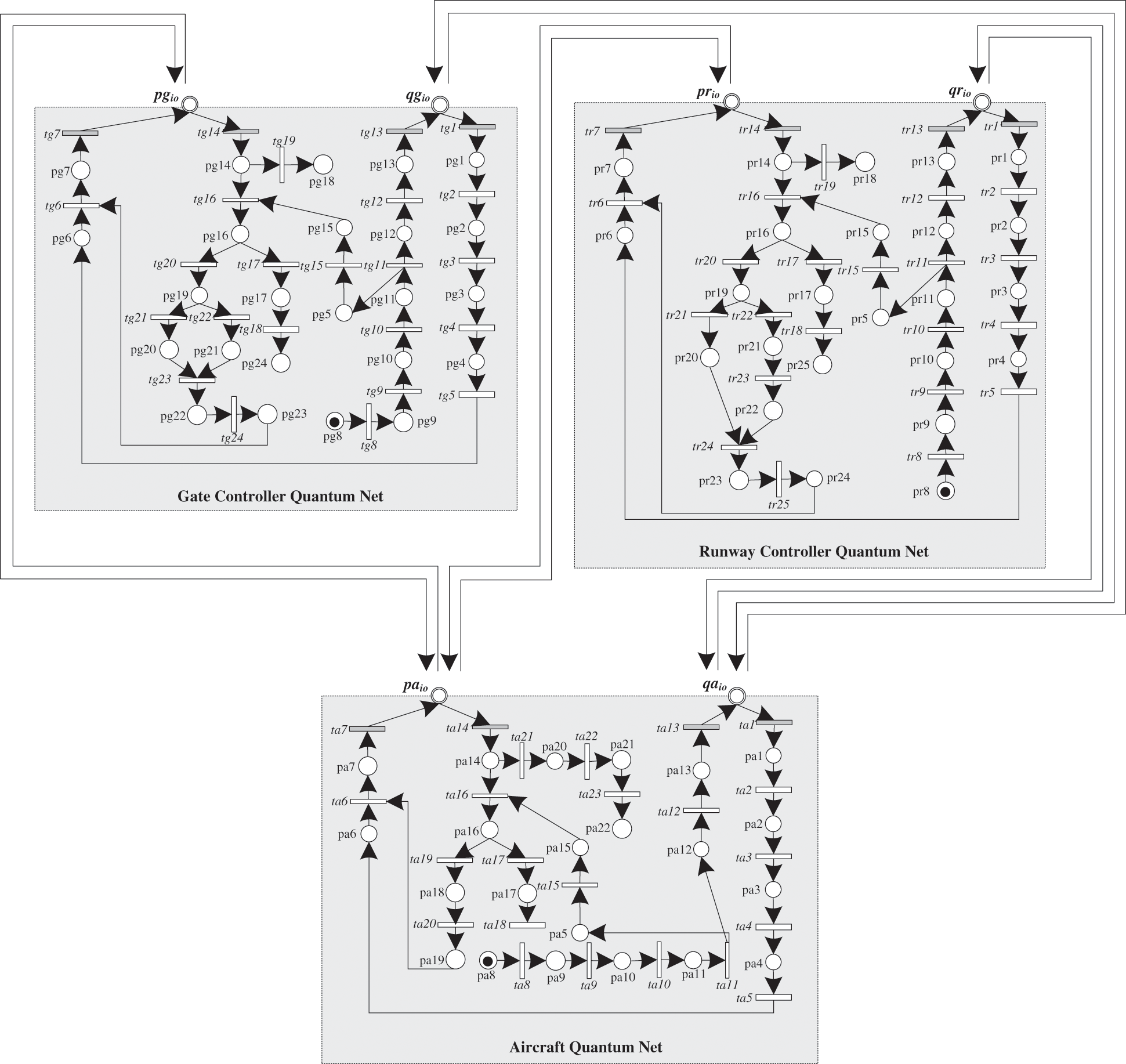
Figure 1: A quantum network for an aircraft takeoff
When an aircraft quantum net is ready for takeoff, it contacts the gate controller quantum net. The controller net verifies identity of an aircraft net by encrypting a stream of qubit (tg8 to tg10) and sends them (tr12 to tr13) via its quantum channel qgio. The controller net also stores the basis values of sent qubits in pg5, for later matching. The aircraft net receives the qubits (ta1) via its quantum channel qaio and decrypts them (ta3 to ta4) on random basis. It then sends the decrypted values of qubits (ta6 to ta7) back to the controller net through its public channel paio. After receiving decrypted values (tg14) through its public channel pgio, the controller net matches the decrypted values with the sent qubit values. If the matching entries are less than or equal to a pre-decided threshold (tg15) then the controller net authenticates the aircraft net, otherwise the communication is aborted (tg18). Once an aircraft is successfully authenticated, the controller net looks for favorable weather condition and a vacant ramp. If both conditions are met, then it prepares a ramp route and grant permission to aircraft net (tg21 to tg24) through its public channel pgio. After receiving permission (ta14) via its public channel paio, the aircraft transits the defined area according to the route specified by the controller net (ta22 to ta23).
When an aircraft quantum net enters the ramp, it ends its communication with the gate controller and then it contacts the runway controller quantum net. The controller net verifies identity of an aircraft net by encrypting a stream of qubits (tr8 to tr10) and sends them (tr12 to tr13) via its quantum channel qrio. The controller net also stores the basis values of sent qubits in pr5, for later matching. The aircraft net receives the qubits (ta1) via its quantum channel qaio and decrypts them (ta3 to ta4) on random basis. It then sends the decrypted values of the qubits (ta6 to ta7) back to the controller net through its public channel paio. After receiving decrypted values (tr14) through its public channel prio, the controller net matches the decrypted values with the sent qubit values. If the matching entries are less than or equal to a pre-decided threshold (tr15) then the controller net authenticates the aircraft net, otherwise the communication is aborted (tr18). Once an aircraft is successfully authenticated, the controller net looks for favorable weather condition, a vacant taxiway, and a vacant runway. If all three conditions are met, then it prepares a runway route and grant permission to aircraft net (tr21 to tr25) through its public channel prio. After receiving permission (ta14) via its public channel paio, the aircraft transits through the defined area according to the route specified by the controller net (ta22 to ta23). Therefore, the visual representation of three communicating quantum nets namely aircraft, runway controller and gate controller are successfully shown in this section. The interaction between the three quantum nets for a successful takeoff is demonstrated through proposed BB84 quantum nets and results are demonstrated in Tab. 3.
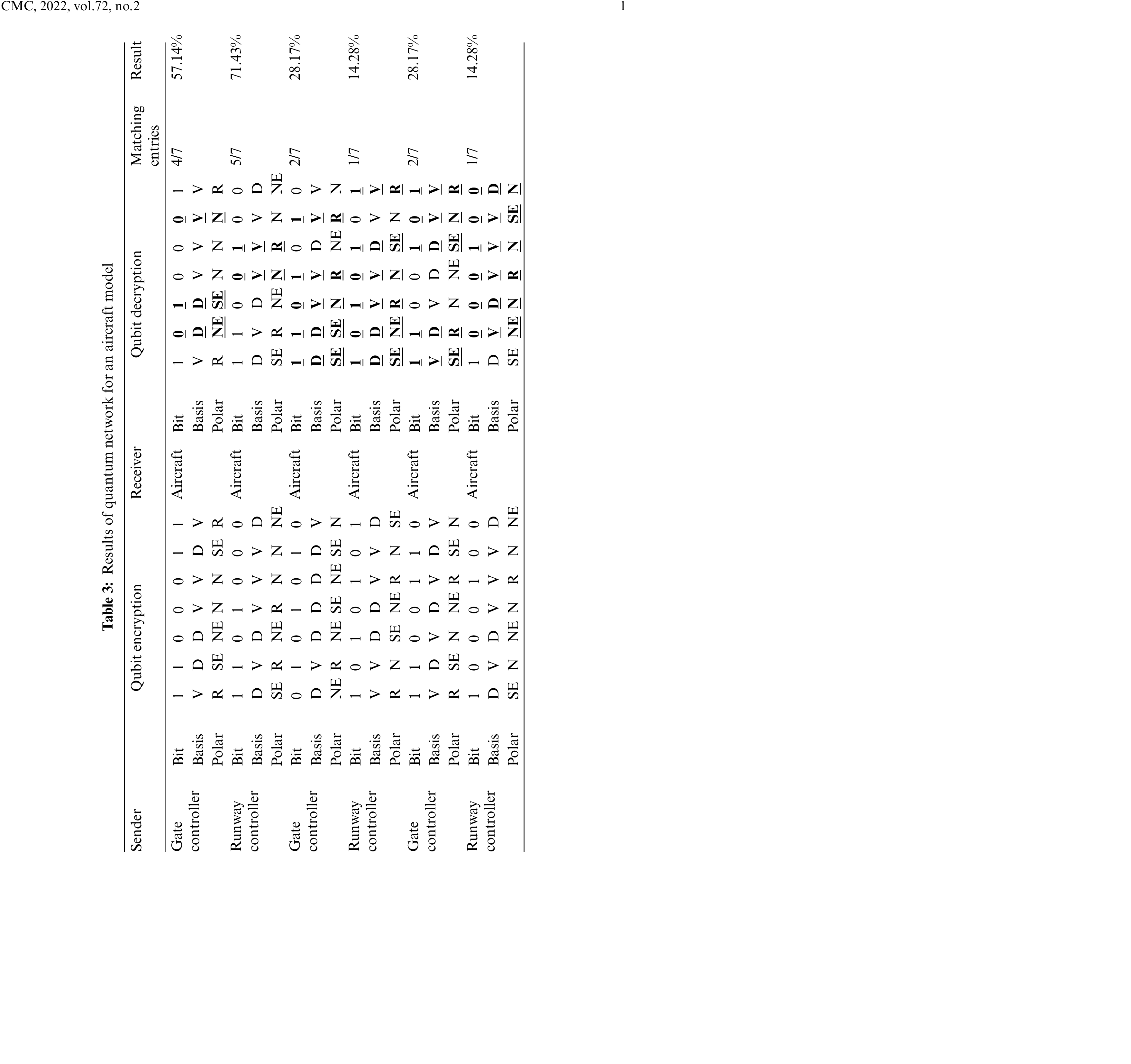
First row of Tab. 3 shows the interaction between gate controller quantum net and an aircraft quantum net. The controller net being the sender sends an encrypted stream of seven qubits. The aircraft net being the receiver decodes the qubit on random basis and it successfully decrypts four qubit values yielding a result within threshold value. Therefore, the aircraft net is authenticated successfully by the gate controller net. In row two, the sender is a runway controller net, and the receiver is the aircraft net. Out of seven encrypted qubits, the aircraft net successfully decodes five qubits’ values, yielding a result within threshold value. Therefore, the aircraft net is authenticated successfully by the runway controller net. In row third, the sender is a gate controller net, and the receiver is the aircraft net. Out of seven encrypted qubits, the aircraft net successfully decodes just two qubits’ values, yielding a result out of the threshold value. Therefore, the aircraft net is not authenticated by the gate controller net and their communication is aborted. In row fourth, the sender is a runway controller net, and thereceiver is the aircraft net. Out of seven encrypted qubits, the aircraft net successfully decodes just one qubit value, yielding a result out of the threshold value. Therefore, the aircraft net is not authenticated by the runway controller net and their communication is aborted. The last two rows of Tab. 3 show the intrusion detection scenarios. In row fifth, the sender is a gate controller net, and the receiver is the aircraft net. Out of seven encrypted qubits, the aircraft net wrongly decodes the pre-decided polarization values. For instance, the polarization decided for basis V and bit 1 was R which was wrongly decrypted in first qubit of fifth row as NE which shows the presence of an intruder who does not know the pre-set values. Therefore, the last two rows of Tab. 3 are unsuccessful authentications, and their respective interactions are aborted.
In this section, the verification results of aircraft takeoff quantum network have been discussed. In the quantum network of an aircraft takeoff the encrypted qubit and decrypted values are matched for authentication purposes, the results are shown in Tab. 3. In the takeoff quantum network, two types of communication are involved: firstly, between an aircraft and gate controller and then between an aircraft and runway controller. Let us assume that for both interactions the pre-decided threshold is 50%. The bit values are 0 and 1; the basis values are D for diagonal and V for vertical; and Polarization represents a photon polarization which is generated from bit and basis value. For instance, basis V with bit 0 is represented as North, N, and basis V with a bit 1 is shown as Right, R. A basis D with bit 0 is marked as North East, NE and basis D with a bit 1 is represented as South East, SE.
5.3 Reachability Tree (RT) Analysis
The reachability analysis for quantum network of an aircraft takeoff is presented in this sub-section. It helps to find that the system under study is free from any unexpected behavior. The external transitions are also used to represent communication between nets labeled as T1, T2, and so on. First, a RT is constructed in Fig. 2 to represent the successful authentication between a gate controller and an aircraft net. The nodes of the tree are based on places and transitions of either an aircraft net or a gate controller net. The external transitions defined are T1 to T3. The marking and labels are also narrated in Fig. 2.

Figure 2: RT of successful authentication between aircraft and gate controller nets
An RT is constructed in Fig. 3 to represent the unsuccessful authentication between a gate controller and an aircraft net. The nodes of the tree are based on places and transitions of either an aircraft net or a gate controller net. The external transitions defined are T1 and T3.

Figure 3: RT of unsuccessful authentication between aircraft and gate controller nets
The defined marking of the tree and their labels are also narrated in this Fig. 4. An RT is constructed in Figs. 4 and 5 to represent the successful and unsuccessful authentication between a runway controller and an aircraft net, respectively. The nodes of the trees are based on places and transitions of either an aircraft net or a gate controller net. The external transitions defined in Fig. 4 are T1 to T3 and T1 and T2 in Fig. 5, respectively. The defined marking of each tree and their labels are also narrated in their respective figures. Each RT shows that the system exhibits no unexpected error and there are no unreachable markings in the quantum network of an aircraft takeoff.

Figure 4: RT of successful authentication between aircraft and runway controller nets

Figure 5: RT of unsuccessful authentication between aircraft and runway controller nets
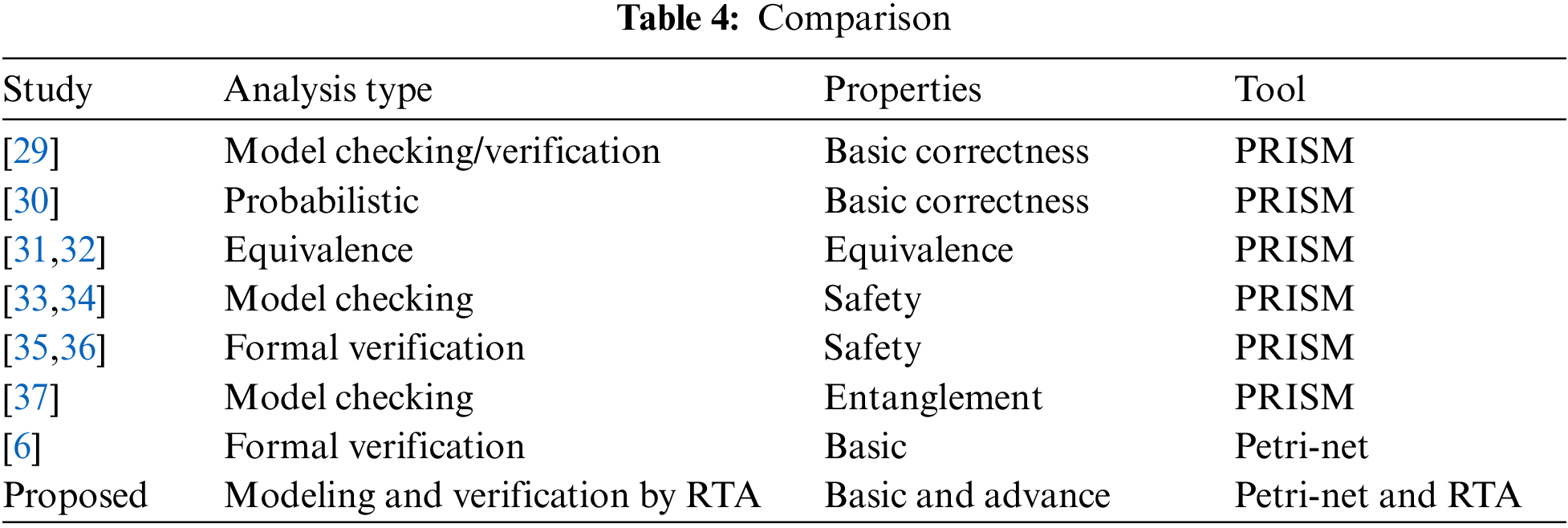
Tab. 4 shows a qualitative comparison of the proposed approach with the scheme given in [6] and [29–37] in terms of analysis type, protocol properties and tool used for analysis. Mainly it is observed that the types of analysis are performed by means of model checking and model verification.
This research provides an integration of BB84 with petri-nets for formal modeling and verification of aircraft takeoff procedure. A new variant of traditional petri-nets, coined as the “Quantum Nets” are developed to integrate quantum characteristics of BB84. The strong static foundations of quantum nets are developed whereas the dynamic properties such as tokenization, external transitions, transition, enabling, and system dynamics are also formalized. Furthermore, the properties like reachability, boundedness, liveness, safety, and concurrency have been abstractly defined. By using the defined Quantum Nets formal model of aircraft takeoff is developed which constitute of three quantum nets namely aircraft, runway controller, ground controller and secure communication between them is described by using BB84 protocol. The model is checked through simulator of CPN Tools, and it is also verified through proof technique of RT analysis. This research reveals some fruitful outcomes and opens the horizons for future research of quantum cryptography. The expressivity of traditional petri-nets has been enhanced by developing its new variant, coined as a Quantum net, which can be used in future for modeling similar systems. The modeling and verification of a quantum system helps to identify errors and abnormal system behavior from a system to be built long before the system is physically implemented. Identification of errors and bugs spotted during modeling are easier and cheaper to be fixed. In this research only some properties of a quantum system are stated at an abstract level. Many more properties can be defined for further analysis and all the defined properties can also be extended for an intense and comprehensive verification. In this research we have only demonstrated the use of RT for verifying a quantum cryptographic system. Also, some more proof techniques like liveness, deadlock, simulations etc., can be exploited to analyze various other dimensions of the cryptographic system such as an earlier work demonstrated the strength of agent-based mobile petri-nets in modeling security policy [50]. The quantum nets proposed in this research also has some limitations. As the public channel is not secure, it is vulnerable to some kinds of security threats like eavesdrop, integrity etc., any intruder can access the secure data. So, security of this channel needs to be focused for overall privacy of the system. Other limitation of quantum net is inherent in physical characteristics of a quantum channel. BB84 works on a photon polarization state and a quantum channel is designed to carry photons. Other than an intrusion attack, the state of a photon may change based on the environmental factors such as intense light and noise. It inhibits the receiver to correctly decode the qubits and authentication becomes unsuccessful, and communication is aborted since it takes time when exposed to the factors. More studies can be conducted to overcome these limitations by means of using quantum nets in contrast to CPN tool and RT analysis.
Acknowledgement: Acknowledged to our families whose unconditional support enabled us to work.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. N. A. Zafar, “Safety control management at airport taxiing to take-off procedure,” Arabian Journal for Science and Engineering, vol. 39, no. 8, pp. 6137–6148, 2014. [Google Scholar]
2. C. H. Bennett and G. Brassard, “Quantum cryptography: Public key distribution and coin tossing,” arXiv preprint arXiv:2003.06557, 2020. [Google Scholar]
3. N. Papanikolaou, “An introduction to quantum cryptography,” Crossroads, vol. 11, no. 3, pp. 3, 2005. [Google Scholar]
4. H. W. Li, Q. Z. Yin, S. Wang, Y. J. Qian, W. Chen et al., “Randomness determines practical security of BB84 quantum key distribution,” Scientific Reports, vol. 5, no. 1, pp. 1–8, 2015. [Google Scholar]
5. F. Yang, G. Yang and Y. Hao, “The modeling library of eavesdropping methods in quantum cryptography protocols by model checking,” International Journal of Theoretical Physics, vol. 55, no. 7, pp. 3414–3427, 2016. [Google Scholar]
6. S. Zhang, Y. Ma, C. Meng and H. Wang, “Formal verification of quantum communication protocols using petri nets,” arXiv preprint, arXiv:1704.07031, 2017. [Google Scholar]
7. F. Yang and Y. J. Hao, “The formal study of quantum cryptography protocols,” in Proc. ICCWAMTIP, Chengdu, China, pp. 29–33, 2013. [Google Scholar]
8. M. Elboukhari, M. Azizi and A. Azizi, “Analysis of quantum cryptography protocols by model checking,” Journal of Universal Computer Science, vol. 1, no. 1, pp. 34–40, 2010. [Google Scholar]
9. E. D'hondt and M. Sadrzadeh, “Classical knowledge for quantum security,” Electronic Notes in Theoretical Computer Science, vol. 270, no. 1, pp. 155–163, 2011. [Google Scholar]
10. T. Davidson, S. J. Gay, H. Mlnařík, R. Nagarajan and N. K. Papanikolaou, “Model checking for communicating quantum processes,” International Journal of Unconventional Computing, vol. 8, no. 1, pp. 73–98, 2012. [Google Scholar]
11. T. Davidson, S. J. Gay, R. Nagarajan and I. V. Puthoor, “Analysis of a quantum error correcting code using quantum process calculus,” arXiv preprint, arXiv:1210.0614, 2012. [Google Scholar]
12. N. A. Saqib, A. A. Salam, A. Rahman and S. Dash, “Reviewing risks and vulnerabilities in web 2.0 for matching security considerations in web 3.0,” Journal of Discrete Mathematical Sciences and Cryptography, vol. 24, no. 3, pp. 1–17, 2021. [Google Scholar]
13. S. J. Gay and R. Nagarajan, “Communicating quantum processes,” ACM Sigplan Notices, vol. 40, no. 1, pp. 145–157, 2005. [Google Scholar]
14. Y. Kakutani, “A logic for formal verification of quantum programs,” in Proc. Annual Asian Computing Science Conf., Berlin, Heidelberg, Springer, pp. 79–93, 2009. [Google Scholar]
15. T. Kubota, Y. Kakutani, G. Kato, Y. Kawano and H. Sakurada, “Semi-automated verification of security proofs of quantum cryptographic protocols,” Journal of Symbolic Computation, vol. 73, no. 1, pp. 192–220, 2016. [Google Scholar]
16. T. Kubota, Y. Kakutani, G. Kato, Y. Kawano and H. Sakurada, “Automated verification of equivalence on quantum cryptographic protocols,” in Proc. SCSS, Castle of Hagenberg, Austria, pp. 64–69, 2013. [Google Scholar]
17. J. Ribeiro and F. Grosshans, “A tight lower bound for the bb84-states quantum-position-verification protocol,” arXiv Preprint, arXiv:1504.07171, 2015. [Google Scholar]
18. T. Kubota, Y. Kakutani, G. Kato, Y. Kawano and H. Sakurada, “Application of a process calculus to security proofs of quantum protocols,” in Proc. FCS, Las Vegas, Nevada, USA, pp. 1–7, 2012. [Google Scholar]
19. Y. Feng and M. Yin, “Toward automatic verification of quantum cryptographic protocols,” arXiv Preprint, arXiv:1507.05278, 2015. [Google Scholar]
20. T. Kubota, Y. Kakutani, G. Kato and Y. Kawano, “A formal approach to unconditional security proofs for quantum key distribution,” in Proc. UCNC, Berlin, Heidelberg, pp. 125–137, 2011. [Google Scholar]
21. M. Elboukhari, A. Azizi and M. Azizi, “Security oriented analysis of B92 by model checking,” in Proc. IEEE 2008 New Technologies, Mobility and Security, Tangier, Morocco, pp. 1–6, 2008. [Google Scholar]
22. B. Huang, Y. Huang, J. Kong and X. Huang, “Model checking quantum key distribution protocols,” in Proc. ITME, Fuzhou, China, pp. 611–615, 2016. [Google Scholar]
23. S. Kuppam, “Modelling and analysis of quantum key distribution protocols, BB84 and B92, in communicating quantum processes (CQP) language and analysing in PRISM,” arXiv preprint, arXiv:1612.03706, 2016. [Google Scholar]
24. A. Ghilen, M. Azizi and R. Bouallegue, “Integration of a quantum protocol for mutual authentication and secret key distribution within 802.11i standard,” in Proc. IEEE/ACS 12th Int. Conf. of Computer Systems and Applications, Marrakech, Morocco, pp. 1–7, 2015. [Google Scholar]
25. D. A. Almubayedh, G. Alazman, M. Alkhalis, M. Alabdali, N. Nagy et al., “Quantum bit commitment on IBM QX,” Quantum Information Processing, vol. 19, no. 55, pp. 1–27, 2020. https://doi.org/10.1007/s11128-019-2543-8. [Google Scholar]
26. M. Nagy and N. Nagy, “Coding in the entanglement domain,” Quantum Inf Process, vol. 19, no. 4, pp. 1–20, 2020. https://doi.org/10.1007/s11128-020-02632-6. [Google Scholar]
27. N. U. Ain and A. Rahman, “Quantum cryptography: A comprehensive survey,” Journal of Information Assurance and Security, vol. 11, no. 1, pp. 31–38, 2016. [Google Scholar]
28. N. Ain, A. Rahman, M. Nadeem and A. G. Abbasi, “Quantum cryptography trends: a milestone in information security,” in in Proc. HIS’15, Seoul, Korea, pp. 25–39, 2015. [Google Scholar]
29. M. Elboukhari, M. Azizi and A. Azizi, “Verification of quantum cryptography protocols by model checking,” Int. J. Network Security & Appl, vol. 2, no. 4, pp. 43–53, 2010. [Google Scholar]
30. S. Gay, R. Nagarajan and N. Papanikolaou, “Probabilistic model-checking of quantum protocols,” arXiv preprint, quant-ph/0504007, 2005. [Google Scholar]
31. E. Ardeshir-Larijani, S. J. Gay and R. Nagarajan, “Equivalence checking of quantum protocols,” in Proc. TACAS, Rome, Italy, pp. 478–492, 2013. [Google Scholar]
32. E. Ardeshir-Larijani, S. J. Gay and R. Nagarajan, “Verification of concurrent quantum protocols by equivalence checking,” in Proc. TACAS, Grenoble, France, pp. 500–514, 2014. [Google Scholar]
33. M. Elboukhari, M. Azizi and A. Azizi, “Analysis of the security of BB84 by model checking,” arXiv preprint, arXiv:1005.4504, 2010. [Google Scholar]
34. J. R. Sahoo and S. Satapathy, “Simulation and analysis of BB84 protocol by model checking,” International Journal of Engineering Science and Technology, vol. 3, no. 7, pp.5695, 2011. [Google Scholar]
35. R. Nagarajan, N. Papanikolaou, G. Bowen and S. J. Gay, “An automated analysis of the security of quantum key distribution,” arXiv preprint, cs/0502048, 2005. [Google Scholar]
36. V. Fernández, M. J. García-Martínez, L. Hernández-Encinas and A. Martín, “Formal verification of the security of a free-space quantum key distribution system,” in Proc. the Int. Conf. on Security and Management (SAM), Las Vegas, Nevada, USA, pp. 1–7, 2011. [Google Scholar]
37. S. Rochanapratishtha and W. Pijitrojana, “Analysis of security of quantum key distribution based on entangled photon pairs by model checking,” Journal of Quantum Information Science, vol. 5, no. 3, pp. 103–108, 2015. [Google Scholar]
38. S. U. Rehman, M. Mahmud, A. Rahman, I. U. Haq and M. Safdar, “Information security in business: A bibliometric analysis of the 100 top cited articles,” Library Philosophy and Practice (e-Journal), vol. 5354, no. 1, pp. 1–49, 2021. [Google Scholar]
39. M. Mahmud, A. Rahman, M. Lee and J. Choi, “Evolutionary-based image encryption using RNA codons truth table,” Optics & Laser Technology, vol. 121, no. 1, pp. 1–8, 2020. [Google Scholar]
40. M. T. Naseem, I. M. Qureshi, A. Rahman and M. Z. Muzaffar, “Robust and fragile watermarking for medical images using redundant residue number system and chaos,” Neural Network World, vol. 30, no. 3, pp. 177–192, 2020. [Google Scholar]
41. A. Rahman, “Optimum information embedding in digital watermarking,” Journal of Intelligent and Fuzzy Systems, vol. 37, no. 1, pp. 553–564, 2019. [Google Scholar]
42. A. Rahman, K. Sultan, N. Aldhafferi, A. Alqahtani and M. Mahmud, “Reversible and fragile watermarking for medical images,” Computational and Mathematical Methods in Medicine, vol. 2018, no. 1, pp. 1–8, 2018. https://doi.org/10.1155/2018/3461382. [Google Scholar]
43. A. Rahman, K. Sultan, D. Musleh, N. Aldhafferi, A. Alqahtani et al., “Robust and fragile watermarking for medical images: A joint venture of coding and chaos theories,” Journal of Healthcare Engineering, vol. 2018, no. 1, pp. 1–12, 2018. https://doi.org/10.1155/2018/8137436. [Google Scholar]
44. A. Rahman, M. Mahmud, K. Sultan, N. Aldhafferi, A. Alqahtani et al., “Medical image watermarking for fragility and robustness: A chaos, ECC and RRNS based approach,” Journal of Medical Imaging and Health Informatics, vol. 8, no. 6, pp. 1192–1200, 2018. [Google Scholar]
45. A. Rahman, M. Azam, G. Zaman, “Performance comparison of product codes and cubic product codes using FRBS for robust watermarking,” International Journal of Computer Information Systems and Industrial Management Applications, vol. 8, no. 1, pp. 57–66, 2016. [Google Scholar]
46. M. Z. Muzaffar, I. M. Qureshi, A. Rahman, F. A. Alhaidari and M. A. A. Khan, “Compressed sensing for security and payload enhancement in digital audio steganography,” Journal of Information Hiding and Multimedia Signal Processing, vol. 15, no. 6, pp. 1506–1517, 2018. [Google Scholar]
47. M. Zaheer, I. M. Qureshi, K. Sultan, A. Rahman, M. Z. Muzaffar et al., “High-capacity image steganography based on prime series representation and payload redundancy removal,” Journal of Information Assurance and Security, vol. 14, no. 3, pp. 40–47, 2019. [Google Scholar]
48. M. Zaheer, I. M. Qureshi, A. Rahman, J. Alhiyafi and M. Z. Muzaffar, “Improved and secure differential LSB embedding steganography,” Journal of Information Assurance and Security, vol. 11, no. 1, pp. 170–178, 2018. [Google Scholar]
49. N. A. Zafar, “Formal specification and analysis of take-off procedure using VDM-SL,” Complex Adaptive Systems Modeling, vol. 4, no. 4, pp. 1–26, 2016. https://doi.org/10.1186/s40294-016-0014-y. [Google Scholar]
50. M. Jamal and N. A. Zafar, “Formalizing the resurrecting duckling into hierarchical coloured petri nets,” in Proc. ICET, Islamabad, Pakistan, pp. 1–6, 2016. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |