Computers, Materials & Continua DOI:10.32604/cmc.2022.021519
Article

Image Encryption Using Multi-Scroll Attractor and Chaotic Logistic Map

R. Anitha* and B. Vijayalakshmi

Department of Electronics & Communication Engineering, B. S. Abdur Rahman Crescent Institute of Science & Technology, Chennai, 600045, Tamilnadu, India
*Corresponding Author: R. Anitha. Email: anitharajesh29@gmail.com
Received: 05 July 2021; Accepted: 24 December 2021

Abstract: In the current scenario, data transmission over the network is a challenging task as there is a need for protecting sensitive data. Traditional encryption schemes are less sensitive and less complex thus prone to attacks during transmission. It has been observed that an encryption scheme using chaotic theory is more promising due to its non-linear and unpredictable behavior. Hence, proposed a novel hybrid image encryption scheme with multi-scroll attractors and quantum chaos logistic maps (MSA-QCLM). The image data is classified as inter-bits and intra-bits which are permutated separately using multi scroll attractor & quantum logistic maps to generate random keys. To increase the encryption efficiency, a hybrid chaotic technique was performed. Experimentation is performed in a Qiskit simulation tool for various image sets. The simulation results and theoretical analysis show that the proposed method is more efficient than its classical counterpart, and its security is verified by the statistical analysis, keys sensitivity, and keyspace analysis. The Number of changing pixel rate (NPCR) & the Unified averaged changed intensity (UACI) values were observed to be 99.6% & 33.4% respectively. Also, entropy oscillates from 7.9 to 7.901 for the different tested encrypted images. The proposed algorithm can resist brute force attacks well, owing to the values of information entropy near the theoretical value of 8. The proposed algorithm has also passed the NIST test (Frequency Monobit test, Run test and DFT test).

Keywords: Chiper key; image encryption; logistic map; quantum chaos; qiskit

1  Introduction

The growth in digital communication and information technology fields creates a high requirement for data generation, transmission and storage. Medical images are highly sensitive data and need to be protected while transmitting [1–3]. Digital images exhibit more detailed information as a shared correlation among nearby pixels. Encryption of digital images is highly challenging and it does not suit the traditional Advanced Encryption Standard (AES) and Data Encryption Standard (DES) encryption algorithm. Chaotic encryption schemes are preferable because of their randomness property in a key generation [4–7].

The existing chaos-based encryption model needs more improvisation to withstand vulnerable cyber-attacks including botnet, Denial of Service (DoS) and Man in the Middle (MITM) attacks [7]. The requirement of an efficient chaos scheme must expel high randomness and complex key generation. The dynamic complex nature of the data introduces more possibilities for introducing chaotic models. Though the data are non-dynamic, complex encryption is required to withstand the security requirements [8,9]. The encryption algorithm thus needs a complex chaotic key generation system to withstand malicious encoding of protected data [10].

Quantum-based chaos encryption models are preferred for their complexity behavior. Quantum computing in image processing applications is introduced to perform classical image processing problems with quantum mechanics techniques. This invasion enhances the efficiency in the field of imaging and excels with its parallel processing skills. The images are represented as quantum bits say qubits are encoded to perform a specific task. The quantum encoding process requires [(2*n) + 1] qubits to encode a raw image. The main goal of the quantum image encryption scheme is to preserve the original content of the input image bits that are encoded. The permutation of bits in the image by changing their coordinates can result in image encryption. Quantum encryption exhibits classical state behavior and they are highly sensible for dynamic behaviors in any system. Many types of research propagate the advantage of quantum-based chaotic encryption [11–14].

From the above observations, a novel encryption scheme with multi-scroll attractor and quantum chaotic logistic maps is proposed for data encryption. The various stages of novel MSA-QCLM include,

1)   Chaotic key generation using multi-scroll attractor model and quantum logistic Maps.

2)   The newly encrypted data is permutated with the initial condition of logistic maps.

3)   New encrypted data by diffusion process ready for transmission.

The paper discussion starts with a literature Survey followed by the proposed MSA-QCLM algorithm. Experimentation setup results with comparative analysis were discussed and concluded with the future scope.

2  Literature Review

Ranjeet et al. [15] developed a method of security system for the transmission of computerized imaging. They used a quantum confusion map to encrypt the staggered picture data. The image data is quad-tree divided and each part is encrypted separately to produce a non-shrinkable new structure for transmission. The encryption is based on the frequency of the corresponding blocks. The shuffling of pixels in each block constitutes to new measurement matrix which acts as the random key. The model is sensitive to edge-based pixel values of each block of the image.

Zakariya et al. [16] developed an image encryption model for computerized signature transmission using quantum cryptographic schemes. The input is divided into quantum gates for the encryption process. The quantum gates are used to solve both classical and quantum issues. The data is encrypted, decrypted, matched and transmitted to three output parties. Quantum entry-based keys are generated and checked for tampering in the pathways. In the receiving end, the unscrambled data is retrieved with the quantum key received at the end. The model is tested using MATLAB using the Quad Quantum library. The communication established is slower due to the complex process.

Guodong [17] developed an image encryption model that depends on confusing guideline entropy. This includes the various parameters for a confused guide such as change, regulation and dissemination. The keys are generated in regard concerning the pixel position. Thus, the change of position is communicated and resolved to upgrade the security. Even a slight change in plain data generates a significant difference in encryption. This shows highly excelled encryption in the majority of instances. The pixel distribution is limited beforehand of diffusion operation.

Xingbin et al. [18] proposed an encryption scheme that develops the encryption circuit based on bit logic. The inter-bit and intra-bit are arranged and disordered to calculate q-bit using XOR logic. These q-bit planes constitute the generation of chipper text. There will create a uniform change in pixel position. This encryption scheme withstands brute-force attacks. The key generated thus by pixel detangling shows more proficient security.

Jian et al. [19] developed an encryption scheme based on generating confused guide maps. It also uses the Lorenz tumultuous guide map for DNA coding. The image is recreated based on the generated maps. Histogram, correlation and entropy are evaluated. Though the input image has ups and downs, the encrypted image is relatively uniform thus withstanding statistical attacks. The encryption scheme is often unstable in highly dynamic environments.

Xing et al. [20] developed encryption based on the Region of Interest (ROI) principle. The image is partitioned into ROI and encrypted. This is introduced in real-time Internet of Things (IoT) gadgets and observed that the power consumption for establishing the disordered encryption is high. Lia et al. [21] made a detailed idea of chip-based cryptography. The features in the images constitute the structure and encryption key requirements for chip generation. They also summarized the attacks prone in communication at various levels. They highlighted the chosen plain text attack and its need for consideration to build strong encryption schemes.

Motivated from these papers and proposed the novel hybrid encryption algorithm to ensure the better security against the different statistical attacks.

3  Proposed MSA-QCLM Method

The proposed algorithm based on multi-scroll attractor and quantum logistic maps create a strong encryption scheme with multiple key generations at an intermediate level. The input image is divided into inter-bits and intra-bits & permuted based on the fractal scroll and logistic maps to generate a random encryption key. These keys are combined with the original image information to create a highly sensitive chiper key for efficient encryption.

3.1 Multi-Scroll Attractor Model

Dynamical systems with multi-scroll are more complex dynamics than chaotic systems with mono-scroll attractors. The state-space equation for automatic chaotic system is given by,

x˙1=−ax1+bx2x3(1)

x˙2=−cx23+dx1x3(2)

x˙3=ex3−fx1x2(3)

The above Eqs. (1)–(3) can be adapted using hyperbolic function and modified in Eq. (6).

Eqs. (4) and (5) are similar to Eqs. (1) and (2).

x˙1=−ax1+bx2x3(4)

x˙2=−cx23+dx1x3(5)

x˙3=ex3−fx1x2+p1tanh(x2+h)(6)

Chaotic attractor is obtained when a=2, b=6, c=6, d=3, e=3, f=1, p1=1, h=2 and the preferred initial conditions include (x1[0],x2([0],x3[0])=(0.1,0.1,0.6). Once the hyperbolic function is activated with the parameter, h=−3 and for the initial conditions generated, Fig. 1 illustrates various conditions of hyperbolic function. The second phase is initiated with the parameters p1=−1, h=3 with the newly defined initial conditions as [0.1,−0.1,−0.6]. Fig. 2 illustrates the function regarding the new initial condition values. In the third phase, the parameters p1=1, h=3 and initial conditions are similar to the initially chosen values [0.1,0.1,0.6]. This is demonstrated in Fig. 3 which shows a single scroll. From the models, it is evident that the scheme is multi-scroll property.

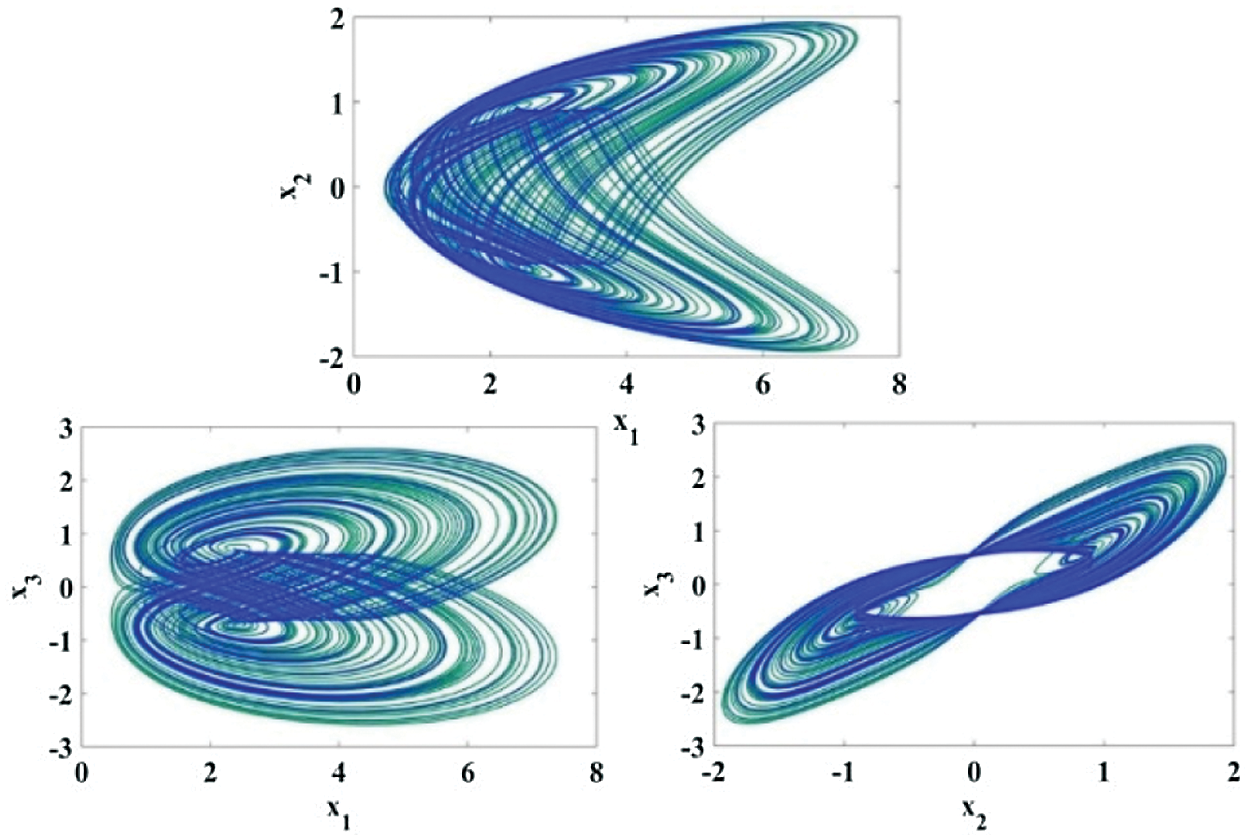
Figure 1: Portraits of phase for cubic nonlinear models of p1tanh⁡(x2+h) function in 1st phase

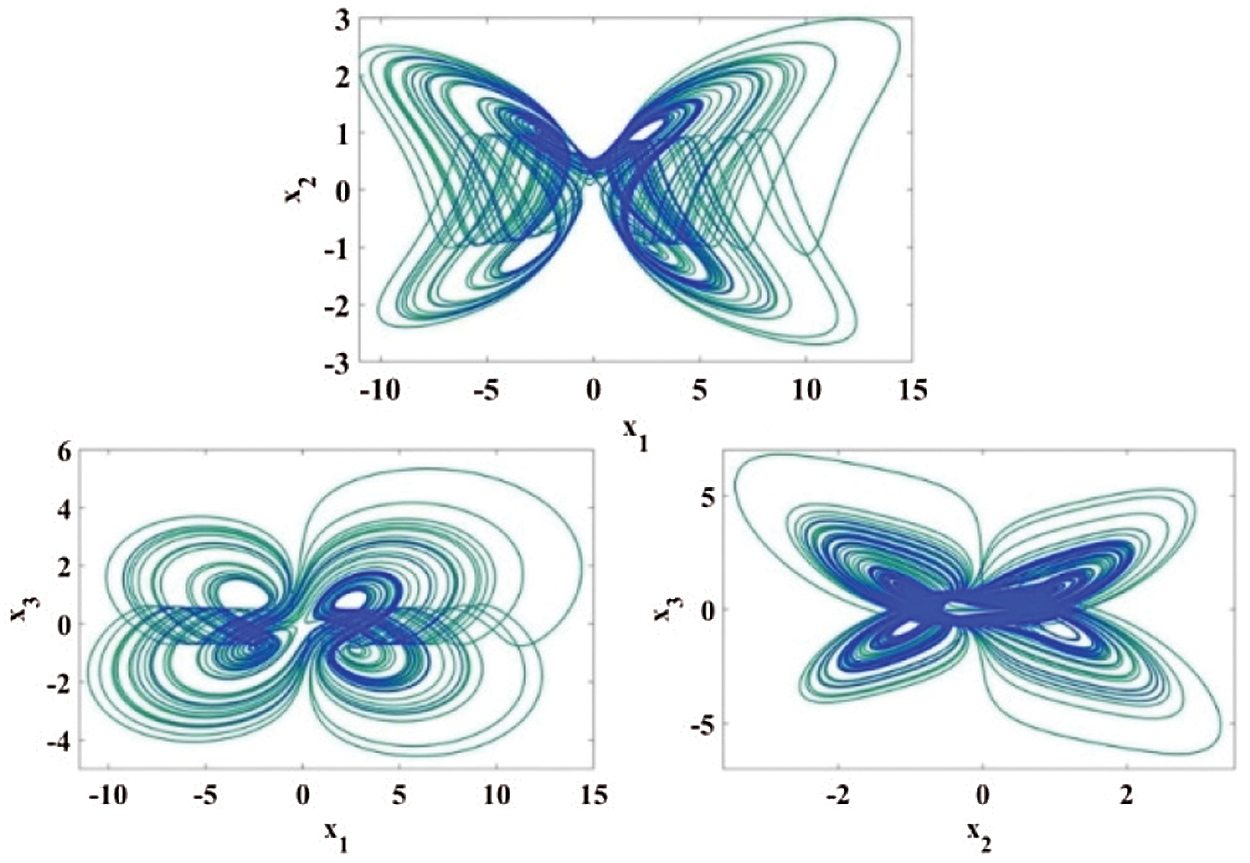
Figure 2: Portraits of phase for cubic nonlinear models of p1tanh⁡(x2+h) function in 2nd phase

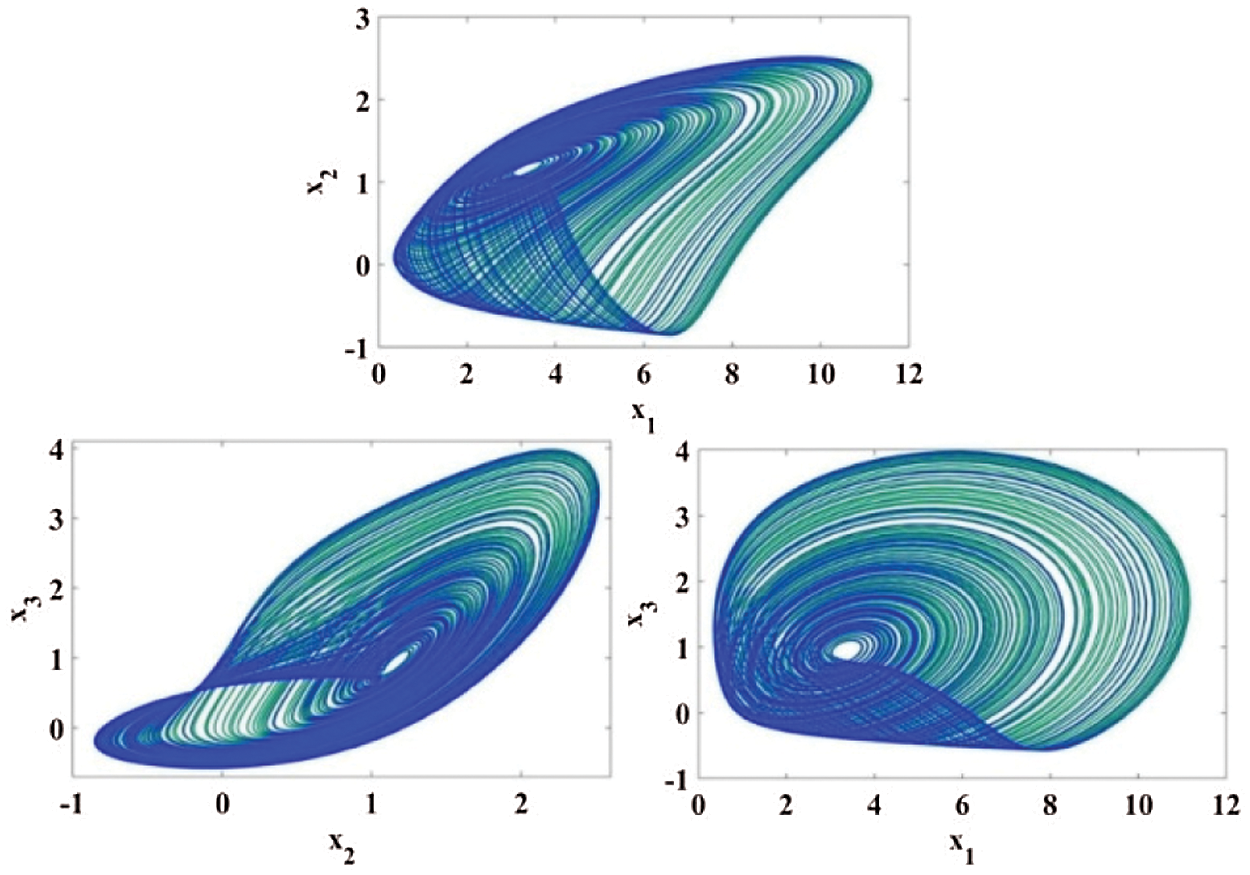
Figure 3: Portraits of phase for cubic nonlinear models of p1tanh⁡(x2+h) function in 3rd phase

To perform fractional estimates of chaotic systems, Eqs. (4) to (6) are adapted with the first, second and third-order derivative functions represented by Eqs. (7) to (9).

The newly derived models include,

dqx1dtq=−ax1+bx2x3(7)

dqx2dtq=−cx23+dx1x3(8)

dqx3dtq=ex3−fx1x2+p1tanh(x2+g)(9)

The bifurcation diagrams of the proposed multi-scroll system is shown in the following Fig. 4.

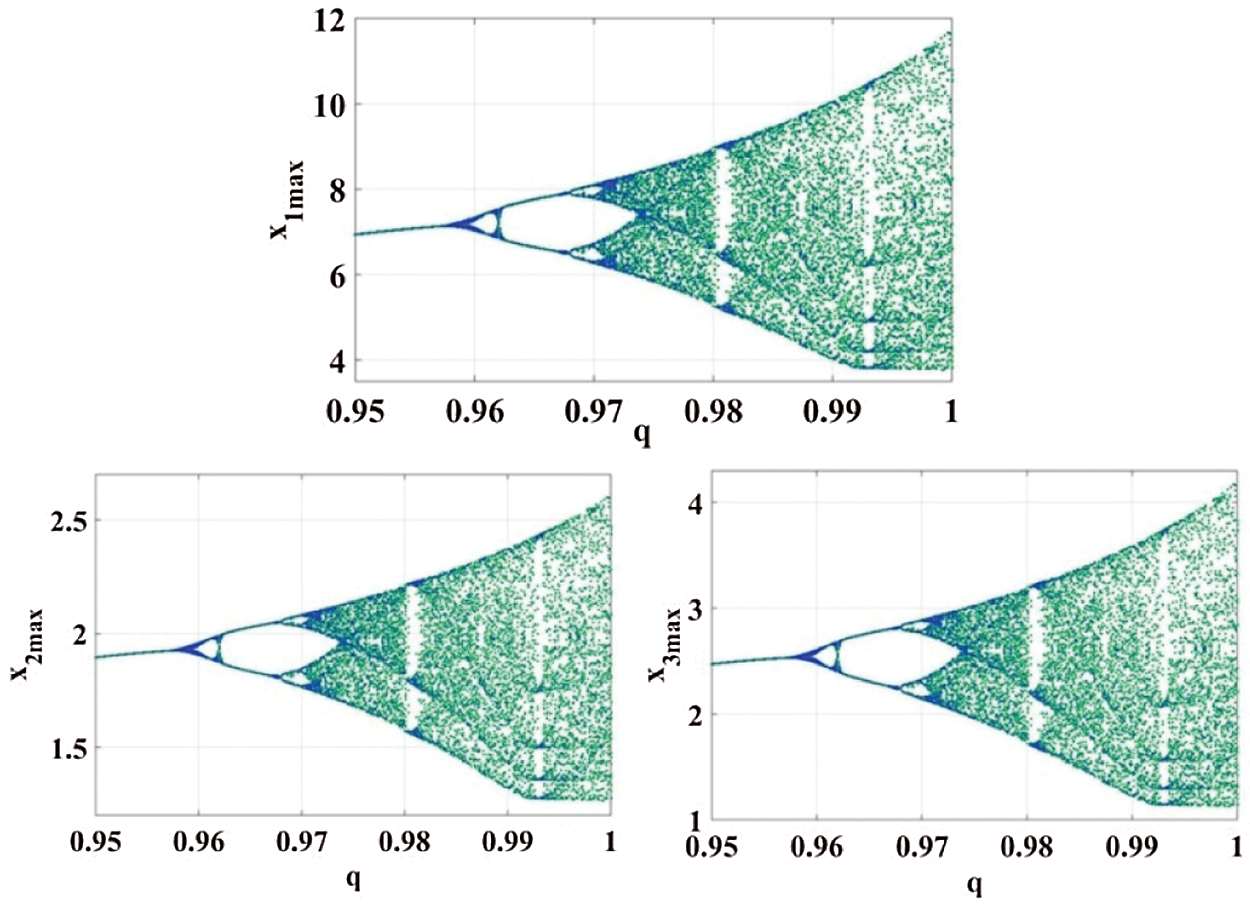
Figure 4: Bifurcation diagram of the proposed chaotic system

3.2 Logistic Maps

Chaotic systems are highly sensitive and are unpredictable in nature. The logistic maps are generated initially with basic permutation parameters. The bifurcation parameter varies from 0 to 4 when the iteration proceeds. The quantum logistic chaos maps are mainly generated with highly random outcomes.

The chaotic logistic maps are expressed as,

xm+1=μxm(1−xm)(10)

where, μ is the bifurcation parameter of logistic maps, with range 0 ≤ μ ≤ 4. The initial condition is chosen as x0∈(0,1) and as the iteration continues for ‘m’ numbers of sequences the threshold 3.5699456 ˂ μ ≤ 4 defines the chaotic nature of the system. As Kulsoom et al. [14] proposed the quantum logic maps is expressed as,

{am+1=C∗(am−|am|)−C∗fmbm+1=−fm∗h−2α+h−αC[(2−2am)fm−2amdm]em+1=−dm∗h−2α+h−2αC[2(1−am)dm−2amfm−am]}(11)

where, C denotes the control parameter, α is the dissipation constant, am & dm are complex conjugate coordinates. Thus, the model is highly sensible such that a small change in data generates different pseudo-random sequences. As the iteration proceeds, the model exhibits the non-linearity required for medical image encryption.

3.3 Proposed MSA-QCLM Encryption Process

The complete encryption scheme using the proposed hybrid algorithm is given as a model in Fig. 5.

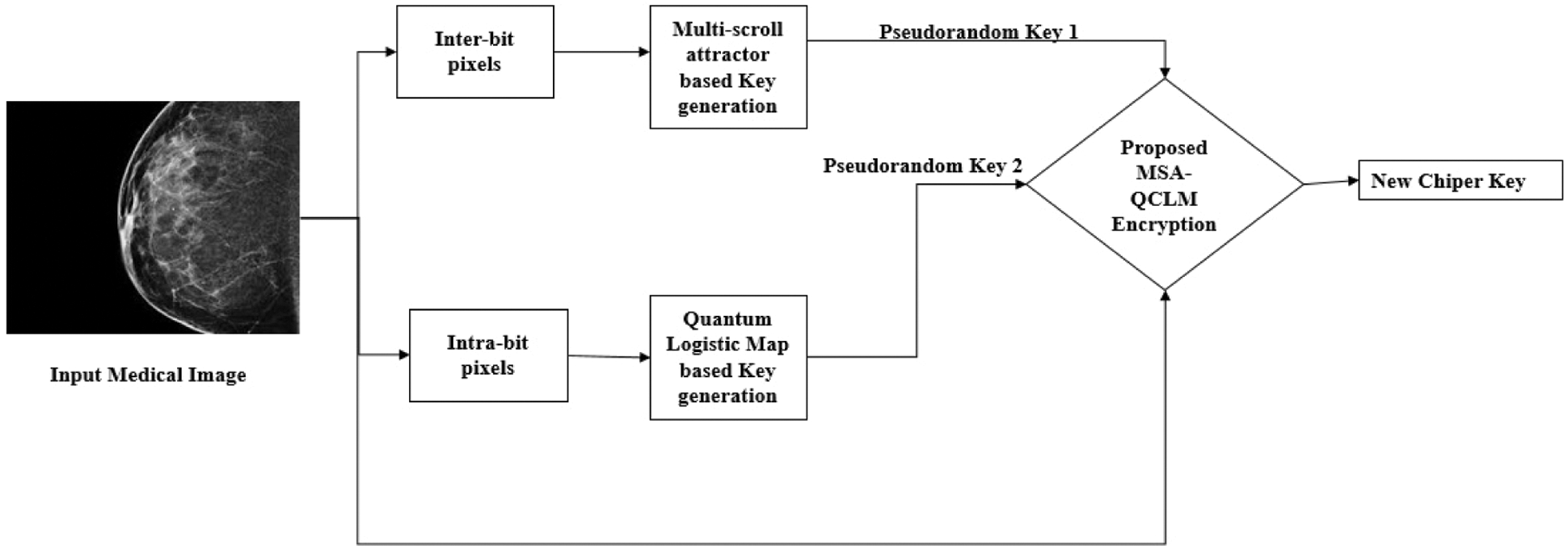
Figure 5: Proposed MSA-QCLM encryption process

The encryption process is described as follows,

1.   The Input Medical Images (grayscale images) are sub-divided into the inter-bit (pixels) I (m) and I(b) intra-bit (pixels) and rearranged into two M × N matrics

2.   The intermediate keys are generated using the multi-scroll attractors using the Eqs. (4)–(6) which are denoted by the matrix S(m).

3.   The matrix S(m) and I(m) are then diffused and permutated to form the new intermediate key K1 using the diffusion process given by,

β(1)=mod  256  {∑I(m)}(12)

μ(1)=Fi+β(1)+mod  256  {I(m)}(13)

Again,

β(2)=mod  256  {∑S(m)}(14)

μ(2)=Fi+β(2)+mod  256  {S(m)}(15)

Total First key=K1=β(1)permutatedβ(2)(16)

4.   The intermediate keys are generated using the 3D logistic maps using the Eqs. (7)–(9) which are denoted by the matrix Sl.

5.   The matrix S(l) and I(b) are then diffused and permutated to form the new intermediate key K2 using the diffusion process given by,

β(3)=mod  256  {∑I(b)}(17)

μ(1)=Fi+β(3)+mod  256  {I(b)}(18)

Again,

β(4)=mod  256  {∑S(l)}(19)

μ(4)=Fi+β(4)+mod  256  {S(l)}(20)

Total Second    key = K1 =β(3)permutatedβ(4)(21)

6.   The total random key is generated by adding the Eqs. (16) and (21) which is given as the K matrix.

7.   Again, the input image and newly formed key K is diffused to form the new encrypted images, the corresponding quantum circuit is given in Fig. 6

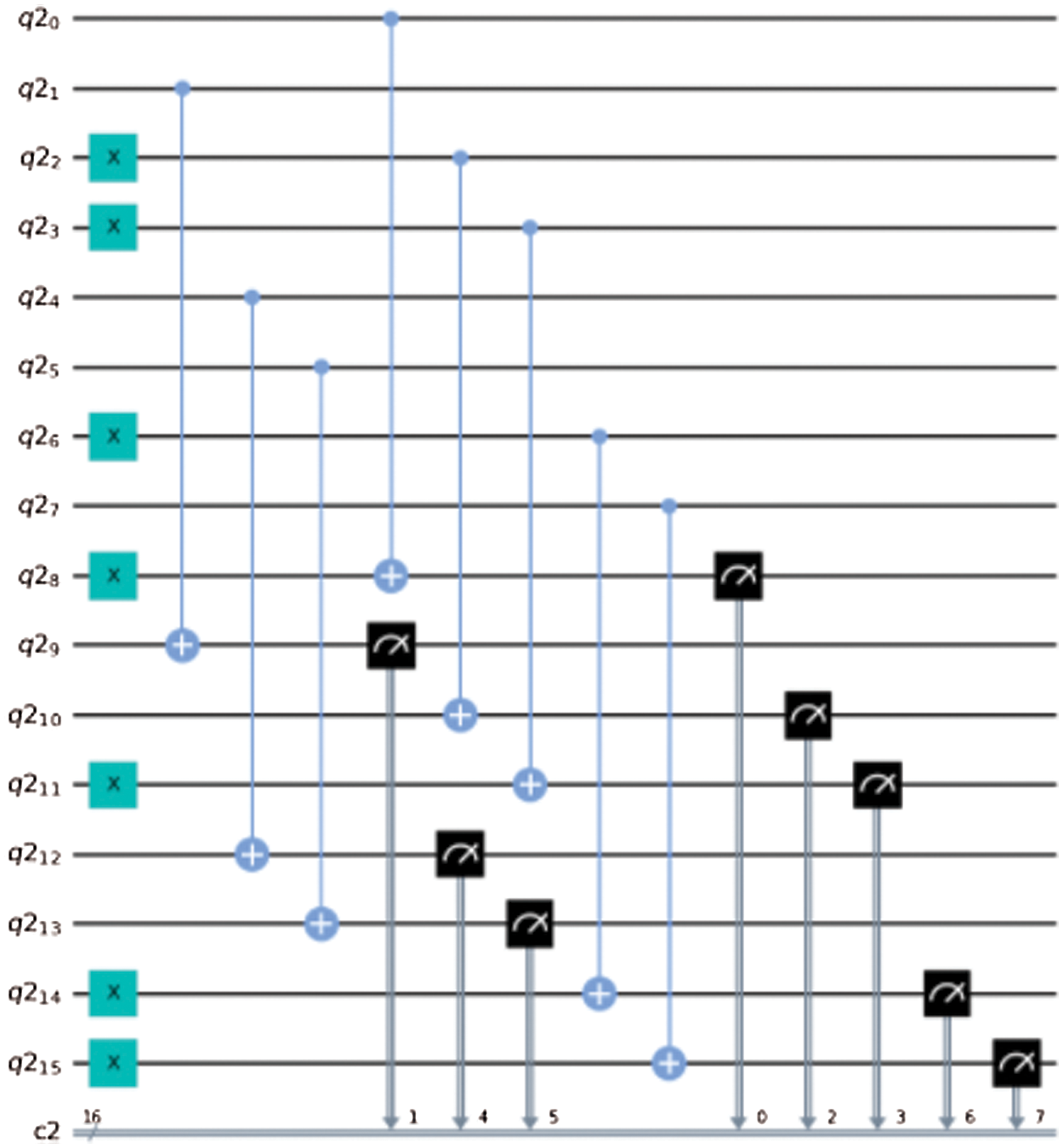
Figure 6: Quantum circuits for the implementation of proposed encryption

4  Results and Discussion

The performance of the proposed MSA-QCLM system is evaluated for the algorithm capability and the security ensured.

4.1 Performance of Security Analysis

The security assured by the proposed hybrid system is tested in distinct image sets. The general image set including Lena, Pepper, Baboon and medical data from the Mammogram Image Analysis Society (MIAS) model is utilized for experimentation. The image is chosen with a size of 256×256, shown in Fig. 7. The encrypted outputs of images are shown in Fig. 8 that has the better susceptible to different attacks. The whole experimentation has been implemented on i5 CPU with 4GB RAM, 1TBHDD, 3.2 GHZ frequency and Qiskit with necessary libraries were used for the complete development of the proposed algorithm.

Figure 7: Input images

Figure 8: Encrypted output images

4.2 Key Sensitivity Analysis

It is of utmost importance to validate the sensitivity of key generated for its resistance towards mild to strong attacks. The number of changing pixel rate (NPCR) and the unified averaged changed intensity (UACI) are the parameters used to test the performance of the encryption algorithm.

4.2.1 Randomness Test

NPCR focuses on the number of pixels that change due to attacks and UACI on the averaged difference between two paired ciphertext images. The NPCR & UACI metrics are calculated according to the Eqs. (22) and (23) to examine the proposed MSA-QCLM system. Tab. 1 shows the NPCR & UACI values for the input image set.

NPCR=∑i,j⁡E(i,j)L∗100(22)

UACI=1L∑i,j⁡|f(i,j)≠f(i,j)|256∗100(23)

where,

E(p,q)=[1,f(p,q)≠f(p,q)0,f(p,q)=f(p,q)(24)

The obtained results are compared with the other encryption algorithms and tabulated in Tab. 2. It gives the clear idea on strength of the proposed algorithm.

4.2.2 National Institute of Standards and Technology (NIST) Test

The strength of any encryption system will be highly related to the generated key. To ensure the key generated by the proposed algorithm is random, the paper employs the National Institute of Standards and Technology (NIST) procedural tests. The keys which are generated are converted into binary sequences and employed for the testing.

Frequency Monobit Test

The emphasis of the analysis is the ratio of one's and zero's throughout the whole series. The objective of this analysis is to decide whether the number of one's and zero's in a series is roughly the same as predicted. The measure evaluates the proximity of the percentage of one to 1/2, represents the number of one and zero in the series must be roughly the same. In this test, the zeros are assigned to −1 and the zeros are assigned to +1 and combined to generate the aggregate figures whose total mathematical formulation is presented as follows,

S=||S(n)||/n0.5(25)

where, ‘S(n)’ is the sum of the values attained and ‘n’ is the over-all sample count. Once the sum of values is calculated, the randomness is estimated by the ‘P’ value and is expressed as,

P=erfc(S2)0.5(26)

Run Test

The objective of this measure is to determine the cumulative number of cycles in a series even if the loop is a repeated series of the same pieces. The length ‘k’ run comprises precisely the same k bits and is connected pre and post with a bit of the contrary value. The objective of the training session is to decide if the number of tries of ones and zeroes of different lengths is as predicted in a random sequence. In specific, this measure decides if the oscillation among ones and zeros is too rapid or too sluggish.

This test uses a frequency test as a prerequisite. The key's continuity is examined for the randomness using the mathematical expression,

P=erfc(|V(n)(obs)−2nπ(1−π)|)/2.828nπ(1−π)(27)

where, V(n) (Obs) indicates the more rapid oscillations, when there is a lot of changes in the bitstreams.

DFT Test

The objective of this test seems to be the maximum height of the series in the Discrete Fourier Series. It identifies the recurrent characteristics (i.e., repeated structures that are close to one another) in the series which would imply a variation from the presumption of randomness. The complete test analysis of the key generated using the proposed hybrid chaotic applications are given in Tab. 3

Tab. 3 clearly shows the randomness of the keys is achieved by using the proposed hybrid algorithm and it has been proved that the generated key can defend any attacks in the networks for effective secured data transmission.

4.3 Adjacent Pixel Point Correlation Analysis

It is interesting to estimate the correlation factor of encrypted image and it has to be relatively low for an efficient encryption scheme. By comparing a set of 100 medical images, the correlation is estimated as follows,

Rxy=cov(a,b)E(x)E(y)(28)

cov(a,b)=D{[a−D(a)][b−D(b)]}(29)

e(a)=1n∑i=1n⁡ai(30)

L(x)=1n∑i=1n⁡[ai−a(x)]2(31)

where e(a) and L(x) indicates the expectations and variance of the normal image and encrypted images. Tab. 4 shows the correlation coefficient of the input and encrypted images. From the results, it is clear that the adjacent pixels are highly correlated in input but less correlation between the pixels in encrypted images.

4.4 Information Entropy Analysis

Entropy analyzes the randomness of information distribution in encrypted images. The higher entropy value relates to better irregularity in the encrypted images. Mathematically it is represented as,

g(m)=∑ll−1⁡q(m)log21q(mi)(32)

The values of entropy vary from 1 to 8. The different entropy values observed for various data sets are shown in Tab. 5.

Tab. 5 shows the various entropies of the various image sets that were observed to be nearly equal to 8.

4.5 Computational Time Complexity Analysis

A faster response rate is another requirement for any system to encrypt data. By injecting few attacks, the algorithm was tested for its response time. The input images with dimensions 256 × 256 are considered and assessed the time frame which is shown in Tab. 6

4.6 Diehard Randomness Test

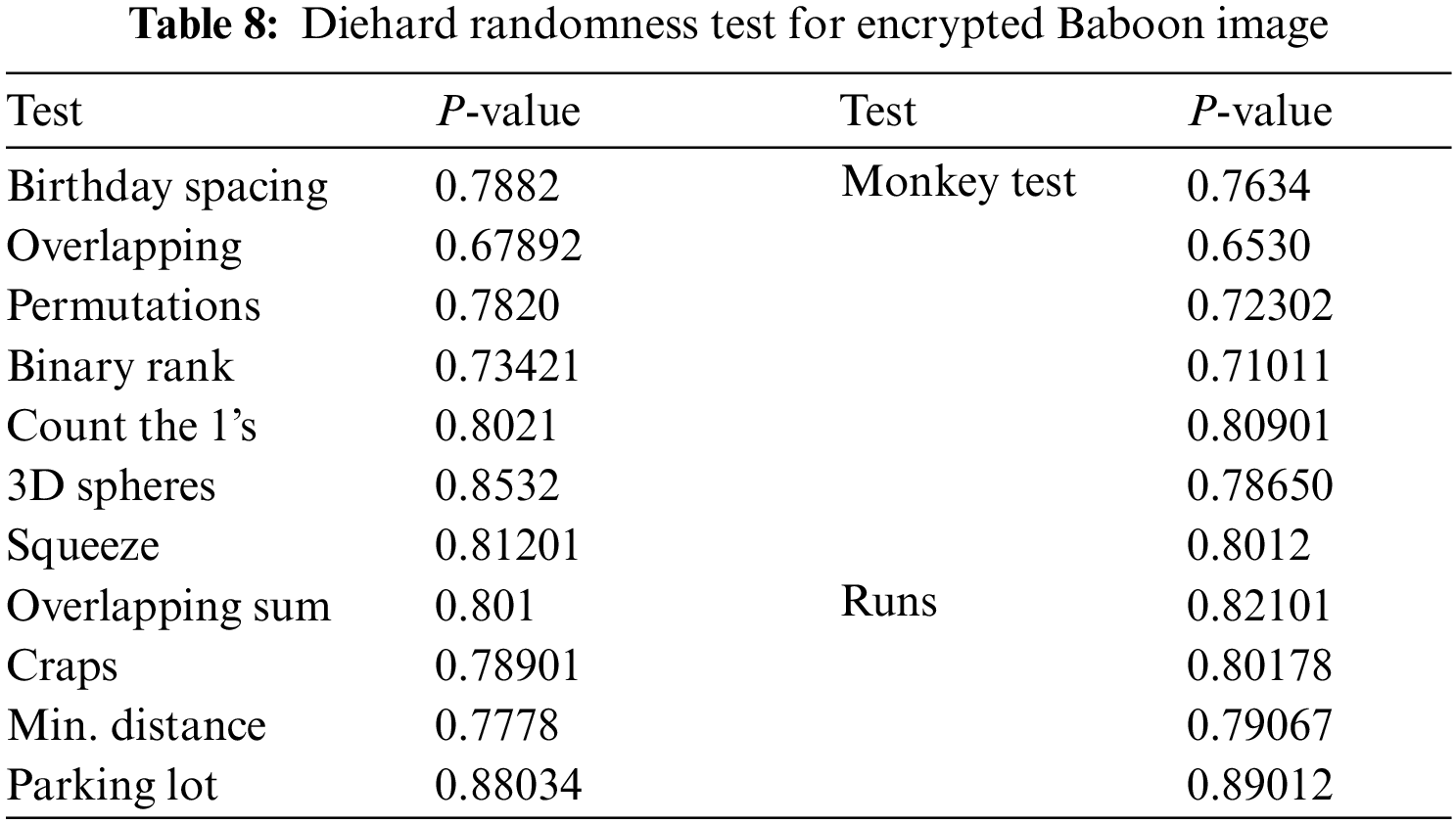
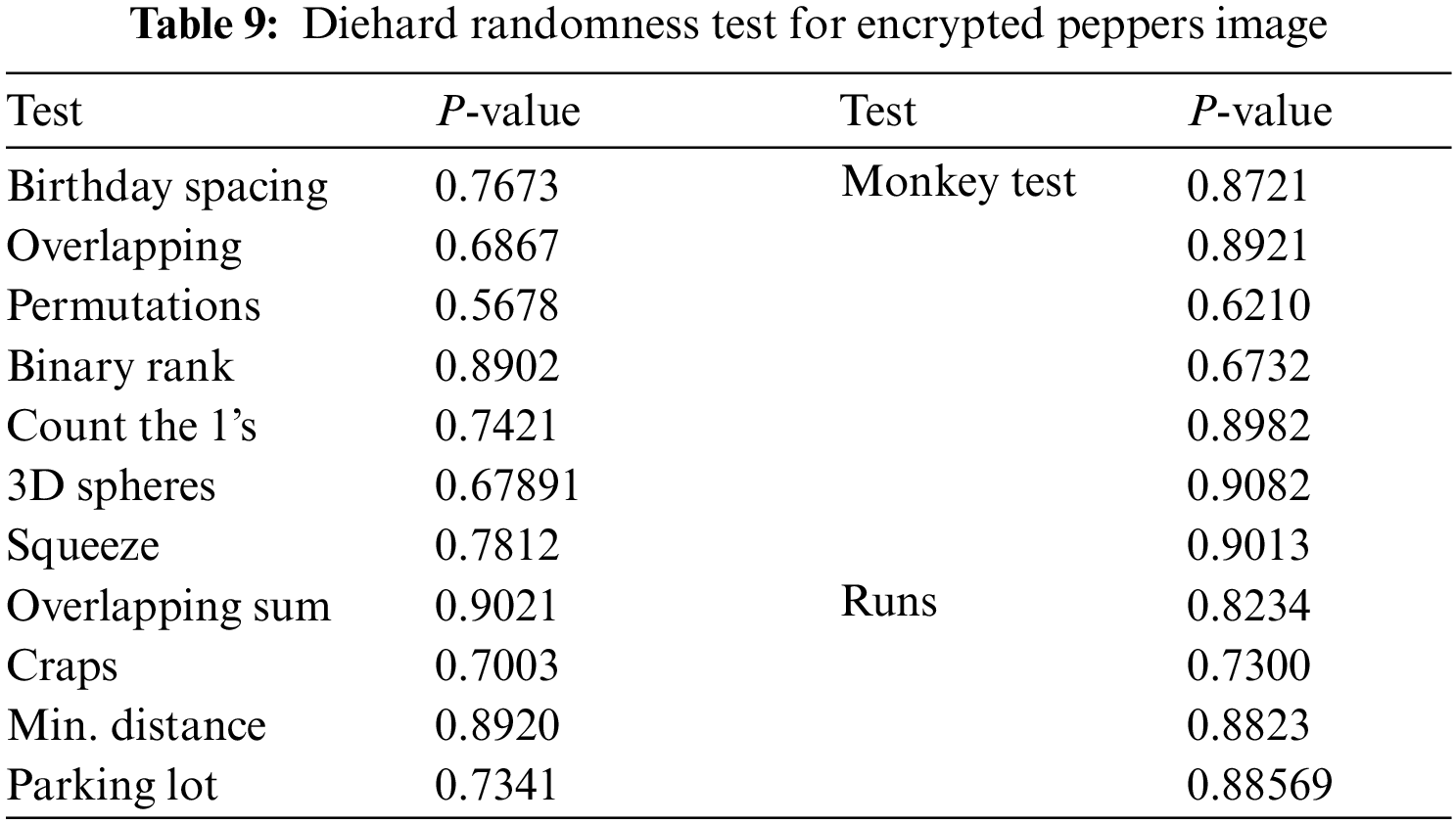
To prove the randomness of the proposed encryption algorithm, we have conducted Diehard test which gives measurable indicators of randomness of cipher-text. The diehard battery includes twelve tests of which few are repeated with different parameters. As mentioned in [22], we conducted 12 test such as birthday test, overlapping test, permutations, binary rank, 3D-spheres, squeeze, overlapping sum, craps, minimum distance, parking lot, monkey test and runs. Tabs. 7 to 10 shows the different p-values of encrypted images. It is found from the Tabs. 7 to 10, p-values are found to be greater than 0.01 as mentioned in [23], which proves the proposed encryption can defend network and statistical attacks.

Tab. 11 shows the comparative analysis between the proposed algorithm and other state of art algorithms.

5  Conclusion

The proposed hybrid encryption algorithm enhances data security in dynamic environments. The proposed MSA-QLCM system is aware of the threats that occur during data transmission with a strong encryption key. The simulation results and theoretical analysis show that the proposed method is more efficient than its classical counterpart. The statistical analysis, keys sensitivity analysis, and key space analysis have been done. For the given medical data and standard images, the NPCR and UACI are found to be in the range of 99.8% and 33.5% respectively. Also, it has passed the NIST test and correlation values were very less after the encryption process. The entropy values oscillate between 7.9 to 8.0. Even though the proposed algorithm finds its applications in medical data transmission; the algorithm still requires profound improvement in terms of implementing the high intelligent algorithm. Future work can be extended to X dimensional hybrid chaotic system integrating the complex operations over the hybrid maps.

Acknowledgement: Thanks to the reviewing committee for their valuable points and notes.

Funding Statement: The author received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  M. Axenides, E. Floratos and S. Nicolas, “The quantum cat map on the modular discretization of extremal black hole horizons,” The European Physical Journal C, vol. 78, pp. 1–15, 2018. [Google Scholar]

 2.  A. Akhshani, A. Akhavan, A. Mobaraki, S. Lim and Z. Hassan, “Pseudo random number generator based on quantum chaotic map,” Communications in Nonlinear Science and Numerical Simulation, vol. 19, no. 1, pp. 101–111, 2014. [Google Scholar]

 3.  E. Ahmed, A. Anees, V. Abbas and M. Siyal, “A noisy Channel tolerant image encryption scheme,” Wireless Personal Communication, vol. 77, no. 4, pp. 2771–2791, 2014. [Google Scholar]

 4.  A. Bakhshandeh and Z. Eslami, “An authenticated image encryption scheme based on chaotic maps and memory cellular automata,” Optics and Lasers in Engineering, vol. 51, no. 6, pp. 665–673, 2013. [Google Scholar]

 5.  A. Akhshani, A. Akhavan, S. Lim and Z. Hassan, “An image encryption scheme based on quantum logistic map,” Communications in Nonlinear Science and Numerical Simulation, vol. 17, no. 12, pp. 4653–4661, 2012. [Google Scholar]

 6.  G. Ye and K. Wong, “An efficient chaotic image encryption algorithm based on a generalized Arnold map,” Nonlinear Dynamics, vol. 69, no. 4, pp. 2079–2087, 2012. [Google Scholar]

 7.  X. Ji, S. Bai, Y. Guo and H. Guo, “A new security solution to JPEG using hyper-chaotic system and modified zigzag scan coding,” Communications in Nonlinear Science and Numerical Simulation, vol. 22, no. 1, pp. 321–333, 2015. [Google Scholar]

 8.  Y. He, Y. Q. Zhang and X. Y. Wang, “A new image encryption algorithm based on two-dimensional spatiotemporal chaotic system,” Neural Computing and Applications, vol. 32, pp. 247–260, 2020. [Google Scholar]

 9.  A. Alghafis, N. Munir, M. Khan and I. Hussain, “An encryption scheme based on discrete quantum map and continuous chaotic system,” International Journal of Theoretical Physics, vol. 59, pp. 1227–1240, 2020. [Google Scholar]

10. Q. Zhang, L. Guo and X. Wei, “Image encryption using DNA addition combining with chaotic maps,” Mathematical and Computer Modeling, vol. 52, no. 11–12, pp. 2028–2035, 2010. [Google Scholar]

11. X. Y. Wang, Y. Q. Zhang and Y. Y. Zhao, “A novel image encryption scheme based on 2-D logistic map and DNA sequence operations,” Nonlinear Dynamics, vol. 82, no. 3, pp. 1269–1280, 2015. [Google Scholar]

12. X. Aqeelur Rehman, X. Liao, A. Kulsoom and S. Ullah, “A modified (Dual) fusion technique for image encryption using SHA-256 hash and multiple chaotic maps,” Multimedia Tools and Applications, vol. 75, no. 18, pp. 11241–11266, 2016. [Google Scholar]

13. A. Belazi, A. A. El-Latif and S. Belghith, “A novel image encryption scheme based on substitution-permutation network and chaos,” Signal Processing, vol. 128, pp. 155–170, 2016. [Google Scholar]

14. A. Kulsoom, D. Xiao, Aqeel-Ur-Rehman and S. A. Abbas, “An efficient and noise resistive selective image encryption scheme for gray images based on chaotic maps and DNA complementary rules,” Multimedia Tools and Applications, vol. 75, no. 1, pp. 1–23, 2016. [Google Scholar]

15. S. Ranjeet Kumar Singh, K. Binod Kumar, W. Dilip Kumar Shaw and D. Danish Ali Khan, “Level by level image compression encryption algorithm based on Quantum chaos map,” Journal of King Saud University-Computer and Information Sciences, vol. 33, no. 7, pp. 844–851, 2021. [Google Scholar]

16. C. Zakariya Qawaqneh, M. Khaled Elleithy, A. Bandar Alotaibi and V. MunifAlotaibi, “A new hardware quantum-based encryption algorithm,” in IEEE Long Island Systems, Applications and Technology (LISAT) Conf. 2014, Farmingdale, NY, pp. 1–5, 2014. [Google Scholar]

17. R. Guodong Ye, “A chaotic image encryption algorithm based on information entropy,” International Journal of Bifurcation and Chaos, vol. 28, no. 1, pp. 1850010, 2018. [Google Scholar]

18. R. Xingbin Liu, W. Di Xiao and I. Yanping Xiang, “Quantum image encryption using intra and inter-bit permutation based on logistic map,” IEEE Access, vol. 7, pp. 6937–6946, 2019. [Google Scholar]

19. D. Jian Zhang and R. DaHuo, “Image encryption algorithm based on quantum chaotic map and DNA coding,” Multimedia Tools Applications, vol. 78, pp. 15605–15621, 2019. [Google Scholar]

20. E. Xing Zhang, W. Seung-Hyun Seo and A. Changda Wang, “A lightweight encryption method for privacy protection in surveillance videos,” IEEE Access, vol. 6, pp. 18074–18087, 2018. [Google Scholar]

21. C. Lia, Y. Zhang and E. Y. Xie, “When an attacker meets a cipher-image in 2018: A year in review,” Journal of Information Security and Applications, vol. 48, 2019. https://doi.org/10.48550/arXiv.1903.11764. [Google Scholar]

22. M. Mohammed Alani, “Testing randomness in cipher text of block-ciphers using diehard tests,” International Journal of Computer Science and Network Security, vol. 10, no. 4, pp. 53–57, 2010. [Google Scholar]

23. L. Sleem and R. Couturier, “Testu01 and practrand: Tools for a randomness evaluation for famous multimedia ciphers,” Multimedia Tools and Applications, vol. 79, pp. 24075–24088, 2020. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.