DOI:10.32604/cmc.2022.019764

| Computers, Materials & Continua DOI:10.32604/cmc.2022.019764 |  |
| Article |
Metaheuristics Algorithm for Tuning of PID Controller of Mobile Robot System
1Indian Institute of Information Technology, Nagpur, India
2School of Computing & Information Technology, Manipal University, Jaipur, Rajasthan, India
3Faculty of Computing and Informatics, University Malaysia Sabah, Jalan UMS, Kota Kinabalu, 88400, Sabah, Malaysia
4Faculty of Computing & Informatics, Multimedia University, Persiaran Multimedia, Cyberjaya, 63100, Selangor, Malaysia
5Maulana Azad National Institute of Technology, Bhopal, India
6Department of Electronics and Communication Engineering, JECRC University, Jaipur, Rajasthan, India
7Department of Computer Science and Engineering, Hanyang University, Seongdong-gu, Seoul, 04763, Korea
*Corresponding Author: Kashif Nisar. Email: kashif@ums.edu.my
Received: 24 April 2021; Accepted: 08 June 2021
Abstract: Robots in the medical industry are becoming more common in daily life because of various advantages such as quick response, less human interference, high dependability, improved hygiene, and reduced aging effects. That is why, in recent years, robotic aid has emerged as a blossoming solution to many challenges in the medical industry. In this manuscript, meta-heuristics (MH) algorithms, specifically the Firefly Algorithm (FF) and Genetic Algorithm (GA), are applied to tune PID controller constraints such as Proportional gain Kp Integral gain Ki and Derivative gain Kd. The controller is used to control Mobile Robot System (MRS) at the required set point. The FF arrangements are made based on various pre-analysis. A detailed simulation study indicates that the proposed PID controller tuned with Firefly Algorithm (FF-PID) for MRS is beneficial and suitable to achieve desired closed-loop system response. The FF is touted as providing an easy, reliable, and efficient tuning technique for PID controllers. The most suitable ideal performance is accomplished with FF-PID, according to the display in the time response. Further, the observed response is compared to those received by applying GA and conventional off-line tuning techniques. The comparison of all tuning methods exhibits supremacy of FF-PID tuning of the given nonlinear Mobile Robot System than GA-PID tuning and conventional controller.
Keywords: Metaheuristic algorithm; genetic algorithm; PID controller; mobile robot system; firefly algorithm
In the medical area, robotics is straight linked to human healthiness. The application of robotics in the medical field is becoming widespread in daily routine. It has several benefits like a fast response, minimum human interferes, high reliability, better hygiene, and less aging effect. That is why Robotic assistance came out as a burgeoning solution to many problems associated with the medical field in the last few years [1–3]. An appliance class of mobile robot is track follower wheelchair. To assist and care for citizens with disabilities and specific requirements to achieve particularly advanced assignments, e.g., spiritual customs, two ideas of planned wheelchair are presented in [4].
For many such applications, appropriate and precise controller design is a challenging task of researchers in this field. In process industries, if the process is linear and time-invariant, conventional controllers with fixed gain can be designed and implemented successfully. Calculating the PID gains using several offline tuning methods like Ziegler and Nichols (ZN) and Chien-Hrones-Reswick (CHR) has been proposed. In these conventional offline PID tuning methods, tuning of PID parameters are often not suitable for nonlinear and time-varying systems. Robotics are mainly nonlinear and time-varying systems, so conventional PID controllers with fixed gain may not be suitable for these applications. The system parameters are normally changed in such applications with times that need continuous monitoring and online PID tuning accordingly [5–8].
Due to this problem, various control techniques based on metaheuristic methods have been employed to get the optimum result and enhance the controller's performance. These AI techniques comprise of Genetic Algorithm (GA), Particle Swarm Optimization (PSO), Artificial Bee Colony (ABC) [9–12]. Even Nowadays, scientists and researchers are solving future-driven network security problems in Software-Defined Networking (SDN) [13–19], Named Data Networking (NDN) [20,21], and cloud computing network [22] with applications such as voice over IP (VoIP) [23–25], worldwide interoperability for microwave access (WiMAX) [26–28] with the support of AI, Machine Learning (ML) [29], Deep learning (DL) techniques [30], and robotic system [31]. Xin-She Yang introduced a novel meta-heuristic called Firefly Algorithm (FF). As per the literature, the FF is very influential, achievable, and better than other algorithms, such as GA, to solve several mathematical problems. According to the bibliography outcomes, the situation is clear that the FF is a robust and innovative population-based technique for solving various mathematical or optimization problems [32].
Aim of this paper to design the Metaheuristic Algorithms to tune PID controller parameters. An optimization algorithm based on FA and GA is proposed and compared with conventional PID for MRS. However conventional Chien-Hrones-Reswick (CHR) method of tuning is also implemented for comparison purpose.
In the past decade, researchers within MRS have been growing fast, particularly due to their several advantages over their disadvantages regarding the workplace. It's well known that mobile robots are nowadays used within the medical field, different industries, and for many purposes to develop the technologies necessary to obtain mobile robots that support or substitute certain operations performed by humans [33]. Numerous complex control algorithms used in robotics, such as adaptive control theory and/or robust control theory, have been projected and executed for natural systems. However, these complex and delicate control algorithms present a less complicated PID system than the popularly utilized controller in robotics and process industries [34]. Such a category of algorithms has already been shown to provide adequate functioning in controlling various linear and nonlinear processes. However, the asking of improved approaches to enrich the PID is an emerging domain of investigation. In recent times, the Metaheuristics Algorithm-based PID controller is getting a growing interest along with its suitability and practicality through various explorations. The applications of PID controllers have been described in recent literature [35].
Traditional controllers offer secure and suitable functions for linear time-invariant processes. Nevertheless, when the procedure is performed in the scope sufficiently near to a provided functioning point, this may not guarantee a decent control performance by variants in functional points or ecological situations. For solving such an issue, a considerable attempt has been placed on merging intellectual characteristics of Genetic Algorithm, PSO, FF to fine-tune factors for regulators (controllers) involuntarily. A stochastic, deterministic, population-based, and iterative optimization procedure is recognized as a population-based tuning technique. In current literature, several optimization methods may be found that enhance process operation and transaction with vagueness throughout the process operation. According to the allied literature, PID tuning in robotics and process industries is suitable and academic supports are described in articles. Although various Metaheuristics algorithm-based PID controller techniques are existing in the literature, according to [36–39].
This section presents the mathematical model of MRS for designing and tuning of PID controller to investigate the system performance under various situations. Without a controller, the existing system's model gives the oscillatory response and shows high steady-state error, which is undesirable for an application like a wheelchair for the physically challenged person. Tuning of conventional controllers for such systems is a bit challenging.
This paper considers MRS, which consists of electrical and mechanical components with electrical input and speed as output. The transfer function of MRS is shown by Eq. (1). Different controllers will be now designed to enhance the performance of the system.
The schematic design of the control scheme for MRS is presented in Fig. 1. In this article, the main aim is to regulate or control the speed of the wheel. The desired step input voltage Vin(s) is applied and speed wMRS (s) of the MRS is controlled with suggested controllers and through feedback loop. Consequently, an error e(t) is generated through comparison between required speed and real speed of MRS which is given to the PID controller. The optimized values of controller parameters are calculated by GA and FF using the objective function defined by Eq. (3).
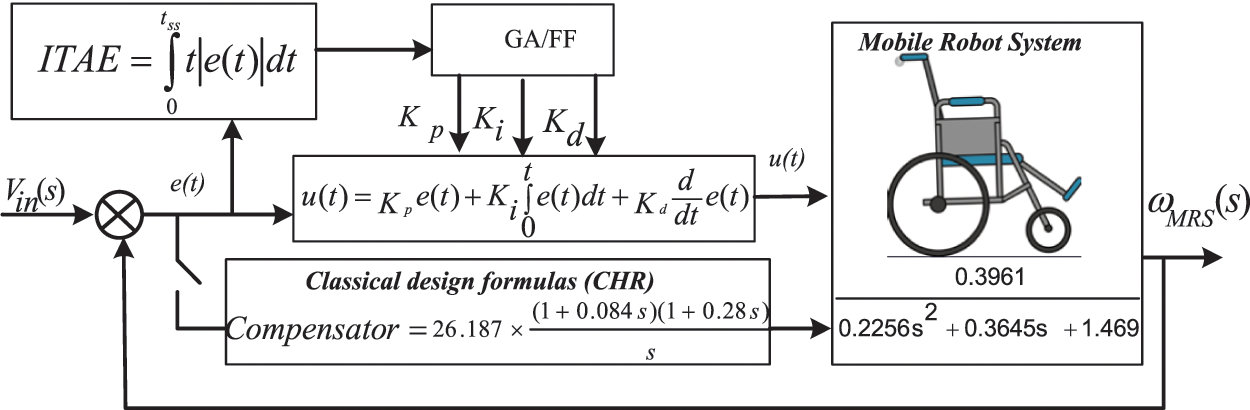
Figure 1: A schematic diagram of control action
The corresponding response is the new setpoint of the MRS. Then MRS is operated accordingly to set a new set point until the error is minimized. The performance of the MRS is analyzed in the context of response time conditions settling time. The performance of the MRS is analyzed in context of response time conditions settling time ts, rise time tr and maximum overshoot Mp. The control signal u (t) produced by the controller is the function of three tuning parameters
where
t: Time
These PID parameters are chosen to meet prescribed performance criteria for system response. The system performance mainly depends on the appropriate tuning of the controller parameters. In this paper, FF and GA algorithms are proposed to calculate the controller gain
Here, the objective function is to reduce Integral Time Absolute Error (ITAE) given by Eq. (3) for controller gains. Individually chromosome (in GA), swarm (in FF) for the population would be chosen through the fitness function just one time. Swarm& chromosomes are created through 3 values that relate to the three controller improvements to be set for keeping a satisfactory performance of the PID control. The assessments made up for calculating the functionalities of an individual element of the swarm & chromosome.
This section provides the design procedure of the tuning method along with the detailed simulation study. The MRS was considered and simulated in a MATLAB environment and controlled by applying CHR-PID, GA-PID, and FF-PID tuning methods, the time responses of the MRS were plotted and analyzed.
5.1 MRS Performances with Conventional PID Tuning with Chien-Hrones-Reswick (CHR) Using SISOTOOL
‘SISOTOOL’ is one of the advanced features in the Control System Toolbox in MATLAB that facilitates software-based controller configuration for single-input-single-output (SISO) systems. A typical design workflow with the SISOTOOL involves the following steps:
• Run the transfer function of an inherently unstable system in the editor or command window of MATLAB.
• Type ‘SISOTOOL’ at the command prompt.
• A new window SISO Design task is open.
• Import the system model (transfer function) of an inherently unstable system.
• Design controllers using PID Tuning method in Classical design formulas (CHR) Automated Tuning and update compensator.
• Now Eq. (4) of compensator is found.
• Click on show analysis plot and investigate control system designs using frequency-domain responses and time-domain such as step responses graphs.
The time response characteristic of the MRS with CHR-PID tuning is shown in Fig. 2. It can be observed by Fig. 2 that with the CHR technique, the system shows the higher overshoot and oscillation in the response curve, which is not acceptable. In such a situation, we require a series of fine-tuning techniques until a satisfactory outcome is obtained.
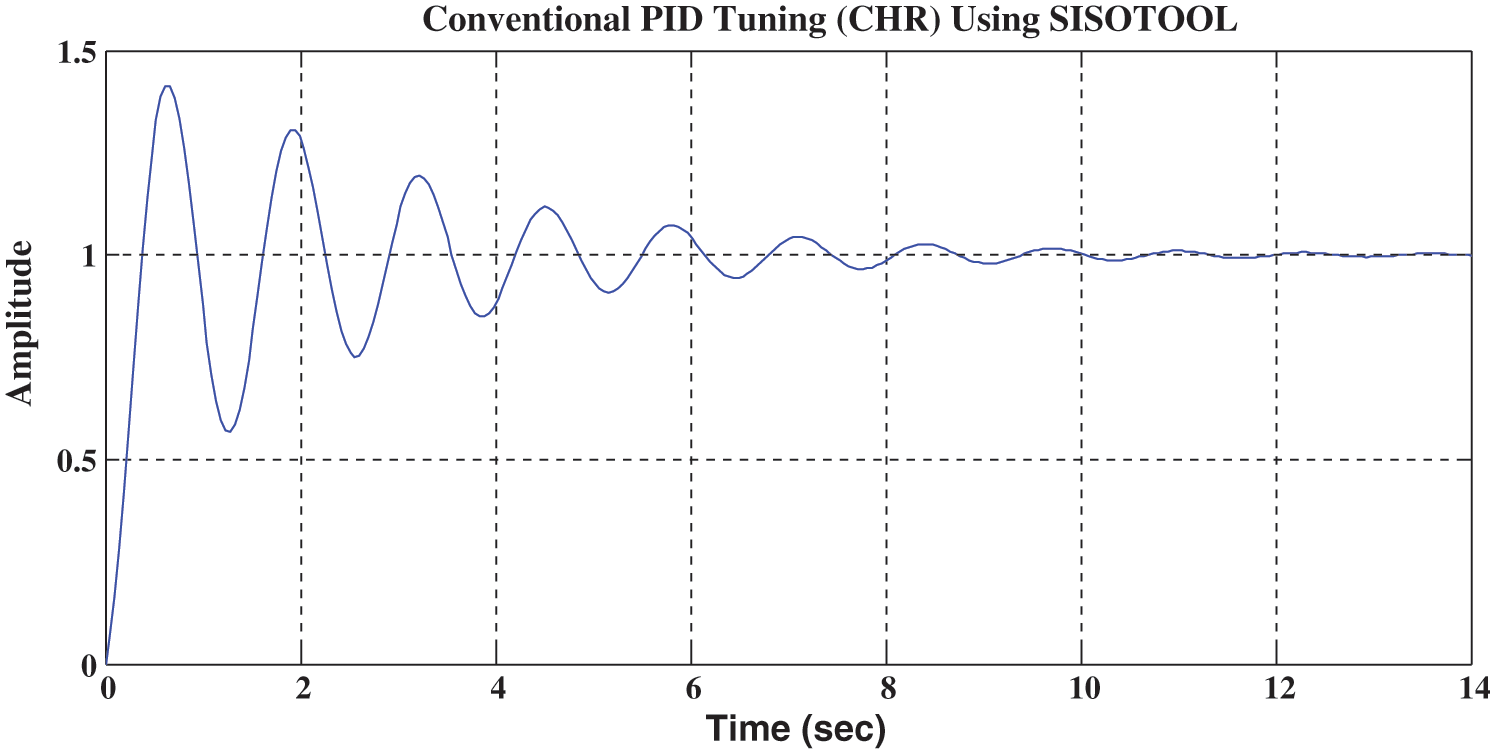
Figure 2: Time response graph with tuned CHR tuning technique
5.2 MRS Performance Analysis Using Metaheuristics Algorithm
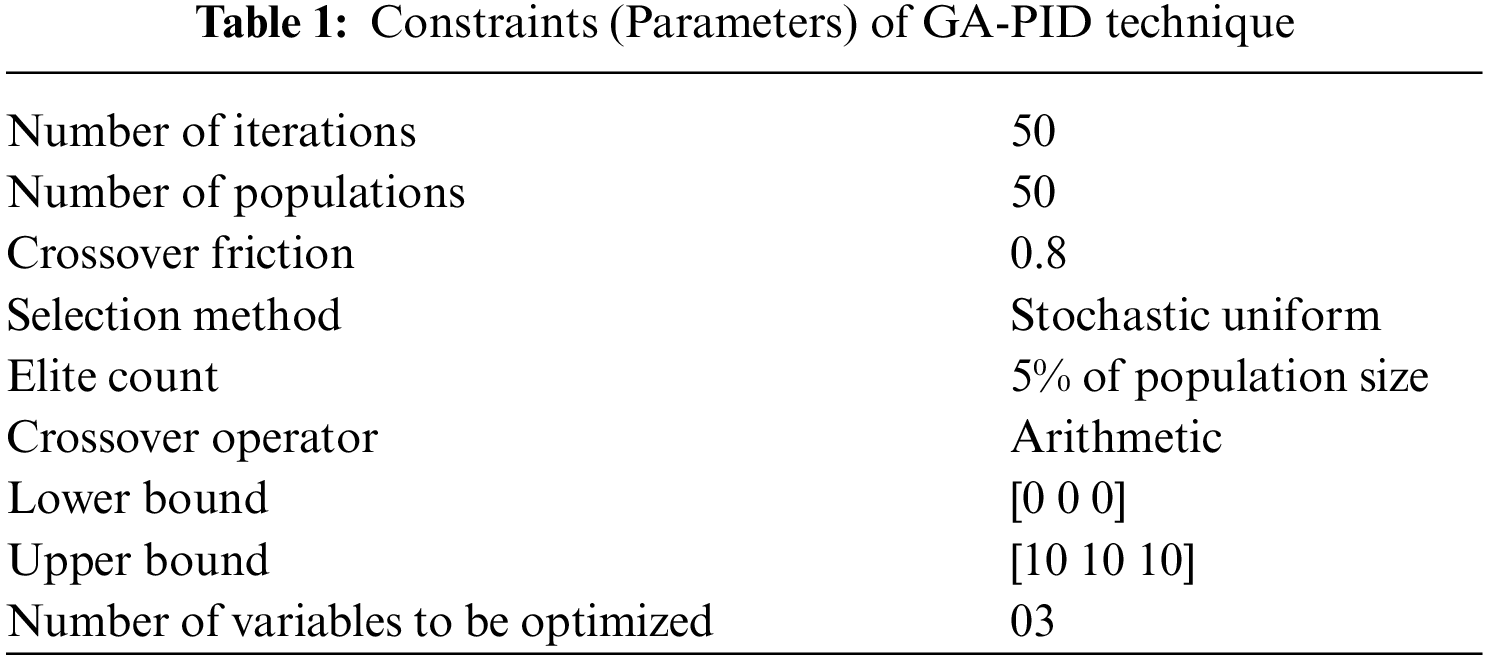
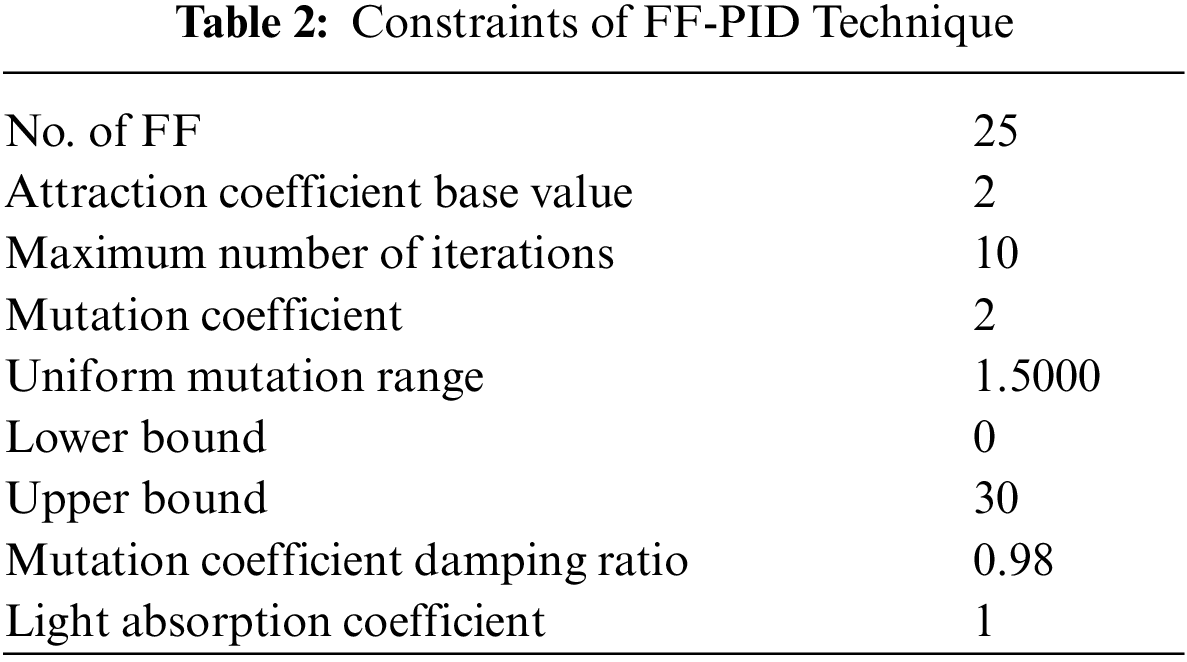
In this section, system response or outcomes are found by MATLAB encoding, and the comparative investigation is shown to prove the utility of the GA-PID and FF-PID Controller design for the following values of MRS variables. Tabs. 1 and 2 presents the initial constraints selected for GA and FF, respectively.
5.3 Fitness's Convergence for GA and FF
Next, Fig. 3 exhibits the graph between the best fitness and mean fitness for genetic algorithm. It can be observed that in 20 generations, experimental reading points of the best fitness and mean fitness appear nearby each other. Further, the mean fitness stops near the best fitness value, which does not vary with addition in generations, hence presenting the optimal or estimated optimal outcomes for the controller constraints specified values. Fig. 4 exhibits the iterations of the best fitness value for FF. Next to 6 iterations, the best fitness does not fluctuate by additional iterations, therefore, giving optimal or near-optimal results for the PID parameter values. Tab. 3 confers the values of the controller parameters obtained by GA and FF PID tuning technique.

Figure 3: Convergence of fitness for GA-PID

Figure 4: FF-PID's convergence of fitness
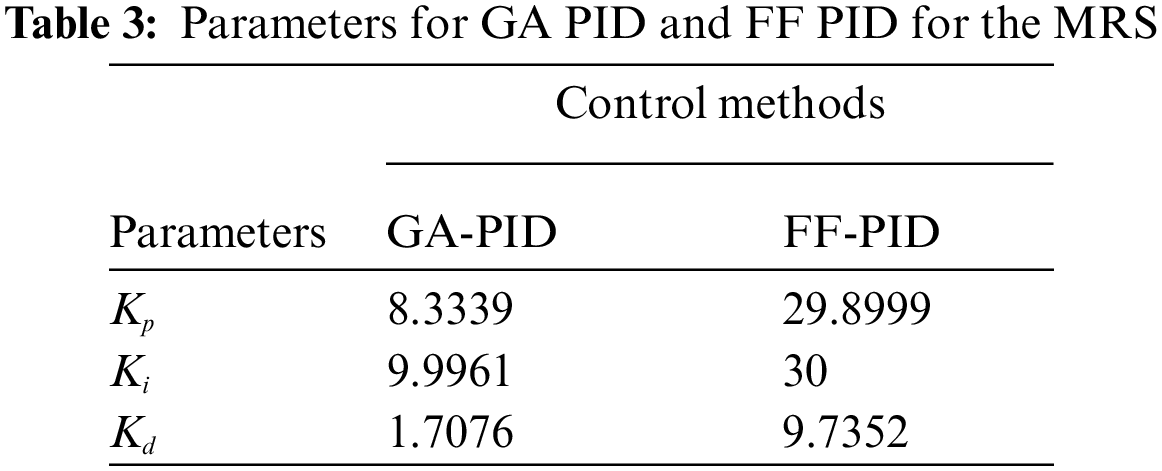
Fig. 5 shows the performance investigation of MRS with PID controller tuned with metaheuristic algorithms. A comparative analysis of the system has been performed for MRS without the controller, with GA-PID and FF-PID. GA-PID and CHR-PID have faster peak times compared when no controller is employed, which is 1.1401 s. Further, FF- PID tuning has a faster settling time and less maximum overshoot than GA-PID, 2.0065 s and 1.4365%, respectively.

Figure 5: Comparative analysis of MRS performance with GA-PID and FF-PID
Hence FF-PID proves perfection in other time response specifications. Tab. 4 compares system performance in relation to time outcome conditions like rising time, peak times, overshoot, and settling time for CHR PID, GA-PID, and FF-PID.
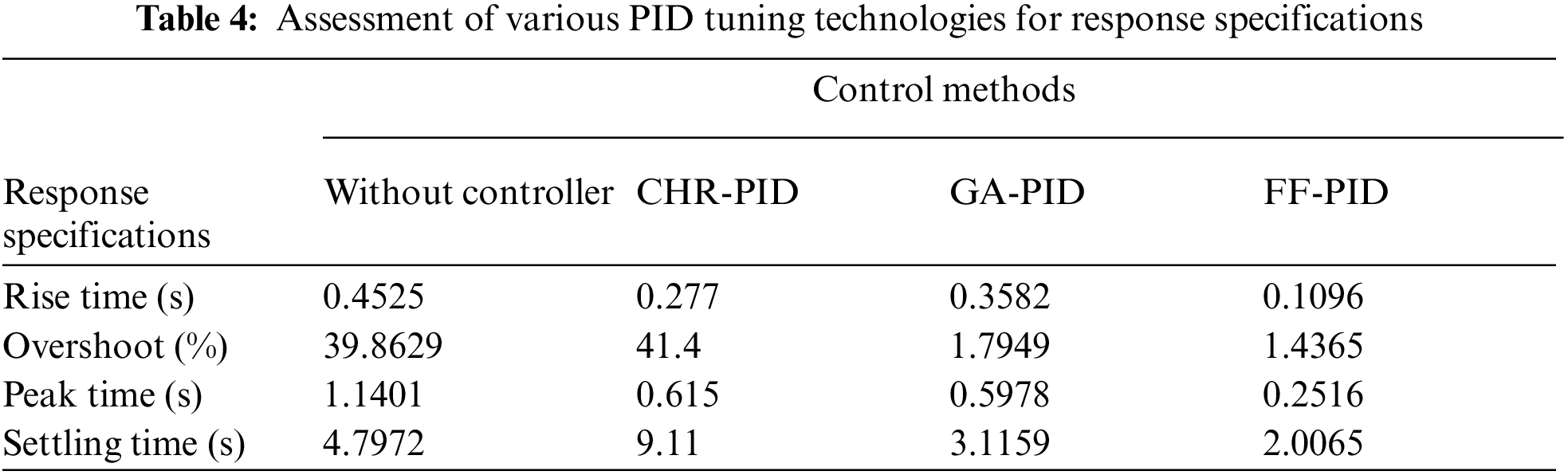
The resulting frequency response (Bode plot) of an MRS with CHR controller is given in Fig. 6, in which the Gain margin and Phase margin of the MRS with CHR controller are positive, so the system is stable. Similarly, Fig. 7 shows the Bode plot of an MRS without a controller with GA-PID and FF-PID. The gain margin and Phase margin of the MRS without a controller are infinite, so the system is unstable. While using suggested controllers, the gain margin and phase margin are positive, so the system is stable. Minimum stability criterion of MRS calculated from Bode plots presented in Tab. 5.

Figure 6: Bode plot for MRS unstable system with CHR controller

Figure 7: Bode plot for stability analysis of MRS performance with GA-PID and FF-PID
The paper exhibits optimal tuning of controller parameters, utilizing metaheuristic algorithm GA and the newly advanced FF algorithm. The controller is employed to regulate the speed of MRS and keep it up to reference value. It is described that the FF provides an easy, reliable, and efficient procedure for tuning of PID controller. According to the display in the time response, the most suitable optimal performance is achieved with FF-PID. The system with FF-PID took less time to reach the desired set-point. Hence, stable MRS performance is obtained. To examine the obtained results with other GA-PID and FF-PID controller techniques, CHR-PID is also designed and implemented. Based on the time response specification, it could be resolved that FF-PID exhibits excellent performance for fine-tuning the analyzed nonlinear MRS control system. Eventually, this is confirmed that the PID tuning through FF may be counted when an adequate procedure for the execution of better appearance and unusual quality of the designed control scheme for Mobile Robot System is available.
Acknowledgement: The authors would like to thank the editors of CMC and anonymous reviewers for their time and for reviewing this manuscript and Professor Dr. Yong-Jin Park (IEEE Life member and former Director IEEE Region 10) for his valuable comments and suggestions on improving the paper.
Funding Statement: This research work is fully supported by Universiti Malaysia Sabah (USM). Fund received by K. Nisar. Sponsors’ Websites: https://ums.edu.my.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. M. S. Qureshi, P. Swarnkar and S. Gupta, “A supervisory on-line tuned fuzzy logic-based sliding mode control for robotics: An application to surgical robots,” Robotics and Autonomous Systems, vol. 109, pp. 68–85, 2018. [Google Scholar]
2. M. S. Qureshi, G. N. Kaki, P. Swarnkar and S. Gupta, “Robust control techniques for master–slave surgical robot manipulator,” in Harmony Search and Nature Inspired Optimization Algorithms, Springer, Singapore, pp. 599–609, 2019. [Google Scholar]
3. S. Singh, M. S. Qureshi and P. Swarnkar, “Comparison of conventional PID controller with sliding mode controller for a 2-link robotic manipulator,” in Int. Conf. on Electrical Power and Energy Systems (ICEPES), Bhopal, India, pp. 115–119, 2016. [Google Scholar]
4. A. A. Mahfouz, A. A. Ayman and A. S. Farhan, “Mechatronics design of a mobile robot system,” International Journal of Intelligent Systems and Applications, vol. 5, no. 3, pp. 23, 2013. [Google Scholar]
5. C. Moler, “Matlab optimization toolbox, the math works, Inc,” Natick, MA, USA, 2021. [Online]. Available: https://www.mathworks.com/products/optimization.html. [Google Scholar]
6. L. Priyadarsini, S. Kundu and M. K. Moharana, “Motion control of AUV using IMC-PID controller,” International Journal, vol. 9, no. 3, pp. 3632–3636, 2020. [Google Scholar]
7. H. Goud and P. Swarnkar, “Investigations on metaheuristic algorithm for designing adaptive PID controller for continuous stirred tank reactor,” MAPAN, vol. 34, no. 1, pp. 113–119, 2019. [Google Scholar]
8. H. Goud and P. Swarnkar, “Signal synthesis model reference adaptive controller with genetic algorithm for a control of chemical tank reactor,” International Journal of Chemical Reactor Engineering, vol. 17, no. 7, pp. 2018-0119, 2019. https://doi.org/10.1515/ijcre-2018-0199. [Google Scholar]
9. H. Goud and P. Swarnkar, “Signal synthesis model reference adaptive controller with artificial intelligent technique for a control of continuous stirred tank reactor,” International Journal of Chemical Reactor Engineering, vol. 17, no. 2, pp. 2018-0145, 2019. https://doi.org/10.1515/ijcre-2018-0145. [Google Scholar]
10. H. Goud and P. Swarnkar, “Analysis and simulation of the continuous stirred tank reactor system using genetic algorithm,” in Harmony Search and Nature Inspired Optimization Algorithms, Springer, Singapore, pp. 1141–1151, 2019. [Google Scholar]
11. O. Roeva and T. Slavov, “Firefly algorithm tuning of PID controller for glucose concentration control during e. coli fed-batch cultivation process,” in 2012 Federated Conference on Computer Science and Information Systems (FedCSIS), Wroclaw, Poland, pp. 455–462, 2012. [Google Scholar]
12. I. Fister, I. F. Jr, X. Yang and J. Brest, “A comprehensive review of firefly algorithms,” Swarm and Evolutionary Computation, vol. 13, pp. 34–46, 2013. [Google Scholar]
13. K. Nisar, A. M. Said and H. Hasbullah, “Enhanced performance of packet transmission using system model over voip network,” in IEEE Int. Symp. on Information Technology, Kuala Lumpur, Malaysia, pp. 1005–1008, 2010. http://dx.doi.org/10.1109/ITSIM.2010.5561593. [Google Scholar]
14. K. Nisar, E. R. Jimson, M. H. A. Hijazi, I. Welch, R. Hassan et al., “A survey on the architecture, application and security of software defined networking,” Internet of Things, vol. 12, pp. 1–27, 2020. http://dx.doi.org/10.1016/j.iot.2020.100289. [Google Scholar]
15. M. R. Haque, S. C. Tan, Z. Yusoff, K. Nisar, C. K. Lee et al., “Automated controller placement for software-defined networks to resist DDoS attacks,” Computers, Materials & Continua, Tech Science Press, USA, vol. 68, no. 3, pp. 3147–3165, 2021. http://dx.doi.org/10.32604/cmc.2021.016591. [Google Scholar]
16. K. Nisar, G. Chen and A. Sarrafzadeh, “A review: Software defined networks management,” in Network Research Workshop, Proc. of the APAN, Japan, vol. 39, pp. 1–09, March 2015. http://dx.doi.org/10.7125/APAN.39.2. [Google Scholar]
17. N. F. Ali, A. M. Said, K. Nisar and I. A. Aziz, “A survey on software defined network approaches for achieving energy efficiency in wireless sensor network,” in IEEE Conf. on Wireless Sensors (ICWiSe), Miri, Malaysia, pp. 28–33, 2017. http://dx.doi.org/10.1109/ICWISE.2017.8267157. [Google Scholar]
18. M. R. Haque, S. C. Tan, Z. Yusoff, K. Nisar, R. Kaspin et al., “Unprecedented smart algorithm for uninterrupted SDN services during DDoS attack,” Computers, Materials & Continua, Tech Science Press, Henderson, Nevada, USA, 2021. http://dx.doi.org/10.32604/cmc.2021.018505 [Google Scholar]
19. E. R. Jimson, K. Nisar and M. H. A.d Hijazi, “The state of the art of software defined networking (SDN) issues in current network architecture and a solution for network management using the SDN,” in Int. Journal of Technology Diffusion, (IJTD), IGI Global Publishers, Hershey, PA, USA, vol. 10, no. 3, pp. 33–48, September 2019. http://dx.doi.org/10.4018/IJTD.2019070103. [Google Scholar]
20. A. A. A. Ibrahim and K. Nisar, “Future internet and named data networking hourglass, packet and node architecture,” Journal of Industrial Information Technology and Application, Daegu University, Republic of Korea, vol. 2, no. 3, pp. 115–123, September, 2018. [Google Scholar]
21. S. Harada, Z. Yan, Y. Park, K. Nisar and A. A. A. Ibrahim, “Data aggregation in named data networking,” in IEEE Region 10 Conf. (TENCON), Penang, Malaysia, pp. 1839–1842, November 2017. http://dx.doi.org/10.1109/TENCON.2017.8228157. [Google Scholar]
22. Y. Zhang, X. Lan, J. Ren and L. Cai, “Efficient computing resource sharing for mobile edge-cloud computing networks,” in IEEE/ACM Transactions on Networking, vol. 28, no. 3, pp. 1227–1240, June 2020. Accessed on: Feb. 13, 2021. http://dx.doi.org/10.1109/TNET.2020.2979807. [Google Scholar]
23. K. Nisar, A. Amphawan, S. Hassan and N. I. Sarkar, “A comprehensive survey on scheduler for VoIP over WLANs,” Journal of Network and Computer Applications, (JNCA), Norman, OK, USA, vol. 36, no. 2, pp. 933–948, 2013. http://dx.doi.org/10.1016/j.jnca.2012.07.019. [Google Scholar]
24. K. Nisar, A. M. Said and H. Hasbullah, “Enhanced performance of packet transmission using system model over VoIP network,” in ITSim, IEEE 2010, Malaysia, pp. 1005–1008, 15, June 2010. http://dx.doi.org/10.1109/ITSIM.2010.5561593. [Google Scholar]
25. N. I. Sarkar, K. Nisar and L. Babbage, “Performance studies on campus-wide focus on ftp, video and VoIP ethernet network,” in International Journal of Advanced Pervasive and Ubiquitous Computing, (IJAPUC), IGI Global Publishers, Hershey, PA, USA, vol. 4, no. 1, pp. 49–59, 2012. http://dx.doi.org/10.4018/japuc.2012010106. [Google Scholar]
26. J. Shuja, R. W. Ahmad, A. Gani, A. I. A. Ahmed, A. Siddiqa et al., “Greening emerging IT technologies: Techniques and practices,” Journal of Internet Services and Applications (JISA), Springer, London, UK, vol. 8. no. 9, pp. 01–11, July 2017. http://dx.doi.org/10.1186/s13174-017-0060-5. [Google Scholar]
27. I. A. Lawal, A. M. Said, K. Nisar and A. A. Mu'azu, “A distributed QoS-oriented model to improve network performance for fixed WiMAX,” International. Journal on Recent Trends in Engineering and Technology, Association of Computer Electronics and Electrical Engineers, vol. 10, no. 1, pp. 186–202, January 2014. [Google Scholar]
28. I. A. Lawal, A. M. Said, K. Nisar, P. A. Shah and A. R. A. Mu'azu, “Throughput performance improvement for VoIP applications in fixed WiMAX network using client–server model,” Journal of Science International-Lahore, Pakistan, vol. 26, no. 3, pp. 999–1002, August 2014. http://www.sci-int.com/pdf/636639048130555148.%20Lawal--.pdf. [Google Scholar]
29. M. R. Haque, S. C. Tan, Z. Yusoff, K. Nisar, C. K. Lee et al., “SDN architecture for UAVs and EVs using satellite: A hypothetical model and new challenges for future,” in IEEE 18th Annual Consumer Communications & Networking Conf. (CCNC), Las Vegas, NV, USA, 2021. pp. 1–6, http://dx.doi.org/10.1109/CCNC49032.2021.9369464. [Google Scholar]
30. N. Salam, M. K. Abbas, M. K. Maheshwari, B. Chowdhry and K. Nisar, “Future mobile technology: Channel access mechanism for LTE-LAA using deep learning,” in 2021 IEEE 18th Annual Consumer Communications & Networking Conf. (CCNC), Las Vegas, NV, USA, pp. 1–5, 2021. http://dx.doi.org/10.1109/CCNC49032.2021.9369598. [Google Scholar]
31. I. Haider, K. B. Khan, M. A. Haider, A. Saeed and K. Nisar, “Automated robotic system for assistance of isolated patients of coronavirus (COVID-19),” in 2020 IEEE 23rd Int. Multitopic Conf. (INMIC), Bahawalpur, Pakistan, pp. 1–6, 2020. http://dx.doi.org/10.1109/INMIC50486.2020.9318124. [Google Scholar]
32. S. Shamshirband, F. Esmaeilbeiki, D. Zarehaghi, M. Neyshabouri, S. Samadianfard et al., “Comparative analysis of hybrid models of firefly optimization algorithm with support vector machines and multilayer perceptron for predicting soil temperature at different depths,” Engineering Applications of Computational Fluid Mechanics, vol. 14, no. 1, pp. 939–953, 2020. [Google Scholar]
33. A. Bârsan, “Position control of a mobile robot through PID controller,” Acta Universitatis Cibiniensi, Technical Series, Sciendo, vol. 71, no. 1, pp. 14–20, 2019. http://dx.doi.org/10.2478/aucts-2019-0004. [Google Scholar]
34. M. H. A. Talib, I. Z. M. Darus, P. M. Samin, H. M. Yatim, M. I. Ardani et al., “Vibration control of semi-active suspension system using PID controller with advanced firefly algorithm and particle swarm optimization,” Journal of Ambient Intelligence and Humanized Computing, vol. 12, pp. 1–19, 2020. [Google Scholar]
35. B. N. Kommula and V. R. Kota, “Direct instantaneous torque control of brushless DC motor using firefly algorithm based fractional order PID controller,” Journal of King Saud University-Engineering Sciences, vol. 32, no. 2, pp. 133–140, 2020. [Google Scholar]
36. S. Taran, P. C. Sharma and V. Bajaj, “Automatic sleep stages classification using optimize flexible analytic wavelet transform,” Journal of Knowledge-Based Systems, Elsevier, vol. 192, pp. 1–8, 2020. [Google Scholar]
37. P. C. Sharma and N. S. Chaudhari, “A tree based novel approach for graph coloring problem using maximal independent set,” Journal of Wireless Personal Communication,” Springer, vol. 110, no. 3, pp. 1143–1155, 2020. [Google Scholar]
38. H. Goud, P. C. Sharma, P. Swarnkar, V. G. Shankar, V. P. Sharma et al., “A comparative analysis of conventional PID tuning techniques for single link robotic Arm,” Solid State Technology, vol. 64, no. 2, pp. 565–574, 2021. [Google Scholar]
39. H. B. Patel and S. N. Chaphekar, “Developments in PID controllers: Literature survey,” International Journal of Engineering Innovation & Research, vol. 1, no. 5, pp. 425–430, 2012. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |