DOI:10.32604/cmc.2022.016410

| Computers, Materials & Continua DOI:10.32604/cmc.2022.016410 |  |
| Article |
Finger Vein Authentication Based on Wavelet Scattering Networks
1Artificial Intelligence & Data Analytics Lab, CCIS Prince Sultan University, Riyadh, 11586, Saudi Arabia
2Department of Computer Engineering, Dolatabad Branch, Islamic Azad University, Isfahan, Iran
3Faculty of Computer Engineering, Najafabad Branch, Islamic Azad University, Isfahan, Iran
4MIS Department College of Business Administration, Prince Sattam bin Abdulaziz University, Alkharj, 11942,Saudi Arabia
*Corresponding Author: Majid Harouni. Email: majid.harouni@gmail.com
Received: 31 December 2020; Accepted: 14 January 2022
Abstract: Biometric-based authentication systems have attracted more attention than traditional authentication techniques such as passwords in the last two decades. Multiple biometrics such as fingerprint, palm, iris, palm vein and finger vein and other biometrics have been introduced. One of the challenges in biometrics is physical injury. Biometric of finger vein is of the biometrics least exposed to physical damage. Numerous methods have been proposed for authentication with the help of this biometric that suffer from weaknesses such as high computational complexity and low identification rate. This paper presents a novel method of scattering wavelet-based identity identification. Scattering wavelet extracts image features from Gabor wavelet filters in a structure similar to convolutional neural networks. What distinguishes this algorithm from other popular feature extraction methods such as deep learning methods, filter-based methods, statistical methods, etc., is that this algorithm has very high skill and accuracy in differentiating similar images but belongs to different classes, even when the image is subject to serious damage such as noise, angle changes or pixel location, this descriptor still generates feature vectors in a way that minimizes classifier error. This improves classification and authentication. The proposed method has been evaluated using two databases Finger Vein USM (FV-USM) and Homologous Multi-modal biometrics Traits (SDUMLA-HMT). In addition to having reasonable computational complexity, it has recorded excellent identification rates in noise, rotation, and transmission challenges. At best, it has a 98.2% identification rate for the SDUMLA-HMT database and a 96.1% identification rate for the FV-USM database.
Keywords: Biometrics; finger veins; wavelet scattering; vein authentication; disaster risk reduction
For more than two decades, biometric-based authentication systems have replaced traditional authentication systems such as ID cards, passwords, etc. During this time, many unique features of the human body have been identified, and much research has been carried out to improve the methods of identification using these features. The most famous of these features are fingerprint, face and iris [1–5]. Each of these features had its difficulties and challenges. Fingerprints and palm lines were constantly exposed to physical damage, leading to changes in these lines’ patterns and increased system error rates. Face-based systems were considered one of the most challenging authentication systems because factors such as ageing, facial hair growth, wearing glasses, etc., significantly reduced these systems’ error rate [6–8]. Iris-based systems were considered to be susceptible systems with meager error rates. However, these systems still had a major challenge due to the iris images’ complex texture.
Furthermore, implementing iris-based systems was very costly and had high computational complexity [9,10]. According to all the aspects discussed, the researcher decided to introduce techniques that were not firstly subject to destruction and had the least changes. Second, the imaging type and its computation have the least computational and implementation complexity. Therefore, the patterns of finger and palm veins were of interest to researchers. Third, researchers less favored the use of finger vein patterns because of their complexity in imaging and implementation. Since this feature was first recognized in 2003 as biometrics, extensive research has been launched to identify and respond to biometrics’ challenges [11,12]. These challenges were categorized into finger vein recognition problems, identity identification rate, and temporal complexity. This section will investigate the challenges and part of this research.
Based on analysis of literature reviewed, it is found that this field of research has not yet reached to its maturity level and emerging research focus on deep learning applications [13–15]. But these methods have been accompanied by two problems of computational complexity and low identification rates. Therefore, the need for an authorization system that, in addition to low error, has a high identification rate and low computational complexity is increasingly felt. The use of finger-vein based systems is associated with a major challenge called pixel misalignment. This challenge occurs when the test image is not similar to the image recorded in the database [16,17]. The important point is that this challenge was inevitable. The user may place the finger at an incorrect angle or location when placing the finger on the scanner for identification and the test image may not be the same as the training image. It is also possible to apply noise to the scanner, reducing the identification rate like the challenges mentioned above [18–20]. This paper attempts to introduce a method based on the response to the challenge. Scattering wavelets is one way of extracting a feature from images considered deep learning but did not have neural networks’ time and computational complexity. Scattering wavelet extracts image features from Gabor wavelet filters in a structure similar to convolutional neural networks. What distinguishes this algorithm from other feature extraction methods is its very high skill and accuracy in differentiating similarities. Different classes of images, even when the image is subject to severe damage such as noise, angle changes or pixel location, this descriptor still generates feature vectors in a way that minimizes the classifier error. This paper aims to evaluate the proposed method's performance compared to some other machine learning methods under two finger vein databases.
This section investigates the conducted research in two types of machine learning-based research and neural network-based research. Machine learning-based research consists of three principal tasks: preprocessing, feature selection and classification [21]. However, deep neural networks receive images directly and perform self-identification at the output [22]. For example, a machine learning-based approach for authentication for finger vein images is presented in [23]. In the preprocessing step, after extraction of the wristband, the size images are also fitted. Then, with the PCA and the linear discriminant analysis (LDA), the appropriate features have been extracted and finally classified with SVM. For example, in [24], authors used machine learning to identify finger vein-based identity. After the preprocessing process, only PCA has been used to extract the features.
Two post-propagation neural networks and adaptive network-based fuzzy inference system (ANFIS) based fuzzy classifier methods have been used in the pattern classification stage. The fuzzy classifier is less sensitive to noise and conforms to the nature of biometric data. But the results of both methods were satisfactory. First, similar to previous research, this research indicates that PCA-generated data have a very high degree of differentiation. Second, deep learning has an excellent result in the authentication. The following year, the researchers used a Gaussian adaptive filter to improve image quality in the preprocessing stage. Feature extraction was performed using the variance of practical binary patterns. The proposed classification is based on global adaptation and SVM, demonstrating the importance of the support vector machine in pattern recognition research [21].
Moreover, in [24], the implemented approach employed a complex preprocessing process, including histogram equation, contrast enhancement, intermediate filtering, and Gabor filtering. Finally, the extracted features include global thresholds and Gabor filters, in which the classifier used is also SVM. The proposed method is very complex and the results are desirable. The study in [25] used a hard-adaptive algorithm for classification. Still, only the Region of Interest (ROI) was extracted in the preprocessing phase. The feature extractor used only the HCGR (Histogram of Competitive Gabor Responses), a new method. This research shows that Gabor based approaches can be very effective in the feature extraction. The research in [26] applied the rigid and complex pattern matching algorithm to classify the proposed method. The proposed method is also complicated in the preprocessing and feature extraction stages. After extraction of ROI and normalization of light and illumination of infrared images near Mumford shah have been used for minimization in the preprocessing phase. Interestingly, in the extraction stage of the local entropy threshold, characteristic of morphological refusal and morphological filtering have been suggested, despite all the complexities, their accuracy was low. Vlachos et al. [26] proposed a multidimensional biometric system using palm and finger vein patterns. Input images are preprocessed first and using a modified two-dimensional Gabor filter, gradient-based approaches are employed to extract features. These features are matched using Euclidean distance metrics and are merged using fuzzy logic techniques using the scoring level. Similarly, Liu et al. [27] used a distance calculation-based method for authentication. In the preprocessing stage after extraction of the finger normalization, a Sobel edge filter is used to improve finger vein detection. A 2-D Rotated Wavelet Filters (RWF) have been used in the zoning step. Finally, the feature vectors’ distance has been calculated with a distance calculation mechanism and authentication has been done. In this way, the effect of Gabor-based features on the extraction of distinct features is well evident. Also, Shrikhande et al. [28] proposed a Sobel-based approach to finger–vein-based authentication. In this research, after the finger region's normalization, a histogram parameters alignment stage has been used for preprocessing. At the feature extraction stage, Sobel operators have been used to extract the features and finally, a matching mechanism has been used for finger vein authentication.
Various preprocessing processes have been employed to improve the quality of IR infrared images. These include ROI extraction, then median filtering, and histogram equation. Morphological operators and maximum curve points are used as extracted features for the multilayer perceptron neural network [29,30]. The proposed method is implemented and the results are significant, indicating that the combination methods of deep learning and machine learning effectively identify finger vein. Convolutional neural networks are modeled to classify finger vein images [31]. Convolutional neural networks are one of the deep learning methods that have recently attracted many researchers’ attention. These methods do not require feature extraction anymore, and convolutional neural network performs the classification image by creating a data pool. The results show that the convolutional neural network-based methods can significantly improve the identification rate with finger vein images. In the following, Fang et al. [32], a technique has again used the convolutional neural network to identify finger vein-based authentication. In this study, unlike many highly complex analyses, images are convoluted and prolonged immediately after entering the neural network, and ultimately authentication is done. In this study, we used the rectified linear unit (ReLU) cost function, which is one of the fundamental functions for the convolutional neural network and more optimized cost functions have been introduced in previous years; however, the identification rate obtained is acceptable, and this again emphasizes the efficiency of the convolutional neural network in identifying finger vein patterns. Radzi et al. [33] also used a deep learning convolutional neural network for finger-vein-based authentication. The proposed neural network capabilities have been evaluated through four databases. This study's main purpose is that the proposed deep learning method can deliver consistent and highly accurate results in the face of different quality finger images. The extensive set of experiments shows that the proposed method's accuracy can be ideal. A series of these papers suggests that methods based on support vector machines, Gabor filters, and convolutional neural networks can significantly impact finger vein identification techniques. While a combination of the methods mentioned has been used in this study. Fig. 1 illustrates the evolutionary process of this research in the last decade.
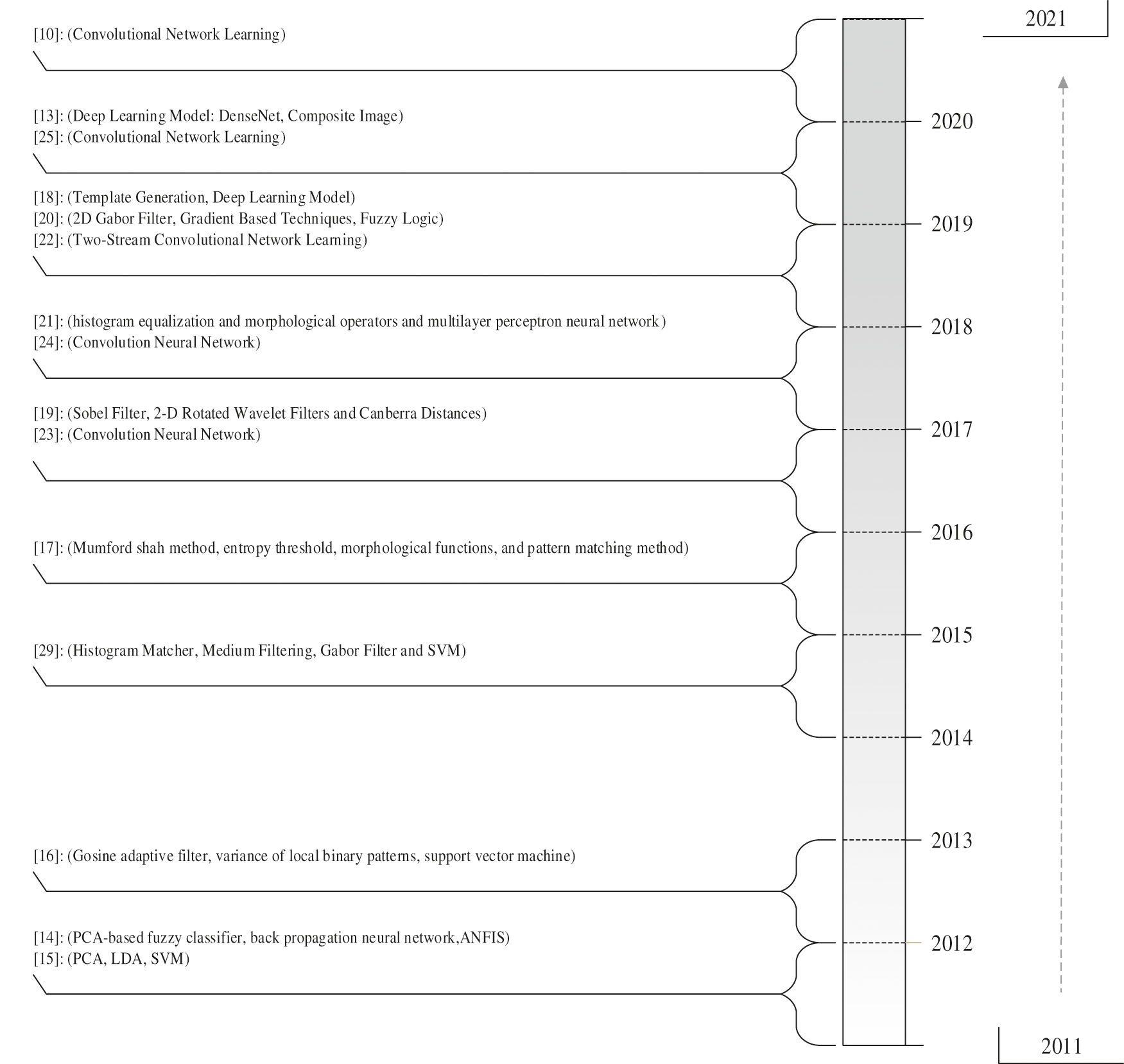
Figure 1: The evolutionary process of related research
This paper has been organized and implemented as follows. Section 3 explains the scattering wavelet, Section 4 describes the proposed method for this paper, and Section 5 discusses this study's results. The final section concludes research.
The Fourier transform and coefficients of the subset family of this transform are somewhat stable to the transition. However, this transform is highly unstable against deformation, especially at high signals, and any signal deformation at large signals causes major changes [34]. For this reason, wavelets were used more extensively to resist deformation. Wavelet has a local waveform, unlike the Fourier Sine waveform, that causes its stability against the changes [35].
On the other hand, the wavelet transform calculates the convolutions with the wavelet filters, so the covariance transform is unstable against the changes. For this purpose, as described in [36], a set of wavelet filters is required to produce descriptors with a set of stable features resistant to deformation, transition, scale, direction and dilation. The two-dimensional directional wavelets are obtained by scaling and rotating a single bandpass filter
If the Fourier transform
A wavelet transforms filters the signal x using a family of wavelets
Finally, it should be noted that these filter banks make them more resistant to rotation and dilation. But the important point is that a wavelet transform is obtained with the translation, so it is not stable against the translation. Therefore, to produce a stable feature vector against change, it must be produced in a nonlinear (subjected to an operator) structure. For example, suppose R is a linear or nonlinear operator calculated by the translation
Now, if we consider
A scattering transform in the path p has been defined as an integral normalized by the Dirac response. Each scattering factor
Eq. (6) defines a scattering transform in the neighborhood of
This ultimately results in Eq. (7):
If a set has the length of M, it
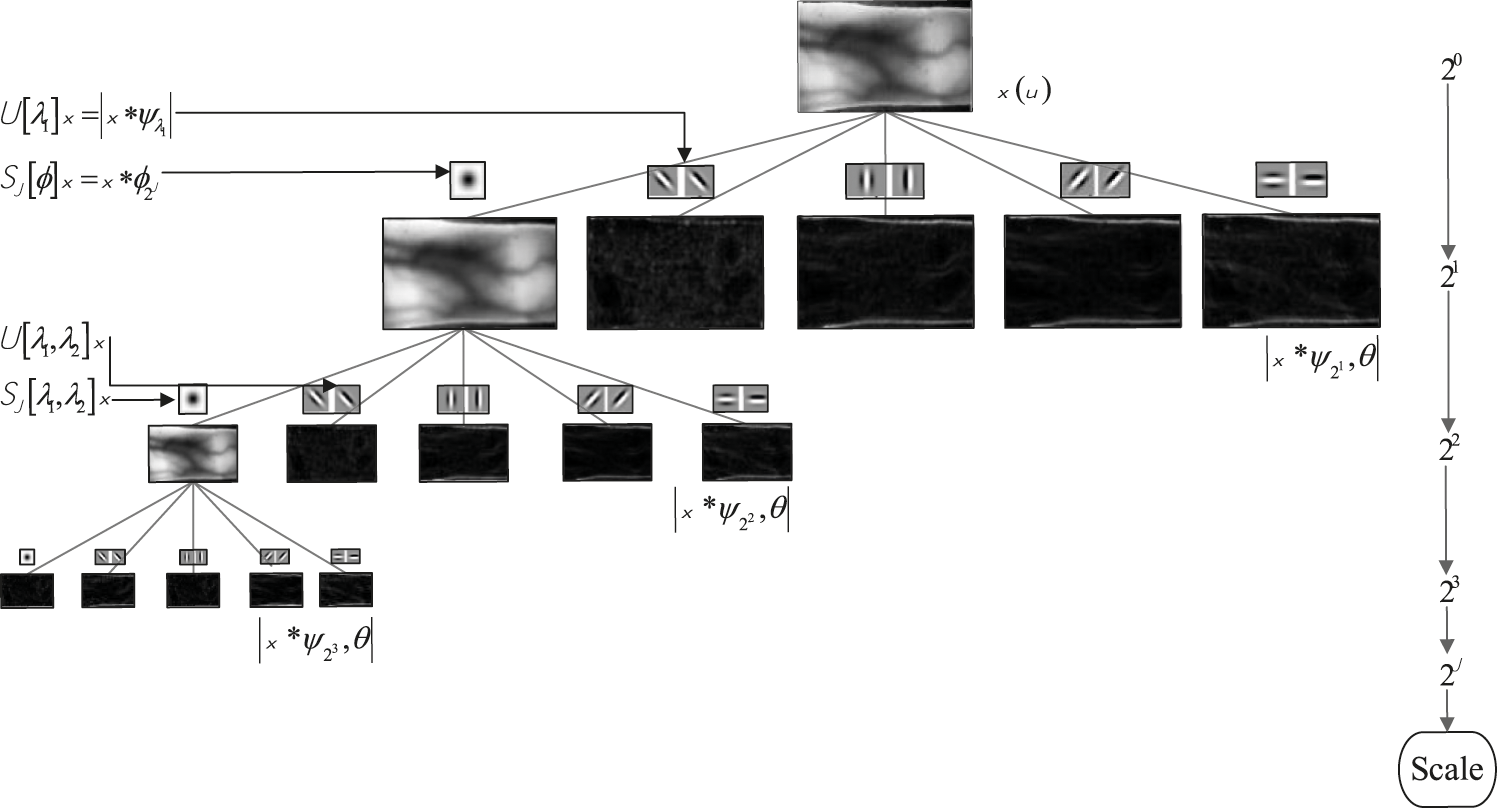
Figure 2: An example of a scattering wavelet step on an image
The proposed authentication system has been implemented based on the scattering wavelet descriptor and the K Nearest Neighbors (KNN) classifier. Like many authentication methods, this consists of four main parts: preprocessing, feature extraction, dimension reduction and authentication. The finger region is first separated in the raw image in preprocessing section. The image is then sharpened using a Butterworth filter and the image contrast is improved at the end. In the feature extraction part of the research, the wavelet scattering algorithm is used and the basic component analysis has been used in the dimension reduction part. Finally, the identification section also uses the KNN classifier [21]. Fig. 3 shows the block diagram of the proposed method.
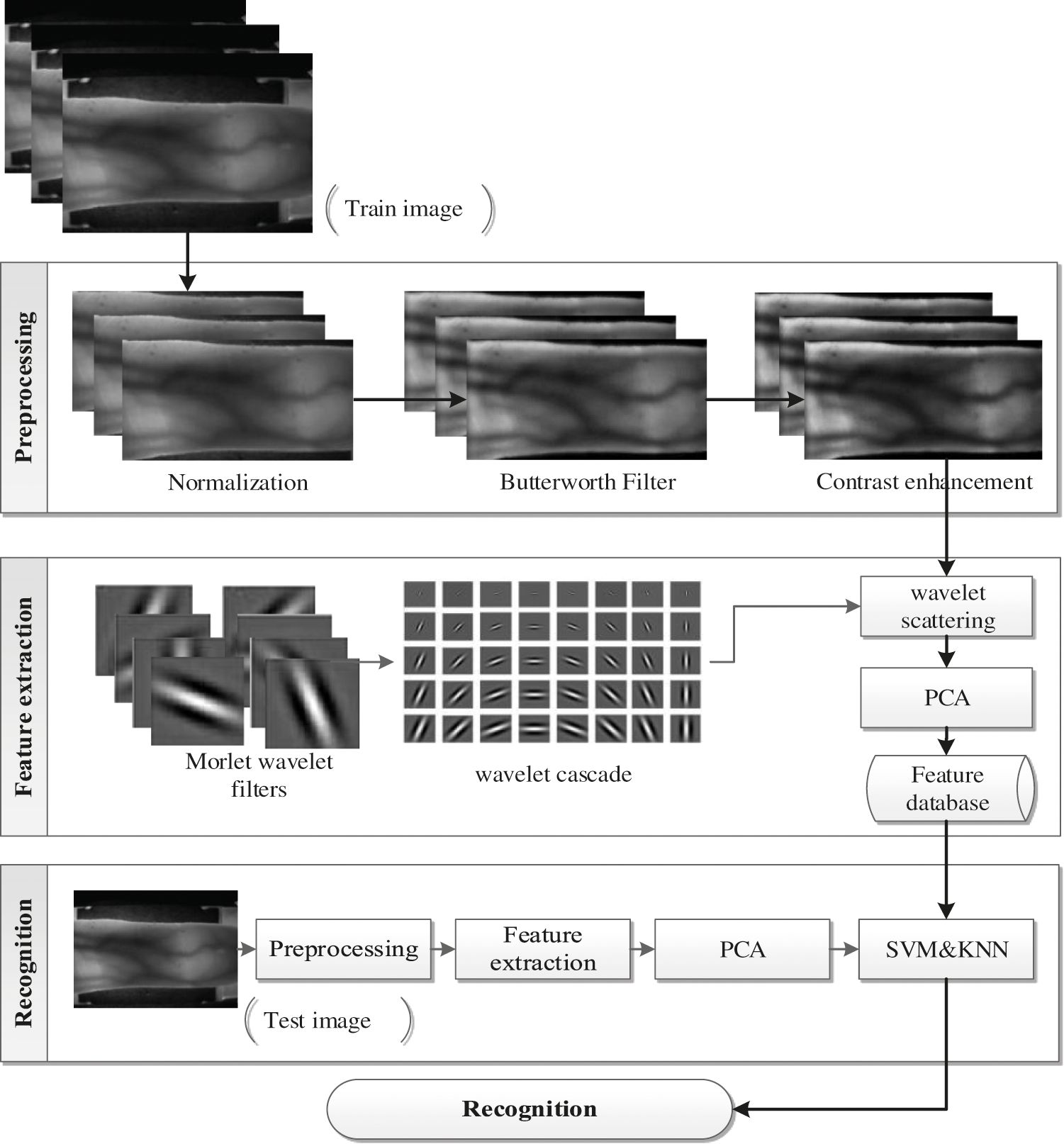
Figure 3: The block diagram of the proposed method
In the preprocessing phase, three operations of normalization, filtering and contrast enhancement are performed. The raw image's finger region is first identified using an active contour algorithm in image normalisation. This algorithm has been widely used in finger vein related research [36]. Then, using the edge detection algorithm, the normal finger area from the raw image, as shown in Fig. 4. Following the preprocessing, the normalized image has been sharpened using the Butterworth filter to enhance the clarity of the image veins and, this improves the differentiation of image feature vectors. Finally, the image's contrast is improved to provide the image for feature extraction. During the contrast enhancement stage, the clarity of the vein segments is distinguished from the whole image.

Figure 4: The results of an image normalization phase: (a): raw image, (b): normalized image, (c): normal finger area
The discriminative features extraction and selection are challenging tasks in the authentication process. In this research, required wavelet cascade is generated using the Gabor wavelet filters and proportional to the image size. In the second step, the iris image's scattering transform is calculated using the generated wavelet cascade. This transform calculates the features of each depth of image separately and in the final step, by combining the vectors of each depth, the feature vector is developed for each image. These feature vectors have the differentiation feature to fall into the right classes according to most classifiers’ distance criterion. But one of the major problems in deep learning research is the production of feature vectors of immense dimensions, which is not an exception. For example, the feature vectors extracted from finger vein images have over 30000 features. The critical point is that classifying these dimensions of feature vectors for each classification is complicated and time-consuming. Secondly, feature vectors with large dimensions will have a correlation feature.
For this reason, PCA has been used to quantitatively and qualitatively improve the properties of feature vectors. The generated feature vector contains new values that are quantitatively much smaller than the original feature vector. In terms of the vector quality, it is more distinct than the feature vector extracted by the descriptor.
After the preparation of the feature vectors, the authentication procedure is performed using the classifier. At this stage, the test data is classified with the feature vectors collected in the feature database, and the identity recognition procedure is performed. In this paper, the K Nearest Neighbors classifier has been used for classification. In addition to its high accuracy, this classifier has very low computational complexity in recognizing, which reduces the chronology.
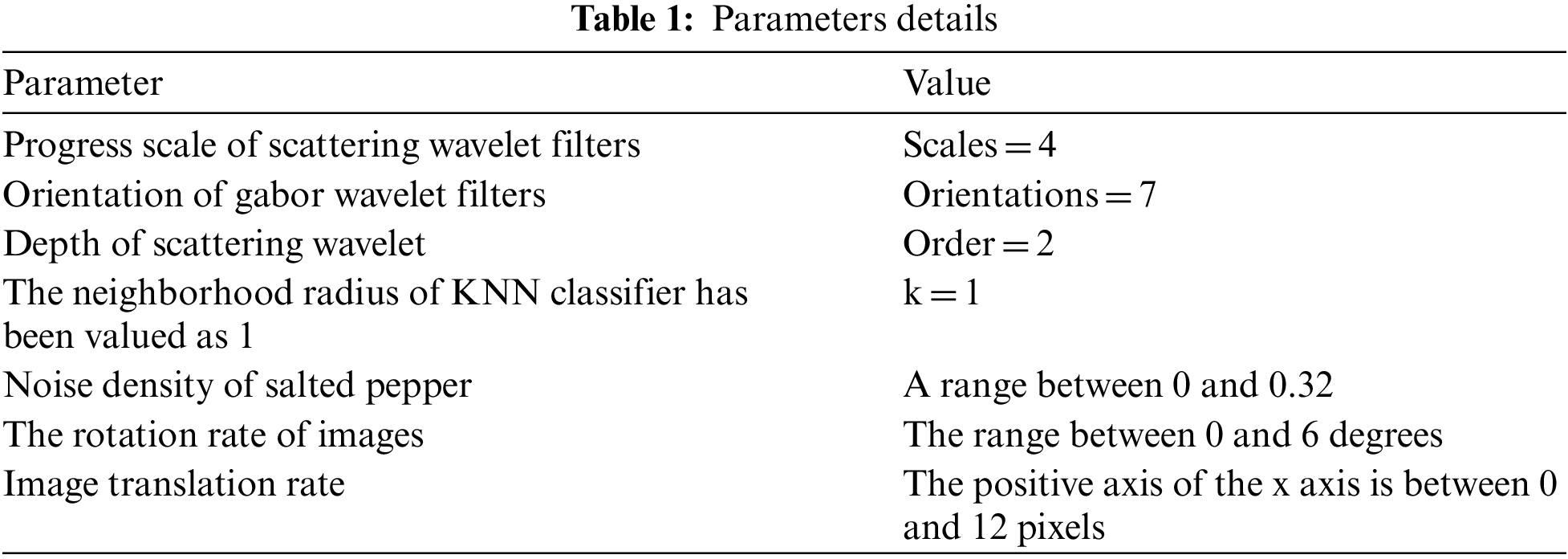
In this section, the proposed method's efficiency is evaluated using SDUMLA-HMT [37] and FV-USM [38] database images. Unfortunately, the finger veins in the FV-USM database had less clarity than the SDUMLA-HMT database, which will cause a challenge to the proposed method. The parameters of the proposed method are presented in Tab. 1
To evaluate the proposed method, palm-line images of two databases SDUMLA-HMT [37] and FV-USM [38] have been used. For experiments, databases are distributed into three segments. The first segment contains images by which the best parameters in the proposed method's descriptor and classifier are identified. The second segment, contains training images that comprise 40% of the database images and third segment of the proposed method's images. Tab. 2 shows the specifications of the two databases.
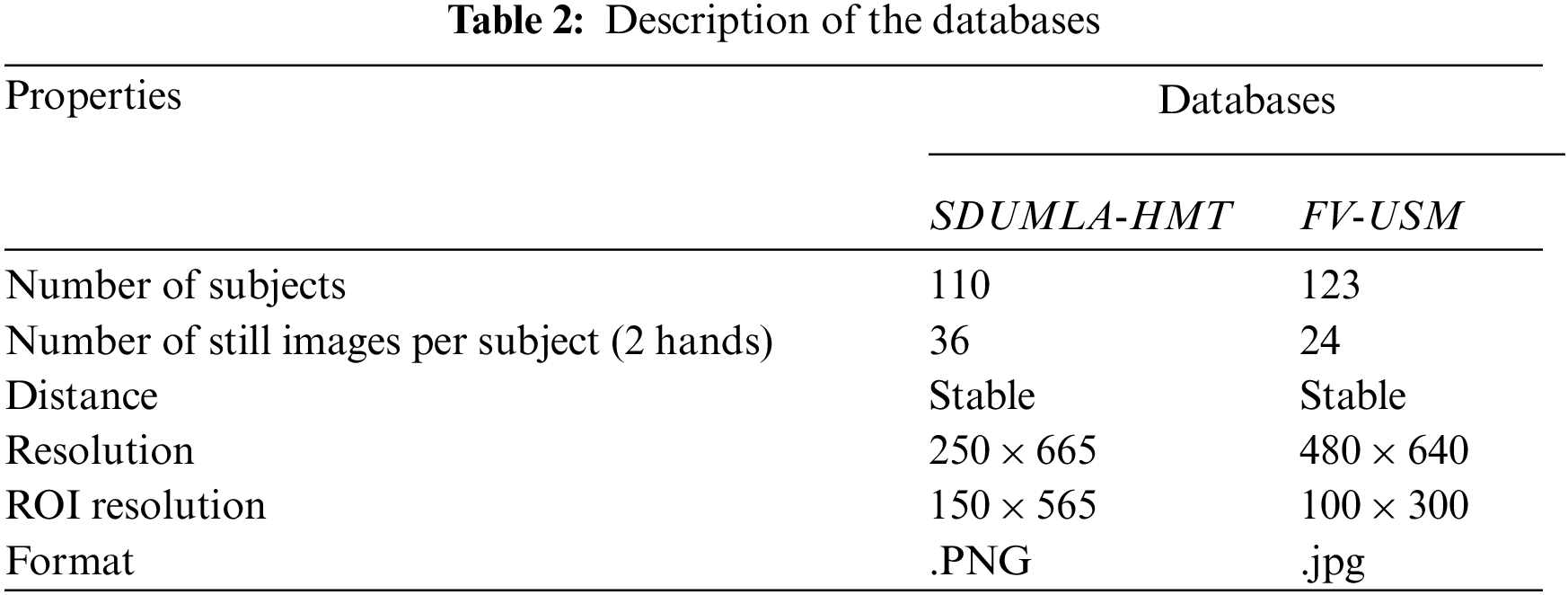
Several important points should be noted in describing the implementation of the proposed method. Sampling the training and test images were randomly sampled in all experiments and 4 of 6 images were selected for training and two images were randomly selected to apply the rotation, translation and noise effects on the image as illustrated in Fig. 5. The dataset used in these tests for both databases was 600 images from 100 individuals (4 images per person for training and 2 images for testing). Then the method was introduced. The comparison method is repeated 10 times with random sampling for test and training set and calculated and recorded for each run of the identification accuracy [39]. The identification accuracy recorded in the results table is the average of 10 times tests’ implementation. The confidence interval range has also been calculated by considering the identification accuracy obtained from 10 repetitions of each trial and the confidence level of 95%. Tabs. 3 to 5 show the results of this study. The first challenge described in this section is the challenge of noise in the image. Noise challenge is one of the most common challenges from the users and the devices. It is expected that the proposed methods in this field will be resilient to this important challenge. Tab. 3 exhibits the results of recommended noise challenge method.

Figure 5: Different image challenges: (a): raw image, (b): translation, (c): rotation, (d): noise
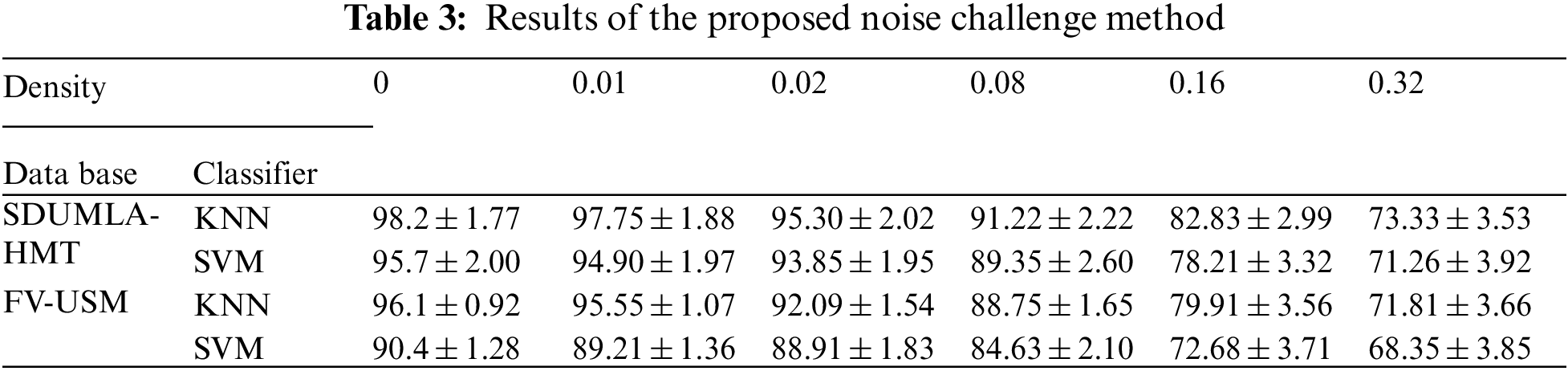
According to Tab. 3, the proposed method has high stability against noise due to Gabor wavelet filters, which are high-pass filters and eliminate a wide range of noises. Therefore, the proposed method based on scattering wavelets against noise will be stable. Fig. 6 shows the results of Tab. 3 on the graph.
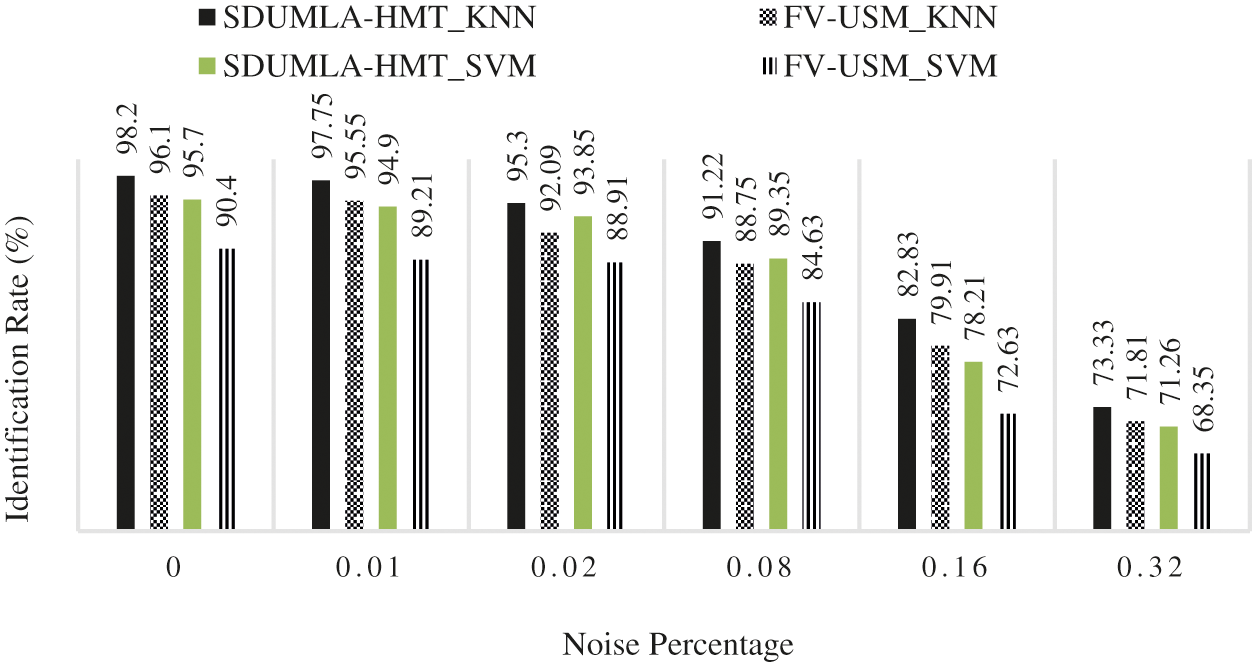
Figure 6: The results of the proposed method with noise challenge
Fig. 6 shows that the KNN classifier has evaluated both databases and results relative to the SVM. It can also be seen that the identification rate did not decrease significantly as the noise density increased. However, the proposed method's failure point against noise is somehow the density of 0.08 because, after this density, the proposed method's identification rate is 90%. The proposed method's rotation challenge will be discussed in the following section and its results shown in Tab. 4.
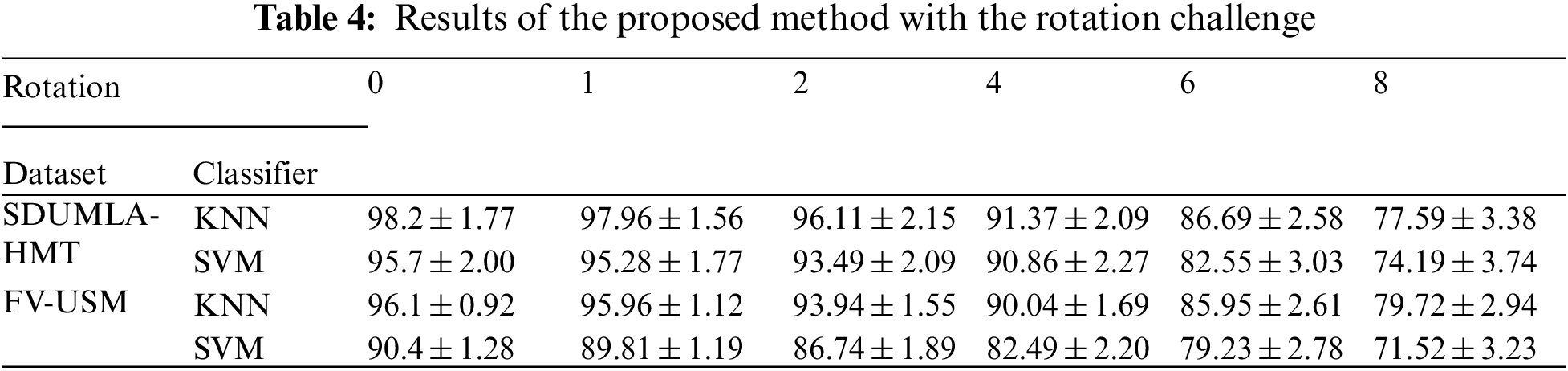
The results shown in Tab. 4 illustrate well the impact of wavelet cascade performance on the rotation challenge. Several filters with different angles and orientations are applied to the image. As a result, it usually understands minor rotations due to user error in placing the hand on the scanner and reducing the system error rate. However, this error is inevitable, and the proposed systems must have the required predictions to respond to this challenge. Fig. 7 shows a comparison of the rotation results in Tab. 4.
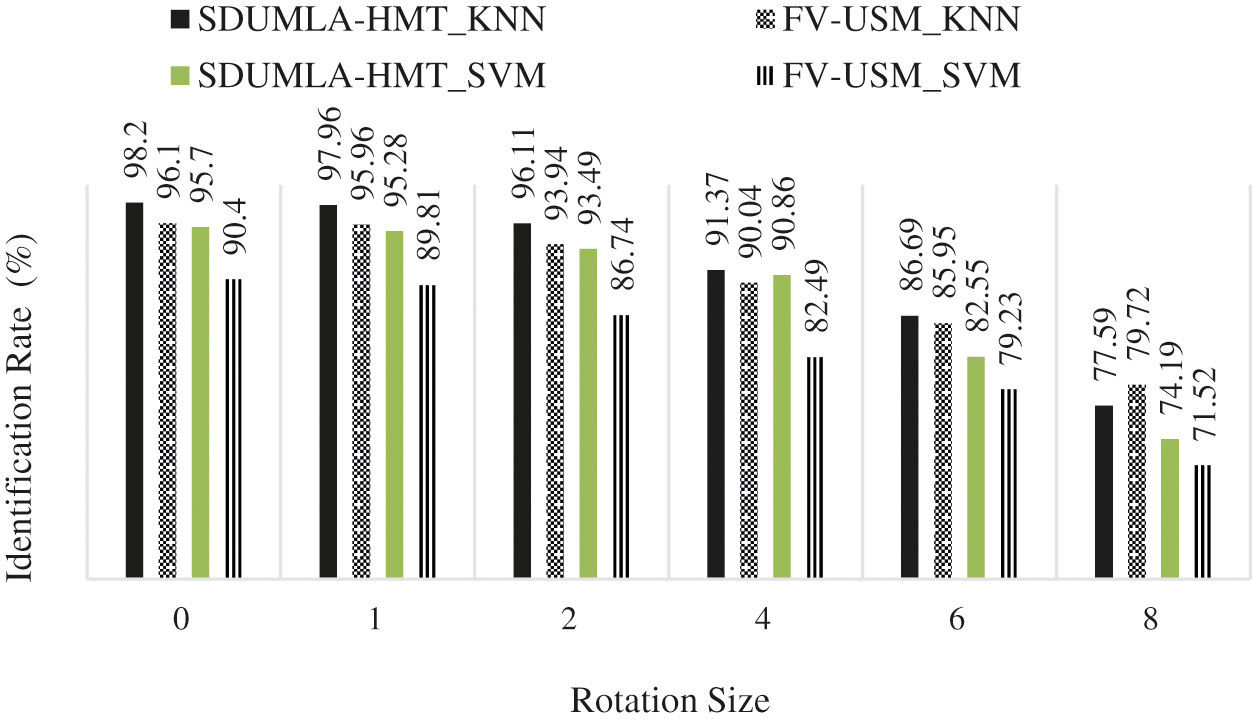
Figure 7: Results of the proposed method with the rotation challenge
Fig. 7 also shows superiority of the K Nearest Neighbors classifier to the SVM. However, what is visible is the stability of the proposed method in partial rotations, which is especially important in business authentication systems. At the end of this article, the impact of the proposed challenge with the translation challenge will be examined, as shown in Tab. 5.
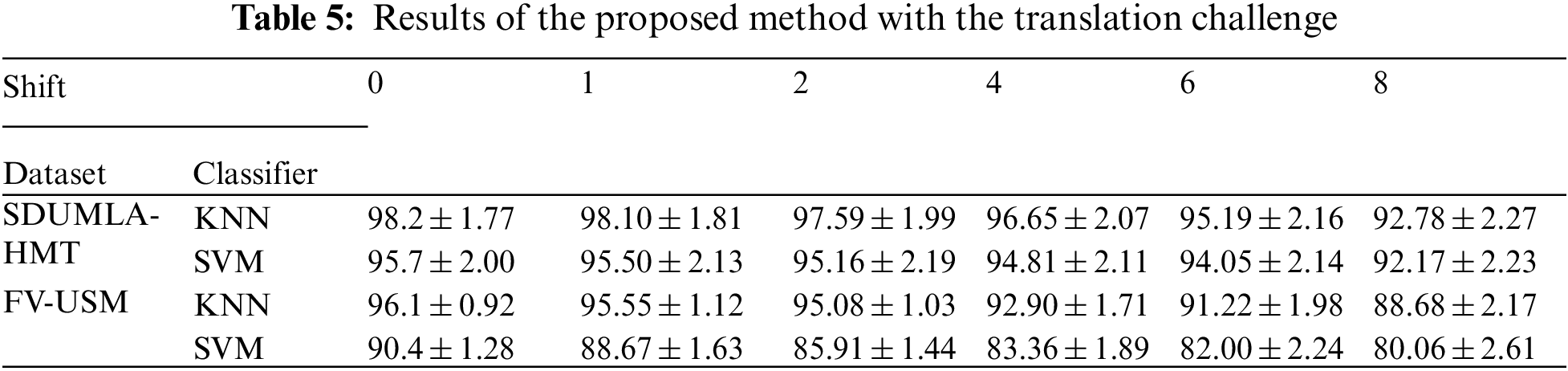
In all types of biometrics, especially biometrics that contain microscopic images, the dimensions of the images and the imaging area are extremely important. By losing part of the image by moving the finger along the x-axis or the y-axis, a portion of the area considered for imaging disappears and reduces the identification rate. Because this error occurs from the user, this error is inevitable and the proposed algorithm must be responsive to this challenge and have the necessary stability to meet this challenge. The proposed scattering wavelet-based method has been stable against this challenge by producing very accurate feature vectors for each class of images. Fig. 8 shows a diagram of the proposed method with this challenge.
Fig. 8 shows the stability of the proposed method in the translation challenge. Thus, the KNN classifier's use in this system greatly maintains the identification rate stable against translation.
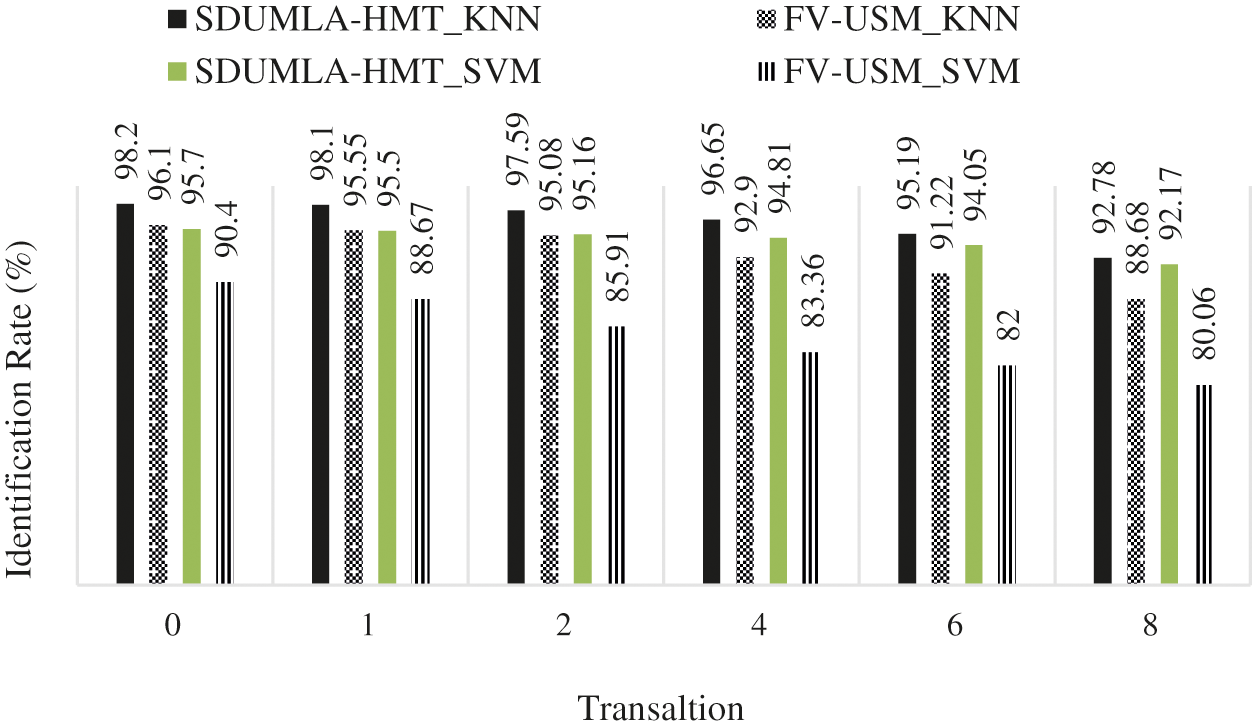
Figure 8: Results of the proposed translation challenge method
Biometric finger veins are a unique biometric in humans for authentication. This biometrics has changed in various conditions, such as changes in veins’ clarity, angles, scales, veins orientation, etc. These changes make the structure of the images unstable and therefore challenging for authentication algorithms. This paper has presented an improved scattering wavelet-based authentication approach with fundamental component analysis. For authentication purpose, proposed method has several stages including preprocessing, normalization, feature extraction using wavelet scattering, dimension reduction using PCA, classification with SVM and KNN. The proposed method has shown a tangible superiority over the compared methods with a very favorable identification rate in noise, translation, rotation, and scaling. Appropriate preprocessors and stable descriptors against changes have caused the authentication results to have significant superiority in different challenges. Finally, 98.2% authentication rate for the SDUMLA-HMT database and a 96.1% authentication rate for the FV-USM database attained.
Acknowledgement: This research is supported by Artificial Intelligence & Data Analytics Lab (AIDA) CCIS Prince Sultan University, Riyadh 11586 Saudi Arabia. The authors also would like to acknowledge the support of Prince Sultan University for paying the Article Processing Charges (APC) of this publication.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no interest in reporting regarding the present study.
1. K. Meethongjan, M. Dzulkifli, A. Rehman, A. Altameem and T. Saba, “An intelligent fused approach for face recognition,” Journal of Intelligent Systems, vol. 22, no. 2, pp. 197–212, 2013. [Google Scholar]
2. K. Neamah, D. Mohamad, T. Saba and A. Rehman, “Discriminative features mining for offline handwritten signature verification,” 3D Research, vol. 5, no. 1, pp. 1–6, 2014. [Google Scholar]
3. M. Harouni, M. Rahim, M. A. Rodhaan, T. Saba, A. Rehman et al., “Online persian/arabic script classification without contextual information,” The Imaging Science Journal, vol. 62, no. 8, pp. 437–448, 2014. [Google Scholar]
4. S. Joudaki, D. Mohamad, T. Saba, A. Rehman, M. A. Rodhaan et al., “Vision-based sign language classification: A directional review,” IETE Technical Review, vol. 31, no. 5, pp. 383–391, 2014. [Google Scholar]
5. F. Ramzan, M. U. G. Khan, A. Rehmat, S. Iqbal, T. Saba et al., “A deep learning approach for automated diagnosis and multi-class classification of Alzheimer's disease stages using resting-state fMRI and residual neural networks,” Journal of Medical Systems, vol. 44, no. 2, pp. 1–16, 2020. [Google Scholar]
6. M. A. Khan, M. Sharif, T. Akram, M. Raza, T. Saba et al., “Hand-crafted and deep convolutional neural network features fusion and selection strategy: An application to intelligent human action recognition,” Applied Soft Computing, vol. 87, no. 105986, pp. 1–14, 2020. [Google Scholar]
7. J. W. J. Lung, M. S. H. Salam, A. Rehman, M. S. M. Rahim and T. Saba, “Fuzzy phoneme classification using multi-speaker vocal tract length normalization,” IETE Technical Review, vol. 31, no. 2, pp. 128–136, 2014. [Google Scholar]
8. A. Jamal, M. H. Alkawaz, A. Rehman and T. Saba, “Retinal imaging analysis based on vessel detection,” Microscopy Research and Technique, vol. 80, no. 7, pp. 799–811, 2017. [Google Scholar]
9. S. Elnasir, S. M. Shamsuddin and I. Farokhi, “Accurate palm vein recognition based on wavelet scattering and spectral regression kernel discriminant analysis,” Journal of Electronic Imaging, vol. 24, no. 1, pp. 013031, 2015. [Google Scholar]
10. R. S. Kuzu, E. Piciucco, E. Maiorana and F. Campisi, “On-the-fly finger-vein-based biometric recognition using deep neural networks,” IEEE Transactions on Information Forensics and Security, vol. 15, pp. 2641–2654, 2020. [Google Scholar]
11. T. Saba, M. Kashif and E. Afzal, “Facial expression recognition using patch-based lbps in an unconstrained environment,” in 1st Int. Conf. on Artificial Intelligence and Data Analytics, Riyadh Saudi Arabia, IEEE, pp. 105–108, 2021. [Google Scholar]
12. M. Adnan, M. S. M., Rahim, A. Rehman, Z. Mehmood, T. Saba et al., “Automatic image annotation based on deep learning models: A systematic review and future challenges,” IEEE Access, vol. 9, pp. 50253–50264, 2021. [Google Scholar]
13. A. M. Ahmad, G. Sulong, A. Rehman and H. M. Alkawaz, “Data hiding based on improved exploiting modification direction method and huffman coding,” Journal of Intelligent Systems, vol. 23, no. 4, pp. 451–459, 2014. [Google Scholar]
14. M. Rashid, M. A. Khan, M. Alhaisoni, S. H. Wang, S. R. Naqvi et al., “A sustainable deep learning framework for object recognition using multi-layers deep features fusion and selection,” Sustainability, vol. 12, no. 12, pp. 5037–5059, 2020. [Google Scholar]
15. M. Elarbi-Boudihir, A. Rehman and T. Saba, “Video motion perception using optimized gabor filter,” International Journal of Physical Sciences, vol. 6, no. 12, pp. 2799–2806, 2011. [Google Scholar]
16. M. S. M. Rahim, A. Rehman, F. Kurniawan and T. Saba, “Ear biometrics for human classification based on region features mining,” Biomedical Research, vol. 28, no. 10, pp. 1–5, 2017. [Google Scholar]
17. A. Naz, M. U. Javed, N. Javaid, T. Saba, M. Alhussein et al., “Short-term electric load and price forecasting using enhanced extreme learning machine optimization in smart grids,” Energies, vol. 12, no. 5, pp. 866, 2019. [Google Scholar]
18. K. Aurangzeb, I. Haider, M. A. Khan, T. Saba, K. Javed et al., “Human behavior analysis based on multi-types features fusion and von nauman entropy based features reduction,” Journal of Medical Imaging and Health Informatics, vol. 9, no. 4, pp. 662–669, 2019. [Google Scholar]
19. N. Abbas, T. Saba, D. Mohamad, A. Rehman, A. S. Almazyad et al., “Machine aided malaria parasitemia detection in giemsa-stained thin blood smears,” Neural Computing and Applications, vol. 29, no. 3, pp. 803–818, 2018. [Google Scholar]
20. A. R. Khan, F. Doosti, M. Karimi, M., Harouni, U. Tariq et al., “Authentication through gender classification from iris images using support vector machine,” Microscopy Research and Technique, vol. 84, no. 11, pp. 2666–2676, 2021. [Google Scholar]
21. A. R. Khan, S. Khan, M. Harouni, R. Abbasi, S. Iqbal et al., “Brain tumor segmentation using K-means clustering and deep learning with synthetic data augmentation for classification,” Microscopy Research and Technique, vol. 84, no. 7, pp. 1389–1399, 2021. [Google Scholar]
22. S. Soleimanizadeh, D. Mohamad, T. Saba and A. Rehman, “Recognition of partially occluded objects based on the three different color spaces (RGB, YCbCr, HSV),” 3D Research, vol. 6, no. 3, pp. 1–10, 2015. [Google Scholar]
23. J. M. Song, W. Kim and K. R. J. I. A. Park, “Finger-vein recognition based on deep DenseNet using composite image,” IEEE Access, vol. 7, pp. 66845–66863, 2019. [Google Scholar]
24. J. D. Wu and C. T. Liu, “Finger-vein pattern identification using principal component analysis and the neural network technique,” Expert Systems with Applications, vol. 38, no. 5, pp. 5423–5427, 2011. [Google Scholar]
25. K. Q. Wang, A. S. Khisa, X. Q. Wu and Q. S. Zhao, “Finger vein recognition using LBP variance with global matching,” in IEEE Int. Conf. on Wavelet Analysis and Pattern Recognition, Adelaide, Australia, pp. 196–201, 2012. [Google Scholar]
26. M. Vlachos and E. Dermatas, “Finger vein segmentation from infrared images based on a modified separable mumford shah model and local entropy thresholding,” Computational and Mathematical Methods in Medicine, vol. 2015, no. 868493, pp. 1–21, 2015. [Google Scholar]
27. Y. Liu, J. Ling, Z. Liu, J. Shen and C. Gao, “Finger vein secure biometric template generation based on deep learning,” Soft Computing, vol. 22, no. 7, pp. 2257–2265, 2018. [Google Scholar]
28. S. P. Shrikhande and H. Fadewar, “Finger vein recognition using rotated wavelet filters,” International Journal of Computer Applications, vol. 149, no. 7, pp. 28–33, 2016. [Google Scholar]
29. S. Bharathi and R. Sudhakar, “Biometric recognition using finger and palm vein images,” Soft Computing, vol. 23, no. 6, pp. 1–13, 2019. [Google Scholar]
30. T. Saba, A. Rehman, Z. Mehmood, H. Kolivand and M. Sharif, “Image enhancement and segmentation techniques for detection of knee joint diseases: A survey,” Current Medical Imaging, vol. 14, no. 5, pp. 704–715, 2018. [Google Scholar]
31. C. H. Hsia, J. M. Guo and C. S. Wu, “Finger-vein recognition based on parametric-oriented corrections,” Multimedia Tools and Applications, vol. 76, no. 23, pp. 25179–25196, 2017. [Google Scholar]
32. Y. Fang, Q. Wu and W. J. N. Kang, “A novel finger vein verification system based on two-stream convolutional network learning,” Neurocomputing, vol. 290, pp. 100–107, 2018. [Google Scholar]
33. S. A. Radzi, M. K. Hani and R. Bakhteri, “Finger-vein biometric identification using convolutional neural network,” Turkish Journal of Electrical Engineering & Computer Sciences, vol. 24, no. 3, pp. 1863–1878, 2016. [Google Scholar]
34. G. Meng, P. Fang and B. Zhang, “Finger vein recognition based on convolutional neural network,” MATEC Web of Conferences, vol. 128, pp. 4015–4020, 2017. [Google Scholar]
35. R. Das, E. Piciucco, E. Maiorana and P. Campisi, “Convolutional neural network for finger-vein-based biometric identification,” IEEE Transactions on Information Forensics and Security, vol. 14, no. 2, pp. 360–373, 2019. [Google Scholar]
36. S. Soatto, Actionable Information in Vision. In: Cipolla R., Battiato S., Farinella G. (eds) Machine Learning for Computer Vision. Studies in Computational Intelligence, vol. 411. Springer, Berlin, Heidelberg. 2013. https://doi.org/10.1007/978-3-642-28661-2_2. [Google Scholar]
37. Y. Yin, L. Liu and X. Sun, “SDUMLA-HMT: A multimodal biometric database,” in Chinese Conf. on Biometric Recognition, Beijing, China, pp. 260–268, 2011. [Google Scholar]
38. M. S. M. Asaari, S. A. Suandi and B. A. Rosdi, “Fusion of band limited phase only correlation and width centroid contour distance for finger based biometrics,” Expert Systems with Applications, vol. 41, no. 7, pp. 3367–3382, 2014. [Google Scholar]
39. M. Harouni and H. Y. Baghmaleki, “Color image segmentation metrics,” %J arXiv preprint arXiv:.09907, 2020. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |