Computers, Materials & Continua DOI:10.32604/cmc.2022.026074
Article

Game Theory-Based IoT Efficient Power Control in Cognitive UAV

Fadhil Mukhlif1,*, Norafida Ithnin1, Omar B. Abdulghafoor2, Faiz Alotaibi3 and Nourah Saad Alotaibi4

1Information Assurance and Security Research Group (IASRG), School of Computing, Faculty of Engineering, Universiti Teknologi Malaysia, Johor, Malaysia
2Electronic and Telecommunication Department, College of Engineering, The American University of Kurdistan, Iraq
3Faculty of Computer Science and Information Technology, Universiti Putra Malaysia, Selangor, Malaysia
4Computer Department, Faculty of Applied College, Imam Abdulrahman Bin Faisal University, Dammam, Saudi Arabia
*Corresponding Author: Fadhil Mukhlif. Email: mafadhil@utm.my
Received: 14 December 2021; Accepted: 14 January 2022

Abstract: With the help of network densification, network coverage as well as the throughput can be improved via ultra-dense networks (UDNs). In tandem, Unmanned Aerial Vehicle (UAV) communications have recently garnered much attention because of their high agility as well as widespread applications. In this paper, a cognitive UAV is proposed for wireless nodes power pertaining to the IoT ground terminal. Further, the UAV is included in the IoT system as the source of power for the wireless nodes as well as for resource allocation. The quality of service (QoS) related to the cognitive node was considered as a utility function based on pricing scheme that was modelled as a non-cooperative game theory in order to maximise users’ net utility function. Moreover, an energy efficiency non-cooperative game theory power allocation with pricing scheme (EE-NGPAP) is proposed to obtain an efficient power control within IoT wireless nodes. Further, uniqueness and existence of the Nash equilibrium have been demonstrated mathematically and through simulation. Simulation results show that the proposed energy harvest algorithm demonstrated considerable decrease in transmitted power consumption in terms of average power reduction, which is regarded to be apt with the 5G networks’ vision. Finally, the proposed algorithm requires around 4 iterations only to converge to NE which makes the algorithm more suitable in practical heterogeneous scenarios.

Keywords: UAV; drones; WSN; IoT; game theory; energy efficiency; 5G & B5G networks

1  Introduction

Rapid advancement in mobile internet has also brought in serious challenges pertaining to the design of mobile wireless networks, particularly when offering ultra-high data rate as well as very low time delay. As per a recent International Telecommunication Union (ITU) report, there will be an increase by 10000 times in wireless data traffic by next few years compared to 2010 [1]. The ultra-dense network (UDN) technique is regarded suitable to meet the needs pertaining to explosive data traffic [2]. With the help of flexible deployment as well as deployment of massive, small cell base stations (SBSs) with low transmit power, the network coverage can be broadened effectively as well as the overall throughput can be improved [3]. Majority of the current studies on UDNs concentrate on performance enhancement of terrestrial heterogeneous cellular networks by managing different parameters such as the coexistence of resource allocation, energy efficient frequency reuse in heterogeneous small cell networks, Wi-Fi and heterogeneous ultra-dense scenarios user association, amongst others [4,5].

Furthermore, UAV communications as well as networking have gained much popularity recently because of their high agility as well as their use in many applications. When UAVs are introduced into UDNs, significant gains can be achieved by completely exploiting their potential [6]. Rapid deployment of UAVs to serve wireless users can be achieved without being impacted by geographical constraints compared to the traditional terrestrial infrastructure. It could also be used as flying base stations (BSs) to improve wireless coverage as well as enhance throughput at hotspots like sport stadium and campuses or in areas that do not have cellular infrastructure [7]. They could also behave as flying relays in regions where the separated users do not possess reliable direct communication links. Thus, UAVs can be incorporated to achieve efficient relocation with regards to user's mobility. Almost line of sight (LOS) communication links can be established in most situations by adjusting the locations of UAVs dynamically. Thus, this allows considerable improvement in the performance of the system. Therefore, UAVs could also carry an energy source or at times act as an energy source for charging wireless nodes to extend the network lifetime. Some of the usual applications are internet of things (IoT) and wireless sensor networks, wherein wired charging is not available [8].

In tandem, The Internet of Things (IoT) plays a leading role in wireless networks as well as in the next generation of mobile communications, and now works in a variety of everyday life services [9]. With recent advances in IoT implementation, transmit data has become more intense and the volume of information interchange has increased significantly [10]. Hence, it is necessary to equip communication technologies with higher bandwidth, higher speeds, less arrival times and less energy consumption to ensure successful implementation of the internet [11]. However, applications and developments of IoT technologies need to also handle unprecedented as well as severe challenges due wireless devices’ energy limitation. An urgent issue is how to implement sustainable energy to smart devices connected in IoT, which is the main hindrance in IoT development. Thus, wireless power transfer (WPT) technology is considered for sustainable energy supply to be an appropriate solution to provide sustainable energy and can efficiently resolve the bottleneck associated with the limited energy issue in IoT [12]. More wireless devices in the nearest future will be used WPT technology to reduce immoderate dependency on batteries. Further, wireless power transfer is widely used in smart wireless, implanted medical, smart homes devices and electric vehicle etc. UAV allows dynamic movement of the IoT devices, data gathering, transmitting services and also powering IoT devices in comparison to conventional wireless networks [13,14]. The UAV assisted WPT are not only improving the performance of IoT-UDNs by dynamically adjusting the power source, but high UAV navigation in the proposed scenario can also provide comprehensive power for wireless devices in large distribution areas faster and more flexible [15,16].

1.1 Contribution

In this research work, the UAV assisted IoT wireless powered that has been studied and the resource allocation of IoT system has been solved. With regards to the non-cooperative game theory, the issue of resource allocation between UAV nodes and wireless IoT is investigated. In this proposed system, the IoT nodes harvest energy from hovering drones. Drones act as a floating power source to supply wireless nodes using wireless power transmission. Game theory based on the proposed model for the problem of resource allocation between drones and wireless nodes is presented and Nash equilibrium is obtained for the proposed model based on the game theory approach. By accounting for the Nash Equilibrium, optimal allocation is made by UAV based on its energy sources to facilitate the transmission of wireless power. Key contributions of this research are summarised below:

•   IoT wireless power is provided with the help of UAVs including one UAV and wireless node density. Drones attempt to harvest wireless nodes based on wireless power transmission technology. The harvested energy is employed by wireless nodes to transmit information.

•   The resource allocation issue existing between wireless nodes and UAV could be formulated in terms of a non-cooperative power control game. In the proposed game, the drone controls its source perfectly for energy transfer and the wireless node controls its source perfectly for transmitting information.

•   For the coexisting ultra IoT ground sensors, assessment of the issue pertaining to non-cooperative power control game theoretic is done.

•   Obtaining of the Nash Equilibrium with regards to the non-cooperative power control game is done. Also, the existence, as well as uniqueness pertaining to the put forward game to its Nash, has been established.

•   An iterative power control algorithm is developed those fits well with the UAV scenario as well as its trajectories.

•   The simulation results support the superiority pertaining to the put forward algorithm strategy.

1.2 Organisation

The remaining paper is organised as follows: Section 2 discusses the general system model and Game Formulation. Section 3 presents a mathematically ratified mechanism for the suggested equations as a game theory approach. The recommended algorithm is elucidated in Section 4. Section 5 discusses the simulation outcomes and the throughput performance through which green transmission algorithm insights are attained. Section 6 investigates the limitations and challenges of this study and the possibility for further enhancement. Finally, Section 7 concludes the paper and summarizes the key findings.

2  System Model and Game Theoretic Formulation

UAVs offer unparalleled benefits because of their inherent mobility compared to the conventional terrestrial infrastructures which are in fixed location. With UAV support it will bring major changes and development to UDNs. Fig. 1 demonstrates the support provided by UAV in energy transfer when it functions as mobile energy sources. Moreover, to charge wireless nodes for extended lifetime of the network, UAVs could carry an energy source or at times become that source of energy. Some of the common applications are wireless IoT and sensor networks, when wired charging is not available.

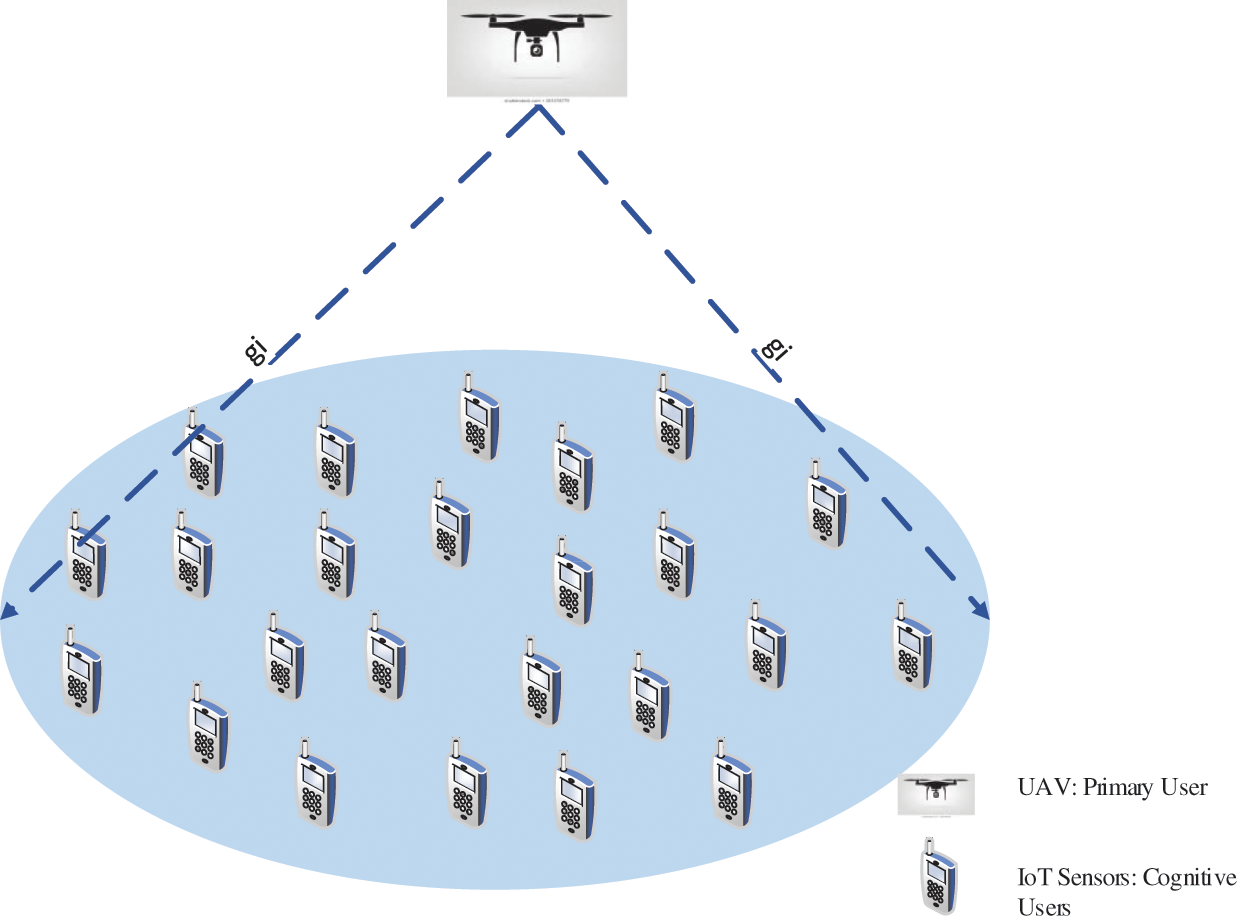
Figure 1: System model of UAV supported IoT energy transfer

Moreover, UDNs usually include massive spatially distributed wireless nodes, like device-to-device (D2D) communications, machine-to-machine (M2M) communications as well as sensor nodes. For these networks, the challenge is to minimise energy consuming as well as extending the network lifetime, as currently batteries remain the primary source of energy. If batteries for massive nodes requires constant recharging or replaced regularly, it can be costly as well as inconvenient [8]. It is envisioned that the UAV can hover around the wireless nodes to transfer power wirelessly to the nodes as well as to transmit information. we aimed to determine the optimal way to allocate resources for wireless power transmission and information transfer to the Internet of Things (IoT) that offers the system. In our advanced systems, IoT nodes sending information to UAV and its need energy form it. UAV or drone act as a moving source for charging wireless nodes. Drones can also collect all information from wireless nodes. In this study, wireless nodes were distributed at locations located in the IoT environment and assumed to be charged by UAVs.

We consider the general characteristics of UAV based wireless communication, the general communication model consists of UAV-drones and ground IoT nodes. For three-dimension (3D) location, within the completion time T and trajectory design UAVs location is denoted as q(t)=[x(t),y(t),H(t)]T∈R3 at time t. It is presumed that the final and initial time pertaining to UAVs location conforms to t(0)=0,t(N)=T. By introducing the elemental time slot length δt, the horizon time T is divided into M time slots, this means T=Mδt. The selection of elemental time slot length is done to ensure that the location of UAVs and ground nodes could be assumed as constants within each slot. Or else, UAV's 3D location in time slot m could be expressed as:

q[m]=[x(m),y(m),H(m)]T,m=1,2,…,M(1)

For trajectory design, we consider three fundamentals of the trajectory of UAV including trajectory location {q[m]}m=1M, speed {v[m]}m=1M and acceleration {acc[m]}m=1M. For the fixed altitude of UAV at H the trajectory location of UAV in the mth time slot can simply as the horizontal location q[m]=[x[m],y[m]]T, m=1,…,M where M is the final time slot at the end of trajectory.

The trajectory of UAV in a typical time slot is defined as:

q[m+1]=q[m]+v[m]δt+0.5acc[m]δt2,m=0,1,2,…,M(2)

v[m+1]=v[m]+acc[m]δt,m=0,1,2,…,M(3)

For a constant of velocity (acc[m]=0) and allowable maximum velocity of the UAV (Vmax), the trajectory constraints of the UAV are as:

‖q[m+1]−q[m]‖≤Vmaxδt,m=0,1,2,…,M(4)

Here, q[0]=[x[0],y[0]]T represents the UAV's initial horizontal location.

In channel model, a difference exists in air to ground (ATG) channel and the ground channel because of line of sight (LoS) higher chance propagation through 3D location [17]. In such conditions, the impact cast by the environment on LoS occurrence becomes even more important. However, the effects of propagation blockage [18] like building blockage still exist for the complete channel models. Due to this, for ATG channels, large scale Rayleigh, as well as free space fading models, is optimum.

With regards to an arbitrary elemental timeslot, the distance between the ith ground nodes and the UAV located at (x,y,H) can be represented as:

Ri=di2+H2(5)

Here, di=(x−xi)2+(y−yi)2 denotes the horizontal distance existing between the ith ground nodes and the UAV and xi,yi signifies the location pertaining to the ith ground nodes. The simple distance pathloss that exists between the ith ground nodes and the UAV could be signified as [19]:

L(Ri)=10log(4πfcRic)α(6)

where α>2 is the path loss exponent, c is the speed of light (m/s), fc is carrier frequency (Hz). On the other hand, the probability of LoS is given by [20]:

PLoS=11+aexp(−b(arctan⁡(Hdi)−a))(7)

where a,b are constants. Thus, one has PNLoS=1−PLoS.

Then the total path loss expression from UAV to ith ground nodes is as:

PL(Ri)=L(Ri)+ηLoSPLoS+ηNLoSPNLoS(8)

where ηLoS and ηNLoS are average additional losses for LoS and NLoS respectively.

Assuming Los dominated in free space path loss model [21]. For time slot t, the channel gain in the free space model is defined as:

gi(t)=β0ρ2Ri−α(t)(9)

where gi is the channel power gain from UAV to ground IoT, Ri(t)=(x−xi)2+(y−yi)2+H2 is the distance between UAV and ground IoT nodes, ρ Reduction Factor, α is the Pathloss exponent, β0 is the Channel power gain at the reference distance [22].

By using the required energy from the drones, the information is passed by the wireless node to the drone. When a wireless contract derives its energy from drones, they can use the acquired energy to transfer information and generate revenue from the information transfer process. Because IoT nodes are in the same class that carry information in the same channel, there is overlap between IoT nodes in protected areas. At this point, the SIR can be employed to signify the revenue based on the information transmission, which can also be presented as power level pertaining to information transmission:

γi(pi)=pi(t)gi(t)∑j≠iN⁡pj(t)gj(t)+σi2(t)≥Γi,i=1,2,,3,…,n(10)

Here, Γi denotes the threshold SIR and σi2 signifies the Gaussian noise power. Representation of the sum of interference by considering the noise as the denominator of Eq. (10) could be done as Ii(p−i), and thus Eq. (1) could be presented in the form of a function of user transmission power as well as the transmission power pertaining to other users:

γi(pi,p−i)=pi(t)gi(t)Ii(p−i)=pi(t)gi(t)∑j≠iN⁡pj(t)gj(t)+σi2(t)(11)

The subscript −i represents the interference that is dependent on the power transmitted by all users excepting the ith node.

The total interference power generated by the Cognitive IoTs must be below a given limit which is known as interference temperature limit and it is expressed as below:

∑i=1N⁡pig0i≤ITL(12)

Mathematically, the expression of non-cooperative game theoretic power allocation strategy pertaining to spectrum sharing could be done as an issue with regards to decreasing the power consumption for each node subject to predefine the requirements for SIR to identify the target as well as to establish a maximum interference tolerant limit pertaining to the communication system. If IoT nodes pertaining to the system behave as greedy and selfish in order to increase their own utilities, exploiting of the non-cooperative game theory is done in order to effectively model the interactions between various nodes in terms of a Nash game. Thus, analytically, the existence of the Nash equilibrium as well as its uniqueness is verified successfully. Ultimately, we have put forward an iterative power allocation algorithm that possesses low computational complexity and it has been established that quick convergence plays the game amongst various nodes. However, the key aim of this work pertains to decreasing the power consumption applicable to each node along with the optimisation of transmission power allocation, which has been seen to be limited by a predefined SIR requirement pertaining to target identification as well as a maximum interference tolerant limit associated with the communication system. Thus, the game theory is regarded as an appropriate mathematical tool that also accounts for player's rational as well as self-interested behaviour. In particular, the IoT nodes that behave like players compete amongst each other and then select a strategy space pertaining to transmission power to achieve a payoff, which can also be presented by their utility functions.

In the non-cooperative power allocation game, the features pertaining to the players’ interaction can be strategically presented as:

Φ=[N,{Pi},{Ui(.)}](13)

Here, N={1,2,…,N}   denotes the player's index set of IoT nodes, wherein the key aim of each player would be to increase its utility by selecting a suitable action to transmit power. Pi=[0,Pimax] represents the users’ transmission power strategy pertaining to set i, while Pimax denotes the maximum transmission power i of the users. The utility function pertaining to user i can be defined as Ui(.), where each user associated with the network tries to maximise in a selfish manner its utility. When applying the non-cooperative game theory, it is crucial to choose an ideal utility function. Mathematically, the utility function representing the user i can be expressed as the received number pertaining to information bits in the form of per joule of the consumed energy [23]:

Ui(pi,p−i)=LRf(γi)Mpi(14)

Here, in cognitive networks, information is sent by transmitters to receivers as well as wireless data as frames or packets pertaining to length M bits. This involves L<M information bits as a data rate along with R bits/s, in which f(γ) denotes the efficiency function with regards to the transmission. The efficiency function f(γ) has been seen to depend on the achieved SIR in the channel, wherein the value lies in the range from 0 to 1 (i.e., f(γ)∈[0,1]). Furthermore, power pi represents the power that has been transmitted by the user i.

Moreover, a novel utility function has been put forward by accounting for power function besides a new sigmoid efficiency function with regards to pricing function for the user's transmit power. Furthermore, we introduce a sigmoid efficiency function in the form of a fraction by considering an exponential ratio power multiplied by tuning factor (z) along with the entire power to target SIR as expressed below:

f(γi)=1(1+exp(1−zsiri))≀i(15)

where z is the tuning factor where its change will change the response of the efficiency function proposed as shown in Fig. 2, since proposed sigmoidal function part of utility function, changing of tuning factor (z) will also affect on the proposed utility function as shown in Fig. 3. With regards to Eq. (14), the utility function pertaining to the ith cognitive nodes can be expressed as:

Ui=LRMpi1(1+exp(1−zsiri))≀ibitjoule(16)

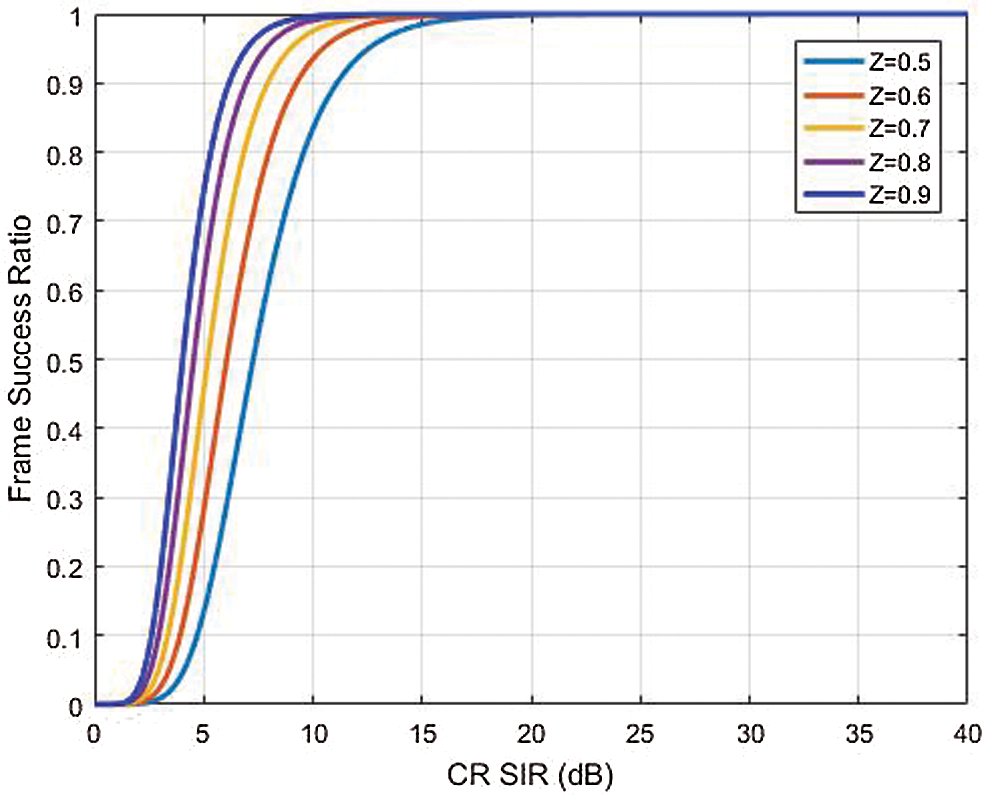
Figure 2: Proposed efficiency function different z

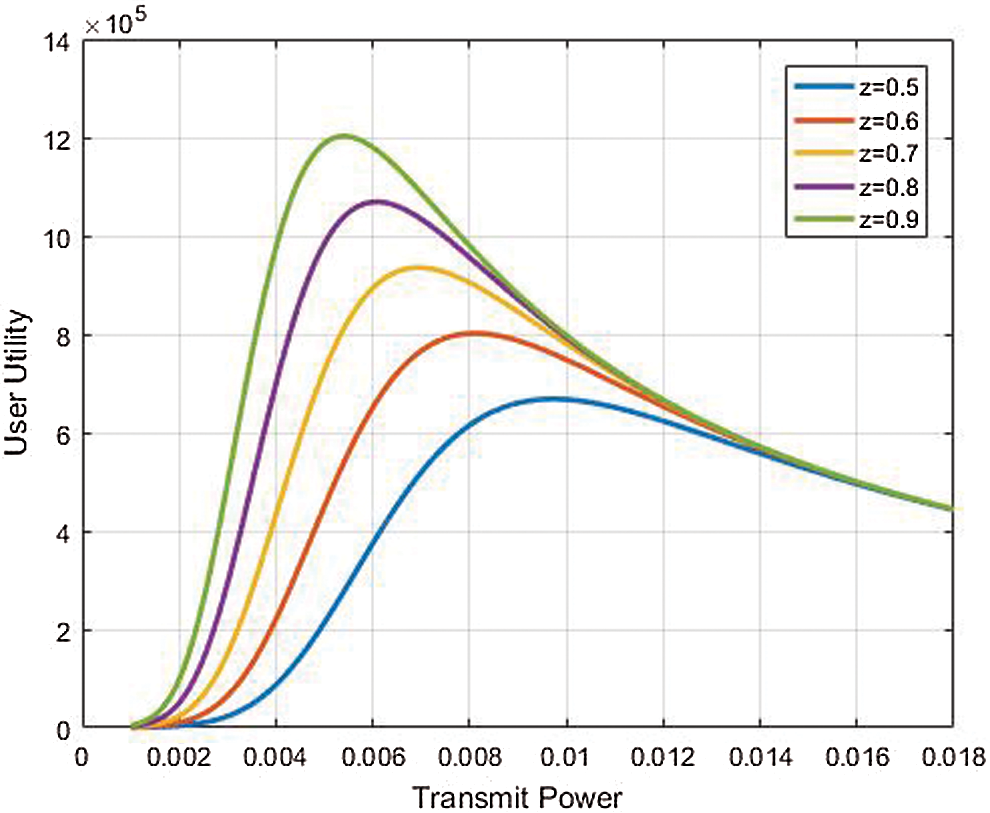
Figure 3: Utility function for different values of z factor

The Nash Equilibrium because of non-cooperative power control is not deemed to be efficient as it fails to account for the cost that it enforces on other nodes via the generated interference. Therefore, the pricing idea was introduced to motivate users to efficiently use resources associated with the network. A general representation pertaining to pricing-based non-cooperative power control game can be expressed as follows:

Φc=[N,{Pi},{Uic(.)}c](17)

Here, Uic(.) denotes the utility function employing pricing and is expressed as:

Uic(pi,p−i)=Ui(pi,p−1)−Ci(pi,p−1)(18)

Hence, the suggested pricing function is stated as:

Ci(pi,p−i)=cpiexp(piα)(19)

We present a new structure for pricing to improve the system's efficiency of the system by promoting CRs to utilise the system's resources effectively. This design contributes by applying a higher cost for users who are farthest from the base station and use more power. Thus, we present an exponential power function of the transmission power rather than the conventional linear pricing. Fig. 4 displays an instance of the disparity among the power pricing and the linear pricing methods. We supposed that the power transmitted by different users ranges from minimum to maximum limit for power strategy [0, 1], and a numeric calculation is made for the price functions. The pricing obtained by using the power function is lesser than that of the linear pricing CRs function using low transmission power and who are closer to the network while it is higher for the farthest CRs which use high power.

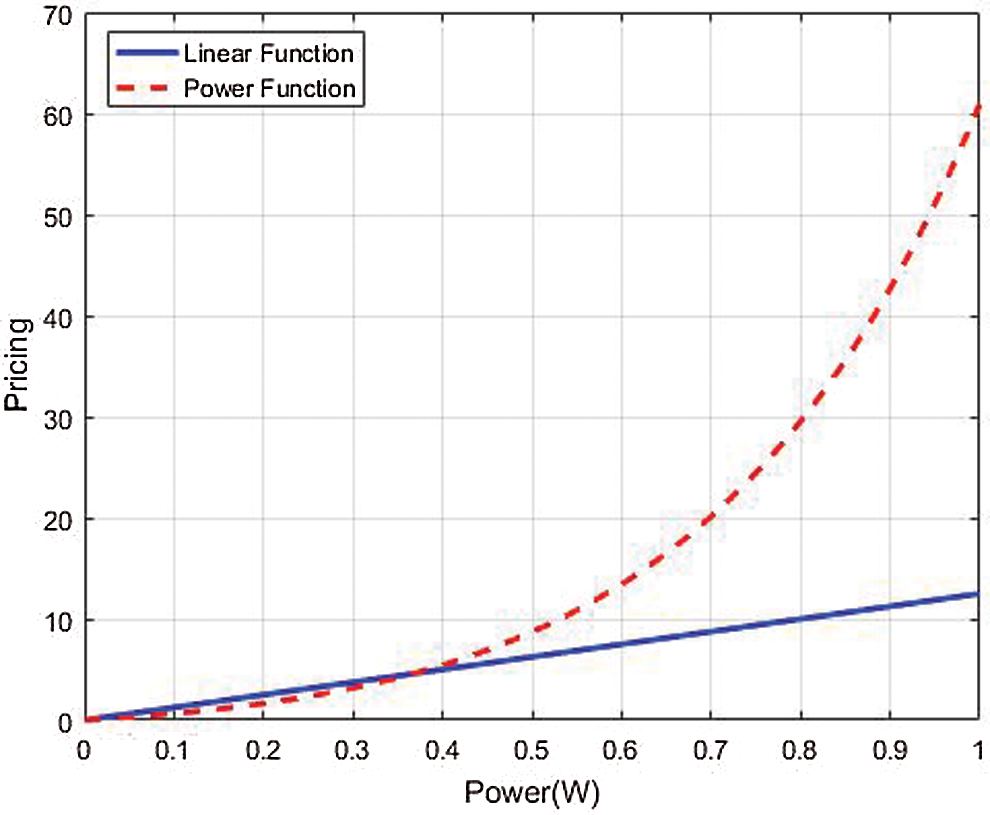
Figure 4: Comparison of pricing for linear and power function

Furthermore, in this article pricing technique has been adopted and the utility function can be written as:

UiC(pi,p−i)=LRMpi1(1+exp(1−zsiri))≀i−cpiexp(piα)(20)

where c and α represent the pricing factor. Thus, in the game of the recommended green non-cooperative power control with pricing is written as:

EE−NGPAP:maxpi∈Pi⁡UiC(pi,p−i)=LRMpi1(1+exp⁡(1−zsiri))≀i−cpiexp⁡(piα)(21)

3  Nash Equilibrium Existence and Uniqueness

With regards to non-cooperative power control game, the ith Cognitive Sensor (CS) boosts its utility by selecting an appropriate strategy based on the strategy set Pi=[0,Pimax].

In non-cooperative power control game, there exists a Nash Equilibrium when all i=1,2,…,n comply with the two conditions given below [24,25]:

1- The action set Pi can be defined as non-empty, compact and convex subset pertaining to certain Euclidean RN.

2- The utility function UiC(pi,p−i) can be defined as continuous pertaining to p and (∂2UiC/∂pi∂pj)≥0∀j≠i∈N.

For each Cognitive IoT sensor in our game, the transmit power space strategy can be described with the help of maximum and minimum powers and the value pertaining to the powers lie between such values. Thus, the first condition pertaining to action set Pi can be satisfied.

To demonstrate quasi-concave characteristics of the cognitive IoT sensor utility function in pi, obtaining of the second derivative with regards to UiC(pi,p−i) could be done with pi:

∂UiC∂pi=LRMpi2(γi∂f(γi)∂γi−f(γi))−ceαp−cpαeαp(22)

∂2UiC∂pi∂pj=LRMpi2(∂γi∂pj∂f(γi)∂γi+γi∂γi∂pj∂2f(γi)∂γi2−∂γi∂pj∂f(γi)∂γi)=LRMpi2(γi∂γi∂pj∂2f(γi)∂γi2)(23)

Since the first order derivative pertaining to γi with regards to pj could be stated as:

(∂  γi/∂pj)=−(hihjpi/∑j≠i⁡hjpj+σ2)<0, so we need the second order derivative of our efficiency function with respect to γi be ∂2f(γi)/∂γi2≤0.

∂f(γi)∂γi=∂(1(1+e(1−zγi))≀i)∂γi=z≀ie−zγi(1+e1−zγi)≀i(1+e1−zγi)(24)

∂2f(γi)∂γi2=гi2 z2 (1+e1−zγi)2(1+e1−zγi)гi (1+e1−zγi)2−гi z2 e1−zγi(1+e1−zγi)гi  (1+e1−zγi)     +гi z2 (1+e1−zγi)2(1+e1−zγi)гi (1+e1−zγi)2(25)

Is simplified to:

∂2f(γi)∂γi2=−≀iz2e1−zγi(1+e1−zγi)≀i(1+e1−zγi)(1−e1−zγi(≀i−1)(1+e1−zγi)2)(26)

Due to:

e1−zγi(≀i−1)(1+e1−zγi)2<1(27)

As per Eq. (27), the second condition can be satisfied by cautiously choosing the pricing factors. Thus, the put forward power control game was seen to possess a unique Nash Equilibrium solution.

4  Proposed EE-NGPAP Algorithm

In this article, development of a distributed iterative power allocation algorithm is done to measure the Nash Equilibrium point pertaining to the put forward model beginning from any initial feasible point. Execution of the proposed algorithm strategy is done by considering each cognitive node at every time step in a distributed way in order to determine the Nash Equilibrium point pertaining to the put forward model, i.e., optimal transmission power achieved SIR value is determined by each node. Because of this, EE-NGPAP is deemed to be apt for this model in which each IoT node needs just the transmit strategies pertaining to all the other nodes with no information on the system. Therefore, the iteration power allocation along with pricing algorithm can be defined as a completely distributed process whose pseudo-code may be summarised by considering the existence of unique Nash Equilibrium with the put forward model.

However, we suppose that each cognitive node updates it's transmit power at time instances ti={ti1,ti2,…}, where tik<ti(k+1), and we assume the strategy set of power of the ith IoT node is Pi=[Pimin,Pimax]. We set an infinity small quantity ε where (ε>0) and by considering the proposed algorithm as given Eq. (21) generates sequence of powers as follows:

Where ri(tk) is used as the representative of the collection of the best transmit powers that correspond to the ith IoT nodes. This can be obtained when the objective function is applied with EE-NGPAP algorithm during time instant k. Moreover, the proposed algorithm is based on power allocation using pricing function. Hence, the computational complexity directly depends on the number of users and the available channels which resulted in O(log(N)).

5  Simulation Results & Discussion

In this segment, the proposed game is simulated to achieve the best harvesting for energy as well as efficient resource allocation pertaining to the IoT nodes on the ground based on UAV as an energy source. To develop the simulation environment, MATLAB software has been employed. Moreover, a series of experiments is conducted to assess the put forward algorithm's performance pertaining to an energy harvesting in 1,000×1,000m2 area, in which random distribution of the 20×20 IoT nodes is done, while the maximum distance between UAV and nodes were 50 and 100 m. Such low power nodes could be regarded as sensor nodes containing much important information for the transmission. However, these nodes are regarded to lack any fixed energy source. Unless specified, the associated system parameters have been set as presented in Tab. 1.

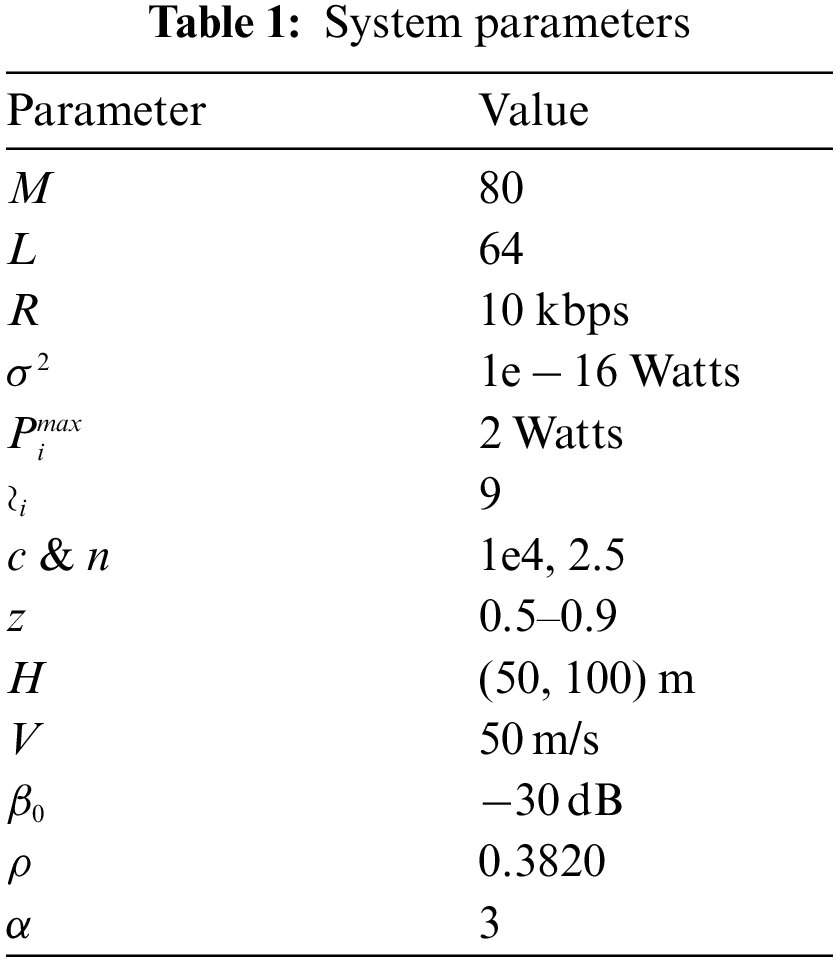
In this scenario, the trajectory employed can be regarded as spiral trajectory along with distributed IoT sensor nodes demonstrating system model as presented in Fig. 5, wherein the default nodes are coloured as blue. However, drones need to transfer power to wireless nodes based on contract requirements and maximize profits during power transfers. As the game continuous, drones need to increase their power level to transmit wireless power to meet the requirements of wireless contracts and increase their profitability. Moreover, implementation of energy harvesting technology is done under spiral trajectory along with put forward power control game to satisfy energy requirements pertaining to the nodes.

Figure 5: UAV scenario based dense IoT sensors

Without loss of generality, the maximum flight speed is assumed to be fixed with 50m/s. Considering in our algorithm two types of results shown in Fig. 8 with 50 m height and Fig. 9 with 100 m height, results with applying the effect of game theory which is in sub-figures of (b, d and f) within Figs. 8 and 9 and results without game theory effects which is in sub-figures of (a, c and e) within Figs. 8 and 9 for both cases in order to compare between results and showing the positive effect of applying multi-decision mathematical approach which is familiar used in many scientific areas. Also, we are performing multi average flying time with fixed hovering speed, these average flying times are in seconds for 350s for Fig. of (a & b), 450s for Fig. of (c & d) and 550 for Fig. of (e & f) all of these sub-figures within Figs. 8 and 9.

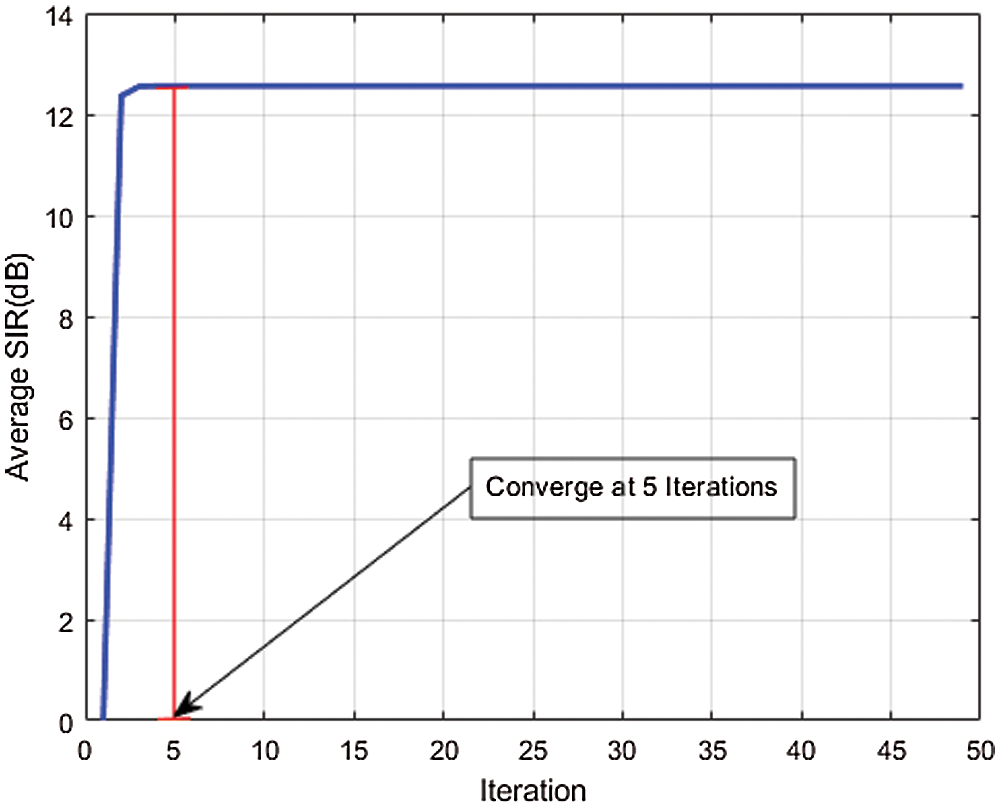
Figure 6: Average SIR convergence

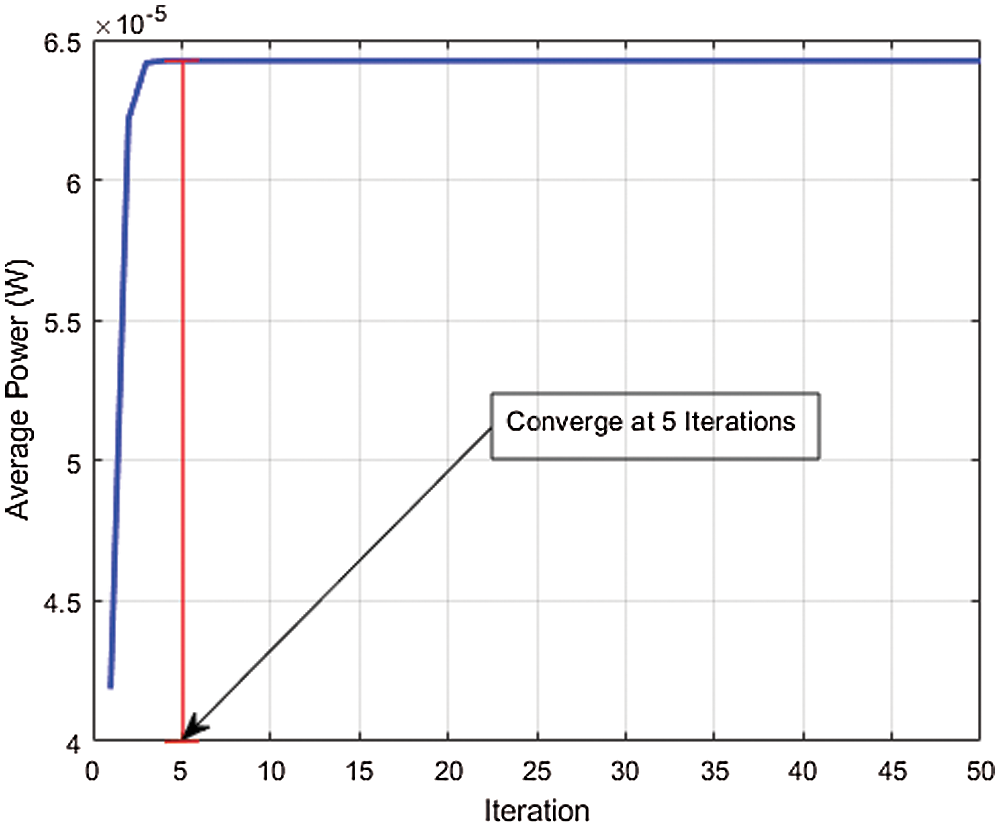
Figure 7: Average power convergence

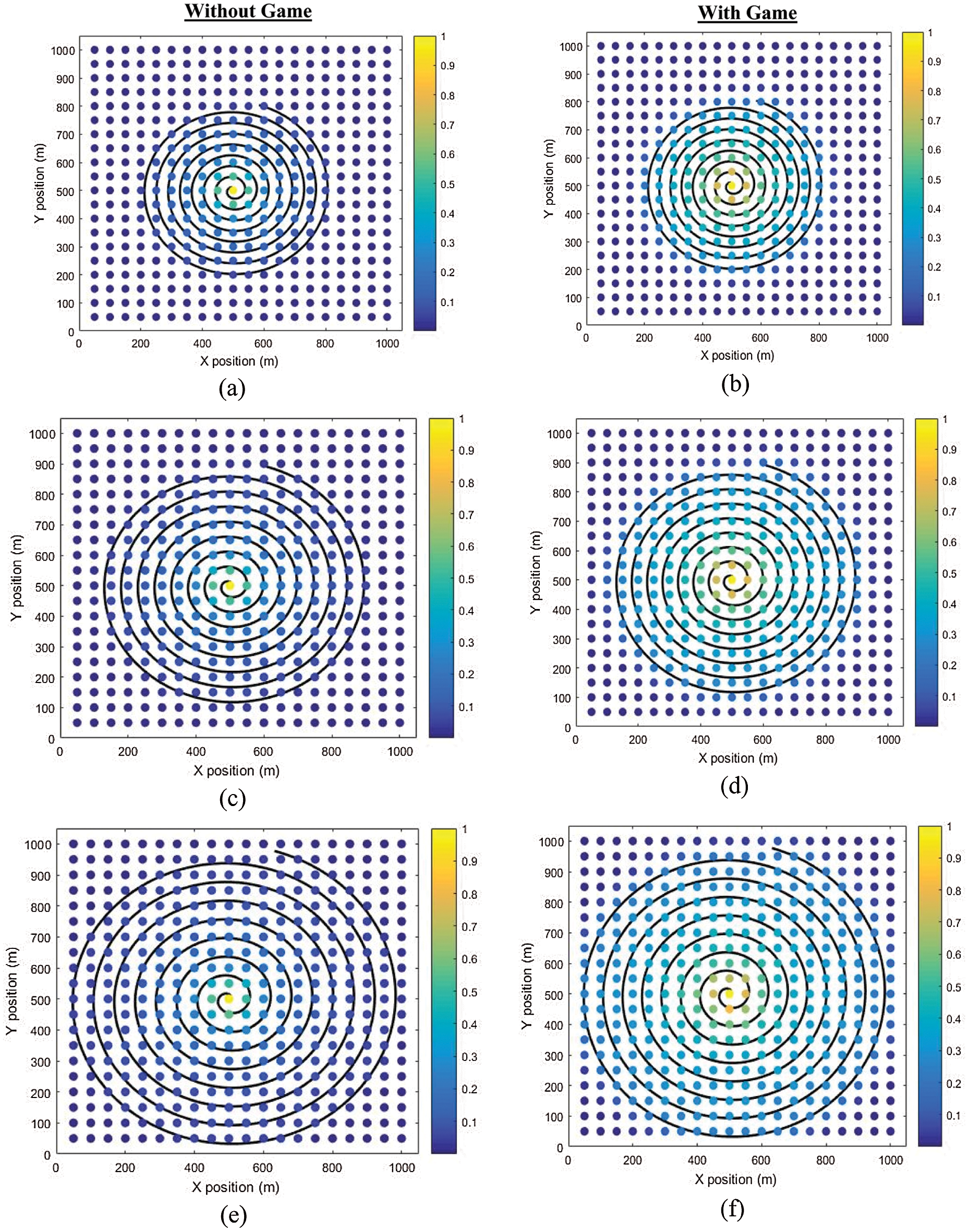
Figure 8: With & without game for UAV with different flying time for H = 50 m

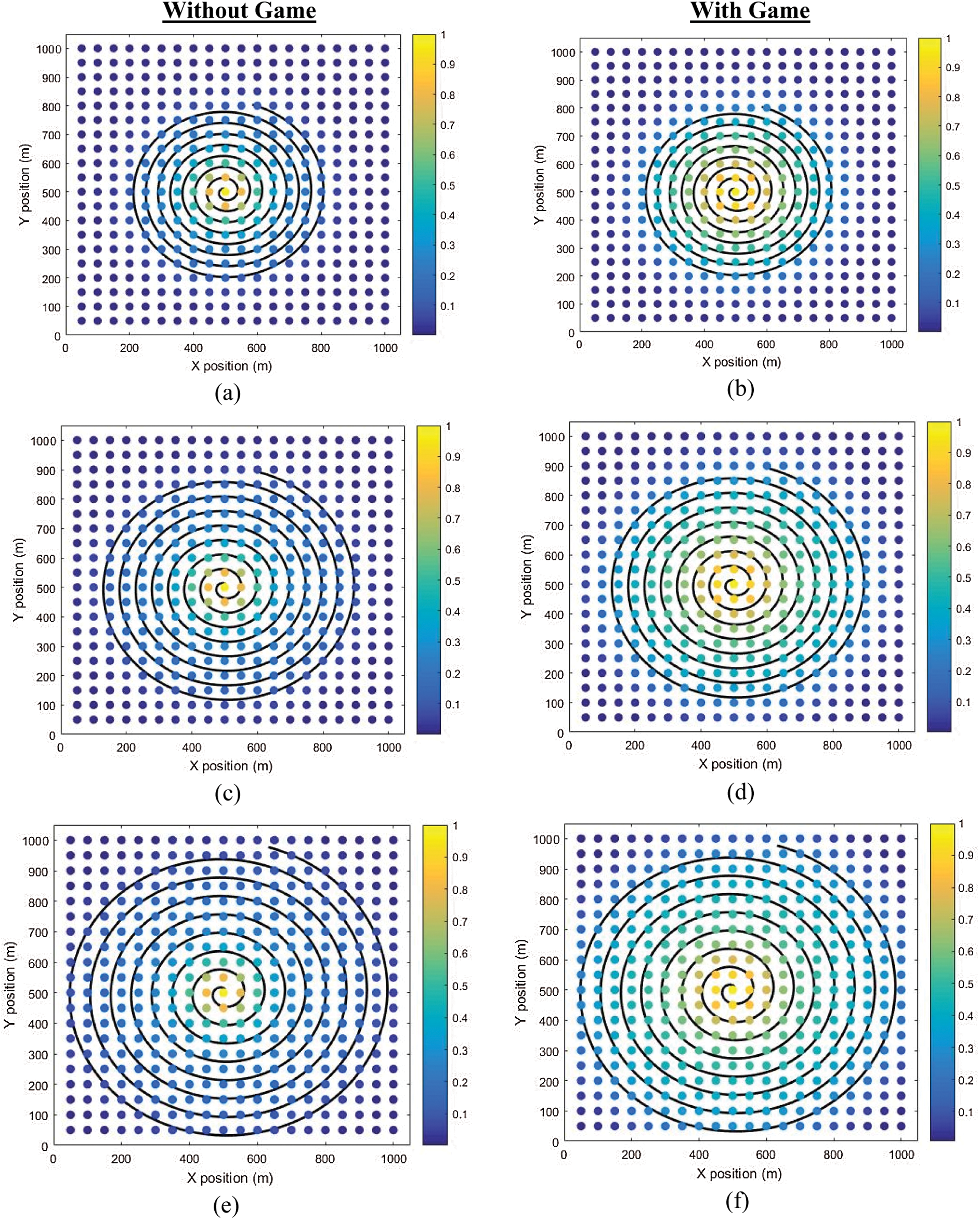
Figure 9: With & without game for UAV with different flying time for H = 100 m

Additionally, we examine the average SIR and average power. In this experiment, the iteration time is shown on the horizontal axis that is required to achieve the Nash Equilibrium, while the average power and average SIR are shown on the vertical axis. It is observed that our recommended EE-NGPAP method can achieve Nash Equilibrium with just 5 iterations as displayed in Fig. 6. Alternatively, Fig. 7 displays the curve of average transmission power obtained by the recommended algorithm. Fig. 7 reflects that the usage of average power of the recommended EE-NGPAP method has a considerable decrease and that is the most important thing in implementing potential 5G wireless networks. We succeeded in decreasing the transmission power to micro-Watt as can be seen in Fig. 7. The outcome attained from Fig. 7 signifies interference's extent gauged at the main system from the suggested EE-NGPAP. This attribute of the suggested EE-NGPAP algorithm makes it appropriate for maximising the sharing of spectrum and guarantees QoS in either system. The convergence speed of the recommended algorithm is apparent from Fig. 7.

However, with the 50 meters height besides multi average flying time (ft.) in which ft=350s as in Fig. 8b, ft=450s as in Fig. 8d and ft=550s as in Fig. 8f and applying Nash Equilibrium between players which is represented in our algorithm as an IoT nodes, the discount factor affects the optimal policies for wireless nodes which is shown in Figs. 8b, 8d, 8f, 9b, 9d and 9f. As time goes on, the drones will increase the price of the transferred unit as the higher the transmission time, the higher the cost of transporting the drone. Because the power conversion efficiency is low for wireless power transmission and long distance for wireless power transmission, drones must have more power to transmit wireless power. All of these factors will lead to a significant increase in the cost of power transmission. UAVs will then increase the price of transmitted power units when required time to transmit wireless power is large. In Figs. 8, 9b, 9d and 9f with game the optimal solutions for the IoT nodes are given as compared to Figs. 8 and 9 without game (a, c and e). We have considered that all nodes that fall within the same category are standard and uniform to provide simple simulations for the users. From Figs. 8 and 9 with game we have found that drones will increase the energy sent to transfer information to make more profit, even as energy unit prices are transferred over time by increasing hover time. Based on Figs. 8f and 9f we can see that IoT contracts are getting more and more power over time as drones increase the level of wireless power delivery by increasing average flight time to meet more wireless contract requirements. Also, the IoT node harvesting more energy and it will be there more energy to transfer information.

6  Research Limitations & Challenges

A major challenge is the limited energy as UAVs that fly in the air do not contain a fixed energy supply. Firstly, a dominant part pertaining to the UAV power consumption is the mechanical power consumption, which also considerably limits the applications. Secondly, the communications between UAV and IoT ground sensors or amongst UAVs take up much energy, which at times is even higher vs. those consumed when serving users. Typically, UAV devices possess limited energy storage capacity when executing flying operation. When considering the long-term operation pertaining to UAV networks, the energy constraints become tighter further. Under lower power, signals are transmitted, which makes the outage probability much higher since the links could be intermittent. These nodes dynamically function allowing frequent reorganisation of the network. This suggests that their routing protocols require confirming changes over time and employing more energy to extend the network stability. Thus, to enable efficient utilisation in UAV-based applications, we need to consider the resource allocation as well as deployment.

7  Conclusion

This study proposed an energy efficiency non-cooperative game theory power allocation with pricing scheme termed as EE-NGPAP to obtain an efficient power control in cognitive UAV network within IoT wireless nodes. Further, a new energy harvesting function, apart from the utility functions, was introduced and both uniqueness and existence of the Nash equilibrium have been demonstrated mathematically and via simulation. Moreover, simulation results showed that the proposed non-cooperative power control algorithm possess better power saving properties compared to other studies in the literature. Further, the convergence of the proposed algorithm to the NE requires only 4 iterations which makes the proposed energy harvesting algorithm more suitable for future development in IoT technology. For future work, further evaluation is needed for the scenario wherein UAV behaves as a mobile energy provider. Finally, the adoption of machine learning in UAV communications is another direction of our future work.

Funding Statement: This work is supported by the School of Computing, Faculty of Engineering, Universiti Teknologi Malaysia (UTM) and funded by the PRGS Project (Grant ID: R.J130000.7806.4L706).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  F. Mukhlif, K. A. B. Noordin, A. M. Mansoor and Z. M. Kasirun, “Green transmission for C-RAN based on SWIPT in 5G: A review,” Wireless Networks, vol. 25, no. 5, pp. 1–29, 2018. https://doi.org/10.1007/s11276-018-1718-z. [Google Scholar]

 2.  N. Bhushan, J. Li, D. Malladi, R. Gilmore, D. Brenner et al., “Network densification: The dominant theme for wireless evolution into 5G,” Ieee Communications Magazine, vol. 52, no. 2, pp. 82–89, 2014. [Google Scholar]

 3.  M. Kamel, W. Hamouda and A. Youssef, “Ultra-dense networks: A survey,” IEEE Commununications Surveys and Tutorials, vol. 18, no. 4, pp. 2522–2545, 2016. [Google Scholar]

 4.  L. Y. Su, C. Y. Yang and I. Chih-Lin, “Energy and spectral efficient frequency reuse of ultra dense networks,” Ieee Transactions on Wireless Communications, vol. 15, no. 8, pp. 5384–5398, 2016. [Google Scholar]

 5.  S. Samarakoon, M. Bennis, W. Saad, M. Debbah and M. Latva-Aho, “Ultra dense small cell networks: Turning density into energy efficiency,” Ieee Journal on Selected Areas in Communications, vol. 34, no. 5, pp. 1267–1280, 2016. [Google Scholar]

 6.  Y. Zeng, R. Zhang and T. J. Lim, “Wireless communications with unmanned aerial vehicles: Opportunities and challenges,” Ieee Communications Magazine, vol. 54, no. 5, pp. 36–42, 2016. [Google Scholar]

 7.  F. Yang, J. Song, W. Xiong and X. Cui, “UAV-based collaborative electronic reconnaissance network for 6G,” Wireless Communications and Mobile Computing, vol. 2021, 2021. [Google Scholar]

 8.  H. C. Wang, G. R. Ding, F. F. Gao, J. Chen, J. L. Wang et al., “Power control in UAV-supported ultra dense networks: Communications, caching, and energy transfer,” Ieee Communications Magazine, vol. 56, no. 6, pp. 28–34, 2018. [Google Scholar]

 9.  H. Yu and Y. B. Zikria, “Cognitive radio networks for internet of things and wireless sensor networks,” Ed: Multidisciplinary Digital Publishing Institute, vol. 20, no. 18, pp. 5288, 2020. [Google Scholar]

10. C. Lee, G. Jang, N. N. Dao, D. S. Lakew, C. Le et al., “Competitive game theoretic clustering-based multiple UAV-assisted NB-IoT systems,” Electronics, vol. 10, no. 3, pp. 356, 2021. [Google Scholar]

11. A. Majeed, R. Bhana and S. Parvez, “Retracted: Controlling energy consumption by internet of things (IoT) applications,” Journal of Fundamental and Applied Sciences, vol. 10, no. 4S, pp. 608–611, 2018. [Google Scholar]

12. S. Y. R. Hui, W. X. Zhong and C. K. Lee, “A critical review of recent progress in mid-range wireless power transfer,” IEEE Transactions on Power Electronics, vol. 29, no. 9, pp. 4500–4511, 2014. [Google Scholar]

13. Z. Zhang, H. L. Pang, A. Georgiadis and C. Cecati, “Wireless power transfer-an overview,” IEEE Transactions on Industrial Electronics, vol. 66, no. 2, pp. 1044–1058, 2019. [Google Scholar]

14. S. Y. Lien, K. C. Chen and Y. H. Lin, “Toward ubiquitous massive accesses in 3GPP machine-to-machine communications,” Ieee Communications Magazine, vol. 49, no. 4, pp. 66–74, 2011. [Google Scholar]

15. B. Liu, H. Xu and X. Zhou, “Resource allocation in unmanned aerial vehicle (UAV)-assisted wireless-powered internet of things,” Sensors, vol. 19, no. 8, pp. 1908, 2019. [Google Scholar]

16. F. Mukhlif, J. O. Hodonu-Wusu, K. A. Bin Noordin and Z. M. Kasirun, “Major trends in device to device communications research: A bibliometric analysis,” in 2018 Ieee Student Conf. on Research and Development, (IEEE Student Conference on Research and Development SCOReD, New York, IEEE, pp. 1–6, 2018. [Google Scholar]

17. R. I. Bor-Yaliniz, A. El-Keyi and H. Yanikomeroglu, “Efficient 3-D placement of an aerial base station in next generation cellular networks,” in 2016 Ieee Int. Conf. on Communications, (IEEE International Conference on Communications, New York, IEEE, pp. 985–989, 2016. [Google Scholar]

18. A. Al-Hourani, S. Kandeepan and A. Jamalipour, “Modeling air-to-ground path loss for low altitude platforms in urban environments,” in 2014 Ieee Global Communications Conf., (IEEE Global Communications Conference, New York, IEEE, pp. 2898–2904, 2014. [Google Scholar]

19. M. Mozaffari, W. Saad, M. Bennis and M. Debbah, “Efficient deployment of multiple unmanned aerial vehicles for optimal wireless coverage,” Ieee Communications Letters, vol. 20, no. 8, pp. 1647–1650, 2016. [Google Scholar]

20. A. Al-Hourani, S. Kandeepan and S. Lardner, “Optimal LAP altitude for maximum coverage,” Ieee Wireless Communications Letters, vol. 3, no. 6, pp. 569–572, 2014. [Google Scholar]

21. J. Xu, Y. Zeng and R. Zhang, “UAV-enabled wireless power transfer: Trajectory design and energy optimization,” Ieee Transactions on Wireless Communications, vol. 17, no. 8, pp. 5092–5106, 2018. [Google Scholar]

22. L. D. Nguyen, A. Kortun and T. Q. Duong, “An introduction of real-time embedded optimisation programming for UAV systems under disaster communication,” EAI Endorsed Transactions on Industrial Networks & Intelligent System, vol. 5, no. 17, pp. e5, 2018. [Google Scholar]

23. D. Goodman and N. Mandayam, “Power control for wireless data,” Ieee Personal Communications, vol. 7, no. 2, pp. 48–54, 2000. [Google Scholar]

24. D. M. Topkis, “Supermodularity and complementarity," in The Froniers of Economic Research, 1st edition, vol. 1. Princeton, New Jersey, United States of America: Princeton University Press, pp. 7–93, 1998. [Google Scholar]

25. Y. A. Al-Gumaei, K. A. Noordin, A. W. Reza and K. Dimyati, “A novel utility function for energy-efficient power control game in cognitive radio networks,” PLoS ONE, vol. 10, no. 8, pp. 1–21, Art no. e0135137, 2015. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.