Computers, Materials & Continua DOI:10.32604/cmc.2022.026026
Article

Dipper Throated Optimization Algorithm for Unconstrained Function and Feature Selection

Ali E. Takieldeen1, El-Sayed M. El-kenawy1,2, Mohammed Hadwan3,4,5,* and Rokaia M. Zaki6,7

1Faculty of Artificial Intelligence, Delta University for Science and Technology, Mansoura, 35712, Egypt
2Department of Communications and Electronics, Delta Higher Institute of Engineering and Technology, Mansoura, 35111, Egypt
3Department of Information Technology, College of Computer, Qassim University, Buraydah, 51452, Saudi Arabia
4Department of Computer Science, College of Applied Sciences, Taiz University, Taiz, Yemen
5Intelligent Analytics Group (IAG), College of Computer, Qassim University, Buraydah, Saudi Arabia
6Higher Institute of Engineering and Technology, Kafrelsheikh, Egypt
7Department of Electrical Engineering, Shoubra Faculty of Engineering, Benha University, Egypt
*Corresponding Author: Mohammed Hadwan. Email: m.hadwan@qu.edu.sa
Received: 13 December 2021; Accepted: 13 January 2022

Abstract: Dipper throated optimization (DTO) algorithm is a novel with a very efficient metaheuristic inspired by the dipper throated bird. DTO has its unique hunting technique by performing rapid bowing movements. To show the efficiency of the proposed algorithm, DTO is tested and compared to the algorithms of Particle Swarm Optimization (PSO), Whale Optimization Algorithm (WOA), Grey Wolf Optimizer (GWO), and Genetic Algorithm (GA) based on the seven unimodal benchmark functions. Then, ANOVA and Wilcoxon rank-sum tests are performed to confirm the effectiveness of the DTO compared to other optimization techniques. Additionally, to demonstrate the proposed algorithm's suitability for solving complex real-world issues, DTO is used to solve the feature selection problem. The strategy of using DTOs as feature selection is evaluated using commonly used data sets from the University of California at Irvine (UCI) repository. The findings indicate that the DTO outperforms all other algorithms in addressing feature selection issues, demonstrating the proposed algorithm's capabilities to solve complex real-world situations.

Keywords: Metaheuristic optimization; swarm optimization; feature selection; function optimization

1  Introduction

Optimization is the process of obtaining the greatest or least objective function value for a set of inputs. It is the subject of various machine techniques that draw on artificial neural networks. Hundreds of famous optimization algorithms have become accessible, and dozens of technologies are available in major scientific code libraries. Given the problems of optimization, selecting what methods can thus be challenging [1]. Optimization is how a function has the lowest or highest output of input parameters or arguments. In machines where the input parameters of the tasks like the floating-point values are numerical, continuous functions optimization frequently arises. The function returns an evaluation of the parameter of real-life [2].

Continuous function optimization may be used to distinguish between such problems with discrete variables, known as combined optimization problems [3]. Different techniques may be resolved, organized, and called to optimize the problems involving continuous functions. The information about the objective function utilized and used throughout the optimization process depends on one technique of optimization classification [4]. The more information about the target function is generally understood, the easier it is to optimize because knowledge can be applied effectively [5]. Perhaps the significant difference between optimization techniques is identifying the destination function in one location [6]. It means that the first derivative of the feature may be used to identify a possible solution (gradient or route). It distinguishes itself from other not-calculated gradient data [7]. Metaheuristic optimization is the optimization process utilizing metaheuristic techniques. Almost every area of life is involved, much from engineering to business, holiday preparation to internet travel [8]. The use of those readily available resources must be maximized due to the continuous scarcity of money, resources, and time. The vast majority are non-linear, multimodal, and quite restrictive in real-life problems [9]. Different objectives frequently collide. Even if one goal is set, Optimum solutions are not always available [10]. Usually, a faultless or failed response is not simple to find. Many metaheuristic algorithms have been published, including swarm intelligence, anthrax optimization, optimization of the particulate swarm. In previous articles [11]. The feature selection issue may be seen as a multi-objective optimization problem in which two conflicting objectives must be met: picking the fewest possible features while attaining maximum classification accuracy [12]. The solution with the most distinctive features and the maximum classification accuracy is deemed optimal [13].

2  Literature Review

Meta-heuristics refers to generic methods that normally used to solve complex and challenging combinatorial search problems. Generally, the problems solved by metaheuristic algorithms are challenging for computer scientists due to the need to examining a huge number of combinations that usually exponential with conflicting objectives [14]. Many metaheuristic algorithms have been proposed to tackle real-world situation such as image segmentation [15], water allocation and crop planning [16], Nurse Rostering [17], power load dispatch [18], and Parkinson diagnosis [19]. Several survey papers are available for more information about metaheuristic algorithms [20–23].

Nature-inspired metaheuristic algorithms to solve complex real-world situation have attracted the attention of the researchers in the scientific community. Many new nature-inspired metaheuristic algorithms have been developed, including Symbiotic Organisms Search [24], Bat Algorithm (BA) [25], Bacterial Foraging Opt [26], Gravitational Search Algorithm [27], Firefly Algorithm (FA) [28], Krill Herd [29], Grey Wolf Optimization (GWO) algorithm [30,31], Cuckoo Search [32], Harmony search algorithm [33], Whale optimization [34], Social spider optimization [35], and Biogeography-based Opt [36].

Several research paper can be found in the literature tackling feature selection as in [37–40]. When it comes to feature selection, metaheuristic algorithms are instrumental because they deal with the dimensions of the data set to make predictions [38]. However, when the dimensionality of the data sets is increased, the performance of classification methods suffers because of this. Furthermore, high-dimensional data sets have several drawbacks, including a long model creation time, redundant data, and reduced performance, making data analysis very challenging [40]. The feature selection step is a major preprocessing step that is used to resolve this problem. Its goal is to select a subset of features from an extensive data set while also increasing the accuracy of the classification or clustering model, resulting in the removal of noisy, extraneous, and ambiguous data. The following section present the proposed DTO optimizer.

3  Proposed Dipper Throated Optimization Algorithm

Dipper Throated bird is a member of the genus Cinclus in the bird family Cinclidae, so-called because of their bobbing or dipping movements see Fig. 1. They are unique among passerines for their ability to dive, swim, and hunts underwater. Besides, it can fly rapidly and straight without pauses or glides because it has short and flexible wings. Dipper Throated bird has its unique hunting technique, it performs rapid bowing movements, enhanced by the pure white of the breast. Once the prey is detected, it dives headfirst into the water, even into the turbulent and fast-flowing water. When it became on the bottom, it turns up stones and pebbles, to disturb aquatic invertebrates, aquatic insects, and small fish. the Dipper walks on the bottom by grasping stones. It often walks against the current, with the head downwards to locate prey, it can be stable for a long time with its strong feet, also, it can walk into the water and deliberately submerge, by using its wings effectively and walk along with the bottom keeping its head well down and its body oblique to secures its food.

3.1 Mathematical Formulation

Mathematically, the Dipper Throated Optimization (DTO) algorithm assumes the birds are swimming and flying to search for food resources Nfs available for n birds. The birds’ locations, BP, and velocities, BV, can be represented by the following matrices:

BP=[BP1,1BP1,2BP1,3…BP1,dBP2,1BP2,2BP2,3…BP2,dBP3,1BP3,2BP3,3…BP3,d……………BPn,1BPn,2BPn,3…BPn,d](1)

BV=[BV1,1BV1,2BV1,3…BV1,dBV2,1BV2,2BV2,3…BV2,dBV3,1BV3,2BV3,3…BV3,d……………BVn,1BVn,2BVn,3…BVn,d](2)

where BPi,j indicates ith bird in the jth dimension for i∈1,2,3,…,n and j∈1,2,3,…,d. BVi,j indicates ith bird velocity in the jth dimension for i∈1,2,3,…,n and j∈1,2,3,…,d. The initial locations of BPi,j are uniform distribution within lower and upper bounds. The fitness values f=f1,f2,f3,…,fn are calculated for each bird as in the following array

f=[f1(BP1,1,BP1,2,BP1,3,…,BP1,d)f2(BP2,1,BP2,2,BP2,3,…,BP2,d)f3(BP3,1,BP3,2,BP3,3,…,BP3,d)…fn(BPn,1,BPn,2,BPn,3,…,BPn,d)](3)

where the fitness value indicates the quality of food source searched by each bird. The optimal value means mother bird. These values are then sorted in ascending order. The first best solution in declared to be BPbest. The remaining solutions are supposed to be normal birds BPnd for follower birds. The global best solution in declared to be BPGbest.

First DTO mechanism by this optimizer to update the swimming bird position is based on the following equation:

BPnd(t+1)=BPbest(t)−C1.|C2.BPbest(t)−BPnd(t)|(4)

where BPnd(t) is a normal bird position at iteration t and BPbest(t) is the best bird position. The “.” is pairwise multiplication. BPnd(t+1) is the updated bird position for the solution.

The C1 and C2 are updated within the iterations by the following

C1=2c.r1−c,C2=2r1,c=2(1−(tTmax)2)(5)

where c changes from 2 to 0 exponentially, r1 is a random value in [0,1] and Tmax in the total number of iterations.

Second DTO mechanism is based on updating the flying bird position and velocity by the following equations. The flying birds’ positions are updated as

BPnd(t+1)=BPnd(t)+BV(t+1)(6)

where BPnd(t+1) is the new bird position for normal birds, and the updated velocity of each bird BV(t+1) is calculated as

BV(t+1)=C3BV(t)+C4r2(BPbest(t)−BPnd(t))+C5r2(BPGbest−BPnd(t))(7)

where C3 is a weight value, C4 and C5 are constants. BPGbest is the global best position and r2 is a random number in [0;1].

The DTO algorithm can be described by this equation

BPnd(t+1)={ BPbest(t)−C1.| M |if R<0.5BPnd(t)+BV(t+1)otherwise(8)

where M=C2.BPbest(t)−BPnd(t) and R is a random value in [0,1].

Figure 1: White throated dipper

3.2 Complexity Analysis

The computational complexity of the DTO algorithm can be expressed as follow. For population n and iterations tmax, the time complexity will be defined as follows:

▪ Initialization BPi(i=1,2,…,n), BVi(i=1,2,…,n), Tmax, c, C1, C2, C3, C4, C5, r1, r2, R, t=1: O(1).

▪ Calculate objective function fn for each bird BPi: O(n).

▪ Finding best bird BPbest: O (n).

▪ Updating position of current swimming bird: O(tmax×n).

▪ Updating velocity of current flying bird: O(tmax×n).

▪ Updating position of current flying bird: O(tmax×n).

▪ Calculating objective function fn for each bird BPi: O(tmax).

▪ Updating c, C1, C2, R: O(tmax).

▪ Finding best bird BPbest: O(tmax).

▪ Setting BPGbest = BPbest: O(tmax).

▪ Setting t=t+1: O(tmax).

▪ Producing the best bird BPGbest: O(1)

From this analysis, the complexity of computations is O(tmax×n) and O(tmax×n×d) with d dimension.

4  Experimental Results

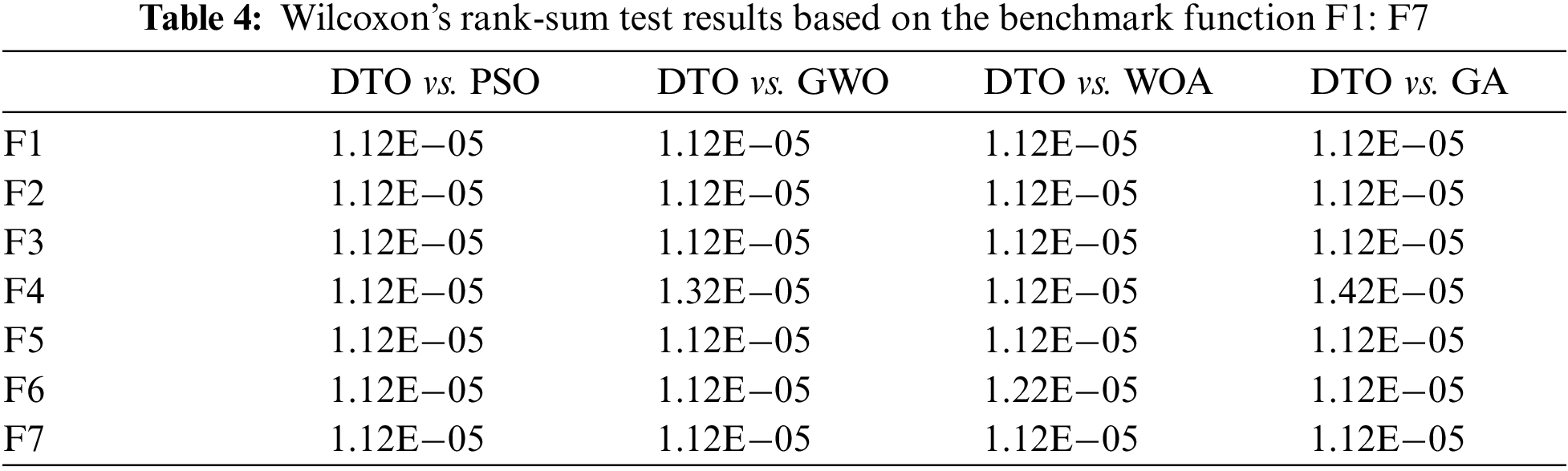
The experiments in this section are explained in two sets. The first set of experiments is designed to evaluate the proposed DTO algorithm performance. The proposed DTO algorithm is tested compared to the algorithms of Particle Swarm Optimization (PSO), Whale Optimization Algorithm (WOA), Grey Wolf Optimizer (GWO), and Genetic Algorithm (GA) based on the seven unimodal benchmark functions [19]. Then, ANOVA and Wilcoxon rank-sum tests are performed to confirm the effectiveness of the proposed algorithm compared to other optimization techniques. The second is experimental in feature selection [20].

4.1 Evaluation of DTO Algorithm Unconstrained Function

Tab. 1 shows a list of the unimodal benchmark function tested in the first experiment. Tab. 1 shows the compared algorithms configuration. To be fair in the comparison, all the algorithms start with 20 agents, same objective function, 100 iterations, same dimensions, and boundaries.

Fig. 2 shows the convergence curves of the proposed DTO algorithm compared to the PSO, WOA, and GWO algorithms for the benchmark mathematical functions. Note that, the best convergence is achieved by the DTO algorithm. Tab. 2 shows the mean and the standard deviation results based on the benchmark function, F1-F7, for different algorithms.

Figure 2: The sample functions’ graphical representations and convergence curves

To test the statistical difference between the proposed DTO algorithm and the compared algorithms, a one-way analysis of variance (ANOVA) test is applied. In this test, two hypotheses are considered; the first is null hypothesis (H0: μDTO=μPSO=μWOA=μGWO=μGA) and the alternate hypothesis (H1: Means are not all equal). The ANOVA test results are shown in Tab. 3. Fig. 3 shows the ANOVA test for proposed and the compared algorithms vs. the objective function. From the results, the alternate hypothesis H1 is accepted. The ANOVA test confirms the effectiveness of the proposed algorithm compared to other optimization techniques.

Figure 3: ANOVA test for the proposed DTO and compared algorithms based on the benchmark functions

Wilcoxon's rank-sum test is employed between every two algorithms to get the p-values between the proposed DTO algorithm and other algorithms to show that DTO has a significant difference. The two hypotheses are the null hypothesis (H0: μDTO=μPSO, μDTO=μGWO, μDTO=μWOA, and μDTO=μGA) and the alternate hypothesis (H1: Means are not all equal). Tab. 4 shows that the p-values are less than 0.05 between the proposed algorithm and other algorithms. This confirms the superiority of the DTO algorithm and that it is statistically significant. Thus, the alternate hypothesis H1 is accepted.

4.2 Evaluation of DTO Algorithm on Feature Selection Problem

In the case of the feature selection issue, the output solution should be modified from a continuous solution to a binary solution utilizing the numbers 0 or 1. This function is often used to convert the continuous solution of an optimizer to a binary solution in an optimization problem.

Xd(t+1)={0ifSigmoid(XBest)<0.51otherwise,Sigmoid(XBest)=11+e−10(XBest−0.5)(9)

4.2.1 Fitness Function

The quality of an optimizer's solutions is determined by the fitness function that has been given to it. The error rate of classification and regression, as well as the features that have been picked from the input dataset, are the primary determinants of the function. It is advisable to choose a solution based on the collection of characteristics that can provide the bare minimum of features with the lowest classification error rate. The following equation is used in this study to evaluate the quality of the solutions provided.

Fn=αErr(O)+β|s||f|(10)

As part of the experiments and comparative findings, the DTO evaluated our proposed algorithm against six datasets from the UCI machine learning library to determine its effectiveness. The datasets were chosen because they had a diverse range of features and occurrences that were reflective of the many types of problems that the proposed approach would be evaluated against. For more details about the UCI datasets, refer to Tab. 5.

4.2.2 Evaluation Metrics

The evaluation metrics used in this research are presented in Tab. 6 as follows:

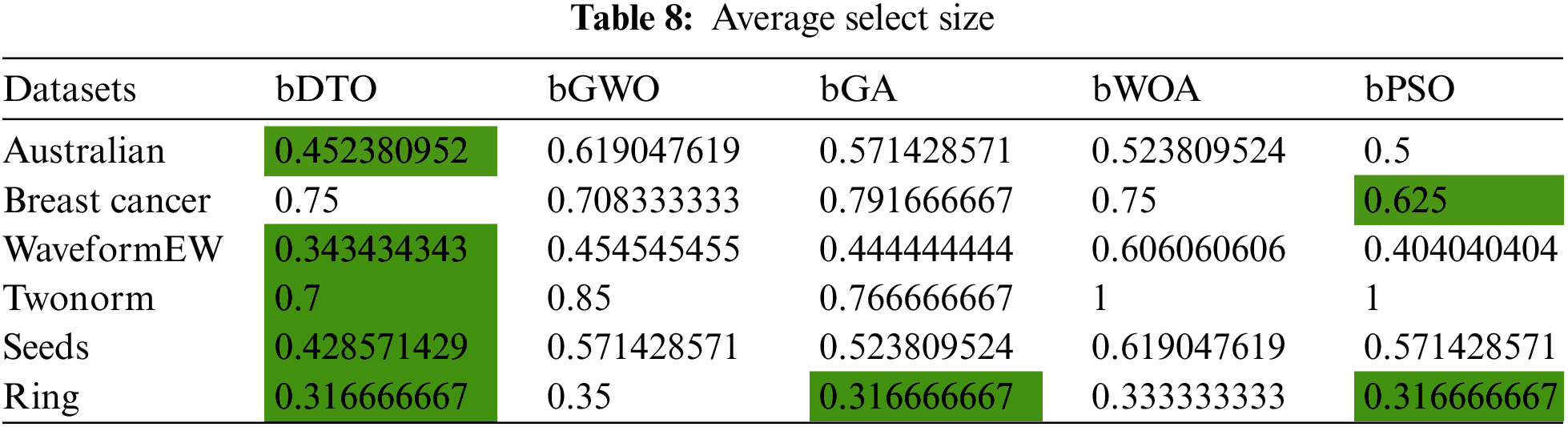
The average error of several algorithms is shown in Tab. 7. Due to the decreased error, the optimizer has identified the optimal collection of features that can train the classifier while also producing a smaller error on the concealed test data. Tab. 8 bellow shows the average features selected. Tab. 9 for average fitness, Tab. 10 for standard deviation fitness, Tab. 11 for best fitness, and Tab. 12 for worst fitness. The DTO has been able to find the superiority fitness for all datasets.

5  Conclusion

In this paper, a novel Dipper Throated Optimization (DTO) is introduced which is inspired by the throated dipper bird. Six UCI machine learning database datasets and unconstrained function are used to prove the consistency of the suggested optimizer and guarantee that the proposed solution is dependable and stable to evaluate its quality and effectiveness. ANOVA and Wilcoxon rank-sum tests are used to compare the proposed algorithm to different optimization methods. The results showed clearly that, DTO outperformed all other compared methods. For future work, DTO needs more investigation by applying it to solve other well-known real-world combinatorial optimization problems. Based on the great success of DTO, the researchers can investigate the hybridizations between DTO and other metaheuristic optimization algorithms as it is proved that hyper metaheuristic algorithms perform well compared to single metaheuristic algorithms.

Acknowledgement: The researcher would like to thank the Deanship of Scientific Research, Qassim University for funding the publication of this project.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  A. Ibrahim, H. A. Ali, M. M. Eid and E. -S. M. El-kenawy, “Chaotic harris hawks optimization for unconstrained function optimization,” in 16th Int. Computer Engineering Conf. (ICENCO), Cairo, Egypt, pp. 153–158, 2020. [Google Scholar]

 2.  M. M. Eid, E. -S. M. El-kenawy and A. Ibrahim, “A binary sine cosine-modified whale optimization algorithm for feature selection,” in National Computing Colleges Conf. (NCCC), Taif, Saudi Arabia, pp. 1–6, 2021. [Google Scholar]

 3.  E. -S. M. El-Kenawy, S. Mirjalili, A. Ibrahim, M. Alrahmawy, M. El-Said et al., “Advanced meta-heuristics, convolutional neural networks, and feature selectors for efficient COVID-19 X-ray chest image classification,” IEEE Access, vol. 9, pp. 36019–36037, 2021. [Google Scholar]

 4.  E. S. M. El-Kenawy, S. Mirjalili, S. S. M. Ghoneim, M. M. Eid, M. El-Said et al., “Advanced ensemble model for solar radiation forecasting using sine cosine algorithm and Newton's laws,” IEEE Access, vol. 9, pp. 115750–115765, 2021. [Google Scholar]

 5.  A. Ibrahim, S. Mirjalili, M. El-Said, S. S. M. Ghoneim, M. Alharthi et al., “Wind speed ensemble forecasting based on deep learning using adaptive dynamic optimization algorithm,” IEEE Access, vol. 9, pp. 125787–125804, 2021. [Google Scholar]

 6.  A. A. Salamai, E. -S. M. El-kenawy and A. Ibrahim, “Dynamic voting classifier for risk identification in supply chain 4.0,” Computers, Materials & Continua, vol. 69, no. 3, pp. 3749–3766, 2021. [Google Scholar]

 7.  E. -S. M. El-Kenawy, M. M. Eid, M. Saber and A. Ibrahim, “MbGWO-SFS: Modified binary grey wolf optimizer based on stochastic fractal search for feature selection,” IEEE Access, vol. 8, pp. 107635–107649, 2020. [Google Scholar]

 8.  E. -S. M. El-kenawy, H. F. Abutarboush, A. W. Mohamed and A. Ibrahim, “Advance artificial intelligence technique for designing double T-shaped monopole antenna,” Computers, Materials & Continua, vol. 69, no. 3, pp. 2983–2995, 2021. [Google Scholar]

 9.  M. M. Fouad, A. I. El-Desouky, R. Al-Hajj and E. -S. M. El-Kenawy, “Dynamic group-based cooperative optimization algorithm,” IEEE Access, vol. 8, pp. 148378–148403, 2020. [Google Scholar]

10. E. -S. M. El-Kenawy, A. Ibrahim, S. Mirjalili, M. M. Eid and S. E. Hussein, “Novel feature selection and voting classifier algorithms for COVID-19 classification in CT images,” IEEE Access, vol. 8, pp. 179317–179335, 2020. [Google Scholar]

11. A. Ibrahim, M. Noshy, H. A. Ali and M. Badawy, “PAPSO: A power-aware VM placement technique based on particle swarm optimization,” IEEE Access, vol. 8, pp. 81747–81764, 2020. [Google Scholar]

12. E. M. Hassib, A. I. El-Desouky, L. M. Labib and E. -S. M. T. El-Kenawy, “Woa + brnn: An imbalanced big data classification framework using whale optimization and deep neural network,” Soft Computing, vol. 24, pp. 5573–5592, 2020. [Google Scholar]

13. S. Mirjalili, “Sca: A sine cosine algorithm for solving optimization problems,” Knowledge-Based Systems, vol. 96, pp. 120–133, 2016. [Google Scholar]

14. J. Hao and C. Solnon, “Meta-heuristics and artificial intelligence,” in P. Marquis, O. Papini, H. Prade, (Eds.A Guided Tour of Artificial Intelligence Research: AI Algorithms, 1st ed., vol. 2. Cham, Denmark: Springer, pp. 27–52, 2020. [Google Scholar]

15. M. Ahmadi, K. Kazemi, A. Aarabi, T. Niknam and M. S. Helfroush, “Image segmentation using multilevel thresholding based on modified bird mating optimization,” Multimedia Tools Applications, vol. 78, pp. 23003–23027, 2019. [Google Scholar]

16. O. Mohammadrezapour, I. YoosefDoost and M. Ebrahimi, “Cuckoo optimization algorithm in optimal water allocation and crop planning under various weather conditions (case study: Qazvin plain, Iran),” Neural Computing and Applications, vol. 31, pp. 1879–1892, 2017. [Google Scholar]

17. M. Hadwan, M. Ayob, N. R. Sabar and R. Qu, “A harmony search algorithm for nurse rostering problems,” Information Sciences, vol. 233, pp. 126–140, 2013. [Google Scholar]

18. K. B. O. Medani, S. A. Sayah and A. Bekrar, “Whale optimization algorithm based optimal reactive power dispatch: A case study of the Algerian power system,” Electric Power Systems Research, vol. 163, pp. 696–705, 2018. [Google Scholar]

19. D. Gupta, S. Sundaram, A. Khanna, A. E. Hassanien, and V. H. C. Albuquerque, “Improved diagnosis of Parkinson's disease using optimized crow search algorithm,” Computer and Electrical Engineering, vol. 68, pp. 412–424, 2018. [Google Scholar]

20. K. Hussain, M. N. Mohd Salleh and S. Cheng, “Metaheuristic research: A comprehensive survey,” Artificial Intelligence Reviews, vol. 52, pp. 2191–2233, 2019. [Google Scholar]

21. E. N. Dragoi and V. Dafinescu, “Review of metaheuristics inspired from the animal kingdom,” Mathematics, vol. 9, no. 18, pp. 1–52, 2021. [Google Scholar]

22. R. Rajakumar, P. Dhavachelvan and T. Vengattaraman, “A survey on nature inspired meta-heuristic algorithms with its domain specifications,” in 2016 Int. Conf. on Communication and Electronics Systems (ICCES), Coimbatore, India, pp. 1–6, 2016. [Google Scholar]

23. T. El-Ghazali, “Machine learning into metaheuristics: A survey and taxonomy of data-driven metaheuristics,” ACM Computer Survey, vol. 54, pp. 1–32, 2020. [Google Scholar]

24. C. Min-Yuan and D. Prayogo, “Symbiotic organisms search: A new metaheuristic optimization algorithm,” Computers and Structures, vol. 139, pp. 98–112, 2014. [Google Scholar]

25. X. S. Yang, “A new metaheuristic bat-inspired algorithm,” in Nature Inspired Cooperative Strategies for Optimization (NICSO 2010), 1st ed., vol. 284. Berlin, Heidelberg: Springer, pp. 65–74, 2010. [Google Scholar]

26. K. M. Passino, “Biomimicry of bacterial foraging for distributed optimization and control,” IEEE Control Systems Magazine, vol. 22, pp. 52–67. 2002. [Google Scholar]

27. E. Rashedi, H. Nezamabadi-Pour and S. Saryazdi, “Gsa: A gravitational search algorithm,” Information Sciences, vol. 179, no. 13, pp. 2232–2248, 2009. [Google Scholar]

28. X. -S. Yang, “Firefly algorithm, stochastic test functions and design optimization,” arXiv preprint arXiv:1003.1409, 2010. [Google Scholar]

29. A. H. Gandomi and A. H. Alavi, “Krill herd: A new bio-inspired optimization algorithm,” Communications in Nonlinear Science and Numerical Simulation, vol. 17, no. 12, pp. 4831–4845, 2012. [Google Scholar]

30. E. -S. El-Kenawy and M. Eid, “Hybrid gray wolf and particle swarm optimization for feature selection,” International Journal of Innovative Computing, Information and Control, vol. 16, no. 3, pp. 831–844, 2020. [Google Scholar]

31. S. Mirjalili, S. M. Mirjalili and A. Lewis, “Grey wolf optimizer,” Advances in Engineering Software, vol. 69, pp. 46–61, 2014. [Google Scholar]

32. X. -S. Yang and S. Deb, “Cuckoo search via lévy flights,” in 2009 World Congress on Nature & Biologically Inspired Computing (NaBIC), IEEE, Coimbatore, India, pp. 210–214, 2009. [Google Scholar]

33. M. Hadwan, M. Ayob, M. A. Rassam and E. A. Hezam, “Deluge harmony search algorithm for nurse rostering problems,” in 2019 First Int. Conf. of Intelligent Computing and Engineering (ICOICE), Hadhramout, Yemen, pp. 1–5, 2019. [Google Scholar]

34. S. Mirjalili and A. Lewis, “The whale optimization algorithm,” Advances in Engineering Software, vol. 95, pp. 51–67, 2016. [Google Scholar]

35. E. Cuevas, M. Cienfuegos, D. ZaldíVar and M. Pérez-Cisneros, “A swarm optimization algorithm inspired in the behavior of the social-spider,” Expert Systems with Applications, vol. 40, no. 16, pp. 6374–6384, 2013. [Google Scholar]

36. D. Simon, “Biogeography-based optimization,” IEEE Transactions on Evolutionary Computation, vol. 12, no. 6, pp. 702–713, 2008. [Google Scholar]

37. P. Agrawal, H. F. Abutarboush, T. Ganesh and A. W. Mohamed, “Metaheuristic algorithms on feature selection: A survey of one decade of research (2009–2019),” IEEE Access, vol. 9, pp. 26766–26791, 2021. [Google Scholar]

38. B. Xue, M. Zhang, W. N. Browne and X. Yao, “A survey on evolutionary computation approaches to feature selection,” IEEE Transaction on Evolutionary Computing, vol. 20, no. 4, pp. 606–626, 2016. [Google Scholar]

39. P. Y. Lee, W. P. Loh and J. F. Chin, “Feature selection in multimedia: The state-of-the-art review,” Image and Vision Computing, vol. 67, pp. 29–42, 2017. [Google Scholar]

40. M. Sharma and P. Kaur, “A comprehensive analysis of nature-inspired meta-heuristic techniques for feature selection problem,” Archives of Computational Methods in Engineering, vol. 28, pp. 1–25, 2020. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.