DOI:10.32604/cmc.2022.025334

| Computers, Materials & Continua DOI:10.32604/cmc.2022.025334 |  |
| Article |
Comparative Study of Machine Learning Modeling for Unsteady Aerodynamics
Mechanical Engineering Department, Abu Dhabi University, Abu Dhabi, United Arab Emirates
*Corresponding Author: Mohammad Alkhedher. Email: mohammad.alkhedher@adu.ac.ae
Received: 20 November 2021; Accepted: 27 December 2021
Abstract: Modern fighters are designed to fly at high angle of attacks reaching 90 deg as part of their routine maneuvers. These maneuvers generate complex nonlinear and unsteady aerodynamic loading. In this study, different aerodynamic prediction tools are investigated to achieve a model which is highly accurate, less computational, and provides a stable prediction of associated unsteady aerodynamics that results from high angle of attack maneuvers. These prediction tools include Artificial Neural Networks (ANN) model, Adaptive Neuro Fuzzy Logic Inference System (ANFIS), Fourier model, and Polynomial Classifier Networks (PCN). The main aim of the prediction model is to estimate the pitch moment and the normal force data obtained from forced tests of unsteady delta-winged aircrafts performing high angles of attack maneuvers. The investigation includes three delta wing models with 1, 1.5, and 2 aspect ratios with four determined variables: change rate in angle of attack (0 to 90 deg), non-dimensional pitch rate (0 to .06), and angle of attack. Following a comprehensive analysis of the proposed identification methods, it was found that the newly proposed model of PCN showed the least error in modeling and prediction results. Based on prediction capabilities, it is seen that polynomial networks modeling outperformed ANFIS and ANN for the present nonlinear problem.
Keywords: Unsteady aerodynamics; supermaneuverability; identification; neuro-fuzzy; polynomial networks; neural networks
In the past, aircraft designers avoided post stall maneuvering of fighter aircraft which is characterized by large flow separation. Today's tactical fighters are using the supermaneuverability, which is defined as the ability of an aircraft to perform transient moves beyond the stall angle in a controlled manner of attack up to 90 degrees [1]. Additionally, the concept also refers to the ability of aircraft to alter its flight path in space whilst holding constant fuselage attitude or equivalently, possessing the ability to pitch and yaw without having to change the path of flight. This in return would enhance air-to-air combat on a short range performance at subsonic speeds where transients of angle of attack to 50 degrees and above can be achieved [2]. The characterized wings are delta-winged aircrafts which possess extreme high angles of attack, Fig. 1.

Figure 1: Delta wing nomenclature, where α is angle-of-attack, Λ is swept angle, V∞ is free-stream velocity, CN is the normal force coefficient, CD is the drag force coefficient and CL is the lift force coefficient
Consequently, numerous experimental attempts have been accomplished to model and study complex unsteady delta wing aerodynamics and its characteristics of, vortex sheets, vortex bursting, and flow separation [3]. For many years, the aerodynamic functions are approximated by linear expressions in the form of stability derivatives with an addition of nonlinear terms to express high-angle-of-attack maneuvers. The aforementioned type of formulation makes the assumption that moments and aerodynamic forces can be represented by differential function, and thus can be expanded using Taylor series while only possessing the first order terms (represents stability and control derivatives). However, the mentioned mathematical structure ultimately lacks the capability of modeling aerodynamic responses during occurrences of unsteady nonlinear effects, and is only sufficient for portions of the flight envelope [4,5].
Many researchers conducted experiments on unsteady high alpha maneuvers for various aspect ratios delta wings and with alpha excursions range from 0 deg to over 90 deg. It was found that flow separation, vortex bursting and attachment play vital roles in the production of aerodynamic loads. Therefore, aerodynamic coefficients vary with motion variables in a non-linear manner and depend on the motion history [6]. This study implements different aerodynamic prediction tools, including: adaptive neuro fuzzy logic inference system, artificial neural networks, and Fourier nonlinear model to estimate the pitch moment and the normal force of unsteady aerodynamics for delta-winged aircrafts at high attack angles. These methods are compared to an original tool of polynomial classifier networks to determine most suitable prediction tool in terms of relative precision, less complexity and stability of all models. The motivation behind this work is to achieve a highly accurate, less computational, and stable prediction model of associated aerodynamic instability due to a high angle of attack maneuvers.
2 Unsteady Aerodynamic Experimental Tests
Wind tunnel tests are often utilized to investigate and accurately describe the unsteady aerodynamic effects in prior- and post-stall regimes for fighter aircrafts at high angle of attack. The experimental data in this study is obtained for a range of delta wings aspect ratios performing fighter like supermaneuvers [7]. The experiments were carried out for several data ranges of system variables, i.e.,α (angle of attack), K (Reduced Frequency), and AR (Aspect Ratio). The hysteresis loops are found to become larger at high angles of attack; they also enlarge with an increase of the reduced frequency.
The aerodynamic tests are acquired by generating sinusoidal and ramp variations of the angle of attack. The simulated maneuvers are characterized by wind tunnel-matched dimensionless time constants (reduced frequencies) as K = wCR/2V∞. The sinusoidal and ramp simulated maneuvers are described in Eqs. (1) and (2) respectively.
where: αmin is the minimum angle of attack during one cycle test; τ is preprogrammed time when maximum angle of attack αmax reached. The reduced frequency is chosen to be 0.0 to 0.08 as often used for advanced fighters. More than 2500 measurements for normal Force coefficients and pitching moment coefficients have been employed in this study.
3 Model Formulations of Unsteady Aerodynamic Data
Researchers have previously unveiled numerous techniques for prediction aerodynamic loading at extremely high angle of attack maneuvers. Utilizing linear terms in the Expansion of the aerodynamic forces and moments using the Taylor series has been one of the most prominent and regularly used methodologies for the aircraft's forces’ and moments’ formulation [8]. The aforementioned terms are referred to as aerodynamic stability derivatives; this is due to the fact that their signs and magnitudes can be used to determine the stability at the equilibrium [9]. The indicated method has proven its high effectiveness specifically for flow attachments with low attack angles [1]. Moreover, the useful range of flight conditions of practical applications can further be extended by adding quadratic terms in Taylor expansions, which thereby expresses the stability derivatives’ changes [10].
The indicial response method is also an alternative approach to the modelling of aerodynamic loading. Since the theory of the linear Indian can approximate as a linear time-invariant system, knowing the system's indicial functions can also the way it would react to any random motion. Therefore, a reduction in computational requirements is achieved [11]. Moreover, the development of nonlinear indicial prediction models has permitted the prediction of unsteady time-dependent aerodynamic loads which are correlated with aircraft maneuvers at high pitch rates and high angle of attack [11,12]. The basis of this model lays on the nonlinear indicial theory in addition to the parameterization of the indicial and crucial state responses efficiently that stem from local information; for instance, the pitch rate and instantaneous angle of attack. However, there is great complexity in the aerodynamic transient that occurs when a critical state is crossed, and thus this model is unable to provide correct predictions in such cases. Nonetheless, researchers have shed a light on a solution that uses a dynamic simulation of state space which determines the state of Separation of unsteady flows in terms of the complementary state variable [13]. Aerodynamic coefficients have been obtained when utilizing the preceding state and corresponding inputs (α, q) state variable [13]. the aerodynamic coefficients were acquired using (α, q).
Precise time solutions of Euler or Navier-Stokes system equations are computationally expensive approach where several parameters have to be identified, as in maneuvers involving a high angle of attack. To demonstrate this problem's complexity, CFD analysis is performed in Figs. 2 and 3 to show the velocity streamlines and pressure profiles of different α for AR = 1, Re (Reynolds Number) = 4.5 × 105 and K = 0.01. The shown time dependent aerodynamic nonlinearity in velocity streamlines demonstrates the variations of aerodynamic loads that are time-dependent and correlated with aircraft movements at high pitch rates and high angles of attack. Large time delays and hysteresis are used to examine the vortex breakup over delta wings in unsteady flows. which resulted in increased lift and delayed stall [14].

Figure 2: Velocity streamlines for different angle of attack simulations for Re = 4.5 × 105 and K = 0.01

Figure 3: Pressure profiles for different angle of attack simulations for Re = 4.5 × 105 and K = 0.01
Several researchers have implemented a converged CFD simulation for data generation and learning. The time frame data of the unsteady flow was recorded, including velocity, pressure, and aerodynamic force of the wings at different α. The generated data set for training, testing and validation was composed with different extracted variables, such as point coordinates, aerodynamic lift and drag force coefficients for varied angles of attack at a fixed Reynolds number and wing aspect ratio [15]. Under transonic circumstances, the flow across delta wings is quite complicated and they are highly affected by different parameters. Different researchers have investigated the occurrence of vortex breakdown in order to provide a description for the contrariety between computational and experimental results based on the under-prediction of the vortex core axial velocity [16]. In previous work, generalized aerodynamic force coefficients related to the time and frequency domains are investigated. The Fourier analysis of the time series of the harmonic responses allows for the transmission of the time domain results into frequency domain [17].
This research describes a study which aims to analyze multiple modeling techniques of aerodynamic loading for a delta wing like aircraft's entire flight regime. A novel method is introduced, alongside artificial intelligence methods, based on polynomial networks technique which produces a model to identify aerodynamic instability up to a high angle of attack regime. The temporal history of motion and the wing aspect ratio act as the system's variable inputs, whereas both unsteady normal force and pitch moment exerted on a delta wing in the range 0 to 90 degrees angles of attack act as its outputs.
Aerodynamic responses result from a Fourier analysis of harmonic forced oscillation at high angles of attack when changing frequency. This analysis technique is efficient in assessing the resulting time integrals based on a concept of equivalent harmonic motion [18]. Fourier method is conducted in this study to analyze normal force and pitching moment data collected in Forced oscillation experiments with huge amplitudes at high attack angles.
In the modeling of aerodynamic data from wind tunnel tests on a variety of aircraft, a utilization of the neural network method occurred [19]. In [20,21], a rectangular wing with the NACA0015 profile, pitching from α = 0° to α = 60 about the 1/4 chord location °, is introduced using the ANN model. At varying span locations, the pressure coefficients and sectional force in the model was predicted using the neural network. The applied ANN is characterized as a feed-forward network consisting of three network layers, i.e., input layer (α, AR, and K), hidden trained layer and output layer (which represents normal force and pitching moment coefficients). The neural network structure is shown in Fig. 4 which uses supervised backpropagation training method. In an effort to diminish the mean square error (MSE) and keep it to a minimum, the optimal number of neurons in the hidden layer is found.

Figure 4: ANN Model, where: bik+1 is node i bias at k + 1 layer, wijk+1 is the connecting weight for node i at layer k + 1 and node j, k = 0, 1, 2…(total layers-1)
4.3 Adaptive Neuro-Fuzzy Modeling
A favorable comparison between Neuro-fuzzy model and semi-empirical approaches for unstable aerodynamic normal force coefficients was conducted [22]. In modeling the aerodynamic unsteady normal force coefficient, three inputs comprised the model: non-dimensional pitch rate, aspect ratio and angle of attack. The system's root mean square error was less than 6% for the 0 to 90 degrees angle of attack range., which indicated highly reliable results for CN prediction. In this work, similar input vector as the ANN method (α, AR, and K) was included in the selected model as displayed in Fig. 5. The ANFIS model comprised of three stages of several learning algorithms [23]: The first layer involved unsupervised learning of the membership functions (Centers and widths), the second layer involved unsupervised learning of the Rules (rules computation), and the third layer included error back propagation to improve the membership functions [24].

Figure 5: Adaptive-neuro-fuzzy modeling system. where: (x1–x4) are input vectors, k: is node number, Ai,j: are input fuzzy sets, wm: the rule output, fm is a output crisp variable of mth rule
Polynomial networks algorithm is a nonlinear mapping technique of all possible input polynomial terms which are essential to model the system [25,26]. The model desired output vector (normal force or pitching moment coefficient) is symbolized by C:
where: N is the output vector's length(coefficients of normal force and pitch moment). The corresponding input vector I is defined as:
The vector P is a sequence of polynomial basis terms represented by the input vector sequence IP and expressed as P(IP) = [1 IP], where IP is defined as:
The first term in the polynomial vector P is to model any present DC output, where other terms refer to first order linear terms and second order nonlinear terms. Mapping of input sequence IP into the desired output sequence C is achieved by using mean-squared error as the objective criterion is:
where: w is the network mapping gain. Solving Eq. (6) for C when error approaches zero:
In this section, to improve the accuracy and learning rate of the polynomial model, a novel strategy is proposed. The modified polynomial model, shown in Fig. 6, is based on closed loop identification by assuming a new sequence of polynomial basis terms P′(IP) as:

Figure 6: Block diagram of closed loop model training based on polynomial networks
The lines’ thicknesses indicate the dimensionality of the data. MSE is calculated based on the difference measurement between C and (Pw) [27].
The addition of feedback loops of the estimated output enabled the improved model to include more nonlinear terms without additional computations. Therefore, the new methodology shall enhance the convergence rate of the system with lower degree of polynomial order. The least squares error (LSE) method is used to optimize the weights for the proposed network. To further improve the model estimates, it is vital to eliminate ineffectual terms in the polynomial sequence vector before implementing the LSE.
The aerodynamic load coefficients were classified for three different delta wings according the three categories: training, testing, and validation. The distribution of the data was as follows: 80% for training, 10% validation and 10% testing. One thousand data vectors exist in the training data, and each data vector has system inputs comprised of angle of attack, aspect ratio, angle of attack rate change, and the reduced frequency, while the system outputs consist of the coefficients pitching moment and normal force. Three hundred data vectors comprise the testing data and are utilized to ensure the accuracy of implemented models. Finally, validation of the model's performance is achieved by using MSE percentage error.
A simple model is built to obtain the Fourier expansion for the fifth term in the sequence. Tab. 1 is a brief conclusion of this algorithm results. The performance was very responsible with an average percentage error of around 5%. The model produced the envelope shape of the coefficients of normal force and pitch moment, without any overshooting in this response.

5.2 Neural Network Model Results
The Neural Networks-based model is comprised of two layers of adjustable weights: an output layer and a hidden layer. A manually optimizing technique of the hidden layer neurons was attained to minimize MSE. The model's performance results proved that the first 20 epoch are where the most significant advancement took place, the MSE error was recorded as 1.5046e − 3. Furthermore, hyperbolic tangent (TAN) sigmoid and logarithmic (LOG) sigmoid were utilized to attain back propagation network training.
Aerodynamic normal force coefficients for aspect ratios of 1, 1.5, and 2 are modeled with K = 0.01, 0.02, 0.04, and 0.06.as in Tab. 2. Outstanding performance is shown in the obtained results; however, at aspect ratios = 1.5 and 2, the model's response showed a different performance than that of an aspect ratio = 1. The cause of this difference is the smaller size of the data used in training which is less than that at AR = 1. The unsteady aerodynamics pitch moment loading was also modeled by implementing the neural network technique. Tab. 3 depicts the results that show that the agreement between the model and the experiment is less than that of the CN model. This arises from the degree of difficulty and convolution of estimating the pitch moment since the unsteady load distribution is represented by it as well.


In comparison with the learning functions of hyperbolic tangent sigmoid, the performance of the ANN model was improved through the utilization of logarithmic sigmoid training function. Furthermore, the accuracy of the model was enhanced to a settling limit by incrementing the number of epochs. On the other hand, increasing the hidden layer's neurons to a number larger than 200 neurons did not achieve any notable enhancement in the performance or precision of the model.
5.3 Adaptive Neuro-Fuzzy Model Results
With the aim of optimizing and increasing the efficiency of the membership function's (MFs) distribution, ANFIS model is used to minimize MSE errors and divergence between experimental data used for training and the model output. The implementation of Gaussian bell shape membership function occurred.
A summary presenting the result's iterations and percentage errors in Tabs. 4 and 5 that were collected to model the pitch moment and normal force coefficients with ANFIS. The results of the model were representative and accurate with a minimum percentage error of around 0.01%. The model accuracy was improved by having a higher number of MFs and epochs. The training data of the model is rigidly tracked at an extremely high epochs number. However, this leads to a tradeoff in the predictive abilities of the model.


5.4 Polynomial Networks Results
The results for open loop and closed loop polynomial models are shown in Fig. 7. The closed loop output is always following the experimental data and minimizes the error rapidly. This improvement made the polynomial network model able to perform modeling with high accuracy for unsteady nonlinear aerodynamics systems.
The polynomial network has shown a competitive efficiency in modeling all conditions with almost same accuracy regardless of the number of data points used to train the model. For instance, at AR = 1.5, the data set was fewer than the data used to train the model at AR = 1, but the model results showed a similar performance for both data sets. The same range of angle of attack and aerodynamic parameters are used to model CN and CM. The improvement in feedback modeling is apparent compared to classical polynomial structure.

Figure 7: Unsteady aerodynamic (a) normal force and (b) pitching moment coefficients for checking data points using polynomial networks model
The model demonstrates rapid enhancement in the output performance when polynomial network order increase. Figs. 8 and 9 showed that using feedback loops improved significantly the model estimation ability. The polynomial networks model for normal force and pitch moment unsteady aerodynamics coefficients showed significant performance improvement compared to earlier models. Figs. 8 and 9 also show the global minima of model evaluation curves as an optimization point. With no feedback loops, the best result was obtained with fourth order polynomial model, where using the feedback loops resulted in a better convergence without higher order terms. The results of modeling normal force coefficients showed the possibility of getting an outstanding performance with lower order polynomial model by using only one feedback loop, therefore, reducing the computations cost needed for such modeling technique. These results were not as accurate for modeling the pitch moment unsteady aerodynamics.

Figure 8: Evaluation of polynomial networks model of unsteady aerodynamics (a) normal force and (b) pitching moment coefficients with no feedback loops

Figure 9: Evaluation of polynomial networks model of unsteady aerodynamic (a) normal force and (b) pitching moment coefficients with two feedback loops
Flow separations and dynamic lags for vortex bursting are the two flow mechanisms that cause the unsteady effects. Thus, it can be predicted a comparable hysteresis loop will be demonstrated in the pitch oscillatory maneuvers. This investigation has provided results that present the adaptive Neuro fuzzy model as the one with the lowest percentage error, as shown in Fig. 10. This signifies that there is an over fitting in the training data by the adaptive Neuro fuzzy model which allows is to act similarly to a lookup table, which will be distinctly depicted in the prediction results discussed later.

Figure 10: Testing results of modeling (a) normal force coefficients, AR = 1 and K = 0.01 (b) pitching moment coefficients, AR = 2, K = 0.04, using fourier, NN, ANFIS and PCN modeling techniques
The standard deviation of the results was found the lowest for ANFIS model and the highest for PCN model. Comparison of the four modeling schemes for modeling normal force coefficients at AR = 1 and K = 0.01 is shown in Fig. 10a Also Fig. 10b shows the comparison results for modeling pitch moment coefficients at AR = 2, K = 0.04.
7 Modeling Prediction Performance
7.1 Neural Network Model Prediction
The neural network model's prediction capability was put to the test. Fig. 11 presents an evaluation of the prediction performance at a unique data set which the system had not tested before with the values K = 0.03 and AR = 2; this case lies in the confines of the training data's scale. Agreeable results between the experimental and estimated data sets were obtained.

Figure 11: Prediction of unsteady aerodynamics for (a) normal force (b) pitch moment coefficients, where K = 0.03, reynolds number = 4.5 × 105, and AR = 2 using NN
As depicted in Tab. 6, the model predicts the largest error to be at AR = 1.5, which reached 28.54% when predicting CM ; the low number of training cases at this specific value is the main cause of this error. Inversely, 1.06% was the least error recorded, at Tan-sig training function and 200 neurons.

An alternate case of novel prediction is explored where the reduced frequency and highest angle of attack (model inputs) lie outside the training range. The results showed that the neural network's model proved to be incapable of predicting such a case, especially when compared with in-range cases. The MSE percentage error was wide-ranging between 4%–25%, and thus the model is not suitable for generalizations to unknown aerodynamics.
7.2 Adaptive Neuro-Fuzzy Model Prediction
As shown in Fig. 12, the data set K = 0. 03 and AR = 1 was used to validate the ANFIS model, within the trained scale of inputs. The model was quite unstable with and low performance in modeling CN while being highly accurate in modeling cases of CM.

Figure 12: Prediction of unsteady aerodynamics for (a) normal force (b) pitch moment coefficients, where K = 0.03, reynolds number = 4.5 × 105, and AR = 2 using ANFIS
Tab. 7 depicts a list of iterations which attempt to enhance the adaptive neuro-fuzzy technique's prediction ability through varying the number of epochs and altering MF's. On account for the over-fitting in the training process, the obtained results give very high MSE reaching up to 72% in certain cases.
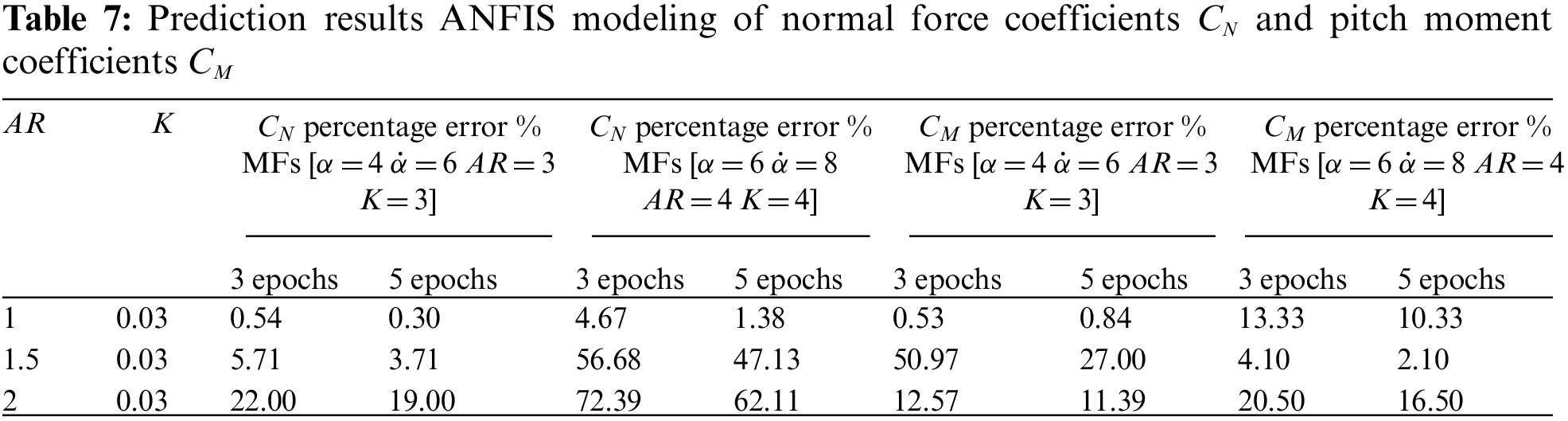
7.3 Polynomial Networks Prediction Results
Based on the results of PCN model identification of unsteady aerodynamics, shown in Fig. 13, this model has predicted the normal force and pitch moment coefficients for various values of aspect ratios. The close loop configuration of PCN has shown a remarkable enhancement over classical PCN.

Figure 13: Prediction of unsteady aerodynamics for (a) normal force and (b) pitch moment coefficients, where K = 0.03, reynolds number = 4.5 × 105, and AR = 1 using PCN model
It is noticed that the range of MSE for prediction results is similar to the MSE of testing phase as seen it Tabs. 8 and 9. This clearly demonstrates the stability, steadiness, and generalization of polynomial networks model is a vital outcome of this new method.
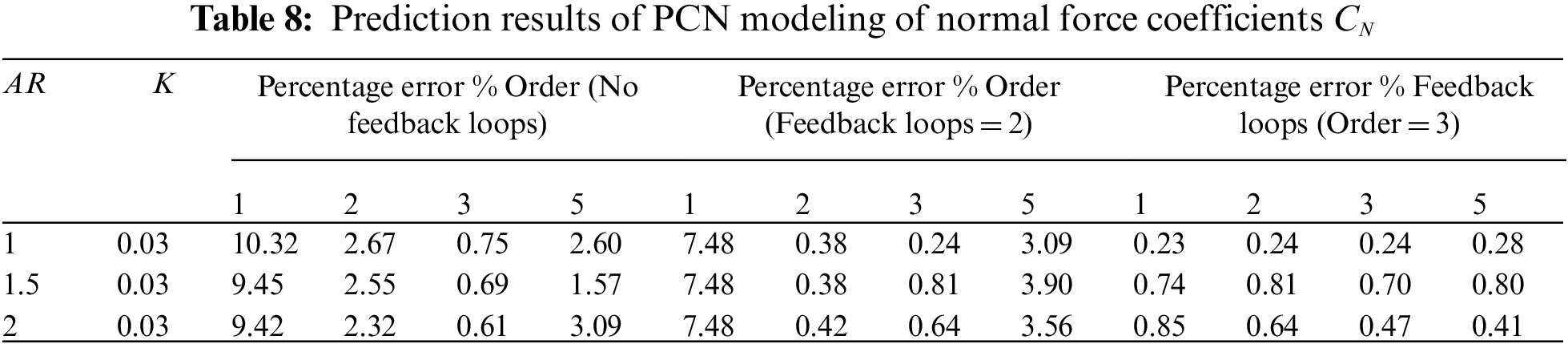

To further explore the extent of model generality, novel aerodynamic data set is used where AR = 1.5 and K = 0.02 with a maximum angle of attack = 60°. Tab. 10 shows that polynomial networks model satisfies this issue undoubtedly. The feedback PCN improved prediction capability of open loop polynomial model. Even though the system was not trained with this new range of maneuvering data, it showed extremely accurate performance.

8 Models Prediction Comparison
The crucial issue of this work is to study models’ ability in predicting the unsteady aerodynamics of new maneuvers, for both pitch moment and normal force coefficients. Tab. 11 shows an assessment of predicting capabilities of discussed models.

The results illustrate the prediction accuracy and stability for polynomial networks model, where other models demonstrates lower precision or instability at certain points. The average achieved prediction accuracy with PCN was less than 0.9%. Although, these results were lower for predicting pitch moment coefficients due to limited data set and complexity of CM profiles.
Using a new data set to test the ability of each system in predicting the unsteady aerodynamics at high angle of attack regimes with new maneuvering data is discussed in Tab. 12. The polynomial network showed a remarkable accuracy compared to other modeling techniques. The MSE of PCN was 0.78% compared to the second best method, NN, with MSE of 6.89%.

This paper presents a comparative study of nonlinear modeling of unsteady aerodynamics loading. Neural networks, adaptive neuro fuzzy logic inference system, Fourier nonlinear expansion, and polynomial classifier networks were utilized as identification methods. Such models serve the objective of predicting the aerodynamic normal force and pitching moment coefficients for aircrafts with differently shaped delta-wings that carry out unsteady maneuvers at diverse values of maximum angle of attack. Acquired results proved that the polynomial networks model is a reliable and capable technique in the prediction of unsteady aerodynamics at high angle of attack maneuvers, whereas alternate models were impeded by problems of generalization and memorization. Moreover, using them ensues many difficulties such as their requirement for exhaustive and slow training with numerous parameters to adjust, as well the possibility of falling into local minima. In contrast, the polynomial networks model was very efficient and comprehensive in the prediction of unsteady aerodynamics. Further enhancement of this method is presented by introducing a feedback state, which improved the model's performance; it was optimized using several feedback loops and polynomial orders. The proposed model proved capable in foretelling novel maneuvering data. The proposed model is inherently a parallel algorithm, which is ideal for multiprocessor hardware.
Funding Statement: The author received no specific funding for this study.
Conflicts of Interest: The author declares that they have no conflicts of interest to report regarding the present study.
1. A. Krzysiak, “Wind tunnel tests of aircraft aerodynamic characteristics at overcritical angles of attack,” Journal of KONES. Powertrain and Transport, vol. 23, no. 1, pp. 169–176, 2016. [Google Scholar]
2. C. Kostic and B. Rasuo, “Aerodynamic airfoil at critical angles of attack,” Vojnotehnicki Glasnik, vol. 64, no. 3, pp. 784–811, 2016. [Google Scholar]
3. T. Faure and C. Leogrande, “High angle-of-attack aerodynamics of a straight wing with finite span using a discrete vortex method,” Physics of Fluids, vol. 32, no. 10, pp. 104109, 2020. [Google Scholar]
4. W. Ruffles and S. M. Dakka, “Aerodynamic flow characteristics of utilizing delta wing configurations in supersonic and subsonic flight regimes,” Journal of Communication and Computer, vol. 13, no. 6, pp. 299–318, 2016. [Google Scholar]
5. P. Viswanath and S. Patil, “Aerodynamic characteristics of delta wing–body combinations at high angles of attack,” The Aeronautical Journal, vol. 98, no. 975, pp. 159–170, 1994. [Google Scholar]
6. P. Murphy, V. Klein and N. Frink, “Nonlinear unsteady aerodynamic modeling using wind-tunnel and computational data,” Journal of Aircraft, vol. 54, no. 2, pp. 659–683, 2017. [Google Scholar]
7. M. A. Jarrah, “Unsteady aerodynamics of delta wings performing maneuvers to high angles of attack,” Ph.D. dissertation, Dept. of Aeronautics and Astronautics, Stanford University, Dec. 1988. [Google Scholar]
8. D. Hao, L. Zhang, J. Yu and D. Mao, “Modeling of unsteady aerodynamic characteristics at high angles of attack,” Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, vol. 233, no. 6, pp. 2291–2301, 2018. [Google Scholar]
9. B. Mi, H. Zhan and S. Lu, “An extended unsteady aerodynamic model at high angles of attack,” Aerospace Science and Technology, vol. 77, pp. 788–801, 2018. [Google Scholar]
10. M. Baigang and Y. Jingyi, “An improved nonlinear aerodynamic derivative model of aircraft at high angles of attack,” International Journal of Aerospace Engineering, vol. 2021, pp. 1–12, 2021. [Google Scholar]
11. A. Da Ronch, A. Ventura, M. Righi, M. Franciolini, M. Berci et al., “Extension of analytical indicial aerodynamics to generic trapezoidal wings in subsonic flow,” Chinese Journal of Aeronautics, vol. 31, no. 4, pp. 617–631, 2018. [Google Scholar]
12. M. Ghoreyshi and R. Cummings, “Unsteady aerodynamic modeling of aircraft control surfaces by indicial response methods,” AIAA Journal, vol. 52, no. 12, pp. 2683–2700, 2014. [Google Scholar]
13. M. Goman and A. Khrabrov, “State-space representation of aerodynamic characteristics of an aircraft at high angles of attack,” Journal of Aircraft, vol. 31, no. 5, pp. 1109–1115, 1994. [Google Scholar]
14. I. Gursul, “Recent developments in delta wing aerodynamics,” The Aeronautical Journal, vol. 108, no. 1087, pp. 437–452, 2004. [Google Scholar]
15. A. Boutemedjet, M. Samardžić, L. Rebhi, Z. Rajić and T. Mouada, “UAV aerodynamic design involving genetic algorithm and artificial neural network for wing preliminary computation,” Aerospace Science and Technology, vol. 84, pp. 464–483, 2019. [Google Scholar]
16. M. Patil, R. Gawade, S. Potdar, K. Nadaf, S. Suresh et al., “Effect of vortex generator on the flow field over a conventional delta wing in subsonic flow condition at higher angles of attack,” FME Transactions, vol. 49, no. 2, pp. 395–400, 2021. [Google Scholar]
17. A. Epikhin, “Numerical simulation of the unsteady aerodynamic loads on the tail fin in the vortex breakdown flow,” Progress in Computational Fluid Dynamics, an International Journal, vol. 21, no. 5, pp. 274, 2021. [Google Scholar]
18. S. Chin and C. Lan, “Fourier functional analysis for unsteady aerodynamic modeling,” AIAA Journal, vol. 30, no. 9, pp. 2259–2266, 1992. [Google Scholar]
19. L. Hu, J. Zhang, Y. Xiang and W. Wang, “Neural networks-based aerodynamic data modeling: A comprehensive review,” IEEE Access, vol. 8, pp. 90805–90823, 2020. [Google Scholar]
20. D. Ignatyev and A. Khrabrov, “Neural network modeling of unsteady aerodynamic characteristics at high angles of attack,” Aerospace Science and Technology, vol. 41, pp. 106–115, 2015. [Google Scholar]
21. D. Ignatyev and A. Khrabrov, “Experimental study and neural network modeling of aerodynamic characteristics of canard aircraft at high angles of attack,” Aerospace, vol. 5, no. 1, pp. 26, 2018. [Google Scholar]
22. S. Jović, “Prediction of aerodynamics performance of continuously variable-speed wind turbine by adaptive neuro-fuzzy methodology,” Engineering with Computers, vol. 36, no. 2, pp. 597–602, 2019. [Google Scholar]
23. A. Kumar and A. Ghosh, “ANFIS-delta method for aerodynamic parameter estimation using flight data,” Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, vol. 233, no. 8, pp. 3016–3032, 2018. [Google Scholar]
24. S. Nanda, V. Kulkarni, N. Sahoo and V. Menezes, “Sensitivity studies of ANFIS based force recovery technique towards prediction of aerodynamic load,” Flow Measurement and Instrumentation, vol. 80, pp. 101969, 2021. [Google Scholar]
25. T. Shanableh and K. Assaleh, “Feature modeling using polynomial classifiers and stepwise regression,” Neurocomputing, vol. 73, no. 10–12, pp. 1752–1759, 2010. [Google Scholar]
26. Y. Shin and J. Ghosh, “Ridge polynomial networks,” IEEE Transactions on Neural Networks, vol. 6, no. 3, pp. 610–622, 1995. [Google Scholar]
27. K. Assaleh and T. Shanableh, “Robust polynomial classifier using L 1-norm minimization,” Applied Intelligence, vol. 33, no. 3, pp. 330–339, 2009. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |