DOI:10.32604/cmc.2022.024989

| Computers, Materials & Continua DOI:10.32604/cmc.2022.024989 |  |
| Article |
A Chaotic Oppositional Whale Optimisation Algorithm with Firefly Search for Medical Diagnostics
1Singidunum University, 32 Danijelova Str., 11010, Belgrade, Serbia
2Department of Applied Cybernetics, Faculty of Science, University of Hradec Králové, 50003, Hradec Králové, Czech Republic
*Corresponding Author: K. Venkatachalam. Email: venkatachalam.k@ieee.org
Received: 07 November 2021; Accepted: 10 December 2021
Abstract: There is a growing interest in the study development of artificial intelligence and machine learning, especially regarding the support vector machine pattern classification method. This study proposes an enhanced implementation of the well-known whale optimisation algorithm, which combines chaotic and opposition-based learning strategies, which is adopted for hyper-parameter optimisation and feature selection machine learning challenges. The whale optimisation algorithm is a relatively recent addition to the group of swarm intelligence algorithms commonly used for optimisation. The Proposed improved whale optimisation algorithm was first tested for standard unconstrained CEC2017 benchmark suite and it was later adapted for simultaneous feature selection and support vector machine hyper-parameter tuning and validated for medical diagnostics by using breast cancer, diabetes, and erythemato-squamous dataset. The performance of the proposed model is compared with multiple competitive support vector machine models boosted with other metaheuristics, including another improved whale optimisation approach, particle swarm optimisation algorithm, bacterial foraging optimisation algorithms, and genetic algorithms. Results of the simulation show that the proposed model outperforms other competitors concerning the performance of classification and the selected subset feature size.
Keywords: Whale optimisation algorithm; chaotic initialisation; opposition-based learning; optimisation; diagnostics
Constructing algorithms to solve non-deterministic polynomial time hard problems (NP-hard) is not typically hard to do. However, executing such an algorithm can, in extreme cases, take thousands of years on contemporary hardware. Such problems are regarded as nearly impossible to solve with traditional approaches for finding a deterministic algorithm. Metaheuristics, as stochastic optimisation approaches, are useful for solving such problems. These approaches do not guarantee an optimum solution. Instead, they provide tolerable sub-optimal outcomes in a reasonable amount of time [1]. The optimisation process aims to discover a solution that is either optimum or near-to-optimal regarding the stated goals and given constraints. Since the turn of the century, many population-based stochastic metaheuristics have been developed to address challenging optimisation issues in both combinatorial and global optimisation [2].
Stochastic population-based metaheuristics begin the search process using a set of random points, but the process is led and directed by some mechanism from iteration to iteration. Natural systems and processes can be used to inspire the concepts that underpin the search mechanism. Some algorithms, such as genetic algorithms (GA) frequently become trapped in local optima. Hybridisation is one method for overcoming the aforementioned difficulties with metaheuristics.
The hybridisation should not be based on a random mix of hybridising algorithms, but rather on a specific analysis of the benefits and drawbacks of each method. Under some situations, the drawback of one algorithm (slow convergence, tendency to quickly become trapped in the local optimum, etc.) is overcome by combining with the structural portion of other algorithms. This can help fix common issues of the original optimal solution search method.
In contrast to deterministic optimisation methods that ensure the optimum answer, heuristic algorithms aim to discover the best possible solution, without ensuring that the optimal solution is obtained [3,4] Many practical and benchmarking problems cannot be solved using deterministic approaches as their solving is dawdling. Since heuristic algorithms are robust, academics worldwide have been interested in their improvement. This has led to the development of metaheuristics for a variety of problems. Metaheuristics is used to create heuristic techniques for solving different kinds of optimisation problems. Two main groups of metaheuristics are those which are inspired and which are not nature-inspired. Metaheuristics inspired by nature can be additionally categorised as evolutionary algorithms (EA) and swarm intelligence. Swarm intelligence has recently become a major research field and they are proven as methods that are able to achieve outstanding results in different fields of optimisation [5–8].
Besides metaheuristics, machine learning is another important domain of artificial intelligence. Notwithstanding good performance of machine learning models for various classification and regression tasks, there are still some challenges from this domain that should be addressed. Among two most important challenges are feature selection and hyper-parameters’ optimisation. Performance of machine learning models to the large extend depend on the un-trainable parameters, which are known as the hyper-parameters and finding optimal or suboptimal values of such parameters for concrete problem is NP-hard task itself. Moreover, machine learning models utilize large datasets with many features and typically only subset of such features has significant impact on the target variable. Therefore, the goal of feature selection is to choose a subset of features and to eliminate redundant ones.
Study shown in this article proposes a new approach based on the well-known whale optimisation algorithm (WOA), which belongs to the group of swarm intelligence metaheuristics. Proposed improved WOA was first tested for standard unconstrained CEC2017 benchmark suite and it was later adapted for simultaneous feature selection and support vector machine (SVM) hyper-parameter tuning and validated for medical diagnostics by using breast cancer, diabetes, and erythemato-squamous datasets. The contributions of this research are twofold. First, an improved version of the WOA, that addresses known deficiencies of the basic version by implementing the concepts of chaotic initialisation and opposition-based learning (OBL), and by incorporating the firefly search (FS), has been proposed, Second, proposed method was adopted for simultaneously optimisation of SVM hyper-parameters and feature selection and achieved better performance metrics than other contemporary classifiers for three medical benchmark datasets.
The rest of the manuscript is structured as follows. Section 2 presents an overview of the recent swarm intelligence applications. Section 3 introduces the WOA metaheuristics, their improvements, and proposes the hybrid SVM optimisation approach. Section 4 exhibits the experimental findings and the discussion. The last section brings the final remarks, proposes a future work, and concludes the article. The authors hope to provide an accurate feature detection method used for their diagnostics.
Swarm intelligence is based on natural biological systems, and function with a population of self-organising agents who interact with one another locally and globally with their environment. Although there is no central component that governs and directs individual behaviour, local interactions between agents result in the formation of globally coordinated behaviour. The swarm intelligence algorithm can produce quick, inexpensive and high-quality solutions for challenging optimisation problems [9].
In swarm intelligence algorithms, a swarm is a population consisting of simple homogeneous agents. The swarm might have direct or indirect interactions. Direct interactions refer to audio or visual situations, touch, etc. In indirect interactions, agents are affected by the environment and changes made to it, which can be a result of other agents’ actions, or from external influences.
The operators of evolutionary algorithms, notably selection, crossover and mutation, also employ swarm metaheuristics. The crossover operator is employed to look for quicker convergence in a single sub-domain. Mutations help avoid local optima and are used for random searching. The selection operator enables the system to move to the desired conditions.
Popular implementations of swarm intelligence algorithms are the particle swarm algorithm (PSO) [10], the ant colony optimisation (ACO) algorithm [11], the wasp swarm (WS) algorithm [12], the stochastic diffusion search (SDS) algorithm [13], the artificial bee colony (ABC) algorithm [14], the firefly search (FS) algorithm [15], whale optimisation algorithm (WOA) [16], the multi-swarm optimisation (MSO) algorithm [17], the krill herd (KH) algorithm [18], the dolphin echolocation (DE) algorithm [19], etc. Each of these algorithms, as well as many others which fall into this category, have strengths and weaknesses for different optimisation problems. One algorithm may outperform the other when applied to one problem and significantly under perform on another.
As already noted in Section 1, swarm intelligence has seen successful application to different areas of optimisation. Research proposed introduces a variety of the swarm intelligence algorithm, tested on Himmelblau's nonlinear optimisation and speed reducer design problems, and used to attempt to solve problems such as the travelling salesman problem, the robot path planning problem etc. The study presented in [20] reviews earlier works and concludes that there is strong applicability of swarm intelligence algorithms for solving complex practical problems. Authors give overviews of the application of the swarm intelligence algorithm for swarm robotics. A chapter in [21] presents interesting insights and predictions about the use of the swarm intelligence algorithm for swarm robotics in the future. Study presented in [22] provides detailed reviews of the swarm intelligence algorithm and its practical implementation, from early conceptions in the late 80s onward. Aside from application in robotics, swarm intelligence algorithms have found application in computer networks [23,24], power management [25], engineering [26,27], Internet of things [28], social network analysis [29], medical diagnostics [30,31], data mining [32], etc.
Algorithms such as PSO and GA are known to get trapped in sub-optimal search space regions. Algorithms based on maritime animal behaviour are a relatively recent addition to the field of swarm intelligence algorithm research. Aside from the WOA, there are several notable algorithms reported in the literature, inspired by animal behaviour. Review [33] gives a review of other evolutionary algorithms inspired by animals for a specific problem optimisation. However, their review covers a range of maritime animal-inspired algorithms. Study [34] gives an overview of other animal behaviour inspired algorithms, not limited to maritime animals. Research proposed in [35] modifies the salp swarm algorithm optimisation [36,37], based on the salps sailing and foraging behaviour. Work presented introduces a dolphin inspired swarm optimisation algorithm with mimics the dolphins hunting technique, using their available senses. Research presented in demonstrates an optimisation algorithm modification on five real-life engineering problems, etc.
In recent years, SI was frequently applied in different scientific fields with promising results, usually targeting NP-hard problems from the fields of computer science and information technology. Applications include global numerical optimisation problem wireless sensor network efficiency [38], localisation and prolonging the overall lifetime [39,40] and cloud task scheduling [41,42].
Finally, swarm intelligence has also been successfully combined with machine learning models and in this way hybrid methods were devised. Some example of such approaches include: training and feature selection of artificial neural network (ANN) [43–49], assisting prediction of COVID-19 cases [50,51], hyper-parameters tuning [52–54] etc.
The methodology of this research can be expressed in seven steps, of which the first step was performed manually when all input datasets were acquired from different sources, and the second-to-last step was also automated for the ease of multiple re-runs when needed, like others those before it, but its execution is done manually upon successful completion of the following steps:
■ Download and normalise the datasets;
■ Randomly split the datasets into 10 sets of training and testing data;
■ Execute the optimisation algorithm for the given number of iterations;
■ Randomly split the originally downloaded datasets into 10 new validation sets;
■ Perform predictions with the trained model using the validation sets;
■ Evaluate the prediction results;
■ Compare results of this study to results from previous research.
3.1 Overview of Basic Whale Optimisation Algorithm
Whales are highly intelligent animals that have twice the number of brain cells similar to human spindle cells, which are responsible for emotions, decision making and social behaviour. Whales are often found in social groups, of families. Most whales prey on fish. Fish are much faster than whales. Because of this, some whales have developed a hunting method that allows them to hunt schools of fish. This method is often called the bubble-net feeding method. Researchers have found two variations of this method, which whales use. A part of this method is an approach where whales encircle their prey in a spiral manoeuvre. They dive down below the school of fish and start circling in a spiral path, slowly working their way to the surface, all the while creating a wall of bubbles above their traversed path. This wall of bubbles directs fish in an ever-smaller area as the circular path becomes smaller and smaller. Finally, the whale can capture large parts of the school as it reaches the surface. Whales do not know where the school of fish is located, ahead of time. This method helps them locate the fish after the manoeuvre. This feeding method is a direct inspiration of the WOA, which is mathematically modelled and used to perform optimisation [55]. This method can be used to search for the optimal location within the search space, and can be presented by these equations:
In Eqs. (1)–(5),
In Eq. (6),
By assigning random values to
In Eqs. (8) and (9),
The pseudo-code of the WOA can be found in a paper whereas a modified WOA with simultaneous hyper-parameter tuning is implemented.
The model representing this experimental setup is further explained in the model section. The proposed model balances the searching and utilising features of the algorithm. These results can be further improved by using multi-swarm mechanisms, as reported in the original paper. In addition to this modification, the paper suggests modifying the population generation process. Instead of using a random feature selection for each agent in a population, it suggests generating the population-based on chaos theory. In this approach, a chaos progression, sensitive to initial conditions, is used to modify the best agents from the previous population when generating the next population.
This can be achieved by introducing a self-adapting chaotic disturbance mechanism, expressed as:
In Eq. (10),
3.2 Drawbacks of the Original WOA and Proposed Improved Method
The basic WOA implementation has impressive performances, and it is considered to be a very powerful optimiser. However, the extensive experimentations with different benchmark functions sets have revealed drawbacks that can hinder the performances of the WOA under some circumstances. Namely, the basic WOA suffers from scarce exploration and inappropriate intensification-diversification trade-off, which can limit the algorithm's power to explore different promising areas of the search domain and lead to getting stuck in the local optima. Consequently, in some runs, the basic WOA will not converge to the optimal areas of the search domain, obtaining poor mean values. To address these deficiencies, the proposed enhanced WOA metaheuristics incorporate three mechanisms: chaotic population initialisation, OBL, and FS [60].
The first proposed enhancement is the chaotic population initialisation, which was first proposed in [61]. The majority of the metaheuristics depend on random generators, but recent publications suggest that the search can be more intense if chaotic sequences are utilised Numerous chaotic maps exist today, including circle, Chebushev, iterative, sine, tent, logistic, singer and many more. After thorough experimentations with all mentioned maps, the most promising results were obtained with a logistic map, which has been consequently chosen for implementation in WOA.
The second mechanism that was incorporated in the proposed modified WOA is OBL, first introduced in [62]. The OBL procedure gained popularity fast as it can significantly improve both intensification and diversification processes. The OBL procedure is applied in two stages, first when the initial population is spawned and when a new population is spawned after completing the evaluation and finding the best agent
In Eq. (11),
In Eq. (12),
In Eq. (13), the new population becomes the original population P, afterwards joined with the opposing population
To incorporating the FS mechanism in the proposed modified WOA,
In Eq. (14),
In Eq. (15), the distance is calculated for each dimension of the given solution s and parameter p on all agents of the population, where
Inspired by introduced enhancements, proposed method is named chaotic oppositional WOA with firefly search (COWOAFS-SVM).
The proposed modified WOA can be expressed with the pseudo-code depicted in Algorithm 1.

Experimental result cross-validation analysis is performed. These results are averaged to attain the result for each of the datasets and aggregated by each of the features of these datasets. Results are presented in the experimental results section and further explained in the discussion section of the paper.
4 Experimental Setup, Comparative Analysis and Discussion
For this research, the original algorithm and the algorithm created using the meta-heuristic approach with feature selection and simultaneous hyper-parameter tuning driven by the modified swarm intelligence algorithm are evaluated. This approach was proven to give favourable results in earlier research. Finally, both these algorithms were tested using 30 standard unconstrained benchmarking functions. To test the modified algorithm, first a set of standard benchmark functions retrieved from the well-known Congress on Evolutionary Computation (CEC) benchmark function suite, and afterwards, the proposed method vas validated for SVM hyper-parameter tuning and feature selection. In both experiments, proposed improved WOA was tested with the parameters as suggested in the original paper.
4.1 Standard CEC Function Simulations
The proposed method is tested on a set of standard bound-constrained benchmarks from the CEC benchmark suite [63]. Statistical results of these benchmarks are presented in the results section. Functions with a single global optimum (F1–F7) are used to evaluate the capability of exploitation. Functions with many local optimums (F8–F23) are used to evaluate the capability of exploration. Functions (F24–F29) are used to evaluate the algorithms ability to escape local minima, as they are a set of very challenging functions. The proposed algorithm was run 30 times for each benchmark function, every time with a different population. Algorithms included in comparative analysis were implemented for the purpose of this study and tested with default parameters. Opponent algorithms include: Harris hawks’ optimisation (HHO) [64], improved HHO (IHHO) [65], differential evolution (DE) [66], grasshopper optimisation algorithm (GOA) [67], grey wolf optimizer (GWO) [68], moth-flame optimisation (MFO) [69], multi-verse optimizer (MVO) [70], particle swarm optimisation (PSO), whale optimisation algorithm (WOA), sine cosine algorithm (SCA) [71] and firefly algorithm (FA).
This research utilizes the same approach presented. The research presented in reported the results with N = 30 and T = 500. Since the proposed COWOAFS-SSVM algorithm uses more FFE in every run, the max FFE was utilised as the finish criteria. All other methods use one FFE per solution during the initialisation and update phase, and to provide fair analysis, max FFE was set to 15,030 (N + N
The reported results from the Tab. 1 show that the proposed COWOAFS-SVM metaheuristics obtained the best results on 30 benchmark functions, and was tied for the first place on seven more occasions. By conducting a comparison of the results of COWOAFS-SVM against the basic WOA and FA, it is clear that hybrid algorithm outperformed basic versions on every single benchmark instance.
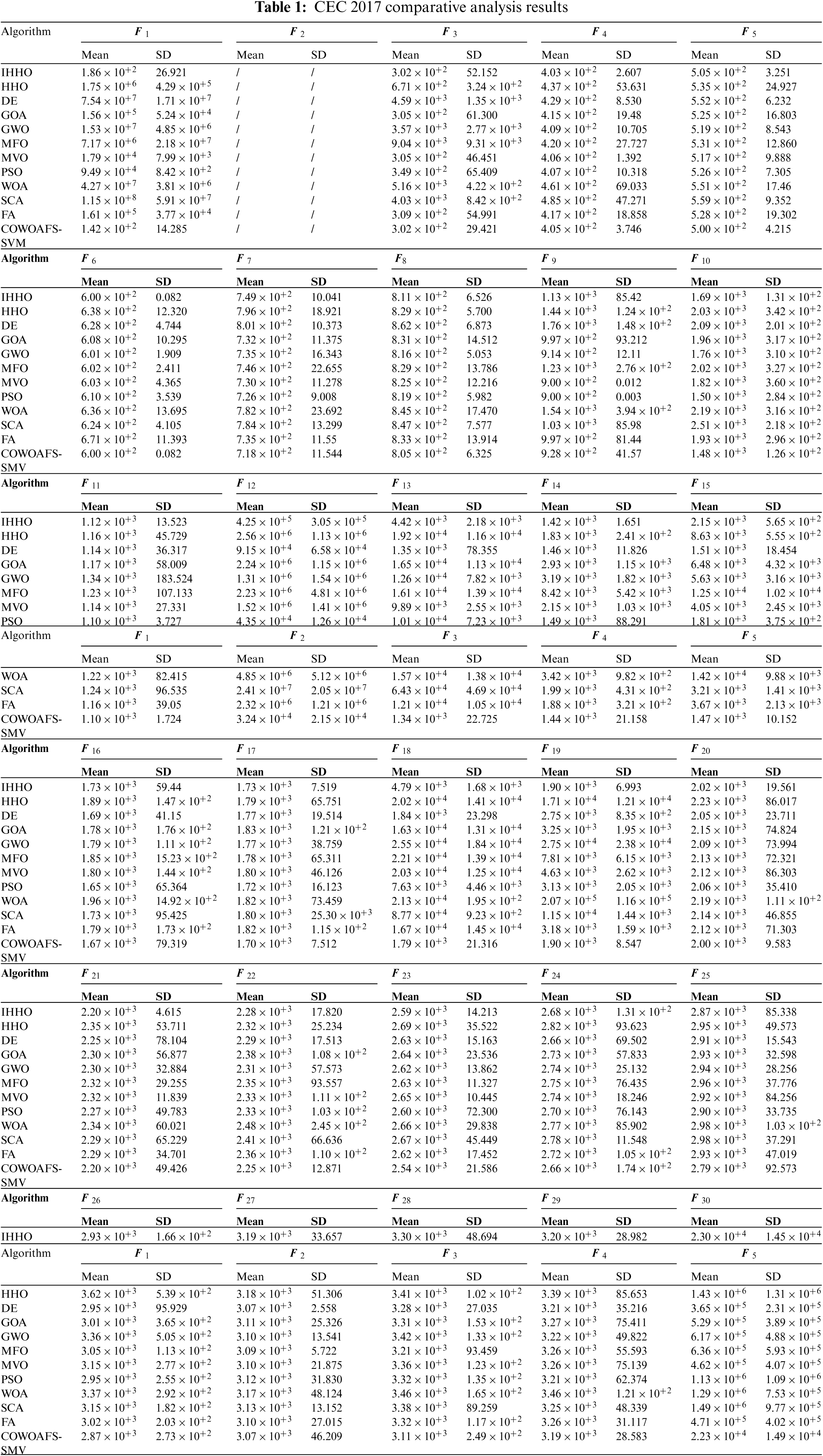
On some functions, the proposed COWOAFS-SVM drastically improved the results of the basic variants; such is the example of F1, where it obtained 1000 times better results than the basic WOA and FA. Overall results indicate that the proposed COWOAFS-SVM outperformed significantly all approaches covered by the research.
Dispersion of solutions over 50 runs for some algorithms and chosen functions are shown in Fig. 1.
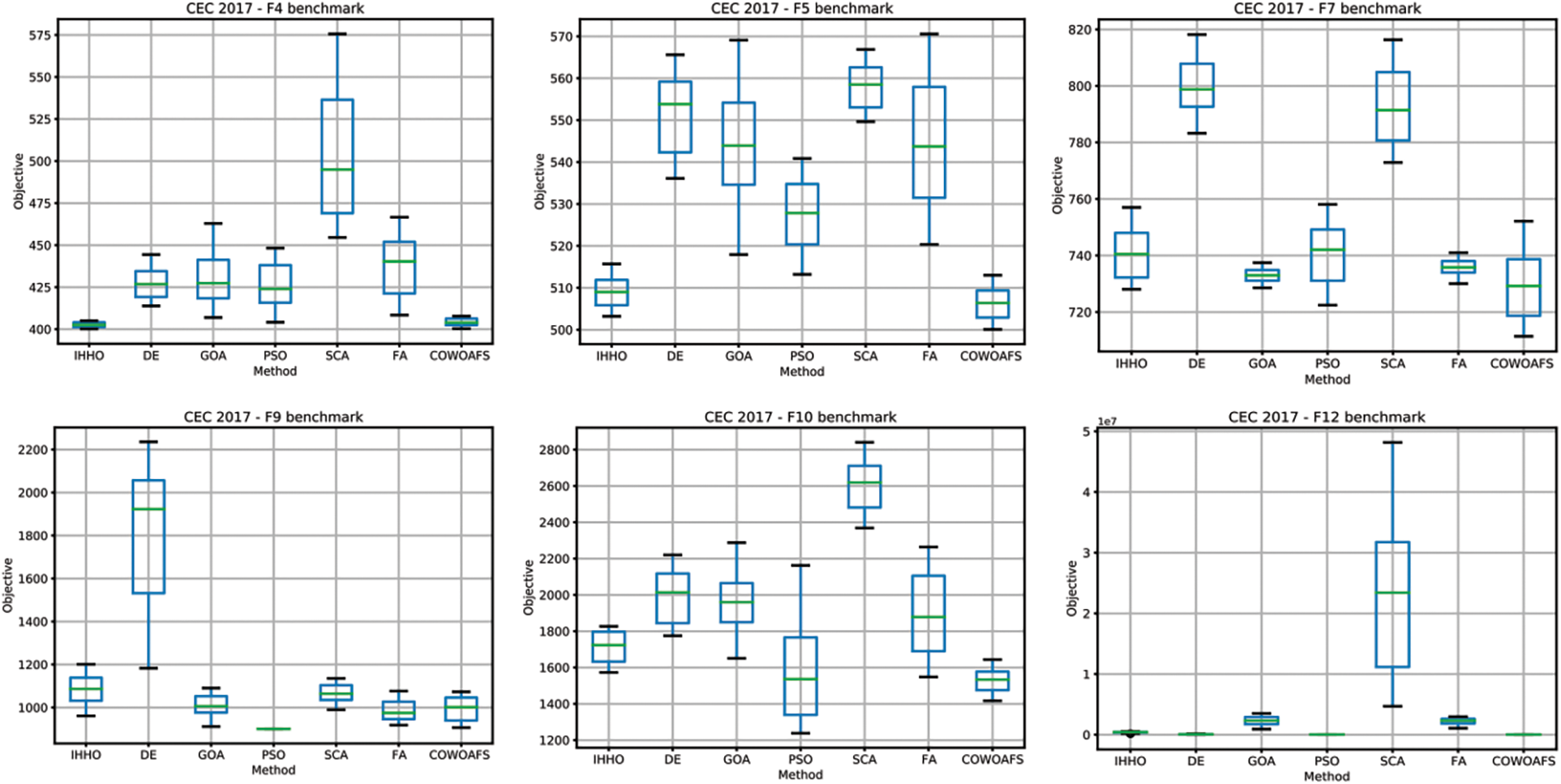
Figure 1: Dispersion of solutions of benchmark functions F4, F5, F7, F9, F10 and F12
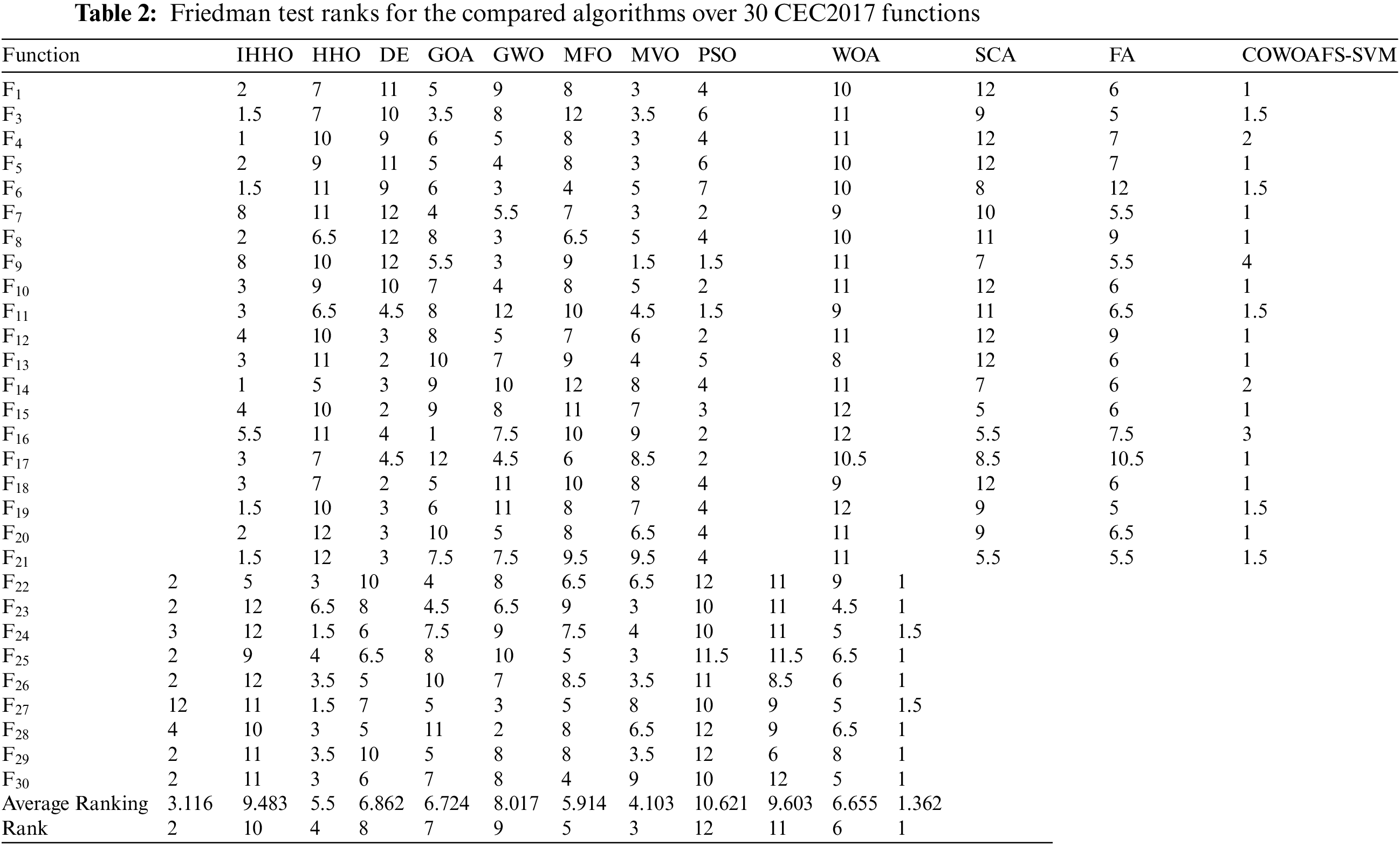
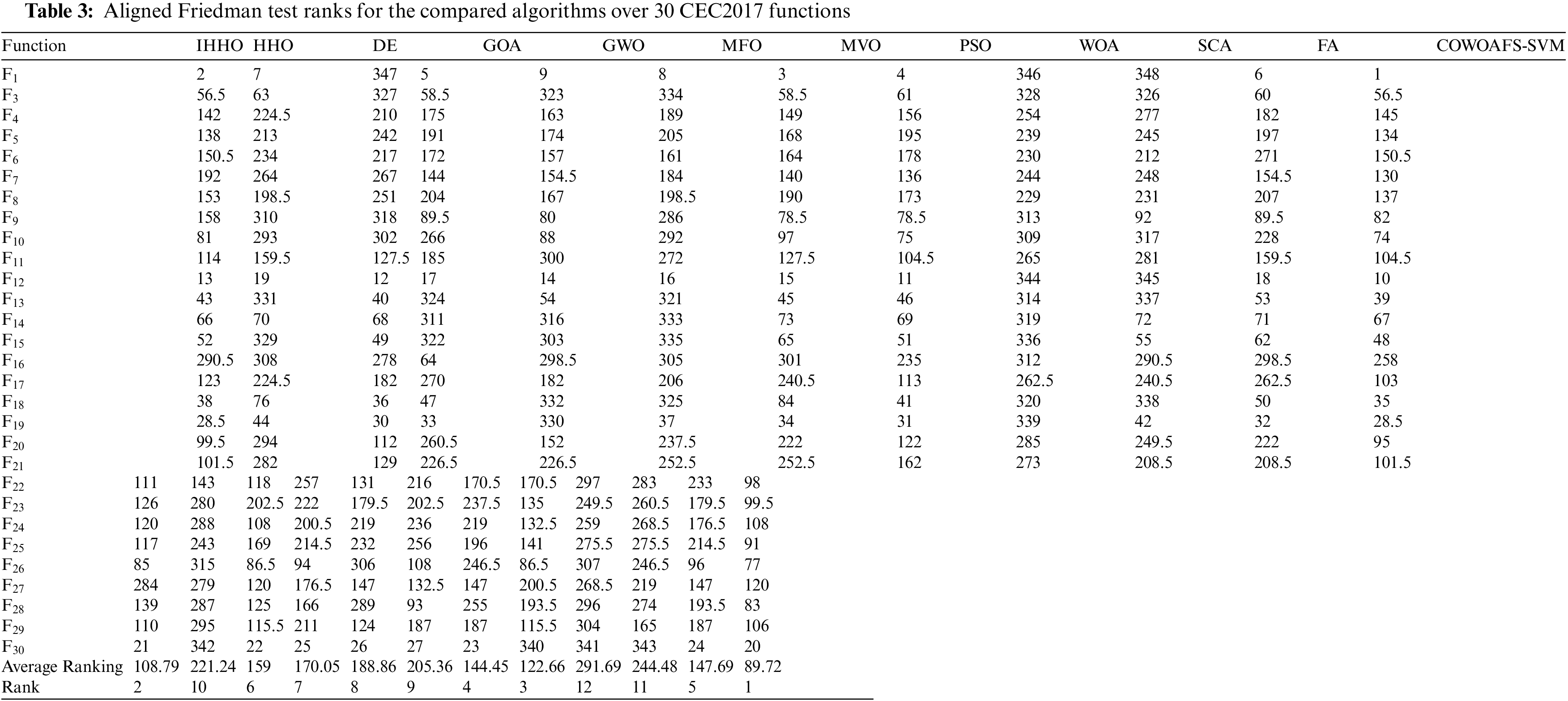
To statistically validate the significance of the proposed method, the Friedman test and the two variance ranking analysis were performed. Tabs. 2 and 3 depict the results obtained by twelve observed algorithms on the set of 30 CEC2017 benchmark functions for Friedman test ranks and aligned Friedman ranks, respectively. It is clear from both tables that the proposed COWOAFS-SVM significantly outperformed all other algorithms.
Finally, the Iman and Davenport test has also been conducted, as it can provide better results than

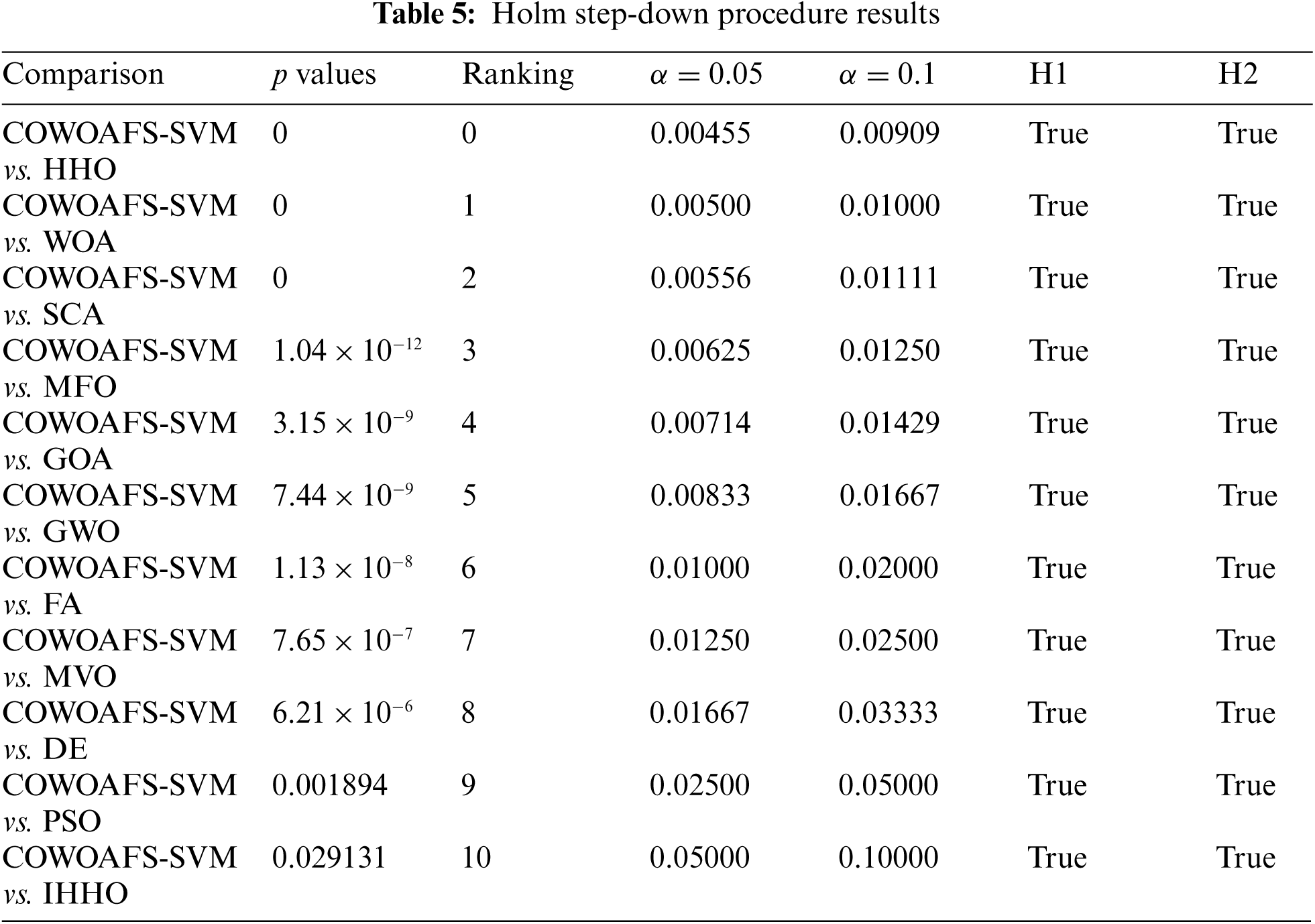
Additionally, Friedman statistics (184.40) is larger than the
As the null hypothesis has been rejected by both statistical tests that were executed, the non-parametric Holm step-down procedure was also performed, and results are shown in Tab. 5.
4.2 Hyper Parameters Tuning and Feature Selection Experiments
This section first describes the SVM parameters that have been subjected to the optimisation process, followed by the short description of the datasets, pre-processing and metrics utilised to measure the performances. Lastly, in this section, results of the conducted experiments are presented, with the comparative analysis against other current methods, tested on the same problem instances.
For the purpose of this study, all methods included in comparative analysis are implemented and tested with control parameters, as suggested in the original paper [30]. All methods were tested over the course of 150 iterations and the results are average of 10 independent runs, as per the restraints of the experimental setup, suggested in [30]. The experiment was conducted in following the specifications laid out in the proposed methodology, starting with the acquisition, normalisation and preparation of all input datasets for the experiment, following a series of steps, as explained earlier, securing separate training and testing sets, using the former in the proposed algorithm and the later to evaluate the prediction results.
This section proposes the application of the devised COWOAFS-SVM algorithm to improve the efficacy of the SVM model (with and without the feature selection) on three standard benchmark medical diagnostic datasets, as described in the referred paper [5]. The datasets included in the research deal with common illness, namely breast cancer, diabetes and erythemato-squamous (ES) disease.
Similarly as in [5], only two SVM hyper-parameters were considered: penalty parameter (C) and kernel bandwidth of kernel function (γ). Each agent is encoded as an array of two elements (C and γ). The search boundaries for C parameter are in range {2−7.5, 2−3.5,…, 27.5}, and for γ in range {2−7.5, 2−3.5,…, 27.5}.
This article presents the experimental results of the modified WOA on several datasets, inherited from the original study. Datasets used for this experiment cover diseases affecting many people, such as breast cancer, diabetes and erythemato-squamous. Breakthroughs in diagnostic and detection methods for these diseases are unquestionably beneficial. All features commonly extracted from input sources, used in the diagnostic of these diseases are available in digitised forms from different databases:
■ The breast cancer dataset was acquired from the Wisconsin breast cancer database.
■ The database dataset was acquired from Pima Indian heritage and contains anonymized data about their female patients.
■ The dermatology database has clinical and histopathological data, acquired, normalised, and prepared in the same manner as explained in [30].
The original study gives full descriptions and details of all three datasets.
Values from these datasets are normalised to [−1, 1] to avoid calculation issues and dominance and drag that much lower or much greater values may have on results. This normalisation strategy is performed on the dataset at the very beginning. Each dataset was split into ten segments to ensure more reliable and stable experimental results. Each run was repeated ten times to improve these results.
The final results are averaged. To assure comparability of the results of this study with the results reported in the earlier study, this setup was limited to the same parameters of the population, iteration count, repetitions and segmentation of the datasets. This way, the hardware impact is eliminated and only the final performance of the optimisation of the target function is measured.
The algorithm performance evaluation was inherited from the original research [30], to ensure result comparability. These metrics are:
In Eqs. (16)–(18), formulas are given for the classification accuracy, and measurements are the sensitivity and the specificity, all referring to the tested algorithm. Values TP, TN and FN are numbers of true positives, true negatives and false negatives, respectively. All values are expressed in percentage.
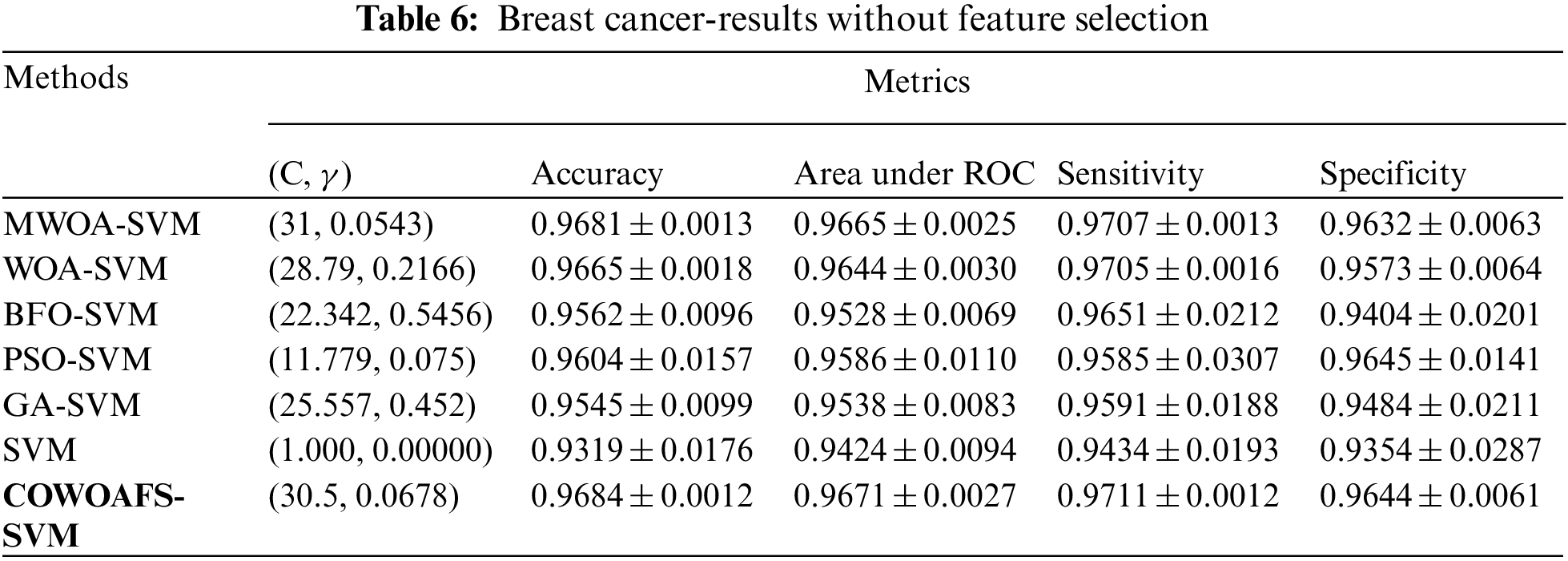
The results of this experimental research are shown in this section. The performances of the proposed COWOAFS-SVM method were compared to the results published in [30]. To provide valid grounds for the comparisons, this research utilised the same experimental setup and datasets as in [30]. The results for MWOA-SVM, WOA-SVM, BFO-SVM, PSO-SVM, GA-SVM and pure SVM were also taken from [30].
Results Pertaining to Breast Cancer Diagnostics
The breast cancer dataset is comprised of 699 entries, 458 of which were benign, while 241 were malignant. The performances of the proposed COWOAFS-enhanced SVM method without feature selection are shown in Tab. 6 and with feature selection in Tab. 7. The results show average values obtained through 10 independent runs of ten-fold CV. The results indicate that the SVM structure generated by the COWOAFS-SVM algorithm outperforms all other SVM approaches, in terms of accuracy, area under curve, sensitivity and specificity. COWOAFS-SVM achieved average accuracy of 96.84%, together with the standard deviation that is smaller than the results of the MWOA-SVM and other compared methods, indicating that the COWOAFS-SVM is capable of producing consistent results.
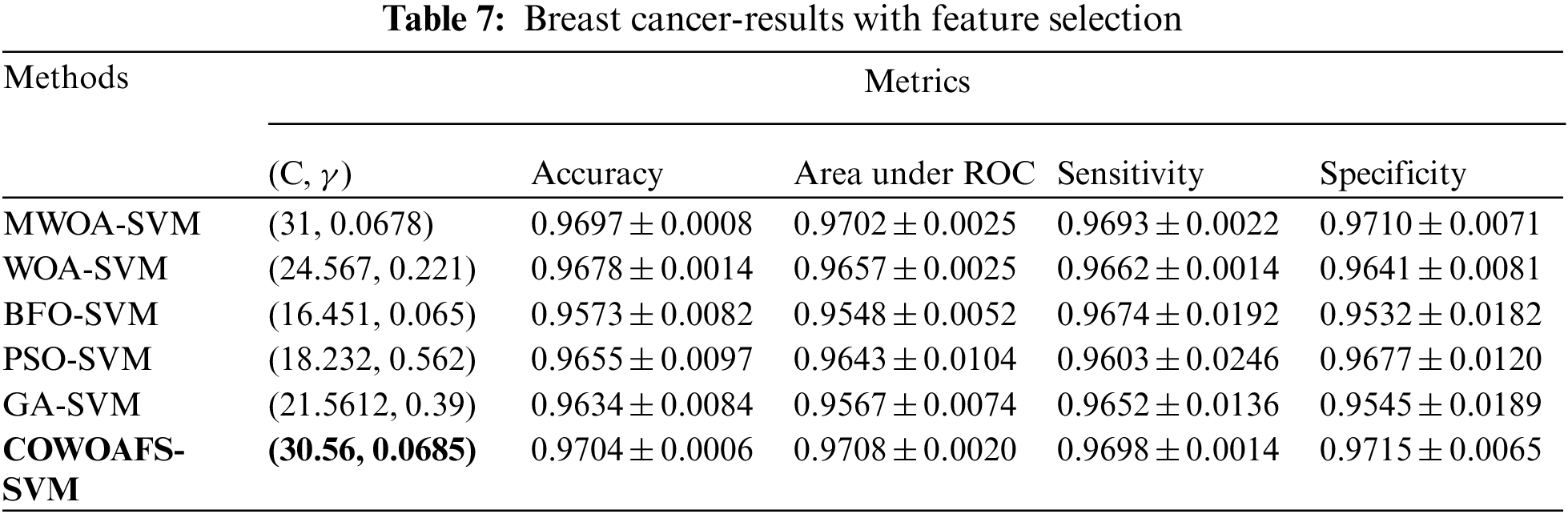
Similarly as in [30], the performances of the proposed COWOAFS-SVM method were further enhanced by performing the optimisation of the SVM structure and feature selection together. The proposed method once again outperformed all competitors, by achieving the accuracy of 97.04%, the best values for area under curve, sensitivity and specificity, while having the smallest standard deviation.
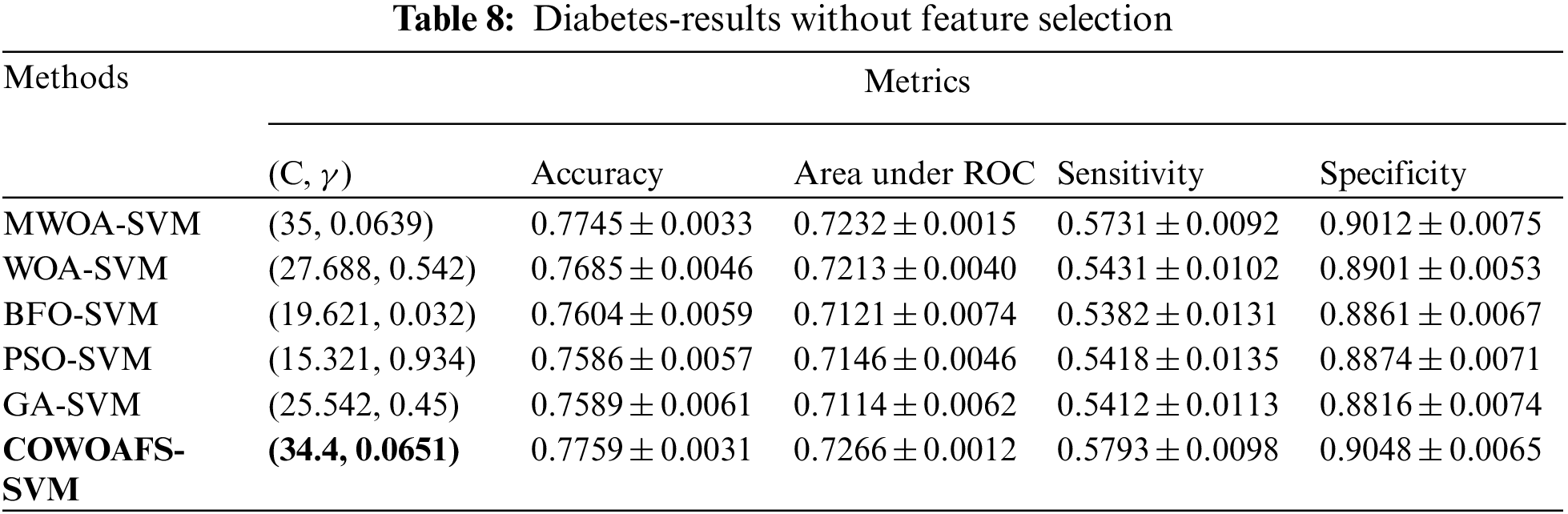
Results Pertaining to Diabetes Diagnostics
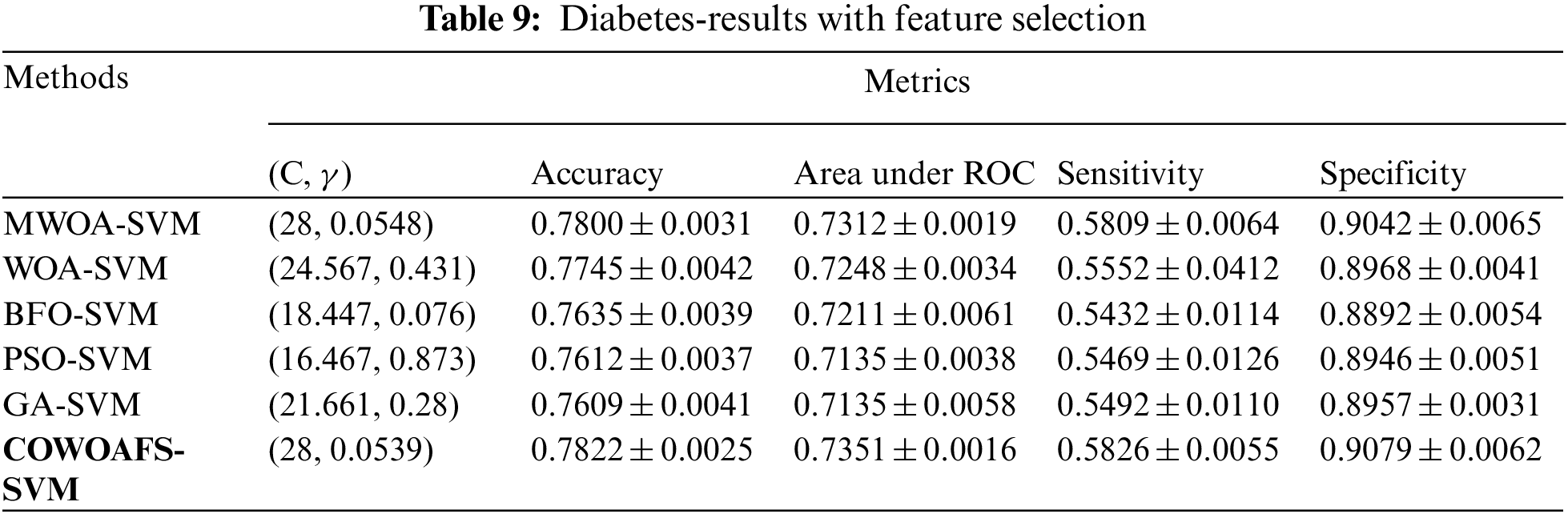
The second dataset related to the diabetes diagnostics consisted of 768 entries, 268 belonging to the diabetic patients, while 500 were normal healthy instances. The results of the proposed approach without feature selection are shown in Tab. 8. It can be clearly seen that the proposed COWOAFS-SVM approach outperformed all other competitors, for which the results were taken from paper [30]. The average metrics of ten runs show the accuracy of 77.59%, which is slightly better than MWOA-SVM, and significantly better than other compared methods. Other metrics are also in favour of the proposed COWOAFS-SVM method, including the smallest standard deviation values.
Tab. 9 depicts the results obtained by the proposed COWOAFS-SVM approach with feature selection, from ten runs of ten-fold CV. Once again, the results clearly indicate that the proposed method outperformed other Metaheuristic based approaches in terms of accuracy, area under curve, sensitivity and specificity, while having the smallest values of the standard deviation.
Results Pertaining to ES Disease Diagnostics
The ES disease dataset consisted of 358 instances with 34 features and six classes of diseases. As in paper [30], the only metric that was utilised is the accuracy, because of the multi-classification nature of the challenge. Tabs. 10 and 11 contain results attained using the proposed COWOAFS-SVM method compared to competitor approaches, averaged on 10 runs of 10 ten-fold CV, without and with feature selection, respectively.
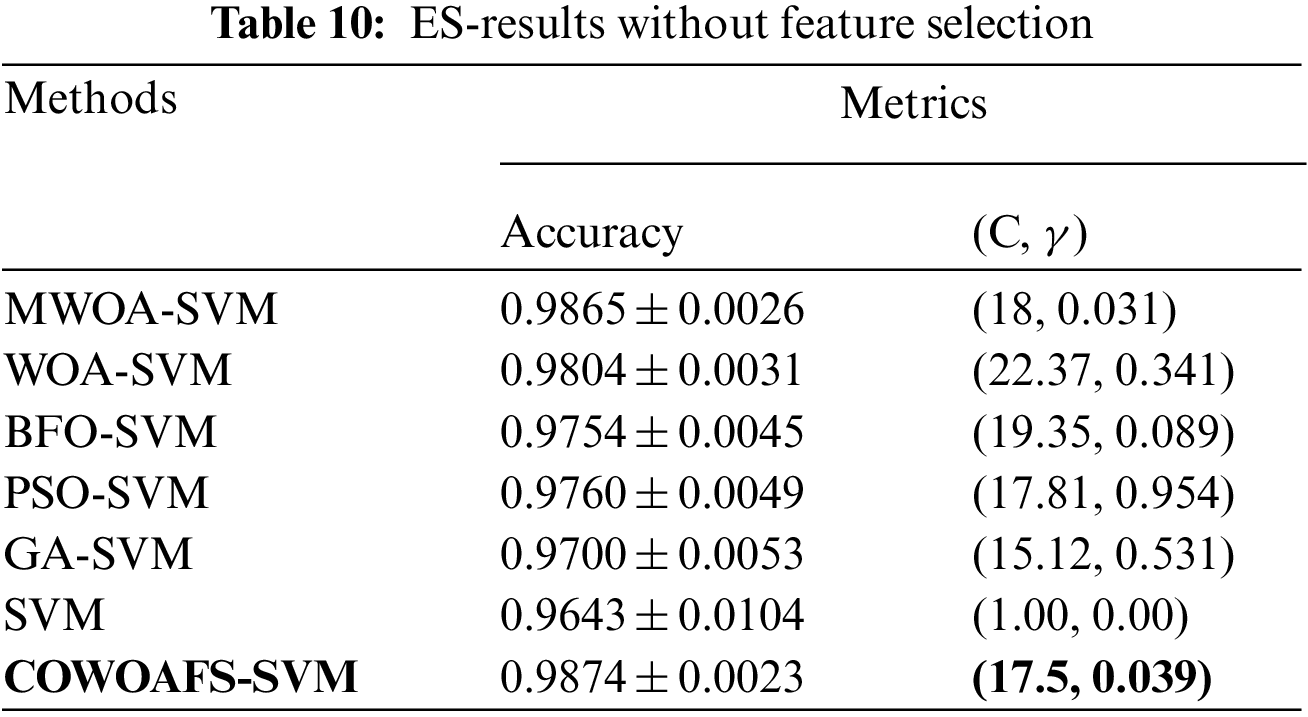
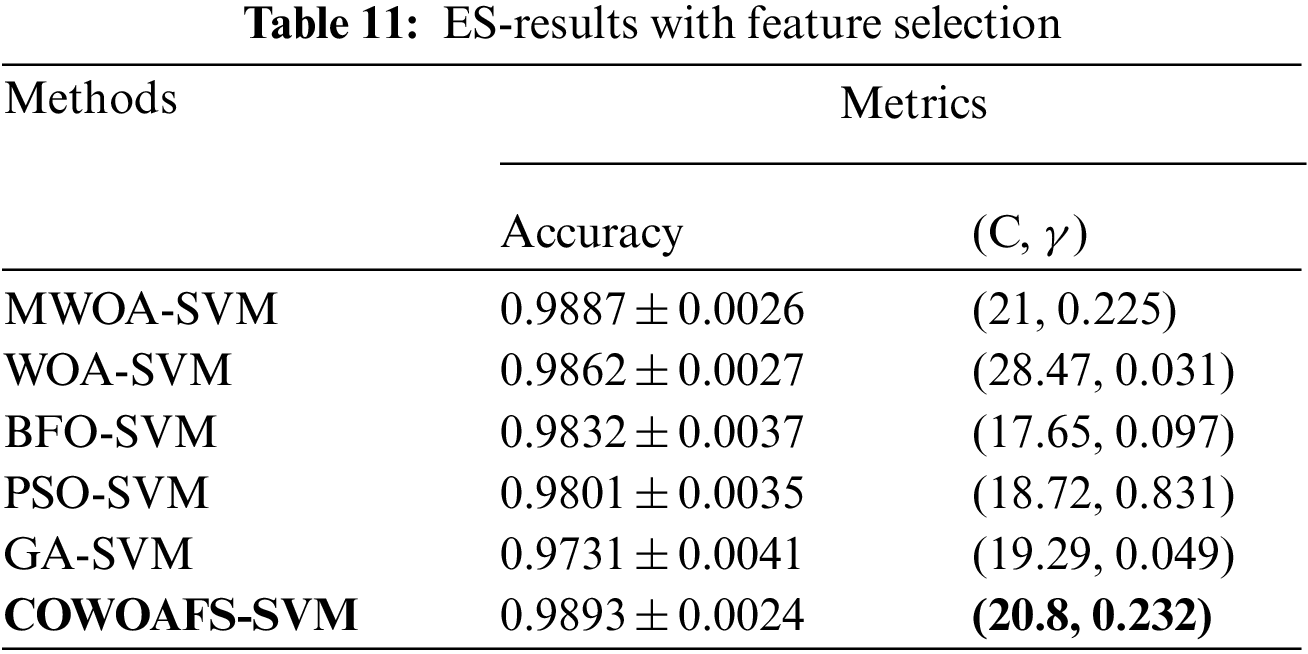
In both cases, the proposed method outperformed other competitors both in terms of highest accuracy achieved and smallest standard deviation, indicating consistent performances of the approach.
The presented research proposed a novel WOA method, enhanced with chaotic initialisation, opposition-based learning and firefly search, which was later utilised to improve the performances of the SVM for medical diagnostics. The experimental findings listed in the preceding section plainly show that the proposed COWOAFS-SVM enhanced SVM model obtained superior performances than other modern approaches subjected to the comparative analysis [5]. The proposed COWOAFS-SVM is capable of constructing a superior SVM with higher accuracy and consistency than other competitor methods. It is particularly interesting to compare the results of the proposed COWOAFS-SVM against the CMWOAFS-SVM, which obtained the best results in [5]. It is possible to conclude from the presented results that the proposed COWOAFS-SVM achieved significantly enhanced performances than CMWOAFS-SVM on all datasets used in the experiments. The improvement were observed both for the accuracy and other indicators (area under curve, sensitivity and specificity), as well as for the consistency of the results, that is reflected in the smaller average standard deviation.
To gain better insights into methods’ performance, convergence speed graphs for all methods included in comparative analysis with respect to accuracy are shown in Fig. 2.
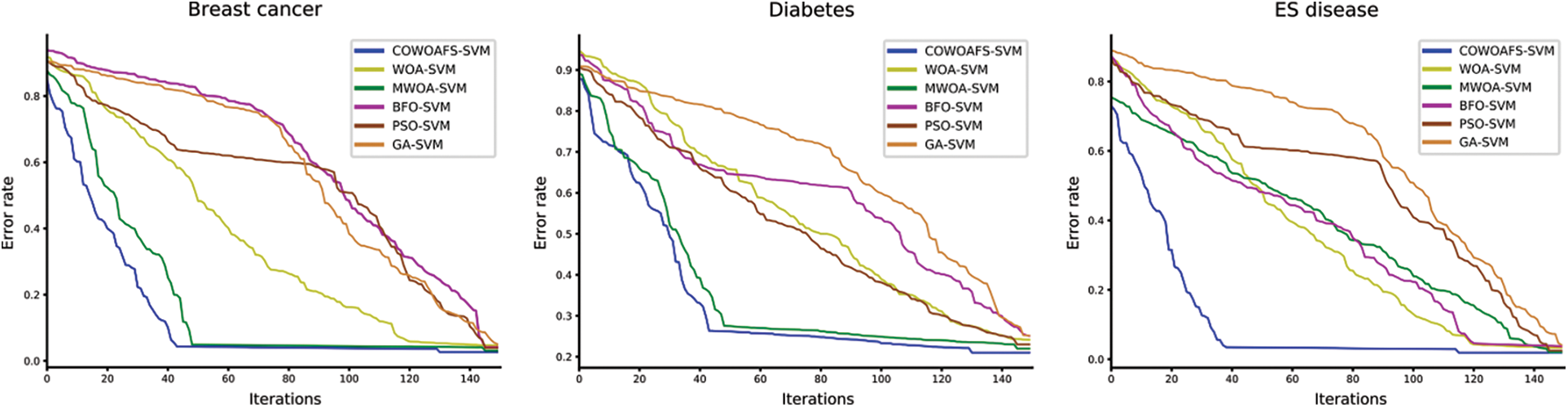
Figure 2: Average convergence speed graphs for classification error rate metrics for 150 iterations
In this paper, an improved model for simultaneous feature selection and hyper-parameter tuning for SVM is proposed. The algorithm that was utilised for improving SVM performances was based on the WOA SI metaheuristics. The proposed method was then used to improve the SVM for medical diagnostics of breast cancer, diabetes, and erythemato-squamous illnesses. COWOAFS-SVM was evaluated and compared to other state-of-the-art metaheuristics based approaches, and achieved superior performances both in terms of higher accuracy and consistency reflected through smaller values of the standard deviation on all three observed datasets. The achieved promising results indicate the possible direction of the future research, which will focus on validating the proposed model on other datasets from different application domains. The other direction of the possible future work is to apply the proposed COWOAFS-SVM metaheuristics in solving other challenging problems from wide spectrum of application domains, including cloud computing, optimisation of the convolutional neural networks, and wireless sensor networks.
Funding Statement: The authors state that they have not received any funding for this research.
Conflicts of Interest: The authors state that they have no conflicts of interest regarding this research.
1. J. C. Spall, “Stochastic Optimization,” in Handbook of Computational statistics, Berlin, Heidelberg: Springer, pp. 173–201, 2012. [Google Scholar]
2. Z. Beheshti and S. M. H. Shamsuddin, “A review of population-based meta-heuristic algorithms,” International Journal of Advances in Soft Computing and Its Applications, vol. 5, pp. 1–35, 2013. [Google Scholar]
3. L. T. Biegler and I. E. Grossmann, “Retrospective on optimization,” Computers & Chemical Engineering, vol. 28, pp. 1169–1192, 2004. [Google Scholar]
4. S. Desale, A. Rasool, S. Andhale and P. Rane, “Heuristic and meta-heuristic algorithms and their relevance to the real world: A survey,” International Journal of Computer Engineering in Research Trends, vol. 351, pp. 2349–7084, 2015. [Google Scholar]
5. J. Xue and B. Shen, “A novel swarm intelligence optimization approach: Sparrow search algorithm,” Systems Science & Control Engineering, vol. 8, pp. 22–34, 2020. [Google Scholar]
6. X. Dai, S. Long, Z. Zhang and D. Gong, “Mobile robot path planning based on ant colony algorithm with A heuristic method,” Frontiers in Neurorobotics, vol. 13, pp. 15, 2019. [Google Scholar]
7. W. Yong, W. Tao, Z. Cheng-Zhi and H. Hua-Juan, “A new stochastic optimization approach-dolphin swarm optimization algorithm,” International Journal of Computational Intelligence and Applications, vol. 15, pp. 1650011, 2016. [Google Scholar]
8. G. Dhiman and V. Kumar, “Spotted hyena optimizer: A novel bio-inspired based metaheuristic technique for engineering applications,” Advances in Engineering Software, vol. 114, pp. 48–70, 2017. [Google Scholar]
9. M. Mavrovouniotis, C. Li and S. Yang, “A survey of swarm intelligence for dynamic optimization: Algorithms and applications,” Swarm and Evolutionary Computation, vol. 33, pp. 1–17, 2017. [Google Scholar]
10. J. Kennedy and R. Eberhart, “Particle swarm optimization,” in Proc. of ICNN'95-Int. Conf. on Neural Networks, Perth, Australia, 1995. [Google Scholar]
11. M. Dorigo, V. Maniezzo and A. Colorni, “Ant system: Optimization by a colony of cooperating agents,” IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), vol. 26, no. 1, pp. 29–41, 1996. [Google Scholar]
12. P. Pinto, T. A. Runkler and J. M. Sousa, “Wasp swarm optimization of logistic systems,” in Adaptive and Natural Computing Algorithms, Vienna: Springer, 2005. [Google Scholar]
13. J. Bishop, “Stochastic searching networks,” in Proc. First IEE Int. Conf. on Artificial Neural Networks, London, UK, No. 313, pp. 329–331, 1989. [Google Scholar]
14. D. Karaboga, “An idea based on honey bee swarm for numerical optimization,” Computer Science Journal, vol. 200, pp. 1–10, 2005. [Google Scholar]
15. X. S. YANG, “Nature Inspired Metaheuristic Algorithms,” Bristol, UK: Luniver Press, 2008. [Online]. Available: https://dl.acm.org/doi/book/10.5555/2655295. [Google Scholar]
16. M. Seyedali and L. Andrew, “The whale optimization algorithm,” Advances in Engineering Software, vol. 95, pp. 51–67, 2016. [Google Scholar]
17. T. Hendtlass, “WoSP: A multi-optima particle swarm algorithm,” in Proc. IEEE Congress on Evolutionary Computation, Edinburgh, UK, Vol. 1, pp. 727–734, 2005. [Google Scholar]
18. A. H. Gandomi and A. H. Alavi, “Krill herd: A new bioinspired optimization algorithm,” Communications in Nonlinear Science and Numerical Simulation, vol. 17, no. 12, pp. 4831–4845, 2012. [Google Scholar]
19. A. Kaveh and N. Farhoudi, “A new optimization method: Dolphin echolocation,” Advances in Engineering Software, vol. 59, pp. 53–70, 2013. [Google Scholar]
20. L. Cao, Y. Cai and Y. Yue, “Swarm intelligence-based performance optimization for mobile wireless sensor networks: Survey, challenges, and future directions,” IEEE Access, vol. 7, pp. 161524–161553, 2019. [Google Scholar]
21. A. Nayyar and N. G. Nguyen, “Introduction to swarm intelligence,” Advances in Swarm Intelligence for Optimizing Problems in Computer Science, pp. 53–78, 2018. https://www.taylorfrancis.com/chapters/edit/10.1201/9780429445927-3/introduction-swarm-intelligence-anand-nayyar-nhu-gia-nguyen. [Google Scholar]
22. B. Jakimovski, B. Meyer and E. Maehle, “Swarm intelligence for self-reconfiguring walking robot,” in 2008 IEEE Swarm Intelligence Symp., St. Louis, MO, USA, pp. 1–8, 2008. [Google Scholar]
23. D. Liu and B. Wang, “Biological swarm intelligence based opportunistic resource allocation for wireless ad Hoc networks,” Wireless Personal Communications, vol. 66, pp. 629–649, 2011. [Google Scholar]
24. Y. Qawqzeh, M. T. Alharbi, A. Jaradat and K. N. Abdul Sattar, “A review of swarm intelligence algorithms deployment for scheduling and optimization in cloud computing environments,” PeerJ Computer Science, vol. 7, pp. e696, 2021. [Google Scholar]
25. S. Naka, T. Genji, T. Yura and Y. Fukuyama, “A hybrid particle swarm optimization for distribution state estimation,” IEEE Transactions on Power Systems, vol. 18, pp. 60–68, 2003. [Google Scholar]
26. S. Yuan, S. Wang and N. Tian, “Swarm intelligence optimization and its application in geophysical data inversion,” Applied Geophysics, vol. 6, pp. 166–174, 2009. [Google Scholar]
27. W. Zhao, Z. Zhang and L. Wang, “Manta ray foraging optimization: An effective bio-inspired optimizer for engineering applications,” Engineering Applications of Artificial Intelligence, vol. 87, pp. 103300, 2020. [Google Scholar]
28. S. Mishra, R. Sagban, A. Yakoob and N. Gandhi, “Swarm intelligence in anomaly detection systems: An overview,” International Journal of Computers and Applications, vol. 43, pp. 109–118, 2021. [Google Scholar]
29. R. Olivares, F. Muñoz and F. Riquelme, “A Multi-objective linear threshold influence spread model solved by swarm intelligence-based methods,” Knowledge-Based Systems, vol. 212, pp. 106623, 2021. [Google Scholar]
30. M. Wang and H. Chen, “Chaotic multi-swarm whale optimizer boosted support vector machine for medical diagnosis,” Applied Soft Computing, vol. 88, pp. 105946, 2020. [Google Scholar]
31. C. A. de Pinho Pinheiro, N. Nedjah and L. de Macedo Mourelle, “Detection and classification of pulmonary nodules using deep learning and swarm intelligence,” Multimedia Tools and Applications, vol. 79, pp. 15437–15465, 2019. [Google Scholar]
32. B. H. Nguyen, B. Xue and M. Zhang, “A survey on swarm intelligence approaches to feature selection in data mining,” Swarm and Evolutionary Computation, vol. 54, pp. 100663, 2020. [Google Scholar]
33. M. Jahandideh-Tehrani, O. Bozorg-Haddad and H. A. Loáiciga, “A review of applications of animal-inspired evolutionary algorithms in reservoir operation modelling,” Water and Environment Journal, vol. 35, pp. 628–646, 2021. [Google Scholar]
34. L. Torres Treviño, “A 2020 taxonomy of algorithms inspired on living beings behavior,” 2021. [Online]. Available: https://arxiv.org/. [Google Scholar]
35. Q. Zhang, H. Chen, A. A. Heidari, X. Zhao, Y. Xu et al., “Chaos-induced and mutation-driven schemes boosting salp chains-inspired optimizers,” IEEE Access, vol. 7, pp. 31243–31261, 2019. [Google Scholar]
36. T. Bezdan, A. Petrovic, M. Zivkovic, I. Strumberger, V. K. Devi et al., “Current best opposition-based learning salp swarm algorithm for global numerical optimization,” in Proc. Zooming Innovation in Consumer Technologies Conf., Novi Sad, Serbia, pp. 5–10, 2021. [Google Scholar]
37. N. Bacanin, A. Petrovic, M. Zivkovic, T. Bezdan and A. Chhabra, “Enhanced salp swarm algorithm for feature selection,” in Intelligent and Fuzzy Techniques for Emerging Conditions and Digital Transformation, Cham: Springer, 2021. [Google Scholar]
38. M. Zivkovic, T. Zivkovic, K. Venkatachalam and N. Bacanin, “Enhanced dragonfly algorithm adapted for wireless sensor network lifetime optimization,” in Proc. Data Intelligence and Cognitive Informatics, Springer, Singapore, pp. 803–817, 2021. [Google Scholar]
39. M. Zivkovic, N. Bacanin, E. Tuba, I. Strumberger, T. Bezdan et al., “Wireless sensor networks life time optimization based on the improved firefly algorithm,” in Proc Int. Wireless Communications and Mobile Computing, Harbin, China, pp. 1176–1181, 2020. [Google Scholar]
40. N. Bacanin, E. Tuba, M. Zivkovic, I. Strumberger and M. Tuba, “Whale optimization algorithm with exploratory move for wireless sensor networks localization,” in Proc. Int. Conf. on Hybrid Intelligent Systems, Springer, Porto, Portugal, pp. 328–338, 2019. [Google Scholar]
41. T. Bezdan, M. Zivkovic, M. Antonijevic, T. Zivkovic and N. Bacanin, “Enhanced flower pollination algorithm for task scheduling in cloud computing environment,” in Proc. Machine Learning for Predictive Analysis, Springer, Singapore, pp. 163–171, 2020. [Google Scholar]
42. M. Zivkovic, T. Bezdan, I. Strumberger, N. Bacanin and K. Venkatachalam, “Improved harris hawks optimization algorithm for workflow scheduling challenge in cloud-edge environment,” in Computer Networks, Big Data and IoT, Springer, Singapore, pp. 87–102, 2021. [Google Scholar]
43. N. Bacanin, N. Vukobrat, M. Zivkovic, T. Bezdan and I. Strumberger, “Improved harris hawks optimization adapted for artificial neural network training,” in Pro. Int. Conf. on Intelligent and Fuzzy Systems, Springer, Cham, pp. 281–289, 2021. [Google Scholar]
44. I. Strumberger, E. Tuba, N. Bacanin, M. Zivkovic, M. Beko et al., “Designing convolutional neural network architecture by the firefly algorithm,” in Proc. 2019 Int. Young Engineers Forum (YEF-ECE), Lisboa, Portugal, pp. 59–65, 2019. [Google Scholar]
45. S. Milosevic, T. Bezdan, M. Zivkovic, N. Bacanin, I. Strumberger et al., “Feed-forward neural network training by hybrid bat algorithm,” in Int. Conf. on Modelling and Development of Intelligent Systems, Springer, Cham, pp. 52–66, 2021. [Google Scholar]
46. T. Bezdan, C. Stoean, A. A. Naamany, N. Bacanin, T. A. Rashid et al., “Hybrid fruit-fly optimization algorithm with K-means for text document clustering,” Mathematics, vol. 9, pp. 19–29, 2021. [Google Scholar]
47. N. Bacanin, T. Bezdan, M. Zivkovic and A. Chhabra, “Weight optimization in artificial neural network training by improved monarch butterfly algorithm,” in Mobile Computing and Sustainable Informatics, Springer, Singapore, pp. 397–409, 2022. [Google Scholar]
48. L. Gajic, D. Cvetnic, M. Zivkovic, T. Bezdan, N. Bacanin et al., “Multi-layer perceptron training using hybridized bat algorithm,” in Computational Vision and Bio-Inspired Computing, Singapore, Springer, pp. 689–705, 2021. [Google Scholar]
49. N. Bacanin, K. Alhazmi, M. Zivkovic, K. Venkatachalam, T. Bezdan et al., “Training multi-layer perceptron with enhanced brain storm optimization metaheuristics,” Computers Materials & Continua, vol. 70, no. 2, pp. 4199–4215, 2022. [Google Scholar]
50. M. Zivkovic, N. Bacanin, K. Venkatachalam, A. Nayyar, A. Djordjevic et al., “COVID-19 cases prediction by using hybrid machine learning and beetle antennae search approach,” Sustainable Cities and Society, vol. 66, pp. 102669, 2021. [Google Scholar]
51. M. Zivkovic, K. Venkatachalam, N. Bacanin, A. Djordjevic, M. Antonijevic et al., “Hybrid genetic algorithm and machine learning method for COVID-19 cases prediction,” in Proc. Int. Conf. on Sustainable Expert Systems, Springer, Singapore, pp. 169–184, 2021. [Google Scholar]
52. T. Bezdan, M. Zivkovic, E. Tuba, I. Strumberger, N. Bacanin et al., “Glioma brain tumor grade classification from MRI using convolutional neural networks designed by modified FA,” in Proc. Int. Conf. on Intelligent and Fuzzy Systems, Istanbul, Turkey, pp. 955–963, 2020. [Google Scholar]
53. T. Bezdan, S. Milosevic, K. Venkatachalam, M. Zivkovic, N. Bacanin et al., “Optimizing convolutional neural network by hybridized elephant herding optimization algorithm for magnetic resonance image classification of glioma brain tumor grade,” in Proc. 2021 Zooming Innovation in Consumer Technologies Conf. (ZINC), IEEE, serbia, pp. 171–176, 2021. [Google Scholar]
54. J. Basha, N. Bacanin, N. Vukobrat, M. Zivkovic, K. Venkatachalam et al., “Chaotic harris hawks optimization with quasi-reflection-based learning: An application to enhance CNN design,” Sensors, vol. 21, pp. 6654, 2021. [Google Scholar]
55. N. Rana, M. S. Abd Latiff and H. Chiroma, “Whale optimization algorithm: A systematic review of contemporary applications, modifications and developments,” Neural Computing and Applications, vol. 32, pp. 1–33, 2020. [Google Scholar]
56. G. Zhenyu, C. Bo, Y. Min and C. Binggang, “Self-adaptive chaos differential evolution,” Advances in Natural Computation, vol. 4221, pp. 972–975, 2006. [Google Scholar]
57. M. A. El-Shorbagy, A. A. Mousa and S. M. Nasr, “A Chaos-based evolutionary algorithm for general nonlinear programming problems,” Chaos, Solutions & Fractals, vol. 85, pp. 8–21, 2016. [Google Scholar]
58. I. Fister, M. Perc and S. M. Kamal, “A review of chaos-based firefly algorithms: Perspectives and research challenges,” Applied Mathematics and Computation, vol. 252, pp. 155–165, 2015. [Google Scholar]
59. X. Lu, Q. Wu, Y. Zhou, Y. Ma, C. Song et al., “A dynamic swarm firefly algorithm based on chaos theory and Max-min distance algorithm,” Traitement du Signal, vol. 36, pp. 227–231, 2019. [Google Scholar]
60. N. Bacanin, R. Stoean, M. Zivkovic, A. Petrovic, T. A. Rashid et al., “Performance of a novel chaotic firefly algorithm with enhanced exploration for tackling global optimization problems: Application for dropout regularization,” Mathematics, vol. 9, no. 21, pp. 1–33, 2021. [Google Scholar]
61. R. Caponetto, L. Fortuna, S. Fazzino and M. Xibilia, “Chaotic sequences to improve the performance of evolutionary algorithms,” IEEE Transactions on Evolutionary Computation, vol. 7, no. 3, pp. 289–304, 2003. [Google Scholar]
62. H. R. Tizhoosh, “Opposition-based learning: A new scheme for machine intelligence,” in Int. Conf. on Computational Intelligence for Modelling, Control and Automation and International Conf. on Intelligent Agents, web Technologies and Internet Commerce (CIMCA-IAWTIC'06), Vienna, Austria, IEEE, vol. 1, pp. 695–701, 2005. [Google Scholar]
63. N. Awad, M. Ali, J. Liang, B. Qu, P. Suganthan et al., “Evaluation criteria for the CEC 2017 special session and competition on single objective real-parameter numerical optimization,” Technology Report, 2016. [Google Scholar]
64. A. A. Heidari, S. Mirjalili, H. Faris, I. Aljarah, M. Mafarja et al., “Harris hawks optimization: Algorithm and applications,” Future Generation Computer Systems, vol. 97, pp. 849–872, 2019. [Google Scholar]
65. A. G. Hussien and M. Amin, “A Self-adaptive harris hawks optimization algorithm with opposition-based learning and chaotic local search strategy for global optimization and feature selection,” International Journal of Machine Learning and Cybernetics, vol. 12, pp. 1–28, 2021. [Google Scholar]
66. A. K. Qin, V. L. Huang and P. N. Suganthan, “Differential evolution algorithm with strategy adaptation for global numerical optimization,” IEEE Transactions on Evolutionary Computation, vol. 13, no. 2, pp. 398–417, 2009. [Google Scholar]
67. S. Z. Mirjalili, S. Mirjalili, S. Saremi, H. Faris and I. Aljarah, “Grasshopper optimization algorithm for multi-objective optimization problems,” Applied Intelligence, vol. 48, no. 4, pp. 805–820, 2018. [Google Scholar]
68. S. Mirjalili, S. M. Mirjalili and A. Lewis, “Grey wolf optimizer,” Advances in Engineering Software, vol. 69, pp. 46–61, 2014. [Google Scholar]
69. S. Mirjalili, “Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm,” Knowledge-Based Systems, vol. 89, pp. 228–249, 2015. [Google Scholar]
70. S. Mirjalili, S. M. Mirjalili and A. Hatamlou, “Multi-verse optimizer: A nature-inspired algorithm for global optimization,” Neural Computing and Applications, vol. 27, pp. 495–513, 2016. [Google Scholar]
71. S. Mirjalili, “SCA: A sine cosine algorithm for solving optimization problems,” Knowledge-Based Systems, vol. 96, pp. 120–133, 2016. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |