Computers, Materials & Continua DOI:10.32604/cmc.2022.024736
Article

Archery Algorithm: A Novel Stochastic Optimization Algorithm for Solving Optimization Problems

Fatemeh Ahmadi Zeidabadi1, Mohammad Dehghani2, Pavel Trojovský2,*, Štěpán Hubálovský3, Victor Leiva4 and Gaurav Dhiman5

1Department of Mathematics and Computer Sciences, Sirjan University of Technology, Sirjan, Iran
2Department of Mathematics, Faculty of Science, University of Hradec Králové, 50003, Hradec Králové, Czech Republic
3Department of Applied Cybernetics, Faculty of Science, University of Hradec Králové, 50003, Hradec Králové, Czech Republic
4School of Industrial Engineering, Pontificia Universidad Católica de Valparaíso, Valparaíso, 2362807, Chile
5Department of Computer Science, Government Bikram College of Commerce, Patiala, Punjab, India
*Corresponding Author: Pavel Trojovský. Email: pavel.trojovsky@uhk.cz
Received: 29 October 2021; Accepted: 29 November 2021

Abstract: Finding a suitable solution to an optimization problem designed in science is a major challenge. Therefore, these must be addressed utilizing proper approaches. Based on a random search space, optimization algorithms can find acceptable solutions to problems. Archery Algorithm (AA) is a new stochastic approach for addressing optimization problems that is discussed in this study. The fundamental idea of developing the suggested AA is to imitate the archer's shooting behavior toward the target panel. The proposed algorithm updates the location of each member of the population in each dimension of the search space by a member randomly marked by the archer. The AA is mathematically described, and its capacity to solve optimization problems is evaluated on twenty-three distinct types of objective functions. Furthermore, the proposed algorithm's performance is compared vs. eight approaches, including teaching-learning based optimization, marine predators algorithm, genetic algorithm, grey wolf optimization, particle swarm optimization, whale optimization algorithm, gravitational search algorithm, and tunicate swarm algorithm. According to the simulation findings, the AA has a good capacity to tackle optimization issues in both unimodal and multimodal scenarios, and it can give adequate quasi-optimal solutions to these problems. The analysis and comparison of competing algorithms’ performance with the proposed algorithm demonstrates the superiority and competitiveness of the AA.

Keywords: Archer; meta-heuristic algorithm; population-based optimization; stochastic programming; swarm intelligence; population-based algorithm; Wilcoxon statistical test

1  Introduction

The technique of finding the optimal solution among all possible solutions to a problem is known as optimization. An optimization problem must first be modeled before it can be solved. Modeling is the process of defining a problem with variables and mathematical relationships in order to simulate an optimization issue [1]. Optimization is employed in the design and maintenance of many economic, engineering, and even social systems to reduce waste, minimize cost, optimal process design, or maximize profits. Because of the widespread use of optimization in numerous disciplines, this issue has developed significantly, and it is now researched in mathematics, management, industry, and many other fields of science. An optimization problem should be optimized using the proper approach after mathematical modeling and design. There are two types of optimization problem solving approaches: deterministic and stochastic [2].

Deterministic methods can provide solutions to optimization problems using derivatives (gradients-based) or initial conditions without using derivatives (non-gradient-based). The advantage of deterministic methods is that they guarantee the proposed solution as the main solution to the problem. In fact, the solution to the problem of optimization using these types of methods is the best solution. Among the problems and disadvantages of deterministic methods is that they lose their efficiency in nonlinear search spaces, non-differentiable functions, or by increasing the dimensions and complexity of optimization problems [3].

Many science optimization problems are naturally more complex and difficult than can be solved by conventional mathematical optimization methods. Stochastic approaches, which are based on random search in the problem-solving space, can yield reasonable and acceptable solutions to optimization problems [4]. Optimization algorithms are one of the most extensively used stochastic approaches for addressing optimization problems that do not need the use of objective function gradient and derivative information. The process of optimization algorithms begins with the random proposal of a number of feasible solutions to the optimization problem. The proposal solutions are then enhanced in each iteration through a repeated process based on different steps of the algorithm. The algorithm converges to a viable solution to the optimization problem after a sufficient number of iterations [5].

Among the conceivable solutions to each optimization issue is a main best solution known as the global optimum. The important issue with optimization algorithms is that because they are stochastic methods, there is no guarantee that their provided solutions be global optimal. As a result, the solutions derived through optimization algorithms for optimization problems are known as quasi-optimal solutions [6]. When the performance of different optimization algorithms on solving an optimization issue is compared, the algorithm that is capable of providing a quasi-optimal solution that is closer to the global optimal is the superior algorithm. This has led researchers to make great efforts to design new algorithms with the aim of providing quasi-optimal solutions that are more appropriate and closer to the global optimal [7–9]. Optimization algorithms have been used to achieve better solutions in various scientific fields: energy carriers [10,11], electrical engineering [12–17], protection [18], and energy management [19–22].

The contribution of this study is the development of a novel optimization method known as Archery Algorithm (AA) that provides quasi-optimal solutions to optimization problems. The procedure of updating the members of the population in each dimension of the search space in AA is based on the guidance of a randomly selected member of the population by the archer. The proposed AA's theory is provided, as well as its mathematical model for use in addressing optimization problems. The proposed algorithm's capacity to find acceptable answers is demonstrated using a standard set of twenty-three standard objective functions of various unimodal and multimodal varieties. The proposed AA's optimization results are also compared to those of eight well-known algorithms: Grey Wolf Optimization (GWO), Particle Swarm Optimization (PSO), Marine Predators Algorithm (MPA), Teaching-Learning Based Optimization (TLBO), Whale Optimization Algorithm (WOA), Gravitational Search Algorithm (GSA), Tunicate Swarm Algorithm (TSA), and Genetic Algorithm (GA).

The remainder of this paper is structured in such a way that Section 2 presents research on optimization algorithms. Section 3 introduces the proposed Archery Algorithm. Section 4 contains simulation studies. Finally, in Section 5, findings, conclusions, and recommendations for further research are offered.

2  Background

Because of the intricacy of optimization issues and the inefficiency of traditional analytical approaches, there is a perceived need for more powerful tools to address these problems. In response to this need, optimization algorithms have been emerged. These methods do not require any gradient or derivative information of the objective function of the problem, and with their special operators are able to scan the search space and provide quasi-optimal and even in some cases global optimal. Optimization algorithms have been constructed using ideation based on various natural phenomena, behavior of living things, physical laws, genetic sciences, game rules, as well as evolutionary processes. For example, simulations of ants’ behavior when searching for food have been used in the design of the Ant Colony Optimization (ACO) algorithm [23], modeling of the cooling process of metals during metalworking has been used in the design of the Simulated Annealing (SA) algorithm [24], and simulation of the human immune system against viruses have been used in the design of the Artificial Immune System (AIS) algorithm [25]. From the point of view of the main design idea, optimization algorithms can be classified into four groups: swarm-based, game-based, physics-based, and evolutionary-based algorithms.

Swarm-based algorithms have been created using models of natural crowding behaviors of animals, plants, and insects. Particle Swarm Optimization (PSO) is one of the oldest and most widely used methods based on collective intelligence, inspired by the group life of birds and fish. In PSO, a large number of particles are scattered in the problem space and simultaneously seek the optimal global solution. The position of each particle in the search space is updated based on its personal experience as well as the experience of the entire population [26]. Teaching-Learning Based Optimization (TLBO) is designed based on imitating the behavior of students and teachers in the educational space of a classroom. In TLBO, the position of members of the algorithm population is updated in two phases of teaching and learning. In this way, in the teacher phase, similar to the real classroom where the teacher is the best member of the population, she/he teaches the students and leads to the improvement of the students’ performance. In the learning phase, students share their information with each other to improve their knowledge (performance) [27]. Grey Wolf Optimization (GWO) is a collective intelligence algorithm that, like many other meta-heuristic algorithms, is influenced by nature. GWO is built on a hierarchical framework that mimics gray wolf social behavior when hunting. In order to represent the hunt, four varieties of gray wolves, such as alpha, beta, delta, and omega, have been utilized to mimic the hierarchical leadership of gray wolves, as well as three main phases including (i) search for prey, (ii) siege of prey, and (iii) attack the prey [28]. Whale Optimization Algorithm (WOA) is a swarm-based algorithm that is inspired by the bubble-net hunting technique and is based on simulation of humpback whale social behavior. WOA updates population members based on modeling whale hunting behavior in three stages: (i) search for prey, (ii) encircling prey, and (iii) bubble-net attacking method [29]. Some of other swarm-based algorithms are: Marine Predators Algorithm (MPA) [30], Emperor Penguin Optimizer (EPO) [31], Cat and Mouse based Optimizer (CMBO) [32], Following Optimization Algorithm (FOA) [33], All Members Based Optimizer (AMBO) [34], Donkey Theorem Optimization (DTO) [35], Mixed Leader Based Optimizer (MLBO) [36], Good Bad Ugly Optimizer (GBUO) [37], Mixed Best Members Based Optimizer (MBMBO) [38], Grasshopper Optimization Algorithm (GOA) [39], Mutated Leader Algorithm (MLA) [40], and Tunicate Swarm Algorithm (TSA) [41].

Game-based algorithms have been proposed by simulating various game rules and player behavior in various individual and group games. Football Game Based Optimization (FGBO) is one of the game-based algorithms inspired by the behavior of players and clubs in the football league. FGBO updates the members of the population in four phases, including (i) holding the league, (ii) training, (iii) transferring the player, and (iv) promote and relegate of the clubs [42]. Some of other game-based algorithms are: Hide Object Game Optimizer (HOGO) [43], Darts Game Optimizer (DGO) [44], Ring Toss Game Based Optimizer (RTGBO) [45], Orientation Search algorithm (OSA) [46], Dice Game Optimizer (DGO) [47], and Binary Orientation Search algorithm (BOSA) [48].

Physics-based algorithms have been introduced according to the modeling of diverse principles and physical phenomena. Gravitational Search Algorithm (GSA) is a physics-based algorithm developed based on the inspiration of the force of gravity and Newton's laws of universal gravitation. In GSA, the members of the population are assumed to be different objects which are updated in the problem search space according to the distance between them and based on the simulation of the force of gravity [49]. Momentum Search Algorithm (MSA) is based on the modeling of the physical phenomenon of impulse between objects and Newton's laws of motion. In MSA, the process of updating population members is such that each member in the search space moves in the direction of the optimal member based on the impulse received by an external object [50]. Some of other physics-based algorithms are: Henry Gas Solubility Optimization (HGSO) [51], Spring Search Algorithm (SSA) [52], and Charged System Search (CSS) [53].

Evolutionary-based algorithms have been developed based on simulation of rules in natural evolution and using operators inspired by biology, such as mutation and crossover. Genetic Algorithm (GA), which is an evolutionary-based algorithm, is one of the oldest widely used algorithms in solving various optimization problems. GA updates population members based on simulations of the reproductive process and according to Darwin's theory of evolution using selection, crossover, and mutation operators [54]. Some of other evolutionary-based algorithms are: Genetic Programming (GP) [55], Evolutionary Programming (EP) [56], and Differential Evolution (DE) [57].

3  Archery Algorithm

The suggested optimization method and its mathematical model are described in this section. Archery Algorithm (AA) is based on mimicking an archer's behavior during archery towards the target board. In fact, in the proposed AA, each member of the population is updated in each dimension of the search space based on the guidance of the member targeted by the archer. In population-based algorithms, each member of the population is actually a feasible solution to the optimization problem that determines the values of the problem variables. Therefore, each member of the population can be represented using a vector. The algorithm's population matrix is made up of the members of the population. This population matrix can be modeled as a matrix representation using Eq. (1).

X=[X1⋮Xi⋮XN]N×m=[x1,1⋯x1,d⋯x1,m⋮⋱⋮...⋮xi,1⋯xi,d⋯xi,m⋮...⋮⋱⋮xN,1⋯xN,d⋯xN,m]N×m,(1)

where X is the matrix of AA's population, Xi is the vector of ith AA's population member, xi,d is the dth dimension of ith population member, N is the number of population members, and m is the number of problem variables.

Each member of the population can be used to evaluate the objective function of optimization problems. Proportional to the number of members of the population, different values are obtained for the objective function, which is specified as a vector using Eq. (2).

F=[F1⋮Fi⋮FN]N×1=[F(X1)⋮F(Xi)⋮F(XN)]N×1,(2)

where F is the vector of various obtained values for objective function from population members and Fi is the objective function value obtained from ith population member.

In the proposed AA, the target panel is considered as a page (square or rectangle). The target panel is segmented so that the number of sections in its “width” is equal to the number of population members, and the number of sections in its “length” is equal to the number of problem variables. The difference in the width of the different parts is proportional to the difference in the value of the objective functions of the population members.

In order to determine the width proportional to the value of the objective function, the probability function is used. The probability function similar to the objective function is calculated using a vector according to Eq. (3).

P=F−Fworst∑i=1N⁡(Fi−Fworst)(3)

Here,P is the probability vector and Fworst is the objective function value of worst population member.

In the proposed algorithm, in order to update the position of each member in the search space in each dimension, a member is randomly selected based on the archery simulation. In archery simulation, the member that performs better on the objective function value has a higher probability function and, in fact, a better chance of being selected. Cumulative probability has been used to simulate archery and randomly select a member. This process can be modeled using Eq. (4).

k={1,0≤rk,di≤C1⋮i,Ci−1<rk,di≤Ci⋮N,CN−1<rk,di≤CN,(4)

where, k is the row number of selected member by archer, Ci is the cumulative probability of ith member, and rk,di is a random number in interval [0,1] which is a criterion for simulating the selection of the kth member to lead the ith member in the dth dimension.

Therefore, in the proposed AA, the position of the population members is updated based on the said concepts, using Eqs. (5) to (7).

xi,dnew={xi,d+r×(xk,d−I×xi,d),Fk<Fixi,d+r×(xi,d−I×xk,d),else(5)

I=round(1+rand)(6)

Xi={Xinew,Finew<FiXi,else,(7)

where, Xinew is the new status of the ith member, Finew is the its objective function value, xi,dnew is the its dth dimension, r is a random number with normal distribution belonging to the closed interval [0,1], xk,d is the dth dimension of selected member by archer, and Fk is the its objective function value.

The proposed AA is an iteration-based algorithm like other population-based algorithms. After updating all members of the population, the algorithm enters the next iteration and the various steps of the proposed AA based on Eqs. (3) to (7) are repeated until the stop condition is established. Once fully implemented, the algorithm provides the best proposed solution to the problem. The various steps of the proposed AA are presented its pseudo-code in Alg. 1 and as a flowchart in Fig. 1.

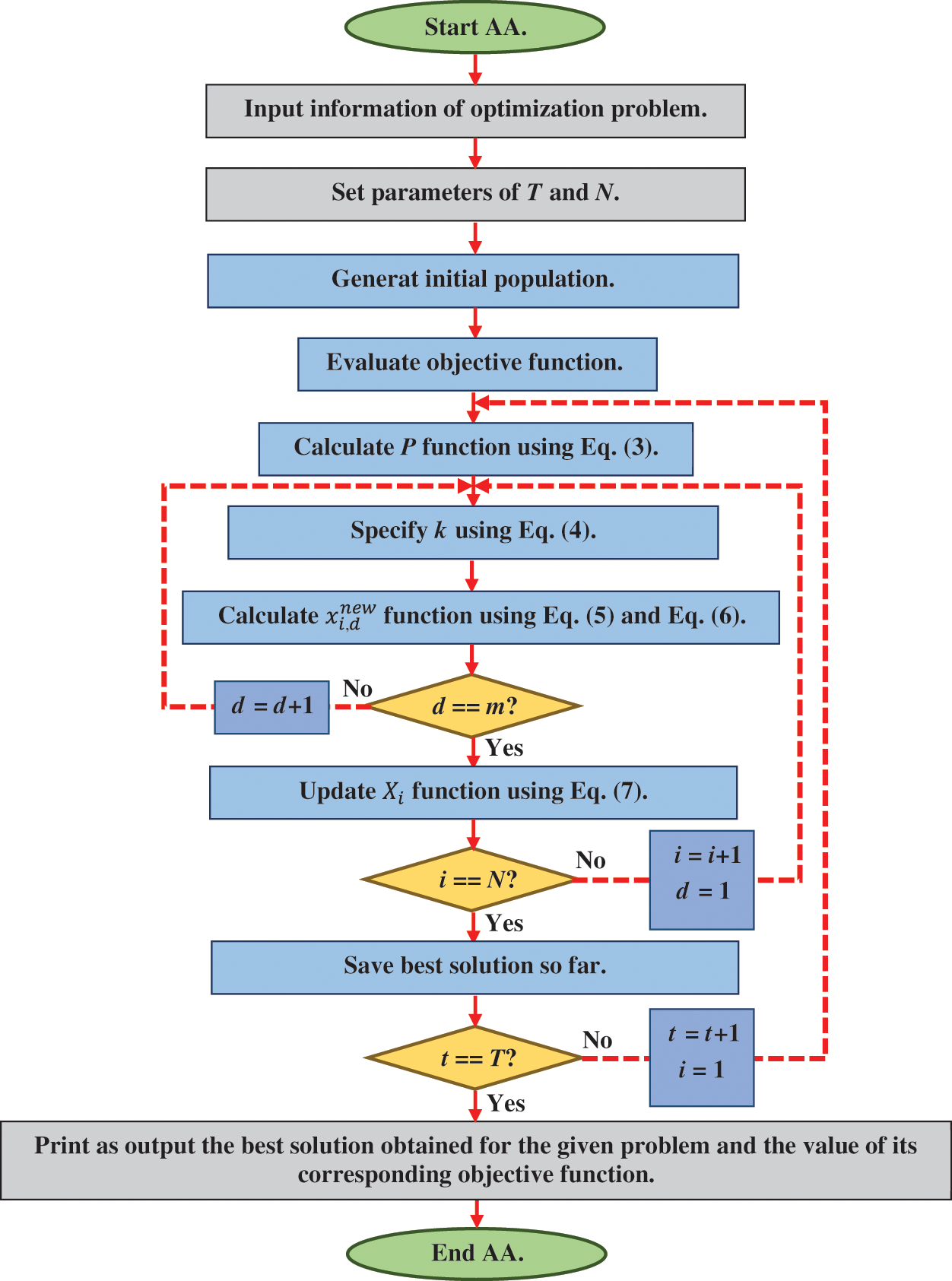
Figure 1: Flowchart of AA

4  Simulation Studies and Results

This section presents simulated experiments on the proposed AA's performance in addressing optimization problems and giving acceptable quasi-optimal solutions. To examine the proposed algorithm, a standard set of twenty-three functions from various types of unimodal, high-dimensional multimodal, and fixed-dimensional multimodal models is used. Furthermore, the AA findings are compared to the performance of eight optimization techniques, including Particle Swarm Optimization (PSO) [26], Teaching-Learning Based Optimization (TLBO) [27], Grey Wolf Optimization (GWO) [28], Whale Optimization Algorithm (WOA) [29], Marine Predators Algorithm (MPA) [30], Tunicate Swarm Algorithm (TSA) [41] Gravitational Search Algorithm (GSA) [49], and Genetic Algorithm (GA) [54]. In order to report the results of function optimization, two indicators of the average of the best obtained solutions (avg) and the standard deviation of the best obtained solutions (std) are used.

4.1 Evaluation of Unimodal Functions

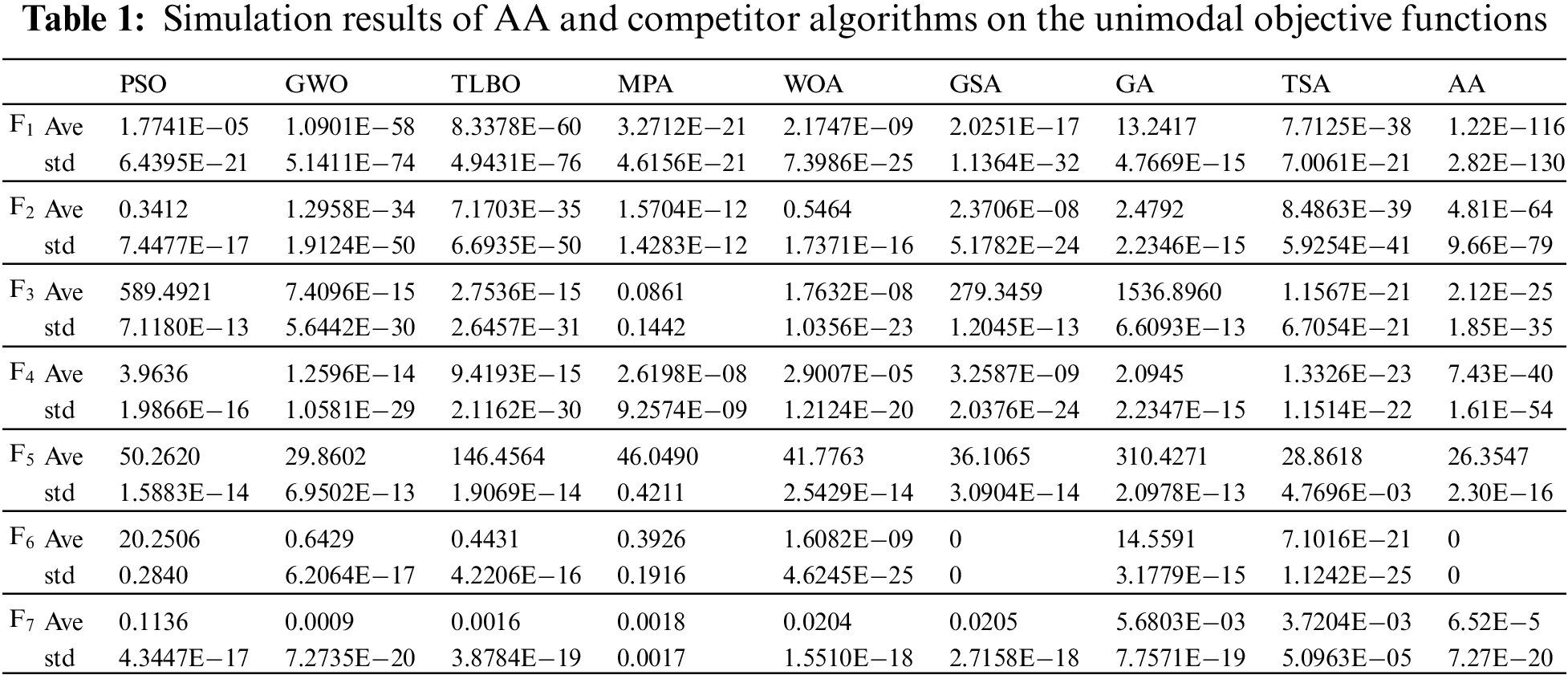
The objective functions of F1 to F7 of the unimodal type have been selected to evaluate the performance of the optimization algorithms. The results of the implementation of the proposed AA and eight compared algorithms are presented in Tab. 1. Based on the results of this table, the AA is the best optimizer for F1, F2, F3, F4, F5, and F7 functions and is also able to provide the global optimal for the F6 function. The proposed AA has a strong capacity to optimize unimodal functions and is significantly more competitive than the eight compared algorithms, according to analysis and comparison of optimization algorithm performance.

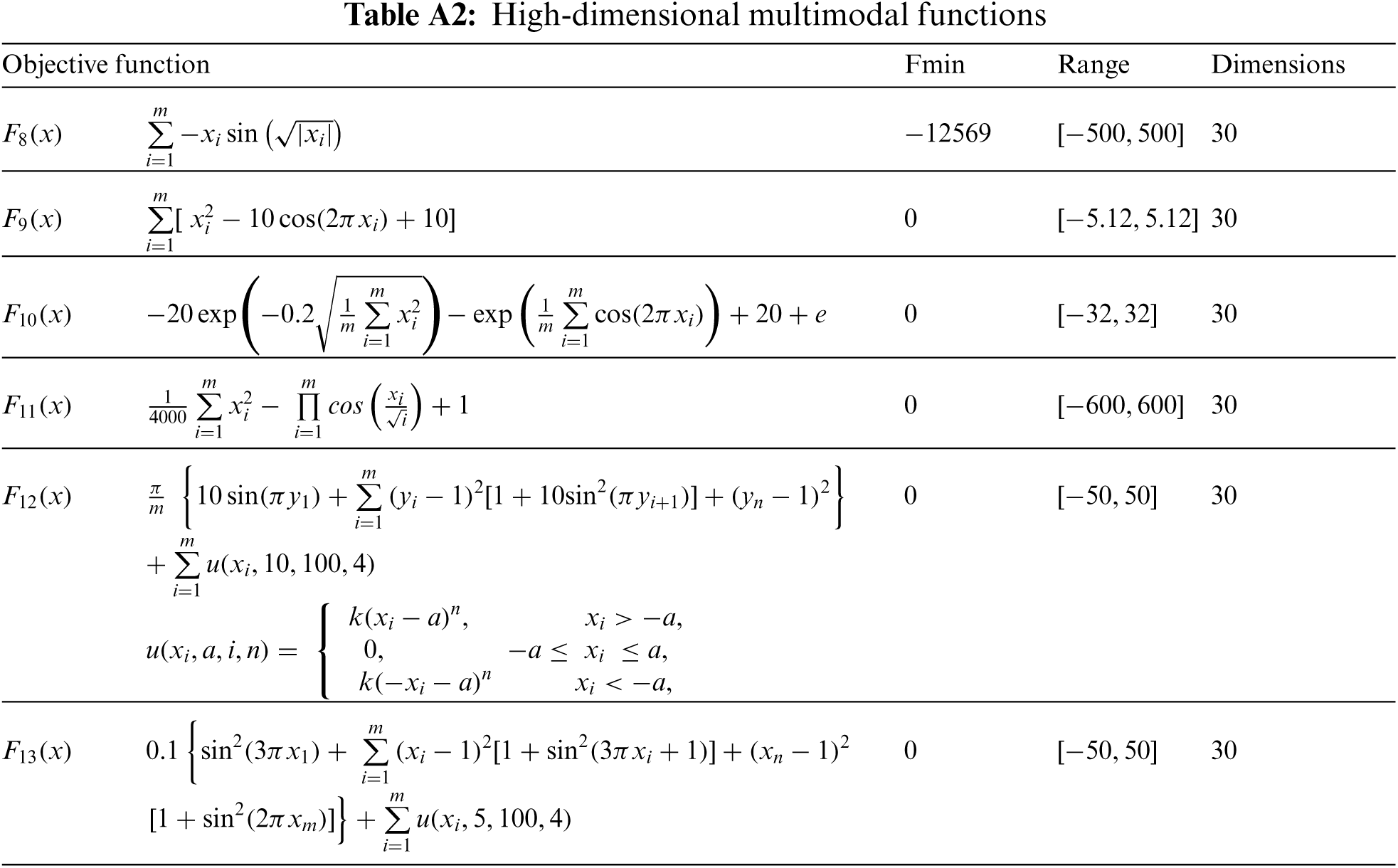
4.2 Evaluation of High-Dimensional Multimodal Functions

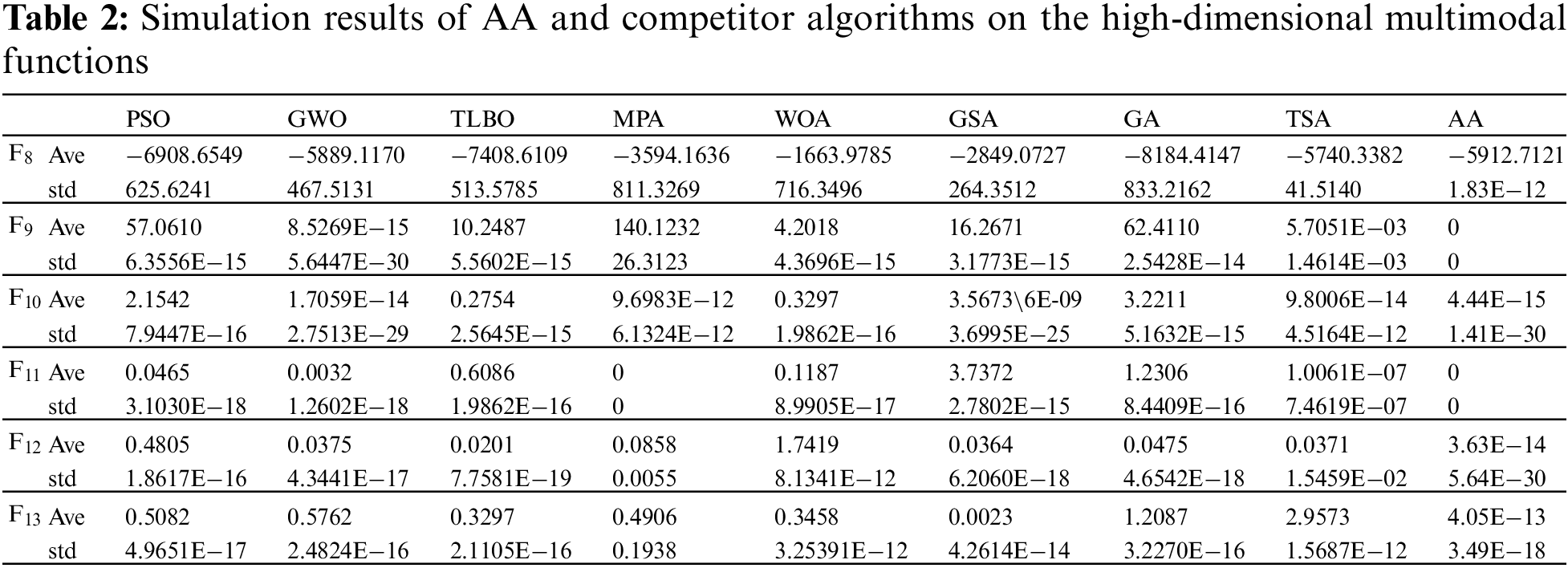
Objective functions of F8 to F13 are selected to evaluate the performance of optimization algorithms in solving high-dimensional multimodal problems. The results of optimization of this type of objective functions using the proposed AA and eight compared algorithms are presented in Tab. 2. The simulation results show that AA is the best optimizer for F10, F12, and F13 functions and is also able to provide the global optimal for F9 and F11 functions. The reported findings demonstrate that the suggested AA approach is capable of optimizing high-dimensional multimodal objective functions.

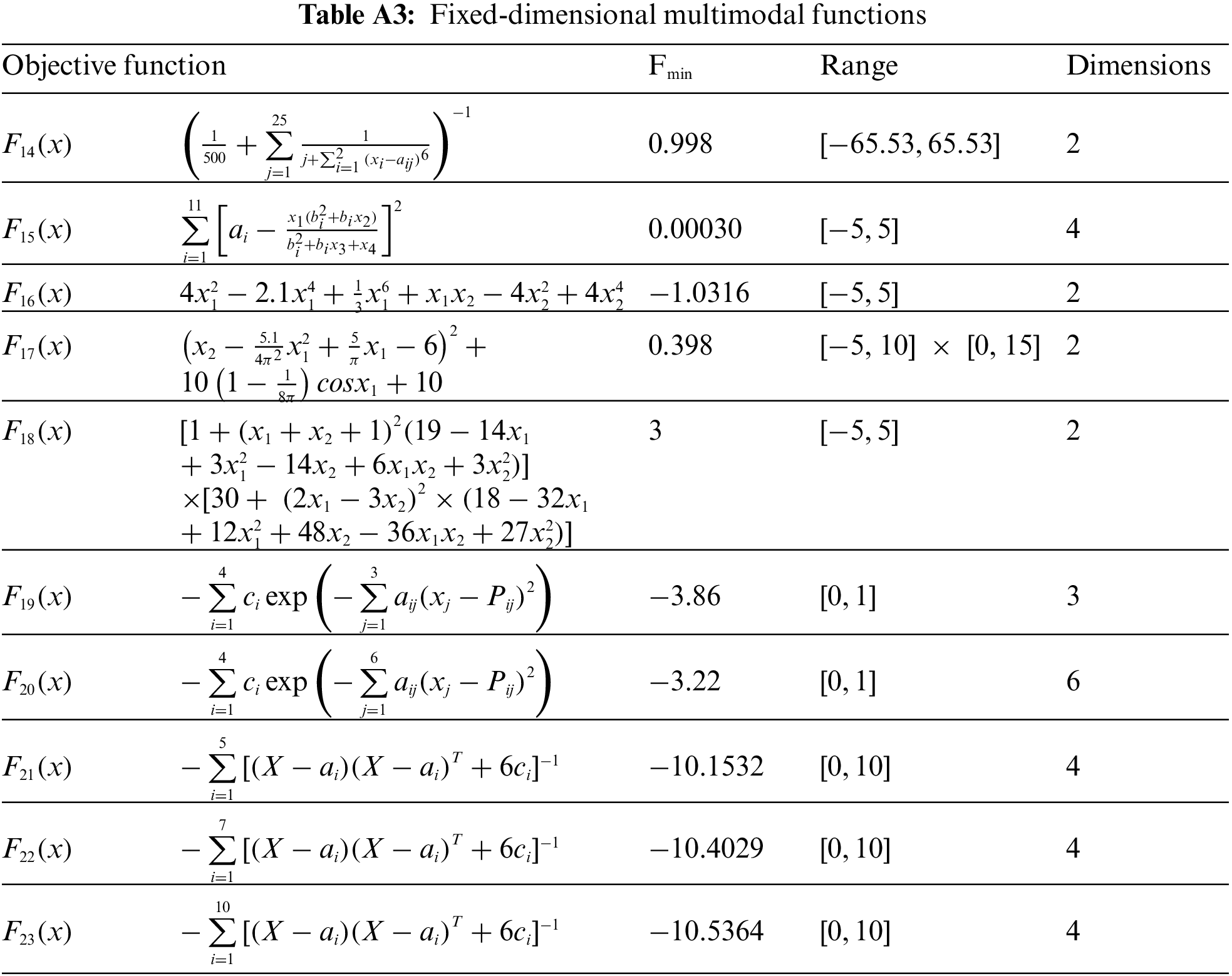
4.3 Evaluation of Fixed-Dimensional Multimodal Functions

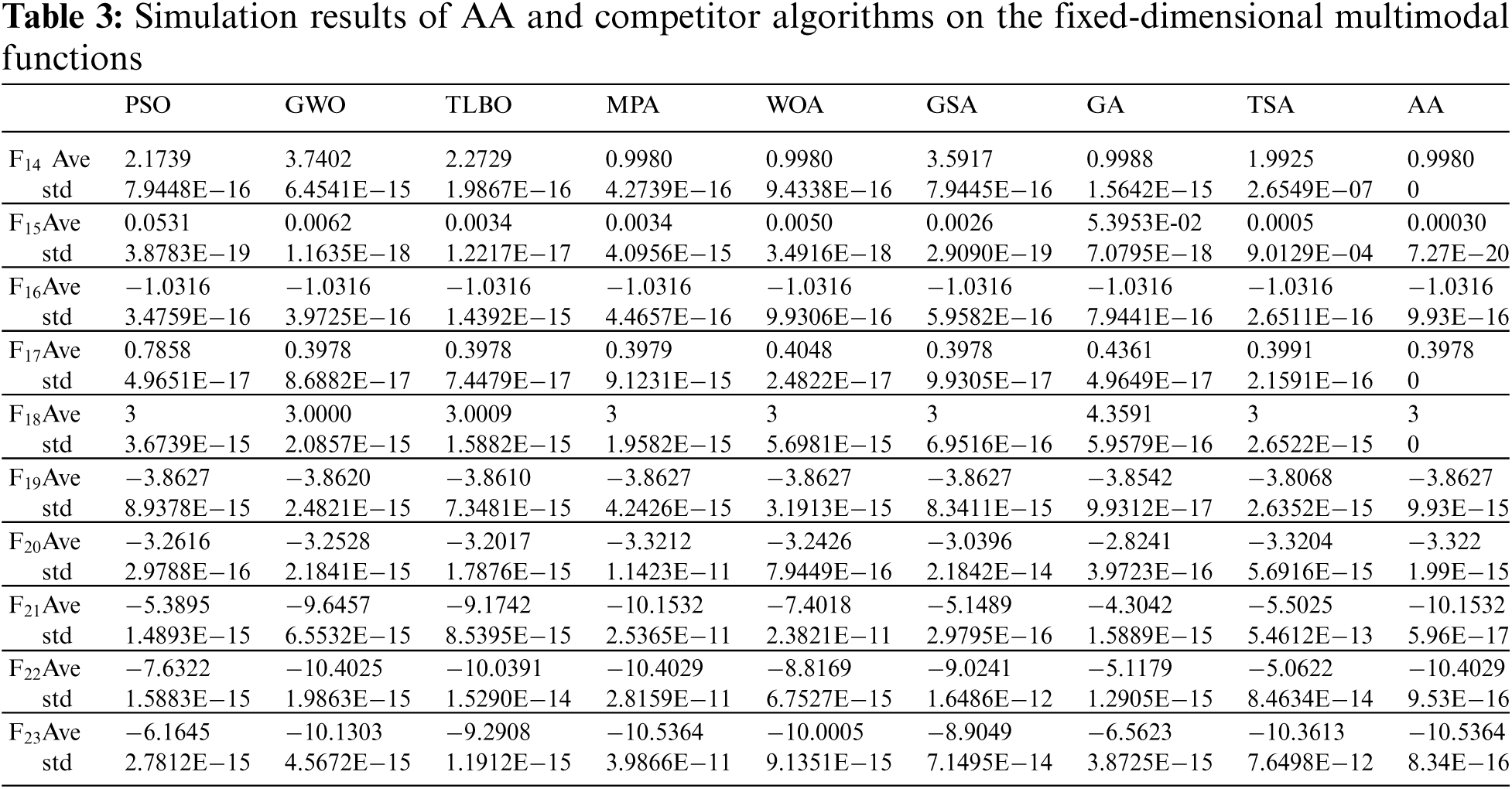
Objective functions of F14 to F23 are selected to analyze the ability of optimization algorithms to solve fixed-dimensional multimodal problems. The results of the implementation of the proposed AA and eight comparative algorithms on these objective functions are presented in Tab. 3. Based on the analysis of the results in this table, the proposed AA is able to provide the global optimal for the F14, F17, and F18 functions. In addition, AA with optimal quasi-optimal solutions and less standard deviation is the best optimizer for F15, F16, F19, F20, F21, F22, and F23 functions. Analysis and comparison of the results of the compared algorithms against the performance of the proposed algorithm shows that AA has a very high ability to solve fixed-dimensional multimodal type objective functions.

4.4 Statistical Analysis

Although analyzing and comparing optimization algorithms based on two criteria, the average of the best solutions and its standard deviation, gives important information, the superiority of one algorithm over other algorithms may be random, even with a very low probability. This section presents a statistical analysis of the performance of optimization techniques. The Wilcoxon rank sum test [58], a non-parametric statistical test, is used to assess the significance of the results. Tab. 4 displays the outcomes of this test. This table specifies the significant superiority of the suggested AA over the other methods based on p-values less than 0.05.

4.5 Sensitivity Analysis

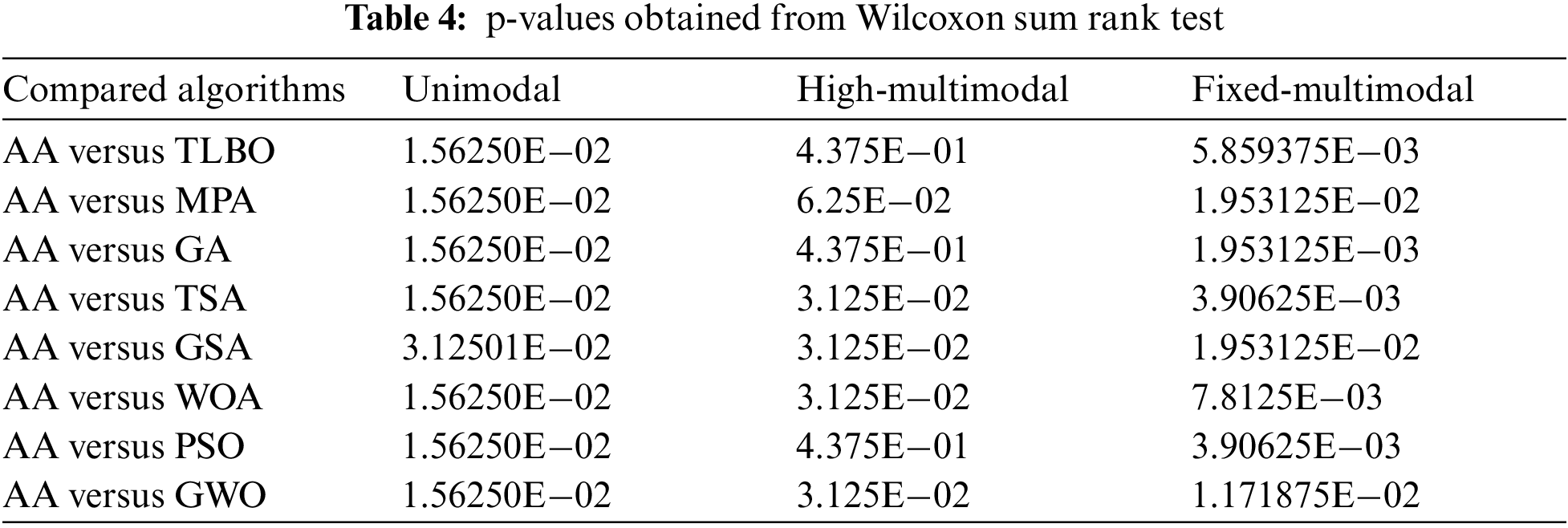
A sensitivity analysis is provided in this subsection to evaluate the influence of “number of population members” and “maximum number of iterations” parameters on the performance of the proposed AA.

The AA is implemented in separate performances for different populations with 20, 30, 50, and 80 members on all twenty-three objective functions to give a sensitivity analysis of the proposed algorithm to the “number of population number” parameter. The simulation results are reported in Tab. 5. What can be deduced from the analysis of these results is that the values of the objective function decrease as the number of members of the population increases.

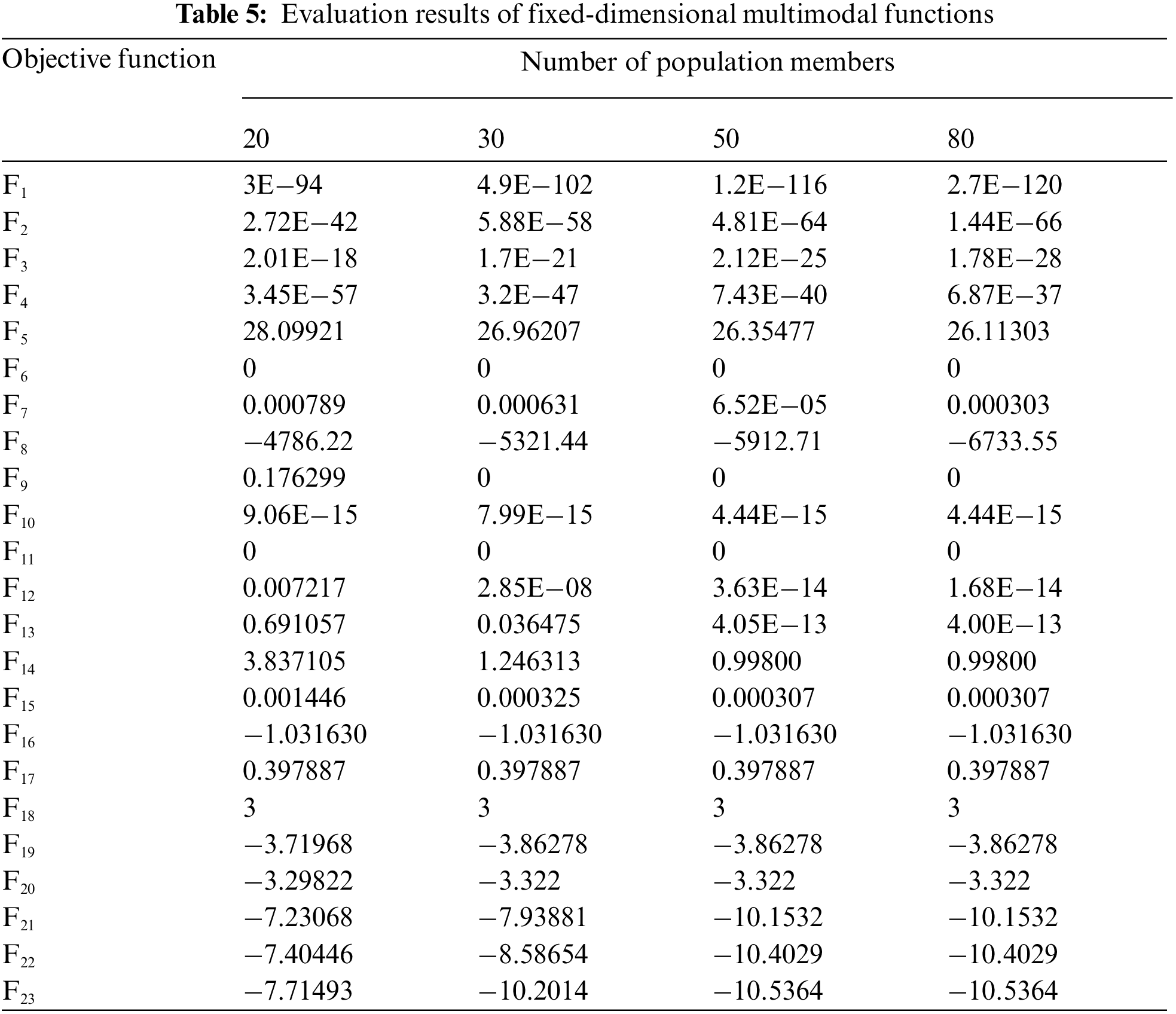
In order to provide a sensitivity analysis of the proposed algorithm to the “maximum number of iterations” parameter, the AA is implemented in independent performances for the number of 100, 500, 800, and 1000 iterations on all twenty-three objective functions. Tab. 6 displays the findings of this sensitivity analysis. The simulation results demonstrate that raising the algorithm's maximum number of iterations leads to convergence towards the best solution and decreases the value of the objective functions.

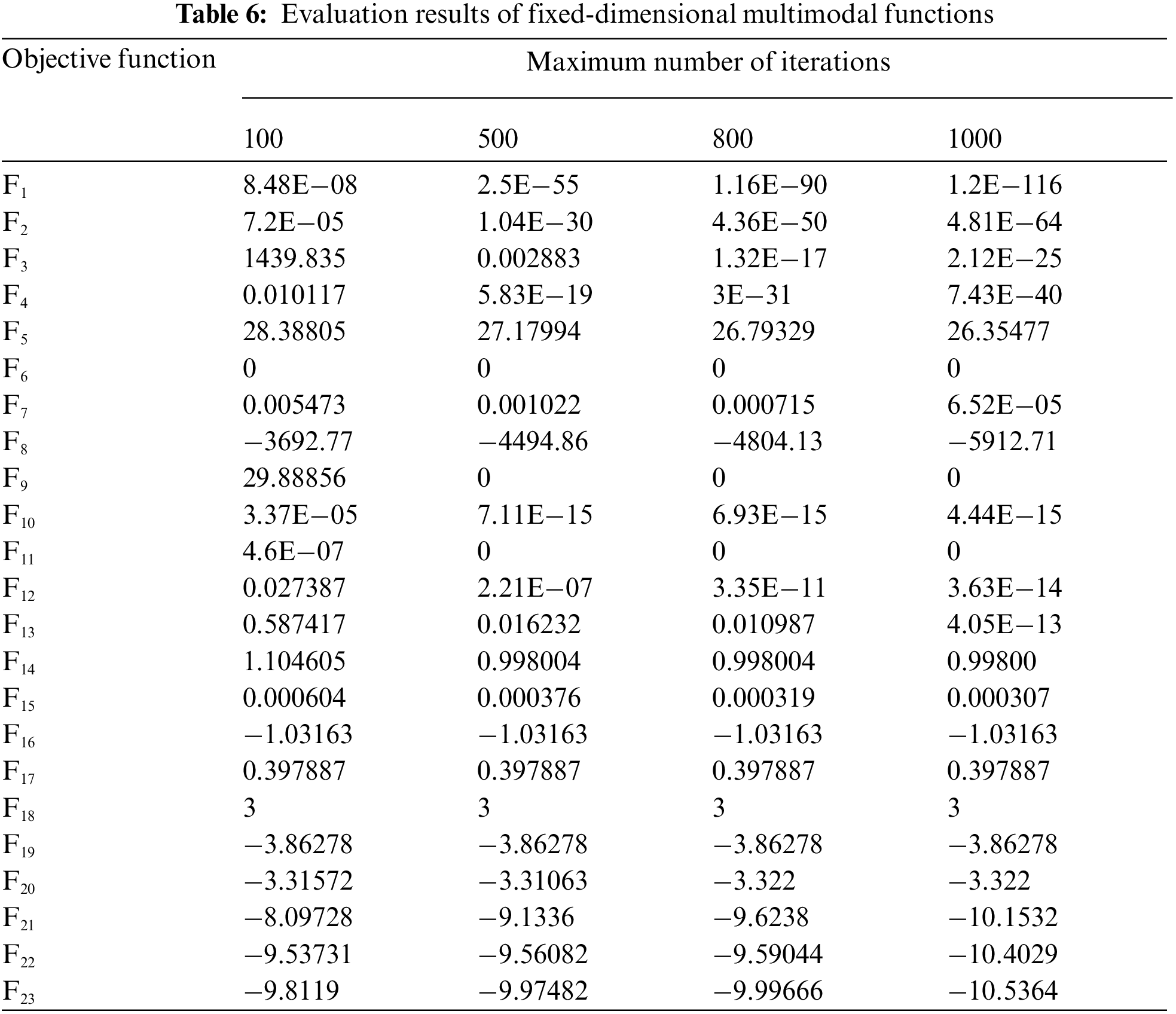
5  Conclusions and Future Works

A vast variety of scientific optimization issues in many areas must be tackled using proper optimization approaches. One of the most extensively utilized tools for solving these issues is stochastic search-based optimization algorithms. In this study, Archery Algorithm (AA) was developed as a novel optimization algorithm for providing adequate quasi-optimal solutions to optimization problems. Modeling the archer shooting behavior towards the target panel was the main idea in designing the proposed algorithm. In the AA, the position of each member of the population in each dimension of the search space is guided by the member marked by the archer. The proposed algorithm was mathematically modeled and tested on twenty-three standard objective functions of different types of unimodal, and multimodal. The results of optimizing the unimodal objective functions show that the suggested AA has a strong exploitation potential in delivering quasi-optimal solutions near to the global optimal. The results of optimization of multimodal functions showed that the proposed AA has high power in the index of exploration and accurate scanning of the search space in order to cross the optimal local areas. Furthermore, the suggested AA's results were compared to the performance of eight methods, including: Particle Swarm Optimization (PSO), Grey Wolf Optimization (GWO), Teaching-Learning Based Optimization (TLBO), Marine Predators Algorithm (MPA), Whale Optimization Algorithm (WOA), Gravitational Search Algorithm (GSA), Genetic Algorithm (GA), and Tunicate Swarm Algorithm (TSA). The results of the analysis and comparison revealed that the proposed AA outperforms the eight mentioned algorithms in addressing optimization problems and is far more competitive.

The authors offer several suggestions for further studies, including the design of multi-objective version as well as binary version of the proposed AA. In addition, the application of the proposed AA in solving optimization problems in various sciences and the real-world problems are another suggested study ideas of this paper.

Funding Statement: The research was supported by the Excellence Project PřF UHK No. 2208/2021–2022, University of Hradec Kralove, Czech Republic.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  M. Dehghani and P. Trojovský, “Teamwork optimization algorithm: A new optimization approach for function minimization/maximization,” Sensors, vol. 21, no. 13, pp. 4567, 2021. [Google Scholar]

 2.  M. Dehghani, Z. Montazeri, A. Dehghani, R. R. Mendoza, H. Samet et al., “MLO: Multi leader optimizer,” International Journal of Intelligent Engineering and Systems, vol. 13, no. 6, pp. 364–373, 2020. [Google Scholar]

 3.  M. Dehghani, Z. Montazeri, A. Dehghani, H. Samet, C. Sotelo et al., “DM: Dehghani method for modifying optimization algorithms,” Applied Sciences, vol. 10, no. 21, pp. 7683, 2020. [Google Scholar]

 4.  S. A. Doumari, H. Givi, M. Dehghani, Z. Montazeri, V. Leiva et al., “A new two-stage algorithm for solving optimization problems,” Entropy, vol. 23, no. 4, pp. 491, 2021. [Google Scholar]

 5.  M. Dehghani, Z. Montazeri and Š Hubálovský, “GMBO: Group mean-based optimizer for solving various optimization problems,” Mathematics, vol. 9, no. 11, pp. 1190, 2021. [Google Scholar]

 6.  A. Sadeghi, S. A. Doumari, M. Dehghani, Z. Montazeri, P. Trojovský et al., “A new “good and bad groups-based optimizer” for solving various optimization problems,” Applied Sciences, vol. 11, no. 10, pp. 4382, 2021. [Google Scholar]

 7.  M. Dehghani, Z. Montazeri, A. Dehghani, O. P. Malik, R. Morales-Menendez et al., “Binary spring search algorithm for solving various optimization problems,” Applied Sciences, vol. 11, no. 3, pp. 1286, 2021. [Google Scholar]

 8.  M. Dehghani, Z. Montazeri, A. Dehghani, N. Nouri and A. Seifi, “BSSA: Binary spring search algorithm,” in Proc. of IEEE 4th Int. Conf. on Knowledge-Based Engineering and Innovation, Tehran, Iran, pp. 0220–0224, 2017. [Google Scholar]

 9.  M. Dehghani, Z. Montazeri, G. Dhiman, O. Malik, R. Morales-Menendez et al., “A spring search algorithm applied to engineering optimization problems,” Applied Sciences, vol. 10, no. 18, pp. 6173, 2020. [Google Scholar]

10. M. Dehghani, Z. Montazeri, A. Ehsanifar, A. R. Seifi, M. J. Ebadi et al., “Planning of energy carriers based on final energy consumption using dynamic programming and particle swarm optimization,” Electrical Engineering & Electromechanics, no. 5, pp. 62–71, 2018. https://doi.org/10.20998/2074-272X.2018.5.10. [Google Scholar]

11. Z. Montazeri and T. Niknam, “Energy carriers management based on energy consumption,” in Proc. of IEEE 4th Int. Conf. on Knowledge-Based Engineering and Innovation (KBEI), Tehran, Iran, pp. 0539–0543, 2017. [Google Scholar]

12. M. Dehghani, Z. Montazeri and O. Malik, “Optimal sizing and placement of capacitor banks and distributed generation in distribution systems using spring search algorithm,” International Journal of Emerging Electric Power Systems, vol. 21, no. 1, pp. 20190217, 2020. [Google Scholar]

13. M. Dehghani, Z. Montazeri, O. P. Malik, K. Al-Haddad, J. M. Guerrero et al., “A new methodology called dice game optimizer for capacitor placement in distribution systems,” Electrical Engineering & Electromechanics, no. 1, pp. 61–64, 2020. https://doi.org/10.20998/2074-272X.2020.1.10. [Google Scholar]

14. S. Dehbozorgi, A. Ehsanifar, Z. Montazeri, M. Dehghani and A. Seifi, “Line loss reduction and voltage profile improvement in radial distribution networks using battery energy storage system,” in Proc. of IEEE 4th Int. Conf. on Knowledge-Based Engineering and Innovation (KBEI), Tehran, Iran, pp. 0215–0219, 2017. [Google Scholar]

15. Z. Montazeri and T. Niknam, “Optimal utilization of electrical energy from power plants based on final energy consumption using gravitational search algorithm,” Electrical Engineering & Electromechanics, no. 4, pp. 70–73, 2018. https://doi.org/10.20998/2074-272X.2018.4.12. [Google Scholar]

16. M. Dehghani, M. Mardaneh, Z. Montazeri, A. Ehsanifar, M. J. Ebadi et al., “Spring search algorithm for simultaneous placement of distributed generation and capacitors,” Electrical Engineering & Electromechanics, no. 6, pp. 68–73, 2018. https://doi.org/10.20998/2074-272X.2018.6.10. [Google Scholar]

17. M. Premkumar, R. Sowmya, P. Jangir, K. S. Nisar and M. Aldhaifallah, “A new metaheuristic optimization algorithms for brushless direct current wheel motor design problem,” Computers, Materials & Continua, vol. 67, no. 2, pp. 2227–2242, 2021. [Google Scholar]

18. A. Ehsanifar, M. Dehghani and M. Allahbakhshi, “Calculating the leakage inductance for transformer inter-turn fault detection using finite element method,” in Proc. of Iranian Conf. on Electrical Engineering (ICEE), Tehran, Iran, pp. 1372–1377, 2017. [Google Scholar]

19. M. Dehghani, Z. Montazeri and O. P. Malik, “Energy commitment: A planning of energy carrier based on energy consumption,” Electrical Engineering & Electromechanics, no. 4, pp. 69–72, 2019. https://doi.org/10.20998/2074-272X.2019.4.10. [Google Scholar]

20. M. Dehghani, M. Mardaneh, O. P. Malik, J. M. Guerrero, C. Sotelo et al., “Genetic algorithm for energy commitment in a power system supplied by multiple energy carriers,” Sustainability, vol. 12, no. 23, pp. 10053, 2020. [Google Scholar]

21. M. Dehghani, M. Mardaneh, O. P. Malik, J. M. Guerrero, R. Morales-Menendez et al., “Energy commitment for a power system supplied by multiple energy carriers system using following optimization algorithm,” Applied Sciences, vol. 10, no. 17, pp. 5862, 2020. [Google Scholar]

22. H. Rezk, A. Fathy, M. Aly and M. N. F. Ibrahim, “Energy management control strategy for renewable energy system based on spotted hyena optimizer,” Computers, Materials & Continua, vol. 67, no. 2, pp. 2271–2281, 2021. [Google Scholar]

23. M. Dorigo, V. Maniezzo and A. Colorni, “Ant system: Optimization by a colony of cooperating agents,” IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), vol. 26, no. 1, pp. 29–41, 1996. [Google Scholar]

24. S. Kirkpatrick, C. D. Gelatt and M. P. Vecchi, “Optimization by simulated annealing,” Science, vol. 220, no. 4598, pp. 671–680, 1983. [Google Scholar]

25. S. A. Hofmeyr and S. Forrest, “Architecture for an artificial immune system,” Evolutionary Computation, vol. 8, no. 4, pp. 443–473, 2000. [Google Scholar]

26. J. Kennedy and R. Eberhart, “Particle swarm optimization,” in Proc. of ICNN'95-Int. Conf. on Neural Networks, Perth, WA, Australia, pp. 1942–1948, 1995. [Google Scholar]

27. R. V. Rao, V. J. Savsani and D. Vakharia, “Teaching–learning-based optimization: A novel method for constrained mechanical design optimization problems,” Computer-Aided Design, vol. 43, no. 3, pp. 303–315, 2011. [Google Scholar]

28. S. Mirjalili, S. M. Mirjalili and A. Lewis, “Grey wolf optimizer,” Advances in Engineering Software, vol. 69, pp. 46–61, 2014. [Google Scholar]

29. S. Mirjalili and A. Lewis, “The whale optimization algorithm,” Advances in Engineering Software, vol. 95, pp. 51–67, 2016. [Google Scholar]

30. A. Faramarzi, M. Heidarinejad, S. Mirjalili and A. H. Gandomi, “Marine predators algorithm: A nature-inspired metaheuristic,” Expert Systems with Applications, vol. 152, pp. 113377, 2020. [Google Scholar]

31. G. Dhiman and V. Kumar, “Emperor penguin optimizer: A bio-inspired algorithm for engineering problems,” Knowledge-Based Systems, vol. 159, pp. 20–50, 2018. [Google Scholar]

32. M. Dehghani, Š Hubálovský and P. Trojovský, “Cat and mouse based optimizer: A new nature-inspired optimization algorithm,” Sensors, vol. 21, no. 15, pp. 5214, 2021. [Google Scholar]

33. M. Dehghani, M. Mardaneh and O. P. Malik, “FOA: ‘following’ optimization algorithm for solving power engineering optimization problems,” Journal of Operation and Automation in Power Engineering, vol. 8, no. 1, pp. 57–64, 2020. [Google Scholar]

34. F. A. Zeidabadi, S. A. Doumari, M. Dehghani, Z. Montazeri, P. Trojovský et al., “AMBO: All members-based optimizer for solving optimization problems,” Computers, Materials & Continua, vol. 70, no. 2, pp. 2905–2921, 2022. [Google Scholar]

35. M. Dehghani, M. Mardaneh, O. P. Malik and S. M. NouraeiPour, “DTO: Donkey theorem optimization,” in in: Proc. of Iranian Conference on Electrical Engineering (ICEE), Yazd, Iran, pp. 1855–1859, 2019. [Google Scholar]

36. F. A. Zeidabadi, S. A. Doumari, M. Dehghani and O. P. Malik, “MLBO: Mixed leader based optimizer for solving optimization problems,” International Journal of Intelligent Engineering and Systems, vol. 14, no. 4, pp. 472–479, 2021. [Google Scholar]

37. H. Givi, M. Dehghani, Z. Montazeri, R. Morales-Menendez, R. A. Ramirez-Mendoza et al., “GBUO: “the good, the bad, and the ugly” optimizer,” Applied Sciences, vol. 11, no. 5, pp. 2042, 2021. [Google Scholar]

38. S. A. Doumari, F. A. Zeidabadi, M. Dehghani and O. P. Malik, “Mixed best members based optimizer for solving various optimization problems,” International Journal of Intelligent Engineering and Systems, vol. 14, no. 4, pp. 384–392, 2021. [Google Scholar]

39. S. Saremi, S. Mirjalili and A. Lewis, “Grasshopper optimisation algorithm: Theory and application,” Advances in Engineering Software, vol. 105, pp. 30–47, 2017. [Google Scholar]

40. F. -A. Zeidabadi, S. -A. Doumari, M. Dehghani, Z. Montazeri, P. Trojovský et al., “MLA: A new mutated leader algorithm for solving optimization problems,” Computers, Materials & Continua, vol. 70, no. 3, pp. 5631–5649, 2022. [Google Scholar]

41. S. Kaur, L. K. Awasthi, A. L. Sangal and G. Dhiman, “Tunicate swarm algorithm: A new bio-inspired based metaheuristic paradigm for global optimization,” Engineering Applications of Artificial Intelligence, vol. 90, pp. 103541, 2020. [Google Scholar]

42. M. Dehghani, M. Mardaneh, J. M. Guerrero, O. Malik and V. Kumar, “Football game based optimization: An application to solve energy commitment problem,” International Journal of Intelligent Engineering and Systems, vol. 13, no. 5, pp. 514–523, 2020. [Google Scholar]

43. M. Dehghani, Z. Montazeri, S. Saremi, A. Dehghani, O. P. Malik et al., “HOGO: Hide objects game optimization,” International Journal of Intelligent Engineering and Systems, vol. 13, no. 4, pp. 216–225, 2020. [Google Scholar]

44. M. Dehghani, Z. Montazeri, H. Givi, J. M. Guerrero and G. Dhiman, “Darts game optimizer: A new optimization technique based on darts game,” International Journal of Intelligent Engineering and Systems, vol. 13, no. 5, pp. 286–294, 2020. [Google Scholar]

45. S. A. Doumari, H. Givi, M. Dehghani and O. P. Malik, “Ring toss game-based optimization algorithm for solving various optimization problems,” International Journal of Intelligent Engineering and Systems, vol. 14, no. 3, pp. 545–554, 2021. [Google Scholar]

46. M. Dehghani, Z. Montazeri, O. P. Malik, A. Ehsanifar and A. Dehghani, “OSA: Orientation search algorithm,” International Journal of Industrial Electronics Control and Optimization, vol. 2, no. 2, pp. 99–112, 2019. [Google Scholar]

47. M. Dehghani, Z. Montazeri and O. P. Malik, “DGO: Dice game optimizer,” Gazi University Journal of Science, vol. 32, no. 3, pp. 871–882, 2019. [Google Scholar]

48. M. Dehghani, Z. Montazeri, O. P. Malik, G. Dhiman and V. Kumar, “BOSA: Binary orientation search algorithm,” International Journal of Innovative Technology and Exploring Engineering, vol. 9, no. 1, pp. 5306–5310, 2019. [Google Scholar]

49. E. Rashedi, H. Nezamabadi-Pour and S. Saryazdi, “GSA: A gravitational search algorithm,” Information Sciences, vol. 179, no. 13, pp. 2232–2248, 2009. [Google Scholar]

50. M. Dehghani and H. Samet, “Momentum search algorithm: A new meta-heuristic optimization algorithm inspired by momentum conservation law,” SN Applied Sciences, vol. 2, no. 10, pp. 1–15, 2020. [Google Scholar]

51. F. A. Hashim, E. H. Houssein, M. S. Mabrouk, W. Al-Atabany and S. Mirjalili, “Henry gas solubility optimization: A novel physics-based algorithm,” Future Generation Computer Systems, vol. 101, pp. 646–667, 2019. [Google Scholar]

52. M. Dehghani, Z. Montazeri, A. Dehghani and A. Seifi, “Spring search algorithm: A new meta-heuristic optimization algorithm inspired by Hooke's law,” in Proc. of IEEE 4th Int. Conf. on Knowledge-Based Engineering and Innovation (KBEI), Tehran, Iran, pp. 0210–0214, 2017. [Google Scholar]

53. A. Kaveh and S. Talatahari, “A novel heuristic optimization method: Charged system search,” Acta Mechanica, vol. 213, no. 3–4, pp. 267–289, 2010. [Google Scholar]

54. D. E. Goldberg and J. H. Holland, “Genetic algorithms and machine learning,” Machine Learning, vol. 3, no. 2, pp. 95–99, 1988. [Google Scholar]

55. W. Banzhaf, P. Nordin, R. E. Keller and F. D. Francone, “Genetic programming: An introduction on the automatic evolution of computer programs and its applications,” in Library of Congress Cataloging-in-Publication Data, 1st ed., vol. 27. San Francisco, CA, USA: Morgan Kaufmann Publishers, pp. 1–398, 1998. [Google Scholar]

56. R. G. Reynolds, “An introduction to cultural algorithms,” in Proc. of the Third Annual Conf. on Evolutionary Programming, river edge, NJ: World Scientific, vol. 24, pp. 131–139, 1994. [Google Scholar]

57. R. Storn and K. Price, “Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces,” Journal of Global Optimization, vol. 11, no. 4, pp. 341–359, 1997. [Google Scholar]

58. F. Wilcoxon, “Individual comparisons by ranking methods,” Breakthroughs in Statistics, vol. 1, no. 6, pp. 196–202, 1992. [Google Scholar]

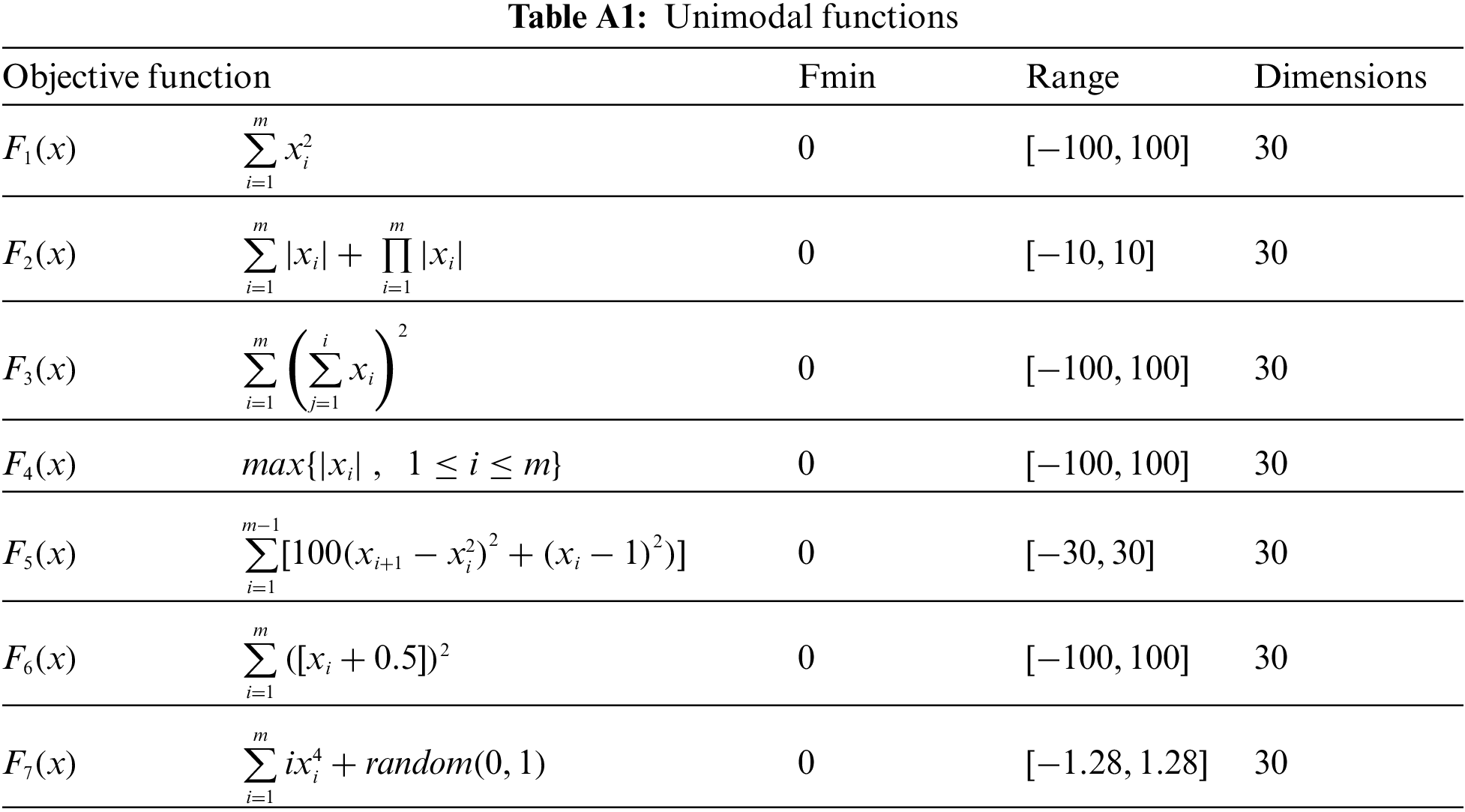
Information of test objective functions

The information of the objective functions used in the simulation section is presented in Tab. A1 to Tab. A3

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.