Computers, Materials & Continua DOI:10.32604/cmc.2022.024585
Article

Locomotion of Bioinspired Underwater Snake Robots Using Metaheuristic Algorithm

Souad Larabi-Marie-Sainte1, Taiseer Abdalla Elfadil Eisa2, Fahd N. Al-Wesabi3,4, Amani Abdulrahman Albraikan5, Manar Ahmed Hamza6,*, Abdelwahed Motwakel6, Ishfaq Yaseen6 and Mesfer Al Duhayyim7

1Department of Computer Science, College of Computer and Information Sciences, Prince Sultan University, Riyadh, 11586, Saudi Arabia
2Department of Information Systems-Girls Section, King Khalid University, Mahayil, 62529, Saudi Arabia
3Department of Computer Science, College of Science & Art at Mahayil, King Khalid University, 62529, Saudi Arabia
4Faculty of Computer and IT, Sana'a University, Sana'a, 1247, Yemen
5Department of Computer Science, College of Computer and Information Sciences, Princess Nourah Bint Abdulrahman University, 11564, Saudi Arabia
6Department of Computer and Self Development, Preparatory Year Deanship, Prince Sattam bin Abdulaziz University, 16278, Saudi Arabia
7Department of Natural and Applied Sciences, College of Community-Aflaj, Prince Sattam bin Abdulaziz University, 16278, Saudi Arabia
*Corresponding Author: Manar Ahmed Hamza. Email: ma.hamza@psau.edu.sa
Received: 23 October 2021; Accepted: 06 December 2021

Abstract: Snake Robots (SR) have been successfully deployed and proved to attain bio-inspired solutions owing to its capability to move in harsh environments, a characteristic not found in other kinds of robots (like wheeled or legged robots). Underwater Snake Robots (USR) establish a bioinspired solution in the domain of underwater robotics. It is a key challenge to increase the motion efficiency in underwater robots, with respect to forwarding speed, by enhancing the locomotion method. At the same time, energy efficiency is also considered as a crucial issue for long-term automation of the systems. In this aspect, the current research paper concentrates on the design of effectual Locomotion of Bioinspired Underwater Snake Robots using Metaheuristic Algorithm (LBIUSR-MA). The proposed LBIUSR-MA technique derives a bi-objective optimization problem to maximize the Forward Velocity (FV) and minimize the Average Power Consumption (APC). LBIUSR-MA technique involves the design of Manta Ray Foraging Optimization (MRFO) technique and derives two objective functions to resolve the optimization issue. In addition to these, effective weighted sum technique is also used for the integration of two objective functions. Moreover, the objective functions are required to be assessed for varying gait variables so as to inspect the performance of locomotion. A detailed set of simulation analyses was conducted and the experimental results demonstrate that the developed LBIUSR-MA method achieved a low Average Power Consumption (APC) value of 80.52 W under δ value of 50. The proposed model accomplished the minimum PAC and maximum FV of USR in an effective manner.

Keywords: Bio-inspired robots; underwater snake robots; locomotion efficiency; forwarding velocity; average power consumption; objective function

1  Introduction

Bioinspired robots imitate animal movement and this phenomenon has led to numerous technical developments that transformed the locomotion mode of man-made machines over land, air, and water [1]. Scientists and engineers still follow the fluidity and elegance of animal motion. A number of such fascinating biological systems is yet to be understood, programmed, built and designed as robotic systems. Biological stimulation can be taken from various forms of animals which involves the physical structure of their bodies, organization of their nervous system, and their behavioural approaches [1]. The main drawbacks that need to be considered including the degree of realism is that the advantages of biological stimulation and the division of relevant biological information from these essentials must be leveraged to the core, so as to achieve the task of interest [2]. In general, a roboticist gets inspired for concepts from biology as a springboard for novel engineering design but they consequently neglects the biological realism. As a technological endeavour, the achievement of bio-stimulated robotic projects should not be determined by its realism to biological data [2]. Instead, it should be determined by the extent up to which the efficiency of biological-stimulated robot enhances the current technological methods with the help of efficacy parameters as a benchmark for that technology.

The current study considered the transformation from Snake-to-snake Robots (SR) [3]. In land, an individual can view a snake which climbs in the woods based on which an extended mechanical creature can be constructed. But, this construction process can be driven only when essential macroscopic standards are in place and are examined in-depth so that the muscles and skeleton can be transmitted into mechanical linkages and traditional motors successfully. Swimming SRs are bio-inspired robotic systems which imitate the biological movement of eels/snakes with its own essential manipulation abilities. This characteristic could be deliberated as a good candidate for these kinds of applications [3]. Various bio-inspired swimming SRs have been introduced so far by distinct groups of researches [4]. USR, being a potential candidate, brings a possible solution to improve the efficiency of next generation underwater vehicles [5], and help in the development of significant applications for underwater monitoring, exploration, inspection, and surveillance [6]. Further, it also has the ability to inspect gas installation and subsea oil. Furthermore, for biology and marine archaeology communities, SRs are capable of swimming efficiently without much noise and could navigate in complex environments like wrecks which are highly stimulating [7].

In order to realize the functioning of SRs for underwater applications, various control design problems should be resolved [8,9]. Significant control problems arise with regards to the device's capability of achieving an effective movement, preferably with minimal number of expended energies and this process can take a long time to accomplish. In literature [8], the researchers analysed the relationship among gait variables, expended energy, and the forwarded velocity for distinct movement forms to USRs. Additionally, depending on simulative study results, empirical rules have been presented to select the most-efficient movement pattern. Moreover, in the study conducted earlier [9], the researchers compared Remotely Operated Vehicles (ROVs) and SRs and the results were attained for underwater power utilization. Particularly, it is displayed that the biologically-stimulated swimming robots are highly effective than ROVs. Such simulative researches have been proposed to achieve stimulating perceptions about power utilization and the efficacy of USRs.

1.1 Paper Contribution

The current research paper proposes the model i.e., efficient Locomotion of Bioinspired Underwater Snake Robots using Metaheuristic Algorithm (LBIUSR-MA). The proposed LBIUSR-MA technique derives a bi-objective optimization problem to maximize the Forward Velocity (FV) and minimize the power consumption level. While the latter can be achieved through Manta Ray Foraging Optimization (MRFO). MRFO algorithm is chosen over other algorithms due to the fact that MRFO optimizer can achieve promising improvements on the precision of the solution with less computation cost than other well-established optimizers. In addition, effective weighted sum technique is also used for the integration of two objective functions of MRFO technique. Besides, the objective functions are required to be assessed for varying gait variables in order to inspect the locomotion performance. To examine the enhanced outcomes of the proposed LBIUSR-MA technique, a set of experiments was conducted and the results were inspected under different performance measures.

1.2 Organization of the Paper

Rest of the paper is organized as follows. Section 2 provides a detailed review of existing works and Section 3 defines the modelling of USRs. Next, Section 4 introduces the proposed model and Section 5 validates the performance of the proposed model. Finally, Section 6 concludes the paper.

2  Existing Works About Bio-Inspired USRs

The current section reviews the existing works related to locomotion efficiency and power consumption of USRs. Kelasidi et al. [10] proposed the conversion of two objective functions into a single one with the help of weighted sum approach. In this study, for a distinct groups of weight factors, Particle Swarm Optimization (PSO) is employed and a group of optimum points is subsequently attained. Trade-off curves/Pareto fronts are demonstrated for swimming snake and land-based robots respectively using different number of links. Particularly, the designers/operators of the bioinspired SRs selected Pareto optimum points on the basis of trade-off curves, provided the preferable link number is available. The optimum gait variable for robot controlling systems is directly provided for underwater snake and land-based robots.

Kelasidi et al. [11] presented a bioinspired USR armed with passive caudal (tail) fin. To be specific, a very stretchy USR structure was proposed in this study. This structure has the ability to travel in both underwater and ground, owing to its modular design and robust mechanism that enables the involvement of added effector under distinct models of the robot, based on the requirement of applications. It could select appropriate configurations based on the task to be executed in several uncertain underwater and ground surroundings. Kelasidi et al. [12] focused on novel types of USR armed with thruster that integrates the manoeuvrability and flexibility of traditional USR with thruster using the locomotive abilities of conventional marine vessels. Such vehicle structures represent a possible solution for the operation, inside the narrow and constrained parts of subsea configurations. The study considered the locomotive efficacy of such novel kind of USR with thruster by examining the essential characteristics of velocity and the consumed energy of USR with and without thruster, for eel-like motion and lateral undulation.

Kelasidi et al. [13] considered the energy efficacy of swimming SRs by examining and presenting the essential characteristics of velocity and the consumed energy of USR for eel-like motion and lateral undulation. To be specific, the researchers examined the relations among gait variables, FV, and the consumed energy for distinct motion patterns. The experimental and simulation outcomes were observed to support the theoretical results. Kelasidi et al. [14] formulated a multi-objective optimization problem to maximize FV and minimize energy consumption. Particularly, the optimum values of gait variable for distinct motion patterns were evaluated in the presence of tradeoffs between consumed energy and velocities. When using multi-objective optimization problem, the solution is not a single point, instead a set of points. The study presented a weighted sum technique to integrate FV with energy consumption optimization problems. PSO was employed in this study to obtain the optimum gait variables for distinct weighting factors.

Kelasidi et al. [15] presented the results about power consumption of USRs. Particularly, the researchers analysed the relations among gait variables, FV, and the energy consumed for distinct motion patterns of USRs. According to a simulative research, the authors proposed empirical rules to select the gait variable, considering FB and desirable consumed energy. Jia et al. [16] presented a new Bayesian-based controller for SRs in cluttered environments. Sequential density propagation rules were derived in this study by presenting various likelihood densities in a unified architecture. Especially, two input influence densities were presented to model the increasing effects of several external forces endured by SR. Furthermore, the measurement probability method was exploited in this research work to provide a powerful closed-loop feedback. Virgala et al. [17] presented an arithmetical locomotive method for SR in a pipe of rectangular cross section.

Zhang et al. [18] designed an underwater swimming SR made up of soft joints and rigid links. The study presented an accurate, completely dynamic and kinematic method with hydrodynamics to describe the underwater undulatory motion of robot. The result verifies the efficacy of the method and shows that SR has a significant capacity that can be utilized in marine applications. Cao et al. [19] investigated locomotive efficacy optimization and adoptive path following of snake-like robots in difficult environments. In order to optimize the locomotive efficacy, FV and the consumed energy were taken and the optimum locomotive parameter of snake-like robots, managed via Central Pattern Generator (CPG) controller, was investigated. A Cuckoo Search (CS) approach is employed to optimize the locomotive parameters of robot for environment with obstacle distribution and variable fraction. An adoptive path following approach was presented for steering the snake-like robot forward and desirable paths. Though few research works have been conducted in the literature, USRs need to be explored in detail with much insights about real-time applications.

3  Modelling of USRs

This section concisely presents the dynamics and kinematics of USR movements in a virtual horizontal plane. The complete demonstration of the module follows the literature [20]. The USR contains n rigid link of equivalent length 2l, connected with n−1 joint. The link is supposed to have a similar mass m and moment of inertia, J=13ml2. The mass of every link is uniformly distributed in such a way that the link CM is placed at middle point (at length l from all sides of the joint). Hence, the overall mass of the robot is denoted by nm. The succeeding vector and matrix are utilized as given herewith.

A=[11⋱⋱11],D=[1−1⋱⋱1−1]

Whereas, D∈R(n−1)×n. Moreover,

e=[1,  .  .  .  ,  1]T∈Rn,E=[e0n×10n×1e]∈R2n×2,

Sθ=diag(sin  θ)∈Rn×n,Cθ=diag(cos  θ)∈Rn×n

θ˙=[θ˙,...,θ˙]T∈Rn,K=AT(DDT)−1D.

3.1 Kinematics of USR

The SRs are supposed to pass in a virtual horizontal plane which is entirely immersed in water, and possess n+2 degrees of freedom. The link angles of every link i∈1,…,n of SR is represented through θi∈R. However, the joint angle of joint i∈1,  …,  n−1 is denoted via φi=θi−θi−1. Both link angle and the joint angle are gathered in the vector θ=[θ1,  …,  θn]T∈Rn and φ=[φ1,  …,  φn−1]T∈Rn−1, Correspondingly. The orientation (or heading) θ¯∈R of the snake is determined as the average of link angle, viz., as θ¯=1n∑i=1n⁡θi [21]. A global frame location PCM∈R2 of CM in the robot is provided as follows.

pCM=[pxpy]=[1nm∑i=1n⁡mxi1nm∑i=1n⁡myi]=1n[eTXeTY](1)

Here (xi,yi) denotes the global frame coordinates of the CM of link i, X=[x1,  …,  xn]T∈Rn & Y=[y1,  …,  yn]T∈Rn.

3.2 Hydrodynamic Modelling

The dynamic modelling of contact force is highly complex compared to the modelling of entire rigid movement. It is displayed that the link between torque and fluid forces can be formulated as follows.

f=[fxfy]=[fAxfAy]+[f  DIxf  DIy]+[f  DIIxf  DIIy].(2)

and

τ=−Λ1θ¨−Λ2θ˙−Λ3θ˙|θ˙|(3)

Here, the vectors fAx and fAy represent the effect from additional mass forces whereas the vectors fDxI,fDyI & fDxII,fDyII represent nonlinear d linear drag forces correspondingly. It is possible to execute a complete derivation of fAx,fAy,fDxI,fDyI,fDxII,fDyII vectors and Λ1, Λ2 & Λ3 matrices.

3.3 Modelling Motion

This sub-section presents the equation of motion for USR. The acceleration of CM might be stated as follows.

[p¨xp¨y]=−Mp[k11k12k21k22][lKT(Cθθ˙+Sθθ¨)lKT(Sθθ˙−Cθθ¨)]−Mp[k12−k11k22−k21][VxaVya]θ˙+Mp[eTfDxeTfDy](4)

Whereas a thorough derivation of the matrix Mp and vectors Vxa, Vya, k11, k12, k21 and k22 are provided herewith. Additionally, it is displayed that the effects of fluid force (2), torque (3) and the whole equations of motion of USRs are attained by (4).

Mθθ¨+wθP2+Vθθ˙+A3|θ˙|θ˙+KDxfDx+KDyfDy=DTu(5)

Here, fDx=fDxI+fDxII and fDy=fDyI+fDyII which demonstrates that the drag forces in x and y directions and u∈Rn−1 remains the control input.

4  Design of the Proposed LBIUSR-MA Technique

In current research work, a new LBIUSR-MA technique has been proposed to resolve the multi-objective optimization issue. In movement optimization issue, the stated multi-objectives undergo optimization by iterating on the gait variable which is subjected to USR’ dynamic method i.e., highly complicated owing to hydrodynamic impacts. Resolving an optimization issue involves the development of a solution from each possible perspective in order to maximize (or minimize) an objective function. In this study, a bi-objective optimization issue was considered to optimize objectives functions namely, FV and power consumption. The familiar weighted sum method is executed to combine the two objective functions and is resolved by MRFO algorithm.

MRFO algorithm is developed based on Manta Rays (MRs), an exclusive species with terrific appearance. Being a marine species, MR is highly efficient in detecting the dense plankton [22]. The foraging standard has been developed out of cyclone foraging. The tail outcomes connect to the heads in a spiral form so as to create a spiralling vertex in a cyclone-like form and attains the water flow in a surface. When MR detects a food source, it performs a series of back somersaults due to which a circle is created around the plankton that draws the latter towards MR. Somersault is usually done in the form of cyclic, arbitrary, frequent, and with local motion. These movements help MR to consume the optimal food sources. Although the foraging behaviours are arbitrary, it is highly effective. It can be modelled mathematically and a new meta-heuristic method called MRFO is placed herewith to compute global optimization. MRFO was developed using cyclone, somersault, and chain behaviours. The mathematical method is determined as discussed herewith.

4.1 Chain Foraging

In MRFO, MR can notice the location of planktons and moves towards it. When the location of planktons becomes broader, it is deliberated as the optimum one. Though the optimal solution is not explicitly known, MRFO considers that position as the optimum solution since the MR with high plankton attains an optimal food source. An individual, without an initial move toward food, does not function yet it develops in the future. Therefore, an individual is updated with an optimum solution prior to the recognition. The mathematical method for chain foraging is given herewith.

xid(t+1)={xid(t)+r⋅(xbestd(t)−xid(t))+α⋅(xbestd(t)−xid(t))i=1xid(t)+r⋅(xi−1d(t)−xid(t))+α⋅(xbestd(t)−xid(t))i=2,…,N(6)

α=2⋅r⋅|log(r)|(7)

Whereas, xid(t) denotes the location of i th individual at time t in dth dimension, r determines an arbitrary value from [0,1],  a signifies the weight coefficient and xbestd(t) indicates the plankton with greater attention. The location upgrade of ith   individual is determined using the location xi−1(t) of the (i−1)th current individual and location xbest(t) of the food.

4.2 Cyclone Foraging

When a set of MR detects dense plankton in marine water, it develops a long foraging chain and moves toward the food in a spiral way. The mathematical operation for spiral-shaped motion of MR, in two-dimensional space, is given below.

{Xj(t+1)=Xbest+r⋅(Xi−1(t)−Xi(t))+ebw⋅cos⁡(2πw)⋅(Xbest−Xi(t))Yi(t+1)=Ybest+r⋅(Yi−1(t)−Yi(t))+ebw⋅sin⁡(2πw)⋅(Ybest−Yi(t))(8)

Whereas w denotes an arbitrary number I between 0 and 1. The movement behaviours are transferred to n-D space. For easiness, the mathematical method of cyclone foraging is given herewith.

xid(t+1)={xbestd+r⋅(xbestd(t)−xid(t))+β⋅(xbestd(t)−xid(t))i=1xbestd+r⋅(xi−1d(t)−xid(t))+β⋅(xbestd(t)−xid(t))i=2,…,N(9)

β=2er1T−t+1T⋅sin(2πr1)(10)

whereas β denotes the weight coefficient, T indicates high number of iterations, and r1 indicates rand value between 0 and 1. An individual starts exploration with food as reference location; therefore, cyclone foraging has optimal exploitation for an area with the recognition of optimum solution. Further, it is also employed to enhance the searching procedure. The searching process is defined and activates the MRFO to achieve the global search as given herewith.

xrandd=Lbd+r⋅(Ubd−Lbd)(11)

xid(t+1)={xrandd+r⋅(xrandd−xid(t))+β⋅(xrandd−xid(t))i=1xrandd+r⋅(xi−ld(t)−xid(t))+β⋅(xrandd−xid(t))i=2,…,N(12)

Whereas xrandd denotes the arbitrary location created from search space and Lbd & Ubd denotes lower limit and upper bounds of dth dimension, respectively.

4.3 Somersault Foraging

Now, the position of food is stated as ‘pivot’. Then, the position is updated near the optimum location considered so far. The mathematical approach can be established as follows.

xid(t+1)=xid(t)+S⋅(r2⋅xbestd−r3⋅xid(t)),  i=1,  …,  N(13)

Whereas S denotes the somersault factor that selects the somersault rank and S=2,r2 and r3 denotes two arbitrary values between zero and one. From Eq. (13), and the depiction of somersault range, it is possible for an individual to swim towards the position for the purpose of searching an application located between current location and the symmetrical location in an optimal location. Since the distance between better and individual positions gets decreased, the perturbation on the present location gets minimized. An individual is explored by an optimal solution in search space. The sample point is distributed between symmetrical and current locations on xbest, and the sample point, assigned as sparse in the distance, gets decreased. The abundant point from xbest contributes towards the search and sparse one involves in optimum exploration. Fig. 1 illustrates the flowchart of MRFO technique [22]. Algorithm 1 is the pseudocode for MRFO algorithm.

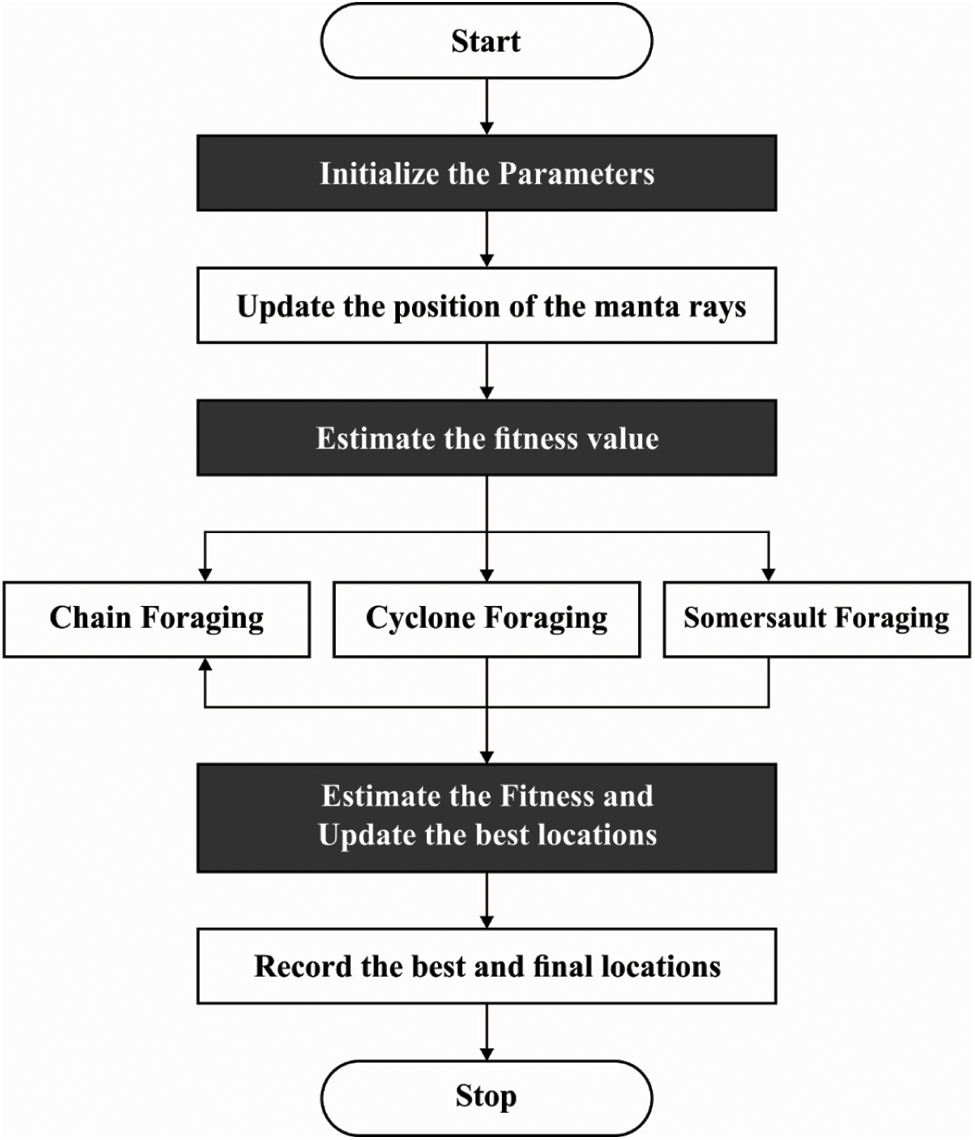
Figure 1: Flowchart of MRFO algorithm

4.4 Objective Function

Firstly, the overall energy utilization is derived as a function of actuation torque and angular velocity of the joint as given herewith.

Es=∫0T⁡(∑i=1n−1⁡|ui(t)φ˙(t)|)dt(14)

Whereas T denotes the time of a whole cycle movement. The actuation torque ui and the angular velocity φ˙ for joint i are estimated φ˙=θ˙−θ˙, correspondingly [23]. The joint is considered as an ideal one. Thus, the overall energy of the scheme is equivalent to the summation of kinetic energy and the energy dissipated due to ground friction for land-based SR or nearby fluid for USR. The average power utilization is evaluated as follows.

Pavg=1T∫0T⁡(∑i=1n−1⁡|ui(t)φ˙(t)|)dt(15)

Eq. (15) provides the average power utilization considering the accurate value of power spent for joint movement. The average power utilization could be evaluated as follows.

Pavg=1T∫0T⁡(∑i=1n−1⁡ui(t)φ˙(t))dt(16)

For USR, Eqs. (15) and (16) are studied. In the last cast, it is displayed that by taking into account, the negative work affects the simulated robot is capable of recovering energy too. But, for land-based SR, the accurate value of theoretic joint power is taken into account since the ground friction utilizes energy, if the robots move on land. For this scenario, Eq. (15) is utilized.

Additionally, the succeeding equation is utilized for calculating FV.

v¯=(px(T)−px(0))2+(py(T)−py(0))2T(17)

Whereas (px(0),  py(0)) and (px(T),  py(T)) denote the first and last locations of CM of the robot. The movement optimization issue could be created with the help of succeeding bound constraints and objective functions as given herewith.

minα,ω,δ⁡Jopt=[Pavg,  −v¯](18)

s.t:|φi∗|≤φi max  ,  |φ˙|≤φ˙,  |ui|≤ui max  

0≤α≤α max  ,  0≤ω≤ω max  ,  0≤δ≤δ max  

The equation denotes the physical limitation of joint, due to servo motor and specific structure of SR. The equation limits the potential range of the parameter for sinusoidal movement pattern. Fig. 2 showcases the framework for optimization process [11].

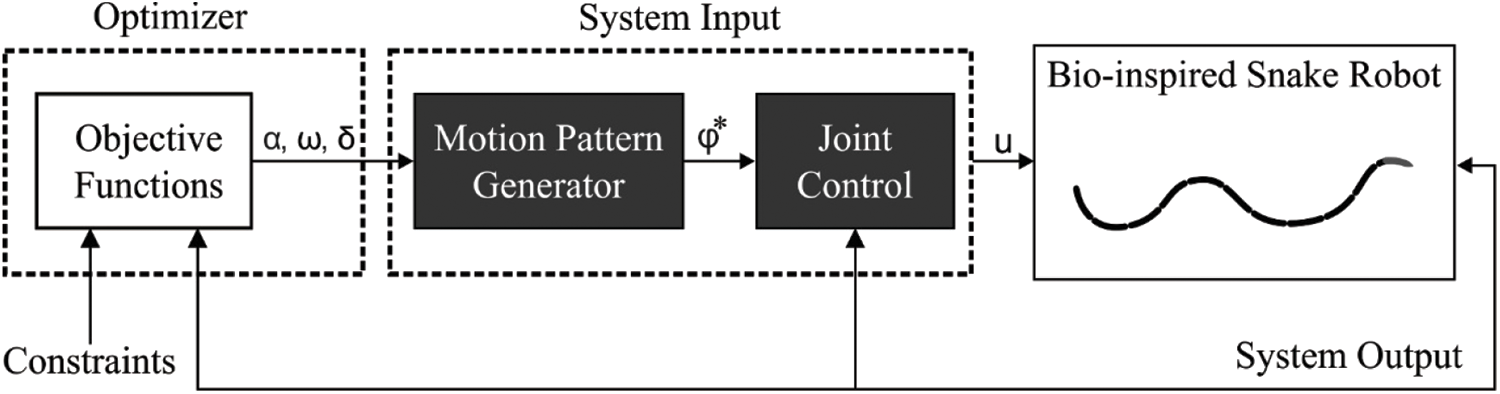
Figure 2: Illustration of the optimization framework [11]

As mentioned above, in case of bi-objective optimization issue Eq. (18), rather than a global solution, there is a group of optimum solutions available already. Furthermore, in such problems, the objective function is in contradictory to each other which further reduces the utilization of power. This phenomenon obviously leads to decrease in velocity. So, a Pareto optimality idea was recommended to overcome the bi-objective optimization issue. In this optimization issue Eq. (18), Pareto optimum solution is proposed. When power utilization cannot be improved through other means without attaining penalty of reducing FV, it could not have a great value without the need for additional power. Pareto optimum solutions are known as Pareto frontier or effective frontier. The current study considered two objective functions while it has the potential to display the frontier in Cartesian coordinate. As mentioned earlier, weighted-sum method is one of the familiar ways to create multi-objective optimization issue for normal objective function problems:

Jbal=wp(Pavg)sc−wU(v¯)sc′(19)

wp=1−wU′(20)

whereas (Pavg)sc and (v¯)sc represent the scaled value of power utilization and FV, correspondingly whereas wp and wv denote the weighting coefficients.

5  Performance Validation

The current section validates the performance of the proposed LBIUSR-MA technique under varying gait variables. The results were investigated under different values of α, ω and δ which correspond to amplitude, frequency, and phase shift amongst the joints respectively. The result was examined in two ways namely, FV and power consumption. Tab. 1 and Fig. 3 portrays the results achieved from FV analysis of the proposed LBIUSR-MA technique under different values of α. The figure showcases that FV got increased when α increased. The results were determined under FV of analytical model v¯tm, the Vortex model v¯tv, and average values from experimentation v¯te. For instance, with α=6, the LBIUSR-MA technique offered FV with v¯te, v¯tv, and v¯tm such as 0.070, 0.028, and 0.010 m/s respectively. In line with this, with α=10, LBIUSR-MA algorithm attained FV with v¯te, v¯tv, and v¯tm such as 0.111, 0.059, and 0.027 m/s respectively. Eventually, with α=20, the LBIUSR-MA approach accomplished FV with v¯te, v¯tv, and v¯tm of 0.220, 0.131, and 0.083 m/s correspondingly. Also, with α=30, LBIUSR-MA technique obtained FV with v¯te, v¯tv, and v¯tm of 0.278, 0.198, and 0.132 m/s correspondingly. Besides, with α=40, the LBIUSR-MA method attained FV with v¯te, v¯tv, and v¯tm of 0.270, 0.219, and 0.157 m/s respectively.

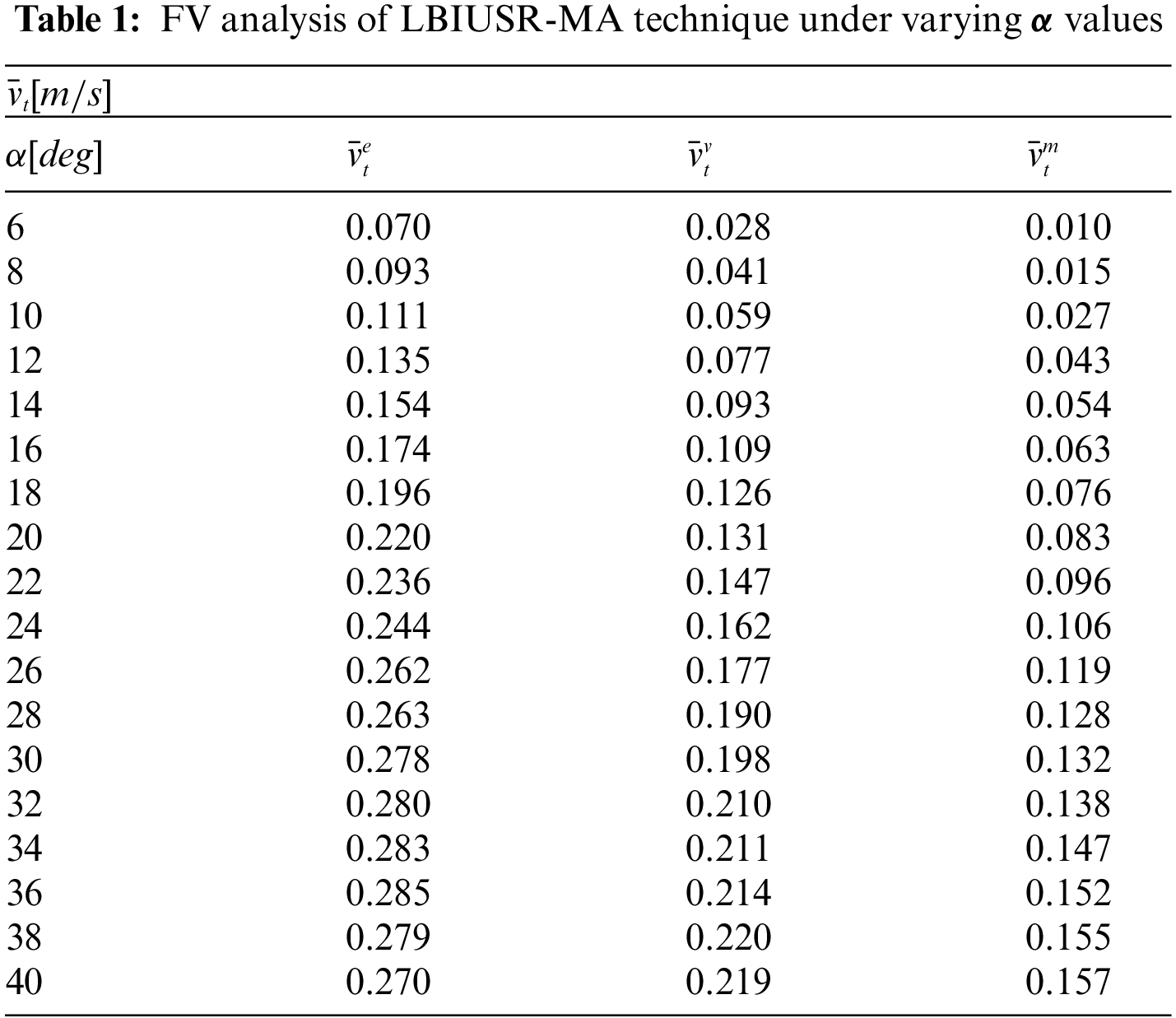
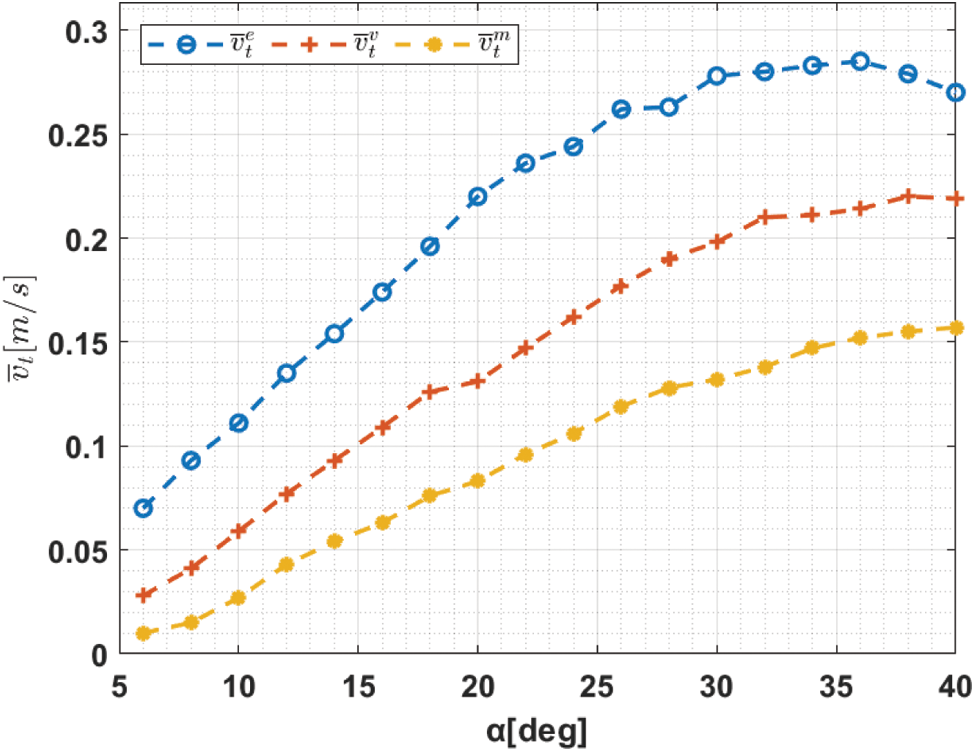
Figure 3: FV analysis of LBIUSR-MA technique under different values of α

Tab. 2 and Fig. 4 shows the results of FV analysis achieved by LBIUSR-MA method under varying values of ω. The figure showcase that FV got increased with an increase in ω. The outcomes were defined under FV of analytical approach v¯tm, the Vortex manner v¯tv,   and the average values from experimentation v¯te. For sample, with ω=10, the LBIUSR-MA approach offered a FV with v¯te, v¯tv, and v¯tm such as 0.041, 0.033, and 0.004 m/s correspondingly. Similarly, with ω=30, LBIUSR-MA technique attained a FV with v¯te, v¯tv, and v¯tm such as 0.083, 0.050, and 0.031 m/s correspondingly. Likewise, with ω=90, the LBIUSR-MA manner accomplished a FV with v¯te, v¯tv, and v¯tm such as 0.218, 0.137, and 0.098 m/s respectively. Moreover, with ω=120, the LBIUSR-MA algorithm accessed FV with v¯te, v¯tv, and v¯tm such as 0.235, 0.183, and 0.132 m/s correspondingly. Lastly, with ω=150, the LBIUSR-MA manner obtained FV with v¯te, v¯tv, and v¯tm such as 0.257, 0.232, and 0.157 m/s correspondingly.

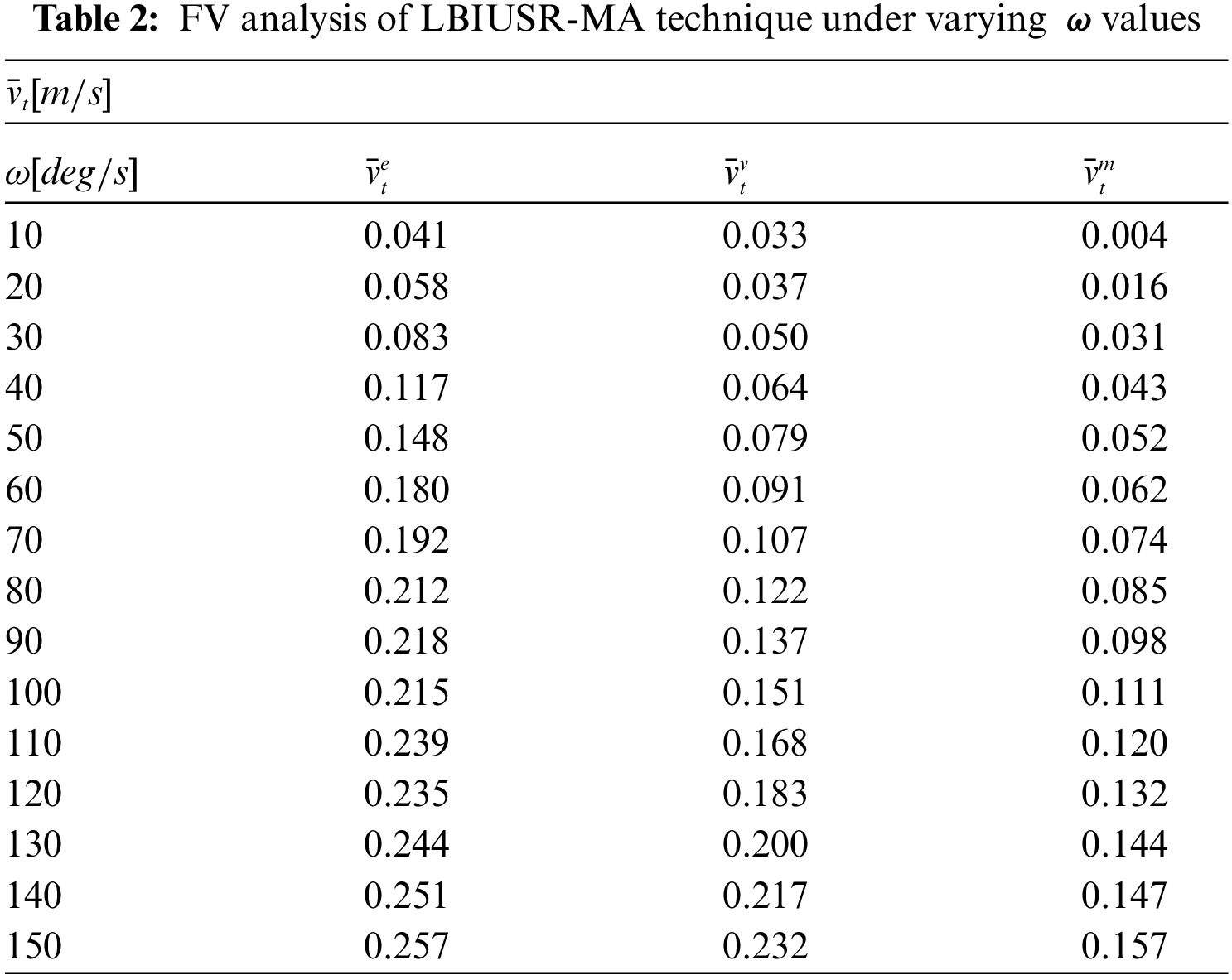
Figure 4: FV analysis of LBIUSR-MA technique under different values of ω

Tab. 3 and Fig. 5 inspects the results of FV analysis accomplished by LBIUSR-MA manner under different values of δ. The figure demonstrates that FV got improved with an increase in δ. The outcomes were defined under FV of analytical technique v¯tm, the Vortex model v¯tv,   and the average values from experimentation v¯te. For sample, with δ=20, the LBIUSR-MA method obtained FV with v¯te, v¯tv, and v¯tm such as 0.264, 0.354, and 0.187 m/s correspondingly. Along with that, when δ=25, the LBIUSR-MA method accomplished FV with v¯te, v¯tv, and v¯tm such as 0.256, 0.324, and 0.184 m/s correspondingly.

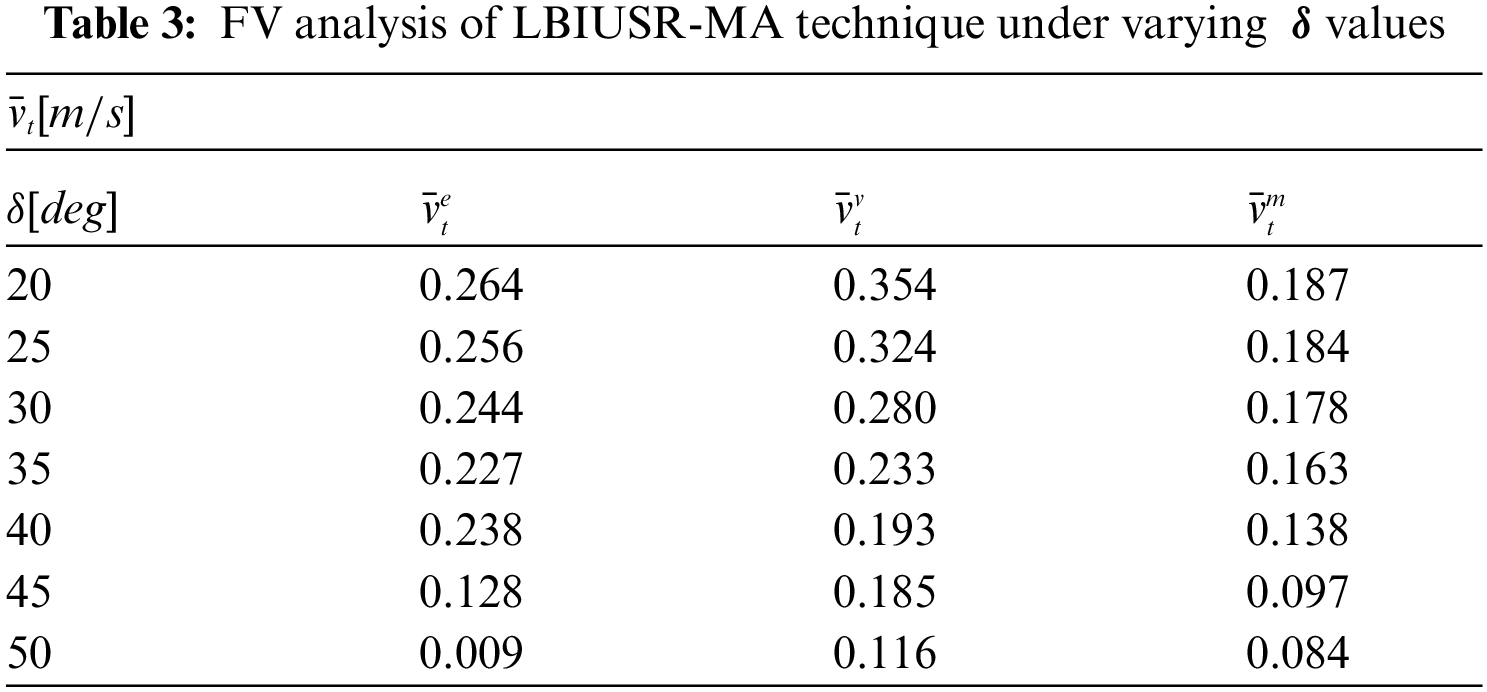
Figure 5: FV analysis of LBIUSR-MA technique under different values of δ

Followed by, with δ=35, the LBIUSR-MA technique accessed FV with v¯te, v¯tv, and v¯tm such as 0.227, 0.233, and 0.163 m/s correspondingly. Besides, with δ=45, the LBIUSR-MA method attained FV with v¯te, v¯tv, and v¯tm such as 0.128, 0.185, and 0.097 m/s respectively. Finally, with δ=50, the LBIUSR-MA algorithm accomplished FV with v¯te, v¯tv, and v¯tm such as 0.009, 0.116, and 0.084 m/s correspondingly.

The Average Power Consumption (APC) analysis was conducted for LBIUSR-MA technique under different values of α and the results are shown in and Fig. 6. The figure demonstrates that the proposed LBIUSR-MA technique attained effective APC which got increased with an increase in α. For instance, the LBIUSR-MA technique obtained APC values of 51.52, 54.97, and 59.85 W under α values such as 16, 18, and 20 respectively. Additionally, LBIUSR-MA method achieved APC values of 69.62, 70.20, and 71.35 W under α values such as 26, 28, and 30 correspondingly. Likewise, the proposed LBIUSR-MA technique gained APC values of 68.19, 66.75, and 70.20 W under α values such as 38, 40, and 42 respectively. At the same time, the proposed LBIUSR-MA approach attained APC values such as 73.36, 71.63, and 71.63 W under α values namely, 46, 48, and 50 correspondingly.

In order to showcase that the proposed model perform better, a comparison study was conducted with existing methods such as USR with thrusters and USR with and without caudal fin (USR-WWOCF) [11,12] and the results are shown in Fig. 6. The figure shows that USR-Thrusters model obtained a high APC over other two techniques. Besides, USR-WWOCF technique managed to obtain a slightly reduced APC over USR-Thrusters method, but not less than the proposed model. Among the techniques compared, the proposed LBIUSR-MA technique accomplished a superior performance with low APC.

Figure 6: Comparative results analysis of LBIUSR-MA with existing techniques

6  Conclusion

In current research work, a new LBIUSR-MA technique was proposed, developed and implemented to resolve the problem of maximization of FV and minimization of power consumption. The proposed LBIUSR-MA technique involves the design of MRFO algorithm in which two objective functions were derived to address the optimization issue. Moreover, the objective functions are required to be assessed for various values of the gait variables for the purpose of inspecting locomotion efficiency. In order to validate the enhanced performance of LBIUSR-MA technique, a set of experiments was carried out and the results were inspected under different performance measures. The resultant experimental outcomes exhibit that LBIUSR-MA methodology achieved a low APC of 80.52 W under 50 δ   value. The proposed model has effectively accomplished the minimum PAC and maximum FV of USR. The results of the analysis exhibit the supremacy of the proposed LBIUSR-MA technique over recent state-of-the-art techniques. In future, the performance of the sinusoidal motion pattern can be inspected, while other designing parameters of USRs (such as link count) can also be considered as optimization variables.

Funding Statement: The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work under Grant Number (RGP 1/282/42). https://www.kku.edu.sa. The authors would like to acknowledge the support of Prince Sultan University for paying the Article Processing Charges (APC) of this publication. This research was funded by the Deanship of Scientific Research at Princess Nourah bint Abdulrahman University through the Fast-track Research Funding Program.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  G. Picardi, M. Chellapurath, S. Iacoponi, S. Stefanni, C. Laschi et al., “Bioinspired underwater legged robot for seabed exploration with low environmental disturbance,” Science Robotics, vol. 5, no. 42, pp. eaaz1012, 2020. [Google Scholar]

 2.  A. H. Hofman, I. A. v. Hees, J. Yang and M. Kamperman, “Bioinspired underwater adhesives by using the supramolecular toolbox,” Advanced Materials, vol. 30, no. 19, pp. 1704640, 2018. [Google Scholar]

 3.  E. Kelasidi, P. Liljeback, K. Y. Pettersen and J. T. Gravdahl, “Innovation in underwater robots: Biologically inspired swimming snake robots,” IEEE Robotics and Automation Magazine, vol. 23, no. 1, pp. 44–62, 2016. [Google Scholar]

 4.  T. I. Fossen, Handbook of Marine Craft Hydrodynamics and Motion Control: Fossen/Handbook of Marine Craft Hydrodynamics and Motion Control, Chichester, UK: John Wiley & Sons, Ltd, 2011. [Google Scholar]

 5.  F. Boyer, M. Porez and W. Khalil, “Macro-continuous computed torque algorithm for a three-dimensional eel-like robot,” IEEE Transactions on Robotics, vol. 22, no. 4, pp. 763–775, 2006. [Google Scholar]

 6.  A. J. Wiens and M. Nahon, “Optimally efficient swimming in hyper-redundant mechanisms: Control, design, and energy recovery,” Bioinspiration & Biomimetics, vol. 7, no. 4, pp. 046016, 2012. [Google Scholar]

 7.  E. Kelasidi, K. Y. Pettersen, J. T. Gravdahl and P. Liljeback, “Modeling of underwater snake robots,” in 2014 IEEE Int. Conf. on Robotics and Automation (ICRA), Hong Kong, China, pp. 4540–4547, 2014. [Google Scholar]

 8.  S. Hirose, Biologically Inspired Robots: Snake-Like Locomotors and Manipulators, Oxford; New York: Oxford University Press, 1993. [Google Scholar]

 9.  E. Kelasidi, K. Y. Pettersen and J. T. Gravdahl, “Energy efficiency of underwater robots,” IFAC-PapersOnLine, vol. 48, no. 16, pp. 152–159, 2015. [Google Scholar]

10. E. Kelasidi, M. Jesmani, K. Pettersen and J. Gravdahl, “Locomotion efficiency optimization of biologically inspired snake robots,” Applied Sciences, vol. 8, no. 1, pp. 80, 2018. [Google Scholar]

11. E. Kelasidi, A. M. Kohl, K. Y. Pettersen, B. H. Hoffmann and J. T. Gravdahl, “Experimental investigation of locomotion efficiency and path-following for underwater snake robots with and without a caudal fin,” Annual Reviews in Control, vol. 46, pp. 281–294, 2018. [Google Scholar]

12. E. Kelasidi, K. Y. Pettersen, P. Liljeback and J. T. Gravdahl, “Locomotion efficiency of underwater snake robots with thrusters,” in 2016 IEEE Int. Symposium on Safety, Security, and Rescue Robotics (SSRR), Lausanne, Switzerland, pp. 174–181, 2016. [Google Scholar]

13. E. Kelasidi, P. Liljebäck, K. Y. Pettersen and J. T. Gravdahl, “Experimental investigation of efficient locomotion of underwater snake robots for lateral undulation and eel-like motion patterns,” Robotics and Biomimetics, vol. 2, no. 1, pp. 8, 2015. [Google Scholar]

14. E. Kelasidi, M. Jesmani, K. Y. Pettersen and J. T. Gravdahl, “Multi-objective optimization for efficient motion of underwater snake robots,” Artificial Life and Robotics, vol. 21, no. 4, pp. 411–422, 2016. [Google Scholar]

15. E. Kelasidi, K. Y. Pettersen and J. T. Gravdahl, “Energy efficiency of underwater snake robot locomotion,” in 2015 23rd Mediterranean Conf. on Control and Automation (MED), Torremolinos, Malaga, Spain, pp. 1124–1131, 2015. [Google Scholar]

16. Y. Jia and S. Ma, “A Bayesian-based controller for snake robot locomotion in unstructured environments,” in 2020 IEEE/RSJ Int. Conf. on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, pp. 7752–7757, 2020. [Google Scholar]

17. I. Virgala, M. Kelemen, E. Prada, M. Sukop, T. Kot et al., “A snake robot for locomotion in a pipe using trapezium-like travelling wave,” Mechanism and Machine Theory, vol. 158, pp. 104221, 2021. [Google Scholar]

18. J. Zhang, Y. Chen, S. Yang, J. Li, F. Song et al., “Dynamic modeling and analysis of underwater swimming snake robot with soft joint,” in Proc. of the Thirty-First (2021) Int. Ocean and Polar Engineering Conf., Rhodes, Greece, pp. 258, 2021. [Google Scholar]

19. Z. Cao, D. Zhang, B. Hu and J. Liu, “Adaptive path following and locomotion optimization of snake-like robot controlled by the central pattern generator,” Complexity, vol. 2019, pp. 1–13, 2019. [Google Scholar]

20. E. Kelasidi, K. Y. Pettersen, J. T. Gravdahl and P. Liljeback, “Modeling of underwater snake robots,” in 2014 IEEE Int. Conf. on Robotics and Automation (ICRA), Hong Kong, China, pp. 4540–4547, 2014. [Google Scholar]

21. P. Liljebäck, K. Y. Pettersen, O. Stavdahl and J. T. Gravdahl, “Snake robots: Modelling, mechatronics, and control,” in Advances in Industrial Control, London New York: Springer, 2013. [Google Scholar]

22. W. Zhao, Z. Zhang and L. Wang, “Manta ray foraging optimization: An effective bio-inspired optimizer for engineering applications,” Engineering Applications of Artificial Intelligence, vol. 87, pp. 103300, 2020. [Google Scholar]

23. A. J. Wiens and M. Nahon, “Optimally efficient swimming in hyper-redundant mechanisms: Control, design, and energy recovery,” Bioinspiration & Biomimetics, vol. 7, no. 4, pp. 046016, 2012. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.