Computers, Materials & Continua DOI:10.32604/cmc.2022.024507
Article

Efficient Approach for Resource Allocation in WPCN Using Hybrid Optimization

Richu Mary Thomas and Malarvizhi Subramani*

Department of Electronics and Communication Engineering, SRMIST, Kattankulathur, 603203, India
*Corresponding Author: Malarvizhi Subramani. Email: malarvig@srmist.edu.in
Received: 20 October 2021; Accepted: 24 December 2021

Abstract: The recent aggrandizement of radio frequency (RF) signals in wireless power transmission combined with energy harvesting methods have led to the replacement of traditional battery-powered wireless networks since the blooming RF technology provides energy renewal of wireless devices with the quality of service (QoS). In addition, it does not require any unnecessary alterations on the transmission hardware side. A hybridized global optimization technique uniting Global best and Local best (GL) based particle swarm optimization (PSO) and ant colony optimization (ACO) is proposed in this paper to optimally allocate resources in wireless powered communication networks (WPCN) through coordinated operation of communication groups, in which the wireless energy transfer and information sharing take place concomitantly by the aid of a cooperative relay positioned in between the communicating groups. The designed algorithm assists in minimizing power consumption and maximizes the weighted sum rate at the end-user side. Thus the principal target of the system is coordinated optimization of energy beamforming along with time and energy allocation to reduce the total energy consumed combined with assured information rates of the communication groups. Numerical outputs are presented to manifest the proposed system's performance to verify the analytical results via simulations.

Keywords: Wireless powered communication networks; cooperative communication; relay; hybrid optimization technique; ant colony optimization; particle swarm optimization

1  Introduction

A while back, batteries were used to power up the traditional wireless communication systems, which had a limited lifespan resulting in a reduced lifetime of a wireless communication system. Many pieces of research have been conducted in the past [1–3,4] to investigate this issue and offer a solution to either improve/save energy or replace the battery to enhance the energy consumption in wireless communication. However, they were ineffective due to high costs and inconvenience. Thus, thenceforward to provide limitless power to wireless communication systems, wireless power transfer has been introduced since it proved to be eco-friendly, favorable and secure [5]. Wireless powered communication networking (WPCN) is an emerging study in which the microwave wireless power transfer (WPT) technique is used to power several wireless devices by wireless power transmitters to supply continuous and steady RF energy through the air and to delete the necessity for recurrent manual battery management. Even though WPCN has improved device lifespan with high throughput and low operating cost, it has a few challenges such as complexity, low power transfer efficiency for long-distance. As a result, the integration of RF-based energy harvesting schemes with wireless technology has been blooming in the recent past [6–8].

Compared to microwaves with high attenuation over distance, Radio Frequency (RF) enabled WPT is utilized chiefly to supply low-power communication devices like RFID devices. The progressing research attention towards RF energy harvesting, where received RF signals are changed into electric energy, which appears to be a potential clarification for energy-constrained wireless networks. The RF-based WPT energy harvesting network from a radio environment provided an enduring power supply compared to conventional wireless networks that have a short lifespan and hindered network performance. This study was scrutinized by [9]. Widely used WPT methods are electromagnetic radiation, inductive coupling and magnetic resonance coupling. Of these three, electromagnetic radiation is predominantly used in radio frequency energy harvesting to transfer radio power signals with a bandwidth around 300 GHz to 3 kHz. The efficiency of energy transmission during this electromagnetic broadcasting could be low if only a part of the energy is transmitted due to isotropic antennas. Hence to enhance the energy transfer, there is a necessity to focus the transmitting direction in accordance with the receiver called energy beamforming [10] and [11].

1.1 Simultaneous Wireless Information and Power Transfer (SWIPT)

Thus far, several types of research have been carried out to combine the WPT as an energy harvesting scheme into communication networks. In WPT, the nodes charge their batteries through electromagnetic radiation. Also, WPT can provide green energy by taking advantage of solid nodes in base stations that utilize renewable energy as a power source. The current investigation and interests in radio waves have led to the development of the RF-based SWIPT concept, in which the energy and data can be transmitted simultaneously. The underlying notion of this aspect is that the signals employed to transfer data transmission could also carry energy that the node could acquire at the receiver. Wireless devices can send data between nodes utilizing this gathered energy, thereby attaining better throughput than traditional battery-based wireless networks [12]. Numerous works have been conducted on SWIPT based WPCNs with [13] where multiple antenna WPCN with energy beamforming vectors and WPT to improve the throughput amid individual user was considered [14], without considering the energy beamforming scheme. Reference [15] also suggested a concurrent operation of uplink and downlink SWIPT to increase the performance of the network. For the combined power and Resource allocation scheme, the RF signal in SWIPT plays the carrier role to transfer both data and energy. The constraints for such transmission include power sensitivity to harvest energy and decoding of data. Hence the united operation of energy and scheduling of users becomes prominent. A fair trade-off could be achieved by this mechanism, as a user with significant gains can opt for energy transfer so as to improve its lifespan.

Still, the existing works did not explore the coordinated operation of different communication groups to improve the weighted sum rate and power consumption in WPCN. This issue can influence the network performance directly and affect the network to a large extent which needs to be addressed. The potential process to overcome this issue is to enhance the weighted sum rate (WSR) and lessen the total power consumption by framing this dilemma as a maximization or minimization problem by utilizing global optimization techniques such as Ant colony and GL based PSO optimization techniques. The suggested approach offers a flexible selection of individual energy efficiency weights in comparison to other existing systems. The steps involved are framing the optimization problem not considering QoS condition followed by joint allocation of time and power control based derivation of interpretations for energy efficiency optimization, finally acquiring an optimal solution for the maximization of the optimization problem. The obtained results validate their conceptual findings in addition to the effectuality of their suggested method. We shall incorporate these optimization methods to shape hybridized techniques to help in minimizing the power consumption and reducing the WSR effectively. The contributions of the work include constructing a coordinated set of two communication groups and designing an optimization problem utilizing a hybrid global optimization technique to get high throughput by improving WSR and minimizing the total power consumption in Wireless powered communication network.

The proposed work includes:

•   Both the groups modeled and simulated to meet satisfactory data transmission rate by cooperative energy and time-sharing between two groups.

•   Secondly to optimize the main objective function, which is WSR maximization.

•   Finally, numerically obtained results are demonstrated to assess the system performance behaviors, giving valuable ideas to design future WPCN models.

1.2 Organization of the Paper

The sections in this manuscript are organized as stated here. Section 2 deliberates a compendious explanation of the existing methods incorporated with the research work and is demonstrated in related works. The overall architecture and implementation of the proposed system ACO and PSO is depicted in Section 3, and Section 4 demonstrates the comparative analysis of the proposed method with existing methods. The proposed work culminates in the last section.

2  Literature Review

Reference [16] considered a single antenna system and presented a wireless power transfer protocol in which, in the downlink phase, an HAP (Hybrid Access Point) transmits the power signal to numerous users. In contrast, in the uplink phase, the information was decoded. TDMA scheme, which improves the uplink throughput, was utilized to identify the various users in hybrid-AP. The TDMA scheme is based on the optimal allocation of time slots to every user. [17] extended the work of [18] and proposed a hybrid-AP for multiple antenna WPCN contemplating over a flawed channel prediction presumption. Reference [19] investigated resource allocation scheme in WPCN to obtain high energy efficiency considering the initial state of the battery by joint time allocation and energy management through energy harvest by a multitude of users from an unwavering power station and broadcast data with a receiving station. From a base station, energy was harvested first. Later the acquired energy was used to transfer signals to a receiving station. They have investigated the energy efficiency maximization problem in WPCN considering with and without throughput to identify the pattern of the optimal solution to design the desired iterative algorithm to solve the problem, thereby attaining the optimal solution. Efficient performance results were obtained from the simulated experiment. They proposed a harvest then transmit model for effective harvesting of energy in a WPCN containing multiple users. The energy required can be harvested from a base station as per requirement after transferring the harvested energy using signals to send to an end receiver. This work considers three-fold, and the receiving network need not be at the power station itself. It can be at a nearby location, thereby eliminating the distance problem. At the transmission region, the users in these networks were permitted to store the extra harvested energy such that it could add more flexibility for the power usage activities. They have intended to improve the system throughput without degrading the quality of the system and also maintain the power transfer efficiency. They also aimed to enhance the receivers’ efficiency of energy by increasing the weighted sum of the energy in multiple users’ wireless powered communication networks. The energy was acquired through a dedicated power station, and communication was carried out through an information receiving station. The joint allocation of time and power control approach was used to frame a non-convex optimization problem and find an optimal solution based on that model.

An acausal energy network was suggested for joint power and time allocation algorithms to maximize the user's weighted rate. Nevertheless, this acausal energy network was impractical under certain circumstances in case the users have limited energy storage. A balanced energy allocation was done through generalizing the technique used by [20] and improving the sum rate of uplink in limited as well as unlimited power storages, joint allocation of energy and information strategy was employed for performance in both the infinite and the finite capacity of storage cases of energy. Initially considering the unlimited storage of energy, an optimal downlink power transfer strategy allows the H-AP to transmit RF signals containing maximum energy for a particular time slot, then it was turned off. These results were used to design the solution to allocate the necessary power and time optimally. They recommended an alternate system with causal energy to address this issue for full-duplex wireless power transmission [21] and considering limitless energy storage capability with balanced energy allocation. [22] proposed a SWIPT based energy harvesting [23] model for resource allocation and to find the solution for a non-convex optimization problem in a system consisting of numerous information and energy receivers. The algorithm was built to increase the total harvested energy that can be acquired by the receiver, in addition to providing needed SINRs to the numerous information receivers. The iterative algorithm gives an optimal solution. Compared to the traditional linear scheme, the acquired results proved this suggested method to be much more effective than the traditional linear energy harvesting design. Since most of the energy harvesting structure follows a non-linear fashion, the conventional linear harvesting method had much power loss and discrepancies in resource allocation.

Reference [24] had also taken into account the causal energy systems in which, during uplink transmission, the users could access the acquired energy in previously allotted time slots alone. Also, [25] proposed a two scheme-based heuristic optimization algorithm in WPCN using a HAP and number of wireless nodes utilizing Time Division Multiple Access (TDMA) protocol. The nodes in various allotted time slots with the ability to acquire energy can gain energy from different nodes and HAP. The energy harvesting for peer nodes in the allotted time slot is done first. In the latter scheme, energy harvesting for every node is carried out for the WPCN that performs energy harvesting amidst the peer nodes. Enhancing network throughput along with the reduction of the necessary harvested energy were investigated. The results exhibit the efficiency of the suggested techniques in WPCN. [26] proposed a fare-based cooperative wireless power transmission. All transferred information has a price for the energy consumed, and the charge varies according to the individual users. A cooperative strategy is implemented amid source and helping users by making the primary user (PU) provide their excess energy to the secondary user (SU), thereby employing a fair trade between them. The energy efficiency optimization problem of the multi-users was the principal objective function and joint allocation [27] of energy and time considering every user's initial charge state of batteries. Furthermore, the energy consumption of the users and base stations were also taken into account. They have analyzed the pattern of the optimization problem in multi-user WPCN, and optimal solutions were obtained accordingly, portraying the expected results.

3  Research Methodology

3.1 System Model

A wireless network having two communication groups are taken into consideration. They are assumed to have two Hybrid Access Points (HAPs) referred to as S1 and S2 and two users denoted by D1 and D2, as shown in Fig. 1. S1 and S2 can also be considered as sources. D1 and D2 can be considered as destinations. The source S1 is provided with N antennas whereas D1 and D2 are provided with single antenna each. D1 and D2 desire to transmit information to S1 and S2 which have fixed energy supply. D1 and D2 are nodes who have limited energy and hence have to derive energy from RF signals which are transmitted by S1 to support the transmission of information. We presuppose that the fading channel is quasi-static, such that coefficients of all the channels are assumed to be constant at every state of fading. Moreover, the between any two nodes, reciprocity of the channel is presumed. That is, at every fading state, the coefficient of channel from node x to y is identical to from y to x.

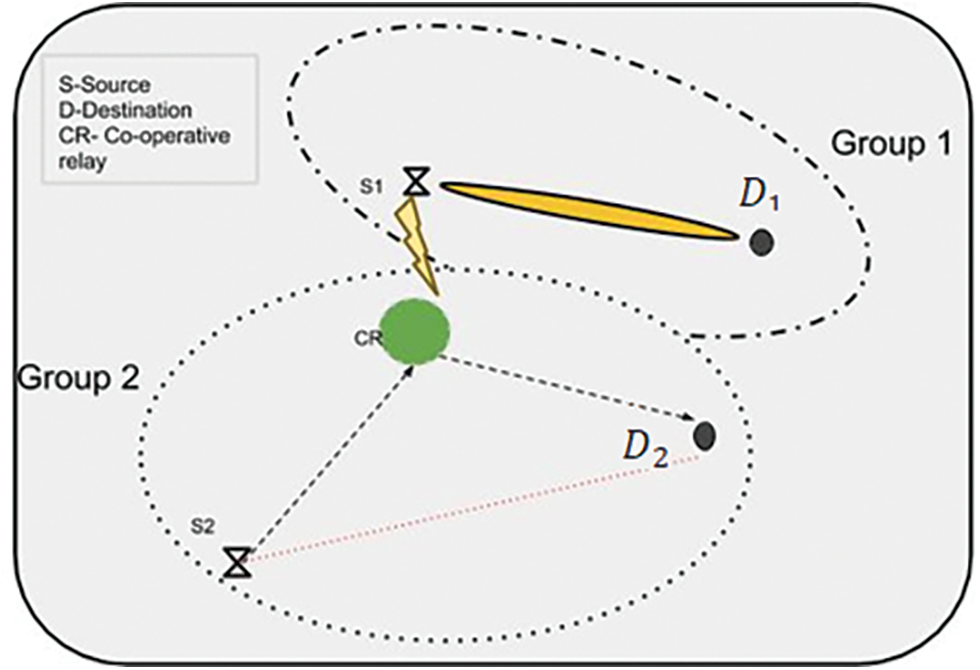
Figure 1: Communication groups with source, relay and node

Since D1 and D2 do not have any power to commence the transmission of information, the entire period of transmission is split into two stages, i.e., the downlink energy initiation (EI) stage and the uplink information transmission (IT) stage.

3.2 Transmission Protocols

In order to achieve cooperative power and information transmission, the entire duration of τ is divided into EI phase with the time length of τ0 and IT stage with the time length of τ1, such that it satisfies

1Tτ=1, 𝜏 ≥0  (1)

where 1 is a column vector with every entry as 1.

Phase 1:

In the Energy Initiation (EI) stage with time length of τ0, S1 transfers energy to both Di where i = 1, 2 and the cooperative relay (CR) Re through RF transmission.

The transmitted symbol from S1 is |xs1(k)|2=1

At destinations Di, (∀ i = 1, 2) the received signals are represented respectively as

yDi(k)=PS1(1)hS1HDi(k)ωxS1(k)+n(k)(2)

yRe(k)=PS1(1)hS1HRe(k)ωxS1(k)+n(k)(3)

where hS1D1,∈CNX1 and  hS1Re∈CNX1 are the complex channel vectors from S1 to D1 and from S1toRe respectively. PS1(1) is the transmitting power available at the source S1 for the energy initiation phase τ0 and ω∈CNX1 corresponds to the energy beamforming vector, which is deliberated and used at S1 and meeting the expectation

∥ω∥2≤1.(4)

The harvested energy at D1 is given by

ED1(1)=ητ0PS1(1)|hS1HD1ω|2(5)

The harvested energy at D2 is given by

ED2(1)=ητ0PS1(1)|hS1HD2ω|2(6)

where the constant η is for energy conversion efficiency. The larger the η value, the higher is the energy conversion efficiency. Achievable rates of information in phase 1 at τ0 from S1 to Di(i = 1, 2) is provided as

RS1(1)=τ0ρ(PS1(1)|hS1HD1ω|N0)2(7)

where ρ(x)=Δlog2(1+x) and the energy harvested at the relay is

ERe(1)=ητ0PS1(1)|hS1hReω|2(8)

where η∈(0,1] is energy conversion efficiency constant. In particular, when η = 1, it means that all the signal power received could be converted into energy available at the receiver.

Phase 2:

The IT (Information Transmission) phase τ1 is additionally divided into three durations of time length τ2, τ3 and τ4 as D1 and D2 take different times to complete the information transmission to S1 owing to the fact that they are at different distances from S1. Cooperative relay (CR) helps in sharing the resources among different links. Specifically, in the first duration of τ1, D1 broadcasts information to S1 and D2. Let the symbol transmitted by D1 be xd1(k) with |xd1(k)  |2=1. The received signal at S1 and D2 from D1 can be respectively given as:-

AtS1:Y0′=PD1(2)(1)hD1S1(k)xD1(k)+n(k):(9)

AtD2:Y2′PD1(2)(1)hD1D2(k)xD1(k)+n(k)(10)

where PD1(2) is the transmit power available at D1 during τ2 and hD1S1 ϵ CNX1 and hD1D2 ϵ CNX1 are the complex channel vectors from D1 to S1 and D1 to D2 respectively. n(k) represents the AWGN vector at S1 and D2, in which each element has mean as zero and N0 variance. By employing the MRT (Maximum Rate Transmission) method, the rate of information achievable from D1 to S1 in this time interval can be represented as

RS1(2)=τ2ρ(PS1(2)||hS1HD1||N0)2(11)

where transmit power PS1(2) is available at S1 in the second phase. Owing to the broadcasting mode of the wireless channels, the transmitted signals from D1 can be fetched by D2 and the co-operative relay (CR) as well. The energy harvested at the cooperative relay is represented as

ERe(2)=ητ2PS1(2)|hHS1RehS1D1∥hS1D1∥|2(12)

where hS1D1∥hS1D1∥ is the precoding transmission vector adopted at S1 for Maximum Rate Transmission (MRT). The consumed total energy at D1 has to be lesser than the energy which is harvested (ED1(1)), it must satisfy that

τ1PD1(2)≤ED1(1)(13)

i.e.,τ1PD1(2)≤ητ0PS1(1)|hS1HD1ω|2(14)

Decode-and-Forward (DF) relaying is used at the CR, such that during τ2, D2 can decode the received information from D1 and can forward it to S1.

Phase: 3

In the time interval τ3 of the Information Transmission (IT) phase, S2 broadcasts the decoded information to the CR and D2. Let the symbol transmitted by S2 be xS2(k) with |xS2(k)|2 = 1. The signal that is received at the CR and D2 can be represented respectively as

yRe(k)=PS2(3)hS2Re(k)xS2(k)+n(k)(15)

yD2(k)=PS2(3)hS2D2(k)xS2(k)+n(k)(16)

where PS2(3) is the transmit power which is available at S2 at the third time interval τ3.

Phase: 4

In the fourth time interval τ4 of the information transmission phase, the cooperative relay decodes the information from S2 and then assists in forwarding this information that is decoded to D2 by utilising the energy that was harvested from S1 in phase 1, i.e., the Energy Initiation (EI) phase. Here, signal received at D2 from cooperative relay in this phase can be shown by

yD2(k)=PRehReD2(k)xRe(k)+n(k)(17)

where PRe is the transmit power which is available at the cooperative relay and is constrained by the total of the energy harvested in the energy initiation phase and information transmission phases, i.e., ERe(1) in Eq. (7) and ERe(2) in Eq. (11). That is,

τ4PRe≤ERe(1)+ERe(2)=ητ0PS1(1)|hS1hReω|2+ητ2PS1(2)|hHS1RehS1D1∥hS1D1∥|2(18)

On combining RS1(1) in (6) andRS1(2) in (10) we obtain the total information rate achievable from D1 to S1 in the nth fading block being

RS1≤RS1(1)+RS1(2)

RS1≤τ0ρ(PS1(1)|hS1HD1ω|N0)2+τ2ρ(PS1(2)||hS1HD1||N0)2(19)

The information rate available at the nth fading block can be given as

RSi≤min{τ3ρ(PS2(3)|hS2Re|2N0),τ3ρ(PS2(3)|hS2D2|2N0)+τ4ρ(PRe|hReD2|2N0)}(20)

Presuming that the minimum needed information rate (threshold) for group i is rSi where i ∈{1,2}, the achievable end-to-end rate of information RSi should meet the condition

RSi≥rSi,∀i=1,2.(21)

The communication groups coordinate and follow the give and take policy to manage energy and transfer time effectively. The secondary user has steady, adequate energy stock yet no authorized frequency band in the group with S1. In contrast, in the group with S2, the primary user has an authorized frequency band, but is situated at a great distance from D2. In traditional networks, in this situation transfers data only if the other group is silent. Furthermore, group 1 will not have a chance to transfer data when there is a continuous transmission from group 2 with a poor data rate. Regardless, this suggested system group with abundant time slots is encouraged to offer its energy to the other group such that it can gain some energy in return from that group, consequently obtaining an improved rate of data transmission. At the same time, the group with some extra energy can transmit without anticipating an opportunity to transfer data at the cost of providing energy to the other group, which is offering its transmission time. In this manner, with the help of WPT, both the groups are benefitted. For improved energy transfer efficiency, S1 has N number of antennas presumably whereas other nodes with just a single antenna. As a follow-up of Rayleigh distribution, each channel coefficient is observed to be constants in block fading. The time period of all fading blocks is indicated by T.

3.3 Flow Diagram

The flow diagram of the procedure involved in the proposed network is depicted in the Fig. 2. The signal and power required for the source and destination nodes in the system are initially assigned, and the values are mentioned in the results. The system model is designed with two communication groups with users, destinations and a cooperative relay. The signals generated initially are passed into the system model. The input signals generated at the transmitting side are received at the destinations and cooperative relay. These are passed into the objective functions for WSR maximization and power minimization. The optimized values obtained are checked whether they meet the desired outputs. The iteration stops when the required outputs are obtained.

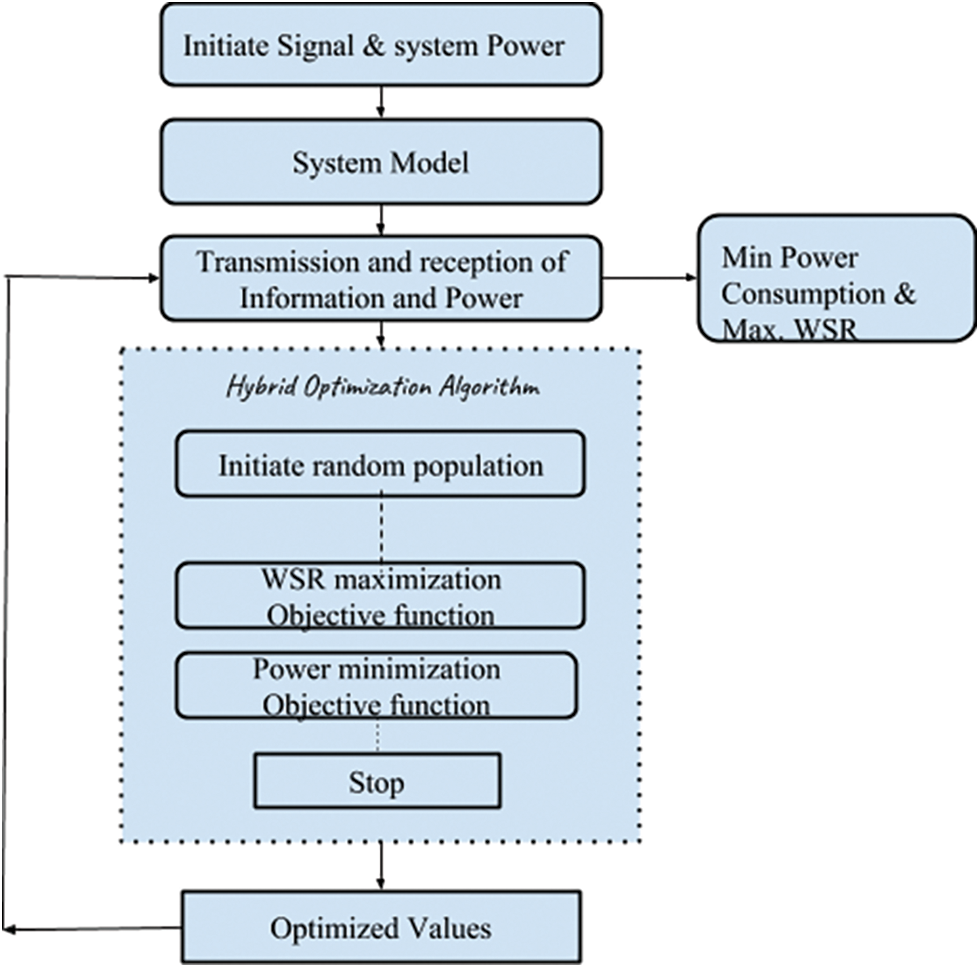
Figure 2: Proposed implementation flow diagram

3.4 Hybridized Global Optimization Technique

Before designing the hybridized global optimization technique, a brief summary of each optimization technique is given below for understanding.

a) GL Based Particle Swarm Optimization

PSO is a population-based heuristic method for optimization which Eberhart and Kennedy introduced. The possible participants of the population under consideration, called particles, adjoin and grow together by splitting knowledge amid adjacent particles. When working on the global search of a problem under study, each particle has a solution with a velocity vector. The particles continuously update their position during the global search by modifying their corresponding velocity vector using the memory of their best position and the global best shared by adjacent particles.

Initially, the search is started having a group of random variables under study and their solutions with a value. Then as the iterations increase, the values are updated for optimum solutions. PSO follows the present particle position rather than crossover and mutation like conventional GA algorithms. The generations are updated for an optimum solution by particles modifying themselves using their velocity vector internally and memory. The PSO is different from the other genetic algorithms, and its transfer of information scheme is unique. Only the global best and local best provides the information to others in a linear one-way fashion scheme. The update looks upon only the best solution, and convergence of the algorithm is quick compared to traditional genetic algorithms.

b) Ant Colony Optimization

Marco Dorigo first introduced ACO, which is based on the behaviour of real ants. Ants as social insects work together to survive their entire ant colony than that of an individual colony. Co-operated rummaging and working on a complex problem from scratch is a noteworthy characteristic of an ant colony. The general concept behind this algorithm is that the searching operation is handled by the agents that imitate the fundamental behaviour of ants, creating artificial ant colonies with memory and discrete-time. The ant colony made ordered local decisions to solve the optimization problem. The ant agent selects a more optimized path at every step to expand the present incomplete solution. The objective rules over the optimal solution finding building scheme in ACO exclusively sketch the investigating space considered the problem to a search tree. The ant colony agents leave a trail from the source to the destination, thus making it easy for other ants to find the shortest paths and optimal solution. Using this approach, continuous complex optimization problems can be solved quickly.

3.5 Implementation Process of Hybrid Optimization Algorithm

The hybrid algorithm used here combines two optimization algorithms called Ant Colony algorithm, and Global best and Local best model termed as GL best PSO. Recent shreds of evidence show that the PSO and ACO are more favorable in solving complex optimization problems. Particle swarm combined with ant colony optimization algorithm seems to be a robust scheme for deriving solutions to highly non-convex problems. The ACO aids the PSO in the influential global investigation along with in achieving optimal solutions quickly. When a comparison is made with other hybrid combinations of PSO and non-PSO strategies, ACO aided PSO hybrid algorithm displays assuring results in solving complex continuous optimization problems [28–30].

Steps used in the hybrid algorithm are given below.

•   Random values are generation depending on available resource boundaries.

•   Random generation is based on the minimum and maximum WPCN resource values. The equation used in MATLAB

I = min_val + (max_val-min_val)*rand

•   Initial size (I) is based on the considered size of the population.

•   Pass all these values to the objective functions.

•   Objective function 1: weighted sum rate

•   Objective function 2: total power consumed by WPCN

•   Best value is selected from the fitness function for best maximum WSR and minimum total power consumed by WPCN.

•   The initial random values are updated by integrating the parameters, i.e., constrained values are updated depending on the best fitness values selected.

•   Select the optimum value; redo the steps till the number of iterations is completed.

•   Select the number of iterations centered on the desired accuracy required.

•   Display the results by comparing existing techniques with optimization algorithms.

Fig. 3 explains the implementation of the proposed algorithm using GL-based particle swarm optimization aided by the ant colony approach. The suggested hybridized algorithm is designed according to the combined characteristics of GL-based PSO and ACO algorithm, the existence of both and cohabitation as a colony through coordination and cooperation. The ants search for the best trail and share the details with swarm particles through local and global best information sharing. First, the GL-based PSO is implemented in the initial stage, and later the ant colony optimization is carried out. The local information is gathered by the ACO, then using the scent-guided scheme, the ants utilize the positions provided from the PSO search. The number of ants involved in the ACO is proportional to the number of particles in PSO. Every ant creates a solution in the global best position amid every swarm particle. Then according to the objective function, the values and positions are updated. Here the maximum weighted rate is solved through the swarm optimization, and the ant colony finds the shortest path with the best position aiding the PSO in finding an optimal solution. As the iteration increases, the ants intensify the search from ample space to near the particles and look for the best solutions to arrive at the optimal solution. As a result, the ACO aids the performance of GL PSO in the influential global search to achieve the feasible and optimal solution quickly. The algorithm is begun by initializing the parameters PSO and ACO methods, as shown in Fig. 3. The values are updated according to the objective function as given below.

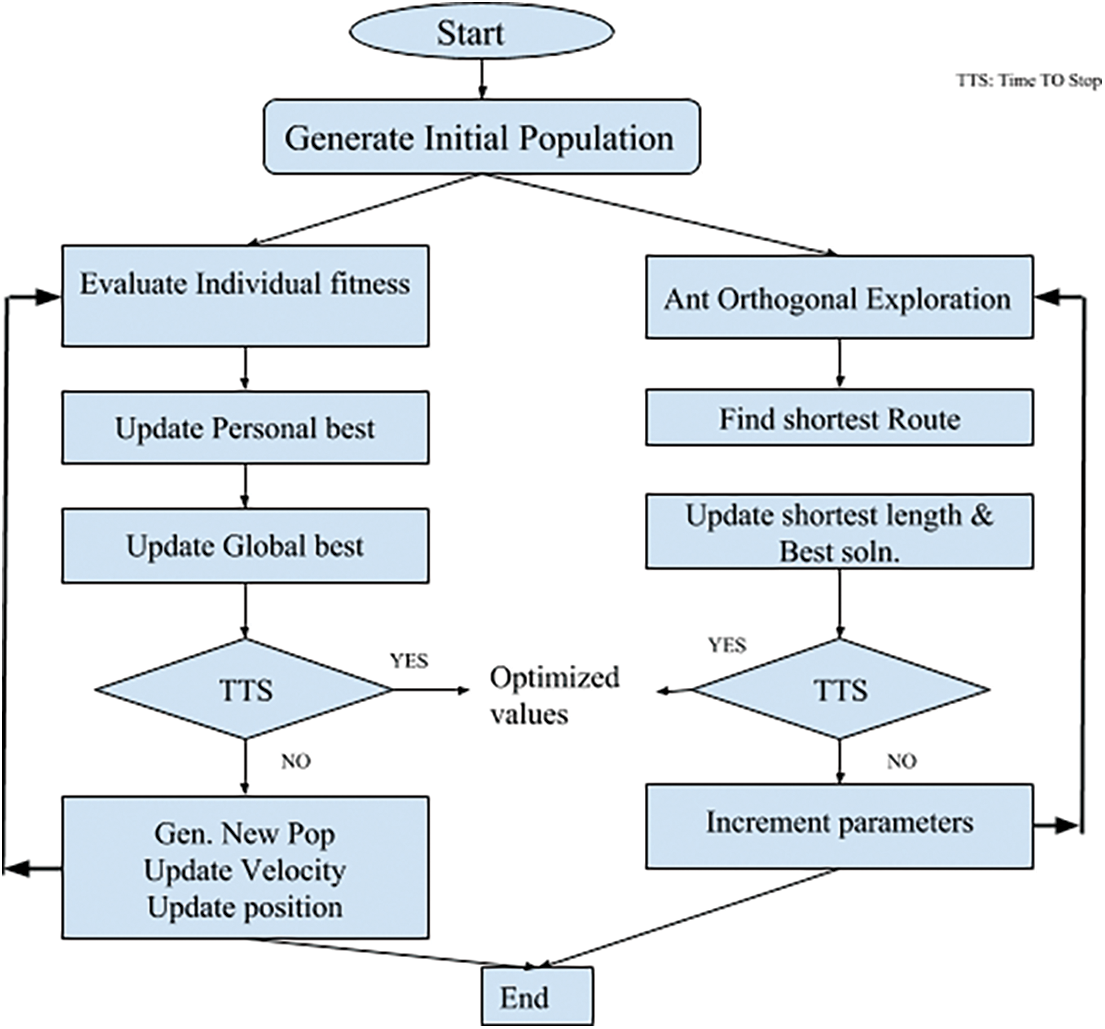
Figure 3: Hybrid optimization algorithm flow diagram

a) WSR maximization

The node S1 has fixed instant power in transmission phases 1 and 2 and are assumed to be the same. i.e., PS1(1)=PS1(2). In phase 3, S2 transmits signals with transmit power PS2(3). We symbolize PS1(1)=PS1(2)=PS1 and let PS2(3) be PS2 and subsequently from Eqs. (18) and (19), the objective function for WSR maximization could be rewritten as:

RS1≤τ0ρ(PS1|hS1HD1ω|N0)2  +τ2ρ(PS1||hS1D1||N0)2(22)

AndRS2≤min{τ3ρ(PS2|hS2Re|2N0),τ3ρ(PS2|hS2D2|2N0)+τ4ρ(PRe|hReD2|2N0)}(23)

where N0 is the variance.

Let us assume αi ≥ 0 as the weights of the information rates achievable for the group i, where i = 2. Hence, for the system, the WSR can be expressed as

Rwsum=α1RS1+α2RS2(24)

and mathematically as

P1:maximize  τ,ω,RS1,RS2⁡α1RS1+α2RS2(25)

Subject to (1), (4), (18), (21), (22), (23)

Where Eq. (25) is the passing function for WSR maximization.

b) Power-minimization design

Apart from maximizing the throughput, the other main objective is power minimization for real energy-constrained WPT networks to enhance their lifespan. This segment deals with constructing a model design with a minimum power consumption objective for the coordinated WPCN under study. The ultimate target is coordinated optimization of energy beamforming and time and energy allocation to reduce the total energy consumed combined with assured information rates of the two communication groups. As discussed earlier, the energy consumed at S1 is τ0PS1(1)∥ω∥2, where ∥ω∥2≤1. The energy consumed during the second phase at S1 is τ2PS1(2) and the energy consumed during the third phase at S2 is τ3PS2(3). Therefore the the sum of the energy consumed for transmission of information is τ0∥ω∥2 + τ2PS1(2) + τ3PS2(3).

For the fading block, its T (total time period) is normalized as 1 and the total power consumed for transmissions could be represented as

Pavg=τ0PS1(1)∥ω∥2+τ2PS1(2)+τ3PS2(3)(26)

where PS1 and PS2 are the corresponding power values of communication groups during iterations. Under minimum required data rates, the total power minimization problem could be expressed as follows.

P2:minimizeτ,ω,ρτ0PS1(1)∥ω∥2+  τ2PS1(2)  +  τ3PS2(3)(27)

Where Eq. (27) is the passing function for power minimization.

4  Results and Discussion

Here, we furnish our numerically obtained results for proving the efficacy of the system through the proposed work of hybrid optimization in co-operative WPCN, using ACO as well as PSO. The outputs are compared with three benchmark systems from the literature. In the first benchmark OBRT (Optimized Beamforming with Random Time) assignment, random assignment of time is adopted and beamforming is optimized. The second benchmark compared is RBOT (Random Beamforming with Optimized Time) assignment where PS1 is allocated randomly to the antennae with optimized assignment of time. In the third benchmark JOBT (Joint Optimization of Beamforming and Time) assignment with fixed and flexible power scenarios are compared.

The following are the simulation parameters.

The transmit power at S1is set asPS1 = 2 W, and at S2asPS2 = 0.2 W, variance N0 = 10−6 W. The minimum information rates for group 1 and group 2 are set as rS1=0.5 bits/s and  rS2 = 0.2 bits/s respectively. The distances between the various nodes are set as dS1D1=9m,dS1Re=2m, dS2Re = 10 m,dReD2 = 20 m and dS2D2 = 100 m. The exponent of path loss is set as 4, the number of antennae is set to 4 and the co-efficiency of conversion of energy η = 0.9. These configurations remain unchanged unless mentioned.

Final simulated results are as given here:

The simulated results with and without optimization schemes are shown in the Figs. 4–9. It shows the effectiveness of the proposed methodology. The WSR is improved with respect to other methods, finally arriving at an optimal result. Fig. 4 represents the gradual increase in WSR with respect to the number of iterations and has reached 9 bits/sec. According to the MATLAB simulation results, the maximized WSR optimization was found to be 33% when compared to non-optimized scenario.

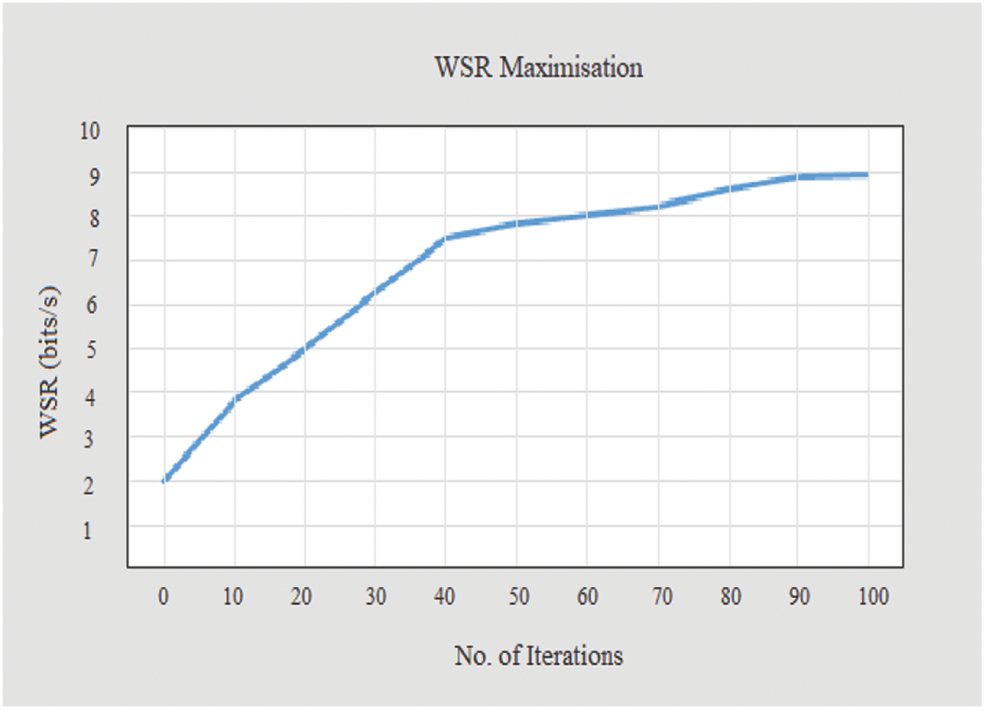
Figure 4: WSR maximization using PSO

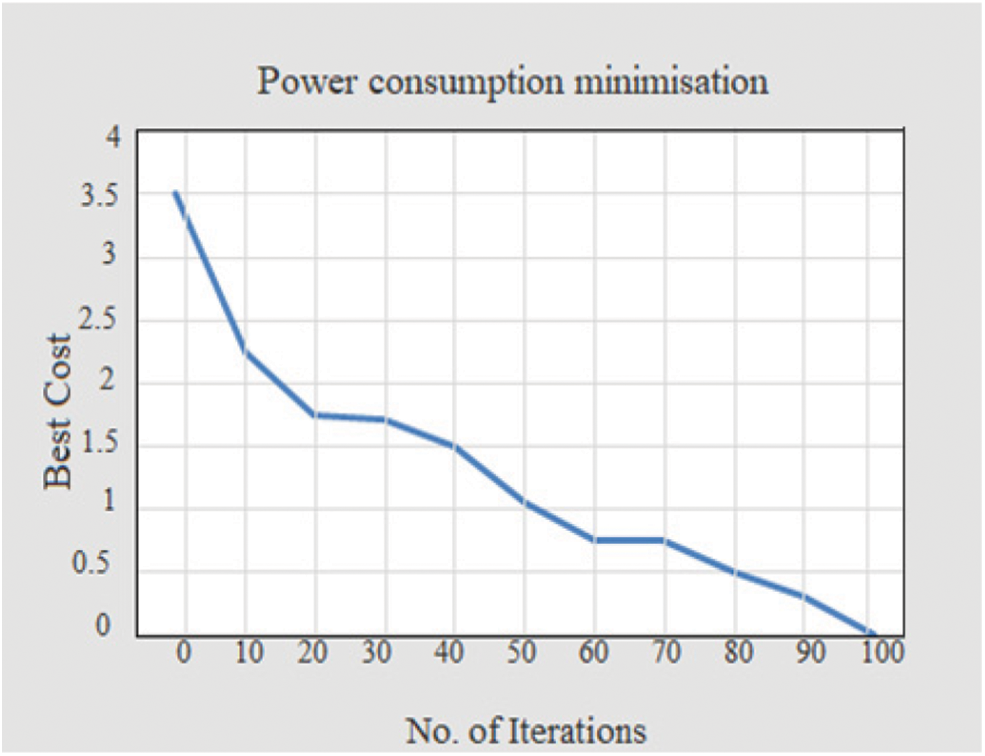
Figure 5: Power consumption minimization using ant colony optimization

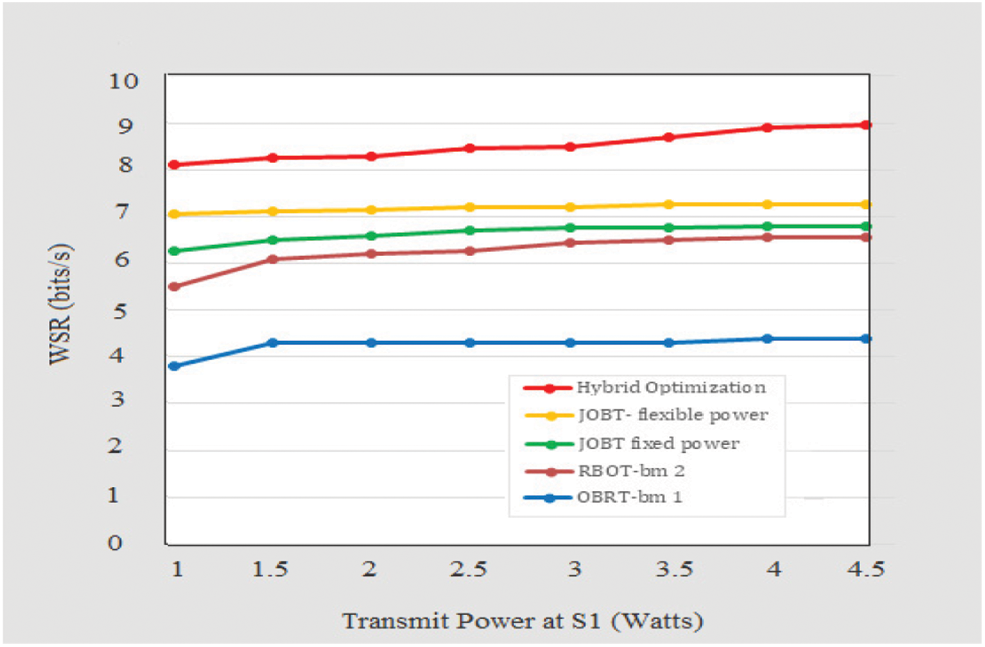
Figure 6: WSR vs. transmit power at S1

Figure 7: WSR vs. transmit power at S2

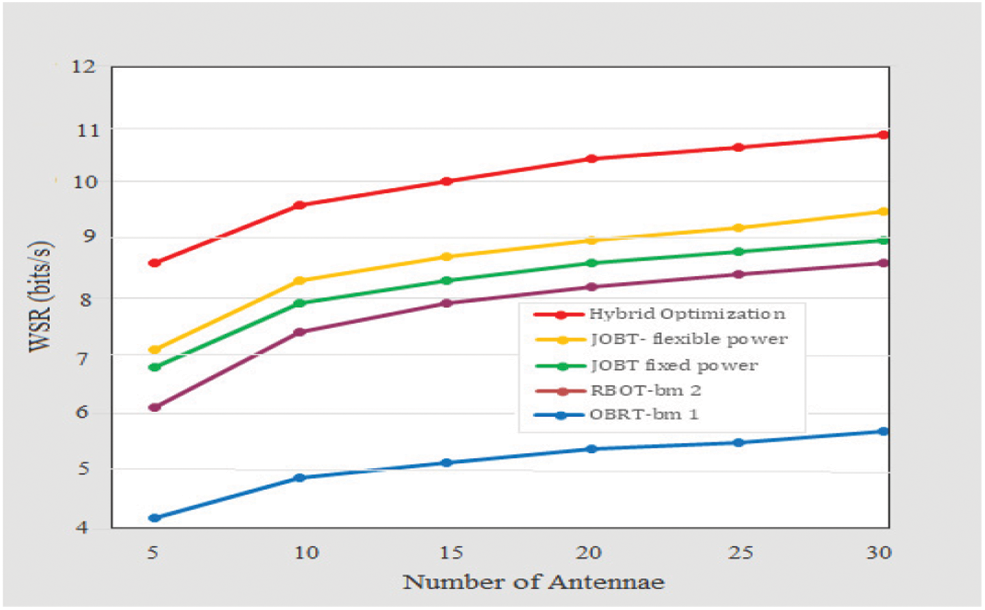
Figure 8: WSR vs. number of antennae of S1

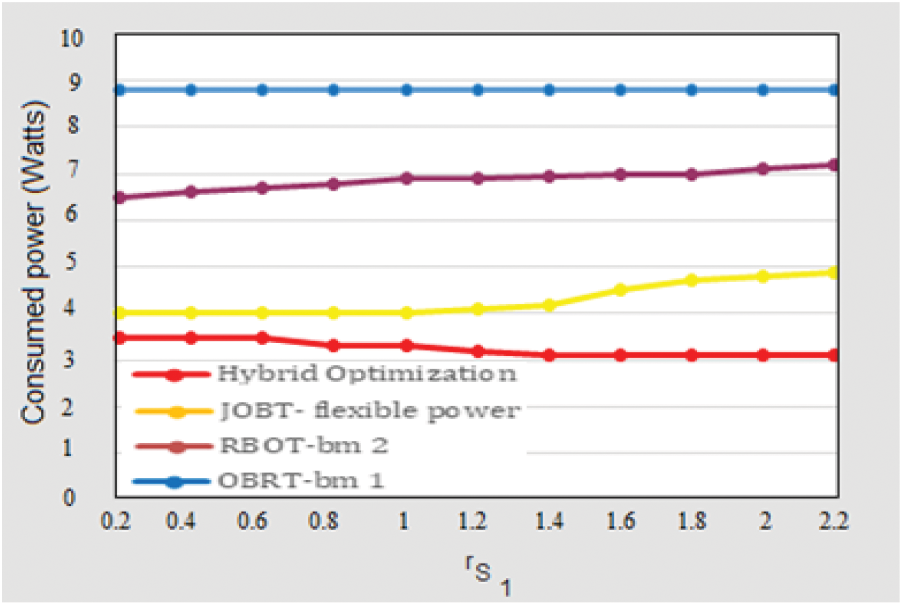
Figure 9: Minimum consumed power vs. rate threshold

Fig. 5 shows the decrease in the consumption of power in 100 iterations. The power consumption has reduced from 3.5 Watts to negligent values. From the Figs. 6 and 7, it was inferred that with PS1 and PS2 increment, the WSRs of the systems under study increase since, an increase in the transmit power will result in an increased information rate. It can also be noticed that RBOT beats ORBT and RBRT, and RBRT brings about the least WSR among all the systems. These results indicate that in the proposed WPCN system, the assignment of time has a greater impact on the system performance than the beamforming at node S1.

The beamforming affects the system's performance by energy transfer, which directly affects the relay and destination 1. Since the transfer of power over a wireless environment fades solemnly, its effects are relatively bounded. Concurrently, the time allotment acts on all source and relay nodes, systematically allocating the system resources. Therefore, time assignment significantly impacts system performance, and it is more crucial in the performance of the system enhancement.

In Fig. 8, the WSR is seen to be improving with the rise in the number of antennae at S1. It corroborates that with the enhancement in the number of antennas, the increasing rate of the WSR decreases roughly, meaning that enhancing the count of antennas can also improve the WSR of the system. Nevertheless, it cannot improve the WSR of the system to an infinite extent. The consumed power for all the benchmark systems was studied concerning the minimum rate required, and the proposed system is shown to have much lesser power than all the other benchmark systems.

In Fig. 9, it can also be noted that, with the RSi increment, the total power consumed by the compared systems in the literature also increases. It is since the higher the requirements of data rates of the two groups, the higher the power required. This indicates that meeting the data rate requirement consumes more power. This is because the power available at the cooperative relay is transferred from node S1, and some energy is lost due to path loss fading during the transfer of energy.

5  Conclusion

In recent past, RF signals were regarded to be an alternative for conventional energy harvesting which was based on renewable energy sources. RF based energy harvesting could provide required energy to charge devices whenever demanded. SWIPT was developed based on RF signals, for wireless information and energy transmission. But coordinated operation between communication groups has been used only in few researches; this paper implemented a coordinated operation of time, energy and resource allocation in WPCN together. The communication groups benefitted equally with the proposed methodology. They shared data and energy in designed time slot with enhanced throughput, by maximizing weighted sum rate (WSR) as the objective function along with minimization of power consumption optimization. The mechanism is executed through global hybridized algorithm uniting the GL based PSO and ACO. The swarm optimization is aided by ACO to attain a feasible and optimal solution for the complex convex optimization problem. The experimental simulated results are provided too along with the optimized values; they prove the efficiency of the suggested coordinated group system mechanism.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  A. Aziz, Y. A. Sekercioglu, P. Fitzpatrick and M. Ivanovich, “A survey on distributed topology control techniques for extending the lifetime of battery powered wireless sensor networks,” IEEE Communications Surveys and Tutorials, vol. 15, no. 1, pp. 121–144, 2013. [Google Scholar]

 2.  F. Zhao, L. Wei and H. Chen, “Optimal time allocation for wireless information and power transfer in wireless powered communication systems,” IEEE Transactions on Vehicular Technology, vol. 65, no. 3, pp. 1830–1835, 2016. [Google Scholar]

 3.  S. Bi, C. K. Ho and R. Zhang, “Wireless powered communication: Opportunities and challenges,” IEEE Communications Magazine, vol. 53, no. 4, pp. 117–125, 2015. [Google Scholar]

 4.  L. Shi, L. Zhao and K. Liang, “Battery state based power and time allocation in wireless powered MIMO uplink transmission,” in IEEE 27th Annual Int. Symposium on Personal, Indoor, and Mobile Radio Communications (PIMRC), Valencia, Spain, pp. 1–5, 2016. [Google Scholar]

 5.  J. Kang, R. Yu, S. Maharjan, Y. Zhang, X. Huang et al., “Toward secure energy harvesting cooperative networks,” IEEE Communications Magazine, vol. 53, no. 8, pp. 114–121, 2015. [Google Scholar]

 6.  H. Lee, K. J. Lee, H. Kim, B. Clerckx and I. Lee, “Resource allocation techniques for wireless powered communication networks with energy storage constraint,” IEEE Transactions on Wireless Communications, vol. 15, no. 4, pp. 2619–2628, 2016. [Google Scholar]

 7.  X. Di, K. Xiong, P. Fan, H. C. Yang and K. B. Letaief, “Optimal resource allocation in wireless powered communication networks with user cooperation,” IEEE Transactions on Wireless Communications, vol. 16, no. 12, pp. 7936–7949, 2017. [Google Scholar]

 8.  C. Zhong, X. Chen, Z. Zhang and G. K. Karagiannidis, “Wireless-powered communications: Performance analysis and optimization,” IEEE Transactions on Communications, vol. 63, no. 12, pp. 5178–5190, 2015. [Google Scholar]

 9.  X. Lu, P. Wang, D. Niyato, D. I. Kim and Z. Han, “Wireless networks with RF energy harvesting: A contemporary survey,” IEEE Communications Surveys and Tutorials, vol. 17, no. 2, pp. 757–789, 2015. [Google Scholar]

10. Q. Sun, G. Zhu, C. Shen, X. Li and Z. Zhong, “Joint beamforming design and time allocation for wireless powered communication networks,” in IEEE Communications Letters, vol. 18, no. 10, pp. 1783–1786, 2014. [Google Scholar]

11. G. Amato, A. Caruso and S. Chessa, “Application-driven, energy-efficient communication in wireless sensor networks,” Computer Communications, vol. 32, no. 5, pp. 896–906, 2009. [Google Scholar]

12. A. Gambhir and R. Arya, “An extensive survey on energy optimization techniques based on simultaneous wireless data and energy transfer to wireless sensor network,” in Soft Computing: Theories and Applications, Singapore: Springer, pp. 469–475, 2018. [Google Scholar]

13. L. Liu, R. Zhang and K. C. Chua, “Multi-antenna wireless powered communication with energy beamforming,” IEEE Transactions on Communications, vol. 62, no. 12, pp. 4349–4361, 2014. [Google Scholar]

14. D. Hwang, D. I. Kim and T. J. Lee, “Throughput maximization for multiuser MIMO wireless powered communication networks,” IEEE Transactions on Vehicular Technology, vol. 65, no. 7, pp. 5743–5748, 2016. [Google Scholar]

15. H. Ju and R. Zhang, “Throughput maximization in wireless powered communication networks,” IEEE Transactions on Wireless Communications, vol. 13, no. 1, pp. 418–42, 2014. [Google Scholar]

16. H. Zhang, S. Huang, C. Jiang, K. Long, V. C. Leung et al., “Energy efficient user association and power allocation in millimeter-wave-based ultra-dense networks with energy harvesting base stations,” IEEE Journal on Selected Areas in Communications, vol. 35, no. 9, pp. 1936–1947, 2019. [Google Scholar]

17. G. Yang, C. K. Ho, R. Zhang and Y. L. Guan, “Throughput optimization for massive MIMO systems powered by wireless energy transfer,” IEEE Journal on Selected Areas in Communications, vol. 33, no. 8, pp. 1640–1650, 2015. [Google Scholar]

18. H. Ju and R. Zhang, “Optimal resource allocation in full-duplex wireless-powered communication network,” in IEEE Transactions on Communications, vol. 62, no. 10, pp. 3528–3540, 2014. [Google Scholar]

19. Q. Wu, M. Tao, D. W. K. Ng, W. Chen and R. Schober, “Energy-efficient transmission for wireless powered multiuser communication networks,” in IEEE Int. Conf. on Communications (ICC), London, UK, pp. 154–159, 2015. [Google Scholar]

20. X. Kang, C. K. Ho and S. Sun, “Full-duplex wireless-powered communication network with energy causality,” IEEE Transactions on Wireless Communications, vol. 14, no. 10, pp. 5539–5551, 2015. [Google Scholar]

21. S. Mao, S. Leng, Q. Zhao and Z. Zhao, “Joint power and time resource optimization in full-duplex wireless-powered communication networks,” in IEEE Int. Conf. on Internet of Things (iThings) and IEEE Green Computing and Communications (GreenCom) and IEEE Cyber, Physical and Social Computing (CPSCom) and IEEE Smart Data (SmartData), Exeter, United Kingdom, pp. 429–436, 2017. [Google Scholar]

22. E. Boshkovska, D. W. K. Ng, N. Zlatanov and R. Schober, “Practical non-linear energy harvesting model and resource allocation for SWIPT systems,” IEEE Communications Letters, vol. 19, no. 12, pp. 2082–2085, 2015. [Google Scholar]

23. J. S. Liu, C. H. R. Lin and J. Tsai, “Delay and energy tradeoff in energy harvesting multi-hop wireless networks with inter-session network coding and successive interference cancellation,” IEEE Access, vol. 5, no. 1, pp. 544–564, 2017. [Google Scholar]

24. Q. Yao, T. Q. Quek, A. Huang and H. Shan, “Joint downlink and uplink energy minimization in WET-enabled networks,” IEEE Transactions on Wireless Communications, vol. 16, no. 10, pp. 6751–6765, 2017. [Google Scholar]

25. Z. Xie, Y. Chen, Y. Gao, Y. Wang and Y. Su, “Wireless powered communication networks using peer harvesting,” IEEE Access, vol. 5, no. 1, pp. 3454–3464, 2017. [Google Scholar]

26. H. Chen, L. Xiao, D. Yang, T. Zhang and L. Cuthbert, “User cooperation in wireless powered communication networks with a pricing mechanism,” IEEE Access, vol. 5, no. 1, pp. 16895–16903, 2017. [Google Scholar]

27. X. Lin, L. Huang, C. Guo, P. Zhang, M. Huang et al., “Energy-efficient resource allocation in TDMS-based wireless powered communication networks,” IEEE Communications Letters, vol. 21, no. 4, pp. 861–864, 2017. [Google Scholar]

28. P. S. Shelokar, P. Siarry, V. K. Jayaraman and B. D. Kulkarni, “Particle swarm and ant colony algorithms hybridized for improved continuous optimization,” Applied Mathematics and Computation, vol. 188, no. 1, pp. 129–142, 2007. [Google Scholar]

29. L. Lhotska, M. Macaš and M. Burša, “PSO and ACO in optimization problems,” in Int. Conf. on Intelligent Data Engineering and Automated Learning, Berlin, Heidelberg, pp. 1390–1398, 2006. [Google Scholar]

30. A. Kaveh and S. Talatahari, “Particle swarm optimizer, ant colony strategy and harmony search scheme hybridized for optimization of truss structures,” Computers and Structures, vol. 87, no. 5, pp. 267–283, 2009. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.